A maladaptive combination of traits contributes to the maintenance of a Drosophila hybrid zone

SUMMARY

Drosophila teissieri and D. yakuba diverged approximately 3 million years ago and are thought to share a large, ancestral, African range [1–3]. These species now co-occur in parts of continental Africa and in west Africa on the island of Bioko [1,4]. While D. yakuba is a human commensal, D. teissieri seems to be associated with Parinari fruits, restricting its range to forests [4–6]. Genome data indicate introgression, despite no evidence of contemporary hybridization. Here, we report the discovery of D. yakuba-D. teissieri hybrids at the interface of secondary forests and disturbed, open habitats on Bioko. We demonstrate that hybrids are the F₁ progeny of D. yakuba females and D. teissieri males. At high temperatures like those found on Bioko, D. teissieri females are generally less receptive to mating; and in combination with temperature effects on egg lay and egg-to-adult viability, this decreases the potential for gene flow between ♀D. teissieri and ♂D. yakuba relative to the reciprocal cross. Field and laboratory experiments demonstrate that F₁ hybrids have a maladaptive combination of D. yakuba behavior and D. teissieri physiology, generating additional barriers to gene flow. Nevertheless, analysis of introgressed and non-introgressed regions of the genome indicate that, while rare, gene flow is relatively recent. Our observations identify precise intrinsic and extrinsic factors that, along with hybrid male sterility, limit gene flow and maintain these species. These data contribute to a growing body of literature that suggests the Gulf of Guinea may be a hotspot for hybridization.

eTOC Blurb

Cooper et al. document hybridization between Drosophila yakuba and D. teissieri on Bioko in west Africa. Temperature-dependent reproductive isolation limits the production of hybrids produced by D. teissieri females. A maladaptive combination of D. yakuba behavior and D. teissieri physiology in hybrids generates additional barriers to gene flow.

RESULTS AND DISCUSSION

Drosophila yakuba and D. teissieri hybridize along forest edges on Bioko

During three separate collection expeditions between 2009 and 2016, we sampled Bioko for D. yakuba-clade individuals. Using morphological variation to classify genotypes in the field (STAR Methods, Figure S1), we discovered that D. teissieri occurs mostly in higher altitude forests; in contrast, D. yakuba occurs primarily in open areas at all altitudes (200 – 2,020 m), but is most common at lower altitudes (Table S1). This suggests D. teissieri and D. yakuba are largely geographically separated on Bioko. However, we identified putative D. yakuba-D. teissieri hybrids near the center of the forest-open habitat ecotone at 1,200–2,020m. Hybridization has been long hypothesized between these two species [7,8], but this discovery is striking given that these species are twice as divergent (Ks = 11%, the synonymous substitutions per synonymous site) as the other naturally hybridizing pairs in the genus [9,10].

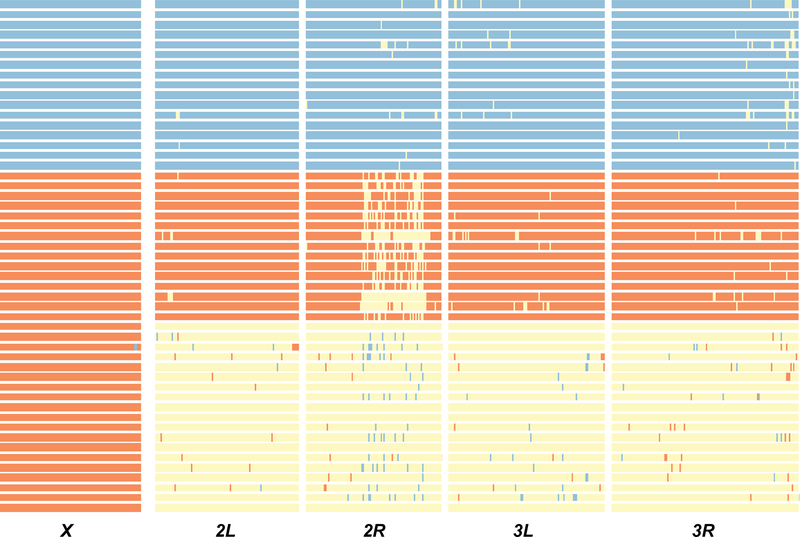
To confirm our discovery of hybrids based on morphology in the field, we sequenced the genomes of D. yakuba, D. teissieri, and putative-hybrid males. All 19-sequenced, putative-hybrid males were heterozygous for D. yakuba and D. teissieri ancestry across their autosomes and hemizygous for the D. yakuba X chromosome (Figure 1). This indicates that all hybrids were the F₁ sons of D. yakuba females and D. teissieri males [denoted F₁(♀yak × ♂tei)]. Interestingly, the strength of reproductive isolation (RI) between reciprocal D. yakuba-D. teissieri crosses does not differ under standard laboratory conditions [11,12], leaving an open question about our inability to sample hybrids produced by D. teissieri females [denoted F₁(♀tei × ♂yak)] on Bioko (see below).

FIGURE 1. Chromosome view of inferred ancestries of wild-caught male D. yakuba (orange), D. teissieri (blue), and predicted hybrids based on morphology (lower third).

Chromosomes are denoted at the bottom of the plot. All individuals classified as hybrids in the field were heterozygous across the autosomes for both parental genotypes (yellow). Hemizygous D. yakuba ancestry on the X chromosome indicates that hybrids were F₁ progeny of D. yakuba females and D. teissieri males. Small regions for which genotypes could not be confidently called are colored gray.

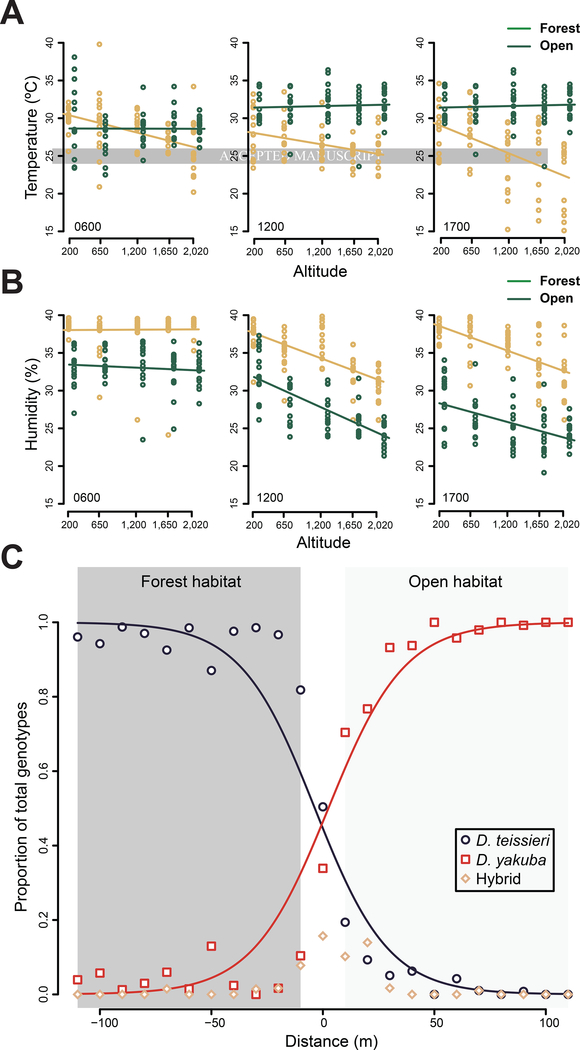
To understand habitat preferences, we performed mark-recapture field experiments on Bioko. We recaptured 8.45% (N = 91) of the D. teissieri, 11.31% (N = 137) of the D. yakuba, and 30% (N = 43) of the hybrid males that we released. In all cases, recaptured hybrid males did not have motile sperm, confirming our genotype assignments [11]. The estimated mean probability of choosing forest habitat differed among D. teissieri (0.97), D. yakuba (0.08), and hybrids (0.32) (LRT: P < 0.0001). Approximately 3% of D. teissieri, 15% of D. yakuba, and 19% of hybrids were recaptured at the center of the forest-open habitat ecotone. Because parental species and hybrids differ in their habitat preferences, we measured the temperature and humidity of each habitat on Bioko across several altitudes—these factors are known to influence the physiology and geographical distributions of Drosophila [13,14]. Both temperature and humidity decreased with altitude (Table S2, Figure 2A and 2B), and forest sites had lower temperatures than open areas at all times of day except at 0600hrs at low altitudes (Figure 2A). Forests were also more humid (Figure 2B). Together, these data indicate that D. yakuba and hybrids prefer warmer and drier conditions than those preferred by D. teissieri.

FIGURE 2. The preferred habitats of D. yakuba and D. teissieri.

A. Temperature conditions (°C) at different altitudes vary between forests and open habitats on Bioko (|t-value|= 2.357; P = 0.019) B. Humidity (%) is generally higher in forests than in open habitats (|t-value|= 2.634; P = 0.009). C. D. teissieri occurs in forests, D. yakuba occurs in open areas, and hybrids occur in a very narrow region centered on the forest-open habitat ecotone. Fitted lines from logistic regressions are plotted for D. yakuba and D. teissieri. For both A and B each panel reports conditions for a specific time of the day labeled in the bottom left corner of each plot. Regression lines for effects of altitude on each environmental condition are plotted. See also Tables S1 and S2.

We next estimated the prevalence of D. yakuba, D. teissieri, and their hybrids across the forest-open habitat ecotone. Including all flies visiting our traps, we captured 951 D. teissieri, 1,172 D. yakuba, and 59 hybrid males during the recapture portion of our mark-recapture experiment. Ninety-eight percent of the captured hybrids traveled less than 30m from the ecotone, and hybrids were never sampled more than 70m from the center of the ecotone (Figure 2C). D. teissieri was mostly absent from open habitat and became more common with distance into forest habitat (z = −22.147, P < 0.0001). In contrast, D. yakuba was mostly absent from forests and became more common with distance into the open habitat (z = 22.267, P < 0.0001; Figure 2C). These data indicate a sharp transition in the distributions of D. teissieri and D. yakuba at the center of the forest-open habitat ecotone where hybrids occur in a very narrow range.

Opposing patterns of dominance between parental alleles in hybrids contribute to the paucity of advanced-generation hybrids on Bioko

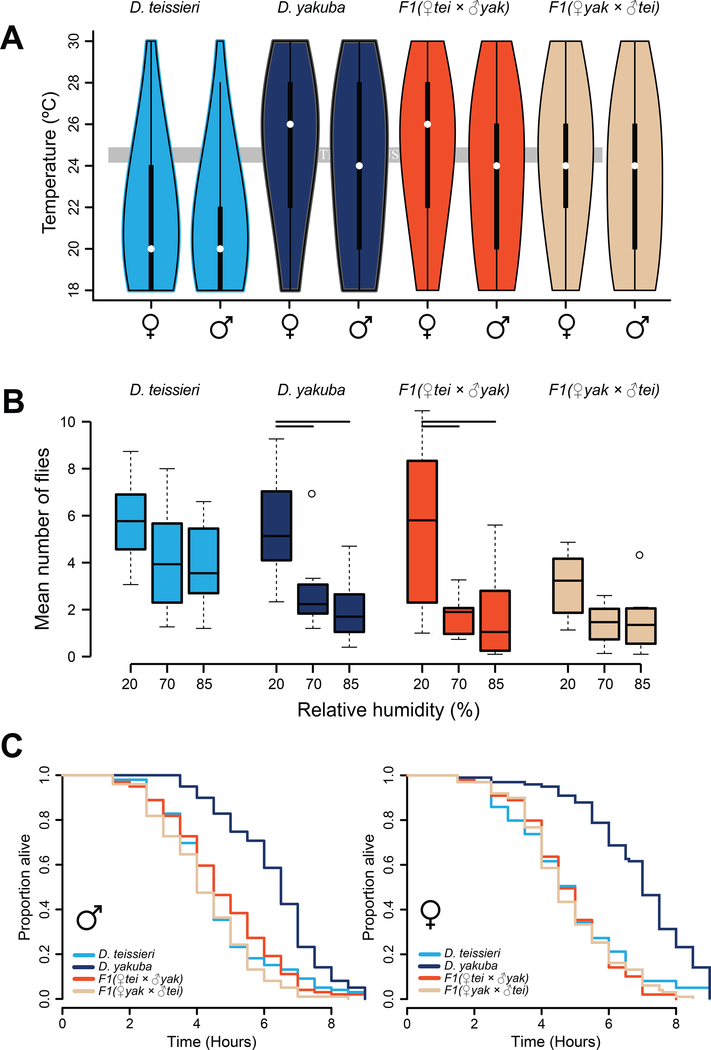
Our field measurements indicate that D. yakuba and hybrid males prefer warmer temperatures than D. teissieri males. To confirm this, we measured the temperature preferences of parental species (as in [11]) and F₁ hybrids in the laboratory (Figure 3A). The mean temperature preference of D. teissieri (21.29°C ± 2.91 SD) is 13% lower than D. yakuba (24.51°C ± 3.68 SD), 12% lower than F₁(♀tei × ♂yak) (24.12°C ± 3.72 SD), and 10% lower than F₁(♀yak × ♂tei) (23.74°C ± 3.82 SD) preferences. Across all genotypes females prefer higher temperatures (23.87°C ± 3.70 SD) than males (22.95°C ± 3.78 SD) (F_1,4792 = 57.361, P < 0.0001). F₁(♀tei × ♂yak) males (23.59°C ± 3.83 SD), which we did not observe on Bioko, prefer temperatures nearly 12% higher than those preferred by D. teissieri males (21.09°C ± 2.77 SD)—this preference is statistically indistinguishable from D. yakuba (23.91°C ± 3.87 SD) (t = −1.458, df = 2396, P = 0.464) and F₁(♀yak × ♂tei) (23.21°C ± 3.87 SD) (t = −1.839, df = 2396, P = 0.2551) preferences. These results indicate that in hybrids D. yakuba’s preference for warm temperatures is dominant or semi-dominant to D. teissieri’s preference.

FIGURE 3. D. yakuba-D. teissieri hybrids have a maladaptive combination of pure species traits.

A. D. yakuba and hybrid genotypes prefer warmer temperatures than D. teissieri, as measured in a laboratory thermocline. Tukey’s HSD post hoc comparisons revealed the temperature preference of F₁(♀tei × ♂yak) hybrids differs from D. teissieri (P < 0.0001), but only marginally from D. yakuba (P = 0.05). In contrast, F₁(♀yak × ♂tei) hybrids that occur on Bioko differ from both D. teissieri (P < 0.0001) and D. yakuba (P < 0.0001). These patterns stem from a slight, but statistically significant, difference between the two reciprocal hybrids (P = 0.03). B. Like D. yakuba, F₁ hybrids tend to prefer lower relative humidity. Horizontal bars represent significant pairwise contrasts (P < 0.01) between humidity conditions fit separately for each genotype (see text for details). C. Both male and female D. yakuba individuals have higher desiccation tolerance than D. teissieri and hybrids. Across sexes F₁(♀yak × ♂tei) have the lowest desiccation tolerance indicating that these hybrids are ill-equipped to cope with the dry environments they prefer on Bioko. See also Table S3 (Summary statistics for males and females) and Table S6.

Our field measurements indicate that D. yakuba and hybrids prefer dryer conditions than D. teissieri. To confirm this, we measured the relative humidity (RH) preferences of parental species and F₁ hybrids in the laboratory (Figure 3B). Males and females do not differ in RH preference (χ² = 0.25, P = 0.62); however, D. yakuba and both types of F₁ hybrids tend to prefer lower RH (D. yakuba, χ² = 15.2, P < 0.001; F₁(♀yak × ♂tei), χ² = 7.8, P = 0.02; F₁(♀tei × ♂yak), χ² = 24.4, P < 0.0001), although F₁(♀yak × ♂tei) hybrids have weaker preference than do F₁(♀tei × ♂yak) hybrids. In contrast, D. teissieri do not prefer a specific RH in the lab (χ² = 4.1, P = 0.13). These data indicate that in hybrids D. yakuba’s preference for low humidity is dominant or semi-dominant to D. teissieri’s lack of preference.

Because hybrids have D. yakuba’s behavioral preference for warm and dry conditions, we assessed whether hybrids also have desiccation tolerances similar to D. yakuba. Body size did not influence desiccation tolerance (F_{3, 392} = 2.434, P = 0.07), but genotype did (χ² = 143.55, df = 3, P < 0.0001) (Figure 3C, Table S3). The desiccation tolerance of D. teissieri (4.73 hr ± 1.69 SD) was 40% lower than D. yakuba (6.63 hr ± 1.54 SD), consistent with the distribution of these species in nature. Strikingly, hybrids had approximately 28% lower desiccation tolerance than did D. yakuba [F₁(♀yak × ♂tei), 4.50 hr ± 1.47 SD; F₁(♀tei × ♂yak), 4.76 hr ± 1.50 SD], despite preferring similarly dry conditions. These results indicate that D. teissieri’s low desiccation tolerance is dominant or semi-dominant to D. yakuba relatively high tolerance. We predict this leaves hybrids physiologically ill-equipped to cope with their preferred conditions in the lab and on Bioko.

Although we did not sample advanced-generation hybrids on Bioko, genome data provide evidence for some introgression [1,8]. We used the distribution of haplotype lengths and possible generation times to estimate the timing of admixture. We estimate admixture between D. teissieri and D. yakuba 611 to 1,124 generations ago assuming a single pulse model and 1,243 to 2,356 generations ago assuming a continuous pulse model [15](Figure S2). Using the temperature dependence of development time to convert generations to absolute ages, we estimate admixture occurred between 23 and 320 years ago (Table S4). Previous simulations using introgressed haplotype size estimated admixture between 1,600 and 8,100 generations ago, assuming very low rates of migration [1]. These prior estimates correspond to admixture between about 60 and 1,100 years ago, which overlaps with our estimates here. Our calculations using the distribution of haplotype sizes assume all haplotypes are neutral (i.e., no hybrid incompatibilities) which will overestimate the age of admixture; further, selection will purge incompatibilities making haplotypes shorter than expected by purely neutral introgression [16].

Intermediate traits in hybrids are a common reason for fitness reduction [17,18], but our results indicate that opposing patterns of dominance between parental alleles decouple behavior and physiology in hybrids (see [19] for a review). A similar situation, but involving only a single trait, has been observed in Heliconius butterflies where hybrids show a combination of wing pattern elements from both parental species and thus do not belong to any of the parental mimicry rings, which leads to higher predation [20]. How often such maladaptive combinations of pure species traits contribute to RI will depend on the genetic bases of the traits and the extent to which the ecological niches of parental species differ. The number of genes involved in deleterious traits specific to hybrids increases with parental divergence time and has been demonstrated for hybrid inviability [21,22] and hybrid sterility [23]. However, a systematic assessment of the number of potential incompatible traits, and their genetic basis, in multiple species is needed to determine the prevalence and rate of evolution of these incompatibilities [24].

Temperature-dependent asymmetries in the strength of RI contributes to the paucity of F₁(♀tei × ♂yak) hybrids on Bioko

Under standard laboratory conditions, non-ecological RI is equally strong between ♀D. teissieri × ♂D. yakuba and ♀D. yakuba × ♂D. teissieri crosses, and reciprocal hybrids do not differ in their survival rate [11,12,25]. This presents a conundrum; namely, what barriers might limit the prevalence and/or production of F₁(♀tei × ♂yak) hybrids in nature that are not revealed in the laboratory? Both species are infected with maternally transmitted Wolbachia bacteria that cause weak cytoplasmic incompatibility (CI) when uninfected females mate with infected males. However, the strength of CI does not differ between reciprocal crosses, and Wolbachia seem to have no influence on RI in this clade [12], indicating that Wolbachia do not contribute to the paucity of F₁(♀tei × ♂yak) hybrids.

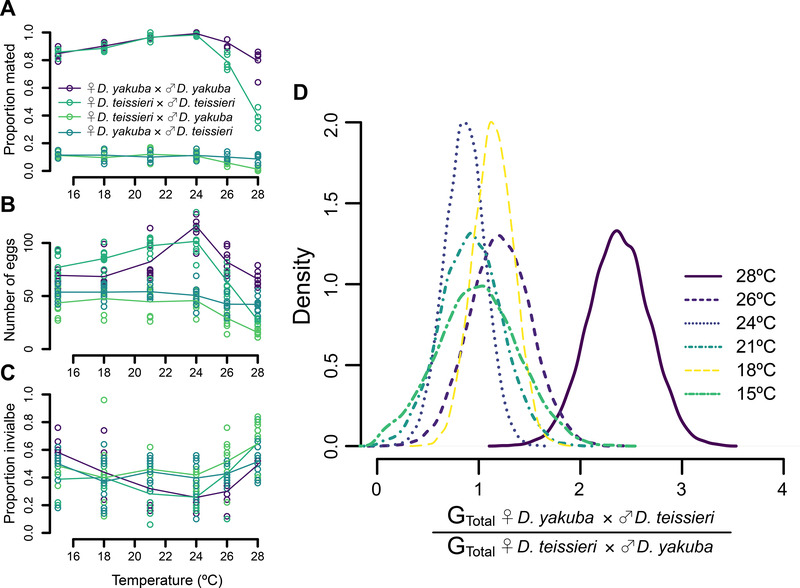
Because D. yakuba and D. teissieri differ in their thermal preferences, we evaluated temperature effects on mating (Figure 4A), egg lay (Figure 4B), and egg-to-adult viability (Figure 4C) for conspecific and heterospecific pairings. This enabled us to estimate the potential for gene flow (G_Total) for each cross at several temperatures. In agreement with past analyses, our estimates of G_Total at 24°C are similar for both crosses (♀D. yakuba × ♂D. teissieri = 0.017 and ♀D. teissieri × ♂D. yakuba = 0.019) with the ratio of G_Total for ♀D. yakuba × ♂D. teissieri to G_Total for ♀D. teissieri × ♂D. yakuba near 1 (Figure 4D). However, at higher temperatures (28°C) like those found on Bioko (Figure 2A), this ratio is more than two times higher at 28°C (2.38) than at the coolest temperatures (15°C = 0.98, 18°C = 1.14, 21°C = 0.92, and 24°C = 0.86) and nearly two times higher than at 26°C (ratio = 1.22) (Figure 4D). This difference is largely caused by adverse effects of high temperature on D. teissieri females in conspecific and heterospecific pairings. At 28°C ♀D. yakuba × ♂D. teissieri matings are seven times more likely to occur than are ♀D. teissieri × ♂D. yakuba matings (8.6% vs 1.2% respectively). In combination with temperature effects on egg lay (Figure 4B) and egg-to-adult viability (Figure 4C), we predict this reduces the potential for gene flow between ♀D. teissieri and ♂D. yakuba crosses on Bioko (Figure 4D).

FIGURE 4. Temperature influences female mating, egg lay following a single mating, and egg-to-adult viability for conspecific and heterospecific crosses.

A. The proportion of mated females paired with conspecific or heterospecific matings for 24 hours depends on cross type (X² = 8,087.5, P < 0.0001), temperature (X² = 166.4, P < 0.0001), and their interaction (X² = 135.3, P < 0.0001) with D. teissieri females being less receptive to conspecific and heterospecific mates at high temperatures. B. The number of eggs laid by females over 10 days following a single mating depends on cross type (F_3,192 = 221.96, P < 0.0001), temperature (F_5,192 = 61.025, P < 0.0001), and their interaction (F_15,192 = 12.81, P < 0.0001) with D. teissieri egg lay reduced at high temperatures found on Bioko. C. The egg-to-adult viability depends on cross type (F_3,216 = 6.51, P = 0.0003), temperature (F_5,216 = 20.03, P < 0.0001), and their interaction (F_15,216 = 3.70, P < 0.0001) with D. teissieri egg-to-adult viability reduced at high temperatures found on Bioko. D. The ratio of GTotal for ♀D. yakuba × ♂D. teissieri to GTotal for ♀D. teissieri × ♂D. yakuba is about two times higher at 28°C than at cooler temperatures. The legend shown in A also applies to B and C.

Selection on ecologically relevant traits such as coloration (e.g. [26,27]) and habitat choice (e.g.[28,29]) can reduce gene flow between locally adapted populations (reviewed in [30]). More recently, studies have begun to test how selection shapes the distribution of hybrid genotypes found in nature using genome-wide data (e.g., [24,31,32]). By measuring ecologically relevant phenotypes of D. yakuba, D. teissieri, and their hybrids in the lab and the field, our findings extend this knowledge to demonstrate temperature-dependent asymmetries in the strength of RI between reciprocal crosses. Notably, these two species also show other barriers to gene flow [11,12]. The role of biotic and abiotic conditions on facilitating hybridization and introgression remain largely understudied (but see [33]).

CONCLUSIONS

Identifying ecological and intrinsic barriers that limit gene flow is crucial to explain the persistence of species in areas of contact. This is especially true for Drosophila where about half of all closely related species have overlapping geographical ranges [34], and several species pairs show evidence of past introgression [1,35–37]. Our results demonstrate that temperature-dependent asymmetries in the strength of RI and a maladaptive combination of D. yakuba behavior and D. teissieri physiology in hybrids generate barriers to gene flow and contribute to the maintenance of the Bioko hybrid zone. These species are the most divergent pair in Drosophila known to form a hybrid zone; indeed, similarly diverged pairs produce inviable or sterile hybrids in the laboratory (e.g., D. melanogaster-D. simulans hybrids, Ks = 0.10, [22]). At least two cases of stable, insect hybrid zones between species with more extreme levels of divergence have been reported: multiple parallel hybrid zones occur between color pattern races of Heliconius erato and H. melpomene whose genomes differ extensively (K_S = 0.15) [38], and two species of termites (Blattodea: Coptotermes) estimated to have diverged 17 million years ago (mya) show little evidence of premating RI and produce hybrid colonies [39]. Hybrid zones between highly diverged vertebrate species seem more common [40,41]. In birds 9 out of 23 hybrid zones are formed between species with divergence times greater than 2 mya ([42] and references therein). The existence of these hybrid zones indicates that the possibility of hybridization, and perhaps introgression, exists after deep divergence between hybridizing species. Finally, our discovery of the Bioko hybrid zone may not be surprising given that hybridization seems to be common in Afronesia (Table S5). Colonial establishment of Bioko occurred in the last 600 years (~1,472), and our inferred interval for the timing of admixture overlaps with the period of time where cocoa plantations and livestock were common in Equatorial Guinea (end of the XIX century-1968; [43,44]). We hypothesize that this hybrid zone may be another example of human disturbance facilitating secondary contact (reviewed in [45]). A systematic exploration of the factors controlling the formation of hybrid zones, and their genomic consequences, is sorely needed.

STAR METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Requests for further information and resources should be directed to, and will be fulfilled by, the Lead Contact, Daniel R. Matute (dmatute@email.unc.edu)

EXPERIMENTAL MODEL AND SUBJECT DETAILS

The Drosophila stocks used for new genomic analyses, and their availability, are described in the Key Resources Table.

METHOD DETAILS

Distinguishing among D. yakuba, D. teissieri, and F₁ hybrids using morphology

We sought to heavily sample Bioko for D. yakuba, D. teissieri, and their putative hybrids. However, conducting experiments in the field requires a method for reliably identifying and distinguishing living individuals of each genotype. Based on our experience with D. yakuba-clade flies, we predicted that three male morphological characteristics would enable us to achieve this goal: the number of chitinized spines on anal plates, the number of sex combs on forelegs, and the lengths of tibia. We first measured each trait in a training set of D. yakuba (N = 500) and D. teissieri (N = 500) males, and also in F₁(♀tei × ♂ yak) (N = 500) and F₁(♀yak × ♂ tei) (N = 500) hybrid males that we created in the laboratory (Figure S1). This provided a distribution of values for each trait within each genotype. We next blindly measured each of the three morphological traits in an additional set of 100 males of each genotype and calculated Mahalanobis distances for each individual [46]. The Mahalanobis distance between a focal individual (i) and the average for a given genotype (i.e., centroids for D. teissieri, D. yakuba, and the two hybrid F₁ genotypes estimated using the training set) was calculated as:

$$M{D}_i={\left(F_i-{\mu }_{LB}\right)}^T\times \left[{S_{LB}}^{-1}\times \left(F_i-{\mu }_{LB}\right)\right]$$ (1)

where the super-index T denotes matrix transpose, S denotes the covariance matrix of a given dataset, F_i is the vector of phenotypic observations in a focal individual, i, and μ_LB is the vector of average phenotypic observations of the training set. To estimate the accuracy of this approach, we calculated the proportion of our blind assignments that were correct. We were able to reliably identify pure species (D. yakuba: 100/100, D. teissieri: 100/100) and F₁ hybrids (single class, 196/200). We attempted to gain further resolution and assessed our ability to discriminate between F₁(♀tei × ♂yak) and F₁(♀yak × ♂tei) reciprocal hybrids, but due to their similar morphology our assignments were incorrect 53% of the time. Thus, we sequenced the genomes of a subset of the putative-hybrid males to confirm genotypes.

Sampling and mark-recapture experiments on Bioko

In 2013, we completed a preliminary experiment to first determine the distance flies travel in ~24 hr. D. melanogaster subgroup species males (D. yakuba, D. teissieri, D. simulans, and D. melanogaster) were collected using baited traps, anesthetized with FlyNap, and assigned to one of the four species based on genital morphology [47]. This approach yielded at least 500 male individuals of each species that we dusted with micronized fluorescent powder (Signal green; Day-Glo Color Corporation, Cleveland, OH) and released at once from a single location (1,650 m). Prior to this release, traps that consisted of small buckets with a mixture of banana and yeast were placed every 100 m in six radially arranged transects around the release area (8 traps per transect for a total of 49 traps, including a trap at the intersection of the transects). Traps were sampled between 23 and 25 hr later, and the number of recaptured flies was determined using a UV light. Species were again identified by their genital morphology. These experiments revealed that D. yakuba and D. teissieri flies rarely moved more than 100 m over a period of 24 hr (Table S6).

We next carried out our primary mark-recapture experiment to determine habitat preferences of D. yakuba-clade genotypes. We next lightly dusted D. yakuba, D. teissieri, and hybrid males with one of three types of micronized fluorescent powder (Signal green, Horizon blue, and Fire orange; Day-Glo Color Corporation, Cleveland, OH) and released them from a trap placed at the center of the forest-open habitat ecotone, at an altitude of approximately 1,650m. Buckets baited with a mixture of banana and yeast were evenly spaced by ~10m, with 11 running into the forest and 11 into the open habitat perpendicular to the interface of the two habitats, which our preliminary analysis of fly travel suggested is sufficient (Table S6). After an average of 24hr, we recaptured flies by netting over the buckets. Upon collection, genotypes were identified by dust color under UV light. To further confirm genotype assignments, we dissected and mounted testes from all recaptured males on slides in Ringer’s solution and assessed sperm motility. Hybrid males are sterile and have no motile sperm, while non-hybrids are fertile with motile sperm [11,12].

Distributions of D. yakuba, D. teissieri, and their hybrids across the ecotone

The male individuals that we recaptured during our mark-recapture experiment enabled us to estimate the rate of hybridization and to assess the distributions of each genotype across the ecotone. Flies collected during this experiment included both dusted flies and any other D. yakuba-clade flies visiting our traps at the time of recapture. We combined these data with our original capture data to estimate the prevalence of D. yakuba genotypes across the ecotone. We first calculated the dilution factor, for each genotype, defined as the number of non-dusted flies captured divided by the number of dusted flies recaptured [48]. We then multiplied the number of flies that we originally released by the dilution factor to estimate the census size of each genotype at this single altitudinal sliver of habitat. The estimated census size of hybrids divided by the sum of the three estimated census sizes (D. yakuba, D. teissieri, and hybrids) provides an estimate for hybrid prevalence. To assess variation in the prevalence of D. teissieri and D. yakuba with distance from the center of the ecotone, we fitted logistic models using the ‘MASS’ library [49].

Genomic sequencing of field-sampled hybrids

We sequenced a subset of the male individuals sampled from Bioko in 2013 to confirm our genotype assignments based on Mahalanobis distances in the field. Genomic DNA was extracted from each individual using the Beckman-Coulter DNAdvance magnetic bead protocol for insects (Beckman Coulter, Indianapolis, IN, USA). Libraries were made for each individual using the Tagmentase protocol detailed in Picelli et al. [50], and barcoded for multiplexing (see supplement for barcode sequences). Libraries were then sequenced to low coverage with Illumina 100 bp single end reads (Cornell Genomics Facility). In total, 17 parental D. teissieri, 15 parental D. yakuba, and 19 individuals of putative-hybrid phenotype were sequenced to sufficient coverage (i.e., > 10,000 reads). The mean number of markers per individual was 6.87, and the mean coverage was 2.29X.

Genotypes of the individuals were determined by the Multiplexed Shotgun Genotyping (MSG) pipeline described by Andolfatto et al. [51], which uses a hidden Markov model (HMM) to assign ancestry along a genome with low-coverage read data. Because this approach utilizes linkage disequilibrium on a large physical scale, it is well-suited for assigning genome-wide ancestry in recently formed hybrids (within several generations of backcrossing). The D. yakuba Flybase assembly (version 1.05, [52]) was masked for repeats (RepeatMasker, [53]) and used as the first parental reference. The second parental input for MSG was made by mapping reads from the outbred individual Bioko_cascade_2_2 [1] to the D. yakuba flybase assembly and creating an updated FASTA file with genotype calls from GATK [54,55]. The updated FASTA file uses only single nucleotide polymorphisms (SNPs), and masks all inferred indels plus 5 bases both up and downstream. Some regions of the genome are error-prone in terms of assigning ancestry, due in part to low sequence divergence, poor reference genome assembly, or high polymorphism in the parental species. To reduce the rate of miscalled ancestry, known intermediate frequency SNPs in each parental population (identified by realigning whole-genome Illumina sequencing data to the D. yakuba reference) were masked in the corresponding reference genomes using sequence data from several wild-caught individuals:

Bioko_Cascade_21 (yak), Bioko_Cascade_19_16 (yak), Bioko_NE_4_6 (yak),

Bioko_Balancha_1 (tei), Bioko_cascade_4_3 (tei), Bioko_House_Bioko (tei),

Bioko_cascade_4_2 (tei), Bioko_cascade_4_1 (tei), Bioko_cascade_2_4 (tei),

Bioko_cascade_2_2 (tei), Bioko_cascade_2_1 (tei). The performance of MSG is also influenced by user-specified parameters in the HMM, in particular, those that describe the error-rate of genotypes and the rate at which transitions between ancestries occur (rfac, deltapar1, and deltapar2). To determine the appropriate parameter values for this study, MSG was run iteratively on pure-species individuals while adjusting parameters to achieve the lowest genotyping error rate, assuming that all individuals are homozygous genome-wide for their ancestry. After parameter-tuning, MSG was run on all individuals and ancestry genotypes were called with a posterior probability filter of 0.99.

Approximate timing of introgression

A previous approach had quantified the amount of introgression between D. yakuba and D. teissieri using whole genome data [1]. Using these results, we estimated the age of admixture by converting the physical length of each haplotype to genetic distances, calculating the age of introgression in generations, and inferring the number of generations per year in the field.

Converting physical distances to genetic distances.

We calculated an approximate age of first contact using the mean haplotype size in cM observed in deduced introgression between D. yakuba and D. teissieri. 146 segments have been transferred between the two species: 70 from D. teissieri to D. yakuba, and 76 from D. yakuba to D. teissieri [1]. To convert the haplotype length from physical distances (Mb) to genetic distances (cM) we assumed that the rates of recombination were similar for D. yakuba, D. teissieri, and D. melanogaster at orthologous regions of the genome. We first generated a lift-over table between the three genomes, and we then used this information to identify the orthologous blocks to the introgressed regions in D. melanogaster. Finally, we used the recombination rates experimentally measured for each orthologous interval [56] to convert to genetic distance using [57]. We focused on the Comeron start point rate but other recombination rates yield similar results.

Calculating the age of introgression in generations from genetic distances.

We converted the bootstrapped means to time of admixture. We used two models: a single pulse of introgression and continuous admixture using the expected these two situations derived by [15] where the expected mean haplotype (in cM) is

$$E(T)=\frac{1}{(1-m)T}$$ (2)

for a single pulse of admixture, and

$$\widehat{E}(T)=\frac{2}{(1-m)T}$$ (3)

for a continuous model of admixture. T is the age of admixture and m is the rate of migration. In both cases, we assumed that m is small (m < 0.05, following simulations from [1] and number of F₁ hybrids reported here). The time of admixture then simplifies to

$$T=\frac{1}{\overline{haplotypesize}}$$ (4)

for a single pulse of admixture and

$$T=\frac{2}{\overline{haplotypesize}}$$ (5)

for a continuous admixture model. In both cases T is expressed in number of generations. We used these equations to obtain an admixture time for each inferred introgressed haplotype. This produced a distribution of T values whose mean reflects the approximate time of admixture. We bootstrapped the distribution of obtained T to find confidence intervals of the mean using the library boot (functions boot and boot.ci, [58,59]). Admixture time in generations were converted to years using the average generation time for each of the two species (see Figure S2, Table S4 and below).

Laboratory experiments

Isofemale lines.

For laboratory crosses, we used D. yakuba line cascade21 and D. teissieri line Balacha1. Both lines were collected in the highlands of Bioko in 2013 and are infected with maternally transmitted, endosymbiotic, Wolbachia bacteria. We chose this approach as low titer Wolbachia infections in males, that we might not detect, could in principle generate cytoplasmic incompatibility (CI) when crossed to uninfected females. However, CI is not possible between infected females and infected males, regardless of titer and cross type [11,12].

Temperature preference.

We measured temperature preferences of D. teissieri, D. yakuba, F₁(♀tei x ♂ yak) and F₁(♀yak x ♂ tei) hybrids in the laboratory. Flies were randomly placed in a thermocline that consisted of a plexiglass chamber (12cm wide × 45cm long × 1cm high) with an aluminum floor. The thermocline was placed in an 18°C room and heat plates (120 VAC Thermo Scientific Cimarec Hot Plate, Thermo Scientific Cimarec, # UX-04600–01, Waltham, MA, USA) were used to generate a thermal gradient ranging from 18°C to 30°C, with a change in temperature of approximately 2°C every 6cm. Flies were allowed to move freely along this gradient over a period of one hour. At the end of each trial we isolated flies into seven chambers, each 10.5 × 6 × 1 cm, by pushing a rod connected to six plexiglass partitions across the width of the chamber. We then recorded the temperature within each partition using a Digi-Sense thermometer equipped with a type-T thermocouple (Cole-Parmer Instrument Co., Chicago, IL; catalog number: 86460–05) and counted the number of flies within each partition [60]. Males and females of each genotype were evaluated separately to avoid sexual attraction that might influence results (N = 3 separate replicates per sex; 400 individuals per replicate).

Humidity preference.

Relative humidity (RH) preferences of D. teissieri, D. yakuba, and F₁(♀tei × ♂ yak) and F₁(♀yak × ♂ tei) hybrids were evaluated by giving flies the choice of orienting themselves along a humidity gradient. Rows of a 48-well polystyrene tissue culture plate (8 rows by 6 columns; Corning Incorporated, Life Sciences, Tewksbury, MA, USA) were filled with one of three super-saturated salt solutions: LiCl, NaCl, or KH₂PO₄. Each of these solutions generates a RH of ~20%, ~70%, and ~85%, respectively, in the headspace above the rows. We filled the wells of two adjacent end rows with LiCl, the three following rows with NaCl, and the three remaining rows with KH₂PO_4. This generates a gradient of RH ranging from ~20% to 85%. The top of each plate was covered with 300 micron nylon netting (MegaView Science Co., Ltd. Taichung, Taiwan) and covered with the culture plate lid on top of the mesh; this left ~1 cm for flies to move freely around the plate. This experimental design is a modified approach from Enjin and colleagues [61]. We lightly anesthetized approximately 50, 4 to 7-day old virgin, males or females of a given genotype and placed them along the long axis of a plate. We ran eight plates simultaneously—one plate for each of the parental and hybrid genotypes, with sexes evaluated separately. Flies were allowed to orient themselves for the first hour after which pictures were taken every 15 min, for an additional two hours. This procedure was repeated on four separate days with the position of each plate and the orientation of the ‘low’ and ‘high’ RH end of the plates relative to the room randomized each day. (This avoids confounding effects of non-uniform lighting and other conditions among days in the laboratory.) In total, we assayed ~200 individuals of each genotype and sex. To score preference, we counted the number of flies over each well of the plates, for each of the eight images generated over the 2 hr assay, and summed counts of flies oriented over wells containing the same super-saturated salt solution. All scoring was double blinded.

Desiccation tolerance in the laboratory.

Desiccation resistance was measured by placing ten, 4-day old virgin, females or males in 30mL empty vials (N = 11 vials per sex), which in turn were placed in a glass desiccator with 200g of Drierite (Sigma Aldrich Catalog number: 7778–18-9; St. Louis, MO) and kept at 21°C (42). The relative humidity was kept under 20% and was measured with a hygrometer. Flies were checked every 30min and the time of death was recorded for each fly.

Conspecific and heterospecific mate preference.

To establish whether temperature influences the magnitude of female choice, we conducted no-choice mating experiments en masse [62–64] at six different temperatures (15°C, 18°C, 21°C, 24°C, and 26°C and 28°C). We collected virgin males and females within eight hours of eclosion from D. teissieri and D. yakuba, and maintained each sex in isolation for four days. In the morning of the fifth day, we paired groups of approximately 100 virgin females with approximately 100 males in vials with cornmeal food, so that each vial contained 200 flies—this was completed for all four possible pairings (♀D. yakuba × ♂ D. teissieri, ♀ D. teissieri × ♂ D. yakuba, ♀ D. teissieri × ♂D. teissieri, ♀ D. yakuba × ♂ D. yakuba). These males and females were kept together for 24 hours. After 24 hours, all individuals were anesthetized with CO₂. We extracted the reproductive tracts from females and then mounted them in chilled Ringer’s solution. If we observed sperm on either the seminal receptacle or any of the spermathecae, females were considered mated. We repeated this assay five times per temperature for a total of 30 experimental blocks and ~3,000 females. We calculated the proportion of mated heterospecific to conspecific females as:

$$Proportionmated=\frac{Numberofmatingsinheterospecificcrosses}{\overline{Numberofmatingsincospecificcrosses}}$$ (6)

Conspecific and heterospecific fecundity.

We evaluated fecundity after conspecific and heterospecific crosses at the six focal temperatures. For all four possible crosses (♀D. yakuba × ♂ D. teissieri, ♀ D. teissieri × ♂ D. yakuba, ♀ D. teissieri × ♂D. teissieri, ♀ D. yakuba × ♂ D. yakuba), one virgin female and one virgin male were housed in a 20mL vial with corn meal. We watched each pair and assess whether mating occurred. We obtained 60 females per cross by watching copulating pairs for a period of eight hours. Once copulation finished, we removed the males from the vial (each vial contained only one female). Females were then randomly assigned to one of six batches which were then placed at the six different temperatures. Every 24 hours, we counted the number of eggs laid. Females were then transferred to a fresh vial. The procedure was repeated for ten days. We calculated the proportion of eggs laid for heterospecific to conspecific crosses as:

$$Proportioneggslaid=\frac{Numberofeggsinheterospecificcrosses}{\overline{Numberofeggsincospecificcrosses}}$$ (7)

Conspecific and heterospecific egg-to-adult viability.

We scored the proportion of embryos from conspecific and heterospecific crosses that molt successfully into adults. To score embryo viability, we housed virgin individuals from the two sexes in the four possible combinations (♀D. yakuba × ♂ D. teissieri, ♀ D. teissieri × ♂ D. yakuba, ♀ D. teissieri × ♂D. teissieri, ♀ D. yakuba × ♂ D. yakuba) in oviposition cages (Flystuff, San Diego, CA, USA) with apple juice agar at 24°C. From these cages, we collected freshly deposited eggs (less than six hours after oviposition). Eggs were then collected in batches of 50, placed into black filter paper and housed in 30mL plastic vials containing cornmeal food. For each cross, we obtained 3,000 embryos which were then divided into five batches. Each batch was placed into the six different temperatures listed above. Vials were tended daily. Once marks of larvae were seen on the side of the food, we added a Kimwipe (Kimberly Clark, Delicate Task) dampened with 0.5% propionic acid solution as a pupation substrate. Adult flies were counted as they hatch every two days. There were ten replicates per cross per temperature (500 individuals). We calculated hybrid inviability as:

$$Hybridinviability=\frac{Numberofdeadhybrids}{\overline{Numberofdeadpurespecies}}$$ (8)

Hybrid sterility.

F₁ hybrids between D. yakuba and D. teissieri are sterile at 24°C [11,25]. We scored whether hybrid males were also sterile at different temperatures. Hybrid males were produced as described above at six different temperatures (Section ‘Conspecific and heterospecific egg-to-adult viability’). Four to eight day old males from conspecific and heterospecific crosses were then lightly anesthetized with CO₂. Their testes were then extracted with forceps and mounted in Ringer’s solution; we assessed sperm motility for 100 males per cross (2 conspecifics and 2 heterospecifics). We assumed all hybrid females were fertile. The index of sterility (‘hybrid male sterility’ in equation 9) was the number of sterile hybrid males.

Temperature dependence of development times.

Since the temperature in Bioko varies substantially, we measured generation times at four different temperature regimes. We collected 40 batches of similarly aged embryos (within 3 hours of deposition) for each of the two species. Each batch was placed in a corn meal vial and randomly assigned to one of four temperature regimes: 11°C/16 °C, 16°C/21 °C, 21°C/26 °C, and 26°C/31 °C. The first temperature corresponds to the night (dark cycle) temperature and the second one to the day (light cycle) temperature. Temperatures were controlled by housing all experiments in incubators (Percival DR-36VL with a H3X pan-type humidifier). Vials were tended daily by adding hydration (propionic acid 0.05%), and added a pupation substrate (Kimwipe). We scored the time of emergence of each fly and calculated the mean time of emergence for each vial. The mean generation time for D. teissieri was significantly longer than D. yakuba (F_1,736 = 305.710, P < 0.0001). Moreover, the life history of the two species also differs; D. teissieri is mostly associated to Parinari fruits, which means the species is most likely to breed during the dry period, when Parinari fruits are commonly found in the ground (6 months out of the year, [65,66]). On the other hand, D. yakuba is found in a multitude of substrates and is likely to be collected year round. The number of generations per year is thus likely to differ for the two species. We used both numbers as the generation time to convert the bootstrapped distribution of T. We thus obtained sixteen different mean values—with their respective confidence intervals—for the time of admixture (2 admixture models × 4 temperature regimes × 2 life histories).

QUANTIFICATION AND STATISTICAL ANALYSIS

Distributions of D. yakuba, D. teissieri, and their hybrids across the ecotone

We modeled the probability of male D. teissieri, D. yakuba, and their hybrids choosing forest habitat over open habitat. We fitted a generalized linear mixed model with binomially distributed error using the ‘lme4’ library [67]. The full model included genotype (either D. teissieri, D. yakuba, or their hybrids) and the random effect of block (N = 3 blocks). We calculated mean values using parameter estimates from the most likely model, and took the inverse logit of these values to calculate the estimated mean probabilities of choosing forest habitats. To estimate P-values, we fitted the same model again using the mixed function within the ‘afex’ library [68]. This approach first fits the full model, and then individual fixed effects are removed to compare the reduced model to the full model. P-values were calculated using the likelihood ratio test (LRT) method within mixed. These analyses and all others were conducted using the R Statistical Package (version 3.3.1; [69]).

Variation in temperature and humidity in the field

To assess variation in temperature and humidity, we fitted two linear models, one for temperature and one for humidity. The two models followed the same form and assessed the effect of altitude, type of habitat, and time of the day on each of the two environmental factors. We also included all possible interactions. We compared temperature and humidity at open versus forest habitats using the Tukey’s Honest Significant Difference (HSD) post hoc pairwise comparisons in the ‘multcomp’ library [70].

Temperature preference, humidity preference, and desiccation tolerance in the laboratory

Because temperature preference was not normally distributed, and remained non-Gaussian after both log (Shapiro Wilk test, W = 0.914, P < 0.0001) and square root (Shapiro Wilk test, W = 0.919, P < 0.0001) transformations, we used the ‘ARTool’ library to complete analyses of variance on aligned rank transformed data [71]. We specifically assessed the effects of genotype, sex, and their interactions on temperature preference. We then used lsmeans to conduct post hoc pairwise comparisons [72].

Because there was no effect of sex on the number of flies choosing a given RH (LRT: χ² = 0.25; P = 0.62), sexes were analyzed together. We first tested whether humidity preference varied across genotypes by modeling the mean number of individuals choosing a given RH as a function of genotype, RH, and the interaction between genotype and RH. We assumed a Poisson distribution of error. To explicitly test whether different genotypes displayed preferences for different RH, we also modeled the mean number of individuals choosing a given humidity, for each genotype separately, as a function of RH (fixed effect) and plate identity (random effect). We tested for variation in humidity preference using LRTs comparing these genotype-specific models to those lacking the fixed effect of RH.

Differences in desiccation resistance between genotypes were analyzed using a survival analysis and a Cox regression (‘rms’ library, [73]) using the cph function. Plots were generated with the ‘survplot’ function [73]. To assess any effects of body size on desiccation tolerance, we measured the thorax length of 4-day old males and females (N = 50 of each sex from each genotype) reared at 24°C. We then fitted a linear model to evaluate the fixed effects of sex and genotype, and the interaction between these factors, using the function lm function in the ‘stats’ package [69].

Conspecific and heterospecific mating, egg laying, and egg-to-adult viability

We modeled the probability of mating by fitting a generalized linear mixed model with binomially distributed error using the lme4 library in the R Statistical Package [67].

Because the number of eggs laid was not normally distributed (Shapiro Wilk test, W = 0.979, P = 0.003), we used the ‘ARTool’ library to complete analyses of variance on aligned rank transformed data [71]. We specifically assessed the effects of cross type (♀D. yakuba × ♂ D. teissieri, ♀ D. teissieri × ♂ D. yakuba, ♀ D. teissieri × ♂D. teissieri, ♀ D. yakuba × ♂ D. yakuba) and temperature on the eggs laid over 10 days.

Because the number of eggs laid was not normally distributed (Shapiro Wilk test, W = 0.985, P = 0.015), we used the ‘ARTool’ library to complete analyses of variance on aligned rank transformed data [71]. We specifically assessed the effects of cross type (♀D. yakuba × ♂ D. teissieri, ♀ D. teissieri × ♂ D. yakuba, ♀ D. teissieri × ♂D. teissieri, ♀ D. yakuba × ♂ D. yakuba) and temperature on egg-to-adult viability.

Potential for gene flow for ♀D. yakuba × ♂ D. teissieri and ♀ D. teissieri × ♂ D. yakuba crosses

We calculated the magnitude of possible gene flow for the two reciprocal crosses using a modification of the serial isolation equation of Coyne and Orr [74] Sobel et al. [75] using mean values for each trait where:

$$\begin{gathered} {\text{G}}_{\text{Total}}=(Proportionmated)\times (Proportioneggslaid)\times (1-hybridinviability) \\ \times \left(1-\frac{hybridmalesterility}{2}\right) \end{gathered}$$ (9)

We calculated 12 mean G_Total values, one for each reciprocal cross at the six studied temperatures. We also calculated the minimum and maximum G_Total values for each temperature by finding the lowest and highest value of G_Total from all possible combinations of individual trait values for a total of 450 values per temperature.

DATA AND SOFTWARE AVAILABILITY

All new data reported in this paper are available as described in the Key Resources Table.

Highlights.

• Drosophila yakuba prefers open areas and D. teissieri prefers forests on Bioko

• These species hybridize at the center of the forest-open habitat ecotone

• Temperature-dependent reproductive isolation limits gene flow

• A maladaptive combination of parental traits in hybrids also limits gene flow