Microscopic Characterization of Membrane Transporter Function by in silico Modeling and Simulation

Abstract

Membrane transporters mediate one of the most fundamental processes in biology. They are the main gatekeepers controlling active traffic of materials in a highly selective and regulated manner between different cellular compartments demarcated by biological membranes. At the heart of the mechanism of membrane transporters lie protein conformational changes of diverse forms and magnitudes, which closely mediate critical aspects of the transport process, most importantly the coordinated motions of remotely located gating elements and their tight coupling to chemical processes such as binding, unbinding and translocation of transported substrate and co-transported ions, ATP binding and hydrolysis, and other molecular events fueling uphill transport of the cargo. An increasing number of functional studies have established the active participation of lipids and other components of biological membranes in the function of transporters and other membrane proteins, often acting as major signaling and regulating elements. Understanding the mechanistic details of these molecular processes require methods that offer high spatial and temporal resolutions. Computational modeling and simulations technologies empowered by advanced sampling and free energy calculations have reached a sufficiently mature state to become an indispensable component of mechanistic studies of membrane transporters in their natural environment of the membrane. In this article, we provide an overview of a number of major computational protocols and techniques commonly used in membrane transporter modeling and simulation studies. The article also includes practical hints on effective use of these methods, critical perspectives on their strengths and weak points, and examples of their successful applications to membrane transporters, selected from the research performed in our own laboratory.

Nanoscale Effects Governing Membrane Transporter Function

Lipid bilayers are an impermeable barrier, actively compartmentalizing life into cells and organelles that are clearly distinct at the nanoscale (Schneider et al., 2010; Medalia, 2002). Membrane transporters are incredibly specific in their capacity as the conduit of molecular transit across the membrane, serving as the Maxwellian “demon” that selectively permits specific substrates to cross while barring the path for others (Thomson, 1874). Unlike Maxwell’s fictional demon, membrane transporters function by well established thermodynamic principles, exploiting cellular sources of chemical energy such as ATP or pre-established ion gradients to drive conformational or enzymatic changes that facilitate the movement of substrate. Transporter-driven processes are found throughout biology, and are used to drive not only exchange of nutrients, ions, and metabolites across the membrane, but also more complex processes such as ATP synthesis (Weber et al., 2003), cellular signaling (Blakely & Edwards, 2012), and the excretion of cellular toxins (DeGorter et al., 2012).

The structure of the membrane transport proteins themselves are as diverse as their function, with over 10000 different transporters classified into 49 superfamilies (Saier et al., 2014). Despite their large diversity in function, there are however also similar constraints that evolution has placed upon membrane transporters. Transport is an active process that requires chemical energy to be fueled, either a pre-existing electrochemical gradient as in passive carriers and secondary transporters, or ATP hydrolysis in primary transporters. Thus unregulated transport can effectively act like a short circuit in biology, insidiously draining the capacity for the cell to do work, ultimately leading to disease (Hediger et al., 2013) or death (Feng et al., 2015; Ajao et al., 2015) if not ameliorated. The centrality of transporters to biological function has made them an attractive topic of study to a broad field of researchers, including computational scientists using techniques detailed in this chapter after a brief overview of the fundamental question of membrane transporter function.

Alternating Access Mechanism in Membrane Transporters

Membrane transporters mediate the translocation of specific substrate from one side of the membrane to the other. Although seemingly straightforward, this task cannot be accomplished by simply creating an open pathway at the membrane to allow free passage of the substrate. Under physiological conditions, many membrane transporter substrates move against their concentration gradient across the membrane. Uncontrolled flow of the substance through a wide open pathway, therefore, would be detrimental and even deadly to the cell.

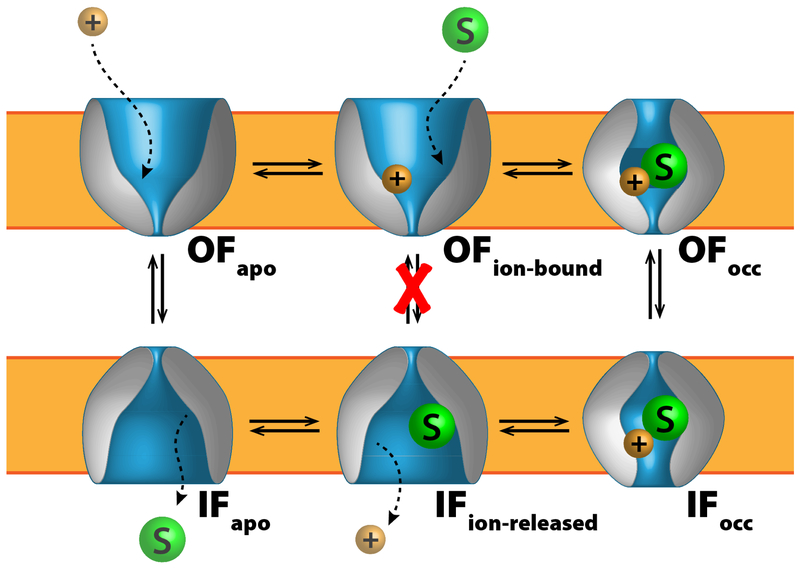
To fulfill this important requirement, virtually all membrane transporters utilize the “alternating access” mechanism (Jardetzky, 1966) to carry out their function. According to this mechanism, as the transport protein undergoes conformational changes to move the substrate from one side to the other, coordinated closing and opening motions of specific gating elements within the protein ensure that the bound substrate is only accessible from one side of the membrane at any given time (Fig. 1).

Figure 1.

An exemplary scheme of the alternating access mechanism adopted by a cation-coupled symporter, where ions and substrate move in tandem. Here the coupling mechanism only permits conformational transitions when the binding site is either completely vacant or bound with both chemical species, forbidding transitions of partially bound states (red X). Different types of transporters have different coupling mechanisms, however all share this feature of certain forbidden transitions to regulate substrate transit and to prevent draining membrane potential.

At least two major conformational states are visited by a membrane transporter during its functional cycle: the “inward-facing” (IF) and the “outward-facing” (OF) states. In a microscopic view, however, a series of events including the coordinated substrate binding/release, the engagement/discharge of the energy source, and the interconversion between these two major conformational states, need to take place in a particular order during each transport cycle. Key functional aspects, such as transport directionality, mechanism, and efficiency, rely on free energy landscapes controlling the interconversion of these states and how they are affected by chemical events within the protein.

The requirement for global conformational changes renders membrane transporter structures highly flexible and dynamic, and often difficult to capture experimentally. Nevertheless, detailed, atomistic descriptions of the structures and dynamics of these molecular machines are highly relevant, and pivotal to studies of the activities/pathologies of membrane transporters. Thus, simulating these movements with molecular dynamics and characterizing their thermodynamic properties using free energy calculations can be of great value to mechanistic studies of membrane transporters (J. Li et al., 2015).

Augmenting Mechanistic Studies of Membrane Transporters Using Simulation

In addition to traditional experimental approaches, simulation with classical molecular dynamics (MD) (Hug, 2013) is a compelling addition to the scientific arsenal, going beyond the resolution and interpretation limitations of conventional experiment to provide models of these systems at arbitrary resolution. Crucially, MD permits atomic events (such as a side chain rotation or the formation of a salt bridge) to be observed on a single molecule level, allowing the effect of specific mutations or binding events to be captured for biological assemblies (Perilla et al., 2015).

The resolution offered by MD is particularly important because transporters are inherently dynamic, which can cause difficulties for experimental observation. Substrate arrives on one side of the bilayer, finds a transporter, and follows it as the transporter undergoes a conformational change and unbinds on the other side of the bilayer. Thus, while static methods such as X-ray crystallography (Barends et al., 2014) or cryo-EM (R. Y.-R. Wang et al., 2015; Jackson et al., 2015) are indispensable to determining a 3D structure, they are missing some of the rich details that can only be obtained by exploiting the unparalleled simultaneous spatial and temporal resolution of MD simulation (Dror et al., 2012; E. H. Lee et al., 2009). Instead, ensemble spectroscopy techniques such as NMR (Oxenoid & Chou, 2013; Murray et al., 2013) or EPR (McHaourab et al., 2011) as well as single molecule techniques such as FRET (Vitrac et al., 2015) have had the greatest success in probing transporter conformational change. However, due to resolution restrictions on these techniques, computational modeling and MD also have a role to play.

The relationship between simulation and experiment can best be thought of as a symbiotic one (Karplus & McCammon, 2002; Papaleo, 2015). Simulation is impossible without the high-resolution experimentally-derived structures. Likewise, experiment is driven forward by understanding of the interactions present in the system at the nanoscale. While later sections of the chapter will emphasize computational techniques used to probe a transporter system of interest, fruitful collaboration with experiment only improves the final scientific result.

Modeling Membrane Transporters in their Native Environment

Having established the role of molecular simulation in investigating the mechanism of transporter function, actually carrying out the simulations involves a number of decisions that need to be made and procedures that need to be carried out prior to simulation. The aim of this section is to serve as a guide through the process of setting up membrane transporter simulations, complete with recommendations for state of the art tools and techniques that are expected in the larger field of biomolecular simulation, and a special emphasis on where membrane systems would differ from their soluble counterparts. The set of steps for complete system construction is expanded below, and are broadly applicable to any membrane-embedded protein.

1. Decide on a level of simulation detail.

2. Obtain a starting conformation for the membrane protein of interest.

   1. Choose a 3D structure.
   2. Fill in missing elements of the chosen structure.
   3. Determine protonation and termination.
3. Assemble a complete simulation system.

   1. Choose a membrane composition.
   2. Build the membrane.
   3. Embed the model structure into the generated membrane.

4. Equilibrate the system under appropriate simulation conditions.

Choosing a Level of Detail: Atomistic or coarse-grained?

The first decision prior to any simulation is to choose the level of detail for the simulation. Since classical MD simulations propagate Newton’s equations of motion forward in time for each particle by using an empirical force field (Karplus & McCammon, 2002; Hug, 2013), stable integration of the position demands that the timestep between force evaluations be approximately ten times shorter than the timescale of the fastest degree of freedom (Hess, 2008). In the original formulation of biomolecular MD, each particle in the simulation system represents a specific atom, and the fastest degrees of freedom are the bond vibrations to hydrogen. The relevant vibrational modes are observed at ~ 3000 cm⁻¹ in IR spectra (de Vries & Hobza, 2007), implying ~ 10¹⁴ vibrations of the bond per second, limiting unconstrained atomic MD timesteps to 1 fs. If the length of bonds to hydrogen atoms are fixed, the next fastest modes are heavy atom vibrations, which limit the timesteps to 2–2.5 fs each.

Many biological processes happen on the ns-ms timescale, so for atomic simulation, approximately 10⁶ – 10¹² timesteps need to be taken. At a reasonable simulation rate of ~ 10 ms of wallclock time per simulation timestep, a rate dictated by current hardware communication performance, a μs of simulated time would take approximately 4 months for a fully unconstrained atomic system, and a ms would be unrealistic except on specialized hardware (Shaw et al., 2014). To achieve longer to timescales economically, coarse grained alternatives to atomic simulation have been developed, which fundamentally depart from an atomic representation to make larger particles that represent multiple atoms (Marrink & Tieleman, 2013), multiple residues (Saunders & Voth, 2012, 2013), simply omit hydrogen (S. Lee et al., 2014), or a combination of these approaches (Han & Schulten, 2012). As a consequence of the increased particle mass, coarse grained particle vibration is retarded, allowing for substantially longer timesteps of 20–40 fs in these representations, lengthening the timescale accessible to the simulation.

Both atomic and coarse-grained representations are frequently used for production simulations, and have different strengths. Coarse grained simulations are frequently favored when the timescale required for the process is large and the interaction specificity is not central to the result, such as simulations of lipid membrane mixing (Ingólfsson et al., 2014) or sampling the organization of larger lipids around membrane supercomplexes (C.-K. Lee et al., 2015). Atomic scale simulations are indispensable if specific interactions are essential to the function, such as salt bridges breaking to precipitate a large conformational change in a transporter (Moradi et al., 2015) or a single hydrogen bond tuning the redox state of a protein cofactor (Vermaas, Taguchi, et al., 2015). Again emphasizing that both approaches are accepted practice, it should be noted that there is always a danger of oversimplifying the system and missing essential features in a coarse grained simulation. If more detailed interactions are required, reverse coarse graining approaches have been developed to convert simulation systems back to an atomic representation (Stansfeld & Sansom, 2011; Wassenaar et al., 2014). The examples in the sections to follow will all focus on atomic simulation.

Initial Structural Model Construction and Refinement

For any level of biomolecular simulation, a correct starting structure is essential to the validity of the results. Structural resources such as the protein databank (PDB) (H. M. Berman et al., 2000; H. Berman et al., 2003) provide vital starting points for a 3D structure. However choosing a single structure for the protein of interest can be quite difficult simply due to the number of options available. Generally speaking, there are no hard and fast rules about which structure is “best”, although low resolution structures are best avoided if at all possible. Additionally, the structure should make sense in terms of membrane topology. For some membrane transporters, crystal contacts between neighbors can cause significant artifacts, as discussed by Y.-J. Chen et al. (2007) and Wisedchaisri et al. (2014) when comparing their crystal structures against other structures. Once a starting point is obtained, there are a number of additional technical elements that should be checked prior to starting simulation, including the completeness of the structure and protonation.

PDB structures from crystallographic data are often missing pieces of the native protein, which were too floppy or dynamic to be well resolved in the crystal lattice. Many tools exist to fill in these gaps, and broadly speaking come in two different flavors, those that use population-based statistics to generate candidate models, and those that directly use additional experimental inputs to refine the structure. Given a protein structure with gaps, tools such as MODELLER (Webb & Sali, 2014), Rosetta (Das & Baker, 2008; Chaudhury et al., 2010), or particularly SuperLooper (Hildebrand et al., 2009), which has been optimized for membrane protein loops, can fill in those gaps and complete the protein structure. This obviates the need to restrain the geometry of what would otherwise be loose ends, although they should be monitored during simulation. Additionally, PDB structures may contain cis-peptide bonds or chirality errors (Schreiner et al., 2011; Touw et al., 2015; Croll, 2015), which can be detected using tools included in webservers such as MolProbity (V. B. Chen et al., 2010) or WHAT IF (Rodriguez et al., 1998), and corrected through model rebuilding and/or re-refinement of the crystal structure. These stereochemical errors, nevertheless, can be easier addressed during system construction using the Chirality/Cispeptide (Schreiner et al., 2011) plugins of VMD (Humphrey et al., 1996).

Refinement methods depend on experimental observables to apply additional constraints to the protein structure. CryoEM or X-ray derived electron densities can be used as a biasing potential for the protein structure using molecular dynamics flexible fitting (MDFF) (Trabuco et al., 2009; McGreevy et al., 2014), where the classical MD force field is supplemented by forces acting on the atoms to bring them to electron dense regions of space. EPR/DEER data can similarly be incorporated into simulation structures using restrained ensemble simulations applying a series of distance restraints (Islam et al., 2013). In principle, with the advent of complex collective variables available in easy to use packages (Fiorin et al., 2013; Tribello et al., 2014), NMR observables such as NOEs (nuclear Overhauser effect) and RDCs (residual dipolar couplings) can also be included in structure determination protocols (Fu et al., 2014; Camilloni & Vendruscolo, 2015).

Another often overlooked feature of the structure preparation process is the determination of the protonation states for each and every ionizable residue. Now the N- and C- termini tend to be fairly clear decisions, as they are nearly always protonated and deprotonated respectively according to their pK_a and general environment. However if the protein is incomplete, such as if only one domain is being simulated, it may be appropriate to use a neutral terminating patch instead. For ionizable residues such as histidine or aspartate, their pK_a can shift dramatically depending on their protein environment. If the ionization state is unknown, the pK_a of each residue can be estimated using tools such as PROPKA (Søndergaard et al., 2011; Olsson et al., 2011), or H++ (Gordon et al., 2005), allowing the protonation state to be assigned. PROPKA is particularly suitable to this task, as when combined with the PDB2PQR originally designed for Poisson-Boltzmann electrostatics calculations (Dolinsky et al., 2007), it generates an output that assigns protonation locations, including the always ambiguous histidine, which has two neutral forms. Neither PROPKA or H++ takes into account which residues interact with the membrane, and instead assumes the proteins are soluble, so caution should be exercised with their output on the protein periphery and inspected carefully for transporter systems.

Membrane Composition and Construction Considerations

Prior to assembling a membrane-embedded transporter simulation system, it is important to consider what lipid composition is most appropriate for the transporter in question. Due to the desire to improve performance by limiting the size of the simulation, there may be fewer than 100 lipids per leaflet for modeled membranes surrounding transport proteins. As a result, single composition membranes form the zero-order approximation of a cell membrane in vivo. Phosphatidylcholine (PC) and phosphatidylethanolamine (PE) lipids are commonly used because they represent the largest components of steady state mammalian and bacterial cell membranes respectively (van Meer et al., 2008; Dowhan, 1997).

A more complete approach, however, would be to include other membrane actors, such as sterols or signaling lipids that have been experimentally shown to influence transporter function (Hong & Amara, 2010; Hamilton et al., 2014). Sterols are generally abundant, and can be included in mixed systems without difficulty at their experimental concentration (E. Wu et al., 2014; Jo et al., 2009), keeping in mind that lipid mixing processes are slow, and require extensive simulation for full equilibration (Ingólfsson et al., 2014). Rare signaling lipids represent significantly below 1 percent of membrane phospholipid in vivo (van Meer et al., 2008), and should be strongly enriched in typical simulations so that the embedded protein may have a chance to interact with the lipid. This enrichment depends on the assumption that the transporters locally enhance the concentration of certain lipids from the heterogeneous lipid distribution in live cells, and is likely true for proteins with specific lipid binding sites.

The location of the transporter must also be considered; mitochondrion, for example, have high levels of cardiolipin, a bacterial lipid not found elsewhere in mammalian cells (Paradies et al., 2014). Similarly, yeast and bacterial cells have a membrane composition that can differ substantially from mammalian cells, and the membrane composition must be changed accordingly. Context in which the transporter operates should be taken into account as well. If, for example, a transporter functions on activated platelets or cells undergoing apoptosis, it is likely to interact more frequently with charged lipids flipped from the inner membrane (Fadok et al., 1992). This can be summarized into the following series of steps.

1. Review the available literature to determine if the transporter function is influenced by specific lipids. If a specific lipid plays a major role in the activity of the transporter, it may be advisable for a larger-than-physiological concentration of the moiety be included to ensure the critical interaction is sampled. Multiple initial membrane configurations should be generated, as the protein-lipid interactions will be biased towards the initial conformation.

2. Review the membrane context for implications as to the lipid environment surrounding the transporter, including the species from which the transporter was isolated, and the localization of the transporter within the cell. If a particular lipid has a significant presence, it may be advisable to include it to reproduce the conditions of the specific functional environment of interest.

3. Review experimental studies on the transporter to inform the design of the simulation. Since it is known that the choice of lipid changes the behavior of transporters in vitro, direct comparisons between simulation and experiment are best made at similar membrane compositions.

One final thing to consider is that once the lipid composition for the simulation has been determined, a lipid patch of appropriate size for the system must be generated. Many tools exist for this step, including both webservers and stand-alone programs (Wassenaar et al., 2015; Bovigny et al., 2015; Jo et al., 2008). The CHARMM-GUI membrane builder is an exemplary tool for this step, as it includes most physiological mammalian and bacterial phospholipids and sterols (E. Wu et al., 2014). CHARMM-GUI also permits the membrane geometry to be selected, and contains an interface to alternative membrane representations that accelerates lipid diffusion (Qi et al., 2015). This Highly Mobile Membrane Mimetic (HMMM) representation (Ohkubo et al., 2012) can be used to accelerate sampling of the lipid environment around proteins, capturing headgroup-specific interactions (Vermaas, Baylon, et al., 2015; Baylon et al., 2016).

Membrane-Embedded Transporter System Assembly

Aside from membrane considerations, the protein itself needs to be oriented and placed correctly relative to this membrane. Transporter proteins typically have a very distinct belt-like region in contact with the membrane. This region may not be obvious merely through visual inspection alone. Commonly, a web server such as the PPM (Positioning of Proteins in Membrane) (M. A. Lomize et al., 2006; A. L. Lomize et al., 2006, 2007, 2011), is used to automatically identify the hydrophobic belt region of a transmembrane protein. This is done by minimizing the transfer energies of the membrane protein from water to an artificial lipid bilayer (A. L. Lomize et al., 2011). This is a crucial step because the function of the membrane protein is greatly affected by the lipid-protein interactions. Misplacement of the orientation of the protein and mismatch of the protein hydrophobic belt and membrane bilayer may lead to long equilibration requirements or misleading conclusions.

Following the orientation of the membrane protein, it must be inserted into the bilayer. For simple cylindrical transporters, the protein can simply be superimposed onto the membrane. Lipids that overlap with the protein can be programmatically removed via structure building tools such as VMD (Humphrey et al., 1996) or CHARMM (Brooks et al., 2009) (Fig. 2A). Usually this will leave large gaps at the interface between the protein and the lipids. This artifact can be equilibrated away, as the lipids will naturally pack against the transporter during simulation. With the new CHARMM36 lipid forcefield parameters (Klauda et al., 2010) and constant pressure condition applied to the lateral (membrane plane) and perpendicular directions, the area per lipids will match the experimental values once equilibrated, i.e., ~ 70 Å2 lipid (Leftin et al., 2014). However this protocol may change the protein structure, which is frequently ameliorated by restraining the protein backbone via a harmonic potential to its initial position. The restrained equilibration relaxes the lipid tails prior to production simulation. This step should continue until the unit cell dimension of the membrane settle to near a fixed value, when the restraints can be released. Alternatively, a repulsive force centered around the protein and pointing outwards can be applied to the lipids to remove clashes (Shen et al., 1997; Tieleman & Berendsen, 1998; Faraldo-Gómez et al., 2002).

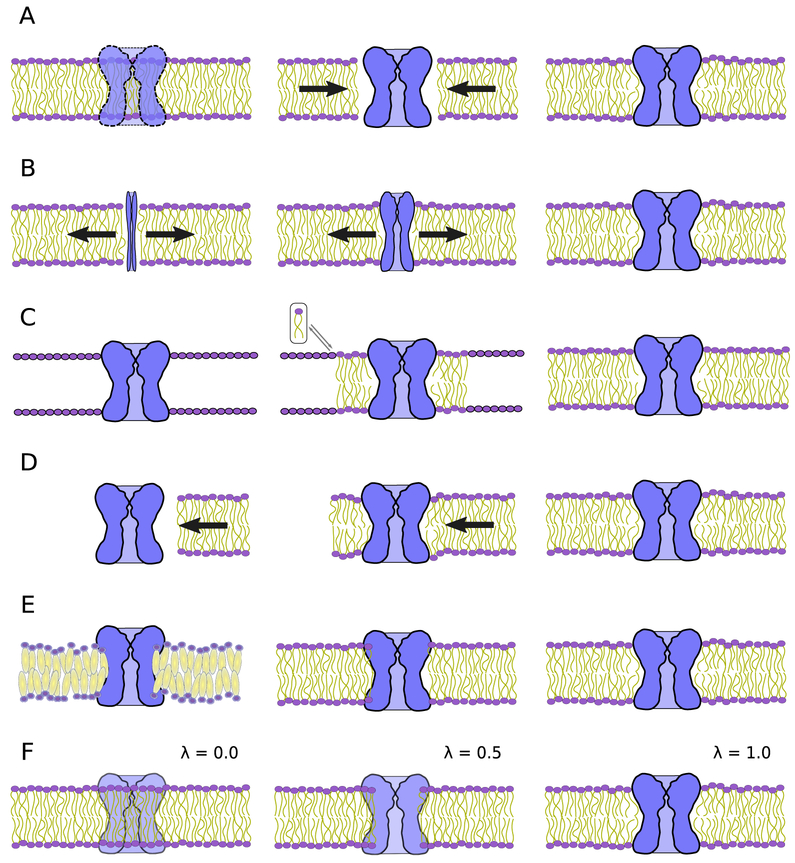
Figure 2.

Schematic diagrams of the many membrane embedding protocols outlined here. The protein is colored blue and the phospholipid bilayer is shown with a purple head group and yellow lipid tails. (A) The naive lipid deletion method carried out within VMD (Humphrey et al., 1996) or CHARMM (Brooks et al., 2009), where overlapping lipids are removed from the bilayer and equilibration eliminates the gap as denoted by the arrows. (B) The method of Wolf et al. (2010), where the protein, initially a thin rod, expands to make space for itself within the membrane. Outward displacement of lipids is illustrated by the arrows. (C) Pseudo atoms replaced by lipid conformers taken from a lipid library that results in a nearly equilibrated membrane-protein complex (Jo et al., 2007). (D) The membrane is introduced to the protein by a pressure applied to the membrane, resulting in an embedded complex (Javanainen, 2014). Flow of the membrane is indicated by the direction of the arrow. (E) Stansfeld et al. (2015) use coarse grained simulation to reach equilibrium. Reversion of coarse grain lipids to atomistic allows further equilibration. (F) Alchemical techniques (Jefferys et al., 2015) gradually introduce protein-lipid interactions by using a soft-core Van der Waals potential as indicated by the λ parameter.

For non-cylindrical transporters, many other methods exist (Kandt et al., 2007; E. Wu et al., 2014; Wolf et al., 2010; Javanainen, 2014; Stansfeld et al., 2015; Jefferys et al., 2015). In all these methods, the lipids that have severe overlaps with the membrane protein are removed first. They differ in the strategy for removing minor clashes and wrapping lipids around the protein. In method from Kandt et al. (2007), the X and Y coordinates of the pre-equilibrated membrane are first scaled up to remove clashes and then gradually scaled towards the target lipid density to accommodate lipids around the membrane protein. In the method of Wolf et al. (2010), the X and Y coordinates (along the membrane plane) of the transporter protein are first scaled down and then scaled back to the original to allow the lipids to tightly fit to the hydrophobic belt of the transporter using molecular dynamics (Fig. 2B). In Javanainen’s method (Javanainen, 2014), the lateral pressure along the membrane plane is used to wrap the lipids around the restrained target membrane protein (Fig. 2D). In the MemProtMD method developed by Stansfeld et al. (2015), the key idea to change the representation of the target system to a coarse-grained version and take advantage of the fast dynamics in new resolution-reduced system to accelerate the the lipid diffusion process (Fig. 2E). This coarse-grained system is subsequently converted back to the all-atom system with some equilibration. In the Alchembed method developed by Jefferys et al. (2015), interactions between the protein and the lipids are replaced by alchemical soft-core potentials with gradually increasing intensity to remove clashes between lipids and the protein including aromatic ring piercing (Fig. 2F). Last but not least, a module named the “Membrane Builder” from the web application CHARMM-GUI (Jo et al., 2007, 2008; E. Wu et al., 2014) can also be used for preparing the membrane-protein system. The algorithm used by CHARMM-GUI “Membrane Builder" first determines the lipid head group position on the two membrane surfaces via a simulation with pseudo atoms that surround the embedded protein (Jo et al., 2007) (Fig. 2C). The pseudo atoms are then replaced by full lipids selected from a conformer library with 2000 distinct conformations taken from a MD trajectory, generating a membrane embedded membrane protein.

All the methods mentioned above have been demonstrated to be well suited for building simulation systems with membrane proteins embedded in pure or mixed biological membranes. However each of them have a different learning curve, and CHARMM-GUI stands out for its simple interface and rich customization features for different lipid types (E. Wu et al., 2014).

Simulation Condition Considerations

Membrane protein simulation conditions differ from their soluble counterparts in a number of aspects. The membrane is an anisotropic medium, with distinct stress moduli along the membrane normal and membrane parallel directions. Barostats in simulation should take this asymmetry into account. MD engines include an option for a barostat that can change the shape of the dimensions of the periodic cell independently between the membrane normal and membrane parallel axes, based on the seminal work of Martyna et al. (1994). The two membrane parallel axes should grow and shrink in a constant ratio with one another, lest the membrane deform anisotropically and allow the embedded protein to contact itself across the periodic boundary.

While the thermostat used for simulation of membrane transporters follows the same general advice as soluble proteins, using a Nose-Hoover (Evans & Holian, 1985) or Langevin thermostat (Brünger et al., 1984; J. C. Phillips et al., 2005), the target temperature of membrane protein systems needs to be carefully chosen. Membranes undergo phase transitions near physiological temperature, which have been hypothesized by Gray et al. (2015) to be a way by which the cell can reorganize its membranes in response to different growth conditions. Thus unlike soluble proteins, which are frequently simulated near room temperature (300 K) to mimic experimental conditions, membrane protein simulations are typically a bit warmer (310 K) to stay above the liquid-gel transition temperature for the lipids being simulated and to mimic natural disordered lipids (Coppock & Kindt, 2010).

Membrane protein simulation conditions differ from solution simulations in one final respect: rather than only needing a forcefield to describe the interactions within the protein and between the protein and water, membrane protein simulations also require accurate parameters for protein-membrane interactions. Amber (Dickson et al., 2012), Gromos (Reif et al., 2013), OPLS (Siu et al., 2012) and CHARMM (Klauda et al., 2010) lipid force fields have all been validated for these mixed interactions at the atomic level, and all continue to be improved and updated as more experimental data becomes available. Currently, either the combination of the CHARMM36 lipid (Klauda et al., 2010) and protein (Best et al., 2012) force fields or the SLIPID (Jämbeck & Lyubartsev, 2013) and AMBER99SB-ILDN (Aliev et al., 2014) force fields would be recommended for new simulation having been consistently found to outperform their competitors in membrane properties (Paloncýová et al., 2014) and correctly capture membrane-protein interaction (Sun et al., 2015).

Modeling Substrate Binding and Unbinding Processes in Membrane Transporters

The activity of membrane transporters is tightly coupled to their substrates, and may additionally be modulated by other small molecules present in the system under study. While experimental quantities such as a dissociation constant (K_d) are often readily available for many compounds and transporter combinations, those are missing the details of the interaction, and thereby have difficulty making predictions on how the dynamics change once a substrate is bound. Since the binding fundamentally lowers the barrier to conformational transition, determining the interactions that take place and quantifying their effect through free energy calculation is a frequent addition to traditional equilibrium simulation of the unbound state. Furthermore, quantifying the energy change is frequently used to compare with experiment and connect back in silico observables with those determined in vitro, and is a crucial sanity check on the validity of the results. An additional complication to adding substrates or drugs to the system is that they may be missing parameters that describe their interaction with other elements of the system. Techniques commonly used to add these features to transporter simulation are discussed in this section (Fig. 3), and should be used in conjunction with equilibrium MD of the apo state to elucidate how substrates trigger conformational change.

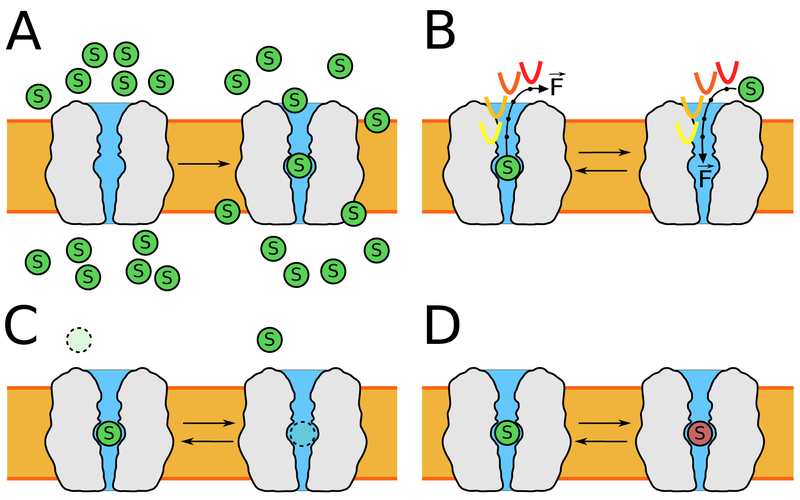
Figure 3.

Schematic of widely employed techniques for characterizing substrate association and dissociation, including their energetics. (A) Flooding simulations are where a high concentration of substrate (green circle) is allowed to interact with the transporter. (B) Steered molecular dynamics (SMD) and umbrella sampling (US) use biasing forces applied along a reaction coordinate (curved arrows) to steer a binding or unbinding process. (C & D) Alchemical methods such as free energy perturbation (FEP) or thermodynamic integration (TI) permit absolute binding (C) and relative binding (D) free energies to be computed without knowing the binding or unbinding pathway.

Determining Substrate Force Field Parameters

Classical MD simulations are founded on molecular mechanics (MM) force fields, a mathematical description of interatomic (comprising intra- and intermolecular) interactions (Ponder & Case, 2003; Mackerell, 2004; Guvench & MacKerell, 2008; Monticelli & Tieleman, 2013). MM potential energy functions are comprised of terms to describe each individual topological and intermolecular element, in which each term is tuned for a specific interaction using parameters. For the transporters themselves and their environment, decades of research has led to the availability of robust parameter sets for commonly studied biopolymers (e.g., proteins (MacKerell, Jr. et al., 1998, 2004; Best et al., 2012; Cornell et al., 1995; Lindorff-Larsen et al., 2010; D.-W. Li & Brüschweiler, 2010; Oostenbrink et al., 2004; Kamisnki et al., 2001), DNA/RNA (MacKerell Jr. & Banavali, 2000; Denning et al., 2011; Hart et al., 2012; Pérez et al., 2007; Aduri et al., 2007; Soares et al., 2005), carbohydrates (Guvench et al., 2009; Raman et al., 2010; Guvench et al., 2011; Glennon & Merz, Jr., 1997; Kirschner et al., 2008; Damm et al., 1997; Kony et al., 2002)) and other biological structures for which dynamic studies are required (e.g., lipids (Feller et al., 1997; Klauda et al., 2010; Skjevik et al., 2012; Dickson et al., 2014; Maciejewski et al., 2014)). The substrates of membrane transporters are generally classified as small molecules which, in contrast to biopolymers, frequently contain unique functional groups not shared with the biopolymers they interact with, and demand parameters not necessarily covered by existing parameter sets. Despite lacking an inherent repeated structure, transporter substrates often share common substructure or functional groups (e.g., aromatic rings, alcohols, amines, amides, alkyl chains, olefins, etc). Efforts towards developing parameter sets covering these common elements are the basis for generalized extensions to popular biopolymer force fields, such as the CHARMM General Force Field (CGenFF) (Vanommeslaeghe et al., 2010) and the Generalized AMBER Force Field (GAFF) (J. Wang et al., 2004).

While such parameter sets provide coverage for common substructures, it is unreasonable to expect that they can provide coverage for the exponential combinations required to describe small molecule parameter space (estimated at 10¹⁸–10²⁰⁰ molecules!) (Drew et al., 2011). The focus of obtaining parameters is thus shifted from parameterizing entire molecules, to focusing on linkages between substructures that lack parameters. Although this does not represent a complete solution to obtaining parameters, it significantly reduces the complexity and practical challenges associated with parametrization. There are several tools available that facilitate filling in the remaining missing parameters for small molecules, and take one of two approaches: assigning parameters by analogy to molecules for which parameters are already known, or by optimizing parameters against target data, typically high level quantum mechanical calculations. Traditionally, comparisons to determine molecular analogy has been performed by hand. While this allows for a high degree of control, it requires that the researcher has an in-depth knowledge of chemical similarity and what types of molecules are already present in the parameter set. Recently, several programs have been developed that automate the process of determining parameters by analogy, such as the CGenFF Program (Vanommeslaeghe & MacKerell, Jr., 2012; Vanommeslaeghe et al., 2012) and MATCH (Yesselman et al., 2012) for the CGenFF force field, AnteChamber (J. Wang et al., 2006) and R.E.D. (Vanquelef et al., 2011) for the AMBER force field, and the Automated Topology Builder (ATB) (Malde et al., 2011) and PRODRG (Schüettelkopf & van Aalten, 2004) for the GROMOS force field.

In addition to targeting different force fields, each of these resources uses its own methodology to make parameter assignments. It is critical to understand how each tool arrives at the a parameter set and to make sure that this method is consistent with the target force field for the desired application, as this has been shown to strongly impact the quality of subsequent simulations (Lemkul et al., 2010). Each resource also relies upon a different database of parameter knowledge, which can impact the results. The CGenFF program, for instance only crosschecks against the main CGenFF parameter set, excluding many chemotypes for which parameters are well-known but are distributed as add-on specialty parameters, such as parameters for lipids, sterols, carbohydrates, fluoroalkanes, and amines, amongst many others that are contained in separate “stream files” and are not part of the CGenFF Program similarity search.

Assigning parameters by analogy is often expedient, and in some cases sufficient; however, there are many cases which require computing the parameters directly, such as refining parameters for a specific system or obtaining parameters for novel chemotypes where no suitable analogy exists. Computing parameters directly is a significantly more involved process that requires multiple calculations to fit parameters to target data than for the analogy method (Fig. 4). The availability of toolsets for performing these tasks are less widespread, with the most options available for the CHARMM family of force fields (i.e., CHARMM, CGenFF). The General Automated Atomic Model Parametrization (GAAMP) webserver (L. Huang & Roux, 2013) is the simplest to use, requiring only modest input and employing a highly automated, albeit blackbox, approach to optimizing parameters. The Force Field Toolkit (ffTK) (Mayne et al., 2013), distributed as a plugin within the popular VMD molecular modeling package (Humphrey et al., 1996), is designed specifically with usability in mind by automating tedious and error-prone tasks, providing reasonable defaults for novice users, and featuring a set of analytical tools to assess the details of the optimization calculations and allow for extensive customization by expert users. Expert users may be interested in the stand-alone program lsfitpar (Vanommeslaeghe et al., 2015), which provides users with the same routines employed by the developers of CGenFF in a command-line environment, or the Force Balance program (L.-P. Wang et al., 2013), which is written in Python and furnishes an infrastructure that accommodates a diversity of target data, such as experimental data, and optimization techniques, such as MD-simulated properties, to fit parameters. In addition to these tools, the Paramfit program (Betz & Walker, 2015) supports parametrization of for the AMBER force field, and the ForceFit program (Waldher et al., 2010) provides general routines that are not specific to any particular force field.

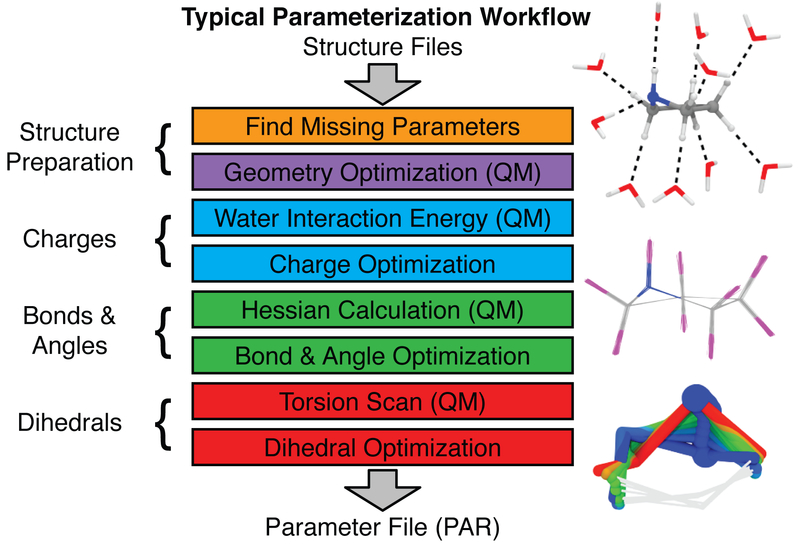
Figure 4.

General parameterization workflow for developing CHARMM-compatible parameters. These steps are implemented in the Force Field Toolkit (ffTK) (Mayne et al., 2013), and are grouped by color to highlight how quantum mechanical target data feeds into each step of the parameter optimization process. Molecules showing the water interactions, bond stretching, and torsional scanning are presented on the right beside the workflow.

Following the steps to obtain parameters, it is critical to assess the quality of the parameters. Depending on the molecule in question, the availability of experimental data, assessments towards the parameter quality range greatly in terms of complexity and rigor. The CGenFF Program provides a “penalty score” for each parameter which describes how close the term matches by analogy to the existing term (Vanommeslaeghe et al., 2012). Using this penalty score, the authors of the tool suggest that the parameter is fair, requires basic validation, or extensive validation/optimization. When computing parameters directly, ffTK provides a significant amount of data and analytical tools to assess the degree of fit between the MM-computed properties and the driving target data (Mayne et al., 2013). The most rigorous assessment of parameter performance, however, is the ability to reproduce condensed phase properties from MD simulations. The simplest calculations are to compute the density and enthalpy of vaporization (Vanommeslaeghe et al., 2010). These properties are only relevant to molecules that are liquids under simulation conditions, and are largely defined by the Lennard-Jones term of the force field; therefore, they are not ideal for assessing charge assignments or bonded parameters. Currently, the most rigorous approach is to compute the free energy of solvation, where experimental values are frequently available (Mobley et al., 2011; Mayne et al., 2013; Mobley & Guthrie, 2014; Zhang et al., 2015). Experimental partition coefficients for octanol/water solvent systems are also frequently available for lipophillic compounds (Sangster, 1989; CRC, 2015) and can be approximated from free energy calculations using alchemical simulations (Garrido et al., 2012; Vermaas, Taguchi, et al., 2015).

Ensemble Docking to Identify Putative Substrate Binding Sites

In cases where the substrate binding site of the transporter is unknown, small molecule docking can be used to search for possible binding conformations of a ligand in the binding site of a protein (Mihasan, 2012; Strynadka et al., 1996; Dolghih et al., 2011). The identified favorable protein-ligand conformations through docking provide a clear picture of the key molecular interactions that facilitate binding. Not all docking programs use the same scoring functions and docking protocols, so users should evaluate the reliability of available software for the ligands and proteins of interest to compare their results (Cross et al., 2009; Plewczynski et al., 2011). Following are a few ways to obtain reliable docking results, (i) a consensus approach (Clark et al., 2002), where a few docking programs are used to predict the protein/ligand complex and a predominant pose is selected, (ii) re-docking a crystallographically solved similar protein/ligand complex of interest to validate the programs in predicting the x-ray identified complex (Thangapandian et al., 2012), (iii) using a benchmark dataset (Hevener et al., 2009), which includes known binders and non-binders of the protein of interest, to evaluate the predictive ability of the docking programs.

Molecular docking was first carried out on static or nearly static structures, where only a few protein side chains were allowed to change their orientation (Meng et al., 2011; Morris & Lim-Wilby, 2008; Thangapandian et al., 2010). However this static approach misses binding sites that might become accessible only due to the motion of a protein or only exist after membrane interaction changes protein conformation, a feature that is common among membrane-associated proteins (Lin et al., 2002; Denisov et al., 2015; Rinne et al., 2015; Rodríguez et al., 2015). To take these conformational changes into account, a so called “ensemble docking” technique is used. Ensemble docking is performed against a series of protein conformations taken from a MD trajectory or experimentally solved conformations of a protein (Lin et al., 2002; S.-Y. Huang & Zou, 2007; Amaro et al., 2008; Korb et al., 2012; Campbell et al., 2014; Tian et al., 2014; Ellingson et al., 2015). The breathing motions from MD may find even more poses and states, rather than relying on a single or a few experimental snapshots to be representatives of the ensemble of conformations encountered in vivo.

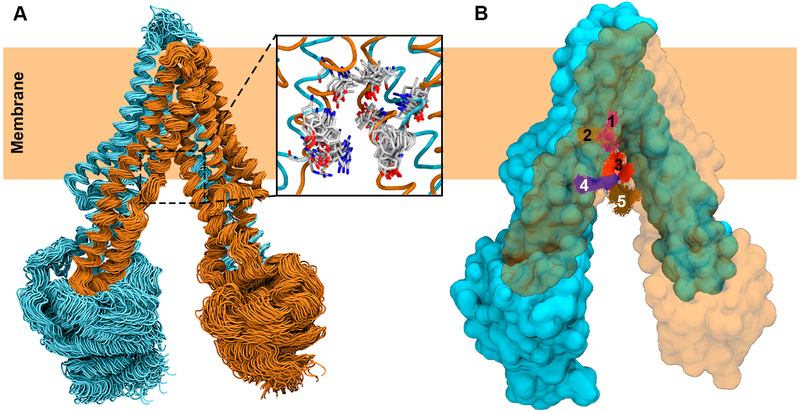
As an example, ensemble docking of a drug substrate on to P-glycoprotein (P-gp), an ATP-binding casette (ABC) transporter that exports toxins and drugs out of the cell (Aller et al., 2009; J. Li et al., 2014), is demonstrated. Here, an ensemble of 1000 protein conformations obtained from a long MD trajectory (Fig. 5A) is used. Then the docking region is defined, keeping in mind that it should comprise the complete translocation compartment and not just the final binding site, as transport proteins usually have multiple binding sites (Dolghih et al., 2011; Safa, 2004; Martin et al., 2000; Sharom, 2014). A drug substrate was docked in to the defined docking region using AutoDock (Morris et al., 2009), generating 10 docked poses for each protein conformation. For this example, ensemble docking has resulted a total of 10,000 docked poses of the drug molecule (1000 conformations × 10 poses) covering the entire translocation compartment. A clustering method was then used to cluster all the docked poses, which in turn provided a set of possible binding sites (Fig. 5B). Repeating the same protocol for both end states of the transport cycle would provide additional insight as to the complete path of a substrate during the large-scale transition of the transporter.

Figure 5.

Ensemble docking of a drug substrate into the translocation lumen of P-gp. (A) MD simulation-generated ensemble of conformations used in molecular docking. Two pseudosymmetric halves of P-gp are colored in cyan and orange, respectively. Only 100 out of 1000 conformations used in ensemble docking are shown. A set of translocation path residues is shown to display the diverse side chain conformations represented by the MD-generated ensemble (inset). (B) Top 5 RMSD-based clusters of docked poses of the drug molecule are shown in different colors with P-gp in surface representation. One half of the protein is shown transparent to clearly show the clusters of the docked drug molecule.

Substrate Binding and Unbinding from Unbiased Simulation

The docking methods presented in the previous section provide starting points for substrates bound to their binding site. However, only through simulation is it possible to explore the detailed dynamics of substrate binding or unbinding (Fig. 6). Through extended equilibrium MD simulation, important dynamical elements of substrate binding have been observed, including the specific interactions that bind the substrate to the transporter, and gating residues that prevent premature translocation (Z. Huang & Tajkhorshid, 2008; Yin et al., 2006; Zomot & Bahar, 2012; Simmons et al., 2014; Watanabe et al., 2010; Enkavi & Tajkhorshid, 2010; Y. Wang et al., 2008; Andersson et al., 2012; X. Jiang et al., 2014; Zhao et al., 2011). Conceptually, these simulations are simple equilibrium simulations, although an unprepared investigator can find analyzing their results surprisingly counterintuitive.

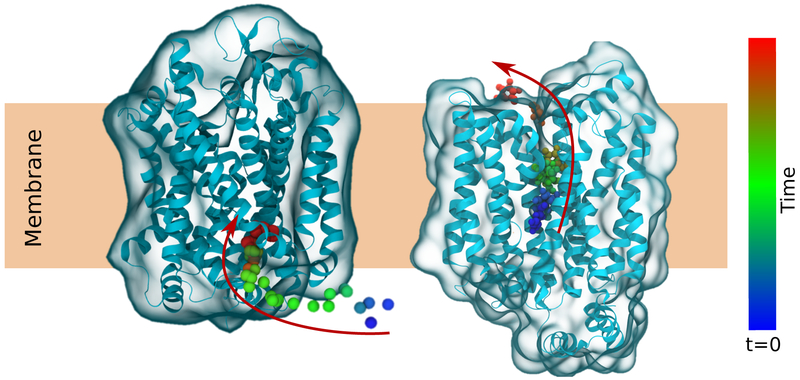
Figure 6.

Binding of an ion (left) or unbinding of substrate (right) from membrane transporters captured in unbiased equilibrium simulations. The color of the ion and substrate changes with time to show movement in the direction of the arrows.

For instance, despite calculating forces based on a potential energy function, the exact value of that function for interaction strength between substrate and protein has no meaning in isolation, as it neglects the contribution of water and other species to the sum of the forces acting upon the substrate. Instead, dedicated free energy methods are required to compute experimentally relevant quantities, and are detailed in subsequent sections. However, these types of analyses can be useful in identifying specific interactions, such a hydrogen bonds, that restrain substrate dynamics and are liable to play a larger role in governing the substrate binding and unbinding behavior, as exemplified by numerous applications (Koldsø et al., 2013; Kantcheva et al., 2013; Cheng & Bahar, 2015). In cases where the substrate bound form is being studied, it is recommended to release any equilibrating restraints placed upon the substrate binding site first, such that the residues surrounding the binding site can adopt their final favored conformation (J. Li & Tajkhorshid, 2012; Tavoulari et al., 2016). If this is insufficient, additional harmonic distance restraints can be applied to enforce a hypothesized binding geometry, though it may not prove to be stable during simulation.

Studies of binding or unbinding processes can focus on specific binding residues, such as those that form an intricate H-bonding network between the substrate and the binding site that needs to be disrupted for the substrate to be released from the binding site (Zomot & Bahar, 2012; Watanabe et al., 2010). However in some instances, other protein side chains can block binding or unbinding based on their rotameric state, acting as “gate” controlling the flow of substrate (Zomot & Bahar, 2010; Watanabe et al., 2010). The coupling between the substrate rearrangement and gate opening is frequently accomplished by water solvating the binding site and lubricating the unbinding event (Choe et al., 2010; Cheng & Bahar, 2014). Analyzing the trajectories for these features is frequently first done by eye, using visualization tools such as VMD (Humphrey et al., 1996), Chimera (Pettersen et al., 2004), or PyMOL (Schródinger, LLC, 2015), and then measuring quantities of interest via trajectory analysis tools such as VMD (Humphrey et al., 1996), MDTraj (McGibbon et al., 2015), or MDAnalysis (Michaud-Agrawal et al., 2011).

Unlike substrate unbinding, binding events are difficult to capture using unbiased MD simulation, as the entropy decreases substantially upon binding relative to the unbound state. Additionally, substrate binding requires the reformation of interaction between the substrate and the binding site which is generally accompanied by local conformation reorganization of the amino acids in the binding site. Nevertheless, binding of small ions (Zomot et al., 2015) and gaseous molecules (CO and O₂) has been observed previously in MD simulations (Baron et al., 2009; Ruscio et al., 2008). Furthermore, strong interactions, such as those between charged substrates and their binding site, have also been captured spontaneously in MD simulations (Enkavi & Tajkhorshid, 2010; Y. Wang et al., 2008; Dehez et al., 2008).

For uncharged substrates, the simplest simulation approach to apply to the transporter system to identify substrate binding sites and pathways would be to increase the concentration of the substrate, which may increase the probability of binding at the simulation timescale. In this “flooding” approach, a high concentration of substrate is placed in the simulation system and allowed to diffuse in an unbiased manner (Brannigan et al., 2010; Murail et al., 2011). Copies of substrate can be generated by substituting water molecules or using softwares such as PACKMOL (Martínez et al., 2009). Binding sites and transport pathways of substrate can be identified by visualizing simulated trajectories and by clustering analysis (Ruscio et al., 2008; Brannigan et al., 2010; Buch et al., 2011; P. H. Wang et al., 2011; LeBard et al., 2012). As an example of such analysis, the entire trajectory of a simulation can be clustered into a three-dimensional occupancy map using tools integrated into VMD (Humphrey et al., 1996), which indicates regions within the protein where substrate is frequently sampled, and can be applied to a diverse set of transmembrane proteins (Mahinthichaichan et al., 2016; Arcario et al., 2014).

Implicit ligand sampling (ILS) is an alternative and complementary approach to these flooding simulations to characterize substrate binding and transport pathways in proteins (Cohen et al., 2006; Saam et al., 2007, 2010; Y. Wang et al., 2007; Y. Wang & Tajkhorshid, 2010). Rather than explicitly simulating copies of the substrate, ILS is a post-processing method where substrates are probed to see if they would fit and bind favorably in different regions of a dense grid during a substrate-free simulation. ILS is most suitable for small hydrophobic gases, such as O₂, NO and CO₂, since the approach implicitly assumes that there are no strong interactions between the substrate and protein that might perturb the overall protein structure dynamics (Cohen et al., 2006). In this manner, ILS can be viewed as “systematic docking”, in that snapshots of the protein taken from a trajectory of MD simulation in the absence of a targeting molecules may be used to quantitatively identify high affinity sites for substrate binding over the entire structure (Fig. 7). ILS has been successfully employed to study gas transport in membrane proteins, which include aquaporins (Y. Wang et al., 2007; Y. Wang & Tajkhorshid, 2010) and bioenergetic proteins (photosystem II and cytochrome c oxidase) (Vassiliev et al., 2013; Mahinthichaichan et al., 2016).

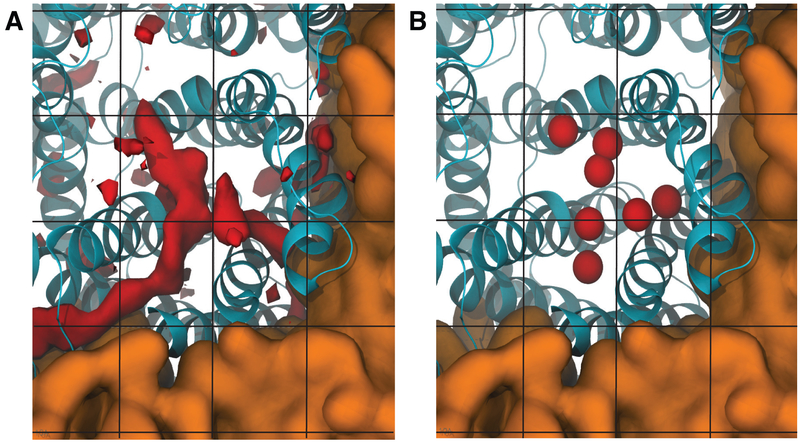
Figure 7.

Probing substrate binding sites and pathways using Implicit Ligand Sampling (ILS) technique. (A) Substrate binding sites predicted by ILS are shown in red isosurfaces. Blue helices represent the protein. The brown surface represents lipid bilayer. Black lines represent the grid on which the substrate is placed systematically during ILS analysis. (B) Experimental observed substrate binding sites taken from crystal structures. Substrates are shown in balls.

Substrate Binding Pathway and Mechanism from Biased Simulation

Binding and particularly unbinding are relatively rare events in the lifetime of a transporter. Over a transport cycle of approximately 10 ms, a small substrate such as a sugar will travel ~ 1 μm if left to freely diffuse, and so transporters bind their substrates tightly to confine the substrate during the cycle. Thus the barrier to unbinding is sufficiently high such that equilibrium MD may not capture and unbinding event. Similarly, the high entropy of a single substrate in solution can render binding too slow of a process to capture with equilibrium MD. By applying forces in addition those of the force field, the membrane binding and unbinding process can be examined in detail.

The simplest of these approaches is steered molecular dynamics (SMD, Fig. 3B), where a force is applied to induce a change within the simulation, in this case to force the binding or unbinding of the substrate. SMD comes in two major flavors, a constant force mode that was originally implemented, and a constant velocity mode analogous to that adopted in atomic force miscroscopy (AFM) which records the force required over a chosen pathway. In order to be consistent with an AFM setup, the pulling reaction coordinate should be in a constant direction, although the freedom of working in silico permits other reaction coordinates to be explored as well that might better reflect the unbinding or binding reaction coordinate, such as coordination number or the distance to a binding site (Fiorin et al., 2013; Tribello et al., 2014). In either context, the choice of a proper force constant determines the accuracy of the SMD simulation. The force constant must be high enough so that the free energy barrier for the substrate transport in the membrane transporter is overcome, but ideally not so high that the measurement is far from equilibrium (Isralewitz et al., 2001). A common rule of thumb is to make sure that the thermal fluctuations as a result of pulling lies in the order of 0.5 Å (Isralewitz et al., 2001).

For SMD, it is critical to think statistically. A single SMD pull has limited significance in elucidating the binding and unbinding pathway. The nonequilibrium work from repeated pulls places an upper bound on the free energy difference of the process at hand (Jarzynski, 1997), thereby providing a method by which different candidate pathways can be evaluated. For as far as is possible, these pulls should start from different starting configurations, such as by taking different timepoints from a trajectory as the starting point for individual pulls.

SMD does not overcome the fundamental problem of equilibrium simulation however, in that high energy states are still only rarely sampled. To sample these rarely visited states of a binding process, an additional external potential can be added to constrain the reaction coordinate to force sampling of a small region of reaction coordinate space (Kästner, 2011), typically taken along a SMD trajectory to seed the initial positions (Fig. 3B). Since the added potential is known, the underlying free energy profile near this highly sampled region can be deduced through self-consistently solving for the unweighted free energies given the weighted population distribution in each local environment. By repeating this procedure for many adjacent regions of reaction coordinate space, the total free energy profile can be estimated in a self-consistent manner (Kumar et al., 1992) via a number of different packages (Grossfield, 2013; Hub et al., 2010; Chodera et al., 2007). Since the individual applied potential looks like an umbrella, and each “umbrella” spans a region of the reaction coordinate, this sampling method is called umbrella sampling (Torrie & Valleau, 1977).

Setting up umbrella sampling calculations to study substrate binding to transporters requires carefully balancing the force constants used to add the external, usually harmonic, potential. If the force constant is too weak, the underlying potential energy surface can overpower the biasing potential, causing specific regions of the free energy landscape to be undersampled that remain too high in energy to be thermally accessible. If the force constant is too strong, each umbrella will span only a small amount of the reaction coordinate. Since the sampled regions must overlap for a complete profile, strong force constants can dramatically increase the computational cost by forcing additional umbrellas to be placed in undersampled gaps. Umbrella placement and strength can be approached algorithmically (Sabri Dashti & Roitberg, 2013), although as a rule of thumb, the spacing between adjacent umbrellas should be such that the potential bias is ~3kT at the center of the adjacent umbrellas.

A more modern development in the field has been the proliferation of replica exchange umbrella sampling (REUS) studies, based on studies by Sugita et al. (2000), where the biasing potentials are exchanged over the course of the simulation set. The goal of this approach is to overcome a shortcoming of conventional umbrella sampling studies, where the simulations may be exploring conformational space orthogonal to the measured reaction coordinate, thereby changing the free energy profile in a hidden way (Neale et al., 2008). Replica exchange methods eliminate the effect of these hidden degrees of freedom, and can dramatically accelerate free energy profile convergence (W. Jiang et al., 2012; Kokubo et al., 2013).

Less structured exploration methods have also been employed to study substrate dynamics in membrane transporters, namely metadynamics (Laio & Parrinello, 2002) and the adaptive biasing force (ABF) method (Darve & Pohorille, 2001; Darve et al., 2002). The basic approach in these biased sampling techniques is to smooth the energy landscape of the system along a predefined reaction coordinate by the addition of biases during the simulation that let the system overcome energetic barriers, with the goal of uniformly sampling the entire reaction coordinate (Darve et al., 2008). One advantage of these methods over umbrella sampling is that they can be significantly cheaper computationally, requiring only a single simulation to produce a result. However the robustness of both methods improves substantially with multiple copies, whose results can be agglomerated into a single free energy profile (Raiteri et al., 2006; Minoukadeh et al., 2010).

Alchemical Perturbation Applied to Substrate Binding

There are times when rather than an unbinding or binding process, the relative or absolute binding free energies are the critical observable comparable to experiment (Chipot & Pearlman, 2002; Chipot & Pohorille, 2007). For example, many transporters use ionic gradients to fuel their transition, and so the relative affinity of two similar ions (eg. Na⁺ or Li⁺) may be the quantity of interest (Thompson et al., 2009). Alchemical method such as free energy perturbation (FEP) (Zwanzig, 1954) and thermodynamic integration (TI) (Kirkwood, 1936) exploit the fact that free energy is a state function (i.e., it is path independent) by computing a free energy difference from in silico alchemical transmutation to complete a thermodynamic cycle (Pohorille et al., 2010). By carefully choosing the thermodynamic cycle, complicated absolute (Fig. 3C) or relative (Fig. 3D) binding free energies can be computed far more efficiently than via other methods (Tembre & Cammon, 1984; W. L. Jorgensen & Thomas, 2008).

From the perspective of membrane transporter binding calculations, there is very little difference between FEP and TI methods, and the two methods become equivalent in the limit of infinitesimal step sizes (Christ et al., 2010; W. L. Jorgensen & Thomas, 2008). They differ in their formalism of how the free energy difference is computed, but generally speaking both operate by slowly decoupling one set of atoms from the calculation while coupling an originally decoupled set of atoms. The progress of this alchemical process is characterized by the scaling parameter λ, which varies between 0 and 1 to represent the initial and final states (Beveridge & DiCapua, 1989). This setup makes the free energy change a continuous function of λ between the initial and final states (Frenkel & Smit, 2002). The intermediate values of λ must be chosen for both methods, and are frequently not equally spaced between the end points, as the largest free energy changes occur when a particle is being grown into or out of existence, where the non-bonded interactions may introduce large values as the weakly-coupled atoms overlaps with other atoms in the system (Goette & Grubmüller, 2009). These “end-point catastrophes” (Lu et al., 2004) are generally handled by altering the non-bonded interactions when λ is near extrema, however it is still a good idea to sample more in these regions (W. L. Jorgensen & Thomas, 2008).

The principle differences between FEP and TI comes in analysis. FEP takes discrete steps, and so one basic estimate of the error comes from taking the steps forward (from λ = 0 to λ = 1) and backward (from λ = 1 to λ = 0) and evaluating the hysteresis (W. Jorgensen & Ravimohan, 1985). This approach is implemented with the ParseFEP tool in VMD to analyze NAMD simulations (Liu et al., 2012), and other MD packages have other tools such as g_bar in GROMACS (Pronk et al., 2013) to evaluate the output of alchemical simulations.

Emerging Techniques to Simulate Large-Scale Structural Transitions in Membrane Transporters

Large-scale structural transitions are perhaps the defining functional features of membrane transporters, enabling them to regulate the accessibility of their binding site(s) to one side of the membrane at a time and allowing a chemical energy source to be used to drive the uphill motion of substrates. Unfortunately, while conventional MD simulation is well suited to work out the details of the interactions that might drive these processes, the millisecond or (often) longer time scales required for large-scale conformational changes rule out unbiased equilibrium MD simulation as a technique for studying these changes. We present here a recently developed procedure (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015) involving an array of advanced nonequilibrium MD techniques that can be used to study these conformational changes. In essence, this procedure simplifies to the following set of steps:

1. Obtain atomistic models of the states.

2. Choose collective variables and biasing protocols to drive the system from one state to another.

3. Relax the transition pathway with a refinement technique.

4. Sample along the pathway to obtain a free energy profile.

5. Analyze the profile quality and return to Step 2 if need be.

Defining Target End States

Before any kind of transition can be investigated, the end states of that transition must be defined. For a few transporters (e.g., a glutamate transporter homolog called Glt_ph (Yernool et al., 2004; Reyes et al., 2009) and a bacterial ABC exporter called MsbA (Ward et al., 2007)), X-ray crystal structures have captured the transporter in multiple states in their transport cycles. In these select few cases, two crystal structures can be used as the end states, and the conformational transition between the structures can be investigated. However, for most transporters, X-ray crystal structures are only available for a single state, so the structure of a second state must be modeled before the large-scale structural changes can be investigated. There are currently two main approaches available to model unknown states in transporters: homology modeling and repeat-swap modeling.

Homology modeling is a general tool in which an unknown structure for a protein is generated using a known structure of a homologous protein as a template (Martí-Renom et al., 2000). Homology modeling can be performed by many programs, and MODELLER (Webb & Sali, 2014) and SWISS-MODEL (Biasini et al., 2014) are popular examples. While the specific techniques used by different software packages differ, the basic procedure they use is the same (Martí-Renom et al., 2000). First, a sequence alignment is used to identify corresponding portions of the two proteins. The local conformations of these portions in the protein with unknown structure are then made to match the conformations in the template, which causes the global conformation of the entire protein to approximately match that of the template. Finally, the resulting model is refined to increase its quality (e.g., by eliminating steric clashes between residues).

Recently, it has been found that many transporters are composed of pairs of pseudo-symmetric structural elements called inverted repeats (Forrest et al., 2008; Crisman et al., 2009; Vergara-Jaque et al., 2015). When inverted with respect to the plane of the membrane, the topology of one repeat is (nearly) identical to the topology of the other (Fig. 8A). While their topologies are (nearly) identical, the conformations of the repeats are quite different, and it has been shown that swapping the conformations of the repeats will swap the overall conformation of the transporter from an IF to OF state or vice versa (Fig. 8B) (Forrest et al., 2008; Crisman et al., 2009; Vergara-Jaque et al., 2015). The sequence similarity between the individual repeats is usually fairly low, but it is high enough that homology modeling techniques can be used to swap the conformations of the repeats (Forrest et al., 2008; Crisman et al., 2009; Vergara-Jaque et al., 2015). Once the conformations of the repeats have been swapped, the repeats can be fit back together, and the resulting global conformation of the model can be empirically refined to generate a model of a missing state in a transport cycle (Forrest et al., 2008; Crisman et al., 2009; Vergara-Jaque et al., 2015).

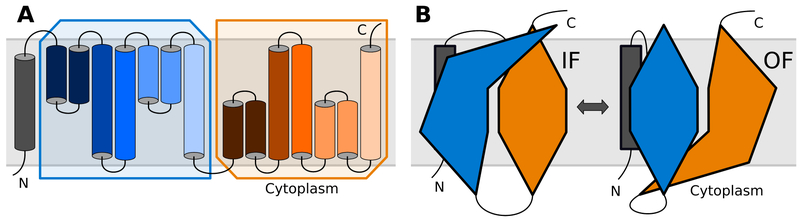
Figure 8.

Schematic of the inverted repeats of a transporter. (A) The topologies of the inverted repeats, boxed in blue and orange, are identical when inverted with respect to the plane of the membrane. The color lightness of the helices can be used to identify corresponding helices in the two repeats. (B) In any given state, the conformations of the repeats differ. When the IF conformations of the repeats are swapped, they form the OF state and vice versa.

Before investigating the transition between a known and a modeled state, rigorous investigation of the quality of the modeled state is essential. If the modeled state does not correspond sufficiently well to a physiological state visited by the transporter, the subsequent steps involved in this procedure will yield results that are of limited value at an extremely high computational cost. Standard modeling techniques attempt to maximize the internal quality of the model but cannot take into account the transporter’s environment. The stability of any model in the context of a membrane should be verified through equilibrium simulations (Moradi et al., 2015). If the quality of the model is not sufficient, it is common for the transporter to revert from the modeled state back to the known crystallographic state within a few dozen nanoseconds of simulation.

Generating a Biasing Protocol to Induce Transporter Transitions

One common way of inducing a structural transition is through a targeted MD (TMD) simulation, which makes use of the root-mean-square displacement (RMSD) of a selection of atoms in the transporter (Schlitter et al., 1993; Fiorin et al., 2013). RMSD is a common measure of differences in protein conformations (the lower the RMSD, the more similar the conformations) and is calculated using the equation$\sqrt{\frac{1}{N}{\sum }_j\Vert {\mathbf{x}}_j-{\mathbf{x}}_j^{\prime }{\Vert }^2},$, where N represents the number of atoms in the selection, x_j represents the 3D coordinates of atom j in one conformation, and ${\mathbf{x}}_j^{\prime }$ represents the 3D coordinates of the atom in a reference conformation. When an RMSD calculation is performed for large-scale conformational differences, only the protein’s heavy or C_α backbone atoms are selected, as side chain rotations and the movement of lighter atoms are small-scale conformational changes that may obscure the progress of the global transition. In a TMD simulation, the starting conformation is driven to the final (target) conformation by inducing a linear reduction of the RMSD, measured with reference to the target conformation, from its initial value to zero (Schlitter et al., 1993; Fiorin et al., 2013). This is done by applying forces to the selected atoms, and the forces are calculated using the gradient of a harmonic energy potential of the form $U=\frac{k}{2}(\zeta -{\zeta }^{\prime }{)}^2$ (Schlitter et al., 1993; Fiorin et al., 2013). Here, k is a user-specified force constant, ζ represents the RMSD of the transporter’s conformation and ζ′ represents a target RMSD value that changes throughout the simulation.

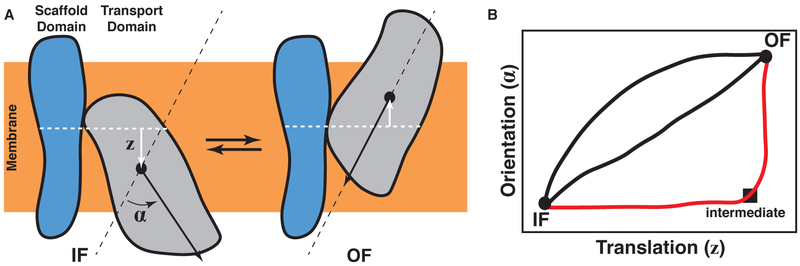
The TMD approach of investigating transporter transitions is popular due to its simplicity, but its use commonly results in transitions that approximately correspond to linear interpolations between the end states. Unfortunately, such transitions are often inconsistent with the alternating-access mechanism (i.e., substrate is accessible from both sides of the membrane at the same time), which makes them nonphysiological and therefore of limited scientific value (Moradi & Tajkhorshid, 2013, 2014). To avoid this problem, it is better to induce changes in ways specific to the transporter under investigation. By investigating the large-scale differences in conformation between the two end states and any experimental clues about the structural nature of the transporter’s mechanism, one can qualitatively predict the kinds of motion that must be induced in the transporter to transition it from one state to the next (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015). To induce these motions in a simulation, forces derived from harmonic potentials involving so-called “collective variables” (i.e., reaction coordinates) can be applied to the atoms in the transporter in the same way as is done with RMSD in TMD simulations (Fiorin et al., 2013). Generally, a collective variable is a quantity that is calculated from the positions of the atoms and is used to represent a specific conformational element in the transporter (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015). Besides RMSD, examples of collective variables include distances between centers of mass of two atom selections within the transporter along a user-defined axis, which can be useful for translating the selections with respect to one another, and the orientation quaternion (Coutsias et al., 2004; Horn, 1987; Fiorin et al., 2013), which quantifies the differences in orientation between two states (Fig. 9A).

Figure 9.

Two important considerations in the design of a biasing protocol. (A) The choice of collective variables. The differences between an exemplary IF and OF state are decomposed into two collective variables. One, z, represents the position of the center of mass of the transport domain relative to the center of mass of the scaffold domain along the membrane normal axis. The other, α, represents the change in orientation of the transport domain. (B) The choice of the transition pathway. Three possible transition pathways are shown in the collective variable space. If a crystal structure or other experimental evidence identified an intermediate state, two of the transition pathways could immediately be eliminated from consideration.

By modeling each of the structural differences between the end states with a separate collective variable, one can represent these structural differences quantitatively and induce the predicted motions associated with the transporter’s mechanism using a biasing protocol. Nonequilibrium driven MD simulations are defined by the biasing protocols they use, which include the set of collective variables utilized to induce transitions as well as the parameters associated with the applied harmonic potentials. Transporters’ large-scale structural transitions are complex, so it is necessary to test a variety of biasing protocols to refine initial mechanistic predictions and to find good candidates for transition pathways through the collective variable space (Fig. 9B). Three criteria are used to judge the quality of a biasing protocol and the associated transition pathway (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015). First, it is necessary to check whether the desired conformational changes were actually induced by the biasing protocol by ensuring that the collective variables reach their final target values during the simulation. Second, the functional relevance of the pathway should be verified. For example, the pathway must be consistent with the alternating-access mechanism, and unphysical deformations of the membrane (which tend to arise as a result of inducing large-scale conformational changes in unrealistically short time scales) should be minimized. Finally, the nonequilibrium work required to induce the transition (defined as $W(t)={\int }_0^t\frac{\partial U(t^{\prime })}{\partial t^{\prime }}d{t}^{\prime }$ should be minimized. A pathway that reproducibly requires less work corresponds to a pathway with a lower free energy barrier between the end states. The lower the free energy barrier, the easier and more likely it is for the transporter to use the associated pathway in reality.

Several refinements to the initial biasing protocol can and should be made when investigating a transition pathway. For example, the initial choice of collective variables may not adequately represent the conformational elements of the transporter, in which case different collective variables will need to be tested. The ideal force constants k associated with the harmonic potentials must also be determined empirically for each collective variable (Moradi & Tajkhorshid, 2013, 2014). Force constants should be high enough that the desired conformational changes are induced but low enough that the transporter has some freedom to avoid high energy barriers (e.g., steric clashes) and keep the work low. With the choice of collective variables and force constants established, changes in the collective variables should be induced in different orders and at different rates, and transitions that explore a variety of areas in the collective variable space should be tested (Moradi & Tajkhorshid, 2013, 2014). The relative quality of different pathways is never known a priori, so it is necessary to be as comprehensive as possible in this exploratory phase. It must be stated that the extreme complexity involved in this problem necessarily prohibits one from conducting a systematic search to find an ideal biasing protocol and transition pathway. There are an infinite number of possible biasing protocols that use different combinations of collective variables and induce changes in them in unique ways. Intuition and knowledge of the transporter are the best guides for empirically designing a finite number of biasing protocols that have the best chance of capturing an acceptable transition pathway (Moradi & Tajkhorshid, 2013, 2014).

Due to the number of different biasing protocols that should be tested (e.g., ~ 200 in previous transporter studies (Moradi & Tajkhorshid, 2013, 2014)), it is advisable that preliminary simulations be made quite short (~ 5ns). Progressively fewer candidate transition pathways can be extended to longer and longer simulation time scales as the best pathways are identified at shorter time scales. Also, since these simulations are stochastic, the best candidate biasing protocols should be repeated several times to ensure their best qualities (especially low work) are reproducible (Moradi & Tajkhorshid, 2013, 2014). Before proceeding to the following steps involved in characterizing a transition pathway, it is advisable to reduce the work to less than ~100 kcal·mol⁻¹. This is desirable because reducing the work required by the transition in this step greatly reduces the computational cost of subsequent steps. Once a satisfactory biasing protocol and transition pathway have been found, the pathway can be refined using a more advanced computational technique.

Refining the Transition Pathway

Refinement of the transition pathway found in the previous step can be accomplished by applying a path refinement technique like the string method with swarms of trajectories (SMwST). SMwST is a method that relaxes the initial pathway to the nearest minimum free energy pathway through the following steps (Pan et al., 2008; Gan et al., 2009). First, a set of images (i.e., conformations) are obtained at evenly spaced intervals along the initial pathway. Distances along the pathway are calculated using a metric (e.g., weighted Euclidean distance) based on the collective variables used in the driven transition. Multiple independent copies of the images (swarm of trajectories) are then harmonically restrained near their initial collective variable values before being released into short equilibrium simulations. The average drift observed during the equilibrium simulations is used to calculate a new image center for each swarm of trajectories, and the positions of the image centers are refined such that they remain evenly spaced along the new relaxed pathway. Iterations of this restrain-release cycle are performed until the pathway has converged and no longer changes (Fig. 10). A convenient method of evaluating the convergence of SMwST is through the use of the the Fréchet distance, which is able to quantify the similarity between two curves (W. Jiang et al., 2014; Seyler et al., 2015).

Figure 10.

Schematic representation of SMwST. A series of paths, iteratively refined by SMwST, connecting two minima in a schematic 2D free energy surface are shown. The color gradient represents different iterations, while the red line represents the converged lowest free energy path.

In a recent study on the large-scale conformational changes in a transporter called GlpT (glycerol-3-phosphate:phosphate antiporter), 50 images along the initial pathway were used, and 20 copies per image were simulated (Moradi et al., 2015). In each iteration, the copies were restrained for 5ps and released for 5ps, and ~20 iterations were required for convergence (Moradi et al., 2015). Such a small number of iterations was required due to the high quality (low free energy) of the initial pathway. Because SMwST is so computationally expensive, careful refinement of the initial transition pathway by evaluating a variety of different biasing protocols should be performed before using SMwST. SMwST is also quite sensitive to the collective variables used, so great care should be taken to ensure that the collective variables chosen in the previous step adequately capture the transporter’s motion (Moradi & Tajkhorshid, 2014). Finally, it is worth noting that a convenient feature of SMwST is that it can be implemented either serially or in parallel (Moradi et al., 2015). That is, each transporter copy associated with each window can either be simulated one after the other on a small computing cluster or at the same time on a massive supercomputer.

Obtaining a Free Energy Profile

As described previously, US is a technique that is used to obtain free energy profiles and other thermodynamic information through enhanced conformational sampling along a reaction coordinate. By using the refined transition pathway found previously as the reaction coordinate, US can be applied not only to binding processes but also to the structural changes involved in transport cycles. To obtain an accurate free energy profile along such a transition pathway, it is essential to use REUS since there are many orthogonal degrees of freedom in the transporter that are not directly sampled. When REUS is applied to large-scale conformational changes in transporters, it is more commonly called bias-exchange umbrella sampling (BEUS) (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015). Just as for a conventional US calculation, the number of umbrellas and force constants applied during a BEUS simulation are important parameters, and empirical or systematic efforts to optimize them must be made. Additionally, all umbrellas should have roughly equal exchange rates with their neighbors in a BEUS simulation to ensure convergence of the free energy profile (Moradi & Tajkhorshid, 2013, 2014; Moradi et al., 2015). Once the BEUS simulation has been run, the free energy profile along the pathway can be reconstructed using the Weighted Histogram Analysis Method (WHAM) (Kumar et al., 1992), a method which is considered standard, or other techniques (H. Wu et al., 2014; Shirts & Chodera, 2008). If multiple transition pathways within a transport cycle are investigated, it is possible to structurally elucidate and thermodynamically characterize the entire transport cycle for a transporter. Using this approach, an engineered cycle for GlpT, composed of three natural transition pathways from the transport cycle and one that is considered forbidden, has recently been characterized. (Moradi et al., 2015). In Fig. 11, a schematic of the engineered cycle is shown alongside the free energy profile obtained for the entire cycle. Importantly, the location and height of major barriers in this profile are quantitatively available, and it is clear that the structural transition induced along the natural pathways is significantly more energetically favorable than the one induced along the forbidden pathway.

Figure 11.

Thermodynamic characterization of the transport mechanism of GlpT. Adapted from (Moradi et al., 2015). (A) Schematic representation of the engineered cycle with gating helices highlighted in pink and blue. The substrate is inorganic phosphate (P_i), and the cycle consists of transitions between four states: the apo OF (OF_a) and IF (IF_a) states and the bound OF (OF_b) and IF (IF_b) states. (B) Free energy profile along the entire cycle with the important states denoted explicitly.

Before the free energy profile resulting from a BEUS simulation can be considered accurate, the BEUS data must first be analyzed for poor sampling, which would make the free energy profile unreliable. If poor sampling is observed along any of the collective variables used, a better biasing protocol must be employed (Moradi & Tajkhorshid, 2014). Evaluation of sampling is fairly straightforward, as one simply needs to create a histogram, using a collective variable as the independent variable for the plot, from the conformations visited in the BEUS simulation and verify that it is uniform over the range of collective variable values between the end states (Moradi & Tajkhorshid, 2014). Whether or not poor sampling along one of the collective variables is observed, it is also useful to identify the important degrees of freedom present in the BEUS simulation. One way this can be done is by using principal component analysis (PCA) (Amadei et al., 1993), which is a method used to determine the orthogonal combinations of degrees of freedom that show the greatest variation within a data set, on the conformations generated in the BEUS simulation. If n collective variables were used in a biasing protocol, the first n principal components (PCs) should correspond roughly to these collective variables (Moradi & Tajkhorshid, 2014). If more than n significant PCs are found, the result indicates that there are combinations of degrees of freedom that must be accounted for to ensure reliable sampling (Moradi & Tajkhorshid, 2014). To account for these degrees of freedom, collective variables must be added to a revised biasing protocol, the steps required to obtain a new free energy profile must be completed, and PCA must be performed once more.

In addition to BEUS simulations along a refined pathway, which are inherently one dimensional, it is also possible to perform multidimensional BEUS simulations to obtain informative free energy landscapes. While more general configurations are possible, these landscapes are most commonly generated by performing two dimensional (2D) BEUS simulations on a rectangular grid (Moradi & Tajkhorshid, 2014). Due to the computational cost associated with such simulations, only approximate free energy landscapes can be generated (Moradi & Tajkhorshid, 2014). Before such a simulation can be performed, the collective variables that represent the transporter’s important structural elements must be well established, but an extensive exploration of the collective variable space does not need to have been performed. A 2D BEUS simulation can either be used to guide pathway exploration, or it can be used after exploration is finished to generate a more complete understanding of the thermodynamics that govern the transporter’s transition. To set up a 2D BEUS simulation, conformations corresponding to the points in the BEUS grid must be generated, and the grid points must be spaced following the same considerations as for 1D BEUS simulations. If large areas of the collective variable space have been explored during pathway exploration, these grid conformations can be generated by driving nearby conformations from previous simulations to the grid points. If such data is not available, conformations representing the grid points can also be generated systematically using driven simulations. After verifying the quality of the sampling and reconstructing the free energy landscape, one can then identify the minimum free energy path connecting any two points in the landscape using a variety of path-finding algorithms (Moradi et al., 2015), and this path can be further refined using SMwST.

The Direction of Future Membrane Protein Studies

The membrane protein field is progressing rapidly, currently experiencing exponential growth in the number of available 3D structures of distinct membrane proteins (White, 2009). With the growing success of cryo-EM in determining membrane protein structures to high resolution (Vinothkumar, 2015), this trend is expected to continue for the foreseeable future. Similarly, the methods of the modeling community will not remain static. While much of the groundwork for current simulation techniques was established in the 1990’s, the continued advancement of computing power granted by Moore’s Law, replica exchange and other enhanced sampling techniques have become much more common and have become far more routine to a degree not foreseen even a few years ago.

The wealth of available structural information is also pushing simulation in new directions. For instance, crowding on the membrane surface is generally currently neglected, despite suggestions that interplay between different membrane actors is critical to membrane protein function in general (R. Phillips et al., 2009; Guigas & Weiss, 2015) and to understand cellular membrane topology (Stachowiak et al., 2012). This will require a substantial increase in the simulation scope in the years to come, as the community moves from studying individual transporters to collective action by the membrane-embedded community of proteins.