Modelling Sex-Specific Crossover Patterning in Arabidopsis

Males and females of many organisms show distinct patterns of inheritance. Here, Lloyd and Jenczewski model crossover patterning in Arabidopsis to gain insights into what causes the large differences in recombination rates and patterns...

Abstract

“Interference” is a major force governing the patterning of meiotic crossovers. A leading model describing how interference influences crossover patterning is the beam-film model, a mechanical model based on the accumulation and redistribution of crossover-promoting “stress” along the chromosome axis. We use the beam-film model in conjunction with a large Arabidopsis reciprocal backcross data set to gain “mechanistic” insights into the differences between male and female meiosis, and crossover patterning. Beam-film modeling suggests that the underlying mechanics of crossover patterning and interference are identical in the two sexes, with the large difference in recombination rates and distributions able to be entirely explained by the shorter chromosome axes in females. The modeling supports previous indications that fewer crossovers occur via the class II pathway in female meiosis and that this could be explained by reduced DNA double-strand breaks in female meiosis, paralleling the observed reduction in synaptonemal complex length between the two sexes. We also demonstrate that changes in the strength of suppression of neighboring class I crossovers can have opposite effects on “effective” interference depending on the distance between two genetic intervals.

MEIOTIC crossovers (COs) shuffle parental genetic information generating new combinations of alleles. In most species, the presence of one CO inhibits nearby CO formation, so that the distances between COs are greater and more uniform than if placed at random. This phenomenon, CO interference, was first noted in genetic studies over a century ago (Sturtevant 1915; Muller 1916); however it is only in the last few years that insights into its mechanistic basis have begun to surface.

The inhibitory effect of interference is thought to spread a defined distance along the chromosome axis, a linear proteinaceous structure formed by each chromosome at the base of the chromatin loop array in early prophase [reviewed Zickler and Kleckner (2015)]. By midprophase, homologous chromosome axes are joined by additional proteins comprising the transverse filament and central element to form the synaptonemal complex (SC). Although the interference signal likely propagates prior to polymerization of the SC (Zickler and Kleckner 2015), the distance across which interference spreads is usually specified in micrometers SC, as SC length is easier to measure cytologically and is proportional to the length of the axis prior to synapsis. In yeast, interference is, at least in part, mediated by Topoisomerase II (Zhang et al. 2014b), and wild-type levels of interference require small ubiquitin-like modifier (SUMO)ylation of TopoII and the axis component Red1/Asy3, as well as ubiquitin-mediated removal of SUMOylated proteins (Zhang et al. 2014b). These findings are consistent with suggested roles for the chromosome axis and local stress relief via DNA remodeling in mediating interference.

Several approaches have been used to model crossover (CO) patterning, the most notable being the γ model and the beam-film model. The γ model is a statistical model based on the observation that the distances between two COs are relatively uniform, following a γ distribution (McPeek and Speed 1995; Broman and Weber 2000; Housworth and Stahl 2003). Under this model “effective interference strength” is highest when distances between COs show the least variation. This results in a large value of the γ shape parameter.

In contrast, the beam-film model is a mechanistic model whose various parameters have biological correlates (Kleckner et al. 2004; Zhang et al. 2014a). In the beam-film model, each bivalent has a number of “precursor” sites [double-strand breaks (DSBs)] that are subject to mechanical stress. CO designation at precursor sites is promoted by stress and this stress is relieved locally following CO designation. As stress promotes COs, stress relief propagating out from CO sites inhibits the formation of additional COs nearby. In the beam-film model, interference strength is highest when stress relief propagates furthest from designated CO sites.

In most species, there are multiple CO pathways. The majority of COs occur via the interference-sensitive class I pathway and are dependent on the ZMM group of proteins identified initially in yeast (Zip1, Zip2, Zip3, Zip4, Mer3, Msh4, and Msh5) (Sym et al. 1993; Ross-Macdonald and Roeder 1994; Hollingsworth et al. 1995; Chua and Roeder 1998; Nakagawa and Ogawa 1999; Agarwal and Roeder 2000; Tsubouchi et al. 2006; Lynn et al. 2007). COs occurring via this pathway are specifically marked by Zip3/Hei10 and MLH1 foci at late pachytene (Agarwal and Roeder 2000; Lhuissier et al. 2007; Chelysheva et al. 2012). A number of secondary “clean-up” pathways repair DSBs not metabolized by the class I pathway (Hollingsworth and Brill 2004; Kurzbauer et al. 2018). These clean-up pathways mostly repair DSBs as non-COs, but also contribute a smaller number of COs (i.e., class II COs). Class II COs are insensitive to interference (Housworth and Stahl 2003; Mercier et al. 2005; Cooper et al. 2018) and usually make up 10–30% of the total CO number (Mercier et al. 2005; Lhuissier et al. 2007; Falque et al. 2009; Cooper et al. 2018). In their simplest forms, the γ and beam-film models deal exclusively with class I COs and several studies have explored CO patterning in yeast using the single-pathway beam-film model (Zhang et al. 2014a,b; Wang et al. 2015; White et al. 2017a).

While the biological processes underlying meiosis and the various recombination pathways are remarkably conserved across eukaryotes (Loidl 2016), differences in CO patterning exist both between and within species (Mercier et al. 2015; Loidl 2016). In Arabidopsis (Giraut et al. 2011), as in many species (e.g., Singer et al. 2002; Tortereau et al. 2012; Gruhn et al. 2013; Phillips et al. 2015), there are marked sex-specific differences in CO patterning. Recombination rates are highest in the male Arabidopsis germline, with particularly high levels of recombination in distal regions (Giraut et al. 2011). In contrast, distal regions have the lowest recombination rates in females (Giraut et al. 2011). Female meiosis has also been reported to have higher levels of interference (Giraut et al. 2011). While these differences have been repeatedly observed (Giraut et al. 2011; Fernandes et al. 2018), there has so far been little insight into the biological factors contributing to them. Beam-film modeling offers an attractive means to provide such insight, through estimating and comparing sex-specific values for the various model parameters, each of which has a biological correlate.

Theoretically, such analyses are possible for both genetic and cytological data. However, while cytological analyses are routine in the Arabidopsis male germline, they remain challenging for female meiosis. In addition, as the number of COs per chromosome is low for female Arabidopsis, well over a 1000 cells would need to be analyzed to achieve the same number of interinterval distances (IIDs; the limiting factor for analyses) commonly reported for yeast chromosomes (Zhang et al. 2014a,b). For this reason, we took advantage of a previously published large Arabidopsis reciprocal backcross recombination data set (∼1500 individuals and ∼380 markers for both males and females) (Giraut et al. 2011). Being genetically derived, this data set comprised COs arising from both the class I and class II recombination pathways.

To identify likely biological determinants of sex-specific differences in Arabidopsis CO patterning, we determined and compared sex-specific parameter values for various beam-film model parameters. In addition, we comprehensively explored the behavior of the two-pathway beam-film model, providing novel insights into how the patterning of class I and class II COs interact to influence patterns of inheritance. Such insights have not been possible from previous beam-film analyses focusing on the single-pathway model.

Materials and Methods

Experimental data

The experimental data set used has been previously published (Giraut et al. 2011) and was derived from large Arabidopsis reciprocal backcross populations. On average, 1505 plants were genotyped for 380 SNPs in the male population and 1507 plants genotyped for 386 SNPs in the female population (380 in common). As the average distance between markers is small in this data set, 316 kb in males and 311 kb in females, the number of double COs (DCOs) in a single interval are expected to be negligible (the average distance between DSBs is ∼480 kb). It was therefore assumed during analysis that all recombination events were identifiable. Genotyping and recombination data sets are provided (Supplemental Material, data sets S1 and S2, respectively).

Beam-film-parameter optimization

Beam-film simulations were performed and best-fit parameters determined using MADpatterns (White et al. 2017a) and custom perl scripts with an approach based on that described in Zhang et al. (2014a). For each chromosome and each sex, at least three rounds of analysis were undertaken. In each round of each analysis, 30,000 bivalents were simulated for a range of parameter values. In the first round, to ensure the full parameter space was sampled, relatively broad value ranges of optimized parameters (Smax: 2–10 L: 0.4–1.7; T2Prob: 0.002–0.008; cL: 0.3–1.3, and cR: 0.3–1.3) were chosen based on values described in Zhang et al. (2014a) and comparison of ad hoc simulations with analysis of experimental data sets (Basu-Roy et al. 2013). Parameters N, B, E, Bs/Be/Bd, A, and M were set at appropriate default values (see below). In the next two rounds, progressively smaller step sizes between values were used to arrive at the final parameter values. Descriptions of each parameter are provided below.

For each round of analysis, the CO distributions, coefficient of co-incidence (CoC) curves, and event distributions (distribution of number of COs per gamete) simulated for each chromosome were determined using MADpatterns (White et al. 2017a), and compared to those obtained for the relevant sex and chromosome from the experimental data set. For CO distributions and CoC curves, each chromosome was split into 13 equal-sized adjacent intervals for analysis. Importantly, the experimental data are gamete data, while the MADpatterns program simulates (and outputs) bivalent data (i.e., all COs on a pair of homologous chromosomes). Therefore, all simulated bivalent CO frequencies were halved to convert to gamete CO frequencies. Bivalent event distributions were also converted to gamete event distributions, assuming random assignment of each CO to two of the four chromatids, i.e., each CO has a 50% chance of being inherited by a gamete arising from that meiosis. Parameter sets were ranked based on the difference between simulated and experimentally determined CoC distributions [Score_CoC = Σ_IID abs(log₂(CoC_sim/CoC_exp))], CO distributions [Score_CO = Σ_Int (CO_sim – CO_exp)²], and event distributions [Score_ED = Σ_Enum (ED_sim – ED_exp)²]. Simulations were ranked for each score and final parameter values chosen were those with the lowest rank-sum. For graphical representation, CoC curves were smoothed using locally estimated scatterplot smoothing (span 0.3–0.5).

Optimized parameters

Beam-film model parameters Smax, L_BF, cL/R, and T2Prob were optimized (see above). Parameters N, B, E, Bs/Be/Bd, A, and M were fixed based on known values of the biological correlates, parameters that tend to be stable between species (Zhang et al. 2014a), or suggested default values (White et al. 2017b). A description of each of these parameters is given below and further explanations can be found in the references. Zhang et al. (2014a), White et al. (2017a).

Beam-film parameters:

The beam-film program requires three kinds of parameters: (1) precursor array parameters, which determine the position and number of potential CO sites (DSBs) along each bivalent; (2) CO patterning parameters that determine which precursor sites become designated CO sites; and (3) the maturation efficiency parameter, which determines the likelihood of designated CO sites maturing to become true COs.

Precursor array parameters:

N: precursor sites per bivalent:

Parameter N sets the number of potential recombination sites or precursors on a bivalent. The biological correlate is the number of meiotic DSBs for that bivalent. For the first round of simulations, we assumed 250 DSBs per meiosis in both males and females. For any given chromosome, N was set to 250 × proportion of total genome size (in megabases) contributed by that chromosome. For modeling of reduced DSB formation in female N, we calculated as above assuming 150 DSBs genome-wide.

B: similarity in total precursor number between bivalents:

B sets the similarity of precursor number between the multiple bivalents simulated for a given chromosome in each round of analysis. Precursor number for any given chromosome was set to be constant for each bivalent simulated (B = 1).

E: evenness of precursor spacing:

There is considerable experimental evidence that DSB spacing is nonrandom, being more evenly spaced than if placed at random (Berchowitz and Copenhaver 2010; Choi et al. 2018). For numerous organisms, a parameter value of 0.6 has been found to be appropriate (Zhang et al. 2014a) and we therefore set E to 0.6 for all simulations (0 = random, 1 = even).

A: intrinsic precursor sensitivities:

In the early steps of the model, each precursor is assigned a “sensitivity,” reflecting the fact that not all DSBs have an equal chance of becoming a CO; local factors, e.g., SNP density, local structural diversity, and the epigenetic landscape, may also influence the fate of each precursor site. Parameter A determines how precursor sensitivities are assigned. For all simulations A was set to 1 – sensitivities assigned from a uniform distribution.

Bs/Be/Bd: recombination “black hole” start/end/precursor density:

Recombination black hole start (Bs) and end (Be) points delineate the start and end of the heterochromatic centromeric region, which has reduced DSB formation. Parameter Bd indicates the relative precursor density of the black hole and was set to 0.01 for all simulations (1 = no reduction in precursors and 0 = no precursor formation). Values were determined based on recombination frequencies observed in the backcross data (Figure S1 and Table S1) and correspond to regions of the Arabidopsis genome with high DNA methylation, low H3K4me3, and reduced DSB formation (Choi et al. 2018).

CO patterning parameters:

Smax: maximum stress level per bivalent:

COs are promoted at precursor sites by CO-promoting stress (S). Smax is the maximum level of stress that a bivalent is subject to during simulation. The biological correlate of the CO-promoting stress is not precisely defined but may relate to the expansion of chromatin during early prophase (Kleckner et al. 2004).

Bsmax: similarity in maximum stress levels between bivalents:

Bsmax sets the similarity of Smax between simulated bivalents and was set to be constant for all simulations (Bsmax = 1).

L_BF: stress-relief distance:

The parameter L_BF corresponds to the length of the chromosomal interval over which a CO relieves stress, i.e., stress relief propagates out from COs a distance of one-half of the L_BF in either direction.

cL/R: left- and right-end “clamping”:

In the beam-film model, clamping at chromosome ends determines how stress is supported in terminal regions. Unclamped chromosome ends (cL = 0; cR = 0) cannot support stress and so locally relieve stress, behaving as if there were a CO at the chromosome end. Clamped chromosome ends (cL = 1; cR = 1) experience stress as elsewhere along the bivalent.

T2Prob: probability that a non-CO designated precursor will form a class II CO:

The parameter T2Prob defines the probability that a precursor site (i.e., an DSB) not designated to become a class I CO will become a class II CO.

Maturation parameter:

M: CO maturation efficiency:

In the beam-film model, it is possible to model failure of CO maturation. If failure occurs, the CO-designated site inhibits nearby COs but does not itself develop into a CO. We assumed 100% CO maturation efficiency for all simulations (M = 1).

DCO class determination:

The proportion of each class of DCO for a given IID was determined from simulations modeling for the formation of class I COs only (T2Prob = 0), class II COs only (Smax = 0), or both class I and II COs. For each simulation, numbers of DCOs were tallied for each IID (the distance between a pair of genetic intervals). For each IID, numbers of DCOs involving two class I COs (DCO_{I_I}), two class II COs (DCO_{II_II}), or all DCOs (DCO_ALL) were calculated from the respective simulations. DCO_{I_II} = DCO_ALL – (DCO_{I_I} + DCO_{II_II}).

Response of model to parameters L, Smax, T2Prob, and N:

To investigate the response of the model to parameters L, Smax, and T2Prob, we simulated 30,000 bivalents for an “idealized” male Arabidopsis chromosome (N = 60, B = 1, E = 0.6, Bs = 0.45, Be = 0.55, Bd = 0.01, Smax = 9, Bsmax = 1, A = 1, L = 0.7, cL = 0.8, cR = 0.8, M = 1, and T2Prob = 0.004) as described above, varying one specified parameter.

Data availability statement

Data set S1 contains male and female genotyping data originally reported in Giraut et al. (2011). Data set S2 contains male and female recombination location data. Code used for parameter optimization is available at https://github.com/andrewhmlloyd/BeamFilmBestFit. Supplemental material available at Figshare: https://doi.org/10.25386/genetics.7610921.

Results

Beam-film simulations replicate CO patterning in Arabidopsis

To determine the likely biological determinants of differences in CO patterning between male and female meiosis, we compared beam-film-parameter estimates obtained for the two sexes. To obtain these estimates, we ran a series of beam-film simulations using a broad range of parameter values and compared simulated recombination data to our experimental data set. Independent simulations were run for each of the five Arabidopsis chromosomes for each sex. Parameter best-fits for each chromosome and sex were then obtained by comparing CO number and distribution, and interference relationships (CoC curves) of simulated recombination and experimental data (Figure 1, and Figures S1 and S2). Global parameter estimates were then derived for male and female meiosis by averaging the individual estimates of the five chromosomes (Figure 2). As parameter estimates for male and female meiosis are drawn from the same parameter space, the female best-fit simulations are an example of a parameter set that did not fit the male data and vice versa. Figure S3 shows several other examples.

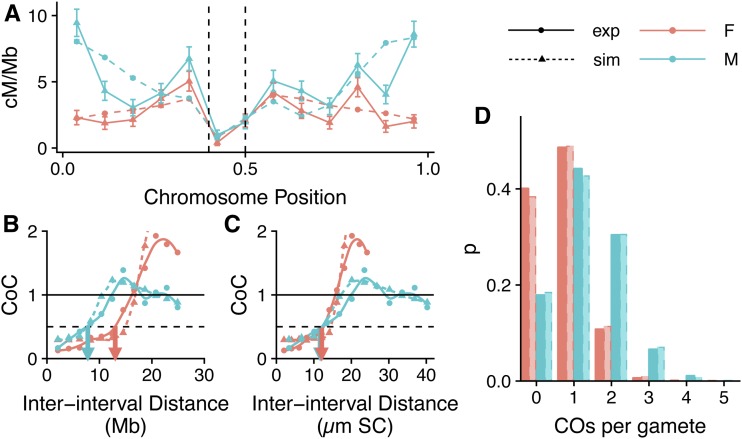
Figure 1.

CO analysis for Arabidopsis chromosome 5. Each analysis includes experimental (solid lines) and simulated (dashed lines) data for males (blue) and females (orange). (A) CO distributions for Arabidopsis chromosome 5. Vertical dashed lines represent the limits of the centromeric region over which precursor (DSB) number is markedly reduced, both biologically (Choi et al. 2018) and during simulations. Error bars indicate 95% C.I.s. (B and C) CoC curves for chromosome 5 with IID (the distance between a pair of genetic intervals) measured in megabases (B) or micrometers SC (C). L_CoC for males and females (blue and orange arrows, respectively) differed when IIDs were measured in megabase but not when measured in micrometers SC. (D) Event distribution for chromosome 5. Male and female simulations shown assume 250 DSBs genome-wide. Chromosomes were divided into 13 equal-sized adjacent intervals for analysis. CO, crossover; CoC, coefficient of co-incidence; DSB, double-strand break; exp, experimental; F, female; IID, interinterval distance; M, male; SC, synaptonemal complex; sim, simulated.

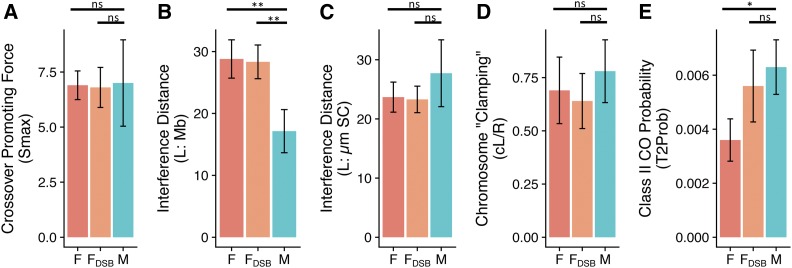
Figure 2.

Beam-film best-fit parameter estimates. (A) Estimates of CO-promoting force (Smax) were identical for males and females with 250 DSBs (M and F, respectively) and females with 150 DSBs (F_DSB). Estimates of interference distance (L) were longer in males when measured in megabases (B) but not significantly different when measured in micrometers SC (C). (D) There was no significant difference in estimates of chromosome clamping. (E) The probability of nonclass I-designated precursors becoming class II crossovers was estimated to be lower in females than males if both sexes had 250 DSBs, but not significantly different if there were reduced DSBs (150) in females. For each parameter and condition, the mean of the estimates for the five chromosomes is shown. Error bars indicate 95% C.I. * P < 0.05 and ** P < 0.01, after Bonferroni multiple comparison correction. CO, crossover; DSB, double-strand break; F, female; M, male; ns, not significant; SC, synaptonemal complex; Smax, maximum stress level per bivalent; T2Prob, probability that a non-CO designated precursor will form a class II CO.

CO distribution:

Simulated CO distributions using optimized parameter sets reproduced CO distributions observed in the experimental data. Simulations captured the broad-scale trends, rather than fine-scale differences in CO frequency. Highest recombination in males was found in distal regions and highest recombination in females in regions adjacent to the centromere (Figure 1 and Figure S1). The exception was the short arms of chromosomes 2 and 4 in males, which have high experimental recombination rates but had low levels of recombination when simulated using the global best-fit parameters (Figure S1). It is possible that this is related to the presence of nucleolar organizer regions on the short arms of these two chromosomes, which are not explicitly modeled in simulations.

CoC curves:

The CoC is the ratio of the observed and expected numbers of DCOs for a given pair of intervals, given the rates of single COs in the two intervals. When interference strength is high, CoC values tend to be low as there are fewer DCOs observed than expected. CoC shows a characteristic curve when plotted against the IID (Figure 1, B and C), with low CoC for small IIDs (when a CO in one interval suppresses the occurrence of a CO in the neighboring interval) and CoC approximating 1 for large IIDs (over which the interference signal no longer spreads along the chromosomes). A useful measure when analyzing such curves is L_CoC (Zhang et al. 2014a), the IID at which the observed number of DCOs is half the expected number (CoC = 0.5, dashed line, Figure 1, B and C). For all analyses, the simulated data gave L_CoC values that were no different from those determined from the equivalent experimental data (Table 1). For both experimental and simulated data, L_CoC was significantly smaller in males than in females if measured in megabases, but showed no difference when measured in micrometers SC (Figure 1, Figure S2, and Table 1). This confirms that genetic measurements of interference (e.g., L_CoC in megabases) are lower in males than in females, but suggests that the physical distance over which interference spreads (measured in micrometers SC) may be similar.

Table 1. L_CoC values.

	Megabases			Micrometer SC
	Male	Female	P-valuea	Male	Female	P-valuea
Experimental	7.05 ± 0.50	12.84 ± 1.50	7.90E−07	11.65 ± 0.86	12.83 ± 1.50	1
Simulated	6.30 ± 1.05	11.60 ± 0.83	1.40E−05	10.21 ± 1.75	11.20 ± 0.78	1
P-valuea	1	1		1	1

SC, synaptonemal complex.

^aBonferroni multiple-comparison corrected.

In the beam-film model, the CO patterning process is primarily determined by the strength of the CO designation (S and Smax) and by the distance over which interference spreads (L_BF). Thus, we compared estimates of these two parameters between male and female meiosis.

Estimates of CO promoting stress are the same for male and female meiosis

In the beam-film model, precursor (DSB) fate is determined by the CO-promoting stress (S) experienced by that precursor as well as the precursor’s sensitivity (a random value between 0 and 1, determined by parameter A, see Materials and Methods). When simulating each bivalent, the value of S is progressively increased until S = Smax, with each precursor experiencing stress equal to the product of S and the precursor’s sensitivity. At some point, the stress experienced by the most sensitive precursor reaches the critical value of 1 and will undergo CO designation. Stress relief will then extend out from that position. As S increases to Smax, additional precursors usually experience sufficient stress to promote the designation of further COs, although in these subsequent rounds of CO designation, the stress experienced by precursors is reduced by the sum of any stress relief caused by interference from nearby COs. If Smax is set < 1, then no precursor will achieve the critical stress value and therefore no class I COs will be designated.

According to this model, the higher the final maximum stress value (Smax), the more CO designations. However, despite males having significantly more COs than females, the predicted levels of maximum stress for the five chromosomes were similar for both sexes: Smax for males 7 ± 1.9 and females 6.9 ± 0.7, P = 1 (Bonferroni corrected) (Figure 2 and Table S1). Thus, our modeling suggests that increased CO frequencies in males are not due to differences in the CO-designation driving force.

Interference propagates the same physical distance along male and female bivalents, but has a greater effective strength in females

The parameter L_BF determines the length of the chromosomal region, centered on a CO, over which stress is relieved by that CO. In the beam-film model, the magnitude of the stress relief decreases exponentially with distance from the CO, such that there is maximal stress relief immediately surrounding the CO and almost no stress relief at a distance one-half of the L_BF in either direction from the CO (Kleckner et al. 2004; Zhang et al. 2014a).

When running simulations, L_BF is specified as the proportion of total chromosome length (i.e., chromosome length is set to 1), but is converted to length in megabases or micrometers SC to enable comparisons between chromosomes of different lengths. For some chromosomes, the estimated distance over which stress is relieved was greater than the length of the chromosome in question. While this may at first seem contradictory, it is in fact required if a CO suppresses the formation of additional COs more than one-half the length of the chromosome away. An example can be seen for chromosome 2 in females, which has an estimated SC length of 16.2 µm and an estimated stress-relief distance (L_{BF_SC}) of 25.9 µm. As can be seen from the CoC curve for this chromosome (Figure S2), it is clear that the observed number of DCOs are less than expected (i.e., CoC < 1), even when intervals are at opposite ends of the chromosome (e.g., IID ∼14 µm).

When measured in megabases (L_{BF_Mb}) the average best-fit estimates of stress-relief distance were significantly higher in females: L_{BF_Mb} – male 17.1 ± 3.5 Mb and female 28.8 ± 3.1 Mb, P = 0.0095, Bonferroni corrected (Figure 2 and Table S1). However, when the distance metric was converted to micrometers SC (L_{BF_SC}) using the best available estimates of SC length in the two sexes (Drouaud et al. 2007), there was no longer any difference in the estimated stress-relief distance between the two sexes: L_{BF_SC} – male 27.7 ± 5.6 µm and female 23.7 ± 2.5 µm, P = 1, Bonferroni corrected (Figure 2). These results indicate that the physical distance over which interference spreads is the same in both males and females, but that the effect of interference on patterns of inheritance is greater in females than it is in males. This is because the same physical distance (micrometers SC) covers a greater proportion of total chromosome length (megabases) in females.

These findings highlight a key distinction between different possible interpretations of interference that can be broadly defined as mechanistic and effective. For clarity, we here define our use of these terms which we will use in the remainder of this manuscript. We use the term interference when speaking broadly of the phenomenon, we use “mechanistic interference” when referring specifically to interference as defined in the beam-film model, i.e., the distance along the chromosome (measured in micrometers SC) that the interference signal propagates, and we use the term effective interference to refer to interference as measured genetically (e.g., CoC or γ, calculated from genetic data and expressed in megabases). Effective interference can be influenced by stress-relief distance (in micrometers SC), but is also affected by other factors like rates of class II COs and chromatin loop size (megabases per micrometer SC). Thus, although mechanistic interference is identical for male and female meiosis, effective interference is stronger in female meiosis, resulting in fewer interference-sensitive class I COs in females.

Estimates of chromosome end tethering (cL/R) are the same for male and female meiosis

In addition to Smax and L_BF, several other beam-film parameters commonly vary within or between species, and might contribute to sex-specific patterns of CO formation (Zhang et al. 2014a). The first of these we focused on was the effect of clamping or tethering of chromosome ends, which determines how stress is supported in terminal regions. A probable biological correlate is the tethering of telomere ends to the nuclear envelope. If a chromosome is clamped/tethered it can support CO-promoting stress. If unclamped, stress can dissipate from the loose chromosome end, which, according to the beam-film model, would tend to suppress CO formation. As the interference signal (stress relief) cannot come from beyond the end of the chromosome, recombination frequencies will tend to be highest in distal regions when chromosomes are clamped and there is > 1 CO per bivalent. Total clamping averages (cL/R) for males and females were calculated from the estimated values of cL and cR for each sex. Clamping values were variable between chromosomes but there was no significant difference between the average clamping values: cL/cR males 0.78 ± 0.16 and females 0.69 ± 0.13, P = 1 Bonferroni corrected (Figure 2). Differences in chromosome-end tethering are therefore unlikely to contribute to sex-specific differences in CO patterning.

Fewer class II COs occur through the female germline

The number of class II COs in a simulation is determined by parameter N, the number of recombination precursor sites (DSBs), and parameter T2Prob, which specifies the probability of a non-CO-designated precursor site becoming a class II CO. Assuming the same number of DSBs in males and females, the estimated likelihood of a precursor becoming a class II CO was significantly higher in male than female meiosis: T2Prob - 0.0063 ± 0.0010 and 0.0036 ± 0.0008, respectively (P = 0.026, Bonferroni corrected, Figure 2 and Table 1). As male and female meiosis have the same number of precursors (DSBs) in these analyses, males have a proportionately higher number of class II COs: 1.575 ± 0.5 and 0.9 ± 0.2, respectively (P = 0.026, Bonferroni corrected). We also determined what proportion of the total number of COs occur via the class II pathway (i.e., P = CO_II/(CO_I + CO_II). These values were equivalent for the two sexes: 0.14 ± 0.02 male and 0.14 ± 0.03 female, P = 1, Bonferroni corrected. A lower probability of class II CO formation in females may therefore, in addition to the decrease in class I COs described above, contribute to sex-specific CO patterning in Arabidopsis.

Fewer DSBs in females would explain lower class II CO numbers, and unify estimates of beam-film parameters for male and female meiosis

One of the parameters fixed for each round of analysis is the number of DSBs. While there are relatively good estimates for the number of DSBs in male meiosis in Arabidopsis, cytological analyses of female meiosis are more challenging and there are no reliable estimates of DSB numbers. Thus, while we have assumed equal numbers of DSBs in male and female meiosis in the analyses described above, it is possible that DSB numbers differ between the two sexes. Meiotic DSBs occur in loop DNA that has been recruited to the chromosome axis (Panizza et al. 2011). In Arabidopsis female meiosis, there are fewer (albeit larger) chromatin loops and the chromosome axis is 40% smaller than in male meiosis (Drouaud et al. 2007), which could feasibly result in a similar reduction in DSBs (Gruhn et al. 2013; Baier et al. 2014). To understand whether reduced DSB numbers would have any effect on CO patterning and/or estimates of parameter values in female meiosis, we repeated the best-fit simulations assuming a reduction in DSBs equal to the reduction in SC length, i.e., ∼40% reduction, or 150 (rather than 250) DSBs per meiosis.

Optimized estimates of CO-promoting stress (Smax), interference strength/stress-relief distance (L_{BF_Mb}, L_{BF_SC}), and chromosome tethering (cL/cR) were identical for both sets of simulations (F and F_DSB, Figure 2). Estimates of class II CO likelihood (T2Prob) were higher for simulations of female meiosis with reduced DSB numbers, and the optimized value no longer differed from that estimated for male meiosis (Figure 2). Although the probability of class II CO formation was the same for males with 250 DSBs and females with 150 DSBs, the absolute number of class II COs was lower in females (due to the reduced number of DSBs): males - 250 DSBs × T2Prob 0.0063 ± 0.001 = 1.58 ± 0.25; Females - 150 DSBs × T2Prob 0.0056 ± 0.001 = 0.90 ± 0.17 COs.

Taken together, these results suggest that the smaller SC length in females, if accompanied by an equivalent reduction in DSBs, can account for all differences in CO patterning between the two sexes, even if the mechanics of CO patterning remain identical. The smaller SC in females accounts for stronger effective interference, and therefore reduced COs, despite identical estimates of L_{BF_SC}. Similarly, a reduction in DSB density (per megabase), due to the shorter SC, could account for the reduction in class II COs.

Behavior of the two-pathway beam-film model

We next comprehensively explored the behavior of the two-pathway beam-film model, to better understand how the patterning of class I and class II COs interact to influence patterns of inheritance. To do this, we simulated COs, independently varying the stress-relief distance (L_BF, Figure 3, A–C), CO-promoting stress (Smax, Figure 3, D–F), and class II CO probability (T2Prob, Figure 3, G–I).

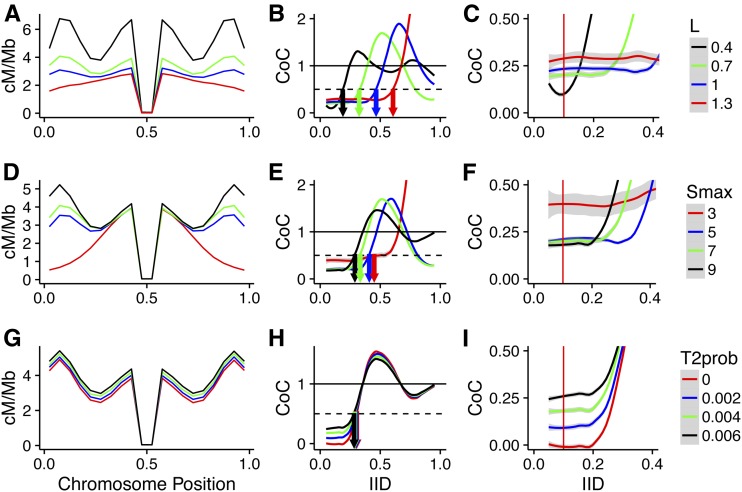
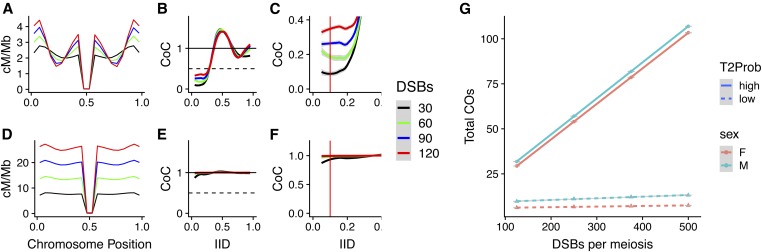
Figure 3.

Effect of beam-film parameters on crossover patterning in Arabidopsis. The effect of altering a single beam-film parameter—L (A–C), Smax (D–F), or T2Prob (G–I)—on crossover distribution (A, D, and G) and CoC (B and C, E and F, and H and I). Red vertical lines in (C, F, and I) represent IID = 0.1. Gray shading in CoC curves indicates 95% C.I. CoC, coefficient of co-incidence; IID, interinterval distance; Smax, maximum stress level per bivalent; T2Prob, probability that a non-CO designated precursor will form a class II CO.

COs tend to increase in regions adjacent to telomeres and pericentromeres

Changes in L_BF and Smax dramatically altered CO distributions (Figure 3, A and D), while changing the proportion of class II COs had little effect (Figure 3G). Changes in CO frequency were primarily observed in terminal regions (Smax and L_BF) and in regions adjacent to the pericentromere (L_BF), and showed increased CO frequencies with greater stress and decreased stress-relief distance (Figure 3, A and D).

L_CoC is primarily influenced by stress-relief distance

As has been observed previously in yeast (Zhang et al. 2014a), the parameter that most influenced CoC curves was the stress-relief distance (L_BF), with higher values of L_BF shifting CoC curves to the right. Because of this shift, increases in L_BF resulted in proportional increases in L_CoC,, highlighting that L_CoC (when measured in micrometer SC) is a useful proxy for stress-relief distance. One major advantage of L_CoC over L_BF is that it can be determined directly from experimental data, without the requirement for beam-film modeling and parameter optimization.

Intriguingly, the behavior of CoCs at small IIDs differed from that observed at larger IIDs. For example, an increase in the distance over which the interference signal is propagated would normally be expected to lead to lower values of CoC as more DCOs are suppressed. However, at small IIDs, increased L_BF resulted in increased values of CoC (Figure 3C). It was also evident that while changes in the probability of class II CO formation had negligible effects on L_CoC and the shape of the CoC curve, it was the parameter that had the largest impact on CoC at small IIDs (IID ∼0.1, red lines, Figure 3I vs. Figure 3, C and F).

Differing classes of DCOs at small and large IIDs cause opposite effects of altered stress-relief distance on CoC:

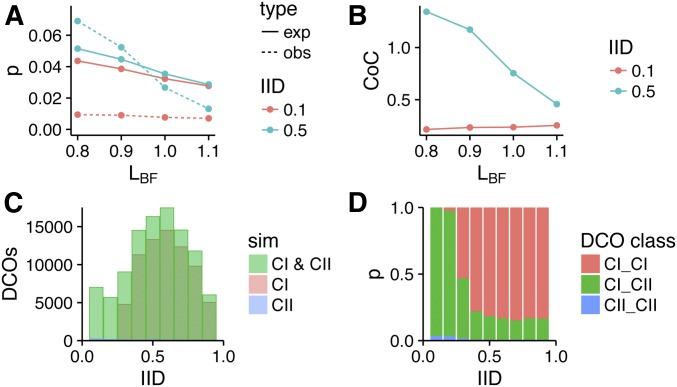
To further understand why CoC might behave differently at different IIDs, we sought to identify how changes in L_BF might differentially affect the expected and observed number of DCOs (the determinants of CoC) for different IIDs. Beam-film simulations demonstrated that increased L_BF resulted in a small decrease in the expected number of DCOs for both small and large IIDs (IID = 0.1 and 0.5; Figure 4A). This was anticipated, given that the expected number of DCOs for a pair of intervals is based purely on the respective rates of COs in the two intervals. In contrast, the observed number of DCOs changed dramatically for IID = 0.5, but only marginally for IID = 0.1 (Figure 4A) in response to changes in L_BF. As a result, CoC dramatically decreased for IID = 0.5 with increased L_BF but increased slightly for IID = 0.1 (Figure 4B).

Figure 4.

Influence of IID on CoC response to changes in L_BF. (A) The expected (solid line) and observed (dashed line) proportion of interval pairs receiving a DCO for two different IIDs; calculated from simulations with varying values of L_BF. (B) CoC values for two IIDs calculated from simulations with varying values of L_BF. (C) The number of DCOs observed for different IIDs from simulations involving CI and CII, CI, or CII crossovers. (D) The proportions of DCOs formed between two CI crossovers (CI_CI), two CII crossovers (CII_CII), or a CI and a CII crossover (CI_CII) for different IIDs. CI, class I crossover; CII, class II crossover; CoC, coefficient of co-incidence; DCO, double crossover; exp, expected; IID, interinterval distance; L_BF, stress-relief distance; obs, observed; sim, simulated.

We reasoned that the difference in behavior might be due to the nature of the DCOs formed at smaller and larger IIDs, which might differ in their sensitivity to interference. For example, DCOs can occur between two class I COs, two class II COs, or between a class I and a class II CO, but interference only directly suppresses those involving two class I COs. Therefore, we ran beam-film simulations with class I COs only (T2Prob = 0), class II COs only (Smax = 0), or both class I and class II COs, and determined numbers of the different classes of DCOs formed for each set of simulations at different IIDs (Figure 4C). From these numbers, we determined the proportions of the different classes of DCOs (Figure 4D) that occur for different IIDs under standard conditions (i.e., when simulating both class I and class II COs). For small IIDs, DCOs are almost exclusively formed between a class I CO and a class II CO (Figure 4D). In contrast, for larger IIDs (≥ 0.4), the majority of DCOs are formed between two class I COs (Figure 4D). Cytological observations in tomato reporting the same phenomenon (Anderson et al. 2014) suggest that this is a general feature of meiosis. As interference only suppresses DCOs involving two class I COs, changes in L_BF will only directly affect DCO formation at larger IIDs. This pattern holds when the proportion of class II COs falls within the range normally observed (5–20%), although when class II COs are absent or make up the majority of COs, then most DCOs involve two class I or two class II COs, respectively, for all IIDs (Figure S4).

Both the expected number of DCOs and observed DCOs at small IIDs are indirectly affected by increased L_BF due to the associated decrease in the frequency of class I COs. The magnitude of the change is greater for the expected number of DCOs, which can be seen from the equations below. Here, CI and CII are the rates of class I and class II COs, respectively, in the two intervals:

$${\text{DCO}}_{exp}=\left(C{I}_{Int1}+CI{I}_{Int1}\right)\times \left(C{I}_{Int2}+CI{I}_{Int2}\right)$$

$${\text{DCO}}_{ob{s}_{Small\_IID}}\sim \left(C{I}_{Int1}\times CI{I}_{Int2}\right)+\left(C{I}_{Int2}\times CI{I}_{Int1}\right)$$

For small IIDs, while CI >> CII, the reduction in the expected number of DCOs is approximately twice that of the observed reduction in DCOs, resulting in an increase in CoC.

CO homeostasis is influenced by the proportion of class II COs

Finally, we assessed the effects of the rate of class II CO formation on CO homoeostasis. CO homoeostasis maintains CO number despite differences in DSB formation (Martini et al. 2006; Rosu et al. 2011; Cole et al. 2012). As described above, we observed few changes in CO number and estimates of beam-film parameters when we modeled a 40% decrease in DSB numbers; therefore, the beam-film model displays strong CO homeostasis when modeling wild-type Arabidopsis meiosis. However, we reasoned that if the proportion of class II COs increased, such as is seen in some mutant contexts (e.g., Fernandes et al. 2018), then DSB number should have a greater influence on the number of COs.

When modeling wild-type meiosis, altered DSB number had relatively little effect on CO distributions or CoC curves (Figure 5, A and B). For CO distribution, increased DSBs resulted in a slight increase in proximal and distal COs, but fewer interstitial COs. The only clear difference in CoC was for small IIDs, where higher DSB numbers resulted in higher values of CoC (Figure 5C). In contrast, altering the number of DSBs in a context where a high proportion become class II COs had a dramatic effect on CO patterning. Here, increased DSBs resulted in proportionate increases in COs (Figure 5D). Regardless of the number of DSBs, CoC values were ∼1 for all IIDs (Figure 5, E and F).

Figure 5.

Influence of DSB number on CO patterning and homeostasis is dependent on the probability of class II COs. (A–C) show results for simulations of wild-type meiosis and (D–F) show results for simulation of meiosis with increased class II CO formation (T2Prob). (A) Increased DSBs in wild-type cells resulted in more proximal and distal COs, but fewer interstitial COs. (D) In mutants with increased class II COs, more DSBs resulted in a uniform increase in crossovers. (B and C) For wild-type cells, CoC values increased at small IIDs with increased DSBs. (E and F) With increased class II COs, CoC values were ∼1 for all IIDs and all DSB numbers. (G) Total CO number for genome-wide simulations using best-fit parameters for male and female meiosis, and varying numbers of DSBs. In wild-type cells (dashed lines), increasing DSBs had a minimal effect on total COs. With increased class II COs (solid lines), doubling DSBs resulted in twice as many COs. Gray shading in CoC curves indicates 95% C.I. CO, crossover; CoC, coefficient of co-incidence; DSB, double-strand break; F, female; IID, interinterval distance; M, male; T2Prob, probability that a non-CO designated precursor will form a class II CO.

We next modeled how DSB number affects the total number of COs for male and female meiosis in both contexts. In wild-type cells, doubling the number of DSBs resulted in a ∼15% increase in COs in males and females (Figure 5G). In a context with a high number of class II COs, doubling the number of DSBs resulted in almost double the number of COs (Figure 5G). The number of DSBs has often been reported to have limited influence on rates of COs due to CO homeostasis (Martini et al. 2006; Rosu et al. 2011; Cole et al. 2012). Our results indicate that the number of DSBs primarily affects the number of COs when the proportion of class II COs is high, and by extension suggests that the probability of class II CO formation has a major influence on CO homeostasis.

For a given number of DSBs, the modeling predicts ∼65% more COs in wild-type males than wild-type females, but essentially equal numbers of COs when the probability of class II COs is high (Figure 5G).

Discussion

CO interference is a well-known genetic phenomenon; however, its mechanistic basis is only just now coming to light. The interference signal is thought to propagate a set physical distance (L_BF, usually measured in micrometers SC) from designated CO sites (Zhang et al. 2014a,b), and analyses commonly use cytological observations and simulations of class I CO positions along the length of a synapsed bivalent (Zhang et al. 2014a,b).

To gain insights into the differences between female and male meiosis in Arabidopsis, we analyzed a large Arabidopsis reciprocal backcross data set (Giraut et al. 2011) and performed two-pathway (i.e., both class I and class II COs) beam-film best-fit simulations. Our modeling suggests that the major differences in CO number, CO distribution, and interference relationships between the sexes can all be explained by the observed difference in SC length between male and female meiosis. The relationship between genome size and SC length is governed by the size/number of chromatin loops, which occur at a conserved density of ∼20 per micrometer SC across a wide range of organisms (Zickler and Kleckner 1999). As genome size is identical for both sexes in Arabidopsis, we would expect loop size in male meiocytes to be ∼60% of that found in female meiocytes. Exactly how chromatin loop size is determined remains unclear, but this decision occurs very early in, or prior to, meiosis (Zickler and Kleckner 2015; Kaiser and Semple 2018). It is therefore probable that the cause of differences in CO patterning also occurs very early in, or prior to, meiosis. Interestingly, humans also display sex-specific differences in chromatin loop size and SC length, although in this case female meiocytes have shorter loop sizes, longer SCs, and more COs (Tease and Hultén 2004).

It has been reported previously that effective CO interference is stronger in females than males in Arabidopsis (Basu-Roy et al. 2013). Our analyses indicate that the interference signal is propagated over the same physical distance (micrometers SC) in both male and female meiosis, and thus, from a mechanistic standpoint, interference is identical in the two sexes. The higher effective interference (i.e., the effect on the inheritance of two linked genetic loci) observed in females can be entirely explained by the difference in SC length between the two sexes, as a given distance in micrometers SC corresponds to a greater length in megabases. It is worth noting that our estimates of L_BF for male (27.7 ± 5.6 µm) and female (23.7 ± 2.5 µm) Arabidopsis are similar to estimates for tomato [14 µm, see Zhang et al. (2014a)], but are 80–90-fold larger than for yeast [0.3 µm, see Zhang et al. (2014a)]. This vast difference in the distance across which interference propagates in different taxa, as estimated by the beam-film model, remains challenging to explain biologically.

In addition to explaining differences in effective interference, SC length also explained the differences in CO distribution observed between the sexes. In male meiosis, COs are high adjacent to the pericentromeres and in the distal regions, while in female meiosis, COs are high adjacent to the pericentromeres but low in the distal regions (Drouaud et al. 2007; Giraut et al. 2011). Our modeling shows that increases in the proportion of the chromosome over which interference spreads (either through a reduction in SC length or an increase in L_BF) reduces COs, particularly in distal regions. The lower SC length in females can therefore account for the observed differences in CO distribution.

In mammals, SC length is correlated with the number of DSBs (Gruhn et al. 2013; Baier et al. 2014; Ruiz-Herrera et al. 2017). If the same holds true in plants, then we might expect fewer DSBs in female meiosis. Our analysis revealed that while the number of DSBs had very little influence on CO distributions and CoC curves, a decrease in the number of DSBs resulted in an increase in the estimated proportion of DSB sites that become class II COs (T2Prob). Thus, the reduction in SC length observed for females, if accompanied by an equivalent reduction in DSBs, can also account for proposed differences in the number of class II COs between male and female meiosis. However, at least one line of evidence suggests that this question may not be fully resolved. In mutant lines with large numbers of additional class II COs, the recombination landscapes of male and female meiosis are roughly equivalent with even a slightly higher number of COs in females (Fernandes et al. 2018). This suggests the possibility of similar numbers of DSBs in male and female meiosis. Further comparative cytological studies of male and female meiosis will be required to fully answer these questions. For example, it would be interesting to see if SC lengths still differ between males and females in these mutant contexts.

Given the substantial differences in CO patterning between female and male meiosis, it is striking that they can all be accounted for by the difference in SC length. It is similarly striking that, despite the differences in CO patterning, there are also no significant differences between the sexes in the estimated beam-film model parameters (if L is expressed in micrometers SC and the number of DSBs is reduced in line with the shorter SC in females). This gives us good confidence in our approach and suggests that similar investigations, in different contexts (e.g., mutants, over expression lines, environmental conditions), could provide further mechanistic insights into the factors governing CO patterning in Arabidopsis.

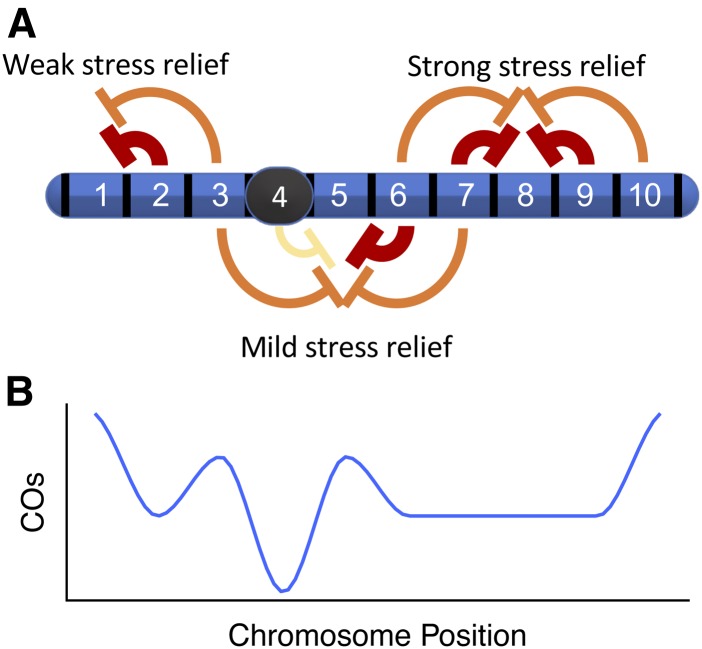
When exploring the impact of varying the beam-film parameters, it was clear that increased CO-promoting stress (Smax) or decreased stress-relief distance (L_BF) resulted in increased COs, particularly in terminal regions. COs also increased in proximal regions but only when the stress-relief distance was low, and so were not suppressed by the increase in terminal COs (e.g., Figure 3A, L = 0.4 compared to L > 0.5 and Figure 3D). This is explained in the beam-film model by the fact that additional COs will tend to occur in regions that experience, on average, less stress relief. Additional COs in terminal regions are only suppressed by prior COs in one direction, i.e., COs located toward the centromere; in contrast, additional COs in interstitial regions are suppressed by both distal and proximal COs (Figure 6). Similarly, the low precursor density at the centromere results in fewer COs and thus regions adjacent to the centromere experience less stress relief than interstitial regions (Figure 6), resulting in more COs. This is particularly true when the stress-relief distance is low and the local environment has greater effect (e.g., Figure 3A).

Figure 6.

CO (crossover) increases tend to accumulate in terminal and proximal regions. (A) Terminal regions (e.g., interval 1) experience weaker stress relief than interstitial regions (e.g., interval 8) as they are surrounded by fewer COs. Similarly, proximal regions (e.g., interval 5) experience less stress relief, due to the lower precursor number and therefore fewer COs in centromeric regions (interval 4). (B) As crossovers increase, the additional crossovers tend to accumulate in terminal and proximal regions due to their lower average levels of stress relief.

In addition to mechanistic insights into the factors governing CO patterning in Arabidopsis, the model can be used to make predictions about how important agricultural goals such as heightened recombination rates could be achieved. For example, with the development of clustered regularly interspaced short palindromic repeats and related technologies, it is possible to modulate the number or location of DSBs in early meiosis, and there is interest in using this approach to alter recombination rates in plant breeding programs (Choi 2017; Filler Hayut et al. 2017; Puchta 2017). In most organisms, CO numbers are thought to be maintained independently from the number of DSBs through CO homeostasis (Martini et al. 2006; Rosu et al. 2011; Cole et al. 2012). Our modeling suggests that the extent to which homoeostasis maintains CO numbers is determined by the proportion of DSBs that become class II COs: the higher the proportion of class II COs, the more DSB number will affect CO number. Thus, we predict that combining the knockout of class II CO-suppressing proteins (e.g., RECQ4, FANCM, and FIGL1) (Crismani et al. 2012; Girard et al. 2015; Séguéla-Arnaud et al. 2015) with approaches to increase meiotic DSBs could maximize increases in recombination and the associated benefit to breeding programs.

One of the surprising findings of our analysis is that, for small IIDs, an increase in the distance over which the interference signal is propagated can result in increased values of CoC (Figure 3), i.e., decreased effective interference. This behavior is not specific to the beam-film model but is expected whenever both class I and class II COs occur, and there is a change in the strength of suppression of closely spaced class I COs. This finding highlights the need for caution when interpreting interference data, and particularly in the distinction between mechanistic (e.g., L_BF) and effective (e.g., CoC from genetic data) measurements of interference. It should also be noted that at small IIDs, the magnitude of the predicted change in CoC is small, and that for specific interval pairs the effect of the local chromosomal landscape (e.g., recombination hotspots etc.) may outweigh the effect predicted by the model. Despite these caveats, it is clear that an increase or decrease in mechanistic interference strength (L_BF) is not expected to result in an equivalent increase or decrease respectively in effective interference for small IIDs. Given the widespread use of reporter lines that determine recombination rates and CoC values for closely linked intervals (Francis et al. 2007), it is important to realize that these lines may give little to no insight into any change in the mechanics of CO interference.

As an example, two recent papers investigated altered recombination rates at temperature extremes in Arabidopsis (Lloyd et al. 2018; Modliszewski et al. 2018). In both cases, increased temperature gave rise to more class I COs, but the increased COs were associated with no change or a decrease in genetic measurements of CoC (i.e., effective interference). In the studies, CoC (or interference ratio) was measured by tracking the inheritance of closely linked fluorescent reporter genes in pollen, and thus combined both class I and class II COs measured at a small IID. While it could be concluded from these studies that temperature increases class I COs without any effect on interference, these results are also consistent with an alternative hypothesis, i.e., that increased temperature decreases the distance over which interference is propagated, resulting in increased class I COs, but with no effect on genetic measurements of interference at small IIDs. Or, to put it another way, high temperature might decrease mechanistic interference but result in an increase (or no change) in effective interference for small IIDs. There is good evidence that heightened temperature might have such a mechanistic effect, given that the chromosome axis is thought to mediate interference (Zickler and Kleckner 2015) and the synaptonemal complex/axis structure is sensitive to temperature (Loidl 1989; Morgan et al. 2017), but this remains to be experimentally validated.

While the beam-film model was able to reliably model genetic recombination data, there are several ways in which models of CO patterning might further be improved with increased understanding of the underlying biology. For example, when calculating L_BF and L_CoC in micrometers SC using back cross data, we assume a direct relationship between SC length and megabases. In Arabidopsis, the relationship between SC length and megabases is constant between whole chromosomes [R² = 0.99, based on data from López et al. (2008)]; however, the relationship may not be constant within a chromosome (Bickmore and Oghene 1996). Establishing how the relationship between megabases and micrometers SC changes for different chromosomal domains would provide one means to improve models of CO patterning when using genetic data. Another question is whether DSB density is constant along the length of the chromosome. If so, is it constant relative to SC length or length in megabases? Recently, Spo11-oligo sequencing has demonstrated relatively constant DSB formation along the length of the chromosome, although there are clearly regions of higher and lower DSB density, particularly at the centromeres where DSB formation is strongly suppressed (Choi et al. 2018). It would be interesting to incorporate such data into future models of CO patterning.

Despite these possible improvements to future models, it is clear that we can gain novel insights into CO patterning using genetic recombination data in combination with beam-film simulations. These are particularly powerful when, as for this study, we have good estimates of SC length for all chromosomes, circumventing the need for cytological determination of CO locations. This enables us to take advantage of the main benefit of genetic data: that it incorporates all CO events, and thus enables us to develop a more nuanced understanding of the interplay between the mechanistic determinants of CO interference and the final effect on patterns of inheritance.