Development of a Fully Cross-Validated Bayesian Network Approach for Local Control Prediction in Lung Cancer

Abstract

The purpose of this study is to demonstrate that a Bayesian network (BN) approach can explore hierarchical biophysical relationships that influence tumor response and predict tumor local control (LC) in non–small-cell lung cancer (NSCLC) patients before and during radiotherapy from a large-scale dataset. Our BN building approach has two steps. First, relevant biophysical predictors influencing LC before and during the treatment are selected through an extended Markov blanket (eMB) method. From this eMB process, the most robust BN structure for LC prediction was found via a wrapper-based approach. Sixty-eight patients with complete feature information were used to identify a full BN model for LC prediction before and during the treatment. Fifty more recent patients with some missing information were reserved for independent testing of the developed pre- and during-therapy BNs. A nested cross-validation (N-CV) was developed to evaluate the performance of the two-step BN approach. An ensemble BN model is generated from the N-CV sampling process to assess its similarity with the corresponding full BN model, and thus evaluate the sensitivity of our BN approach. Our results show that the proposed BN development approach is a stable and robust approach to identify hierarchical relationships among biophysical features for LC prediction. Furthermore, BN predictions can be improved by incorporating during treatment information.

I. INTRODUCTION

IN the era of big data, it is conjectured that the increased amount of available medical data coupled with imaging and genetic information could provide new opportunities to resolve current challenges in precision cancer care. This is driven by recent advances in computational methodologies spearheaded by the application of artificial intelligence and machine learning techniques [1]. Machine learning tools could be used to assist the clinicians in arriving at more informed treatment decisions based on patient records [2]. Recent years have witnessed extensive application of machine learning in different areas of radiotherapy ranging from quality assurance to outcome prediction [3]. Probability theory is a rational approach to analyze uncertainty, since its axioms follow basic principles for measuring belief [4]. As a directed acyclic graph (DAG), a Bayesian network (BN) could be developed by expressing the joint probability distribution of a set of random variables and taking into account the conditional independence between these variables [5]. A BN together with the Bayesian interpretation of probability theory have proven to be a sound and practical framework for reasoning under uncertainty [6–8]. Here, this framework is investigated for building a reliable and interpretable radiation outcomes prediction model for personalized treatment planning based on a large-scale retrospective dataset in lung cancer.

Lung cancer is the second most commonly diagnosed cancer in both man and woman in the US, and it is the leading cause of cancer death with an estimated 155,870 deaths in 2017, accounting for 1 in 4 cancer deaths [9]. The majority of non– small-cell lung cancer (NSCLC) patients are diagnosed at middle or late stages of disease [10]. Radiotherapy is the main treatment for locally advanced NSCLC. While it is designed to achieve tumor local control (LC), it may still cause radiation induced toxicities (RITs). Not all NSCLC patients are expected to benefit from the same treatment interventions due to heterogeneity of lung tumors. Radiation outcomes may depend on radiation dose and patients’ physical, clinical, biological and genomic characteristics before and during a course of radiotherapy. Therefore, it is necessary to explore the relationships between radiation outcomes and these biophysical factors, which can guide optimal dose prescription, selection of fractionation schemes and combined treatments with targeted therapies [11].

The BN approach has been previously employed to provide personalized estimates of radiation outcomes and treatment selection recommendation for breast cancer [12–16], lung cancer [17, 18], pancreatic cancer [19], and colon cancer [20]; however, most of these studies were based on limited dimensional datasets. In our own previous study [21], in order to find the relationship among patients’ biophysical characteristics and radiation induced toxicities from a large- scale data so called pan-Omics dataset including: clinical, physical, genetic, protein, and imaging information [22], we developed a novel two-step BN approach to explore hierarchical biophysical relationships influencing the radiation pneumonitis grade 2 and above (RP2). The developed BN may assist not only in improved prediction of RP2 but also in better understanding of its mechanistic values, which is very valuable for developing informed interventions using radiotherapy. The current work focuses on extending the previous methodology to local control (LC) and compares its performance with an ensemble model building approach of BNs.

Literature reports show that LC is only achieved in less than half of NSCLC patients irrespective of the patients receiving radiotherapy alone or both radiotherapy and chemotherapy based on randomized trials [23, 24]. It has been also long recognized that better LC rates would contribute to improved survival in these populations [25]. In this study, the previous two-step BN approach was used to develop BNs for LC prediction based on the same retrospective discovery and validation dataset with additional radiomics PET imaging data before and during the radiotherapy. Moreover, a nested cross- validation (N-CV) approach is also developed to fully cross- validate our previous single BN approach and compare its performance with a BN ensemble approach.

While several studies developed models based on extracted radiomic features from CT and/or PET images only [26, 27], our BN approach explores the biophysical relationship among clinical, physical, genomic, biological, radiomic features and radiation outcome in terms of different radiation treatment plans in a single BN framework. It is not only able to predict radiation outcome but also can identify appropriate treatment plans before and during radiation treatment to improve patients’ therapeutic satisfaction.

The organization of the rest of this paper can be described as follows. The dataset and our BN approach for LC prediction are introduced in Section 2. The prediction performance of the obtained pre- and during-treatment BNs together with the performance and sensitivity of our BN approach are evaluated in Section 3. Radiobiological interpretation, discussion and conclusions are summarized in Section 4.

II. METHODS

A. Study participants and data collection

The study included a secondary analysis of 68 NSCLC patients treated in and before year 2009 with 20 cases of local progression used for model building and 50 additional patients treated after year 2009 with 12 cases of local progression reserved for independent model testing. The patients had been treated on four prospective protocols under IRB approval. The first three treated patients to standard doses (60–66 Gy) and the fourth was a dose escalation study intensifying doses to persistent positron emission tomography (PET)-avid target volumes during treatment with 2.1–2.85 Gy per fraction up to a total dose of 85.5 Gy over 30 fractions [28–30].

Each patient in the dataset had 288 features from seven categories including 6 dosimetric parameters, 14 clinical factors (e.g., age, stage, KPS), 30 pre-treatment cytokines (e.g., pre_IL- 10), the slopes of 30 cytokine changes during the treatment course (e.g., SLP_fractalkine), 62 microRNAs (e.g., miR-17– 5p), 60 SNPs (e.g., il10ra-Rs3135932), 43 pre-treatment PET radiomics features (e.g., global statistics and textural information), and the relative differences of 43 PET features during the treatment course (e.g., RD_GLRLM-LRLGE). The details of these features are listed in Appendix A. The collection of these data can be described as follows.

1. Dosimetric data

Radiation dose distributions in the tumor were computed within the Varian Eclipse treatment planning system using the AAA dose algorithm [31]. To account for fractionation differences, all total tumor dose values were converted into their 2 Gy equivalents (EQD2) using locally developed software tool by the linear-quadric model with an alpha/beta ratio of 10 Gy. Generalized equivalent uniform dose (gEUD) was calculated with various tissue-specific parameters “a” to describe the volume effect. For a→–∞, gEUD approaches the minimum dose; thus negative values of “a” are used for tumors [32]. In addition to tumor gEUD and MeanDose, values for D5, D90, and D95 were extracted from EQD2-corrected dose- volume histograms, where Dx represents the minimum dose received by the hottest x percent of the tumor volume. In the current BN, a gEUD with a= −10 was selected from these dosimetric data based on our BN approach to provide the best prediction of LC.

2. Biological information

Blood samples were obtained at baseline and after approximately 1/3 and 2/3 of the scheduled radiation doses were delivered. Pre-treatment blood samples were analyzed for cytokine levels [33], miRNAs [34], and single-nucleotide polymorphisms (SNPs) [35, 36]. These variables have been identified as candidates from the literature as related to lung cancer or inflammatory disease. The slopes (SLP) of cytokine changes and the relative differences (RD) of PET radiomics features [37] from before to during treatment were also determined as patients’ responses to radiation treatment.

3. Radiomics

Radiomics features were extracted from only PET images, and the radiomics features in our study were calculated based on the publically available software tool [38], which has been a part of the image biomarker standardisation initiative (IBSI) standard [39]. In addition to pre-treatment, the time used to include during imaging in our study was around mid-treatment (3rd to 4th week of a 6 weeks course), around 40– 46 Gy. The FDG-PET images were acquired on imaging protocols on (Biograph Classic and CPS; Siemens Medical Solutions) scanners. PET images were attenuation corrected and reconstructed using the OSEM algorithm. The voxel spacing varied from 1.2×1.2×3 mm³ to 5×5×5 mm³. For texture calculations, the images were resampled to an isotropic size of 5×5×5 mm³ for texture matrices calculations as performed in the literature [38].

Pre-treatment and intra-treatment PET images were registered to the treatment planning CT using rigid registration. Image analysis was performed using customized routines in MATLAB (The Mathworks, Natick, MA). The metabolic tumor volume (MTV) was extracted by applying a level set algorithm by using the planned tumor volume (PTV) as a region of interest [40]. Radiomics textural features were extracted after images were quantized into 32 levels using the Lloyd’s algorithm [41, 42]. Features that were extracted included widely used global, gray level co-occurrence matrix (GLCM), neighborhood gray-tone difference matrix (NGTDM), run-length matrix (RLM), and grey-level size-zone matrix (GLSZM) features [37].

4. Radiation outcome

Patients were considered to have local progression if clinical, radiographic, or biopsy evidence of progression was observed with a minimum follow-up of six months. Otherwise, patients were considered to achieve LC of lung cancer if they had an initial radiographic response on computed tomography (CT) or PET/CT images to treatment and a stable mass at each follow- up visit.

B. Data pre-processing

Due to only having 68 patients with full information in the retrospective dataset, the Hartemink’s pairwise mutual information method was employed to discretize continuous variables (e.g., Tumor_gEUD, Age, pre_MTV) into three categories [43]. Interval discretization was used for the categorical variables, such as Stage and KPS, except for SNPs, since the SNPs were described by three kinds of genotypes: wild type homozygote, minor allele homozygote, and heterozygote. While the heterozygote is assigned number “1” in this study, the homozygotes with and without the ancestral allele are assigned numbers “0” and “2”, respectively. Statistical methods were implemented in the R-software environment, candidate predictors selection and the BN learning were based on the “bnlearn” package [44].

C. Single structure BN approach

The goals of the current single structure BN approach are twofold; (1) to develop the best pre-and during-treatment stable BNs from large-scale existing dataset for LC prediction and (2) provide better understanding of underlying biophysical interactions. However, the computational complexity of learning the structure of Bayesian networks is super- exponential in the number of nodes in the worst case and polynomial in most real-world scenarios [45]. Thus, a novel BN building approach was generated here, mainly including the following two steps. First, an extended Markov blanket (eMB) approach was developed to determine important factors related to LC from a high dimensional dataset. Secondly, while bootstrap sampling and Tabu Search were employed to optimize the BN structure for a given number of predictors, the best scale for the BN was learned from predictor pruning and arc selection in terms of the prediction performance of resulting BNs based on cross validation (CV). The major components of the current BN approach are summarized as follows.

1. Extended MB (eMB) approach

In this study, an eMB neighborhood approach was developed to find out not only the inner family of inter-related variables as commonly practiced (the variables directly related to LC based on the MB of LC) but also their extended family, i.e., next-of-kin variable relationships (the variables directly related to the inner family based on their MBs). For instance, the MB of LC would be the smallest set containing all variables carrying information about LC that cannot be obtained from any other variable (inner family). Then, for each member in the LC blanket, a next-of-kin MB for this member was also derived. In addition to identifying good feature subsets for BN structure learning, the MB also helps determine causal relationships among various nodes in the BN. Here, the eMBs of LC and next-of-kin were found using the Semi-Interleaved Hiton Parents and Children algorithm (SI-HITON-PC), a fast forward selection technique for neighborhood detection designed to exclude nodes efficiently based on the marginal association [44]. Since the SI-HITON-PC algorithm reduces the number of variables in the prediction models by three orders of magnitude relative to the original variable set while improving or maintaining accuracy [46], it was employed here for the eMB neighborhood approach.

2. BN structure optimization

The purpose of BN structure learning is to explore the possible interactions among the above selected variables from the existing dataset. Before starting to learn the best BN structure, the known causal and logical influence relationships between every two variables were defined as “biophysical rules”. Although there are many biophysical interactions related to LC and the relationships among potential variables in each interaction could be complicated. There exist many known prior biophysical relationships related to LC onset that could be exploited to constrain the search space in the process of building the BN structure. If a connection could be identified from literature or influence of time order, the relationship was considered as an inclusion connection; otherwise, it was an exclusion connection. For instance, the connection from Tumor-gEUD to the relative difference of PET information before and during treatment was considered as an inclusion connection. However, the connection from Tumor-gEUD to a miRNA was an exclusion connection, as radiation treatment cannot influence miRNAs prior to radiotherapy.

Bootstrapping is a random sampling process with replacement that allows for reducing pitfalls of over-/under- fitting [47], and it was used to generate examples of the retrospective dataset with the selected features. Tabu Search, a metaheuristic search method by using local search for mathematical optimization [48], was employed to generate a stable BN structure for pre-or during-treatment. It combined the selected biophysical variables through an iterative statistical resampling based on generating bootstrap samples of the original data to ensure robustness. In the meantime, radio- biologically plausible relationships among a set of selected biophysical variables related to LC were built among them by adding constraints to the Tabu Search and enforcing biophysical rules.

3. Cross validation-guided BN structure learning

While the inter-dependence between two associated biophysical factors is represented by an edge/arc in a BN, the degree of their dependence can be described by the strength of the edge/arc between them [44], and the larger strength value represents stronger dependency. Assuming that the edge can disappear if its strength is less than a threshold, it is possible to remove the relatively weak interactions among the predictors in the BN in terms of LC prediction by increasing the threshold of edge strength towards a stable BN obtained from bootstrap resampling.

A node without any descendant related to LC is considered as a leaf node, and it has limited contribution to LC prediction compared to other predictors. The BN with appropriate biophysical interactions based on the eMB neighborhood approach may or may not have a good LC prediction performance, since when each predictor and edge is able to contribute to biophysical information for LC prediction, they may also cause noise at a certain level. Therefore, the BN’s prediction performance could be improved by removing such leaf nodes and keeping appropriate edge strength threshold to balance loss of information and noise reduction. This was the underlying idea of the BN structure learning to achieve a more robust model.

The BN structure learning was guided by the performance of resulting BN for LC prediction. CV is a re-sampling technique that was employed to prevent over-fitting by assessing how a statistical model will generalize to an independent dataset [49], and Receiver Operating Characteristic (ROC) curves were generated to evaluate the prediction power of a prediction model based on CV. The ROC curves show the trade-offs between true positive and false positive rates for a given diagnostic task, and the Area Under the ROC Curve (AUC) provides a single measure of the performance of a classifier by assigning 0.5 to a random signal and 1.0 to a perfectly discriminant signal. In the training data, there are only 20 local failure events in 68 patients. Therefore, a stratified CV approach was used to avoid the problem of imbalanced event rates [50] in the training and the testing datasets.

D. Performance measurement

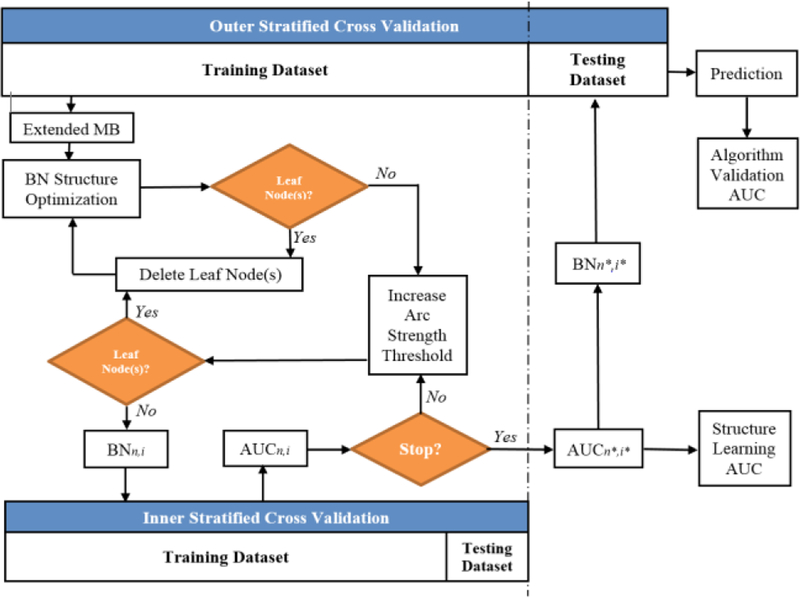
A nested cross-validation (N-CV) approach was also generated to evaluate the performance of the overall BN approach as shown in Fig. 1, where outer loop stratified CV is conducted based on the discovery dataset and inner loop stratified CV is employed to guide BN structure learning within each iteration of the outer CV. Let N or I be the set of predictors or the set of threshold levels of arc strength to build a BN during an iteration of outer CV, n or i be the index of the number of these predictors (n∈ N) or the index of these threshold levels (i∈ I), and a BN generated from the training dataset of the outer loop CV can be described as BN_n,i. The prediction performance of BN_n,i evaluated by the inner loop CV can be denoted as AUC_n,i. During the process of the current BN approach, the values of AUC_n,i vary as the number of the nodes and the thresholds of arc strength change. Let AUC_n*,_i* denote the maximal value of AUC_n,i, and n* and i* indicate the number of predictors and the threshold level associated with it respectively (n* ∈ N, l* ∈ I). Then, the best BN guided by the inner loop CV based on the training dataset of the outer loop CV can be denoted as BNn*,i*, and it was used to predict the patients’ LC in the reserved testing dataset. After stacking the patients’ LC prediction from all iterations of the outer loop CV, the ROC curve for evaluation of the performance of the current BN approach was obtained.

Fig. 1.

The process of validating the current two-step BN approach with N- CV.

E. Sensitivity analysis by ensemble BN

The subset of retrospective data reserved for validation were patients who had incomplete data for more than two categories. In order to obtain stable BN models for LC prediction, these patients (n=50) were not considered in obtaining pre- and during-treatment full BN models although there are many approaches that can be used to impute the missing information. In this study, the stability of the full BN model was measured by developing the following ensemble BN model approach. A leave-one-out CV (LOO-CV) was employed for the outer loop CV as shown in Fig. 1, and the total number of the best BN structures from the N-CV is equal to the number of the patients in the discovery dataset. Each BN was converted into an adjacency matrix where an element in the matrix indicates the strength of connection between each pair of features in the BN. The matrix of ensemble BN models can be obtained by simply combining all these adjacency matrices together, where a number in the combined matrix indicates the importance of a connection in the ensemble BN model.

If a strength threshold is assigned to the ensemble matrix, the numbers become zero when their values are greater than a given threshold, or are kept the same otherwise; a feature with zero in both its column and row of the matrix is redundant and can be eliminated from the ensemble BN. In this fashion, the number of nodes in the ensemble BN model could be adjusted with different thresholds, and its scale could be reduced to meet the rank of the full BN model with appropriate strength threshold. Since the latter could also be converted to an adjacency matrix as well, the sensitivity of the current BN approach was evaluated by the similarity of the matrices from the ensemble BN model and its associated full BN model.

Mantel test [51] is a statistical test of the correlation between two dissimilarity matrices, and it intends to answer the basic question, “How often does a randomization of one matrix result in a correlation as strong or stronger than the observed correlation?”. The standardized Mantel statistic (r) is calculated as the usual Pearson product-moment correlation coefficient between the two matrices.

III. RESULTS

A. Pre-treatment full BN and its prediction performance

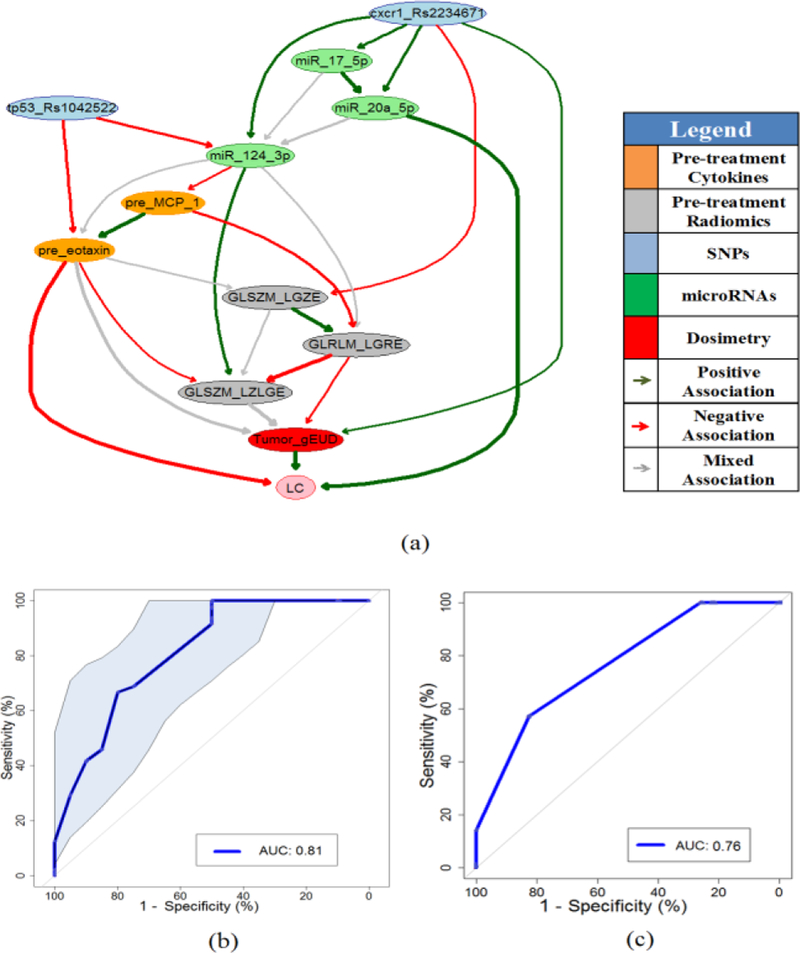
The MB of LC based on the discovery dataset is formed from “miR-20a-5p”, “pre-eotaxin”, “GLSZM-LGZE”. Moreover, each of these variables may have its own MB neighborhood as shown in Fig. 2. For example, “miR-17–5p”, “miR-93–5p”, “miR-124–3p”, and “Tumor-gEUD” from the MB of “miR-20a- 5p”. In this study, the eMB neighborhoods within two layers of LC were used as potential variables of pre-treatment full BN.

Fig. 2.

The extended MB (eMB) neighborhoods of LC before radiation treatment, where the second column shows the inner family of LC and the third column shows the next-of-kin for each of its member.

Fig. 3(a) shows a stable pre-treatment full BN with an edge strength ≥ 0.65, where eleven important biophysical predictors are identified. Their relationships in terms of LC prediction are indicated by directed edges, and the thickness of an edge represents the strength of a connection. While the green and red lines represent positive and negative influences between the connected predictors, respectively, the grey lines indicate the mixed positive and negative influences between them.

Fig. 3.

(a) Pre-treatment full BN for LC prediction. (b) The ROC curve of pre- treatment full BN as shown in Fig.3(a) based on CV with the discovery dataset, where shadow area indicates the 95% confidence interval of the AUC. (c) The ROC curve of pre-treatment full BN for the validation dataset.

A balanced 7-fold cross-validation (about 10 samples per fold), which maintained the same ratio of event-to-no event in each fold in both training and holdout, was employed to guide predictor pruning and to find a robust BN structure with a high LC prediction power. In the meantime, it was also used to evaluate the performance of pre-treatment full BN in the discovery dataset as shown in Fig. 3(b), where the AUC value is 0.81 with a 95% confidence interval of 0.69–0.90 based on 2000 stratified bootstrap replicates. In comparison, the main dosimetric predictor (Tumor_gEUD) had an AUC of only 0.61 with a 95% confidence interval of 0.51–0.75 from 2000 stratified bootstrap replicates. For the validation dataset, the ROC curve of pre-treatment full BN is illustrated in Fig. 3(c) with an AUC=0.76.

B. During-treatment full BN and its prediction performance

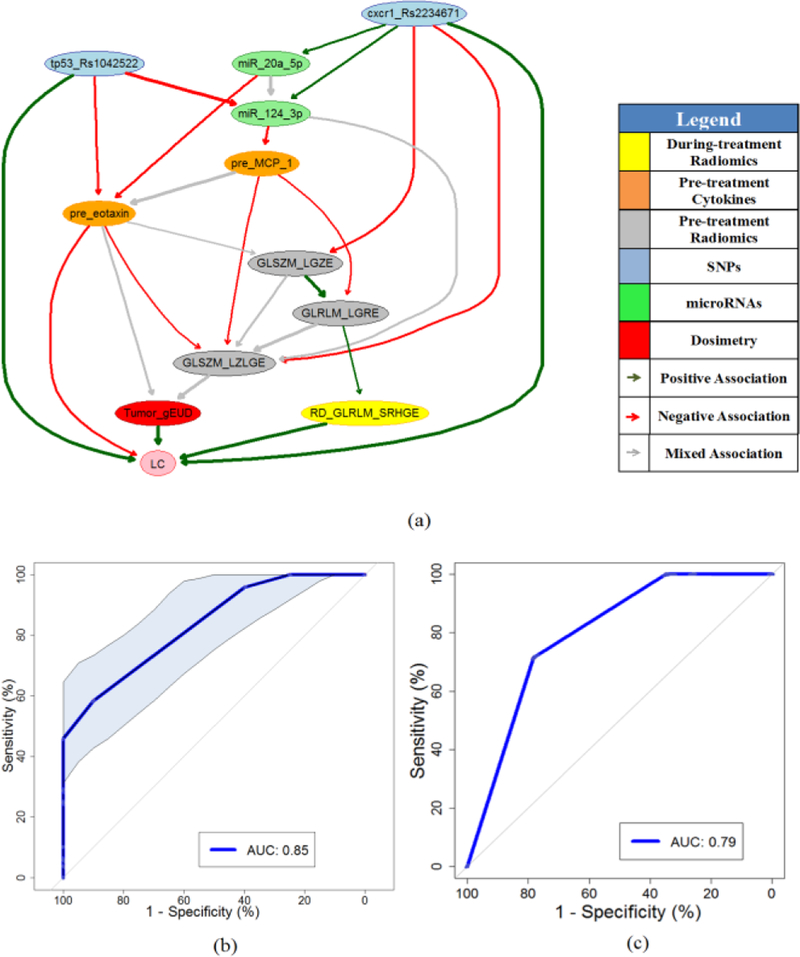
In an extended LC prediction model, the relative changes of PET features before and during-treatment were incorporated as part of the patients’ response during the course of radiotherapy. The important biophysical predictors for LC prediction during radiation treatment can be found from the SI-HITON-PC algorithm. The updated eMB neighbourhoods are shown in Fig. 4.

Fig. 4.

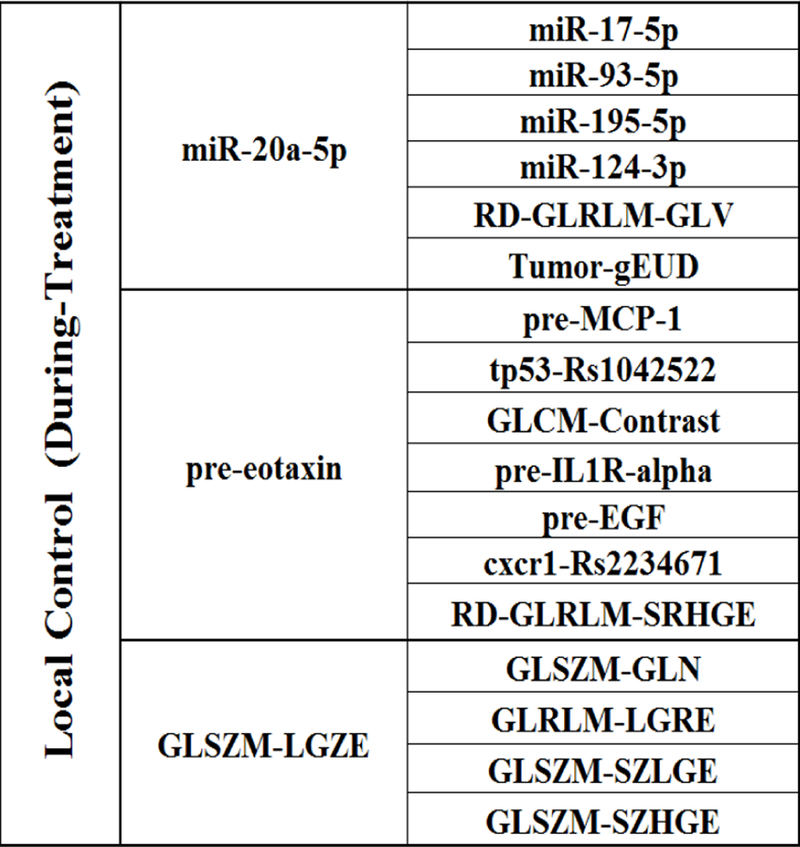
The extended MB (eMB) neighborhoods of LC during radiation treatment, where the second column shows the inner family of LC and the third column shows the next-of-kin for each of its member.

A during-treatment full BN with edge strength ≥ 0.68 was developed via BN structure learning and predictor pruning as illustrated in Fig. 5(a). Fig. 5(b) shows the ROC curve of the during-treatment BN based on 7-fold cross validation within the discovery dataset, and the AUC of the internal testing cross validation is 0.85 with a 95% confidence interval of 0.75–0.93 based on 2000 stratified bootstrap replicates. Fig. 5(c) presents the ROC curve of during-treatment full BN for the validation dataset with an AUC=0.79. The pre- and during-treatment full BN networks are defined by conditional probability tables (CPT) that are associated with each node, and their detailed information are available from the authors.

>Fig. 5.

(a) During-treatment full BN for LC prediction. (b) The ROC curve of during-treatment full BN as shown in Fig.5(a) based on CV with the discovery dataset, where shadow area indicates the 95% confidence interval of the AUC. (c) The ROC curve of during-treatment full BN for the validation dataset.

C. The results of N-CV and Mantel test

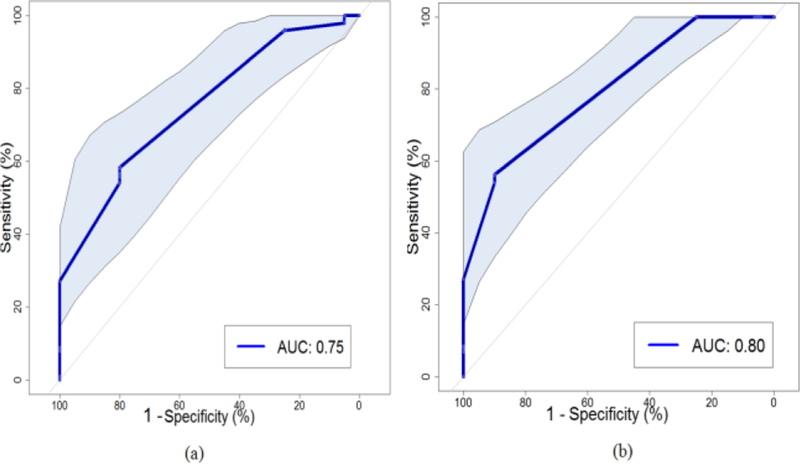
The performance of the two-step BN approach can be validated by the N-CV as shown in Fig. 1. With the pre- treatment discovery dataset, the ROC curve of the current BN approach can be described in Fig. 6(a), and its performance reaches an AUC=0.75 with a 95% confidence interval of 0.64– 0.86 based on 2000 stratified bootstrap replicates. After considering additional during-treatment information, the ROC curve of the BN approach is illustrated in Fig. 6(b), and its performance increases to an AUC=0.80 with a 95% confidence interval of 0.71–0.89 from 2000 stratified bootstrap replicates.

Fig. 6.

(a) The ROC curve of the whole process of single structure BN approach with the pre-treatment discovery dataset based on the N-CV, where shadow area indicates the 95% confidence interval of the AUC. (b) The ROC curve of the whole process of current BN approach with the whole discovery dataset based on the N-CV with 95% confidence interval of the AUC.

The Mantel test was applied to measure the similarity between the ensemble pre- and during-treatment BNs and their corresponding full BNs. Mantel statistic r (original data correlation) of 0.408 or 0.419 show that there is a relatively strong positive correlation between them for the before or the during treatment, and the p-value of 0.001 in both cases indicates the correlations are statistically significant at an alpha of 0.05.

IV. DISCUSSION

A. Main Findings

The contributions of this work can be summarized as follows. First, a large-scale BN analysis was developed to unravel biophysical interactions behind LC through the use of a new eMB approach to demonstrate its utility as a feature selection technique when the ratio of the variables to the samples is high. Secondly, it is noted that mid-treatment information had added value. This could be explained by the fact the initial dose received acts as a probe that would further improve one’s understanding of the response that the patient is likely to have. Thirdly, it was also shown that the full BN model has excellent robustness characteristics to missing information in the case of the validation dataset, and had a consistent performance across the discovery and the validation datasets. Finally, we have demonstrated that our BN approach is a stable and robust approach to find hierarchical relationships among biophysical features for LC prediction before and during the radiotherapy by comparison with ensemble BN models.

The developed BN is not only able to predict LC, but also can be used to provide an understanding of the underlying LC radiobiology, which is essential for understanding molecular mediators of response and for the development of targeted interventions as discussed below. Clinically, this would allow one to conduct personalized treatment planning based on individual’s characteristics. Following the arrows entering node “Tumor_gEUD” in Figs. 3(a) and 5(a), appropriate radiation dose to increase the probability of LC could be predicted by the patient’s characteristics including SNPs, miRNAs, cytokines, and PET information.

B. Mechanistic Biological Interpretation of the Full BN Models

The current study of genetic variants identified two SNPs: tp53-Rs1042522 and cxcr1-Rs2234671 that were specifically prominent in the dataset. TP53, a tumor suppressor gene, plays a critical role in cell cycle control, apoptosis, and DNA damage repair [52]. Mutations in the TP53 tumor suppressor gene are the most frequent genetic alterations in human cancer and commonly compromise the gene’s tumor suppressor activity [53]. Studies showed that the variant genotype of TP53 SNP rs1042522 significantly increased lung cancer risk in the total population [54], and tumor-derived CXCL1 contributes to tumor associated neutrophils infiltration in lung cancer, which promotes tumor growth [55]. Moreover, the polymorphism rs2234671 at position Ex2+860G > C of the CXCR1 gene causes a conservative amino acid substitution (S276T), and this SNP seemed to be functional as it was associated with decreased lung cancer risk [56].

The role of microRNAs was also demonstrated in the early stages of disease progression and metastasis [57]. Mir-20a was found to be associated with lung cancers, and is encoded by a gene located on chromosome 13q31. Mir-20a is involved in several oncogenic processes like proliferation, angiogenesis and apoptosis through the regulation of a multitude of target genes [58]. One example of the regulation of tumor cell proliferation through this family of miRNAs is the transcription factor E2F1, which is involved in cell cycle progression and has been shown to be regulated by two miRNAs of this family, miR-17–5p and miR-20 [59]. Moreover, Lin et al. suggested that miR-124 function as a tumor suppressor miRNA and suppress tumor proliferation and aggression by directly targeting oncogenic CD164 signalling pathway in NSCLC [60]. Taken together, these findings support the relationships between genetic variants and LC in our BNs. However, further testing and validation ae still needed to confirm these relationships.

It has been recently demonstrated that tumor cell growth can be directly regulated by chemokines, a group of proteins originally discovered as chemoattractants and activators of specific subsets of lymphocytes [61–63]. CCL11 (eotaxin-1) is a member of the CC chemokine family most homologous to the monocyte/macrophage chemoattractant protein (MCP) subfamily [64]. Meaney et al. showed that elevated levels of eotaxin-3 were associated with shorter survival (P=0.043) [65]. MCP-1/CCL2 is one of the key chemokines that regulates migration and infiltration of monocytes/macrophages [66], and CCL2 expression in tumor cells is significantly correlated with the extent of tumor-associated-macrophage (TAM) infiltration [67]. Moreover, Cai et al. observed that MCP-1 levels were increased in lung cancer patients with bone metastases compared to patients with localized tumor. This study concluded that MCP-1 expression promotes lung cancer– induced osteoclast activity and thus results in bone resorptive lesions in vivo [68]. Kudo-Saito et al. demonstrated that CCL2/MCP-1 is a critical determinant for both tumor metastasis and immunosuppression induced by SNAIL positive tumor cells, and it is significantly upregulated in various human tumor cells accompanied by SNAIL expression induced by SNAIL transduction or TGF-β treatment [69].

Quantitative imaging information such as PET radiomics can help identify the status of tumor response. Molina et al. pointed out that run length matrix (RLM) allows for a better characterization of tumor heterogeneity, being able to describe complex 3D structures labelled with the same grey level values [70]. Association rule mining with 12 features such as GLRLM- LGRE image textures can distinguish malignant from benign masses with a level of accuracy of 92.3% [71]. Yang et al. also found that texture features derived from GLRLM, SRHGE exhibited significant temporal changes during the course of disease in patients with complete metabolic responders, and LGRE exhibited significant temporal changes in patients with partial metabolic responders/new disease during the course of disease [72]. GLSZM is an extension of GLRLM into a higher dimension (one-dimensional ‘runs’ into two-dimensional ‘zones’) [73], thus the two matrices may carry similar heterogeneity information and these features are expected to correlated [74]. These findings confirm the interaction among PET feature information shown in the current BNs. However, further testing and validation are still needed to confirm these relationships.

C. Limitations

Our approach is a data-driven, response-based to explore the relationship of biophysical factors leading to radiation-induced LC. However, the scope of this BN analysis is limited by the nature of the relatively small dataset used. Therefore, future studies are necessary to confirm and extend on current observations. Radiomics features were extracted from PET images only; it may worth extending the analysis to include CT images in future studies. Moreover, no shape descriptors were considered beyond the MTV, which may be also relevant. However, this would also require larger datasets too.

The novel relationships generated from the BN analysis would require further validation studies in vitro and in vivo. The estimated influences are calculated from the adjacent parent and children nodes, and may not necessarily reflect the accumulative effect or direct causal interaction of all variables along the network in reality. Other intermediate factors which are not included in the study may need to be considered as well. In the next step, we plan to enhance the current Bayesian network analysis, include known biological prior knowledge, validate the LC prediction model with larger external data set, and develop dynamic BNs to guide our personalized radiation treatment practice.

V. CONCLUSIONS

An extended large-scale Markov blanket algorithm was employed to identify treatment-relevant pan-Omics features from SNPs, miRNAs, cytokines, PET imaging and dosimetric information that are related to LC in a heterogeneous dataset. Biophysical interaction networks of LC using BN analyses of pre- and during-treatment information were subsequently developed. These BNs allow probing of the probabilistic relationship among these different factors and their hierarchal relationship with LC from genetic variants, imaging features, and changing cytokine levels induced by radiation, to predict tumor response and personalize radiation treatment. As presented in the discussion section on the mechanistic biological interpretation, our current results are generally aligned with known observations made in the literature of such relationships. Analysis of SNP’s, miRNAs and cytokines show an activation of signalling networks that is consistent with the maintenance of a cancer-permissive microenvironment that supports cancer cell proliferation, reduces treatment sensitivity and allows the establishment of an immune privilege. However, further testing and validation are still needed to confirm these relationships.

APPENDIX A. Table 1. Data Description

Categories	Names
Dosimetric Information (6)	Dosimetric information related to GTV composite: α/β= 10, gEUD with 𝛼 = −10, −20, Mean Dose, D5, D90, D95
Clinical Factors (14)	Smoking, COPD, Chemo, Gender, Adenocarcinoma, Squamous cell carcinoma, Large cell carcinoma, Poorly differentiated carcinomas, Stage, Age, GTV, KPS, Weight, Race.
Cytokines for pre and during treatment (30+30)	EGF, eotaxin, fractalkine, G-CSF, GM-CSF, IFN-γ, IL-10, IL-12p40, IL-12p70, IL-13, IL-15, IL-17, IL-1α, IL-1β, IL- 1ra, IL-2, IL-4, IL-5, IL-6, IL-7, IL-8, IP-10, MCP-1, MIP-1α, MIP-1β, sCD40L, TGFA, TNFA, VEGF, TGF-β1
PET information for pre and during treatment (43+43)*	MTV, Global-Var, Global-Skewness, Global-Kurtosis, GLCM-Energy, GLCM-Contrast, GLCM-Entropy, GLCM- Homogeneity, GLCM-IDM, GLCM-Correlation, GLCM-SumMean, GLCM-Variance, NGTDM-Coarseness, NGTDM-Contrast, NGTDM-Busyness, NGTDM-Complexity, NGTDM-Strength, GLRLM-SRE, GLRLM-LRE, GLRLM-GLN, GLRLM-RLN, GLRLM-RP, GLRLM-LGRE, GLRLM-HGRE, GLRLM-SRLGE, GLRLM-SRHGE, GLRLM-LRLGE, GLRLM-LRHGE, GLRLM-GLV, GLRLM-RLV, GLSZM-SZE, GLSZM-LZE, GLSZM-GLN, GLSZM-ZSN, GLSZM-ZP, GLSZM-LGZE, GLSZM-HGZE, GLSZM-SZLGE, GLSZM-SZHGE, GLSZM-LZLGE, GLSZM-LZHGE, GLSZM-GLV, GLSZM-ZSV
miRNAs (62)	let-7a-5p, miR-100–5p, miR-106b-5p, miR-10b-5p, miR-122–5p, miR-124–3p, miR-125b-5p, miR-126–3p, miR-134, miR-143–3p, miR-146a-5p, miR-150–5p, miR-155–5p, miR-17–5p, miR-17–3p, miR-18a-5p, miR-192–5p, miR-195– 5p, miR-19a-3p, miR-19b-3p, miR-200b-3p, miR-200c-3p, miR-205–5p, miR-21–5p, miR-210, miR-221–3p, miR-222– 3p, miR-223–3p, miR-224–5p, miR-23a-3p, miR-25–3p, miR-27a-3p, miR-296–5p, miR-29a-3p, miR-30d-5p, miR- 34a-5P, miR-375, miR-423–5p, miR-574–3p, miR-885–5p, miR-92a-3p, let-7c, miR-10a-5p, miR-128, miR-130b-3p, miR-145–5p, miR-148a-3p, miR-15a-5p, miR-193a-5p, miR-26b-5p, miR-30e-5p, miR-374a-5p, miR-7–5p, miR- 103a-3p, miR-15b-5p, miR-191–5p, miR-22–3p, miR-24–3p, miR-26a-5p, miR-20a-5p, miR-93–5p, miR-16–5p
SNPs (60)	Rs3857979, Rs235756, Rs1800587, Rs17561, Rs2070874, Rs1801275, Rs1800795, Rs4073, Rs2234671, Rs1800896, Rs3135932, Rs1800872, Rs180925, Rs11556218, Rs4760259, Rs1799983, Rs689470, Rs11939979, Rs11724777, Rs12102171, Rs6494633, Rs4776342, Rs12456284, Rs12913975, Rs12906898, Rs7227023, Rs7333607, Rs1800468, Rs1800469, Rs4803455, Rs1061622, Rs664677, Rs664143, Rs373759, Rs189037, Rs609261, Rs1800057, Rs3212961, Rs3212948, Rs11615, Rs238406, Rs13181, Rs17655, Rs1047768, Rs12917, Rs1805794, Rs1625895, Rs1042522, Rs25489, Rs25487, Rs6464268. Rs3218536, Rs1799796, Rs9293329, Rs1478486, Rs1040363, Rs2075685, Rs2228000, Rs2228001

^*PET features were extracted included widely used global, gray level co-occurrence matrix (GLCM), neighborhood gray-tone difference matrix (NGTDM), run-length matrix (RLM), and gray-level size-zone matrix (GLSZM).