Modelling drug transport during intraperitoneal chemotherapy

Abstract

Despite a strong rationale for intraperitoneal (IP) chemotherapy, the actual use of the procedure is limited by the poor penetration depth of the drug into the tissue. Drug penetration into solid tumours is a complex mass transport process that involves multiple parameters not only related to the used cytotoxic agent but also to the tumour tissue properties and even the therapeutic setup. Mathematical modelling can provide unique insights into the different transport barriers that occur during IP chemotherapy as well as offer the possibility to test different protocols or drugs without the need for in vivo experiments. In this work, a distinction is made between three different types of model: the lumped parameter model, the distributed model and the cell-based model. For each model, we discuss which steps of the transport process are included and where assumptions are made. Finally, we focus on the advantages and main limitations of each category and discuss some future perspectives for the modelling of IP chemotherapy.

Introduction

In 1978, Dedrick et al. [1] hypothesized that the peritoneum-plasma barrier, which was previously considered to be an obstacle for drug transport, might rather offer a unique treatment opportunity for patients with oncological malignancies confined to the peritoneal cavity. The idea was put forward that when cytotoxic drugs are administered directly into the peritoneal cavity, the peritoneum would limit the drug absorption in the systemic circulation. This would result in higher local drug concentrations in the tumour tissue while minimizing the development of systemic side effects, an idea that has been proven to be true by different groups since then [2, 3].

The higher drug concentrations that are locally obtained in the tumour tissue are important because of the steep dose–response relationship for cytotoxic agents on the one hand and because it can prevent the development of resistance of the tumour against the used chemotherapeutic agent. Additionally, some peritoneal metastasis are nearly avascular and are consequently not treatable by intravenous chemotherapy as there is simply no vascular drug source present within the tumour [4]. The direct contact between the cytotoxic drug and the tumour tissue does allow for these poorly vascularized tumours to be exposed to the chemotherapeutic agent. Additional to these high local tumour tissue concentrations, there is uptake of the drug by the vascular component of the tumour tissue which results in a systemic drug effect. This systemic effect is of the same order of magnitude as the one obtained during intravenous (IV) chemotherapy, meaning that for the same systemic toxicity, the local tissue concentration obtained by intraperitoneal chemotherapy can exceed the tissue concentrations that would be obtained by conventional chemotherapy [3].

Even though the rationale behind intraperitoneal chemotherapy (IPC) has been well established, it has not yet become standard of care mainly due to the limited penetration depth of the cytotoxic agent into the tumour tissue [5, 6, 7, 8, 9, 10]. Drug transport during IPC is a complex process that is governed by a multitude of parameters which can be separated in three distinctive categories: tissue-related parameters, drug-related parameters and therapy-related parameters (Table 1). In the next paragraph, an overview of the different steps that occur in the transport process during IPC will be given and all relevant parameters will be briefly discussed.

Table 1:

Summary of the parameters that are involved in the drug transport during intraperitoneal chemotherapy. The parameters are subdivided in three main categories: therapy related, drug related and tumour tissue related.

Therapy related	Drug related	Tumour tissue related
Dose	Molecular weight	Permeability
Temperature	Ionic charge	Vascularity
Carrier fluid	Membrane binding	Interstitial fluid pressure (IFP)
Volume of carrier fluid	Solubility	Cell density
Intra-abdominal pressure	Diffusivity	Extracellular matrix composition
Vaso-active agents
Surfactant use
Duration

Mathematical modelling of drug delivery started in the 1960s [11, 12] and has since then become an important tool for the cancer researcher due to its relative ease and its low cost. Furthermore, modelling of drug transport allows for the variation of single parameters over large ranges of values, which makes it especially suited to study the relative influence of parameters on therapeutic outcome without the need for expensive experiments. In this review, we will focus on the work that has been done on mathematical and computational modelling of intraperitoneally administrated anti-cancer drugs acting on tumour tissues. In this work, we chose to subdivide the existing models based on the used scale of the model. A distinction will be made between three different scales: the whole organ scale, which considers the peritoneum as a single compartment; the tissue scale, which considers the tissue of the tumour as a homogenous mixture of cells, interstitium and vasculature; and finally the cellular model, which models each cell explicitly.

It is important to note that even though mathematical and computational models are designed to mimic and predict natural behaviour, they remain a simplification of the reality and knowing which simplifications or assumptions are made is a crucial factor to consider when conclusions are drawn from the obtained results.

Drug transport steps during intraperitoneal chemotherapy

In this section, we summarize the path along which the intraperitoneally administrated drug will travel, the mechanisms behind this and discuss the barriers it might encounter on its path (Figure 1). Once administered in the peritoneal cavity, the cytotoxic drug has to be absorbed into the peritoneal tumour tissue. It has been shown that the peritoneal mesothelial lining does not constitute an explicit barrier for drug uptake [13, 14]. The administered dose and diffusion coefficient of the drug will determine the amount of drug that is initially available for transport. Cytotoxic agents do not remain stable over prolonged periods of time in the peritoneal cavity and their decay rate is an important factor that will influence the absorption. The remaining concentration of drug in the carrier fluid at each time point will also determine the concentration gradient and therefore the magnitude of the inward diffusive flux. The chosen carrier solution on the other hand will also have an influence on drug absorption: the amount of carrier fluid in the peritoneal cavity will determine how high the hydrostatic pressure is and will provide a driving force for the convectional transport across the peritoneum. Recently there has been an interest in the use of aerosols and an elevated intra-abdominal pressure as a means of increasing the contribution of convective transport to the drug transport [15]. Furthermore, other properties of the carrier fluid such as osmolarity might also influence this first step in the transport process [16, 17, 18]. Finally, temperature is also likely to have an influence as a higher temperature influences the diffusion coefficient through the Einstein–Stokes equation [19].

Figure 1:

Schematic representation of the drug transport process during intraperitoneal chemotherapy and some of its determining factors.

IFP, interstitial fluid pressure; ECM, extracellular matrix; MW, molecular weight. Source: Reprinted with permission from [4].

Once entered in the tumour tissue, the drug will penetrate deeper into the tumour by means of diffusive-convective transport. The diffusive transport will be dependent on the diffusivity constant of the drug in the extracellular fluid and the aforementioned used concentration of the drug. The convective transport on the other hand depends on both the tissue permeability and the fluid velocity. Tissue permeability is a parameter that describes the resistance that a porous medium (like human tissue) exerts on a fluid. The extracellular matrix (ECM) of solid tumours is composed of two main constituents: fibrous proteins (e. g., collagen, elastin) and polysaccharides (e. g., hyaluronan, glycosaminoglycan) [20]. Tumour tissue is characterized by an increased deposition of collagen I [21] and as a result, tumour stroma is characterized by increased stiffness when compared to normal tissue [22]. A difference in ECM composition and the higher cell density that is associated with tumours can lead to a difference in tissue permeability and therefore a different resistance to convective drug flow. The fluid velocity will be radially outward due to the high interstitial fluid pressure (IFP) at the centre of the tumour [23]. This characteristic elevated IFP is caused by a number of contributing factors, including the leaky and irregularly shaped microvasculature, the lack of a functional lymphatic system, a denser ECM, an increased number of cancer-associated fibroblasts (CAFs) and a larger cell density [24]. The higher the IFP is, the larger the drug outwash will be. Furthermore, not all drug molecules entering the interstitial space of the tumour remain available for transport as a fraction will bind (reversibly or irreversibly) to the proteins in the ECM.

As the therapy progresses, part of the drug entering the tumour tissue interstitium will be absorbed by the tumour vasculature and thereby add to the systemic effect of the therapy. The amount of drug that will cross the vascular wall will depend on drug-related parameters such as the osmotic reflection coefficient and the diffusion coefficient and on tissue-dependent parameters such as the surface to volume ratio of the vasculature, the vascular density, the permeability of the vessel wall for the drug, the oncotic pressure in both tissue and vasculature, the IFP and pressure in the vasculature and the plasma concentration of the drug. Uptake by the vascular component is a reversible process and therefore drug molecules can again enter the interstitial space from the blood pool.

From the interstitial space, the drug can then be taken up by cancer cells by both active and passive processes. Depending on the drug used, different mechanisms will be responsible for cellular uptake. The amount of drug that will be incorporated in the cells will depend on the cell-dependent factors such as cell density and drug-dependent parameters including size, charge and molecular weight, but also on other therapy related factors such as temperature, local drug concentration and duration. Table 1 summarizes the parameters that are involved in the drug transport during intraperitoneal chemotherapy that are mentioned above.

Whole body level: compartmental models

As mentioned in the introduction, the rationale and theoretical basics of intraperitoneal drug therapy were first described by Dedrick et al. [1]. In order to do so, a compartmental model consisting of two compartments was used. The first compartment consists of the entirety of all body water (contained intra- and extravascular, and intra- and extra cellular) and communicates with the second compartment, being the fluid in the intraperitoneal cavity. As the clearance for the peritoneal compartment, the product of the peritoneal permeability and the peritoneal surface area was used. Using this model and peritoneal permeability values estimated from literature, the authors predicted a difference of 1–3 logs between the drug concentrations in the two compartments, with the higher concentration predicted in the peritoneal compartment.

A different compartmental model considered the concentrations in and the exchange between extracellular and intracellular cisplatin in order to predict the dependence of cancer cell survival on the time course of extracellular drug exposure [25]. The model was created to test the validity of extracellular area under the curve (AUC) as a predictor of cytotoxicity, as experimental studies on this subject had shown conflicting results [26, 27]. The exchange between the compartments is considered to be reversible. Once it has entered the cells, the drug can either leave the cell again or bind to DNA. The DNA-bound cisplatin can then be released again during DNA repair but it will no longer be available for binding at that point [28]. The authors propose two different models for cell survival based on the calculated drug concentrations, and compare these with four others that were available in literature [29, 30, 31, 32] by fitting all models to three datasets available in literature [30, 33, 34]. It was found that the proposed models relating cell survival to the peak concentration of DNA-bound intracellular platinum provided the best fit for cisplatin cytotoxicity in three different cancer cell lines for a wide range of exposure times. The models were fitted to in vitro datasets and several transport parameters are therefore not included in this model (i.e. the vascular uptake, the uptake of the drug from the peritoneal cavity). It does however offer the opportunity to be incorporated in models that do include these transport steps and to serve as a bridge to the scale gap and offer an extra step in predicting therapeutic outcome.

In 2005, a three compartment model developed by Miyagi et al. [3] compared the resulting AUCs obtained by intravenous and intraperitoneal carboplatin administration. The three described compartments were the peritoneal cavity, the serum and the peripheral tissue compartment. The model contained five a priori unknown transfer coefficients: four inter-compartmental clearances and a plasma elimination factor. In order to estimate all parameters, a group of 22 patients received randomized treatment (11 IV/11IP) plasma and peritoneal drug concentrations were used to estimate all parameters on a patient to patient basis. Using these estimated parameters in the described three-compartment model to predict both the intraperitoneal AUC and plasma AUC yielded a good agreement between the calculated and experimental values. This work demonstrates an interesting technique to predict platinum AUC in the different compartments based on the total dose delivered, regardless of the administration route. The omission of the tumour as a separate compartment makes it however difficult to gain insight into therapeutic outcome and the dataset that was used to estimate the pharmacokinetic parameters was rather limited, resulting in high standard deviations for certain parameters.

To study the influence of co-administration of anti-angiogenic therapies on the drug penetration in tumours after intraperitoneal chemotherapy a physiologically based multi-compartment model was described by Shah et al. [35] Although the model presented in this work is a compartmental model, it does allow for the visualization of concentration profiles as the tumour is not modelled as a single compartment, but rather as five concentric spheres. Each of these five tumour layers communicates with both adjacent tumour layers and the vascular compartment except the innermost, which only communicates with the second layer and the vascular compartment and the outermost layer, which communicates with the layer below, the vascular component and the peritoneal space. The model predicted that when tumour blood flow was reduced by anti-angiogenic drugs (to 50, 75, and 90 %, of the baseline value of 0.06 mL/min/g) an increase in tumour drug concentration after intraperitoneal chemotherapy would be found.

Colin et al. studied the influence of the dosing of intraperitoneally administrated paclitaxel in a pharmacokinetics /pharmacodynamics (PK/PD) model [36]. Key findings of the models include the observation that the AUC of the drug in the tumour compartment reaches a maximum at a particular paclitaxel concentration and increasing the concentration beyond this point will not increase the AUC in the tumour anymore. Given the fact that the AUC in the plasma compartment does not exhibit this saturation behaviour, the model can then be used to estimate, for each therapy duration, an optimal paclitaxel dose for which the AUC in the tumour compartment over the AUC in the plasma compartment ratio is as high as possible.

Although these compartmental parameter (Figure 2) models can accurately predict peritoneal, plasma, intracellular and extracellular drug concentrations based on the pharmacological data present in literature, there are certain inherent features of all compartmental models that limit their relevance. The first limitation is the assumption that each compartment is a homogeneous well-mixed entity. It is therefore impossible to obtain concentration gradients within a certain compartment (e. g. tumour tissue) using a lumped parameter model. Furthermore, as the name suggests, these lumped parameters do not reflect a single physiological process but are rather representing the lumped effect of several processes and it might therefore be difficult to gain more insight into the exact physiological processes that underlie the result.

Tissue level: distributed models

Due to the need for a better understanding of the actual transport process within the tissue and to have the possibility of calculating concentration gradients and profiles (Figure 3), a first distributed model for peritoneal drug transport was described by Flessner et al. [37]. In this model, the tissue space is considered to be distributed. A mass balance equation for the drug, taking into account the diffusion and convection in the tissue surrounding the peritoneal cavity as well as the exchange with a vascular component is solved in the distributed peritoneal tissue compartment. Simulations were performed using drug properties of sucrose. One of the assumptions made in this early work was that the rate of convection in tissue can be approximated by an average value. In a follow-up paper the group validated the model using autoradiographic images and an agreement was found between measured and simulated pressure profiles [38]. A clear overview of the differences between a lumped parameter compartmental model and a distributed model of IPC was published in 1985 by Dedrick et al. [39]. Further advances using this model were done by Statchowska-Pietka et al. [40] and Flessner et al. [41] in order to include pressure gradients.

Figure 3:

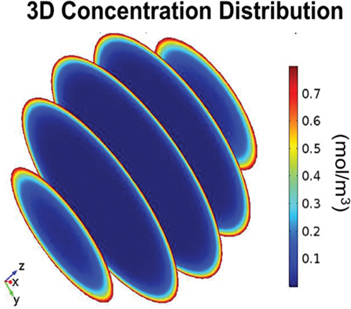
Spatially varying cisplatin concentration after intraperitoneal chemotherapy in a spherical tumour nodule.

Source: Reprinted from [50].

Figure 2:

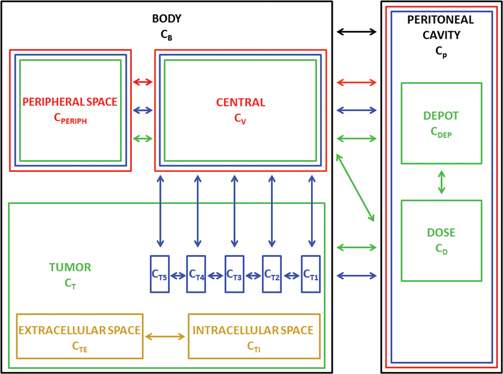
Schematic representation of the five different compartmental models highlighting their mutual relationships.

The model by Dedrick et al. [1] is shown in black, the one of El-Kareh et al. [24] in yellow, the one of Myjagi et al. [3] in red, the one by Colin et al. [35] in green and the one by Shah et al. [34] in blue.

Similarly, further research on the lumped parameter model by El-Kareh et al. [42] included the simulation of the effect of hyperthermia on the drug penetration distance. As opposed to their previous work however, the peritoneal surface was considered separately and an equation was formulated that described the (one-dimensional) transport of drugs into the peritoneal tissue. Factors included in this equation were the inward diffusive drug transport from the peritoneal cavity and the clearance between extracellular and intracellular compartment. To account for the effect of hyperthermia, two different approaches are pursued. The first one involves the use of extracorporeal heat sources, resulting in a uniform tissue temperature and the second one involves the administration of heated drugs. In the latter case, the temperature gradient along the tissue is described by the bioheat equation, which describes the temperature distribution in the living tissues based on the provided boundary conditions [43]. The effect of the temperature on the vascular component is included by changing the surface to volume ratio of the vasculature as well as the perfusion parameter. Furthermore, based on the experimental observation that cellular uptake of cisplatin increases for increasing temperatures [44, 45], the clearance from the interstitial towards the intracellular component was increased. A similar choice to increase the rate of DNA binding was made based on the experimental observation that the same concentration of cisplatin causes a higher cytotoxic effect at higher temperatures [45, 46]. A notable result of the model was that the elevated intracellular platinum levels up to a depth of 3–5 mm [6] were due to penetration of heat, causing increased cell uptake of drug. Limitations of the model included the omission of the high IFP and resulting radially outward convective flow, the ECM drug binding and the effect of increased temperature on the diffusion coefficient.

In 2014, a spatiokinetic model for interperitoneal administration of paclitaxel was described by Au et al. [47]. In a single spherical tumour nodule model (r=2 mm) which consists of three separate layers, the cellular level of the tumour tissue was averaged and modelled as a homogeneous, isotropic porous medium. Similarly, vasculature was not explicitly taken into account, but the vascular component of the tissue was considered to represent a homogeneous source and sink term for both paclitaxel and interstitial fluid. These assumptions reduced the momentum conservation equation to Darcy’s law and allowed for the incorporation of a source term of interstitial fluid in the mass conservation equation to represent the build-up of the high IFP. This mass source term was modelled after the Starling law, an approach first described in the context of IFP build-up by Baxter and Jain [48]. Three different equations for drug transport were written for each of the considered species: the transport of drug in the vascular component, transport of the unbound drug and the transport of the drug immobilized on the cells. Data used to describe the relation between bound and unbound drug was based on previous experimental studies of the same group [49, 50]. The drug concentration boundary conditions imposed at the edge of the tumour and in the vascular component were also based on prior experiments by this group. This model is, to the best of our knowledge, the first model for IP tumour that incorporates spatially varying parameters by assigning three different zones. Parameters that were assumed to be spatially varying were the volume fractions of the different components (interstitium, vasculature and cellular), the drug diffusivity, the surface to volume ratio of the vascular component, and the tissue permeability. The model was validated using the data of a mouse model with IP tumours (n=4) and the experimental results were in good agreement with the simulated results with a 1 % deviation for the total drug AUC and 23 % deviations for individual data points [47].

Based on the groundwork done by Baxter and Jain on the drug transport in solid tumours [48], our group created a parametric single tumour nodule model to study the influence of several different parameters on the penetration depth of various drugs (cisplatin, paclitaxel)[51]. Six different geometries were created to mimic the wide variety in shape and size existing among peritoneal tumour nodules (r_min=1 mm, r_max=4 mm). In each of these geometries, equations of mass and momentum conservation were solved as well as a drug transport equation in which vascular re-uptake (both by diffusion and convection) and cell uptake were included in addition to the diffusion and convection terms. Interestingly, the model showed that the presence of a necrotic core and permeability of the tumour tissue had very little effect on the penetration depth of the drug. Smaller tumours showed better penetration than larger ones, which could be attributed to the lower IFP in smaller tumours. Furthermore, the model demonstrated significant improvements in penetration depth by subjecting the tumour nodules to vascular normalization therapy, and illustrated the importance of the drug that is used for therapy. Overall, a shape effect could also be noted in the non-symmetrical geometries, highlighting the importance of using 3D geometries. The obtained penetration depths were compared to values in literature and a close agreement was found (simulated penetration depth range of 0.36–0.49 mm; experimentally defined range of 0.41–0.56 [9]). Similar agreements were found when vascular normalization therapy was applied in our model and the resulting penetration depths were then compared to the recent experimental data in which IP tumours were pre-treated with several different VEGF (R) inhibitors to normalize the microvasculature before subjecting them to IP chemotherapy [52] (simulated penetration depth range 1.6–2.1 mm; experimentally defined 1.68 mm).

Cellular models

To study the tumour penetration of cisplatin and pertuzumab when delivered by two alternative routes (IV/IP) in disseminated ovarian cancer a cellular Potts model (CPM) was used by Winner et al [53]. In this type of model a lattice-based computational modelling method is used to simulate the collective behaviour of cellular structures [54, 55]. Each lattice site represents a single cell and during each timestep transport equations for IL-8, Growth Factor 2, VEGF and oxygen were solved for each cell (Figure 4). According to their local chemical concentrations, each cell will then update their current state after which the cell lattice is then updated assuming chemical concentrations stay constant. The CPM model for ovarian cancer (OvTM) was first proposed by the same group to study ovarian cancer cell attachment, chemotaxis, growth and vascularization [56] and was then extended to include a transport equation for the used drug. The drug concentration in both the vasculature and the peritoneal fluid at each timepoint was estimated from data in which simultaneous measurements of the drug concentration in plasma and ascites were performed after administration by either route [56]. In addition to avascular tumours, small vascular tumours with vascular densities ranging between 2 and 10 % were also studied. This range of used vascular densities was based on the analysis of nine ovarian cancer patient samples. Using this model, the authors found that the intraperitoneal infusion route is the superior route for drug delivery for both investigated drugs (cisplatin and pertuzumab) and both investigated tumour types (avascular tumours and small vascular tumours). The vascular density did influence the accumulation of drug in the tumour and a sink effect could be noted due to the presence of the vessels. These sinks caused drug accumulation patterns that were noticeably less spatially homogeneous. This is, to the best of our knowledge, the only spatial model currently available in the context of intraperitoneal drug therapy that explicitly models the tumour vasculature instead of a distributed source. Limitations include the omission of the effect of the convective bulk interstitial fluid flow on drug concentrations and the use of fixed concentration profiles obtained from literature in both the IP and IV compartment during both delivery routes. Also, the very high spatial and temporal resolution of the model results in simulation durations in the range of 6–9 days for a single simulation.

Figure 4:

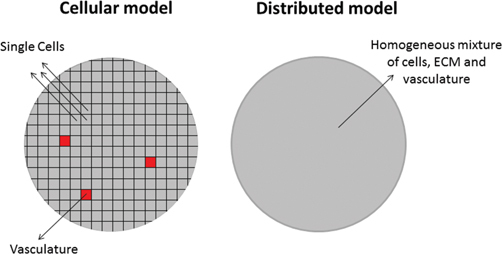
Schematic representation of the lattice used in the described cellular Potts model [53].

Each computational cell represents either a single cell or a vascular component. This method differs from distributed models (right-hand side) where all cells in the computational domain represent a homogeneous mixture of cells, extracellular matrix and vasculature.

Conclusions and future directions

In this review, we discussed various models that were created to study the drug transport that occurs during intraperitoneal chemotherapy. Although all relevant transport steps during IP chemotherapy have been modelled, there is to date no model that is able to fully model all the complex processes that are occurring during IP chemotherapy such as the uptake of the drug from the carrier fluid, the diffusive-convective transport of the drug in the interstitium, the cell binding and uptake of the drug, the vascular uptake and systemic effect of the drug, etc.. The existing models are diverse and each one is neither good nor bad but comes with its own set of advantages and limitations.

The models were categorized based on the length scale over which the drug concentration was averaged. Traditionally, the most abundant models in this context were the compartmental models. These models have the advantage that they are easy to fit to experimental data, and can accurately predict the concentrations of the drug in multiple organs. They, however, cannot describe gradients within different compartments nor can their parameters be directly related to the underlying transport processing.

The distributed models considered tissue to be a continuous mixture of several cell types. The advantage of this technique is that resulting drug profiles can easily be visualized and the processing of larger tumours can still be done in a reasonable timeframe. It is however not possible to gain information from these models on the single cell level.

In cell-level models, modelling single cell uptake of nutrients and drugs becomes possible. These models are a good fit to describe the naturally very heterogeneous nature of cancerous tissues. The main limitation of these models is that the high spatial resolution comes at a high computational cost. Furthermore, due to the high spatial resolution, the temporal resolution also has to be sufficiently high, thereby further adding to the computational cost.

In numerous works the drug transport is said to be diffusion driven, and often the radially outward convective flow is neglected in these models. Given the strong influence of the high IFP on the drug penetration both in IV and IP chemotherapy models [51, 57], models incorporating this convective interstitial fluid (IF) flow might be more suited to determine which transport processes are limiting in different cases. In the context of IV chemotherapy, there have been some reports of the use of spatially varying parameters that were determined on a pixel to pixel basis from imaging data [58, 59]. The incorporation of accurate IFP profiles might offer a significant advantage over using an idealized pressure profile. Au et al. [47] created three different tumour zones in their model to account for the spatial variations of certain parameters within the tumour tissue.

For IV and intratumour drug delivery, several distributed models have been described based on patient datasets [60, 61, 62, 63]. To date, no such patient-specific models have been described in the context of IP chemotherapy. Given the size and shape effect of the tumour on drug penetration that our group found, the accuracy of the model might benefit of the use of realistic geometries. Furthermore, none of the distributed models accounted for the vasculature in an explicit way. Vessels have been shown to act as local sinks for drug molecules [64] and drug distribution in the tumour is expected to be more heterogeneous than predicted by these distributed models. The CPM described by Winner et al. [53] does model the vascular component explicitly and their findings illustrate the occurrence of a more heterogeneous drug distribution.

Most investigated models limited the studied timeframe to a period in which it is safe to say that no tissue growth or remodelling will occur. This assumption allows for all tissue-related parameters to remain constant during the procedure duration. Exception here is the work by Winner et al. in which growth and tissue remodelling are explicitly present in the model on a single cell level [53]. Additionally, the work by Colin et al. [36] does estimate the changes in tumour volume based on a PDPD link suggested by Ait-Oudhia et al. [65]. Given the recent interest in metronomic chemotherapy in the context of IP chemotherapy [66], extending models to include growth and cell survival might become more frequent.

A main limitation of mathematical models in the context of cancer is that validation of the model can be quite difficult. Two different types of validation are necessary: the single parameter validation and the full model validation. The behaviour of each of the different presented models in this work is governed by a number of parameters. Reliable values for these parameters might not be available in literature and experimental determination of these single parameters is needed. These single parameters can be notoriously difficult to quantify due to the interference with other parameters. The full model also has to be validated, this can be done in vitro, in animal models and using clinical data. It is important to note however that due to the high number of parameters in most models, and the often limited sample sizes in validation studies, care should always be taken not to over-fit the model to a certain dataset.

In summary, mathematical modelling has shown some promising insights into the transport processes of drugs during IP chemotherapy and could identify new strategies to improve penetration deeper into the tumour tissue. The amount of work done in this field is however still quite limited. Far more work has been done in the modelling of IV chemotherapy and extensive reviews about mathematical modelling of drug penetration in tumour tissue and multiscale cancer modelling have recently been published [67, 68].