Visual control of walking speed in Drosophila

Summary

An animal’s self-motion generates optic flow across its retina, and it can use this visual signal to regulate its orientation and speed through the world. While orientation control has been studied extensively in Drosophila and other insects, much less is known about the visual cues and circuits that regulate translational speed. Here we show that flies regulate walking speed with an algorithm that is tuned to the speed of visual motion, causing them to slow when visual objects are nearby. This regulation does not depend strongly on the spatial structure or the direction of visual stimuli, making it algorithmically distinct from the classical computation that controls orientation. Despite the different algorithms, the visual circuits that regulate walking speed overlap with those that regulate orientation. Taken together, our findings suggest that walking speed is controlled by a hierarchical computation that combines multiple motion detectors with distinct tunings.

eTOC Blurb

During navigation, animals regulate both rotation and translation. Creamer et al. investigated how visual motion cues regulate walking speed in Drosophila. They found that orientation and walking speed are stabilized by algorithms with distinct tunings but employ overlapping circuitry.

Introduction

As animals navigate the world, they use visual information to regulate both their orientation and their speed (Etienne and Jeffery, 2004; Gibson, 1958; Srinivasan et al., 1999). When an animal rotates or moves, stationary objects in the world generate optical flow fields across its retina. These fields contain many motion cues that could guide navigational behaviors (Heeger and Jepson, 1992; Koenderink and van Doorn, 1987; Lappe et al., 1999). In many animals, including flies, the circuits and behaviors underlying orientation control have been the subject of extensive study (Oyster, 1968; Oyster et al., 1972; Portugues and Engert, 2009; Silies et al., 2014; Waespe and Henn, 1987), but the circuits and behavioral algorithms underlying translational control have been far less studied. Here, we use the fruit fly as a model system to dissect the behavioral algorithms and visual circuits that regulate walking speed and to investigate how multiple motion-detecting circuits drive different navigational behaviors.

In visual circuits, motion-detecting cells are often categorized into two broad classes: those that are tuned to the temporal frequency (TF) of the stimulus and those that are tuned to its velocity. These classes are simplified descriptions of response properties, yet they serve as a useful abstraction for thinking about the properties and algorithms involved in direction-selectivity. Cells can be categorized into these classes based on their responses to drifting sine wave gratings. Responses that are TF-tuned respond most strongly to a single TF (the ratio of the stimulus velocity to its wavelength). Thus, responses depend on both the stimulus velocity and its spatial structure, making them pattern-dependent (Srinivasan et al., 1999). Such cells are found near the periphery of visual processing in mammalian retina (Grzywacz and Amthor, 2007; He and Levick, 2000), in mammalian V1 (Foster et al., 1985; Talebi and Baker, 2016; Tolhurst and Movshon, 1975), and in wide-field motion detectors in insects (Haag et al., 2004; Ibbotson, 1991; Schnell et al., 2010; Theobald et al., 2010). TF-tuning can be obtained from models with only a single timescale and length scale (Egelhaaf et al., 1989; Reichardt and Varju, 1959), suggesting an elemental underlying computation. In insect behavior, flies turn in the direction of wide-field motion in a TF-tuned response that acts as a negative feedback control mechanism for course stabilization (Borst and Egelhaaf, 1989; Fermi and Reichardt, 1963; Gotz, 1964; Kunze, 1961; McCann and MacGinitie, 1965; Reichardt and Poggio, 1976; Reichardt and Varju, 1959). This behavior is known as the optomotor rotational response and is well-described by the Hassenstein Reichardt correlator (HRC) model for motion detection (Egelhaaf et al., 1989; Hassenstein and Reichardt, 1956). Over the past 60 years, this behavior and the HRC model have been the subject of intensive research and have been foundational in understanding direction-selective algorithms and circuitry across many animals (Adelson and Bergen, 1985; Hassenstein and Reichardt, 1956; van Santen and Sperling, 1984), and especially in insects (Silies et al., 2014).

Cells in the second classification are tuned to the speed of drifting sine wave grating stimulus, independent of its spatial structure (i.e., wavelength). These sorts of speed-tuned neurons are found in pigeons (Crowder et al., 2003), monkey cortical area MT (Perrone and Thiele, 2001a; Rodman and Albright, 1987), and insect descending command circuits (Ibbotson, 2001). The tuning to speed rather than TF suggests that the computations underlying these signals integrate multiple timescales and length scales (Hildreth and Koehl, 1987; Simoncelli and Heeger, 1998; Srinivasan et al., 1999). In insect behavior, observations of flying honeybees and flies have shown that visual control of flight speed appears to be independent of the spatial structure of the stimulus (David, 1982; Fry et al., 2009; Srinivasan et al., 1996), suggesting that they employ speed-tuned algorithms to regulate flight speed. However, the behavioral algorithms and visual circuits used to regulate translation remain largely unknown.

Little is known about how the fruit fly Drosophila regulates its walking speed. It is unknown whether it employs the same visual algorithms that regulate orientation and whether walking speed is governed by the same visual circuits that regulate optomotor turning responses. It has been shown that visual motion stimuli cause flies to slow (Götz and Wenking, 1973; Katsov and Clandinin, 2008) and that some early visual neurons contribute to both optomotor turning and walking speed (Silies et al., 2013). Here, we combine behavioral measurements, genetic silencing, imaging, and modeling to investigate how walking speed is regulated in Drosophila. We find that flies stabilize and modulate walking speed with a computation that is tuned to the speed of a visual stimulus, not to its temporal frequency, and thus cannot be represented by the classical HRC algorithm. The computation causes flies to slow as they pass nearby objects or surfaces. Interestingly, the visual stabilization of walking speed is implemented by circuits that overlap with those that control orientation, suggesting that these circuits play multiple roles in multiple classes of motion computation. These findings reveal the first instance of speed-tuning in a model organism that permits genetic circuit dissection.

Results

Flies turn and slow in response to visual motion

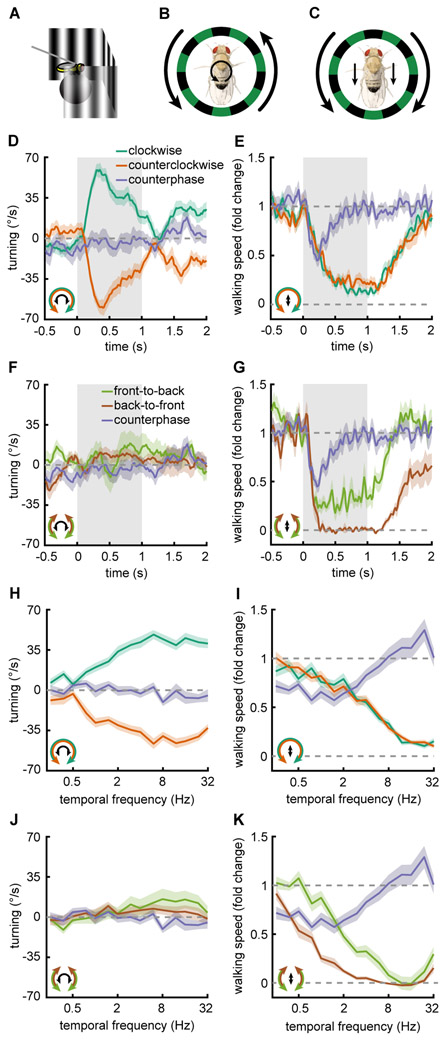
Walking Drosophila rotate (Buchner, 1976; Geiger, 1974; Götz and Wenking, 1973) and slow (Götz and Wenking, 1973; Katsov and Clandinin, 2008; Silies et al., 2013) in response to full-field visual stimuli. To measure these two optomotor responses, we tethered flies above an air-supported ball and presented panoramic visual stimuli (Fig. 1A) while monitoring ball rotations to infer a fly’s turning and walking speed (Clark et al., 2011; Salazar-Gatzimas et al., 2016). When presented with rotational sine wave gratings (Fig. 1B, Fig. S1A), flies turned in the direction of the motion (Fig. 1D, Fig. S1B, Supp. Movie M1). We refer to this response as the turning response. During the turning response, flies also slowed their walking speed in response to rotational stimuli (Fig. 1E). We term this behavior the slowing response. Because there is variability in the baseline walking speed among flies, we plotted walking speed as a fold change from baseline (Fig. S1C) (Götz and Wenking, 1973; Silies et al., 2013). To simulate optic flow caused by a fly’s translation through the world, we created a translational stimulus consisting of mirror-symmetric sine wave gratings that moved either front-to-back (FtB) or back-to-front (BtF) on two halves of a virtual cylinder around the fly (Fig. 1C, Fig. S1A). This stimulus possesses qualities of a real translational flow field, such as symmetric flow on both eyes, and it has a well-defined spatial and temporal frequency. When presented with FtB and BtF motion, flies showed no net rotational responses (Fig. 1F). The absolute level of turning slightly increased during FtB presentations and decreased during BtF presentations (Fig. S1D), consistent with previous measurements (Reiser and Dickinson, 2010; Tang and Juusola, 2010). In response to translational stimuli, flies reduced their walking speed regardless of the direction of the presented stimulus motion (Fig. 1G, Fig. S1B), though BtF motion generated stronger slowing than FtB. While rotational stimuli of opposite directions generated turning in opposite directions, translational stimuli generated the same sign of modulation, regardless of direction. Thus, the sign of the slowing response is insensitive to the stimulus direction, and qualitatively different from the rotational optomotor response.

Figure 1. Flies turn and slow in response to visual motion.

Error patches represent standard error of the mean. Icons in the bottom left indicate the stimulus presented (outside) and the behavioral response measured (inside).

(A) Behavioral responses were measured by tethering the fly above an air suspended ball and monitoring the rotation of the ball as visual stimuli were presented on 3 screens surrounding the fly.

(B, C) Diagram of the stimuli and fly behavioral response for (B) rotational and (C) translational motion stimuli.

(D) Fly turning velocity over time in response to clockwise (green, n=69), counterclockwise (orange, n=69), and counterphase (purple, n=19) sine wave gratings. Counterphase gratings are equal to the sum of clockwise and counterclockwise stimuli. Stimulus is presented during gray shaded region.

(E) As in D but measuring the fly’s walking speed.

(F) Fly turning velocity over time in response to front-to-back (FtB, green, n=18), back-to-front (BtF, brown, n=14) and counterphase (purple, n=19) sine wave gratings. Counterphase gratings are equal to the sum of FtB and BtF stimuli. Stimulus is presented during gray shaded region.

(G) Same as in F but measuring the fly’s walking speed.

(H) Mean fly turning to rotational sine wave gratings (green, orange, n=69) and counterphase gratings (purple, n=19) at a variety of temporal frequencies. Data colored as in (D).

(I) Same as in H but measuring the fly’s walking speed.

(J) Mean fly turning to FtB (green, n=18) and BtF (brown, n=14) sine wave gratings and counterphase gratings (purple, n=19) at a variety of temporal frequencies. Data colored as in (E).

(K) Same as in J but measuring the fly’s walking speed.

Throughout, error patches represent standard error of the mean.

See also Figure S1 and Supplemental Movie M1.

Since the slowing response is relatively direction insensitive, we asked whether flies were responding to the motion or simply to the spatiotemporal flicker of the stimulus. To test this, we presented flies with a counterphase grating, which was equal to the sum of a leftward- and rightward-moving sine wave grating (Fig. S1A, see STAR Methods). This stimulus contains no net motion, but has the same spatial and temporal frequencies as the sine wave gratings. Flies did not turn in response to this stimulus, and they slowed relatively little in response to it (Fig. 1D-G purple curves), indicating that walking speed depends on visual motion, not merely on flicker. It is noteworthy that flies slowed in response to both FtB and BtF motion, less strongly and more transiently to the sum of the stimuli. This result implies that the signals from the two opposite motion directions cancel each other out, rather than add to each other, a feature associated with motion opponency (Heeger et al., 1999; Levinson and Sekuler, 1975). Thus, the slowing response is an opponent, approximately non-direction-selective (non-DS) behavior. To measure mean responses to stimuli with different TFs, we integrated behavioral responses over time for each stimulus (Fig. 1H-K, Fig. S1EF). We found that the turning and slowing responses each depended strongly on the TF of the stimulus (Fig. 1H-K). However, the counterphase grating elicited only moderate slowing over a range of TFs (Fig. 1K, Fig. S1F).

Slowing to visual motion stabilizes walking speed

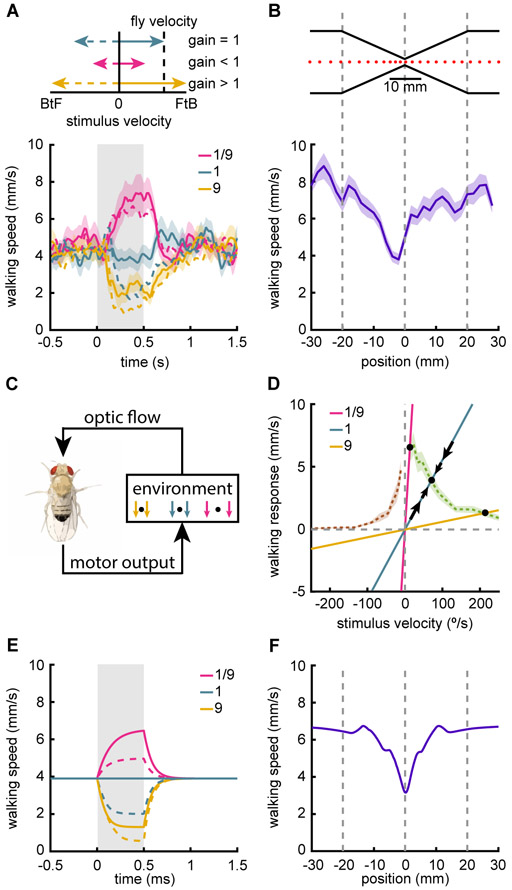
To investigate how flies use visual information to regulate walking speed, we created a closed-loop virtual environment, in which the walking speed of the fly controlled the velocity of a translational sine wave grating (Fig. 2A top). In this setup, as the fly walked forward, the sine wave grating moved FtB. As the fly walked faster, the grating moved faster, with a proportionality determined by the gain, reflecting how much the visual stimulus moves when the fly moves. For walking speed, the gain is inversely proportional to the distance to a virtual object, with close objects showing higher gains. We set the gain to a value that generated walking speeds in the middle of the fly’s dynamic range, and termed that a gain of 1 (see STAR Methods). When we increased the gain between fly behavior and stimulus velocity, the fly slowed down and when the gain was decreased, the fly sped up (Fig. 2A bottom). Thus, the fly uses visual stimuli to regulate and stabilize its walking speed. We also presented the fly with negative gain stimuli, in which the stimulus moved BtF when the fly walked forward. Interestingly, when presented with negative gain stimuli, the fly’s response was similar to the positive gain stimuli (Fig. 2A dotted lines) and this held true for a wide variety of gain changes (Fig. S2A). The similarity between positive and negative gain responses is consistent with the open-loop experiments, which showed that the slowing response is relatively insensitive to the stimulus direction (Fig. 1GK).

Figure 2. Slowing to visual motion stabilizes walking speed.

Error patches represent standard error of the mean.

(A) Flies were presented with translational sine wave gratings with velocity determined by the walking speed of the fly. The gain relating the visual stimulus to the walking speed of the fly was set to 1 during the pre-stimulus interval, and then transiently changed to ±1/9 or ±9 during the stimulus presentation. Different gains correspond to different visual stimulus speeds for a given walking speed (top). Gain of 1 corresponded to 18 °/s for 1 mm/s walking speed and was changed during gray shaded region (bottom). Dotted lines indicate negative gains. n=29.

(B) Flies were placed in a one-dimensional closed-loop environment, consisting of a hallway with an hourglass narrowing (top). Mean fly locations are plotted every 400 ms (top). Fly walking speed is plotted as a function of position in the hallway (bottom). n=35.

(C) Schematic of the model of fly walking behavior in closed-loop. Walking forward generates a visual flow field that is determined by distances in the environmental. The fly changes its walking speed based on the visual flow.

(D) Simple model of fly walking behavior in closed-loop. Open-loop slowing responses (Fig. 1K) for FtB (green) and BtF (brown) are plotted as a function of stimulus velocity. Natural stimulus gain (indicating the visual velocity experienced for a given fly walking speed) for environments with distant (pink), intermediate (blue), and close (yellow) objects. Stable fixed points are indicated by black circles. Black arrows indicate the change in walking speed for fluctuations near the intermediate distance fixed point. See STAR Methods for a detailed analysis.

(E) Predictions of the closed-loop model of fly behavior, colored as in (A).

(F) Prediction of the closed-loop model of fly behavior for the hourglass hallway experiment in (B).

See also Figure S2 and Supplemental Movie M2.

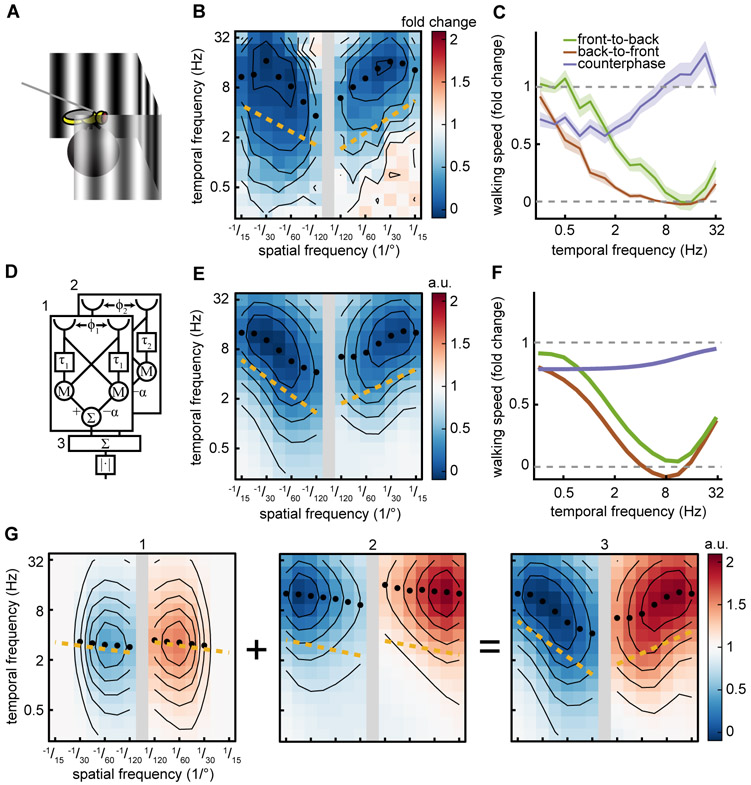
We wished to investigate how this stabilization of walking speed under different gain conditions related to real visual cues a fly might encounter. When an observer moves, nearby objects pass across the visual field more quickly than distant objects, which is equivalent to the different gains present in the stabilization experiments (Fig. 2A). Since flies slow more to faster stimuli (Fig. 1K) and walk slower with higher gain stimuli (Fig. 2A), we hypothesized that they should slow when passing nearby objects. To test this possibility, we designed a narrowed virtual hallway with an hourglass shape through which the flies walked on a one-dimensional track (Fig. 2B top, Supp. Movie M2). When flies moved along this virtual hallway, they reduced their speed as they approached the neck of the hourglass and sped up again after passing it (Fig. 2B bottom). This behavior closely resembles distance-dependent regulation of flight speed in honeybees (Srinivasan et al., 1996) and birds (Schiffner and Srinivasan, 2016), and represents the use of motion parallax to reduce speed near objects to avoid collisions (Sobel, 1990; Srinivasan et al., 1996).

A simple model relates closed-loop data to open-loop data

We wished to relate the open-loop slowing behavior we observed (Fig. 1K) to the closed loop behaviors in which flies regulated their walking speed (Fig. 2AB). To develop a simple dynamical model to describe walking speed stabilization, following classic work on orientation regulation in flies (Reichardt and Poggio, 1976). In that model, the fly’s behavior is solely a function of its visual input, while the fly’s behavior feeds back onto its visual input through the environment (Fig. 2C, Fig. S2B). We developed a simple model to show how walking speed could be stabilized using visual input (Fig. 2D, see STAR Methods). In this model, for every visual velocity, the fly has an internal target walking speed. This target was measured explicitly by our open-loop behavioral experiments (Fig. 1K), so we used that experimental data directly in the model (Fig. 2D, green and brown dashed lines). Crucially, the visual flow that the fly sees depends on its behavior as it navigates an environment. If the fly walks faster, then the stimulus moves at a higher velocity, as determined by the environmental gain. As a result, fly walking speed and stimulus velocity exist along a line with slope equal to the inverse gain (Fig. 2D lines through the origin).

To understand what walking speed this model predicts, one must examine the coupling between the target walking speeds and the environmental gain (Fig. 2D). In the model, changes in the fly’s walking speed (black arrows) are proportional to the difference between the target walking speed (determined by the current stimulus velocity) and the current walking speed. Black circles indicate where the environmental gain lines intersect with the target walking speed (dashed green and brown lines). At these points there is no difference between the actual walking speed and the target walking speed for that visual velocity. Thus, an intersection represents a fixed point of the system for a given gain. Furthermore, at that fixed point, small deviations away from the point are pushed back towards it, so it is stable and fly walking speed will approach that point (see STAR Methods). When objects are nearer (yellow line), this model predicts fixed points at slower walking speeds, and when objects are more distant it predicts faster walking speeds (pink line).

We first used this model to simulate closed-loop responses to the gain change experiments (Fig. 2A). These simulations recapitulated the closed-loop walking speed results, predicting the speed-up and slow-down of the flies, as well as the largely similar responses even under gain inversion, when the world moves BtF as the fly walks forward (Fig. 2E). This agreement is noteworthy because the only free parameter in the model was the timescale at which the fly could modulate its behavior. While our open-loop experiments showed only slowing, the closed-loop gain change experiment and model each showed that flies sped up when the gain was reduced (Fig. 2A). The model demonstrates that this is occurs because the flies are not walking at their maximum speed during the pre-stimulus interval, since they have been slowed by the translational visual flow induced by their own walking. When this translational visual flow is reduced by reducing the gain, the flies speed up. Moreover, open-loop experiments in which there is FtB visual flow during the interstimulus interval period show the same phenomenon (Fig. S2D).

This model also recapitulated the slowing observed in the narrowed virtual hallway (Fig. 2F), in which the faster visual flow at the narrowing causes the fly to slow. This slowing occurs because the gain becomes larger during the narrow portion of hallway, moving the fixed point to a lower walking speed.

Interestingly, because this model treats the fly’s behavior as function only of the visual stimulus, it predicts that flies that experience the identical visual inputs should respond identically, whether they are in closed-loop or open-loop conditions. To test this, we measured the walking speed of flies that were presented (under open-loop conditions) the stimulus generated by a different fly under closed-loop conditions. These flies in this replay condition behaved similarly to the flies with closed-loop control of the visual stimulus (Fig. S2EF), in agreement with our model. Overall, this model shows that a simple model can qualitatively explain the observed closed-loop slowing behaviors using open-loop data, even though navigational behaviors are known to feed back onto the responses of visual neurons (Chiappe et al., 2010; Fujiwara et al., 2016; Kim et al., 2015).

The slowing response is speed-tuned while the turning response is temporal-frequency-tuned

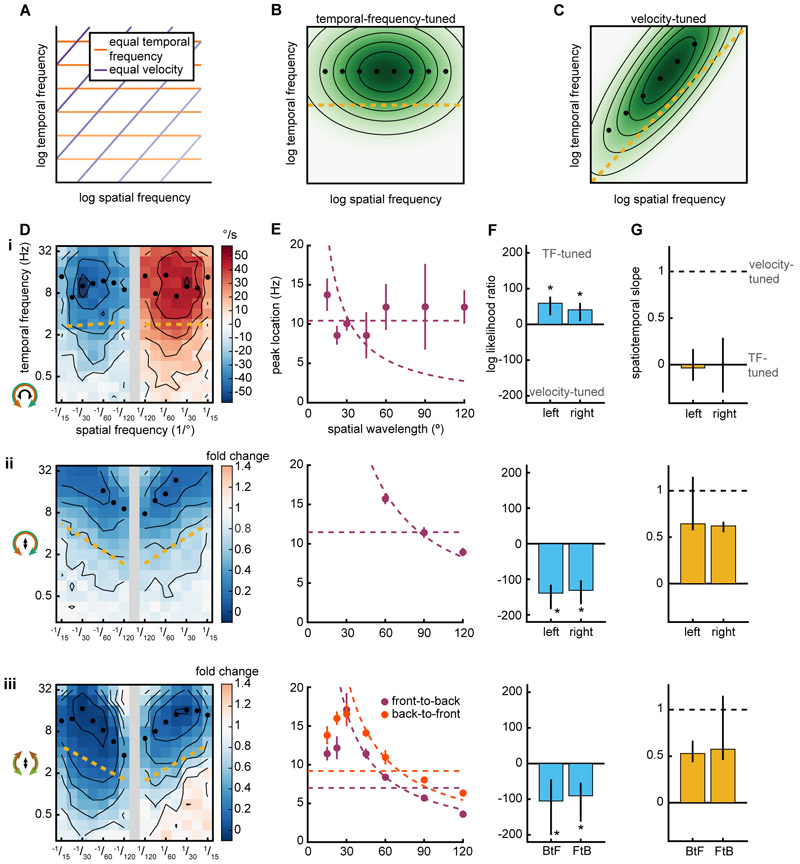
Since walking speed control is sensitive to object depth (Fig. 2B) and the velocity of objects across the retina can be used to infer depth (Sobel, 1990), we hypothesized that the algorithm regulating walking speed might be tuned to the velocity of the stimulus. In insects, the turning response is tuned to the TF of the stimulus, not to its velocity (Borst and Egelhaaf, 1989; Fermi and Reichardt, 1963; Gotz, 1964; Kunze, 1961; McCann and MacGinitie, 1965) and this TF-tuning is consistent with predictions of the HRC model (Borst and Egelhaaf, 1989; Fermi and Reichardt, 1963; Reichardt and Varju, 1959). The tuning of a motion detection circuit can be determined by the responses to sine wave gratings of different temporal and spatial frequencies. TF-tuning is usually defined as a response whose peak occurs at a single TF, independent of spatial wavelength. Analogously, velocity-tuning is defined as a response whose peak occurs at a single velocity, independent of spatial wavelength. On a log-log axis, TF and spatial frequency pairs with equal velocity exist along lines with a slope of 1 (Fig. 3A) (Priebe et al., 2006). A TF-tuned response in spatiotemporal frequency space will have maxima that occur at a single TF (Fig. 3B). A velocity-tuned response in spatiotemporal frequency space will be oriented such that maxima occur along a line with slope 1, corresponding to a single velocity (Fig. 3C).

Figure 3. The slowing response is speed-tuned while the turning response is temporal-frequency-tuned.

(A) Lines of equal temporal frequency (TF) (orange) and velocity (purple) shown in log-log spatiotemporal frequency space. Darker lines indicate greater velocities and temporal frequencies.

(B) Spatiotemporal response of a TF-tuned model. Black circles mark the TF of the maximal response for each wavelength. Gold line is the spatiotemporal slope (STS) (see STAR Methods).

(C) Spatiotemporal response of a speed-tuned model. Plot features are as in B.

(D) Mean fly turning (i) and slowing (ii, iii) to sine wave gratings as a function of spatial and temporal frequency. Positive/negative spatial frequencies indicate rightward/leftward (i, ii) or front-to-back/back-to-front (iii) sine waves. Icons on the left indicate the stimulus presented (outside) and the behavioral response measured (inside). Black isoresponse lines are plotted every 10 °/s for turning (i) and every 0.2 fold change for walking speed (ii, iii). Black circles mark the TF of the maximal response for each wavelength and only reported when the maxima occurs within the TF range measured. Gold line is the spatiotemporal slope (STS). (i, ii) n=467. (iii) FtB n=124. BtF n=104.

(E) TF at which the response is maximal plotted as a function of spatial wavelength. Error bars are standard error of the mean. Dashed lines indicate average TF or average velocity across all maxima. When plotting TF against spatial wavelength, lines of equal TF have slope 0 while lines of equal velocity are proportional to inverse spatial wavelength.

(F) The log likelihood ratio of TF-tuned to speed-tuned models (see STAR Methods). Positive values indicate that a TF-tuned model is more likely while negative values indicate that a velocity-tuned model is more likely. Error bars are 95% confidence intervals and asterisks represent significant difference from 0 at α=0.05.

(G) STS of plots in D, where a value of 0 corresponds to perfect TF-tuning and 1 corresponds to perfect speed-tuning (see STAR Methods). Error bars are 95% confidence intervals.

See also Figures S3 and S4.

We measured the tuning of both the turning and slowing responses to both rotational and translational stimuli with many spatial and temporal frequencies (Fig. 3D). Since these are laborious measurements, we developed a rig that allowed us to measure individual psychophysical curves in 10 flies simultaneously (see STAR Methods). We found that the rotational TF that elicited the maximal turning response did not strongly depend on spatial wavelength (Fig. 3E i), in agreement with many previous measurements (Borst and Egelhaaf, 1989; Fermi and Reichardt, 1963; Gotz, 1964; Kunze, 1961; McCann and MacGinitie, 1965). In contrast, the stimulus TFs that elicited the maximal slowing response depended strongly on spatial wavelength (Fig. 3E ii, iii). At low spatial frequencies, the dependence looked very much like velocity-tuning. Since this response is not direction-selective, we concluded the slowing response is speed-tuned. These tunings remained when turning responses were quantified using a different rotation metric and integration window (Fig. S3ABC i) or if walking speed was not normalized (Fig. S3ABC ii). Interestingly, the slowing response was speed-tuned when the fly was presented with either rotational (Fig. 3E ii) or translational (Fig. 3E iii) stimuli. Thus, the speed-tuning is a property of the behavior, independent of the stimulus. When presented with rotational stimuli, the fly simultaneously engaged in TF-tuned turning and speed-tuned slowing (Fig. 3E i, ii).

Examining the maximal responses at each wavelength is informative, but it does not make full use of the rich dataset we obtained over many wavelengths and temporal frequencies. To take advantage of this data, we developed two models to characterize the entire set of spatiotemporal responses as either TF-tuned or velocity tuned. This characterization was based on the mathematical concept of separability, asking whether the responses could be characterized by single functions of either stimulus TF or velocity (Fig. S4ABC, see STAR Methods). This method does not make strong assumptions about the shape of the spatiotemporal responses. We then asked which of the two models was most likely to underlie the measured data. We found that the turning response was significantly better explained as TF-tuned (Fig. 3F i) and the slowing response was significantly better explained as speed-tuned (Fig. 3F ii, iii). However, the true tuning could be somewhere in between pure speed-tuned and pure TF-tuned. To examine this possibility, we created a third model, which, like the first two, also incorporates data from all spatial and temporal frequencies. In the third model, a parameter could be varied continuously between TF-tuning and speed-tuning. We call the best fit of this parameter the spatiotemporal slope (STS). It corresponds to the slope along which the data is best aligned (Fig. S4D, see STAR Methods). We found that the turning response was best fit by a nearly perfectly TF-tuned model, in which the STS equals zero (Fig. 3G i). The slowing response was more speed-tuned than TF-tuned (Fig. 3F ii, iii), although it did not achieve perfect speed-tuning because the STS was less than 1. These measurements indicate that the TF-tuned HRC, which has classically been used to describe fly motion detection, cannot explain walking speed regulation.

Visual control of slowing and turning requires overlapping circuits

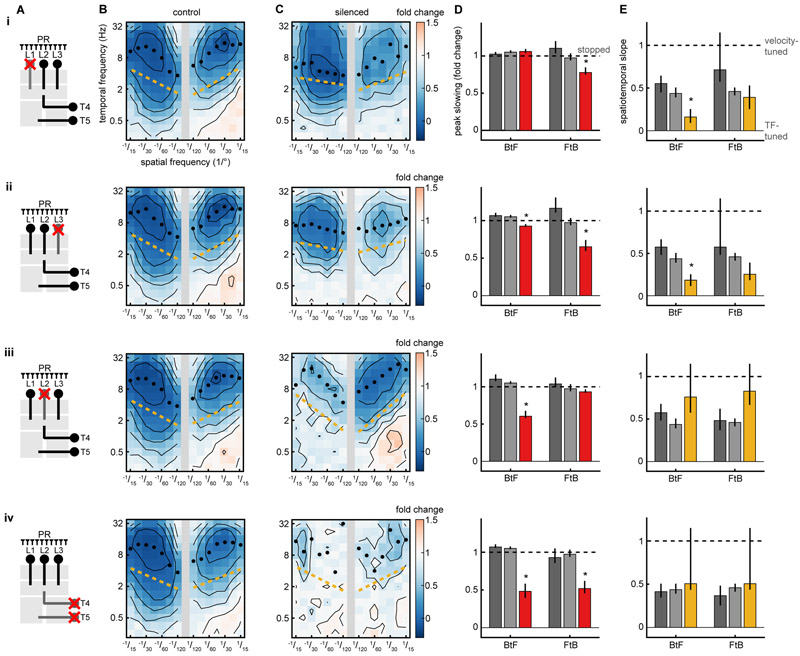
Our results show that the turning response and the slowing response are controlled by distinct algorithms. Are they implemented by distinct or by overlapping neural circuitry? We expressed the protein shibire^ts (Kitamoto, 2001) to silence specific cell types within the fly optic lobes (Fig 4A) using the GAL4/UAS system (Brand and Perrimon, 1993). The neurons L1, L2, and L3 receive direct inputs from photoreceptors and project to the medulla, where they feed into ON and OFF motion pathways (Clark et al., 2011; Joesch et al., 2010; Maisak et al., 2013; Takemura et al., 2013), visual pathways that influence walking speed (Silies et al., 2013), object detection (Bahl et al., 2013), and flicker responses (Bahl et al., 2015). When either L1 or L3 was silenced, the slowing response to FtB motion was significantly diminished relative to control genotypes (Fig. 4BCD i, ii). Interestingly, in both cases, the behavior also lost its characteristic speed-tuning to BtF motion and became more TF-tuned (Fig. 4E i, ii). When L2 was silenced, responses to BtF sine wave gratings were reduced (Fig. 4BCD iii), while the speed-tuning of the behavior was unaffected (Fig. 4E iii). These results suggest that different subcircuits are responsible for FtB and BtF slowing, and that silencing subcircuits can revert speed-tuning to TF-tuning.

Figure 4. Visual control of slowing and turning requires overlapping circuits.

Synaptic transmission was silenced acutely by expression of shibire^ts using the GAL4/UAS system.

(A) Schematic of the fly optic neuropils, with silenced neuron types crossed out. In this diagram, light is detected by photoreceptors (PRs) at top and visual information is transformed as it moves down through the neuropils.

(B) Average fly response as a function of spatial and temporal frequency. Control is the average of the neuron-GAL4/+ and UAS-shibire/+ genetic controls (see STAR Methods). Black isoresponse lines are plotted every 0.2 fold change in walking speed. Black circles mark the TF of the maximal response for each wavelength. The gold line is the spatiotemporal slope (STS). Shibire control FtB n=274, BtF n=247 (i-iv). GAL4 control: (i) FtB n=109, BtF n=115. (ii) FtB n=83, BtF n=98. (iii) FtB n=121, BtF n=116. (iv) FtB n=95, BtF n=105.

(C) Fly response when each cell type is silenced by expressing shibire under the GAL4 driver. (i) FtB n=126, BtF n=146. (ii) FtB n=134, BtF n=126. (iii) FtB n=120, BtF n=131. (iv) FtB n=99, BtF n=96.

(D) Maximal slowing response of each genotype across all spatiotemporal frequencies, where 0 represents no walking speed modulation and 1 represents stopping completely. GAL4/+ is in dark gray, shibire^ts/+ is in light gray, and GAL4>shibire^ts is in red. Error bars are 95% confidence intervals and asterisks represent significant difference from both controls at α=0.05.

(E) Spatiotemporal slope (STS) for each map, where 0 corresponds to perfect TF-tuning and 1 corresponds to perfect speed-tuning. GAL4/+ is in dark gray, shibire^ts/+ is in light gray, and GAL4>shibire^ts is in gold. Error bars are 95% confidence intervals and asterisks represent significant difference from both controls at α=0.05.

See also Figure S4 and Table S3.

The neurons T4 and T5 are the earliest known direction-selective neurons in the fly; they are required for the turning response and the responses of wide-field direction-selective neurons (Maisak et al., 2013; Schnell et al., 2012). When T4 and T5 were silenced, translational motion stimuli no longer elicited robust slowing (Fig. 4BCD iv). Intriguingly, there remained some residual responses at high spatiotemporal frequencies, hinting that parallel, unsilenced pathways might contribute to the slowing response.

Elementary motion detectors T4 and T5 are temporal-frequency-tuned

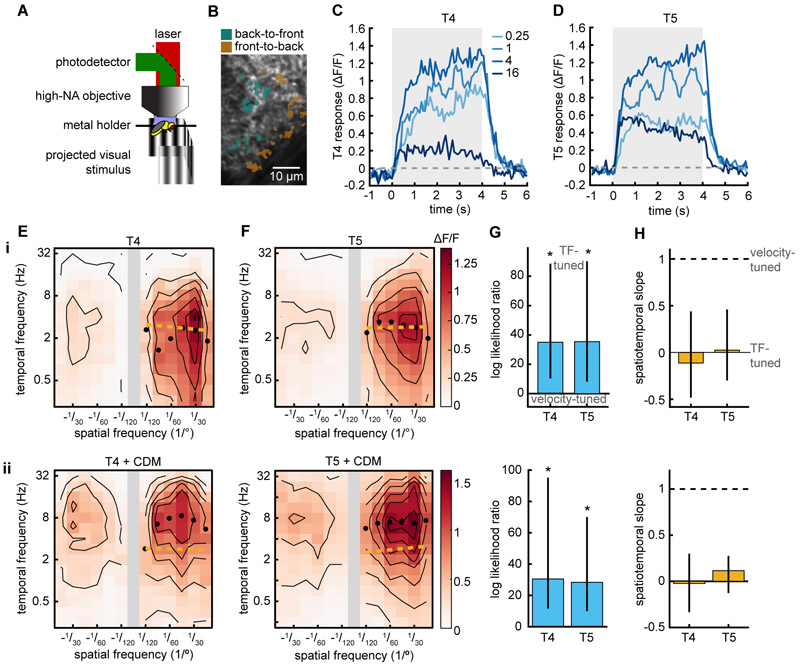
We asked whether the speed-tuning of the slowing response could be inherited from T4 and T5 themselves. T4 and T5 cells with opposite selectivity are subtracted from each other in downstream neurons (Mauss et al., 2015), and models based on the HRC have obtained velocity-tuned responses from the individual HRC multiplier arms before subtraction (Srinivasan et al., 1999; Zanker et al., 1999). We imaged the calcium responses of T4 and T5 axon terminals in the lobula plate (Fig. 5AB) (Salazar-Gatzimas et al., 2016). Consistent with previous findings (Maisak et al., 2013), we found that the axon terminals responded to moving gratings (Fig. 5CD, Fig. S5). We then measured the calcium signals in response to a suite of different spatiotemporal frequencies (Fig. 5EF i). Both T4 and T5 neurons were strongly direction-selective across all spatiotemporal frequencies measured, apparent in the differential responses to positive and negative spatial frequencies, which correspond to preferred and null direction motion. Counter to predictions for single multiplier motion detectors (Zanker et al., 1999), both neuron types showed responses that were TF-tuned (Fig. 5GH i). Thus, taken together with our silencing results, we find that the non-DS, speed-tuned slowing response requires direction-selective, TF-tuned cells. Studies in neurons downstream of T4 and T5 have found differences between T4’s and T5’s responses to fast moving edges (Leonhardt et al., 2016), but we found that T4 and T5 showed similar tuning to sine wave gratings over many spatial and temporal frequencies. We found a response peak at TFs of ~2-3 Hz and spatial wavelength of ~30°, both of which are different from the maximal responses observed in behavior. These differences in tuning have been previously observed in the tuning of T4 and T5 (Maisak et al., 2013; Salazar-Gatzimas et al., 2016; Schnell et al., 2010) compared to behavior (Clark et al., 2011; Fry et al., 2009; Tuthill et al., 2013).

Figure 5. Elementary motion detectors T4 and T5 are temporal-frequency-tuned.

(A) Diagram of two-photon imaging setup.

(B) Image of the lobula plate with T4 and T5 FtB and BtF regions of interest (ROIs) highlighted.

(C, D) Responses of T4 (C, n=7) and T5 (D, n=8) to rotational sine wave gratings measured with GCaMP6f. Legend denotes the temporal frequency (TF) of the sine wave stimulus.

(E, F) Mean calcium response of T4 and T5 (F, n=22) when presented with sine wave gratings of different spatiotemporal frequencies. Black isoresponse lines are plotted every 0.2 ΔF/F. Black circles mark the TF of the maximal response for each wavelength. Gold line is the spatiotemporal slope (STS).

(G) The log likelihood ratio of TF-tuned and speed-tuned models of T4 and T5 responses (see STAR Methods). Positive values indicate that the TF-tuned model is more likely. Error bars are 95% confidence intervals and asterisks represent significant difference from 0 at α=0.05.

(H) Spatiotemporal slope (STS) for T4 and T5 responses, where 0 represents to perfect TF-tuning and 1 represents to perfect speed-tuning (see STAR Methods). Error bars are 95% confidence intervals.

(i) Imaging without pharmacological stimulation. T4, n = 20; T5, n=22.

(ii) Imaging in the presence of octopamine agonist chlordimeform (CDM). T4, n = 13; T5, n=12.

See also Figures S4 and S5.

In flies, motor activity can change the tuning of direction-selective neurons in the visual system (Chiappe et al., 2010), an effect mediated by octopamine released during motor activity (Strother et al., 2018; Suver et al., 2012). To see whether octopaminergic activation of the visual system could convert the spatiotemporal tuning of T4 and T5 from TF-tuned to velocity-tuned, we added chlordimeform hydrochloride (CDM) to the perfusion solution during imaging (Arenz et al., 2017). We found that both T4 and T5 responses shifted to higher temporal frequencies (peak ~6-7 Hz), in agreement with previous studies (Fig. 5EF ii) (Arenz et al., 2017; Strother et al., 2018). However, the spatiotemporal tuning under these conditions was still strongly tuned to the stimulus TF, not to its velocity (Fig. 5GH ii). Thus, T4 and T5 activity may account for the TF-tuned turning response, but the velocity-tuning of slowing cannot be explained by the mean responses of the neurons T4 and T5.

A model with multiple detectors is sufficient to explain the slowing response

We propose a simple mathematical model to explain the spatiotemporal tuning we observed in walking speed regulation. The slowing response is non-DS, opponent, and speed-tuned, all while relying on TF-tuned direction-selective subunits that we observed (Figs. 1, 3-5). To account for our mean behavioral data (Fig. 6ABC), we constructed a model consisting of the sum of two TF-tuned, opponent HRCs with different spatial and temporal scales (Fig. 6D). To model the imbalance between FtB and BtF responses, we permitted the HRCs also to have an imbalance in weighting when subtracting the two directions. We fit the spatial and temporal scales of this model to match our measured behavioral responses to FtB motion (Fig. 3D iii, Fig. 6B). The spatiotemporal frequency responses of the model successfully reproduce the non-DS speed tuning of the original behavior, including the slight FtB/BtF imbalance (Fig. 6E). Moreover, like the data, the model responds strongly to FtB and BtF sine wave gratings, but responds minimally to counterphase gratings, as a result of the imbalance in the two HRCs (Fig. 6F). The spatiotemporal frequency response of the model is velocity-tuned because the two correlators in the model are offset from one another in spatiotemporal frequency space (Fig. 6G). Thus, our behavioral measurements, silencing data, and calcium imaging data is consistent with a hierarchical model in which at least two TF-tuned circuits with different tuning are combined to generate the speed-tuning observed in the fly’s slowing to visual motion.

Figure 6. A model with multiple detectors is sufficient to explain the slowing response.

Black isoresponse lines are plotted every 0.2-fold change for walking speed. Black circles mark the TF of the maximal response for each wavelength. Gold line is the spatiotemporal slope (STS).

(A) Diagram of the behavioral setup from Fig. 1A.

(B) Mean fly responses to sine wave gratings as a function of spatial and temporal frequency. Data is from Fig. 2D. Positive/negative spatial frequencies indicate front-to-back/back-to-front sine waves. FtB n=124. BtF n=104.

(C) Mean fly walking to FtB (green, n=18) and BtF (brown, n=14) sine wave gratings and counterphase gratings (purple, n=19) at a variety of temporal frequencies. Error patches represent standard error of the mean. Data is from Fig 1G.

(D) Schematic of the model consisting of two Hassenstein-Reichardt correlators (HRC) summed together, marked as 1 and 2. Their sum is marked as 3. Distance between the two visual inputs for each correlator is denoted by Φ. τ indicates a first-order low-pass filter. M denotes a multiplication of the two inputs. Σ indicates summation of the inputs. ∣·∣ indicates taking full-wave rectifying the signal.

(E) The model’s average response as a function of spatial and temporal frequency. Positive/negative spatial frequencies indicate front-to-back/back-to-front sine waves.

(F) Mean model response to FtB sine wave, BtF sine wave, and counterphase gratings at a spatial wavelength of 45°. Colors the same as (C).

(G) Average spatiotemporal frequency response of each of the two HRC’s individually (left, center). Average spatiotemporal frequency response of the two correlators summed before taking the magnitude (right). Red indicates a positive response, blue indicates a negative response. Numbers correspond to (D).

See also Figures S4 and S6 and Table S5.

Although the model above is sufficient to explain our data, we wished to investigate whether other models proposed in the literature could explain our observations. We found that the properties of the slowing response and its visual circuitry rule out a variety of models that have been proposed to explain speed or velocity-tuning (Fig. S6). Since most of these models generate direction-selective responses, we rectified each model’s output before averaging, so that only the response amplitude mattered and not its sign (see STAR Methods). Using this procedure, the standard HRC model cannot explain this behavior because it exhibits TF-tuning (Borst and Egelhaaf, 1989) (Fig. S6ABC i). Models based on the sum, rather than the difference, of two HRC subunits (Dyhr and Higgins, 2010a; Higgins, 2004) also do not fit our data, since they are not opponent and respond strongly to counterphase gratings (Fig. S6 ii). Models based on the predicted velocity-tuning of a single, multiplicative HRC subunit (Zanker et al., 1999) can be excluded because our data shows that the earliest direction-selective cells involved in the slowing response are TF-tuned, not velocity-tuned (Fig. 5 i, Fig. S6 iii). Since these published models could not account for our behavioral results, we asked whether it was possible for any model with only one direction-selective, opponent signal to explain our data. We therefore constructed a model that combined a single TF-tuned direction-selective signal with a non-DS signal. With the right tuning, such a model could account for our observations (Fig. S6ABC iv, see STAR Methods). This emphasizes that the model using two correlators with different tuning is sufficient, but a second correlator with different tuning is not required to explain the behavioral results presented here.

Discussion

Our results demonstrate that walking speed is regulated by an algorithm that is non-direction-selective, opponent, and speed-tuned (Figs. 1 and 3). The algorithm produces a stabilizing effect on walking speed, and causes the fly to slow when objects are nearby (Fig. 2). The HRC model, which predicts the TF-tuning of the turning response, has long been central to the study of motion detection in insects (Hassenstein and Reichardt, 1956; Silies et al., 2014). The characterization of walking behavior in this study demonstrates that a second motion-detection algorithm — distinct from a single HRC — exists in flies. However, our dissection of the circuitry underlying this behavior shows that the slowing response and the classical turning response employ overlapping neural circuitry (Fig. 4) and that the slowing response relies on TF-tuned, direction-selective cells (Fig. 5). Several classical models thought to explain speed-tuned responses cannot explain our observations (Fig. S6), but our results are consistent with a hierarchical model for speed-tuning that combines multiple motion detectors (Fig. 6).

Advantages of speed-tuning and temporal-frequency-tuning

Our results show that different motion cues guide distinct navigational behaviors. Why is walking speed regulation speed-tuned while orientation regulation is TF-tuned (Fig. 3)? As an observer translates through the world, objects move across the retina with a speed that is inversely proportional to their distance from the observer. As a result, an observer can use retinal speed to estimate object depth using motion parallax (Sobel, 1990). Importantly, TF is less informative about depth. As a simple example, when an observer moves parallel to a wall with a sine wave pattern, the pattern’s wavelength and velocity on the retina both vary inversely with the distance from the wall, keeping TF constant with depth. The speed-tuning of the slowing response could therefore be critical to the distance-dependent walking speed regulation that we observed in closed-loop experiments (Fig. 2). Interestingly, Drosophila also use visual cues to measure distance when crossing narrow gaps (Pick and Strauss, 2005), a behavior that could employ a motion detection algorithm similar to the one described here.

It is less clear what advantage TF-tuning confers on the turning response, since pattern dependent responses appear at first glance disadvantageous for estimating real world motion. However, with the regularity of spatial frequencies in naturalistic inputs, TF-tuning can be equivalent to velocity-tuning (Dror et al., 2001). If natural optomotor turning behaviors were primarily guided by the direction of motion, rather than the speed, then the pattern-dependence of the tuning would also be less important (Srinivasan et al., 1999). Interestingly, psychophysical experiments in humans indicate that the perception of speed can depend on both stimulus velocity and wavelength, and that perception may be speed-tuned in some regimes and TF-tuned in others (Shen et al., 2005; Smith and Edgar, 1990). These two regimes suggest there may be flexibility in the algorithm used to guide a behavior.

Modeling speed-tuned motion detection circuits in the fly

We have proposed that the speed-tuning of walking speed regulation could originate as the sum of differently tuned, opponent HRC motion detectors. While we represent this as a sum of multiple correlators with different tunings, the underlying structure need not be an HRC; any mechanism that has a compact TF-tuned spatiotemporal response would be sufficient. In primate visual cortex, cells in V1 show TF-tuning while those in MT show speed-tuning (Perrone and Thiele, 2001a; Priebe et al., 2006; Rodman and Albright, 1987). Previous theoretical work has proposed that the approximate speed-tuning observed in MT could be generated by summing V1 cells with different spatiotemporal frequency tunings (Simoncelli and Heeger, 1998). The model presented here is analogous to that V1-MT transformation. An alternative model for speed-tuning has been proposed in honeybees; it combines multiple TF-tuned cells in a different way but could also explain our data (Srinivasan et al., 1999). Fundamentally, these models each approximate speed- or velocity-tuning by combining responses at two or more spatiotemporal scales.

In Drosophila, we suggest that speed tuning could arise from combining the TF-tuned output from T4 and T5 neurons with separate neural signals that possess a different spatiotemporal tuning. According to this suggestion, one might expect to find direction-selective fly neurons with different TF tuning than T4 and T5. Consistent with this, measurements in the fly Calliphora found direction-selective cells with tuning similar to T4 and T5, but also cells with peak responses at 15-20 Hz (Horridge and Marcelja, 1992). Intriguingly, when T4 and T5 were silenced in our experiments we observed residual slowing at high spatial and temporal frequencies, which could originate in such pathways (Fig. 4C iv). Moreover, silencing visual subcircuits can revert the slowing response to TF-tuning (Fig. 4CE i,ii), consistent with models that generate speed-tuned responses by combining responses from multiple TF-tuned direction-selective cells. A model that adds two differently-tuned DS cells is plausible, simply because it only requires the fly to do again what it has already done: create a TF-tuned direction-selective cell, this time with a distinct tuning.

Non-DS regulation of walking speed

Perhaps surprisingly, the algorithm that regulates walking speed is not strongly direction-selective, since flies slow to both FtB and BtF visual flows (Fig. 1 and 3). When different neuronal subcircuits were silenced, it selectively suppressed responses to either FtB or BtF motion (Fig. 4). This implies that non-direction-selectivity is a deliberate function of the circuit, with different directions explicitly computed by different subcircuits. Why might direction-insensitivity be a feature of the circuit? If the fly were using motion parallax to compute distance, then the depth of an object may be computed from only the magnitude of the motion, independent of its direction (Sobel, 1990). Such motion parallax signals could be used to avoid collisions by slowing when objects are near (Fig. 2B), a behavior that is also observed in other insects (Srinivasan et al., 1996) and birds (Schiffner and Srinivasan, 2016). Interestingly, BtF optic flow has been predicted to be useful in collision avoidance (Chalupka et al., 2016). An alternative explanation for direction-insensitivity is that if an observer rotates and translates at the same time, self-motion can induce simultaneous FtB and BtF motion across the retina (Fig. S6D). Non-direction-selectivity might allow the fly’s walking speed regulation to remain sensitive to such conflicting optic flow.

Direction insensitive, speed-tuned circuits and behaviors exist in other animals. Locusts use motion parallax to estimate distance when jumping to visual targets, and this computation is independent of the direction of the motion (Sobel, 1990). Likewise, honeybees regulate flight speed using algorithms that are insensitive to the direction of visual motion (Srinivasan et al., 1996). In primates, direction insensitive speed-tuned cells have been reported in cortical region MT (Rodman and Albright, 1987). It would be interesting to investigate whether there exist speed-tuned, non-DS behaviors in mammals, as has been shown in Drosophila and other insects.

Implications for mechanisms of motion detection

Although the HRC serves as an excellent model for some insect direction-selective neurons and for optomotor turning behaviors, many recent results have shown that the cellular mechanisms implementing motion detection are not consistent with simple multiplication (Behnia et al., 2014; Clark et al., 2011, 2014; Fitzgerald and Clark, 2015; Gruntman et al., 2018; Haag et al., 2016; Joesch et al., 2010; Leong et al., 2016; Salazar-Gatzimas et al., 2016; Strother et al., 2017, 2014; Wienecke et al., 2018). The TF-tuning of T4 and T5 demonstrates that a simple multiplicative nonlinearity cannot account for their direction-selectivity, since such a model would imply a non-TF-tuned response (Zanker et al., 1999). Instead, these tuning results could be consistent with other mechanisms for direction-selectivity that include more complex spatiotemporal filtering (Leong et al., 2016) or multiple direction-selective nonlinearities (Haag et al., 2016). In our modeling we use correlators for their simplicity; the exact structure of the underlying TF-tuned subunit is not specified by our results. Regardless, our result that silencing subcircuits reverts velocity-tuned behavior to TF-tuned behavior (Fig. 4 i, ii) suggests that velocity-tuning in the fly could arise from a hierarchical set of visual processes, similar to the processing found in visual cortex (Felleman and Van Essen, 1991).

Visual control of rotation and translation across phyla

Although vertebrates and invertebrates are separated by hundreds of millions of years of evolution, they must both navigate the same natural world, which could provide convergent pressures on their algorithms to control orientation and translation. For instance, analogous to insect optomotor orientation stabilization, mammals show an optokinetic response, in which the eye rotates to follow wide-field motion (Ilg, 1997). Behavioral studies in fish show that they exhibit optokinetic responses and body-orienting behaviors, and they regulate their translation in response to visual motion (Portugues and Engert, 2009; Severi et al., 2014). Analogous to the translational stabilization measured here, humans use visual feedback to regulate walking speed, slowing down when gain between behavioral output and visual feedback is increased, and walking faster when the gain is reduced (Mohler et al., 2007; Prokop et al., 1997). In mouse retina, direction-selective cells are organized to match translational flow fields (Sabbah et al., 2017), suggesting they play a role in detecting translational self-motion. Analogous to honeybees and our results in Drosophila, birds also slow when passing nearby objects (Schiffner and Srinivasan, 2016). These examples show that navigating vertebrates and insects display many of the same behaviors. In these two evolutionarily distant phyla, the circuits and computations in motion detection show remarkable parallels (Borst and Helmstaedter, 2015; Clark and Demb, 2016). It will be interesting to compare the stabilizing algorithms across these animals and determine whether rotational and translational regulation also show parallel structure. If mammals employ TF-tuned behaviors, as insects do in rotation, then the TF-tuned cells in mammalian cortex might be useful in their own right, rather than serving solely as inputs for later speed-tuned computations.

Neural circuits and behaviors that are speed- or velocity-tuned have been investigated in the visual systems of honeybees (Srinivasan et al., 1996, 1999), pigeons (Crowder et al., 2003), and in primate MT (Perrone and Thiele, 2001b), all animals where genetic tools are not easily applied to dissect circuits and behavior. The slowing response in walking Drosophila represents an opportunity to use genetic tools to dissect how speed-tuning arises, how it interacts with other motion estimates, and how multiple motion signals drive distinct navigational behaviors.

STAR Methods

Contact for reagent and resource sharing

Further information and requests for resources should be directed to and will be fulfilled by the Lead Contact, Damon Clark (damon.clark@yale.edu).

Experimental model and subject details

Fly Husbandry

Flies for behavioral experiments were grown at 20° C. Flies for imaging experiments were grown at either 25 or 29° C. All flies were grown at 50% humidity in 12-hour day/night cycles on a dextrose-based food. All tested flies were non-virgin females between 24-72 hours old. Fly genotypes are reported in Table S1.

Method Details

Psychophysics

We constructed a fly-on-a-ball-rig to measure walking behaviors, as described in previous studies (Clark et al., 2011; Salazar-Gatzimas et al., 2016). Each fly was anesthetized on ice and glued to a surgical needle using UV epoxy. The fly was then placed above a freely turning ball which the fly can grip and steer as if it were walking. The rotation of the ball was measured at 60 Hz using an optical mouse sensor with an angular resolution of 0.5°. Panoramic screens surrounded the fly, covering 270° azimuth and 106° elevation. The stimuli were projected on to the screens by a Lightcrafter DLP (Texas Instruments, USA) using monochrome green light (peak 520 nm and mean intensity of 100 cd/m²). Stimuli were projected such that the fly experienced a virtual cylinder. For higher throughput we built 2 rigs with 5 stations in parallel, enabling us to run 10 flies simultaneously. Flies were tested 3 hours after lights on or 3 hours before lights off at 34-36° C to allow us to use thermogenetic tools (Clark et al., 2011; Salazar-Gatzimas et al., 2016).

Stimuli

All stimuli were drifting sine wave gratings of a single spatial and temporal frequency, which had contrasts c(x, t) = A sin(ω₀t + k₀x), or were counterphase gratings, which had contrasts c(x, t) = A sin(ω₀t + k₀x) + A sin(ω₀t − k₀x) = 2A sin(ω₀t) cos(k₀x). Each presentation of the stimulus was preceded by a period of a blank mean luminance screen. Behavioral experiments used an amplitude A of 0.25 and imaging experiments used an amplitude of 0.5. Behavioral experiments had a prestimulus interval of 5s, a stimulus duration of 1s, and was presented for 20 minutes. Imaging experiments had a prestimulus interval of 5s, a stimulus duration of 4s, and was presented for 15 minutes.

Each open-loop stimulus presentation was chosen at random from the full set of TFs at a single spatial wavelength. Each fly was presented with two spatial wavelengths. Each closed-loop stimulus presentation was chosen at random from the full set of gains.

Stimuli were generated in Matlab using Psychophysics Toolbox (Brainard, 1997; Kleiner et al.; Pelli, 1997). Stimuli were mapped onto a virtual cylinder before being projected onto flat screens subtending 270° of azimuthal angle. This provided the fly with the visual experience of being in the center of a cylinder. The spatial resolution of the stimulus was ~0.3° and the stimuli were updated at either 180 or 360 Hz. Stimulus spatiotemporal frequency is reported in Table S2.

Virtual hourglass hallway

The virtual hallway stimulus consisted of three 20 mm segments with infinitely high walls diagrammed in the top of Fig. 2B. The first segment had walls were 20 mm apart, the second segment had walls that narrowed from 20 mm to 2mm, and the third segment had walls that widened from 2mm to 20mm. The spatial pattern on the walls was a sine wave with a 5.4 mm spatial wavelength. Supplemental Movie M2 moves through the virtual hallway at a constant speed. The stimulus has two phases. The first phase is the pre-stimulus interval where the fly is held in open-loop position but closed-loop with the sine wave texture. The second phase the fly is in closed-loop with its position in the hallway while the texture remains fixed.

2-photon Calcium Imaging

Neurons were imaged in a two-photon rig as previously described (Clark et al., 2011; Salazar-Gatzimas et al., 2016). The fly was anesthetized on ice and placed in a stainless-steel holder which pitched the head forward. The cuticle, fat, and trachea were removed from the back of the fly’s head and the brain was perfused with a ringer solution (Wilson et al., 2004). Chlordimeform (CDM, Sigma-Aldrich 31099) was added to the ringer solution at a concentration of 20 μM during the experiments shown in Fig. 5ABC ii (Arenz et al., 2017). All imaging was performed on a two-photon microscope (Scientifica, UK). Stimuli were displayed using a digital light projector (DLP) on screen in a setup similar to behavior. The screen covered 270° azimuth and 69° elevation and the virtual cylinder was pitched forward 45° to account for the angle of the head. A bandpass filter was applied to the output of the DLP to prevent the stimulus light from reaching the emission photomultiplier tubes (PMTs). The filters had centers/FWHM of 562/25 nm (projector) and 514/30 nm (PMT emission filter) (Semrock, Rochester, NY, USA). A precompensated femtosecond laser (Spectraphysics, Santa Clara, CA, USA) provided 930 nm light at power <30 mW. Images were acquired at ~13 Hz using ScanImage (Pologruto et al., 2003). Regions of interest for T4 and T5 were defined as in previous studies (Salazar-Gatzimas et al., 2016).

Data analysis

Blinding

Experimenters were not blinded to fly genotype or presented stimuli. All analyses were automated.

Data exclusion

Flies were excluded from behavioral analysis based on three criteria applied to behavior during the prestimulus intervals. These criteria were intended to exclude flies that did not walk, did not turn, or had an extreme bias in turn direction. Flies were excluded if (1) their mean walking speed was less than 1 mm/s; (2) the standard deviation of their turning was less than 40°/s; or (3) the mean turning exceeded two-thirds of the standard deviation in turning.

Average response and standard error of the mean

Fig. 1, 2AB, 3D, 4BC, 5CDEF, 6BC, S1CDEF, S2, S3AD, S4AD, S5

To calculate a fly’s average behavioral response to a given stimulus we first averaged over stimulus presentations to find a mean time trace per fly; then over time, to find an average response per fly to each stimulus; then over flies to find the mean response over flies. For imaging data, the same process was applied but regions of interest were averaged before averaging across flies. The reported standard error of the mean is calculated across the flies’ average responses to a stimulus, using the number of flies as N. Responses to rotational stimuli were averaged over the first 250 ms of stimulus and responses to translational stimuli were averaged over the first 1000 ms of stimulus. For rotational behavioral stimuli, leftward and rightward stimuli were averaged together. For imaging stimuli progressive and regressive T4 and T5 were averaged together. Time traces of responses are calculated identically but without averaging over the time of stimulus presentation.

Normalized walking speed

Before averaging, each walking speed trace was divided by the average walking speed of the fly in the 500 ms of the preceding the stimulus. After this normalization operation, the trace represents a fold change from baseline walking. Average fly walking speed for each genotype is reported in Table S3.

Gain

Fig. 2ADE, S2ACE

The gain the closed-loop stimuli is the multiplicative factor (°/mm) that relates the walking speed of the fly (mm/s) to the stimulus velocity (°/s). The exact number chosen is arbitrary and roughly corresponds to a depth to an object in the real world. For this study we used 18 °/mm which corresponds to a stimulus velocity of 18 °/s per every 1 mm/s of fly walking speed. We refer to this as a gain of 1.

Averaging controls

Fig. 4B

Each experimental genotype had two associated controls; shibire/+ and GAL4/+ (Table S2). These controls behaved similarly so we present their averaged spatiotemporal response under the control column. The controls are split apart for statistical tests.

Peak slowing calculation

Fig. 4D

The mean slowing is equal to 1 minus the normalized walking speed. The peak slowing was found by averaging over the 6 spatiotemporal frequencies flies slowed most to.

Measuring Maxima

Fig. 3DE, 4BC, 5EF, 6BEG, S3A, S6B

The temporal frequency (TF) of a sine wave grating which produced the maximum measured response was identified. Then a 3^rd order polynomial was fit to the 3 TFs before and after the maximum location for a total of 7 points. The location of the maximum of this polynomial was reported. This method reduced susceptibility to noise.

Testing for temporal-frequency-vs. velocity-tuning and spatiotemporal slope (STS)

Fig. 3DFG, 4BCE, 5EFGH, S6BEG, S3AC, S3, S6B

A temporal-frequency-tuned system has the property that the temporal frequency (ω) of a sine wave grating that produces the peak response does not depend on the spatial frequency (k) of the grating. More broadly, a temporal-frequency-tuned response has a response r that is separable, such that r(ω, k) = f(ω)g(k). Analogously, a velocity-tuned system has a response r that is separable such that r(v, k) = f(v)g(k), where $\nu =\frac{\omega }{k}$ is the velocity. We therefore modeled the response as r(β, k) = f(β)g(k) where β ≡ ωk^−γ If γ = 0 then β = ω and one has a temporal-frequency-tuned model, while if γ = 1, then $\beta =\frac{\omega }{k}=\nu$ and one has a velocity-tuned model. Varying γ between those limits allows the model to move smoothly between velocity-tuning and temporal-frequency-tuning. In log-log space, log(β) = log(ω)-γlog(k). This means that regions of constant log(β) correspond to lines with slope γ when plotting log(ω) against log(k) (Fig. S4D). We calculate the likelihood that the data is separable for many values of γ to find the maximum likelihood γ (Fig. S4Dii) and term this the spatiotemporal slope (STS) of the response. We also specifically consider the case of perfect TF-tuning (γ = 0) and perfect velocity-tuning (γ = 1), fit a separable model to each case, and determine which model has a higher likelihood (Fig. S4ABC).

In order to compute the STS, we had to test for separability of many different models. For each value of γ, we resampled spatiotemporal responses along the new axes k and β using Delaunay triangulation (Fig. S4D). We then fit the resampled data to a separable model that maximized the explained variance. We computed the log likelihood for that model (Fig. S4Dii) from the sum of the squared residuals, using an estimate of error (the denominator in the log likelihood) equal to the variance in response averaged over all spatiotemporal frequencies.

Model of walking speed stability

For turning, the fly’s rotational velocity can be modeled as a simple function f of the rotation stimulus it sees:

$$\begin{array}{cc}\hfill \tau \stackrel{.}{r}& =f(v_r)-r\hfill \\ \hfill & v_r=-r\hfill \end{array}$$

Where r is the fly’s rotational velocity, f is the fly’s average open-loop response to a stimulus with rotational velocity v_r. In the natural world, every rotation of the fly corresponds to an opposite rotation in the world so v_r = −r. The rotational velocity adjusts to new stimuli with a time constant τ. Since f is odd (direction-selective) and f(0) = 0, this system ensures that a fixed point is zero rotation. If f′ > 0 at the origin, then the system will be stable to small perturbations in r. This acts as a negative feedback on rotation, and this sort of model has been previously explored in depth (Reichardt and Poggio, 1976). The curves described are shown in Figure S2B.

Following a similar approach to rotational responses, we define fly walking speed as w. The flow field created by translation through an environment is not spatially homogeneous, and depends on the angle and depth of objects relative to the trajectory (Sobel, 1990). However, the flow field is proportional to the translation speed w, and inversely proportional to a positive environmental lengthscale R. We assume that the flow field is weighted over space in some way, so that the constant of proportionality α is positive, and a scalar quantity v_t = αw/R represents the translational velocity signal. Then:

$$\begin{array}{cc}\hfill \tau \stackrel{.}{w}& =g(v_t)-w\hfill \\ \hfill & v_t=\alpha w∕R\hfill \end{array}$$

where g is the open-loop response to a specific translational velocity. The walking speed adjusts itself with time constant τ until it reaches g(v_t).

Combining these two equations, we find

$$\tau \stackrel{.}{w}=g(\alpha w∕R)-w$$

This has a fixed point at w* = g(αw*/R). By changing the gain in closed-loop, or by placing the fly in a virtual wasp-waist corridor, we modulate R, and change the fixed point of the system. Furthermore, this fixed point will be stable when g′(αw*/R) < 0. Since the g(x) is measured empirically to be approximately even (non-direction-selective) and is decreasing as ∣x∣ increases, then this system will be stable to small perturbations in walking speed even when the gain is negative. As long as v_t is less than the velocity the fly responds maximally to, then this mechanism will act as a feedback to stabilize the walking speed of the fly, achieving a slower walking speed when objects are closer (R is smaller). The curves described are shown in Figure 2D.

Model requirements

We evaluated the ability of different models to explain our results based on 4 characteristics of the slowing response: non-direction-selectivity, opponency, temporal-frequency-tuned subunits, and speed tuning (Fig. S6).

Non-direction-selective

The model must respond to both front-to-back (FtB) and back-to-front (BtF) stimuli with the same sign and similar magnitude. Most models in the field are direction-selective; to make such models non-DS, we rectified model outputs before averaging over space and time so as to measure the (non-DS) amplitude of response.

Opponent

An opponent system is often defined as one that responds positively to motion in one direction (preferred direction) and negatively to motion in the opposite direction (null direction) (Adelson and Bergen, 1985; van Santen and Sperling, 1984). However, consider the case that such an opponent system is operated on by a full-wave rectifying nonlinearity. The system now responds equally to stimuli of different directions, hiding its internal opponency.

To probe this internal opponency, one can show the system motion in the preferred direction and add motion in the null direction. If the system was not opponent, then adding motion in the null direction should not change its response, or its response should become larger. An opponent system, even one acted upon by a rectifying nonlinearity, should not respond to such a stimulus because the preferred and null direction motion should cancel out. Counterphase gratings are equal to the sum of FtB and BtF stimuli. We define a model as opponent if it responds individually to FtB and BtF stimuli, but not to their sum (Heeger et al., 1999; Levinson and Sekuler, 1975).

Temporal-frequency-tuned subunits

We observed that T4 and T5 are necessary for the walking response (Fig. 4 iv) and that they are temporal-frequency-tuned (Fig. 5EFGH). Therefore, to agree with the data, a model must use temporal frequency tuned subunits as part of its computation rather than achieving velocity tuning in a single step from non-direction-selective neurons.

Speed-tuning

The model must have a positive spatiotemporal slope (STS).

We examined several candidate models, which we could rule out based on one or more of the criteria above.

Model summaries

Hassenstein-Reichardt Correlator (HRC)

The HRC has been the favored model to describe fly turning response for over 50 years (Borst, 2014; Silies et al., 2014). The HRC consists of two “half correlator” subunits which are spatially reflected versions of one another. While the HRC is predictive of the turning response, it is does not explain the slowing response, since the model is temporal-frequency-tuned (Egelhaaf et al., 1989) and thus has a STS of 0 (Fig. S6 i).

Sum of half -correlators

The HRC consists of two multiplicative units that are subtracted from one another. Instead of subtracting the two subunits, one could add them to remove the direction-selectivity of the model (Fig. S6 ii). The resulting model is not direction-selective, but it is also not opponent. While this model is approximately speed tuned by some metrics (Dyhr and Higgins, 2010b; Higgins, 2004), it is separable in spatiotemporal frequency space and thus has an STS of 0. Finally, this model predicts that the behavioral slowing response should be maximal at low spatial frequencies, which we did not observe.

Half-correlator

An HRC half correlator is approximately velocity tuned and has a positive STS (Zanker et al., 1999). However, this model is direction-selective, not opponent, and achieves velocity tuning in a single step without using TF-tuned subunits (Fig. S6 iii).

Combining a single correlator with non-DS cells

We constructed a model to generate the non-DS, speed-tuned, opponent average behavioral responses by combining a single TF-tuned HRC with other non-DS cells (Fig. S6 iv). By combining the two components multiplicatively, the entire model possessed the opponency of the HRC, while the non-DS cells could sculpt the response to be speed-tuned.

Multiple correlators

This model uses TF-tuned subunits with different spatial and temporal characteristics to measure stimulus velocity. This model is capable of reproducing all the features of our results (Fig. 6). It is worth noting that there are multiple ways to combine differently-tuned correlators to achieve velocity-tuning (Simoncelli and Heeger, 1998; Srinivasan et al., 1999). Furthermore, it is not necessary that the units be correlators; they need merely be TF-tuned and respond to a limited range of spatiotemporal frequencies.

Quantification and statistical analysis

Statistical analysis

Fig. 3FG, 4DE, 5GH, S3BC

Confidence intervals for the spatiotemporal slope (STS), slowing amplitude, and log likelihood ratio were created by bootstrapping the spatiotemporal responses 1000 times across flies and recalculating the metric. We report the 95% confidence intervals of this bootstrap distribution. Bootstrapping is a nonparametric method for generating confidence intervals and does not make strong assumptions about the distribution of the data. We assume that each fly is independent and comes from the same underlying distribution. This method also assumes that our datasets have adequately sampled the population.

Sample-size

Sample-sizes for imaging experiments were chosen based on typical sample sizes in the field. Sample-sizes for behavioral experiments were chosen based on a pilot study used to determine how many flies were required to measure response tuning. Once this pilot study was completed, we acquired the data sets in the paper with approximately this sample-size. The number of flies for each figure is reported in Table S4.

All wildtype behavioral data was reproduced multiple times over several years. All neural silencing data was reproduced from several independent crosses over two years.

Model equations and parameters

The functions p and q represent the temporal filtering steps and the spatial filtering steps at the input to an HRC model.

$$\begin{array}{cc}\hfill p_1(t)& =\mathrm{\delta }(\mathrm{t})\hfill \\ \hfill p_2(t)& =\Theta (t)\frac{1}{\tau }{e}^{-\frac{t}{\tau }}\hfill \\ \hfill p_{hp}(t)& =p_1-p_2\hfill \\ \hfill q_1(x)& =\frac{1}{\sqrt{2\pi {\left(\frac{\varphi }{2}\right)}^2}}{e}^{-\frac{x^2}{2{\left(\frac{\varphi }{2}\right)}^2}}\hfill \\ \hfill q_2(x)& =\frac{1}{\sqrt{2\pi {\left(\frac{\varphi }{2}\right)}^2}}{e}^{-\frac{(x-\varphi {)}^2}{2{\left(\frac{\varphi }{2}\right)}^2}}\hfill \end{array}$$

The function p₁ acts as the non-delay line, while p₂ low pass filters input to delay light signals in time. The two spatial filters are Gaussian with width ϕ/2, displaced by a distance φ. The function is Θ(t) is the Heaviside step function and the function δ(t) is the Dirac delta function.

We combine p and q into 4 different spatiotemporal filter combinations:

$$\begin{array}{cc}\hfill h_{1,1}(x,t)& =p_1(t)q_1(x)\hfill \\ \hfill h_{2,1}(x,t)& =p_2(t)q_1(x)\hfill \\ \hfill h_{1,2}(x,t)& =p_1(t)q_2(x)\hfill \\ \hfill h_{2,2}(x,t)& =p_2(t)q_2(x)\hfill \end{array}$$

The HRC computes the net, oriented spatiotemporal correlations. To compute the output of the HRC model, one convolves each of the filters with the stimulus contrast at each point in time and space, s(x, t), and then takes the difference between pairs of products of those filtering steps:

$$R(x,t)=\beta \left(\left[s\ast h_{2,1}\right]\left[s\ast h_{1,2}\right]-\alpha \left[s\ast h_{1,1}\right]\left[s\ast h_{2,2}\right]\right)$$

Here, the parameter β is an overall scaling factor for fitting. The parameter α represents an imbalance between the two correlators. When α = 1, this is a classical HRC.

Each of the models tested is a modified version of R. The fit parameters for each model are presented below. Note that the model in Fig. S6 ii, as published, contained a high-pass filter in time on all inputs to the model, an operation we also performed in our version of that model, using p_hp(t) from above. Parameters for each model are in Table S5. Parameters in parenthesis were not fit, but were set to generate the model.

To construct a model that was opponent everywhere but contained only 1 opponent DS cell (Fig. S6 iv), we generated two non-DS cells that would be summed together. To do this, we generated the form of the response in frequency space by adding together two TF-tuned responses.

$$R_{NDS}(\omega ,k)=\frac{1}{2\pi {\sigma }_{{\omega }_1}{\sigma }_{k_1}}{e}^{-\frac{\log {\left[\frac{\mid \omega \mid }{{\mu }_{{\omega }_1}}\right]}^2}{2{\sigma }_{{\omega }_1}^2}-\frac{\log {\left[\frac{\mid k\mid }{{\mu }_{k_1}}\right]}^2}{2{\sigma }_{k_1}^2}}+\frac{A}{2\pi {\sigma }_{{\omega }_2}{\sigma }_{k_2}}{e}^{-\frac{\log {\left[\frac{\mid \omega \mid }{{\mu }_{{\omega }_2}}\right]}^2}{2{\sigma }_{{\omega }_2}^2}-\frac{\log {\left[\frac{\mid k\mid }{{\mu }_{k_2}}\right]}^2}{2{\sigma }_{k_2}^2}}$$

This form could be the result of adding the squared outputs of two cells with different spatiotemporal selectivity; this generates the speed tuning of the final model. This form takes the response as averaged over time and space, which could be accomplished with spatial integration (as in HS- or VS-like cells) and low-pass temporal filtering. This non-DS response is then multiplied by a similarly averaged HRC of the form above. The model parameters that fit our data were: τ = 10.4 ms, ϕ = 3.26 °, α = (1), β = 3000, μ_ω1 = 1.12 Hz, ${\mu }_{k_1}=0.011\frac{1}{\circ }$, σ_ω1 = 1.4, σ_k1 = 0.67, A = 25.6, μ_ω2 = 0.72 Hz, ${\mu }_{k_2}=0.017\frac{1}{\circ }$, σ_ω2 = 5.48, σ_k2 = 1.61.

Supplementary Material

2

Supplemental Movie M1. Related to Figure 1. Movie of a fly in the behavioral rig during stimulus presentation.

3

Supplemental Movie M2. Related to Figure 2. Movie of an observer traveling at 4 mm/s through the virtual hourglass hallway in the top of Fig. 2B. In experiments, the walls of the hallway extended to the full height of the screen. For more details, see STAR Methods.

Key Resource Table:

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Chemicals, Peptides, and Recombinant Proteins
Chlordimeform	Sigma-Aldrich	31099
Experimental Models: Organisms/Strains
D. melanogaster: WT: +; +; +	Gohl et al., 2011	N/A
D. melanogaster: shibirets: +/hs-hid; +; UAS-shibirets	Kitamoto, 2001; Silies et al., 2013	N/A
D. melanogaster: GCaMP6f: +; UAS-GC6f; +	Chen et al., 2013 Bloomington Drosophila Stock Center	RRID:BDSC_42747
D. melanogaster: L1: +; L1-GAL4; +	Rister et al., 2007; Silies et al., 2013	N/A
D. melanogaster: L2: +; +; L2-GAL4	Rister et al., 2007; Silies et al., 2013	N/A
D. melanogaster: L3: +; +; L3-GAL4	Silies et al., 2013	N/A
D. melanogaster: T4 and T5: +; +; R42F06-GAL4	Maisak et al., 2013 Bloomington Drosophila Stock Center	RRID:BDSC_41253
D. melanogaster: T4 and T5: w; R59E08-AD; R42F06-DBD	Schilling and Borst, 2015	N/A
Software and Algorithms
MATLAB and Simulink, R2017a	Mathworks	http://www.mathworks.com/
Psychtoolbox 3	Psychtoolbox	http://psychtoolbox.org/

Highlights.

• Drosophila slows in response to visual motion to stabilize its walking speed

• Slowing is tuned to the speed of visual stimuli

• Walking speed modulation relies on T4 and T5 neurons

• A model combining multiple motion detectors can explain the behavioral results