A Bayesian Approach for Estimating Dynamic Functional Network Connectivity in fMRI Data

Abstract

Dynamic functional connectivity, i.e., the study of how interactions among brain regions change dynamically over the course of an fMRI experiment, has recently received wide interest in the neuroimaging literature. Current approaches for studying dynamic connectivity often rely on ad-hoc approaches for inference, with the fMRI time courses segmented by a sequence of sliding windows. We propose a principled Bayesian approach to dynamic functional connectivity, which is based on the estimation of time varying networks. Our method utilizes a hidden Markov model for classification of latent cognitive states, achieving estimation of the networks in an integrated framework that borrows strength over the entire time course of the experiment. Furthermore, we assume that the graph structures, which define the connectivity states at each time point, are related within a super-graph, to encourage the selection of the same edges among related graphs. We apply our method to simulated task-based fMRI data, where we show how our approach allows the decoupling of the task-related activations and the functional connectivity states. We also analyze data from an fMRI sensorimotor task experiment on an individual healthy subject and obtain results that support the role of particular anatomical regions in modulating interaction between executive control and attention networks.

1. Introduction

Functional magnetic resonance imaging (fMRI) provides an indirect measure of neuronal activity by evaluating changes in blood oxygenation over different areas of the brain. In a typical fMRI experiment, time series of blood oxygenation-level dependent (BOLD) responses are collected at each location of the brain, for example in response to a stimulus (Poldrack et al., 2011). Statistical methods play a crucial role in understanding and analyzing fMRI data (Lazar, 2008; Lindquist, 2008). Bayesian approaches, in particular, have shown great promise in applications. A remarkable feature of fully Bayesian approaches is that they allow a flexible modeling of spatial and temporal correlations in the data, see Flandin and Penny (2007); Bowman et al. (2008); Quiros et al. (2010); Woolrich (2012); Stingo et al. (2013) and Zhang et al. (2014, 2016), among others. A comprehensive review of Bayesian methods for fMRI data can be found in Zhang et al. (2015).

In neuroscience, it is now well established that brain regions cooperate within large functional networks to handle specific cognitive processes (Bullmore and Sporns, 2009). FMRI data, in particular, allow scientists to learn on two distinct types of brain connectivity, which are referred to as effective and functional connectivity (Friston et al., 1994). Effective connectivity refers to the direct, or causal, dependence of one region over another, while functional connectivity investigates the undirected relationships between separate brain regions characterized by similar temporal dynamics. In this paper we are concerned in particular with this latter form of connectivity. Early model-based approaches for the estimation of functional connectivity included Bayesian frameworks (Patel et al., 2006a,b) that first dichotomised the time series data based on a threshold, to indicate presence or absence of elevated activity at a given time point, and then estimated the relationships between pairs of distinct brain regions by comparing expected joint and marginal probabilities of elevated neural activity. Also, Bowman et al. (2008) developed a two-step modeling approach that employs measures of task-related intra-regional (or short-range) connectivity as well as inter-regional (or long-range) connectivity across regions. More recently, Zhang et al. (2014, 2016) proposed Bayesian nonparametric frameworks that capture functional dependencies among remote neurophysiological events by clustering voxels with similar temporal characteristics within-and across multiple subjects.

Some of the most commonly used approaches to functional connectivity are not model-based, but simply rely on measures of temporal correlation. For example, Pearson correlation coefficients are calculated between regions of interest, or between a “seed” region and other voxels throughout the brain (Cao and Worsley, 1999; Bowman, 2014; Zalesky et al., 2012). These methods result in a network characterization of brain connectivity, with correlations indicating the strength of the connections between nodes. However, there are well-known limitations in using simple correlation analysis as this only captures the marginal association between network nodes. Indeed, a large correlation between a pair of nodes can appear due to confounding factors such as global effects or connections to a third node (Smith et al., 2011). Partial correlation, on the other hand, measures the direct connectivity between two nodes by estimating their correlation after regressing out effects from all the other nodes, hence avoiding spurious effects in network modeling. A partial correlation value of zero implies absence of a direct connection between two nodes given all the other nodes. Consequently, methods for graphical models, that estimate sparse precision matrices, as inverses of the covariance matrix, have been recently applied to fMRI data. These include the graphical LASSO (GLASSO) (Cribben et al., 2012; Varoquaux et al., 2010) and Bayesian graphical models based on G-Wishart priors (Hinne et al., 2014). Also, Pircalabelu et al. (2015) developed a focused information criterion for Gaussian graphical models to determine brain connectivity tailored to specific research questions. Their proposed method selects a graph with a small estimated mean squared error for a user-specified focus.

All approaches described above assume static connectivity patterns throughout the course of the fMRI experiment. Under such an assumption, functional brain connectivity is represented by spatially and temporally constant relationships among the regions of the brain. However, in practice, the interactions among brain regions may vary during an experiment. For example, different tasks, or fatigue, may trigger varying brain interactions. Therefore, more recent work has pointed out that it is more appropriate to regard functional connectivity as dynamic over time (Chang and Glover, 2010; Hutchison et al., 2013; Calhoun et al., 2014; Chiang et al., 2015). Thus, some approaches have considered estimating precision matrices on small intervals of the fMRI time course determined by using a sliding window. The estimated matrices are then clustered together, e.g., by using a k-means algorithm, and the clustered connectivity patterns are finally used to inform a classification of the cognitive processes generated along the experiment (Allen et al., 2012). Although straightforward, these approaches have limitations. For example, the length of the window is arbitrarily selected before the analysis, through a trial-and-error process. Indeed, Lindquist et al. (2014) show that the choice of the window length can affect inference in unpredictable ways. To partially obviate the issue, Cribben et al. (2012) and Xu and Lindquist (2015) have recently investigated greedy algorithms, which automatically detect change points in the dynamics of the functional networks. Their approach recursively estimates precision matrices using GLASSO on finer partitions of the time course of the experiment, and selects the best resulting model based on the Bayesian Information Criterion (BIC). The algorithm estimates independent brain networks over noncontiguous time blocks, whereas instead it may be desirable to borrow strength across similar connectivity states in order to increase the accuracy of the estimation. Furthermore, greedy searches often fail to achieve global optima.

In this paper, we propose a principled, fully Bayesian approach for studying dynamic functional network connectivity, that avoids arbitrary partitions of the data. More specifically, we cast the problem of inferring time-varying functional networks as a problem of dynamic model selection in the Bayesian setting. We do this by first adapting a recent proposal for inference on multiple related graphs put forward by Peterson et al. (2015). This model formulation further assumes that the connectivity states active at the individual time points may be related within a super-graph and imposes a sparsity inducing Markov Random field (MRF) prior on the presence of the edges in the super-graph. MRF priors have been used extensively in recent literature to capture network structures, particularly in genomics (Li and Zhang, 2010; Stingo et al., 2011, 2015) and in neuroimaging (Smith and Fahrmeir, 2007; Zhang et al., 2014; Lee et al., 2014). We then embed a Hidden Markov Model on the space of the inverse covariance matrices, automatically identifying change points in the connectivity states. Our approach is in line with recent evidence in the neuroimaging literature which suggests a state-related dynamic behavior of brain connectivity with recurring temporal blocks driven by distinct brain states (Baker et al., 2014; Balqis-Samdin et al., 2017). In our approach, however, the change points of the individual connectivity states are automatically identified on the basis of the observed data, thus avoiding the use of a sliding window. Furthermore, in our approach the latent state-space process which governs the detection of the change points naturally induces a clustering of the networks across states, avoiding the use of post-hoc clustering algorithms for estimating shared covariance structures. In contrast to standard approaches, where the connectivity networks are estimated separately within each window, within our framework the estimation of the active networks between two change points is obtained by borrowing strength across related networks over the entire time course of the experiment.

We consider task-based experimental designs and show how our modeling framework allows the decoupling of the task-related activations and the functional connectivity states, to understand how a particular task affects (e.g., either modulates or inhibits) functional relationships among the networks. We first assess the performance of our model on simulated data, where we compare estimation results to recently developed methods for network estimation. We then apply our method to the analysis of task-based fMRI data from a healthy subject, where we find that our approach is able to reconstruct known connectivity networks, both under task and resting state. The results also support the role of particular anatomical regions in modulating interactions between executive control and attention networks.

The remainder of the paper is organized as follows. In Section 2 we describe the proposed modeling framework and discuss posterior inference. In Section 3 we assess performances of our method on simulated data. Section 4 describes the application of our model to actual fMRI data. Section 5 provides some final remarks and conclusions.

2. Bayesian model for dynamic functional connectivity

Brain networks can be mathematically described as graphs. A graph $G=(\mathcal{V},\mathcal{E})$ specifies a set of nodes (or vertices) $\mathcal{V}=\{1,2,\dots ,V\}$ and a set of edges $\mathcal{E}\subset \mathcal{V}\times \mathcal{V}$. Here, the nodes represent the neuronal units, whereas the edges represent their interconnections. Let Y_t = (Y_t1,..., Y_tV)^T, with the symbol (·)^T indicating the transpose operation, be the vector of fMRI BOLD responses of a subject measured on the V nodes at time t, for t = 1,..., T. Unlike other fields (e.g., social networks), in brain imaging the best definition of a node is unclear, with some consensus settling toward the consideration of general pragmatic issues and the use of data-driven approaches able to capture differences in the functional connectivity profiles (Cohen et al., 2008; Zalesky et al., 2010). Thus, nodes could be intended as either single voxels or macro-areas of the brain which comprise multiple voxels at once. For example, in the application we discuss in Section 4 we define the nodes of the functional networks using independent component analysis (ICA), an increasingly utilized approach in the fMRI literature, which decomposes a multivariate signal into components that are maximally independent in space (McKeown et al., 1998). ICA components can be interpreted as group of voxels that covary in time, providing a spatial mapping of anatomical regions, and have been found to effectively identify functional networks in both task-based and resting-state data (Garrity et al., 2007; Yu et al., 2013). In our modeling framework, the use of ICA components allows us to also considerably reduce dimensionality, as the number of components of interest is typically low, with most authors considering between 20 and 30 components (Erhardt et al., 2011; Damaraju et al., 2014). We note, however, that our modeling approach does not depend on the particular choice of ICA-based regions, as it is generally applicable to any well-defined set of brain regions for which connectivity is of interest.

ICA components, being linear weighed sums of the original source signal at each time point, preserve the hemodynamic structure of the underlying BOLD signal (Calhoun et al., 2004). In particular, in the analysis of task-based fMRI data, assuming an experiment with K distinct stimuli, we can write a linear regression model of the type

$${\mathit{Y}}_t=\mathit{\mu }+{\displaystyle \sum _{k=1}^K{\mathit{X}}_t^k\circ {\beta }_k+{\epsilon }_t,}$$ (1)

with o denoting the element-by-element (Hadamard) product, and where ${\mathit{X}}_t^k$ is the V × 1 design vector for the k-th stimulus, μ the V-dimensional global mean and β_k = (β_1k,..., β_Vk)^Τ the stimulus-specific V-dimensional vector of regression coefficients. The mean term in (1) allows to decouple the estimation of the brain activations from that of the spatio-temporal correlation of the fMRI time series, which is captured by the error term, while the baseline mean μ is included to represent the base signal during periods where no stimulus is present. We assume that standard pre-processing has been applied to the fMRI data, including smoothing, spatial standardization, motion and slice-timing correction, as well as high-pass filtering, and therefore do not include a drift term in the model. Furthermore, we follow the predominant literature on task-based fMRI modeling and assume that the BOLD signal is characterized by a hemodynamic delay, which accounts for the lapse of time between the stimulus onset and the vascular response (Friston et al., 1994). We then model the elements of ${\mathit{X}}_t^k$ as the convolution of the stimulus pattern with a hemodynamic response function (HRF), h(t),

$$X_{vt}^k={\displaystyle {\int }_0^t{x}_k(\tau )}{h}_{\lambda }(t-\tau )d\tau ,t=1,\dots ,T,v=1,\dots ,V,$$ (2)

with x_k(τ) representing the time dependent stimulus (e.g., a block or event-related design). We assume a Poisson HRF with a region-dependent delay parameter, i.e., $h_{{\lambda }_v}(t)=\exp (-{\lambda }_v){\lambda }_v^t/t!$, and impose a uniform prior on the delay parameters, λ_ν ~ Unif(u_1,u₂), with u₁ and u₂ to be chosen based on prior knowledge on physical ranges of hemodynamic delay (Zhang et al., 2014). We also impose normal priors on the components of the baseline mean vector, μ, that is, ${\mu }_v\stackrel{iid}{~}N(0,{\sigma }_{\mu })$, with σ_μ a hyper-parameter to be specified.

We follow recent literature in Bayesian modeling of task-based fMRI data and identify brain activations by imposing spike-and-slab priors, also known as Bernoulli-Gaussian prior (or degenerated mixture model) in the fMRI community, on the coefficients β_vk (Kalus et al., 2013; Lee et al., 2014; Zhang et al., 2014, 2016). First, we introduce binary latent indicator variables, γ_vk, such that γ_vk = 1 if component v is active, and γ_vk = 0 otherwise. Then, we assume

$${\beta }_{vk}~(1-{\gamma }_{vk}){\delta }_0+{\gamma }_{vk}N(0,{\sigma }_{\beta }),$$ (3)

where δ₀ denotes a Dirac-delta at 0 and σ_β is some suitably large value encouraging the selection of relatively large effects. We place Bernoulli priors on the selection indicators, ${\gamma }_{vk}\stackrel{iid}{~}\mathrm{Bern}(p_k)$, where p_k can be fixed at a small value to induce sparsity.

2.1. Modeling functional networks and dynamic connectivity

An accurate modeling the error term in (1) is key in the analysis of fMRI data. This term, in fact, captures not only acquisition or measurement noise but also spontaneous brain activity, which means all effects that are not directly evoked by the paradigm (i.e. the task-related component) (Yu et al., 2016). In our model formulation, we capture spontaneous brain activity via Gaussian graphical models (GGMs), also known as covariance selection models (Lauritzen, 1996), as a way of estimating functional network connectivity. We assume that subjects fluctuate among different connectivity states during the course of the experiment. We estimate states and corresponding connectivity networks from the data as follows. According to the dynamic paradigm of brain connectivity, fMRI time courses are characterized by possibly distinct connectivity states, i.e., network structures, within different time blocks (Cribben et al., 2012; Allen et al., 2012; Balqis-Samdin et al., 2017). Accordingly, we assume that functional connectivity may fluctuate among one of S > 1 different states during the course of the experiment. Let s = (s₁,..., s_T)^T, with s_t = s, for s ϵ {1,... S}, denoting the connectivity state at time t. Then, conditionally upon s_t, we assume

$$({\epsilon }_t|s_t=s)~N_V(0,{\mathrm{\Omega }}_s),$$ (4)

where Ω_s ϵ ℝ^V x ℝ^V is a symmetric positive definite precision matrix, i.e., ${\mathrm{\Omega }}_s={\sum }_s^{-1}$, with ∑_s the covariance matrix. The zero elements in Ω_s encode the conditional independence relationships that characterise state s, that is graph $G_s=(\mathcal{V},{\mathcal{E}}_s)$. Specifically, ${\omega }_{ij}^{(s)}=0$ if and only if edge $(i,j)\notin {\mathcal{E}}_s$. We discuss the prior distribution on the set of graphs {G₁,..., G_S} in Section 2.2 below.

Many of the estimation techniques for GGMs rely on the assumption of sparsity in the precision matrix, which is generally considered realistic for the small-world properties of brain connectivity in fMRI data (Smith et al., 2011; Varoquaux et al., 2012). We consider general, not necessarily decomposable, graph structures. More specifically, we use the G-Wishart distribution as a conjugate prior on the space of the precision matrices Ω with zeros specified by the underlying graph G (Roverato, 2002; Jones et al., 2005; Dobra et al., 2011). A G-Wishart prior, Ω ~ W_G(b,D), is characterized by the density

$$p(\mathrm{\Omega }|G,b,D)=I_G{(b,D)}^{-1}|\mathrm{\Omega }{|}^{\frac{b-2}{2}}\exp \{\frac{1}{2}\mathrm{tr}({\mathrm{\Omega }}_{t}D)\},\mathrm{\Omega }\in P_G^{+},$$ (5)

where b > 2 is the degrees of freedom parameter, D is a V × V positive definite symmetric matrix, I_G denotes the normalizing constant and $P_G^{+}$ is the set of all V × V positive definite symmetric matrices with off-diagonal elements w_ij = 0 if and only if edge $(i,j)\notin \mathcal{E}$.

We treat the estimation of the unknown connectivity states at each of the time points as a problem of change points detection. More precisely, we identify the functional networks acting at any time point by modeling the temporal dependence of the discrete latent indicators s_t. We assume that at each time point the probability of being within each state is given by a time-dependent probability vector, π(t) = (π₁(t),..., π_S(t))^T, with π_s(t) = p(s_t = s) ≥ 0, for s = 1,...,S, and ${\sum }_{s=1}^S{\pi }_s(t)=1$. Since fMRI experiments are locally stationary in time (Ricardo-Sato et al., 2006; Liu et al., 2010; Messe et al., 2014), we account for the temporal persistence of the states by modeling the selection indicators st through a Hidden Markov Model (HMM). Thus, we assume that two subsequent time points are characterized by connectivity states s_t-1 and s_t according to a law determined by a matrix P of transition probabilities, with elements p(s_t = s|s_t-1 = r) = p_rs, for r, s = 1,...,S and t = 2,...,T. The r-th row of P is assumed to have a Dirichlet distribution with parameter vector a_r = (a_r1,...,a_rS). Marginalizing over the Wishart distribution, we can express the marginal distribution of ε_t as a mixture of type

$${\epsilon }_t~{\sum }_{s=1}^S{\pi }_s(t)p({\epsilon }_t|G_s),t=1,\dots ,T,$$ (6)

with mixing weights ${\pi }_s(t)={\sum }_{r=1}^S{p}_{rs}{\pi }_r(t-1)$ and p(ε_t|G_s) = ∫ p(ε_t|Ω_s) p(Ω_s|G_s)dΩ_s. It is important to note that marginalizing over the Wishart distribution reduces expression (6) to a mixture of scaled multivariate t distributions.

2.2. Joint modeling of the connectivity states

We assume that the graph structures, which define the connectivity states active at each time point, may be related within a super-graph, so to encourage the selection of the same edges in related graphs. In order to achieve such an objective, we adapt a recent proposal by Peterson et al. (2015) for the analysis of (known) cancer subtypes to the analysis of the (unknown) states of fMRI time series. More precisely, we introduce binary vectors of edge inclusion, g_ij = (g_ij1,..., g_ijS)^T with elements g_ijs indicating the presence or absence of edge (i,j) in graph G_s, s = 1,..., S, i.e., g_ij ∈ {0,1}^s, 1 ≤ i < j ≤ V. Then, we assume that the super-graph defines the presence of an edge across graphs through a Markov random field (MRF) prior,

$$p({\mathit{g}}_{ij}|{\nu }_{ij},\mathbf{\Theta })=C{({\nu }_{ij},\mathbf{\Theta })}^{-1}\exp ({\nu }_{ij}{1}^{\mathrm{T}}{\mathit{g}}_{ij}+{\mathit{g}}_{ij}^{\mathrm{T}}\mathbf{\Theta }{\mathit{g}}_{ij}),$$ (7)

where 1 is the unit vector of dimension S, v_ij is a sparsity parameter specific to each vector g_ij, and Θ is an S × S symmetric matrix which captures relatedness among networks. More specifically, the diagonal entries of Θ are set to zero, whereas the off-diagonal entries θ_rs, r ≠ s, are assumed to be non-negative and provide a measure of the strength of the association of two networks. The normalizing constant in (7) corresponds to p(g_ij = 0|v_ij, Θ) = $\frac{1}{C({\nu }_{ij},\mathbf{\Theta })}$ and can be easily computed, especially since the number of identifiable connectivity states S is expected to be low in a typical fMRI experiment. The parameters Θ and ν = (v_ij)_i,j=1,...,V affect the prior probability of selection of the edges in each graph. We impose prior distributions on ν and Θ to help control for multiplicity and allow learning about the networks’ similarity directly from the data. More specifically, we assume a spike-and-slab prior on the off-diagonal entries of Θ, that is

$${\theta }_{rs}|{\xi }_{rs}~(1-{\xi }_{rs}){\delta }_0+{\xi }_{rs}\mathrm{Gamma}(\alpha ,\beta ),$$ (8)

where ξ_rs is a binary random variable that indicates if graph r and s are related, and the parameters (α,β) are chosen to ensure probability to both small and large values of the θ_rs. We set ${\xi }_{rs}\stackrel{iid}{~}\mathrm{Bern}(p_{\xi })$, where p_ξ is selected to promote an overall level of sparsity, and also sharing of information across networks only when it is appropriate, based on the data. The parameter ν in (7) can be used both to encourage sparsity within the graphs G₁,..., G_S and to incorporate prior knowledge on particular connections. In particular, a prior which favors smaller values for ν reflects a preference for model sparsity, and thus can be used for modeling the small-world properties of brain networks (Smith et al., 2011; Varoquaux et al., 2012). We can set a hyper-prior on ν by considering the case of null Θ. In such a case, the probability of inclusion of edge (i,j) in graph G_s is $p(g_{s,ij}|{\nu }_{ij})=\frac{e^{{\nu }_{ij}}}{1+e^{{\nu }_{ij}}}=q_{ij}$, which induces a prior on the elements v_ij, since v_ij = logit(q_ij·). We assume q_ij ~ Beta(a,b).

A schematic representation of the proposed Bayesian model for dynamic functional connectivity is given in Figure 1. A regression model describes the observed BOLD response to a number of different stimuli, via convolution with a HRF. The noise term, capturing spontaneous brain activity, is modeled by a Gaussian graphical model indexed via a HMM, to allow the connectivity structure to change over time. A “super-graph” links the graphs. We note that the modeling construction (1) and (4) induces a marginal distribution on the observed time course data, Y_t, which is multivariate Normal, with the regression component as the mean of the distribution and the Gaussian graphical model imposed on the variance-covariance term. This results in a decoupling of the task-related activations and the functional connectivity states. Furthermore, the characterization of connectivity via latent states and, in particular, the use of the HMM add flexibility to the model formulation, as we can learn on interesting patterns of state persistence in connectivity that may arise during the course of the experiment, as distinct from those induced by the task.

Figure 1:

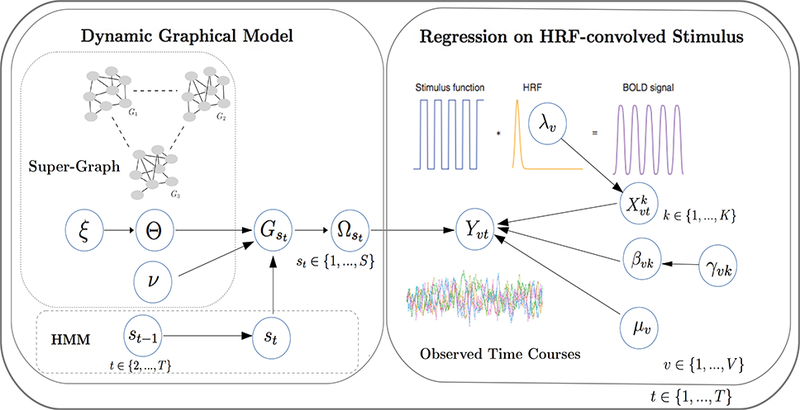
Schematic representation of the proposed Bayesian model for dynamic functional connectivity. A regression model describes the observed BOLD response to a number of different stimuli, via convolution with a HRF. The noise term, capturing spontaneous brain activity, is drawn from a Gaussian graphical model indexed via a HMM, to allow the connectivity structure to change over time. A “super-graph” links the graphs. This results in a marginal multivariate Normal distribution on Y_t, with the regression component as the mean and the Gaussian graphical model imposed on the variance-covariance term.

2.3. Posterior Inference

We rely on Markov Chain Monte Carlo (MCMC) techniques to sample from the joint posterior distribution of (Ω, β, μ, s,v, γ, ξ, Θ, G, λ). We report here a brief description of the sampling steps and give the full details of the algorithm in Appendix A.1.

A generic iteration of the MCMC algorithm comprises the following steps:

• •Update λ: This is a Metropolis-Hastings (MH) step across all λ_ν for v ∈ {1,.., V} with a uniform proposal centered at the current value of the parameter.
• •Update s: For each s ∈ {1,..., S}, the state transition probabilities are sampled from a Dirichlet(α_s) distribution, with α_s an S dimensional vector. Then the stationary distribution of this transition matrix is calculated and accepted or rejected based on an MH step. The states are then sampled using the Forward Propagate Backward Sampling method of Scott (2002).
• •Update G and Ω: For each s ∈ {1,..., S} and pair i ≠ j ∈ {1,..., V}, an edge indicator $g_{ij}^{(s)}$ is proposed with probability $p(\frac{G_{s_{new}H(e,\mathrm{\Omega })}}{G_{s_{old}}})$, where H(e, Ω), with e = (i,j) the edge being updated, is as outlined in Wang and Li (2012). If the proposed value of edge indicator is different, then ${\mathrm{\Omega }}_{s_{new}}|G_{s_{new}}$ is sampled from its conditional distribution and the joint proposal is accepted or rejected in an MH step. This step uses an adaptation of the sampling scheme of Wang and Li (2012), which avoids computation of prior normalizing constants and does not require tuning of proposals.
• •Update Θ and ξ: We update these parameters jointly by performing between-model and within-model MH steps. For the between-model step, for each r ≠ s ∈ {1,..., S} we propose to change the value of ξ_rs from 0 to 1, or vice versa. If the new ξ_rs = 0 we set θ_rs = 0, and if the new ξ_rs = 1 we sample a new θ_rs from a Gamma proposal. For the within-model step, for each pair r ≠ s ∈ {1,..., S} such that ξ_rs = 0 we sample a proposed θ_rs from a Gamma proposal.
• •Update γ and β: We update these parameters jointly by performing between-model and within-model MH steps. For the between-model step, for each k ∈ {1,..., K}, we either add, delete, or swap values of the γ_k vector, then sample β_k conditional on the proposed values of γ_k. For the within-model step, for each k ∈ {1,..., K} and for each v ∈ {1,...,V} such that γ_kv ≠ 0 we sample a proposed from a normal distribution centered at the old value of β_kv.
• •Update μ: For each v ∈ {1,..., V} we sample μ_u from a univariate normal distribution centered at the current value of μ_u, and accept or reject in an MH step.
• •Update v: For each i ≠ j ∈ {1,..., V} we sample q_ij from a Beta proposal, then compute the proposed v_ij = logit(q_ij), and accept or reject the proposed value in an MH step.

For posterior inference, we are primarily interested in the detection of the connectivity states s_t, for t = 1,...,T, and the estimation of the connectivity networks G_s, for s = 1,..., S. Inference on the connectivity states can be achieved by looking at the proportion of iterations in the MCMC samples that a time point is classified to each of the S states, and then assigning the most probable state at each time point. Network connectivity structures can then be estimated by computing marginal probabilities of edge inclusion as proportions of MCMC iterations in which an edge was included. More precisely, for each s = 1,..., S, the posterior p(g_ijs = 1|data) is estimated as the proportion of iterations that g_ijs = 1. Included edges are then selected by thresholding the posterior probabilities to control for the Bayesian false discovery rate (FDR, Newton et al., 2004). For testing a sequence of R null hypotheses H_0r vs alternative hypotheses H_1r, r ∈ R, let h_r = p(H_1r |data) denote the posterior probability of each alternative hypothesis. Then, the Bayesian FDR is defined as

$$FDR(\kappa )=\frac{{\sum }_{r=1}^R(1-h_r)I_{(h_r>\kappa )}}{{\sum }_{r=1}^R{I}_{(h_r>\kappa )}},$$

where I_A is an indicator function such that I_A = 1 if A is true, and 0 otherwise, and κ is a given threshold on the posterior probabilities h_r ‘s. A FDR control at a given level monotonically correspond to a threshold on h_r. In our setting, $R=\mathcal{E}$, i.e. the set of all edges being tested, whereas H_0r and H_1r denote the null and alternative hypotheses that an edge is either absent or present in a connectivity state, respectively. Given the estimated networks, estimates of the strength of the associations can then be obtained from the corresponding precision matrices by averaging sampled MCMC values. In addition to the inference on the estimated graphs, our model returns a spatial map of the activated components obtained by thresholding the posterior probabilities of activation, p( γ_vk = 1| data), for v = 1,...,V and k = 1,..., K, estimated as the proportion of times that γ_vk = 1 across all MCMC iterations, after burn-in.

3. Simulation Study

In order to assess the performance of our proposed method in a controlled setting, we simulated data intended to mimic an actual fMRI time course experiment. We employed the publicly available SimTB toolbox (Erhardt et al., 2012, http://mialab.mrn.org/software/simtb/) which provides flexible generation of fMRI data.

In the simulation setting we present here, we considered a design with rest and K = 2 stimuli over T = 180 time points (see Figure 2, top) and generated data corresponding to the time courses of V =10 separate ICA components. We followed the framework outlined in Erhardt et al. (2012) and modeled the signal for each component time course as an increase or a decrease in the mean value in response to the stimuli. We set the baseline mean μ in model (1) to zero and the stimulus-specific regression coefficients as given at the bottom of Figure 2. The SimTB toolbox implements a canonical hemodynamic response function (Lindquist et al., 2009), which is defined as the linear combination of two Gamma functions that model both the typical response delay observed after activation and the post-stimulus undershoot, that is $h(t)=t^{a_1-1}{b}_1^{a_1}\exp (-b_{1}t)-c{t}^{a_2-1}{b}_2^{a_2}\exp (-b_{2}t)$. For the simulation presented here we set a₁ = 6, b₁ = 1, a₂ = 15, b₂ = 1, and c = 1/3. Within the SimTB toolbox we also added some unique events, generated by uniformly sampling from the interval (−0.025, 0.025) with probability .1, as well as a Gaussian noise component with mean zero and standard deviation .1, which is added at each time point of the convolved hemodynamic time series.

Figure 2:

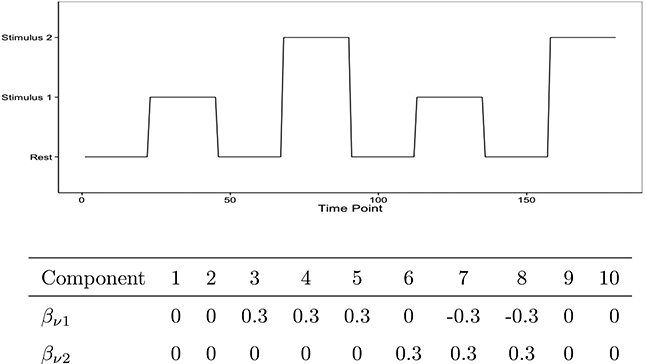
Simulation study design: Resting and stimulus conditions (top figure) and stimulus-specific regression coefficients (bottom table).

The next step in the data generation is to induce dynamic spatio-temporal correlation in the time series, which in our model is captured by the error term ε_t. Our interest is in testing whether our method can recover the functional connectivity states that characterize task and resting conditions. We therefore set S = 3 connectivity states corresponding to the rest and task conditions. We then generated 3 functional networks {G₁,G₂,G₃} as follows. First, a set of cliques, i.e., fully connected subsets of the 10 simulated components, were selected for inclusion in each of the three connectivity states. These cliques define the 3 graphs and their adjacency matrices are provided in Figure 3 (top). Then, at each time point t, given state s_t = s ∈ {1,..., S}, and for each clique in G_s, correlation among the nodes of the clique was induced by randomly adding or subtracting a fixed quantity (0.5) to all node values at that time point with probability 0.95. There may be nodes in a clique which are negatively correlated with the others, and to these nodes we would subtract instead of add, or vice versa. As a result, within a clique there may be nodes either negatively or positively correlated with other components in the same clique. The resulting correlation matrices for each state are depicted in Figure 3 (bottom). We note that our approach simulates errors according to a specified conditional independence structure, while avoiding simulation from a Gaussian graphical model.

Figure 3:

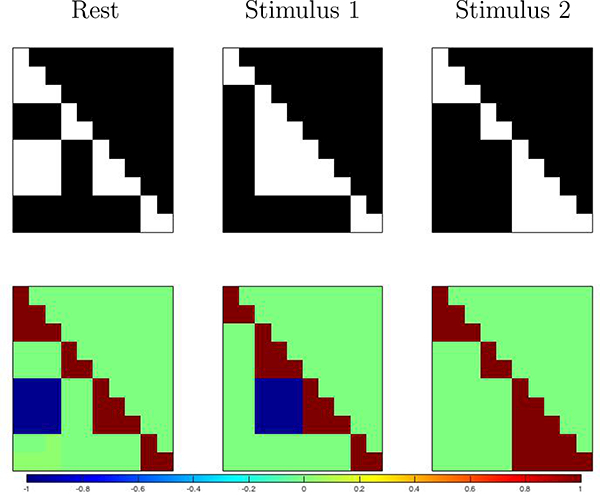
Simulation study design: Simulated connectivity networks (top) and corresponding correlation matrices (bottom - only the lower triangular part is displayed).

For model fitting, we specified independent Unif(0, 8) priors on the Poisson hemodynamic delay parameters λ_ν in (2), to ensure prior mass within a reasonable area of the expected hemodynamic delay. We also specified a N(0,1) prior on the individual components of the baseline mean, μ_ν, and as the slab portion of the spike-and-slab prior (3) on the regression coefficients, ß_vk. The prior probability of a component being activated was specified as p_k = .2, for k = 1, 2. We note that this specification is different from the true proportion of activated components, which is .5 and .3 for stimulus 1 and 2, respectively. As for the parameters of the G-Wishart prior in (5), we specified b = 3 and D = I_V, which corresponds to a vague distribution on the space of precision matrices. For the prior specification on the MRF prior (7) on (G₁,..., G_S}, we recall that v_ij = logit(q_ij), where q_ij defines a marginal probability of edge inclusion. Here, we set q_ij ~ Beta(1,3), which corresponds to a prior marginal probability of edge inclusion of .25. Further, for the prior specification on Θ in (8), we set α = 4 and β = 16, and fixed ρ_ξ = 0.1, in order to further promote sparsity. Peterson et al. (2015) note that monotonically higher values of ρ_ξ correspond to monotonic increases in P(θ_rs ≠ 0|data) ∀r = s ∈ (1,...,S}, and this motivates a low value for ρ_ξ to correspond with our expectation of a reasonable, but small, amount of graph similarity. In our experience, results appeared to be robust to the different choices of ρ_ξ we considered, as long as the prior overall encouraged a reasonable level of sparsity. For example, for the settings we considered here, there were not appreciable differences for values of ρ_ξ < 0.2. The priors on the rows of the HMM transition matrix were set as uniform, i.e., Dir(1,1,1), to characterize lack of prior knowledge on state transitions.

We ran the MCMC algorithm for 20,000 iterations and used a burn in of 10,000. The code took approximately 1 hour and 40 minutes to run on an iMac 3.2 GHz Intel Core i5. Convergence was checked by examining the number of edges included in each iteration, for the graph component, and number of variables included in each iteration, for the regression component (plots not shown). Furthermore, the Geweke diagnostic test (Geweke, 1992), as implemented in the R package coda, was performed on the number of edges, the number of included variables in the regression, and the regression coefficients. The convergence test was significant at the alpha = .01, for all variables.

We comment first on the inference on the connectivity states. Figure 4 displays the posterior probabilities of s_t = s for s ∈ {1,2, 3}, across all T time points. A visual comparison with Figure 2 highlights that State 1 characterizes the absence of any stimulus, that is the resting state, while States 2 and 3 capture the presence of the two stimuli with high probability. As expected, transition points between connectivity states have the highest uncertainty. This result also highlights the fact that our method is able to correctly identifying non-contiguous temporal regions as belonging to the same connectivity state, effectively borrowing strength in estimation across time windows characterized by similar connectivity states. Figure 5 (top) illustrates our inference on the 3 estimated connectivity networks, {G₁,G₂,G₃}, obtained by thresholding the posterior probabilities p(g_ijs = 1|data) at a level corresponding to a Bayesian FDR of .1. Figure 5 (bottom) shows the corresponding estimated precision matrices. Overall, our method appears to capture the main features of the true dependence structures, namely positive and negative correlations, quite well. As a formal comparison, we calculated the RV-coefficient, a measure of similarity between positive semi-definite matrices (Josse et al., 2008), between the true correlation matrices and our estimates. Denoted by R_V ∈ [0,1], the RV-coefficient can be viewed as a generalization of the Pearson’s coefficient, with values closer to one indicating more similarity. For the three correlation matrices we obtained values of .9625, .9802, and .9892, respectively. Formal permutation tests for H₀ : R_V = 0 vs. H₁ : R_V ≠ 0 rejected the null hypotheses, at the .01 significance level after adjusting for multiplicity with a Bonferroni correction.

Figure 4:

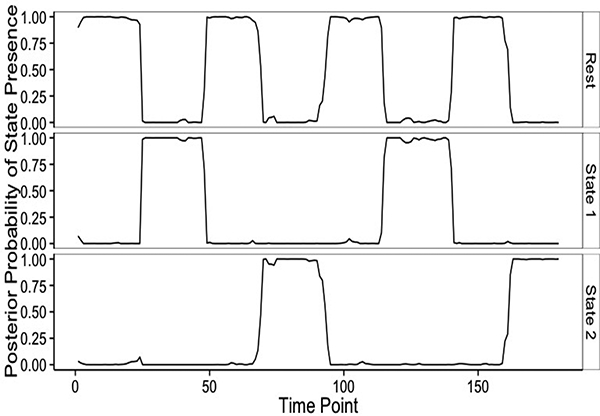
Simulation study: Posterior probability of each connectivity state across all time points, P(s_t = s) for t ∈ (1,..., T} and s ∈ (1, 2, 3}.

Figure 5:

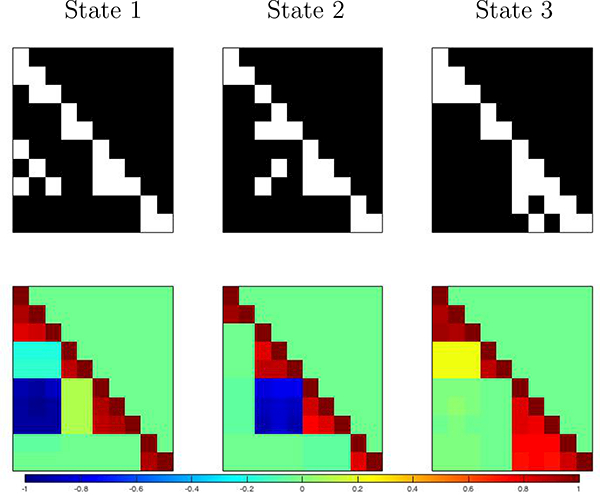
Simulation study: Estimated connectivity networks (top) and correlation matrices (bottom - only the lower triangular part is displayed).

In addition to the inference on the latent connectivity states, our model also allows the detection of brain activations and the estimation of the HRF. Figure 6 shows the marginal posterior probabilities of activation of the 10 components during Stimulus 1 and Stimulus 2 and the estimates of the Poisson HRFs, computed at the posterior mean of λ_υ and scaled to have maximum at one, each of the 10 components v = 1,..., 10. Our method is able to accurately detect the functional units which change their activation status in response to the stimuli, also providing a good estimation of the hemodynamic delay.

Figure 6: Simulation study: Top: Marginal posterior probabilities of activation (p(γ_vk = 1|data) for v ∈ {1,..., V} and k =1, 2 of the V = 10 components during Stimulus 1 and 2.

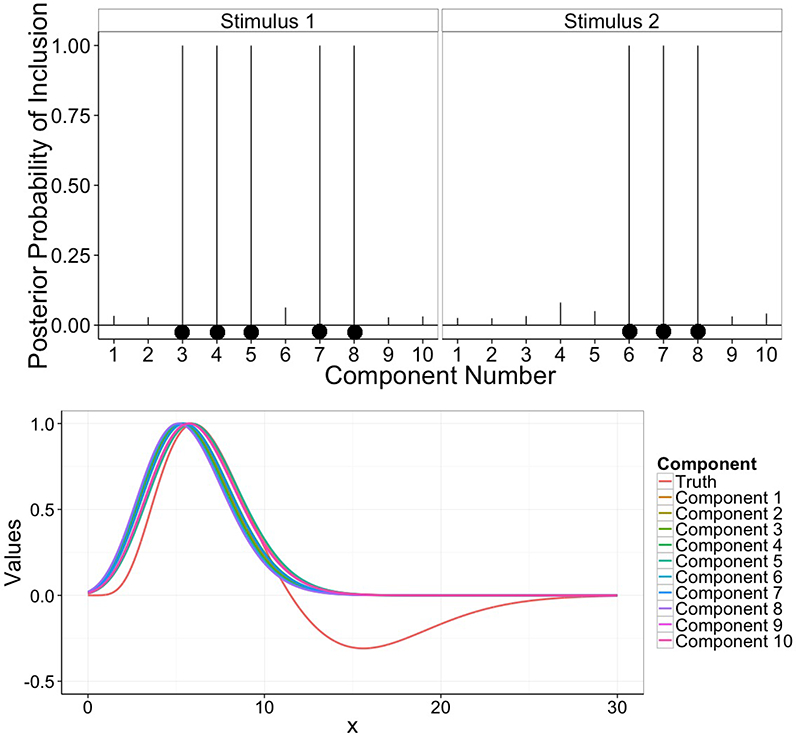
Black dots indicate components simulated as activated by the stimulus. Bottom: Posterior densities of the Poisson HRFs, centered on λ_ν, for v = 1,..., V, and scaled to have maximum at one. The true canonical HRF used to simulate the data is also depicted

3.1. Comparison Study

For a performance comparison, we looked into the sliding window method of Allen et al. (2012), and the methods of Cribben et al. (2012) and Xu and Lindquist (2015), which are based on greedy algorithms. We did not obtain satisfactory results with the greedy algorithm methods, as those estimate independent brain networks over noncontiguous time blocks. As an example, in the simulated scenario presented above, the Dynamic Connectivity Discovery method of Xu and Lindquist (2015) detected three change points (roughly at the 1st, 3rd, and 4th transitions between states in Figure 2) and therefore estimated 4 unique connectivity states with corresponding networks (result not shown) when only 3 states exist. On the other hand, the sliding window clustering approach by Allen et al. (2012) provided a more reasonable comparison with our procedure, although their method also required fixing the number of clusters, which we set to the ground truth, i.e., 3.

In order to measure performances in the estimation of the state-dependent connectivities, we first computed the Frobenius distance between the true correlation matrices, as depicted in Figure 3, and the estimated ones, separately for our approach and the method by Allen et al. (2012). The Frobenius distance of two matrices  and A, is defined as ${\Vert \widehat{A}-A\Vert }_F=\sqrt{\mathrm{tr}((\widehat{A}-A){(\widehat{A}-A)}^{\mathrm{T}})}$, and is often employed to measure the total squared error in matrix estimation. Boxplots of Frobenius distances are reported in Figure 7, for each of the three connectivity states, over 30 replicated datasets, and indicate that our method displays the best performance overall. Furthermore, we calculated precision, accuracy and Matthews correlation coefficient achieved by the two methods, for each network state. Let TP indicate the number of true positive edges detected by a method, TN the number of true negatives, FP the number of false positives and FN the number of false negatives. The precision of the method is defined as the fraction of true positive detections over all detections, i.e. $\frac{TP}{TP+FP}$, whereas the accuracy is defined as the fraction of true conclusions (i.e., both truly present and truly absent edges) over the total number of edges tested, i.e. $\frac{TP+TN}{TP+FP+FN+TN}$. The Matthews correlation coefficient (MCC) is a measure that combines all the above performance measures in a single summary value as

$$MCC=\frac{TP\times TN-FP\times FN}{\sqrt{(TP+FP)(TP+FN)(TN+FP)(TN+FN)}}.$$

The MCC ranges from −1 to 1, with values closer to 1 indicating better performance in the network detection, and it is generally regarded as a balanced representation of the quality of a binary classification. Results are reported in Table 1, averaged over the 30 replicates, and confirm the improved performance of our method.

Figure 7:

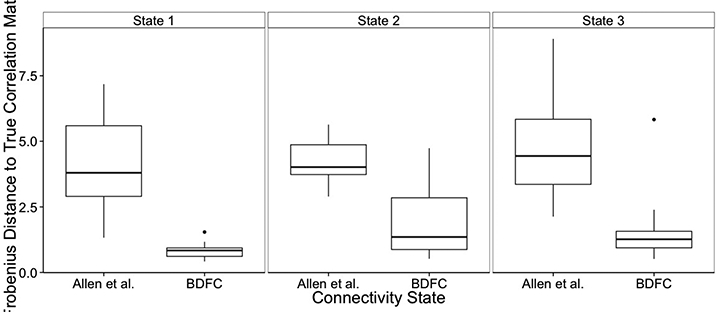
Simulation study: Box plots of Frobenius distances between the true and the estimated correlation matrices, for our method and the method of Allen et al. (2012), across 30 replicated datasets.

Table 1:

Simulation study: Performance comparison of our method (BDFC) and the method of Allen et al. (2012) on edge detection for individual network states. Results are given as precision, accuracy (ACC) and the Matthews Correlation Coefficient (MCC) averaged across 30 simulations. Standard deviations are given in parentheses.

	BDFC			Allen et al.
	Precision (sd)	ACC (sd)	MCC (sd)	Precision (sd)	ACC (sd)	MCC (sd)
State 1	.575 (.067)	.857 (.037)	.611 (.080)	.496 (.255)	.757 (.146)	.547 (.257)
State 2	.500 (.053)	.822 (.024)	.471 (.079)	.537 (.298)	.773 (.177)	.555 (.320)
State 3	.958 (.083)	.890 (.037)	.742 (.092)	.548 (.251)	.691 (.182)	.389 (.348)

Finally, we also compare the performance of our method with respect to the detection of the change points in the connectivity states. Figure 8 illustrates the accuracy of the state classification at each time point along the fMRI time series, by plotting the proportion of correctly identified states at each time point, averaged over the 30 replicated datasets, for both our method and the method by Allen et al. (2012). Both methods are able to capture the 5 change points quite well. However, the method by Allen et al. (2012) appears to be characterized by an increased frequency and uncertainty of state transitions within each interval, most likely due to the nature of the sliding-window estimation. On the other hand, our method is characterized by increased accuracy and stability of state identification at each time point. The transitions between states have the highest uncertainty; however, they are still very consistent with the true timing of the change points.

Figure 8:

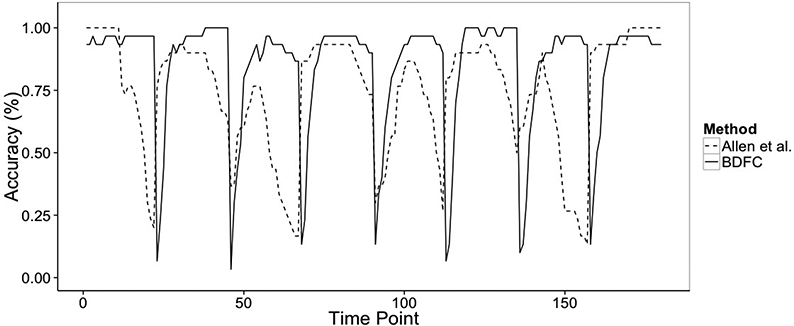
Simulation study: Accuracy of change point detections and state identifications, for the proposed method (solid line) and the method of Allen et al. (2012) (dashed line), averaged across the 30 replicates.

4. Analysis of Sensory Motor Task fMRI Data

We applied our method to data obtained from an actual fMRI experiment conducted by the Mind Clinical Imaging Consortium (MCIC, Gollub et al., 2013). The particular experiment considered here is a block design fMRI study, designed to activate the auditory and somatosensory cortices. The design of the experiment alternated 16 second blocks of auditory stimulus and 16 second blocks of fixation. During the stimulus blocks, the subject, keeping eyes closed for the duration of the scan, was presented with a series of bi-aural audio tones of varying frequencies at irregular intervals and asked to press a button in response to each of the stimuli as quickly as possible. More precisely, the auditory stimulus consisted of 16 different tones of monotonically increasing frequency from 236 Hz to 1318 Hz, with each tone lasting 200 ms. The tones rose to the maximum value, and then descended. This pattern was repeated for 16 seconds, and the subject was asked to press a button with their right thumb after hearing each individual tone. The experiment lasted for 240 seconds, during which the subject was scanned in intervals of 2 seconds. This resulted in a total of 120 time points across the scanning session. The first block of each scanning session is a fixation block, giving a total of 8 fixation blocks and 7 sensory motor blocks. The data were collected on a 3 T Siemens Trio, with a bandwidth of 3125Hz/pixel. The spatial resolution was 3.4mm cubic voxels in a 53 × 63 × 46 cubic grid. Motion correction was performed using SPM12.

Applying ICA, using the GIFT Matlab toolbox (Calhoun et al., 2001), reduced the voxel space to 40 ICA components, representing a spatial map of anatomical regions with associated time courses. Many of these components corresponded to biological structures not of interest here, such as cerebrospinal fluid, the sinuses, or the brainstem, and other components corresponded to motion artifacts. These components do not have any functional relationship with relevant anatomical regions and were removed from the analysis, as a standard data preprocessing step (Allen et al., 2012). After these components were removed, we were left with 14 ICA components corresponding to anatomical regions of interest, as depicted in Figures 9 and 10. As it is known that there is low frequency drift in fMRI time courses, which is not associated with neurological behavior in the subject (Smith et al., 1999), we removed linear and quadratic trends from the time courses of the obtained components.

Figure 9: Case study: Z-score maps of components of interest, overlaid in Montreal Neurological Institute (MNI) space.

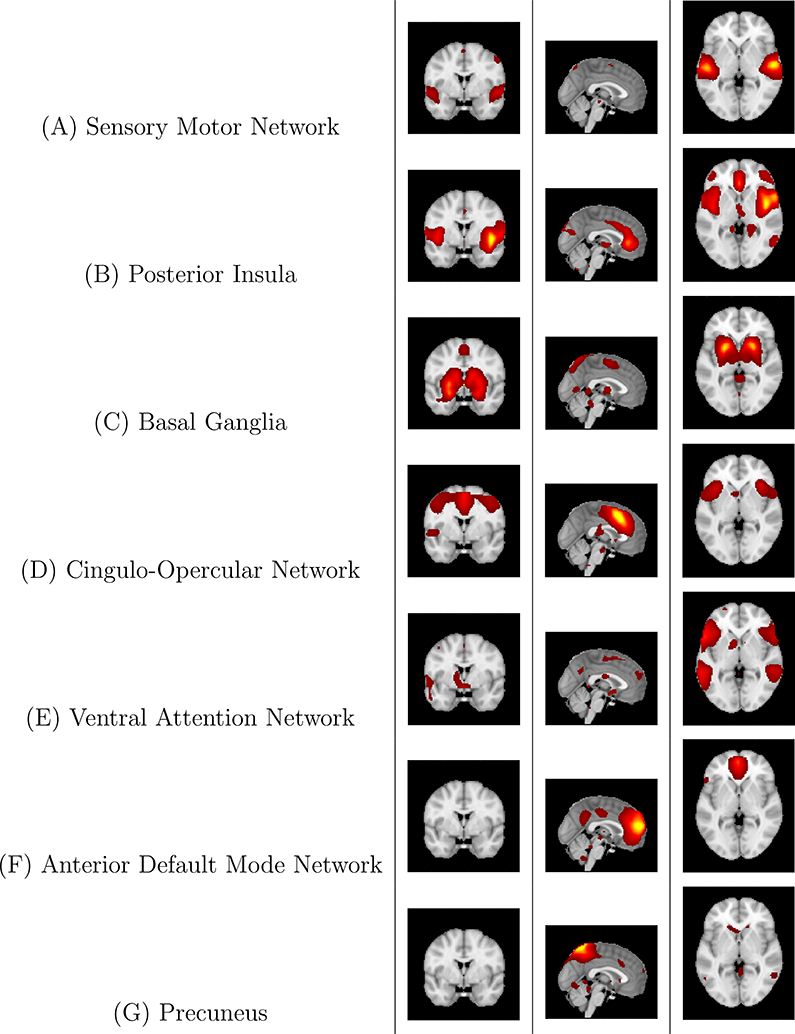
For each component, three representative slices are displayed, in the coronal, sagittal, and axial orientations, respectively. Components are sorted based on their anatomical and functional properties, with the executive control sorted together and all of the Default Mode Network (DMN) components sorted together.

Figure 10: Case study: Z-score maps of components of interest, overlaid in Montreal Neurological Institute (MNI) space.

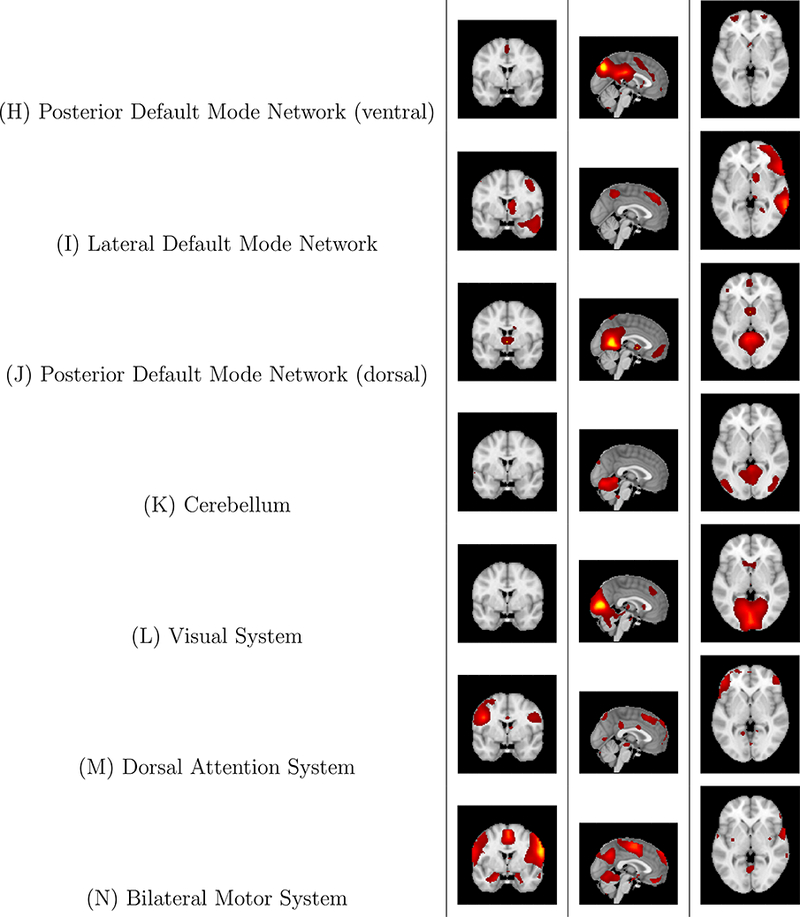
Three representative slices are displayed, in the coronal, sagittal, and axial orientations, respectively, for each component. Components are sorted based on their anatomical and functional properties, with the executive control sorted together and all of the Default Mode Network (DMN) components sorted together.

We used a similar prior specification to the one adopted in the simulation study. In particular, we imposed independent Unif(0, 5) priors on the hemodynamic delay parameter λ_ν in (2) and placed N(0,1) priors on the slab components in (3) and the baseline mean components. Also, we set the prior probability of a component being activated to .2. For the parameters of the G-Wishart prior in (5) we specified b = 3 and D = I_V, which corresponds to a vague distribution on the space of precision matrices. We specified the parameters of the MRF prior (7) on {G₁,..., G_S} to obtain a prior marginal probability of edge inclusion of .25. For the prior specification on Θ in (8), we set α = 4 and β = 16, and fix ρ_ξ = 0.1. Finally, we set the priors on the rows of the HMM transition matrix as uniform Dir(1,1). We ran the MCMC algorithm for 20,000 iterations and used a burn in of 10,000. The code took approximately 2 hours to run on an iMac 3.2 GHz Intel Core i5. As in the simulation study, the model convergence was analyzed by looking at number of edges included in the graphs, number of components included in the regression, and the regression coefficients. These quantities were tested using the Geweke criteria, and were rejected at a .01 significance level.

4.1. Inferred connectivity networks and activations

The experimental design alternates between two conditions, fixation and auditory stimulus. Accordingly, we set S = 2, to understand how the particular task affects (e.g., either by modulating or inhibiting) functional relationships among the networks. This choice was also supported by model selection criteria, such as the BIC and AIC. For example, for S = 2, 3 the corresponding AIC values were (2939, 5544), respectively, whereas for the BIC we obtained (4804, 7409). Figure 11 displays the posterior probabilities of s_t = s for s ∈ {1,2}, across all T time points. Non-contiguous temporal blocks where the method estimates with high posterior probability that the individual is in either State 1 or State 2 are clearly recognizable, and they correspond well to the temporal intervals between the offset of the auditory stimulus and rest in the experiment, respectively.

Figure 11: Case study: Posterior probability of each connectivity state across all time points, p(s_t = s) for t ∈ {1,... ,T} and s ∈ {1, 2}.

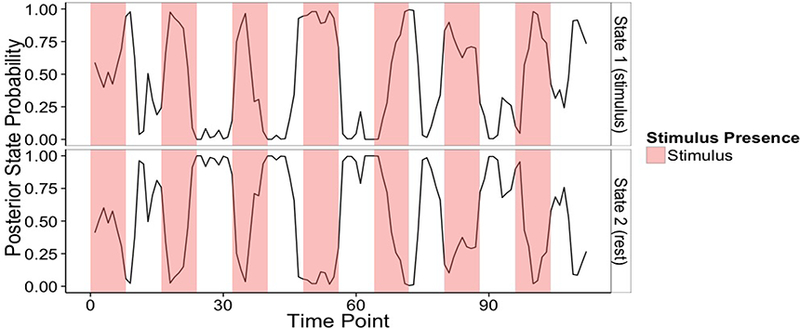
The shaded regions mark the presence of the auditory stimulus.

Figure 12 shows the inferred connectivity networks under the two states, obtained by thresholding the posterior probabilities of edge inclusion at a .1 expected Bayesian FDR, together with the estimated precision matrices. Negative correlations are depicted in blue and positive correlations in red. In the graphs, dashed and solid lines correspond to shared and differential edges, respectively. Our findings on the connectivity networks under task (auditory stimulus - State 1) and rest (fixation - State 2) reveal several interesting features.

Figure 12: Case Study: Estimated precision matrices (left) and connectivity networks (right) corresponding to a .1 Bayesian FDR, under task (auditory stimulus - State 1 - top plots) and rest (fixation - State 2 - bottom plots).

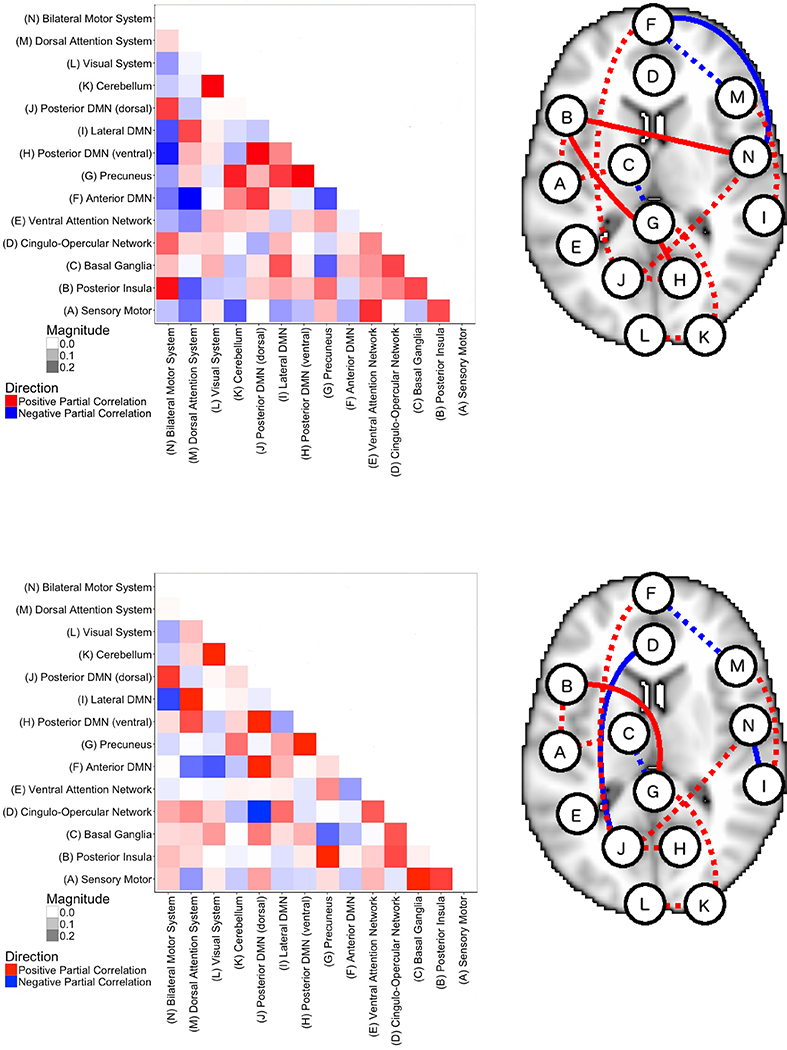
A blue line corresponds to a negative correlation, whereas a red line indicates a positive correlation. Dashed and solid lines correspond to shared and differential edges, respectively.

First, the connectivity network under fixation is characterized by more negatively correlated edges. Those negative correlations are prevalent between regions associated with executive control or task functioning, including the Basal Ganglia (C), Cingulo Opercular Network (D), Dorsal Attention System (M), and Bilateral Motor System (N), and regions in the default mode system (the Precuneus (G), Dorsal Posterior Default Mode (J), Anterior Default Mode (F), and the Lateral Default Mode (I)). Indeed, the default mode network (DMN) has been found to exhibit higher metabolic activity at rest than during performance of externally-oriented cognitive tasks (Uddin et al., 2009), and those negative correlations could suggest an inhibitory effect from these regions over the executive control regions. Furthermore, some researchers have suggested that the DMN is associated with monitoring of the external environment and the dynamic allocation of attentional resources, with some form of depression showing altered DMN patterns during implicit emotional processing (Koshino et al., 2011; Shi et al., 2015). Our estimated networks also identify regions which are typically related to executive control, i.e., the Posterior Insula (B), Basal Ganglia (C), Cingulo-Opercular Network (D), and the Ventral Attention Network (E), as engaged both during the auditory stimulus and fixation. Indeed, this finding is consistent with the expectation that at any time the subject is either controlling a response to a stimuli or waiting for a stimuli to be presented. Also regions belonging to the DMN appear engaged in both the resting and the task networks, a remark consistent with the understanding that DMN processes unconscious task-related information, despite being characterized by general decreased activity levels during task performance (De Pisapia et al., 2011). We also observe a more pronounced correlation between the Sensory Motor Network (A) and the Basal Ganglia (C) during fixation. The Basal Ganglia (C) has been observed to moderate attention networks (Jackson et al., 1994), and specifically to moderate executive attention (Berger and Posner, 2000).

Figure 13 shows the marginal posterior probabilities of activation of the 14 components during task. The Sensory Motor (A), Cingulo-Opercular Network (D), Ventral Attention Network (E), Anterior Default Mode (F), Precuneus (G), Ventral Posterior Default Mode (H), Lateral Default Mode (I), and Dorsal Posterior Default Mode (J) components all have high posterior probability of being activated by the task. The posterior means and 95% credible intervals of the regression coefficients in (1) corresponding to these components are also reported in Figure 13. Interestingly, our method selects all default mode related regions (F-J), while also selecting the sensory motor region (A), and regions associated with attention or executive control (D-E). As expected, the sensory motor region (A) exhibits significantly higher activity during the task, similarly to the two selected executive control regions (D-E). On the contrary, most DMN regions (F, G, H, J) exhibit deactivation during the task, with the interesting exception of the Lateral DMN component (I). As mentioned, it has been established that regions which are part of the DMN are usually characterized by greater activity during task preparation than during task performance (Koshino et al., 2014). The Lateral DMN component (I) includes areas corresponding to the right angular gyrus, which has been shown in meta-analysis reviews to be consistently activated in go/no-go tasks, as it may be involved in the restraining of an inappropriate response from being executed (Wager et al., 2005; Nee et al., 2007).

Figure 13:

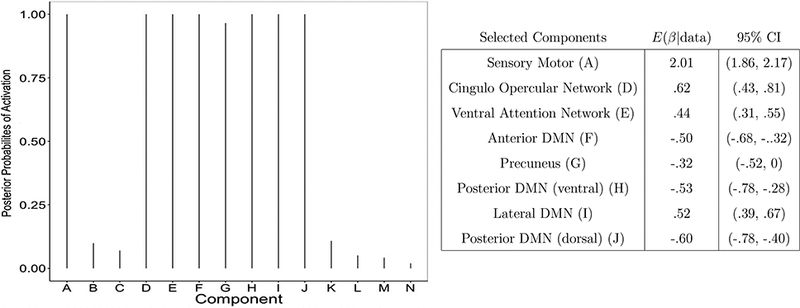
Case study: Marginal posterior probabilities of activation of the V = 14 components during the sensory motor task (left), and posterior means and 95% credible intervals of the regression coefficients in (1) corresponding to the selected components (right)

5. Conclusion

The investigation of dynamic changes in functional network connectivity has recently received increased attention in the neuroimaging literature, as it is believed to provide greater insights into brain organization and cognition (Hutchison et al., 2013). In this manuscript, we have introduced a fully Bayesian approach to the problem, which allows simultaneous estimation of time-varying networks, with corresponding change points, and detection of brain activations in response to a set of external stimuli. With respect to current methods for studying dynamic connectivity, our approach does not require an ad-hoc choice of sliding-windows for estimating the network dynamics, and inference is conducted in a unified framework. By using a Hidden Markov Model formulation to detect change points in the connectivity dynamics, our framework allows posterior assessment of the probability of each connectivity state at each time point, and further allows borrowing of information across the entire fMRI scan to improve accuracy in the estimation of the networks.

We have considered task-based fMRI data, where we have shown how our method achieves decoupling of the task-related activations and the functional connectivity states, to understand how a particular task affects (e.g., either by modulating or inhibiting) functional relationships among the networks. We have shown good performances of our model on simulated data and illustrated the method on the analysis of an actual fMRI dataset obtained from a healthy subject involved in a sensory motor task with an auditory stimulus. The results were consistent with current findings in the neuroimaging literature, showing an increased role of the regions involved in the default mode network at rest. Interestingly enough, regions related to executive control appeared involved both at rest and during task, consistent with the pattern implied by the “wait-to-hear” design of the auditory stimulus. During the task, a stronger connection between the Ventral Attention Network and the Basal Ganglia was observed, relating the attention to the stimulus to the voluntary muscle movements triggered by the task.

In our approach we have fitted a model to fMRI BOLD responses over macro-regions identified via ICA, rather than to the voxel-level data itself. As we have noted, our modeling approach does not depend on the particular choice of ICA-based regions, as it is generally applicable to any well-defined set of brain regions for which connectivity is of interest. In ICA, components are effectively spatial regions that share a common time course, and the shared time course is different enough from those of other regions to be distinct components. This leads to model order. One advantage of ICA, therefore, is that if we want to consider a graph with a small set of nodes, a low-model order ICA decomposition will help decide which structural areas can be grouped based on similar time course activation. Another advantage to ICA is that it chooses spatial components that have time courses that are the most distinct from each other; therefore, unlike in an atlas specification of regions where two regions can be highly functionally connected, ICA gives us the starting point of components that are as temporally unalike as possible. Then, the Bayesian graphical model will find the relationships between these distinct components. For future extensions of the method, an interesting question to explore is the interaction between the results of our model and the pre-processing step. Indeed, it might be possible to have the identification of the macro regions be not a preprocessing step but be included within the Bayesian hierarchical model fitting. This requires addressing the resulting non-trivial computational challenges. In addition, scalability of the methods can be facilitated by the implementation of computationally efficient algorithms for posterior inference, such as Variational Bayes and Hamiltonian Monte Carlo methods constrained on the space of positive definite matrices (Neal, 2011; Holbrook et al., 2016), in place of the more computationally expensive MCMC methods. Such strategy can allow the estimation of graphs with a larger number of nodes than what we have considered in our examples, also making it possible to validate findings on whole-brain parcellations and functional brain atlases, such as the Willard and MSDL atlas, instead of ICA components, in order to ensure the robustness of the results and assess the impact of the pre-processing.

In model (1) we have considered the case of a Poisson hemodynamic response function. Clearly, other parametric HRFs, such as the canonical or the gamma HRFs (Lindquist, 2008), can be used with our model. Also, our approach can be extended to incorporate methods for joint detection-estimation (JDE) of brain activity that allow both to recover the shape of the hemodynamic response function as well as to detect the evoked brain activity (Makni et al., 2008; Badillo et al., 2013). In such approaches, whole brain parcellations are typically used, to make the HRF estimation reliable by enforcing voxels within the same parcel to share the same HRF profile. Extensions that allows simultaneous inference of the parcellation have also been proposed (Chaari et al., 2013; Albughdadi et al., 2017), at the expense of the computational cost.

The use of a Hidden Markov Model for change point detection requires the predetermination of the upper bound, S, on the number of possible states. In task-based fMRI data, a reasonable value for S can often be surmised on the basis of the experiment, e.g., the number of different tasks. However, in our model formulation connectivity is not defined by the presence of a stimulus but rather characterized by a latent state. This adds flexibility to the model, as we can learn on interesting patterns of state persistence that may arise during the course of the experiment. For example, model selection criteria, such as the AIC and BIC, can be employed to determine the optimal value of S. Alternatively, one could use flexible Bayesian nonparametric generalizations of the Hidden Markov Models that do not require fixing S in advance and instead estimate E(S|Y) directly from the data (Beal et al., 2002; Airoldi et al., 2014). This will be an objective of future investigations. Other possible extensions of our modeling framework include incorporating external prior information on the networks, whenever available. For example, estimates of structural connectivity obtained using diffusion imaging data can be incorporated into the sparsity prior on the precision matrices (Hinne et al., 2014). Finally, even though we have discussed here the analysis of fMRI data from a single subject, multiple subjects analyses would also be of interest, as they would allow comparisons of functional connectivity dynamics between groups of subjects, for example healthy controls and patients affected by neuropsychiatric disorders, such as Alzheimer’s and schizophrenia. For such extensions, however, several aspects of the modeling and computations need careful thought, as one might expect the connectivity states and the change points to vary subject-by-subject.

A Appendix

A.1 Markov chain Monte Carlo algorithm

We describe here the MCMC algorithm for posterior inference.

• •
  Update λ_v : This is a Metropolis Hastings (MH) step. Propose ${\lambda }_{v_{new}}~\mathrm{Unif}({\lambda }_{v_{old}}-h,{\lambda }_{v_{old}}+h)$ and adjust the $X_{vt}^k$ element of Xnew to be $X_{vt}^k={\int }_0^t{x}_k(\tau )h_{{\lambda }_{v_{new}}}(t-\tau )d\tau$, then accept ${\lambda }_{v_{new}}$ with probability:

  $$\min \{1,\frac{p({\lambda }_{v_{new}}|Y,{\mathit{X}}_{new},\mathrm{s},\beta ,\mathrm{\Omega })q({\lambda }_{v_{new}},{\lambda }_{v_{old}})}{p({\lambda }_{v_{old}}|Y,{\mathit{X}}_{old},\mathrm{s},\beta ,\mathrm{\Omega })q({\lambda }_{v_{old}},{\lambda }_{v_{new}})}\},$$

  where $p(\lambda |Y,X,\mathrm{s},\beta ,\mathrm{\Omega })\propto {\prod }_{s\in \{1,\dots ,S\}}{\prod }_{t:s_t=s}N(\mathit{\mu }+{\sum }_{k=1}^K{\mathit{X}}_t^k\circ {\beta }_k,{\mathrm{\Omega }}_s)$.
• •Update s: This is an MH step followed by a Gibbs sampler.

  1. Sample state transition probabilities for state i from a Dirichlet(α_i) distribution where [α_i]_j = #i j + 1 is the number of state transitions from i to j plus 1.

  2. Calculate the stationary distribution π_new given the transition probabilities.

  3. Accept resulting transition matrix and stationary distribution with probability:

     $$\min \{1,\frac{{\pi }_{new}(CurrentStates)}{{\pi }_{old}(CurrentStates)}\}$$
  4. Perform Gibbs sampling using Forward Propagate Backward Sampling (Scott, 2002). Obtain the forward transition probabilities for each state at each time point as: P_t = [p_trs] where p_trs is the transition probability from r at time t — 1 to s at time t. The formula for p_trs is obtained by computing:

     $$p_{trs}\propto {\pi }_{t-1}(r|\theta )q(r,s)N(X_t\beta +\mu ,{\mathrm{\Omega }}_s)$$

     and normalizing. The term π_t(r|θ) = ∑_r p_trs is computed after each transition.

  5. Once P_t has been obtained for all t, sample s_T from π_t, and then recursively sample s_t proportional to the s_t+1-th column of P_t+1; until s₁ is sampled.

• •Update G and Ω: This is an MH step.

  1. For each s ∈ {1,..,S}, and each off diagonal pair (i,j) ∈ {1,...,V} propose an edge with probability $\frac{p(G_{new})H(e,\mathrm{\Omega })}{p(G_{old})}$, with e = (i,j) the edge being updated, and with H(e, Ω) as defined in Wang and Li (2012) section 5.2 Algorithm 2. If the new edge / lack of an edge is different from the previous edge state continue with MH step. Otherwise, proceed forward to the next edge.

  2. Sample ${\mathrm{\Omega }}_{s_{new}}|G_{s_{new}}~W_{G_{s_{new}}}(b+n_k,D+\mathrm{cov}(\{Y_t:s_t=s\}))$.

  3. Accept or reject the move with the following probability:

     $$\min \{1,\frac{f({\mathrm{\Omega }}_{new}\backslash ({\omega }_{i{j}_{new}},{\omega }_{j{j}_{new}})|G_{old})}{f({\mathrm{\Omega }}_{new}\backslash ({\omega }_{i{j}_{new}},{\omega }_{j{j}_{new}})|G_{new})}\},$$

     with f(Ω\(w_ij,w_ij)|G) as defined in Wang and Li (2012).
• •Update Θ and ξ: This is done using within-model and between-model MH steps.
  • 1.Between-Model
    • (a)For each r, s G {1,.., S}
      • i.If ξ_rs = 1 set ${\xi }_{r{s}_{new}}=0$ and ${\theta }_{r{s}_{new}}=0$
      • ii.If ξ_rs = 0 set ${\xi }_{r{s}_{new}}=1$ and sample ${\theta }_{r{s}_{new}}$ from the proposal Gamma(α*, β*) distribution.
    • (b)Accept proposal with probability:
      • i.$\min \{1,\frac{\mathrm{\Gamma }(\alpha )}{\mathrm{\Gamma }({\alpha }^{*})}\frac{{({\beta }^{*})}^{{\alpha }^{*}}}{{\beta }^{\alpha }}{({\theta }_{km})}^{{\alpha }^{*}-\alpha }{e}^{(\beta -{\beta }^{*}){\theta }_{rs}}{\prod }_{i<j}\frac{C({\nu }_{ij},\mathbf{\Theta })\exp (-2{\theta }_{rs}{g}_{r,ij}{g}_{s,ij})}{C({\nu }_{ij},{\mathbf{\Theta }}_{new})}\frac{1-w}{w}\}$
      • ii.$\min \{1,\frac{\mathrm{\Gamma }({\alpha }^{*})}{\mathrm{\Gamma }(\alpha )}\frac{{\beta }^{\alpha }}{{({\beta }^{*})}^{{\alpha }^{*}}}{({\theta }_{r{s}_{new}})}^{\alpha -{\alpha }^{*}}{e}^{({\beta }^{*}-\beta ){\mathbf{\Theta }}_{r{s}_{new}}}{\prod }_{i<j}\frac{C({\nu }_{ij},\mathbf{\Theta })\exp (-2{\theta }_{r{s}_{new}}{g}_{r,ij}{g}_{s,ij})}{C({\nu }_{ij},{\mathbf{\Theta }}_{new})}\frac{w}{1-w}\}.$

        Here C(ν, Θ) is the MRF normalizing constant.

  • 2.Within-Model
    • (a)For each r, s ∈ {1,.., S} such that ξ_rs = 1 and θ_rs ≠ 0 sample ${\theta }_{r{s}_{new}}$ from the same proposal Gamma(α*,ß*) distribution.
    • (b)Accept proposal with probability: $\min \{1,{(\frac{{\theta }_{r{s}_{new}}}{{\theta }_{rs}})}^{\alpha -{\alpha }^{*}}{e}^{({\beta }^{*}-\beta )}({\theta }_{r{s}_{new}}-{\theta }_{rs}){\displaystyle \prod _{i<j}\frac{C({\nu }_{ij},\mathbf{\Theta })\exp (2({\theta }_{r{s}_{new}}-{\theta }_{rs})g_{k,ij},g_{m,ij})}{C({\nu }_{ij},{\mathbf{\Theta }}_{new})}}\}$
• •Update γ and β: Updated using between-model and within-model MH steps:
  • 1.Between-Model
    • (a)For each k ∈ {1,...,K} either swap two values of γ_k or select an index and change it’s value.
      • —When swapping two values to obtain ${\gamma }_{k{i}_{new}}$ and ${\gamma }_{k{j}_{new}}$ then, without loss of generality, if ${\gamma }_{k{i}_{new}}$ = 0 set ${\beta }_{k{j}_{new}}$ = 0 and sample ${\beta }_{k{j}_{new}}$ from N(0, σ_β).
      • —When changing the value of an individual index j, then if ${\gamma }_{k{j}_{new}}$ = 0 set ${\beta }_{k{j}_{new}}$ = 0, otherwise sample ${\beta }_{k{j}_{new}}$ from N(0,σβ).
    • (b)
      Accept proposal with probability:

      $$\min \{1,\frac{{\prod }_{t=1}^{T}p(Y_t|\mathit{X},{\beta }_{new},\mathrm{s},\mathrm{\Omega })p({\beta }_{new})p({\gamma }_{new})q(\{{\gamma }_{new},{\beta }_{new}\},\{{\gamma }_{old},{\beta }_{old}\})}{{\prod }_{t=1}^{T}P(Y_t|\mathit{X},{\beta }_{old},\mathrm{s},\mathrm{\Omega })p({\beta }_{old})P({\gamma }_{old})q(\{{\gamma }_{old},{\beta }_{old}\},\{{\gamma }_{new},{\beta }_{new}\})}\},$$

      where $p(Y_t|\mathit{X},\beta ,\mu ,\mathrm{s},\mathrm{\Omega })=N({\mathit{X}}_t\beta +\mu ,{\mathrm{\Omega }}_{s_t})$, and q(o, o) is the transition probability.
  • 2.Within-Model
    • (a)For each k ∈ {1,..., K} and v ∈ {1,..., V} such that γ_kv = 1 propose ${\beta }_{k{v}_{new}}={\beta }_{k{v}_{old}}+N(0,{\sigma }_{\beta }^{prop})$
    • (b)
      Accept the proposal with probability:

      $$\min \{1,\frac{{\prod }_{t=1}^{T}p(Y_t|\mathit{X},{\beta }_{new},\mathrm{s},\mathrm{\Omega })p({\beta }_{new})}{{\prod }_{t=1}^{T}p(Y_t|\mathit{X},{\beta }_{old},\mathrm{s},\mathrm{\Omega })P({\beta }_{old})}\},$$

      where $p(Y_t|\mathit{X},\beta ,\mathrm{s},\mathrm{\Omega })=N({\mathit{X}}_t\beta +\mu ,{\mathrm{\Omega }}_{s_t})$.
• •Update μ: Updated using an MH step:
  • 1.
    ∀v ∈ {1,..., V} perform a random walk on μ_ν to obtain

    $${\mu }_{new}=\{{\mu }_{1_{old}},\dots ,{\mu }_{v_{new}},\dots ,{\mu }_{p_{old}}\}.$$
  • 2.
    Accept or reject ${\mathit{\mu }}_{v_{new}}$ with the following probability:

    $$\min \{1,\frac{{\prod }_{t=1}^{T}P(Y_t|\mathit{X},\beta ,{\mathit{\mu }}_{new},\mathrm{s},\mathrm{\Omega })p({\mathit{\mu }}_{new})}{{\prod }_{t=1}^{T}p(Y_t|\mathit{X},\beta ,{\mathit{\mu }}_{old},\mathrm{s},\mathrm{\Omega })p({\mathit{\mu }}_{old})}\},$$

    where $p(Y_t|\mathit{X},\beta ,\mu ,\mathrm{s},\mathrm{\Omega })=N({\mathit{X}}_t\beta +\mu ,{\mathrm{\Omega }}_{s_t})$.
• •Update v: Updated using an MH step:
  • 1.∀_i,j ∈ {1,.., V} such that i < j, sample q_ij ~ Beta(a*, b*).
  • 2.Obtain ${\nu }_{i{j}_{new}}$ as a function of q_ij by setting ${\nu }_{i{j}_{new}}$ = logit(q_ij).
  • 3.
    Accept ${\nu }_{i{j}_{new}}$ with the following probability:

    $$\min \{1,\frac{exp(({\nu }_{i{j}_{new}}-{\nu }_{ij})(a-a^{*}+1^T{g}_{ij}))C({\nu }_{ij},\mathbf{\Theta }){(1+e^{{\nu }_{ij}})}^{a+b-a^{*}-b^{*}}}{C({\nu }_{i{j}_{new}},\mathbf{\Theta }){(1+e^{{\nu }_{i{j}_{new}}})}^{a+b-a^{*}-b^{*}}}\}.$$