Bayesian and parsimony approaches reconstruct informative trees from simulated morphological datasets

Abstract

Phylogenetic analysis aims to establish the true relationships between taxa. Different analytical methods, however, can reach different conclusions. In order to establish which approach best reconstructs true relationships, previous studies have simulated datasets from known tree topologies, and identified the method that reconstructs the generative tree most accurately. On this basis, researchers have argued that morphological datasets should be analysed by Bayesian approaches, which employ an explicit probabilistic model of evolution, rather than parsimony methods—with implied weights parsimony sometimes identified as particularly inaccurate. Accuracy alone, however, is an inadequate measure of a tree's utility: a fully unresolved tree is perfectly accurate, yet contains no phylogenetic information. The highly resolved trees recovered by implied weights parsimony in fact contain as much useful information as the more accurate, but less resolved, trees recovered by Bayesian methods. By collapsing poorly supported groups, this superior resolution can be traded for accuracy, resulting in trees as accurate as those obtained by a Bayesian approach. By contrast, equally weighted parsimony analysis produces trees that are less resolved and less accurate, leading to less reliable evolutionary conclusions.

1. Introduction

Evolutionary history can be reconstructed using parsimony-based or probabilistic approaches. Because models used with molecular datasets generally share a common probabilistic construction, statistical methods can be used to determine the most appropriate model [1]. With morphological datasets, however, it is more difficult to establish whether probabilistic models or parsimony better reconstruct phylogenetic relationships (which are typically unknown).

A pragmatic approach to this question is to simulate data from a known tree. With the important caveat that generative trees and simulated morphological datasets may be unrealistic [2,3], probabilistic approaches typically reconstruct the generative tree most accurately (i.e. with least conflict), followed by parsimony under equal and implied weights in turn [4–9].

Previous studies have advocated accuracy as the sole criterion by which to select a method [5–11]. Congreve & Lamsdell [9] (problematically [2]) define the most accurate tree as the one that bears the fewest incorrect splits. Other authors [5–8,11] use the Robinson-Foulds (RF) distance as a proxy for accuracy (even though the RF distance is also influenced by precision; a pair of trees can be made two units more similar by replacing an incorrect partition with a correct one, or by collapsing two incorrect partitions). Goloboff et al. [2] propose alternative tree similarity metrics as proxies for accuracy.

Accuracy alone, however, is not the only goal when reconstructing trees [11]. No tree shows less conflict than a single polytomy, for a total absence of relationship information guarantees that no relationship is incorrectly resolved. An emphasis on accuracy therefore disadvantages methods that produce highly resolved trees [11] (and vice versa). This trade-off has been acknowledged by collapsing some poorly supported groups before calculating accuracy (even if accuracy is still equated with ‘performance’) [2,6,8,11]. Naturally [12], methods that yield less resolution are consistently more accurate [2,5,7,8,11].

We should be seeking not the most accurate method, but the method that recovers as much information as possible about the true tree, striking a balance between the complementary quantities [12] of accuracy and resolution. For example, a tree that resolves 20 relationships conveys much information about the correct tree, even if one of those relationships is incorrect; a tree that resolves just one relationship conveys less information, even if that single relationship is correct. If two trees are equally accurate, we should prefer the more precise. Here I explore the impact on previous studies of evaluating trees according to their total shared information content, rather than ‘accuracy’ alone.

2. Material and methods

Congreve & Lamsdell ([9]; CL hereafter) simulated 55-character matrices from a bifurcating 22-tip tree using a Markov k-state (Mk) 1 parameter model with rates sampled from a discretized gamma distribution [13]. Their generative tree is the single most parsimonious tree obtained from a study of Ordovician trilobites; its edges were assigned a unit length.

O'Reilly et al. ([5]; OR hereafter) simulated matrices containing 100, 350 and 1000 characters from a bifurcating 75-tip tree using a modified HKY85 model [14]; they followed a previous simulation study [4] in selecting a single bifurcating tree from a morphological + molecular analysis of Lissamphibia.

I used TNT [15] to conduct parsimony searches on each of these matrices under equal and implied weights, using the parsimony ratchet and sectorial search heuristics (search options: xmult:hits 20 level 4 chklevel 5 rat10 drift10). I took a strict consensus of all optimal trees obtained under equal weights, and under implied weights [16] at the concavity constants used in each respective study (CL: k = 1, 2, 3, 5 and 10; OR: k = 2, 3, 5, 10, 20 and 200). For each dataset, I generated a further strict consensus of all trees that were optimal under any of the concavity constants, excluding the unreasonable value of k = 1, which inadequately penalizes extra steps beyond the first, and thus exhibits undesirable properties of clique analysis [17] (see electronic supplementary material).

I also generated majority-rule consensus trees in MrBayes 3.2.2 [18] using an Mk model, with rates distributed according to a gamma parameter. I combined results from four independent runs, each of which employed four Metropolis-coupled Markov chains. After a burn-in period of 4 000 000 generations, the cold chain in each run was sampled every 10 000 generations for 6 000 000 generations. The sampled topologies faithfully reflected the posterior distribution for each dataset (0.999 < potential scale reduction factor < 1.001; estimated sample size > 400).

To explore the relationship between resolution and accuracy, I generated further trees for each analysis by collapsing poorly supported groups. Under the Mk model, I collapsed groups whose posterior probability was less than 95%, 90%, 85%, … 50%. In parsimony analyses, I compared different measures of node support. Under jackknife and bootstrap resampling, I collapsed groups with (i) absolute frequency supports of less than 0%, 2%, 4% … 100%; (ii) relative frequency (GC) support of less than −100%, −95%, … 95%, 100%. Under Bremer support, I collapsed groups with Bremer support values less than 1, 2, 3, … 20 with equally weighted trees (TNT command subopt x; bbreak;); under implied weighting, Bremer support values were drawn from a logarithmic distribution (0.73^0…19, 2.5 × 10⁻³ → 1 × 10⁰), reflecting the fractional nature of tree scores under implied weights [16].

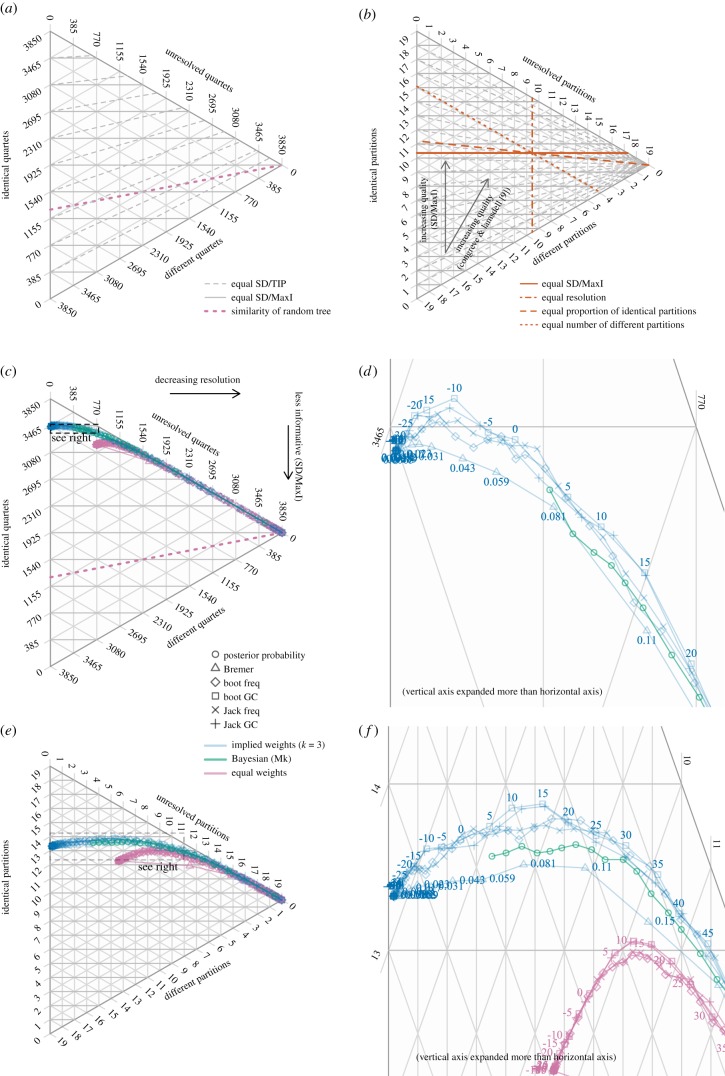
Symmetric difference metrics calculate how much information two trees hold in common [19]—that is, how much information a generated tree contains about the generative tree. Where the generative tree is bifurcating, a particular relationship may be resolved the same way (s) or a different way (d) on each tree, or resolved in the comparison tree only (r) [20,21]. The symmetric difference (‘SD’, also termed the Robinson-Foulds distance) is given by 2d + r. The symmetric difference is conventionally normalized against the total information present (TIP) in the two trees, 2d + 2s + r [21]. Undesirably, this assigns a fully unresolved tree the same score as a tree that is perfectly resolved and completely incorrect (figure 1a). In the present context, therefore, it is more appropriate to normalize against the maximum information (MaxI) that could potentially have been resolved, 2(d + s + r).

Figure 1.

Method selection. (a) Normalizing symmetric difference against the total information present in two trees (SD/TIP, dashed lines) scores a completely incorrect bifurcating tree (all relationships resolved differently; bottom corner) no worse than a polytomy (all relationships unresolved; rightmost corner). Random trees (coloured line) with more relationships resolved receive better scores, as some relationships will by chance be resolved correctly. Normalizing against the maximum possible relationship information (SD/MaxI, solid lines) penalizes misinformation over non-information; random trees with more relationships resolved (which thus contain more misinformation) consequently receive worse scores. (b) Four measures of tree quality. (c–f) Impact on tree quality when least-supported groups are collapsed: (c–d) Counting quartets; (e–f) counting partitions.

The unit of relationship information may be a quartet (a four-taxon statement) [20–22] or a bipartition split [23–25]. (Each clade in a tree corresponds to a bipartition that splits taxa into ‘members' and ‘non-members’.) Partitions offer a simple but incomplete measure of the topological information accommodated in a tree. The trees ((A, (X, B)), (C, D)) and ((A, B), ((C, X), D)) both contain the same information regarding the relationships between (A, B) and (C, D), yet have no partitions in common. As a consequence, the partition difference ( = Robinson-Foulds distance) suffers four essential shortcomings [23]. First, it is imprecise; the number of unique values that the metric can take is two fewer than the number of taxa. (Simply put, a precise method can allocate distinct difference values to two trees that an imprecise method would assign an identical score.) Second, it is rapidly saturated; relatively minor differences can result in the maximum distance value. Third, its value can be counterintuitive; for example, moving a single tip to a particular location can generate a higher difference value than moving both that tip and its immediate neighbour to the same point (electronic supplementary material). Fourth, balanced trees contain proportionally more uneven partitions, and thus attract lower average distances than asymmetric trees (electronic supplementary material).

Quartets, by contrast, represent all topological information within a tree. The quartet dissimilarity measure is precise, does not rapidly reach saturation, generates a meaningful value for random trees, is robust to the placement of wildcard taxa and consistently increases in value as trees become more different; and every quartet represents an equal quantity of information. I consider it to represent a more useful, meaningful and interpretable indicator of tree similarity.

I calculated quartet distances using the tqDist algorithm [26] via the QuartetStatus function in the new R package Quartet [27]. Partition distances were calculated using the Quartet function SplitStatus. To summarize results, s, d and r were calculated for each individual tree relative to the generative tree, and the mean of each parameter was calculated at each resolution in each analysis.

Previous studies (e.g. [5,6]) have plotted unnormalized symmetric difference against the resolution. The unnormalized symmetric difference, however, is a function of both resolution and accuracy: a change in resolution (x) necessarily influences the value, and the range of possible values, of the symmetric difference (y). Because the axes are not independent, this is analogous to plotting x against y/x; the inherent correlation between the axes makes it difficult to interpret the relative contributions of x and y to the plotted function. I instead plotted the proportion of quartets or partitions that are the same in both trees (s), different in both trees (d) and only resolved in the generative tree (r) on ternary plots using the Ternary R package [28], oriented such that SD/MaxI decreases vertically and resolution decreases horizontally (figure 1a). This plotting configuration distinguishes the relative contributions of resolution and accuracy to overall similarity (figure 1b).

Data, scripts and analyses used in this study are archived on GitHub [29,30].

3. Results

Ideally, measures of node support would assign incorrect nodes low support values. With the CL datasets (55 characters, 22 tips), resampling methods accomplished this more effectively than Bremer support (figure 1, c–f), a metric that has attracted criticism [31,32]. The groups contradicted/supported (GC) metric outperformed group frequency (as anticipated by [33]), whereas bootstrap resampling outperformed the jackknife approach (contra [34]); subsequent analyses thus employed the bootstrap GC metric. Differences between methods were not statistically significant (electronic supplementary material).

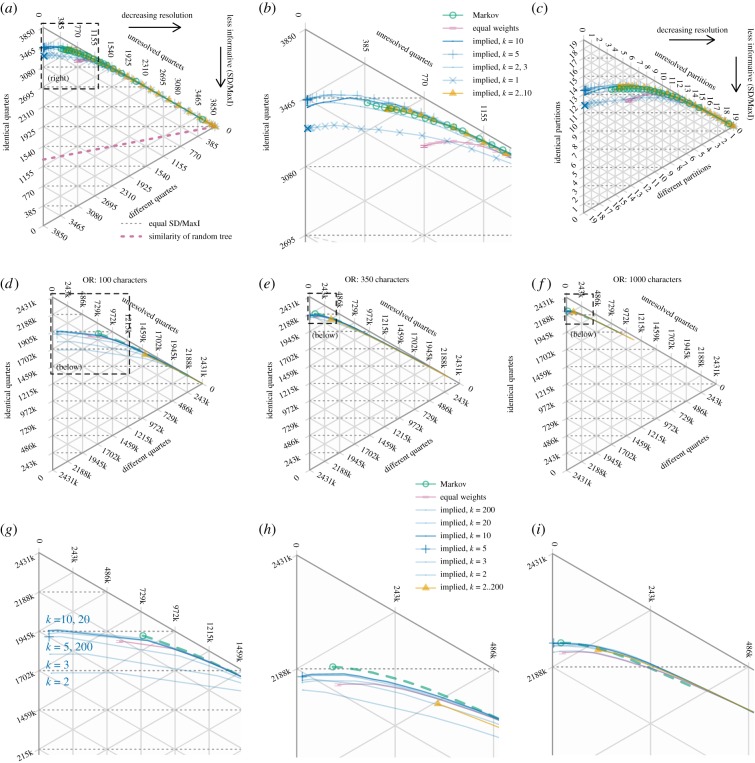
With the CL datasets, there is no significant difference (at p = 0.01) between the MaxI-normalized quartet symmetric difference of the best trees generated by the Mk model or implied weights (k ∈ {2, 3, 5, 10})—but the best trees generated by equal weights, implied weights with k = 1, and the consensus of k values are significantly worse than those produced by the other methods (figure 2a,b; electronic supplementary material).

Figure 2.

Status of quartets and bipartitions in trees recovered from simulated datasets. Points denote the average number of quartets (a–b,d–i) or partitions (c) that are the same as the generative tree, resolved differently to the generative tree, or not resolved. Each series indicates the effect of progressively collapsing the least-supported groups in trees generated by analysis of CL (a–c) and OR datasets (d,g: 100; e h: 350; f,i: 1000 characters) under the specified analytical parameters. The vertical direction corresponds to similarity (i.e. more informative trees); the horizontal direction corresponds to resolution.

Collapsing the least-supported groups initially increases the overall accuracy (as predicted in [2,35]), leading to a slight increase in the overall informativeness of the tree (figure 2a,b). Beyond a GC score of ca −15, the gain in accuracy no longer offsets the resolution lost; collapsing further groups thus removes ‘correct’ information and reduces the similarity between the tree and the reference tree. Indeed, the optimal tree is only perfectly resolved in a minority of cases (CL, 18%; OR: less than 0.2%). Because a Bayesian approach results in less resolution, its most resolved trees cannot generally be improved by collapsing groups (figures 1c,d and 2).

These results hold even if the (problematic) partition difference metric is employed (figure 1e–f), though relatively more groups must be collapsed (those with a GC score of less than 10) to maximize this metric. The results do not meaningfully change when datasets with low consistency indices are excluded.

Similar results are observed in the OR datasets (figure 2d–i): at any given level of resolution, the best trees obtained by the Mk model are similar in accuracy to those obtained under implied weights (except with very small values of k) but are more accurate than those obtained using equal weights.

These datasets also demonstrate the impact of dataset size on tree quality. With larger ratios of characters to taxa (1000 or 350 characters, 75 tips), all methods produced reasonably accurate, well-resolved trees (figure 2e–f, h–i). With the smallest (100 character) datasets (figure 2d,g), trees were much more different from the generative tree, and the choice of method influenced results more strongly: the Bayesian approach could obtain substantially less resolution, and implied weights recovered poor trees at low values of k. No existing method can overcome the inherent limitation of a low character to taxon ratio.

4. Discussion

When accuracy and resolution are recognized as complementary aspects of information [12], parsimony and probabilistic analyses generate equally informative reconstructions of evolutionary history in the simulation studies analysed herein. Parsimony results are most informative when groups with a bootstrap GC value of less than −15 are collapsed, and are as accurate as Bayesian results if nodes are collapsed until trees exhibit an equal resolution. As an important caveat, parsimony analysis must employ a moderate weighting scheme. At low values of the concavity constant (k < 2, say), implied weights begin to exhibit the undesirable properties of clique analysis, whereas at high values (as k → ∞), it converges to the inferior equally weighted parsimony (electronic supplementary material). Each of these extremes yields results that are less accurate and less resolved, making them more different from the generative tree and consequently less informative about evolutionary history; results encountered only under such parameters do not merit biological interpretation.

Quite aside from issues with the validity of data simulation protocol [2,3], previous results that favour Bayesian methods over parsimony [5–8,10], or equal weights over implied weights [9], have arisen because accuracy has been considered the sole measure of a method's performance. Future simulation studies should evaluate methods based on normalized tree similarity metrics that reflect the total information contained within two trees—a quantity that reflects both resolution and accuracy. In the analyses examined herein, neither Bayesian nor parsimony analyses generate consistently superior results. Of course, other factors may influence a researcher's choice of methods: Bayesian models, for instance, can readily integrate non-morphological data [36,37] and allow probabilistic hypothesis testing using Bayes Factors [38]. Such considerations notwithstanding, researchers may wish to explicitly compare the results of both Bayesian and implied weights analyses when conducting phylogenetic analysis; observations common to both approaches and receiving strong node support values are particularly likely to be well supported by underlying data.

Data accessibility

Data and analyses are available on GitHub and archived with Zenodo. CL: https://github.com/ms609/CongreveLamsdell2016 [29]; OR: https://github.com/ms609/OReillyEtAl2016 [30]. The datasets are available in the electronic supplementary material.

Competing interests

I declare that I have no competing interests.

Funding

I received no funding for this study.