Abstract
Background
An angiography‐based supervised machine learning (ML) algorithm was developed to classify lesions as having fractional flow reserve ≤0.80 versus >0.80.
Methods and Results
With a 4:1 ratio, 1501 patients with 1501 intermediate lesions were randomized into training versus test sets. Between the ostium and 10 mm distal to the target lesion, a series of angiographic lumen diameter measurements along the centerline was plotted. The 24 computed angiographic features based on the diameter plot and 4 clinical features (age, sex, body surface area, and involve segment) were used for ML by XGBoost. The model was independently trained and tested by 2000 bootstrap iterations. External validation with 79 patients was conducted. Including all 28 features, the ML model with 5‐fold cross‐validation in the 1204 training samples predicted fractional flow reserve ≤0.80 with overall diagnostic accuracy of 78±4% (averaged area under the curve: 0.84±0.03). The 12 high‐ranking features selected by scatter search were involved segment; body surface area; distal lumen diameter; minimal lumen diameter; length of a lumen diameter <2.0 mm, <1.5 mm, and <1.25 mm; mean lumen diameter within the worst segment; sex; diameter stenosis; distal 5‐mm reference lumen diameter; and length of diameter stenosis >70%. Using those 12 features, the ML predicted fractional flow reserve ≤0.80 in the test set with sensitivity of 84%, specificity of 80%, and overall accuracy of 82% (area under the curve: 0.87). The averaged diagnostic accuracy in bootstrap replicates was 81±1% (averaged area under the curve: 0.87±0.01). External validation showed accuracy of 85% (area under the curve: 0.87).
Conclusions
Angiography‐based ML showed good diagnostic performance in identifying ischemia‐producing lesions and reduced the need for pressure wires.
Keywords: artificial intelligence, coronary angiography, fractional flow reserve, machine learning
Subject Categories: Diagnostic Testing, Imaging, Angiography, Catheter-Based Coronary and Valvular Interventions, Coronary Artery Disease
Clinical Perspective
What Is New?
Using clinical and angiographic features based on the diameter plot, the supervised machine learning model separated the lesions with fractional flow reserve ≤0.80 versus >0.80 with overall accuracy of 82% (area under the curve: 0.87) in the test set.
What Are the Clinical Implications?
Angiography‐based machine learning is useful to predict ischemia‐producing lesions by mitigating the visual–functional mismatch between angiography and fractional flow reserve.
The data‐driven approach may support clinicians in identifying clinically relevant coronary lesions without fractional flow reserve measurement and in making clinical decisions.
Introduction
Fractional flow reserve (FFR), a standard tool for lesion‐specific hemodynamic assessment, has been used to make decisions regarding revascularization of intermediate coronary stenosis.1, 2, 3, 4 Despite the abundant clinical evidence showing significant reduction in major adverse cardiac events by estimating FFR, >70% of treatment decisions still rely on a visual estimation of angiographic stenosis, indicating a worrisome discrepancy between current guidelines and practice.5, 6 The need for drug‐induced hyperemia, a prolonged procedure time and short‐term high costs, insufficient insurance coverage, and overconfidence in visual assessments by physicians may restrict the widespread use of FFR in clinical practice.
Although quantitative coronary angiography is routinely used to assess lesion severity, the integration of anatomic and physiologic parameters remains challenging. A reason for the visual–functional mismatch is that myocardial ischemia is mainly determined by multiple factors including the variable size of the subtended myocardium and the degree of stenosis.7 The overall diagnostic accuracy of quantitative coronary angiography diameter stenosis (DS) as a single morphological parameter for predicting FFR ≤0.80 was reported to be only 60% to 65%.7, 8 Moreover, even with a lot of substantial clinical and angiographic information, the development of prediction models using traditional statistical methods is limited by nonlinearity between factors and outcomes, interactions among variables, and too many predictors.9
Some approaches have used angiography‐based mathematical models to assess hemodynamic significance.8, 10, 11, 12 A virtual functional assessment index and quantitative flow ratio derived from 3‐dimensional quantitative coronary angiography models of computational fluid dynamics have achieved overall diagnostic accuracies of 80% to 86%. As part of an ongoing effort to develop better methods of hemodynamic assessment, we applied a machine learning (ML) technique that has emerged as a highly effective computer algorithm for the identification of patterns in large data sets with a multitude of variables, thus facilitating the building of models for data‐driven prediction.13, 14, 15 The aim of this study was to develop an angiography‐based supervised ML algorithm for classifying intermediate coronary lesions with FFR ≤0.80 versus >0.80.
Methods
The data, analytic methods, and study materials will not be made available to other researchers for purposes of reproducing the results or replicating the procedure.
Study Population
Between November 2010 and July 2015, we initially evaluated a consecutive series of 1717 stable and unstable angina patients who underwent invasive coronary angiography and preprocedural FFR to assess at least 1 intermediate lesion between November 2010 and July 2015 at Asan Medical Center, Seoul, Korea. Native coronary lesions with intermediate stenosis (defined as an angiographic DS of 40–80% on visual estimation) were screened for inclusion in our current analyses. In cases for which the FFR had been measured in multiple lesions, the lesion with the lowest FFR value was chosen. We excluded 25 patients with tandem lesions, 20 patients with a stent within the target vessel, 11 patients with a side branch evaluation, 145 patients with left main coronary artery stenosis (angiographic DS >30%), 4 patients with poor imaging quality, 6 patients with chronic total occlusion, and 5 patients with a scarred myocardium and regional wall motion abnormality. A final cohort of 1501 patients with 1501 lesions were enrolled in this retrospective analysis. They were randomly assigned into a training or test sample group at a 4:1 ratio. Thus, 1204 patients were used for model training (training sample), and a nonoverlapping group of 297 patients was used for evaluating the diagnostic performance of the model (test sample; Table 1). The protocol of retrospective data analysis was approved by the institutional review board of the Asan Medical Center, and a waiver of informed consent was granted.
Table 1.
Baseline Characteristics
| Training Set | Test Set | |
|---|---|---|
| Number of patients/lesions | 1204/1204 | 297/297 |
| Age, y | 62.6±9.7 | 62.1±10.0 |
| Men | 929 (77) | 228 (77) |
| Diabetes mellitus | 393 (31) | 89 (30) |
| Hypertension | 783 (65) | 198 (67) |
| Current smoker | 493 (43) | 134 (45) |
| Hyperlipidemia | 394 (66) | 193 (65) |
| Stable (vs unstable) angina | 987 (82) | 252 (85) |
| Body surface area, m2 | 1.74±0.16 | 1.74±0.16 |
| FFR at maximal hyperemia | 0.79±0.10 | 0.79±0.10 |
| Involved segment | ||
| Proximal LAD | 509 (42) | 115 (39) |
| Mid LAD | 293 (24) | 89 (29) |
| Distal LAD | 11 (1) | 0 (0) |
| Proximal LCX | 67 (6) | 20 (7) |
| Distal LCX | 55 (5) | 13 (4) |
| Proximal RCA | 145 (12) | 33 (11) |
| Mid RCA | 90 (8) | 20 (7) |
| Distal RCA | 34 (3) | 7 (2) |
Data are shown as mean±SD or n (%). FFR indicates fractional flow reserve; LAD, left anterior descending artery lesion; LCX, left circumflex artery; RCA, right coronary artery.
External validation of the ML models was conducted in 79 angina patients (64 patients from CHA University, Seongnam, Korea, and 15 patients from Ajou University, Suwon, Korea) who underwent invasive coronary angiography and FFR to assess an intermediate coronary lesion.
Acquisition of Angiography
Coronary angiography was performed with 5F to 7F catheters through a radial or femoral access after the administration of 250 μg of intracoronary nitroglycerine.
FFR Measurement
FFR is defined as the ratio of maximal coronary blood flow in a diseased artery to the maximal coronary blood flow in the same artery without stenosis.1, 2, 3 “Equalizing” was performed with a guidewire sensor positioned at the guiding catheter tip. A 0.014‐in FFR pressure guidewire (Radi; St. Jude Medical) was then advanced distally to the stenosis. The FFR was measured at the maximum hyperemia induced by an intravenous infusion of adenosine administered through a central vein at 140 μg/kg per minute, which was increased to 200 μg/kg per minute to enhance the detection of hemodynamically relevant stenoses. Hyperemic pressure pullback recordings were performed. FFR was then obtained as the ratio of distal coronary artery pressure to normal perfusion pressure (approximate aortic pressure) during maximal hyperemia.1, 2, 3 An FFR of 0.80 indicates that the stenotic coronary artery supplies 80% of the normal maximal flow. A stenosis was considered functionally significant when the FFR was 0.80 or less than the cutoff.3, 4
Angiographic Segmentation and Diameter Calculation
To clearly show the entire vessel from the ostium to the distal stream to the lesion, an angiographic projection without foreshortening or vessel overlap was selected, and a frame at the end‐diastolic phase of a cardiac cycle was used. Within the region of interest between the ostium and 10 mm distal to the target lesion, angiographic lumen segmentation was done using commercial edge‐detection software (CAAS‐5; Pie‐Medical). By reviewing all segmented images, the erroneous segmentations were manually corrected. To obtain the lumen diameters from the ostium to the distal reference, the centerline of the lumen was extracted. Briefly, we applied the distance transform on the lumen area and converted the result into the speed function, which was a real‐valued image in the range of 0 to 1. These values can be interpreted as speed. The fast marching algorithm was then used to find the optimal path from the proximal to distal points.16 The extracted centerline points were smoothed by convolution with a Gaussian kernel. We linearly sampled the centerline points with equal spacing. In each centerline point, the perpendicular direction to the centerline was computed, and the 2 rays were cast to the opposite direction to find the end position of the lumen area. The distance between the 2 end points was recorded as the lumen diameter at the given centerline points. The lumen dimensions and the distances between the 2 points on a centerline were calibrated by multiplying a scale factor that was calculated as the known caliber (millimeter) of guiding catheter divided by the pixel distance between the 2 edges of the catheter. The series of lumen diameters along the centerline were plotted with median filtering and used for extracting angiographic features.
Computed Segments
Figure 1 shows the computed segments based on the diameter plot with median filtering. The ostium (points A and B) is the 5‐mm segment from the beginning of the region of interest. By selecting the site of the minimal lumen diameter (MLD), the worst segment (points F and G) was defined by a lumen diameter of less than [MLD+0.2 mm]. The proximal plateau (point D) was the proximally closest point from the MLD, where the moving standard deviation was ≈0. The proximal reference (points C~E) was the segment in which the change in the lumen diameter was within ±0.2 mm from the proximal plateau. The distal plateau (point I) was the distally closet point from the MLD, where the moving standard deviation was ≈0. The distal reference (points H~J) was the segment in which the change in the lumen diameter was within ±0.2 mm from the distal plateau. The proximal and distal edges were defined as the distal end of the proximal reference (point E) and the proximal end of the distal reference (point H), respectively. The lesion (points E~H) was the segment between the computed proximal and distal edges. The proximal (or distal) 5‐mm reference was within the 5‐mm segments proximally (or distally) to the lesion, respectively.
Figure 1.
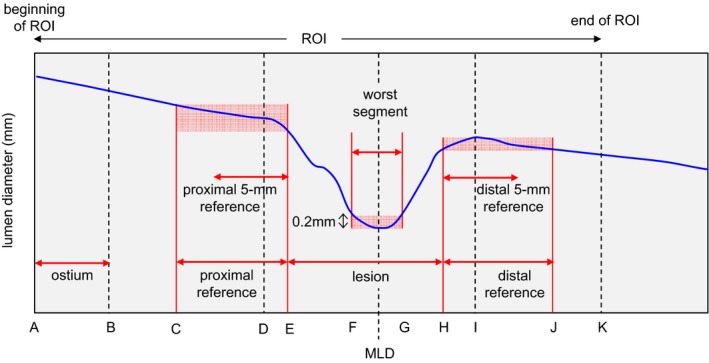
Definition of vessel segmentations on a diameter plot (points A–K). MLD indicates minimal lumen diameter; ROI, region of interest.
Computational Feature Extraction
The definitions of the 24 computed angiographic features are summarized in Table 2. By adding the clinical features (age, sex, body surface area, and the involved segment), a total of 28 features were used in the ML model.
Table 2.
Definitions of Computed Angiographic Features
| Feature | Definition | Feature Importance, %a |
|---|---|---|
| Maximal lumen diameter, mm | Maximal lumen diameter within the ROI (points A~K) | 0 |
| MLD, mm | Minimal lumen diameter within the ROI (points A~K) | 84.0 |
| Proximal lumen diameter, mm | Mean lumen diameter between the ostium and the proximal edge (points A~E) | 0 |
| Distal lumen diameter, mm | Mean lumen diameter between the distal edge and the end of ROI (points H~K) | 90.5 |
| Proximal 5‐mm RLD, mm | Mean lumen diameter within the proximal 5‐mm reference | 46.0 |
| Distal 5‐mm RLD, mm | Mean lumen diameter within the distal 5‐mm reference | 66.0 |
| Averaged RLD, mm | Average of proximal and distal 5‐mm RLDs | 47.5 |
| Lumen diameter within the worst segment, mm | Mean lumen diameter within the worst segment (points F and G) | 75.5 |
| DS, % | [Averaged RLD−MLD]/Averaged RLD×100 | 60.5 |
| Distance to MLD, mm | Distance from the ostium to the MLD (point A~MLD) | 14.0 |
| Length of the proximal reference, mm | Length of the proximal reference (points C~E) | 6.0 |
| Distance to the distal reference, mm | Distance from the ostium to the distal reference (points A~J) | 4.0 |
| Lesion length, mm | Length of the lesion (points E~H) | 40.5 |
| Length‐D <2.0, mm | Total length of the segment with lumen diameter <2.0 mm | 82.5 |
| Length‐D <1.75, mm | Total length of the segment with lumen diameter <1.75 mm | 2.5 |
| Length‐D <1.5, mm | Total length of the segment with lumen diameter <1.5 mm | 71.5 |
| Length‐D <1.25, mm | Total length of the segment with lumen diameter <1.25 mm | 68.0 |
| Length‐D <1.0, mm | Total length of the segment with lumen diameter<1.0 mm | 50.5 |
| Length‐DS >25, mm | Total length of the segment with DS >25% | 34.0 |
| Length‐DS >50, mm | Total length of the segment with DS >50% | 35.0 |
| Length‐DS >70, mm | Total length of the segment with DS >70% | 52.0 |
| Longitudinal eccentricity | Ratio of the length of point E~MLD to the lesion length | 48.0 |
| Proximal slope | [Lumen diameter at the proximal edge−MLD]/length of point E~MLD | 0 |
| Distal slope | [Lumen diameter at the distal edge−MLD]/length of MLD~point H | 12.0 |
| Segment | Involved segment | 100.0 |
| Body surface area | Body surface area | 96.0 |
| Sex | Male or female | 70.5 |
| Age | Years of age | 0 |
DS indicates diameter stenosis; Length‐D, length of the lumen diameter; MLD, minimal lumen diameter; RLD, reference lumen diameter; ROI, region of interest.
Feature importance was based on a scatter search in 200 cases with the best performance from 10 million trials.
Feature Selection and ML
The devised ML algorithm was implemented by using the eXtreme Gradient Boosting (XGBoost) library. Data S1 includes the theoretical overviews and technical details of the integrated ML algorithm based on gradient boosting of a regression tree.17
Including the aforementioned 28 features, the ML model was trained for the binary classification of the lesions as those with FFR ≤0.80 versus >0.80. The receiver operating characteristic curve, which was based on the relative performances considering the whole range of possible probability thresholds (from 0 to 1), has an area that ranges from 0.5 for classifiers without any prediction capability to 1 for perfectly classifying algorithms. With a 5‐fold cross‐validation scheme (Figure S1), the accuracy was calculated by averaging the accuracies over the 5 tests performed in the multiple rounds of cross‐validation. On the basis of the ML model, feature importance was assessed by scatter search as a metaheuristic and a global optimization algorithm in the 200 cases showing the best performance from 10 million trials. The ML classifiers using the 12 high‐ranking features were applied to an independent test sample of 297 lesions that were not used in the training phase.
In the training set, the models were independently trained on the 2000 train‐validation random splits with a 4:1 ratio, and the averaged performances of the 2000 bootstrap replicates and the bootstrap CIs were calculated. In the 2000 bootstrap replicates by random sampling of 80% of the test samples, the averaged performances and bootstrap CIs were also assessed.
The overall flow of the development of the supervised ML model is shown in the Figure 2.
Figure 2.

Workflow for developing the machine learning model. The 12 high‐ranking features selected by scatter search were involved segment; body surface area; distal lumen diameter; minimal lumen diameter; length of a lumen diameter of <2.0 mm, <1.5 mm, and <1.25 mm; mean lumen diameter within the worst segment; sex; diameter stenosis; distal 5‐mm reference lumen diameter; and length of diameter stenosis >70%. CV indicates cross‐validation; FFR, fractional flow reserve.
Statistical Analysis
The statistical analyses used for evaluating patient and lesion characteristics at baseline were performed using SPSS (v10.0; IBM Corp). All values are expressed as mean±SD (continuous variables) or as counts and percentages (categorical variables). Continuous variables were compared using unpaired t tests, and categorical variables were compared using χ2 statistics. P<0.05 was considered statistically significant. Receiver operating characteristic curve analysis was done using MedCalc software to assess the area under the curve (AUC) and the best threshold of each angiographic feature to predict an FFR ≤0.80 with maximal accuracy.
Results
Clinical and Lesion Characteristics
The baseline characteristics of the study patients are summarized in Table 1. Overall, the target vessel was the left anterior descending artery (LAD) in 1017 (67.8%) patients, the left circumflex artery in 155 (10.3%) patients, and the right coronary artery in 329 (21.9%) patients. The frequency of FFR ≤0.80 was 562 (46.7%) in the training set and 134 (45.1%) in the test set (P=0.63). No significant differences in the baseline characteristics were noted between the training and test sets.
Clinical and Computed Angiographic Features
In the training set, FFR ≤0.80 was more frequent in men than in women (49.7% vs, 36.4%, P<0.001). The lesions with FFR ≤0.80 versus >0.80 were associated with younger patient age (61.7±9.6 versus 63.5±9.8 years, P=0.001) and larger body surface area (1.76±0.16 versus 1.72±0.16 m2, P<0.001). The involved segment was the proximal LAD in 58.2% of the lesions with FFR ≤0.80 and 28.3% of the lesions with FFR >0.80 (P<0.001). The frequency of FFR ≤0.80 versus >0.80 was 64.2% in the proximal LAD, 44.4% in the mid‐LAD, 36.4% in the distal LAD, 32.8% in the proximal left circumflex artery, 27.3% in the distal left circumflex artery, 27.6% in the proximal right coronary artery, 20.0% in the mid–right coronary artery, and 17.6% in the distal right coronary artery (Figure S2).
Computed angiographic features were compared between the lesions with FFR ≤0.80 versus >0.80 (Table 3). The lesions with FFR ≤0.80 were more likely to be associated with smaller MLD; higher DS; smaller mean lumen diameter within the worst segment; a longer segment with a lumen diameter <2.0 mm, <1.75 mm, <1.5 mm, <1.25 mm, or <1.0 mm; a longer segment with DS >50% or >70%; shorter distance to the MLD; and smaller reference lumen diameter. On the receiver operating characteristic curve analysis, the computed angiographic DS >54% predicted FFR ≤0.80 with sensitivity of 54% and specificity of 77% (AUC: 0.690). The threshold and the performance of each feature for predicting FFR ≤0.80 are presented in Table 3.
Table 3.
Angiographic Prediction of FFR ≤0.80 in the Training Sample (N=1204)
| ROC Curve Analysis for Predicting FFR ≤0.80 | t test | ||||||
|---|---|---|---|---|---|---|---|
| Cutoff | AUCa | Sensitivity, % | Specificity, % | FFR >0.80 | FFR ≤0.80 | P Value | |
| Maximal lumen diameter, mm | <4.09 | 0.573 | 72 | 41 | 3.93±0.69 | 3.75±0.63 | <0.001 |
| Proximal lumen diameter, mm | <4.04 | 0.551 | 83 | 27 | 3.49±0.79 | 3.34±0.77 | 0.001 |
| Distal lumen diameter, mm | <2.61 | 0.648 | 72 | 51 | 2.70±0.61 | 2.40±0.51 | <0.001 |
| Lumen diameter within the worst segment, mm | <1.73 | 0.783 | 76 | 68 | 1.93±0.41 | 1.54±0.31 | <0.001 |
| Length of the proximal reference, mm | <2.96 | 0.557 | 53 | 59 | 4.05±2.85 | 3.51±2.41 | 0.001 |
| MLD, mm | <1.48 | 0.778 | 77 | 67 | 1.68±0.40 | 1.30±0.31 | <0.001 |
| Distance to MLD, mm | <35.9 | 0.559 | 69 | 42 | 35.97±22.36 | 30.85±17.94 | <0.001 |
| Length‐D <2.0, mm | >3.63 | 0.734 | 88 | 50 | 8.38±11.93 | 17.56±15.96 | <0.001 |
| Length‐D <1.75, mm | >2.23 | 0.763 | 78 | 65 | 3.13±6.06 | 8.81±10.17 | <0.001 |
| Length‐D <1.5, mm | >1.02 | 0.747 | 67 | 77 | 1.07±2.86 | 3.96±5.41 | <0.001 |
| Length‐D <1.25, mm | >0.146 | 0.646 | 39 | 90 | 0.22±1.06 | 0.96±1.99 | <0.001 |
| Length‐D <1.0, mm | >0 | 0.555 | 14 | 97 | 0.03±0.32 | 0.15±0.56 | <0.001 |
| Proximal 5‐mm RLD, mm | <4.08 | 0.549 | 84 | 26 | 3.50±0.79 | 3.35±0.77 | 0.001 |
| Distal 5‐mm RLD, mm | <2.61 | 0.647 | 72 | 51 | 2.69±0.60 | 2.40±0.51 | <0.001 |
| Averaged RLD, mm | <3.19 | 0.607 | 74 | 44 | 3.10±0.59 | 2.87±0.53 | <0.001 |
| Lesion length, mm | >19.4 | 0.532 | 75 | 31 | 17.92±4.72 | 17.38±3.85 | 0.033 |
| Distance to the distal reference, mm | >22.17 | 0.525 | 89 | 18 | 49.93±26.56 | 51.42±23.88 | 0.312 |
| DS, % | >54 | 0.690 | 54 | 77 | 44.8±13.7 | 53.4±13.1 | <0.001 |
| Length‐DS >25, mm | <3.1 | 0.529 | 24 | 81 | 5.03±2.74 | 4.75±2.48 | 0.056 |
| Length‐DS >50, mm | >0.14 | 0.681 | 60 | 72 | 0.65±1.51 | 2.12±3.15 | <0.001 |
| Length‐DS >70, mm | >0 | 0.521 | 5 | 99 | 0.01±0.15 | 0.04±0.23 | 0.009 |
| Longitudinal eccentricity | <0.569 | 0.539 | 69 | 39 | 0.50±0.97 | 0.41±0.62 | 0.050 |
| Proximal slope | <0.0035 | 0.510 | 66 | 40 | 0.0038±0.0041 | 0.0034±0.0030 | 0.072 |
| Distal slope | <0.0016 | 0.560 | 65 | 47 | 0.0023±0.0029 | 0.0019±0.0024 | 0.010 |
| Age, y | <65 | 0.558 | 65 | 46 | 63.52±9.77 | 61.71±9.61 | 0.001 |
| Body surface area | >1.68 | 0.562 | 70 | 40 | 1.72±0.16 | 1.76±0.16 | <0.001 |
AUC indicates area under the curve; DS, diameter stenosis; FFR, fractional flow reserve; Length‐D, length of the lumen diameter; MLD, minimal lumen diameter; ROC, receiver operating characteristic; RLD, reference lumen diameter.
Threshold of predictive score.
Prediction of FFR ≤0.80 by ML
To classify the lesions with FFR ≤0.80 versus >0.80, the performances of ML using all 28 features are shown in Table 4 and Figure 3. Based on the ranking of importance (Table 2), 12 features were selected including segment, body surface area, distal lumen diameter, MLD, length‐D <2.0, lumen diameter within the worst segment, length‐D <1.5, sex, length‐D <1.25, distal 5‐mm RLD, DS, and length‐DS >70. Including these 12 high‐ranking features, the ML model predicted FFR ≤0.80 in the test sample with sensitivity of 84%, specificity of 80%, and overall accuracy of 82% (AUC: 0.87; Table 4 and Figure 3).
Table 4.
Performances of the ML Model for Predicting FFR ≤0.80
| AUC | Sensitivity | Specificity | PPV | NPV | Overall Accuracy | |
|---|---|---|---|---|---|---|
| Using all 28 features | ||||||
| Training set (5‐fold CV)a | 0.84±0.03 | 0.78±0.04 | 0.78±0.05 | 0.77±0.05 | 0.79±0.05 | 0.78±0.04 |
| Test set | 0.86 | 0.82 | 0.79 | 0.79 | 0.82 | 0.80 |
| External validation cohort | 0.90 | 0.72 | 0.89 | 0.75 | 0.87 | 0.84 |
| Using the 12 selected features | ||||||
| Training set | 0.86 | 0.79 | 0.80 | 0.77 | 0.82 | 0.79 |
| Test set | 0.87 | 0.84 | 0.80 | 0.81 | 0.84 | 0.82 |
| External validation cohort | 0.87 | 0.80 | 0.87 | 0.74 | 0.90 | 0.85 |
| By 2000 bootstrap iterations | ||||||
| Training setb | 0.87±0.01 (0.86–0.88) | 0.81±0.01 (0.79–0.83) | 0.77±0.01 (0.74–0.79) | 0.75±0.01 (0.73–0.76) | 0.83±0.01 (0.81–0.84) | 0.79±0.01 (0.77–0.80) |
| Test setb | 0.87±0.01 (0.86–0.87) | 0.84±0.02 (0.81–0.87) | 0.77±0.01 (0.75–0.80) | 0.78±0.01 (0.76–0.80) | 0.83±0.01 (0.81–0.86) | 0.81±0.01 (0.79–0.82) |
AUC indicates area under curve; CV, cross‐validation; FFR, fractional flow reserve; ML, machine learning; NPV, negative predictive value; PPV, positive predictive value.
Mean±SD with 5‐fold CV.
Averaged performances of 2000 bootstrap replicates as mean±SD, (bootstrap CIs).
Figure 3.
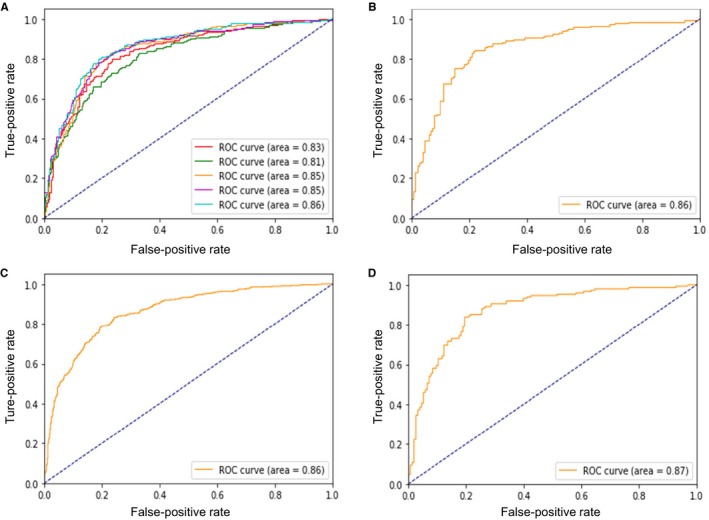
Performance of the machine learning model for classifying lesions as having FFR ≤0.80 vs >0.80. Receiver operating characteristic curves (ROCs) in the training set with 5‐fold cross‐validation using all 28 features (A), in the test set using all 28 features (B), in the training set using the selected 12 features (C), and in the test set using the selected 12 features (D). AUC indicates area under the curve; FFR, fractional flow reserve.
In the test sample, 24 of 148 lesions with FFR ≤0.80 were misclassified as FFR >0.80 by the ML model. Among them, 13 (54%) lesions were revealed to have a gray zone of FFR (0.75–0.80). When the 56 lesions with an FFR 0.75 to 0.80 were excluded, the sensitivity and the overall accuracy were further improved to 88% and 83%, respectively.
External Validation
In the external validation cohort including 79 patients, the age was 59.6±9.0 years, and 58 (73.4%) were men. FFR ≤0.8 was seen in 25 (31.6%) lesions. The angiographic DS and MLD were 48.3±8.0% and 1.64±0.39 mm, respectively. The performances of the ML models for the prediction of FFR<0.8 are shown in Table 4.
Discussion
The main findings of this study are as follows. First, for the binary classification of the intermediate lesions as FFR ≤0.80 versus >0.80, the 12 high‐ranking features were segment, body surface area, distal lumen diameter, MLD, length‐D <2.0, lumen diameter within the worst segment, length‐D <1.5, sex, length‐D <1.25, distal 5‐mm RLD, DS, and length‐DS >70. Second, the ML model using the selected 12 features predicted the lesions with FFR ≤0.80 with an overall accuracy of 82% (AUC: 0.87) in the test set.
Previous studies have provided insights into higher risk populations that can obtain clinical benefits from an approach incorporating ischemia‐guided revascularization.18, 19 The FAME (Fractional Flow Reserve versus Angiography for Multivessel Evaluation) trial demonstrated that FFR‐guided (versus angiography‐guided) percutaneous coronary intervention in multivessel disease significantly reduced the rates of 1‐year major adverse cardiac events.4 In the FAME 2 trial evaluating the lesions with FFR ≤0.80, medical therapy alone (versus FFR‐guided percutaneous coronary intervention) remarkably increased clinical events.5 Although the routine estimation of FFR is recommended as part of treatment decision making, the procedural time and expense and the risk of complications remain concerns. The International Survey on Interventional Strategy suggested that 71% of decisions were based solely on angiographic appearance, which was discordant in 47% compared with a known FFR, using 0.80 as the cutoff. The dominance in clinicians’ decisions by visual estimation indicates a worrisome discrepancy between current guidelines and daily practice. The positive predictive value of the angiographic DS criterion has been <50%, which may lead to a high rate of unnecessary percutaneous coronary intervention.7
Although coronary angiography has been the gold standard for assessing coronary lesion severity, its role in treatment decision making is limited because of poor diagnostic accuracy (60–65%) for predicting FFR ≤0.80.5, 6, 7, 8 A reason for the visual–functional mismatch is that myocardial ischemia is determined by many attributes including the variable size of the supplied myocardium, the degree of stenosis, local geometry, collateral distribution, and other clinical characteristics.8 In addition, quantitative coronary angiographic measurements such as DS and MLD are obtained at only a single point and thus rarely reflect the nature of the entire vessel.
Several approaches for an FFR approximation using angiography‐based models have recently been introduced.10, 11, 12 The DILEMMA score, including an estimate of coronary blood flow, has discriminated FFR ≤0.80 from >0.80 lesions with overall diagnostic accuracy of ≈72%. Moreover, a virtual functional assessment index and a quantitative flow ratio based on computational fluid dynamics have shown overall accuracy of 80–86% in predicting FFR ≤0.80. Those approaches require a 3‐dimensional reconstruction of at least 2 angiographic projections without foreshortening or overlapping vessels and the subsequent computational analyses.
As part of an ongoing effort to develop an angiography‐based model for hemodynamic assessment, we applied the integrated ML algorithm based on gradient boosting of a regression tree. Using clinical parameters and computed angiographic features derived from a single projection image, the ML model showed sensitivity of 84% and specificity of 80% to predict FFR ≤0.80 (AUC: 0.87). Moreover, the averaged accuracy was 81±1% (averaged AUC: 0.87±0.01) in the 2000 bootstrap replicates in the test set. The sensitivity was further improved to ≈88% by the exclusion of the lesions with a gray zone of FFR 0.75–0.80. By efficiently integrating both morphologic and physiologic information, this approach extends the role of angiography in decision making for the management of intermediate coronary stenosis. Furthermore, the data‐driven ML model would continue to learn from new data to make even better predictions.
Our current study findings have provided further clues as to how the clinical and angiographic features of a coronary stenosis affect the FFR value. The high‐ranking features were primarily involved with the size of subtended myocardial territories (proximal LAD segment, larger body surface area, and male sex) and stenosis severity (MLD, DS, and the length of luminal narrowing). The distal RLD positively correlated with the FFR, indicating that the RLD was more likely to reveal the presence of diffuse disease in the reference segment rather than to reflect the vessel size. Although the ranking of the features is specific to the fitted model, the approach suggests that the best performance of these features warrants consideration in future models.
Limitations
With the exclusion of significant left main disease, side branch, and diffuse and tandem lesions, the ML model cannot be generally applied. In addition, this binary classifier cannot provide a numerical hemodynamic index for incremental risk stratification. Using a single angiographic projection, the uncertainly about the eccentricity of luminal stenosis is another limitation. In addition, foreshortening of the coronary centerline because of vascular curvature might affect the length of the stenotic segment; this needs to be further validated by combining 3‐dimensional computed tomography angiography. Although our developed model was validated in the independent test samples and in the 2000 bootstrap replicates, the possibility of overfitting cannot be completely excluded. Thus, the performance and the clinical impact of this approach should be further proved by an external validation study with a large cohort. A prospective randomized study for evaluating clinical outcomes following ML‐ and FFR‐guided diagnostic strategies is also needed. Nonangiographic clinical risk factors such as diabetes mellitus, hyperlipidemia, and smoking were not included in the model. Finally, prespecified angiographic features were used for ML, but an image‐based deep learning strategy using large data sets is warranted for achieving optimal diagnostic performance.
Conclusion
The angiography‐based ML model shows good diagnostic performance for identifying ischemia‐producing lesions and may reduce future need for pressure wires and risk of procedural complications. This approach potentially promotes the utilization of physiologically guided decision making.
Sources of Funding
This study was supported by grants from the Korea Healthcare Technology R&D Project, Ministry for Health & Welfare Affairs, Republic of Korea (HI15C1790 and HI17C1080), the Ministry of Science and ICT (NRF‐2017R1A2B4005886), and the Asan Institute for Life Sciences, Asan Medical Center, Seoul, Korea (2017‐0745).
Disclosures
None.
Supporting information
Data S1. Supplemental Methods and Results.
Figure S1. Five‐fold cross‐validation.
Figure S2. Frequency of fractional flow reserve <0.80 according to the involved segment.
(J Am Heart Assoc. 2019;8:e011685 DOI: 10.1161/JAHA.118.011685.)
References
- 1. Pijls NH, Van Gelder B, Van der Voort P, Peels K, Bracke FA, Bonnier HJ, el Gamal MI. Fractional flow reserve. A useful index to evaluate the influence of an epicardial coronary stenosis on myocardial blood flow. Circulation. 1995;92:3183–3193. [DOI] [PubMed] [Google Scholar]
- 2. Pijls NH, De Bruyne B, Peels K, Van Der Voort PH, Bonnier HJ, Bartunek J, Koolen JJ, Koolen JJ. Measurement of fractional flow reserve to assess the functional severity of coronary‐artery stenoses. N Engl J Med. 1996;334:1703–1708. [DOI] [PubMed] [Google Scholar]
- 3. Tonino PA, Fearon WF, De Bruyne B, Oldroyd KG, Leesar MA, Ver Lee PN, Maccarthy PA, Van't Veer M, Pijls NH. Angiographic versus functional severity of coronary artery stenoses in the FAME study fractional flow reserve versus angiography in multivessel evaluation. J Am Coll Cardiol. 2010;55:2816–2821. [DOI] [PubMed] [Google Scholar]
- 4. Tonino PA, De Bruyne B, Pijls NH, Siebert U, Ikeno F, van't Veer M, Klauss V, Manoharan G, Engstrøm T, Oldroyd KG, Ver Lee PN, MacCarthy PA, Fearon WF; FAME Study Investigators . Fractional flow reserve versus angiography for guiding percutaneous coronary intervention FAME. N Engl J Med. 2009;360:213–224. [DOI] [PubMed] [Google Scholar]
- 5. Toth GG, Toth B, Johnson NP, De Vroey F, Di Serafino L, Pyxaras S, Rusinaru D, Di Gioia G, Pellicano M, Barbato E, Van Mieghem C, Heyndrickx GR, De Bruyne B, Wijns W. Revascularization decisions in patients with stable angina and intermediate lesions: results of the international survey on interventional strategy. Circ Cardiovasc Interv. 2014;7:751–759. [DOI] [PubMed] [Google Scholar]
- 6. Dattilo PB, Prasad A, Honeycutt E, Wang TY, Messenger JC. Contemporary patterns of fractional flow reserve and intravascular ultrasound use among patients undergoing percutaneous coronary intervention in the United States: insights from the National Cardiovascular Data Registry. J Am Coll Cardiol. 2012;60:2337–2339. [DOI] [PubMed] [Google Scholar]
- 7. Park SJ, Kang SJ, Ahn JM, Shim EB, Kim YT, Yun SC, Song H, Lee JY, Kim WJ, Park DW, Lee SW, Kim YH, Lee CW, Mintz GS, Park SW. Visual‐functional mismatch between coronary angiography and fractional flow reserve. JACC Cardiovasc Interv. 2012;5:1029–1036. [DOI] [PubMed] [Google Scholar]
- 8. Westra J, Tu S, Winther S, Nissen L, Vestergaard MB, Andersen BK, Holck EN, Fox Maule C, Johansen JK, Andreasen LN, Simonsen JK, Zhang Y, Kristensen SD, Maeng M, Kaltoft A, Terkelsen CJ, Krusell LR, Jakobsen L, Reiber JHC, Lassen JF, Bøttcher M, Bøtker HE, Christiansen EH, Holm NR. Evaluation of coronary artery stenosis by quantitative flow ratio during invasive coronary angiography: the WIFI II study (Wire‐Free Functional Imaging II). Circ Cardiovasc Imaging. 2018;11:e007107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Goldstein BA, Navar AM, Carter RE. Moving beyond regression techniques in cardiovascular risk prediction: applying machine learning to address analytic challenges. Eur Heart J. 2017;38:1805–1814. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Papafaklis MI, Muramatsu T, Ishibashi Y, Lakkas LS, Nakatani S, Bourantas CV, Ligthart J, Onuma Y, Echavarria‐Pinto M, Tsirka G, Kotsia A, Nikas DN, Mogabgab O, van Geuns RJ, Naka KK, Fotiadis DI, Brilakis ES, Garcia‐Garcia HM, Escaned J, Zijlstra F, Michalis LK, Serruys PW. Fast virtual functional assessment of intermediate coronary lesions using routine angiographic data and blood flow simulation in humans: comparison with pressure wire—fractional flow reserve. EuroIntervention. 2014;10:574–583. [DOI] [PubMed] [Google Scholar]
- 11. Tu S, Westra J, Yang J, von Birgelen C, Ferrara A, Pellicano M, Nef H, Tebaldi M, Murasato Y, Lansky A, Barbato E, van der Heijden LC, Reiber JH, Holm NR, Wijns W; FAVOR Pilot Trial Study Group . Diagnostic accuracy of fast computational approaches to derive fractional flow reserve from diagnostic coronary angiography: the international multicenter FAVOR Pilot study. JACC Cardiovasc Interv. 2016;9:2024–2035. [DOI] [PubMed] [Google Scholar]
- 12. Xu B, Tu S, Qiao S, Qu X, Chen Y, Yang J, Guo L, Sun Z, Li Z, Tian F, Fang W, Chen J, Li W, Guan C, Holm NR, Wijns W, Hu S. Diagnostic accuracy of angiography‐based quantitative flow ratio measurements for online assessment of coronary stenosis. J Am Coll Cardiol. 2017;70:3077–3087. [DOI] [PubMed] [Google Scholar]
- 13. Krittanawong C, Zhang H, Wang Z, Aydar M, Kitai T. Artificial intelligence in precision cardiovascular medicine. J Am Coll Cardiol. 2017;69:2657–2664. [DOI] [PubMed] [Google Scholar]
- 14. Henglin M, Stein G, Hushcha PV, Snoek J, Wiltschko AB, Cheng S. Machine learning approaches in cardiovascular imaging. Circ Cardiovasc Imaging. 2017;10:e005614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Darcy AM, Louie AK, Roberts LW. Machine learning and the profession of medicine. JAMA. 2016;315:551–552. [DOI] [PubMed] [Google Scholar]
- 16. Mueller D, Maeder A. Robust semi‐automated path extraction for visualising stenosis of the coronary arteries. Comput Med Imaging Graph. 2008;32:463–475. [DOI] [PubMed] [Google Scholar]
- 17. Chen T, Guestrin C. Xgboost: a scalable tree boosting system. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, ACM. 2016:785–794.
- 18. Gada H, Kirtane AJ, Kereiakes DJ, Bangalore S, Moses JW, Généreux P, Mehran R, Dangas GD, Leon MB, Stone GW. Meta‐analysis of trials on mortality after percutaneous coronary intervention compared with medical therapy in patients with stable coronary heart disease and objective evidence of myocardial ischemia. Am J Cardiol. 2015;115:1194–1199. [DOI] [PubMed] [Google Scholar]
- 19. Hachamovitch R, Hayes SW, Friedman JD, Cohen I, Berman DS. Comparison of the short‐term survival benefit associated with revascularization compared with medical therapy in patients with no prior coronary artery disease undergoing stress myocardial perfusion single photon emission computed tomography. Circulation. 2003;107:2900–2907. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data S1. Supplemental Methods and Results.
Figure S1. Five‐fold cross‐validation.
Figure S2. Frequency of fractional flow reserve <0.80 according to the involved segment.


