Abstract
This Letter proposes a customised approach for attribute selection applied to the fuzzy rough quick reduct algorithm. The unbalanced data is balanced using synthetic minority oversampling technique. The huge dimensionality of the cancer data is reduced using a correlation-based filter. The dimensionality reduced balanced attribute gene subset is used to compute the final minimal reduct set using a customised fuzzy triangular norm operator on the fuzzy rough quick reduct algorithm. The customised fuzzy triangular norm operator is used with a Lukasiewicz fuzzy implicator to compute the fuzzy approximation. The customised operator selects the least number of informative feature genes from the dimensionality reduced datasets. Classification accuracy using leave-one-out cross validation of 94.85, 76.54, 98.11, and 99.13% is obtained using a customised function for Lukasiewicz triangular norm operator on leukemia, central nervous system, lung, and ovarian datasets, respectively. Performance analysis of the conventional fuzzy rough quick reduct and the proposed method are performed using parameters such as classification accuracy, precision, recall, F-measure, scatter plots, receiver operating characteristic area, McNemar test, chi-squared test, Matthew's correlation coefficient and false discovery rate that are used to prove that the proposed approach performs better than available methods in the literature.
Keywords: lung, fuzzy set theory, cancer, rough set theory, pattern classification, learning (artificial intelligence), sampling methods, approximation theory, medical computing
Keywords: cancer data, fuzzy rough quick reduct algorithm, Lukasiewicz fuzzy implicator, fuzzy approximation, fuzzy rough machine learning approaches, fuzzy triangular norm operator, correlation-based filter, leukaemia, central nervous system, ovarian datasets, lung, McNemar test, chi-squared test, Matthew's correlation coefficient
1. Introduction
The decision-making process in health care is supported by suitable classification techniques in machine learning. Early diagnosis of the disease contributes to higher chances of recovery and cure. The accuracy of the classifier is the most important parameter in medical applications. Hence attribute selection and classification play a significant role in healthcare applications [1]. The attribute selection methods gain importance because of the higher dimensionality of microarray datasets and small sample size that contribute to degradation in the performance of the classifier. The process of attribute selection involves the elimination of redundant genes and preservation of informative genes, thereby reducing the dimensionality and computation cost and increasing the classification accuracy (CA). The dependency between attributes could be used for feature selection in rough sets. The quick reduct algorithm begins with an empty set and adds attributes, one at a time by computing the dependency of each attribute and chooses the best candidates to generate a reduct set that is least exhaustive with the highest dependency value [2].
Fuzzy-based independent component sub-space using fuzzy backward feature elimination is proposed to improve the performance of support vector machine (SVM) and Naive Bayes classifiers. An accuracy of 85% is reported on leukemia and 81% on lung cancer dataset [3]. The particle swarm optimisation (PSO) adaptive K-nearest neighbour-based gene selection method is proposed and SVM is used to reconfirm the usefulness of the identified genes [4]. The method to perform subset evaluation using neighbourhood approximation and attribute grouping is proposed and this approach selects three genes in the final minimal reduct and an accuracy of 84% is reported [5]. A two-phase hybrid model based on improved binary PSO is proposed for the diagnosis of cancer and the CA reported is in the range of 92 –100%. This model also selects the least number of genes (<1.5%) from the raw dataset [6]. The fuzzy rough set method to maximise both relevance and significance of the selected features is proposed that makes use of dependency, relevance, redundancy and significance as criteria for subset selection [7]. Markov blanket is used with an incremental wrapper to generate high-quality feature subset [8]. A formally correct and unified mathematical framework is proposed in [9]. A filter-wrapper approach is proposed to select the best set of features and the fuzzy rough set model using representative instances is proposed in [10]. Feature selection based on large-scale multi-objective binary optimisation is proposed and the method is implemented on cancer microarray gene expression datasets [11]. A hybrid approach to feature selection using correlation coefficient for dimensionality reduction and fuzzy rough quick reduct (FRQR) algorithm for generating the minimal reduct set is proposed in [12]. A correlation-based filter with a PSO-based wrapper is used for dimensionality reduction and FRQR algorithm is used to generate the final reduct set using cancer microarray gene expression datasets [13]. An entropy based filter is used for dimensionality reduction and customised similarity measure using FRQR is used to generate the minimal reduct set [14].
The above-discussed methods used the concept of the fuzzy rough set to generate the minimal reduct set. The two key problems of conventional FRQR approaches are – (i) the complexity in computing the Cartesian product of the fuzzy equivalence classes and (ii) in certain cases, the fuzzy lower approximation gets bigger than the fuzzy upper approximation. To solve the above issues, our proposed approach of correlation-based feature selection (CFS) is used as a dimensionality reduction technique and customised triangular norm-based minimal reduct set generation produces the minimal number of informative genes and produces comparably better CA.
This Letter is organised as follows: Section 2 presents the contributions of the research work, Section 3 discusses the proposed method for attribute subset selection; Section 4 discusses the simulation results and discussions and Section 5 discusses the conclusions.
2. Contributions
This Letter aims to reduce the feature sets and achieve better CA. The contribution of the proposed work is to customise the fuzzy triangular norm (t-norm) operator so that it produces a lesser number of feature genes in the final minimal reduct set and also provides better performance in terms of the different statistical parameters analysed when compared to the conventional FRQR approach.
3. Proposed method for attribute subset selection
The framework for the proposed approach can be described using the block diagram as shown in Fig. 1.
Fig. 1.
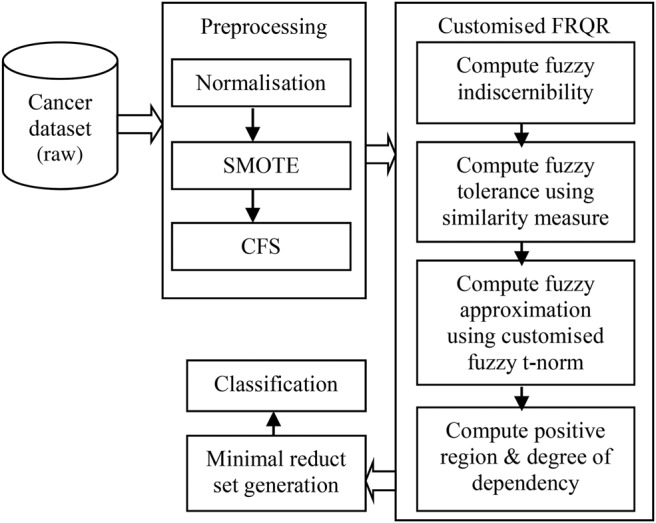
Framework of the proposed approach
The raw dataset is reduced for its dimensionality by using Pearson's correlation coefficient. The dimensionality reduced gene expression dataset is subjected to attribute subset selection using the customised function for Lukasiewicz fuzzy t-norm operator and Lukasiewicz implicator on the FRQR algorithm. The final minimal reduct generated is used to perform different statistical analysis to prove that this new customised operator performs better than those available in the literature.
3.1. Data preprocessing
Min–max normalisation is performed for our raw datasets. Classes are not approximately represented in imbalanced datasets [15]. Hence, the synthetic minority over-sampling technique (SMOTE) is used to create synthetic minority class samples for our normalised datasets. CFS uses Pearson's correlation coefficient to perform dimensionality reduction on the normalised and balanced datasets.
3.2. Proposed customised fuzzy t-norm operator for FRQR
Elimination of redundant features and preserving the quality of the original feature genes are the two main goals of feature selection. Representation of the information system in a concise manner is very much essential for real world applications. Hence the concept of a reduct is introduced that could determine the minimal representation of the original dataset.
3.2.1. Working of FRQR algorithm
The algorithm for FRQR is described as follows: at the beginning of execution of this algorithm, the current best set of attributes represented as a potential reduct is initialised to an empty set. The first step is to compute the fuzzy indiscernibility. The second step in the algorithm is the computation of the tolerance of the attributes using the similarity measure. The fuzzy tolerance relation is used along with the fuzzy t-norm to compute the final reduct. The third step is to compute the fuzzy lower approximation, i.e. generalised by means of an implicator and a fuzzy t-norm. The fourth step is to compute the positive region. The minimal reduct set is computed using the degree of dependency, i.e. the last step in the quick reduct algorithm [16]. This Letter proposes the computation of the indiscernibility relation by using a customised function for Lukasiewicz fuzzy t-norm operator to compute the fuzzy lower approximation.
3.2.2. Computation of reduct set using fuzzy implicator and customised t-norm operator
Fuzzy tolerance, equivalence, and T_equivalence are the various methods used in the computation of the fuzzy indiscernibility. Computation of the minimal reduct set using customised similarity measure is proposed in [14]. This section describes the computation of the minimal attribute subset using the customised function for Lukasiewicz fuzzy t-norm. A fuzzy relation between two patterns ‘p’ and ‘q’ is a mapping such that is a fuzzy set in A. For each , . In fuzzy rough sets, the similarity between any two patterns in a set A is modelled by a fuzzy relation Rat defined as
| (1) |
| (2) |
| (3) |
Equation (1) is called reflexivity, (2) is called symmetricity and (3) is called transitivity relation for all p, q, r in A [17]. Given a triangular norm or t-norm, the concepts of symmetricity and transitivity need not be satisfied. The approximation of a set requires the use of some fuzzy logical counterparts of connectives that are involved in the generalisation of the fuzzy lower and upper approximation. A pair of fuzzy lower and upper approximation operators on a fuzzy set X based on a similarity relation is defined in as
| (4) |
| (5) |
There are two common problems with the fuzzy rough attribute selection using (4) and (5), namely, the complexity of calculating the Cartesian product of fuzzy equivalence classes gets larger and larger in each step and in some cases, the fuzzy lower approximation becomes bigger than fuzzy upper approximation [18]. To solve the above issues, alternate fuzzy lower and upper approximations are proposed in [19, 20] and represented as
| (6) |
| (7) |
where represents the Lukasiewicz implicator (default) used for our proposed method and is represented in (8) as
| (8) |
represents similarity measures available and the proposed method uses the similarity measure represented as
| (9) |
For fuzzy t-norm operators ‘1’ is the neutral element. The region where does not have any impact on the formation of lower approximation membership due to the presence of ‘inf’ operator on it. Hence a region where needs to be found and the lower and upper approximations need to be computed for that region [20]. An operator is called a conjunctor that maps from
| (10) |
where denotes any operation on any two attributes, then (10) satisfies
| (11) |
All sets that satisfy (11) are called the border conjunctors [9]. The fuzzy t-norm operator represented by satisfies the conditions namely single identity in (12), monotonicity in (13), associativity in (14) and commutativity in (15) that can be represented as under:
| (12) |
| (13) |
| (14) |
| (15) |
A border conjunctor that satisfies (10) and (11) is called a t-norm. Equation (16) represents the minimum t-norm, (17) represents the product t-norm and (18) represents the (default) Lukasiewicz t-norm that is used frequently
| (16) |
| (17) |
| (18) |
To improve the statistical parameters such as the accuracy of the classifier, a new customised function for the Lukasiewicz fuzzy t-norm is introduced in (19) as
| (19) |
where [p, q] lies between [0,1]. The maximum value that ‘p’ and ‘q’ can take is 1. Hence at all times
| (20) |
Ignoring the ideal case in (20) where the values of both ‘p’ and ‘q’ will be equal to 1, we can rewrite (18) as
| (21) |
Now, the left-hand side of (19), i.e. can be rewritten as then (19) is rewritten as in (22)
| (22) |
Considering the customised function as represented in (19), it is inferred as
| (23) |
Else (19) returns the value of zero. Hence (19) satisfies the basic condition for fuzzy t-norm in the FRQR algorithm.
3.2.3. Computation of positive region and degree of dependency
For a fuzzy decision system with and , the positive region of D with respect to B is defined as
| (24) |
where The degree of dependency is computed for all the features in the dataset. The final reduct is obtained by taking those feature genes that contribute to the increase in dependency value. The stopping criterion for the algorithm is defined as the point at which an attribute does not contribute to an increase in dependency value and thereby produces the final attribute subset. If P depends totally on Q, then there exists a functional dependency between them. For Q depends on P in a degree denoted by if
| (25) |
where in (25) represents the quality of approximation [14]. The computed dependency value k lies in the range [0 1] where ‘1’ represents total dependency, ‘0’ represents no dependency and any value between ‘0’ and ‘1’ indicates partial dependency. The most significant features are obtained by computing the change in the dependency value when features are removed from the set of candidate gene subsets [14]. High variations in the values indicate that it is a significant feature and needs to be retained and added to the final reduct set. The significance value of zero indicates that the feature can be removed from the reduct set. The output of the proposed method is the reduced gene attributes in the final minimal reduct. The CA, one of the adequate measures in microarray gene expression data gets affected because of the problem of ‘curse of dimensionality’ wherein there are only a few testing and training samples. The solution to this problem is to use the leave-one-out cross validation (LOOCV) strategy for cross validation to compute the CA using a decision stump classifier.
4. Results and discussion
The dataset used for our study is considered as the benchmarked dataset for microarray data used in a number of standard research papers [1, 4, 6, 11–14, 21, 22] and is downloaded from the Kentridge biomedical repository [23]. The binary un-paired dataset samples used for training and testing the classifier are disjoint and non-overlapping. They include leukemia, central nervous system (CNS), lung cancer, and ovarian cancer samples. The binary datasets used for our study consist of unbalanced raw data. Leukemia data consists of 72 samples, CNS data consists of 60 samples, lung cancer or lung carcinoma data consists of 181 patient samples and ovarian cancer data consists of 253 samples. The proposed algorithms are implemented on an Intel Core i7 CPU that has a 3.2 GHz processor and 8 GB RAM running on a 64 bit Windows operating system.
The normalised and SMOTE balanced datasets are reduced for their dimensionality using a correlation-based filter by removing the redundant genes and preserving the informative ones. The dimensionality reduced datasets are subjected to attribute subset selection using the customised function for Lukasiewicz fuzzy t-norm operator on FRQR. The performance of the proposed approach is compared with the conventional FRQR using the decision stump classifier and LOOCV cross validation strategy to generalise the results as the sample size is smaller in cancer gene expression datasets. The performance analysis is done on different datasets using conventional FRQR and proposed customised fuzzy t-norm FRQR and the results are tabulated in Table 1.
Table 1.
Performance analysis on different datasets – conventional FRQR versus proposed customised FRQR
| Dataset | Number of genes in the raw dataset | Number of genes obtained using CFS | Method | No. of feature genes selected | CA, % | FDR | Precision | Recall | F-measure | TP | FN | FP | TN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| leukemia | 7129 | 112 | conventional FRQR | 8 | 87.63 | 0.120 | 0.880 | 0.880 | 0.880 | 44 | 6 | 6 | 41 |
| proposed method | 2 | 94.85 | 0.063 | 0.938 | 0.957 | 0.947 | 45 | 2 | 3 | 47 | |||
| CNS | 7129 | 100 | conventional FRQR | 10 | 69.14 | 0.333 | 0.667 | 0.810 | 0.731 | 34 | 8 | 17 | 22 |
| proposed method | 3 | 76.54 | 0.275 | 0.725 | 0.881 | 0.796 | 37 | 5 | 14 | 25 | |||
| lung cancer | 12,533 | 252 | conventional FRQR | 8 | 96.70 | 0.026 | 0.974 | 0.980 | 0.977 | 147 | 3 | 4 | 58 |
| proposed method | 2 | 98.11 | 0.020 | 0.981 | 0.993 | 0.987 | 149 | 1 | 3 | 59 | |||
| ovarian cancer | 15,154 | 44 | conventional FRQR | 8 | 96.22 | 0.059 | 0.941 | 0.981 | 0.961 | 159 | 3 | 10 | 172 |
| proposed method | 3 | 99.13 | 0.000 | 1.000 | 0.981 | 0.991 | 159 | 3 | 0 | 182 |
TP, true positive; FN, false negative; FP, false positive; TN, true negative.
The false discovery rate (FDR) is the probability of getting a positive test result when the result is actually negative. The formula to compute FDR is given as
| (26) |
The values of precision, recall, and F-measure are found to be better, the CA of the proposed method is found to be higher, FDR (complement of precision) and the number of feature genes in the final reduct set is lesser for all the datasets under study compared to the conventional FRQR method. The scatter plots drawn for the conventional FRQR and customised FRQR show how a feature gene is being influenced by another feature gene and is depicted in Figs. 2 and 3, respectively.
Fig. 2.
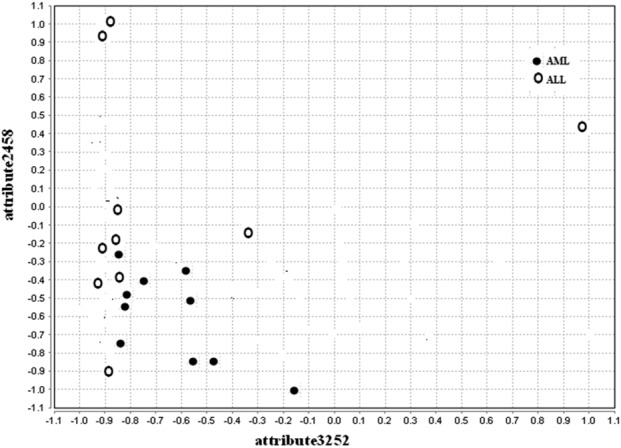
Scatter plot for conventional FRQR for leukemia dataset
Fig. 3.
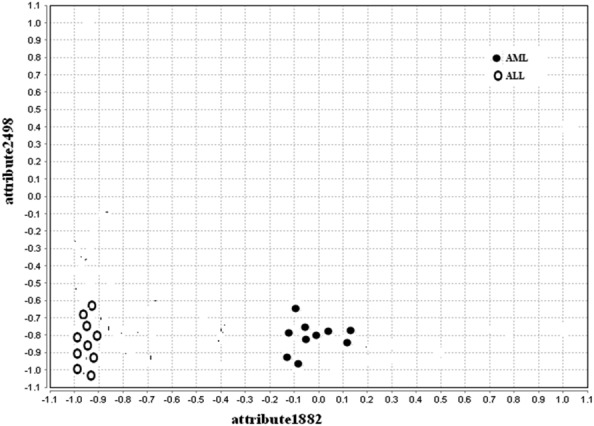
Scatter plot for proposed customised FRQR for leukemia dataset
The execution time is computed for all the four datasets under study. The execution time for leukemia, CNS, lung, and ovarian cancer datasets are 100, 90, 224.9 and 39.6 s respectively. To validate the results, additional measures such as Kappa (ka), mean absolute error (MAE), and root mean squared error (RMSE) are performed for the conventional FRQR and the proposed customised fuzzy t-norm FRQR methods. The Kappa metric is used to make a comparison of observed accuracy against expected accuracy. Higher the value, better the result and hence better the performance of the proposed method. MAE measures the average of absolute differences between the actual and predicted observations where all individual differences have equal weightage. RMSE measures the average magnitude of the error by taking the squared difference between predicted and actual observations. Lower their values, better the result. The values of kappa, MAE, and RMSE are tabulated in Table 2.
Table 2.
ka, MAE, RMSE metrics for conventional FRQR versus proposed customised FRQR
| Dataset | Conventional FRQR | Proposed method | ||||
|---|---|---|---|---|---|---|
| ka | MAE | RMSE | ka | MAE | RMSE | |
| leukemia | 0.752 | 0.147 | 0.340 | 0.900 | 0.089 | 0.225 |
| CNS | 0.377 | 0.365 | 0.475 | 0.526 | 0.347 | 0.420 |
| lung cancer | 0.919 | 0.069 | 0.161 | 0.954 | 0.037 | 0.138 |
| ovarian cancer | 0.924 | 0.064 | 0.191 | 0.983 | 0.036 | 0.097 |
CA is one of the parameters in the field of clinical medicine to evaluate the proposed method. The efficiency of the proposed method is also evaluated using other statistical parameters namely, Matthew's correlation coefficient (MCC), McNemar's test and chi-squared test. MCC is a measure used in machine learning approaches in order to determine the quality of binary classification. It is generally considered as a balanced measure, regardless of the number of instances in each class [24]. The formula to compute MCC is given as
| (27) |
McNemar and chi-squared tests are used to find the statistical significance for paired and un-paired nominal data ,respectively. The values of these metrics are represented in Table 3
Table 3.
MCC, McNemar, chi-squared metrics for conventional FRQR versus proposed customised FRQR
| Dataset | Conventional FRQR | Proposed method | ||||
|---|---|---|---|---|---|---|
| MCC | McNemar chi-squared value (p-value) | Chi-squared test value (p-value) | MCC | McNemar chi-squared value (p-value) | Chi-squared test value (p-value) | |
| leukemia | 0.752 | 0.08 (0.386) | 51.93 (<0.0001) | 0.897 | 0.00 (0.500) | 74.51 (<0.0001) |
| CNS | 0.387 | 3.80 (0.109) | 10.56 (0.0006) | 0.540 | 2.89 (0.213) | 21.44 (<0.0001) |
| lung cancer | 0.920 | 0.04 (0.500) | 174.96 (<0.0001) | 0.954 | 0.02 (0.614) | 188.41 (<0.0001) |
| ovarian cancer | 0.925 | 2.14 (0.096) | 290.71 (<0.0001) | 0.983 | 1.33 (0.248) | 328.22 (<0.0001) |
MCC returns a value in the range −1 to +1. A coefficient value of +1 indicates better prediction, 0 indicates random prediction and −1 indicates total disagreement between the observed and the predicted values. The value of the MCC is higher for the proposed approach for all our datasets under study and hence indicates better prediction over conventional FRQR. McNemar test is performed on disconcordant (lack of agreement in decision class) pairs with 1-degree of freedom. It can be observed that the McNemar test produces McNemar chi-squared values <3.84 (critical value threshold) for all the datasets on pairs of classifiers used for McNemar test and 1-tailed chi-squared test attains statistical significance since it produces ‘p’ value less than 0.005. After a suitable analysis of the above parameters, it can be concluded that the proposed approach using customised fuzzy t-norm operator performs better than the available methods in the literature. The false positive rate (FPR), true positive rate (TPR) are computed and tabulated in Table 4.
Table 4.
TPR, FPR for conventional FRQR versus proposed customised FRQR
| Dataset | Conventional FRQR | Proposed method | ||
|---|---|---|---|---|
| TPR | FPR | TPR | FPR | |
| leukemia | 0.880 | 0.128 | 0.957 | 0.060 |
| CNS | 0.691 | 0.318 | 0.881 | 0.243 |
| lung cancer | 0.987 | 0.081 | 0.993 | 0.048 |
| ovarian cancer | 0.981 | 0.055 | 0.981 | 0.001 |
The TPR for all the datasets under study is higher and FPR is lower for our proposed method compared to conventional FRQR. The receiver operating characteristic area for leukemia, CNS, lung cancer, and ovarian cancer datasets used for our study is 0.910, 0.743, 0.953 and 0.997, respectively, for the proposed customised fuzzy t-norm FRQR method. The proposed method is compared with state-of-the-art attribute selection methods with respect to two aspects, namely, CA, and the number of genes in the reduced subset. The CA and number of genes are presented as the average value obtained across the different datasets under study. They are represented in Table 5.
Table 5.
Comparison with state-of-the-art attribute selection methods
| Attribute selection method | CA, % | Number of genes in the reduced subset |
|---|---|---|
| independent component subspace [3] | 83.00 | 10 |
| neighbourhood approximation [4] | 84.64 | 3 |
| scalable feature selection [5] | 84.64 | 4 |
| CFS-improved binary particle swarm optimisation [6] | 84.53 | 7 |
| max dependency, relevance [7] | 82.83 | 2 |
| CFS-PSO-FRQR [13] | 90.19 | 10 |
| BDE-SVMrankf (binary differential evolution – support vector machine (SVMrankf)) [21] | 91.80 | 4 |
| proposed customised FRQR | 92.16 | 3 |
In the case of all our datasets under study, the proposed customised fuzzy t-norm FRQR method finds a lesser number of informative feature genes and comparatively higher CA compared to many of the available feature selection methods in the literature.
5. Conclusion
This Letter proposes an efficient method for predicting cancer using fuzzy rough machine learning approaches. The proposed method customises the Lukasiewicz fuzzy t-norm operator of FRQR for attribute subset selection. This new technique has reduced the dimensionality of the datasets by using a Pearson's correlation coefficient and the redundant genes are removed by using the customised function for Lukasiewicz fuzzy t-norm operator on the FRQR algorithm. The classification algorithm produces CA of 94.85, 76.54, 98.11 and 99.13% on leukemia, CNS, lung, and ovarian datasets by selecting 2, 3, 2 and 3, feature genes, respectively, for the proposed method. It is evident that the proposed method produces much better accuracy than the other methods available in the literature. The proposed customised fuzzy t-norm operator works well for binary cancer microarray gene expression datasets. Future research is on the way to apply the proposed customised FRQR method that uses the customised fuzzy t-norm operator to multi-class cancer microarray gene expression datasets.
6. Acknowledgments
We would like to express our deep sense of gratitude to the Management team and Chairperson of the Department of Computer Science and Engineering, Amrita Vishwa Vidyapeetham, Coimbatore, India and also the Management, Secretary and Principal of Dr Mahalingam College of Engineering and Technology, Pollachi, India, for supporting us to carry out this research work.
7 References
- 1.Bolon Canedo V., Sanchez Marono N., Alonso-Betanzos A.: ‘Distributed feature selection, an application to microarray data classification’, Appl. Soft Comput., 2015, 30, pp. 136–150 (doi: 10.1016/j.asoc.2015.01.035) [Google Scholar]
- 2.Hannah Inbarani H., Azar A.T., Jothi G.: ‘Supervised hybrid feature selection based on PSO and rough sets for medical diagnosis’, Comput. Methods Programs Biomed., 2014, 113, (1), pp. 175–185 (doi: 10.1016/j.cmpb.2013.10.007) [DOI] [PubMed] [Google Scholar]
- 3.Aziz R., Verma C.K., Srivastava N.: ‘A fuzzy based feature selection from independent component subspace for machine learning classification of microarray data’, Genom. Data, 2016, 8, pp. 4–15 (doi: 10.1016/j.gdata.2016.02.012) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kar S., Sharma K.D., Maitra M.: ‘Gene selection from microarray gene expression data for classification of cancer subgroups employing PSO and adaptive K-nearest neighborhood technique’, Expert Syst. Appl., 2015, 42, (1), pp. 612–627 (doi: 10.1016/j.eswa.2014.08.014) [Google Scholar]
- 5.Jensen R., Parthalain N.M.: ‘Towards scalable fuzzy–rough feature selection’, Inf. Sci., 2015, 323, pp. 1–15 (doi: 10.1016/j.ins.2015.06.025) [Google Scholar]
- 6.Jain I., Jain V.K., Jain R.: ‘Correlation feature selection based improved-binary particle swarm optimization for gene selection and cancer classification’, Appl. Soft Comput., 2018, 62, pp. 203–215 (doi: 10.1016/j.asoc.2017.09.038) [Google Scholar]
- 7.Maji P., Garai P.: ‘On fuzzy-rough attribute selection: criteria of max-dependency, max-relevance, min-redundancy, and max-significance’, Appl. Soft Comput., 2013, 13, pp. 3968–3980 (doi: 10.1016/j.asoc.2012.09.006) [Google Scholar]
- 8.Wang A., An N., Chen G., et al. : ‘Incremental wrapper based gene selection with Markov blanket’. Proc. IEEE Int. Conf. on Bioinformatics and Biomedicine (BIBM), Belfast, UK, 2014, pp. 74–79, doi: 10.1109/BIBM.2014.6999251 [Google Scholar]
- 9.D'eer L., Verbiest N., Cornelis C., et al. : ‘A comprehensive study of implicator–conjunctor-based and noise-tolerant fuzzy rough sets: definitions, properties and robustness analysis’, Fuzzy Sets Syst., 2015, 275, pp. 1–38 (doi: 10.1016/j.fss.2014.11.018) [Google Scholar]
- 10.Zhang X., Mei C., Chen D., et al. : ‘A fuzzy rough set-based feature selection method using representative instances’, Knowl. Based Syst., 2018, 151, pp. 1–14 (doi: 10.1016/j.knosys.2018.04.016) [Google Scholar]
- 11.Shahbeig S., Rahideh A., Helfroush M.S., et al. : ‘Gene selection from large-scale gene expression data based on fuzzy interactive multi-objective binary optimization for medical diagnosis’, Biocybernetics Biomed. Eng., 2018, 38, pp. 313–328 (doi: 10.1016/j.bbe.2018.02.002) [Google Scholar]
- 12.Arunkumar C., Ramakrishnan S.: ‘A hybrid approach to feature selection using correlation coefficient and fuzzy rough quick reduct algorithm applied to cancer microarray data’. Proc. 10th Int. Conf. on Intelligent Systems and Control (ISCO 2016), Coimbatore, India, 2016, pp. 414–419, doi: 10.1109/ISCO.2016.7726921 [Google Scholar]
- 13.Arunkumar C., Ramakrishnan S.: ‘Modified fuzzy rough quick reduct algorithm for feature selection in cancer microarray data’, Asian J. Inf. Technol., 2016, 15, pp. 199–210, doi: 10.3923/ajit.2016.199.210 [Google Scholar]
- 14.Arunkumar C., Ramakrishnan S.: ‘Attribute selection using fuzzy roughset based customized similarity measure for lung cancer microarray gene expression data’, Future Comput. Inf. J., 2018, 3, (1), pp. 131–142 (doi: 10.1016/j.fcij.2018.02.002) [Google Scholar]
- 15.Chawla N., Kevin Bowyer W., Lawrence Hall O., et al. : ‘SMOTE: synthetic minority over-sampling technique’, J. Artif. Intell. Res., 2002, 16, (1), pp. 321–357 (doi: 10.1613/jair.953) [Google Scholar]
- 16.Anarki J.R., Eftekhari M.: ‘Rough set based feature selection – a review’. Proc. 5th Conf. on Information and Knowledge Technology, Shiraz, Iran, 2013, pp. 301–306, doi: 10.1109/IKT.2013.6620083 [Google Scholar]
- 17.Radzikowska A.M., Etieniie Kerre E.: ‘An algebraic characterisation of fuzzy rough sets’. IEEE Int. Conf. on Fuzzy Systems, Budapest, Hungary, 2004, doi: 10.1109/FUZZY.2004.1375698 [Google Scholar]
- 18.Anarki J.R., Eftekhari M.: ‘Improving fuzzy-rough quick reduct for feature selection’. Proc. 19th Iranian Conf. on Electrical Engineering, Tehran, Iran, 2011, pp. 1–6 [Google Scholar]
- 19.Bhatt R.B., Gopal M.: ‘On fuzzy-rough sets approach to feature selection’, Pattern Recognit. Lett., 2005, 26, (7), pp. 965–975 (doi: 10.1016/j.patrec.2004.09.044) [Google Scholar]
- 20.Bhatt R.B., Gopal M.: ‘On the compact computational domain of fuzzy-rough sets’, Pattern Recognit. Lett., 2005, 26, (11), pp. 1632–1640 (doi: 10.1016/j.patrec.2005.01.006) [Google Scholar]
- 21.Apolloni J., Leguizamon G., Alba E.: ‘Two hybrid wrapper-filter feature selection algorithms applied to high-dimensional microarray experiments’, Appl. Soft Comput., 2016, 38, pp. 922–932 (doi: 10.1016/j.asoc.2015.10.037) [Google Scholar]
- 22.Pang S., Havukkala I., Hu Y., et al. : ‘Classification consistency analysis for bootstrapping gene selection’, Neural Comput. Appl., 2007, 16, (6), pp. 527–539 (doi: 10.1007/s00521-007-0110-1) [Google Scholar]
- 23. http://datam.i2r.a-star.edu.sg/datasets/krbd , accessed 10 December 2011.
- 24.Boughorbel S., Jarray F., El-Anbari M.: ‘Optimal classifier for imbalanced data using Matthews Correlation Coefficient metric’, PLoS ONE, 2017, 12, (6), pp. 1–17 (doi: 10.1371/journal.pone.0177678) [DOI] [PMC free article] [PubMed] [Google Scholar]


