Predicting the metabolic capabilities of Synechococcus elongatus PCC 7942 adapted to different light regimes

Abstract

There is great interest in engineering photoautotrophic metabolism to generate bioproducts of societal importance. Despite the success in employing genome-scale modeling coupled with flux balance analysis to engineer heterotrophic metabolism, the lack of proper constraints necessary to generate biologically realistic predictions has hindered broad application of this methodology to phototrophic metabolism. Here we describe a methodology for constraining genome-scale models of photoautotrophy in the cyanobacteria Synechococcus elongatus PCC 7942. Experimental photophysiology parameters coupled to genome-scale flux balance analysis resulted in accurate predictions of growth rates and metabolic reaction fluxes at low and high light conditions. Additionally, by constraining photon uptake fluxes, we characterize the metabolic cost of excess excitation energy. The predicted energy fluxes are consistent with known light-adapted phenotypes in cyanobacteria. Finally, we leverage the modeling framework to characterize existing photoautotrophic and photomixtotrophic engineering strategies for 2,3-butanediol production in S. elongatus. This methodology, applicable to genome-scale modeling of all phototrophic microorganisms, can facilitate the use of flux balance analysis in the engineering of light-driven metabolism.

1. INTRODUCTION

There is significant interest in engineering light-driven metabolism towards the production of fuels and chemicals. Cyanobacteria represent the simplest phototrophs and have been employed to produce a variety of products [38]. Synechococcus elongatus PCC 7942 (hereafter, S. elongatus), a genetically tractable obligate phototroph, has been engineered for the production of a wide variety of chemicals to include 3-hydroxypropinoate [24], succinate [25], and 1,3-propanediol [13]. Despite its classification as an obligate phototroph, this organism has also been engineered for mixotrophic metabolism, using carbon sources such as glycerol [16] and glucose [17] to generate bioproducts of interest. While experimental and computational fluxomics have been central to effective engineering of heterotrophic organisms [2,19], their application to the engineering of phototrophic metabolism has been limited.

Fluxomics contributes to metabolic engineering by identifying the resource partitioning through a metabolic network. Reaction fluxes are determined experimentally via ¹³C metabolic flux analysis (MFA), or computationally using methods such as flux balance analysis (FBA) [39]. Recent developments in ¹³C MFA have resulted in characterization of photoautotrophic metabolic fluxes [51] and the engineering of cyanobacteria such as S. elongatus [15]. Flux balance analysis coupled with genome-scale modeling (GEM) has a long history of facilitating bioprocess design [18], and has the potential to advance the engineering of phototrophic metabolism [27]. Still, despite the availability of several phototrophic GEMs [11], there are few examples of GEMs being employed in the design of light-driven metabolic processes [7].

The potential of a GEM to engineer a metabolic network for bio-production depends on its ability to accurately predict flux through the network. Simple constraints such as the glucose and oxygen uptake rate result in accurate assessments of heterotrophic reaction fluxes [29]. The ability to define the metabolic flux state with as few parameters as possible requires a mechanistic understanding of the governing constraints on the system. Recent modeling in S. elongatus resulted in accurate prediction of photoautotrophic growth through photophysiology constraints [6]. In this study, a mechanistic description of photon uptake coupled with constraints on oxygen evolution resulted in accurate predictions of photoautotrophic growth to include the transition to a linear growth curve as a result of self-shading. With the recent publication of ¹³C MFA reaction fluxes for S. elongatus [15, 1], it is possible to assess the ability of photophysiology constraints to characterize photoautotrophic metabolism.

GEMs can also quantify alternative electron transport (AET) within the metabolic network. Photosynthetic organisms absorb light in excess of basic biomass and maintenance requirements. A fraction of this excitation energy is dissipated upstream of the photosystem as fluorescence, heat or other non-radiative dissipation mechanisms [45]. The remaining fraction is directed to through the photosynthetic apparatus and generates the reductant and chemical energy necessary for growth. Excitation energy in excess of growth requirements is quenched via various alternative electron transport pathways [26]. AET has been shown to constitute up to 40% of the total linear electron flux through the photosystems in cyanobacteria [12]. Characterizing and quantifying AET can facilitate engineering strategies that divert these electrons to bioproducts.

In this study we show constraining a GEM of S. elongatus with the photon uptake rate derived from whole-cell absorbance and the net oxygen evolution rate results in accurate predictions of metabolic fluxes. First, we generate the necessary constraints from the photophysiology of S. elongatus acclimated to two light intensities differing by an order of magnitude. Next, we incorporate these constraints with the GEM to predict growth rates at the two culture conditions. The resulting metabolic reaction fluxes predicted by the model showed good agreement with the experimental ¹³C MFA results. We then use the GEM to assess alternate energy flows in S. elongatus, quantifying excess light energy captured by the system. Finally, we use the modeling framework to characterize existing engineering strategies for 2,3-butanediol production in S. elongatus. Overall we present the governing constraints of photoautotrophic metabolism, obtained by experimentally accessible protocols, that result in accurate prediction of photoautotrophic metabolic reaction fluxes. This methodology, applicable to genome-scale modeling of all phototrophic microorganisms, can facilitate the use of flux balance analysis in the engineering of light-driven metabolism.

2. MATERIALS AND METHODS

2.1. Culture conditions.

Synechococcus elongatus PCC 7942 wild type, stored in our laboratory;s culture collection as AMC06, was cultured at 30°C in 400 mL BG-11 medium in 1 L Roux flasks. Flasks were bubbled with air under continuous illumination in a temperature controlled incubator. Cultures were light acclimated (low light (n=3) at 60 μmol photons m⁻² s⁻¹, high light (n=4) at 600 μmol photons m⁻² s⁻¹) for 72 hours, diluted and grown until mid-exponential phase before being harvested.

2.2. Cell physiology measurements.

Cell densities were manually determined using an improved Neubauer hemocytometer. Growth rates were determined based on the change in cell counts from inoculation to harvest. Cell dry weight was determined by taking 50 mL of culture (n=3) and filtering it onto a GF/C glass microfiber filter (diameter: 47mm). Filters containing cellular biomass and media controls (n=3) were dried at 95°C overnight. Cellular dry weight was determined by subtracting the post-filtration mass from the pre-filtration mass, after normalizing to the media control.

2.3. Determination of cell dimensions.

For imaging, thin pads of 1% (wt/vol) agarose were prepared using Mini-PROTEAN® Tetra Cell Casting Module. From this gel, 1–2 cm square pads were cut and placed onto a microscope slide and 2–5 ul cell culture liquid was added to the pad and let dry. Then a microscope slide cover was gently placed onto of the agarose pad and cells were imaged using a DeltaVision inverted epifluorescence microscope (Applied Precision, Issaquah, WA). Images were captured using a CoolSnap HD charge-coupled device (CCD) camera (Photometrics, Tucson, AZ). Cell length and width were determined using the straight line tool in ImageJ [44]. For high light (n=210) and low light (n=238) acclimated cells the mean and standard deviation were determined and the mean ± 2 standard deviations was used to determine cell volume by modeling the cell shape as a core cylinder capped with two hemispheres according to the following equation:

$$Vol=\pi {\left(\frac{w}{2}\right)}^2\left(l-\frac{w}{2}\right)+\frac{4}{3}\pi {\left(\frac{w}{2}\right)}^3$$ (1)

Where l is the cell length and w is the cell width.

2.4. Pigment extraction.

Cells (4 mL culture) were collected by centrifugation at 10,000 × g at 5°C for 15 minutes. The supernatant was discarded and the cell pellet was frozen at −80°C until processed. Chlorophyll was extracted with 50 μL DMSO and 1950 μL of methanol, incubated in the dark for 30 minutes, and centrifuged at 10,000 × g at 5°C for 15 minutes. The pigment containing supernatant was transferred to a 1 cm path length cuvette. Absorbance spectra were collected used a Cary 60 UV-Vis Agilent spectrophotometer in scan mode (350–800 nm, scan interval of 1 nm). Chlorophyll concentrations were determined using the equations for the appropriate solvent [42].

Phycobilisomes were extracted from the thawed cell pellets by resuspension in 2 mL PBS (10 mM phosphate, 150mM NaCl, pH 7.0) with a protease inhibitor (cOmplete™, Sigma-Aldrich). Cells were lysed by sonication (Fischer Scientific Sonic Dismembrator 500, 50% power, 8 seconds on, 30 seconds off for 5 cycles) with the tube chilled in an ice bath during lysis to prevent overheating. Microscopic observation of post-sonicated samples indicated a lysis efficiency of over 90%. Lysed samples were centrifuged at 45,000 × g at 5°C for 60 minutes. 200 μL of the phycobilisome containing supernatant was transferred to a 96 well plate. Absorbance spectra were collected using an Infinite 200 PRO Multiplate Reader (Tecan) spectrophotometer in scan mode (400–750 nm, scan interval of 1 nm). Phycocyanobilin and apophycocyanobilin concentrations were determined using published extinction coefficients [4] after correcting the well plate path length to a 1 cm equivalent.

2.5. Cellular absorption coefficients.

Cellular absorption coefficients were determined based on published protocols [32]. 1 mL of culture volume was added to 9 mL of BG-11 media and cells were collected by vacuum filtration onto a GF/C glass microfiber filter (47 mm diameter). The filter was placed on top of a 96-well plate with a plate cover along with a negative control consisting of a filter through which 10 mL of BG-11 media had passed. Absorbance spectra were collected using a Infinite 200 PRO Multiplate Reader (Tecan) in scan mode (400–750 nm). Spectra from a total of 6 wells per filter were collected, averaged, blank subtracted and normalized to an OD750 value of 0. The wavelength specific absorption coefficient was determined, along with correcting for filter amplification using the coefficients for Synechococcus WH103 in [32], according to the following equation:

$$a_{\lambda }=2.303\left(0.301\left(A_{\lambda }\right)+0.45\left(A_{\lambda }^2\right)\right)$$ (2)

where A_λ is the absorbance at a given wavelength. The cell normalized absorption coefficient (a*_cell, units: cm² cell⁻¹) and the pigment normalized coefficient (a*_pigm, units: cm² μg⁻¹ pigments) were determined by dividing a_λ by either the total number of cells deposited on the filter or the total pigment mass, respectively, and then multiplying the resulting value by the filter area onto which the cells were deposited (12.7 cm² for the 47 mm diameter GF/C filter).

2.6. Simultaneous oxygen evolution and chlorophyll fluorescence parameters.

Rapid light curves (RLCs) were performed as outlined in [14]. A Walz Dual PAM 100 fluorometer in a temperature controlled custom cuvette holder and a FireSting Optical Oxygen Meter were used for the simultaneous measurement of chlorophyll fluorescence and oxygen evolution. Approximately 30 mL of culture was removed and cells were pelleted by centrifugation (3000 × g, 10 minutes at 30°C). Cell pellets were resuspended in fresh media to the target cell density (HL: 5×10⁸ cells mL⁻¹, LL: 2.5×10⁸ cells mL⁻¹) and kept in the dark for 10 minutes prior to analysis. Dark respiration rates were collected for approximately 10 minutes prior to running RLCs. A red actinic light (635 nm) was used to provide a saturating pulse (600 ms, 10,000 μmol photons m⁻² s⁻¹) for fluorescence measurements. Cells were illuminated for 1 min steps at the following increasing intensities (μmol photons m⁻² s⁻¹):

HL: 0, 8, 24, 43, 75,109,146,195, 259, 339, 435, 547, 674, 844, 1033, 1565, 2386, 2924

LL: 0, 8, 24, 43, 75,109,146,195, 259, 339, 435, 547, 844, 1565, 2386

The chlorophyll fluorescence parameters Fv/Fm, Y(II), qP and NPQ were determined as described [45, 23]. Net oxygen evolution rates were normalized to cell count. Shading in the round cuvette was accounted for by calculating the attenuation across the cuvette path length according the following equation:

$$Q{F}_{I_o}=2{\int }_{\lambda =400}^{\lambda =700}{\int }_{y=0}^{y=r}{I}_{O_{\lambda }}(\lambda )-I_{o_{\lambda }}(\lambda )e^{-a_{cell}^{*}(\lambda )\cdot c\cdot 2{\left(r^2-y^2\right)}^{\frac{1}{2}}}dyd\lambda$$ (3)

where $Q{F}_{I_o}$ is the quantum flux in μmol photons m⁻² s⁻¹ at a given PAR value (I_o), λ is the wavelength, $I_{o_{\lambda }}(\lambda )$ is the fraction of the PAR at a given wavelength λ, r is the radius of the cuvette (0.56 cm), $a_{cell}^{*}$ is the wavelength-specific absorption coefficient in cm² cell⁻¹, and c is the cell density in cells cm⁻³. QF was converted to μmol photons cell⁻¹ s⁻¹ by multiplying $Q{F}_{I_o}$ by the rectangular surface area of the cuvette (width = 0.56 cm, height = 1.15 cm), converted to m² and dividing by the total number of cells in the cuvette. This QF value was used as the independent variable in plots of oxygen-based photosynthesis (Po) versus QF.

2.7. Genome-scale metabolic modeling.

The S. elongatus genome-scale model (GEM) iJB785 [6] was updated to include additional content (Table S1).

Simulations were performed in a similar manner to [6]. The biomass objective function was updated to account for differences in pigments between the low and high light conditions (Table 1). Demand reactions to allow dissipation of excitation energy at PSII and PSI were added to assess the minimum quantum requirement of biomass production:

$$\text{DM}\_\text{chla}\_\text{qy}2\_\text{c}:\text{chla\_qy}2*\_\text{c}\to \text{cholphya\_c}$$

$$\text{DM}\_\text{chla}\_\text{qy}1\_\text{c}:\text{chla\_qy}1*\_\text{c}\to \text{cholphya\_c}$$

Photoautotrophic growth was simulated for a 12 hour time period broken into 20 minute psuedo-steady-state segments. Light was modeled coming from the side of the flask. The Roux flasks had approximately 375 mL of culture at the time of the experiments which resulted in a light-facing surface area of 80 cm² and a path length of 4.7 cm. At the beginning of each simulation, the appropriate constraints were updated. First, the total biomass in the culture was divided by the cell dry weight to determine the total cells in the culture. Next, the photon uptake rate was determined by dividing the culture into 50 slices along the 4.7 cm path length. These slices were considered thin enough that cell shading was assumed to be negligible. Thus, we used the spectral distribution of photon flux for the given light source at the experimental irradiance (I₀(λ)), the cell specific spectral absorption coefficient $\left(a_{\lambda }^{*}\right)$, and the cell count, to determine the photon uptake flux (I_a) in units of μmol photons (time interval)⁻¹ using the following equation:

$$I_a=\frac{cell}{SA}{\int }_{400}^{700}{I}_0(\lambda )a_{cell}^{*}(\lambda )d\lambda$$ (4)

where cell is the total number of cells in the slice and SA is the light-facing surface area of the slice. Light attenuated in one slice was removed from I₀(λ) for the subsequent slices, accounting for shading along the culture path length. A running total of the absorbed light was used to set the reaction bounds of the photon exchange reactions in the GEM.

Table 1.

Physiology parameters of S. elongatus acclimated to low and high light.

	Growth rate (h−1)	Cell volume (μm3)	pgDW cell−1
Low Light	0.047 ± 0.004	3.4 ± 0.6	1.3 ± 0.2
High Light	0.081 ± 0.015	2.8 ± 0.3	1.0 ± 0.2

The P_O vs. QF curves were fit to a Platt [41] equation for photosynthesis prediction (P), using quantum flux as the independent variable.

$$P=P_{max}\left(1-e^{-\frac{\alpha \times QF}{P_{max}}}\right)e^{-\frac{\beta \times QF}{P_{max}}}$$ (5)

P_max is the maximum photosynthetic rate, α and β are the parameters that describe the initial slope of the curve, and the photoinhibition (if present), respectively. These curves were used to determined the oxygen evolution rate at each slice. The total oxygen evolution across the culture path length was used to set the bounds of the oxygen exchange reaction in the GEM (reaction ID: EX_o2_e).

Non-growth associated maintenance (NGAM) was calculated from the experimental dark respiration rate. This value was set as the lower bound for an fictional plastoquinone oxidase (reaction ID: NGAM), which forces a minimal amount of reductant mediated oxygen consumption consistent with the observed dark respiration rate.

The simulation was performed by maximizing the BOF reaction using the parsimonious FBA function [28] as implemented in COBRApy [8]. The flux through this reaction is equal to the biomass accumulation in milligrams over the 20 minute time interval. This biomass was added to a running total of the total culture biomass and used to parameterize the next 20 minute simulation interval. All calculations and simulations were performed using in-house scripts developed in IPython [40].

2.8. Comparison with ¹³C isotopically-nonstationary metabolic flux analysis.

For low light simulations, the predicted flux vector from the model simulation was divided by the flux through the RPBCcx model reaction (RubisCO carboxylase) and multiplied by 100. The experimental data was normalized to 100 units of flux through the RUBP + CO2 → 3PGA + 3PGA reaction in Supplemental Table A2 for wild type S. elongatus PCC 7942 in [15]. For high light simulations, the same process was applied, except fluxes were normalized to the sum of the CO₂ and bicarbonate exchange fluxes, multiplied by 100, and compared with the experimental fluxes reported in Supplemental Table 5 in [1].

3. RESULTS

In this study we set out to assess the ability of genome-scale modeling coupled with photophysiology constraints to predict metabolic capabilities in S. elongatus. To this end, we first collected the necessary physiology data necessary to parameterize the models. This resulted in a comprehensive comparison of low versus high light acclimated cultures. Next, we integrated these data as constraints on the model simulations, comparing model simulations with in vivo growth rates and fluxes. Finally, we assess the alternate energy flows through the photosystems as a result of the absorption of excess excitation energy.

3.1. Photoacclimation of S. elongatus PCC 7942..

S. elongatus was acclimated and cultured at a high light condition of 600 μmol photons m⁻² s⁻¹ (HL, n=4) and a low light condition of 60 μmol photons m⁻² s⁻¹ (LL, n=3). Specific growth rates were 0.081 ± 0.015 and 0.047 ± 0.004 hr⁻¹ respectively for HL and LL cultures. While cells grown at both light levels had approximately the same cell width (1.2 ± 0.1 and 1.1 ± 0.1 μm at HL and LL respectively), LL cells were significantly longer resulting in a 20% increase in cell volume at LL (Table 1).

There were significant differences in light harvesting pigments as a result of photoacclimation. Total pigments (phycocyanin (PC), allophycocyanin (APC) and chlorophyll a (chla) at LL were 4.9 fold higher than at HL (Table 2). Chla and APC increased at a similar rate (3.4 and 3.8 fold respectively). Almost all chla in S. elongatus is contained within the photosystems [48] and APC is a linker pigment-protein complex physically and energetically connecting the light harvesting PC with the photosystems. Thus, this increase in chla and APC is likely attributed to an increase in the number of PSI and PSII complexes present at LL. The light harvesting pigment-protein complex PC increased 5.7 fold at LL compared to HL. The larger-fold increase in PC versus APC suggests not only did the number of phycobilisomes increase but the rod length of each phycobilisome increased at LL compared to HL. The phycobilisomes constituted 28% of the cellular biomass at LL compared to 7% at HL.

Table 2.

Comparison of pigments in S. elongatus acclimated to low and high light.

							Ratios (LL:HL)
	Chl a (pg/cell)	PC (pg/cell)	APC (pg/cell)	PC:Chl a	APC:Chl a	PC:APC	Total pigments	Chl a	PC	APC
Low light	0.037 ± 0.002	0.29 ± 0.05	0.08 ± 0.02	7.8	2.2	3.6	4.9	3.4	5.7	3.8
High light	0.011 ± 0.000	0.05 ± 0.01	0.02 ± 0.00	4.6	1.9	2.4

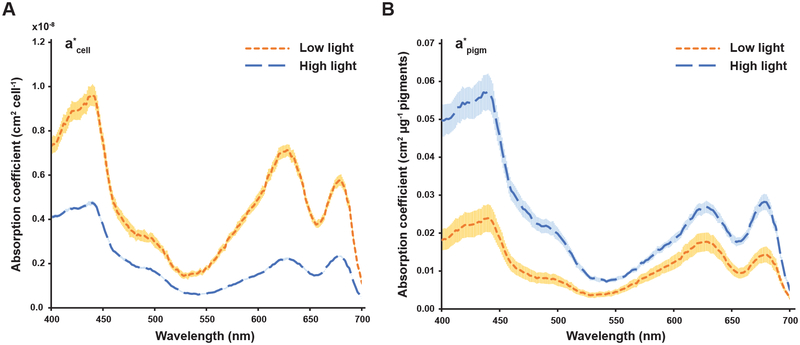
The pigment content and composition of the cell dictates its light harvesting capacity. This cell-specific absorption coefficient is an important modeling parameter as it determines the photon uptake rate and the extent of self-shading that occurs in the culture. We compared the cell normalized absorption coefficient (a*_cell) and the pigment normalized coefficient (a*_pigm) at both light levels (Fig. 1). LL acclimation resulted in 2.3 times more light absorbed per cell than the HL cells, despite the 4.9 fold increase in total pigments. This decrease in light capture efficiency on a per-pigment basis is illustrated in the LL to HL a*_pigm ratio of approximately 0.5 (Fig. 1B, area under the curve: HL: 7.4 vs LL: 3.6 cm² μg⁻¹ nm⁻¹). Thus, while low light acclimation allowed S. elongatus to absorb more light per cell, there were diminishing returns with respect to the resources needed to harvest the light energy.

Figure 1.

Cell- and pigment-specific absorption coefficients for S. elongatus acclimated to low and high light. (A) Cell-specific absorption coefficient. (B) Pigment-specific absorption coefficient. The pigment mass includes phycocyanin, allophycocyanin and chlorophyll a. Shaded areas represent one standard deviation from the mean (HL n=4, LL n=3).

3.2. Photophysiology of S. elongatus at low and high light.

As the GEM requires quantitative incorporation of photophysiology constraints, we converted both the photon uptake and the photosynthesis versus irradiance (P vs. I) curve into a model-compatible format. The photon uptake rate is derived from the PAR spectrum and the a*_cell values. The PAR spectrum is a wavelength density function describing the relative distribution of photons. For example, a red LED exclusively delivers photons in the 600–700 nm range while a white LED distributes the photons over a broader range of wavelengths. The a*_cell describes the wavelength-specific attenuation of light. For example, the cyanobacterial light harvesting pigment phycocyanin preferentially captures orange and red photons and is responsible for the absorption maximum at 620 nm in Fig. 1. Therefore, the intersection of the PAR spectrum and the a*_cell describes the cell-specific attenuation of light, which is the photon uptake rate.

We simultaneously measured chlorophyll fluorescence parameters and oxygen evolution using a rapid light curve (RLC) protocol [14]. In an improvement over previous photoautotrophic modeling of S. elongatus [6], we converted the incident light (photosynthetically available radiation, PAR) to the quanta of light absorbed by the cells (quantum flux, QF). This representation is necessary to convert between light sources of different spectral quality. In the previous study [6], the P vs. I curve was determined with a white LED and the culture light source was a fluorescent lamp. For S. elongatus, these light sources result in similar QF rates. In this study, the oxygen evolution and fluorescence were collected using a red actinic light, while the cells were cultured under fluorescent light. These light sources have dramatically different spectral qualities; thus, necessitating a conversion.

Upon conversion the P vs. I curve becomes a P vs. QF curve and describes the maximum photosynthesis rate as a function of photon uptake. In this study we used oxygen evolution as a proxy for photosynthesis (P_O). While a culture under full diurnal, solar irradiance may experience a wide variety of QF values, constant light cultures only experience a small section of the P_O vs. QF curve. Thus, the only relevant section of the curve is the maximum QF (QF_max), representative of photon capture rates of cells closest to the light source, and the minimum QF (QF_min), representative of the photon capture rate at the point farthest from the light source, attenuated by cell shading. Thus, we report both the maximum QF (QF_max), representative of photon capture rates of cells closest to the light source, and the mean QF (QF_mean), representative of the average photon capture rate across the full path length.

To induce sufficient fluorescence signal, PAM measurements often require high cell densities. The resulting increase in cell shading decreases the quanta of light absorbed across the path length of the sample cuvette. In an improvement over the previous modeling effort [6], we calculated the photon uptake accounting for cuvette shape, path length, cell density and cellular pigmentation [50]. This transformation dramatically affected the calculated oxygen evolution rate at a given photon absorption rate (P_O vs.QF) (Fig. S1).

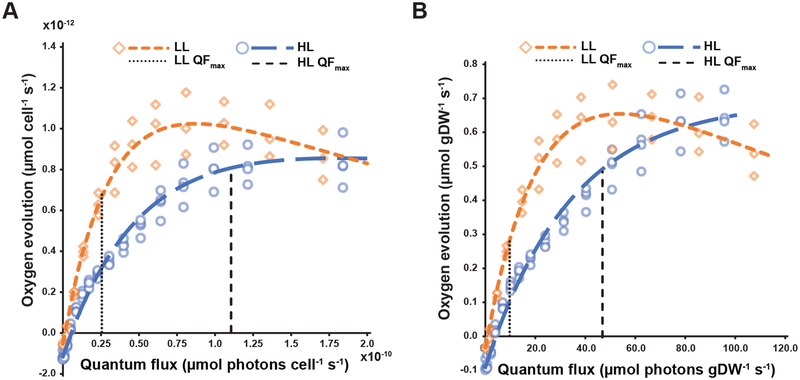
P_O versus QF curves showed the LL acclimated cells had a significantly steeper light limited slope of photosynthesis, α, and a higher maximum photosynthetic rate, P_max, compared to HL cultures (Fig 2A). This resulted in similar cell-specific maximum oxygen evolution rates at the experimental QF for the two light levels with the HL P_O at QF_max approximately 20% higher than the LL condition (Table 3). Comparing the mean oxygen evolution rates, this difference increases to almost 40%, quantifying the impact of cell shading on culture productivity. When the P_O versus QF curves were normalized to gram dry cell weight, the difference in mean oxygen evolution rate increased to 75% (Fig. 2B), which is similar to the difference in specific growth rate (72%, Table 1).

Figure 2.

Oxygen evolution versus quantum flux for S. elongatus acclimated to low and high light. (A) Cell-specific P_o versus QF curves. (B) Dry cell weight-specific P_o versus QF curves. Vertical dashed lines represent the maximum quantum flux received by the cultures at the experimental irradiance. Abbreviations. LL: low light, HL: high light, QF: quantum flux.

Table 3.

Comparison of photosynthetic rates in S. elongatus acclimated to low and high light. The chlorophyll fluorescence parameter qL is reported for QF_mean.

							Ratios (HL:LL)
	QFmax*	QFmean*	${\text{P}}_{{\text{o}}_{\text{max}}}$†	${\text{P}}_{{\text{o}}_{\text{mean}}}$†	Fv/Fm	qL	${\text{P}}_{{\text{o}}_{\text{max}}}$	${\text{P}}_{{\text{o}}_{\text{mean}}}$
Low Light	2.5×10−11	1.6×10−11	6.6 ± 0.8×10−13	4.6 ± 0.5×10−13	0.30	0.93	1.2	1.4
High Light	1.1×10−10	6.0×10−11	8.1 ± 0.7×10−13	6.3 ± 0.4×10−13	0.20	0.71

^*μmol photons cell⁻¹ s⁻¹

^†μmol O₂ cell⁻¹ s⁻¹

Interpretation of chlorophyll fluorescence measurements in cyanobacteria differs from that in algae and higher plants [46, 35]. As such, we report the maximum quantum yield of PSII (Fv/Fm), the effective quantum yield of PSII as a function of QF (Y(II)), and the fraction of open reaction centers (qL) (Table 3 and Fig. S2). However, the values were not quantitatively integrated with our model simulations. S. elongatus PCC 7942 lacks the orange carotenoid protein that confers the blue light activated phycobilisome fluorescence quenching mechanism in cyanobacteria [20] and we did not observe non-photochemical quenching (NPQ) induced fluorescence in either acclimation condition. The effective quantum yield was approximately two-fold higher for the LL acclimated cells (0.33 ± 0.01 vs. 0.15 ± 0.01 at LL and HL respectively), suggesting an increase in excitation energy diverted to PSI, consistent with previous observations in cyanobacteria [35].

3.3. Genome-scale modeling of S. elongatus at low and high light.

The photophysiology results were translated into modeling constraints to simulate photoautotrophic growth of S. elongatus. The a*_cell coupled with the experimental PAR intensity and spectral quality of the fluorescent light was used to determine the photon uptake constraint for the simulations. This uptake value, equivalent to QF, was used to determine the oxygen evolution rate of the culture. This value constrained the oxygen exchange flux for the simulations. The biomass objective function (BOF) [9] defines which metabolites and in what ratio must be synthesized to generate the macromolecular cellular components necessary for growth. We updated the BOF to reflect the differences in pigment mass between the two growth conditions prior to performing simulations.

The quality of the model simulations depends on the accuracy of the experimental photophysiology parameters. Thus, we not only simulated growth using the mean values, but also the upper bound (UB) and lower bounds (LB) of the P_o vs. QF curves, a*_cell and dry cell weight (pg cell⁻¹). As the experimental growth curves are based on cell counts, the dry cell weight converts the biomass accumulation predicted by the model to cell counts; thus, having an impact on the accuracy of the model growth rate predictions.

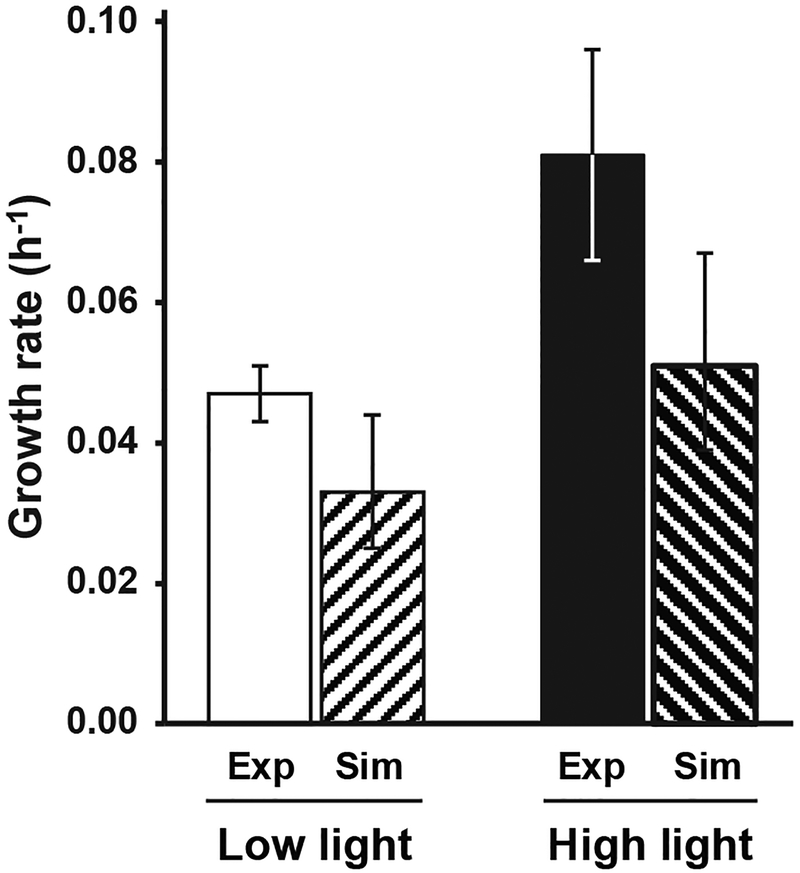
The model predicted a LL mean growth rate of 0.033 h⁻¹(UB: 0.044, LB: 0.025) compared to an experimental value of 0.047 ± 0.004 h⁻¹ representing a 30% underestimation by the model (Fig. 3). For the HL condition the model predicted a mean growth rate of 0.051 h⁻¹ (UB: 0.067, LB: 0.039) compared to an experimental value of 0.081 ± 0.015 h⁻¹ representing a 38% underestimation by the model (Fig. 3). While the upper bound of the simulations values approached the range of the experimental observations, the model tended to underestimate the growth rate at both high and low light.

Figure 3.

Experimental versus simulated growth rates for S. elongatus acclimated to low and high light. For experimental values, error bars represent the standard deviation (HL: n=4, LL: n=3). For the simulation values, the error bars represent the model upper and lower bounds of the model predictions based on the error of the experimental inputs. Abbreviations. Exp: experimental, Sim: simulated.

We explored whether or not maintenance energy requirements forced upon the model could explain the growth rate discrepancies. Maintenance energies in phototrophs differs from that of heterotrophs as the energy source, light, is uncoupled from the carbon source, inorganic carbon. Thus, as long as the culture is not light-limited, maintenance energy costs will not affect growth rate.

Growth-associated maintenance (GAM), represented as growth-dependent ATP consumption, has been inconsistently applied to phototrophic GEMs. Genome-scale models of the cyanobacterium Synechocystis sp. PCC 6803 include GAM values ranging from 53 to 1.3 mmol ATP Gdw⁻¹ h⁻¹ [34, 21]. GAM requirements in our S. elongatus GEM include a growth associated maintenance cost of 30 mmol ATP gDW⁻¹ h⁻¹; however, this is a largely arbitrary value. Our GEM sets the non-growth associated maintenance (NGAM) to the dark respiration rate. This value represents the residual reductant-mediated oxygen consumption that is necessary to maintain viability in the absence of light. This value varies with the incident irradiance. We observed dark respiration rates of 0.41 and 0.15 mmol O₂ gDW⁻¹ h⁻¹ for S. elongatus at HL and LL respectively; with a corresponding reductant consumption rate of 4 mmol electrons per 1 mmol O₂. Finally, there is an NGAM cost associated with the repair of the photosystem II (PSII) D1 subunit. This subunit is damaged at a rate proportional to PSII flux [3], is independent of growth rate, and incurs an ATP and GTP cost at the ribosome to biosynthesize a replacement subunit.

Upon removing all GAM and NGAM requirements, the growth rate was unchanged at LL and HL. Additionally, we quantified the energy in excess of growth and maintenance requirements by fixing the growth rate at the maximum value and optimizing for either an ATP hydrolysis reaction or a plastoquinone-mediated oxygen consumption reaction. At LL, an ATP hydrolysis flux of 19 mmol ATP gDW⁻¹ h⁻¹ and a respiratory flux of 0.7 mmol electrons gDW-1 h⁻¹ could be sustained above and beyond growth and maintenance requirements. At HL, these values increased to 122 mmol ATP and 2.0 mmol electrons gDW⁻¹ h⁻¹, suggesting the cultures are not light limited at either irradiance. Thus, the growth rate discrepancy between our simulations and the observed experimental values was not due to excessive maintenance energy requirements forced on the model.

3.4. Comparison of GEM predicted reaction fluxes with ¹³C MFA.

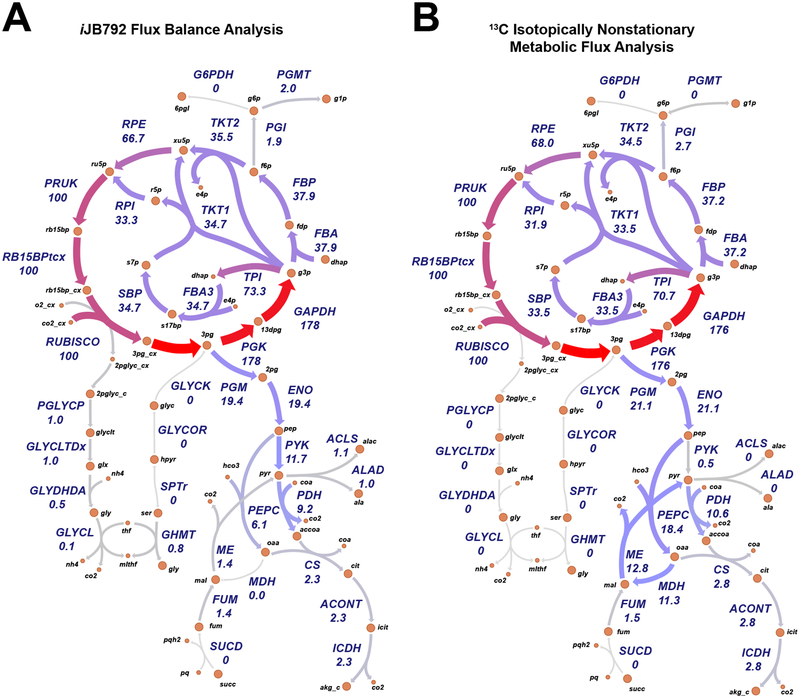
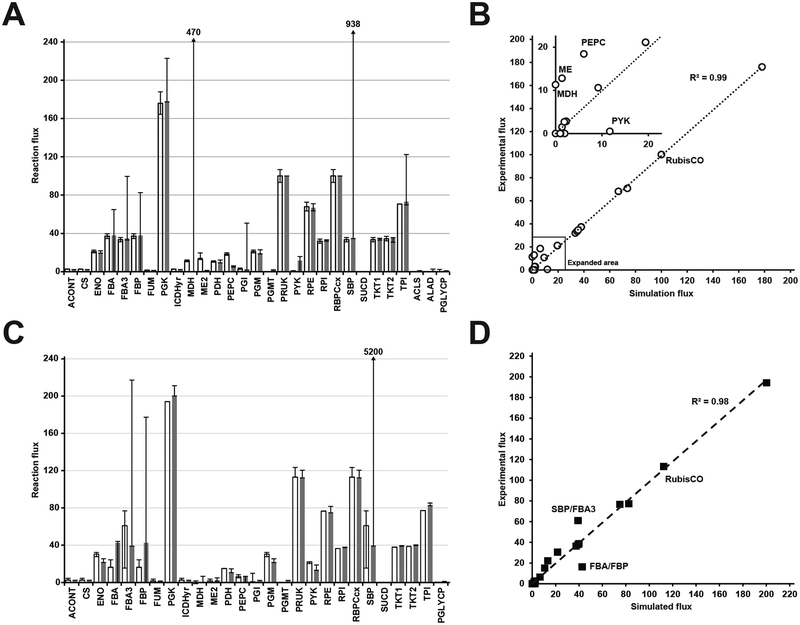
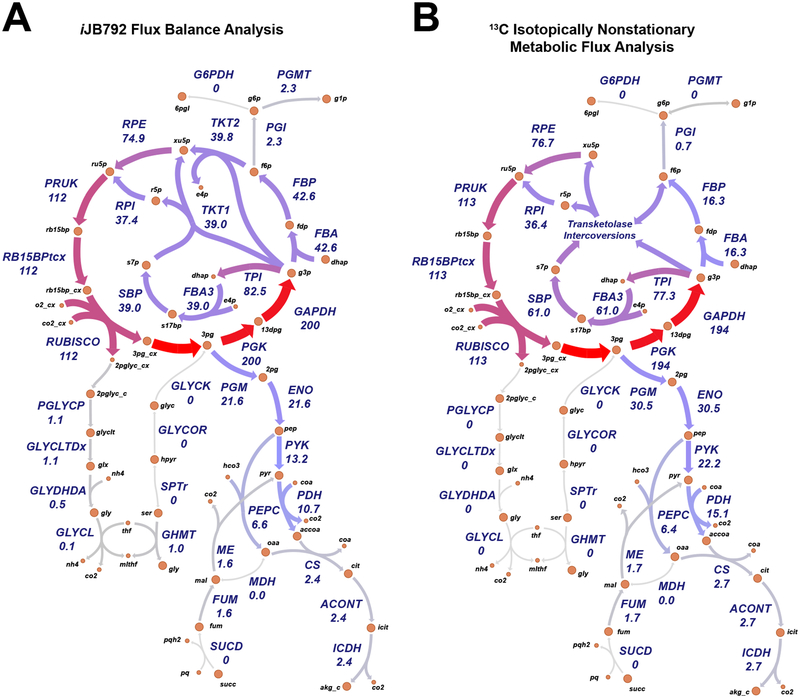
While growth rate can be inferred from empirical models, genome-scale models have the advantage of predicting the flux for all biochemical reactions in the metabolic network. In the case of S. elongatus, constraining the oxygen evolution rate with net P_O, the photon uptake rate with QF and the biomass objective function with the light-condition-specific cellular composition, reaction fluxes are predicted for 861 intracellular reactions. Recent studies have used ¹³C metabolic flux analysis (MFA) to experimentally determine the reaction flux for central metabolism in S. elongatus [15, 1]. We compared our LL condition predicted reaction fluxes with those published for S. elongatus at a similar growth rate [15], normalized to 100 units of RubisCO carboxylase flux to account for the slight difference in growth rate. The predicted reaction fluxes, determined using parsimonious FBA (pFBA) [28], showed remarkable similarity to the experimental values (Fig. 4 and Fig. 5A, B). The primary difference was in metabolic fluxes surrounding the malate dehydrogenase (MDH); a reaction that was inferred from the ¹³C MFA data, but to date the gene responsible for catalyzing this reaction is unidentified in S. elongatus PCC 7942.

Figure 4.

Simulated versus experimental metabolic reaction fluxes for S. elongatus at low growth rates. (A) Predicted fluxes at low light by the S. elongatus genome-scale model iJB792. (B) Experimental reaction fluxes for S. elongatus as reported in [15]. Metabolic reactions and metabolites are indicated by their BiGG identifier (bigg.ucsd.edu). Flux values normalized to 100 units of RubisCO carboxylase flux are shown below the reaction abbreviations.

Figure 5.

Correlation between simulated and experimental metabolic reaction fluxes for S. elongatus. (A) Comparison of low light predicted fluxes (gray bars) and experimental fluxes (white bars) reported in [15]. Flux ranges determined by flux variability analysis are shown for the predicted fluxes. Upper bounds that exceed the Y-axis scale are indicated by an arrow and the upper bound flux value. (B) Correlation between low light predicted fluxes and experimental fluxes reported in [15]. (C) Comparison of high light predicted fluxes (gray bars) and experimental fluxes (white bars) reported in [1]. Flux ranges determined by flux variability analysis are shown for the predicted fluxes. Upper bounds that exceed the Y-axis scale are indicated by an arrow and the upper bound flux value. (D) Correlation between high light predicted fluxes and experimental fluxes reported in [1]. Metabolic reactions and metabolites are indicated by their BiGG identifier (bigg.ucsd.edu). For (A) and (B), flux values are normalized to 100 units of RubisCO carboxylase flux. For (C) and (D) flux values are normalized to 100 units of inorganic carbon uptake. Abbreviations: ACONT: aconitase, CS: citrate synthase, ENO: enolase, FBA: fructose-bisphosphate aldolase, FBA3: sedoheptulose 1,7-bisphosphate D-glyceraldehyde-3-phosphate-lyase, FBP: fructose-bisphosphatase, FUM: fumarase, PGK: phosphoglycerate kinase, ICDH: isocitrate dehydrogenase, MDH: malate dehydrogenase, ME: malic enzyme, PDH: pyruvate dehydrogenase, PEPC: phosphoenolpyruvate carboxylase, PGI: glucose-6-phosphate isomerase, PGM: phosphoglycerate mutase, PGMT: phosphoglucomutase, PRUK: phosphoribulokinase, PYK: pyruvate kinase, RPE: ribulose-5-phosphate 3-epimerase, RPI: ribose-5-phosphate isomerase, SBP: sedoheptulose-bisphosphatase, SUCD: succinate dehydrogenase, TKT1: transketolase (S7P → R5P + X5P), TKT2: Transketolase (F6P → E4P + X5P), TPI: triosephosphate isomerase, ACLS: acetolactate synthase, ALAD: L-alanine-dehydrogenase, PGLYCP: phosphoglycolate phosphatase.

We compared our HL predicted reaction fluxes with those published for S. elongatus PCC 7942 at near optimal growth rates [1]. Again, pFBA flux predictions showed good agreement with the experimental values (Fig. 6 and Fig. 5C, D). The primary discrepancies were in the phosphatase reactions in the Calvin-Benson cycle. However, the net flux into and out of these reactions were in agreement. Overall, the GEM flux predictions constrained by photophysiology constraints were consistent with ¹³C MFA results across the range of observed growth rates.

Figure 6.

Simulated versus experimental metabolic reaction fluxes for S. elongatus at high growth rates. (A) Predicted fluxes at high light by the S. elongatus genome-scale model iJB792 at low light. (B) Experimental reaction fluxes for S. elongatus as reported in [1]. Metabolic reactions and metabolites are indicated by their BiGG identifier (bigg.ucsd.edu). Flux values normalized to 100 units of inorganic carbon uptake are shown below the reaction abbreviations.

Using flux variability analysis (FVA), we explored whether or not alternate optimal solutions existed for the LL and HL models. For both LL and HL conditions, FVA ranges were narrow for all reactions except those connected to an ATP or reductant consuming reaction (Fig. 5a,c). As discussed above, both conditions have ATP and reductant pools in excess of growth and maintenance requirements. As a result, the FVA ranges for these reactions are wide as the available energy pools can drive flux through these energy consuming reactions. Therefore, the discrepancy in flux predictions are likely a result of the minimization of total flux performed by pFBA.

3.5. Predicted excitation energy routes in S. elongatus.

The GEM’s biomass objective function defines the energetic requirements for growth down to the metabolite level. Comparing constrained versus unconstrained photon uptake enabled an assessment of excitation energy absorbed in excess of biosynthesis and maintenance needs. We simulated growth using the upper bound constraints as they more closely recapitulated in vivo growth rates and thus, realistic energy needs.

At low light, with a QF of 2.0×10⁻¹¹ μmol photon cell⁻¹ s⁻¹, the model where all excess excitation energy can be dissipated upstream of the photosystems (unconstrained) predicted only 33% of the excitation energy was necessary to satisfy the electron needs for biomass production and maintenance. We then constrained the photon uptake to account for the entire quanta of absorbed photons. The GEM includes experimentally determined wavelength-specific energy transfer efficiencies [48]. Based on these values and the emission spectra of the growth light, approximately 30% of the QF is lost before reaching the reaction centers. This quanta, along with the biomass and maintenance requirements accounted for 63% of the absorbed photons. The remaining 37% was consumed by alternative electron transport (AET). At high light, with a QF of 7.5×10⁻¹¹ μmol photon cell⁻¹ s⁻¹, the unconstrained model predicted only 11% of the excitation energy was necessary to satisfy the electron needs for biomass production and maintenance. After accounting for wavelength-specific energy transfer efficiencies, 58% of the absorbed QF was consumed by AET.

The AET predicted by the model depends on their relative metabolic cost. The simulations predicted relatively high flux through PSI, even at low light. The model includes a basal PSI superoxide generation rate of 1% [49], while PSII includes a D1 repair cost proportional to flux. The model flux predictions preferentially routed excitation energy through PSI since the combined action of superoxide dismutase and catalase detoxifies the ROS to water with no energy input required. Compared to the unconstrained simulation, the constrained simulation predicted an increase in charge recombination at PSII which increases damage to the PSII D1 protein. This damage is mitigated by de novo synthesis of a new protein at a significant ATP/GTP cost at the ribosome. The model predicted increased cyclic electron flow around PSI is required to generate the chemical energy necessary for D1 protein biosynthesis (Table 4). Thus, the D1 repair cost determines both the predicted bifurcation of excitation energy between PSII and PSI and the cyclic electron flow rate, balancing ATP and reductant ratios necessary to satisfy photodamage mitigation and repair mechanisms. A summary of predicted excitation energy routing, D1 repair costs and quantum yields of carbon fixation and oxygen evolution are shown in Table 4.

Table 4.

Predicted excitation energy flow in S. elongatus acclimated to low and high light. ${\Phi }_{{\text{CO}}_2}$: quantum yield of net carbon fixation, ${\Phi }_{{\text{O}}_2}$: quantum yield of net oxygen evolution. Abbreviations: ET: energy transfer, PSII: photosystem II, PSI: photosystem I, CEF: cyclic electron flow, CR: charge recombination.

	Fraction of absorbed quanta									State Transition
	ET loss	PSII	PSI	CEF	PSII CR	PSI/PSII	D1 repair cost1	${\Phi }_{{\text{CO}}_{\text{2}}}$2	${\Phi }_{{\text{O}}_2}$2	PSI:PSII3	Y(II)4
High light	0.31	0.09	0.60	0.54	0.04	6.7	3.2×10−10	0.009	0.010	2.1	2.1
Low light	0.29	0.17	0.54	0.36	0.03	3.2	0.6×10−10	0.028	0.031

¹μmol ATP cell⁻¹ s⁻¹

²μmol × μmol⁻¹ photon

³(High light PSI/PSII)x(Low light PSI/PSII)⁻¹

⁴(Low light Y(II))x(High light Y(II))⁻¹

3.6. Model-driven engineering of 2,3-butanediol production in S. elongatus.

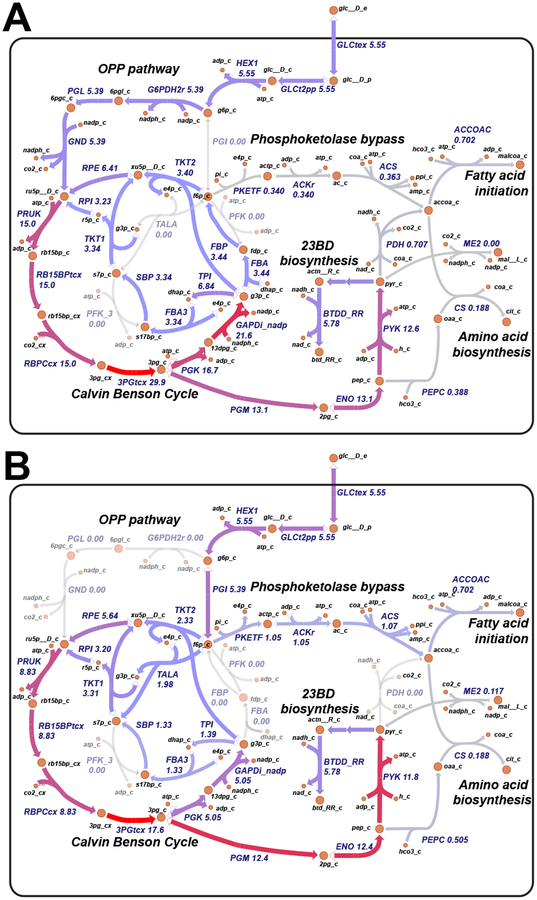
The chemical precursor (R,R)-2,3-butanediol (23BD) has been sccussfully produced in S. elongatus via both phototrophic [37] and photomixotrophic strategies [31, 17]. We explored the ability of the photophysiology constrained GEM to optimize 23BD production in S. elongatus. We added the 23BD biosynthsis pathway to the GEM (Dataset S1) and removed the non-network constraints. These constraints are restrictions on pathway usage and magnitude that were necessary to recapitulate published in vivo gene essentiality data [43, 6]; however, the organism can be engineered to overcome these constraints. The model suggested an optimal solution that uses the phosphoketolase (PKT) pathway to bypass lower glycolysis (Fig. 7b). Previous modeling in S. elongatus also suggested this pathway was optimal; however, based on the essentiality of lower glycolytic enzymes, it was concluded this bypass was not active during photoautotrophic conditions [6]. PKT uses the Calvin-Benson-Bassham (CBB) cycle intermediates frucose-6-phosphate (F6P) or xyulose-5-phosphate as substrates. It has been hypothesized the lack of available substrates, due to high CBB flux, may explain the lack of PKT flux. S. elongatus engineered to consume exogenous glucose was shown to have an elevated F6P pool [17]. Thus, hypothesizing an overexpresed PKT pathway could tap into this F6P pool, we performed an in silico comparison of the PKT pathway to the published oxidative pentose phosphate (OPP) engineered pathway [17] for converting exogenous glucose into 23BD (Fig. 7a,b).

Figure 7.

Comparison of the phosphoketolase engineered pathway with oxidative pentose phosphate pathway. (A) Engineered pathway as described in [17] that routes extracellular glucose through the oxidative pentose phosphate toward 2,3-butanediol production. (B) Engineered pathway as described in this study that routes includes a phosphoketolase bypass toward 2,3-butanediol production. Metabolic reactions and metabolites are indicated by their BiGG identifier (bigg.ucsd.edu). Flux values are in units mmol gram⁻¹ glucose uptake.

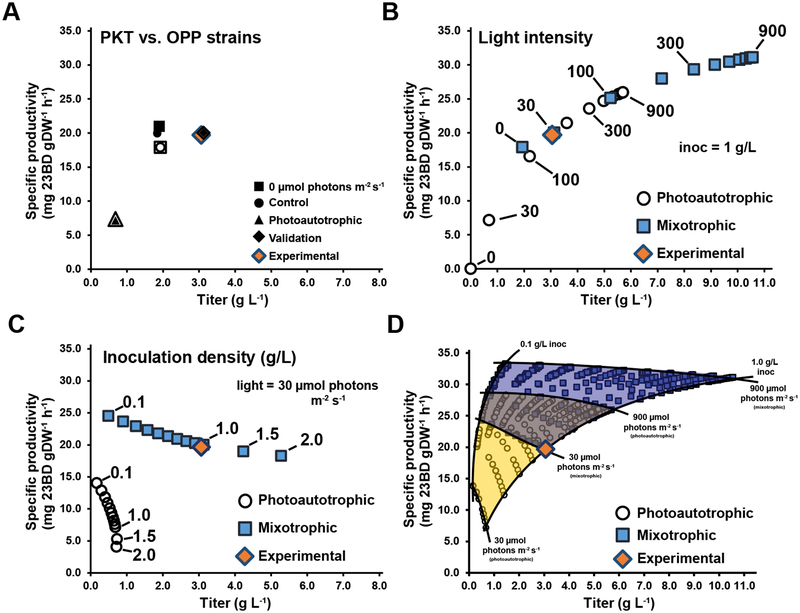
First, using the model as a framework, we characterized the OPP engineered pathway results to derive the necessary parameters for comparison. Based on the published culture conditions, the feedstock was likely low light acclimated (30 μmol photon m⁻² s⁻¹); thus, we used the photophysiology values (a*_cell, PO v. QF, pigment composition, etc.) from our LL acclimated culture as simulation parameters. Using the published results from Kanno et.al. [17], we determined the glucose uptake rate of the optimized strain was approximately 0.29±0.1 mmol glucose gDW⁻¹ h⁻¹ during the first 3 days of culturing. Using a value of 0.27 mmol glucose gDW⁻¹ h⁻¹ and the biomass production rate set to 20% of the maximum, the experimental results were accurately recapitulated (Fig. S3a–c). Thus, these values were used for simulating photomixotrophic production of 23BD.

Using the derived glucose uptake and biomass partitioning values, we compared flux simulations from the OPP engineered pathway and the PKT designed pathway. Both designs resulted in identical titers and specific productivities at the published experimental conditions in Kanno et. al. (30 μmol photon m⁻² s⁻¹, 1 g/L inoculation density) and were consistent with the experimental results (Fig. 8a). Parsimonious FBA flux predictions between the OPP and PKT designs suggested that while both designs resulted in the same 23BD titer, the PKT design required 40% less flux through the CBB cycle (Fig. 7a,b). Additionally, the PKT design avoids carbon loss as CO₂ at both the OPP reaction phosphogluconate dehydrogenase and at the pyruvate dehydrogenase (PDH) reaction. The OPP pathway does generate 2 equivalents of NADPH per glucose; however, these reactions would have to compete with photosynthesis for the oxidized NADP+ pool, which may limit the flux through the OPP pathway. The phosphoketolase enzyme cleaves F6P into acetyl phosphate, which is converted to acetyl CoA and used to generate biomass, and erythrose 4-phosphate, a CBB intermediate. Thus, the PKT pathway coupled with a PDH knockout would result in a maximum biomass partitioning of 33% (2 out of 6 carbons from glucose) and effectively uncouple the CBB from biomass production and towards 23BD biosynthesis. The flux distributions suggest the PKT design could provide advantages over the OPP pathway, especially at high irradiances when the redox state of the NADPH pool may inhibit OPP flux.

Figure 8.

Engineering photoautotrophic and photomixotrophic production of 2,3-butanediol in S. elongatus. (A) Specific productivity versus titer comparison of phosphoketolase (PKT) design (this study) with the oxidative pentose phosphate (OPP) engineered pathway as described in [17]. Solid and open markers represent OPP and PKT values respectively. Control marker: no carbon fixation (Rubisco bounds = 0). Validation marker: in silico simulation of the experimental conditions reported in [17] (inoculation density: 1 g/L, light: 30 μmol photon m⁻² s⁻¹). (B) Specific productivity versus titer as a function of increasing light intensity. Select PAR values, in units of μmol photon m⁻² s⁻¹, are indicated. (C) Specific productivity versus titer as a function of increasing inoculation density. (D) Specific productivity versus titer production envelope as a function of inoculation density and light intensity. Yellow shaded region: photoautotrophy. Blue shaded region: photomixotrophy. For all panels the experimental value as reported in [17] is shown and the total culture duration was 3 days.

Next, we assessed the impact of cell shading on 23BD production. Using an inoculation density of 1 g/L, simulations suggested increases in titer and specific productivity could be achieved for both photoautotrophic and photomixotrophic conditions (Fig. 8b). Holding the light intensity constant at 30 μmol photon m⁻² s⁻¹ and varying the inoculation density indicated the photoautotrophic condition was more sensitive to the cell density compared to the photomixotrophic condition (Fig. 8c). We assessed the full production envelope from an inoculation density of 0.1 to 1 g/L and irradiance values from 30 to 900 μmol photon m⁻² s⁻¹. The simulations suggested dramatic improvements in both 23BD titer and specific productivity could be achieved by increasing the available light (Fig. 8d). Additionally, the impact to production yields caused by high inoculation densities was dramatically attenuated at high irradiances. While it is important to mention these results are based on the photoautotrophic P_O vs. QF curves, even the photoautotrophic condition achieved theoretical titers 2-fold higher than the published photomixotrophic values with increased specific productivity.

4. DISCUSSION

In this study we combined photophysiology constraints with a genome-scale model of S. elongatus PCC 7942 to predict metabolic differences between low and high light acclimated cultures. Overall, the model underestimated the growth rate at both high and low light but flux predictions were in good agreement with experimentally determined values. The genome-scale model predictions allowed for an assessment of excitation energy routing through the photosystem as a result of excess light absorption. Finally, we employed this modeling construct to assess and improve current S. elongatus production strategies for 2,3-butanediol.

The photophysiology constraints resulted in accurate predictions of photoautotrophic growth. Whole cell absorption spectrum, cell dry weight and oxygen evolution are widely accessible experimental techniques that are often used to characterize photophysiology [50]. When coupled to genome-scale modeling, these inputs provided a detailed assessment of cellular metabolism to include growth rate and reaction fluxes. Such inputs could be used for real-time monitoring and/or process control parameters of large-scale, light-driven bioprocesses engineering.

While the upper bound of the simulations values approached the range of the experimental observations, the model tended to underestimate the growth rate at both high and low light. When determining the oxygen evolution rate, we did not supplement the sample with exogenous bicarbonate as it has been reported to affect photophysiology [47]. However, based on the cell densities used and photosythetic rates observed, it is likely the samples became carbon limited during the oxygen evolution experiment. This likely would have reduced P_max of the P_O vs. QF curve used to parameterize the model resulting in a underestimation of the growth rate.

Parsimonious FBA reaction fluxes predicted by the genome-scale model were consistent with experimental ¹³C metabolic flux analysis [15, 1]. The observed accuracy is partially due to the non-redundant nature of the S. elongatus metabolic network. This lack of redundancy decreases the number of feasible flux states at the network level; evident by the similarity in experimental reaction fluxes in both ¹³C MFA studies. The agreement between the model predictions and MFA data suggests the photophysiology parameters are dominant constraints on photoautotrophy and the FBA assumption of optimality is appropriate. These factors coupled with emerging methods for combining constraint-based modeling with quantitative-omics data [52] brings a wide variety of phenotypes of interest to the phototrophic community into scope for in silico modeling.

While there were discrepancies in the simulation flux predictions and experimental data, the experimental values fell within the flux range of equally optimal solutions. For the high light/fast growth rate comparison (Fig. 6), the primary differences were in the Calvin-Benson cycle phosphatase reactions. The experimental values for these reactions did fall within the flux ranges determined by flux variability analysis (FVA) (Fig. 5c). The wide flux ranges reported by FVA are due to the fact these phosphatases are coupled to ATP-consuming kinases. As the GAM/NGAM assessment indicated, there was an excess of ATP at both LL and HL. Thus, when FVA is maximizing flux through the phosphatase, the corresponding kinase reaction has a large pool of ATP to drive the reaction pair resulting in a wide flux range. Despite these discrepancies, the overall flux into and out of the Calvin-Benson cycle was accurately predicted by the model. For the low light/slow growth rate comparison (Fig. 4), the primary differences were around the hypothesized malate dehydrogenase reaction. This MDH bypass of pyruvate kinase is hypothesized to be necessary due to regulatory inhibition of pyruvate kinase [22]. The MDH reaction, which has yet to be ascribed to a gene in S. elongatus, was added to our GEM based on biochemical evidence from MFA [15]. Regulatory mechanisms are not included in the genome-scale model; thus, the default prediction is for the bypass to not carry flux. While the pFBA solution predicted the MDH reaction carried no flux, the FVA flux ranges for this reaction were quite wide. Like the HL/fast growth rate comparison above, this was due to an ATP-coupled reaction (phosphoenolpyruvate synthase) driving flux through a loop that included MDH. Data-dependent incorporation of the PYK regulatory mechanism into a GEM could more accurately constrain the flux through this bypass. Of note, despite the bio-chemical evidence from MFA showing an MDH-mediated bypass of PYK, PYK is essential in vivo [43]. Therefore, in S. elongatus, the in vivo MDH-mediated PYK bypass cannot carry sufficient flux to maintain cell viability in the absence of PYK.

An advantage of genome-scale modeling over ¹³C MFA is the ability to predict reaction fluxes beyond central metabolism. We used this capability to assess alternate energy flows in S. elongatus. Our simulations predicted approximately 37% and 58% of the absorbed photons at low and high light respectively, were in excess of growth requirements and energy transfer losses. These numbers are likely overestimates since the energy transfer losses included in the model are based on measurements in S. elongatus permeaplasts [48] using chemical electron donor and acceptors; thus, they represent the most efficient energy transfer rates. Lever-aging recent developments in cyanobacterial PAM fluorometry techniques [35] may help constrain the physiological values. Still, up to 40% of photosynthetic flux was reportedly directed to the Mehler AET reaction in the cyanobacterium Synechocystis [12], suggesting our simulated values are in a biologically realistic range.

The model predicts an increase in excitation energy directed to PSI with an increase in QF (Table 4), consistent with known state transitions in cyanobacteria [33]. Additionally, our prediction of increased cyclic electron flow at high light, evident by increased flux through the NDH-1 complex, is in agreement with the known role of this complex in cyanobacteria [36][5]. The absolute fluxes through PSII versus PSI depends on accurate accounting of the metabolic cost of ROS detoxification at both reaction centers. Currently, the metabolic cost to repair the D1 protein, as represented in the model, drives the predicted excitation energy routing. Additionally, the GEM assigns a ROS generation rate that scales linearly with reaction flux. The kinetics of ROS generation are likely not linear in vivo and properly constraining the flux-dependent ROS generation rates stands as an area of improvement for the GEM. Still, the fold change in predicted PSI versus PSII flux predicted by the model was in close agreement in the change in Y(II) at the experimental QF (Table 4). This suggests coupling photon uptake constraints with the GEM assumption of optimality results in accurate qualitative assessments of excitation energy routing between low and high light.

It should be emphasized that FBA and MFA are complementary methods. Often GEM simulations result in multiple mathematically-equivalent flux states for a given set of constraints. MFA results restrict these alternate, equivalent optima to a narrower, biologically realistic subset. MFA results also validate or refute assumptions in the GEM. For example, in S. elongatus a phosphoketolase bypass of glycolysis is feasible based on the genome annotation [6]. The GEM uses a hypothesized constraint that limits this bypass flux. The agreement between the model predictions and MFA data validates this constraint on phosphoketolase flux. GEMs also support and extend discovery and engineering in MFA experiments. Metabolic reconstructions define the core metabolism of the organism, assisting in the development of the isotopomer models needed for MFA. Additionally, ¹³C MFA experiments in phototrophs are resource intensive. A validated GEM can explore phenotypes and engineering strategies in silico prior to committing resources on experimental validation of the predictions. Finally, genome-scale models extend MFA flux measurement outside of central metabolism either through direct constraints [30] or by analyzing the full flux distribution from a simulation that was validated against MFA central carbon flux, as we have done in this study.

The framework presented in this study provided insights into an existing 23BD production strain. Computational analysis of the published data [17] established the glucose uptake rate of the photomixotrophic strain as well as constrained the fraction of carbon allocated to biomass. This analysis included the culture vessel geometry, total culture volume, light intensity, inoculation density and photophysiology; all parameters that can be optimized during bioprocess design. Characterization of the engineered strain enabled an assessment of the theoretical yield, suggesting that an increase in irradiance would result in higher production titers. While our assessment assumed photophysiology parameters from our study, replacing the P_O vs. QF curve with an experimentally derived curve from the photomixotrophic strain would enable a more accurate characterization of the production culture. The phosphoketolase design suggested by our flux simulations may provide unique S. elongatus bioengineering solutions. In particular, growth-coupled engineering strategies could be developed for bio-products that are synthesized from the acetyl-CoA pool, such as isoprene [10].

5. CONCLUSIONS

Engineering of cyanobacteria shows promise for generating energy-dense products with minimal input requirements. In this study we presented an in silico methodology for accurately characterizing photoautotrphic metabolism. These experimentally accessible constraints enable phototrophic genome-scale engineering equivalent to classical heterotrophic in silico design. Additionally, by incorporating photophysiology constraints with engineering design, we were able to assess an existing photomixotrophic engineering strategy and revealed the current design was light limited. Coupling genome-scale modeling-driven in silico design with experimental validation, to include ¹³C metabolic flux analysis, is a promising strategy to accelerate the iterative bioprocess design of light-driven metabolic engineering strategies.