Abstract
Explicit solvent molecular dynamics simulations of a macromolecule are slow as the number of solvent atoms considered typically increases by order of magnitude. Implicit methods introduce surface-dependent corrections to the force field, gaining speed at the expense of accuracy. Properties such as molecular interface surfaces, volumes and cavities are captured by Laguerre tessellations of macromolecules. However, Laguerre cells of exterior atoms tend to be overly large or unbounded. Our method, the inclusion-exclusion based Laguerre-Intersection method, caps cells in a physically accurate manner by considering the intersection of the space-filling diagram with the Laguerre tessellation. We optimize an adjustable parameter, the weight, to ensure the areas and volumes of capped cells exposed to solvent are as close as possible, on average, to those computed from equilibrated explicit solvent simulations. The contact planes are radical planes, meaning that as the solvent weight is varied, interior cells remain constant. We test the consistency of our model using a high-quality trajectory of HIV-protease, a dimer with flexible loops and open-close transitions. We also compare our results with interval-arithmetic Gauss-Bonnet based method. Optimal solvent parameters quickly converge, which we use to illustrate the increased fidelity of the Laguerre-Intersection method over two recently proposed methods as compared to the explicit model.
Keywords: Laguerre tessellation, Voronoi tessellation, Implicit Solvation
1. Introduction
Laguerre tessellation (also known as the weighted Voronoi or power tessellation) is a well known mathematical tool used to partition the space containing data points into cells. Each data point is assigned the region which is closest to the given data point (generator of the cell) by the “power distance”. Laguerre methods have been widely used in biochemistry to find volumes of atoms, molecules, and amino acid residues (which we call simply “residues”) in proteins. They are useful for cavity location and in studying packing and deformation of proteins. They may also be used in protein structure prediction to check the quality of predicted structures. For example, residue volume may be considered an “intrinsic” property of amino acid type and is thus a predictable or checkable quantity 12. Laguerre surfaces have been used as a quick and parameter free way to measure accessibility of atoms and residues for quantifying exposure of a molecule with solvent 12. Residue contacts, which are important for protein structure and stability, have been studied using Laguerre surfaces. Interresidue contact surface areas are useful for protein structure analysis and prediction, and in studying structure-function relationships. Preferential contacts between amino acid species and atom-atom contact frequencies have also been found13,26. Differences in contact areas between model and reference structures have been used as a scoring function and for benchmarking protein structure prediction methods 29. Contact surfaces have also been used to characterize interactions between multiple proteins, or proteins and ligands, with important applications in protein docking and formation of complexes 27,30.
Surface area calculations play an increasingly important role in molecular dynamics simulations of macromolecules. For example, explicit solvent molecular dynamics simulations of a macromolecule are slow. The solute is imbedded in an adequately large periodic box filled with solvent and the system is simulated for a sufficiently long time so solvent molecules achieve thermal equilibrium. This typically increases the number of atoms in the system by an order of magnitude and furthermore the solvent viscosity significantly slows global dynamics such as protein folding 36. Using implicit solvent in molecular dynamics is an attractive alternative due to the reduced number of atoms in the simulation, along with the reduced viscosity due to the instantaneous relaxation of solvent following solute conformational changes. Implicit solvent calculations also play an important role in the post-processing of MD trajectories that were carried out in explicit water as a means to estimate binding affinities (the MM-PBSA method 21). Here implicit solvent is often advantageous since it directly provides an estimate of the free energy of (de)solvation, as compared to the enthalpy that is obtained using explicit solvent. This can be valuable in some cases where solvation free energy is needed, since obtaining this value in explicit solvent requires proper averaging over all possible explicit solvent configurations for a given solute configuration, obtaining the entropic contribution as well as the appropriately averaged enthalpy. Popular implicit solvent models include the Poisson-Boltzmann and Generalized Born methods, however these model only the polar contribution to solvation energy. A more accurate treatment involves also including the nonpolar (hydrophobic and dispersion) contributions to solvation, which are typically considered as approximately proportional to the solvent accessible surface area of the solute. Several methods have been developed and are commonly used 7,34,35. The speed and accuracy of these methods is vital to successful application, but due to the computational overhead many recent studies of protein folding omit nonpolar solvation despite the importance of the hydrophobic effect 28.
The Laguerre cell is the region which is closest to the generator of the cell (atom or residue center, for example) by the power distance. The power distance is an appropriate quantity to use as larger areas are assigned to data points with larger weights (larger atoms or residues, for example). The Laguerre cell of a data point depends on its neighbors. This poses a problem for systems that are typically found in a medium such as solvent but for which the surrounding medium is not explicitly known. In this situation, Laguerre cells of points on the convex hull are unbounded and the cells of points otherwise in contact with the surrounding medium tend to be too large. To arrive at a geometrical description of a macromolecule that is both independent of the rapidly changing detailed structure of the surrounding solvent molecules (typically water) while at the same time encoding an “average” geometrical profile as seen by the medium is a challenge that must be overcome in order to enhance the accuracy of implicit solvation modeling.
Researchers have addressed this difficulty in a variety of ways. Some consider only cells in the bulk of the protein which are not affected by the surrounding (unknown) environment. Others surround the structure by a layer of water or an artificial environment of spheres with size equal to the average amino acid size 14,31. However, this causes the size of the problem to increase, typically by an order of magnitude. Soyer et al., bounded Laguerre cells by only considering Laguerre facet vertices from tetrahedra of a small enough size 33. Still cells near the boundary tend to be elongated or have fewer facets than those in the bulk of the protein. Cazals method 'Intervor’ constructs interface surfaces by considering facets of dual Delaunay edges in the space filling diagram and discarding any edges that belong to large tetrahedra 6,4. Discarding these edges causes pertinent information to be lost.
Another class of models prunes and truncates certain Laguerre facets. Mahdavi et al. construct intermolecular interface surfaces by considering truncated facets in the union of extended convex hulls 24,25. The convex hulls are extended in a fashion to mimic a 1.4 Angstrom solvent radius. Ban and coworkers construct a series of interface surfaces based on a sequence of alpha complexes and truncate facets to within alpha complex tetrahedra, but no attempt is made to mimic the effect of the solvent 1,16.
McConkey et al. construct Laguerre-like cells by considering the surfaces of extended radical contact planes between neighboring atoms within a cutoff distance and the surface of an expanded sphere 26. However, the algorithm miscalculates Laguerre volumes when the atom center lies outside its cell (what we term an “engulfing contact”), a situation that our algorithm treats correctly (See Section 3.2). Cazals et al. in their paper “Computing the volume of a union of balls: a certified algorithm” 5 provide a formalization of the McConkey’s algorithm which also correctly calculates engulfing contact volumes. While these algorithms compute the restriction of Laguerre cells to the space-filling model, there are three key differences with our model. McConkey’s and Cazals’ algorithms are based on the Gauss-Bonnet theorem whereas our algorithm is an inclusion-exclusion model which is an extension of Edelsbrunner’s algorithm for calculating atomic and molecular surface areas and volumes 9. Inclusion-exclusion contributions extended to per-restriction quantities are given in equations (12)-(28) and (34)-(36). The inclusion-exclusion method is advantageous in that cycles of intersection points on the surface of the sphere do not need to be calculated which decreases algorithm complexity. The second key difference is that the former algorithms expand nonsolvent atoms by a solvent radius of 1.4 Å while our algorithm expands the squared radius. Expanding cells’ radii means that cells are bounded by extended radical planes rather than radical planes. This poses problems since the cells of atoms in the bulk, which should not be affected by the cutoff distance, are affected. Furthermore, cells of small atoms completely disappear for cutoff distances as small as 1.4 Å. The third difference is that in order to achieve double precision accuracy Cazals’ resorts to interval arithmetic and/or extended precicion (“ exact “) arithmetic which increases runtime by a factor of ten over the floating point models. As we are interested in calculating Laguerre-Intersection quantities at each step in a molecular dynamics (MD) simulation, speed is of utmost importance, and we can achieve desired accuracy using floating point operations. Remarkably, the accuracy of the results achieved by our method in the majority of cases is comparable to the extended precision results of the GB method, and highly more accurate than the GB method employing double precision arithmetic.
The proposed Laguerre-Intersection cell algorithm 19, considers the intersection of Laguerre cells with expanded atoms. The contact planes are the radical planes, which means that as the solvent weight is varied, Laguerre cells stay constant. This method simulates the environment better than using the extended radical plane. The Laguerre cells are capped in a physical manner that enables the study of boundary facets, rather than truncation by convex hulls.
We calculate molecule specific optimal solvent parameters from explicit solvent HIV protease trajectory data. The HIVP dimer has two flexible loops covering the active site that exhibit open-closed dynamics 17. We generated a 100 ns trajectory of HIV in explicit water to use as reference data (see Results). Despite the configurational variability, optimal solvent parameters converge quickly which we use to predict Laguerre quantities in the remainder of the trajectory. We show that these predicted quantities are closer to those found using explicit models than two current alternative methods. Further work is required to determine optimal solvent parameters for an arbitrary molecule.
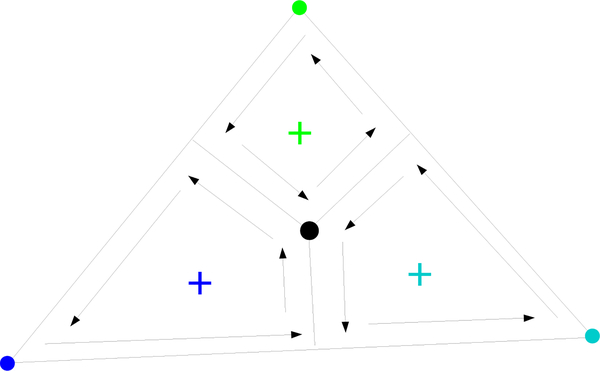
2. Background
2.1. Laguerre and Laguerre-Intersection cells
Consider a molecule represented by a set of spheres or atoms . For we write where is the center of the atom and is the weight or squared radius of the atom. The Laguerre cell, Li, of atom i is defined to be
| (1) |
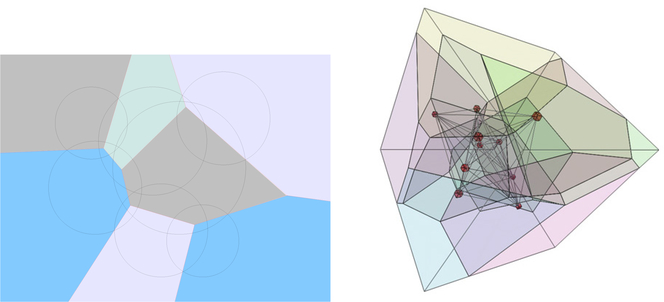
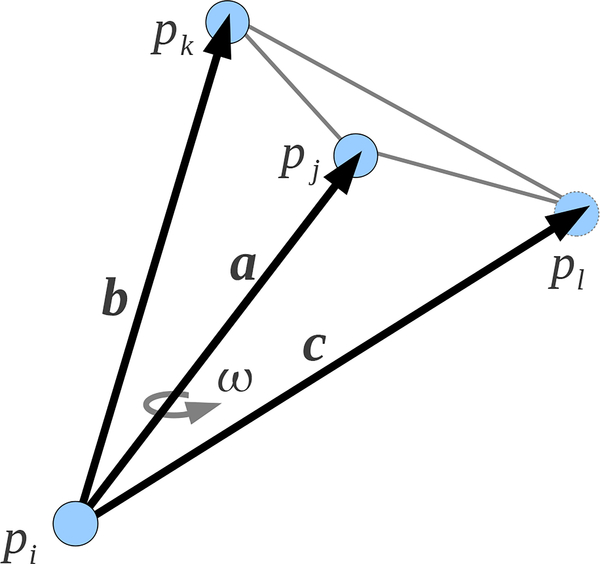
and is a convex polytope (Fig. 1).
Fig. 1.
2d and 3d Laguerre diagram: 2d illustrates how the radical plane partitions space between atoms of different radii; 3d courtesy of Frederick Vanhoutte.
The quantity is called the power distance between pi and x′ and is written as
| (2) |
A Laguerre cell is the set of points whose nearest neighbor by the power distance is pi, and each Laguerre facet lies on the plane which is equi-powerdistant between two points and which is called the radical plane.
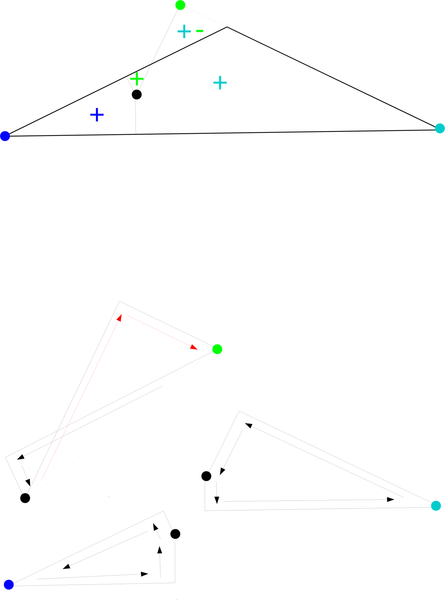
The weights of the atoms in may be increased or decreased by a certain amount w which we call the solvent weight. In this section, we call this modified set where has and wi(w) = wi + w. The Laguerre cell of pi(w) is defined as
| (3) |
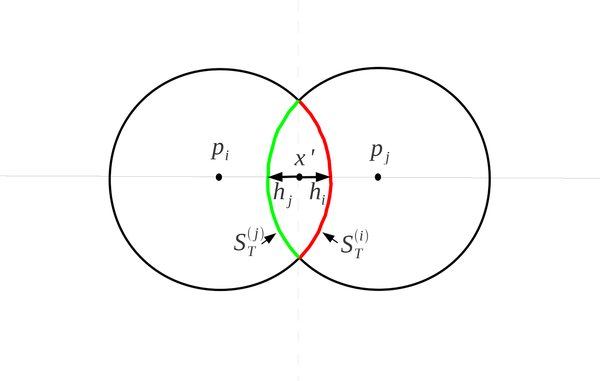
Since Li(w) = Li(0) for all w (See Fig. 2) we simply write the Laguerre cell of atom i as Li.
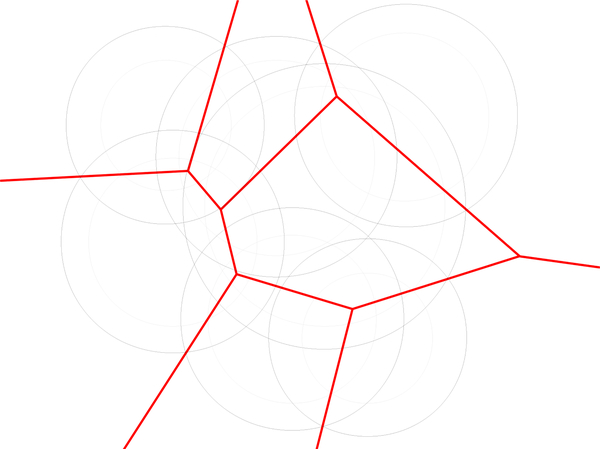
Fig. 2.
Red bounds Laguerre cells of (shown in black) and (shown in gray). Note that the cells are the same for both weights. This is the reason that varying the weight rather than the radius in the space filling diagram gives better agreement between Laguerre-Intersection quantities and Laguerre quantities found using explicit solvent (See Section 5.5).
The Laguerre diagram, , of is the collection of all Laguerre cells and their faces which we call Laguerre facets, segments, and nodes. A Laguerre facet is the intersection of two Laguerre cells and is a subset of the plane which is equipowerdistant from the generator of the two cells. A Laguerre segment is the intersection of at least three Laguerre cells, and a Laguerre node is the intersection of at least four Laguerre cells. For define
| (4) |
The space filling model of with solvent weight w is defined as
| (5) |
We also define the following quantities:
LVi: Volume of the Laguerre cell of atom i.
LSi: Surface area of the Laguerre facets of atom i.
A residue is the collection of atoms in a single amino acid unit in the protein. The Laguerre volume of residue j (residual volume) is the sum of Laguerre volumes of atoms in residue j. The interresidue Laguerre surface area between residues j and k is the sum of areas of Laguerre facets which lie between atoms in residue j and atoms in residue k.
2.2. Laguerre diagram and regular tetrahedrization
The regular tetrahedrization is dual to the Laguerre diagram . There is a one to one correspondence between the (3 − k)-faces in and the k-simplices in . Each node in corresponds to a tetrahedron in whose vertices are equipowerdistant to the node, which we call the characteristic point of the tetrahedron. Each segment in corresponds to a triangle in whose vertices are equipowerdistant to the power segment. For each facet in there is an edge in whose vertices are equipowerdistant to the power facet. Each cell in corresponds to a point in , namely the generator of the cell. We call a point whose center is on the convex hull of exterior to the tetrahedrization. Otherwise a point is called interior to . An edge is called exterior if both of its vertices are exterior to . An edge is called interior if at least one of its vertices is interior. Note that the Laguerre cell of an exterior point is unbounded whereas the Laguerre cells of interior points are bounded. The Laguerre facets corresponding to exterior edges are unbounded whereas Laguerre facets of interior edges are bounded.
In this paper we take for granted robust algorithms for the calculation of the regular tetrahedrization and the α-complex which is a subset of the the tetrahedrization.
3. Methods
3.1. Computation of Laguerre surface areas of interior facets
Interior Laguerre cells are bounded by Laguerre facets. Each of these facets correspond to an edge in the regular tetrahedrization. We call an edge eij if the vertices of that edge are and and call the Laguerre facet corresponding to that edge Lij. The facets are convex polygons whose vertices are nodes in the Laguerre diagram, namely the characteristic points of the tetrahedra which surround that given edge. If a Laguerre cell has n facets, the volume may be divided into n pieces, one for each of its facets. The volume of the Laguerre cell of i corresponding to the edge eij is written and the volume of the Laguerre cell of j corresponding to the edge is written . We call the ordered list of tetrahedra which surround a given edge, i.e. the ordered list of tetrahedra in the edge’s star, a tetrahedra ring or tetraring. A tetraring is called complete if the ring closes, otherwise it is called incomplete. Note that the tetraring of an interior edge is complete, whereas the tetraring of an exterior edge is incomplete (Fig. 3). In this section, we assume that the protein is surrounded by a layer of solvent. This means that all nonsolvent atoms are interior to the regular tetrahedrization as well as all edges which contain a nonsolvent atom as a vertex. We call these “nonsolvent edges”. The computation of the Laguerre volumes and surfaces of each nonsolvent atom proceeds as follows:
Regular tetrahedrization of all atoms is computed
Characteristic points of tetrahedra are found
- For each nonsolvent edge
- Surface area of the corresponding Laguerre facet is computed and assigned to appropriate atoms
- Using the calculated area, corresponding Laguerre volumes are found and assigned to appropriate atoms
- Interresidual Laguerre surface areas are assigned
Laguerre residue volumes are summed
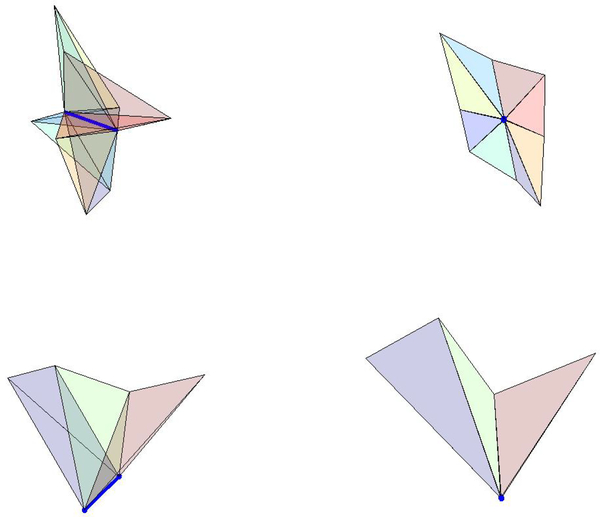
Fig. 3.
Top row: Side and perpendicular views of the complete tetraring of an interior edge (shown in dark blue). Bottom row: Side and perpendicular views of an incomplete tetraring of an exterior edge (shown in dark blue).
3.1.1. Surface areas
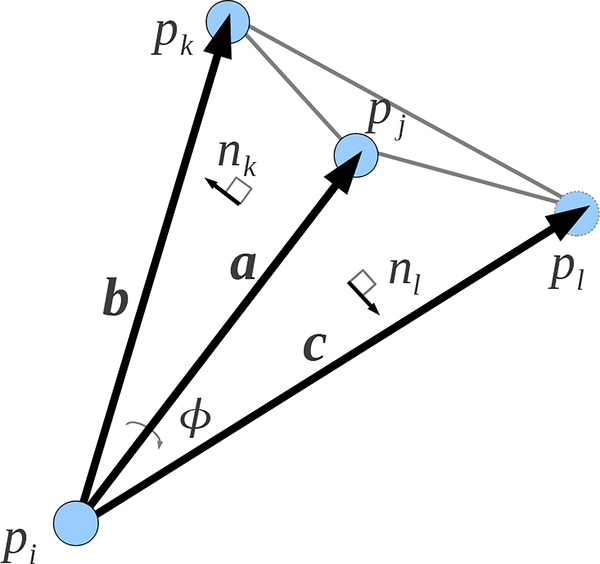
When considering edge eij, we compute the surface area, LSij, of the facet, Lij, between atoms i and j. The ordered vertices in the Laguerre facet are the characteristic points of the tetrahedra in the edge’s tetraring. Note that the edge does not always intersect its Laguerre facet, but it is always perpendicular to it (Fig. 4). Next we define the characteristic point of an edge. The characteristic point, of an edge, eij satisfies
| (6) |
with minimal. The center of this point lies on the intersection of the line containing and and the plane of points which are equipowerdistant to pi and pj. The method computes the surface area as the sum of the areas of the triangles as shown in Fig. 5.
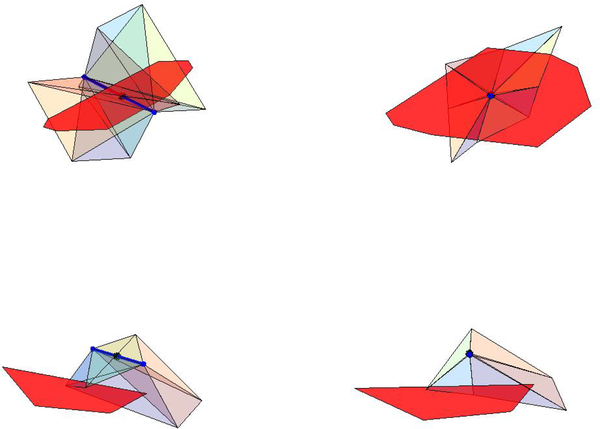
Fig. 4.
Laguerre facet of edge represented in red. The vertices of the facet are the characteristic points of the tetrahedra in the edge’s tetraring. Top row: Two views of a facet which is intersected by its corresponding edge. Bottom row: Two views of a facet which is not intersected by its corresponding edge.
Fig. 5.
Subdivision method for the two facets shown in Fig. 4.
3.1.2. Volumes
The Laguerre volume contributions, and , are pyramids with base Lij, and heights and respectively, with
| (7) |
| (8) |
We can write
| (9) |
Thus the position of the plane containing the edge’s facet with respect to and is encoded in the value of t (Fig. 6). This gives
| (10) |
The term is positive if the corresponding pyramid lies in Li and negative otherwise (Figs. 7, 8). We call the latter case an “engulfing” contact; that is the generator of one cell lies in the Laguerre cell of another atom.
Fig. 6.
The value of t is determined by the relationship of the equi-powerdistant plane with respect to the two edge points and indicates if the center of the generator of the cell is interior or exterior to its cell.
Fig. 7.
Left: Laguerre cell that contains generator’s center. Right: Pyramidal decomposition of Laguerre cell. All volumes are positive.
Fig. 8.
Left: Laguerre cell that does not contain generator’s center (black vertex). Center: Negative pyramidal volume. Right: Positive pyramidal volumes.
Formula 10 is in contrast to the volume calculation (Equation 7b) in McConkey’s method 26 which does not consider signed volumes and thus returns incorrect quantities for engulfing contacts (For example, see Fig. 8).
3.2. Removing solvent
We would like to compute Laguerre-like volumes and surfaces of a molecule that is not surrounded by solvent, so that these quantities are as close as possible to the Laguerre volumes and surfaces that are found when the molecule is in its typical environment. In doing this, we come across two problems:
The Laguerre cells are unbounded for certain atoms on the convex hull of .
The Laguerre cells of atoms that would otherwise be in contact with solvent are too large
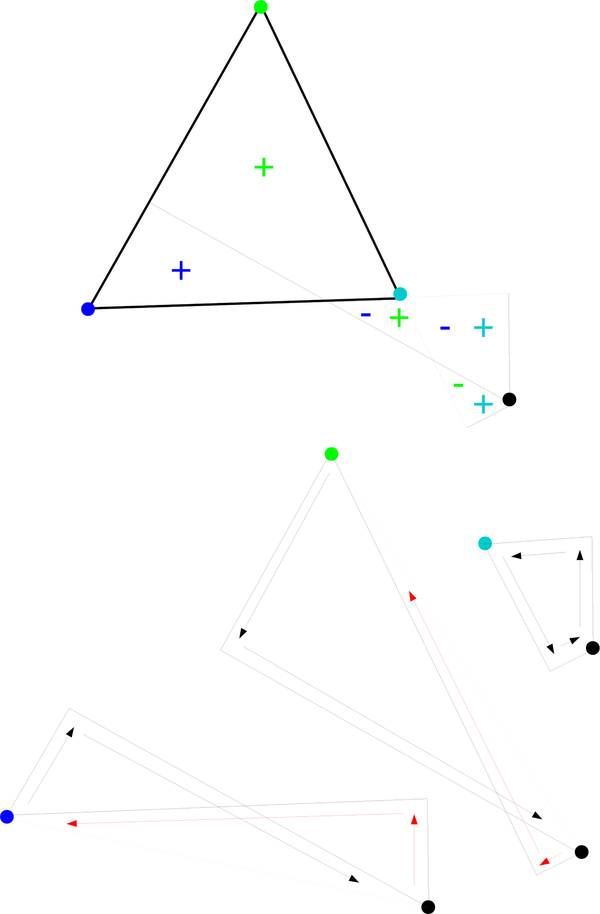
This may be overcome by using Laguerre intersection cells, LI(w). The Laguerre intersection cell of an atom is the intersection of the Laguerre cell of that atom with the expanded atom.
| (11) |
Exterior cells are bounded in a realistic way, and the cells of atoms which would otherwise be in contact with solvent are shrunk to a more appropriate size (Fig. 9). Laguerre cells are constant as a function of w, which means this parameter can be tuned to generate appropriate exterior Laguerre intersection cells while interior cells remain unchanged (Fig. 10).
Fig. 9.
Example of Laguerre-Intersection cells (shown in grays and greens). Solvent is represented by light blue spheres, boundary of Laguerre cells of molecule (minus solvent) are shown in red, and boundary of Laguerre cells of molecule in solvent is represented by the dotted line.
Fig. 10.
Laguerre cell does not depend on w while the Laguerre-Intersection cell does depend on w.
Define LISi(w) and LIVi(w), be the surface area and volume of LIi(w)
| (12) |
Just as the individual atomic surface area and molecular volume can be written as a sum of contributions corresponding to simplices in the alpha complex using the inclusion-exclusion formulas (See Appendix A), LIS and LIV can be split into contributions (Eqs. 13, 14) from simplices in the alpha complex which is a subset of the Delaunay tetrahedrization 8. Define to be the alpha complex of with the set of simplices in the boundary of . For , σT represents the simplex which is the convex hull of the centers of points in T. As we are working in three dimensions we only consider |T| ≤ 4, where |T| is the number of elements in T. Recall that eij = σT for T = {pi, pj}. We also represent vertices and triangles as vi and tijk in a similar manner.
The Laguerre-Intersection cell, LI, of an atom interior to is precisely the Laguerre cell L. The Laguerre-Intersection cell of an atom exterior consists of polyhedral components (contributions from interior simplices) and spherical components (contributions from simplices on ).
The terms and are the surface area and volume contributions of the simplex σT to LIVi(w) and LISi(w) (the analogs to terms in A.3). We can also write for T = {pi(w)}, for T = {pi(w), pj(w)}, etc., and likewise for surface areas (See Fig. 11). The terms and FT for |T| = 2 are pyramidal volumes and facet surface areas that will be discussed shortly. We have
| (13) |
and
| (14) |
where Si(w) is the accessible surface area of atom i with solvent radius w, and cTs are given for the following simplices
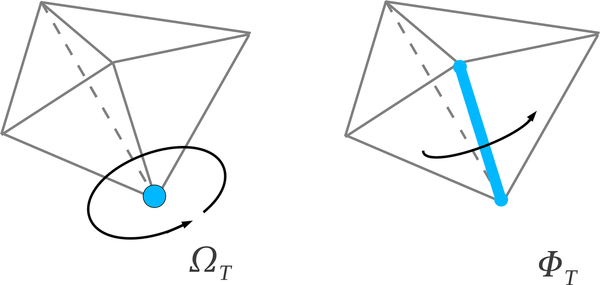
|T| = 1, i.e. a vertex vi: cT = ΩT is the fraction of the ball i outside the tetrahedra in the alpha complex. That is ΩT is the normalized outer solid angle subtended by the union of tetrahedra in which contain vi.
|T| = 2, i.e. an edge eij: cT = ΦT is normalized outer dihedral angle of the union of tetrahedra in which contain the edge eij.
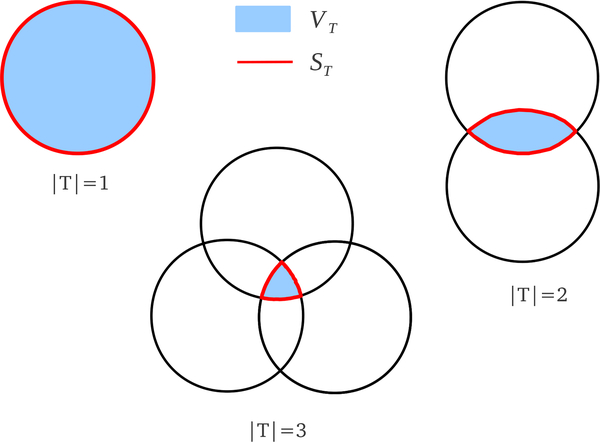
|T| = 3, i.e. a triangle tijk: cT is 1 if the triangle is singular and if the triangle is regular. In other words, cT is the fraction of VT and ST that is outside the union of tetrahedra in the alpha complex.
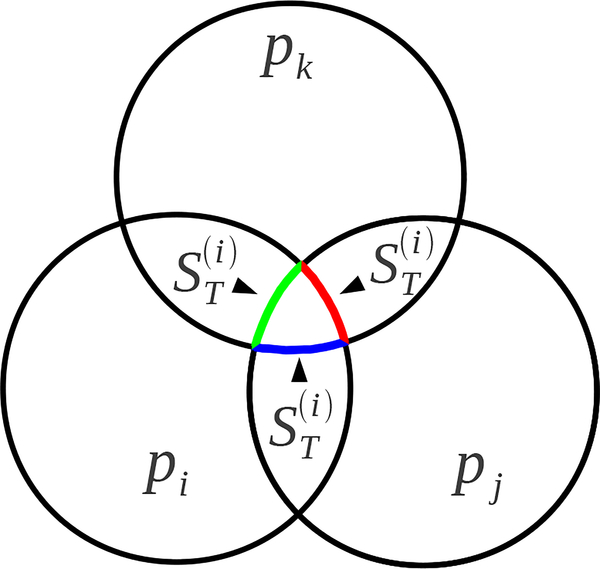
Here , , and .
Fig. 11.
Laguerre-Intersection cell volumes (blue), , , , and surfaces (red) LISij, and LISijk. to atom i from simplices.
Since
| (15) |
where is the contribution of σT to Si(w), we can write
| (16) |
3.3. Equations
3.3.1. Vertices
The Laguerre volume and surface contributions from a vertex, vi, are given by
| (17) |
| (18) |
3.3.2. Edges
The formulas for the volume and surface contributions from the intersection of two balls pi and pj are
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
3.3.3. Triangles
Let be the characteristic point of the triangle tijk. Let p be one of the two points of intersection on the spheres pi(w), pj(w), and pk(w). We can write where n is the normal to the plane containing the triangle,
| (25) |
Let σTc the tetrahedron defined by the centers of T and xT. Then
| (26) |
| (27) |
| (28) |
where ϕij is the fractional inner dihedral angle of σTc along edge σij, ωi is the fractional (inner) solid angle of σTc subtended from , etc. Let , , be the centers of the characteristic points of the triangle’s edges. Then is the sum of the areas of the triangles given by , , p, and , , p. We have
| (29) |
where is the signed volume of the solid with vertices at , xij, xijk, xik, and p. More specifically, let
| (30) |
| (31) |
| (32) |
| (33) |
then
| (34) |
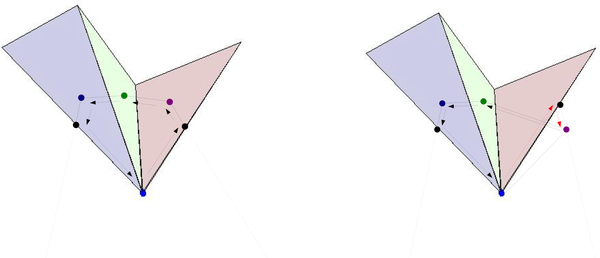
Equivalent equations hold for , , , and . See Figs. 12, 13, 14 for possible configurations.
Fig. 12.
, , , and represented by dark blue, light blue, green, and black dots, respectively. The point p is out of the page. The black arrows represent positive contributions to the volumes , , and .
Fig. 13.
Above: Sample configuration. Below: Black arrows represent positive contributions to , , and , while red arrows represent negative contributions.
Fig. 14.
Above: Sample configuration. Below: Black arrows represent positive contributions to , , and , while red arrows represent negative contributions.
3.3.4. Other contributions
We get additional contributions, FT and , from all edges in . There are two types of these edges:
edges interior to
edges exterior to .
Contributions from interior edges of are computed as in section 3.1. That is
| (35) |
and
| (36) |
The terms and FT are zero for all edges that are not part of at least one tetrahedron in . To calculate the contribution from all other exterior edges, we must know the characteristic points of the triangles on the boundary of the tetraring. The characteristic point of the boundary triangle may or may not be on the Laguerre facet, but it always indicates the direction of one of the facet’s boundary segments (Fig. 15). For each exterior edge, the counterclockwise list of Laguerre nodes corresponding to tetrahedra in the alpha complex is already known. The surface area is computed by using signed surface areas as shown in pseudocode in the appendix. The volume contributions to LIi and LIj are found by multiplying the resulting surface by and , respectively. In this case, a sign is Incorporated into the surface area which means the sign(1 − t) and sign(t) terms in equation 10 are not needed.
Fig. 15.
Two examples of additional contributions from edges which are regular and exterior with respect to . The royal blue points are the characteristic points of edges which are exterior to and which points directly out of the paper. The triangles represent tetrahedra in the tetrahedra ring which are also in . Dark blue, green, and purple dots represent the Laguerre nodes corresponding to the tetrahedra of the same color in the tetraring. The black points are characteristic points of the boundary triangles. In the first case, both triangle characteristic points lie in the Laguerre facet. In the second case, one of the triangle characteristic points is not in the facet but is still needed to determine a line segment (shown in gray). In the first case all Laguerre nodes lie in the union of tetrahedra and all corresponding surface contributions are positive. In the second case, a Laguerre node lies outside the union of tetrahedra in . The triangular surface that is bounded by the right black, purple, and clear dots was originally assigned during contributions from the boundary triangle, and must be subtracted to obtain the correct area.
Note that the tetraring of an edge may not be connected. The pseudocode does not take this into account for simplicity reasons, while the actual implementation does.
4. Experiments: Accuracy of Algorithm
4.1. Monte-Carlo based estimates
We tested the accuracy of our Laguerre-intersection algorithm on a tryptophan dipeptide trajectory (1000 structures) with Monte-Carlo based estimates of Laguerre-Intersection volumes and surfaces. Tryptophan has a near-planar ring which was useful for testing the robustness of our algorithm.
Monte-Carlo Laguerre-Intersection volume estimates were obtained by generating N = 10n with n = 1 : 7 uniformly random points in the volume of each atom. The fraction fij of points in the volume of atom j in structure i which are closest to atom j by the power distance were tabulated. The Laguerre-Intersection volume estimate is
| (37) |
where rj is the radius of atom j.
Laguerre-Intersection atomic surface areas consist of spherical (solvent-accessible) portions and planar portions that lie on discs of intersection between two spheres. The solvent-accessible portions were estimated in a similar manner as Laguerre-Intersection volumes. N = 10n with n = 1 : 7 uniformly random points were generated on each sphere and the estimated surface areas are
| (38) |
where fij is the fraction of points on the surface of atom j in structure i that lie closest to atom j by the power distance.
The planar Laguerre-Intersection surface area for atom j is structure i is
| (39) |
where q is the number of alpha-complex neighbors and LISijk is the portion of LISij that lies on the disc of intersection between atom j and its neighbor k in structure i. Let Aijk be the surface area of this disc and define
| (40) |
Then random points are generated on the disc of intersection between atom j and its neighbor k in structure i and the estimated planar Laguerre-Intersection surface area is
| (41) |
where fijk is the fraction of points on the disc of intersection that are closest to atom j by the power distance.
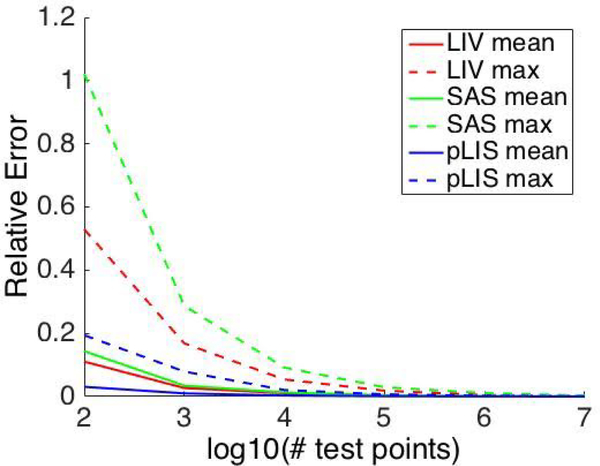
Maximum and mean errors decrease as the number of test points increase (Fig. 16). Final mean errors for LIV, SAS, and pLIS estimates are O(10−4). Maximum relative errors for LIV, SAS, and pLIS estimates are O(10−3).
Fig. 16.
Mean and maximum relative difference over all atoms between estimated and analytic Laguerre-Intersection atomic volumes and surfaces areas for 1000 structure tryptophan dipeptide trajectory.
An analysis of the accuracy of the estimates follows. Let LIV be the Laguerre-Intersection volume for an atom with radius r. Then the probability that a test point x falls in LIV is
| (42) |
Given n trials, the number of points, k, that fall within LIV follows a Binomial distrubution with parameters p and n,
| (43) |
For large np and n(1 − p), B(p, n) is approximated well by the normal distribution .
Given a significance level, α = .01, upper and lower limits, and , on k may be calculated with 99% confidence. Since the normal distribution is symmetric about the mean, we are 99% confident that the relative error of the estimate is bounded by
| (44) |
Note that the right hand side of (44) is a decreasing function of p.
We follow the same analysis for SAS and pLIS. For our trajectory, p ≥ .174, p ≥ .056, and p ≥ .180 for LIV, SAS, and pLIS respectively. This gives 99% probability that
| (45) |
| (46) |
| (47) |
which is consistent with the values in Fig. 16.
4.2. Comparison with Gauss-Bonnet-type algorithm
We compared atomic Laguerre-Intersection volumes and surface areas calculated using our method with those found using vorlume 3, the Gauss-Bonnet-type algorithm adopted in the Structural Bioinformatics Library (SBL) on a diverse set of 1013 proteins in the Protein Data Bank. With the latter algorithm, we used the ‘exact’ option which employs interval arithmetic with extended precision and sufficiently small intervals that the solution is considered ‘exact’. We compared the results from our algorithm and the single number reported by vorlume without the ‘exact’ option in the SBL, to test how our method compares to Gauss-Bonnet-type method when both employ double precision computations. We checked both algorithms’ results of surface and volume to see whether they fall in intervals provided by the algorithm with ‘exact’ option and calculate the correct ratio, which is defined as the ratio of atoms for each protein whose value for surface or volume falls in the interval provided by vorlume with the ‘exact’ option.
Both algorithms do better on computing surfaces than on computing volumes. However, no matter whether surface or volume, our algorithm appears more robust and accurate. We identified the 20 proteins where each one of these two algorithms obtained its lowest correct ratios, respectively. The average correct ratio for vorlume to calculate the surface of its 20 most unfavorable proteins is 3.695%, while the correct ratio of our algorithm for the same 20 proteins is 96.44%. The average correct ratio for vorlume to calculate the volume of its 20 most unfavorable proteins is 2.316%, while the correct ratio of our algorithm for the same 20 proteins is 68.45%. The average correct ratio for our algorithm to calculate the surface of its 20 most unfavorable proteins is 94.99%, while the correct ratio of vorlume for the same 20 proteins is 37.52%. The average correct ratio for our algorithm to calculate the volume of its 20 most unfavorable proteins is 67.377%, while the correct ratio of vorlume for the same 20 proteins is 3.043%. We see that our algorithm’s results do not vary as much as the Gauss-Bonnet-type vorlume when it is calculating the surface/volume for the 2 different sets of 20 proteins.
If we consider the whole 1013 protein database which contain 3710687 atoms, the correct ratio for surface of our algorithm is 3580002/3710687 = 96.48% and the correct ratio for volume of our algorithm is 3295669/3710687 = 88.81%. Correspondingly, the correct ratio for surface of vorlume is 1079062/3710687 = 29.08% and the correct ratio for volume of vorlume is 615823/3710687 = 16.60%. In conclusion, our algorithm gives results more accurate and robust.
From the perspective of computing time, our algorithm has obvious advantages. We take the two modes of the Gauss-Bonnet-type algorithm vorlume in the SBL as a reference. The mode with option ‘exact’ will give results with extended precision at a considerable time cost while the mode without ‘exact’ uses double precision floats, which is less accurate than ‘exact’ model but much faster. Excluding the time for tetrahedralization from the total time budget, we find that over the 1013 protein database, which involved 3710687 atoms in total, the total time spent on computing surface and volume using vorlume with ‘exact’ option is 36982.902331s. The total time spent on computing surface and volume using vorlume without ‘exact’ option is 2948.505325s. The total time spent on computing surface and volume using our algorithm is 73.316s. Our algorithm is about 40 times faster than the much less accurate mode, while it is about as 504 times fast as the exact mode, with which we agree on the great majority of cases.
5. Experiments: Optimizing Solvent Parameter
We test the capability of the Laguerre-Intersection method for predicting explicit water Laguerre quantities. We train on molecular dynamics trajectory data to determine “optimal solvent parameters”; those parameters for which the Laguerre-Intersection volumes and surface areas are, on average, as close as possible to the Laguerre volumes and surfaces of a molecule in its typical solvent environment.
5.1. Data
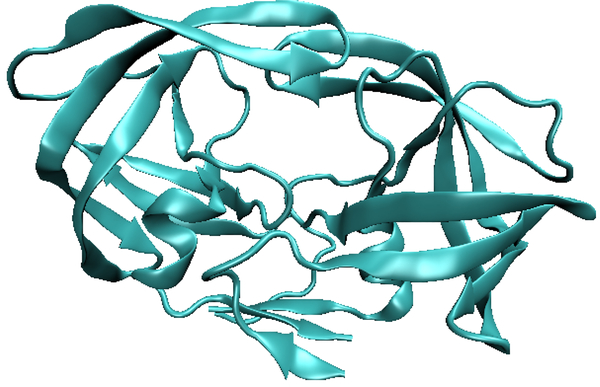
We work with solvated molecular dynamics trajectory data (2500 structures) of the HIV protease dimer (See Fig. 17) to determine optimal solvent parameters. The trajectory was initiated from the 1HVR crystal structure 22, and generated using the Amber software 2 with the ff99SB protein force field 18 and the TIP3p water model 20. Equilibration followed published protocol 32 with a 2fs time step, and the simulation coupled to a thermostat at 300K. A total of 100 ns of data were generated.
Fig. 17.
Sample structure from the HIV protease molecular dynamics trajectory.
Optimal solvent parameters, which converge quickly, determine the capability of the implicit Laguerre-Intersection model to predict explicit water Laguerre quantities. We also compare our method to other implicit models.
First residual and atomic Laguerre volumes, atomic, interresidual, and residue-solvent surface areas (LV_res, LV_atom, LS_atom, LS_interres, LSAS_res, respectively) were calculated for the solvated trajectory.
For various solvent parameters, wk and rk,
equivalent Laguerre-Intersection quantities were computed for each structure (LIV res, LIV_atom, LIS atom, LIS_interres, LISAS_res, respectively). We set dw = .1 Å and chose dr such that
| (48) |
This means that for an atom with atomic radius 1.7 Å (the typical radius of carbon), the initial (k = 0) and final (k = k_max) total weights are the same using both methods.
Laguerre and Laguerre-Intersection quantities were compared and “optimal” solvent parameters were found. The optimal solvent weight (radius) is the value wk (rk) that minimizes the error (Equations 49, 50).
We write the Laguerre volume of residue j in structure i as LV_res(i, j), and the Laguerre-Intersection volume of residue j in structure i with solvent parameter wk (rk) as LIV_res(i, j, k). We write the interresidual Laguerre surface area between residues j and jj in structure i as LS_interres(i, j, jj), and the interresidual Laguerre-Intersection surface area between residues j and jj in structure i with solvent value wk (rk) as LIS_interres(i, j, jj, k). Equivalent formulas hold for the other Laguerre and Laguerre-Intersection quantities.
Using wildcard notation, an arbitrary Laguerre quantity and Laguerre-Intersection quantity are written as L* and LI*. Then with solvent parameter wk (rk) 1-Norm and 2-Norm errors are
| (49) |
and
| (50) |
where N is the number of structures in the MD trajectory.
For LIV_res, LIV_atom, LIS_atom, and LISAS_res
| (51) |
and
| (52) |
where n is the number of residues or atoms and
| (53) |
with
For the first three quantities . The average Laguerre quantity is defined as
| (54) |
With LIS_interres we have
| (55) |
and
| (56) |
where
| (57) |
with
The average interresidual surface area is defined as
| (58) |
In this paper we present the absolute errors divided by the average quantities. We do not compute the relative errors at each step because the exact quantities may be zero.
First we present optimal solvent parameters obtained from HIV protease trajectory data. We show these parameters converge quickly despite the configurational variability of the molecule. We compare the capability of the Laguerre-Intersection, McConkey 26, and Cazals’ 4 method to predict explicit solvent Laguerre quantities. After a brief overview of these methods, We will compare all three methods to explicit water models, followed by a comparison of the radius vs. weight method of expanding atoms.
5.2. Optimal solvent parameters
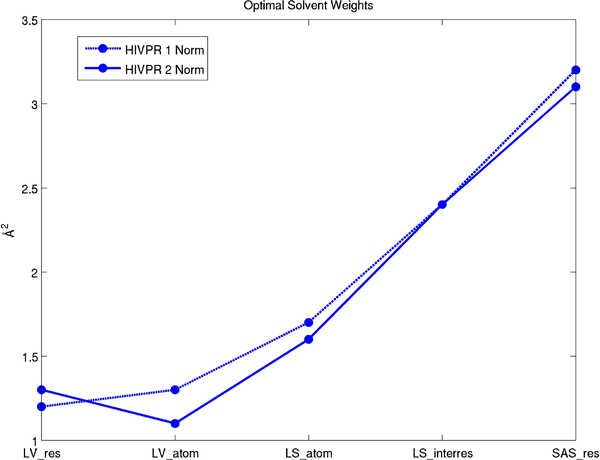
We plot the optimal solvent weights found from the HIV protease trajectory which has 2500 structures (See Fig. 18). The optimal solvent parameters for Laguerre volumes and Laguerre surfaces differ which is expected. One additional benefit of the weight method, is that the weighted Delaunay tetrahedrization is constant for all weights. This means the tetrahedrization (the time limiting step) only needs to be computed once per structure. When using the radius method, the tetrahedrization must be recalculated for each optimal solvent parameter.
Fig. 18.
Optimal solvent weights from the HIV protease trajectory.
Note that these are not “universal” parameters and are not necessarily optimal for an arbitrary molecule. Further work is needed to determine which values should be used in a given molecular dynamics simulation.
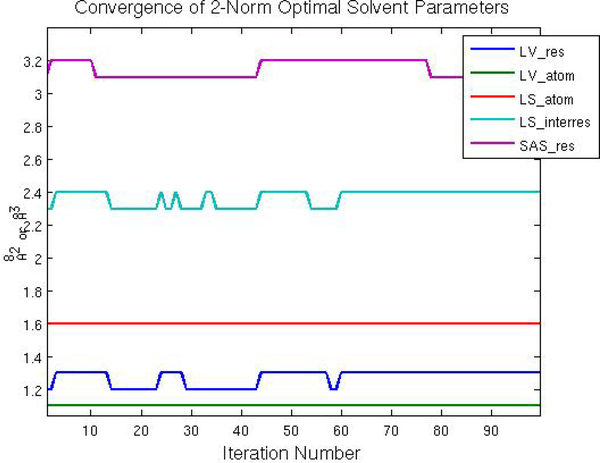
Optimal solvent parameters, as given by Equations 49, 50, 54, and 58, are recorded at each step in the trajectory. The first 100 out of 2500 iterations are shown in Fig. 19. We see that the optimal solvent parameters are immediately within one dw of the global optimal solvent parameters and soon become stationary with each step. Since the HIV protease dimer has flexible loops and open-close transitions we conjecture that most other proteins will exhibit similar or quicker convergence.
Fig. 19.
Convergence of optimal solvent parameters.
5.3. Overview of current methods
5.3.1. McConkey-Cazal method
McConkey-Cazals (MC) algorithm 5,26 constructs Laguerre-like cells by considering the surfaces of extended radical contact planes between neighboring atoms within a cutoff distance and the surface of an expanded sphere. Similar to our Laguerre-Intersection algorithm, this method considers the intersection of cells with the space filling diagram with atom radii expanded by a solvent radius of 1.4 Å. While the McConkey-Cazals method and the Laguerre-Intersection method are algorithmically different, (McConkey-Cazals method is based on the Gauss-Bonnet theorem while ours is an in inclusion-exlusion method), another key difference is that the cells in McConkey-Cazals method are bounded by extended radical planes rather than radical planes. This poses problems since the cells of atoms in the bulk, which should not be affected by the cutoff distance, are affected. Furthermore, cells of small atoms completely disappear for cutoff distances as small as 1.4 Å.
5.3.2. ’Intervor’ for interface surfaces
Another Cazals’ method, ’Intervor’, is used to determine interface surfaces between molecules or a molecule and solvent 6,4 and locates atoms that are in direct contact with each other and those whose contact is mediated by water. This method is more qualitative in nature than the Laguerre-Intersection method, i.e. it does not claim to give contact areas that are similar to those of solvated systems but rather locate and describe topology of interactions.
A solvent radius of r = 1.4 Å to all atoms and the alpha complex, , is computed. Laguerre facets dual to edges not in are thrown out. This is called the α criterion. However, overly large facets still remain. Such facets are discarded according to ’condition β’:
| (59) |
where we is the weight of the smaller of the two balls in the edge and is the size of the largest weighted Delaunay tetrahedron that contains the edge. The value M is set to 5.
5.4. Comparison with explicit model
We compare the Laguerre-Intersection, McConkey-Cazals 26,5 (MC), and Intervor 4 to explicit models for the HIV protease trajectory data. We see a clear improvement in accuracy using the Laguerre-Intersection method (See Table 1). SAS_res is approximately thirty percent more accurate while LV_res is about eight times more accurate when compared to the MC method. Intervor4 gives norms about four times larger than the Laguerre-Intersection method and about two times larger than the MC method.
Table 1.
| Quantity | Method | 1-Norm / Average | 2-Norm / Average |
|---|---|---|---|
| LS_interres | Laguerre-Intersection | .1416 | .2027 |
| MC r=1.4 | .3224 | .5101 | |
| Intervor | .6988 | 1.3150 | |
| LV_res | LI | .05695 | .07097 |
| MC r=1.4 | .4184 | .5487 | |
| LS_atom | LI | .06794 | .09994 |
| MC r=1.4 | .4841 | .5714 | |
| LV_atom | LI | .1039 | .1636 |
| MC r=1.4 | .7573 | 1.0937 | |
| SAS_res | LI | .1176 | .1548 |
| MC r=14. | .2039 | .2536 |
At this point we do not know what effect this improvement might have on the accuracy of statistical potentials developed with these models.
5.5. Radius vs. weight method
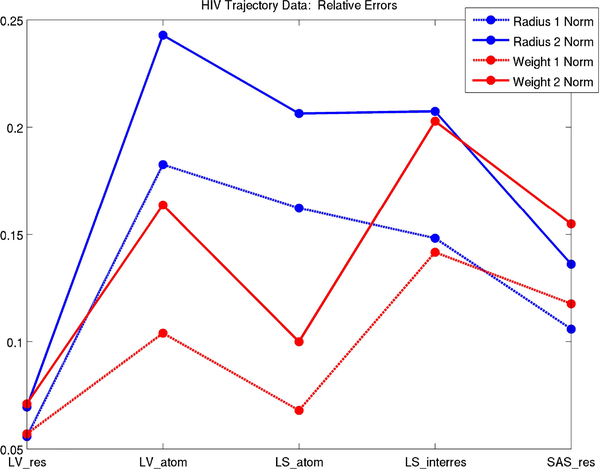
In our simulations, we found that the weight rather than radius method gave smaller errors for atomic quantities and similar errors for residual quantities. This is expected as the Laguerre cell of the molecule does not vary as atom weights are uniformly increased (See Fig. 2). Residual errors decrease relative to atomic errors for the radius method due to cancellation in atomic errors. Fig. 20 compares relative errors for Laguerre-Intersection quantities over the HIV protease trajectory.
Fig. 20.
Relative errors corresponding to optimal solvent parameters.
6. Conclusion
We developed an algorithm to compute the atomic and residual volumes and surface areas of the intersection of the Laguerre diagram with the space filling model of a molecule with applications to implicit solvation. While methods exist which calculate volumes and surface areas of the restriction of the Laguerre diagram to the space filling model, our algorithm is unique in that it is based on inclusion-exclusion rather than Gauss-Bonnet which decreases the complexity of the calculation. We also optimize an adjustable parameter, the weight, so the Laguerre-Intersection atomic and residual volumes and surface areas are as close as possible to Laguerre volumes and surface areas found using explicit solvent. We test our algorithm on an explicit water HIV protease molecular dynamics trajectory. We show that volumes and surface areas computed using our implicit method are 30% to 8 times closer to explicit quantities than those found using current models. We also show that varying the weight rather than the radius in the space-filling diagram gives much better agreement with explicit quantities.
Fig. 22.
Fractional outer solid angle and fractional outer dihedral angle.
Fig. 25.
Normalized dihedral angle ϕ between planes with normals nk and nl.
Acknowledgments
Michelle Hummel and Evangelos Coutsias were supported in part by NIH grant R01GM090205 and Stony Brook University research funds. Carlos Simmerling was supported in part by NIH grant R01GM107104. Evangelos Coutsias and Carlos Simmerling acknowledge support from the Laufer Center for Physical and Quantitative Biology at Stony Brook University. A portion of this work was carried out at the Department of Mathematics and Statistics, Univerisity of New Mexico.
Appendix A. Inclusion-Exclusion Volume and Surface Area Formulas
The equations in sections 3.2 and 3.3 are extensions od the short inclusion-exclusion formulas for the atomic surface areas and volumes of a molecule discussed in 9,10, 23, 11. We use the same notation as in 3.2.
The terms ST and VT are the surface area and volume respectively of the intersection of the balls in T (See Figure 21). The surface area and volume of the union of balls are 9,10,
| (A.1) |
| (A.2) |
where V is the volume of the tetrahedra in the alpha complex and the coefficients, cT, are given in Section 3.2.
Fig. 21.
Volume (blue) and surface area (red) contributions from simplices of dimensions one, two, and three.
The term gives the total surface area of the molecule, but we are also interested in the contribution of an individual atom, pi, to the total surface area. Call this term . Then
| (A.3) |
where is the contribution of ST to with
| (A.4) |
These formulas will be given in subsequent sections. The sum A.3 may also be taken over all σT ∈ ∂C such that pi ∈ T since if .
A.1. Equations
A.1.1. |T| = 1: Volume and Surface Area
Consider T = {pi}. The formulas for the volume and surface area of a ball are
| (A.5) |
| (A.6) |
| (A.7) |
Let be the set of tetrahedra in to which the vertex pi is incident. For define ωI as the normalized inner solid angle subtended by the tetrahedron σI from the point . Then
| (A.8) |
The normalized inner solid angle, ω, of a tetrahedron subtended by the vectors , , and (See Figure 23) is given by the equation
| (A.9) |
where a = |a| and likewise for b and c (See Figure 23).
Fig. 23.
Normalized inner solid angle, ω, subtended by , , and .
A.1.2. |T| = 2: Volume and Surface Area
Consider T = {pi, pj}. The formulas for the volume and surface area of the intersection of the two balls, pi and pj are
| (A.10) |
| (A.11) |
| (A.12) |
| (A.13) |
where hi and hj are the heights of the spherical caps of pi and pj (See Figure 24).
Fig. 24.
Heights of the spherical caps and the partition of the surface area ST between two atoms.
The characteristic point, x ∈ ℝ3 × ℝ, of the edge σT satisfies
| (A.14) |
for some scalar t (See Figure 6). Equations A.14 gives
Define and . Then
| (A.15) |
and
| (A.16) |
Let be the set of tetrahedra in to which the edge σT is incident. For define ϕI as the normalized inner dihedral angle of σI along σT. Then
| (A.17) |
The normalized dihedral angle between planes with normals nk and nl is
| (A.18) |
Assume plane k is defined by the vectors and and the plane l is defined by the vectors a and . Then
| (A.19) |
A.1.3. |T| = 3: Volume and Surface Area
Consider T = {pi, pj, pk}. The volume and surface area of the common intersection of three balls can be written as a weighted sum of the surface area of the single and the double intersections. If pi, pj, and pk have a non-empty intersection then there are two points in common with the surfaces of all three balls. Call one of these points x′, define px = (x′,0) ∈ ℝ3 × ℝ, and let Tx = {pi, pj, pk, px}. Let S2 be the set of edges defined by and S1 the set of vertices in .
The volume and surface areas (See Figure 26) of the intersection of pi, pj, and pk are given by 15
| (A.20) |
| (A.21) |
| (A.22) |
| (A.23) |
| (A.24) |
where Φ{i, j} is the normalized dihedral angle of along the edge σ{i, j}, Ωi is the normalized solid angle of subtended from , and similarly for other combinations i, j, and k.
Fig. 26.
Partition of ST between the three atoms.
The point x satisfies the following equations
| (A.25) |
| (A.26) |
| (A.27) |
Let and , which gives the normal to the plane that contains σT as n = a × b. The characteristic point, xc, of the triangle σT was found in the computation of the alpha complex and satisfies x = xc + hn where h is the height of x above the plane containing σT. Plugging this into equation A.25 gives
| (A.28) |
The vector is orthogonal to n which gives
| (A.29) |
where is the size of the triangle σT.
Given a triangle, σT, its coefficient is given by
| (A.30) |
The triangle, σT, transitions from singular to regular when an incident tetrahedron becomes part of the alpha complex.
A.2. |T| = 4: Volume
Consider T = {pi, pj, pk, pl}. Let , , and . The volume of the tetrahedron σT is given by
| (A.31) |
Appendix B. Exterior Facet Area Computation Pseudocode
!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! !COMPUTE AREA OF LAGUERRE INTERSECTION FACET OF EXTERIOR EDGE !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! ! !surf = area of the Laguerre intersection facet !num_ring = number of nodes in Laguerre intersection facet !nodes = num_ring x 3 matrix ! contains coords of counterclockwise ! Laguerre nodes of tetrahedra in alpha complex ! with characteristic points of appropriate ! boundary triangles inserted !x = center of characteristic point of edge ! !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
surf=0
temp_vec=0
a=nodes(2,:)-x
do i=2,num_ring
b=nodes(i,:)-x
temp_vec=cross_product(b,a)
if (dot_product(temp_vec,edge)>=0 ) then
surf=surf+.5d0*sqrt(temp_vec)
else
surf=surf-.5d0*sqrt(temp_vec)
end if
a=b
end do
b=nodes(1,:)-x temp_vec=cross_product(a,b)
if (dot_product(temp_vec,edge)>=0 ) then surf=surf+.5d0*sqrt(temp_vec) else surf=surf-.5d0*sqrt(temp_vec) end if
Appendix C. Glossary
- π
- Power distance between weighted point and unweighted point; π(p, x′) = |p′ − x′|2 − p″.
- σT
- A simplex which is the convex hull of point centers in set T.
A
- Set of weighted data points (spheres) which represents atoms in a molecule.
- Set of data point centers; .
- Set of expanded points, .
B
- Space filling model of . Equal to .
- Bi(w)
- Closed ball with center at and weight .
C
- Alpha complex of data set with α = w.
- Boundary of the alpha complex .
E
- eij
- Edge connecting the centers of pi and pj.
F
- FT
- Surface area of the intersection of the Laguerre facet corresponding to simplex σT with the interior of the alpha complex.
L
- Laguerre diagram of the data set .
- Li
- Laguerre cell of atom i.
- Li(w)
- Laguerre cell of pi(w) in .
- Lij
- Laguerre facet corresponding to edge eij.
- LI(w)
- Set of Laguerre-Intersection cells.
- LIi(w)
- Laguerre-Intersection cell of atom i with weight w.
- LISi(w)
- Surface area of LIi(w).
- Contribution of the simplex σT to LISi.
- LIVi(w)
- Volume of LIi(w).
- Contribution of the simplex σT to LIVi.
- Equivalent to .
- Equivalent to .
- Equivalent to .
- LSi
- Surface area of the Laguerre cell of atom i.
- LSij
- Surface area of facet Lij.
- LVi
- Volume of the Laguerre cell of atom i.
- Volume contribution of the edge eij to the Laguerre cell of atom i.
P
- p = (p′, p″)
- Weighted point (sphere) in ℝ3 × ℝ with center p′ and weight (radius squared) p″.
- p′
- Unweighted point or location in ℝ3.
- p″
- Weight or radius squared of point p. This can also be written as w.
- p(w)
- Expanded point p(w) = (p′, p″ + w)
- Pyramidal volume contribution of σT to LIVi.
S
- Si(w)
- Accessible surface area of atom i with solvent weight w.
- ST
- Surface area of the intersection of balls represented by points in T.
- Equivalent to where T = {pi}.
- The contribution of ST to Si.
T
- Weighted Delaunay (Regular) tetrahedrization of the data set .
- T
- Set of points corresponding to simplex in .
- |T|
- Number of elements in the set T.
- tijk
- A triangle with vertices at , , .
V
- vi
- Vertex.
- VT
- Volume of the intersection of balls represented by points in T.
W
- w
- Weight or radius squared of a data point
X
- xij
- Characteristic point of the edge eij.
- xijk
- Characteristic point of the triangle tijk.
- xT
- Characteristic point of the simplex σT. where is the center of the characteristic point and the weight is the size of the simplex.
Contributor Information
MICHELLE HATCH HUMMEL, Department of Applied Mathematics and Statistics, Stony Brook University, Stony Brook, NY 11794, USA mhhumme@sandia.gov.
BIHUA YU, Department of Applied Mathematics and Statistics, Stony Brook University, Stony Brook, NY 11794, USA bihua.yu@stonybrook.edu.
CARLOS SIMMERLING, Department of Chemistry and Laufer Center, Stony Brook University, Stony Brook, NY 11794, USA carlos.simmerling@stonybrook.edu.
EVANGELOS A. COUTSIAS, Department of Applied Mathematics and Statistics and Laufer Center, Stony Brook University, Stony Brook, NY 11794, USA evangelos.coutsias@stonybrook.edu.
References
- 1.Ban Yih-En Andrew, Edelsbrunner Herbert, and Rudolph Johannes, Interface surfaces for protein-protein complexes, Journal of the ACM 53 (2006), 361–378. [Google Scholar]
- 2.Case David A. et al. , The Amber biomolecular simulation programs, Journal of Computational Chemistry 26 (2005), 1668–1688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cazals F, Dreyfus T, and Loroit S, User manual: Space filling model surface volume, Structural Bioinformatics Library (Accessed 2017), http://sbl.inria.fr/doc/Space_filling_model_surface_volume-user-manual.html. [Google Scholar]
- 4.Cazals Frederic, Revisiting the Voronoi description of protein-protein interfaces: Algorithms, Lecture Notes in Computer Science 6282 (2010), 419–430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Cazals Frederic, Kanhere Harshad, and Loroit Sebastien, Computing the volume of a union of balls: a certified algorithm, ACM Transactions on Mathematical Software 38 (2011). [Google Scholar]
- 6.Cazals Frederic, Proust Flavien, Bahadur Ranjit P., and Janin Joel, Revisiting the Voronoi description of protein-protein interfaces, Protein Science 15 (2006), 2082–2092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Connolly ML, Analytical molecular surface calculation, Journal of applied crystallography 16 (1983), 548–558. [Google Scholar]
- 8.Edelsbrunner Herbert, Weighted alpha shapes, Technical Report (1992).
- 9.Edelsbrunner Herbert, The union of balls and its dual shape, Proceeding of the ninth annual symposium on Computational Geometry, San Diego, CA, 1993. [Google Scholar]
- 10.Edelsbrunner Herbert and Fu Ping, Measuring space filling diagrams and voids, Proc. 28th Ann. HICSS (1995). [Google Scholar]
- 11.Edelsbrunner Herbert and Koehl Patrice, The geometry of biomolecular solvation, Discrete and Computational Geometry: MSRI publications; 52 (2005), 241–273. [Google Scholar]
- 12.Esque Jeremy, Oguey Christophe, and de Brevern Alexandre G., A novel evaluation of residue and protein volumes by means of Laguerre tessellation, J. Chem. Inf. Model 50 (2010), 947–960. [DOI] [PubMed] [Google Scholar]
- 13.Esque Jeremy, Oguey Christophe, and de Brevern Alexandre G., Comparative analysis of threshold and tessellation methods for determining protein contacts, Journal of Chemical Information and Modeling 51 (2011), 493–507. [DOI] [PubMed] [Google Scholar]
- 14.Gerstein Mark, Tsai Jerry, and Levitt Michael, The volume of atoms on the protein surface: Calculated from simulation, using Voronoi polyhedra, J. Mol. Biol 249 (1995), 955–966. [DOI] [PubMed] [Google Scholar]
- 15.Gibson KD and Scheraga Harold A., Volume of the intersection of three spheres of unequal size: a simplified formula, Journal of Physical Chemistry 91, 4121–4122. [Google Scholar]
- 16.Headd Jeffrey J., Ban Y.E. Andrew, Brown Paul, Edelsbrunner Herbert, Vaidya Madhuwanti, and Rudolph Johannes, Protein-protein interfaces: Properties, preferences, and projections, Journal of Proteome Research 6 (2007), 2576–2586. [DOI] [PubMed] [Google Scholar]
- 17.Hornak Viktor et al. , Hiv-1 protease flaps spontaneously open and reclose in molecular dynamics simulations, PNAS 103 (2005), 915–920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hornak Viktor et al. , Comparison of multiple Amber force fiels and development of improved protein backbone parameters, Proteins: Structure, Function, and Bioinformatics 65 (2006), 712–725. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hummel Michelle H., Delaunay-Laguerre Geometry for Macromolecular Modeling and Implicit Solvation, Ph.D. thesis, University of New Mexico, New Mexico, 2014, Lobovault Repository, http://hdl.handle.net/1928/25782. [Google Scholar]
- 20.Jorgensen William L. et al. , Comparison of simple potential functions for simulating liquid water, The journal of chemical physics 79 (1983), 926–935. [Google Scholar]
- 21.Kollman Peter A. et al. , Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models, Acc. Chem. Res 33 (2000), 889–897. [DOI] [PubMed] [Google Scholar]
- 22.Lam PY et al. , Rational design of potent, bioavailable, nonpeptide cyclic ureas as hiv protease inhibitors, Science 263 (1994), 380–384. [DOI] [PubMed] [Google Scholar]
- 23.Liang Jie, Edelsbrunner Herbert, Fu Ping, Sudhaker Pamidighantam V., and Subramaniam Shankar, Analytical shape computation of macromolecules: I. molecular area and volume through alpha shapes, PROTEINS: Structure, Function, and Genetics 33 (1998), 1–17. [PubMed] [Google Scholar]
- 24.Mahdavi Sedigheh, Mohades Ali, Ali Salehzadeh-Yazdi Samad Jahandideh, and Masoudi-Nejad Ali, Computational analysis of RNA-protein interaction interfaces via the Voronoi diagram, Journal of Theoretical Biology 293 (2012), 55–64. [DOI] [PubMed] [Google Scholar]
- 25.Mahdavi Sedigheh, Ali Salehzadeh-Yazdi Ali Mohades, and Masoudi-Nejad Ali, Computational structure analysis of biomacromolecule complexes by interface geometry, Computational Biology and Chemistry 47 (2013), 16–23. [DOI] [PubMed] [Google Scholar]
- 26.McConkey BJ, Sobolev V, and Edelman M, Quantification of protein surfaces, volumes and atom-atom contacts using a constrained Voronoi procedure, Bioinformatics 18 (2002), 1365–1373. [DOI] [PubMed] [Google Scholar]
- 27.Ray N, Cavier X, Paul JC, and Maigret B, Intersurf: dynamic interface between proteins, J Mol Graph Model 23 (2005), 347–354. [DOI] [PubMed] [Google Scholar]
- 28.Nguyen Hai et al. , Folding simulations for proteins with diverse topologies are accessible in days with a physics-based force field and implicit solvent, Journal of the American Chemical Society 136(40). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Olechnovic Kliment, Kulberkyte Eleonora, and Venclovas Ceslovas, Cad-score: A new contact area difference-based function for evaluation of protein structural models, Proteins 81 (2013), 149–162. [DOI] [PubMed] [Google Scholar]
- 30.Rayand Nicolas, Cavin Xavier, Lorraine Inria, and Maigret Bernard, Interactive poster: visualizing the interaction between two proteins.
- 31.Sadoc JF, Jullien R, and Rivier N, The Laguerre polyhedral decomposition: application to protein folds, The European Physical Journal B 33 (2003), 355–363. [Google Scholar]
- 32.Shang Yi and Simmerling Carlos, Molecular dynamics applied in drug discovery: The case of hiv-1 protease, Methods in Molecular Biology 819 (2012), 527–549. [DOI] [PubMed] [Google Scholar]
- 33.Soyer Alain, Chomilier Jaques, Mornon Jean-Paul, Jullien Remi, and Sadoc Jean-Francois, Voronoi tessellation reveals the condensed matter character of folded proteins, Physical Review Letters 85 (2000), 3532–3535. [DOI] [PubMed] [Google Scholar]
- 34.Tan Chunhu, Tan Yu-Hong, and Luo Ray, Implicit nonpolar solvent models, The journal of physical chemistry 111 (2007), 12263–12274. [DOI] [PubMed] [Google Scholar]
- 35.Weiser Jorg, Shenkin Peter S., and Still W. Clark, Approximate atomic surfaces from linear combinations of pairwise overlaps (lcpo), Journal of Computational Chemistry 20 (1999), 217–230. [Google Scholar]
- 36.Zagrovic Bojan and Pande Vijay, Solvent viscosity dependence of the folding rate of a small protein: distributed computing study, Journal of Computational Chemistry 24 (2003), 1432–1436. [DOI] [PubMed] [Google Scholar]