Abstract
Quantitative risk assessments for physical, chemical, biological, occupational, or environmental agents rely on scientific studies to support their conclusions. These studies often include relatively few observations, and, as a result, models used to characterize the risk may include large amounts of uncertainty. The motivation, development and assessment of new methods for risk assessment is facilitated by the availability of a set of experimental studies that span a range of dose-response patterns that are observed in practice. We describe construction of such an historical database focusing on quantal data in chemical risk assessment, and we employ this database to develop priors in Bayesian analyses. The database is assembled from a variety of existing toxicological data sources and contains 733 separate quantal dose-response data sets. As an illustration of the database’s use, prior distributions for individual model parameters in Bayesian dose-response analysis are constructed. Results indicate that including prior information based on curated historical data in quantitative risk assessments may help stabilize eventual point estimates, producing dose-response functions that are more stable and precisely estimated. These in turn produce potency estimates that share the same benefit. We are confident that quantitative risk analysts will find many other applications and issues to explore using this database.
Keywords: Quantal dose-response data, Bayesian Prior elicitation, BMDS software, Carcinogenicity, Data mining, Knowledgebase, R software, Statistical methods, Toxicology
1. INTRODUCTION: ENVIRONMENTAL RISK ASSESSMENT
Public and environmental health officials studying the impacts of adverse physical, chemical, biological, occupational, or environmental agents rely on scientific studies to assess risk. Statistical modeling of data from these studies can be used to generate quantitative estimates of the risks associated with exposure to such agents. As statisticians, data scientists, and toxicologists develop new techniques to address these risk-analytic questions, it is often of interest to examine performance of the new methods on a ‘sandbox’ or ‘test bed’ of pertinent data sets containing experimental results that span a range of possible dose-response patterns. We describe the development and application of such a database here.
Modeling and analysis for quantal dose-response data has a long history of study and continues to be an active area of research in quantitative risk assessment (1–3). Quantal response data refers to data in the form of proportions, Y/n, where Y is a count of some adverse outcome among n independent subjects under study. Such outcomes are common in a variety of toxicological settings, especially when recorded alongside a concomitant predictor variable such as the dose of a potentially detrimental agent or stimulus. New methodological advances are often applied to existing data of this sort in order to examine and help validate use of the evolving methods and to compare new methods with existing techniques. When employed for purely illustrative purposes the data are typically taken from a single motivating study or experiment; however, when validation or wide-scale demonstration is desired, a test bed of pertinent quantal data would be a more favorable choice. Below, we describe a database constructed to offer investigators a resource for the coordinated study of new (and existing) risk-analytic statistical techniques with quantal-response data. The test bed is aggregated from existing, vetted data sources, and contains data sets that provide a wide range of actual dose-response patterns and shapes. It is intended as a resource for exploring how methods for analyzing quantal response data might operate in practice. Section 2 describes how we constructed the database, identifies its various sources, and details the variables associated with each entry therein. It also shows how to access the database and gives some selected applications to illustrate its use. Section 3 explores use of the database to determine prior distributions for Bayesian analyses with a suite of common quantal-response models. Section 4 ends with a brief discussion. Throughout, we conduct most core operations using the R statistical environment (4) although the database is designed for users to apply any statistical programming language/package, or even code directly, at their discretion.
2. THE QUANTAL RISK ASSESSMENT DATABASE (QRAD)
2.1. Constructing the database
To populate and curate our Quantal Risk Assessment Database (QRAD), we extracted quantal-response data from multiple sources. To begin, we accessed the Integrated Risk Information System (IRIS) data warehouse developed by the U.S. Environmental Protection Agency (EPA, see http://www.epa.gov/iris). IRIS contains information on an extensive number of chemical substances; depending on the study being reported, the adverse health effects can be either cancerous or non-cancerous. We restricted the data from IRIS to include only cancerous outcomes, following the approach taken by Nitcheva et al. (5) for constructing a smaller quantal database. For simplicity, we limited the selection to rat or mouse tumorigenicity and only if the animals’ exposure to the substances was oral (diet, drinking water, or gavage) or thru inhalation, although we did allow for differing response endpoints, such as lung and liver cancer, from the same experiment. The IRIS data provided an initial group of 90 individual quantal data sets for study.
Next, we followed Wignall et al. (6) who included quantal dose-responses over a variety of endpoints and chemical sources. These were originally sourced from IRIS, but also included quantal data from the U.S. EPA’s Provisional Peer Reviewed Toxicity Values (PPRTV), the EPA Office of Pesticide Programs (OPP), and its Health Effects Assessment Summary Tables (HEAST); from the State of California EPA (CalEPA); and from the U.S. Centers for Disease Control and Prevention’s Agency for Toxic Substances and Disease Registry (ATSDR). In particular, the data sets sourced from Wignall et al. contained IRIS entries above and beyond the original 90 quantal data sets from Nitcheva et al. Any duplicate entries were removed, leading to a total of 144 IRIS quantal data sets for our use. Further, many of the CalEPA studies were themselves duplicates of the IRIS studies, and these were also removed.
In all, 733 unique quantal data sets for 333 different chemicals were extracted from these five data sources. The 333 unique chemicals in this database have all been the subject of previous risk assessments. Among them, only 1.6% of the experiments have 7 or more dose groups (the modal number of dose groups including control is 4, the maximum is 16) and over 80% of the experiments had between 3 and 5 dose groups. Also, more than 50% of the database is derived from IRIS (371 entries) with CalEPA contributing 235 entries. Only 3 entries were from ATSDR. Our QRAD can be found online at http://www.users.miamioh.edu/baileraj/research/.
Directions for accessing QRAD can be found in §2.2, below. Approaches for constructing summary descriptions of the database are described in §2.3 and in Sections S.1–S.3 of a Supplemental Document.
Within the database, each data set provides the following information:
a unique identifier code (ID), from 1 to 733 (integer)
each agent’s chemical name (string)
the source from which we compiled the data set (data.source), e.g., “IRIS,” “CalEPA,” etc. (string)
the chemical’s Chemical Abstracts Service Registry Number (CASRN); see http://www.cas.org/content/chemical-substances/faqs (string)
the dose, d, in whatever units were listed in the original data set source (numeric)
doses scaled to the unit interval, i.e., d/max{d}, denoted as r.dose (numeric)
the number of independent subjects, n, studied at each dose (integer)
the number of observed responses, Y, at each dose, denoted as obs (integer)
the organ system in which outcomes were observed to produce the values in Y (above) (string)
the particular toxicological or carcinogenic outcome recorded to produce the values in Y (above), denoted as effect (string)
if available, the publication or other product (study.source) from which the original data were acquired (string)
Supplemental Fig. S.2 displays the various empirical shapes of the dose-response curves within the database, stratified by data source. From this figure, we find that a much larger number and variety of patterns are contributed by the IRIS and CalEPA sources, confirming that these were the source of most of the entries in QRAD. In addition, a wide range of dose-response shapes, from sub-linear to super-linear, is indicated.
2.2. Accessing and manipulating the database
Our collected QRAD construct is fashioned as an R data frame and is also available as a comma delimited table. In what follows we access the database from R. The core file can be read into R using the load command. For example, the following sample code loads the object with the database of dose responses, final.data, into the user’s R Global Environment where the file is located in the directory ‘/users/your_username/Downloads’. This new object is a data frame in R.
setwd(“/users/yourusername/Downloads”) # move to the containing directory load(“database.RData”) # load database
Alternatively, one may wish to load this database from the website. To do this, enter the command
load(url(“http://www.users.miamioh.edu/baileraj/research/database.RData“))
It is simple to list the variables included in QRAD (cf. the list above); e.g., the command
names(final.data)
produces
[1] “ID” “chemical” “data.source” “CASRN” “dose” [6] “r.dose” “n” “obs” “organ” “effect” [11] “study.source”
It is also relatively straightforward to learn more about these data. For example, query which organ systems were tested via unique(final.data$organ).
Additionally, if the database is saved as a csv file, QRAD can be imported into other software platforms. For example, the following code would read the file database.csv into SAS® for additional analysis. Information about the variables in the SAS data set ‘FinalData’ is generated by an application of the PROC CONTENTS procedure (7):
proc import datafile=“path_directory_with_database\database.csv” out=FinalData dbms=csv replace; getnames=yes; run; proc contents data=FinalData; run;
2.3. Basic summaries: number of chemicals and numbers of dose groups
After downloading the database, one might wish to start exploring its features. We often employ the dplyr package in R (8) to build data frames with particular summary information. In the code below, we process the data by ID to calculate the number of dose groups in each ID and to save this as a new data frame.
library(dplyr) Summary1 <- final.data %>% group_by(ID) %>% summarise(nDoseGrps = n())
After constructing this new data frame with counts of the number of dose groups associated with each ID, we can generate relative frequencies for the numbers of dose groups in each experiment. In the sample code below, the table function produces a one-way frequency table, while the length function counts the number of IDs:
with(Summary1, round(table(nDoseGrps)/length(nDoseGrps), digits=3)*100)
The output (edited for presentation) is:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 10 | 13 | 16 |
| 13.0 | 31.8 | 40.0 | 7.9 | 5.7 | 0.5 | 0.1 | 0.4 | 0.3 | 0.3 |
We discern in QRAD that the modal experiment size is 4 dose groups (40% of the studies) and approximately 80% of the studies have between 3 and 5 dose groups. This is consistent with past reports on numbers of dose levels in toxicological assays: Nitcheva et al. (5) found that that the most common number of doses used among the 91 rodent carcinogenicity studies they studied (most of which are contained in our database) was three; next most common was four. Similarly, Muri et al. (9) reported that the most prevalent study design they found among 20 pesticide risk analyses again employed only four doses, and did so almost twice as often as the next most-common design (which used five doses). Within this context, one surprise in our database is the 1% of studies possessing 10 or more dose groups: this appears to be a relatively uncommon occurrence in studies used in support of toxicological risk assessments.
A simple graphical display for the numbers of dose groups can be generated using the ggplot package in R (10). Sample code is
library(ggplot2) ggplot(Summary1,aes(x=nDoseGrps)) + geom_bar() + xlab(“Number of Dose Groups”) + ylab(“Frequency”) + theme_minimal()
which produces the histogram in Fig. 1.
Fig. 1.
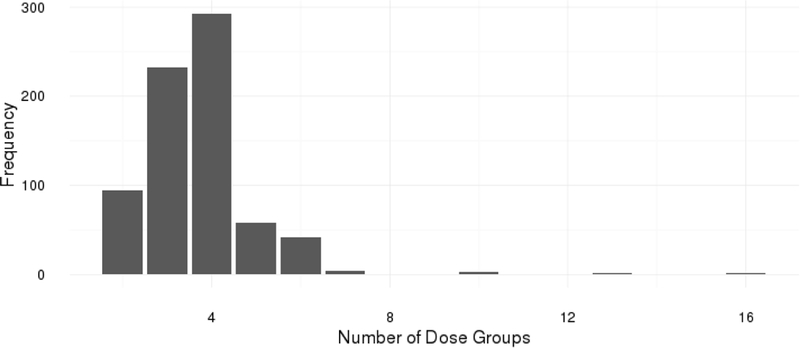
Numbers of dose groups per data set in the quantal-response database
A supplemental document illustrates a few other, basic commands for manipulating QRAD, including ways to subset it and to apply a function to all data sets in the database.
3. MINING QRAD TO FORM PRIOR DISTRIBUTIONS IN BAYESIAN QUANTAL-RESPONSE ANALYSIS
3.1. Quantal-Response Models
We illustrate a more-advanced use of QRAD by addressing an intriguing problem in dose-response analytics: how to specify prior distributions on unknown parameters in a Bayesian quantal-response analysis. We assume the responses Yi are independent binomial variates, Yi ~ Bin.(ni, π(di)), where π(di) is the underlying function describing the response probability P[Yi = 1|di] at dose di (i = 1,..., m). The dose-response function π(d) can take one of several potential forms—see the list below—each of which depends one or more unknown parameters, say, α, β0, β1, γ, etc.
For the possible dose-response function we employed the following quantal-response models, available in the U.S. EPA’s popular BMDS system (11):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
| (8) |
Bayesian analysis of quantal dose-response data has a long and rich history—see, e.g., Ramsay (12); Tsutakawa (13); Messig and Strawderman (14); Kuo and Cohen (15); or Novelo et al. (16). As these sources suggest, Bayesian quantal-response modeling often expands the inferential capacity of the analysis, offering the analyst heightened flexibility, greater connection to the data, and in particular more efficient use of information that can be gleaned from previous studies. Indeed, its application here has the added benefit of enhancing the limited information in the data when only a few doses are studied. As we saw in Fig. 1, the great majority of quantal-response designs employ up to 4, or perhaps 5, dose groups. These small numbers of doses often provide only limited information on the shape of the underlying dose response in an individual experiment. By incorporating a Bayesian hierarchical construction in such cases, information supplied by the prior augments and updates information in the data when conducting posterior inferences on parameters of interest.
To cement the notation, consider use of the quantal-linear model π1(d) from (1), and suppose interest focuses on some function of the β1 parameter, say, g(β1,). Writing the data vector as Y = [Y1 … Ym]T, the likelihood function under the binomial model is . Denote the prior for β1 as p(β1) and the prior for γ as p(γ), so that the posterior for β1 is p(β1|y) ∝ p(β1)ƒ(y|β1); the posterior for γ is similarly defined. For most practical choices on the prior for β1, including those we propose below, the posterior p(β1|y) will be algebraically intractable. To manage the posterior calculations we turn to Monte Carlo Markov Chain (MCMC) methods (17, §6.3): simulate a (long) Markov chain of β1 values whose stationary distribution is designed to converge to p(β1|y), and view the resulting realizations of β1 as an approximation of a random sample from the posterior p(β1|y). Point and interval estimates for g(β1) can be taken from appropriate components of the transformed chain of g(β1) values.
Specification of prior(s) on the parameters for such Bayesian dose-response analyses can be a thorny issue (18–20). When previous experimental results or domain-specific expert knowledge are available from which to elicit the prior, such knowledge should be the first recourse (21). Otherwise, however, determination or specification of prior components in a Bayesian (or any hierarchical) model is often a difficult exercise. Here, we query QRAD to identify potential prior forms for use in a Bayesian quantal-response analysis. Our approach has the flavor of a data mining study (22), where information in a large knowledgebase such as QRAD is employed to expand our understanding of the quantal-response issue(s) under study and to advance the consequent data analysis.
To develop the priors from QRAD we first filtered out those experiments providing only minimal information on the shape of their dose-response relationships, namely, experiments with fewer than 4 dose groups or fewer than 100 observations. The requirement for 100 or more observations ensured that sufficient dose-response information was available to accurately represent the underlying biological processes, while the requirement of four or more dose groups was used to help prevent the three-parameter models from overfitting. This resulted in 269 data sets, which we employed to develop historically-based priors for the various parameters (i.e., the βs, α, and γ, as necessary) of Models (1)–(8), above. In some cases, we enforced a series of monotonicity constraints to match use in practice or avoid numerical instabilities. In particular, we required βj ≥ 0 (j = 1,2) for all models, although we left β0 unconstrained in Models (5)–(8). Also, whenever a background response parameter, γ, was included, we set 0 ≤ γ ≤ 1. Lastly, for models (3) and (4) we required α ≥ 0.2 to avoid numerical problems, rather than the somewhat more-common constraint of α > 0.
3.2. Fitting the models and finding empirical priors
Our strategy adopted a relatively straightforward approach: using the filtered database, Models (1)–(8) were fit to the data and their various parameters were estimated as the posterior modes after imposing vague, flat priors on every parameter; this corresponded to fitting via the method of maximum likelihood. We then took the empirical collection of 269 such estimates for each model/parameter combination and used it to identify a possible parametric distribution for that parameter’s prior. For simplicity, we considered three basic forms: (i) a lognormal distribution LN(μ,σ2) with mean exp{μ + ½σ2} and variance {exp(σ2) – 1}exp{2μ + σ2} for parameters restricted to a positive support and displaying a clear positive skew, (ii) a normal distribution N(μ,σ2) mean μ and variance σ2 for parameters varying over the entire real line and where the empirical pattern was more general, and (iii) a beta distribution Beta(a,b) with shape parameters a and b for parameters restricted to the unit interval.
To produce specific prior recommendations for each model/parameter combination, we kept the effort simple and appealed to moment-type estimation schemes. For (i) the LN(μ,σ2) prior we took a logarithmic transformation of the 269 estimated values for that parameter and then set μ equal to its log-mean and σ2 equal to its log-variance. Cases where the original parameter estimate was zero—corresponding to a ‘boundary’ occurrence for that parameter—were excluded, as were cases where the BMDS software ran the point estimate up to its arbitrary maximum of 18, which we viewed as indicators of aberrant response for that particular model.
For the special case of the α parameter in the Weibull Model (3) and the gamma Model (4) with restricted support 0.2 ≤ α < ∞, we first subtracted the known lower bound, 0.2, to produce a shifted parameter α′ = α – 0.2, and then proceeded to fit the lognormal model as described above.
For (ii) the N(μ,σ2) prior, we found the sample mean and sample variance of the 269 estimated values for the given parameter and set them equal to μ and σ2, respectively.
For (iii) the Beta(a,b) prior—which applied only for the background response parameter γ in Models (1)–(4), (6), and (8)—we found the sample mean of the 269 estimated γ values. We then set these equal to the Beta mean and variance, and , respectively, and solved for a and b.
Our results appear in Table 1. Therein, we see that the majority of recommended priors are lognormal, where we found that the empirical distributions exhibited clear positive skew. We felt the lognormal was a reasonable choice for these recommended priors, which correspond to essentially all the βj coefficients (j ≠ 0) and also the shifted α′ parameters in Models (3) and (4). (Of course, other distributional choices are possible here, and we comment further on this in the Discussion section, below.) We should acknowledge that this selection carries with it an important consequence: for any parameter associated with the dose-response relationship—e.g., the various βj parameters—the lognormal prior forces P[βj = 0] = 0. In effect, this assumes that the associated dose response is real. To incorporate the possibility that the dose response is flat, a more-complex prior needs to be constructed, e.g., a mixture of a continuous density for βj > 0 and a non-zero mass at P[βj = 0] or some other form of spike-and-slab prior (23).
Table 1.
Summary statistics and recommended empirical prior distributions for Models (1)–(8) developed from QRAD. Model numbers and parameters correspond to those described in the text. For recommended priors: N(μ,σ2) indicates a normal distribution with mean μ and variance σ2, LN(μ,σ2) indicates a log-normal distribution with mean and variance , while Beta(a,b) indicates a Beta distribution with shape parameters a and b.
| sample statistics |
|||||||
|---|---|---|---|---|---|---|---|
| Model | parameter | minimum | median | maximum | mean | variance | recommended prior |
| Quantal linear (1) | γ | 0 | 0.041 | 1 | 0.109 | 0.025 | γ~ Beta(0.313, 2.545) |
| β1 | 0 | 0.583 | 17.770 | −0.470* | 1.688* | β1 ~ LN(-0.470, 1.688) | |
| Multi-stage (2) | γ | 0 | 0.041 | 0.947 | 0.112 | 0.025 | γ~ Beta(0.326, 2.582) |
| β1 | 0 | 0.241 | 11.394 | −1.006* | 4.949* | β1 ~ LN(-1.006, 4.949) | |
| β2 | 0 | 0.063 | 15.874 | −1.016* | 5.013* | β2 ~ LN(-1.016, 5.013) | |
| Weibull (3) | γ | 0 | 0.034 | 0.947 | 0.095 | 0.022 | γ~ Beta(0.271, 2.583) |
| α | 0.20 | 1.051 | 17.619 | −0.243* | 2.467* | α-0.2 ~ LN(-0.243, 2.467) | |
| β | 0 | 0.706 | 11.388 | −0.464* | 1.535* | β ~ LN(-0.464, 1.535) | |
| Gamma (4) | γ | 0 | 0.034 | 1 | 0.097 | 0.023 | γ~ Beta(0.276, 2.572) |
| α | 0.20 | 1.098 | 17.799 | −0.153* | 2.637* | α-0.2 ~ LN(-0.153, 2.637) | |
| β | 0 | 0.924 | 16.119 | −0.587* | 5.659* | β ~ LN(-0.587, 5.659) | |
| Logistic (5) | β0 | −16.491 | −2.446 | 2.889 | −2.526 | 3.733 | β0 ~ N(-2.526, 3.733) |
| β1 | 0 | 2.734 | 16.734 | 1.018* | 0.603* | β1 ~ LN(1.018, 0.603) | |
| Log-Logistic (6) | γ | 0 | 0.031 | 1 | 0.097 | 0.023 | γ~ Beta(0.275, 2.571) |
| β0 | −4.789 | 0.095 | 7.353 | 0.203 | 4.061 | β0 ~ N(0.203, 4.061) | |
| β1 | 0.200 | 1.314 | 17.760 | 0.274* | 0.960* | β1 ~ LN(0.274, 0.960) | |
| Probit (7) | β0 | −11.844 | −1.431 | 1.619 | −1.660 | 3.264 | β0 ~ N(-1.66, 3.264) |
| β1 | 0 | 1.537 | 13.519 | 0.473* | 0.638* | β1 ~ LN(0.473, 0.638) | |
| Log-Probit (8) | γ | 0 | 0.050 | 0.947 | 0.104 | 0.022 | γ~ Beta(0.333, 2.877) |
| β0 | −17.400 | 0.047 | 11.176 | −0.514 | 10.337 | β0 ~ N(-0.514,10.337) | |
| β1 | 0.200 | 0.914 | 5.926 | −0.186* | 0.579* | β1 ~ LN(-0.186, 0.579) | |
It is also useful to note that the lognormal priors all correspond to parameters whose parent model places restrictions on their range. Figure 2 gives a representative example of the empirical distribution and the recommended lognormal prior for the β1 parameter from the probit dose-response model (7).
Fig. 2.
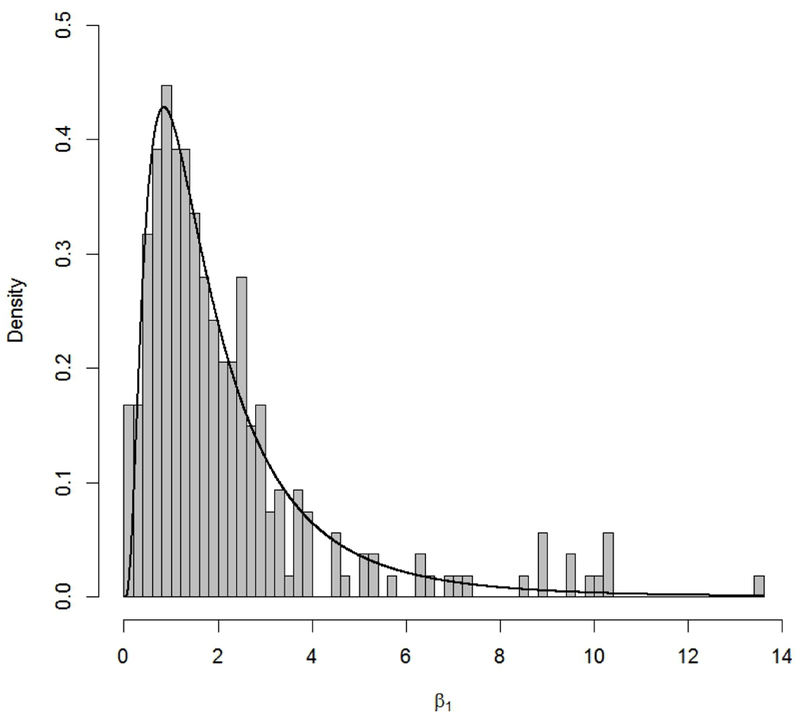
Empirical distribution (histogram) of shape parameter β1 for the probit dose-response model (7) and corresponding recommended prior (black curve), β1 ~ LN(0.473, 0.638), from Table 1.
In those cases from Table 1 where no restriction was placed on the parameter, corresponding to the β0 parameter in Models (5)–(8), we recommend as a starting approximation a Normal prior primarily; Figure 3 gives an example with the log-logistic model (6). Lastly, for the shape parameter α in models (3)–(4) we again found that both empirical distributions exhibited a substantial positive skew. (Recall that, for simplicity, we operate with the shifted shape parameter α′ = α – 0.2 for these two models.) This led us to once more recommend the lognormal for these parameters. Similar graphical displays of the empirical distributions and recommended priors for all the model/parameter configurations in Table 1 are given in the supplemental material.
Fig. 3.
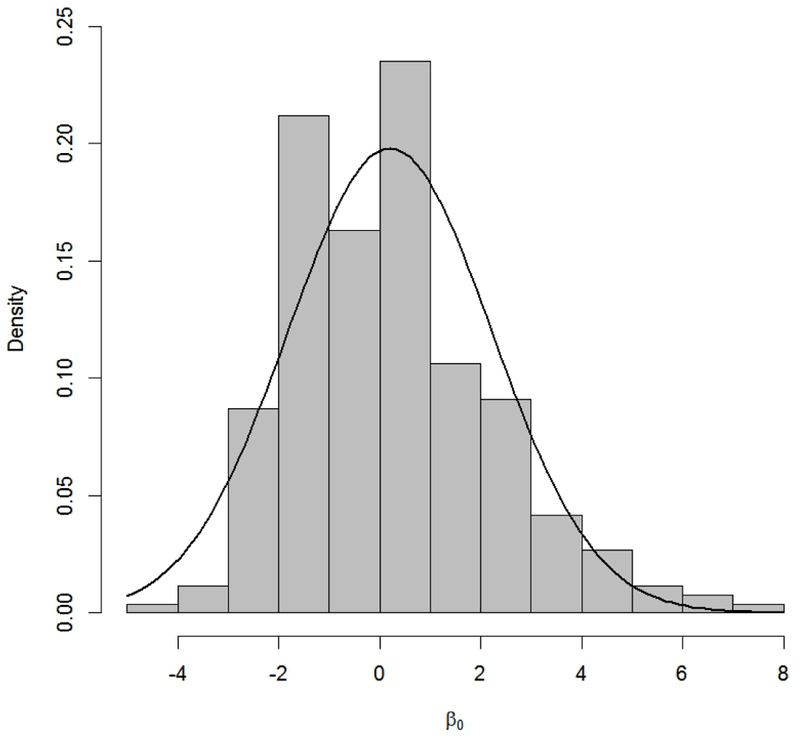
Empirical distribution (histogram) of parameter β0 for the log-logistic dose-response model (6) and corresponding recommended Normal prior (black curve), β0 ~ N(0.203, 4.061), from Table 1.
We list in Table 2 the cases from Table 1 where the lognormal distribution is recommended, along with some additional calculations. For instance, it is instructive to note that all the prior expectations exp{μ + σ2/2} are close to or above 1.0; smallest is the log-probit β1 parameter with prior expectation 1.108. This despite the fact that in no cases were the underlying parameter estimates constrained to be greater than or equal to 1.0, as is sometimes recommended for many of these models. Simply from an empirical perspective this gives evidence that shape parameters for many of the models in Table 1 are typically greater than 1, and it gives credence to the argument for avoiding or at a minimum employing some form of model averaging (2, 24) to down-weight use of supralinear curves—i.e., curves where the shape parameter is less than 1—with dose-response data such as found in QRAD (25).
Table 2.
Summary statistics for various parameters in selected lognormal models from Table 1, as extracted from QRAD. Model numbers and parameters correspond to those described in the text. Reported means and variances are based on QRAD estimates after logarithmic transformation.
| Model (no.) | parameter | mean, μ | variance, σ2 | expected value* | percentiles: | 12.5% | 87.5% |
|---|---|---|---|---|---|---|---|
| Quantal-linear (1) | β1 | −0.470 | 1.688 | 1.453 | 0.130 | 2.902 | |
| Multi-stage (2) | β1 | −1.006 | 4.949 | 4.341 | 0.0 | 2.052 | |
| β2 | −1.016 | 5.013 | 4.440 | 0.0 | 1.303 | ||
| Weibull (3) | α | −0.243† | 2.467† | 2.693† | 0.370 | 2.594 | |
| β | −0.464 | 1.535 | 1.355 | 0.130 | 2.659 | ||
| Gamma (4) | α | −0.153† | 2.637† | 3.206† | 0.315 | 3.510 | |
| β | −0.587 | 5.659 | 9.414 | 0.039 | 5.854 | ||
| Logistic (5) | β1 | 1.018 | 0.603 | 3.744 | 1.100 | 6.620 | |
| Log-Logistic (6) | β1 | 0.274 | 0.960 | 2.125 | 0.448 | 3.777 | |
| Probit (7) | β1 | 0.473 | 0.638 | 2.206 | 0.589 | 3.687 | |
| Log-Probit (8) | β1 | −0.186 | 0.579 | 1.108 | 0.311 | 1.948 |
The empirical distributions as well as the histograms in Figs. 2–4 call into question the large range of values often assigned to parameters in a dose-response analysis. Consider, e.g., the shape parameters in our various models: α for the Weibull (3), α for the gamma (4), β1 for the log-logistic (6), and β1 for the log-probit (8). In EPA’s BMDS system (26) these parameters are constrained to be at or smaller than 18, and options are often available to also force them larger than or equal to 1. Yet, for a majority of occurrences in QRAD—say, 75% of the empirical values for each parameter, between its 12.5% and 87.5% percentiles—these shape parameters appear to lie in a much smaller range of values, with many values less than 1 and few above roughly 4; see Table 2. Large values of these shape parameters lead to high curvature in the dose-response pattern. Indeed, very large values approach extremes such as a “hockey stick” dose response that starts near zero and remains essentially flat until a certain point, after which it rises very quickly to almost 100%. Many authors argue that such patterns are biologically unreasonable, and that a simple maximum likelihood fit leading to them requires adjustment. Use of informative priors for the shape parameter in a Bayesian dose-response analysis may shrink the eventual shape estimate away from large extremes, reducing the number of fitted dose-response curves that take on such biologically unreasonable patterns.
Fig. 4:
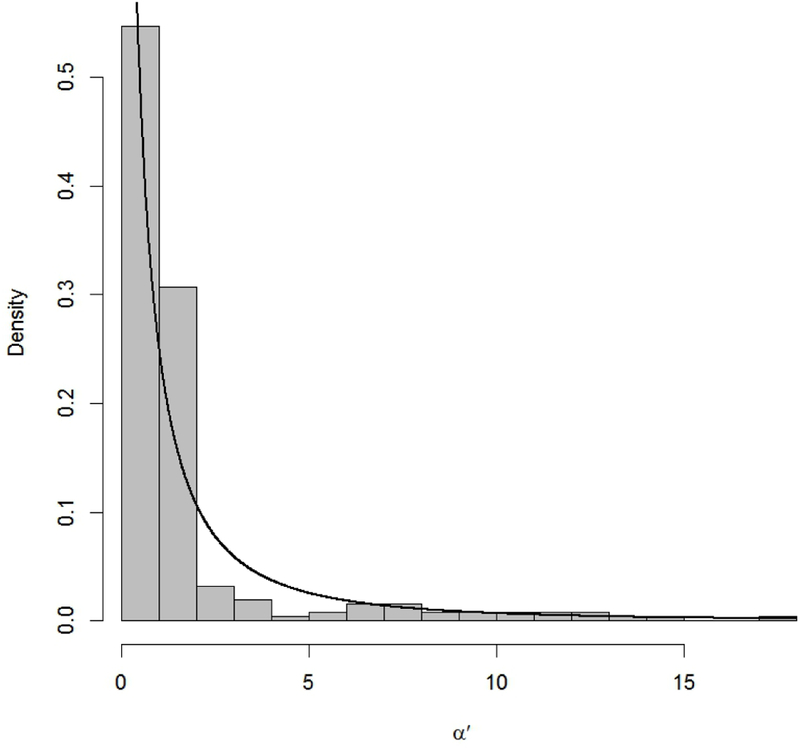
Empirical distribution (histogram) relating to shape parameter α for the Weibull dose-response model (3) and corresponding recommended prior (black curve), α′ = α–0.2 ~ LN(–0.243, 2.467), from Table 1.
Alert readers will no doubt have noticed that the various empirical priors recommended for the background probability parameter γ in Models (1)–(4), (6), and (8) are all almost identical. This stems from the very similar means and variances of the empirical γ values across these six models. This seems reasonable: γ represents the same quantity, π(0) = P[Y = 0|d = 0], for every model in which it appears, and this value would not be expected to vary greatly across the differing models. Indeed, pooling across all 269 dose-response patterns chosen for this analysis to find the empirical background proportions Y/N at d = 0 yields a mean proportion of 0.097, and a corresponding variance of 0.024. These compare favorably with their six analogous combinations in Table 1. The associated, pooled Beta prior is γ ~ Beta(0.262, 2.429), which, again, is roughly similar to the six recommended priors for γ in Table 1. Whether to use this pooled prior for γ or use the individual priors in Table 1 is, we feel, a matter of taste. Lastly, within the context of this discussion on background probabilities, it has not escaped our attention that QRAD can serve the additional value as a source of historical control data (16, 27, §7.4) for risk analysts seeking such a database.
We should also mention that the number of significant digits displayed for the various recommended priors in Table 1 is done so only for the sake of precision. It would certainly be reasonable in practice to set, say, γ ~ Beta(0.25, 2.5) when employing the pooled Beta prior for γ, and apply a similar sort of rounding for any of the other recommended priors in Table 1.
4. EXAMPLE: BAYESIAN BENCHMARK ANALYSIS OF 3-MONOCHLOROPROPANE-1,2-DIOL
As a formal example, we analyze renal tubule hyperplasia data in male Sprague-Dawley rats exposed to 3-monochloropropane-1,2-diol, a chemical food contaminant and suspected mammalian carcinogen (28). At exposure doses of d1 = 0, d2 = 25, d3 = 100, and d4 = 400 ppm the following proportions of affected animals were observed: Y1/N1 = 1/50, Y2/N2 = 11/50, Y3/N3 = 21/50, and Y4/N4 = 36/50 respectively. These data do not appear in QRAD; however, they have been the subject of previous risk assessments by the European Food Safety Authority (EFSA) (29) and by the Food and Agricultural Organization of the United Nations (FAO) in concert with the World Health Organization (WHO) (30). Intriguingly, across both studies carcinogenic potency estimates varied by an order of magnitude. One source of the disparities seen in such previous risk assessments with these data was the different modeling assumptions applied by previous analysts, using the Weibull (3), Gamma (4), Log-logistic (6), and Log-Probit (8) models from Section 3. For the EFSA risk assessment, the shape parameters for these models were left unconstrained, while for the FAO/WHO risk assessment, the shape parameters were constrained to be greater than 1. Our goal here is not to supplant these previous results, but instead simply to investigate the effect of the priors developed from QRAD in Table 1 on the analysis of these data where we permit the shape parameters to take values less than 1.
We conducted a Bayesian analysis similar to the EFSA risk assessment (29) but applied (independent) informative priors developed from QRAD. For comparison purposes, we also applied independent, vague, uniform priors similar to those suggested by Shao and Shapiro (31). In particular, with the Weibull and Gamma models we assumed α ~ U((0.2, 18), β ~ U(0,18), and γ ~ U(0,1) while with the Log-Probit and Log-Logistic models, we assumed β0 ~ U(–18, 18), β1 ~ U(0, 18), and γ ~ U(0,1).
We applied all these various hierarchical models to the 3-monochloropropane-1,2-diol data using RStan ver. 2.14, an R package that implements fully Bayesian statistical analysis via Markov Chain Monte Carlo (MCMC) methods (32). To conduct the MCMC operations for each model fit we sampled 25,000 realizations of the pertinent Markov chain(s), with the first 1,000 samples discarded as burn-in. As a measure of carcinogenic potency/risk, we calculated the benchmark dose (BMD) based on inverting each dose-response model’s extra risk function at a benchmark response (BMR) of 10% (27, §4.3). For reporting purposes, we followed standard practice and found the lower 95% limit on the BMD (a 95% BMDL). The BMDL is taken as the lower 5% percentile from each generated MCMC posterior.
Table 3 reports summary statistics for the posterior distributions of the BMD at BMR=0.10 under each of the four candidate dose-response models. From the table we see that use of the informative priors consistently decreases variation in the posterior BMDs, recognized as lower standard deviations and IQRs vs. the vague uniform (‘flat’) priors, across all four models. Posterior BMD means and 95% BMDLS are also consistently reduced, to where the ratios of mean BMD/BMDL (a measure of precision in the benchmark-dose calculations: higher ratios indicate better precision) are markedly higher under the informative priors for the first three models in Table 3, and are roughly equal for the Log-Probit model (8).
Table 3.
Summary characteristics from MCMC-based posterior distributions of the Benchmark Dose (BMD) at BMR = 0.10 for four dose-response models referenced in Section 3. The benchmark dose lower bound (BMDL) is the lower 5% percentile from the generated MCMC posterior. Results are stratified by type of priors used in the analysis: (i) Informative Priors from Table 1 or (ii) Vague Uniform (‘Flat’) priors as described in the text.
| Model (no.) | Mean | Sth. Dev. | IQR | BMDL | Mean/BMDL |
|---|---|---|---|---|---|
| Informative Priors |
|||||
| Weibull (3) | 0.68 | 0.49 | 0.58 | 0.11 | 6.18 |
| Gamma (4) | 0.55 | 0.45 | 0.53 | 0.06 | 9.17 |
| Log-Logistic (6) | 0.94 | 0.55 | 0.67 | 0.23 | 4.09 |
| Log-Probit (8) | 1.05 | 0.56 | 0.68 | 0.32 | 3.28 |
| Flat Priors |
|||||
| Weibull (3) | 0.99 | 0.68 | 0.77 | 0.20 | 4.95 |
| Gamma (4) | 1.09 | 0.83 | 0.90 | 0.20 | 5.45 |
| Log-Logistic (6) | 1.19 | 0.73 | 0.83 | 0.31 | 3.84 |
| Log-Probit (8) | 1.35 | 1.79 | 0.83 | 0.35 | 3.86 |
Abbreviations: IQR = lower limit. interquartile range; BMDL = (95%) benchmark dose
It is worth noting that the use of models with restrictions such as α > 1, which caused some of the analytic discrepancies with these data between the EFSA and the FAO/WHO, is based upon previous calculations that produced confidence intervals for the individual parameters of wide, often unreasonable, lengths. As seen in our analysis, use of informative priors and their consequent, less-restricted, dose-response models may assuage this concern as the informative priors can help decrease overall uncertainty in the posterior BMD estimates.
5. DISCUSSION
We have described the construction and exploration of a test bed knowledgebase of quantal dose-response data, the Quantal Risk Assessment Database (QRAD), useful for coordinated study of new or existing data-analytic methods in quantitative risk analysis. The database contains 733 separate quantal dose-response data sets, representing 333 unique chemicals and exhibiting a panoply of patterns and shapes.
Our initial analyses with QRAD illustrate the database’s flexibility for addressing different scientific questions of interest to the environmental risk assessment community. Obviously, however, much more could be accomplished; e.g., one might explore QRAD to help define a core range of dose-response configurations typically encountered in toxicological dose-response experimentation. Indeed, our example in §3 with specification of prior distributions for the model parameters in Bayesian dose-response analysis is only one such potential illustration, and even there we only scratch the surface. A deeper analysis would consider other distributional forms for the various priors, along with comparisons of the resulting posterior inferences. For the many positive parameters in Table 1 exhibiting highly skewed patterns, useful alternative priors could include the gamma, inverse gamma, or Weibull—not to be confused with the Weibull response model (3)—or perhaps some more exotic forms such as Erlang, Rayleigh, or inverse Gaussian. For the unrestricted β0 parameters, alternative priors include the extreme value (Gumbel), logistic—not to be confused with the logistic response model (5)—or Cauchy distributions. (See Forbes, et al. (33) or Thomopoulos (34) for details on any of these distributional forms.)
In the end, our hope is that availability of this database will enable risk analysts to answer questions about the shape and type of models used in quantal dose-response analysis. For instance, it is well-known that the probit and logistic models produce very similar fits over large portions of the dose-response curve, and some may question the need for both models in risk assessment practice. As QRAD contains over 700 dose-response data sets—all having been employed for risk assessment purposes—the effect of removing the probit or the logistic model could be explored by analyzing their model fits across the entire database. Such an analysis would add a transparency to any future decisions based on these models, and may allow for the creation of general dose-response modeling guidance based upon data used in risk assessment.
Supplementary Material
ACKNOWLEDGMENTS
Thanks are due Drs. Christine Whittaker and D. Dean Billheimer for their helpful input during the preparation of this material and Drs. Woodrow Setzer and Kan Shao for useful comments on an earlier version of the manuscript. This research was supported in part by grant #R03-ES027394 from the U.S. National Institutes of Health and grant #CCF-1740858 from the National Science Foundation. John Bailer was supported by NIOSH funding via an Intergovernmental Personnel Act appointment. The contents herein are solely the responsibility of the authors and do not necessarily reflect the official views of any Federal agency or external company.
Footnotes
Competing Financial Interests
The authors declare they have no actual or potential competing financial interests.
Supplemental Material
Supplemental material is provide that contains sample computer code for manipulating the new database and exploring its contents, along with graphical summaries of selected parametric models fitted via data extracted from the database.
REFERENCES
- 1.Bailer AJ, Piegorsch WW. From quantal counts to mechanisms and systems: The past, present and future of biometrics in environmental toxicology (Editors’ Invited Paper). Biometrics, 2000; 56 (2):327–36. [DOI] [PubMed] [Google Scholar]
- 2.Wheeler MW, Bailer AJ. Model averaging software for dichotomous dose response risk estimation. J. Statist. Software, 2008; 26 (5):Art. No. 5. [Google Scholar]
- 3.Deutsch RC, Piegorsch WW. Benchmark dose profiles for joint-action quantal data in quantitative risk assessment. Biometrics, 2012; 68 (4):1313–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.R Development Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; 2014. [Google Scholar]
- 5.Nitcheva DK, Piegorsch WW, West RW. On use of the multistage dose-response model for assessing laboratory animal carcinogenicity. Regul. Toxicol. Pharmacol., 2007; 48 (2):135–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Wignall JA, Shapiro AJ, Wright FA et al. Standardizing benchmark dose calculations to improve science-based decisions in human health assessments. Environ. Hlth. Perspect, 2011; 122 (5):499–505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bailer AJ. Statistical Programming in SAS®. Cary, NC: SAS Press; 2010. [Google Scholar]
- 8.Wickham H, Francois R. dplyr: A grammar of data manipulation. R package version 0.5.0. http://CRAN.R-project.org/package=dplyr 2016.
- 9.Muri SD, Schlatter JR, Brüschweiler BJ. The benchmark dose approach in food risk assessment: Is it applicable and worthwhile? Food Chem. Toxicol, 2009; 47 (12):2906–25. [DOI] [PubMed] [Google Scholar]
- 10.Wickham H ggplot2: Elegant Graphics for Data Analysis. 2nd ed. New York: Springer; 2016. [Google Scholar]
- 11.EPA US, Benchmark Dose Software (BMDS) User Manual Version 2.6.0.1. Research Triangle Park, NC: National Center for Environmental Assessment, U.S. Environmental Protection Agency. [Google Scholar]
- 12.Ramsey FL. A Bayesian approach to bioassay. Biometrics, 1972; 28 (3):841–58 (corr. vol. 29, no. 4, p. 30). [PubMed] [Google Scholar]
- 13.Tsutakawa RK. Estimation of cancer mortality rates: A Bayesian analysis of small frequencies. Biometrics, 1985; 41 (1):69–80. [PubMed] [Google Scholar]
- 14.Messig MA, Strawderman WE. The asymptotic behaviour of Bayes estimators for dichotomous quantal response models. Sankhyā, Ser. A, 1998; 60 (3):418–25. [Google Scholar]
- 15.Kuo L, Cohen MP. Bayesian analysis for linearized multi-stage models in quantal bioassay Biomet. J., 1999; 41 (1):53–69. [Google Scholar]
- 16.Novelo LGL, Womack A, Zhu H et al. A Bayesian analysis of quantal bioassay experiments incorporating historical controls via Bayes factors. Statist. Med, 2017; 36 (12):1907–23. [DOI] [PubMed] [Google Scholar]
- 17.Christensen R, Johnson WO, Branscum AJ et al. Bayesian Ideas and Data Analysis: An Introduction for Scientists and Statisticians. Boca Raton, FL: Chapman & Hall/CRC Press; 2011. [Google Scholar]
- 18.Fang Q, Piegorsch WW, Barnes KY. Bayesian benchmark dose analysis. Environmet., 2015; 26 (5):373–82. [Google Scholar]
- 19.Chen M-H, Ibrahim JG, Shao Q-M et al. Prior elicitation for model selection and estimation in generalized linear mixed models. J. Statist. Plann. Inf, 2003; 111 (1–2):57–76. [Google Scholar]
- 20.Bornkamp B Practical considerations for using functional uniform prior distributions for dose-response estimation in clinical trials. Biomet. J, 2014; 56 (6):947–62. [DOI] [PubMed] [Google Scholar]
- 21.O’Hagan A, Buck CE, Daneshkhah A et al. Uncertain Judgements: Eliciting Experts’ Probabilities. Chichester: John Wiley & Sons; 2006. [Google Scholar]
- 22.Hand DJ, Blunt G, Kelly MG et al. Data mining for fun and profit. Statist. Sci, 2000; 15 (2):111–31. [Google Scholar]
- 23.Scheipl F, Fahrmeir L, Kneib T. Spike-and-slab priors for function selection in structured additive regression models. J. Amer. Statist. Assoc, 2012; 107 (500):1518–32. [Google Scholar]
- 24.Piegorsch WW, An L, Wickens AA et al. Information-theoretic model-averaged benchmark dose analysis in environmental risk assessment. Environmet., 2013; 24 (3):143–57. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Slob W, Setzer RW. Shape and steepness of toxicological dose-response relationships of continuous endpoints. Crit. Rev. Toxicol, 2014; 44 (3):270–97. [DOI] [PubMed] [Google Scholar]
- 26.Davis JA, Gift JS, Zhao QJ. Introduction to benchmark dose methods and U.S. EPA’s Benchmark Dose Software (BMDS) version 2.1.1. Toxicol. Appl. Pharmacol, 2012; 254 (2):181–91. [DOI] [PubMed] [Google Scholar]
- 27.Piegorsch WW, Bailer AJ. Analyzing Environmental Data. Chichester: John Wiley & Sons; 2005. [Google Scholar]
- 28.Cho W-S, Han BS, Nam KT et al. Carcinogenicity study of 3-monochloropropane-1, 2-diol in Sprague–Dawley rats. Food Chem. Toxicol, 2008; 46 (9):3172–7. [DOI] [PubMed] [Google Scholar]
- 29.Alexander J, Barregard L, Bignami M et al. Risks for human health related to the presence of 3- and 2-monochloropropanediol (MCPD), and their fatty acid esters, and glycidyl fatty acid esters in food. EFSA J, 2016; 14 (5):Article No. UNSP 4426. [Google Scholar]
- 30.FAO/WHO. Summary Report of the Eighty-third Meeting of Joint FAO/WHO Expert Committee on Food Additives (JECFA). Rome: Food and Agricultural Organization of the United Nations/World Health Organization. [Google Scholar]
- 31.Shao K, Shapiro AJ. A web-based system for Bayesian benchmark dose estimation. Environ. Hlth. Perspect, 2018; 126 (1):017002.1–.14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Stan Development Team. RStan: the R interface to Stan. R package version 2.14.1. http://mc-stan.org/2016.
- 33.Forbes C, Evans M, Hastings N et al. Statistical Distributions. 4th ed Hoboken, NJ: John Wiley & Sons; 2011. [Google Scholar]
- 34.Thomopoulos NT. Statistical Distributions. Applications and Parameter Estimates. Cham, Switzerland: Springer International Publishing; 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


