Abstract
In Hybrid Foraging tasks, observers search for multiple instances of several types of target. Collecting all the dirty laundry and kitchenware out of a child’s room would be a real-world example. How are such foraging episodes structured? A series of four experiments shows that selection of one item from the display makes it more likely that the next item will be of the same type. This pattern holds if the targets are defined by basic features like color and shape but not if they are defined by their identity (e.g. the letters p & d). Additionally, switching between target types during search is expensive in time, with longer response times between successive selections if the target type changes than if they are the same. Finally, the decision to leave a screen/patch for the next screen in these foraging tasks is imperfectly consistent with the predictions of optimal foraging theory. The results of these hybrid foraging studies cast new light on the ways in which prior selection history guides subsequent visual search in general.
Imagine you are cleaning up a child’s room. Yes, of course, they should do it themselves, but what are you going to do? You are looking for laundry that needs to be washed, stuffed animals that go on the bed, building blocks that should be in their box, and those library books that are now three weeks overdue. This is a “hybrid foraging” task (Wolfe, Aizenman, Boettcher, & Cain, 2016). In hybrid foraging tasks, observers are searching for multiple instances of several types of target at the same time. Such tasks are a routine aspect of daily life; for example, driving: Find restaurants, parking places, and traffic signs. Hybrid foraging can also be part of important expert search tasks; for example, in a medical image perception task in radiology where the clinician might have several specific targets to look for plus a general requirement to note any clinically significant “incidental findings” (Lumbreras, Donat, & Hernández-Aguado, 2010; Wolfe, 2017).
The term “hybrid foraging” is an extension of “hybrid search”. In a simple hybrid search task, observers search for one instance of any of several possible targets in a display containing distractor items. Schneider and Shiffrin (1977) used the name “hybrid search” for this combination of a visual search though the display and a memory search through the set of possible targets. A wide range of hybrid search tasks produce similar results. Response time (RT) increases linearly with the number of items in the visual display and logarithmically with the number of items in the memory display (Wolfe, 2012). This is true for specific objects in specific poses as well as for categories of objects (Cunningham & Wolfe, 2014) and words (Boettcher & Wolfe, 2015).
In standard laboratory visual search, there is typically one target or no target in a search display and the search is over when the target is found or when the searcher concludes that there is no target to be found. However, in many important real-world search tasks, including those described above, there are likely to be multiple instances of the target(s). Searches for multiple instances, especially if the number of instances is unknown, fall into the category of foraging tasks. Long studied in the animal behavior literature (Pyke, Pulliam, & Charnov, 1977; Stephens & Krebs, 1986), foraging has more recently become a topic of interest in cognitive science (Hills & Dukas, 2012; Hills, et al., 2015) including, unsurprisingly, information foraging on the internet (Pirolli, 2007; Pirolli & Card, 1999). In human visual foraging, much of the interest to date has focused on the moment when observers decide to stop foraging in the current ‘patch’ (or screen) and move to the next patch (Ehinger & Wolfe, 2016; Wolfe, 2013; Zhang, Gong, Fougnie, & Wolfe, 2017)1. Predictions based on Charnov’s (1976) Marginal Value Theorem (MVT) work quite well, at least on average data. MVT proposes that foragers should leave for a new patch when the current yield from the current patch falls below the average yield for the task as a whole. Thus, you should move to the next blueberry bush when your rate of berry acquisition from the current bush drops below the rate you have established in the field. MVT works well for tasks where there are a large number of targets. It is less well-suited to tasks where targets are found more intermittently. When should you stop looking for missile launchers in the current satellite image and move to the next? There may be multiple targets, but it is likely that there will be relatively long periods where nothing is found and where the instantaneous rate of success drops to zero. Under such circumstances, it would not make sense to abandon search as simple MVT would suggest. However, MVT can be reformulated in a more Bayesian manner to say that the forager should leave when the expected value of staying falls below the expected value of leaving (“potential value theory” Cain, Vul, Clark, & Mitroff, 2012; McNamara & Houston, 1985, Olsson & Brown, 2006).
Hybrid foraging introduces a new degree of complexity. If you are foraging for any of several types of target, how should you structure your search within a patch? Should you search for each target type in turn, switching to a new target type when the rate of acquiring the current target type falls below some level? Should you collect items at random from within the target set? This topic has been the subject of considerable research in the animal behavior literature, typically with a memory set size of just two. The problem is usually framed around a predator with two available forms of prey; for instance, a bird, hunting for moths of two varieties (Bond, 2007; Bond & Kamil, 2002; Dukas, 2002) or pecking for different sorts of seeds. When targets are relatively hard to find – when they are “cryptic” in the language of the animal literature – birds tend to pick the more common item at a rate higher than that item’s prevalence in the population. Only when the common item becomes rarer and harder to find does the bird switch the less common item. If the items are relatively conspicuous, birds switch more readily (Bond, 1983).
Humans show similar behavior (Bond, 1982). In a more recent experiment, Kristjansson et al. (2014) showed observers an iPad screen with four types of items. In the simple color feature condition, items could be red, green, blue, or yellow and observers were asked to touch all of the items showing either of two colors (e.g. red and green). Like pigeons pecking at conspicuous seeds, the observers switched back and forth between items of the two colors. In a second condition, the items were defined by conjunctions of color and shape. Observers were asked to collect red circles and green squares and to ignore green circles and red squares. In this case, the targets do not pop-out of the display. Observers tended to pick all of the items of one type before switching to the other type. This perseverance on one type of target is similar to, but more extreme than, what is seen when birds hunt for ‘cryptic’ prey. The difference may have been influenced by the instructions given to the human observers. Kristjansson’s human observers were asked to search exhaustively. They had to select every red circle. In more typical foraging tasks, observers are allowed to move on to the next patch (or screen) when they wish. Neither of these approaches is the “right” way to do the task. They capture aspects of different real-world search tasks. When foraging for food, the animal is generally free to move to the next bush when the current bush becomes unsatisfactory. In contrast, a radiologist ‘foraging’ for cancer metastases might be under an obligation to find everything before moving to the next patient.
Wolfe et al (2016) had observers memorize between 8 and 64 photographs of objects and then perform a hybrid foraging task in which they searched through displays (henceforth “patches”) that contained multiple instances of those target types. Each patch contained examples of 3–5 of those target types. Observers collected items by ‘clicking’ on them with a computer mouse. They could leave the patch whenever they wished by clicking on a “next” button. This produced a new patch about five seconds later with a new set of 3–5 target types present. The observers’ goal was to collect a designated number of targets as quickly as possible. They were not required to be exhaustive in their search. To thwart systematic strategies (‘reading’ from top-left to bottom-right for example), all items were in continuous movement around the screen.
Observers in this task did not pick randomly among available targets. Instead, observers tended to collect items in runs of one target type. RT data indicated that searching again for the same item was more efficient than searching for any of the other targets held in memory. Results were generally consistent with optimal foraging theory and observers tended to leave 25–33% of targets uncollected when moving to the next screen/patch.
In a subsequent paper, Wolfe, Cain, and Alaoui-Soce (2018) manipulated the value and prevalence of items in a similar foraging task. Observers always held four items (photographic objects) in memory. In the foraging portion of the task, 20–30% of 60–105 items were targets. These could be equally distributed amongst the four possibilities or they could vary in prevalence (7%, 13%, 27%, and 53% of total target items, respectively). Items could also vary in their value (in points) to the forager (2, 4, 8, or 16 points). In the condition where value and prevalence varied, they varied inversely so that a common but less valued target type represented as many points as a valuable but scarce item. Value and prevalence had strong and interacting effects on foraging behavior. Unsurprisingly, foragers tended to favor more valuable items. Interestingly, when values were uneven, they tended to leave patches sooner. This makes sense in the MVT context because, once the valuable items are picked, the rate of return tends to drop more quickly in these conditions. Moreover, uneven value introduced more variability between observers. Some observers tended to collect only valuable items and then move to the next screen/patch. Others did not leave patches so precipitously. On average, foragers tended to abandon patches too soon, in MVT terms, when both prevalence and value were uneven.
As in the other foraging search tasks described above, the item foraged next depended on the item foraged previously (The “selection history”; Awh, Belopolsky, & Theeuwes, 2012; Theeuwes, 2018). This tendency for collection to go in runs longer than predicted by random selection among targets is seen in the animal literature as well (Bond, 1982). In the present paper, we examine the reasons for this tendency for target types to be picked in ‘runs’. There are several hypotheses that can be tested:
1) Selection goes in runs because the previous selections perceptually prime the next selection on the basis of shared basic features (e.g. if you picked red last time, you will be guided to red the next time).
2) Selection goes in runs because the previous selections semantically prime the next selection (e.g. if you picked a tool last time, you are more likely to pick a tool the next time, even if that tool shares no more features with the previous selection than does another type of target).
3) Selection goes in runs because one target type is in the focus of attention (perhaps in working memory) at any given time and, regardless of whether there is semantic or perceptual priming, there is a cost associated with switching a new item into the focus of attention
These hypotheses are not mutually exclusive. Here we report qualified evidence for feature guidance (Hypothesis #1), good evidence for switch costs (#3), but no evidence for semantic guidance (#2).
Experiment 1: Near replication of Kristjansson, Johannesson, & Thornton (2014)
In Experiment 1, we perform a near-replication of Kristjansson, Johannesson, & Thornton (2014). Recall that they had observers forage for two colors in a four-color display or for two mutually exclusive conjunctively defined targets. They found strong evidence for runs in the conjunction case. Like Kristjansson, we had feature and conjunction search conditions. We added a letter search condition, designed to be ‘unguided’. Targets were the lower-case characters p & d among b and q distractors. Here the targets are semantically distinct, in the sense that “b” has a different meaning or identity than “d”, but no basic features can be used to guide attention to a specific target type. Unlike Kristjansson, our observers were allowed to leave the current patch at will and to proceed to the next patch. This turns out to be a critical factor in shaping the pattern of responses.
Methods
Participants
Twenty-four naïve observers (16 females), ages 18 to 47 years (M = 29.7 years, SD = 12.3 years) participated in the experiment. All participants had normal or corrected-to-normal vision and passed the Ishihara Color Test (Ishihara, 1980). Participants provided oral informed consent and were paid $10/hr for their participation. All procedures were approved by the Partners Healthcare Corporation Institutional Review Board. The sample size was determined by the sample size required to see important RT and RT × set size effects in visual search experiments [Wolfe, 1998 #4526]. Twenty-four observers are adequate to detect a 1.5× change in slope with power of 0.95 and 0.01 chance of a Type 1 error.
Stimuli and apparatus
The experiments were written in Matlab 7.10 (The Mathworks, Natick, MA) using the Psychophysics Toolbox (Brainard, 1997; Pelli, 1997, Kleiner et al, 2007) version 3. Stimuli presented on a 55-inch TV (Sony XBR55) with an infrared multitouch detection overlay. Observers responded by touching stimuli on the screen. An item was considered to be selected if the touch fell inside a circle with a diameter of 28 pixels (approximately 0.8 degrees of visual angle) centered on the item. If a touch was ambiguous between a target and a distractor item, the target item was collected. Since some experiments involved a touchscreen and others involved response via computer mouse. We will refer to items as being “collected” or “clicked”, using “clicked” in a generic sense to include touch responses.
Observers were placed at a viewing distance slightly less than arm’s length from the screen. There were three stimulus conditions, cartooned in Figure 1. In all cases, individual stimuli subtended approximately 0.75 deg. They were initially placed randomly in cells of a 15 × 15 grid. However, immediately upon the start of the trial, the items began to drift in a random manner within a 40 × 25 deg region of the screen. Items moved at a constant velocity of 44 pixels/second (approximately 1.2 degrees of visual angle per second), changing directions at pseudo-random intervals. It is useful to have stimuli that move in foraging experiments of this sort to avoid having observers simply “read” a display from, say, top left to bottom right; a reasonable search strategy but not a very interesting one for present purposes (Wolfe, et al., 2016).
Fig 1:
Stimuli for Exp. 1. After starting in this rough grid, items moved about the screen to thwart a strategy of systematically selecting items from, say, top left to bottom right.
In the Feature Condition, stimuli were red, yellow, green, or blue squares. Half of the Observers foraged for blue and green items; the other half, for red and yellow. In the Conjunction Condition, half foraged for green squares and blue circles among blue squares and green circles while targets and distractors were reversed for the other half. Finally, in the letter condition, half searched for p & d among q & b distractors while the other half searched for q & b among p & d. Displays contained 60,100, 140, or 180 total items to start. Of those items, 20–30% were target items.
Procedure
At the start of each condition, observers were tested to assure that they knew their two targets. They were shown each of the types of item for the condition and asked to identify them as target or distractor. Next, they briefly practiced foraging for those targets. Targets were collected by touching it on the touchscreen. Target items disappeared once touched and gave a reward of 2 points. Distractors also disappeared when touched and gave a penalty of −1 point, but they were rarely selected. This small penalty was introduced so that observers would not adopt a strategy of simply clicking everything as quickly as possible. A new screen with a new set of items could be generated at any time by clicking on the “Next” button at the center of the display. In each condition, observers needed to collect 100 points (i.e., 50 targets, assuming no distractor clicks) in the practice period and 1000 points (500 targets) in the experimental block. They were not explicitly told that they needed to collect items of both target types, but everyone did so. Observers could view as many screens as they wished in the process of collecting the required number of points. The block ended when the point goal had been reached. In the practice period, observers were shown the locations of all remaining targets after they clicked on the Next button. They were not given this feedback during the experimental period. Response times were recorded and erroneous clicks were tabulated.
Results & Discussion
Our first interest is in whether the pattern of runs deviates from what would be predicted by chance selection of items from the set of all available targets. A selection is part of a “run” if the target selected is the same as the previous target selected. Runs are not held to continue between screens. Thus, the first trial on a screen is not considered to be a run or a switch trial. Errors (e.g. clicking on a distractor) ended runs. The selection after an error was not coded as a run or a switch trial.
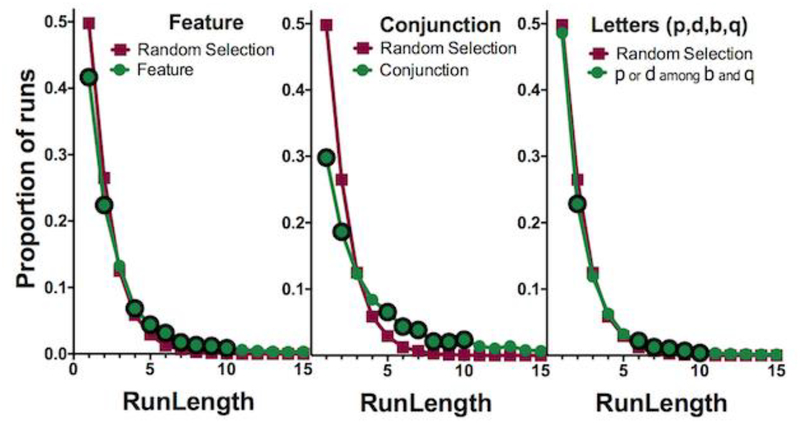
Table One gives overall numbers of patches, targets per patch, and runs per patch as a function of condition. It can be seen that observers changed patch somewhat more quickly in the Letter condition. There are obvious variations in the numbers of runs per patch. When do these deviate from the chance distribution of runs? That is, with two targets in memory and present on screen, it would be expected that the same target type would sometimes be picked on successive selections. That chance distribution of runs is difficult to compute because it changes dynamically during foraging from a patch. That is, if a patch started with 20 red and 20 green targets, the probability of picking one or the other color would be 50%, but as soon as one target is selected, the probabilities change, and continue to change from selection to selection. Moreover, the total number of selections from a single screen/patch varies from trial to trial and observer to observer. Accordingly, it was more straight-forward to simulate random selection. Stimuli were generated with the same mix of targets and distractors as in the real experiment. The number of simulated selections for a specific screen was drawn from the distribution of actual numbers of selections produced by human observers. For both real and simulated data, the numbers of runs of different length were tabulated. The resulting proportions are tabulated in Figure 2.
Table One:
Overall numbers of patches, targets per patch, and runs per patch
| Condition | Total # of patches per condition | Average # of targets per patch | Average # of runs per patch |
|---|---|---|---|
| Feature Search | 20.1 | 25.5 | 9.0 |
| Conjunction Search | 21.0 | 24.5 | 5.6 |
| Letter Search | 27.8 | 19.5 | 8.2 |
Figure 2:
Distributions of runs of different lengths. Green circles show the observed distribution. Red squares show the results of simulating random selection. Circles with black outlines show points where the functions are statistically different by 1-sample t-tests (p<0.01). Significance was not calculated for runs > 10 because the chance probability is extremely low.
Data were compared to the random selection function using a Kolmogorov-Smirnov test. Pooling all the data, each condition is significantly different from random selection (all p<0.001). The deviations are largest for the conjunction condition and minimal for the letter condition. If we look at individual observers using an alpha of 0.001 to correct for multiple comparisons, in the feature condition, 4 of 24 observers’ individual functions reject the null hypothesis of random selection (9 observers would reject the null hypothesis with p<0.01). In the conjunction condition, 23 of 24 observers’ functions reject the null hypothesis of random selection at p < 0.001). In the letter condition, none of 24 observers’ functions reject the null hypothesis of random selection (4 observers would reject at p < 0.01).
Green circles show the observed distribution averaged across all 24 observers. Red squares show the results of the simulation of random selection. The two functions are compared point-by-point by 1-sample t-tests. Circles with black outlines show points where the functions are statistically different (p<0.001 for all significant points except those near the crossover between the two functions. The significant points near the crossover have p < 0.01, not corrected for multiple comparisons). Significance was not calculated for runs > 10 because the chance probability is extremely low. It is clear in the Feature condition and, even more so, in the Conjunction condition, that humans produce longer runs than would be predicted by chance. Runs of length one and two are significantly under-represented and longer runs are significantly over-represented.
For the Letter condition, visual inspection shows that the results from the human observers are much closer to the results of the simulation of chance performance. The two functions deviate significantly for runs of length 2 with a lower proportion than expected by chance. However, there is no difference for lengths of 1, 3, 4, or 5. There is a significant effect at the higher run lengths. These effects are probably the result of observers occasionally making a volitional decision to search for just one item in a screen/patch.
This pattern of results indicates that guidance by basic feature information (Wolfe & Horowitz, 2017) is an important factor in shaping the distribution of runs. After you pick one type of target, it is likely that the next pick will share the same features. This applies to the Feature and Conjunction conditions. In the Letter condition, all of the items have the same basic features and, perhaps as a consequence, there is very little evidence that the letter identity of the current pick primes the selection of the next item. Why does the effect appear to be larger in the Conjunction condition than in the Feature condition? In both cases, basic feature information is available to guide attention to the next item. Indeed, guidance by a single basic feature like color is typically more effective than guidance by a conjunction of features (Wolfe, 1998). One possibility is that it is easier to switch from blue to green in the Feature condition than it is to switch from blue circle to green square in the Conjunction. An alternative account of the color search results would be that observers can maintain two color templates2 at the same time [Hollingworth, 2016 #12813; Gilchrist, 2011 #10925; Berggren, 2016 #12948], though there seems to be some cost for doing so [Grubert, 2014 #11872; Stroud, 2017 #13431]. These hypotheses can be tested by looking at the response times (RTs) defined as the times between successive selections. RTs can be classified as “run” RTs or “switch” RTs depending on whether the preceding selection was the same or different from the current selection. The first RTs in a patch are coded separately and excluded from this analysis. They are typically relatively long.
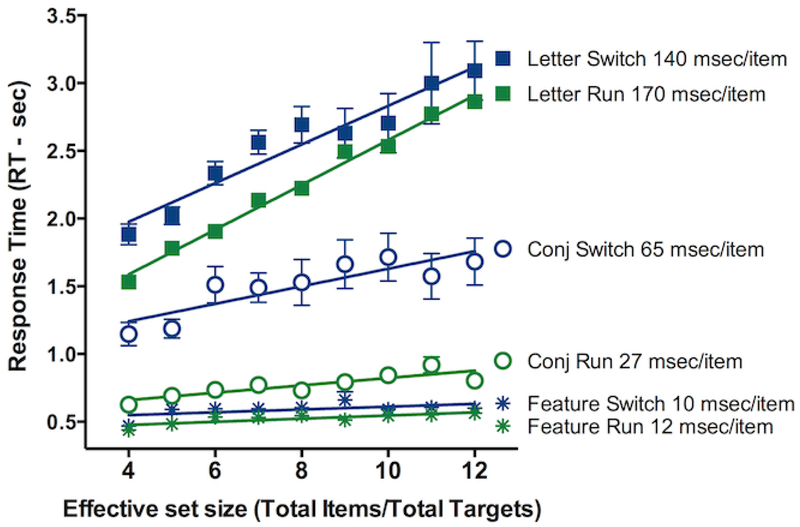
Figure 3 shows run and switch RTs for each of the three conditions as a function of the “Effective Set Size”. For this analysis, RTs were removed if they were less than 200 msec or greater than 7000 msec. In visual search experiments, RTs are typically analyzed as a function of the set size because, as a general rule, it is harder to find a target among a larger number of distractors than among a smaller number. The slope of the RT × set size function is a standard measure of the efficiency of a visual search (for a recent argument about this, see Kristjansson, 2015; Kristjánsson, 2016; Wolfe, 2016). In foraging tasks like those studied here, the Effective Set Size can be defined as the number of items on the screen divided by the number of targets. Thus, the search task is assumed to be roughly the same if one is looking for a single “p” or “d” among 12 other letters or for any of four instances of “p” and “d” among 48 letters. One could define a different effective set size as the number of items on the screen divided by the number of one specific target type (e.g. just the “d”s) but here we are treating all visible targets (“p”s and “d”s) as the denominator. Note that Effective Set Size increases as foraging progresses in a patch because the number of targets decreases proportionally more quickly than the total number of items on the screen.
Figure 3:
RT as a function of Effective Set Size for run and switch trials for each condition. Effective set size is the number of remaining items divided by the number of remaining targets. For graphing, effective set sizes are rounded to the nearest integer and averaged.
Figure 3 shows RT as a function of Effective Set Size for run and switch trials. The number of trials per data point decreases as the Effective Set Size (EffSS) increases from more than 40 repeat trials and more than 14 switch trials per observer at EffSS=4 to 6–11repeat trials and just 3–5 run trials at EffSS=12. The figure shows the expected differences between conditions. As in standard search tasks, feature searches are more efficient than conjunction searches. Those, in turn, are more efficient than spatial configuration tasks like the letter search (Wolfe, Palmer, & Horowitz 2010). An ANOVA with Condition, Run/Switch, and Effective Set Size as factors shows very large main effects of Condition (F(2,46)=337.0, p<0.00001, ) and Effective Set Size (F(8,184)=20.3, p<0.00001, ). The interaction of Condition and Effective Set Size, reflecting the fact that the difference in the slopes of the RT × Effective Set Size functions across conditions is also very robust (F(16, 368)=8.5, p<0.00001, ). The average slope for feature searches (12 msec/item, sd=11) is less than the average for conjunction search (27 msec/item, sd=21, t(23)=3.3, p<0.005). The conjunctions slopes are much shallower than the letter slopes (164 msec/item, sd=120, t(23)=5.6, p<0.0001)
The main effect of the Run/Switch variable is significant (F(1,23)=65.8, p<0.00001, ). Two-way ANOVAs on each of the conditions separately show that there is a Run/Switch effect in each condition (all F(1,23)>10.5, all p <0.004, all ). However, it is clear that the switch costs are much bigger in the Conjunction condition than in either the Feature or Letter condition. This is reflected in a significant interaction of the Run/Switch and Condition in the three-way ANOVA (F(2,46)=20.1, p<0.00001, ).
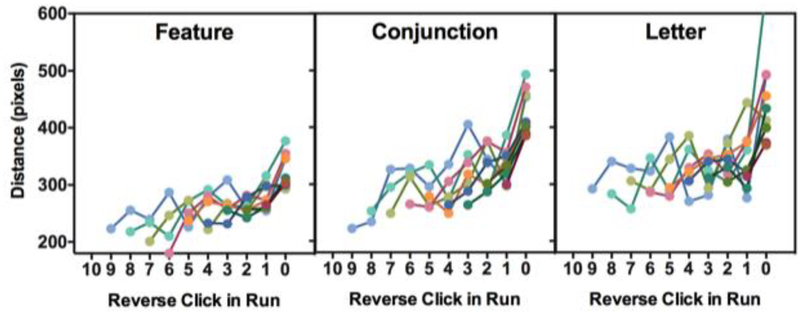
Another way to look at switches and what drives them is to examine the distance between targets. As can be seen in Figure 4, for all three conditions, the first click in a run (i.e., the switch click) is very near to the previous target, and subsequent clicks get further away (Feature: F(1,23)=28.78, p<.001, ; Conjunction: F(1,23)=51.67, p<.001, ; Letter: F(1,23)=18.68, p<.001, ). For all conditions, post-hoc t-tests confirmed that the last click in the run was significantly further away from the previous target location than were any of the previous clicks (Feature: all t>3.5, all p<.001; Conjunction: all t>4.5, all p<.001; Letter: all t>3.0, all p<.005).
FIGURE 4:
Distances in pixels between successive target collections in each condition. Different lines represent runs of different lengths. Data are plotted in terms of reverse clicks, with 0 being the last click in a run before a switch, 1 being the penultimate click in the run, etc.
These results suggest that there are two factors at play in the tendency of items to be collected in runs in these tasks. First, selection of a target type primes the features of that target type, giving other items with those features priority in subsequent search (Failing & Theeuwes, 2017; Theeuwes, 2013). Both the Feature and Conjunction conditions would produce this type of guidance by priming. The letter search is a “spatial configuration search” (Wolfe, 1998) with no guidance beyond that which directs attention to items in the search array and not blank space or objects elsewhere in the room. Second, in line with task switching costs, more generally (Altmann & Gray, 2008; Monsell, 2003), switching the target template can be costly in visual search (Wolfe, Horowitz, Kenner, Hyle, & Vasan, 2004). There are costs associated with switching between two colors (Ort, Fahrenfort, & Olivers, 2017) but these are fairly small (Grubert & Eimer, 2014; Liu & Jigo, 2017) and, as noted above, it could be that two color templates can be active at the same time. The cost is more dramatic in conjunction search (Wolfe, et al., 2004). Thus, in the conjunction foraging condition, observers are least likely to want to switch to a new target and, as a result, the evidence for more and longer runs of responses is clearest in the Conjunction condition. In the letter search, there is no switch of a feature-based attentional set from item to item during the search. Attention is deployed to the next item, more or less at random, and that item is identified as either one of the two targets or as a distractor. Even though there may not be feature guidance in the letter condition, RTs are still faster when target type is repeated. This probably represents the effects of response priming (repetition and/or semantic priming). It is faster to make the same response again than to make a different response and, thus, switch responses are longer than run responses [Krinchik, 1974 #7750; Farah, 1989 #2252
The distance data are consistent with this account. Switches become more likely when available targets of the current type are relatively far away. At that point, it is worth ‘paying’ the switch cost in order to collect a nearby target of the other type.
What is left behind?
In this experiment, observers are free to move to the next screen/patch whenever they wish. Recall that this method differs from the Kristjansson et al (2014) paradigm in which observers were required to collect all targets before moving to the next screen. This leads to interesting question about the targets that are left on screen when the observer chooses to move to the next screen. The targets that are left behind should not be thought of as errors since observers were told to leave each patch whenever they wished. Indeed, as the next section will discuss, Optimal Foraging Theory predicts that items will be left behind (Charnov, 1976).
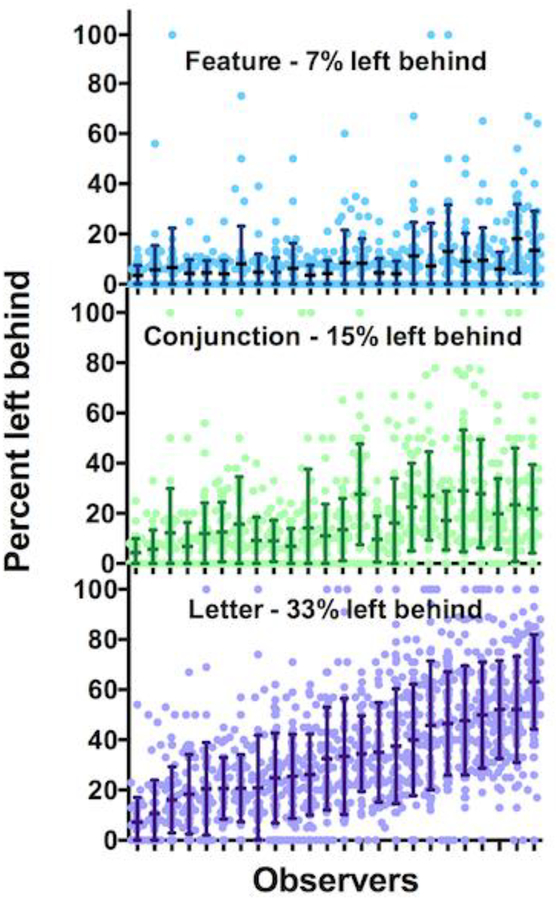
Figure 5 shows the percentages of items left behind in each of the three conditions of the experiment for each observer. The observers are ordered by the percentage left behind in the Letter condition. Several trends are visible. First, the left behind rate is lowest for Feature search and highest for the Letter search. Second, as more items are left behind, the variability across and within observers increases. Observers seem to adopt very different strategies with some observers leaving fewer than 10% of letters, on average, while others leave as many as 60% of letters. Sometimes, observers fail to collect any instances of one type of target from a screen. Faster picking is associated with more items left on screen, but the relationship between the percentage left behind and the rate of picking is weak (Feature: r2=.20, p=0.03, Conjunction: r2=0.08, p=0.17, Letter, r2=.15, p=0.06). A more convincing analysis of these points would require a design with greater statistical power. Finally, individuals have a relatively consistent tendency to leave items behind. The percentage of items left behind in the Letter condition is correlated with the Conjunction condition (r2 = 0.62, p<0.0001) and the Feature condition (r2 = 0.47, p<0.0005).
Figure 5:
Percentage of targets left on the screen when observers chose to move to the next screen. Each data point shows the percentage for one type of target (e.g. p or d) left on screen for each screen for each observer (many data points overlap). Dark bars show mean +/− 1 s.d. for each observer. Observers are sorted by the percentage left behind in the letter task.
Is Foraging Optimal?
Optimal foraging theory (Charnov, 1976) makes predictions about when observers should leave the current patch. Specifically, Charnov’s (1976) Marginal Value Theorem (MVT) says that observers should leave a patch when the current rate of collection from the patch falls below the average rate for the task as a whole. The average rate is reduced by the time between patches when nothing can be collected. This is known as the “travel time” in the foraging literature; the time, for example, that a bee might spend flying to the next flower. The longer that travel time, the lower the average rate and the longer the bee should continue collecting from the current flower. MVT is not the best model for search tasks where target acquisition is intermittent because, under those conditions, the current rate can drop to zero (Cain, et al., 2012; Ehinger & Wolfe, 2016) but in tasks like the ones used here, where observers are picking rapidly and continuously, it has proven to be a good fit to average data, even if it is violated in some specific situations (Wolfe, 2013; Zhang, et al., 2017). Is MVT appropriate to this hybrid foraging task? It would not be a good model for the Kristjansson version of this task because their observers were required to search exhaustively. In Experiment 1, the interesting complication is that there are two types of target in each patch. As the rate of collection drops, our observers can choose between switching patches and switching target types. Under these circumstances, is the overall behavior still consistent with MVT?
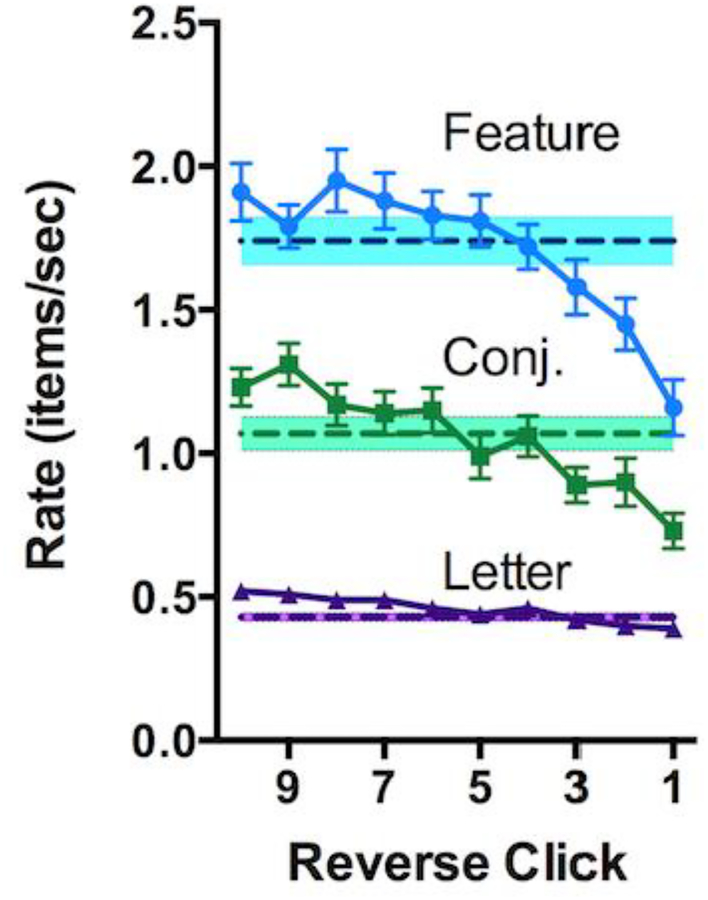
In fact, MVT is not a good predictor of the patch leaving time for the current data. This is shown in Figure 6. Rate of selection is plotted as a function of “reverse click”. The use of reverse clicks as the independent measure allows the data to be aligned to the end of foraging in the current patch rather than the aligning to the start of foraging. Thus, reverse click #1 is the last item selected in a patch. Reverse click #2 is the penultimate click, and so forth. MVT predicts that the penultimate click should be near the average rate (shown as a dashed horizontal line for each task). The rate for the final click then falls below the average rate, triggering patch leaving, according to MVT. In the present data, it is clear that observers continue picking longer than MVT predicts the Feature and Conjunction conditions. The rates for each of the last three clicks in those conditions fall below the average rate (all 6 t(23)>3.2, all p < 0.005). The letter condition conforms more closely to the MVT prediction. The penultimate rate is not different from the average rate (t(23)=1.8, p=0.09). The next, final click is at a significantly lower rate (t(23)=2.2, p=0.04). Alternatively, we can ask where the instantaneous function crosses the average rate. MVT predicts that intercept at about reverse click 2. The next click is then at too slow a rate and the observer leaves the patch. We calculated these crossing points from a linear regression on reverse clicks 1–7 (a roughly linear range). The intercepts were: Feature: 4.8, Conjunction 5.6, Letter 6.5. All of these values are significantly greater than 2 (all t(23) > 5.2, all p < 0.0001, which would survive correction for multiple comparison). By this test, all conditions violate the predictions of MVT.
Figure 6:
Rate of selection as a function of Reverse Click. Reverse Click #1 is the final click in the patch. #2 is the penultimate click and so forth. Horizontal lines are the average rate for the task as a whole. Shaded areas are +/1 s.e.m. around that average. Error bars are +/− 1 s.e.m.
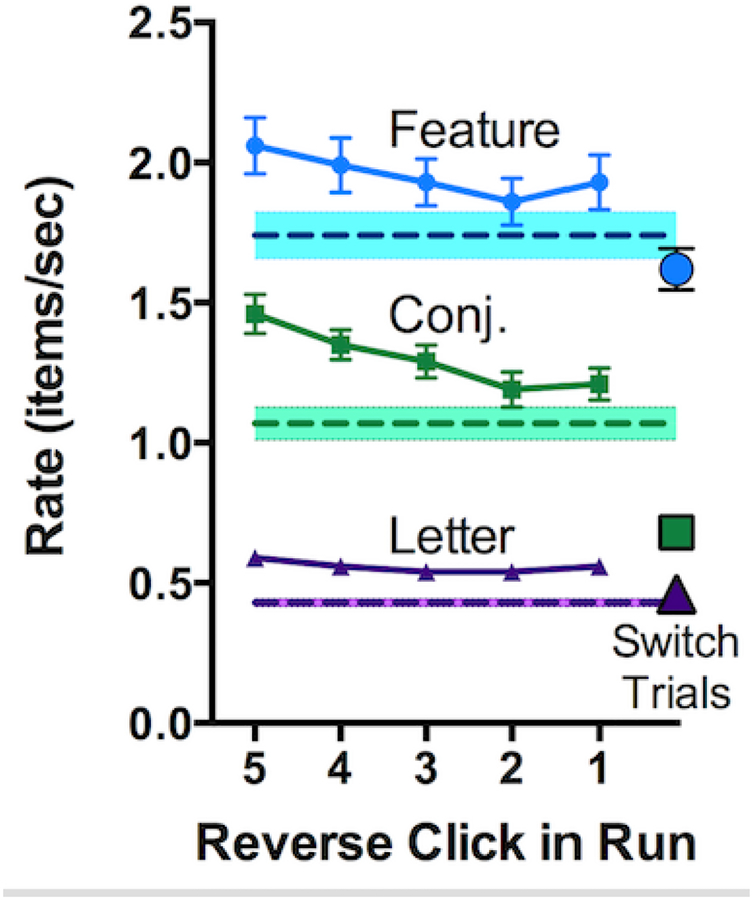
Why are observers staying too long in a patch (at least, from the MVT vantage point)? Looking at the internal structure of foraging within a patch can provide an answer because the observer’s time in each patch can be thought of as a succession of smaller foraging episodes. Just as observers need to decide when to leave a patch, they also need to decide when to leave a run. If an observer is collecting green squares in the Conjunction task, they need to decide if it is worth switching to the blue circle target. The switch costs within a patch are akin to the “travel costs” between patches that drive down the average rate. Thus, we can look at the rate as a function of position of a click relative to the end of a run just the way we would look at the rate relative to the patch leaving time. This is shown in Figure 7. Rather than plotting Reverse Clicks from the last click in the patch, the rates (1/RT) in Figure 7 are plotted relative to the last click in the run. Results are averaged over runs with length longer than 2 because the first trial in each run is a “switch trial”. These trials are much slower (rate is lower) and in Figure 7 are plotted as larger, outlined symbols.
Figure 7:
Rate (1/RT) as a function of reverse click position in a run within a patch. The first trial in a run is a “switch trial” and those lower rates are plotted as larger, outlined symbols. Dashed lines represent the average rates for the entire task.
As in the patch as a whole, the rate drops during a run as the local population of targets of that type is depleted. When the observer decides to switch to a new target, that “switch trial” is markedly slower for Feature and Conjunction conditions. Notice that the effective rate when making a switch trial is lower than the average rate for the task. If the observer followed the usual MVT rules and left the patch when the current rate dropped below the average rate, they would tend to move to a new patch rather than switching to the other target. Perhaps to avoid this, observers only leave the entire patch when the current rate is below the rate for switch trials. Notice that this effect is small for the Letter condition. The switch costs are smaller, perhaps reflecting the random selection of one or the other letter (see Figure 1).
Experiment 2: Replication with complex conjunction stimuli
Experiment 1 found strong evidence that targets were foraged in runs when the target types were differentiated from each other by basic ‘guiding’ features. Notably, when the targets were conjunctions of color and shape, observers were most likely to continue picking one target type (e.g. blue circle) rather than changing both basic features in order to select the other (green squares). In Experiment 2, we replicated this basic result using stimuli defined by conjunctions of several fundamental features in order to vary the number of features shared between different target types.
Method
Twenty-six observers (18 females), ages 19 to 55 years (M = 28.4 years, SD = 10.58) were tested. All observers passed the Ishihara color test and had or were corrected to at least 20/25 vision. Of these, 13 were tested using a touch screen while the other 13 responded with a mouse click. Data from one observer was corrupted, leaving 25. Consent was obtained as approved by the Partners Healthcare Corporation Institutional Review Board.
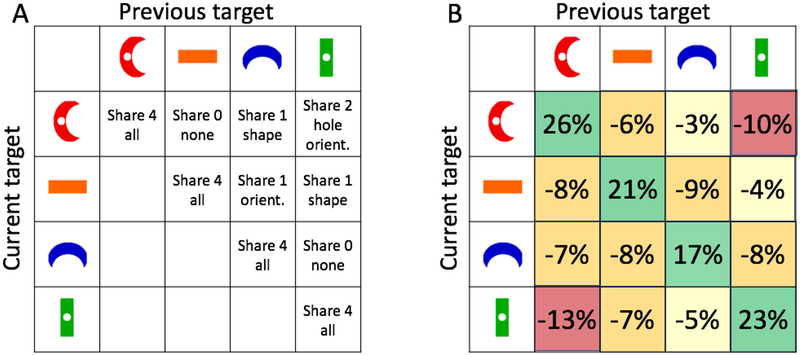
The target types are shown in Figure 8. Items are conjunctions of 4 features: color, orientation, curvature (Wolfe, Yee, & Friedman-Hill, 1992), and the presence or absence of a hole (Chen, 2005). The four items shown were the target types. The distractor set consisted of 124 items created from all the combination of 8 colors × 4 orientations × straight vs curved × hole vs no hole (128 – 4 targets = 124). The distractor set included colors and orientations not present in any target. Each patch started with 60, 80, 100, or 120 items on screen. Of these, 20–30% were target items, divided pseudo randomly amongst the four target types. All four targets were present in 74% of patches. In 24% of patches, three target types were present. Only two types were present in 2% of patches. This meant that the observers could not be assured that a specific target type would be present in a display. In any given patch, a set of distractors was chosen from the remaining 120 types of item in the full set. Distractors were chosen so that the number of instances of a specific distractor type was comparable to the number of instances of target types. On average, there were 18 distractor types in the display with a range from 13 to 23. As in Experiment 1, all items moved randomly about the screen in order to thwart systematic strategies (e.g. reading the display from top left to bottom right).
Figure 8:
(A) Target types for Experiment 2. Targets can share 0, 1, 2, or 4 basic features with each other. (B) Percent deviation from baseline for selection of one type of target on the current click, given selection of one type of target with the previous click. Thus, for example, selection of the horizontal orange target twice in a row occurs 21% more often than would be expected given the prevalence of those targets in the display. Colors are simply a coarse coding of the deviation percentages.
Methods were otherwise similar to those of Experiment 1. Observers learned the four targets. They were tested to confirm that memory using a short recognition memory test. They then collected targets in a series of screens/patches. After a brief practice block, observers collected 2000 points in each of 2 blocks. Observers received 2 points for a correct response and lost 1 point for any false positive click on a distractor item. These were rare, so observers averaged 1013 targets per block. Observers could move to the next patch at will. In practice, they visited an average of 53 patches per block, collecting an average of 19 targets per patch. Each experimental block took an average of 25 minutes. Observers were instructed to reach the point goal as quickly as possible.
Results & Discussion
Half of participants responded with a touchscreen and half with a standard computer mouse. We compared data from the two response modalities and found no broad differences between them. In particular there were no difference in mean collection time (touch M=1.50s, mouse M=1.40s, t(17.82)=0.61, p=.547, d=.25), time to first collection (touch M=2.16s, mouse M=1.84s, t(22.62)=1.40, p=.175, d=.56), response time for last collection in a display (touch M=2.47s, mouse=2.78, t(14.47)=0.544, p=.594, d=.22), or points earned per second (touch M=1.13, mouse=1.31, t(17.76)=1.48, p=.157, d=.60). Given the lack of difference between modalities, groups were combined for all further analyses.
On average, a patch had 22 targets at the start. Observers left an average of 3.4 (15%) target items uncollected when they moved to the next patch. On average, observers collected at least one of every available type of target in 80% of patches.
Of most interest in this experiment is the sequence of target selections within a patch. To determine if observers were picking randomly among the items, we calculated the percentages of each type of target for selections 2–10 in a patch. We restricted this analysis to the first half of the selections in a patch in order to avoid situations where one or more targets were entirely depleted, but the pattern of results reported below is similar if all trials are included. We then tested whether any types of selection were more or less likely than predicted by random selection. Given four target types, there were 16 conditional probabilities for the chance of picking target A given that target B had been picked immediately previously. The first selection was eliminated from the analysis because, of course, it has no preceding selection in the patch.
Figure 8B shows the results of this analysis as percentage deviation from the chance prediction. Green indicates positive deviations while increasing negative deviations are colored from yellow to red. It is clear from the green diagonal that the likelihood of repeating the selection of a target type is higher than would be expected by chance. This is evidence, as in Experiment 1, that responses go in runs. If you are picking blue crescents, you are more likely than chance to continue to do so. This was true for each of the four targets. We can reject the hypothesis that the percentage of repeat targets is the same as would be expected by chance (all four t(24) > 12, all p<10−10). When observers did move to another target type, was that shift influenced by the number of features shared with the previous selection? There are significant differences between transitions to items sharing 0, 1, or 2 features with the preceding item (all t(24)>2.2, all p < 0.04, not corrected for multiple comparison). However, these are not particularly strong effects and, with these particular stimuli, observers are less likely to choose an item that shares two features with the preceding selection. This may be a function of the specific stimuli. The objects that share two features are a red vertical crescent with a hole and a green vertical rectangle with no hole. It is possible that different sets of shapes would yield different results. In these data, there is little or no evidence that switches were anything but random among the possible target types. For instance, if we compare switches where the shape remained the same (crescent to crescent, rectangle to rectangle) to those where the shape changed, there is essentially no difference (t(24)=0.02, p=0.98).
As in Experiment 1, switch trials are slower than repeat trials (1039 vs 2033 msec, t(24)=12.7, p<0.00001). Within the set of switch trials, targets that share 1 feature with the previous selection are slightly faster than targets sharing 2 or 0 features. As noted above, this post-hoc result is hard to explain and would not be statistically reliable if multiple comparisons are considered. We calculated the Effective Set Size as the number of available targets divided by the number of items on the screen. There were an average of at least 50 repeat and 30 switch trials at Effective Set Sizes 4–10. Calculating the slope of the RT × Effective Set Size function over set sizes 4–10, we find that searches for the same item are more efficient than searches for a new type of target (50 msec/item vs 104 msec item, t(24)=4.5, p<0.0002). Targets collected on switch trials were also farther away from the previous target than targets collected as part of a run (553 pixels vs 658 pixels, t(24)=6.1, p<0.00001).
The results of Experiment 2 suggest that observers are simultaneously searching for all four of the target types. This agrees with the conclusion of work on simple hybrid search for a single target in a display (Wolfe, 2012; Wolfe, Drew, & Boettcher, 2014). Selection history (Awh, et al.,2012, Theeuwes, 2018), notably feature priming, biases search in favor of the most recently collected item. Thus, if you have just selected a blue crescent, you are likely to pick another one. However, if that other one is relatively far away, you may find a different type of target before you can confirm another blue crescent. That is the moment when a run ends and you switch to collecting the new target type. Note that, in this case, “simultaneous” means that the observer is not searching for all of one type, then all of the next type, and so forth. These data do not tell us if all four targets were simultaneously active in working memory.
Experiment 3: Forcing Runs and Switches
In the two experiments reported thus far, observers repeat targets in runs more often than would be predicted by chance. RTs on those run trials are faster than the RTs for switch trials. Does that mean that selecting items in runs of the same type of target is an inherently more efficient way to perform these hybrid foraging tasks? Perhaps runs are simply a default strategy and switching would be just as fast if observers could be persuaded to make that the default. In Experiment 3 we tested this hypothesis by requiring that observers switch target types as often as possible. We compared this to a condition where they were instructed not to switch as often as possible. This experiment addresses a second issue as well. In Experiment 2, there is no evidence that selection of a new type is anything but random amongst the set of possible targets. Perhaps we would see more evidence of non-random switching if we forced observers to switch target types. Thus, Experiment 3 was essentially the same as Experiment 2 with one critical change in the instructions. Observers searched for the same four conjunction stimuli, shown in Figure 8. In Experiment 3, there were two blocks. The Run block, observers were given points only if they selected the same target as the previous selection. They lost a point if they switched. Observers needed 900 points to complete the task. In the Switch block, observers were given points only if they selected a target that was different from the previous selection. They lost a point if they repeated the previously selected target. Observers needed 750 points to complete this task. The different point counts roughly equalize the duration of the two blocks. All responses were made by mouseclick in Experiment 3.
Twelve observers (8 females), ages 18 to 43 years (M = 11.5, SD = 4.4) were tested. All had at least 20/25 acuity with correction and could pass the Ishihara color test. All were paid for their participation. Consent was obtained as approved by the Partners Healthcare Corporation Institutional Review Board.
Results & Discussion
The core manipulation worked as intended. In the Run condition, 87% of selections were repeats of the target type selected immediately previously. Of course, targets of one type could be completely depleted in a display, at which point an observer needed to switch or move to the next display. In the Switch condition, just 3% of selections were repeats of the previous target type. We can easily reject the hypothesis that forcing observers to switch as often as possible would make switching as easy as continuing to select the same target. Target collections on forced run trials were markedly faster than on forced switches (M=910 vs 1506 msec, t(11)=16.3, p<0.00001, Cohen’s d=4.1) and markedly more efficient over effective set sizes of 4–10 (14 msec/item vs 70 msec/item, t(11)=5.3, p<0.0001, Cohen’s d=2.7). Switch costs in hybrid foraging are not simply the by-product of a default preference for runs. It would be more correct to say that runs are the default because switching is expensive.
The second hypothesis in Experiment 3 is that forcing observers to switch as often as possible would provide evidence for a preference to switch between target types that shared more basic features. Individual observers do sometimes appear to prefer some transitions over others. For example, some observers seemed to prefer to switch to a target of the same orientation, choosing the target with matching orientation twice as often as either of the other targets. However, on average there is no reliable pattern. Given selection of a particular target on one selection, the probability of selecting one of three other targets on the next selection does not systematically deviate from random selection. The strongest effect is that after picking a horizontal orange rectangle, observers were somewhat more likely to pick a horizontal blue crescent than to pick either of the other two targets. However, the statistical probabilities of 0.03 and 0.05 would not survive correction for multiple comparison. Observers were not more likely to pick items that shared two features with the prior selection than those that shared one feature (t(11)=1.02, p=0.33) or no features (t(11)=1.36, p=0.19). While some observers favored items of the same shape or orientation, these effects were not reliable in aggregate. Thus, while individuals may have specific strategies for finding the next target when forced to find something new, there is no evidence for a general strategy across observers. Experiment 1 showed that observers foraged in runs when basic features like color and shape distinguished different types of targets. When the two targets were “p” and “d”, observers chose between them almost at random. Experiment 2 replicated the finding with different conjunction stimuli. However, Experiments 2 and 3 fail to find evidence for effects of selection history when the match between the previous selection and the current selection is not perfect. While selecting a blue horizontal crescent may prime the subsequent selection of a blue horizontal crescent, it did not give any advantage to items that were merely horizontal or merely crescent-shaped. It is possible that another blue target would have received some benefit but the current experiments were not designed to detect color-specific effects.
Experiment 4: Amnesic foraging
Experiments 1–3 show that, all else being equal, observers prefer to pick the same type of target again over switching to a new one. They are faster and more efficient when they repeat the preceding selection. Perhaps the act of search for the blue crescent creates a priority map (Fecteau & Munoz, 2006; Serences & Yantis, 2006) that favors “blue” and “crescent” across the field. This would make other blue crescents more salient and would predispose observers to select another blue crescent. Alternatively, the selection of a blue crescent might establish a blue crescent search template (Ort, et al., 2017) so that, having found one instance, the system is configured to keep looking for this type of target. These hypotheses sound very similar but they are differentiable. Suppose that, at the moment of selection of one item, contents of all remaining item locations were scrambled. That will reset the current priority map. If runs were based directly on topography of the priority map, then scrambling should eliminate excess runs. On the other hand, if runs were based on the current search template, scrambling should not alter that template. It will take a moment for the template to generate a new priority map to guide attention, but the preference for the preceding target should remain. Experiment 4 tests this hypothesis.
Methods
The task was similar to the task used in Experiment 2. The “Normal” blocks in Experiment 4 were identical to the Experiment 2 task. Twelve observers (6 female), ages 18–51 years (M = 10.3, SD = 13.8) were tested. Observers memorized the same four conjunction targets and selected them as fast as they could in an effort to collect 900 points (2 points for a correct selection, −1 point for a false positive selection). In the “Amnesic” condition, the task was the same, however, each item swapped locations with another item on the screen when a target was collected. Thus, if a second target had been located before the click on the most recent target, that information would not be useful. Observers ran a brief, 100-point practice block with feedback before running the four experimental blocks without feedback. Those blocks were run either in the order (Normal – Amnesic – Amnesic – Normal) or (Amnesic – Normal-Normal – Amnesic). The starting visual set sizes were 60, 100, 140 and 180. Targets constituted 20–30% of the set at the start. Items disappeared when selected. Twelve observers were tested (7 female, mean age = 29 yrs). All observers had at least 20/25 acuity, normal color vision, and gave informed consent. In this experiment, all data were collected by mouse click.
Results and Discussion
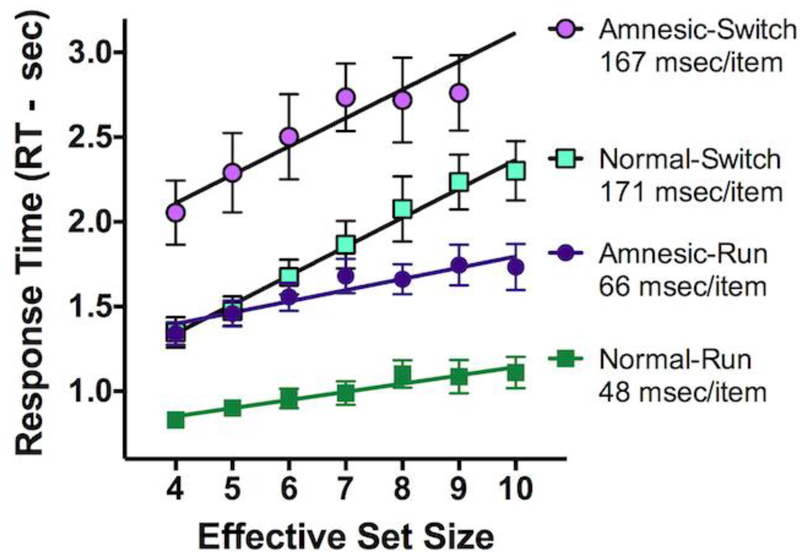
RTs as a function of the Effective Set Size (targets remaining / all items remaining) are shown in Figure 9 for Effective Set Sizes between 4 and 10. The first selection in each patch is removed as it is neither a repeat or switch trial. Correct RTs between 150 and 10,000 msecs are included in the analysis. The upper limit on RTs was extended to 10 seconds because amnesic RTs can be quite long.
Figure 9:
RT × Effective Set Size results for Normal and Amnesic conditions. Run and Switch clicks are plotted separately. The amnesic manipulation produces a substantial, additive increase in RT.
The figure makes it clear that repositioning the items after each selection has a very substantial effect on RT. Amnesic RTs are greater than Normal RTs at all Effective Set Sizes for run clicks (all t(11) > 6.5, all p < 0.00001) and for switch clicks (all t(11) > 3.8, all p < 0.0030). Switch click RTs are greater than Run click RTs at all Effective Set Sizes (all t(11) 4.2, all p < 0.0015). The effect of the random location swapping manipulation appears to be roughly additive. The slopes appear to be similar for Normal and Amnesic blocks. Amnesic Run trials yield a somewhat larger slope but the difference is, at best, marginal (t(11)=2.14, p=0.06, not corrected for multiple comparisons). Amnesic Switch trial slopes do not differ significantly from Normal Switch trial slopes (t(11)=.48, p=0.64).
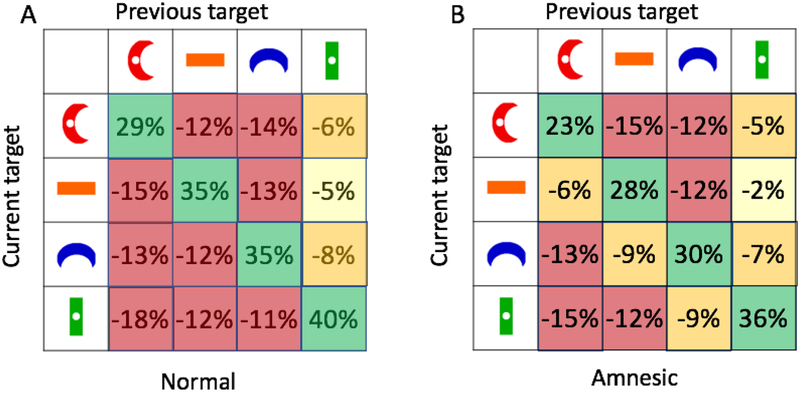
Figure 10 shows that, as in the previous experiments, observers tended to respond in runs. The probability that the next selection will be the same as the previous selection is higher than would be predicted by the frequency of those targets in the displays. This is true for all target types in the Normal and Amnesic conditions (all t(11) > 3.5, all p < 0.005). Runs appear to be a little less prevalent in the Amnesic condition but this is a statistically weak effect (t(11)=2.1, p=0.06).
Figure 10:
Transition probabilities between each of the four types of targets in Normal (A) and Amnesic (B) conditions of Experiment 4. Results show the difference in the percentage of actual transitions and the percentage of possible transitions. Thus, if there were 25% blue crescents in the display but they were selected only 10% of the time following a green rectangle, the table would show a −15% difference. Results do not differ significantly between conditions. Colors coarsely code the percentages.
The results of Experiment 4 show that shuffling all of the items after each click slows foraging. This makes it clear that, in the Normal condition, observers are searching for the next target before they make the motor response to collect the current target. Other than this overall slowing, there is no notable difference between the Normal and Amnesic conditions. This suggests that the excess of runs is not produced by a persistent priority map. The priority map would be flattened or, potentially, worse than useless in the Amnesic condition. The excess of runs is, perhaps, better attributed to the persistent of the current target as a search template in memory.
Discussion
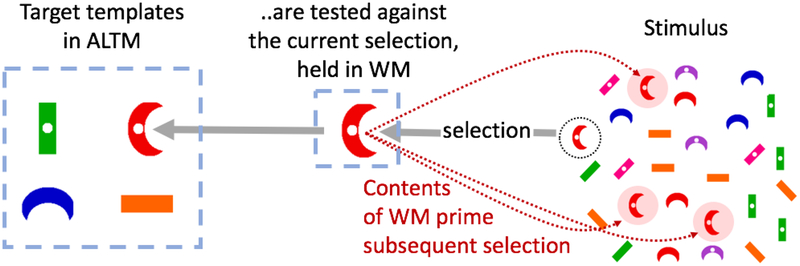
The results reported here, together with those already in the literature, support an account of hybrid foraging, illustrated in Figure 11. For the basic task, used in Experiments 2–4, the observer is holding four items in Activated Long Term Memory (ALTM; Cowan, 1995). These serve as the search templates for hybrid search. It is common to argue that search templates reside in Working Memory (Olivers, Peters, Houtkamp, & Roelfsema, 2011) but we know, from prior work, that can’t be true for hybrid search. First, hybrid search can involve search for, literally, hundreds of target types at the same time (Cunningham & Wolfe, 2014), far in excess of the capacity of working memory. Moreover, loading working memory does not cripple hybrid search (Drew, Boettcher, & Wolfe, 2015). It is better to think of the search templates as being held in a portion of LTM that is relevant to the current task. That is the definition of ALTM. We do not know if there is a limit on the capacity of ALTM. If picture recognition experiments are considered to make use of ALTM, the capacity would be in the thousands of items (Brady, et al; 2008).
Figure 11:
A theoretical snapshot of hybrid foraging. The memory set resides in Activated Long-Term Memory (ALTM). The current object of attention is selected into Working Memory (WM) from the Stimulus. The WM representation is matched to the memory set in ALTM in order to determine if it is a target. If the item, represented in WM, is a target (as it is, in this case), its features prime subsequent selection of similar items in the stimulus.
Working memory must play some role in search since there is a vast literature showing interactions of working memory and search (e.g. Downing & Dodds, 2004; Hollingworth & Luck, 2009; Hutchinson & Turk-Browne, 2012; Luria & Vogel, 2011). Interestingly, many of those interactions look like the priming / selection history effects described here (for a recent example, see Dowd, Pearson, & Egner, 2017). That is, the contents of working memory bias the deployment of attention in search and other tasks. When we tried to block hybrid search by loading working memory, what we found, instead, was that the search task seemed to commandeer the equivalent of one “slot” in working memory (Drew, et al., 2015). We propose that finding a target in a search task, places that target in working memory. Once there, it guides attention to other items that share its basic features. In classic search, this guidance will increase the fluency of search. In hybrid search tasks and, even more, in hybrid foraging tasks, it will bias search to repeat the selection of another instance of the previously selected item. As can be seen in the data presented here, this bias is only a bias, not a requirement to continue selecting the same item. Searches for all the target types are active and an instance of any one of them might be found but, all else being equal, search for the previously selected item will be more fluent. One corollary of this account is that only targets in working memory act to prime subsequent selection. Otherwise, imagine the consequences of attending to an oblique green rectangle. It is not a target. If it primed other oblique green rectangles, that would actively slow search. There is no evidence that this is happening. Indeed, the evidence suggests that features of the distractors are inhibited (Lamy et al, 2008). Presumably, in foraging tasks like those reported here, distractor inhibition must be weaker than the target priming or the distractor inhibition might be expected to completely eliminate the tendency for runs (see figure 10 of Wolfe et al, 2003).
At the outset of this paper, we outlined three hypotheses. Now we can revisit them:
1) Selection goes in runs because the previous selections perceptually prime the next selection on the basis of shared basic features.
The evidence clearly shows that selection of a target, defined by one or more basic features, predisposes the observer to select another example of that type of target. In Experiment 1, those targets could be defined by a single color or by a color × shape conjunction. In Experiments 2–4, the targets were defined by conjunctions of four features. We did not find evidence that, following selection of an item whose definition included a specific feature, selection would be biased toward other items showing that feature. That is, in Experiment 2, selection of a red VERTICAL crescent with a HOLE did not convey any preference to the selection of a green VERTICAL rectangle with a HOLE, even though those items shared two features. This is a case where absence of evidence is not convincing evidence of absence. The experiment should be repeated with different stimuli. In particular, one suspects that color was the strongest guiding feature in this stimulus set and that a red vertical crescent with a hole might well prime other red targets if any had been in the target set.
2) Selection goes in runs because the identity or semantic content of the previous selection primes the next selection
The lack of strong evidence for runs in the search for d & p among d & q is evidence against the hypothesis that the subsequent selection is biased by the identity or semantic content of the targets. Here, when the stimuli are carefully chosen to have no distinguishing basic features, and, thus, elicit no guidance, selection between the two types of target appears to be random. This suggests that neither perceptual priming of the conjunction of shape and orientation nor semantic priming of letter meanings was affecting target selection. Of course, it is possible that other stimuli would produce different results though those stimuli would have to be carefully designed not to contain distinguishing features that could be primed.
3) Selection goes in runs because of the cost associated with switching the target type away from the type that is the current focus of attention.
All of the experiments in this series produce strong evidence for substantial switching costs (see also Kristjánsson & Kristjánsson, 2018). Even in the Letter condition of Experiment 1, switch trials are slower than repeated trials. There appear to be different sorts of switch costs. This is perhaps most clearly seen in Experiment 1 where switch costs for the Conjunction condition are larger than the costs in the Letter or Feature conditions. One can imagine that those costs include the work required to set up new rules for guiding attention to a conjunction of basic features. Consistent with that thought, switch costs are very large in Experiments 2–4, all of which involve conjunction stimuli. Switch trials are a full second slower than repeated trials in Experiment 2. Similarly large costs are seen in Figure 9 for Experiment 4.
The results of these and related experiments hold out the promise that it should be possible to determine with some precision what item will be selected next in a hybrid foraging situation. There will be some bias due to prior selection history, some due to proximity, and some due to the prevalence and/or value of different target types (Wolfe, et al., 2018). Search will not be completely deterministic but we are developing enough of an understanding of the rule to make a good guess about where a searcher will go next and, as a consequence, we may be able to more effectively predict when a searcher will fail to find a target.
Significance.
Many interesting visual search tasks are “hybrid searches” for any of several possible types of target (“Are there guns, bombs, or knives in this bag?”). These combine search through memory with a search of the visible world. Other searches involve foraging for multiple instances of a target (e.g. picking berries). Combining these two, we get “hybrid foraging” tasks, where an observer searches for multiple instances of several types of target. In this paper, we ask how the rules of attentional guidance and priming, studied in simple search tasks, apply to hybrid foraging.
Acknowledgements:
This work was supported by NIH EY017001, NIH CA207490, U.S. Army Natick Soldier Research, Development, and Engineering Center (NSRDEC) W911QY-16-2-0003, and the UC Berkeley Graduate Fellowship. We thank Iris Wiegand and Nurit Gronau for comments and Abla Alaoui-Soce for help conducting the research.
Footnotes
The animal foraging literature discusses when an animal leaves one food ‘patch’ to move to another. In the present work, each screen is the equivalent of a patch and we are interested in when observers chose to finish with one screen and move to the next. We will use the term ‘patch’ here in order to preserve this connection to the foraging literature (and because ‘screen’ introduces other ambiguities into the prose.
We use the term “template” to refer to some internal representation that can guide attention to a target’s features (color, size, etc). A template that is the internal representation of identity (this is the letter, “B”; this is a cat) might or might not be the same template. For purposes of this paper, we are using the term to refer to a template’s role in guidance.
Bibliography
- Altmann EM, & Gray WD (2008). An integrated model of cognitive control in task switching. Psychol Rev, 115(3), 602–639. doi: 10.1037/0033-295X.115.3.602 2008-09896-004 [pii] [DOI] [PubMed] [Google Scholar]
- Awh E, Belopolsky AV, & Theeuwes J (2012). Top-down versus bottom-up attentional control: a failed theoretical dichotomy. Trends in Cognitive Sciences, 16(8), 437–443. doi: 10.1016/j.tics.2012.06.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boettcher S, & Wolfe JM (2015). Searching for the right word: Hybrid visual and memory search for words. Atten Percept Psychophys, 77(4), 1132–1142. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bond A (1982). The Bead Game: Response Strategies in Free Assortment. Human Factors [0018–7208] yr:1982 vol:24 iss:1 pg:101 24(2), 101–110. [Google Scholar]
- Bond AB (1983). Visual search and selection of natural stimuli in the pigeon: the attention threshold hypothesis. J Exp Psychol Anim Behav Process, 9(3), 292–306. [PubMed] [Google Scholar]
- Bond AB (2007). The evolution of color polymorphism: Crypticity searching images, and apostatic selection. Annual Review of Ecology Evolution and Systematics, 38, 489–514. doi: 10.1146/annurev.ecolsys.38.091206.095728 [DOI] [Google Scholar]
- Bond AB, & Kamil AC (2002). Visual predators select for crypticity and polymorphism in virtual prey. Nature, 415(6872), 609–613. [DOI] [PubMed] [Google Scholar]
- Brady TF, Konkle T, Alvarez GA, & Oliva A (2008). Visual long-term memory has a massive storage capacity for object details. Proc Natl Acad Sci U S A, 105(38), 14325–14329. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brainard DH (1997). The Psychophysics Toolbox. Spatial Vision, 10, 433–436. [PubMed] [Google Scholar]
- Cain & Drew (submitted). Visual Working Memory Load has Little Effect on Multiple Target Visual Search Accuracy
- Cain MS, Vul E, Clark K, & Mitroff SR (2012). A Bayesian optimal foraging model of human visual search. Psychol Sci (23), 1047–1054. doi: 10.1177/0956797612440460 [DOI] [PubMed] [Google Scholar]
- Charnov EL (1976). Optimal foraging, the marginal value theorem. Theoretical Population Biology, 9, 129–136. [DOI] [PubMed] [Google Scholar]
- Chen L (2005). The topological approach to perceptual organization. Visual Cognition, 12(4), 553–637. [Google Scholar]
- Cowan N (1995). Attention and Memory: An integrated framework. New York: Oxford U press. [Google Scholar]
- Cunningham CA, & Wolfe JM (2014). The role of object categories in hybrid visual and memory search. J Exp Psychol Gen, 143(4), 1585–1599. doi: 10.1037/a0036313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dowd EW, Pearson JM, & Egner T (2017). Decoding working memory content from attentional biases. [journal article]. Psychonomic Bulletin & Review, 24(4), 1252–1260. doi: 10.3758/s13423-016-1204-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Downing P, & Dodds C (2004). Competition in visual working memory for control of search. Visual Cognition, 11(6), 689–703. [Google Scholar]
- Drew T, Boettcher SP, & Wolfe JM (2015). Searching while loaded: Visual working memory does not interfere with hybrid search efficiency but hybrid search uses working memory capacity. Psychonomic Bulletin & Review, 23(1), 201–212. doi: 10.3758/s13423-015-0874-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dukas R (2002). Behavioural and ecological consequences of limited attention. Philos Trans R Soc Lond B Biol Sci, 357(1427), 1539–1547. doi: 10.1098/rstb.2002.1063 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehinger KA, & Wolfe JM (2016). When is it time to move to the next map? Optimal foraging in guided visual search. Atten Percept Psychophys, 78(7), 2135–2151. doi: 10.3758/s13414-016-1128-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Failing M, & Theeuwes J (2017). Selection history: How reward modulates selectivity of visual attention. [journal article]. Psychonomic Bulletin & Review. doi: 10.3758/s13423-017-1380-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fecteau JH, & Munoz DP (2006). Salience, relevance, and firing: a priority map for target selection. Trends Cogn Sci, 10(8), 382–390. [DOI] [PubMed] [Google Scholar]
- Grubert A, & Eimer M (2014). Rapid Parallel Attentional Target Selection in Single-Color and Multiple-Color Visual Search. Journal of Experimental Psychology: Human Perception and Performance, 41(1), 86–101. doi: 10.1037/xhp0000019 [DOI] [PubMed] [Google Scholar]
- Hills TT, & Dukas R (2012). The Evolution of Cognitive Search In Todd PM, Hills TT & Robbins TW (Eds.), Cognitive Search: Evolution, Algorithms, and the Brain (pp. 11–24). Cambridge, MA: MIT Press. [Google Scholar]
- Hills TT, Todd PM, Lazer D, Redish AD, Couzin ID, & The Cognitive Search Research Group* (*Bateson M, Cools R, Dukas R, Giraldeau L, Macy MW, Page SE, Shiffrin RM, Stephens DW, Uzzi B, Wolfe JW). (2015). Exploration versus exploitation in space, mind, and society. Trends Cogn Sci, 19(1), 46–54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hollingworth A, & Luck SJ (2009). The role of visual working memory (VWM) in the control of gaze during visual search. Atten Percept Psychophys, 71(4), 936–949. doi: 71/4/936 [pii] 10.3758/APP.71.4.936 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchinson JB, & Turk-Browne NB (2012). Memory-guided attention: control from multiple memory systems. Trends Cogn Sci, 16(12), 576–579. doi: 10.1016/j.tics.2012.10.003 S1364–6613(12)00239–2 [pii] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kleiner M, Brainard DH, & Pelli D (2007). What’s new in Psychtoolbox-3? Perception, 36, ECVP Abstract Supplement. [Google Scholar]
- Kristjansson A (2015). Reconsidering visual search. i-Perception, 6(6). doi: 10.1177/2041669515614670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristjánsson Á (2016). The Slopes Remain the Same: Reply to Wolfe (2016). i-Perception, 7(6), 10.1177/2041669516673383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristjansson Å, Johannesson OI, & Thornton IM (2014). Common Attentional Constraints in Visual Foraging. PLoS ONE, 9(6), e100752. doi: 10.1371/journal.pone.0100752 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kristjánsson T, & Kristjánsson Á (2018). Foraging through multiple target categories reveals the flexibility of visual working memory. Acta Psychologica, 183, 108–115. doi: 10.1016/j.actpsy.2017.12.005 [DOI] [PubMed] [Google Scholar]
- Lamy D, Antebi C, Aviani N, & Carmel T (2008). Priming of Pop-out provides reliable measures of target activation and distractor inhibition in selective attention. Vision Research, 48(1), 30–41. doi: 10.1016/j.visres.2007.10.009 [DOI] [PubMed] [Google Scholar]
- Liu T, & Jigo M (2017). Limits in feature-based attention to multiple colors. [journal article]. Attention, Perception, & Psychophysics, 79(8), 2327–2337. doi: 10.3758/s13414-017-1390-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lumbreras B, Donat L, & Hernández-Aguado I (2010). Incidental findings in imaging diagnostic tests: a systematic review. The British Journal of Radiology, 83(988), 276–289. doi: 10.1259/bjr/98067945 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luria R, & Vogel EK (2011). Visual search demands dictate reliance on working memory storage. J Neurosci, 31(16), 6199–6207. doi: 31/16/6199 [pii] 10.1523/JNEUROSCI.6453-10.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNamara J, & Houston A (1985). A simple model of information use in the exploitation of patchily distributed food. Animal Behaviour, 33, 553–560. [Google Scholar]
- Monsell S (2003). Task switching. Trends Cogn Sci, 7(3), 134–140. [DOI] [PubMed] [Google Scholar]
- Olivers CN, Peters J, Houtkamp R, & Roelfsema PR (2011). Different states in visual working memory: when it guides attention and when it does not. Trends Cogn Sci, 15(7), 327–334. doi: S1364–6613(11)00085–4 [pii] 10.1016/j.tics.2011.05.004 [DOI] [PubMed] [Google Scholar]
- Olsson O, & Brown JS (2006). The foraging benefits of information and the penalty of ignorance. Oikos, 112(2), 260–273. doi: 10.1111/j.0030-1299.2006.13548.x [DOI] [Google Scholar]
- Ort E, Fahrenfort JJ, & Olivers CNL (2017). Lack of Free Choice Reveals the Cost of Having to Search for More Than One Object. Psychological Science, 28(8), 1137–1147. doi: 10.1177/0956797617705667 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pelli DG (1997). The VideoToolbox software for visual psychophysics: Transforming numbers into movies. Spatial Vision, 10(4), 437–442. [PubMed] [Google Scholar]
- Pirolli P (2007). Information Foraging Theory. New York: Oxford U Press. [Google Scholar]
- Pirolli P, & Card S (1999). Information foraging. [Article]. Psychological Review, 106(4), 643–675. [Google Scholar]
- Pyke GH, Pulliam HR, & Charnov EL (1977). Optimal Foraging: A Selective Review of Theory and Tests. The Quarterly Review of Biology, 52(2), 137–154. [Google Scholar]
- Schneider W, & Shiffrin RM (1977). Controlled and automatic human information processing: I. Detection, search, and attention. Psychol. Rev, 84, 1–66. [Google Scholar]
- Serences JT, & Yantis S (2006). Selective visual attention and perceptual coherence. Trends Cogn Sci, 10(1), 38–45. [DOI] [PubMed] [Google Scholar]
- Stephens DW, & Krebs JR (1986). Foraging Theory. Princeton, NJ: Princeton U. Press. [Google Scholar]
- Theeuwes J (2013). Feature-based attention: it is all bottom-up priming. Philosophical Transactions of the Royal Society B: Biological Sciences, 368(1628). doi: 10.1098/rstb.2013.0055 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Theeuwes J (2018). Visual Selection: Usually fast and automatic; seldom slow and volitional. J. of Cognition, in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM, Butcher SJ, Lee C, & Hyle M (2003). Changing your mind: On the contributions of top-down and bottom-up guidance in visual search for feature singletons. J Exp Psychol: Human Perception and Performance, 29(2), 483–502. [DOI] [PubMed] [Google Scholar]
- Wolfe JM, Horowitz T, Kenner NM, Hyle M, & Vasan N (2004). How fast can you change your mind? The speed of top-down guidance in visual search. Vision Research, 44(12), 1411–1426. [DOI] [PubMed] [Google Scholar]
- Wolfe JM (1998). What do 1,000,000 trials tell us about visual search? Psychological Science, 9(1), 33–39. [Google Scholar]
- Wolfe JM (2012). Saved by a log: How do humans perform hybrid visual and memory search? Psychol Sci, 23(7), 698–703. doi: 10.1177/0956797612443968 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM (2013). When is it time to move to the next raspberry bush? Foraging rules in human visual search. Journal of Vision, 13(3), 10.1167/13.3.10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM (2016). Visual Search Revived: The Slopes Are Not That Slippery: A comment on Kristjansson (2015). i-Perception, May-June 2016, 1–6. doi: 10.1177/2041669516643244 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM (2017). Mixed hybrid search: A model system to study incidental finding errors in radiology. paper presented at the 2017 Medical Image Perception Meeting in Houston TX (July 12–15, 2017). [Google Scholar]
- Wolfe JM, Aizenman AM, Boettcher SEP, & Cain MS (2016). Hybrid Foraging Search: Searching for multiple instances of multiple types of target. Vision Res, 119, 50–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM, Cain MS, & Alaoui-Soce A (2018). Hybrid value foraging: How the value of targets shapes human foraging behavior. Atten Percept Psychophys, 10.3758/s13414-017-1471-x [DOI] [PubMed] [Google Scholar]
- Wolfe JM, Drew T, & Boettcher SEP (2014). Hybrid Search: Picking up a thread from Schneider and Shiffrin (1977) In Raaijmakers J (Ed.), Cognitive Modeling in Perception and Memory: A Festschrift for Richard M. Shiffrin New York: Psychology Press. [Google Scholar]
- Wolfe JM, & Horowitz TS (2017). Five factors that guide attention in visual search. [Review Article]. Nature Human Behaviour, 1, 0058. doi: 10.1038/s41562-017-0058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM, Palmer EM, & Horowitz TS (2010). Reaction time distributions constrain models of visual search. Vision Res, 50, 1304–1311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolfe JM, Yee A, & Friedman-Hill SR (1992). Curvature is a basic feature for visual search. Perception, 21, 465–480. [DOI] [PubMed] [Google Scholar]
- Zhang J, Gong X, Fougnie D, & Wolfe JM (2017). How humans react to changing rewards during visual foraging. Atten Percept Psychophys, 79(8), 2299–2309 doi: 10.3758/s13414-017-1411-9 [DOI] [PubMed] [Google Scholar]