Abstract
Accessing the network through which a propagation dynamics diffuses is essential for understanding and controlling it. In a few cases, such information is available through direct experiments or thanks to the very nature of propagation data. In a majority of cases however, available information about the network is indirect and comes from partial observations of the dynamics, rendering the network reconstruction a fundamental inverse problem. Here we show that it is possible to reconstruct the whole structure of an interaction network and to simultaneously infer the complete time course of activation spreading, relying just on single epoch (i.e. snapshot) or time-scattered observations of a small number of activity cascades. The method that we present is built on a belief propagation approximation, that has shown impressive accuracy in a wide variety of relevant cases, and is able to infer interactions in the presence of incomplete time-series data by providing a detailed modelling of the posterior distribution of trajectories conditioned to the observations. Furthermore, we show by experiments that the information content of full cascades is relatively smaller than that of sparse observations or single snapshots.
Keywords: epidemics, statistical physics, probabilistic modelling
1. Introduction
Much effort has been devoted recently to the inverse problem of reconstructing the topology of a network from time-series of a dynamical process acting on it [1–4]. When observation of the full time-series of the process is available, the problem can be, and has been, recast into relatively simple terms, since a sequence of time-consecutive states of a pair of nodes gives direct information about the potential interaction between them. In many cases, however, the set of available observations is much sparser, possibly on a much slower time scale than that of the dynamics, and often skipping the initial stages of the propagation which would give precious information about the initial condition. In particular, in an observation consisting of a single snapshot of the system there is no direct information about the interaction of nodes, as evidence of interaction indeed comes from variation of the state of nodes in time. Examples of important applications in which such a complete measurement of dynamical quantities in a full time-series is inaccessible are second messenger cascades in a cell, rapid-firing neuron cascades in the human brain during epileptic seizures or in the context of epidemic and/or information spreading in a network of individuals. In all these examples, typically, there is no information about which was the first active node, little is known about the underlying networks of contacts, which may even be dynamically changing over time and moreover an observation of the full time-series is prohibitive or plainly impossible.
Even though direct experimental data about contact networks in diverse contexts are being collected at a fast rate [5–7], there are some strong experimental and technical limitations to this collection, sometimes due to privacy protection regulations or concerns. However, knowledge of propagation networks would have a large list of benefits. First, it may allow one to understand the propagation process better, including finding entry-points (e.g. the so-called index case or patient zero in epidemiological jargon) of an ongoing epidemic. Second, it may allow one to devise strategies to control the process in various ways, for example, hindering the propagation (e.g. targeted vaccination) or favouring it (e.g. in the context of maximizing information diffusion on social networks, in viral or targeted advertising, etc.). In this respect, a number of computational studies have introduced optimization methods based on message-passing that address the problem of containing [8] or maximizing spreading [9,10].
Recently, several approaches have been proposed for the problem of deducing the propagation network from time-series, based on Bayesian approaches [3,11,12] (we also mention [13,14] where computations are based on efficient dynamic message-passing equations), maximum-likelihood approach [3], compressed sensing schemes [15], genetic [16] and dynamic programming algorithms [17], tensor decomposition [18] or on Monte Carlo sampling [19]. We also mention [20,21] in which the network inference is performed model-free, namely without any a priori knowledge about the dynamic rules and the kind of interaction among nodes. These methods all share the need for observations at consecutive epochs. An attempt to infer a network from a single snapshot is proposed in [22] where the authors, using a topology-based method, limit the set of possible candidate networks to d-dimensional grids or Erdos–Rényi (ER) graphs.
Despite this recent progress, in most contexts the available observations of each cascade are sparse, noisy and especially discontinuous in time. One example is the problem of inferring functional contacts in signalling pathways, in which interacting proteins generate cascades of phosphorylation which eventually transmit signals from the cell membrane to the nucleus. Observations come in general from gene expression data, and the network to be inferred is a sub-network of a large-scale protein–protein interaction (PPI) network, also known as interactome. Although several experimental and computational approaches are able to identify candidate links of these networks, they lack in distinguishing false positive (FP) from true positive (TP) links [23–25] that seems to be a challenging task. Social science and epidemiology offer another interesting domain of application, as one generally tries to infer the network of social contacts (even through the Web [26,27]) from a limited amount of sparse and noisy observations of some propagation histories.
Here we present a Bayesian technique that allows one to uncover the complete functional structure (including its topology and parameters) of a network from a limited amount of single snapshots of the state of the network cascades. We assume that the dynamics is well described by progressive propagation models like susceptible–infected (SI), susceptible–infected–recovered (SIR), independent cascades and variants, including models with hidden variables (e.g. representing latency times). Reversible processes, like susceptible–infected–susceptible epidemics, cannot be treated by our algorithm as, in this case, the probability space of a single-site trajectory can grow exponentially with the time horizon, making the method impractical. Note that these models have absorbing states (all states with no individuals in state I), that limit severely the amount of information that it is possible to retrieve from a single time-series.
Starting from a functional parametrization of the posterior probability distribution of propagation trajectories, our technique builds on a message passing procedure that allows one to compute, and then maximize, the likelihood of a given network structure. This computation can be performed efficiently thanks to belief propagation (BP), which is proven to be exact for tree graphs and has been successfully used in a variety of problems in general graphs with loops. Upon convergence, the parameters allow one to identify both the network and the sources of the infection for each cascade with great accuracy. We called this method gradient ascent belief propagation (GABP).
Although the proposed inference machinery is very general, we focus on the well-known SIR [28] model, which describes those diseases in which infected individuals become immune to future infections after recovery (such as measles, rubella, chicken pox and generic influenza) or the interaction dynamics among proteins. We also propose some results using the SI model when dealing with the spreading of rumour and information over a network. In particular, we evaluate the performances of GABP comparing our results to a ground-truth when dealing with synthetic cascades of both synthetically generated and real-world networks; we also use real cascades measurements and apply our method for inferring the graph structure underlying several websites that have published the same trend topic [29].
Our minimal model of activity propagation in a network is very simple: if a node i is active (infected) at time t, it has a finite probability λij to activate (or infect) any of its neighbours j, which will in turn be active at time t + 1. Exclusively in the SIR model, an active node will recover in each time-step with a (generally site-dependent) recovery probability μi. Once recovered, nodes do not become active anymore, and will not be able to infect other nodes. This will result in a propagation throughout the network, that we call a cascade.
Let us then suppose that a number M of statistically independent realizations (or cascades) of the SIR dynamics can be observed. In the prototypical situation, the complete history of the propagation is unavailable and we do not assume any a priori knowledge about the network structure: all we can observe is, for each cascade, a number of ‘frozen’ snapshots of a wavefront of the activity at a given time T, when all the states of the nodes in the network can be assessed to a reasonable extent of accuracy. Our aim is to identify the hidden network structure and the set of transmission probabilities for each link. Our method could in principle accommodate cases with different types and/or amount of information (including even partial and noisy observations from previous time-steps) but we limit ourselves to consider a limit ‘worst’ case in which a single snapshot of nodal states, per cascade, is observed. Figure 1 shows a cartoon representation of the problem. Each column represents an epidemic process that evolves in time t (the evolution of nodal states is shown in the rows of figure 1). What we observe is the collection of final states within the ampoule, for all the cascades.
Figure 1.
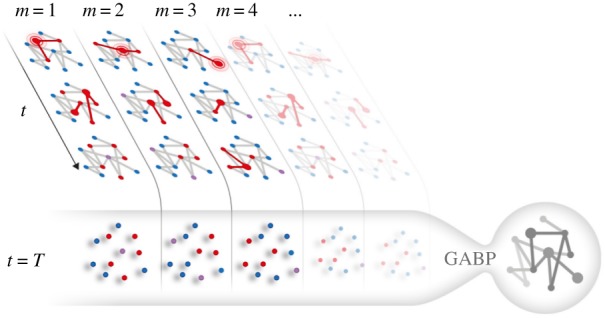
Cartoon representation of the network reconstruction problem: M independent cascades starting from different sources (highlighted in the first frame of each vertical stripe) are represented, with time flowing downward. Infected nodes are red, susceptible nodes are blue and recovered nodes are purple. The GABP algorithm is provided a set of M snapshots taken T time steps after the cascade onset: the goal is to reconstruct the functional interactions in the network G as well as to identify the source of each cascade. (Online version in colour.)
We underline that if the states of the nodes were known for the whole process, namely the time-series of all the states, estimating the infection and recovery probabilities reduces to an easier problem, as the likelihood of the parameters has a closed expression that can, in principle, be climbed by local gradient algorithms. Here we consider cases in which we reduce the observations of each epidemic at a specific time T: the past states of the nodes are unknown dynamical variables over which we need to consider all their possible realizations.
2. Results
2.1. A static formulation of the dynamical process
Reconstructing the unknown connectivity structure of the network is inevitably coupled to that of tracing back in time the entire history of the spreading process for each cascade m ∈ {1, …, M}, which in turn results in the identification of the sources of diffusion. Our approach builds on computing a joint posterior probability distribution over all cascades that are compatible with the observations, and then maximizing the likelihood of interaction parameters of the network at the same time. To set our notation, let us consider a weighted undirected graph G = (V, E, Λ, Ω) with a number |V| of nodes, where Λ = {λij}ij∈E play the role of edge-dependent infection probabilities in an SIR stochastic model, and that is also equipped with a set Ω = {μi}i∈V of site-dependent recovery probabilities. For directed graphs, we allow parameters λij ≠ λji. Focusing, for the moment, on a single cascade, at any point in time each node i will be in one of three possible states: susceptible (S), infected (I) and recovered/removed (R). The state of node i at time t in each cascade m is represented by a variable xi(t) ∈ {S, I, R}, with t in some discrete set. At each time step (e.g. a day) of the stochastic dynamics, an infected node i can first spread the disease to each susceptible neighbour j with given probability λij, then recover with probability μi. Each cascade is defined by the set of vectors xm(t), with m labelling the cascade, and we assume that for each cascade the initial state xm(0) is composed of just one infected node , with all the other nodes in the network being in the susceptible state. We will assume that we have access to the state of the nodes in the networks only Tm = T steps after the initiation of each cascade.
Let us consider a node i which gets infected at its infection time ti: since it has a finite probability to pass the disease to a neighbour j in each time step, this results in a stochastic transmission delay sij. In addition, the individual i recovers at time ti + gi, with gi a stochastic recovery delay. Owing to the irreversibility of the spreading process, each cascade is fully specified by the quantities {ti, gi}i∈V and {sij}(i,j)∈E for each node and each link in the network. It is then possible to construct a simple static graphical model representation of the dynamical process for each cascade on the grounds of the following simple observation: the time at which a given node i gets infected only depends on the infection times of its neighbours j, and the infection delays of these nodes. Infection times ti > 0 are related by the deterministic equations
| 2.1 |
which are a set of |V| constraints encoding the infection dynamics, involving only local quantities at each node. Once the initial condition x(0) and stochastic quantities sij and gi are thrown independently from their own distributions, the infection times are given deterministically by virtue of equation (2.1).
This observation was exploited in a series of works [9,30,31] to develop a fully Bayesian method for approximating the whole probability distribution of the time evolution of the system, conditioned on some observations, and was originally used to identify the origin of the epidemic outbreak in SIR and similar models. The method is built on a BP approximation (see Methods), which is exact on tree graphs and has proven successful in general networks with loops.
What if the underlying network is unknown, and so are the epidemic parameters {λij, μi}? In a maximum-likelihood approach, one needs to define the quantity namely the likelihood of epidemic parameters with respect to observations, and then be able to maximize over the relevant parameters. Note that in a fully Bayesian framework, incorporating a priori information on the network topology or epidemic parameters is straightforward: it would lead to adding a log-prior term to the log-likelihood to obtain a log-posterior. The log-likelihood of the parameters coincides with the so-called free-entropy of the system , which can be computed, consistently with the BP approximation, employing the Bethe decomposition (see Methods).
The BP method for the (cavity) marginal distributions of infection times can be then interleaved with simple log-likelihood climbing steps in a gradient ascent (GA) scheme, leading to a unique set of equations that are solved by iteration. In this setting, the computation of the gradient of the log-likelihood relies only on local updates involving the BP cavity messages. Ultimately, all the information has to be processed locally at each node. That, in addition to other simplifications, entails a huge reduction of computational time, making the analysis of large-scale networks feasible efficiently (see Methods). One starts from a flat assignment of the parameters, and the initial fully connected network gets progressively pruned by means of the GA updates, eventually leading to a reconstructed network strongly resembling the real one.
2.2. Reconstructing random networks
We start by investigating three basic random network structures, namely random regular (RR), ER and Barabási–Albert (BA) scale-free networks: an impressive level of accuracy may be reached with a small number M of observations. In an RR network, each node is connected at random with a fixed number of neighbours in the networks, whereas in the ER graph the number of neighbours is Poisson distributed. Scale-free networks, on the other hand, possess a power-law degree distribution, and are known to capture some key ingredients of many real networks encountered in practical applications (for a review, see [32]).
As a first step, a random graph is constructed, and a set of M cascades are simulated, each one being an independent realization of the stochastic SIR process with a random initial source . GABP is then run until the parameters λij and μi reach a stable value. Since the goal of the inference is twofold, we use two different measures of the inference performance. For each cascade m, the nodes in the network are ranked in decreasing order with respect to the estimated probability of being the origin of the observed epidemic: the ability to identify the sources of the spreading is easily quantified by the rank of , namely the position of in the ordered list.
On the other hand, a simple method for quantifying the accuracy of network reconstruction is the receiver operating characteristic (ROC) curve, namely a plot of the TP rate against the FP rate in a binary classification problem. Constructing the ROC curve in the present case is very easy: the inferred values of λij are ranked in decreasing order, and one step upward in the ROC is taken if the link is present in the original graph (TP) or one step rightward if the link is absent (FP). The area under the ROC curve is a good indication of the discrimination ability: areas close to one signal a good discrimination between true links and non-existent links. The reconstruction performances are compared to those of an empirical correlations based method. For each possible couple of nodes we compute, at the time of the observation T, the probability of having an edge (i, j) as the mutual information (MI) between node i and j; details of the calculations are reported in the Methods section. As for the case of parameters λij, we construct ROC curves and we compute ROC areas from the set of correlation measures mij.
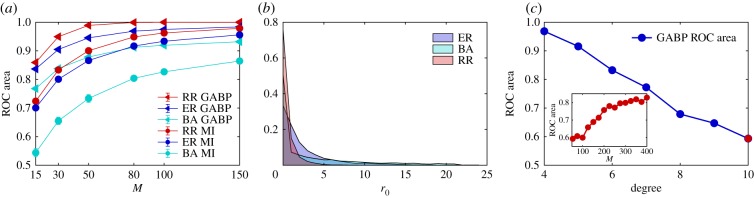
We report in figure 2a a systematic investigation of the reconstruction performances of GABP and MI in the three types of random networks with an increasing number of cascades M. The parameters of the infection are λ = 0.6 and μ = 0.4 for all the experiments (except when differently noted). These parameters seem to ensure a reasonable infection size at the observation time in a way that we can use sufficient information for inferring the network.1 For all values of M GABP outperforms the MI method as the ROC areas associated with the GABP predictions are notably greater than the one obtained from MI. In the case of BA graphs, we notice smaller values of the ROC areas because, for these values of the parameters of the SIR dynamics, we observe huge epidemics in which at time T almost all nodes are infected or recovered. This efficient spreading is caused by the presence of hubs that easily infect a good portion of the network in one time-step. In this regime and even for large value of M, there is not sufficient information to fully recover the true links of the graphs.
Figure 2.
(a) Reconstruction accuracy in three types of random networks using GABP and MI. Each curve is an average over 30 random instances of the area under the ROC curve, as a function of the number of observed cascades M at time T = 5. Epidemic parameters, λij = 0.6 and μi = 0.4, are the same for all the three types of networks. The size of the network is |V| = 50. Red curve: RR graphs with degree d = 4; light blue curve: BA (scale-free) networks with average degree dav = 4; blue curve: ER graphs with average degree dav = 4. Triangular and circular marks show GABP and MI results, respectively. (b) Identification of initial spreaders. Each filled curve is the histogram of the rank of the true patient zero at M = 150 for the three types of network. Histograms refer to 30 random instances, thus considering a total of 30 × 150 = 4500 independent cascades. (c) Reconstruction accuracy versus connectivity. The blue curve is the area under the ROC curve in different instances of RR graphs of size |V| = 50 with increasing degree d. In each case, M = 50 cascades are observed at time T = 7. Recovery rate is fixed to μi = 0.4, λij is scaled down as degree increases in order to keep the size of epidemics roughly constant. Inset: area under the ROC curve as a function of the number of observed cascades M in a random regular graph with degree d = 10 (corresponding to the red point at the end of the blue curve in the main plot). (Online version in colour.)
The ability to identify the sources of spreading (patient zero) is easily quantified by the rank of the true patient zero in each of the M cascades: if M is high enough so that enough information is conveyed on the underlying network structure, GABP is able to successfully identify most of the true initial spreaders in each cascade. This can be seen in figure 2b, that shows the distribution of for a value of M = 150 in the three types of random networks considered here, which is fairly concentrated on low values of .
The reconstruction performance is expected to be substantially related to the density of the network. This can be investigated by systematically varying the degree of connectivity of a network, as is shown in figure 2c, where the performance of GABP is assessed in a RR graph of size |V| = 50 with an increasing connectivity degree d, from d = 4 to 10. The accurate reconstruction of denser networks requires, consequently, a larger number of cascades M.
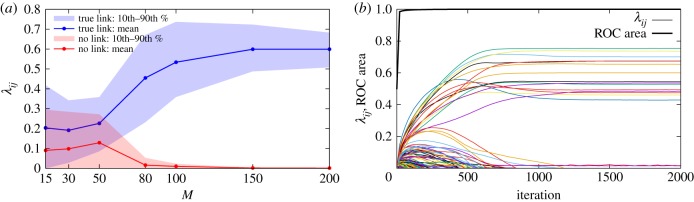
As can be seen in figure 3a, the distribution of inferred values of true links rapidly separates from the one of non-existent ones, that concentrates around vanishing values even for a very small number of observations. The strict separation of the two distributions confirms the results from the area under the ROC curve.
Figure 3.
GABP rapidly identifies true links. (a) Average value of λij for true links (blue) versus non-existent ones (red) as a function of the number of observed cascades in an RR graph with size |V| = 50, λij = 0.6, μi = 0.4 and d = 4; shaded areas correspond to the intervals between the 10th and the 90th percentile in each distribution. (b) The thin lines represent the λij values of a random subset of 200 links in the case with M = 200 cascades as a function of iterations of the GABP algorithm; black thick line: area under the ROC curve. (Online version in colour.)
It is worth noting that GABP achieves a good level of reconstruction accuracy in a very small number of steps. The dynamics of the inferred λij as a function of iterations of the algorithm is exemplified in figure 3b. Even after a very small number of iterations, true links are clearly distinguished from non-existent ones, as can be seen from the steep rise of the area under the ROC curve as a function of iterations: we observe that this kind of behaviour is quite general and not restricted to the case .
2.3. Reconstructing real networks
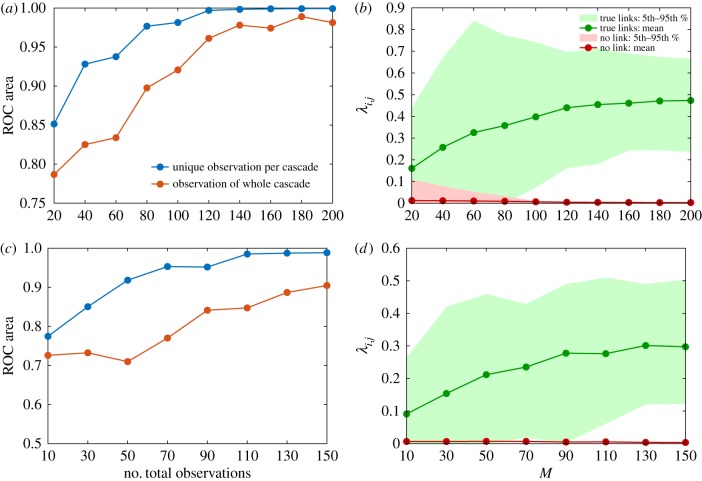
We tested the GABP algorithm on two different real interaction networks on which information about contacts is available for validation purposes. The first dataset consists of a network of Twitter retweets [33,34]: the network is composed of |V| = 96 nodes, which represent Twitter users, linked through |E| = 117 edges corresponding to retweets (these were collected from various social and political hash-tags). The average degree of a node in the network is dav = 2, with a minimum degree of 1 and a maximum degree of 17. Figure 4a,b shows the reconstruction performance in the retweet network using two different observation paradigms: in the single-observation-per-cascade paradigm (which we considered as the standard case), the node state is available only once per cascade, whereas in the whole-cascade paradigm all nodes are observable at all times. In the first algorithm, the number of cascades coincides with the number of observations O while in the whole-cascade reconstruction the number of observations is still O but the number of available cascades is normalized with respect to the number of time-steps, namely O/T . We simulate several spreading cascades with infection probability λij = 0.5 and recovery probability μi = 0.4. It is apparent that an extremely accurate reconstruction is achievable with a number of cascades M quite small compared with |V| and furthermore it is worth noting that when a number of possible observations is fixed, considering many cascades at a single time instead of the full time-series of a smaller number of cascades leads to better predictions.
Figure 4.
Reconstruction performance of GABP in the network of retweets (|V| = 96) with increasing number of independent cascades M. Epidemic parameters are λij = 0.5 and μi = 0.4, observation time T = 5. (a,c) Blue curve: area under ROC curve in the case where the state of the networks is fully observed at each time t ∈ {1, …, T} for each cascade m. Red curve: area under ROC curve in the case where the network is observed only at time T in each cascade. (b,d) Average value of λij for true links (green) versus non-existent ones (red) as a function of the number of observed cascades in the standard case (observation at time T only); shaded areas correspond to the intervals between the 5th (10th in (d)) and the 95th (90th in (d)) percentile in each distribution. (Online version in colour.)
We repeat the same experiment using an SI dynamics with true infection probability λij = 0.3; figure 4c shows that as for the SIR case few cascades suffice to reach a very high value of the area under the ROC curve and that the single-observation paradigm has to be preferred to the whole-cascade one when few observations are available. As for the SIR results, the value of the infection probability is correctly estimated for a large number of cascades and the presence of a link (characterized by a non-zero λij) is clearly detectable after about 100 cascades as shown in figure 4d.
As another illustrative example, in figure 5 we show a pictorial representation of the reconstruction of the Zachary’s Karate Club network, a small social network which consists of |V| = 34 nodes and |E| = 78 edges, documenting the pairwise interactions over the course of three years among members of a university-based karate club. In this case, we simulated up to M = 102 cascades and investigated the performance of the inference method with homogeneous parameters λ = 0.3 and μ = 0.4 at increasing M. In figure 5, links not present in the actual graph are coloured in red, and appear clearly distinguished from the true ones (coloured in black) even for very small values of M.
Figure 5.
Pictorial representation of the GABP performance in Zachary’s Karate Club network with an increasing number of cascades M. An edge is thrown between node i and node j if λij in non-zero, the width of the edge being proportional to the value λij. True links are coloured in black, red links are not present in the original network. (Online version in colour.)
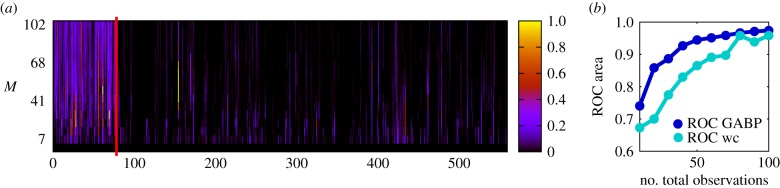
For a more thorough representation of the reconstruction process in the Karate Club network, we show in figure 6a a colour intensity plot of the dynamics of inference as the number of cascades is increased: true links are immediately identified, as the ROC area indicates (figure 6b, blue curve).
Figure 6.
(a) Reconstruction performance of GABP in the Zachary’s Karate Club network with different numbers M of independent cascades. M is on the y-axis. The links are on the x-axis, ordered in such a way that the first 78 are the true links in the original graph. The colour intensity is proportional to the value λij for each putative link (i, j) at increasing values of M. (b) Area under the ROC curve (y-axis) for increasing total observations (see text) of the entire networks (x-axis, scale as in the left part). The blue curve corresponds to a single final observations per cascade at time T = 5, the light-blue curve shows the case in which cascades are fully observed. (Online version in colour.)
It is very interesting to note that, while observing cascades in their entirety clearly conveys a lot of information on the network structure, if the total number of observations of the full state of the network is constrained, distributing these observations far apart in time (or better, on independent cascades) pays better. This is clearly shown in figure 6b by the difference in the area under the ROC curve between the whole cascade (light-blue curve) scenario and the single-observation-per-cascade paradigm.
2.4. Detecting false positive links in protein–protein interaction networks
A challenging problem in reconstructing PPI networks consists in discriminating between TP and FP links. We show in this section how GABP algorithm can be used as a post-processing method to tackle this issue.
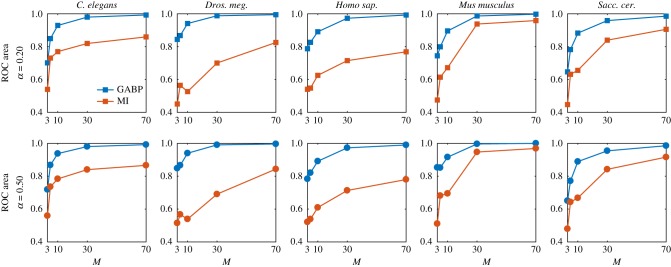
In our experiments, we consider as ground-truth networks the giant components of five interactomes of the PSICQUIC dataset [35] available in the software Cytoscape 3.5.1 [36] (properties are summarized in table 1), while contact cascades are synthetically simulated with infection parameters λ = 0.8 and μ = 0.3. To the true networks, we add Z = α|E| extra edges, for α ∈ [0.2, 0.5], that mimic the presence of FP interactions. This step is performed in a ‘scale-free’ fashion: we first pick a node i with probability proportional to its degree and then we connect it to a node chosen uniformly at random. We then simulate M ∈ [3, 150] cascades on the true network and, from the final observations (at time T = 5), we try to infer the transmission parameters λij associated with both TP and FP edges of the extended graph that, at variance with the cases examined before, is not a fully connected graph. We compare our reconstructions to the ones obtained by an MI-based method. In figure 7, we plot the areas under the ROC curves as a function of the number of cascades of the five interaction networks. Each row of the main figure corresponds to the extreme values of α = {0.2, 0.5}. For all organisms, the areas under the ROC curves of GABP results are significantly larger than those of MI reconstructions and they reach values above 0.9 even when few cascades are available, i.e. M = 10. Quite surprisingly, performances seem to be independent of α, i.e. the number of extra edges, suggesting that our method is quite robust in detecting FP links when the extended graph to be pruned has a reasonable number of edges.
Table 1.
Properties of the interactomes. This table shows the name of the organisms, the number of nodes and edges of the PPI networks and the name of the public datasets supported by PSICQUIC.
Figure 7.
Plots of the ROC areas for GABP and MI in predicting TP links of five different interactomes. Each row corresponds to a different α, the fraction of extra edges, while each column to one of the five studied interactomes. Subplots show the areas under the ROC curves as a function of the number of cascades M for GABP (blue line) and MI (red line). (Online version in colour.)
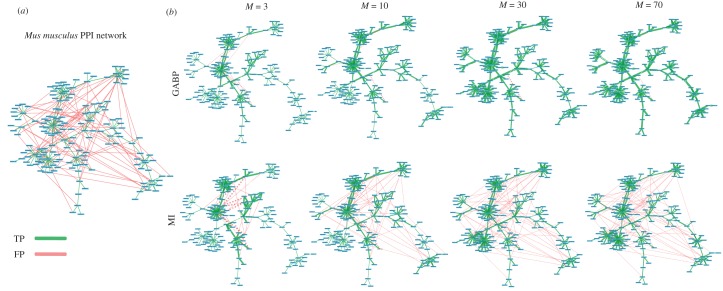
To underline the performances of GABP, we show in figure 8a the Mus musculus interactome containing the TP (green links) and 80 FP edges (red links). The retrieved network for an increasing number of cascades is plotted in figure 8b; edge thickness is proportional to the inferred values of λij for GABP and to mij for MI. It is worth noting that, for very few cascades (M = 3), both GABP and MI are able to recognize almost all true links but GABP misclassifies fewer FP than MI. When M increases, GABP detects all true edges as the associated λij significantly increase and it incorrectly classifies only few FP edges that, in any case, exhibit values of the infection parameters close to zero and negligible if compared to the ones associated with TP links. On the contrary, MI distributes the weights over all the edges and, for large M, it is not able to sharply distinguish the two sets of links as some of the FP edges have values of mij comparable to those of TP links.
Figure 8.
FP edge detection in PPI networks. (a) Mouse interactome of 172 nodes and 297 edges (217 TP in green and 80 FP in red). (b) The first (second) row shows the networks reconstructed by GABP (MI) for M = {3, 10, 30, 70}. The thickness of each edge is proportional to the infection parameters of GABP and the mutual information among couples of nodes for MI; edges with weights smaller than 10−3 are not shown. (Online version in colour.)
2.5. Reconstructing the website influence network through trend topic cascades
Epidemic spreading is also a good model for describing trend topic dynamics in ‘information’ networks such as the World Wide Web. In [29], the authors present a huge dataset containing more than 108 webpages that from August 2008 to April 2009 were involved in about tracked trend topics. With each cascade they associate a temporal window in which the news was ‘viral’, a representative sentence appearing in all the tracked articles and the list of webpages publishing the topic within the temporal window. In [3], they try to infer the links among the webpages using the full time-series of the spreading events.
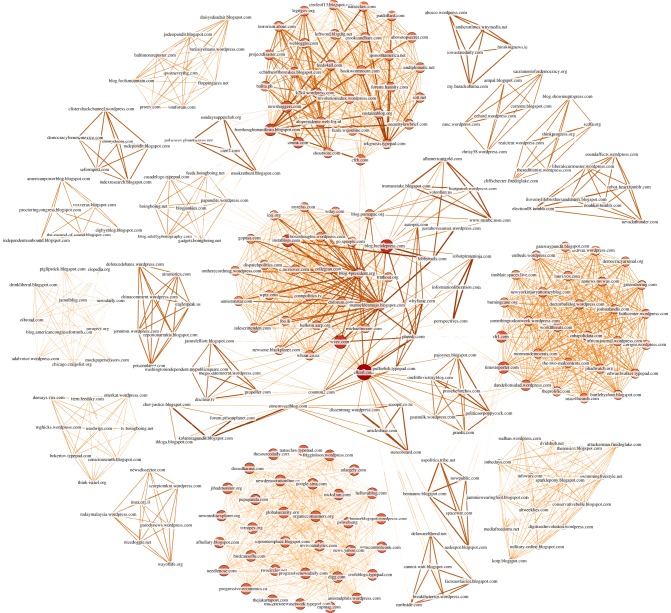
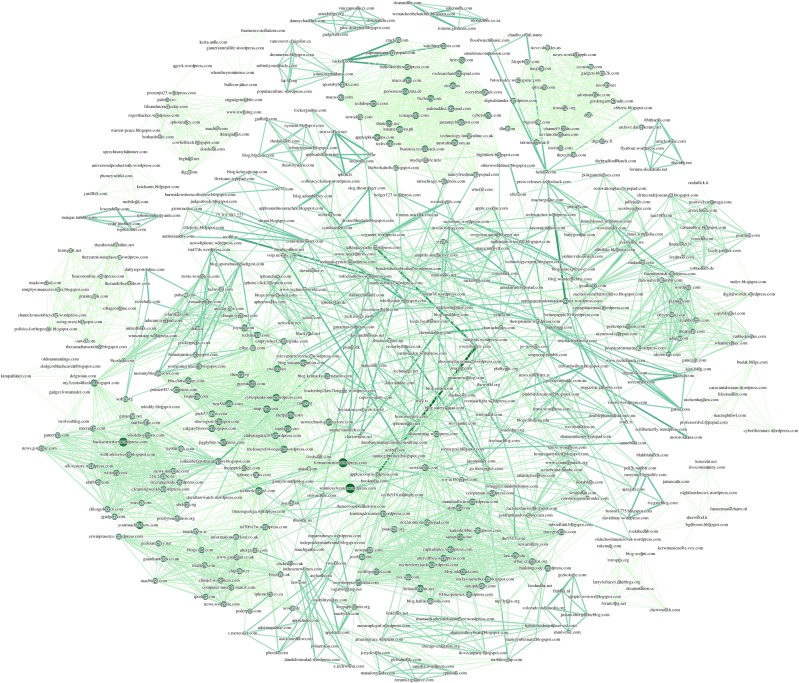
In this section, we show how to use GABP to infer influence sub-network links from only the final observations of some selected trend topic cascades. Within the SI model formalism, each website (the nodes of our graph) will be characterized by the state ‘I’ if it participates to the cascade or ‘S’ otherwise; webpages that have published in the same day are considered as ‘infected’ in the same time-step. The size of the network makes the use of the entire dataset impractical. We therefore analyse single cascades that (a) contain a keyword of our choice in the representative sentence; (b) the number of web-pages involved in the epidemics is larger than a certain threshold (usually 5–10) and (c) the whole spreading event does not last more than T days (usually 10–20). These three conditions are able to isolate sub-sets of nodes labelled by our chosen keyword. We show in figure 9 the sub-network structure of the nodes participating to cascades that contain the word ‘Korea’. Edge thickness and colour are proportional to the values of the inferred infection probabilities, with the most infectious links having the darkest and thickest arrows. Node sizes instead reflect the degree of the nodes. A giant component is clearly visible in the centre of the picture, where edge colour and thickness are inhomogeneous. Several disconnected cliques are also apparent on the sides. These homogeneously connected nodes are observed only once in a unique cascade: our algorithm thus predicts a ‘flat’ assignment of small λij for all possible links of the disconnected components, since there is not enough information to discriminate between zero and non-zero infection probabilities. This is less evident in figure 10 for tag ‘iPhone’. Other reconstructed networks are shown in the electronic supplementary material.
Figure 9.
Reconstruction of website influence network participating in 30 trend topic cascades having the word ‘Korea’ in the representative sentence. The number of nodes is 269 while the number of edges is 2306. (Online version in colour.)
Figure 10.
Webpage networks publishing trend topics containing the word ‘iPhone’. Here M = 91, |V| = 562 and |E| = 3831.
2.6. Inferring transmission probabilities
Let us now briefly consider a slightly different application of the general formalism presented so far. Suppose that the underlying network structure is known but little or any information is available on the transmission probabilities λij, which are, in the general case, inhomogeneous. Our method can be easily accommodated so as to provide the maximum likelihood estimation of the quantities λij. Starting from an initial assignment of the coupling parameters (we used λij ≡ 0.5) defined over a known topology, one seeks a fixed point of the coupled BP and gradient equations using GABP.
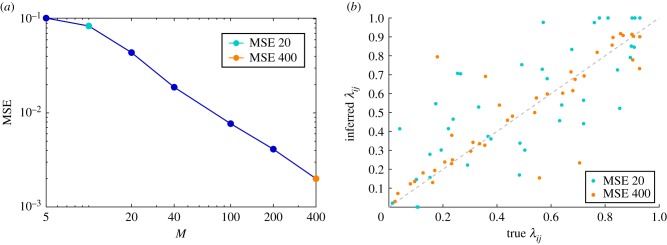
As an example, we consider an RR graph of size |V| = 20 with degree d = 4, and evaluate the inference performance with increasing number of cascades M. Figure 11a shows the value of the mean square error between the inferred transmission probabilities λij and the true ones, . To better appreciate the quality of the inference, we show a scatter plot for two different values of M in figure 11b.
Figure 11.
Reconstructing spreading couplings in inhomogeneous networks. (a) Mean squared reconstruction error in a random regular graph of size |V| = 20 and degree d = 4, as a function of the number of observed cascades M. The network structure is known in advance. The spreading couplings have been extracted randomly from the homogeneous distribution in the interval [0, 1]. The state of the network is observed only at time T = 5 for each cascade. (b) Scatter plot of reconstructed transmission probabilities λij versus true spreading couplings for the cases M = 20 and M = 400, corresponding to the golden and green points in (a), respectively. (Online version in colour.)
2.7. Mutual information based pruning
GABP is an iterative algorithm where fixed-point equations are efficiently updated until convergence as explained in the Discussion section and in the electronic supplementary material. The epidemic parameters are inferred through an expectation maximization (EM) scheme (see also the electronic supplementary material) which does not affect the performances of the method. The running time is thus governed by the O(T|E′|) operations of the main BP algorithm, where |E′| is the number of candidate edges. In all the cases we have considered so far, no a priori knowledge of the network structure is assumed and therefore this number scales as |V|2, except for the PPI networks in which, along with the existing edges, we consider Z additional FP links, |E′| = |E| + Z. We show in this section how to reduce the number of parameters to be inferred by pruning the network of all possible connections.
Consider the case in which two variables appear to be correlated (e.g. their mutual information is very large). This can be a direct effect due to the presence of a link between the two or an indirect effect carried by paths that connect the two nodes (either exploiting other mediator nodes or because co-infections are the consequence of a single initial event). From pure correlation evaluation, we cannot distinguish the two cases. However, if two variables are uncorrelated, the presence of a link is unlikely.
As an example, we consider here M = 50 cascades spreading in an RR graph of |V| = 50 nodes and fixed degree d = 6. We take as candidate edges E′ a certain percentage of the most correlated links (computed via (4.15)) among all the possible ones. When |E′| reaches 800 edges, 65% of the possible edges, we achieve an area under the ROC curve of 0.84, which is equivalent to the one obtained when considering all connections.
3. Discussion
We have presented a new method that allows one to reconstruct a hidden network from limited information of activity propagations, and showed that the reconstruction performance is extremely accurate even when the number of snapshot observations is very small. This scheme can be effectively applied to the detection of FP links in PPI networks even when the number of candidate false edges is comparable to the effective number of TP contacts. In this particular case, it suffices very few independent cascades to correctly classify the great majority of the links.
There are several advantages of this approach over existing ones. The main one is that several inference problems can be treated under a unique formulation. Our technique can be easily extended to incorporate effects of unreliable observations, taking into account noisy measurements, and/or cases where susceptible nodes cannot be distinguished from recovered ones [31]. When a complete list of contact times between nodes is available, the construction of an equivalent network of time-dependent infection probability is straightforward, and the current approach has been proven to be effective.
Owing to the generality of the Bayesian method, the described technique is capable of dealing with a wide variety of irreversible spreading processes on networks. A possible simple generalization is to the (random) bootstrap percolation case where each node gets activated when the aggregated input from neighbours overcomes an intrinsic stochastic activation threshold of the node. These models are widely used to describe the features of dynamical processes in neuronal networks, and we consider this an exciting research direction.
4. Methods
4.1. Graphical model formulation of the spreading process
Let us first consider a single cascade on a network with a fixed topology. For a fixed initial configuration x(0), a realization of the stochastic process can be generated by drawing randomly a set of infection transmission delay sij for all pairs (ij) and the recovery times gi of each node i. The recovery times {gi} are independent random variables extracted from the geometric distributions , the delays {sij} are conditionally independent random variables distributed according to a truncated geometric distribution
| 4.1 |
Note that we concentrate in the value sij = ∞ the mass of the distribution beyond the hard cut-off gi imposed by the recovery time. The joint probability distribution of infection and recovery times conditioned on the initial state is easily written as
| 4.2 |
where
| 4.3 |
is a characteristic function which imposes on each node i the dynamical constraint of equation (2.1).
Using the Bayes formula, the posterior probability of the initial configuration given an observation at time T reads
| 4.4 |
| 4.5 |
where is a factorized prior on the initial infection with
| 4.6 |
for a generally small constant γ (we do not allow state (R) at time 0). Note that the network state x(t) is a deterministic function of the set of infection and recovery times (t, g), so that we obtain
| 4.7 |
with Note that assuming xi(0) ∈ {(S), (I)}, then ψi(ti, {tk, ski}k∈∂i) could be also rewritten equivalently as . Now, if we introduce a set of observational weights , one for each observation m, together with a set of priors , the posterior distribution of the initial states conditioned to observations, because of the assumption of independence, will be proportional to the product over all the single probability weights for each cascade that taking into account equation (4.5) will take the form
| 4.8 |
where all the factors have been labelled with an extra cascade index m and x1 : M(T) = (xm(T))m=1, … ,M. Since we have no a priori information on the graph topology, the product in the term runs over all the possible pairs i and j in the set V, meaning that we always work in the setting of a fully connected network with weights {λij}. If the number of cascades M is large enough, the non-zero elements of the matrix {λij} will signal, upon convergence of the GABP algorithm, the true links in the original graph, their value being informative of the heterogeneity of infection probabilities. The same holds for the set of recovery parameters {μi}. Note that for λij = 0, (4.1) imposes the condition sij = ∞, meaning that (ij) can be ignored in (2.1), effectively pruning the link from the equations.
4.2. Belief propagation approach
Given a high-dimensional probability distribution M(z) with a locally factorized interaction structure, computing marginals and aggregated quantities may be addressed with the use of a message passing procedure built on a cavity approximation for locally tree-like graphs [39–41]. In the present problem, we obtain a full set of (cavity) marginal probabilities over the set of all the possible cascades compatible with the observations. BP is proven to be exact on tree graphs, and has been successfully employed on general loopy graphs under mild regularity conditions [9,42].
To briefly describe the essence of the method, let us consider a probability distribution over the variables z = {zi} that has the following factorized form:
| 4.9 |
where each χa is called a compatibility function, or factor. We write za = {zi}i∈∂a as the set of variables it depends on, ∂a the subset of indices of variables in factor χa, and accordingly ∂i will be the subset of factors that depend on zi. BP equations are a set of self-consistent equations for the so-called cavity messages (or beliefs), a set of single-site probability distributions which are associated with each directed link in the graphical model representing the joint distribution of equation (4.9). The general form of the BP equations is the following:
| 4.10 |
| 4.11 |
| 4.12 |
where the terms Zia, Zai and Zi are local partition functions, serving as normalizers. To solve equations (4.10) and (4.11), an iterative procedure is typically used, where the cavity messages are initialized with uniform distributions and they are asynchronously updated until convergence to a fixed point (see [39,41] for an introduction). The BP equations can be thought of as local update rules for messages in a so-called factor graph, a bipartite graph where each term χa is associated with a factor node, connected to all the variable nodes in the set za it depends on. A naive implementation of the BP scheme at the level of equation (4.8) would simply not work, since the corresponding graphical model has a loopy structure both at local and global scale. It is however possible to construct a disentangled factor graph by means of a re-parametrization of the cavity messages. We provide a brief description of this procedure in the electronic supplementary material, Methods. For a thorough discussion, we refer the reader to previous works [30,31]. Here we just want to stress that the modified factor graph is an enriched dual version of the original graph, whence the particular appeal of the method. In particular, this implies that BP provides the exact Bayesian solution when the underlying network is acyclic.
While the computation of equation (4.11) is straightforward, the sum in equation (4.10) generally involves a number of steps growing exponentially with the size of ∂a. An efficient implementation of the BP equations for the posterior distribution is given in the electronic supplementary material, Methods. Once BP converges, equation (4.12) can be used to compute the marginal probability , which brings a posterior estimation of the probability for the node i to be active at time t = 0 in the mth cascade.
4.3. Network reconstruction algorithm
We employ an alternating optimization scheme in which BP is coupled to a maximum-likelihood strategy, implemented with a GA method. In the BP phase, the network parameters {λij, μi} are kept fixed and a solution is searched iteratively for equations (4.10) and (4.11). At this stage, the source can be located independently for each cascade looking at the single-site marginals . In the maximum likelihood phase, the log-likelihood of network parameters is maximized by means of a simple GA procedure. The gradient may be computed efficiently in the BP approximation. The likelihood with respect to the network parameters is
The logarithm of this quantity (log-likelihood) corresponds to the negative free energy of the model , and can be expressed as a sum of local terms depending only on the BP messages (see electronic supplementary material, Methods). BP updates for the distribution in equation (4.8) are then coupled to GA updates with respect to each network parameter, that take the form
| 4.13 |
and
| 4.14 |
with ε a small multiplier parameter (we found ε = 10−4 yields good results and stable convergence and used this value for all our simulations). The results presented in this work have been obtained by interleaving one BP step with a GA step: this simple scheme suffices to provide good joint estimates for the patient zero in each cascade, together with a remarkably good reconstruction of the underlying network. An alternative method would consist of applying an EM scheme, in which alternatively BP equations are iterated to convergence (BP step) and parameters are fully optimized for fixed BP messages (EM step). However, the EM step requires the maximization of a high-order polynomial that must be solved numerically in any case (e.g. in a GA scheme). We obtained faster convergence by alternating single GA and BP steps rather than alternating full convergence cycles of both steps.
4.4. Mutual information
For comparison, we tried to reconstruct the networks of interest using correlation-based measures. At the observation time, we have computed the probabilities of observing edges (i, j) as the mutual information between nodes i and j:
| 4.15 |
where fij, fi are empirical probabilities computed as
| 4.16 |
and
| 4.17 |
Supplementary Material
Acknowledgements
We warmly thank L. Dall’Asta for useful discussions, and Riccardo Refolo for providing us with figure 1.
Endnote
Suppose of observing some spreading cascades in a network where the infection probability is very small (or the recovery probability is huge in the SIR model). At the observation times the majority of nodes might not have been touched by any of the spreading events and thus no information can be extracted on a huge fraction of the edges. At the same time, a huge infection probability in the SI (SIR) model may let the epidemics propagate so fast that at the observation time all nodes are in the ‘I’ state (‘R’ state). Also in this case, there is no way of inferring the epidemic parameters with this type of observations.
Data accessibility
Retweet data are openly available at http://networkrepository.com/rt_retweet.php. Interactome networks are openly available as part of the PSICQUIC dataset in Cytoscape 3.5.1 (https://cytoscape.org/), and the memetracker phrase cluster data are available at http://www.memetracker.org/data.html.
Authors' contributions
A.B., A.I. and A.P.M. contributed equally to this work.
Competing interests
We declare we have no competing interests.
Funding
A.B. and A.P.M. acknowledge support by Fondazione CRT, project SIBYL under the initiative ‘La Ricerca dei Talenti’, INFERNET, European Union’s Horizon 2020 research and innovation programme under Marie Sklodowska-Curie grant agreement no. 734439, and PRIN project 2015592CTH_003 from the Italian Ministry of University and Research.
References
- 1.Timme M, Casadiego J. 2014. Revealing networks from dynamics: an introduction. J. Phys. A: Math. Theor. 47, 343001 ( 10.1088/1751-8113/47/34/343001) [DOI] [Google Scholar]
- 2.Wang W-X, Lai Y-C, Grebogi C. 2016. Data based identification and prediction of nonlinear and complex dynamical systems. Phys. Rep. 644, 1–76. ( 10.1016/j.physrep.2016.06.004) [DOI] [Google Scholar]
- 3.Gomez Rodriguez M, Leskovec J, and Krause A. 2010. Inferring networks of diffusion and influence. In Proc. 16th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Washington, DC, USA, 25–28 July 2010, pp. 1019–1028. New York, NY: ACM; ( 10.1145/1835804.1835933) [DOI] [Google Scholar]
- 4.Choi B, Rempala GA. 2012. Inference for discretely observed stochastic kinetic networks with applications to epidemic modeling. Biostatistics 13, 153–165. ( 10.1093/biostatistics/kxr019) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Salathé M, Kazandjieva M, Lee JW, Levis P, Feldman MW, Jones JH. 2010. A high-resolution human contact network for infectious disease transmission. Proc. Natl Acad. Sci. USA 107, 22 020–22 025. ( 10.1073/pnas.1009094108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Isella L, Stehlé J, Barrat A, Cattuto C, Pinton J-F, Van den Broeck W. 2011. What’s in a crowd? Analysis of face-to-face behavioral networks. J. Theor. Biol. 271, 166–180. ( 10.1016/j.jtbi.2010.11.033) [DOI] [PubMed] [Google Scholar]
- 7.Rocha LEC, Liljeros F, Holme P. 2010. Information dynamics shape the sexual networks of internet-mediated prostitution. Proc. Natl Acad. Sci. USA 107, 5706–5711. ( 10.1073/pnas.0914080107) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Altarelli F, Braunstein A, Dall’Asta L, Wakeling JR, Zecchina R. 2014. Containing epidemic outbreaks by message-passing techniques. Phys. Rev. X 4, 021024 (doi:0.1103/PhysRevX.4.021024) [Google Scholar]
- 9.Altarelli F, Braunstein A, Dall’Asta L, Zecchina R. 2013. Optimizing spread dynamics on graphs by message passing. J. Stat. Mech: Theory Exp. 2013, P09011 ( 10.1088/1742-5468/2013/09/P09011) [DOI] [Google Scholar]
- 10.Lokhov AY, Saad D. 2016 Optimal deployment of resources for maximizing impact in spreading processes. (http://arxiv.org/abs/1608.08278. ) [Google Scholar]
- 11.Lokhov AY, Misiakiewicz T. 2015 Efficient reconstruction of transmission probabilities in a spreading process from partial observations. (http://arxiv.org/abs/1509.06893. ) [Google Scholar]
- 12.Pajevic S, Plenz D. 2009. Efficient network reconstruction from dynamical cascades identifies small-world topology of neuronal avalanches. PLoS Comput. Biol. 5, e1000271 ( 10.1371/journal.pcbi.1000271) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Karrer B, Newman MEJ. 2010. Message passing approach for general epidemic models. Phys. Rev. E 82, 016101 ( 10.1103/PhysRevE.82.016101) [DOI] [PubMed] [Google Scholar]
- 14.Lokhov AY, Mézard M, Ohta H, Zdeborová L. 2014. Inferring the origin of an epidemic with a dynamic message-passing algorithm. Phys. Rev. E 90, 012801 ( 10.1103/PhysRevE.90.012801) [DOI] [PubMed] [Google Scholar]
- 15.Shen Z, Wang W-X, Fan Y, Di Z, Lai Y-C. 2014. Reconstructing propagation networks with natural diversity and identifying hidden sources. Nat. Commun. 5, 4323 ( 10.1038/ncomms5323) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wan X, Liu J, Cheung WK, Tong T. 2014. inferring epidemic network topology from surveillance data. PLoS ONE 9, e100661 ( 10.1371/journal.pone.0100661) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wang JB, Wang L, Li X. 2016. Identifying spatial invasion of pandemics on metapopulation networks via anatomizing arrival history. IEEE Trans. Cybern. 46, 2782–2795. ( 10.1109/TCYB.2015.2489702) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Yang B, Pei H, Chen H, Liu J, Xia S. 2017. Characterizing and discovering spatiotemporal social contact patterns for healthcare. IEEE Trans. Pattern Anal. Mach. Intell. 39, 1532–1546. ( 10.1109/TPAMI.2016.2605095) [DOI] [PubMed] [Google Scholar]
- 19.Li X, Li X. 2017. Reconstruction of stochastic temporal networks through diffusive arrival times. Nat. Commun. 8, 15729 ( 10.1038/ncomms15729) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li J, Shen Z, Wang W-X, Grebogi C, Lai Y-C. 2017. Universal data-based method for reconstructing complex networks with binary-state dynamics. See /paper/Universal-data-based-method-for-reconstructing-with-Li-Shen/7ad7eb5e8af6ae92adf98de2cd91590a2e5818b0. [Google Scholar]
- 21.Casadiego J, Nitzan M, Hallerberg S, Timme M. 2017. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 8, 2192 ( 10.1038/s41467-017-02288-4) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Milling C, Caramanis C, Mannor S, Shakkottai S. 2012. On identifying the causative network of an epidemic. In 2012 50th Annual Allerton Conf. on Communication, Control, and Computing (Allerton), Monticello, IL, USA, 1–5 October 2012, pp. 909–914. ( 10.1109/Allerton.2012.6483315) [DOI] [Google Scholar]
- 23.Bork P, Jensen LJ, von Mering C, Ramani AK, Lee I, Marcotte EM. 2004. Protein interaction networks from yeast to human. Curr. Opin. Struct. Biol. 14, 292–299. ( 10.1016/j.sbi.2004.05.003) [DOI] [PubMed] [Google Scholar]
- 24.Valencia A, Pazos F. 2002. Computational methods for the prediction of protein interactions. Curr. Opin. Struct. Biol. 12, 368–373. ( 10.1016/S0959-440X(02)00333-0) [DOI] [PubMed] [Google Scholar]
- 25.Yu J, Fotouhi F. 2006. Computational approaches for predicting protein–protein interactions: a survey. J. Med. Syst. 30, 39–44. ( 10.1007/s10916-006-7402-3) [DOI] [PubMed] [Google Scholar]
- 26.Adar E, Adamic LA. 2005. Tracking information epidemics in blogspace. In Proc. 2005 IEEE/WIC/ACM Int. Conf. on Web Intelligence, WI ’05, Compiegne, France, 19–22 September 2005, pp. 207–214. ( 10.1109/WI.2005.151) [DOI] [Google Scholar]
- 27.Liben-Nowell D, Kleinberg J. 2008. Tracing information flow on a global scale using Internet chain-letter data. Proc. Natl Acad. Sci. USA 105, 4633–4638. ( 10.1073/pnas.0708471105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Kermack WO, McKendrick AG. 1927. A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. A 115, 700–721. ( 10.1098/rspa.1927.0118) [DOI] [Google Scholar]
- 29.Leskovec J, Backstrom L, Kleinberg J. 2009. Meme-tracking and the dynamics of the news cycle. In Proc. 15th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Paris, France, 28 June–1 July 2009, pp. 497–506. New York, NY: ACM; ( 10.1145/1557019.1557077). [DOI] [Google Scholar]
- 30.Altarelli F, Braunstein A, Dall’Asta L, Lage-Castellanos A, Zecchina R. 2014. Bayesian inference of epidemics on networks via belief propagation. Phys. Rev. Lett. 112, 118701 ( 10.1103/PhysRevLett.112.118701) [DOI] [PubMed] [Google Scholar]
- 31.Altarelli F, Braunstein A, Dall’Asta L, Ingrosso A, Zecchina R. 2014. The patient-zero problem with noisy observations. J. Stat. Mech: Theory Exp. 2014, P10016 ( 10.1088/1742-5468/2014/10/P10016) [DOI] [Google Scholar]
- 32.Albert R, Barabási A-L. 2002. Statistical mechanics of complex networks. Rev. Mod. Phys. 74, 47–97. ( 10.1103/RevModPhys.74.47) [DOI] [Google Scholar]
- 33.Rossi RA, Ahmed NK. 2013. rt-retweet - retweet networks. See http://networkrepository.com/rt_retweet.php. [Google Scholar]
- 34.Rossi RA, Ahmed NK. 2015. The network data repository with interactive graph analytics and visualization. In Proc. 29th AAAI Conf. on Artificial Intelligence. See http://networkrepository.com. [Google Scholar]
- 35.Orchard S. 2012. Molecular interaction databases. Proteomics 12, 1656–1662. ( 10.1002/pmic.201100484) [DOI] [PubMed] [Google Scholar]
- 36.Shannon P, Markiel A, Ozier O, Baliga NS, Wang JT, Ramage D, Amin N, Schwikowski B, Ideker T. 2003. Osgi alliance cytoscape: a software environment for integrated models of biomolecular interaction networks. Genome Res. 13, 2498–2504. ( 10.1101/gr.1239303) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Orchard S. 2014. The MIntAct project—IntAct as a common curation platform for 11 molecular interaction databases. Nucleic Acids Res. 42, D358–D363. ( 10.1093/nar/gkt1115) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.The UniProt Consortium. 2017. UniProt: the universal protein knowledgebase. Nucleic Acids Res. 45, D158–D169. ( 10.1093/nar/gkw1099) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Yedidia JS, Freeman WT, Weiss Y. 2000. Generalized belief propagation. In Proc. 13th Int. Conf. on Neural Information Processing Systems, pp. 668–674. Cambridge, MA: MIT Press. [Google Scholar]
- 40.Yedidia JS, Freeman WT, Weiss Y. 2003. Exploring artificial intelligence in the new millennium. In Understanding belief propagation and its generalizations (eds G Lakemeyer, B Nebel), pp. 239–269. San Francisco, CA: Morgan Kaufmann Publishers Inc. [Google Scholar]
- 41.Mézard M, Montanari A. 2009. Information, physics, and computation. Oxford, UK: Oxford University Press. [Google Scholar]
- 42.Altarelli F, Braunstein A, Dall’Asta L, Zecchina R. 2013. Large deviations of cascade processes on graphs. Phys. Rev. E 87, 062115 ( 10.1103/PhysRevE.87.062115) [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Retweet data are openly available at http://networkrepository.com/rt_retweet.php. Interactome networks are openly available as part of the PSICQUIC dataset in Cytoscape 3.5.1 (https://cytoscape.org/), and the memetracker phrase cluster data are available at http://www.memetracker.org/data.html.