Locating the source of large-scale outbreaks of foodborne disease

Abstract

In today’s globally interconnected food system, outbreaks of foodborne disease can spread widely and cause considerable impact on public health. We study the problem of identifying the source of emerging large-scale outbreaks of foodborne disease; a crucial step in mitigating their proliferation. To solve the source identification problem, we formulate a probabilistic model of the contamination diffusion process as a random walk on a network and derive the maximum-likelihood estimator for the source location. By modelling the transmission process as a random walk, we are able to develop a novel, computationally tractable solution that accounts for all possible paths of travel through the network. This is in contrast to existing approaches to network source identification, which assume that the contamination travels along either the shortest or highest probability paths. We demonstrate the benefits of the multiple-paths approach through application to different network topologies, including stylized models of food supply network structure and real data from the 2011 Shiga toxin-producing Escherichia coli outbreak in Germany. We show significant improvements in accuracy and reliability compared with the relevant state-of-the-art approach to source identification. Beyond foodborne disease, these methods should find application in identifying the source of spread in network-based diffusion processes more generally, including in networks not well approximated by tree-like structure.

1. Introduction

The complexity and globalization of food production have made foodborne disease a widespread public health problem in both developed and developing countries. Most outbreaks of foodborne disease involve a source of contamination at the point of preparation or sale and affect a small group of people in a localized area. However, a small but worrisome minority of outbreaks are generated by a contamination originating at the site of production or processing, generating a widespread diffusion of contamination through the supply chain and affecting a potentially much greater number of people across geographically distributed locations. When large-scale outbreaks do occur the impact on the public’s health may be massive. In the summer of 2011, an outbreak caused by Shiga toxin-producing Escherichia coli (STEC) O104:H4, spread by sprouts grown in Germany, caused 54 deaths and 4321 illnesses in 16 countries over a nine-week period [1,2]. As the food system continues to become interconnected, driven by large-scale production practices and distribution over ever-larger distances, both the prevalence and the severity of consequences of large-scale outbreaks are increasing. From 2005 to 2014, nearly 200 multi-state outbreaks were identified and investigated in the USA when compared with 85 over the years 1995–2004; these multi-state outbreaks accounted for 3% of total outbreaks, but were responsible for 34% of hospitalizations and 56% of deaths [3].

In the event of a large-scale outbreak, rapidly identifying the contamination source is essential to minimizing impact on public health and industry. There are three standard components to the regulatory response and investigation process, each contributing to the challenge of identifying the source: (i) detecting that an outbreak is occurring, (ii) identifying the food vector causing the outbreak and (iii) identifying the location source of the outbreak at a farm or processing centre. Novel strategies facilitated by new analytical tools and the increasing availability of data sources are being developed to improve to the ability to (i) detect outbreaks, e.g. by crowdsourcing self-reported foodborne illness concerns from popular social networking sites [4–6] and (ii) implicate the food type or even specific product carrying the disease, e.g. by analysing retail-scanner data from grocery stores [7]. This paper addresses part (iii) of the outbreak investigation, identifying the location of origin.

Tracing the location of the source of an outbreak is a challenging problem due to the complexity of the food supply network and the absence of integrated labelling and distribution records. However, current investigation methods represent a missed opportunity to use valuable information to solve the source localization problem. The regulatory approach generally involves triangulation, or tracing back the unique distribution paths of products from several locations to determine if there is a point of convergence in the supply network, such as a common date and location of harvest or place of manufacture [8–10]. Because of resource limitations, investigators are only able to make use of a small subset of the reported cases of illness—data that serve as evidence in the source location problem. With only a few pieces of evidence, the time-consuming traceback will often be unsuccessful in narrowing down the problem significantly. As a result, investigations are completed in many cases after the outbreak has ended and the contamination has made its way through the supply network, meaning that no cases of illness are averted. Furthermore, the majority of outbreaks remain unsolved, meaning that the food and/or location source of the outbreak is never identified [10,11].

1.1. A network approach to source identification

Food distribution is a complex system that can be seen as a network of trade flows connecting supply network actors. Identifying the source of an outbreak of contamination distributed across a network can best be solved by considering this network structure and the dimensions of information it contains.

The food supply network consists of a layered, directed structure typically consisting of the four transformation stages of production, distribution, storage and consumption. Food products travel according to a transport-mediated diffusion process between supply nodes. Owing to the staged structure of the food supply network, paths from source to observation will be close to the same length in terms of number of network edges. Furthermore, there exist multiple paths of travel of similar probability. This is due to the existence of multiple competitors in food production, trade and retailing markets: any given food type will be distributed through multiple larger retailers or wholesalers, each dealing with similarly large volumes of product (see, for example, the turnover distribution of retailers in Germany [12]). In the network model, this translates into homogeneity in path lengths and the existence of multiple paths of similar probability.

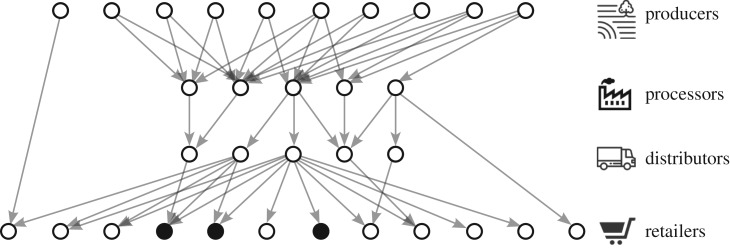
A large-scale outbreak occurs when contaminated food departs from a source node in an early stage of the network that is able to reach downstream retailers and other point-of-sale nodes in geographically distributed locations. The contaminated food eventually makes its way to consumers who develop illness some time after consumption. Case reports of illness are associated with the network node at which the offending product was purchased and exits the supply chain; these nodes can be considered observed or contaminated. The network in figure 1 represents a supply network in which contamination at a food producer has spread through the supply network, leading to reports of illness at three different retailers.

Figure 1.

Illustration of a food distribution network with three reported cases of illness (at the shaded nodes) linked to retailer nodes.

Over the past couple of decades, there has been significant effort devoted to studying the dynamics of outbreaks on networks [13–19]; for a comprehensive review of epidemic spreading on complex networks, see [20]; for a review of information diffusion on complex networks including a comparative evaluation of available models and algorithms, see [21]. Most of this work has focused on the forward problem of understanding and forecasting the diffusion process and its dependence on the structure of the underlying network. However, in recent years much work has emerged on the inverse problem of identifying the source of an outbreak spread in a network. This work covers problems in various real-world contexts, including contagious disease infecting a human population; rumours or information diffusing through a social network; the spread of viruses on the Internet; and the transport-mediated diffusion of contaminated individuals between cities. These contexts represent different spreading scenarios that require different modelling approaches for forward dynamics and inverse solutions. Accordingly, most of the existing approaches to source detection cannot be directly implemented in the foodborne disease context because they are designed for a different purpose—identifying the source of an epidemic contagion [18–22], whereas foodborne disease spreads according to a transport-mediated diffusion process, or because they require data that are not realistically available—complete observations of the contamination status of all nodes in the network [22–25] or timed network data [26–30]. Furthermore, much of this work has focused on studying this problem in analytically tractable frameworks, designing approaches to work on trees and extending to general network structures in an ad hoc manner [22,23,26,29–32]. These simplified frameworks lack many features of real-world networks and problem contexts that can dramatically impact transmission dynamics, and therefore, backwards inference of the source. For further discussion of these features and a review of the literature on the source identification problem in the context of foodborne disease outbreaks, see [33].

A single source detection approach has been evaluated in application to an outbreak of foodborne disease, the 2011 outbreak of STEC in sprouts [32,34], also considered as an application case in §3. This method does not assume contagious transmission, complete observations or timed data and is therefore implementable. However, it makes a tree-like assumption that is unrealistic in the context of food distribution and foodborne disease transmission: it assumes that the contamination always travels from a source to an observation along the shortest, highest probability path. While this type of approximation may be justified in certain network contexts, including the global air mobility networks the method was designed for, it is not adapted for the structure of food supply networks which are characterized by homogeneity in path lengths and the existence of multiple paths of similar probability (see the beginning of this section). Moreover, this method is by definition a heuristic that does not explore the full set of trajectories between each source and observation. Recent work has demonstrated that failing to consider multiple paths can lead to significant error in estimating diffusion trajectories in global air mobility networks [35]. In food supply networks where paths will be significantly less differentiated in length and probabilistic weight, the single-path assumption will lead to greater error.

1.2. Problem statement and contributions

To solve the source detection problem in the context of foodborne disease, we assume as given a network model of the supply of a specific food commodity and a probabilistic model of the transmission process of contamination spreading through this network. At some point in time, a single contamination source begins to send out contaminated products, which travel through the network resulting in observations of illness at a set of network nodes. Our objective is to minimize the error between our estimate of the location of the source and the true location of the source in the network, given the locations of the observations of illness.

We formulate the transmission process of contaminated food items travelling through the supply network as a discrete Markov chain, i.e. a random walk on the network where transmission probabilities correspond to the edge weights. This is a natural transmission model for non-contagious diffusion on a weighted, directed network. To estimate the true source location, we adopt a maximum-likelihood (ML) approach, by definition minimizing the estimation error. The ML estimator chooses the highest probability source node according to the likelihood of observing the reports of illness.

By formulating the transmission process as a weighted random walk, we are able to develop a computationally tractable representation of the ML estimator that accounts for all possible paths of all possible lengths travelled by each contaminated food item. This is in contrast to the relevant (implementable) state-of-the-art approach to source detection [32,34], which develops a heuristic approach that considers only the dominant (i.e. highest-probability and shortest) path between each source and each observation.

Practically, we demonstrate that a source estimator that accounts for all possible transmission paths can locate the outbreak source with greater timeliness, accuracy, and reliability than other methods, and more robustly across extreme cases of network structures. This is shown through the application to different network topologies, including stylized models of food supply network structure and simulated outbreaks, and real network and illness data from the 2011 STEC contaminated sprout outbreak in Germany. Compared with the relevant state-of-the-art approach [32,34], the improvement in accuracy with our source estimator is always observable and can be substantial, with the improvement depending on the network topology evaluated. Furthermore, application to the STEC outbreak demonstrates that our approach is not only more accurate but also more reliable, consistently identifying the source location region over the time course of the outbreak.

The remainder of this paper is organized as follows. In §2, we introduce the probabilistic foodborne disease transmission model and derive the source estimator. In §3, we demonstrate the effectiveness of our source estimation framework through application to both stylized networks and real data from 2011 STEC outbreak. In §4, we conclude and discuss future work.

2. Source detection model

2.1. Problem statement

Our goal is to identify the source of a foodborne disease outbreak based on the reports of illness and information about the underlying network structure. We assume as given a network model and a probabilistic model of the transmission process of contamination spreading through this network. At some point in time, a single contamination source s* begins to send out contaminated products, which spread through the network according to the transmission model, resulting in a list of observations of illness Θ associated with a set of network nodes O. Our objective is to minimize the error of our estimate of the source location in the network and the location of the true source, given the information from the observations of illness. To estimate the true source location, we adopt an ML approach that chooses the highest probability source node according to the likelihood of observing the reports of illness, by definition minimizing the estimation error.

In the following, we describe our model of the food supply network and the foodborne disease transmission process. We then define the ML source estimator for food distribution networks.

2.2. Food supply network model

We model the food supply network as a directed graph G = {V, E}, where V is the set of nodes representing supply network actors. G consists of two types of nodes: the set of absorbing nodes V_R and the set of transient nodes V_Q, such that V = {V_Q, V_R}. Absorbing nodes represent the point at which product is purchased for consumption and departs the supply network, never to reenter (e.g. retailers or restaurants). All other nodes are transient, representing the points at which food is generated or produced, processed and stored. E is the set of edges of the form $(i,j)\in V_Q\times V_Q\cup V_Q\times V_R$, representing trade relationships. Each edge (i, j) is weighted by the volume of food shipped over a certain time period from i to j, w_ij. The following model assumes that these network data are given.

2.3. Foodborne disease transmission model

The process leading to foodborne disease illness presentation consists of the initial inoculation of contaminated product somewhere in production and subsequent dispersal through the food supply network, followed by the transmission of contamination from product to person, ending in illness.

At the core of our model of this process are the following assumptions:

• (i)The contaminated quantity is fixed, and is composed of individual contaminated units that neither spread nor recover from contamination as they travel through the supply network.
• (ii)Each contaminated unit travels independently through the supply network.
• (iii)Each transition of a unit from one node to the next entails an independent transmission direction.

Taken together, these assumptions describe a unit-centric diffusion process that can be visualized as a large number of ‘pinballs’ travelling through a pinball machine, each ball’s trajectory determined according to a stochastic process described below.

Given these assumptions, we introduce the diffusion model. First, some initial quantity of product produced at a single unknown source s* is contaminated. We model s* as a random variable with a predefined prior probability distribution, P(s* = s) over s ∈ V_Q. The contamination diffusion process is initiated when batches or units of contaminated product depart from s*.

Owing to the second assumption, a discrete-time Markov process determines the movement of a contaminated unit, i.e. a weighted random walk through the supply network. The sequence of states X_n obtained in successive transitions are determined by the state-to-state Markov transition probabilities,

$$P(X_{n+1}=j|X_n=i)=p_{ij}.$$

The p_ij taken together compose P, the row-stochastic Markov transition matrix for the transmission process of a contaminated unit occurring on network G. The probability of self-transition is defined as p_ii = 1 for absorbing nodes i ∈ V_R; for transient nodes j ∈ V_Q, the self-transition probability is strictly p_jj < 1. Because of the supply network structure, it is convenient to consider P in an aggregated, ordered form such that the absorbing nodes come last. We can then unite the transient nodes and the absorbing nodes so that the form of the transition matrix becomes

$$P=\left[\begin{array}{cc}{P}_Q& P_R\\ 0& I_R\end{array}\right],$$

where P_Q is the |V_Q| × |V_Q| submatrix concerning transitions between transient nodes, P_R is the |V_Q| × |V_R| submatrix concerning transitions from transient nodes into absorbing nodes, 0 is a matrix of zeroes and I_R is the |V_R| × |V_R| submatrix representing absorption at a consumer node.

Starting from s*, the diffusion of a contaminated unit through the supply network is fully determined by the Markov transmission matrix P. The process ends when an absorbing node o ∈ V_R is reached, generating a list of directed edges connecting s* and o, the network path γ_s*o. After departing the supply network at o, the contaminated unit is consumed. A set of K individuals consuming contaminated units will report or observe illness. We label the node linked to observation k by o_k, resulting in the multiset Θ = (o₁, …, o_K), which may contain repeated elements. The observation locations in this multiset will be linked to the network at the unique set of nodes o ∈ O ⊆ V_R, such that |O| ≤ K. An important implication of the ‘pinball’ assumption is that the transmission paths ${\gamma }_{s{o}_k}$ through the supply network, and thus the observations o_k, are mutually independent.

The final step in developing the transmission model involves connecting the stochastic process with the physical quantities defined in the network model. The volumes shipped from i to j can be seen as a proxy for the conditional probability that a contaminated item is sent along that direction. We, therefore, define the transition probabilities p_ij as the proportion of volume-flux sent from i to j,

$$p_{ij}=\frac{w_{ij}}{\sum _{\hspace{0.17em}j}{w}_{ij}}\in [0,1].$$

2.4. Source estimator: Bayesian inference

Our goal is to find the most ‘probable’ source s* ∈ V_Q based on the list of observations Θ. We introduce a Bayesian formulation for the probability that a feasible source node s is the true source s*, given the observations and the prior distribution over s*:

$$P(s^{\ast }=s|\mathit{\Theta })=\frac{P(s^{\ast }=s)P(\mathit{\Theta }|s^{\ast }=s)}{P(\mathit{\Theta })}.$$ 2.1

To identify the source, we adopt a maximum probability of detection approach, designing an estimator $\hat{s}$ that selects the feasible source node s that maximizes the probability P(s* = s|Θ), i.e.

$$\hat{s}=\underset{s\in \mathrm{\Omega }}{\text{arg max}}\hspace{0.17em}P(s^{\ast }=s)P(\mathit{\Theta }|s^{\ast }=s),$$ 2.2

where s ∈ Ω is the set of feasible source nodes. Here, we have observed that only a subset of nodes V_Q will be feasible source candidates (i.e. Ω ⊆ V_Q): the set of nodes in V_Q that share at least one path through the network to all contaminated nodes o ∈ O. Unless any prior information regarding the source location is available¹ we assume the prior distribution over s* is uniform, i.e. P(s* = s) = 1/|Ω| for all nodes s ∈ Ω, making the estimator $\hat{s}$ the ML estimator, i.e.

$$\hat{s}=\underset{s\in \mathrm{\Omega }}{\text{arg max}}\hspace{0.17em}P(\mathit{\Theta }|s^{\ast }=s),$$ 2.3

since the constant prior probability P(s* = s) = 1/|Ω| will not contribute to the maximization problem.

The main challenge in solving (2.3) is estimating the likelihood P(Θ|s* = s). The probability of observing illnesses at the locations in Θ from a contamination originated at s will depend on the paths taken through G from s to all observations o_k ∈ Θ. However, there are multiple possible paths ${\gamma }_{s{o}_k}$ from s to each observation node o_k ∈ Θ. The exact probability that s is the source is equal to the total probability over every permutation of paths for which s is the source. We now introduce a few definitions that allow us to write the source likelihood defined over all permutations:

• —${\mathit{\Gamma }}_{s{o}_k}=$ The set of all paths ${\gamma }_{s{o}_k}^{\{n\}}$ through G from s to $o_k,\{{\gamma }_{s{o}_k}^{\{1\}},\dots ,{\gamma }_{s{o}_k}^{\{N\}}\}$.
• —π_s = An s-cascade, or a specific permutation of the K paths connecting feasible source s to each observation location o_k ∈ Θ. Formally, π_s is an element of the Cartesian product over the sets of paths ${\{{\mathit{\Gamma }}_{s{o}_k}\}}_{o_k\in \mathit{\Theta }}$, i.e. $({\gamma }_{s{o}_1},\dots ,{\gamma }_{s{o}_K})\in {\mathit{\Gamma }}_{s{o}_1}\times \cdots \times {\mathit{\Gamma }}_{s{o}_K}$.
• —
  Π_s = The set of all s-cascades, or all permutations of paths from s to each o_k ∈ Θ, i.e.

  $${\mathit{\Pi }}_s={\mathit{\Gamma }}_{s{o}_k}\times \cdots \times {\mathit{\Gamma }}_{s{o}_k}=\{({\gamma }_{s{o}_1},\dots ,{\gamma }_{s{o}_K})\hspace{0.17em}:\hspace{0.17em}{\gamma }_{s{o}_k}\in {\mathit{\Gamma }}_{s{o}_k}\}.$$ 2.4

With these definitions, the source likelihood can be written as the total probability of all permutations of paths where s is the source of the cascade,

$$P(\mathit{\Theta }|s^{\ast }=s)=\sum _{{\pi }_s\in {\mathit{\Pi }}_s}P({\pi }_s|s)P(\mathit{\Theta }|s,{\pi }_s)=\sum _{{\pi }_s\in {\mathit{\Pi }}_s}P({\pi }_s|s),$$ 2.5

where the term P(Θ|s, π_s) is equal to 1, since by definition, the observation locations o_k ∈ Θ are the endpoints of the paths ${\gamma }_{s{o}_k}\in {\pi }_s$.

Solving equation (2.5) amounts to finding the total probability over all s-cascades π_s ∈ Π_s. The probability of an individual s-cascade P(π_s|s) can be expanded in terms of the constituent paths ${\gamma }_{s{o}_k}\in {\pi }_s$ and transition probabilities p_ij between each adjacent node pairs $(i,j)\in {\gamma }_{s{o}_k}$ as

$$\begin{array}{rl}P({\pi }_s|s)& =P({\gamma }_{s{o}_1},\dots ,{\gamma }_{s{o}_K}|s)\\ & =\prod _{{\gamma }_{s{o}_k}\in \hspace{0.17em}{\pi }_s}P({\gamma }_{s{o}_k}|s)\\ & =\prod _{{\gamma }_{s{o}_k}\in \hspace{0.17em}{\pi }_s}\prod _{(i,j)\hspace{0.17em}\in \hspace{0.17em}{\gamma }_{s{o}_k}}{p}_{ij},\end{array}$$ 2.6

where the second equality follows from the independence of paths to each observation o_k and the third equality follows from the total probability associated with path ${\gamma }_{s{o}_k}$. The likelihood can then be found in terms of the transition probabilities as

$$P(\mathit{\Theta }|s^{\ast }=s)=\sum _{{\pi }_s\hspace{0.17em}\in \hspace{0.17em}{\mathit{\Pi }}_s}\prod _{{\gamma }_{s{o}_k}\in \hspace{0.17em}{\pi }_s}\prod _{(i,j)\hspace{0.17em}\in \hspace{0.17em}{\gamma }_{s{o}_k}}{p}_{ij}.$$ 2.7

Evaluating the likelihood by solving equation (2.7) explicitly requires enumerating all paths ${\gamma }_{s{o}_k}$ contained in each s-cascade π_s, over all cascades Π_s, which becomes combinatorially difficult for large networks given even very few illness observations. Existing methods have dealt with this complexity by assuming the contamination travels along a single s-cascade: the set of shortest, highest probability paths [32,34]. In the following, we introduce an alternative representation of the likelihood P(Θ|s* = s) that allows us to develop a simple algebraic expression that is probabilistically equivalent to equation (2.7), from which we can tractably compute the total probability over all s-cascades.

We begin by showing that equation (2.5) can be rearranged from an expression that enumerates over each s-cascade π_s ∈ Π_s to one that enumerates over each observation o_k ∈ Θ. Starting from the right-hand side of (2.5) we have

$$\sum _{{\pi }_s\hspace{0.17em}\in \hspace{0.17em}{\mathit{\Pi }}_s}P({\pi }_s|s)=P({\mathit{\Pi }}_s|s)=P({\mathit{\Gamma }}_{s{o}_1}\times \cdots \times {\mathit{\Gamma }}_{s{o}_K}|s),$$

by total probability and the definition of Π_s. Then,

$$P({\mathit{\Gamma }}_{s{o}_1}\times \cdots \times {\mathit{\Gamma }}_{s{o}_K}|s)=P(\prod _{o_k\hspace{0.17em}\in \hspace{0.17em}\mathit{\Theta }}{\mathit{\Gamma }}_{s{o}_k}|s)=\prod _{o_k\hspace{0.17em}\in \hspace{0.17em}\mathit{\Theta }}P({\mathit{\Gamma }}_{s{o}_k}|s),$$

where the last equality follows from the independence of observations o_k ∈ Θ. Therefore,

$$\sum _{{\pi }_s\hspace{0.17em}\in \hspace{0.17em}{\mathit{\Pi }}_s}P({\pi }_s|s)=\prod _{o_k\in \mathit{\Theta }}P({\mathit{\Gamma }}_{s{o}_k}|s).$$ 2.8

The term $P({\mathit{\Gamma }}_{s{o}_k}|s)$ represents the total probability of reaching location o_k from starting point s along all possible paths ${\gamma }_{s{o}_k}^{\{n\}}\in {\mathit{\Gamma }}_{s{o}_k}$. Let us denote this probability as $P({\mathit{\Gamma }}_{s{o}_k}|s)=a_{s{o}_k}$, so that we are interested in evaluating

$$P(\mathit{\Theta }|s^{\ast }=s)=\prod _{o_k\in \mathit{\Theta }}{a}_{s{o}_k}.$$ 2.9

To compute $a_{s{o}_k}$ we could sum over the probability of all individual paths $\{{\gamma }_{s{o}_k}^{\{1\}},\dots ,{\gamma }_{s{o}_k}^{\{N\}}\}\in {\mathit{\Gamma }}_{s{o}_k}$, but this again requires enumerating all possible paths between s and o_k, which is as combinatorially difficult as evaluating (2.7).

An alternative representation involves recognizing $a_{s{o}_k}$ as the absorbing probability for a Markov chain, or the probability that a contaminated item starting at s gets ‘captured’ at o_k. The absorbing probability can be written as [36]

$$a_{s{o}_k}=\sum _{n\hspace{0.17em}=\hspace{0.17em}0}^{\mathrm{\infty }}\sum _{l\hspace{0.17em}\in \hspace{0.17em}{V}_Q}{p}_{sl}^{(n)}{p}_{l{o}_k},$$ 2.10

where $p_{sl}^{(n)}$ denotes the probability of transitioning from transient node s to transient node l ∈ V_Q in exactly n steps, and $p_{l{o}_k}$ denotes the probability of transitioning from l to observation location o_k in one step, where it is absorbed. Equation (2.10) represents the probability of starting at s and being absorbed at o_k in one or more steps—that is, over paths of any length.² The probability of being absorbed in a single step is equal to $p_{s{o}_k}$ and if this does not happen, the contamination may move either to another absorbing state (in which case it never reaches o_k ), or to transient state l. In fact, it may move among the transient states for any number of transitions before landing at l, which occurs after n steps with probability $p_{sl}^{(n)}$. From l it then has probability $p_{l{o}_k}$ of going to o_k.

The probability $p_{sl}^{(n)}$ that the contamination travels from s to l in exactly n steps is found as the $(s,l)\mathrm{th}$ element of the transition-state matrix P_Q raised to the nth power. Therefore, we can write equation (2.10) in matrix form as [36]

$$A=\sum _{n=0}^{\mathrm{\infty }}{P}_Q^n{P}_R,$$ 2.11

where we have also recognized $p_{l{o}_k}$ as the $(l,o)\mathrm{th}$ element of the absorbing-state matrix P_R. Here, we distinguish o and o_k, since o describes the unique node in V_R corresponding to the observation o_k and therefore (l, o) points to a specific entry in P_R. Summing the geometric series, equation (2.11) can be expressed in closed form as

$$A={(I-P_Q)}^{-1}{P}_R,$$ 2.12

which is well defined because for any absorbing Markov chain, I − P_Q will have an inverse [36].

Combining equations (2.9) and (2.12), we can fully define the likelihood over all observations,

$$P(\mathit{\Theta }|s^{\ast }=s)=\prod _{o_k\in \mathit{\Theta }}{[{(I-P_Q)}^{-1}{P}_R]}_{s{o}_k}.$$ 2.13

Evaluating this equation requires only a single operation to compute the matrix A.

We can now see the full advantage of the relation derived in equation (2.8): whereas the left-hand term requires enumerating all possible paths ${\gamma }_{s{o}_k}$ between s and each observation o_k, by rearranging to order over the observations, the right-hand term can be evaluated through a single algebraic computation.

Equation (2.13) can be used in the ML source estimator in equation (2.3) to select the source node that maximizes the posterior probability P(Θ|s* = s) over all possible sources s ∈ Ω,

$$\hat{s}=\underset{s\in \mathrm{\Omega }}{\text{arg max}}\prod _{o_k\in \mathit{\Theta }}{[{(I-P_Q)}^{-1}{P}_R]}_{s{o}_k}.$$ 2.14

We can also construct a posterior probability for each feasible source s ∈ Ω,

$$P(s^{\ast }=s|\mathit{\Theta })=\frac{1}{c}P(\mathit{\Theta }|s^{\ast }=s),$$ 2.15

for some normalizing constant c, forming a probability distribution over the set s ∈ Ω, which can be used to identify a set of the most probable sources.

It is important to note that by the formulation in equation (2.10), $a_{s{o}_k}$ represents the total probability of reaching location o_k from starting point s, considering all possible paths of all possible lengths. Given the transmission model of §2.3, which assumes observations are independent, the likelihood in (2.13) thus represents the exact total probability of all observations resulting from s.

This source detection approach relies on the independent observation assumption. The implication of this assumption is that contamination trajectories or s-cascades containing paths with shared edges are not assigned higher probabilistic weighting during inference of the source. This assumption may introduce some error in situations where contaminated items have travelled in the same batch through early legs of their journey through the supply network, for example, being shipped together from producer to distributor before being divided into separate pallets. Nonetheless, the condition of independence between observations can reasonably be expected to be validated in practice, since it is possible for food items from the same contaminated batch to depart from the source in separate (and independent) trucks; indeed, for large contamination incidents where the contaminated quantity will be larger than what fits in one truck, this is necessarily the case. We, therefore, expect the error caused by failing to consider shared pathways to be of second order and that our solution is a good approximation of the ML source estimator.

3. Evaluation

In this section, we demonstrate the performance benefits of the probabilistically exact source estimator in application to different network topologies. First, we apply the method to stylized network models of the food supply. This allows us to evaluate the performance of our ML source estimator and its robustness to differences in network structure in an idealized setting. In practice, food supply networks are never exactly known, and illness data are imperfect, especially during an unfolding outbreak when data are emerging. In order to evaluate the robustness of our conclusions in these non-ideal settings we also apply our method to illness data from a real outbreak, using an estimated model of the relevant food supply network structure. This estimated model allows us to work around the issue of data deficits by estimating all links since access to complete supply chain data across companies is not a current possibility.

3.1. Evaluation on stylized networks

3.1.1. Stylized network structures

We first evaluate our method on stylized models of food supply networks and simulated outbreaks of contamination. We choose for application the standard food supply structure: a layered, directed network consisting of four layers of supply, for which nodes in each layer trade expressly with nodes in the subsequent layer; this is the structure exhibited by the network in figure 1. Formally, this is a network of the form G = V, E with four layers V = {V₁, V₂, V₃, V₄}, and directed edges of the form (i, j) ∈ E for i ∈ V_n, j ∈ V_n+1, n = 1, 2, 3.

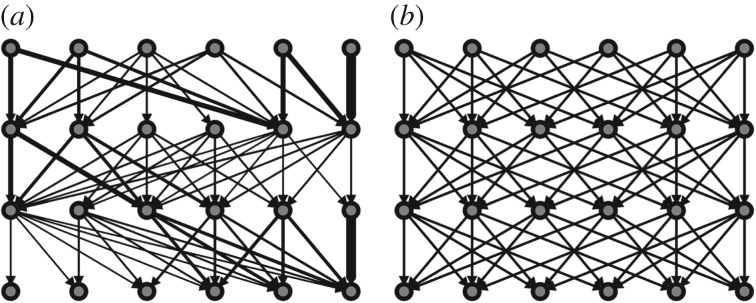
We consider two probabilistically different network topologies based on this characteristic structure, which we use to evaluate the source detection methods. On one extreme is a structure for which a small percentage of edges carry the majority of the probability weight. The dominant probabilities will capture a large fraction of the product flowing through the network; therefore, we call this the dominant paths network. On the other extreme is a structure for which each edge is probabilistically equivalent to every other. Paths through this network will also be probabilistically equivalent and no path will capture more of the flow through the network than any other; we, therefore, call this the non-dominant paths network. For details on how these networks are generated, see electronic supplementary material, §I.

For the simulations presented in this section, we fix 25 nodes per layer, and we choose an average degree of μ_D = 4. Many different network structures with these parameters can be created both for dominant and non-dominant paths connection schemes; we illustrate stylized versions of these structures in figure 2.

Figure 2.

Illustrative figure representing the structure of the stylized networks analysed in §3.1. Both networks have the same number of nodes, links and average degree, but the degree distributions vary: (a) the dominant paths network is generated according to a heterogeneous (geometric) degree distribution, while (b) the non-dominant paths network is generated according to a deterministic degree distribution. Line widths are proportional to link probabilities.

3.1.2. Benchmarks

Throughout this section, we will compare the performance of our method to the effective distance method for source identification proposed in [32,34]. We also compare results to the network baseline, a benchmark that is equivalent to guessing at random between all feasible sources s ∈ Ω.

The effective distance method is the state-of-the-art approach for source detection in problems where a contagion model of transmission is not assumed and data on observations of contamination at every node or timed network data are not available, and the only method that has been implemented in the context of foodborne disease outbreaks. The method involves a measure of effective distance, defined such that the shortest, highest probability path from a source to an observation has the shortest effective distance through the network [32,34]. To identify the source of an outbreak, the single shortest effective distance (i.e. shortest, highest probability) path to each observation is identified. To infer the source location, feasible source nodes are ranked according to the average and variance of the effective distances to each observation and the source chosen as the node that minimizes these two quantities. An explanation of the effective distance method for source identification is provided in terms of the notation introduced in §2 in electronic supplementary material, §II.

3.1.3. Simulation setting

Outbreaks are generated using a Monte Carlo simulation model to determine the trajectories of contamination through the supply chain, leading to observations of illness at the multiset of node locations o_k ∈ Θ. The source detection methods are applied and feasible sources are rank-ordered according to their probability values or effective distances. We run 1000 outbreak simulations using nodes in layer V₁ as the source. Source detection performance is quantified according to simulation accuracy, which measures the percentage of times the true source is accurately identified across all simulations.

3.1.4. Results

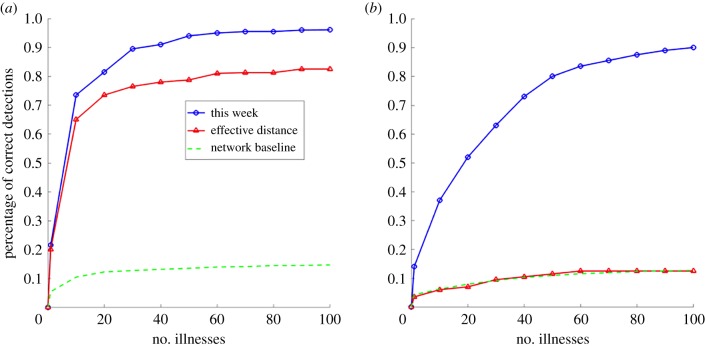
Figure 3 demonstrates results for simulation accuracy with our source detection method, the effective distance method and the network baseline as a function of the number of cases for the dominant paths network (figure 3a) and the non-dominant paths network (figure 3b). The network baseline is included to demonstrate that results are not attributable to the number of feasible sources decreasing, and with it the opportunities for connectivity through the network, as the number of contaminated nodes increases. If this were the case the network baseline (or random guessing between feasible sources) would increase quickly in accuracy, which does not happen.

Figure 3.

Simulation accuracy for the networks introduced in §3.1 for our method for source detection (blue, ⊙), the effective distance method for source detection (red, Δ), and the network baseline (green, - -) as a function of the number of illnesses reported. (a) Accuracy: dominant paths; (b) accuracy: non-dominant paths. (Online version in colour.)

For both networks, our method performs well (figure 3a,b) and follows expected properties, increasing in accuracy with data on the number of illness reports. We can make good inferences about the source location after only a limited number of illnesses have been reported, and very accurate inferences if we wait a bit longer. The accuracy of source identification is faster and more accurate for the dominant paths network; this is as expected since high probability edges will dominate the paths travelled by contaminated product as well as the calculation of the source identification likelihood. Despite the lack of dominant path probabilities, simulation accuracy is also high for the non-dominant paths network. What is happening is that when the probabilities of all paths are equal, our method reduces to calculating the number of possible s-cascades between a source and set of observations; this can be seen by replacing the p_ij in equation (2.7) with a constant. This effectively turns our source estimator into a centrality-based method that chooses the source that connects to the observations across the greatest number of paths.

The comparison of simulation accuracy results for our source estimator and the effective distance method makes apparent the benefit of considering all paths in estimating the source rather than selecting only the set of highest probability paths. On the non-dominant paths network, the effective distance method cannot compete; because all paths appear the same, the method chooses one at random, and as a result performs identically to the network baseline. Still, this network is a stylized and extreme case; most real-world food supply networks will exhibit some degree of heterogeneity in path probabilities. On the dominant paths network, which exhibits significant heterogeneity in path probabilities, the effective distance method performs much better. This is as expected: for each feasible source the method considers the highest probability s-cascade; when path probabilities vary greatly, this will often be the actual set of paths travelled by the contamination. However, because the contamination does not always travel along the highest probability s-cascade, by accounting for all possible s-cascades our method performs better by a substantial margin of around 10% for the particular network topologies investigated.

Since these two networks represent extremes in the way probabilities might be distributed across a food supply network, the results presented here suggest that source identification in the context of foodborne disease is robustly and substantially more accurate across wide-ranging network topologies when the total probability across all possible paths between a feasible source and the observation set is considered.

3.2. Application: 2011 STEC O104:H4 outbreak

In this section, we evaluate our method in application to the STEC O104:H4 outbreak in Germany in 2011, which affected over 4000 people with STEC gastroenteritis or severe hemolytic uremic syndrome [1,2,37].

Electronic supplementary material, figure S1, depicts the epidemic curve of the outbreak. The first confirmed illness case began on 1 May, marking the beginning of week 1. The case count grew dramatically starting on 8 May, at the beginning of week 2. The outbreak peaked on 21 and 22 May, between week 3 and week 4, and the majority of cases had been reported by the end of week 5. By week 6 investigators had narrowed the search down to contaminated sprouts and at the end of that week, on 10 June, confirmed the origin of the outbreak as a small organic farm in Bienenbüttel, in the district Uelzen in northern Germany.

The last illness associated with the outbreak was reported on 4 July, at the end of week 9 going into week 10, but the outbreak was declared over three weeks later, on 26 July [1,2,37]. Further background on the outbreak, timeline and investigation is provided in electronic supplementary material, §IIIA.

3.2.1. Case data

The illness case data come from the Robert Koch Institute (RKI), Germany’s national public health authority, by way of the ServStat tool [38]. We query this tool for data on all cases of E. coli reported in Germany during the dates 1 May to 4 July 2011, corresponding to outbreak weeks 1 through 9. This includes all cases of any strain of E. coli contamination reported in Germany during this time period, including cases unrelated to the STEC O104:H4 outbreak. Since the number of cases during the outbreak far exceed the routine baseline of E. coli cases during this time period in previous years, these unrelated cases likely represent a minor source of noise in the data (see electronic supplementary material, figure S2). Cases are reported in association with the German administrative district (Landkreise) where the patient resides. There are a total of 402 districts in Germany. We use only these data and do not consider cases reported outside of Germany. Further information on these data is provided in electronic supplementary material, §IIIB.

3.2.2. Network model

The source identification method assumes a model of the underlying food supply network structure. Because exact, fine-grained data on the supply network of food commodities are not available, we develop a model of the network based on publicly available data and a practical understanding of food supply chain logistics. We focus this model on the supply of vegetables in Germany because (i) raw vegetables were suspected as the source of infection early in the investigation and (ii) most of the reported cases of illness were inside Germany. Nodes in this network represent the producers, processors, wholesalers, retailers and consumers spatially aggregated into each of the 402 German administrative districts. Our model is based on the approach of [12,39]. Details are provided in electronic supplementary material, §IIIC.

3.2.3. Results and discussion

To evaluate source identification ‘in real time’, we run the source detection method on data available at the end of each week of the outbreak. Results are reported for our method in combination with the vegetable network model described above and for the effective distance method in combination with the network modelling approach reported in [34], a gravity model network of spatial food transportation within Germany based on population statistics.³ Despite using different network models, our results are comparable because the feasible sources in both network models are the same set of administrative districts in Germany. Both methods are evaluated on the publicly available record of general request E. coli cases (no particular E. coli serotype selected) from the SurvStat database.

We report on accuracy according to two metrics: (i) the rank of the true source, the position of the true source in the ordered ranking; and (ii) the top-3 distance to the true source, the average distance to the true source in Bienenbüttel from the centre of the top three ranked locations.

Table 1 reports the source identification performance metrics for our method and the effective distance method by each week of the outbreak. During an outbreak, accurate and timely identification of the source is essential to stem impact on the public. In the context of the STEC outbreak, this would have meant identifying the source before week 4, when the outbreak peaked. However, the source was only identified at the end of week 6, by which time the epidemic was at its tail end (see electronic supplementary material, figure S1), and therefore limited cases were averted. Our approach is accurate, timely and consistent, identifying the source district Uelzen in rank 3 by week 2, and in the top 2 ranked locations for the remainder of the outbreak. Importantly, though not reported in the table, the district in rank 1 during weeks 2–4, Lüchow–Dannenberg, is adjacent to Uelzen and its centre is as close in distance (kilometre) to the origin farm in Bienebüttel as the centre of Uelzen. Furthermore, the consistency of the result in the ordered ranking and the top-3 distance to the true source indicates convergence of the method, signifying a reliable signal for investigators. The effective distance method also demonstrates high accuracy, identifying the source region in Uelzen in the first position in three of the weeks (out of weeks 3–9, for which results are reported). However, it is notably less consistent, identifying the source location within the top 10 ranks in some weeks but not in others, including the critical period around the peak of the outbreak in week 4.

Table 1.

Source identification performance metrics for our method and the effective distance method applied to data from the 2011 STEC O104:H4 outbreak. The investigation identified the source at the end of week 6, as indicated by the asterisk.

		rank of true source location		top-3 distance from true source (in km)
outbreak week	no. ill	this work	effective distance [34]	this work	effective distance [34]
1	65	38	—	180.0	—
2	104	3	—	148.8	—
3	85	2	1	83.7	71.3
4	155	2	>10	40.8	98.3
5	319	1	3	28.7	43.7
6*	363	1	1	28.7	30.3
7	346	1	1	28.7	30.3
8	305	1	5	28.7	135.0
9	279	1	2	28.7	65.0

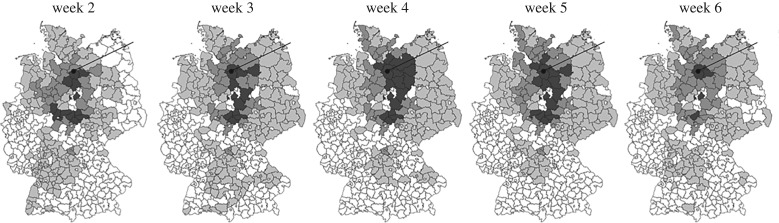
Figure 4 visualizes on a map of Germany the probability distribution resulting from applying the source identification method to the case data available at the end of weeks 2–6, with darker shading representing higher probabilities. The true source in Bienebüttel, district Uelzen, is indicated with the black dot and line. As can be seen in the images, the highest probability locations (also the top-ranked locations) frame the outbreak into a small regional area around the true source.

Figure 4.

Geographical representation of the probability of each of the 402 German administrative districts being the source based on source identification results using our model. Darker shading represents higher probability. The true source in Bienenbüttel, district Uelzen, is indicated.

By developing a source identification approach that accounts for the specific features of foodborne disease transmission and combining it with a network model based on food supply data, we are able to demonstrate significant and timely improvements to source identification on a real case. While our source identification is only as granular as the geographical districts in the network, this information could have been used during the critical early period of the investigation, supplementing conventional methods to inform spatially targeted sampling and narrowing down the list of potential source locations, e.g. to farms located within the black shaded regions in figure 4. These results also might have prevented investigators from pursuing false leads, which happened notably during the early stages of the 2011 STEC outbreak investigation. In this case, during week 4 of the outbreak, investigators wrongly implicated cucumbers produced by a Spanish produce cooperative [40]; this incorrect prediction resulted in the wiping out of over a month’s worth of production and caused lasting damage to the reputation of the Spanish cucumber industry as a whole.⁴ Although international imports are not included in our network model, the early convergence of the source detection method around a region within Germany would have signalled to investigators that a likely local source existed, informing a sampling strategy that could have led to earlier identification of the source location.

4. Conclusion and outlook

This paper develops a methodology to identify the source of large-scale outbreaks of foodborne disease. We formulate a probabilistic model of the foodborne disease contamination transmission process as an absorbing random walk on a network and derive an estimator for the source location. This is the ML source estimator for a diffusion process on a weighted, directed network with absorbing nodes.

The primary methodological contribution of this work is the development of a probabilistically exact source location estimator that is not limited to tree-like approximations but includes multiple possible paths to a destination. Application to stylized networks and a real outbreak case demonstrate the benefits of the method. Given the exact food supply network data, our approach shows significant improvements in accuracy and robustness, especially for particular network structures without a unique set of dominant paths. Furthermore, application to real data from the STEC outbreak demonstrates that our approach is more consistent in converging on the geographical origin of the outbreak. This demonstrated consistency suggests that the inclusion of multiple paths makes our approach less sensitive to fluctuations in case data over the course of an epidemic.

4.1. Limitations

There are two limitations that we want to explicitly mention. First, the source identification method is only as precise as the network model data it relies on. Fine-grained network data on a company level, as well as dynamic changes in network data during an outbreak, are not easily available. However, we demonstrate with the STEC example that the source identification method can produce good results even with approximated (modelled) network data. In these cases, it is important for the method that the network be highly interconnected and possible paths are not excluded.

Second, the transmission process is modelled as a random walk, assuming independence between paths. With this assumption, we are able to develop a computationally tractable solution to the source detection problem that accounts for all possible paths. While we do not exclude that cases with interdependencies exist, we argue that this assumption is true for many cases in food networks and outbreaks and does not make a large difference even when paths are shared.

4.2. Future work

The source detection method described in this paper has been implemented at the German Federal Institute for Risk Assessment (BfR), Germany’s federal-level food safety authority. The use of this method to investigate outbreaks in practice will provide further insights into its real performance and cost. Additionally, multiple extensions to the method may be investigated. First, information on time stamps of outbreaks is not yet used in the model. To play a role in the inference problem, the travelling times through the network need to be significantly different between sources. Second, information on path dependencies, as mentioned above, can be incorporated. Third, information on contamination within the network (for example, by in-line sampling performed by investigators) could be assumed. And lastly the model can be extended to cases with multiple sources.

Other aspects of the investigation process can also be improved. We are currently working on a combined system of the source detection method and network model to identify the food vector source of an outbreak (part (ii) of the investigation process as described in the Introduction). Cases are reported in the outbreak dataset according to the county where the patient resides, while food purchasing or consumption is not limited to a person’s location of residence and frequently occurs at other locations where people work, travel, or go on holiday. Attempts may be made either in the data registry or in the network model to geographically smooth these cases to account for mobility. Finally, the investigator could consider changes in the network (feedbacks) during the outbreak.

Beyond foodborne disease, a natural extension of this work is the application to identifying the source of network-based diffusion processes more generally, such as infectious disease spread through global metapopulation type transport networks or bacterial contaminations spread through water distribution networks.

Data accessibility

The source identification model was written in Matlab and is available at https://github.com/AbigailHorn/Foodborne-Source-Location. Details on the methodology used to generate the stylized and Germany network models evaluated in combination with the source identification model in §3 are described in the electronic supplementary material. The STEC outbreak illness data come from the Robert Koch Institute (RKI), Germany’s national public health authority, by way of the ServStat tool [38].

Authors' contributions

A.L.H. conceived the study, designed the study, developed the model, implemented the evaluations and wrote the paper. H.F. developed the Germany food supply network model, and helped to design the study and draft the paper. Both authors gave final approval for publication.

Competing interests

We have no competing interests.

Funding

This work was developed within the scope of a Robert Wood Johnson Foundation (RWJF) Public Health Services and Systems Research (PHSSR) award and a German Research Foundation (DFG) award. A.L.H. was additionally supported by the Federal Institute for Risk Assessment (BfR) and a Bayer FoundationAward.