Autocatalytic networks in biology: structural theory and algorithms

Abstract

Self-sustaining autocatalytic networks play a central role in living systems, from metabolism at the origin of life, simple RNA networks and the modern cell, to ecology and cognition. A collectively autocatalytic network that can be sustained from an ambient food set is also referred to more formally as a ‘reflexively autocatalytic food-generated’ (RAF) set. In this paper, we first investigate a simplified setting for studying RAFs, which is nevertheless relevant to real biochemistry and which allows an exact mathematical analysis based on graph-theoretic concepts. This, in turn, allows for the development of efficient (polynomial-time) algorithms for questions that are computationally intractable (NP-hard) in the general RAF setting. We then show how this simplified setting for RAF systems leads naturally to a more general notion of RAFs that are ‘generative’ (they can be built up from simpler RAFs) and for which efficient algorithms carry over to this more general setting. Finally, we show how classical RAF theory can be extended to deal with ensembles of catalysts as well as the assignment of rates to reactions according to which catalysts (or combinations of catalysts) are available.

1. Introduction

A central property of the chemistry of living systems is that they combine two basic features: (i) the ability to survive on an ambient food source and (ii) each biochemical reaction in the system requires only reactants and (most often) a catalyst that are provided by other reactions in the system (or are present in the food set). The notion of a self-sustaining ‘collectively autocatalytic set’ tries to capture these basic features formally, and was pioneered by Stuart Kauffman [1,2] who investigated a simple binary polymer model to address questions that relate to the origin of life. The notion of a collectively autocatalytic set was subsequently formalized more precisely as ‘reflexively autocatalytic and food-generated’ (RAF) sets (defined shortly) and explored by others [3–5].

RAFs are related to other notions such as Rosen’s (M;R) systems [6], autopoietic systems [7], and ‘organizations’ in chemical organization theory [8,9]. The application of RAFs has expanded beyond toy polymer models to analyse both real living systems (e.g. the metabolic network of Escherichia [10]) and simple autocatalytic networks that have been constructed in laboratory studies, either with RNA molecules [11] or with peptides [12]. They are also believed to have played an important role in the origin of life [13–15].

The generality of RAF theory also means that a ‘reaction’ need not refer specifically to a chemical reaction, but to any process in which ‘items’ are combined and transformed into new ‘items’, and where similar ‘items’ facilitate (or ‘catalyse’) the process without being used up in the process. This has led to application of RAF theory to processes beyond biochemistry, including biodiversity [16,17], cognitive psychology [18] and (more speculatively) economics [19].

In this paper, we show how RAF theory can be developed further to:

• —provide an exact and tractable characterization of RAFs and subRAFs when reactants involve just food molecules;
• —extend this last concept to general catalytic reaction networks by defining a new type of RAF (generative) which couples realism with tractability; and
• —include reaction rates into RAF theory and show that an optimal RAF can be calculated in polynomial time.

We begin with some definitions.

1.1. Catalytic reaction systems

A catalytic reaction system (CRS) consists of a set X of ‘molecule types’, a set $\mathcal{R}$ of ‘reactions’, an assignment C describing which molecule types catalyse which reactions, and a subset F of X consisting of a ‘food set’ of basic building block molecule types freely available from the environment. Here, a ‘reaction’ refers to a process that takes one or more molecule types (the ‘reactants’) as input and produces one or more molecule types as output (‘products’). C can be viewed as a subset of $X\times \mathcal{R}$.

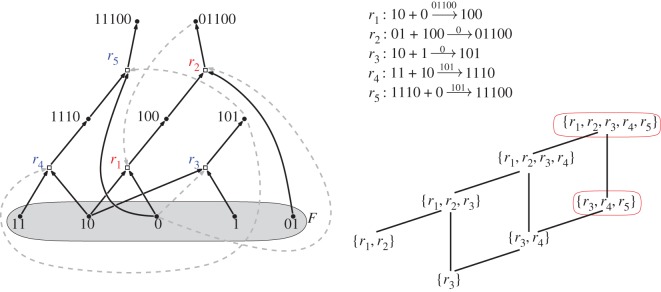
A CRS can be represented mathematically in two essentially equivalent ways. The first is a directed bipartite graph where the two types of vertices are: (i) molecule types (some of which lie in the food set F) and (ii) reactions; this graph also has two types of arcs: (i) from molecule types into and out of reaction vertices, as reactants and products, respectively, and (ii) from molecule types that act as catalysts to reactions, representing the layer of catalysis. Figure 1 provides a simple example of a CRS represented in this way.

Figure 1.

A simple RAF (arising from an instance of the binary polymer model [19]) involving five reactions, r₁, …, r₅ and 10 molecule types (binary polymers), with the food set comprising monomers and dimers. Catalysation arcs are shown as dashed arrows on the left, and are indicated above the reaction arrows on the right. This RAF contains six other subRAFs, as indicated in the Hasse diagram (bottom right). The three circled RAFs are closed (defined below). In this example, each reaction has exactly two reactants, one product and one catalyst; however a CRS can have reactions with an arbitrary number of reactants, products and possible catalysts. (Online version in colour.)

The second way to represent an RAF is to list the reactions explicitly, writing each in the form

$$r\hspace{0.17em}:\hspace{0.17em}A\stackrel{c_1,c_2,\dots }{---⟶}B,$$

where A denotes the set of reactants of reaction r, B the set of products of r, and c₁, c₂, … are the possible catalysts for r. For example, for r₂ in the CRS of figure 1 we write

$$r_1\hspace{0.17em}:\hspace{0.17em}10+0\stackrel{01100}{--⟶}110$$

to denote that r₁ is catalysed by 01100.

1.1.1. Self-sustaining autocatalytic networks (RAFs, maxRAF)

Given a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$, a subset ${\mathcal{R}}^{\prime }$ of $\mathcal{R}$ is a said to be an RAF for $\mathcal{Q}$ if ${\mathcal{R}}^{\prime }$ is non-empty and satisfies the following two conditions.

• —Reflexively autocatalytic (RA): each reaction $r\in {\mathcal{R}}^{\prime }$ is catalysed by at least one molecule type that is either present in the food set or is generated by another reaction in ${\mathcal{R}}^{\prime }$.
• —Food-generated (F): The reactions in ${\mathcal{R}}^{\prime }$ can be ordered so that each reactant of each reaction in ${\mathcal{R}}^{\prime }$ is either a product of an earlier reaction in the sequence or is present in the food set.

In other words, an RAF is a subset of reactions that is both self-sustaining (from the food set) and collectively autocatalytic. In forming an RAF from the food set, some (or all) reactions may initially need to proceed uncatalysed (and thereby at a lower rate) but once formed every reaction in the RAF will be catalysed. A simple example of an RAF is the pair of reactions {r₁,r₂} shown in the CRS of figure 1. Note that in this example either r₁ or r₂ must first proceed uncatalysed, but once one reaction has occurred, the system continues with both reactions catalysed.

An alternative and equivalent way to define an RAF is as follows. Let ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$ denote the set of molecule types that are generated by applying the following procedure until no further molecule types can be added: start with the food set and sequentially add to it any molecule type (from X) that is the product of a reaction r from ${\mathcal{R}}^{\prime }$ provided that r has all its reactants present in the set of molecule types so far constructed (catalysts are ignored in this step). In this way, the (F) condition can be restated more simply as the condition that each reactant of each reaction in ${\mathcal{R}}^{\prime }$ is present in ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$. Moreover, assuming the (F) condition holds, the (RA) condition becomes equivalent to the stronger condition that each reaction $r\in {\mathcal{R}}^{\prime }$ is catalysed by at least one molecule type that is present in ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$. Thus, ${\mathcal{R}}^{\prime }$ is an RAF if and only if each of its reactions has all its reactants and at least one catalyst present in ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$.

Two fundamental combinatorial results concerning RAFs (from [20]) which will be applied in this paper are the following:

• —If $\mathcal{Q}$ has an RAF then it has a unique maximal RAF which contains all other RAFs for $\mathcal{Q}$ (referred to as the maxRAF of $\mathcal{Q}$, denoted $\text{maxRAF}(\mathcal{Q})$).
• —Determining whether or not $\mathcal{Q}$ has an RAF, and if so constructing $\text{maxRAF}(\mathcal{Q})$ can be solved by an algorithm that is polynomial time in the size of $\mathcal{Q}$.

By contrast to the second point, finding a smallest RAF in a CRS $\mathcal{Q}$ has been shown to be NP-hard [21].

1.1.2. Further autocatalytic concepts (subRAFs, irrRAFs, closure, closed RAFs, CAFs)

We now introduce some further notions related to different types of RAFs. The maxRAF of a CRS $\mathcal{Q}$ may contain one or more subsets of reactions that are themselves RAFs for $\mathcal{Q}$, in which case we call any such subset a subRAF of the maxRAF. An RAF ${\mathcal{R}}^{\prime }$ is said to be an irreducible RAF (irrRAF) if it contains no proper subset of ${\mathcal{R}}^{\prime }$ that is an RAF. In other words, removing any single reaction from an irrRAF ${\mathcal{R}}^{\prime }$ gives a set of reactions that does not contain an RAF for $\mathcal{Q}$. Constructing an irrRAF for $\mathcal{Q}$ (or determining than none exists when $\mathcal{Q}$ has no RAFs) can also be carried out in polynomial time [20]; however the number of irrRAFs can grow exponentially with the size of the CRS [22]. To illustrate this notion, the RAF {r₁, r₂} and {r₃} are the only irrRAF for the CRS in figure 1.

Given any subset ${\mathcal{R}}^{\prime }$ of reactions from $\mathcal{R}$, we now define the closure of ${\mathcal{R}}^{\prime }$ in $\mathcal{Q}$, denoted $\overline{{\mathcal{R}}^{\prime }}$. This is the (unique) minimal subset ${\mathcal{R}}^{″}$ of $\mathcal{R}$ that contains ${\mathcal{R}}^{\prime }$ and satisfies the property that if a reaction r from $\mathcal{R}$ has each of its reactants and at least one catalyst present in the food set or as a product of a reaction from ${\mathcal{R}}^{″}$ then r is in ${\mathcal{R}}^{″}$.

It is easily seen that the closure of any RAF is always an RAF. We say that an RAF ${\mathcal{R}}^{\prime }$ is a closed RAF if it is equal to its closure (i.e. ${\mathcal{R}}^{\prime }=\overline{{\mathcal{R}}^{\prime }}$). In particular, the maxRAF is always closed. Referring again to figure 1, the closure of the RAF {r₃} is the subRAF {r₃, r₄, r₅}.

A minimal closed RAF for a CRS $\mathcal{Q}$ is a closed RAF ${\mathcal{R}}^{\prime }$ for $\mathcal{Q}$ that does not contain any other closed RAF for $\mathcal{Q}$ as a strict subset. Any closed irrRAF is a minimal closed RAF but a minimal closed RAF need not be an irrRAF. Once again figure 1 illustrates this last concept: for this CRS, the minimal closed RAF is the maxRAF {r₃, r₄, r₅} but it is not an irrRAF since it contains the RAF {r₃, r₄}.

Given a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$, a stronger notion than an RAF is that of a constructively autocatalytic F-generated (CAF) set for $\mathcal{Q}$ (introduced in [23]). A CAF for $\mathcal{Q}$ is a non-empty subset ${\mathcal{R}}^{\prime }$ of $\mathcal{R}$ for which the reactions in ${\mathcal{R}}^{\prime }$ can be ordered in such a way that for each reaction r in ${\mathcal{R}}^{\prime }$, each reactant and at least one catalyst of r is either produced by an earlier reaction from ${\mathcal{R}}^{\prime }$ or is present in the food set. In other words, a CAF is like an RAF with the extra requirement that no uncatalysed reactions are required for its formation (i.e. the catalyst needs to be already present when it is first needed). For example, in figure 1, {r₃, r₄} is a CAF but {r₁, r₂} is not.

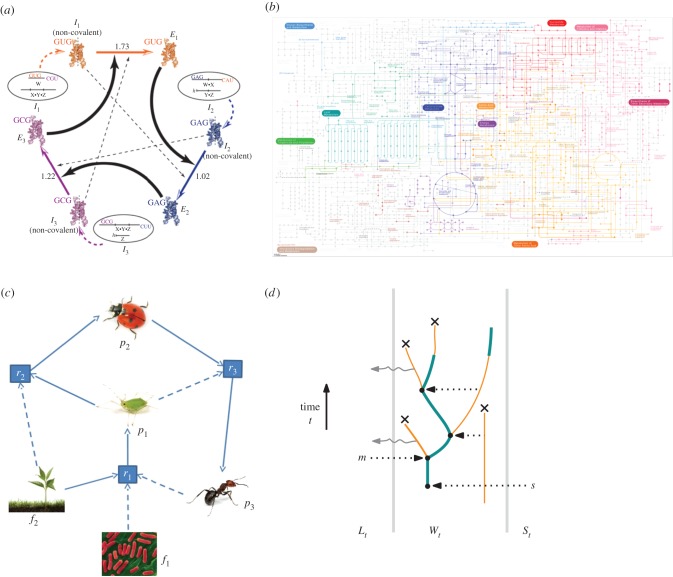
RAFs are not just a theoretical concept, though. They have been constructed in the laboratory with real molecules, either with RNA [24] or with peptides [25], and it has been shown that the metabolic network of E. coli forms a large RAF set [10]. This is illustrated in figure 2, where in [10] cofactors are used as catalysts rather than enzymes. These cofactors are either in the food set or they are produced by the metabolic network.

Figure 2.

RAFs arising across a range of biochemical and biological settings: (a) a catalytic RNA system produced in a laboratory study [24] forms an RAF [11]; (b) the E. coli metabolic network [26] contains a large RAF [10] (metabolic map drawn with iPath [26]); (c) an example of an ecosystem RAF [17]; (d) an RAF proposed in a cognitive model from [18]. (Online version in colour.)

2. The structure of RAFs in ‘elementary’ catalytic reaction systems

Let CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$. We say that $\mathcal{Q}$ is elementary if it satisfies the following condition:

• —Each reaction r in $\mathcal{R}$ has all its reactants in F.

An elementary CRS is a very special type of CRS; however, it has arisen both in applications to real experimental chemical systems [24,25] and in theoretical models [27]. The CRS shown in figure 1 is not an elementary CRS, but it becomes so if reactions r₁, r₂, r₅ are removed (recall here that the food set consists of monomers and dimers). It is possible to extend the definition of elementary CRS to also allow for reversible reactions, by requiring only one side of the reaction to contain molecule types that are exclusively from F.

In this section, we show that elementary RAFs have sufficient structure to allow a very concise classification of their RAFs, closed subRAFs, irrRAFs and ‘uninhibited’ closed RAFs (a notion described below), something which is problematic in general. We then extend this analysis to more complicated types of RAFs in the next section.

Our analysis in this section relies heavily on some key notions from graph theory, so we begin by recalling some concepts from that area.

2.1. Review of graph theoretic terms

In this paper, all graphs will be finite. Given a directed graph $\mathcal{D}=(V,A)$, recall that a strongly connected component of $\mathcal{D}$ is a maximal subset W of V with the property that for any vertices u, v in W, there is a path from u to v and a path from v to u.

It is a classical result that for any directed graph $\mathcal{D}=(V,A)$, the vertex set V can be partitioned into strongly connected components. This, in turn, induces a directed graph structure, called the condensation (digraph) of $\mathcal{D}$, which we will denote by ${\mathcal{D}}^{\ast }$. In this directed graph, the vertex set is the collection of strongly connected components of $\mathcal{D}$ and there is an arc (U, V) in ${\mathcal{D}}^{\ast }$ if there is an arc (u, v) in $\mathcal{D}$ with u ∈ U and v ∈ V. By definition, ${\mathcal{D}}^{\ast }$ is an acyclic directed graph. Moreover, the tasks of partitioning V into strongly connected components and constructing the graph ${\mathcal{D}}^{\ast }$ can both be carried out in polynomial time [28]. Note that the strongly connected component containing v will consist just of v if v is not part of a cycle (i.e. a path that returns to its start) involving another vertex.

We now introduce some further definitions. Given a directed graph $\mathcal{D}=(V,A)$:

• —We say that a strongly connected component S of $\mathcal{D}$ is a core if either |S| = 1 (say S = {r}), and there is an arc from r to itself, or if |S| > 1. Note that $\mathcal{D}$ has a core if and only if $\mathcal{D}$ has a directed cycle.
• —A chordless cycle in a directed graph $\mathcal{D}=(V,A)$ is a subset U of vertices of $\mathcal{D}$ for which the induced graph $\mathcal{D}|U$ is a directed cycle (here $\mathcal{D}|U=(U,A^{\prime })$ where the arc set A′ for $\mathcal{D}|U$ is given by A′ = {(u, v) ∈ A : u, v ∈ U}). Note that if |U| = 1, this means that there is an arc from the vertex in U to itself.
• —A vertex v in V is reachable from some subset S of V if there is a directed path from some vertex in S to v. More generally, a subset U of V is reachable from S if there is some vertex v ∈ U that is reachable from S.

The terminology ‘core’ follows a similar usage by Vasas et al. [3], in which the set of vertices (molecule types) that are reachable from a core is referred to as the ‘periphery’ of the core.

2.2. First main result

The following theorem provides graph-theoretic characterizations of RAFs, irrRAFs, closed RAFs and minimal closed RAFs within any elementary CRS.

Given any CRS, $\mathcal{Q}$, consider the directed graph ${\mathcal{D}}_{\mathcal{Q}}$ with vertex set $\mathcal{R}$ and with an arc (r, r′) if a product of reaction r is a catalyst of reaction r′. In addition, for any reaction r that has a catalyst in F, we add the arc (r, r) (i.e. a loop) into ${\mathcal{D}}_{\mathcal{Q}}$ if this arc is not already present; this step is just a formal strategy to allow the results to be stated more succinctly, and does not necessarily mean that a product of r is an actual catalyst of r.

The proof of the following theorem can be found in the electronic supplementary material.

Theorem 2.1. —

Let $\mathcal{Q}$ be an elementary CRS. Then:

• (i)$\mathcal{Q}$ has an RAF if and only if ${\mathcal{D}}_{\mathcal{Q}}$ has a directed cycle, and this holds if and only if ${\mathcal{D}}_{\mathcal{Q}}$ contains a chordless directed cycle. The RAFs of $\mathcal{Q}$ correspond to the subsets ${\mathcal{R}}^{\prime }$ of $\mathcal{R}$ for which the induced directed graph ${\mathcal{D}}_{\mathcal{Q}}|{\mathcal{R}}^{\prime }$ has the property that each vertex has in-degree at least 1.
• (ii)The irrRAFs of $\mathcal{Q}$ are the chordless cycles in ${\mathcal{D}}_{\mathcal{Q}}$. The closed irrRAFs of $\mathcal{Q}$ are chordless cycles from which no other vertex of ${\mathcal{D}}_{\mathcal{Q}}$ is reachable. The smallest RAFs of $\mathcal{Q}$ are the shortest directed cycles in ${\mathcal{D}}_{\mathcal{Q}}$.
• (iii)The closed RAFs of $\mathcal{Q}$ are the subsets of $\mathcal{R}$ obtained by taking the union of any one or more cores of ${\mathcal{D}}_{\mathcal{Q}}$ and adding in all the reactions in $\mathcal{R}$ that are reachable from this union.
• (iv)Each minimal closed RAF of $\mathcal{Q}$ is obtained by taking any core C of ${\mathcal{D}}_{\mathcal{Q}}$ for which no other core of ${\mathcal{D}}_{\mathcal{Q}}$ is reachable from C, and adding in all reactions in $\mathcal{R}$ that are reachable from C.
• (v)The number of minimal closed RAFs of $\mathcal{Q}$ is at most the number of cores in ${\mathcal{D}}_{\mathcal{Q}}$, and thus it is bounded above by $|\text{maxRAF}(\mathcal{Q})|$. These can all be found and listed in polynomial time in $|\mathcal{Q}|$.
• (vi)The question of whether or not a given RAF for $\mathcal{Q}$ (e.g. the maxRAF) contains a closed RAF as a strict subset can be solved in polynomial time.

Figures 3–5 illustrate parts (i)–(iv) of theorem 2.1. Some of these examples are based on reaction networks that come from actual experimental RAF sets.

Figure 4.

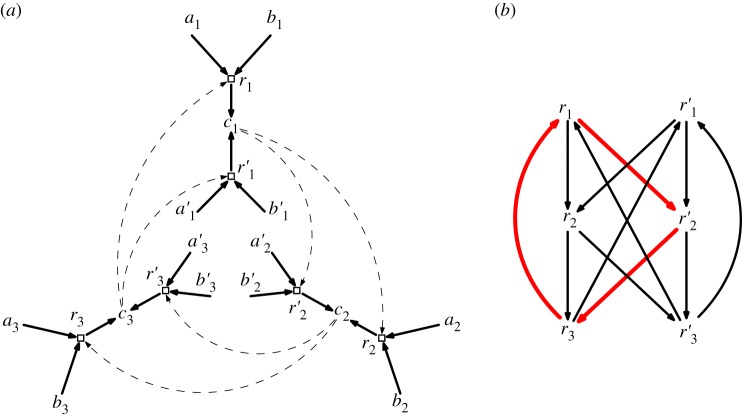
(a) An elementary CRS (with food set F equal to the 12 elements labelled a_i, a_i′, b_i, b_i′ for i = 1, 2, 3) that has eight irrRAFs, each of which has size 3 (this example can be extended to produce an elementary CRS with 2n reactions and 2ⁿ irrRAFs [22]). These irrRAFs correspond to the eight chordless cycles in the graph ${\mathcal{D}}_{\mathcal{Q}}$ shown in (b), with one of these chordless cycles indicated by the three bold arcs. None of these irrRAFs is closed. There are 27 RAFs for $\mathcal{Q}$ in total. (Online version in colour.)

Figure 3.

The directed graph ${\mathcal{D}}_{\mathcal{Q}}$ for an elementary CRS $\mathcal{Q}$ (adapted from an experimental system of [25]) that has three strongly connected components (S₁, S₂, S₃), of which S₁ and S₂ are cores. The associated (acyclic) condensation digraph ${\mathcal{D}}_{\mathcal{Q}}^{\ast }$ is shown on the right. The unique minimal closed RAF is $S_2\cup S_3$; the other closed RAF is the full set itself, namely $S_1\cup S_2\cup S_3$. The reaction subsets S₁, S₂, $S_1\cup S_2$ and $S_1\cup S_3$ are all RAFs but not closed RAFs. A computer-based search finds 305 RAFs altogether. There are six chordless cycles in this CRS, which correspond to the six irrRAFs: {r₂}, {r₅}, {r₈}, {r₁, r₄}, {r₄, r₇} and {r₃, r₇}. Note that this representation of the CRS is in terms of the molecules produced by reactions that have reactants in the food set. However, each reaction produces a single (and unique) product so we can identify the product with the reaction in this example. (Online version in colour.)

Figure 5.

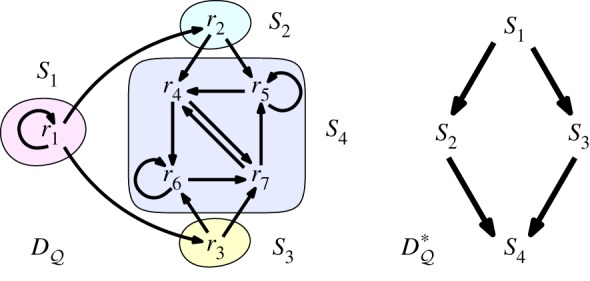
The directed graph ${\mathcal{D}}_{\mathcal{Q}}$ for an elementary CRS (from an experimental system of [24] analysed in [11]), shown on the left, has 67 RAFs and two closed RAFs (the whole set and {r₄, r₅, r₆, r₇}). The strongly connected components of ${\mathcal{D}}_{\mathcal{Q}}$ are {r₁}, {r₂}, {r₃} and {r₄, r₅, r₆, r₇}, two of which are cores (namely, {r₁} and {r₄, r₅, r₆, r₇}). The associated condensation digraph ${\mathcal{D}}_{\mathcal{Q}}^{\ast }$ is shown on the right. For this RAF, there are four irrRAFs, namely {r₁}, {r₅}, {r₆} and {r₄, r₇}. (Online version in colour.)

Remarks —

• —Parts (ii)–(vi) of theorem 2.1 hold even when $\mathcal{Q}$ is not elementary, provided that ${\mathcal{Q}}^{\prime }=(X,{\mathcal{R}}^{\prime },C,F)$ is elementary where ${\mathcal{R}}^{\prime }$ is the maxRAF of $\mathcal{Q}$.
• —Cores cannot share reactions, but it is possible for minimal closed RAFs to do so.
• —The last sentence of part (ii) implies that the size of the smallest RAF is equal to the length of the shortest directed cycle in ${\mathcal{D}}_{\mathcal{Q}}$ and this can be found in polynomial time in $|\mathcal{Q}|$ (by a depth-first-search or network flow techniques). This is in contrast to the problem of finding the size of a smallest RAF in a general CRS, which has been shown to be NP-hard in [21].
• —An important extension of the RAF concept allows for molecule types to inhibit reactions (as well as being able to catalyse reactions). Here we consider the conservative extension of the RAF concept whereby each reaction in the system must be catalysed and, in addition, no reaction in the RAF is inhibited (i.e. inhibition of a reaction is considered a strong property that cannot be remedied by having other catalysts present). For a general CRS $\mathcal{Q}$, it is known that determining whether or not a CRS $\mathcal{Q}$ has an RAF ${\mathcal{R}}^{\prime }$ for which no reaction is inhibited by any molecule produced by ${\mathcal{R}}^{\prime }$ is NP-hard [23]. However, for any elementary CRS, theorem 2.1(v) provides the following positive result.

Corollary 2.2. —

When inhibition is also allowed in an elementary CRS $\mathcal{Q}$, it is possible to determine in polynomial time whether $\mathcal{Q}$ contains a closed RAF ${\mathcal{R}}^{\prime }$ for which no reaction of ${\mathcal{R}}^{\prime }$ is inhibited by any molecule type produced by ${\mathcal{R}}^{\prime }$.

Proof. —

There is a closed RAF for $\mathcal{Q}$ that has no inhibition if and only if there is a minimal closed RAF for $\mathcal{Q}$ that has no inhibition. By part (v) of theorem 2.1, there are at most $|\text{maxRAF}(\mathcal{Q})|$ minimal closed RAFs for an elementary CRS $\mathcal{Q}$, and these can all be checked in polynomial time to determine if any of them have the property that no reaction is inhibited by any molecule type produced by the reactions in the set.  ▪

• —Part (v) of theorem 2.1 raises the question of whether this result might apply without the restriction that $\mathcal{Q}$ is elementary. In other words, is the number of minimal closed RAFs in a (general, non-elementary) CRS bounded polynomially in the size of $\mathcal{Q}$? The answer turns out to be ‘no’, and an example is described in the electronic supplementary material.
• —Another question that part (v) of theorem 2.1 suggests is the following: does an elementary CRS always have at most a polynomial number of closed RAFs? Again, the answer is ‘no’, and the construction to show this is much simpler than the previous example. Consider the elementary CRS with F = {f₁, …, f_n}, $X=F\cup \{x_1,\dots ,x_n\},$ together with the set $\mathcal{R}$ of k catalysed reactions $r_i\hspace{0.17em}:\hspace{0.17em}{f}_i\stackrel{x_i}{⟶}{x}_i$ for i = 1, …, k. This CRS has 2^k − 1 closed RAFs, one for each non-empty subset of $\mathcal{R}$.

2.3. The probability of an RAF in an elementary CRS

Given an elementary CRS $\mathcal{Q}$, suppose that catalysis is assigned randomly as follows: each molecule type catalyses each given reaction in $\mathcal{R}$ with a fixed probability p, independently across all pairs (x, r) of molecule type x and reaction r. The probability $p_{\mathcal{Q}}$ that $\mathcal{Q}$ has an RAF is simply the probability that ${\mathcal{D}}_{\mathcal{Q}}$ has a directed cycle (by theorem 2.1(i)).

In the case where each reaction in $\mathcal{R}$ has just a single product, then the asymptotic behaviour of $p_{\mathcal{Q}}$ as $|\mathcal{R}|\to \mathrm{\infty }$ is equivalent to the emergence of a directed cycle in a large random directed graph, which has been previously studied in the random graph literature by Bollobas & Rasmussen [29].

Here we provide a simple lower bound on $p_{\mathcal{Q}}$. Let $\lambda =p|\mathcal{R}|$ be the expected number of reactions that each molecule type catalyses. The following result gives a lower bound on $p_{\mathcal{Q}}$ that depends only on λ and which converges towards 1 as λ grows (the proof is in the electronic supplementary material).

Proposition 2.3. —

$p_{\mathcal{Q}}\ge 1-{(1-\lambda /|\mathcal{R}|)}^{|\mathcal{R}|}\sim 1-{\text{e}}^{-\lambda }$, where ∼ denotes asymptotic equality as $|\mathcal{R}|$ grows.

The value p required for RAFs to arise in an elementary CRS is lower than the corresponding value of p required for RAFs to emerge in polymer models [1]. This is because, in the former setting, an RAF requires only a subset of reactions that forms a directed catalytic cycle, since the F-generated property ‘comes for free’ in an elementary system; however, F-generation is an additional constraint that has to be simultaneously satisfied in the polymer setting. Moreover, the sizes of RAFs when they first emerge in an elementary CRS with random catalysis are quite different from that in the polymer setting. In the former case, small RAFs (consisting of just a few reactions) are likely to be present (from theorem 11 of [29]), whereas in the binary polymer small RAFs are provably absent at catalysis rates at which RAFs first form (by theorem 4 of [21]).

2.4. Eigenvector analysis

A previous study by Jain & Krishna [27] considered the dynamical aspects of an ‘autocatalytic set’ in a CRS, which is closely related to the notion of an RAF (our graph ${\mathcal{D}}_{\mathcal{Q}}$ differs from theirs in two respects: firstly the vertices here represent reactions rather than molecule types, and we also permit self-loops from a reaction to itself). We now present the analogues of these earlier dynamical findings in our setting (and formally, with proofs).

Given an elementary CRS $\mathcal{Q}$, let $A_{\mathcal{Q}}$ denote the adjacency matrix of the directed graph ${\mathcal{D}}_{\mathcal{Q}}$. Thus, the rows and columns of $A_{\mathcal{Q}}$ are indexed by the reactions in $\mathcal{R}$ in some given order, and the entry of A_Q corresponding to the pair (r, r′) is 1 precisely if (r, r′) is an arc of ${\mathcal{D}}_{\mathcal{Q}}$ and is zero otherwise. By Perron–Frobenius theory for non-negative matrices, A_Q has a non-negative real eigenvalue λ of maximal modulus (among all the eigenvalues) and if ${\mathcal{D}}_{\mathcal{Q}}$ is strongly connected (i.e. A_Q is irreducible), then A_Q has a left (and a right) eigenvector with eigenvalue λ whose components are all positive.

The following results are analogues of the former study by Jain & Krishna [27] to our setting (the proof is in the electronic supplementary material).

Proposition 2.4. —

• (i)If $\mathcal{Q}$ contains no RAF, then λ = 0.
• (ii)If $\mathcal{Q}$ contains an RAF, then λ ≥ 1.
• (iii)If A_Q has an eigenvalue > 0 with an associated left eigenvector w, then the set of reactions r for which w_r > 0 forms an RAF for $\mathcal{Q}$.

To illustrate an application of proposition 2.4, consider the system of nine reactions from figure 3 which comes from an experimental system [25]. In this case, λ ≥ 1 since the system contains an RAF (cf. proposition 2.4(ii)). Regarding part (iii), three of the eigenvalues of ${\mathcal{A}}_{\mathcal{Q}}$ are strictly positive, and for the three corresponding left eigenvectors, one has strictly positive entries for the three reactions r₂, r₆, r₈, which form the subRAF S₁ shown in figure 3. A second left eigenvector has strictly positive entries for the reactions r₁, r₃, r₄, r₅, r₇, r₉, and these form the minimal closed subRAF $S_2\cup S_3$ shown in figure 3. The third left eigenvector has strictly positive entries for the reactions r₁, r₄, r₇ which forms a subRAF of S₂.

3. Generative RAFs

We now introduce a new notion which describes how simple RAFs can develop into more complex ones in a progressive way. This section will build on, and apply the results concerning elementary CRSs, particularly theorem 2.1.

Given a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$ and a subset Y of X containing F, let $\mathcal{R}|Y$ be the subset of reactions in $\mathcal{R}$ that have all their reactants in Y, and let

$$\mathcal{Q}|Y:=(X,\mathcal{R}|Y,C,Y).$$

In other words, $\mathcal{Q}|Y$ is the CRS obtained from $\mathcal{Q}$ by deleting each reaction from $\mathcal{R}$ that does not have all its reactants in Y, and by expanding the food set to include all of Y.

Definition 3.1 (genRAFs). —

Given a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$, we say that an RAF ${\mathcal{R}}^{\prime }$ for $\mathcal{Q}$ is a genRAF (or generative RAF) if there is a sequence ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_k$ of subsets of $\mathcal{R}$ with ${\mathcal{R}}_k={\mathcal{R}}^{\prime }$ and that satisfy the following properties:

• (i)${\mathcal{R}}_1$ is the closure in $\mathcal{Q}$ of an RAF of $\mathcal{Q}|F$;
• (ii)for each i > 1, ${\mathcal{R}}_i$ is the closure in $\mathcal{Q}$ of an RAF of $\mathcal{Q}|Y_i$ where $Y_i=F\cup \pi ({\mathcal{R}}_{i-1})$, and where $\pi ({\mathcal{R}}_{i-1})$ refers to all molecule types that are produced by a reaction from ${\mathcal{R}}_{i-1}$.

Thus, a genRAF is any RAF for $\mathcal{Q}$ that can be formed by taking ${\mathcal{R}}_1$ to be the closure (within $\mathcal{Q}$) of an RAF within the elementary CRS $\mathcal{Q}|F$, and for each i > 1, adding the products of ${\mathcal{R}}_{i-1}$ to the food set F of $\mathcal{Q}$ and taking ${\mathcal{R}}_i$ to be the closure (within $\mathcal{Q}$) of the resulting (induced) elementary CRS. In other words, the next closed RAF in the sequence is built upon an enlarged food set generated by the previous closed RAFs in the sequence and considering just those reactions that use this enlarged food set as reactants, and then forming the closure of this set in $\mathcal{Q}$.

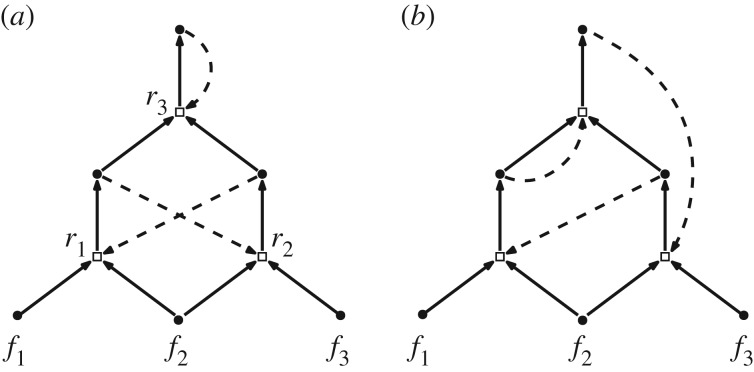
As an example, the CRS in figure 6a is itself a genRAF as it has the generating sequence ${\mathcal{R}}_1,{\mathcal{R}}_2$ where ${\mathcal{R}}_1=\{r_1,r_2\}$ and ${\mathcal{R}}_2=\{r_1,r_2,r_3\}$. This genRAF is not a CAF as r₁ or r₂ need to occur uncatalysed once for the RAF to form. The CRS in figure 6b has the same molecules and reactions as figure 6a, but a different pattern of catalysis, making it an RAF but not a genRAF.

Figure 6.

(a) This CRS is a genRAF (a generating sequence starts with the elementary closed RAF {r₁, r₂}, and then adds r₃). (b) A different pattern of catalysis converts the three reactions into an RAF that is no longer a genRAF. In both cases, the food set is F = {f₁, f₂, f₃}.

The motivation for considering the notion of genRAFs is twofold. Firstly, a genRAF can be built up from simpler RAFs (starting with an elementary one) by generating the required catalysts at each step (i.e. some reactions may still need to proceed initially uncatalysed, but a catalyst for the reaction will be generated by some other reaction by the end of the same step). This avoids the possibility of long chains of reactions that need to proceed uncatalysed until a catalyst for the very first link in the chain is produced, which seems biochemically less plausible. A second motivation for considering genRAFs is that they combine two further desirable properties: namely an emphasis on RAFs that are closed (i.e. all reactions that are able to proceed and for which a catalyst is available will proceed), and genRAFs are sufficiently well-structured that some questions can be answered in polynomial time that are problematic for general RAFs (theorem 3.3(iv) provides an explicit example).

We will call the sequence ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_k$ in the above definition a generating sequence for ${\mathcal{R}}^{\prime }$. We now make two observations, that are proved in the following lemma (the proof is provided in the electronic supplementary material).

Lemma 3.2. —

Suppose that a genRAF ${\mathcal{R}}^{\prime }$ has generating sequence ${\mathcal{R}}_1,{\mathcal{R}}_2,\dots ,{\mathcal{R}}_k$. Then:

• (i)${\mathcal{R}}^{\prime }$ and each set in its generating sequence is a closed RAF for $\mathcal{Q}$.
• (ii)${\mathcal{R}}_i\subseteq {\mathcal{R}}_{i+1}$ for all i ∈ {1, …, k − 1}.

A natural question in the light of lemma 3.2(i) is the following: Is every closed RAF in a CRS generative? The answer to this is ‘no’ in general; for example, a CRS may have a maxRAF that requires too much ‘jumping ahead’ with catalysis (chains of initially spontaneous reactions) to be built up in this way, as in figure 6b. Shortly (theorem 3.3), we will provide a precise, and efficiently checkable, characterization for when a closed RAF is a genRAF.

Another instructive example is the following maxRAF that arose in a study of the binary polymer model from [19]:

$$\begin{array}{rl}{r}_1& \hspace{0.17em}:\hspace{0.17em}10+0\stackrel{01100}{⟶}100,\\ r_2& \hspace{0.17em}:\hspace{0.17em}01+100\stackrel{0}{⟶}01100,\\ r_3& \hspace{0.17em}:\hspace{0.17em}10+1\stackrel{0}{⟶}101,\\ r_4& \hspace{0.17em}:\hspace{0.17em}11+10\stackrel{101}{⟶}1110\\ \mathrm{and}{r}_5& \hspace{0.17em}:\hspace{0.17em}1110+0\stackrel{101}{⟶}11100,\end{array}$$

where F = {0, 1, 00, 01, 10, 11}. This maxRAF contains six subRAFs, two of which are closed, namely, the full set of all five reactions, which is not generative, and the subset {r₃, r₄, r₅}, which is a genRAF.

A maximal generative RAF: Given a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$, consider the following sequence $({\overline{\mathcal{R}}}_i,i\ge 1)$ of subsets of $\mathcal{R}$. Let ${\mathcal{Q}}_1:=\mathcal{Q}|F$, let ${\mathcal{R}}_i=\text{maxRAF}({\mathcal{Q}}_1)$ and let ${\overline{\mathcal{R}}}_1$ be the closure of ${\mathcal{R}}_1$ in $\mathcal{Q}$. For i > 1, let

$${\mathcal{R}}_i=\text{maxRAF}({\mathcal{Q}}_i),\text{ where }{\mathcal{Q}}_i:=F\cup \pi ({\overline{\mathcal{R}}}_{i-1}),$$

and let ${\overline{\mathcal{R}}}_i$ be the closure of ${\mathcal{R}}_i$ in $\mathcal{Q}$.

Note that ${\mathcal{R}}_1$ may be empty even if $\mathcal{Q}$ has an RAF (as figure 6b shows), in which case, ${\overline{\mathcal{R}}}_i=\mathrm{\varnothing }$ for all i ≥ 1. However, if ${\mathcal{R}}_1$ is non-empty, then ${\overline{\mathcal{R}}}_i$ forms an increasing nested sequence of closed RAFs for $\mathcal{Q}$ and so the sequence stabilizes at some subset of reactions that we denote by $\overline{\mathcal{R}}(\mathcal{Q})$. Thus, $\overline{\mathcal{R}}(\mathcal{Q})={\bigcup }_{i\ge 1}{\overline{\mathcal{R}}}_i$, and this set is identical to ${\overline{\mathcal{R}}}_k$ for some sufficiently large value of k (with $k\le |\mathcal{R}|$).

We can now state the main result of this section. Its proof is provided in the electronic supplementary material.

Theorem 3.3. —

Suppose that $\mathcal{Q}=(X,\mathcal{R},C,F)$ is a CRS.

• (i)$\mathcal{Q}$ contains a genRAF if and only if ${\mathcal{R}}_1\ne \mathrm{\varnothing }$, in which case $\overline{\mathcal{R}}(\mathcal{Q})$ is a genRAF for $\mathcal{Q}$ that contains all other genRAFs for $\mathcal{Q}$.
• (ii)If ${\mathcal{R}}^{\prime }$ is a closed RAF for $\mathcal{Q}$ then ${\mathcal{R}}^{\prime }$ is a genRAF for $\mathcal{Q}$ if and only if ${\mathcal{R}}^{\prime }=\overline{\mathcal{R}}({\mathcal{Q}}^{\prime })$, where ${\mathcal{Q}}^{\prime }=(X,{\mathcal{R}}^{\prime },C,F)$.
• (iii)The construction of $\overline{\mathcal{R}}(\mathcal{Q})$ and determining whether an arbitrary closed RAF ${\mathcal{R}}^{\prime }$ for $\mathcal{Q}$ is generative can be determined in polynomial time in $|\mathcal{Q}|$.
• (iv)Determining whether a given closed genRAF ${\mathcal{R}}^{\prime }$ contains a strict subset that is a closed RAF for $\mathcal{Q}$ can be solved in polynomial time in $|\mathcal{Q}|$.

Remarks —

• —If a CRS has a CAF (defined at the end of the Introduction), then the (unique) maximal CAF is generative. However, a genRAF need not necessarily correspond to a maximal CAF.
• —Part (iv) of theorem 3.3 provides an interesting contrast to the general RAF setting. There the question of determining whether a closed RAF (e.g. the maxRAF) in an arbitrary CRS contains another closed RAF as a strict subset has unknown complexity.

4. RAFs with reaction rates

In this section, we consider a further refinement of RAF theory, by explicitly incorporating reaction rates into the analysis. This can allow for future more realistic uses of the RAF theory in biological contexts, particularly in biochemistry, with the introduction of kinetic constants in the network representation. Although it remains a challenge to obtain kinetic data at a genome scale for real cells, advances have been achieved with E. coli [30,31] and erythrocyte models [32] and others are expected to emerge as new methodologies will convert thermodynamic and metabolomic data to kinetic constants [33]. The advantage of RAF theory here is that it can be applied to networks of any size, as long as a CRS can be drawn for the network [10].

Moreover, this conveniently addresses one shortcoming implicit in the generative RAF definition from the last section—namely a generative RAF necessarily grows as a monotonically increasing nested system with the length of its associative generating sequence (lemma 3.2). However, once a sufficiently large generative RAF is established, one or more of its subRAFs may then become dynamically favoured if it is more ‘efficient’ (i.e. all its reactions proceed at higher reaction rates than the generative RAF it lies within), as we shortly illustrate with a simple example.

Suppose that we have a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$ and a function $f\hspace{0.17em}:\hspace{0.17em}C\to {\mathbb{R}}^{\ge 0}$ that assigns a non-negative real number to each pair (x, r) ∈ C. The interpretation here is that f(x, r) describes the rate at which reaction r proceeds when the catalyst x is present.

Given $\mathcal{Q}$ and f, together with an RAF ${\mathcal{R}}^{\prime }$ for $\mathcal{Q}$, let:

$$\phi ({\mathcal{R}}^{\prime })=\underset{r\in {\mathcal{R}}^{\prime }}{min}\{max\{f(x,r)\hspace{0.17em}:\hspace{0.17em}(x,r)\in C,x\in {\text{cl}}_{{\mathcal{R}}^{\prime }}(F)\}\}.$$

In other words, $\phi ({\mathcal{R}}^{\prime })$ is the rate of the slowest reaction in the RAF ${\mathcal{R}}^{\prime }$ under the most optimal choice of catalyst for each reaction in ${\mathcal{R}}^{\prime }$ among those catalysts that are present in ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$.

Example. —

Figure 7 provides an example to illustrate the notions above. In this CRS, the three reactions comprise an RAF, with a φ-value equal to 1. However there are three subRAFs, and one of these (namely {r₂, r₃}) has a higher φ-value. However, the less optimal closed subRAF {r₁, r₂} is generative and likely to have formed before the optimal one; otherwise {r₂,r₃} would require a chain of two reactions to occur uncatalysed (r₂ followed by r₃) before the catalysts for them become available. The closed RAF {r₁, r₂} may then expand to {r₁, r₂, r₃} before this second closed RAF is subsequently out-competed by its subRAF {r₂, r₃}, since the catalysed reactions in this subRAF run twice as fast as the reaction r₁.

Figure 7.

(a) An RAF in which the catalysis arcs have associated rates (namely, the values 1 and 2 as indicated). The poset consisting of the maxRAF and its three subRAFs (partially ordered by set inclusion) is shown by the Hasse diagram in (b). All four RAFs have φ-values of 1 except for the subRAF {r₂, r₃}, which has a φ-value of 2. This optimal RAF {r₂, r₃} is not a generative RAF (whereas the other three RAFs are generative; indeed, {r₁} and {r₁, r₂} are elementary). Nevertheless, once the generative maxRAF {r₁, r₂, r₃} has formed, {r₂, r₃} can then emerge as the dominant subRAF.

Our main result in this section shows that finding an RAF to maximize φ can be achieved by an algorithm that runs in polynomial time in the size of $\mathcal{Q}$. Its proof is provided in the electronic supplementary material.

Theorem 4.1. —

There is a polynomial-time algorithm to construct an RAF with largest possible φ-value from any CRS $\mathcal{Q}$ that contains RAF. Moreover, this constructed RAF is the maximal RAF with this φ-value.

Remark. —

For the example in figure 7, we have the subRAFs ${\mathcal{R}}_1=\{r_1\},{\mathcal{R}}_2=\{r_2,r_3\}$ with $\phi ({\mathcal{R}}_1)<\phi ({\mathcal{R}}_2)$. In this case, there is a path in the poset from ${\mathcal{R}}_1$ to ${\mathcal{R}}_2$ on which φ is non-decreasing (this path goes ‘up’ then ‘down’ in figure 7b). An interesting question might be to determine when this holds: in other words, from a sub-optimal RAF, can a more optimal RAF be reached by a chain of RAFs that, at each stage, either adds certain reactions or deletes one or more reactions, and so that the optimality score (as measured by φ) does not decrease?

4.1. Rates for ‘catalytic ensembles’

We can extend the results on rates in the previous section to accommodate the following feature: a reaction for which a combination of two or more molecules can act collectively as a catalyst, and possibly at a different rate from that of an alternative single catalyst. An example relevant to early metabolism would be primitive catalysts that combine metals and other inorganic cofactors, as opposed to an evolved enzyme.

We formalize this as follows. Recall that in a CRS $\mathcal{Q}=(X,\mathcal{R},C,F)$, the set C represents the pattern of catalysis and is a subset of $X\times \mathcal{R}$. Thus, (x, r) ∈ C means that x catalyses reaction r. Now suppose we wish to allow a combination (ensemble) of one or more molecules to act as a catalyst for a reaction. In this case, we can represent the CRS as a quadruple $\mathcal{Q}=(X,\mathcal{R},\mathcal{C},F)$ where $\mathcal{C}\subseteq (2^X-\mathrm{\varnothing })\times \mathcal{R}$ and where $(A,r)\in \mathcal{C}$ means that the ensemble of molecules in A acts as a (collective) catalyst for r, provided they are all present. We refer to $\mathcal{Q}$ as a generalized CRS. The notions of RAF, subRAF, CAF and so on can be generalized naturally. For example, the RA condition for a subset ${\mathcal{R}}^{\prime }$ is that for each reaction r, there is a pair $(A,r)\in \mathcal{C}$ where each of the molecule types in A is in the closure of F relative to ${\mathcal{R}}^{\prime }$.

Note that an ordinary CRS can be viewed as a special case of a generalized CRS by identifying (x, r) with the pair ({x}, r). Note also that each reaction may have several ensembles of possible catalysts, and some (or all of these) may be just single molecule types.

Given a generalized CRS $\mathcal{Q}=(X,\mathcal{R},\mathcal{C},F)$, we can associate an ordinary CRS ${\mathcal{Q}}^{\prime }=(X^{\prime },{\mathcal{R}}^{\prime },C^{\prime },F)$ to $\mathcal{Q}$ as follows. Let

$${\mathcal{A}}_{\mathcal{C}}:=\{A\subseteq 2^X-\mathrm{\varnothing }\hspace{0.17em}:\hspace{0.17em}\mathrm{\exists }r\in \mathcal{R}\hspace{0.17em}:\hspace{0.17em}(A,r)\in \mathcal{C}\}\hspace{0.17em}$$

(so ${\mathcal{A}}_{\mathcal{C}}$ is the collection of catalyst ensembles in $\mathcal{Q}$). For each $A\in {\mathcal{A}}_C$, let x_A be a new molecule type, and let r_A be the (formal) reaction A → x_A. Now let

$$\begin{array}{rl}{X}^{\prime }& :=X\hspace{0.17em}\dot{\cup }\hspace{0.17em}\{x_A\hspace{0.17em}:\hspace{0.17em}A\in {\mathcal{A}}_{\mathcal{C}}\},\\ {\mathcal{R}}^{\prime }& :=\mathcal{R}\hspace{0.17em}\dot{\cup }\hspace{0.17em}\{r_A\hspace{0.17em}:\hspace{0.17em}A\in {\mathcal{A}}_{\mathcal{C}}\}\\ \mathrm{and}{C}^{\prime }& :=\{(x_A,r)\hspace{0.17em}:\hspace{0.17em}(A,r)\in \mathcal{C}\}\hspace{0.17em}\dot{\cup }\hspace{0.17em}\{(x_A,r_A)\hspace{0.17em}:\hspace{0.17em}A\in {\mathcal{A}}_C\}.\end{array}$$

Note that $C^{\prime }\subseteq X^{\prime }\times {\mathcal{R}}^{\prime }$.

In other words, ${\mathcal{Q}}^{\prime }$ is obtained from $\mathcal{Q}$ by replacing each catalytic ensemble A by a new molecule type x_A and adding in the reaction r_A : A → x_A catalysed by x_A. The proof of the following lemma is straightforward.

Lemma 4.2. —

A generalized CRS $\mathcal{Q}$ has an RAF if and only if the associated ordinary CRS ${\mathcal{Q}}^{\prime }$ has an RAF that contains at least one reaction from $\mathcal{R}$. Moreover, in this case, the RAFs of $\mathcal{Q}$ correspond to the non-empty intersections of RAFs of ${\mathcal{Q}}^{\prime }$ with $\mathcal{R}$.

Now suppose that we have a generalized CRS $\mathcal{Q}=(X,\mathcal{R},\mathcal{C},F)$ and a function $f\hspace{0.17em}:\hspace{0.17em}\mathcal{C}\to {\mathbb{R}}^{\ge 0}$. The interpretation here is that f(A, r) describes the rate at which reaction r proceeds when the catalyst ensemble A is present.

Given an RAF ${\mathcal{R}}^{\prime }$ for $\mathcal{Q}$, let:

$$\phi ({\mathcal{R}}^{\prime }):=\underset{r\in {\mathcal{R}}^{\prime }}{min}\{max\{f(A,r)\hspace{0.17em}:\hspace{0.17em}(A,r)\in \mathcal{C},A\subseteq {\text{cl}}_{{\mathcal{R}}^{\prime }}(F)\}\}.$$

In other words, $\phi ({\mathcal{R}}^{\prime })$ is the rate of the slowest reaction in the RAF ${\mathcal{R}}^{\prime }$ under the most optimal choice of catalyst ensemble for each reaction in ${\mathcal{R}}^{\prime }$ among catalyst ensembles that are subsets of ${\text{cl}}_{{\mathcal{R}}^{\prime }}(F)$.

Lemma 4.2 now provides the following corollary of theorem 4.1.

Corollary 4.3. —

There is a polynomial-time algorithm to construct an RAF for $\mathcal{Q}$ with largest possible φ-value from any CRS $\mathcal{Q}$ that contains an RAF. Moreover, this constructed RAF is the maximal RAF for $\mathcal{Q}$ with this φ-value.

5. Concluding comments

In this paper, we have considered special types of RAFs that allow for exact yet tractable mathematical and algorithmic analysis, and which also incorporate additional biochemical realism (restricting the depth of uncatalysed reactions chains in generative RAFs and allowing reaction rates).

We first considered the special setting of ‘elementary’ systems in which all reactions (or at least those present in the maxRAF) have all their reactants present in the food set. This allows for the structure of the collection of RAFs, irrRAFs and closed subRAFs to be explicitly described graph-theoretically. As a result, some problems that are computationally intractable in the general CRS setting turn out to be polynomial time for an elementary CRS. For example, one can efficiently find the smallest RAFs in an elementary CRS, which is an NP-hard problem in general [21]. Also, the number of minimal closed subRAF in an elementary CRS is linear in the size of the set of reactions (for a general CRS, they can be exponential in number). For future work, it may be of interest to determine if there are polynomial-time algorithms that can answer the following questions for an elementary CRS: (i) What is the size of the largest irrRAF? (ii) If inhibition is allowed, then is there an RAF that has no inhibition?

The relevance of elementary RAFs to biology is that two experimental laboratory systems for modelling biochemistry at the origin of life (one based on peptides [25], the other on RNA [24]) turn out to be elementary CRSs, and our results allow for a fast, systematic and complete combinatorial analysis of the RAFs and subRAFs within these systems. This methodology should, in turn, be applicable to more complex systems in future studies, either for elementary systems or for generative RAFs within a non-elementary system. The biological relevance of RAF theory is further supported by its recent applications to E. coli metabolism [10], and to the structure of ecological networks [16,17].

The concept of an ‘elementary’ CRS is an all-or-nothing notion. One way to extend the results above could be to define the notion of ‘level’, whereby a CRS has level k if the length of the longest path from the food set to any reaction product goes through at most k reactions (an elementary CRS thus has level 1). We have not explored this further here but instead, we consider the related alternative notion of a generative RAF. Briefly, a generative RAF allows an RAF to form by effectively enlarging its ‘food set’ with products of reactions, so that each step only requires catalysts that are either present or produced by reactions in the RAF at that stage. Although generative RAFs are more complex than elementary ones, their close connection to elementary RAFs (in a stratified way) allows for a more tractable analysis than for general RAFs. Moreover, unlike elementary RAFs, no special assumption is required on the underlying CRS; generative RAFs are just a special type of RAF that can be generated in a certain sequential fashion in any CRS.

In the final section, we considered the impact of rates of RAFs (which need not be generative), and particularly the algorithmic question of finding an RAF that maximizes the rates of its slowest reaction. Not only is this problem solvable in the size of the CRS, but it can also be extended to the slightly more general setting of allowing ‘catalytic ensembles’. The introduction of rates allows for the study of how a population of different closed subRAFs might evolve over time, in which primitive subRAFs are replaced (out-competed) by efficient ones that rely on new catalysts in place of more primitive ones. We hope to explore these extensions further in future work.

Data accessibility

This article has no additional data.

Authors' contributions

All three authors contributed to the conceptual design and writing of the paper. The mathematical statement of theorems and their proofs was handled by M.S.

Competing interests

We declare we have no competing interests.

Funding

J.C.X. thanks the European Research Council (grant no. 666053 to William F. Martin) for financial support. W.H. thanks the Institute for Advanced Study, Amsterdam, for financial support in the form of a fellowship.