Going with the flow: hydrodynamic cues trigger directed escapes from a stalking predator

Abstract

In the coevolution of predator and prey, different and less well-understood rules for threat assessment apply to freely suspended organisms than to substrate-dwelling ones. Particularly vulnerable are small prey carried with the bulk movement of a surrounding fluid and thus deprived of sensory information within the bow waves of approaching predators. Some planktonic prey have solved this apparent problem, however. We quantified cues generated by the slow approach of larval clownfish (Amphiprion ocellaris) that triggered a calanoid copepod (Bestiolina similis) to escape before the fish could strike. To estimate water deformation around the copepod immediately preceding its jump, we represented the body of the fish as a rigid sphere in a hydrodynamic model that we parametrized with measurements of fish size, approach speed and distance to the copepod. Copepods of various developmental stages (CII–CVI) were sensitive to the water flow caused by the live predator, at deformation rates as low as 0.04 s⁻¹. This rate is far lower than that predicted from experiments that used artificial predator-mimics. Additionally, copepods localized the source, with 87% of escapes directed away (greater than or equal to 90°) from the predator. Thus, copepods' survival in life-threatening situations relied on their detection of small nonlinear signals within an environment of locally linear deformation.

1. Introduction

The coevolution of predators and prey has produced a series of exquisite and escalating adaptations [1]. For prey, the ability to rapidly detect and evade a predator is the evolutionary result of sensitive directional detectors keyed to predatory cues, minimized response latencies and rapid specialized motor responses [2–6]. Predatory detection and evasion have been characterized among prey that inhabit terrestrial, benthic and demersal habitats that provide refuge and stable reference frames [7–9]. However, it remains unclear which principles from these systems apply to the ocean's pelagic realm, the largest habitat on the Earth, where the unique physics of the environment imposes particular constraints on predators and prey. Here, we have combined hydrodynamic models with experimental observations of planktonic interactions to elucidate both the physical conditions and the biological adaptations that allow freely suspended prey to detect stealthy predators.

Prey depend on various sensory modalities to detect and escape from would-be predators. Photoreception, mechanoreception (near-field and far-field) and chemoreception all mediate different aspects of predator detection, either pre- or post-encounter [10]. When photoreceptive capabilities (e.g. vision) are limited, a prey typically depends on its mechanosensory system to detect imminent predatory threats. Slight changes in air or water flow induced by the ‘bow wave’ of an approaching predator can be detected through the movement of the medium past receptors on the body of the organism. Examples include the cercal system of insects [11,12], the lateral line system of fishes [13,14] and the setae of crustaceans [15,16]. The best-studied cases are animals that live on or near a substrate, with a fixed frame of reference with respect to an approaching predator, as with crickets that escape from running spiders [17,18]. These substrate-dwelling animals can detect bulk flow past their bodies aligned with the direction of approach, with stronger stimulation of receptors occurring as the predator gets closer. From this, organisms obtain information on the direction of the attacker and the immediacy of the danger.

A neutrally buoyant, free-swimming and small organism perceives a different world, as it is embedded in the bulk flow of the surrounding fluid. This has three profound effects on sensory detection. First, being carried in bulk flow reduces the flow past the sensors on the prey's body, in turn, reducing the magnitude of the mechanosensory cues available to the organism. Second, from the perspective of a small prey (less than or equal to 3 mm), the surrounding water deforms with an approximately linear flow field [19], hereafter referred to as ‘primary flow’. In this, the water along the axis of the approach of a predator flows inward toward the prey from both sides, compressing along that axis, and flows outward, expanding along perpendicular axes. The deformation produced is nearly symmetric about the prey's body such that the deformation on one side of the prey is perceived as a mirror reflection of that on the other side. This deprives the prey of the directional information that is available to substrate-dwelling organisms. A directional response requires detection of the relatively weak asymmetric ‘secondary flow’ derived from the fall-off of the deformation with distance from the predator. This secondary flow becomes stronger relative to the primary flow as the predator nears the prey [20]. Third, many predator–prey interactions occur at intermediate Reynolds numbers (Re), a hydrodynamic regime in which both viscous and inertial forces are prevalent, and one that remains little explored or understood in comparison with either low or high Re conditions [21]. The combination of these physical effects must be accounted for to understand interactions among free-swimming planktonic organisms.

Planktonic calanoid copepods provide a good model for elucidating the principles of pelagic predator–prey interactions in the intermediate Re regime. Among the most abundant metazoans in the world's oceans, these small crustaceans are at the base of marine food webs [22]. Lacking image-forming eyes, mechanoreception is critical for their detection of predatory threats [23]. Escape behaviour in response to changes in flow can occur in under 2 ms [24], which is at least several times faster than those in response to photic or chemical cues. In addition, copepods have evolved remarkable escape responses, moving hundreds of body lengths (BL) from a threat stimulus in a second [25,26].

Hydrodynamic cues, specifically the amount and/or rate of fluid deformation, mediate escapes of copepods [27–31]. These cues are detected by mechanosensory hairs known as setae, distributed along the antennules (A1) of copepodite (juvenile) and adult copepods [30,32]. Most behavioural studies of this group have used predator-mimics, such as suction tubes and rapid or slow movements of a solid object, to elicit escape responses [25,27,28,30,31,33–35]. However, few studies have measured sensitivities of calanoids to and escapes from live predators [36–39] and none have done so with larval fish whose predatory adaptations have co-evolved with those of their zooplankton prey [40].

We combined behavioural experiments with a computational model to (1) assess the hydrodynamic properties ahead of an approaching predator that cue a copepod to escape prior to an attack and (2) determine the directionality and kinematics of subsequent escapes. Our experiments pitted a visual predator, the larval clownfish, Amphiprion ocellaris, during the first two weeks of its life, against various developmental stages of a calanoid copepod prey, Bestiolina similis. We found that the prey was far more sensitive than previously reported and that it showed directional responses to a predatory approach. This implies that the prey is capable of detecting the asymmetric secondary flow, which is generally weaker than the linear primary flow considered in most previous studies. By analysing copepods under real and life-threatening situations, we have gained better insight into the remarkable evasion capabilities of copepods and the evolutionary adaptations that underlie them.

2. Material and methods

2.1. Behavioural experiment

Our behavioural observations were derived from a larger experimental dataset on predation strategies of larval Amphiprion ocellaris clownfish (Pomacentridae) on Bestiolina similis copepods (Paracalanidae), the protocols of which are reported in [41]. Briefly, we reared larval fish from late-stage eggs we received from a breeder (K. Brittain, Kaneohe, Hawaii, USA) and fed them live food twice daily: rotifers (Brachionus plicatilis, Brachionidae, also from K. Brittain) and mixed developmental stages of Parvocalanus crassirostris copepods (Paracalanidae). The experimental copepods, P. crassirostris and B. similis, were isolated from Kaneohe Bay, Oahu, Hawaii, USA and have been in continuous culture since 2009 [42–44]. Three copepodid stage-classes of B. similis were used as prey: early copepodites (CII–CIII stages), late copepodites (CV stage) or adults (CVI stage).

Predator–prey interactions were investigated in experimental trials between larval fish ages 1 to 14 days post-hatch (dph) and the three developmental stage-classes of B. similis prey. We designated fish into early (1–4 dph), mid (6–9 dph) and late (11–14 dph) stages based on species-specific changes in size, diet and jaw morphology [41,44,45]. A. ocellaris is a social fish, so to observe natural feeding behaviour, we placed two fish at a time in the 700-ml observation chamber (glass and acrylic cylinder, 20 cm in diameter, 2.5 cm in height), along with 0.1–0.4 copepods ml⁻¹. Each pair of fish was used in only one trial, which was terminated after six fish–copepod interactions or after 1 h. The closest bounding surfaces were the air–water interface and floor of the tank. These were at distances longer than the typical fish length and greater than the viscous boundary layer thickness; thus, boundary effects were expected to be negligible in our calculations of water deformation (see below).

Individual interactions were recorded with a high-speed, high-resolution camera (Photron FastCAM SA4, 500 frames per second, 1024 × 1024 pixels, with a 35 × 35 mm field-of-view) mounted on a vertical optical rail that viewed animals from above [41]. The camera was connected to a video monitor that allowed us to instantaneously view digital images of the observation chamber and manually focus the lens (Nikon micro-NIKKOR 60 mm) on individual interactions. Captured footage was reviewed and trimmed to include behavioural interactions-of-interest, then downloaded as a sequence of TIFF images.

2.2. Predator-approach and prey-escape behavioural analysis

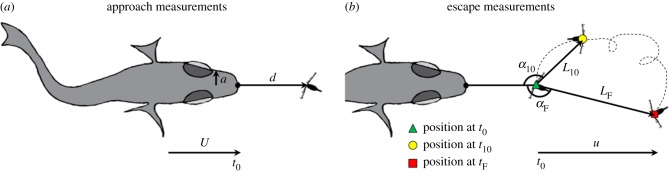
Our goal was to assess cues alerting a copepod in advance of an attack, so we analyse and report only those interactions that resulted in an escape without a strike. Even without a strike, we are confident that these were predatory approaches because the trajectories, postures and speeds of the clownfish matched those previously described for predatory approaches by the same larval clownfish [41]. The frame just prior to the first perceptible escape movement of the copepod was designated t₀, with time in milliseconds on either side of t₀ designated by a negatively or positively signed subscript (before or after t₀, respectively). To calculate the approach speed of the fish (U; figure 1a), we measured the distance between the leading edge of the fish's mouth and the copepod's rostrum at multiple time points leading up to t₀ (d; figure 1a). Reaction distance (d₀) was d at t₀. For each approach, we then created linear regressions of d over time, for which the slope was U (in mm s⁻¹). For n = 22 of the 30 approaches, the speed of the fish over the final 118 ms was well fitted with a linear regression (R² values greater than 0.98) measured at 4 to 6 time points. For n = 8 of the 30 approaches, the speed of the fish over 118 ms was nonlinear (due to acceleration or deceleration), so we calculated fish speed over shorter time intervals (46 or 72 ms) over which the speed was linear (R² > 0.96 measured at 3 to 6 time points). To reduce underestimates of distance measurements owed to the lack of three-dimensional information, we analysed only fish and copepods that remained within the same narrow plane of focus (less than 2 mm) during the approach. At t₀, we measured the width of the fish head just in front of the eyes, from which we derived an effective ‘radius,’ or half-width, for the hydrodynamic model (a; figure 1a; see below). All approach measurements were made using the Fiji software package (built on ImageJ v1.51) [46] for each pre-strike escape.

Figure 1.

Schematic drawing of parameters measured during interactions between a larval clownfish predator (Amphiprion ocellaris) and a calanoid copepod prey (Bestiolina similis), during (a) the stealthy approach of the fish, and (b) the escape of the copepod. Abbreviations: a: half-width of the fish's head immediately anterior of the eyes; d: distance between the leading edge of the fish's mouth and the rostrum of the copepod (reaction distance is d₀ at t₀); L₁₀: displacement of copepod over the initial 10 ms of its escape; L_F: final displacement after the copepod ceased moving; U: fish approach speed (mm s⁻¹) just prior to the copepod's initiating its escape (at time t₀); u: escape speed; α₁₀: angle of escape during the initial 10 ms; and α_F: final angle of escape. Positions of the copepod's rostrum at times t₀, t₁₀ and t_F are indicated as a green triangle, yellow circle and red square, respectively. (Online version in colour.)

Displacements during the copepod's escape were measured at two time points with respect to its starting position at t₀: an ‘initial’ displacement, L₁₀, 10 ms (5 frames) after the jump began, and a final displacement, L_F, when the jump ended (figure 1b). We calculated escape speeds (u in mm s⁻¹; figure 1b) at the midpoints between two successive frames as the displacement between the frames divided by 2 ms (500 fps). The duration of an escape jump was the time in milliseconds between t₀ (start) and cessation (finish) of the copepod's movement (t_F) (figure 1b). We also measured the angle of escape by using the ImageJ angle tool to draw a line from the leading edge of the fish's mouth to the copepod's position at t₀, and thence to either its position at t₁₀ (for the initial angle of escape, α₁₀) or its final position (for the final angle of escape, α_F) (figure 1b). The durations and angles of each escape were measured using Fiji, and coordinate positions of copepods were manually tracked using the Tracker software package v. 4.8 (Open Source Physics, Douglas Brown). We calculated displacements and speeds of escape using Microsoft Excel v. 16.10. Statistical analyses were conducted in R for RStudio v. 1.0.153 [47] with associated package FSA v0.8.20 [48] for Kruskal–Wallis multiple comparisons [49,50], with p-values adjusted with the Benjamini–Hochberg method [51].

Copepod escapes involved power strokes produced by the swimming legs (pereiopods). To distinguish a true escape from a repositioning jump (hop and sink), we evaluated both maximum speeds and the duration of the jump. Escape jumps are three to four times faster than ‘hops’ (which were rare in our experimental video sequences), include multiple power strokes, and scaled by the size of copepod are an order of magnitude above maximum speeds of other aquatic organisms [25,52,53]. Speeds calculated in two dimensions for those copepods that escaped vertically out of the plane of focus were underestimated. However, these estimates were conservative insofar as their purpose was to distinguish escapes from repositioning jumps.

2.3. Modelling water deformation

Based on several earlier studies, the proximate stimulus eliciting pre-strike escape in the copepod was water deformation caused by the flow disturbance, or ‘bow wave’, as it has been termed (e.g. [23]) in front of the approaching fish [28,31]. To estimate the threshold level for this stimulus, we modelled the water flow and deformation (i.e. the rate of strain along the axis of approach) ahead of the swimming fish by representing its body as a rigid sphere, as previously done by Kiørboe & Visser [54] (see also [55]). We partly validated the model by observing that in the region where viscous effects are expected to be negligible ahead of a larval fish swimming at speed 20 mm s⁻¹ (Reynolds number, Re = 28), tracer particles followed streamlines very much like those ahead of a sphere translating steadily through an inviscid fluid (valid in the large Re limit).

To digitally track the coordinate positions of tracer particles (20 µm Polybead^® polystyrene microspheres, Polysciences, Inc.) suspended in the water column, we used a combination of Tracker's automatic and manual tracking functions. We tracked two points on the fish's body—the leading edge of its mouth and a pigment on top of its head—and multiple particles in the immediate path of the moving fish that were both (1) in focus and therefore in the plane of the fish and (2) within a 90° range of the fish's anteroposterior axis, as determined by the orientation of its mouth and pigment. To determine how the particles moved with respect to the swimming fish, we translated and rotated the coordinates of particles such that the x and y axes, respectively, pointed along and across the anteroposterior axis of the fish, and the origin was located at a distance a behind the leading edge of the fish's mouth. This ensured that the leading edge of the mouth coincided with the leading edge of a sphere in the model. Potential flow theory predicts that particles follow streamlines given by setting Ψ to be a constant in

$$\mathit{\Psi }=\frac{1}{2}U{y}^2(1-a^3{(x^2+y^2)}^{-3/2}),$$

with velocity given by the gradient of

$$\varphi =Ux\left(1+\frac{1}{2}{a}^3{(x^2+y^2)}^{-3/2}\right),$$

where U is the constant swimming speed of fish estimated from our video clips. We plotted and compared the particle trajectories with streamlines in the model. The trajectories fitted best with streamlines around a sphere of radius a within 40% of the radius (half-width) of the fish head.

We used the model to predict the deformation rate (D) of water, defined as the gradient of the x-component velocity v in the x direction from the copepod to the fish, that is ∂v/∂x with v = ∂ϕ/∂x, evaluated at the location of the copepod at the moment just prior to initiating its escape (t₀). We also estimated the cumulative deformation (C) experienced by the copepod by integrating the deformation rate over the long period of time prior to t₀ (electronic supplementary material, table S1). Using experimental parameters (radius of fish head a, distance to the copepod from the centre of the sphere Z, and from the leading edge of the sphere d₀ = Z − a, and approach speed U) and Re (=2aU/ν) ranging from 0 to 20, we simulated steady axisymmetric flow around a sphere using a classical method relying on the streamfunction–vorticity formulation (e.g. [56]). This method has been widely used in the past to analyse the flow structure behind the sphere and the drag on the sphere (e.g. [57]). Here, we focus instead on the deformation of the flow ahead of the sphere. This extends the analysis performed previously at extremely low and high Re [54] to the intermediate range of Re, matching those in our experiments. Our simulations computed the steady velocity field by reformulating the governing Navier–Stokes equations for incompressible flow as a system consisting of the Poisson equation for streamfunction and the vorticity transport equation, which were solved in modified spherical coordinates using an explicit forward-time central-space finite-difference scheme with small enough time steps to ensure numerical stability. The polar angle of the modified spherical coordinates was incremented by 6°, and the radial coordinate r = e^z was incremented by z = 0.05. This steady-flow velocity field was used to compute both D and C at the copepod's location at t₀.

3. Results

3.1. Predator-approach and prey-escape behaviours

The majority of predator–prey interactions in this experimental series involved a slow and stealthy approach by the larval fish that did not alert the copepod prey and culminated in a rapid strike [41]. However, in 18% of approaches (n = 46 of 259), the copepod initiated an escape before the fish could strike, 30 of which were of sufficiently high quality to obtain quantitative data on both the predator and the prey. As an example of these interactions, figure 2 shows the approach measurements and subsequent escape trajectory of a late copepodite (CV stage) from a 3-dph fish (early stage).

Figure 2.

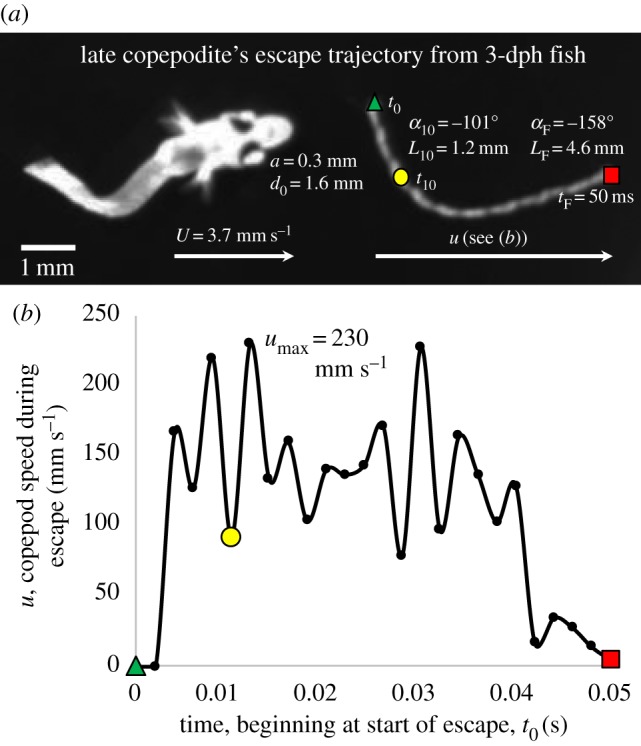
Exemplar for the interaction between an approaching larval fish (3 dph) and an escaping copepod (late copepodite, CV stage) following early detection of the approaching predator by the prey. (a) Overlaid images of copepod escape trajectory from start (t₀, green triangle) to initial escape position (t₁₀, yellow circle) to final escape position (t_F, red square), with fish approach and copepod escape measurements listed, as defined in figure 1 (see also Material and methods). (b) Escape speed of the copepod computed at 2-ms intervals. (Online version in colour.)

To identify a copepod's behaviour as an escape, distinguishing it from other forms of locomotory behaviour, we examined the distribution of peak speeds (u_max) and final displacements (L_F) of observed locomotory events involving power strokes of the swimming legs. Peak speeds ranged from just over 70 mm s⁻¹ (200 BL s⁻¹) to just over 370 mm s⁻¹ (800 BL s⁻¹), along with a minimum in final displacement (L_F) of 1.6 mm (5 BL), values that are comparable to or higher than those for other calanoid species responding to artificial predator-mimics [25,52,58]. Both u_max and L_F differed among copepod developmental stage-classes (u_max: ANOVA F_2,27 = 5.58, p = 0.009; L_F: ANOVA F_2,27 = 4.36, p = 0.02). Adults reached greater peak speeds and distances from the predator than both early and late copepodites (table 1).

Table 1.

Copepod escape parameters and deformation parameters at t₀, by developmental stage-class. All values shown as mean ± s.d. with the range given in parentheses.

	copepod developmental stage-class
	early copepodite (CII–CIII)	late copepodite (CV)	adult copepod (CVI)
peak escape speed, umax (mm s−1)	172 ± 97 (73–305)	172 ± 58 (84–245)	263 ± 55 (167–374)
escape displacement, LF (mm)	4.6 ± 3.1 (1.9–11.1)	3.7 ± 2.2 (1.6–7.5)	7.2 ± 3.1 (2.0–13.9)
reaction distance, d0 (mm)	1.2 ± 0.6 (0.4–2.6)	1.6 ± 0.5 (0.7–2.5)	1.9 ± 0.3 (1.3–2.3)
deformation rate at t0, D (s−1)	0.53 ± 0.64 (0.04–1.78)	0.21 ± 0.15 (0.05–0.51)	0.33 ± 0.30 (0.04–1.09)
cumulative deformation at t0, C	0.17 ± 0.17 (0.00–0.44)	0.06 ± 0.08 (0.00–0.24)	0.04 ± 0.03 (0.01–0.12)

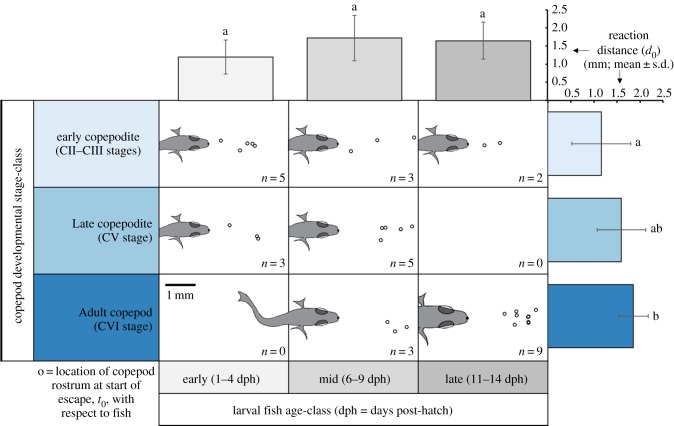
3.1.1. Reaction distance

Copepods initiated escapes at different distances (d₀; reaction distance) from the approaching fish. Average d₀ was 1.6 mm over all three stage-classes of copepod development, with the average distances differing across stage-classes, as shown in figure 3. Early copepodites allowed fish to approach around 40% (0.7 mm) closer than did adult copepods (95% CI 0.2–1.2 mm; ANOVA F_2,27 = 5.29, Tukey p = 0.009). While there was a trend in both mean and median reaction distances increasing with copepod stage-class (table 1), the differences between early versus late copepodites and late copepodites versus adult copepods were not statistically significant (figure 3; ANOVA F_2,27 = 5.29, both Tukey p > 0.1).

Figure 3.

Relative positions of copepods and fish at t₀, just prior to escape, shown in a 3 × 3 matrix of copepod developmental stage-classes (rows) and fish age-classes (columns) (n = number of observations). Fish drawn to scale, showing the average head half-width for each predator–prey category. Bar graphs show means for reaction distance (d₀) as a function of copepod developmental stage-class (to the right, in shades of blue) and fish age-class (top, in shades of grey). The results of statistical tests (ANOVA with Tukey multiple, post hoc comparisons) are represented by letters near each bar, whereby different letters indicate significant differences (p < 0.05) between prey stage-classes (no significant differences among fish age-classes). (Online version in colour.)

3.1.2. Approach characteristics

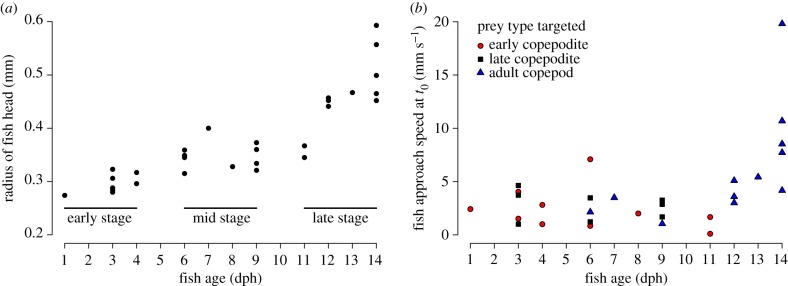
Two parameters of the fish approach affect the strength of its ‘bow wave’ (i.e. flow disturbance [23]) that could alert the copepod: the fish's size, a (head half-width), and approach speed, U. During the first two weeks post-hatch, median a increased by 5% per day (95% CI 4–6%) or more than 80% over 14 days (figure 4a; table 2, statistical test 1). The reaction distance did not change significantly with fish size (table 2, statistical test 2). While approach speed of the two younger fish age-classes (dph 1–9) was independent of fish age (mean = 2.7 mm s⁻¹; coeff. var. = 60%), it more than doubled in the late-stage larvae (mean = 6.4 mm s⁻¹; coeff. var. = 85%). Thus, overall median approach speed increased by 10% per day (95% CI 4–17%) over the first two weeks post-hatch, after removing one outlier (very slow 11-dph fish, U = 0.1 mm s⁻¹) (figure 4b; table 2, statistical test 3). Neither fish age (table 2, statistical test 4) nor fish age-class (figure 3; ANOVA F_2,27 = 2.43, p > 0.1) affected reaction distance of the copepod, despite fish size (a) and approach speed (U) changing with age. Thus, we investigated the water deformation rates predicted for the copepod at the moment of its escape.

Figure 4.

Developmental progression of fish parameters during the first 14 dph of larval life. (a) Fish size, measured as the half-width of head. (b) Approach speed (U) of fish during individual interactions with early copepodites (red circles), late copepodites (black squares) and adult copepods (blue triangles). (Online version in colour.)

Table 2.

Statistical results from linear models testing for significant effects of larval fish age-class and copepod developmental stage-class on predator-approach, prey-escape and deformation rate measurements. Explanatory variables in italics are significant indicators (p < 0.05) of the response.

	statistical test	explanatory variable	coefficient	s.e.	t	p
1	simple linear regression (SLR): log of fish head radius (a)∼age of fish (dph)	intercept	−1.369	0.038	−35.630	<0.001
		dph	0.045	0.004	10.760	<0.001
		residual s.e. = 0.09 on d.f. = 28 R2=81% adjusted R2 = 80%
2	SLR: reaction distance (d0)∼log of fish head radius (a)	intercept	0.724	0.471	1.536	0.136
		dph	2.205	1.223	1.803	0.082
		residual s.e. = 0.55 on d.f. = 28 R2 = 10% adjusted R2 = 7%
3	SLR: log of approach speed (U)∼dph	intercept	0.326	0.269	1.212	0.236
		dph	0.098	0.030	3.312	0.003
		residual s.e. = 0.66 on d.f. = 27 R2 = 29% adjusted R2 = 26%
4	SLR: d0∼dph	intercept	1.219	0.227	5.363	<0.001
		dph	0.041	0.025	1.649	0.110
		residual s.e. = 0.55 on d.f. = 28 R2 = 9% adjusted R2 = 6%
5	multiple linear regression (MLR): log of deformation rate (D)∼dph + early copepodite (ecop) + late copepodite (lcop)	intercept	−1.611	0.792	−2.033	0.052
		dph	0.017	0.063	0.273	0.787
		ecop (versus adult)	0.204	0.570	0.359	0.723
		lcop (versus adult)	−0.255	0.579	−0.439	0.664
		ecop (versus lcop)	0.459	0.470	0.975	0.338
		residual s.e. = 0.99 on d.f. = 26 R2 = 4% adjusted R2 = 7%

3.2. Modelling water deformation

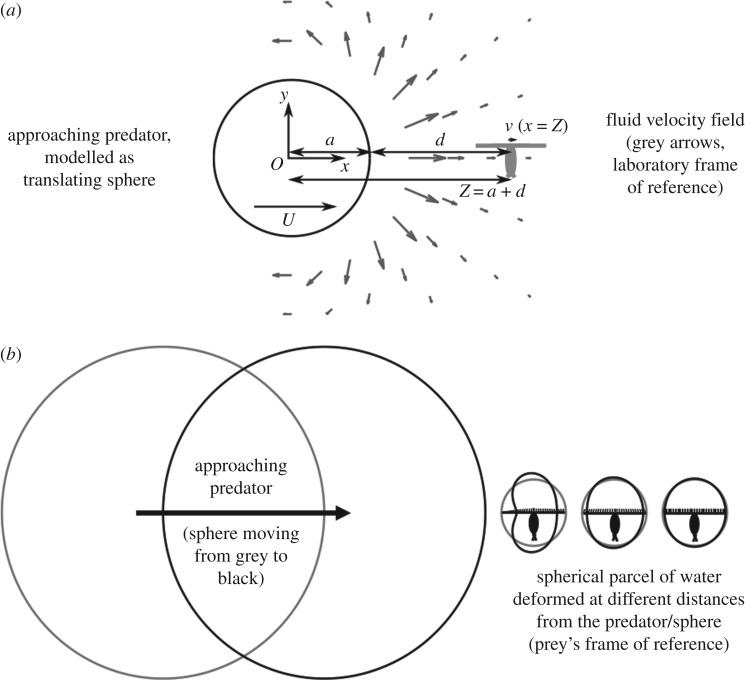
The copepod's escape response is elicited by hydrodynamic disturbances created by the approaching fish. The water around the copepod deforms, thus generating flows that deflect mechanosensory hairs along its long pair of antennules, which can inform the presence and approximate location of the fish [20]. From the perspective of a copepod located in the path of the fish, represented in our model as a sphere (see Material and methods), the water in the copepod's vicinity is compressed along the axis parallel to the direction of approach (figure 5). The amount of compression depends on the distance Z = d + a, approach speed U, sphere radius a and kinematic viscosity ν of water as quantified below.

Figure 5.

Schematic representation of the fluid velocity field (a) and water deformation (b) produced by a slowly approaching predator (modelled as a sphere translating in water). (a) Geometry and coordinate axes in the laboratory frame with the sphere translating at speed U from left to right. A relatively small copepod would translate as shown by the grey arrows that represent the fluid velocity field. The predator velocity and the flow velocity field have the same scale. (b) Water deformation that might provide mechanosensory cues to copepods at various distances. Grey circles show the predator's position and the shapes of three water parcels in the frames of reference of copepods at different initial distances. Similarly, black shapes show the predator's position after moving closer to the copepods, and the resulting deformation of water parcels. Deformation increases as distance between the predator/sphere and copepod decreases, which would result in larger movements of hinged mechanosensory setae on the antennules (A1) of copepods. Drawing to scale, except for cartoon of copepod.

We illustrate this using the water deformation around a copepod located ahead of a sphere translating at high Reynolds number $Re=2Ua/\nu \gg 1$. At a distance Z much greater than radius a, the flows generated by the deformation are approximately symmetric. The deformation rate ∂v/∂x along the axis of approach is given by 3Ua³Z⁻⁴, which decays more rapidly with distance Z, as Z decreases (figures 5 and 6, Re = infinity line). Thus, the flows around a copepod closer to the fish become less symmetric, owing to a stronger compression in the regions closer to the fish (figure 5). A measure of the degree of flow asymmetry is given by (∂²v/∂x²)A1, which is proportional to (∂v/∂x)A1/Z, where A1 is the antennule length [20]. Theory thus predicts that a copepod in sufficient proximity to the fish can distinguish from which direction the fish approaches and will consequently direct its escape away from the fish.

Figure 6.

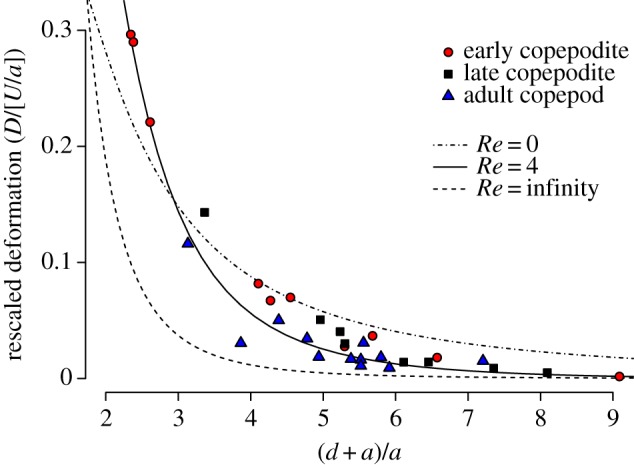
Deformation rate, unitless after rescaling by fish approach speed and size (D/[U/a]), versus reaction distance, also unitless after rescaling by fish size ([d + a]/a). Points represent individual predator–prey interactions, coded by prey developmental stage-class. Upper and lower broken lines show theoretical curves for, respectively, Re = 0 (y = 3x⁻⁴) and Re = infinity (y = 1.5x⁻²–1.5x⁻⁴). Solid line shows the model output for Re = 4, a representative value in these experiments. (Online version in colour.)

Ahead of a sphere translating at lower Reynolds numbers, the water deformation still decreases in rate, and the attendant flows become more asymmetric with decreasing distance. However, the deformation rate along the axis of approach falls off less steeply, because it is given by the formula 1.5 UaZ⁻² for an externally driven sphere translating at $Re\ll 1$ (figure 6, Re = 0 line) [20]. At intermediate Reynolds numbers as in our experiments, the deformation rate cannot be expressed by a single formula and must be computed using simulations (see Material and methods). The simulated deformation rate at a representative Reynolds number of 4 for our experiments is plotted against distance Z/a in figure 6. The deformation rate at close distances is elevated by the viscous boundary layer at the surface of the sphere, while further away it approaches the curve at high Reynolds number due to the reduced effects of viscosity. We ran simulations at Reynolds numbers corresponding to each experiment to estimate the water deformation around the copepod at the instant it initiated its escape, as observed experimentally.

3.3. Copepods’ sensitivity to deformation and directionality of escape

Considering that fish larvae increase in size and speed as a function of age, one might predict that deformation rates of water produced by older fish larvae would be greater than those produced by younger fish larvae. However, there was no evidence that the deformation rate at the point of copepod escape changed with fish age (table 2, statistical test 5). One might also predict that adult copepods would be more sensitive to water deformation rates than copepodites, because the antennules bearing the mechanosensory setae of adults are longer, and thus for a given deformation rate, adult setae experience greater deflecting water motion than copepodite setae. While we found no evidence that mean deformation rate at escape differed among copepod developmental stage-classes (table 2, statistical test 5), the variance in deformation rates at escape was greater for early copepodites than for late copepodites or adult copepods (figure 7a; Fligner–Killeen test: χ² = 6.3, p = 0.04). Deformation values for individual stage-classes are shown in figure 7 and table 1. For all stage-classes combined, deformation rates at t₀ ranged from 0.04 to 1.78 s⁻¹ (mean ± s.d. = 0.37±0.43), and cumulative deformation at t₀ ranged from less than 0.001 to 0.44 (mean ± s.d. = 0.09 ± 0.12).

Figure 7.

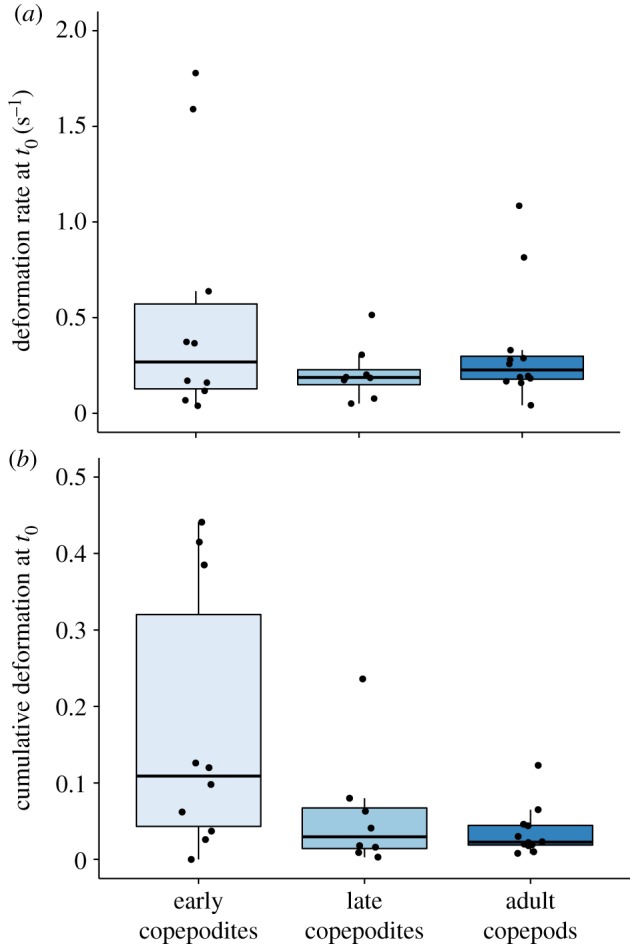
Deformations calculated by the hydrodynamic model at the moment just prior to escape (t₀), displayed as boxplots by copepod developmental stage-class: horizontal lines represent medians for each stage-class, the blue boxes represent the middle 50% of the data, and the vertical lines (whiskers) represent the ranges for the bottom and top 25% of the data, excluding outliers. Points overlaying the boxes represent values for individual copepods within each stage-class. (a) Deformation rate (D; in s⁻¹); (b) cumulative deformation (C; unitless). (Online version in colour.)

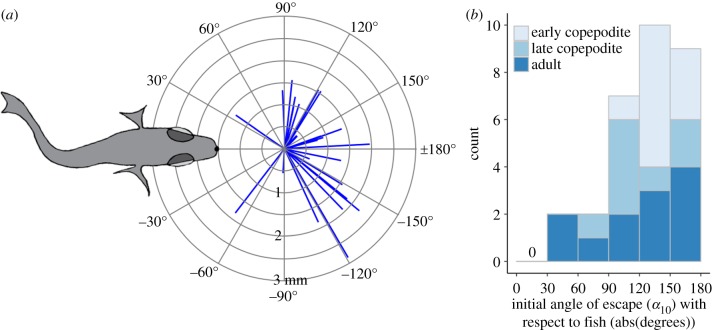
Copepods escaped away from fish, always at initial angles (α₁₀) greater than 30° with respect to the angle of approach (0°), and most often between 90° and 180° (figure 8; n = 26 of 30, 87%; all angles reported as absolute values of α₁₀). Neither median α₁₀, nor the final angle of escape, α_F, depended on the developmental stage-class of the copepod (Kruskal–Wallis rank-sum tests for α₁₀: χ² = 2.96, d.f. = 2, p > 0.1; α_F: χ² = 5.06, d.f. = 2, p = 0.08). The prevailing directionality of escape (i.e. away, defined as greater than or equal to 90°) occurred regardless of the copepod's original heading: toward (n = 11), away (n = 15) or perpendicular (n = 4) to the axis of approach.

Figure 8.

Directionality of copepod escapes. (a) Initial escape vectors traversed by the copepod (n = 30) during the first 10 ms of escape, referenced to its initial location and direction of approach. The fish is shown at the average reaction distance (d₀ = 1.5 mm). (b) Initial angle of escape (α₁₀) shown by copepod developmental stage-class, all as absolute values with respect to the direction of approach. (Online version in colour.)

Theory predicts that when the distance between fish and copepod is greater, the asymmetric secondary flow is smaller in comparison with the symmetric primary flow, which would make it more difficult for copepods to detect the asymmetry and predict the direction of the fish's approach. If this is true, then we would expect copepods to be unable to direct escapes predominantly away with respect to the predator when the fish is further away [20]. However, for the escapes observed in these experiments, this predicted trend was not evident (figure 9a). Because the secondary flow increases relative to the primary flow with antennule length, we might also predict that when antennules are longer, it would be easier for copepods to detect the direction of the fish's approach. If this were true, then we would expect copepods with a greater A1/Z ratio to escape more consistently away from the approach. However again, this prediction was not supported by our experimental data (figure 9b). In all but four cases (out of 30), and regardless of distance or developmental stage-class, copepod escapes were directed more away from (α₁₀ > 90°) than toward the approaching fish (figure 8).

Figure 9.

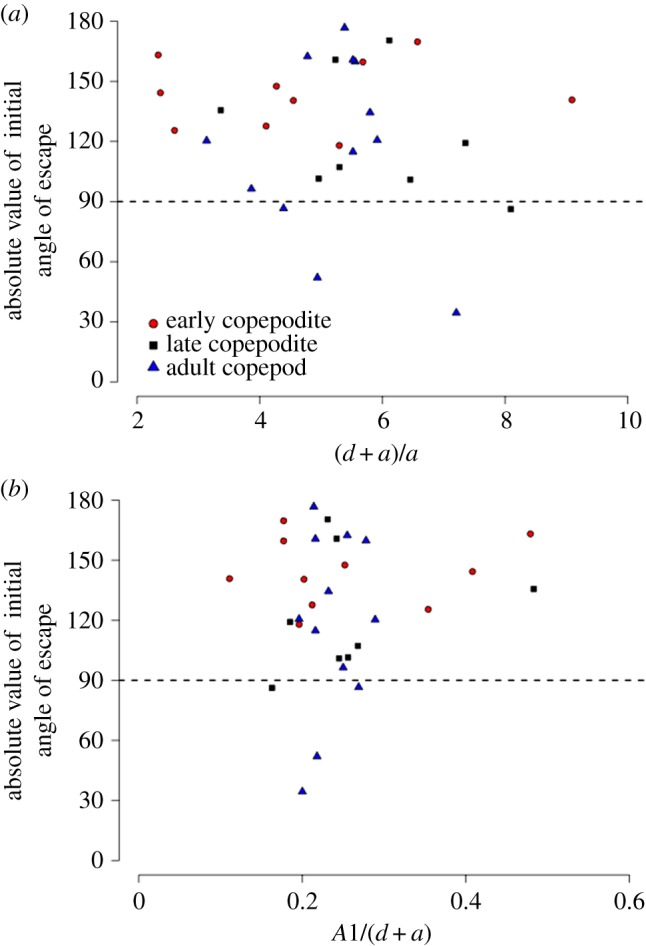
Directionality as a function of reaction distance. Theoretical considerations [20] suggest that copepods should be less able to detect the direction of the predator's approach and thus will be less able to orient escapes consistently away from it: (a) when the distance between fish and copepod relative to the fish size ([d + a]/a) is large; and (b) when copepods have shorter antennules, because when antennules are long relative to the distance to the fish (A1/[d + a]), it is easier for copepods to detect the secondary flows that signal the direction of approach. There was no support for these predictions in the data. A1 is the length of antennule based on average, stage-specific prosome lengths from McKinnon et al. [59] for B. similis: CII–CIII (early copepodite) mean = 0.318 mm; CV (late copepodite) mean = 0.455 mm; and CVI (adult) mean = 0.538 mm. (Online version in colour.)

4. Discussion

4.1. Prey sensitivity

Predator–prey coevolution is a common process across the world's habitats, and yet we barely understand the mechanisms that produce it within the ocean's planktonic community. Relying on mechanosensory cues for detection of a stealthy predator can be challenging for neutrally buoyant prey in pelagic environments. The prey must determine whether a disturbance is a true threat, and therefore, whether and how to escape [60,61]. Our study demonstrates that a calanoid copepod can use minute hydrodynamic cues to detect and direct its escape away from a stealthily approaching larval fish, well before the fish is within its typical striking distance of 1 mm [41]. Our hydrodynamic model estimated the deformation rate of water around the copepod at the instant of its escape by accounting for viscous and inertial effects. Figure 6 shows that the deformation rate is higher than would be estimated had the viscosity been neglected. For B. similis, with antennules ca 0.4 mm in mean length, the deformations as low as 0.04 s⁻¹ would correspond to flow rates at the sensors on the antennular tips as low as 16 µm s⁻¹, near the lower limit of both physiological and behavioural thresholds reported in copepods [30,32,62,63]. The median deformation rate for escapes in our experiments, ca 0.2 s⁻¹ (corresponding to a cumulative deformation of 0.04), represents a 50% escape probability that includes variables such as sub-optimal antennule orientations [20].

Previous studies that used artificial stimuli to elicit escapes in free-swimming copepods (copepodite and adult stages) report threshold deformation rates much less sensitive, e.g. in the typical range approximately 1–10 s⁻¹ [64] with values at times down to approximately 0.2 s⁻¹ [25,28,31,35,58]. These studies found significant differences in sensitivity depending on species, developmental stage and stimulus type. The high sensitivity reported here might have been modulated by additional cues associated with a real predator, such as fish kairomones [65,66] or prior experience. For example, Waggett & Buskey [67] noted that copepods respond with more powerful escapes from real predators than from predator-mimics. Thus, the presence of real fish in these experiments could have also contributed to the observed high sensitivities.

The unprecedentedly high sensitivity of copepods that we report has an additional important implication. Some mechanosensors might be adapted to trigger escapes to the gradual build-up of water deformation, rather than the rate of deformation, by integrating the flow signal over time, as investigated (inconclusively) by Haury et al. [28]. This contrasts with the common assumption in most previous studies that copepods respond to instantaneous signals that exceed a threshold. In the former case, the deformation rate increases gradually and continuously for a prolonged period as the fish approaches stealthily. In the latter case, the strength and direction of the deformation might change suddenly, e.g. due to turbulent ocean currents. In the mixed layer near the ocean surface, copepods are expected to experience random deformation rates of the order of 0.1–1 s⁻¹, which is obtained from the Kolmogorov-scale shear rate $\sqrt{\left({\displaystyle \frac{\epsilon }{\nu }}\right)}$, where ν approximately 10⁻⁶ m² s⁻¹ is the kinematic viscosity of water and ɛ is the energy dissipation rate ranging from 10⁻⁶ to 10⁻⁸ m² s⁻³ [68]. This noise level in turbulence is comparable to the instantaneous deformation rate of an approaching predator. The key difference, however, is that in the cumulative case the deformation increases in the same direction for a prolonged period, smoothing out random fluctuations in rate. In addition, copepods, like many other organisms, habituate to ambient noise levels. This reduces the incidence of spurious escapes, but at the expense of increasing their potential susceptibility to predation [27,69–71].

4.2. Directionality of escape

Copepods typically escaped away from approaching fish, contrary to predictions based on the primary flow symmetry that escapes would be randomly oriented or at right angles to the approach [20]. The copepods must thus have detected asymmetric secondary flow, defined here as the difference between the actual flow and the symmetric primary flow. The distal tips of antennules have the most sensitive mechanosensory setae, meaning that the secondary flow would be best detected by copepods whose distal setae are at different distances from the predator (in n = 21 of 30 of our interactions). The magnitude of the secondary flow along antennules oriented along the line of approach is approximately 2A1/(d + a) times the primary signal in the limit of high Reynolds number [20]. For example, with a = A1 = 0.4 mm and the most extreme reaction distance, d₀ = 2.3 mm, the secondary flow adds 30% to the primary flow on the near side of the copepod and subtracts 30% from the far-side flow. Therefore, the difference between the signals at the two distal ends of the antennules is 60% of the primary flow, providing an ample basis for the directional orientation of escapes. Even a small fraction of the signal being secondary should elicit a turn away from the fish. Two studies have noted that unilateral stimulation of the antennular sensors elicits ipsilateral adduction of the antennule, which rotates the copepod away from the stimulated side [29,72]. Thus, any time the tip of one antennule is closer to the fish than the other, the copepod will reflexively turn away. In summary, the ability of copepods to escape away from the predator at relatively large distances implies that they are capable of detecting the small primary flow and the smaller secondary flow.

4.3. Ontogeny of escape

Ontogenetic changes in escapes involved small changes in sensitivity depending on developmental stage-class, with fish larvae able to approach early copepodites (CII–CIII stages) more closely than adults (CVI stage), on average. This was expected because for a given deformation rate, the setae on the longer antennules of adults experience a greater water motion and hence deflection than do those on the shorter antennules of less developed copepodites (e.g. [28]). The corollary prediction of an ontogenetic increase in sensitivity to deformation rate did not materialize. However, we noted greater variance in threshold sensitivity of early copepodites, which is consistent with greater variance in the expected antennule length of early copepodites due to this developmental category containing two stages (CII and CIII) instead of one. Our findings contrast with those of Kiørboe et al. [31] who found lower sensitivities in earlier developmental stages of Acartia tonsa and concluded that the absolute sensitivity of the mechanosensors was the same across all stages.

4.4. Implications

The stealthy approach of the larval fish and the extraordinary mechanosensory system of copepods are results of an evolutionary ‘arms race’ that has led to unusual adaptation in predator and prey, as we have shown here. As reported by others, copepods always escape from less stealthy fish larvae, such as those of early cod, which initially depend exclusively on non-evasive prey for food [73]. Furthermore, many studies have documented and commented on the adaptations for high sensitivity by the setae on the antennules of calanoid copepods, drawing on evidence from behaviour [25,29,35], morphology [74,75] and physiology [30,32]. Here, we have quantified how these structures enable the copepod to use the primary flows and still smaller secondary flows of the remarkably small hydrodynamic disturbances produced by a stealthy predator to detect, locate and thwart the threat.

Our results inform models that use estimates of encounter rates with zooplankton prey to predict foraging success, growth and survival rate of larval fish (e.g. [76,77]). Calanoid copepods are not passive particles; their extraordinary ability to escape underscores the importance of post-encounter events in determining the outcome of a predation sequence [44,73]. Should our numbers be representative of predation sequences in the natural environment, approximately one-fifth of encounters may result in the prey escaping before a predator can strike. Furthermore, an additional 25–50% of copepods escape after a strike has been initiated [41]. Thus, overall, the copepods' sensorimotor adaptations give them a 40–60% chance of surviving a predator–prey encounter despite the predator's stealth.

Ethics

Animal husbandry and experimental protocols followed institutional guidelines and were approved by the University of Hawai'i Institutional Animal Care and Use Committee (IACUC protocol no. 2099).

Data accessibility

The datasets and code that support this article have been uploaded as part of the supplementary material and are publicly available on Dryad [78]. The original images from which these analyses were based are also publicly available at BCO-DMO [79].

Authors' contributions

L.J.T. participated in data analysis, conducted statistical analyses and drafted the manuscript; H.E.R. carried out the behavioural experiment and participated in data analysis; D.T. helped conceive of the study, created the hydrodynamic model and helped draft the manuscript; J.R.S. helped conceive of and design the study, set up the behavioural experiment and apparatus and interpret results; D.K.H. helped conceive of and design the study, participated in data analysis and helped draft the manuscript; P.H.L. conceived of and designed the study, participated in data analysis and helped draft the manuscript. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

Financial support was provided by the National Science Foundation (OCE 12-35549 to P.H.L. and D.K.H. and CBET 16-03929 to D.T.) and the US Army Research Office (W911NF-17-1-0442 to D.T.).