The role of adhesion in contact mechanics

Abstract

Adhesive (e.g. van der Waals) forces were not generally taken into account in contact mechanics until 1971, when Johnson, Kendall and Roberts (JKR) generalized Hertz’ solution for an elastic sphere using an energetic argument which we now recognize to be analogous to that used in linear elastic fracture mechanics. A significant result is that the load–displacement relation exhibits instabilities in which approaching bodies ‘jump in’ to contact, whereas separated bodies ‘jump out’ at a tensile ‘pull-off force’. The JKR approach has since been widely used in other geometries, but at small length scales or for stiffer materials it is found to be less accurate. In conformal contact problems, other instabilities can occur, characterized by the development of regular patterns of regions of large and small traction. All these instabilities result in differences between loading and unloading curves and consequent hysteretic energy losses. Adhesive contact mechanics has become increasingly important in recent years with the focus on soft materials (which generally permit larger areas of the interacting surfaces to come within the range of adhesive forces), nano-devices and the analysis of bio-systems. Applications are found in nature, such as insect attachment forces, in nano-manufacturing, and more generally in industrial systems involving rubber or polymer contacts. In this paper, we review the strengths and limitations of various methods for analysing contact problems involving adhesive tractions, with particular reference to the effect of the inevitable roughness of the contacting surfaces.

1. Introduction

Adhesive interactions between contacting solids have a major impact in many areas of engineering and everyday life. For example, the degree of adhesion is critical for the assessment of the quality of glued joints, in designing human joint prostheses, or in understanding the sense of touch. Adhesive forces are also central to most modern theories of frictional interaction, as well as to Archard’s theory of adhesive wear. Coatings have been applied widely in aerospace, biomedical, electronic and many other industries with a view to obtaining desired frictional/adhesive characteristics.

In recent years, the need to include adhesion in contact analysis has become increasingly pressing as micro- and nano-electromechanical systems have been developed. In everyday life, objects at the ‘human scale’ do not stick to each other, principally as a result of inevitable surface roughness which reduces the proportion of the surface in intimate contact. However, this does not always hold true at smaller scales, where surface forces, including adhesion, becomes greater in proportion to volume forces.

Designing surfaces for optimal adhesive performance is now a hot topic in the engineering community, where nature is an important source of inspiration. Indeed we are still far from being able to achieve the astonishing capability of insects and reptiles to control interface adhesive strength. The most famous case is perhaps that of the gecko, whose feet can sustain several times its weight, while also being able to completely detach its foot in 15 ms. This remarkable achievement is attributed to the hierarchical structures of gecko feet which are split into many fibrils in order to reach the optimal nanoscale size for the attachment to be robust and close to the theoretical strength. This has stimulated the growth of the field of bioinspired engineering, which attempts to replicate natural solutions with patterns in polymer films having micron- or submicron-sized protrusions.

In this paper, we review (principally analytical) attempts to predict the effect of adhesive forces between deformable bodies in contact. The manuscript is organized as follows: §2 reviews the contact of a sphere on a plane in the presence of adhesion, §3 deals with the experimental measurements of adhesive effects, §4 discusses the instabilities of thin elastic layers, §5 considers the effect of surface roughness on adhesion of elastic bodies, §6 reviews the engineering solutions inspired by nature to improve adhesive performance and in §7 the interplay between adhesion and friction is discussed.

1.1. Interfacial interaction law

Classical contact mechanics is typically characterized by the Signorini inequalities, which demand that the tractions between interacting solid bodies be non-tensile, and that interpenetration of material is inadmissible. We can then partition the surface of a body into regions of contact, where the gap between the bodies is zero and the normal component of traction is compressive, and separation, where there are no tractions and the gap is positive. However, at very small length scales, this dichotomy is an oversimplification. The local tractions between the bodies will be a continuous function of relative approach and van der Waals forces and other physical mechanisms can cause regions of tensile (or adhesive) traction. Most authors assume that the Lennard–Jones 6–12 law [1] defines the relation between the force and separation of two individual molecules, and if a continuum is approximated as a uniform distribution of molecules, the resulting traction σ (tensile positive) between two half spaces is then found to be [2,3]

$$\sigma (g)=\frac{8\mathrm{\Delta }\gamma }{3\epsilon }[\frac{{\epsilon }^3}{g^3}-\frac{{\epsilon }^9}{g^9}],\text{where}\hspace{0.17em}\mathrm{\Delta }\gamma ={\int }_{\epsilon }^{\mathrm{\infty }}\sigma (g)\hspace{0.17em}\text{d}g$$ 1.1

is the interface energy or the work done per unit area of interface in separating the two bodies from the equilibrium position g = ɛ, at which σ = 0. This expression is shown in figure 1. The maximum tensile traction occurs at a separation g = 3^1/6ɛ and is ${\sigma }_0=16\mathrm{\Delta }\gamma /9\sqrt{3}\epsilon$. The definitions of symbols used in this paper are listed in table 1.

Figure 1.

The traction law defined in equation (1.1). The interface energy Δγ corresponds to the shaded area.

Table 1.

Nomenclature.

Aatt	attractive contact area
Ac	total contact area
Anom	‘nominal’ or ‘apparent’ contact area
Arep	repulsive contact area
A0	contact area at null tangential load
B(Δ)	bearing area
C(ζ)	surface heights power spectral density (PSD)
$C_{\parallel }$	compliance in the direction of the applied load
C0	power spectrum value within the roll-off bandwidth
D	fractal dimension
Dp	pillar diameter
Ei	Young modulus
E*	plain strain elastic modulus
G	energy release rate
Gc	interfacial toughness
H	Hurst parameter
Ki	stress intensity factor
L	pillar height
M = ζ1/ζ0	magnification
P	compressive indentation force
$\hat{P}$	dimensionless compressive indentation force
PC(Δ)	compressive force in the corresponding elastic contact problem without adhesion
Pn	pull-off force of a micropattern with n contacts
P0	pull-off force
R	sphere radius
Rp	full contact pressure ‘asperity’ radius
S	amplitude of the sinusoidal traction distribution
T	tangential load
U	elastic strain energy
a	the smallest length scale associated with the geometry
drep	characteristic diameter of repulsive contact areas
f(ψ)	mode mixity function
g	separation
gmax	critical separation in Maugis potential, gmax = Δγ/σ0
h	layer thickness
$h_{\mathrm{rms}},h_{\mathrm{rms}}^{\mathrm{\prime }},h_{\mathrm{rms}}^{\mathrm{\prime }\mathrm{\prime }}$	respectively, surface height, slope, curvature root mean square
k	Winkler foundation modulus
k(ζ)	wavenumber-dependent stiffness
krep	repulsive area–load slope
l	interfacial crack advancing at the interface
la = Δγ/E*	characteristic adhesion length
mn	nth order moment of height PSD
$m_n^{\hspace{0.17em}p}$	nth order moment of traction PSD
pnom	nominal pressure
s	contact splitting efficiency
s0	length scale associated with the singular traction field
u	elastic deformation
un	Fourier series coefficients
Γ	interface energy
Δ	indentation depth, or (for the layer) gap that would exist between a layer and a plane surface in the absence of elastic deformation
$\hat{\mathrm{\Delta }}$	dimensionless indentation depth
Δγ	interface energy per unit area
Δr	range of attractive forces in PR theory
Π	total potential energy
Ω	potential energy of external forces
Φ(g)	probability distribution function of gaps
Φ(p)	probability distribution function of pressure
α	interaction parameter
αA	fitting area reduction coefficient
β = Eɛ2/hΔγ	dimensionless parameter for layer instability
γ	fitting parameter in Persson load-separation theory
ɛ	equilibrium position
ζ = 2π/λ	wavenumber, with λ the corresponding wavelength
ζL	low wavenumber truncation
ζ0	roll-off wavenumber
ζ1	high wavenumber truncation
θFT	Fuller & Tabor parameter
μ	Tabor parameter
νi	Poisson’s ratio
ξ = x/h	dimensionless coordinate
σ	traction [tensile positive]
σP	pull-off stress
σy	yield strength
σ0	maximum tensile traction [theoretical strength]
ψ	phase angle

2. Contact of a sphere on a plane

Equation (1.1) can be integrated to determine the force transmitted between two rigid bodies of known shape and relative position. In particular, if a sphere of radius R is placed near a half plane, the maximum tensile force (the pull-off force) occurs when the point of closest approach is equal to ɛ and is of magnitude 2πRΔγ. Bradley [4] obtained this result by integrating the intermolecular force law over two finite spheres of radius R₁, R₂ and then dropping terms of the order ɛ/R_i, i = 1, 2. This approach was extended by Rumpf [5] and Rabinovich et al. [6] to estimate the adhesive force between a small spherical particle and a rough surface, characterized as a set of spherical asperities. These equations showed that even small amplitude of roughness decreases pull-off by large factors.

2.1. The Johnson, Kendall and Roberts theory

If the contacting bodies are deformable, equation (1.1) can be combined with an analysis of the deformation, but the resulting boundary-value problem is highly nonlinear and generally can only be solved by numerical methods. An approximation introduced by Johnson et al. [7] retains the Signorini dichotomy between regions of contact and separation, but relaxes the requirement that contact tractions be non-tensile. The total potential energy Π = U + Ω − Γ is then computed as the sum of elastic strain energy U, potential energy of external forces Ω and interface energy Γ = A_cΔγ, where A_c is the total contact area. The partition into areas of contact and separation is then determined so as to minimize Π. This is now generally known as the JKR solution. Conceptually, it is identical to Griffith’s theory of fracture and hence is equivalent to linear elastic fracture mechanics (LEFM), with Δγ playing the role of the critical energy release rate G_c. It follows that an alternative formulation is to demand that the contact traction be square-root singular at all edges of the contact area, with stress intensity factor

$$K_{\mathrm{I}}=\sqrt{2E^{\ast }\mathrm{\Delta }\gamma },\text{where}\hspace{0.17em}\frac{1}{E^{\ast }}=\frac{1-{\nu }_1^2}{E_1}+\frac{1-{\nu }_2^2}{E_2}$$ 2.1

and E_i, ν_i are Young’s modulus and Poisson’s ratio, respectively, for the two bodies, with i = 1, 2. For the sphere, the (compressive) indentation force P, the contact radius a and the indentation depth Δ are related by the equations

$$\hat{P}=\frac{4{\hat{a}}^3}{3\pi }-\frac{4{\hat{a}}^{3/2}}{\sqrt{2\pi }}\hat{\mathrm{\Delta }}={\hat{a}}^2-\sqrt{2\pi \hat{a}},$$ 2.2

where the dimensionless parameters

$$\begin{array}{rl}\hat{P}& =\frac{P}{\pi R\mathrm{\Delta }\gamma };\hat{a}={\left(\frac{E^{\ast }R}{\mathrm{\Delta }\gamma }\right)}^{1/3}\frac{a}{R}\text{and}\\ \hat{\mathrm{\Delta }}& ={\left(\frac{E^{\ast }R}{\mathrm{\Delta }\gamma }\right)}^{2/3}\frac{\mathrm{\Delta }}{R}.\end{array}$$ 2.3

The resulting relation between $\hat{P}$ and $\hat{\mathrm{\Delta }}$ is shown in figure 2.

Figure 2.

JKR solution for the relation between dimensionless compressive force $\hat{P}$ and indentation $\hat{\mathrm{\Delta }}$ for the contact of a sphere and a plane.

In this figure, the pull-off force under force control is defined by point B and corresponds to P = −3πRΔγ/2, which differs from Bradley’s rigid-body value only by a factor 3/4. Under force control, only points to the right of B are stable, whereas, under displacement control, stability is retained to the maximum negative indentation at A. In either case, once the limiting point is reached, the sphere will jump out of contact and some energy will be dissipated, presumably in the form of elastodynamic waves. Similarly, if the sphere is slowly brought to approach the half space, it will jump into contact from the origin to point B, again with a loss of energy. A sequence of contact and separation cycles, therefore, implies a hysteretic loss of energy.

The original JKR solution considered only the contact of a sphere on a plane, but the same technique can be applied to any geometry for which the corresponding boundary-value problem can be solved. For example, Johnson [8] gave the solution for a body with a sinusoidal surface in partial contact with a plane. Also, the energetic argument can be used to obtain numerical solutions using a boundary-element approach. For example, Popov et al. [9] used this approach to determine the pull-off force–displacement relation for flat rigid punches of various planforms. They showed that under displacement control, final detachment occurs from a contact area approximately identified with a circle inscribed in the planform, but that the maximum tensile force occurs before this state is reached.

2.2. A generalization of the Johnson, Kendall and Roberts calculation

Johnson et al. [7] determined the elastic strain energy U for the sphere problem by following the two-step scenario shown in figure 3. The contact is first loaded in compression to load P₁ establishing a contact area A₁. The contact area is then held constant whilst the load is reduced to P₂. During this second phase, the load–displacement relation is linear as shown in the figure, and hence

$$P_2=P_1-({\mathrm{\Delta }}_1-{\mathrm{\Delta }}_2){\left(\frac{\mathrm{\partial }P}{\mathrm{\partial }\mathrm{\Delta }}\right)}_{{\mathrm{\Delta }}_1}.$$ 2.4

Figure 3.

Two-step loading scenario. (i) ‘Repulsive’ loading without adhesive forces until a given contact area is reached (point A in the figure). (ii) Unloading at constant total contact area up point B.

If the final value of displacement Δ₂ is prescribed (displacement control), the contact area A₁ and hence Δ₁ must be chosen so as to minimize the total potential energy

$$\mathit{\Pi }=U-A_1\mathrm{\Delta }\gamma .$$ 2.5

We obtain

$$\frac{\mathrm{\partial }\mathit{\Pi }}{\mathrm{\partial }{A}_1}=0\text{and hence}\hspace{0.17em}\frac{\mathrm{\partial }U}{\mathrm{\partial }{A}_1}=\frac{\mathrm{\partial }U}{\mathrm{\partial }{\mathrm{\Delta }}_1}\frac{\mathrm{\partial }{\mathrm{\Delta }}_1}{\mathrm{\partial }{A}_1}=\mathrm{\Delta }\gamma .$$ 2.6

Using figure 3 to determine U as a function of Δ₁, Δ₂, we finally obtain

$${\mathrm{\Delta }}_2={\mathrm{\Delta }}_1-\sqrt{2\mathrm{\Delta }\gamma \frac{\mathrm{\partial }{A}_1}{\mathrm{\partial }{\mathrm{\Delta }}_1}/\frac{{\mathrm{\partial }}^2{P}_1}{\mathrm{\partial }{{\mathrm{\Delta }}_1}^2}}$$ 2.7

[10], which defines a general relation between the adhesive solution and that without adhesion. Strictly, the argument requires that the contact area be such as to give a uniform stress intensity factor around the perimeter as in axisymmetric problems, but it might reasonably be expected to give good approximations in other cases.

2.3. The Tabor parameter

A numerical solution [11] of the problem for a sphere using the traction law of equation (1.1) shows that the pull-off force P₀ is a continuous function of the Tabor parameter

$$\mu ={\hspace{0.17em}}^3\sqrt{\frac{R{(\mathrm{\Delta }\gamma )}^2}{{E^{\ast }}^2{\epsilon }^3}},$$ 2.8

[12], tending to the Bradley rigid-body value of 2πRΔγ at μ = 0 and to the JKR value of (3/2)πRΔγ as μ → ∞. Equation (2.8) contains the radius R and hence is specific to the spherical contact problem. However, since the JKR solution is formally identical to linear elastic fracture mechanics, a more general expression can be obtained by analogy with the ‘small-scale yielding’ criterion. The tensile contact tractions near the boundary of the contact region are given by

$$\sigma (x)=\frac{K_{\mathrm{I}}}{\sqrt{2\pi x}},$$ 2.9

where x is the perpendicular distance from the boundary, so the width of the region in which this traction exceeds the theoretical strength σ₀ is

$$s_0=\frac{E^{\ast }\mathrm{\Delta }\gamma }{\pi {\sigma }_0^2}.$$ 2.10

As in LEFM, the JKR solution is expected to provide a good approximation if s₀ ≪ a_min, where a_min is the smallest length scale associated with the geometry of the problem—e.g. the smallest width of the contact region, or of the separation region. We can then define a generalized Tabor parameter [13]

$$\mu =\sqrt{\frac{0.21a_{min}}{s_0}},$$ 2.11

where the numerical factor is included to ensure that it reduces to the conventional definition in the case of the sphere, with a_min then being the radius of the circular contact area at pull-off. To put this in perspective, if we make an ‘engineering’ interpretation of s₀ ≪ a_min as being roughly equivalent to s₀ < 0.05a_min, equation (2.11) implies that the JKR solution should provide a reasonable approximation for μ > 2, and this is consistent with results for the sphere [11].

2.4. Solutions for lower values of μ

The JKR solution approaches the exact solution asymptotically as μ → ∞, and it is natural to seek a corresponding solution for the case μ → 0. For small values of μ, many authors use a strategy which can be summarized as

• (i)Solve the problem neglecting adhesive tractions—i.e. using the Signorini boundary conditions.
• (ii)Find the gap between the surfaces in the separation region in step 1.
• (iii)Calculate a ‘correction’ to the contact force based on the adhesive tractions that would be predicted in such a gap.
• (iv)Neglect any further elastic deformation that might be expected from these adhesive tractions.

This approach has come to be known as the DMT method, since it was first introduced by Derjaguin et al. [14], who however used only the van der Waals term from equation (1.1) in step 3. If the bodies are strictly rigid so μ = 0, no elastic deformation occurs in step 1 and the DMT solution so defined is exact. However, it cannot be regarded as an asymptotic solution for small but finite μ, though many authors refer to this as the ‘DMT regime’. Indeed, Pashley [15] showed that the DMT method can give unrealistic predictions, notably that the pull-off force is always overestimated for any μ (the error increases with μ), and occurs at separations larger than zero, which contradicts the results of rigorous numerical solutions. Greenwood [16] gives a detailed criticism of the DMT method and offers an alternative ‘semi-rigid’ approach based on determining the elastic displacements due to the tractions predicted by the rigid theory. Derjaguin et al. [14] did not obtain a load–displacement relation analogous to the ‘JKR equation’ (2.2), but Maugis [17] developed an approximate relation by adding a constant ‘adhesive force’ 2πRΔγ to the Hertzian load, obtaining

$$\hat{P}=\frac{4{\hat{\mathrm{\Delta }}}^{3/2}}{3\pi }-2.$$ 2.12

Following Greenwood [18], we shall refer to this as the ‘DMT-M (DMT-Maugis) solution’.

Figure 4 shows a schematic of the DMT solution, where repulsive pressures only act in the area of contact, and adhesive forces only add to the Hertz problem outside the contact area. In the JKR solution, instead, both compressive and tensile stresses act in the area of contact, and nothing else occurs outside. Obviously, there are two very different necks: the Hertz neck of DMT, and the LEFM neck of JKR.

Figure 4.

Sketch of traction distributions in DMT and JKR type of solution. In DMT, the contact area coincides with that obtained from the non-adhesive problem, the adhesive tractions are thus confined in the separated zone. In a JKR solution, both compressive and adhesive tractions are exchanged within the contact area. (Online version in colour.)

2.4.1. Approximation of the traction law

An alternative strategy appropriate for intermediate values of μ is to approximate the traction law (1.1) to make the resulting boundary-value problem more tractable. Maugis [17] used a law in which the tensile tractions in the separation region are assumed to be constant and equal to the maximum value σ₀ from (1.1) over a range 0 < g < g_max, beyond which they are zero. The value of g_max is chosen such that the interface energy Δγ = σ₀g_max. This reduces the contact problem to a linear three-part boundary-value problem which can be solved in closed form for the case of the sphere. Alternatively, Greenwood & Johnson [19] showed that the superposition of two axisymmetric Hertzian traction distributions, one tensile and one (over a smaller circle) compressive, could be chosen so as to satisfy the contact condition in the smaller circle. The traction in the surrounding annulus is then a single-valued function of the gap and parameters can be chosen so as to ensure that the maximum tensile traction is σ₀ and the implied interface energy is Δγ. Both these approaches predict a dependence of pull-off force on μ that is qualitatively similar, but not identical to the numerical solution [11].

2.4.2. Bearing area method

A much simpler approximation [20] appropriate for μ ≪ 1 is to use the Maugis–Dugdale force law [17], but to estimate the attractive area A_att (i.e. the area in which there is separation, but where 0 < g < g_max) as

$$A_{\mathrm{att}}(\mathrm{\Delta })\approx B(\mathrm{\Delta }+g_{max})-B(\mathrm{\Delta }),$$ 2.13

where B(Δ) is the bearing area—i.e. the area over which the bodies would need to interpenetrate each other if they were moved together through a distance Δ and there were no elastic deformation. The total compressive force applied to the indenter is then estimated as

$$P(\mathrm{\Delta })=P_{\mathrm{C}}(\mathrm{\Delta })-{\sigma }_{max}{A}_{\mathrm{att}}(\mathrm{\Delta }),$$ 2.14

where P_C(Δ) is the compressive force in the corresponding elastic contact problem without adhesion. For the sphere, this procedure gives exactly the DMT-M force–displacement relation of equation (2.12) and [17].

2.5. An adhesion map

The map of the contact of elastic spheres is given in figure 5 as given by Johnson & Greenwood [21], as the theory which dominates a certain range of (i) load and (ii) Tabor (or Maugis) parameter. For large compressive loads, it is seen that little is gained by using adhesive theories, as Hertz theory is a good approximation. For tensile loads (not shown in the figure), there is no alternative to adhesive theories, and intermediate cases depend on the Bradley [4] to JKR [7] transition. Recently, Ciavarella et al. [22] have shown that μ > 5 is not sufficient if one wants to model accurately the jump-in phenomenon and hence the hysteresis associated with the instabilities in getting in and out of contact. Strictly speaking, JKR is a solution valid only for very large Tabor parameters, and DMT is never an accurate solution. Maugis–Dugdale is a convenient solution for representing a transition between the DMT-M and the JKR regime, and Schwartz [23] has given an alternative solution which divides the surface energy into a JKR contribution and a DMT-M one.

Figure 5.

Adhesion map for a sphere. Depending on the dimensionless load and the Tabor parameter, the most appropriate model is indicated. M-D refers to Maugis–Dugdale model, see [17].

2.6. Effect of plastic deformation

If plastic deformation occurs during compressive loading, the effective (unloaded) profile of the contacting bodies is modified and this affects the pull-off force. If there is extensive plastic deformation, a crude approximation can be obtained by assuming that contact pressure p₀ at maximum compressive load P₀ is approximately uniform and equal to the hardness H, so the contact area is a circle of radius a₀ (larger than the Hertzian radius) where

$$P_0=\pi a_0^{2}H.$$ 2.15

We also note that H ≈ 3σ_Y, where σ_Y is the uniaxial yield stress. Johnson [24] used this result to estimate an equivalent radius R^′ for the sphere after elastic unloading as

$$R^{\mathrm{\prime }}=\frac{4E^{\ast }{a}_0}{3\pi H},$$ 2.16

by assuming that unloading is approximately defined by the Hertzian analysis from load P₀ and contact radius a₀. Using this value in the JKR solution (2.3) he then obtained an increased pull-off force

$$P_{\mathrm{c}}^{\mathrm{\prime }}=\frac{3\pi R^{\mathrm{\prime }}\mathrm{\Delta }\gamma }{2}=\frac{2E^{\ast }\mathrm{\Delta }\gamma a_0}{H}=2E^{\ast }\mathrm{\Delta }\gamma \sqrt{\frac{P_0}{\pi H^3}}.$$ 2.17

Note that the pull-off force now depends on the material properties H, E* and also increases with the square root of the maximum load during initial compression.

A more precise solution requires a full analysis of the elastic–plastic loading process, in particular, to determine the exact contact radius and traction distribution at maximum compressive load, followed by the exact elastic solution corresponding to unloading from this condition. Mesarovic & Johnson [25] showed that even at large compressive preloads, Johnson’s approximation (2.17) underestimates the JKR pull-off force by a factor of 3π/4 due to Johnson’s unrealistic Hertzian assumption during unloading.

They also presented results using the Maugis–Dugdale cohesive-zone model, which they characterized in a space defined by the dimensionless parameters

$$\chi =\frac{\pi }{(2\pi -4)}\frac{E^{\ast }\mathrm{\Delta }\gamma }{p_0^2{a}_0};S=\frac{{\sigma }_0}{p_0}.$$ 2.18

The pull-off force is always close to the JKR value, to which it tends asymptotically when χ^2/3/S² → 0.

3. Experimental measurement of adhesive effects

Johnson et al. [7] conducted experiments on the contact between rubber and gelatin spheres and an optically smooth glass plate and confirmed some of the predictions of the theory described in §2. The spheres were carefully manufactured to have very low surface roughness to avoid the reduction of effective adhesion discussed in §5 below. In particular, they were able to observe the radius of the contact area as a function of contact force and showed that with a suitable choice of Δγ the results for spheres of different radii could be condensed onto a single curve close to the theoretical form.

More recently, in the field of tribology at the asperity scale, or ‘nanotribology’, we have seen a number of measurements of either friction or adhesion (or both) by means of two fundamental apparatuses: the surface force apparatus (SFA) and the atomic force microscope (AFM). The SFA was originally designed by Tabor & Winterton [26] at Cambridge University and later adapted by Israelachvili [27] to operate in aqueous solutions. It uses two crossed smooth cylinders, mathematically equivalent to a flat surface in contact with a sphere. The AFM is an apparatus of even higher resolution (of the order of fractions of a nanometre), and was invented by IBM scientists in 1982 (see [28]). Both SFA and AFM have permitted measurement of friction and adhesive forces in a single sliding experiment for a single asperity. Surprisingly the JKR equations are found to apply even down to very low dimensions, suggesting that friction can be characterized in the context of fracture mechanics. We shall discuss this approach in §7.

Measurements of adhesion are of course not restricted to the nanoscale. The theory of peeling of Kendall [29] is a classic which has been applied to the case of gecko feet, extended for multiple peeling by Pugno [30], and has been implemented numerically and verified experimentally by co-workers [31–33]. Experimental studies can be found in the book edited by Gorb [34], with emphasis on the surface features of biological systems (snake skin, adhesive pads, wing-interlocking devices as well as sticky mouthparts of insects, and finally anti-adhesive and adhesive surfaces of plants) clearly devised to increase/decrease friction and adhesion.

4. Thin elastic layers

Many engineering and scientific applications involve thin deformable layers supported by a relatively rigid foundation. Examples include rubber layers bonded to steel components and cartilage layers attached to bones. If an elastic layer of thickness h is bonded to a rigid foundation and then subjected to a uniform tensile traction σ, the only non-zero strain will be that in the thickness direction and the surface will move outwards through a distance

$$u=\frac{\sigma }{k},\text{where}\hspace{0.17em}k=\frac{E(1-\nu )}{(1+\nu )(1-2\nu )h}.$$ 4.1

Johnson [35] argued that this remains a good approximation under more general spatially varying tractions as long as the layer is ‘sufficiently thin’ meaning that h is small compared with the linear dimensions of the loaded area. The layer then acts like a Winkler foundation of ‘modulus’ k, with proportionality between local displacement and local traction. In particular, in non-conformal contact problems (such as indentation of an elastic layer by a sphere), the contact pressure then goes to zero at the edge of the contact area.

Johnson’s argument was extended to problems involving adhesive tractions by Yang [36] and Argatov et al. [37], using an energy argument analogous to that in the JKR theory [7]. They showed that the effect of interface energy was to change the boundary condition at the edge of the contact area from σ = 0 to $\sigma =\sqrt{2k\mathrm{\Delta }\gamma }$, which is independent of the contact geometry (as is the stress intensity factor (2.1) in the JKR theory).

If ν → 0.5, the modulus k → ∞, since the layer becomes incompressible. Deformation is still possible under non-uniform tractions, but involves the displacement of material in the plane of the layer [35]. Approximate solutions for the case with adhesive traction are given by Yang [38], Argatov et al. [37] and Papangelo [39].

4.1. Instabilities

The traction law σ(g) of equation (1.1) and figure 1 can be regarded as a nonlinear spring (with ranges of negative stiffness) in series with the linear spring associated with the modulus k of equation (4.1). For example, if Δ denotes the gap that would exist between a layer and a plane surface in the absence of elastic deformation, the actual gap will be g where

$$\mathrm{\Delta }=g+\frac{\sigma (g)}{k}\text{and hence}\hspace{0.17em}\frac{\mathrm{\partial }\mathrm{\Delta }}{\mathrm{\partial }g}=1+\frac{1}{k}\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }g}.$$ 4.2

The gap g and hence the traction σ(g) will be multi-valued functions of rigid-body approach Δ if there exist ranges where ∂Δ/∂ g < 0. Notice (for example, from figure 1) that any traction law involving adhesive tractions must exhibit a range of values of g in which the slope ∂σ/∂ g < 0, and from (4.2), instability is most likely to occur at the point where the magnitude of this negative slope is maximum. For the traction law of equation (1.1), this maximum slope occurs at g = (15/2)^1/6ɛ and is of magnitude 1.253Δγ/ɛ².

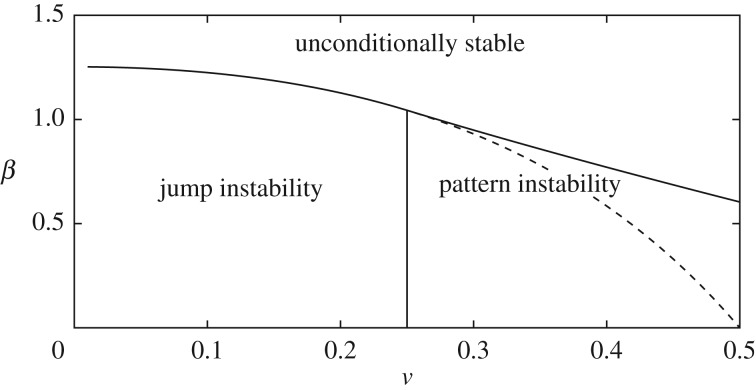
A typical case involving instability is illustrated in figure 6, where ν = 0.25 and the dimensionless parameter

$$\beta =\frac{E{\epsilon }^2}{h\mathrm{\Delta }\gamma }$$ 4.3

is equal to 0.5. If the bodies are initially widely separated, the tractions will be defined by the lower branch of the curve, but if Δ is reduced below Δ_A, there must then be a jump to the point B. A jump in the opposite direction from C to D is anticipated during subsequent separation, so that during an approach–separation cycle, there will be a hysteretic energy loss defined by the area ABCD.

Figure 6.

Adhesive traction σ as a function of rigid-body approach Δ (i.e. the gap that would exist in the absence of elastic deformation) for a layer with ν = 0.25 and β = 0.5. Jumps occur during approach from A to B and during separation from C to D as indicated by the dotted lines.

4.2. Sinusoidal instabilities

The uniform state defined by equation (4.2) can be unstable to non-uniform perturbations even where jumps are not predicted. It is convenient to define a dimensionless coordinate ξ = x/h in the plane of the layer. For a linear elastic layer, a sinusoidal traction distribution σ(ξ) = Scos(ζξ) will produce a surface displacement

$$u(\xi )=\frac{S}{k(\zeta )}\cos (\zeta \xi ),$$ 4.4

where k(ζ) is a wavenumber-dependent stiffness. For a uniform elastic layer bonded to a rigid foundation, we have

$$k(\zeta )=\frac{E\zeta \hspace{0.17em}[(3-4\nu )\cosh (2\zeta )+2{\zeta }^2+5-12\nu +8{\nu }^2]}{2h(1-{\nu }^2)[(3-4\nu )\sinh (2\zeta )-2\zeta ]}$$ 4.5

[40], which reduces to (4.1) in the limit ζ → 0. However, similar arguments can also be applied to more complex elastic systems such as multilayers or functionally graded layers, the only change being in the function k(ζ).

If the layer is placed such that the uniform solution of §4.1 involves a gap g₁, energetic arguments can be used to show that infinitesimal sinusoidal perturbations on this solution of wavenumber ζ will then be unstable if

$${\left(\frac{\mathrm{\partial }\sigma }{\mathrm{\partial }g}\right)}_{g=g_1}<-k(\zeta ),$$ 4.6

[41,42], so instability is most likely to occur at values of g₁ near the maximum negative slope of the traction law. With the Lennard–Jones law, this implies that instabilities are to be anticipated during the approach of an elastic layer to a plane surface unless

$$k(\zeta )>\frac{1.253\mathrm{\Delta }\gamma }{{\epsilon }^2}\text{or equivalently}\hspace{0.17em}\frac{E}{hk(\zeta )}<\frac{\beta }{1.253}$$ 4.7

for all ζ, from equations ((4.3), (4.6)).

Nonlinearity of the traction law (1.1) places limits on the growth of such a perturbation, but if the condition (4.6) is satisfied for some range of values of g₁, ζ, we might then anticipate the development of a spatially periodic deformation pattern during the approach of the layer to a plane surface.

Patterns of this kind have been predicted theoretically [41,42] and observed experimentally [43,44] mainly for incompressible layers for which the ‘uniform’ instability of §4.1 is suppressed. Gonuguntla et al. [43] have shown how this self-patterning behaviour can be used in the manufacture of patterned layers using lithography.

4.3. Periodic deformation patterns

Figure 7 shows contours of the gap g(x, y) for four stages of approach Δ for a layer with β = 0.25, ν = 0.5. These results were obtained using the Green’s function molecular dynamics (GFMD) algorithm of Persson & Scaraggi [45]. Since the material is incompressible, uniform instabilities of the type discussed in §3.1 cannot occur. The contours are defined as multiples of ɛ and the scale bar in figure 7a represents the layer thickness h.

Figure 7.

Contours of dimensionless local gap g(x, y)/ɛ during approach of a uniform incompressible layer to a plane surface. (a) Δ = 2ɛ, (b) 1.7ɛ, (c) 1.4ɛ, (d) 1.2ɛ. The contour scale applies to all four figures. (Online version in colour.)

During approach (Δ decreasing) the morphology is first defined by pillars of ‘contact’ (values of g close to ɛ) surrounded by regions with a much larger gap (a). Further reduction in Δ leads to the labyrinth pattern (b) and then an inverted labyrinth (c) where regions of contact are connected. The last stage (d) comprises a pattern of approximately circular separation regions surrounded by contact. The red line in figure 7d represents the wavelength corresponding to the most unstable sinusoidal perturbation (see §4.5 and figure 9 below).

Figure 9.

Dimensionless layer compliance as a function of wavenumber for an elastic layer bonded to a rigid foundation. We recall from condition (4.7) that instability occurs above the value β/1.253, and hence for ν = 0.5, low and high wavenumbers are both stable.

Theoretically, instability starts at the value of Δ at which an infinitesimal sinusoidal perturbation first becomes unstable. However, once a pattern is established, it persists beyond the range of linear instability and hence the traction curves for loading and unloading are different, as shown in figure 8. During progress from contact to separation, patterns develop before the theoretical point, presumably due to the use of finite increments in the iterative algorithm.

Figure 8.

Relation between mean traction and rigid-body separation Δ for β = 0.25, ν = 0.5. The black line represents the uniform traction solution of equation (1.1). It is unstable between the vertical dashed lines. (Online version in colour.)

4.4. Determination of patterns using series methods

An alternative approach for approximating these patterns is to represent the elastic deformation as a finite Fourier series and use the Rayleigh–Ritz method for determining the coefficients. For example, in two dimensions we write

$$u(\xi )=\sum _{n=0}^N{u}_n\cos (n{\zeta }_0\xi ),$$ 4.8

where ζ₀ is a fundamental wavenumber that might be related to the finite dimension of the contact surface. The elastic strain energy per unit area is then

$$U=\frac{1}{2}k(0)u_0^2+\frac{1}{4}\sum _{n=1}^{N}k(n{\zeta }_0)u_n^2$$ 4.9

and the interface energy per unit area is defined by

$$\mathit{\Gamma }=\frac{{\zeta }_0}{2\pi }{\int }_0^{2\pi /{\zeta }_0}\hspace{0.17em}\text{d}\xi {\int }_{\mathrm{\Delta }-u(\xi )}^{\mathrm{\infty }}\sigma (g)\hspace{0.17em}\text{d}g.$$ 4.10

The coefficients u_n are then determined using an appropriate optimization algorithm so as to minimize the total energy Π = U − Γ for a given value of approach Δ [42]. The same technique was extended to three-dimensional patterns by Gonuguntla et al. [43] using a double Fourier series.

4.5. Effect of material parameters

Figure 9 shows the dimensionless layer compliance (reciprocal of stiffness) E/hk(ζ) as a function of wavenumber ζ for the bonded layer defined by equation (4.5) for various values of Poisson’s ratio ν.

We note from figure 9 that the curves for ν > 0.25 exhibit a maximum at some value ζ = ζ₀ > 0, whereas for ν ≤ 0.25, the maximum occurs at ζ = 0. In both cases, instability will commence when the gap g = g₁ in the uniform solution reaches the value at which ∂σ/∂g first satisfies (4.6). For ν ≤ 0.25 the first unstable condition corresponds to a uniform perturbation [ζ = 0] and hence occurs at the point A during loading and C during unloading in figure 6. The unstable response comprises a sudden change (jump) in uniform traction as indicated.

For ν > 0.25, the maximum compliance occurs at a non-zero wavenumber ζ₀ and we anticipate the development of a pattern with this periodicity, at least near the value of g at which (4.6) is first satisfied. This behaviour is shown schematically in figure 10 for the Lennard–Jones traction law.

Figure 10.

Dependence of stability behaviour on ν and β.

The dashed line in this figure defines the value of β below which a uniform perturbation [ζ = 0] is also unstable. In this region, the non-uniform instability is triggered before the uniform one and generally dominates the subsequent behaviour. However, this requires that a representative in-plane dimension L of the layer be large enough to accommodate at least one wavelength of an unstable sinusoidal perturbation. In most practical cases h ≪ L and which ensures that this condition is satisfied except for values of ν quite close to 0.5.

Similar calculations can be performed for more complex layers. In particular, we note that for a bi-material layer, the dimensionless compliance may exhibit two distinct maxima [46]. In such cases, the absolute maximum of the curve defines the first instability during either approach or separation and generally dominates the subsequent pattern development.

5. Effect of roughness on adhesion

If surfaces were perfectly plane, van der Waals forces would imply that two such bodies brought into contact would be indistinguishable from a single monolithic body and could only be separated by a fracture process involving the application of tractions equal to the theoretical strength σ₀. The fact that this does not generally happen is due to the microscopic roughness of practical surfaces. Numerous authors [47] have developed models to characterize and quantify the effect of surface roughness on solid contact, often motivated by the attempt to explain Amontons’ law of friction. However, most of these models are based on the Signorini dichotomy between contact and separation, and do not include adhesive (tensile) tractions. For ‘stiff’ materials such as metals, with macroscopic roughness (typically much larger in amplitude than the range of attractive tractions), this assumption is reasonable, but recent emphasis on flexible materials such as polymers and biotissues makes the interaction between adhesion and roughness particularly relevant.

5.1. Fuller & Tabor

The first theoretical investigation of the effect of roughness on adhesion was that of Fuller & Tabor [48], who followed Greenwood & Williamson (GW) [49] in modelling the rough surface as a set of identical spherical asperities of radius R whose peak heights follow a Gaussian distribution with standard deviation h_rms, but who used the JKR solution of §2.1 to describe the individual asperity contacts. They predicted that the pull-off force should decrease drastically with h_rms and that this effect is characterized by the dimensionless parameter

$${\theta }_{\mathrm{FT}}=\frac{h_{\mathrm{rms}}^{3/2}{E}^{\ast }}{R^{1/2}\mathrm{\Delta }\gamma },$$ 5.1

where we note that Δγ/E* defines a characteristic adhesion length which for contact of similar materials is related to ɛ of equation (1.1).

Fuller & Tabor also conducted experiments with rubber spheres contacting a perspex plane with varying roughness amplitudes and obtained results that correlate well with the theory (figure 11). This is surprising in view of the fact that the Fuller & Tabor theory suffers from even more limitations than the original GW theory [50] and the theory was developed for the contact of nominally plane bodies, rather than for a sphere on a plane. Strictly speaking, therefore, the good qualitative experimental agreement might be considered fortuitous.

Figure 11.

Relative pull-off decay force for three different elastic moduli and increasing centre line average roughness in Fuller & Tabor experiments (from [48]). Solid lines represent Fuller & Tabor predictions while shaded areas show the regions where experimental measurements lie.

5.2. Fractal surfaces

A not obvious aspect of Fuller & Tabor’s adhesion parameter (5.1) is that it contains the (mean) asperity radius R, which for random rough surfaces is proportional to $m_4^{-1/2}$ [51], where m₄ is the fourth moment of the power spectral density (PSD) of the profile. However, modern studies of nominally flat rough surfaces often assume a Gaussian isotropic two-dimensional roughness with a PSD of the power-law form

$$C(\zeta )=\{\begin{array}{cc}{C}_0,& {\zeta }_L<\zeta <{\zeta }_0\\ C_0{\left(\frac{\zeta }{{\zeta }_0}\right)}^{-2(H+1)},& {\zeta }_0<\zeta <{\zeta }_1\\ 0,& \zeta >{\zeta }_1\end{array}$$ 5.2

as shown in figure 12, where ζ is the wavenumber and to make the surface more closely Gaussian, we have introduced a ‘roll-off’ region of constant PSD. The power-law segment in equation (5.2) typically extends over three or four decades so the roughness has a profound ‘multi-scale’ character and is ‘self-affine’ (a generalization of the concept of ‘self-similarity’), i.e. with a proper rescaling of in-plane and normal coordinates its statistical properties are insensitive to the length scale at which the roughness is observed (figure 13). The slope in the power-law range is characterized by the Hurst exponent H, or equivalently by the fractal dimension D = 3 − H. With this PSD, m₄ depends heavily on the choice of the abrupt truncation at ζ = ζ₁ which in the case of measured surfaces is determined by the resolution or the sampling interval of the measuring instrument. Thus the asperity radii continue to decrease down to atomic scales, where asperities are defined by only a few atoms. This resolution-dependence has been much criticized, and in the fractal limit it means that no real surface should be sticky independently on the rms amplitude of roughness, a result which looks paradoxical. However, we shall see that even many more recent models predict paradoxical resolution dependence of stickiness, and the subject is still controversial. It is perhaps remarkable that in the literature about elastic contact of fractal surfaces, very little or no attention is given to how to really define this ‘magnification’ M = ζ₁/ζ₀ in practical problems, and this is left to the user to address in terms of his application. However, not being a trivial issue for those quantities which strongly depend on this choice of magnification, perhaps more effort is needed in the future and experimental assessment of theories.

Figure 12.

Log–log plot of the typical spectrum of surface roughness which is used today to model idealized nominally flat Gaussian rough fractal surfaces. (Online version in colour.)

Figure 13.

Fractal character of self-affine rough surfaces. After a proper rescaling of in-plane and normal coordinates, the statistical properties of roughness are insensitive to the length scale at which they are observed (M = ζ₁/ζ₀, ‘magnification’). (Online version in colour.)

5.3. Contact of multi-scale surfaces without adhesion

Curiously, a true multi-scale model of rough surfaces was originally discussed (without reference to adhesion) by Archard [52] as long ago as 1957. Ciavarella et al. [53] extended these concepts to a true fractal profile (the Weierstrass series), and found a paradoxical fractal ‘limit’ in which the contact is restricted to an infinite number of infinitesimal contact areas, each sustaining an infinite contact pressure. This anticipated Persson’s ‘resolution-dependent’ solution [54] of the adhesionless rough contact problem which at low nominal pressures p_nom predicted that the total actual contact area A_c is given by

$$\frac{A_{\mathrm{c}}}{A_{\mathrm{nom}}}\sim \frac{\hspace{0.17em}{p}_{\mathrm{nom}}}{E^{\ast }}\frac{1}{\sqrt{m_2}}$$ 5.3

where A_nom is the ‘nominal’ or ‘apparent’ contact area and m₂ is the second moment of the height PSD which also coincides with the slope variance. This dependence on rms slope is sensitive to the PSD truncation, so (e.g.) A_c → 0 as ζ₁ → ∞ in equation (5.2) [55]. Surprisingly, an identical result is obtained from asperity models [56] except for the exact prefactor, and this result caused quite a discussion in the literature [57,58].

An arguably more important conclusion for adhesionless contact due to Persson [59] is that some macroscopic relationships, notably that between load and displacement, tend to a converged result in the fractal limit, whereas asperity model theories remain ill-posed as a result of neglecting interaction effects unless these are introduced numerically [60]. Particularly, rapid convergence is found for the important case of low fractal dimension. Specifically, for D ≃ 2.2 Persson [59] gives

$$\frac{\hspace{0.17em}{p}_{\mathrm{nom}}(g)}{E^{\ast }}\simeq {\zeta }_0{h}_{\mathrm{rms}}\exp \left(\frac{-\overline{g}}{\gamma h_{\mathrm{rms}}}\right),$$ 5.4

where $\overline{g}$ is the mean separation, γ ≃ 0.5 and $h_{\mathrm{rms}}=\sqrt{m_0}$ is the rms height, which depends only weakly on the truncation ζ₁. Note that the height variance m₀ coincides with the zeroth moment of the PSD (see [61]). Another relationship that is only weakly dependent on fine scale roughness is that between electrical contact resistance and nominal pressure [62].

Equations (5.4) and (5.3) are exemplary of two types of result in the contact of fractal rough surfaces: those that are determined primarily at the coarse scale and that are therefore not sensitive to measurement resolution, and those that are not convergent and that give paradoxical predictions when ultrafine scale features are included.

5.4. DMT-type solutions

We first remark that both JKR and DMT solutions of §§2.1 and 2.4, respectively, retain a dichotomy between regions of contact and separation and hence can be expected to give results that are sensitive to the truncation limit ζ₁. Of the two approaches, the JKR method seems to be the less appropriate, since we anticipate large numbers of contact areas whose linear dimensions are likely to be small compared with s₀ of equation (2.10). However, it should be emphasized that the Tabor parameter of §2.3 cannot be directly applied to rough surface contact. Attempts to define a generalized Tabor parameter for rough surface contact [45,63,64] generally predict that this parameter will tend to zero in the fractal limit [ζ₁ → ∞], seeming to imply that a rigid-body (Bradley) solution would be appropriate in this limit. However, elastic deformation occurs on all length scales and is not rendered negligible by the presence of additional arbitrarily short wavelength roughness.

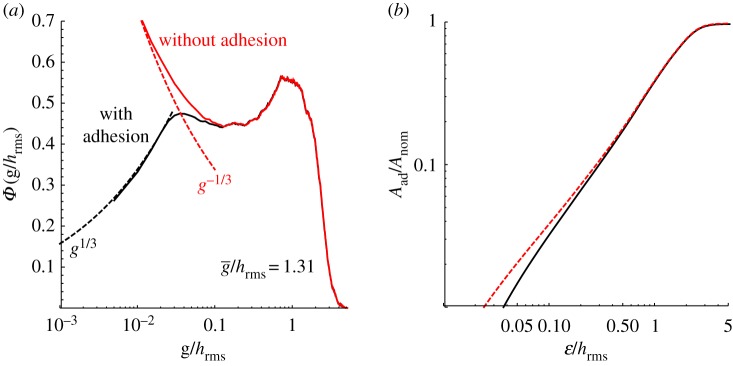
We can obtain some idea of the order of approximation implicit in the DMT solution with respect to the case of a nominally flat rough surface, using the data published in Müser’s recent ‘contact mechanics challenge’ (fig. 8 of [65]). The characteristic length scale of adhesion for the exponential cohesive-zone model used there is ɛ ≃ 2 nm, while h_rms = 0.762 µm, so ɛ/h_rms ≃ 3 × 10⁻³. Figure 14a shows the gap distribution function Φ(g) obtained with accurate numerical solutions (i) without adhesion, where we find a tendency towards the relation Φ(g) ∼ g^−1/3, as predicted by asymptotic analysis at the contact edge, and (ii) with adhesion, where there is no simple theory to predict the asymptotics, but where curiously there is an even better fit with a law Φ(g) ∼ g^1/3, which however we are not able to explain. The results show that the inclusion of adhesive tractions affects the gap distribution only in the range g/h_rms < 0.1, and imply that the DMT solution will tend to overestimate the area of adhesion¹ and the resulting force of adhesion (figure 14b). Note that since Φ(g) is a probability distribution function (PDF) the area under each curve should sum to 1, which they do, despite the differences in the initial trend.

Figure 14.

(a) Gap distribution function Φ(g) obtained with Green’s function molecular dynamics (GFMD) with and without adhesion, for mean gap $\overline{g}/h_{\mathrm{rms}}=1.31$. Data from [65]. (b) Estimated adhesive contact area fraction (dashed/solid line, respectively, with/without adhesion): $A_{\mathrm{ad}}/A_{\mathrm{nom}}={\int }_0^{\epsilon }\mathit{\Phi }(g)\hspace{0.17em}\text{d}g.$ (Online version in colour.)

Persson & Scaraggi [45] developed a DMT-type solution for contact of nominally flat rough surfaces, where the adhesionless Persson’s solution could be used since it contains an approximate expression for the probability distribution Φ(g) for the local gap g between the surfaces in regions of separation which could then be convoluted with any desired traction–separation law to obtain the nominal traction, as in the ‘force’ version of the DMT theory. Their results show a large dependence on the exact shape of the force–separation law when amplitude of roughness is low, which is to be expected since in the limit of no roughness, the traction–separation law itself should be re-obtained. However, comparison with a previous (JKR-based) theory [66] seem to indicate large discrepancies, and there was no detailed investigation of the effect of increasing truncation at ζ = ζ₁ .

5.4.1. Numerical solutions

Persson and Scaraggi compared their theoretical predictions with a numerical solution using a ‘Green’s function molecular dynamics’ (GFMD) algorithm, a method that has been extensively used for such studies. Essentially, the elastic deformation is related to the discretized normal traction using an appropriate Green’s function, but the resulting set of nonlinear equations at nodal points is solved using a molecular dynamics algorithm. Solutions are typically obtained over a rectangular grid with initial nodal heights chosen to approximate a surface with the PSD of equation (figure 12). However, computational considerations place limits on the practical mesh refinement, so that even the most sophisticated codes such as those of Pastewka & Robbins [63] and that used in Müser’s recent ‘contact mechanics challenge’ [65] can only describe surfaces with PSDs spanning about three decades—e.g. nanometre to micrometre scales.

Pastewka & Robbins [63] developed a numerical model in which the nodes are identified with the atoms at the plane surface of an fcc crystal in a square region with sides in the range 512a₀ to 8192a₀, the latter corresponding to around 1 μm with typical interatomic spacings a₀. Periodic boundary conditions were imposed at the edges of the modelled region and the interaction of surface atoms with a rigid indenting rough surface was governed by a force law approximating (and truncating) the Lennard–Jones law [1].

5.4.2. Pastewka & Robbins’ stickiness criterion

In their numerical solution, Pastewka & Robbins [63] define the contact area A_rep as comprising those atoms experiencing repulsive (compressive) forces and observe that at small applied loads N, it remains approximately linear with load [compare with the adhesionless equation (5.4)] even in the presence of adhesion. The morphology of the regions defining A_rep at appropriate force levels was found to be only weakly dependent on adhesion, suggesting that we are in the DMT regime. If this is assumed to be exactly true, we can construct a DMT solution by (i) finding the relation between A_rep and N without adhesion, and then (ii) modifying N by summing the tensile tractions in regions close to the perimeter of A_rep. Based on their numerical observations, Pastewka & Robbins estimate this correction by assuming the existence of a ‘boundary layer’ of tractions, leading to a term proportional to the perimeter, and on the basis of this calculation they define a criterion for ‘stickiness’ such that as we move from the condition A_rep = 0 (complete separation), the normal load initially becomes tensile, implying that there must be another state with N = 0 but A_rep > 0. They also make the interesting observation that the fractal dimension of A_rep is the same as that of its perimeter.

Pastewka & Robbins’ stickiness criterion contains the slope and curvature variances of the surface and if these parameters are expressed in terms of the PSD (figure 12), it can be shown that stickiness requires that

$${\zeta }_1^{(1-5H/3)}<C,$$ 5.5

where C is a positive constant. Hence, in the fractal limit ζ₁ → ∞, all surfaces with D < 2.4 should be sticky, and no surfaces with D > 2.4 should be sticky. This conclusion seems quite counterintuitive and we shall find it in contrast with two more recent theories we discuss in the next two sections, which define stickiness based on ‘pull-off’. There seems to be a possible conflict in the definition of stickiness, but recent investigations [67] have clarified that this is contradicted even by Persson & Scaraggi’s model [45].

5.4.3. Violano and co-authors stickiness criterion

A more precise analysis of Pastewka & Robbins’ theory was conducted by Violano et al. [67] where the authors showed that the probability density function of gaps (obtained by Persson & Scaraggi’s theory as improved by Afferrante et al. [68]) converges with increasing magnification ζ, thus, in the fractal limit, any DMT theory should not depend on the PSD wavenumber cut-off ζ₁. Violano and co-authors [67] showed that the area–load slope, at the origin, depends only on well-defined macroscopic quantities, such as h_rms and the lowest wavenumber ζ₀, which is in contrast with previous stickiness criteria by Pastewka & Robbins [63] and Fuller & Tabor [48]. Violano et al. [67] suggests that for low fractal dimension (D ≃ 2.2) rough hard surfaces stick for

$$\frac{h_{\mathrm{rms}}}{ϵ}<{\left(\frac{9}{4}\frac{{\sigma }_0/E^{\ast }}{ϵ{\zeta }_0}\right)}^{3/5},$$ 5.6

which, when compared with real surfaces measurements, gives justification to the qualitative well known empirical Dalhquist criterion for stickiness which demands adhesives to have elastic modulus lower than about 1 MPa.

5.4.4. BAM solution

Ciavarella [20] applied the BAM approximation (discussed in the context of the spherical contact problem in §2.4.2) to the case of nominally flat bodies with Gaussian random roughness. This approach has the advantage of resulting in a closed form solution and has similarities with DMT-like models in that some parts of the repulsive solution are used for the adhesive problem. However, rather than estimating local separations and convoluting them with a given force–separation law (as done by Persson & Scaraggi [45]), BAM assumes the simplified Maugis–Dugdale force-separation law and makes an independent estimate for the repulsive and adhesive components of the load. The results [20] show that the pull-off traction is principally determined by h_rms, ζ₀ and becomes independent of the short wavelength truncation ζ₁, as in the adhesionless load–separation relation (5.4). Therefore, we can easily construct counterexamples to the predictions of the Pastewka–Robbins criterion (5.5).

5.4.5. Joe et al.’s theory

Persson’s adhesionless theory [54] tracks the evolution of the probability distribution Φ(p) for contact pressure as infinitesimal increments of the roughness PSD are added. Joe et al. [69] adapted this approach using instead the distribution Φ(g) of the local gap g, the evolution of which was determined by performing a linear perturbation on the interaction between elastic deformation and the Lennard–Jones force law. The results agree well with those from the GFMD algorithm due to Persson & Scaraggi [45] for a relatively narrow-band PSD, and in particular they exhibit convergence of the relation between mean traction $\overline{\sigma }$ and mean gap $\overline{g}$ as the truncation wavenumber ζ₁ is increased without limit.

This method can be applied only to relatively fine-scale (short wavelength) roughness, since longer wavelengths interacting with the Lennard–Jones force law exhibit instabilities of the kind discussed in §4.2. However, if a broader PSD is partitioned into two tranches, the theory can be used to determine the relation $\overline{\sigma }(\overline{g})$ for the fine-scale tranche alone, and the complete contact problem can then be regarded as one for the coarse-scale tranche alone, but with $\overline{\sigma }(\overline{g})$ functioning as a modified force law that accounts for the presence of the fine scale roughness. Joe et al. [70] exploited this idea using an iterative approach to predict the relation $\overline{\sigma }(\overline{g})$ for broadband PSDs of the form (5.2). They also presented contour plots for pull-off traction and effective (reduced) interface energy as functions of m₀ and the lower truncated wavenumber ζ₀ for PSDs without the ‘roll-off’ range below ζ₀. Sinusoidal instabilities are still possible (and indeed are physically reasonable) for relatively smooth surfaces with long wavelength content, but in the stable range, the pull-off traction is predominantly determined by the height standard deviation h_rms or equivalently m₀. Figure 15 shows a comparison between the prediction of pull-off traction for three different values of ζ₀ using this theory (points) and using the BAM approximation from §2.4.2 (lines).

Figure 15.

Comparison between BAM (lines) and Joe et al.'s theory (points) for the normalized pull-off traction as a function of height standard deviation for the three cases E*ɛζ₀/σ₀ = 0.053, 0.213 and 0.53. Note that for a pure power law PSD $h_{\mathrm{rms}}\simeq \sqrt{\pi C_0/H}{\zeta }_0$. (Online version in colour.)

5.5. Johnson, Kendall and Roberts models

If we substitute the mean asperity radius for R in the definition of the Tabor parameter (2.8), the resulting value will generally imply that a JKR formulation is inappropriate for rough surface contact, unless an unrealistically small value is taken for the truncation wavenumber ζ₁. With this in mind, Maugis [2] modified Fuller & Tabor’s theory [48] to replace the JKR force–displacement law for an individual asperity by a DMT-M law, and showed that the predicted adhesion reduction was still dependent on the parameter θ of equation (5.1), with very minor differences. This is however most probably due to the very strong assumption of independent asperities behaviour.

Despite the limitation to coarse-scale roughness, the mathematical simplicity of the JKR approach has tempted many authors to use it, but reported results need to be interpreted with caution. Persson & Tosatti [71] defined an effective interface energy as the difference between the theoretical interface energy Δγ and the elastic strain energy in a state of full contact. This is essentially the work per unit area needed to separate the interface from a state of full contact. The elastic interface energy for full contact is unbounded for surfaces with fractal dimension D ≥ 2.5, so this theory would predict that such surfaces could never adhere, even for arbitrarily small height variance m₀. By contrast, for D < 2.5 full contact is predicted to be possible regardless of m₀. These results are inconsistent with the results of Joe et al. [69] and the BAM theory [20]. Persson & Tosatti also considered a possible enhancement of effective interface energy due to the fact that the area of a rough surface exceeds that of the projected plane, but if slopes are sufficiently large to make this term significant, the original basis of the calculation of Δγ from the interaction of adjacent atoms is itself questionable. In a later paper [66], Persson adapted his adhesionless contact theory by modifying the boundary condition at zero traction to include a scale-dependent finite detachment stress (the meaning of this stress is not very clear, and seems related to a ‘remote’ stress rather than a local one: clearly, in a JKR model, infinite negative stresses should be allowed). The predictions of these theories show both qualitative and quantitative discrepancies relative to numerical solutions, even when the latter are based on the JKR assumptions [72,73].

Afferrante et al. [74] extended the Weierstrass–Archard model [53] to include JKR adhesion, and found a similar conclusion: namely that for low fractal dimension, the contact area converges to a finite limit and full contact can occur at all scales. On the other hand, Ciavarella [10] showed that the (approximate) generalized JKR solution of §2.2 introduces a dependence on surface slopes even in the load–separation relationship, and predicts no adhesion in the fractal limit for all fractal dimensions, contrary to the theories of §§5.4.4, 5.4.5. The JKR formulation also leads to erroneous conclusions when applied in the limit ‘almost complete contact’, as we shall see in the next section.

5.5.1. Almost complete contact

In tribology, it is conventional to assume that the actual contact area is much smaller than the nominal area—in other words that A_c/A_nom ≪ 1 in equation (5.3). This view dates back to the pioneering studies of friction due to Bowden and Tabor [75], who argued that full contact (A_c = A_nom) is impossible, at least for rough metal surfaces, due to work hardening. The condition A_c/A_nom ≪ 1 is also a fundamental requirement for asperity models, since these clearly only make sense when contact is restricted to the highest points on the surface. However, with increased interest in flexible materials such as rubber and polymers, the possibility of larger contact ratios must be considered, even in the elastic regime, including cases where actual contact occurs everywhere except at the deepest depressions.

A good starting point for this discussion is Johnson’s surface energy solution [8] for the partial contact of bodies with one- and two-dimensional sinusoidal profiles. Johnson first determines the elastic contact traction required for full contact and then constructs the partial contact solution by superposing a correction comprising a set of ‘pressurized cracks’ opened by pressures equal and opposite to the tractions at full contact. This idea was extended by Xu et al. [76] for a rough surface in the absence of adhesion. In the case of full contact, the PSD for contact traction can be written down in terms of that for surface heights (e.g. equation (5.2)). In particular, the moments $m_n^{\hspace{0.17em}p}$ of the traction PSD are related to those of the height PSD through

$$\begin{array}{rl}{m}_0^{\hspace{0.17em}p}& =\frac{1}{2}{E}^{\ast 2}{m}_2,m_2^{\hspace{0.17em}p}=\frac{1}{3}{E}^{\ast 2}{m}_4\text{and}\\ m_4^{\hspace{0.17em}p}& =\frac{3}{10}{E}^{\ast 2}{m}_6\end{array}$$ 5.7

[77,78], and Nayak’s random surface theory [61] can then be used to determine the distribution and properties of tensile ‘peaks’ of this distribution. Each of these peaks defines a possible separation region and the total out-of-contact area is then determined by a summation analogous to that used in classical asperity model theories.

We note from equation (5.7) that the moments $m_n^{\hspace{0.17em}p}$ of the traction distribution are related to higher moments m_n+2 of the height distribution, which suggests that the results might be very sensitive to the truncation limit ζ₁. However, results show that the normalized total separation area depends only on the Nayak bandwidth parameter

$${\alpha }^{\hspace{0.17em}p}=\frac{m_0^{\hspace{0.17em}p}{m}_4^{\hspace{0.17em}p}}{{(m_2^{\hspace{0.17em}p})}^2}=\frac{27}{20}\frac{m_2{m}_6}{m_4^2}$$ 5.8

for the traction PSD, which is only weakly dependent on the truncation. Also, Ciavarella [79] has shown that if a bearing-area argument is used to estimate the separation area from the full contact pressure, and if a corrective factor 4/3 is used for this area, the Xu model leads exactly to Persson’s well-known solution [54]. A very detailed numerical investigation is difficult under almost full contact, but the comparisons in Ciavarella [79] seem to indicate that Persson’s solution, although asymptotically correct in full contact, may be less accurate than the ‘traction asperity’ theory.

Ciavarella [77] extended this method to include adhesion using the JKR approach, and found that there is now dependence on m₆ independently of the bandwidth parameter. For low fractal dimensions, adhesion enhancement in the form of larger and larger contact area seems to be obtained as ζ₁ is increased. However, if the more realistic Maugis–Dugdale traction law is assumed in the separated region, a transition to a non-hysteretic regime is found [64], depending on the rms surface slope $\sqrt{m_2}$. Hence, in the fractal limit, the contact normalized contact area tends to the value without adhesion. This transition can be characterized by a generalized Tabor parameter, where however the process zone dimension s₀ of equation (2.10) is compared with characteristic dimensions of distinct separation areas, rather than of contact areas.

5.6. Tabor parameter for multi-scale surfaces

For the contact of spheres, we have seen that the exact solution (using the Lennard–Jones traction law, mainly with reference to the pull-off force) is well described by the JKR theory when the Tabor parameter μ is large, and by the DMT theory (or even Bradley’s rigid body solution) when μ is small. Several authors [45,63,64] have defined ‘scale-dependent’ Tabor parameters, all of which tend to zero in the fractal limit ζ₁ → ∞. A naive comparison with the sphere problem would then suggest that the solution in this limit could be obtained by assuming the contacting bodies to be rigid, but this is clearly in error, since a Gaussian surface has no highest point, so a rigid-body solution would imply infinite separation. By contrast, theories based on an interfacial traction law, such as those described in §§5.4.4 and 5.4.5 exhibit progressively weaker dependence on ζ₁ and indeed converge on a meaningful result in the fractal limit. Thus, although we can argue rigorously, as in §2.3, that the JKR solution tends asymptotically to the exact solution when μ → ∞, no such proof exists for the case where μ → 0.

In general, both DMT and JKR solutions (including numerical solutions e.g. [72,73]) for the contact of randomly rough surfaces should be regarded with some caution, not to say skepticism, since the appropriateness of these approximations depends on parameters that are often not well characterized, such as the smallest width of a representative contact area. At present, there is no well-defined ‘map’ of the regions of rough surface parameter space in which these theories might reasonably be applied, not least because numerical solutions are computationally demanding and hence necessarily limited in scope. In this regard, the iterative approach used by Joe et al. [70] defines a method for spanning a broad spectrum PSD without necessitating a choice between the two classical approximations.

5.7. Adhesion enhancement

Experiments by Briggs & Briscoe [80] with rough perspex cylinders rolling on a flat rubber surface showed an interesting result: adhesion energy apparently increased with submicron roughness amplitude as compared with the nominally smooth case. In pure rolling, the resistance must be a combination of viscous losses and adhesive hysteresis, but these authors also reported the results of pull-off experiments some of which also showed enhancement due to roughness.

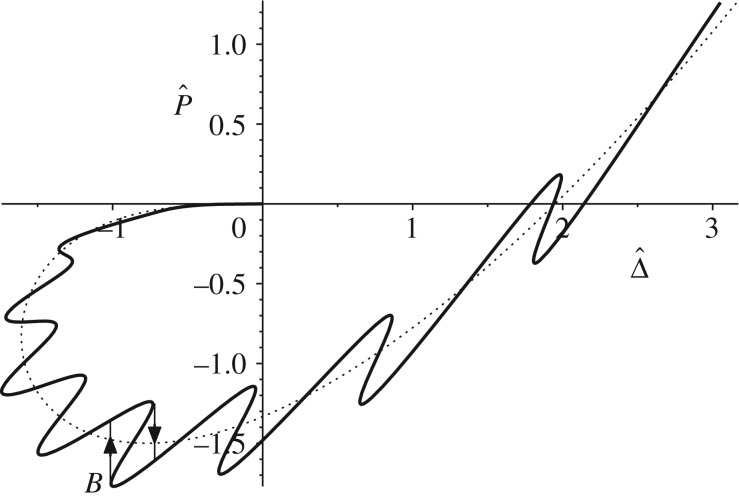
We recall that Persson & Tosatti [71] have suggested that enhancement may result from the fact that the area of a rough surface exceeds that of the projected plane. An alternative model was suggested by Guduru [81] who considered the contact of a sphere with a rough surface modelled as a set of concentric waves. Using the JKR model and assuming that the contact area is simply connected (i.e. a circle), he obtained the load–indentation plot of figure 16, which exhibits oscillations about the ‘smooth’ curve (shown dotted) as the sphere contacts with each successive wave. The maximum tensile force occurs at B and clearly exceeds the value for a smooth sphere, but also loading and unloading under displacement control involve unstable jumps, such as those indicated by the arrows in figure 16, implying that toughness as well as pull-off is enhanced. Kesari & Lew [82] provided an elegant solution for the envelope of Guduru’s curve, and Ciavarella [83] showed that in fact Kesari’s solution corresponds to an increased value of interface energy on unloading (whereas it is reduced during loading), which depends on the parameter introduced by Johnson [8] to characterize the adhesive contact of bodies with two-dimensional sinusoidal roughness. These models predict that enhancement continues to increase with larger roughness amplitudes, which is clearly unrealistic. In particular, a simply connected contact area would then be difficult to achieve, even with a large preload, and the corresponding spatial oscillations would imply the existence of extended regions where the tensile tractions exceed σ₀, thus invalidating the JKR assumption.

Figure 16.

Force–indentation curve for a sphere with axisymmetric waves (solid curve) compared with the classical JKR curve (dotted line). Owing to unstable jumps the dissipated energy is highly increased for the wavy surface (from [81]).

Kesari et al. [84] investigated a more realistic Gaussian form of micro-scale roughness, and reported AFM experiments showing a marked difference between loading and unloading, with the force on unloading depending on the maximum indentation depth (depth-dependent hysteresis (DDH)). Deng & Kesari [85] have also suggested that energy dissipation comes from two sources, one independent of maximum indentation depth and the other mainly due to roughness, which for large enough roughness amplitude essentially comprises dissipation in asperity contacts.

5.8. Effect of roughness on hysteresis

If in a contact problem the load–displacement relation is multi-valued, then different branches will generally be followed during loading and unloading, resulting in hysteretic energy loss. We have reported several cases of this kind in the preceding pages, including for example in §§4.1, 4.3 and 5.7. For the sphere, hysteresis is predicted using the JKR approximation, but not with the DMT approximation. Indeed, the DMT solution of any geometrically defined problem predicts a single-valued relation between force and displacement, since we first solve the adhesionless problem, which has a unique solution, and we then modify the resulting force by a convolution of the interface-traction law with the gap from this same unique solution.

It is then tempting to argue that since fine-scale roughness generally pushes us into the DMT regime, rough surface contact should not involve hysteresis. However, this is not the case. Rough surface contact theories generally (i) assume that the nominal pressure is statistically uniform over an infinite area, and (ii) eliminate the ‘zeroth-order’ [uniform] elastic deformation of the contacting bodies, since for half spaces, this would be infinite except in the special case of an incompressible material. The uniform term is also generally eliminated in numerical models. In effect, these theories generate the properties of a fictitious ‘nonlinear layer’ which, if attached to the surface of a smooth body, would then mimic the effect of roughness in the actual body. This process essentially decouples the roughness scale from the necessarily finite dimensions of the actual contacting bodies and can be seen as a form of homogenization.

The mechanical behaviour of the layer can be described by a relation $\overline{\sigma }(\overline{g})$ between mean traction and mean gap, which would reduce to (e.g.) the Lennard–Jones law in the limit of vanishing roughness, but which in general will have a lower maximum (pull-off) traction and a larger range of effectiveness [70]. As long as $\overline{\sigma }(\overline{g})$ exhibits a tensile range, there must be a range with negative slope, so instabilities and associated multi-valued force–displacement relations are possible under force or displacement control. These may involve ‘jumps’ between states with uniform tractions, or the development of patterns as discussed in §4.3.

In discussing figure 8, we noted that solutions even of the smooth contact problem are very sensitive to numerical perturbations in and just outside the unstable range. This effect is of course even more pronounced if the surfaces have random roughness, provided this is not of such large amplitude as to suppress the instability. The patterns developed analogous to those of figure 7 are now irregular and significant differences are observed between different realizations of the same roughness statistics.

If the JKR approximation is used to describe the roughness scale, the relation $\overline{\sigma }(\overline{g})$ may itself be multi-valued, as in the case of the Fuller & Tabor model. Greenwood [50] showed that the unloading curve then depends on the maximum compressive traction achieved during loading, which is a form of history-dependence. Guduru’s solution (see §5.7) exhibits similar behaviour. However, since length scales cannot be too small for the JKR approach to be valid, there is some question as to whether the micro- and macro-scales can then be effectively decoupled. This question also arises in the broad spectrum results of Joe et al. [70] which show an unstable range at small lower wavenumber ζ₀ that might reasonably be interpreted as a macro-scale effect.

5.9. Effect of plasticity in rough surface contact

In §5.3, we showed that for the elastic contact of multi-scale rough surfaces without adhesion, the predicted actual contact area decreases without limit as ζ₁ increases (see 5.3), implying a corresponding increase in mean contact pressure. Clearly, this process must eventually be limited by inelastic effects. Gao & Bower [86] extended the Weierstrass solution of Ciavarella et al. [53] to an elastic rigid-plastic material and showed that in this case the total actual contact area tends to a finite limit, corresponding to a mean contact pressure close to 6σ_Y. Similar results were reported by Pei et al. [87] based on a finite-element solution for a random rough surface, and these authors also noted an approximately linear relation between total contact area and force—a result that was postulated by Bowden & Tabor [88] as early as 1939.

The present authors are unaware of any investigation of the contact of elastic–plastic rough bodies including adhesion, but based on the arguments in §2.6, we might anticipate that plastic deformation would increase the ‘comformability’ of the surfaces and hence increase (for example) the pull-off traction, and make it strongly load-dependent (that is, in addition to the load-dependence which may already arise in elastic adhesive contacts). In support of this claim, we note that Mesarovic & Johnson [25] predict an increase in pull-off force due to plasticity for a single sphere, and their results might reasonably be incorporated in a modified asperity model theory. Also, Pei et al. [87] reported an increase in the total actual contact area during unloading relative to that during loading which would also conduce to increased pull-off. However, note that roughness spectra generally extend to the nanometre scale and on this length scale conventional plasticity may not provide a good description of the inelastic material behaviour, and this itself needs to be investigated more.

6. Bioinspired adhesion

While we have so far concentrated on theories about idealized geometries, Nature has developed efficient mechanisms to adhere to almost any kind of surface with a lot more freedom of choice, and indeed theoretical solutions based on a perfectly homogeneous, nominally flat geometry fails to explain many of these effects. Non-patterned surfaces exhibit too weak adhesion capabilities, because roughness stress concentrations and defects easily destroy the effect of interface energy. What makes bio-adhesive systems exceptional is their anisotropy, and their self-cleaning and wear resistance properties. The literature on this topic has largely expanded in recent years, and here we shall cover only a very limited amount of material, far less detailed than in some of the previous topics.

Synthetic pressure sensitive adhesives commonly used in domestic or industrial applications deliver either strong or weak adhesion, but require similar energy for detachment. Strong synthetic adhesive are difficult to detach, whereas weak adhesives detach easily. Systems of this kind are unsuitable for locomotion. By contrast, a gecko is able to sustain several times its weight, but is also able to detach its foot in 15 ms and with negligible detachment force [89–91]. Gecko adhesion relies on non-specific van der Walls forces [92] and its pads are covered by millions of hairy setae of characteristic dimension of hundred microns, which split in finer endpoints, called spatulae, of nanometric dimension, leading to a multi-scale hierarchical structure [93,94].

One of the keys to this impressive performance is ‘contact splitting’. Hensel et al. [90] found that in general, the pull-off force P_n for a micropattern with n contacts is related to that for a contact without splitting, P₀, by

$$P_n=n^s{P}_0,$$ 6.1

where s is called the ‘contact splitting efficiency’, which for hemispherical tips is equal to 1/2. Furthermore, if one applies fracture mechanics arguments to the detachment of an elastic flat-ended pillar of diameter D_p perfectly bonded to a rigid substrate, the energy release rate is found as

$$G\sim \frac{{\sigma }^2}{E}{D}_{\hspace{0.17em}p}^{0.81}{l}^{0.19},$$ 6.2

where l is the length of a small crack that advances at the interface. Equating G the work of adhesion Δγ leads to a pull-off stress

$${\sigma }_P\sim \frac{\sqrt{E\mathrm{\Delta }\gamma }}{D_{\hspace{0.17em}p}^{0.406}{l}^{0.094}}.$$ 6.3

For the length scales involved, equation (6.3) gives a scaling very close to that for a crack (−1/2), and indeed the sum of the two powers is 1/2. The weak power in crack length l is due to the assumption of l ≪ D_p. When the pillar diameter is small, there is a cohesive failure regime, with detachment occurring at the theoretical strength of the material σ₀. Note that this analysis predicts that higher modulus pillars have higher pull-off stress, but this needs to be balanced by the effect of roughness, for which lower modulus pillars adapt better.

Although contact splitting provides an explanation for adhesion enhancement in some bio-applications, we are still far for a complete understanding of how adhesion is effectively controlled at the interface. While Artz et al. [95] showed a strong correlation in flies, beetles, spiders and lizards between the areal density of attachment hairs and the body mass, later Peattie & Full [96] surveyed 81 species with hierarchical fibrillar structures and found no such correlation when the data are analysed within the same taxa (see also [97]). Bartlett et al. [98] proposed a more general criterion based on total energy minimization, which predicted that the maximum adhesion force would scale according to the relationship

$$P_0\sim \sqrt{\mathrm{\Delta }\gamma }\sqrt{\frac{A_{\mathrm{c}}}{C_{\parallel }}},$$ 6.4

where A_c is the area of intimate contact and $C_{\parallel }$ is the compliance in the direction of the applied load. Figure 17 shows an impressive correlation between equation (6.4) and results for both natural and synthetic adhesives over 14 orders of magnitudes.

Figure 17.

Scaling relationship for natural and synthetic adhesives. Data align over 14 orders of magnitude (form [98]). (Online version in colour.)

Since Δγ is an uncontrollable parameter that depends on the interface properties, an optimal design requires that we maximize the ratio $A_{\mathrm{c}}/C_{\parallel }$, but this is not an easy task. The system must be soft enough to maximize the contact area and adapt well on any kind of substrate, but also rigid enough in the direction of the applied load. In this respect, hierarchical fibrillar structures are likely to be one of the more promising designs (perhaps the most successful), but not the only one. Bullock et al. [99] compared hairy (Gastrophysa viridula) and smooth (Carausius morosus) pads finding comparable adhesive performance, except that hairy pads can exhibit more anisotropy due to the ability to control each seta individually.

6.1. Patterned surfaces

Inspired by biological design solutions, micro- and nano-patterned surfaces have been developed. These rely on pillars or dimples of various shapes, whose individual small scale makes it possible to have them defect-tolerant and reach high values of strength, close to σ₀. Several authors have attempted to replicate solutions in nature with micropatterned dry adhesives to obtain reversible capabilities to grip, position and release objects [100–104].

For an arrangement of pillars, a simple argument is that the elastic strain energy stored in a single pillar is effectively dissipated during pull-off [90]. The remaining load then has to be redistributed over the remaining surface and the crack needs to nucleate again at the next pillar for pull-off to proceed. Hence ‘crack trapping’ enhances the effective work of separation at the next pillar by $\pi D^2{\sigma }_P^{2}L/2E$, where L is the pillar height. Therefore, a small elastic modulus with long pillars having high individual pull-off stresses is beneficial for this effect to be maximized.

Barreau and co-authors [105] have shown that one strategy for better adaptation to surface roughness is to use a small pillar diameter to take advantage of the contact splitting effect, but not smaller than the mean spacing between local peaks on the substrate, insofar as this can be defined for a multi-scale surface. The problem is that when diameter is too small compared with this criterion, bending and buckling events occur, storing strain energy, which effectively reduce adhesion.

An alternative strategy is to design the contact geometry to include mushroom or funnel-shaped tips. These shapes can increase the pull-off stress even by an order of magnitude because of the shift from the severe singular edge stresses of the flat punch to the more uniform stresses with almost no singularity at the edge of the mushroom flaps [106]. More precisely, the singular stress multiplier is determined by the thickness of the flaps, rather than the diameter of the fibril.

For surfaces with nano/micro-dimples, McMeeking et al. [107] proposed an elegant model comprising essentially the JKR solution for a single depression in one of the surfaces. Interestingly a bi-stable pressure-sensitive adhesive mechanism was obtained, with two distinct states of weak or strong adhesion. As in Johnson’s solution for the sinusoid [8], the model suffers from the weakness that with the JKR assumption a theoretically infinite traction is needed to detach the surface from a state of full contact (see the solid line in figure 18) unless an initial perturbation such as air entrapment as assumed. Papangelo & Ciavarella [108] extended the McMeeking analysis using a Maugis cohesive model to account for the adhesive interaction. The analysis showed that the adhesive behaviour depends not only on the work of adhesion but also on a generalized Tabor parameter μ. Low μ leads to the rigid solution which shows no hysteretic behaviour, while for large μ the cohesive solution tends to the JKR limit.

Figure 18.

Loading curves for smooth (solid lines) and rough dimple (dashed lines). (Online version in colour.)

More recently, Papangelo & Ciavarella [109] studied the effect of an axisymmetric single-scale sinusoidal roughness superimposed on an otherwise smooth dimple, in the JKR regime. As in [81] (see §5.7), the contact area is assumed to be connected, in this case comprising the region outside a single circle. The results show that the nominal compressive traction required to reach the full contact state is increased by the added roughness, but when this is reached, the resistance to pull-off is increased relative to the ‘smooth’ case (see the dashed lines in figure 18). In effect, the rough dimple behaves similarly to the smooth dimple, except that the effective work of adhesion is increased during loading and decreased during unloading. These results are analogous to those of Guduru [81] for the case of a sphere with added a sinusoidal axisymmetric waviness.

7. Adhesion and friction

Everyday life teaches us that relative tangential motion between two contacting bodies is opposed by a friction force. At the macroscopic scale, this force is found approximately to obey the friction law of Amontons and Coulomb—i.e. that it is (i) proportional to the normal contact force, (ii) is independent of the apparent contact area and (iii) is independent on the relative velocity. Many theories have been proposed to explain this behaviour. Bowden & Tabor [88] argued that the inevitable roughness of the contacting surfaces would cause areas of intimate contact to be restricted to a small fraction of the nominal area, resulting in contact stresses sufficient to ensure plastic deformation. They likened these contacts to hardness indentation experiments and concluded that the total actual contact area would be proportional to the normal force. They also suggested that ‘cold-welded junctions’ would form in areas of actual contact, requiring a fixed value of shear stress to allow tangential motion. Archard [110] defined a probability for such an adhesive interaction to lead to the detachment of a wear particle, thus paving the way for the well-known Archard wear theory. Archard [52] also introduced the first purely elastic ‘fractal’ description of the interface (see §5.3) and showed that in the latter case normal load and contact area become nearly proportional independently of material behaviour. This feature remained in more recent multi-asperity [49] or mean-field models [54].

Amontons’ law is recognized as being at best only an approximation to frictional behaviour, and that only at the macro-scale. Rabinowicz [111] showed for example that the static friction coefficient of noble metals is not really a constant, but ranges from 0.3 at high loads to 1.5 at low loads. Rabinowicz was a pioneer of attempting to explain friction in terms of surface energy [112]: he showed that friction coefficients are proportional to surface energy/hardness ratios, although precise correlation suffers from the difficulty to measure these quantities independently.

Recently, there has been much interest in the interplay between adhesion and friction. In many insects, for example, it has been found that the normal force needed to detach adhesive pads is approximately a linear function of the shear force simultaneously applied [89,113,114]. This recalls Amontons’ law for friction, and indeed the model of ‘frictional adhesion’ introduced by Autumn [89], is a modification of the classical Amontons’ law, with two ‘friction coefficients’, one for compressive, and the other for tensile loads.

Classical contact mechanics models for adhesion and friction interaction date back to the seminal work of Savkoor & Briggs [115] who extended the JKR solution for a smooth sphere to friction. They assumed a singular stress field also in tangential direction (mode II), and combined the energy release rate G as

$$G=\frac{1}{2E^{\ast }}[K_I^2+K_{II}^2]=\mathrm{\Delta }\gamma ,$$ 7.1

where K_I and K_II are, respectively, the mode I and II stress intensity factors.

However, Savkoor & Briggs [115] found that the contact area reduction was greatly overestimated by this ‘purely brittle’ model, which, in other words, assumes no frictional resistance when the crack advances. Instead, the interface ‘toughness’ G_c should be considered a function of the phase angle

$$\psi =\arctan \left(\frac{K_{II}}{K_I}\right)$$ 7.2

and, although physical models have been advanced [116], essentially a mode-mixity function f(ψ) that includes a fitting parameter is introduced [117]

$$G_{\mathrm{c}}=\mathrm{\Delta }\gamma f(\psi ).$$ 7.3

Johnson [118] was the first to reconsider Savkoor & Briggs [115] model adding a single empirical constant 0 < α < 1 to tune the ‘interaction’ between modes, where α = 0 corresponds to the ‘ideally brittle’ behaviour of Savkoor & Briggs [115] which implies no frictional resistance in the relative tangential motion of the two surfaces, and α = 1 corresponds to the mode uncoupling with no sensitivity to the tangential load. Later, Johnson [119] introduced more complex cohesive models in both mode I and mode II (mode III was removed by “averaging around the periphery of the contact to maintain axisymmetry in the model), and the number of constants increased. Waters & Guduru [120] came back on this argument proposing their fracture mechanics model and comparing with extensive experimental results, which showed good agreement at least while the contact area remained circular. Cycles of slip instability and reattachment, especially for compressive normal loads, appear in some authors, which have some similarities with Schallamach waves [121], and at the moment there is no complete understanding about when, depending on the particular experimental testing apparatus, method and materials used, they should appear or not (see discussion [120]). Sahli et al. [122] suggest a quadratic decay of the contact area with tangential load T, A_c = A₀ − α_AT², where A₀ is the contact area at null tangential load T = 0 and α_A is a fitting area reduction coefficient. They find that the latter parameter scales with power −3/2 with A₀ over about four orders of magnitude (figure 19), for both smooth (sphere versus plane) and multi-contacts interfaces and that sliding corresponds to the condition when the contact area has reduced such that the tangential load corresponds to the product of a material constant shear strength and the reduced contact area. More recently, Mergel et al. [123], using a similar set-up, but with much lower normal loads, report experimental results in which decay of the contact area is not quadratic for the entire range of observations. Papangelo & Ciavarella [124] have shown that these experiments can be fitted very well by adopting one of the Hutchinson & Suo mode-mixity functions [117], and that the exact form of the mode-mixity function is of crucial importance in such fracture mechanics models.

Figure 19.

Contact area reduction coefficient α_A as a function of the initial apparent contact area A₀ (T = 0) for both sphere and multi-contacts interfaces (from [122]). (Online version in colour.)

8. Conclusion

We have seen that a wide range of interesting physical phenomena can result from the interaction of adhesive (i.e. tensile) tractions between contacting bodies and the underlying contact mechanics. These include, for example, various kinds of instability involving jumping into and out of contact, and also the development of self-generated patterns in systems where one would otherwise expect a nominally uniform state. The ‘JKR’ energetic approach provides a convenient and reliable approximation to the solution in such cases provided that the problem is ‘macroscopic’—i.e. that the resulting contact and separation regions are large relative to the length scale defined by equation (2.10)—but many modern applications of adhesive contact mechanics fail this test, either because the contacting bodies are themselves small, as in many biological and nano-structural problems, or because the more or less inevitable existence of surface roughness causes the contact area to bifurcate into a morphology defined at the nanoscale.

Various approximations have been suggested and used in these cases, including the approximation of the traction law by a piecewise constant function, and the so-called ‘DMT’ approach, where it is assumed a priori that the region where the contact tractions are compressive is unaffected by surrounding regions of tensile traction, which therefore only affect the calculation of the total force. The reliability of such approaches can only be assessed by comparison with nonlinear numerical solutions using the exact form of the interface traction law, but unfortunately computational limitations generally restrict the dimensions of the system that can be so modelled, typically to not exceed the micrometre scale. This problem is particularly challenging when surface roughness is taken into account, since roughness often spans a spectrum covering four or five orders of magnitude, and additional complication is introduced by the fact that the surface is then defined only in a statistical sense. We describe and compare various attempts at treating this challenging multi-scale problem.

In summary, adhesive contact mechanics is an extraordinarily rich source of challenging problems, in which significant advances are regularly being made.

Data accessibility

This article has no additional data.

Authors' contributions

M.C. generally designed the review, J.J. provided some numerical analysis for the patterns in very smooth soft surfaces, and all authors contributed to the organization and text of the final manuscript.

Competing interests

We declare we have no competing interests.

Funding

A.P. is grateful to the German Research Foundation (DFG) for funding the projects HO 3852/11-1 and PA 3303/1-1.