Linguistic laws in chimpanzee gestural communication

Abstract

Studies testing linguistic laws outside language have provided important insights into the organization of biological systems. For example, patterns consistent with Zipf's law of abbreviation (which predicts a negative relationship between word length and frequency of use) have been found in the vocal and non-vocal behaviour of a range of animals, and patterns consistent with Menzerath's law (according to which longer sequences are made up of shorter constituents) have been found in primate vocal sequences, and in genes, proteins and genomes. Both laws have been linked to compression—the information theoretic principle of minimizing code length. Here, we present the first test of these laws in animal gestural communication. We initially did not find the negative relationship between gesture duration and frequency of use predicted by Zipf's law of abbreviation, but this relationship was seen in specific subsets of the repertoire. Furthermore, a pattern opposite to that predicted was seen in one subset of gestures—whole body signals. We found a negative correlation between number and mean duration of gestures in sequences, in line with Menzerath's law. These results provide the first evidence that compression underpins animal gestural communication, and highlight an important commonality between primate gesturing and language.

1. Introduction

The investigation of linguistic laws—the common statistical patterns of human language—is a cornerstone of quantitative linguistics [1,2]. In recent years, studies have begun to explore the universality of linguistic laws beyond our own species, and this work has provided important insights into the basic rules of organization underpinning natural information systems. Most notably, exploration of two such laws—Zipf's law of abbreviation and Menzerath's law—has provided evidence that compression, the information theoretic principle of minimizing the length of a code, is a universal principle not only of human language, but also of animal behaviour and a range of other biological information systems [3–5].

Zipf's law of abbreviation predicts a negative relationship between the length of words and how often they are used [6,7]. It is prevalent across a very wide range of human languages [8], being found in written texts (i.e. in character-based [9,10] as well as letter-based writing systems [8]), in speech [11] and in sign language [12]. Patterns consistent with this law (i.e. an inverse relationship between signal magnitude and frequency of use) have also been documented in the behaviour of a number of animal species: the vocal repertoire of Formosan macaques [5], close-range calls of common marmosets [13], social calls of bat species [14] and non-vocal surface behaviour of dolphins [15].

Menzerath's law predicts that ‘the greater the whole, the smaller its constituents' and in language holds at different scales of analysis: in words with more syllables, the average syllable length is shorter [16], and in sentences with more clauses, the average clause length is shorter [17]. A negative relationship between construct and constituent size has been found in the vocal sequences of male geladas [4] and chimpanzees [18], and at the molecular level—between chromosome number and size across species [19], between exon number and size in genes [20], and between domain number and size in proteins [21].

Mathematical explorations indicate that both these linguistic laws reflect compression, and it has been proposed that this is a universal principle driving coding efficiency [3,4,22]. Further corroboration for the effect of compression in the context of Zipf's law of abbreviation can be found by testing whether the mean code length is significantly small in signalling systems that follow this law [3]. This has been found to be the case in human language and in animal systems where this law holds [3]. With respect to Menzerath's law, an equivalent corroboration has not yet been conducted (in humans or other species).

Although evidence for compression has been found in a range of natural systems, it is important to expand the range of communicative modes in which this principle is investigated if its true extent is to be assessed. Gestural communication is an important signalling mode in anthropoid primates, including humans [23], and it has been proposed that during human evolution, gestural communication played a key role in facilitating the emergence of spoken language [23]. Gestures are defined as non-verbal communication forms involving visible, manual and bodily actions; they typically occur in short-range communication and are used across a diverse range of social interactions including play, sex, aggression, nursing and grooming [24]. Among the best studied primate gestural systems is that of the chimpanzee, a species known for its extensive gesture repertoire, with gestures given singly or flexibly combined in sequences [25]. Chimpanzees produce 50–70% of the gestures from their repertoire during social play [24,25], and this provides a powerful context to test for compression, at the level of both individual gestures and sequences of these signals.

Here, we analyse a comprehensive dataset on play gestures collected from a wild chimpanzee community, to test Zipf's law of abbreviation in individual gesture types and Menzerath's law in gesture sequences. To complement these two tests for compression, we also test whether the mean code length is significantly small in individual gestures and sequences, respectively. This study tests these linguistic laws in a mode of animal signalling in which they have not previously been investigated, and provides the first test of Menzerath's law in the gestural signalling of any species, including humans. Moreover, as these two laws have not been tested simultaneously in the same system outside our own species, our findings provide new insights into the different levels of signal organization at which compression may be prevalent in systems beyond human language.

2. Methods

(a). Study site and subjects

We conducted observations on the chimpanzees of the Sonso community in Budongo Forest Reserve, Uganda. At the time of study, the community consisted of 81 identifiable members. We defined age classes as: infants (0–4 years), juveniles (5–9 years), subadults (female: 10–14 years, male: 10–15 years) and adults (female: greater than or equal to 15 years; male: greater than or equal to 16 years).

(b). Data collection

We collected data in four field periods—October 2007–March 2008; June 2008–January 2009; May 2009–August 2009; January 2011–August 2011—using focal behavioural sampling [26], with observations conducted from 7.30 to 16.30 h. We recorded instances of gestural communication during social play using a Sony Handycam (DCR-HC-55). Social play was defined as situations where two or more individuals engaged in play activities indicated by signs of laughter, play-face and typical body actions such as wrestling, chasing, play-biting or tickling [27].

(c). Coding

In total, we analysed 359 video clips for play gestures that met at least one of the key criteria for intentional communication: (i) sensitivity to the receiver's attentional state, (ii) response waiting, or (iii) goal persistence [28]. For each such gesture, we recorded gesture type (58 types were observed in total; electronic supplementary material, S1), identity of signaller, gesture duration and time between gestures if gestures were given in sequence.

(i). Measuring gesture duration

We measured gesture duration in frames, with each frame lasting 0.04 s, using MPEG Streamclip (v. Squared 5, 2012). We determined gesture start as the commencement of movement of body parts participating in the gestural process. We recorded gesture end either as the cessation of the body movements creating the gesture or as the change of body position if the gesture relied on certain body alignments. If the signaller remained in the gesture position while starting to play, we used this as the gesture's endpoint, as the gesture no longer met criteria for intentional communication [28].

(ii). Intra-observer reliability

As all video clips were analysed by one person (R.H.), to test intra-observer reliability, we randomized the order of clips and remeasured the duration of gestures of every ninth clip (n = 102 gestures from 37 clips). An intraclass correlation coefficient (ICC) test—class 3 with n = 1 rater [29]—revealed very high agreement on measurements of gesture duration (ICC = 0.975, p < 0.0001).

(iii). Defining gesture types and tokens

Linguists distinguish between types and tokens [30,31]. To illustrate this, consider the line from Gertrude Stein's poem ‘Sacred Emily’ [31]: ‘Rose is a rose is a rose is a rose’. The line includes 10 words, and three different types of word. The types are the three word types: rose, is, a. The tokens represent the overall word count: 10 words. In research related to compression, types are used to test Zipf's law of abbreviation and to calculate the mean duration, denoted L [3,5,13,15]. Tokens are used to test Menzerath's law and to calculate the total duration of tokens, denoted M [4]. We therefore considered gesture types when testing Zipf's law of abbreviation and L, and gesture tokens when testing Menzerath's law and M. Gesture types were defined as gestures which occurred repeatedly in the same form of movement and were used singly or in sequence [32]. We considered single gestures to represent a sequence of length 1, following earlier work [4,18]; longer gesture sequences were defined as two or more discrete gestures, with less than 1 s between them [25].

(d). Analysis

(i). Do chimpanzee play gesture types follow Zipf's law of abbreviation?

We used two-tailed Spearman's rank correlation (IBM SPSS v. 22.0) to determine whether the mean duration and frequency of use of gestures types were negatively correlated. The mean duration for each gesture type was calculated as d = D/f, where D is the sum of all the durations of a particular type and f is the frequency of use of that type (i.e. the number of times the gesture occurred in our dataset) [33].

The emergence of patterns consistent with Zipf's law of abbreviation in correlation analyses such as these could be an artefact of using the mean values of signal (here, gesture) duration. Specifically, a negative correlation between two variables, d = D/f and another f, may be inevitable, given d is defined as a quotient involving f, because then d ≈ 1/f [34]. This explanation can be rejected if it can be shown that D and f are significantly correlated [33]. For all analyses related to Zipf's law of abbreviation, therefore, we tested for such relationships between D and f, using Spearman's rank correlation.

In addition to testing Zipf's law of abbreviation in the overall gesture repertoire, we conducted further analyses to test for patterns consistent with the law in specific subsets of the repertoire. These analyses were carried out as previous studies and theoretical arguments indicate this law may be found in parts of a signal repertoire despite not being revealed by analysis of the whole repertoire [13]. For example, in a range of bat species, patterns consistent with the law only emerged when a specific subset of the vocal repertoire—social calls—was considered [14]. In common marmosets, the law was not found in analyses of the entire vocal repertoire [35] but was subsequently found in a subset of the repertoire characterized by low total duration (i.e. calls with low D) [13]. In addition to these empirical studies, theoretical arguments suggest that patterns consistent with Zipf's law of abbreviation may not emerge if pressure for compression is outweighed by other pressures, for example, the need to maximize transmission success and/or reach distant receivers, which are predicted to drive an increase in signal magnitude [3]; such pressures may apply to some signals in the repertoire, but not others.

We therefore conducted four further analyses, informed by previous empirical and/or theoretical work, to test Zipf's law of abbreviation in subsets of the chimpanzee play gestural repertoire. The first divided the repertoire based on values of D, following the general approach of [13] and based on their findings that the law can emerge in low-D but not high-D subsets of the repertoire. The second divided the repertoire based on the frequency of use of gesture types, f, as frequency—or an ordering by frequency—is a fundamental predictor of length in the context of optimal coding according to standard information theory [22,36], while in natural communication systems, compression may act differentially on signals, according to how commonly (or not) they are produced. The third divided the repertoire based on the mean duration of gesture types, d, due to the association between f and d in the context of optimal coding and also for completeness, as D = f d. The final analysis divided the repertoire based on the nature of production of gesture types—simple limb and head movements, known as ‘manual gestures’, or movements involving the whole body, known as ‘whole body signals’ [37]—as it has been proposed that signals that are of greater magnitude (as is the case for whole body signals) may be less likely to reveal patterns consistent with compression [3].

Testing Zipf's law of abbreviation in subsets of the repertoire based on values of D. For these analyses, we adapted the methodology of [13]. In that study, arrangement of signals in order of magnitude of D revealed an obvious breakpoint, demarcating a split between a ‘high-D’ cluster and a ‘low-D’ cluster. No clear breakpoint was seen in our data (electronic supplementary material, S2), so we could not conduct a similar analysis to that of [13]. We therefore adopted an alternative approach, with gesture types first listed in ascending order of D, and subsets then created, starting from either the lowest value of D up to the highest value of D, or the reverse procedure (i.e. from highest to lowest D). So, for example, the subsets starting from the lowest D contain: (i) the gesture type with the lowest D, (ii) the two gesture types with the lowest and second lowest D, …. (lviii) the 58 gesture types with the lowest, 2nd lowest … 58th lowest D (i.e. all gesture types). For all subsets with n > 4, we used Spearman's rank correlation to explore the relationship between d and f.

Finally, we investigated whether the pattern of results produced by such a partitioning provided evidence for compression, or rather was an artefact of the sorting by D, using permutation tests implemented in R (v. 3.2.3) (for rationale, method and R code; see electronic supplementary material, S3).

Testing Zipf's law of abbreviation in subsets of the repertoire based on f, and based on d. We followed the methodology described above for D, to create and analyse subsets based on f, and based on d. As before, we used permutation tests to test whether the pattern of results produced by partitionings provided evidence for compression, or rather could be artefactual.

Testing Zipf's law of abbreviation in subsets of the repertoire based on the nature of gestures. We used Spearman's rank correlation to test Zipf's law of abbreviation in manual gestures (n = 44 types; electronic supplementary material, S4), and whole body signals (n = 14 types; electronic supplementary material, S4).

(ii). Is the mean duration of chimpanzee play gesture types significantly small?

We first calculated the mean duration (L) of gestures types, as defined as in equation (2.1) (following [3]), where n is the number of elements within the repertoire, p_i is the normalized frequency of the ith most probable element and e_i is the magnitude of that element [3]. The normalized frequency of a gesture type was estimated by dividing its frequency by the total frequency of all gesture types. The magnitude of a gesture type was estimated by its mean duration (s).

$$L=\hspace{0.17em}\sum _{i=1}^n{p}_i{e}_i.$$ 2.1

We then used a permutation test executed in R (for R code, see electronic supplementary material, S5A) to test whether L was significantly small [38]. A control of L (L′) was defined over the permutation function π(i), as shown in equation (2.2) [3]. The left p-value was computed by Q_L/Q, with Q_L being the number of uniformly random permutations where L′ ≤ L, and Q the total number of permutations (=10⁵). The right p-value was computed by Q_R/Q, with Q_R being the number of random permutations where L′ ≥ L, and Q the total number of permutations (=10⁵).

$$L^{\mathrm{\prime }}=\hspace{0.17em}\sum _{i=1}^n{p}_i{e}_{\pi (i)}.$$ 2.2

(iii). Do chimpanzee play gesture sequences follow Menzerath's law?

We used Spearman's rank correlation to determine whether sequence size (number of gestures) and mean gesture duration were negatively correlated. It is a moot point whether single signals should be counted as sequences (i.e. of size 1), so analyses were run both for the complete dataset (i.e. sequences of all sizes, including single gestures) and for a dataset excluding single gestures (i.e. sequences of two or more gestures).

In the context of Menzerath's law in chimpanzee gestures, D is defined as the total duration of gestures in a sequence (excluding durations of gaps between consecutive gestures), d as the mean duration of gestures and n as the number of gestures in that sequence. Menzerath's law holds if there is a significant negative correlation between d = D/n and n. It has been argued that patterns consistent with Menzerath's law could emerge as an inevitable consequence of exploring the relationship between variables such as n and d = D/n because d would scale with n automatically as d ≈ 1/n [34]. However, rigorous mathematical analysis has shown that this can only happen in a very special condition, namely when D is the mean independent of n, a property that can be tested with a simple test of the correlation between D and n [39]. To exclude this simplistic explanation for the finding of Menzerath's law, a further analysis was done [39,40], following methods used to explore the robustness of results relating to Menzerath's law in genomes [41]. To test whether Menzerath's law in chimpanzee gestural sequences is an inevitable consequence of trivial scaling, we used Spearman's rank correlation to test the relationship between D and n; a significant negative relationship excludes the trivial explanation.

(iv). Is the expected total sum of the duration of gestures of each sequence significantly small?

The total duration of a collection of sequences is defined as

$$M=\sum _{i=1}^T{D}_i,$$ 2.3

where D_i is the total duration of the ith sequence.

In turn,

$$D_i=\sum _{\hspace{0.17em}j=1}^{n_i}{l}_{ij},$$ 2.4

where n_i is the number of elements of the ith sequence and l_ij is the duration of the jth element of the ith sequence. Defining the mean duration of the ith sequence as ${⟨l_{ij}⟩}_i=D_i/n_i$, M can be expressed as

$$M=\sum _{i=1}^T{n}_i{⟨l_{ij}⟩}_i.$$ 2.5

To test whether the total sum of the duration of gestures of each sequence is significantly small, we calculated M following equation (2.5). The calculation of M is defined over a summation of tokens, with each occurrence of a sequence considered an individual token. We used a similar permutation test as for the testing of significance of L, executed in R (for R code, see electronic supplementary material, S5B), to check whether M was significantly small [3]. n_i has the role of p_i and ${⟨l_{ij}⟩}_i$ has the role of e_i in the test. Namely, n_i and ${⟨l_{ij}⟩}_i$ remain constant during the test.

3. Results

Durations of 2137 play gestures were measured; these comprised 58 gesture types, given by 48 individual chimpanzees. Of these 2137 gestures, 873 occurred as single gestures and the remaining 1264 in sequences ranging from 2 to 45 gestures (table 1). Infants produced 492 (23.02%) gestures, juveniles 940 (43.99%), subadults 638 (29.85%) and adults 67 (3.14%) (electronic supplementary material, S4).

Table 1.

Frequency, n, of gesture sequences according to their size (number of gestures in the sequence).

sequence size	n
1	873
2	267
3	93
4	42
5	17
6	10
7	4
8	1
9	3
14	1
16	1
45	1

(a). Do play gestures follow Zipf's law of abbreviation?

(i). Testing Zipf's law of abbreviation in the overall repertoire

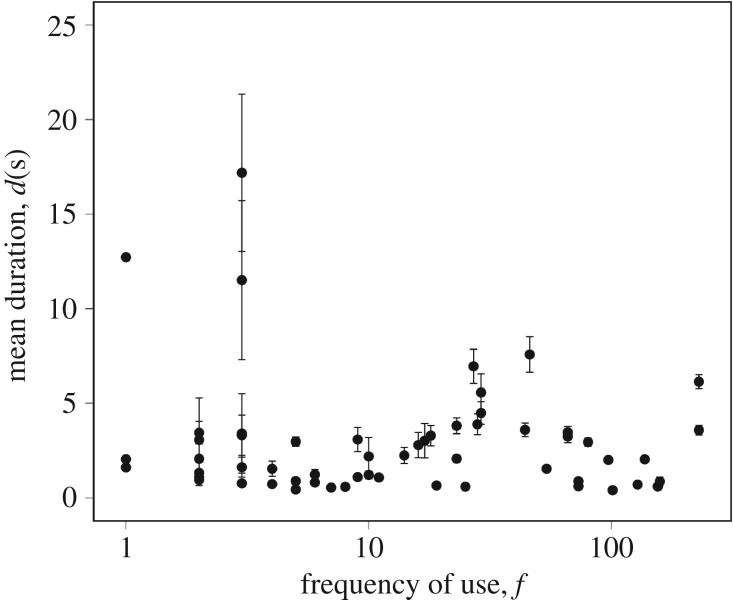
There was no significant correlation between the mean duration (d) and frequency of use, (f) of gesture types (r_s = −0.005, n = 58, p = 0.97, figure 1). The mean duration of gesture types (L) was 2.65 s; this was not significantly small (n = 58, p = 0.42).

Figure 1.

Relationship between the mean duration (d) and frequency of use (f) of gesture types. The x-axis is displayed in log scale. Whiskers indicate s.e.m. The lack of whiskers indicates either small variation of durations within a gesture type or that a gesture type was only used once.

(ii). Testing Zipf's law of abbreviation in subsets of the repertoire based on values of D

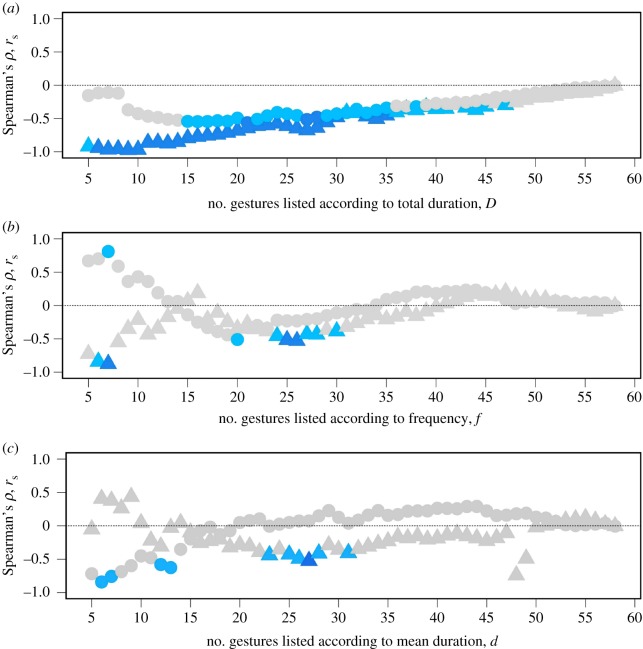
Zipf's law of abbreviation was prevalent in subsets of gesture types with low-D (figure 2a; for full results, see electronic supplementary material, S6). Considering successive subsets of gesture types generated from low-D to high-D (with n > 4), a significant negative correlation between d and f was first seen in the subset comprising gestures with the five lowest D-values; as gesture types with higher D-values were added in one at a time, the correlation between d and f remained significant until the subset of gesture types with the 41 lowest D-values, after which p-values fluctuated around 0.05 until the subset with the 48 lowest D-values, from which point all correlations were non-significant. L was significantly small for all subsets of gesture types generated from low-D to high-D, up to that of gesture types with the 55 lowest values of D (electronic supplementary material, S6). D and f were significantly correlated—and thus agreement with Zipf's law of abbreviation does not appear to be an artefact of analysing mean gesture duration—for the subset containing the gesture types with the nine lowest values of D and for all larger subsets (electronic supplementary material, S6). In addition, the permutations tests provided evidence for compression across a wide range of subsets of gesture types with lowest values of D (electronic supplementary material, S3).

Figure 2.

Coefficients of correlation (Spearman's rank correlation) between the mean duration (d) and frequency of use (f) of gesture types, for the subsets of gesture types generated either by incrementally including gesture types from lowest to highest (triangles) or highest to lowest (circles) values of (a) D, (b) f and (c) d. Symbols in grey indicate p > 0.05, in light blue indicate p < 0.05 but greater than 0.01 and in dark blue indicate p < 0.01.

The pattern of results in subsets generated in the opposite direction—from high-D to low-D—was somewhat different (figure 2a; for full results, see electronic supplementary material, S6). A significant negative correlation between d and f was not seen until the subset containing the 15 gesture types with the highest D-values; the correlation remained significant until the subset containing the 35 gestures types of highest D and then—with the exception of the subset containing the 38 gesture types of highest D—was non-significant in all other, increasingly large, subsets. L was significantly small from the subset containing the 21 gestures types of highest D up to the subset with the 38 gestures types of highest D (electronic supplementary material, S6). While D and f were significantly correlated for the subsets containing the gestures with the 10, 11, 13, 14 and 20 highest values of D and for all subsets larger than this (electronic supplementary material, S6), importantly the permutation tests did not provide evidence for compression in subsets of gesture types with high values of D, indicating significant correlations in these subsets are an artefact of the sorting process (electronic supplementary material, S3).

(iii). Testing Zipf's law of abbreviation in subsets of the repertoire based on values of f

When gestures were grouped in order of f, significant negative relationships between d and f were found only in a small number of subsets and the permutation tests did not provide evidence for compression (figure 2b; for full results, and calculations of L and the correlations between D and f, see electronic supplementary material, S7; for results of the permutation tests, see electronic supplementary material, S3).

(iv). Testing Zipf's law of abbreviation in subsets of the repertoire based on values of d

Analysis of subsets of gestures grouped according to d revealed only a few significant negative relationships between d and f. The permutation tests provided evidence for compression in a narrow range of the subsets of gesture types with highest values of d, but not elsewhere (figure 2c; for full results, and for calculations of L and the correlations between D and f, see electronic supplementary material, S8; for results of the permutation tests, see electronic supplementary material, S3).

(v). Testing Zipf's law of abbreviation in subsets of the repertoire based on nature of gestures

Analysis of manual gestures revealed no relationship between d and f (r_s = −0.125, n = 44, p = 0.419) and L was not significantly small (2.09 s, p = 0.148). Unexpectedly, whole body signals showed a significant positive relationship between d and f (r_s = 0.746, n = 14, p = 0.002)—the opposite pattern to that predicted by Zipf's law of abbreviation—and L was significantly large (5.29 s, p < 0.0001).

(b). Do chimpanzee play gesture sequences follow Menzerath's law?

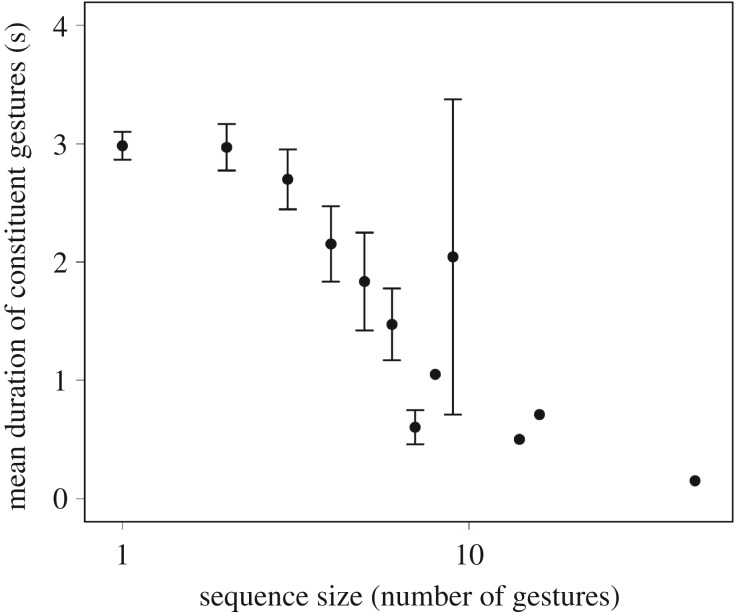
There was a significant negative correlation between sequence size (n_i) and mean constituent gesture duration (${⟨l_{ij}⟩}_i$), both when including single gestures (r_s = −0.077, n = 1313, p = 0.006—figure 3) and when excluding single gestures (r_s = −0.156, n = 440, p = 0.001). These relationships remained significant after removing the outlying data point—a sequence including 45 gestures (including single gestures: r_s = −0.074, n = 1312, p = 0.007; excluding single gestures: r_s = −0.149, n = 439, p = 0.002).

Figure 3.

Relationship between the mean constituent gesture duration and sequence size in terms of the number of gestures in play gesture sequences. The x-axis is displayed in log scale. Whiskers indicate s.e.m. The lack of whiskers indicates that a sequence of this size was only used once.

There was a significant positive correlation between sequence size (n_i) and the total constituent gesture duration (D_i) (including single gestures—r_s = 0.403, n = 1313 and p < 0.0001; excluding single gestures—r_s = 0.209, n = 440 and p < 0.0001), confirming that the finding of Menzerath's law was not an artefact of inevitable, trivial scaling.

The total sum of the duration of gestures of each sequence, M, was 5653.82 s in the complete dataset and 3050.06 s in the dataset excluding single gestures; both values of M were significantly small (including single gestures : n = 1313, p < 0.0001; excluding single gestures: n = 440, p < 0.0001).

4. Discussion

We tested for evidence of compression in chimpanzee play gestural communication, first by investigating whether gesture types and gesture sequences follow linguistic laws that reflect this principle, and second by testing whether measures of the mean code length of types and sequences are significantly small. Individual gesture types were initially found not to follow Zipf's law of abbreviation (which predicts a negative relationship between signal length and frequency of use); however, subsequent analyses of specific subsets of the overall gestural repertoire did reveal strong agreement with this law, and also evidence that the mean code length—here, gesture duration—was significantly small. Unexpectedly, patterns opposite to the law were found in one subset of gestures, whole body signals. Sequences of gestures followed Menzerath's law (according to which longer sequences are made up of shorter constituents), and again the mean code length—here the total sum of the duration of gestures—was significantly small. These findings indicate that compression has shaped chimpanzee play gestural communication at two levels of organization—the pattern of use of individual gesture types, and the construction of gesture sequences. Our results extend the evidence for compression in animal communication for the first time to the gestural mode of signalling; in conjunction with findings from studies of non-vocal behaviour in dolphins [15], a range of animal vocal systems [3–5,14,18], human speech [42] written texts [9,10] and sign language [12], this work provides additional support for the hypothesis that compression is a general principle underpinning diverse forms and modalities of communication.

Such a hypothesis is supported by strong predictions of information theory in relation to three linguistic laws. Concerning Zipf's law of abbreviation, these predictions have in common that the optimal coding of information (minimum L) implies that the correlation between the relative frequency of a type, p, and its length l, cannot be positive [22]. Standard information theory is able to predict the actual relationship between length and frequency in the case of a fully optimized system. In the case of optimal, uniquely decipherable encoding, l should approximate −log p [36]. In the case of optimal non-singular encoding, the length of a type of frequency rank i (the most frequent type has rank 1) should approximate log i [22]. These arguments have been extended to predict Menzerath's law from optimal coding (minimum M) [4]. Finally, the well studied and ubiquitous Zipf's law for word frequencies may also be a consequence of compression [43]. Support for such a powerful and abstract mechanism comes from the ubiquity of the law of abbreviation in human language, independent of modality (speech versus signed) [12,42] or writing system (character-based versus letter-based) [6,9,10].

Results from our analyses of Zipf's law of abbreviation reiterate a key point raised by previous studies [13,14], namely that exploration of linguistic laws in non-human systems may require investigation of patterns at levels below the complete repertoire of signals. Overall, individual play gesture types of chimpanzees did not conform to the pattern predicted by this law; however, very strong agreement was seen in subsets of the repertoire, particularly those for which D, the product of mean duration (d) and frequency of use (f), was small. By contrast, analyses of subsets based on d and f revealed little agreement with Zipf's law of abbreviation. D can be viewed as a ‘total cost’ function, and it may appear counterintuitive that it is gestures that have low total cost in which compression appears most prevalent; greater savings in terms of coding efficiency could, in principle, be gained among gestures with high total cost. However, it is possible that low D gestures are low D precisely because of compression; this principle may have acted to improve coding efficiency not only by aligning frequency of use and duration of such gestures, but also by reducing these two measures (and hence their product) overall.

Alternatively, there may be reasons why among other gestures, patterns consistent with compression are not found. One possibility is that compression does not affect such gestures, contrary to the recent proposal that compression is a universal principle underpinning not just animal behaviour [3], but biological information systems in the broadest sense [4]. Indeed, pressure for efficiency may be reduced in the context we explored—social play—as this behaviour is associated with having excess time and/or energy [44]. However, a lack of agreement with Zipf's law of abbreviation does not preclude that compression acts in a system. Universal principles do not necessarily produce universal patterns. Even when a principle holds, other forces may drive the emergence of patterns that are, superficially, inconsistent with those predicted by the principle alone [3]; this situation appears recurrently in optimization models of communication [45,46]. The challenge is to identify what such forces might be, and to explore under which circumstances they outweigh the underlying principle [3].

Compression is the minimization of redundancy in a system, and absence of a pattern predicted by this principle among a set of chimpanzee play gestures (and the repertoire overall) may be due to redundancy being added in parts of the repertoire. Coding theory indicates that building redundancy into signals—for example, by elongating them—reduces the risk of transmission errors [36]. In our study system, such errors could be costly as social play can become rough and may, in extreme cases, lead to aggressive escalations [47]. Regulatory gesture types used during play (e.g. head stand, dangle, roll over) or which signal play stop or change (e.g. hand on) may therefore need to be used very explicitly to ensure continued peaceful play [32]; notably, these gesture types tend to be characterized by high D. The cost of adding redundancy to certain gestures (increasing their duration) may therefore be outweighed by the cost of aggression resulting from a signal being misinterpreted.

Grouping gestures by their frequency of occurrence, f, did not produce clear patterns of agreement with Zipf's law of abbreviation. This outcome is surprising, as a number of results from standard information theory link the frequency of a type, f, with its length in the context of optimal coding. For example, the length of a type whose relative frequency is p should approximate −log p in the case of optimal uniquely decipherable encoding [36]; and the length of a type of frequency rank i (the most frequent type has rank 1) should approximate log i in the case of optimal non-singular coding [22]. These results indicate that frequency, or an ordering induced by frequency, is fundamental for standard information theory and thus, we might expect this to be the case for animal communication.

However, our results suggest that D captures the pressure for optimization much better than f in this real-world biological system. An intriguing possible explanation for this is that conclusions of standard information theory cannot be extrapolated completely to such systems, for example, because the assumptions of the theory may not be valid. Standard information theory provides a one-way approach to optimal coding: it provides the minimum lengths of the string of each type, given the probability of the types. Thus, the length of a type is caused by its frequency, not vice versa. However, type frequencies vary in natural communication systems and therefore within these systems, there may be pressures reflecting a two-way solution to optimal coding: type frequency may influence its string length (as in standard information theory) and vice versa—the string length of a type may influence its frequency. In a two-way optimization system, natural selection would operate on the product of frequency and duration, not on duration or frequency alone.

Analyses of gestures grouped by the mean duration, d, also revealed little agreement with Zipf's law of abbreviation. The poor performance of d in detecting agreement with this law is not surprising as information theory predicts a strong correlation between d and f (or between d and the frequency rank), and if f has failed to partition the repertoire in a way that reveals agreement with Zipf's law abbreviation, the same should apply to d. Our results for subsets grouped by d, in conjunction with those grouped by f, indicate that it is not among calls that are on average short, or those that are rarely given, that compression is most evident, but rather among calls where both things are the case (the product of f and d is D).

Analyses of Zipf's law of abbreviation in manual gestures and in whole body signals revealed no evidence for the law in the former, but a pattern opposite to that predicted by the law in the latter. While some previous studies of animal communication have found a lack of support for this law [3], to our knowledge, this is the first time that a significant positive relationship has been found—in non-human or human communication—between signal duration and frequency of use. This result provides compelling evidence to refute proposals [34] that patterns consistent with linguistic laws are inevitable, and thus that such laws are scientifically trivial. A pattern opposite to that predicted by Zipf's law of abbreviation may arise via a number of routes: redundancy may have been added in a positive relationship with frequency of use (i.e. more common whole body signals include the greater degree of redundancy); compression may act in positive relationship to rarity (i.e. more rarely used whole body signals are more compressed); or both pressures may be at work. A key factor to consider with respect to whole body signals is that some require a posture to be held in place to be clearly identified as a specific signal; for example, a head stand is only clearly a head stand, and not half a somersault or some other movement, because the signaller stops in the unusual position of standing with their head between their feet and holds that position. This unavoidable extension of certain signals—potentially in conjunction with an absence or relaxation of energetic constraints [44]—may underlie the positive association between whole body signal duration and frequency of use.

Our finding that chimpanzee play gestural sequences follow Menzerath's law, a linguistic law first derived from studies of human language and recently shown also to apply to vocal sequences of geladas [4] and chimpanzees [18], suggests that comparable principles of self-organization [48] underpin these different combinatorial communication systems. This law has not previously been explored in gestural communication in humans or other species; our results provide new evidence of an important commonality between human language and primate gestural communication, with respect to the basic structural patterns underpinning how signals are combined into larger structures. In studies of this law in primate vocal communication [4,18], breathing-related constraints and energetic demands of vocal production were implicated as important drivers of the negative relationship between the number of calls in a sequence and their mean duration. Gestural sequences are not constrained by breathing patterns, as is the case for vocal sequences. Energetic constraints, associated with the increased muscular activity involved in producing gestures, and especially prolonged gesture bouts [49], may underlie the emergence of Menzerath's law in this system.

Our work adds to a growing literature in which statistical laws derived from studies of human language are found to hold in non-human systems [3–5,14,15,18]. Identifying shared common properties of language and other natural systems, and examining the mathematical underpinning of such properties, not only provides new insights into the fundamental principles of natural organization [3], but also presents an important opportunity to explore the evolutionary history of universal linguistic patterns [4]. Many linguistic laws remain to be explored beyond our own species; we hope our work will encourage such investigations across diverse biological information systems.

Ethics

Permission for data collection was provided by the University of St Andrews Animal Welfare and Ethics Committee.

Data accessibility

R codes supporting this article are in electronic supplementary material. Datasets are published at: https://doi.org/10.6084/m9.figshare.5970823.

Authors' contributions

R.H. and S.S. conceived the study; R.H., S.S. and R.F.C. designed the study; C.H. provided the raw data (video recordings and gesture classification); R.H. and R.F.C. analysed data; R.H. and S.S. wrote the paper, with editing by R.F.C. and C.H. All authors gave final approval for publication.

Competing interests

We declare we have no competing interests.

Funding

R.F.C. is funded by grants 2014SGR 890 (MACDA) from AGAUR (Generalitat de Catalunya) and the grant Management and Analysis of Complex Data (TIN2017-89244-R) from MINECO (Ministerio Economía Industria y Competitividad). Fieldwork of C.H. was generously supported by grants from Wenner-Gren Foundation and Russell Trust. S.S. thanks Santander for a Research and Travel grant used to work on this study. R.H. thanks Kölner Gymnasial- und Stiftungsfonds for financial support.