The efficacy of good genes sexual selection under environmental change

Abstract

Sexual selection can promote adaptation if sexually selected traits are reliable indicators of genetic quality. Moreover, models of good genes sexual selection suggest that, by operating more strongly in males than in females, sexual selection may purge deleterious alleles from the population at a low demographic cost, offering an evolutionary benefit to sexually reproducing populations. Here, we investigate the effect of good genes sexual selection on adaptation following environmental change. We show that the strength of sexual selection is often weakened relative to fecundity selection, reducing the suggested benefit of sexual reproduction. This result is a consequence of incorporating a simple and general mechanistic basis for how sexual selection operates under different mating systems, rendering selection on males frequency-dependent and dynamic with respect to the degree of environmental change. Our model illustrates that incorporating the mechanism of selection is necessary to predict evolutionary outcomes and highlights the need to substantiate previous theoretical claims with further work on how sexual selection operates in changing environments.

1. Introduction

In times of rapid change such as increased climate variability, changes in phenology and resource availability, as well as loss of suitable habitat [1], species that do not adapt sufficiently fast face the risk of extinction [2–4]. There is currently much interest in how sexual selection contributes to such evolutionary rescue and whether it generally aligns with the forces of natural selection. This question can be traced back to the early days of evolutionary biology and Darwin [5], who pondered on the evolution of extreme morphological features and behaviours that seemed costly to survival, and ascribed them to selection arising from competition for mating opportunities. Only later came the argument that sexual signals should be costly and only affordable to individuals of high genetic quality, leading to the ‘good genes’ hypothesis of sexual selection [6–8]. According to this hypothesis, sexually selected traits are indicators of overall genetic quality because their expression reflects polygenic variation across large parts of the genome [9]. This logic does not only apply to mate-choice signals, but also to life history, morphological and behavioural traits involved in intrasexual competition and mate searching [10]. Consequently, sexual selection favouring males of high genetic quality could increase the frequency of alleles with positive effects on female fecundity and juvenile viability [9–12].

In the majority of polygamous species, sexual selection acts more strongly in males [10,13–16]. As a consequence, sexual selection in males has the potential to purge deleterious alleles from the population while leaving females, who experience weaker selection, spared of the demographic cost of adaptation [17]. Indeed, under the assumption that population productivity relies mainly on female fecundity, Agrawal [18] and Siller [19] independently showed that the genetic load on population fitness at mutation–selection balance is inversely proportional to the degree of male-bias in selection, and, therefore, potentially lower in sexual relative to asexual lineages. Similarly, Lorch et al. [11] demonstrated that, given a rich polygenic basis for trait variation, condition-dependent male signals and female preference coevolve and can result in more rapid adaptation under environmental change. Male-biased sexual selection for ‘good genes’ could thus be expected to increase rates of adaptation and aid evolutionary rescue in sexually reproducing species experiencing rapidly changing environmental conditions.

The number of empirical studies exploring the effect of environmental change on sexual selection has increased in recent years. Studies have detected temporal and spatial variation in sexual selection metrics such as the Bateman gradient and variance in reproductive success, patterns that are frequently ascribed to ecological factors [20–25]. There is also evidence from laboratory studies that population density and environmental complexity affect interactions between individuals, altering the dynamics of sexual selection and ultimately the rate of adaptation [26–28]. Despite this increase in empirical data, general theoretical predictions for how environmental change may affect the operation of sexual selection are still lacking. Notably, the influential good genes models by Agrawal [18], Siller [19] and Lorch et al. [11] share the assumption that sexual selection remains a strong and unchanged selective force, irrespective of the change in environmental conditions. While this may seem a reasonable null hypothesis, it runs counter to the very basis for how intrasexual competition and intersexual mate choice is expected to operate in nature. Because reproductive success of a given phenotype should depend on the phenotypes of its potential mating partners and competitors, sexual selection is an inherently frequency-dependent process that should be sensitive to any ecological change that affects the relative distribution of adult phenotypes in the population.

Here, we incorporate frequency-dependent sexual selection into a quantitative genetics model to assess the potential for sexual selection to aid evolutionary rescue of a sexually reproducing population experiencing environmental change. Under the simplifying assumptions that population viability is limited only by female fecundity and juvenile survival, the genetic response in population fitness is given by the Robertson–Price identity [29,30],

$$\mathrm{\Delta }{\overline{\omega }}_{\mathrm{POP}}={\displaystyle \frac{1}{2}[{\mathit{I}}_{\mathrm{AF}}\hspace{0.17em}+\hspace{0.17em}\mathrm{CO}{\mathrm{V}}_{\mathrm{MF}}],}$$ 1.1

where $\overline{\omega }$ is the mean relative fitness, I_AF is the additive genetic variance in female relative fitness, measuring the response of female fitness to selection on females and COV_MF is the intersexual genetic covariance for relative fitness, which measures the correlated response of female fitness to selection on males [31]. Thus, sexual selection in males will increase the genetic response of population fitness more than selection in females when COV_MF > I_AF.

To assess the potential for sexual selection to aid evolutionary rescue under environmental change, we compare the strength of frequency-dependent sexual selection in males with that of frequency-independent fecundity selection in females. To estimate the sex-bias in selection, we calculate the opportunity for selection I (i.e. the variance in relative fitness [32]) for each sex and compare the ratios I_M/I_F and COV_MF/I_F for different mating systems. We then study how these ratios are altered for different magnitudes of environmental change that renders the population maladapted. I represents the upper limit for the strength of selection on any trait (independent of whether selection is directional, stabilizing, disruptive or correlational [33,34]), while its additive genetic component I_A represents the response in the mean relative fitness to selection (equation (1.1)) [35,36]. We note that in our model, there is per definition only genetic variance in fitness (see below), so I and I_A are identical. This will of course not be the case in real populations, where measures of I_A should be extracted from I. I has been used extensively in studies of both natural and laboratory populations [15]; therefore, the use of I makes our model accessible to empiricists while providing testable predictions. In electronic supplementary material, appendix S1, we provide a reanalysis of published data to estimate I across benign and stressful environments in two species of seed beetle [37,38], to illustrate the utility of this measure for testing our model predictions.

We find that both I_M and I_F increase as the environment changes and becomes stressful. However, the increase in I_M under environmental change depends on mating system parameters such as the number of locally competing individuals and the degree to which male condition affects fertilization success. We conclude that for mating parameters relevant for most natural systems, the ratios I_M/I_F and COV_MF/I_F decrease with increasing environmental stress, suggesting that the potential for good genes sexual selection to aid evolutionary rescue of maladapted populations may be reduced following environmental change.

2. Model

Our model quantifies the strength of sex-specific selection in a sexually reproducing population that becomes maladapted following a sudden change in environmental conditions. Males are affected by viability selection and subsequently by sexual selection resulting from competition for access to females. Females are subject to the same viability selection as males and then experience fecundity selection. Both juvenile survival and adult reproductive success are dependent on the condition of the individual. Condition, in turn, is determined by an underlying quantitative trait that was under stabilizing selection in the ancestral environment, but whose optimum has been displaced as a result of the environmental change. This causes directional selection on the trait in the novel environment. In contrast with female reproductive success, the reproductive success of a male depends on his own condition as well as on the condition of his direct competitors. Thus, sexual selection in males is frequency-dependent, while fecundity selection in females is frequency-independent.

(a). The population

We consider an organism with non-overlapping generations. Individuals are characterized by a quantitative trait z with frequency distribution f_z (figure 1a). Both sexes have the same trait distribution (i.e. there is no sexual dimorphism). As a result of a long period of stabilizing selection, trait values in the population are normally distributed with mean μ_z and standard deviation σ_z. The frequency distribution of trait z is thus given by

$$f_z(z)=\hspace{0.17em}{\displaystyle \frac{1}{{\sigma }_z\sqrt{2\pi }}{\mathrm{e}}^{-({(z-{\mu }_z)}^2/2{\sigma }_z^2)},}$$

where σ_z is the standard deviation of trait z. The match between the trait value z and the environmentally determined optimal trait value z₀ determines an individual's condition c. We assume that c is bounded between 0 and 1 and that the decrease in condition with increasing deviation from z₀ follows a Gaussian curve. Thus

$$c(z)={\mathrm{e}}^{-{(z-z_0)}^2/{\sigma }_c^2},$$ 2.1

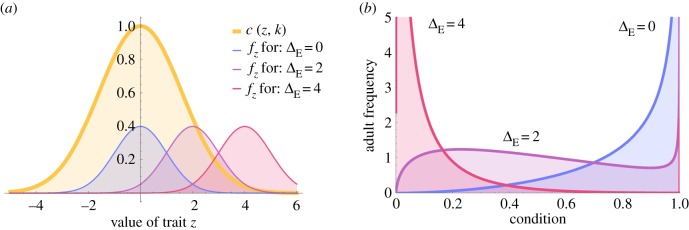
where σ_c is the width of the Gaussian curve and is an inverse measure for the strength of stabilizing selection. The relationship between σ_z and σ_c is shown in figure 1a. The phenotypic standard deviation of quantitative traits is typically on the order of 1/5 to 1/100 of this width-parameter when estimated from studies of stabilizing selection [39]. In our analysis, we use these two extreme values (σ_z/σ_c = 1/5 and σ_z/σ_c = 1/100). However, changing the amount of standing variation in z has little effect on the results and we therefore present only those for σ_z/σ_c = 1/5. From the distribution of trait values f_z and the function c(z), we obtain the distribution of conditions f_c within a population (figure 1b). The mathematical expression of f_c is given in electronic supplementary material, appendix S2, equation (A1).

Figure 1.

Effect of environmental change on the probability density function (PDF) of (a) trait z and (b) condition c. In (a), the yellow Gaussian curve represents the relationship between trait value and condition, and PDFs for z are given for three levels of environmental change: Δ_{E =} |μ_z − z₀| = 0 (blue curve), Δ_E = 2 (purple curve) and Δ_E = 4 (pink curve). In (b), the PDFs for condition c resulting from mapping the three trait distributions in (a) to condition are shown. (Online version in colour.)

(b). Survival to reproduction

The probability s to survive to sexual maturity is determined by the condition c according to the monotonically increasing function

$$s(c)={\displaystyle \frac{c\times (\hspace{0.17em}j+1)}{(\hspace{0.17em}j+c)},}$$ 2.2

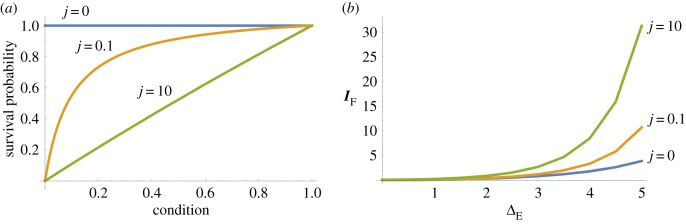
(figure 2). Here, the parameter j determines the intensity of viability selection. For j = 0, there is no viability selection and all individuals survive to reproduction. For positive values of j, we obtain s(0) = 0 and s(1) = 1, and survival increases from 0 to 1 with increasing condition. As j increases, the relationship between c and s changes from a saturating function towards a linear function (figure 2b). We present results for the three levels of viability selection shown in figure 2b: j = 0 (no viability selection), j = 0.1 (weak viability selection) and j = 10 (strong viability selection). The distribution of c in the population after viability selection and before reproduction in both sexes is given by

$$f_{ac}(c)={\displaystyle \frac{\hspace{0.17em}{f}_c(c)\times s(c)}{{\int }_0^1{f}_c(c)\times s(c)\mathrm{d}c},}$$

where the numerator is a standardization factor such that f_ac is a probability density function.

Figure 2.

Effect of parameter j on (a) the relationship between condition and survival probability s and (b) the opportunity for selection in females as the population is exposed to environmental change. Environmental change is given by the distance between optimal trait value and population mean (i.e. Δ_E = |μ − z₀|) in units of standard deviation of the Gaussian fitness landscape. (Online version in colour.)

(c). Sexual selection in males

We define the reproductive success of a male as the number of eggs fertilized by that focal male, taken from the total pool of eggs available to the group of competing males. Reproductive success is the outcome of a competition, which is determined by the condition c₁ of the focal male and the conditions c = (c₂, … ,c_n) of its n − 1 competitors. Since condition is distributed equally in the sexes and condition-dependent survival is assumed to be the same for males and females, we assume an equal sex-ratio within groups at the reproductive stage. We assume furthermore that females do not differ in their preferences and groups contain random samples of males and females from the population. Male reproductive success is then given by

$$p(c_1,\hspace{0.17em}\mathit{c})=n\hspace{0.17em}\overline{q}\hspace{0.17em}{\displaystyle \frac{c_1^g}{c_1^g+{\sum }_{i=2}^{i=n}{c}_i^g}}$$ 2.3

Here, the ratio on the right-hand side of equation (2.3) gives the proportion of eggs fertilized by the focal male. This ratio is multiplied by the total number of available eggs, which is given by the product of the number of females, n, and their average fecundity $\hspace{0.17em}\overline{q}$.

The positive constant g determines the degree to which differences in condition among competing males result in differences in fertilization success. We refer to g as the skew parameter (cf. [40]). With g = 0, fertilization success is independent of male condition and there is no sexual selection on condition. As soon as g > 0, males effectively compete and the fertilization success of a given male depends on its own condition and the conditions of its competitors. When g = 1, the fertilization success of a male is proportional to its condition relative to the total condition within the mating group. This scenario could, for example, represent a sessile broadcast spawning organism for which reproductive success is proportional to the investment in gamete production relative to the investment of competitors. With increasing g, fertilization success becomes increasingly skewed towards individuals with higher condition and in the limit of g = ∞, the single best individual fertilizes all offspring. The reproductive success of such a male equals n$\hspace{0.17em}\overline{q}$. High values of g can be thought of as a mating system where males compete for full control of fertilization in a harem of females, such as often suggested for elephant seals or lions. Note that the average fertilization success equals 1 because, as a result of an even sex-ratio, on average one male fertilizes one female [35,41,42].

For each trait value z, the expected value of p can be calculated by integrating over the distribution of conditions of all competitors in a group. However, solving this integral analytically proved unfeasible for larger groups and we used a numerical approximation as described in electronic supplementary material, appendix S2. Combining equations (2.2) and (2.3) allows us to calculate absolute male fitness w_m, which is the product of survival probability s and reproductive success p,

$$w_{\mathrm{m}}(c_1)=p(c_1,\hspace{0.17em}\mathit{c})s(c_1).$$

The mean and variance in male fitness are then approximated by another numerical procedure described in the electronic supplementary material, appendix S2. With this, we can calculate the opportunity for selection on males (variance in relative fitness) as

$${\mathit{I}}_{\mathrm{M}}={\displaystyle \frac{V(w_{\mathrm{m}})}{{\overline{w}}_{\mathrm{m}}^2}.}$$

Note that in this last step, the mean female fecundity cancels out and therefore does not have to be computed.

(d). Fecundity selection in females

Female fecundity is assumed to be linearly increasing with condition c. Female fitness w_f is the product of the probability to survive to sexual maturity, given by equation (2.2), and fecundity. Thus

$$w_{\mathrm{f}}(c)=f_{\max }\times c\times s(c),$$

where f_max is the maximal possible fecundity. The mean and variance in female fitness is determined by a similar procedure as described for male fitness (see electronic supplementary material, appendix S2). The opportunity for selection in females (variance in relative fitness) is

$${\mathit{I}}_{\mathrm{F}}={\displaystyle \frac{V(w_{\mathrm{f}})}{{\overline{w}}_{\mathrm{f}}^2}.}$$

Animal taxa vary widely in the allometric relationship between fecundity and body size (e.g. [43–46]). To account for this variation, we also explored the consequences of different power functions describing the relationship between condition and female fecundity for our predictions (electronic supplementary material, appendix S4). Changing this power function has little effect on the environmental dependence of the log-ratio and we therefore focus in the following on the case of isometry (power exponent = 1).

(e). Environmental stress

In the ancestral environment, the population mean trait value μ_z equals the trait value that maximizes condition, μ_z = z₀. Environmental change Δ_E is modelled by moving the optimal trait value z₀ away from μ_z while keeping the Gaussian selection function (determined by the parameter σ_c) constant. With increasing difference Δ_E = |μ_z − z₀|, the condition c decreases for the majority of individuals in the population. In the ancestral environment (Δ_E = 0), the distribution of conditions is skewed towards high values close to 1 as most individuals in the population are well adapted (figure 1). At intermediate stress (0 < Δ_E < σ_c /2, reducing mean reproductive success by 0–35%), the distribution of conditions is more symmetric and has a lower peak (figure 1). Finally, under high stress (Δ_E > σ_c /2, reducing mean reproductive success by 40–90%), the distribution of conditions becomes skewed towards low values close to 0 (figure 1).

3. Results

(a). Selection in the ancestral environment

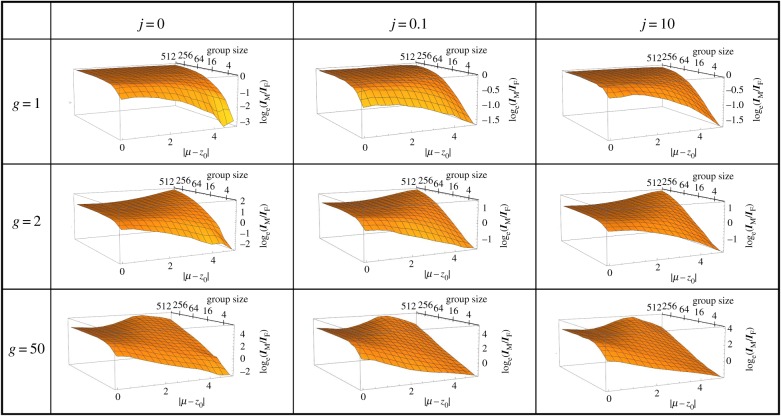
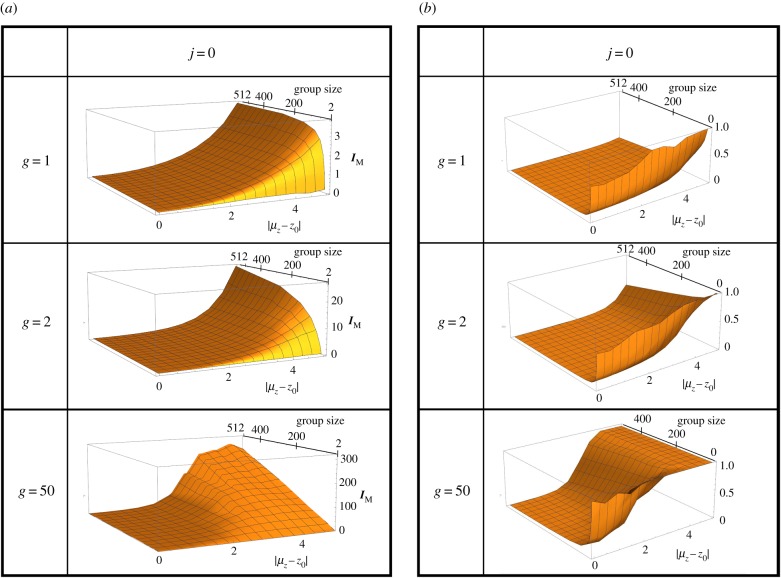
Here, we describe the effect of the skew parameter g and group size n on selection in males and on the ratio I_M/I_F in the absence of environmental change (Δ_E = 0). First, the strength of selection in males I_M increases with the skew parameter g (figure 3). Since the strength of selection in females I_F is unaffected, this results in an increased ratio I_M/I_F. Second, a larger mating group size n provides a chance for the best males to monopolize a larger number of females, which increases I_M and consequently I_M/I_F (figure 3). However, I_M is a saturating function of n and the reproductive success of the best male rarely reaches the absolute maximum set by group size, as can be seen from figure 4b. For low values of g (i.e. differences in male condition affect fertilization success only weakly), this saturation starts already at a rather low group size because males are not able to monopolize all the females in the group. At higher values of g, saturation is reached only for larger groups as high condition males can monopolize a larger number of females in this type of mating system (figure 3).

Figure 3.

Log_e-ratio of male over female strength of selection as a function of group size and environmental change for three different values of the skew parameter g (rows) and three different strengths of survival parameter j (columns). Environmental change is represented by the distance between optimal trait value and population mean (Δ_E = |μ − z₀|) in units of standard deviation of the Gaussian fitness landscape. Group size is plotted on a log₂ scale. Note that the scale of the y-axis may differ across plots (necessary to make the variation in log ratio of strength of selection readable in all parameter combinations). (Online version in colour.)

Figure 4.

(a) Male opportunity for selection and (b) reproductive success of the best male as a function of environmental change and group size, presented for several values of the skew parameter g. To make the reproductive success of the best male more comparable across different group sizes, it is presented as the proportion of fertilized females relative to the total number of females in the group. The absolute limit to male reproductive success is equal to group size, and the ratio presented in (b) equals 1 when this limit is reached. Survival selection parameter j is set to zero (no survival selection). (Online version in colour.)

(b). Selection following environmental change

Environmental stress increases directional selection on z. This results in increased strength of selection I in both sexes (see figures 2b and 4a). However, in males, the effect of stress on I also depends on characteristics of the mating system. In figure 3, we summarize the effect of environmental stress on the relative strength of selection in males and females (log_e(I_M/I_F)) for different combinations of parameters g and n under the three different intensities of viability selection.

In order to understand the effect of group size on sexual selection, it is useful to consider the case g = 1. In this case, the fertilization success of a focal male equals the proportion of its condition relative to the sum of conditions of all males in a group. Since reproductive success of a female equals the ratio of her fecundity over the population average, adult selection then operates in a similar way in the sexes. The only difference is that selection in females acts across the whole population, while males compete to fertilize only the eggs that are available locally within a group (frequency-independent selection in females versus frequency-dependent selection in males). Consequently, with g = 1, males and females experience the same strength of selection when group size becomes infinite (i.e. the group becomes the entire population). Indeed, for a group size of 512, the log-ratio I_M/I_F is very close to 0 (i.e. the strength of selection is equal in the sexes; figure 3, g = 1). When group size is significantly smaller than population size, selection is weaker in males compared to females, demonstrating that group size can limit the strength of sexual selection.

For small groups, increasing stress decreases the ratio I_M/I_F independently of the other model parameters. This is because variance in male reproductive success is bounded by the size of the group, which in our model equals the number of females that the best male can monopolize. However, for larger groups, stress either uniformly increases the ratio I_M/I_F weakly (observed for g = 2), or first increases this ratio and then decreases it at very high levels of stress (observed for g = 50). To understand these results, it is helpful to inspect the reproductive success of the best male as shown in figure 4b. First, males in well-adapted populations never monopolize a large proportion of females in their group regardless of the value of the skew parameter g. The reason is that in benign environments, most individuals are in good condition, and therefore even the highest-condition males will frequently encounter almost equally good competitors. This phenomenon explains why I_M/I_F is never extremely male-biased in well-adapted populations (figure 3). Second, the maximum reproductive success is for most parameter combinations lower than group size. This is true even under high levels of stress and means that the best male in a group rarely can father all offspring. For g > 1, stress tends to increase the maximum male reproductive success towards its upper limit which is set by the size of the mating group (figure 4). This is because high condition individuals become rarer as stress increases, allowing such individuals to monopolize females in their group because their competitors are of comparatively low condition. This phenomenon is magnified by increasing g (figure 4b) and explains why selection becomes more male-biased under stress for high group sizes as can be seen in figure 3 for g = 2.

Finally, the observation that for g = 50, the male-bias in selection is maximal at intermediate stress and then decreases at higher stress can be understood based on figure 4b. Owing to the extreme intensity of competition, high-condition males can monopolize all females in the group already before extreme levels of stress are reached and therefore, the most extreme value of reproductive success ceases to increase after intermediate stress is reached. As variance in female reproductive success is directly proportional to variance in condition c, which increases indefinitely with environmental stress, this results in a decreasing ratio of I_M/I_F from intermediate to high stress.

The ratio COV_MF/I_F responds to environmental change and to the mating system characteristics in qualitatively identical ways as the ratio I_M/I_F (electronic supplementary material, appendix S3), thus confirming that the efficacy of good genes sexual selection is generally reduced relative to fecundity selection following environmental change for group sizes smaller than 30.

4. Discussion

Previous theoretical findings have shown that sexual reproduction can offer a population-level benefit if purifying selection is stronger in males than in females, sparing the latter of the cost of adaptation [10,17–19]. Our work asks whether this conclusion persists under environmental change. We find that while environmental change increases selection in both males (I_M) and females (I_F), the effect on the ratio I_M/I_F depends on the size of the group (i.e. the number of males that compete for matings over the same number of females), and on the degree to which differences in condition among competing males result in differences in fertilization success (embodied in the skew parameter g). For small groups, the ratio I_M/I_F decreases strongly with environmental stress, indicating that the efficiency of sexual selection relative to fecundity selection is reduced under stress. This occurs because group size imposes an upper boundary on variance in male reproductive success, which limits the increase in variance in male reproductive success with stress, an effect not present in females. For large group sizes, I_M/I_F remains qualitatively unchanged or can even increase with environmental stress. These findings highlight the subtle but important interplay between mating system characteristics and ecological condition in determining the strength of sexual selection.

Our results show that the benefit of sexual selection through competition among males can be reduced by a rapid environmental change if males compete in groups below a certain size (here approx. 30, although this number depends on model details). We suggest that this scenario best represents sexual selection in nature because in most natural populations, the maximum number of females that a male can monopolize is likely not very high. Indeed, even if a male can achieve a status of dominance over other males, there should be a limit to the number of females this male can monopolize due to ecological factors such as population density and the mobility and mode of mate finding of the species. We can make an attempt at estimating the maximum number of partners that a male can monopolize across its lifetime using data from natural populations. Of course, this number estimated from data can only be an underestimation of the size of the mating group (model parameter n), which represents the upper theoretical limit of the number of mating partners monopolized. However, we propose that the most successful individuals from long-term datasets represent extremes of the distribution of the best males' reproductive success, and therefore give reasonable indications of our group size parameter in natural mating systems. In the long-term data of Soay sheep on the island of St Kilda, the most successful male ever recorded since the 1960s, OG023, sired around 40 lambs (http://soaysheep.biology.ed.ac.uk/). If we consider that adult females reproduce on average during five breeding seasons and produce one offspring per season, OG023 monopolized the reproductive success of eight females throughout his lifetime, making the upper limit for the ‘group size’ (corresponding to our model parameter n) of this population 8. Another example is the field cricket [47], where a similar calculation indicates that the most successful male monopolized a bit more than nine females over its lifetime. Data from a long-term study in the collared flycatcher [48] suggest that the most successful male monopolized around nine females. Finally, field data on the elephant seal, a harem species, suggest that alpha males may be able to monopolize up to 80 females during a particular breeding season [49], but this is most probably a large overestimation of the lifetime mating success of the best male, because it is probable that the investment necessary to reach dominance in such systems can be achieved only during a single breeding season in the life of a male [50]. Thus, while information on natural variation in male fertilization success is scant for most species and the calculations above are rough approximations, the currently available data seem to indicate that ecology constrains ‘group size’ so that it rarely becomes very large, imposing a limit on variance in male mating success.

Empirical studies under laboratory conditions [26–28] have shown effects of population density on the dynamics of sexual selection. These results suggest that environmental conditions may directly influence parameters of the mating system. Thus, if environmental stress reduces population density, this could have unpredictable effects on the strength of sexual selection [26]. Moreover, changes in ecological conditions are also likely to sometimes influence the dynamics of mate choice and the outcome of different mating strategies [22]. Our model could in principle be modified to incorporate scenarios where environmental change affects mating system parameters directly (e.g. stress reduces group size). However, exactly how such relationships materialize in natural systems remains unclear, and one of our major aims was to highlight that, even when keeping the underlying mechanistic process of sexual selection unmodified, environmental stress can fundamentally change its outcome due to frequency-dependent processes.

Our model assumes that female fitness relies mainly on fecundity while male fitness results mainly from competition for matings. These are simplifying assumptions because females also compete for resources and mating opportunities, and males also vary in fertility. Take, for example, the studies we used above to assess natural variation in ‘group size’. Male and female flycatchers have similar variance in reproductive success and maximum reproductive success [48], and male and female field crickets benefit equally from re-mating (i.e. they have similar Bateman gradients) [47]. This means that sexual selection seems to act with equal strength in both sexes. In some species, females may also compete more strongly than males do (e.g. [51–54]). A key finding of our exploration is that frequency-dependent selection and frequency-independent selection are affected differently by environmental change (see also [55]). This result should hold qualitatively even if the sexes are not subject to only one type of selection, but the model must be adapted to the ecology of the species studied to accurately predict environmentally mediated changes in the strength of sex-specific selection. Nevertheless, sexual selection itself is an inherently frequency-dependent process, and this form of selection acts more strongly in males in most species (e.g. [15,16]), which was the main motivation for our model.

In our model, we also relax the assumption that female fecundity scales linearly with female condition (see ‘Fecundity selection in females’) as natural systems can vary widely in their observed fecundity-body size allometry. In insects, for example, it has been suggested that reduced opportunities for egg laying may impose greater constraints on large females with more egg reserves, making realized female fecundity scale with an allometric exponent less than 1 in nature [43,56,57]. There are, however, also many examples of taxa showing positive allometries [45,46]. More generally, variation in the allometric relationship between fecundity and body condition should result from a combination of developmental and ecological constraints [58] and adaptive growth decisions [59]. In electronic supplementary material, appendix S4, we show that variation in this female allometry only affects the overall log-ratio I_M/I_F, but does not qualitatively modify the effect of environmental stress on the sex-bias in selection. Hence, our model results should be widely applicable across taxa with varying female reproductive allometries, as long as these are not themselves the result of frequency-dependent processes (see above).

Our model presents a snapshot of the strength of selection experienced by a population immediately after environmental change. Because there is no environmental component to trait variation in the model, variance in relative fitness I is equivalent to its additive component I_A, which represents the response of relative fitness to selection. Our model therefore predicts the initial response of female fitness to selection, I_AF, but does not include a multigenerational evolutionary response to the novel environmental conditions. However, quantitative genetic theory often makes similar assumptions (e.g. constant genetic variances and trait distributions in the face of continuous directional selection) that may not be valid over longer time periods, but nevertheless may give reasonable predictions of short-term evolution [60]. Assuming that population demography is mainly regulated through the reproductive output of females, we thus asked how population fitness evolves through female viability and fecundity. These genetic responses are driven by direct selection on females, as well as by correlated responses to selection in males. Following equation (1.1), comparing COV_MF to I_AF quantifies whether selection in males leads to a greater genetic response in female fitness than direct selection in females. In the present model, the responses of the ratios I_M/I_F and COV_MF/I_F to environmental change and mating system characteristics are qualitatively identical (electronic supplementary material, appendix S3), because male and female fitness are strongly correlated as a result of the assumed shared genetic architecture and mapping function of trait z in the sexes. Therefore, selection in males automatically benefits females and I_M is a good proxy for the population-level benefits of sexual selection in our model. We note, however, that while the assumption that phenotypic condition shares a common genetic basis in males and females should hold true when studying effects of de novo mutations (e.g. [61,62]), this may or may not be the case for standing genetic variation contributing to adaptation in quantitative traits. In fact, in both laboratory and natural populations, selection measured on quantitative characters is often found to act in opposing directions in the two sexes (reviewed in [63]). When traits under such sexually antagonistic selection share a strong genetic basis in the sexes, selection on males would act to decrease female fitness by displacing the mean trait value from the female optimum [31,64]. These dynamics are captured by the covariance term in equation (1.1), which describes the change in female fitness attributed to selection in males as a function of the combined effects of variance in male fitness and the alignment of selection in the sexes: $\mathrm{CO}{\mathrm{V}}_{\mathrm{MF}}=\hspace{0.17em}{r}_{\mathrm{MF}}\hspace{0.17em}\sqrt{I_{\mathrm{M}}{I}_{\mathrm{F}}}$, where r_MF is the intersexual genetic correlation for fitness which can range from −1 (selection is maximally opposed in the sexes) to 1 (selection is maximally concordant, as assumed in our model). Recent theoretical (e.g. [65,66]) and empirical [37,38] work has highlighted that while the r_MF often can be negative in well-adapted populations, environmental stress may align selection in the sexes and make the r_MF more positive (but see [38,67]). This influence of the environment could thus act to increase the population benefits of sexual selection in maladapted populations, potentially counteracting the reduced benefits of sexual selection predicted by our model via effects on the ratio of I_M/I_F. While some studies have tried to simultaneously separate environmental effects on these two components [37], more studies are certainly needed to shed light on how these two facets of environmental dependence affect the net effect of sexual selection in maladapted populations.

5. Conclusion

Our model suggests that the relative efficiency of sexual selection should be reduced under environmental stress due to its frequency-dependent nature, but that this effect can be modulated by characteristics of the mating system and the ecology and life history behind sex-specific reproductive competition. Our model on sexual selection dynamics is also a special case, yet broadly applicable to all sexually reproducing species, exemplifying how frequency-dependent selection can thwart evolutionary rescue [55]. This prediction holds unless mating group size is very large. The range of natural variation in group size is difficult to estimate but a simple approximation based on available long-term data suggests that relatively small ‘realized’ group sizes (n < 30) are the rule in animals, indicating that the predicted reduced efficacy of sexual selection may apply to most species. We have illustrated how our model predictions can be evaluated in experimental systems by a reanalysis of our own previously published datasets [37,38] on two species of seed beetle (electronic supplementary material, appendix S1). This analysis confirms the model predictions at low ‘group size’ (n = 2–3), and we hope that this example encourages further research efforts exploring the strengths of sex-specific selection in changing environments. We also note that the current build-up of large datasets from wild populations may allow testing of the model (e.g. [16,68]), although many confounding factors would need to be controlled for.

Data accessibility

The Mathematica code supporting this study has been uploaded as part of the electronic supplementary material in both .pdf and .nb formats.

Authors' contributions

I.M.-A., C.R., G.A. and D.B. all contributed to the development of the original idea. I.M.-A. and C.R. contributed equally to the conception of the mathematical model with frequent input from D.B. I.M.-A. wrote the first draft of the manuscript and all authors contributed substantially to revisions.

Competing interests

We declare we have no competing interests.

Funding

This work was funded by a grant from the Swedish Research Council VR to D.B. (grant no. 2015-05233) and G.A. (621-2014-4523).