Abstract
The concept of cognitive reserve (CR) can explain individual differences in susceptibility to cognitive or functional impairment in the presence of age or disease-related brain changes. Epidemiologic evidence indicates that CR helps maintain performance in the face of pathology across multiple cognitive domains. We therefore tried to identify a single, “task-invariant” CR network that is active during the performance of many disparate tasks. In imaging data acquired from 255 individuals age 20–80 while performing 12 different cognitive tasks, we used an iterative approach to derive a multivariate network that was expressed during the performance of all tasks, and whose degree of expression correlated with IQ, a proxy for CR. When applied to held out data or forward applied to fMRI data from an entirely different activation task, network expression correlated with IQ. Expression of the CR pattern accounted for additional variance in fluid reasoning performance over and above the influence of cortical thickness, and also moderated between cortical thickness and reasoning performance, consistent with the behavior of a CR network. The identification of a task-invariant CR network supports the idea that life experiences may result in brain processing differences that might provide reserve against age- or disease-related changes across multiple tasks.
Keywords: Cognitive aging, Cortical thickness, fMRI, IQ, Multivariate imaging analysis
Introduction
The concept of cognitive reserve (CR) explains individual differences in susceptibility to cognitive or functional impairment in the presence of age- or disease-related brain changes (e.g. Stern, 2002). The goal of this study was to better understand the neural implementation of CR. While most fMRI studies of CR have evaluated activation on a particular task, our intention was to identify an aspect of CR that was active across multiple tasks. We approached this by attempting to identify a network of brain areas 1) whose expression correlates with IQ, a proxy of CR, 2) is expressed during the performance of multiple tasks, and 3) whose expression moderates the relationship between brain or pathology status and cognitive performance. We posit that such a network would be a candidate for a task-invariant CR network.
CR refers to the resilience or plasticity of cognitive networks in the face of disruption. It suggests that the brain actively attempts to cope with brain damage by using pre-existing cognitive processes or by enlisting compensatory processes (Stern, 2002). A set of factors including IQ, educational or occupational attainment, exercise and leisure activities may account for differences in CR across individuals. Numerous epidemiologic studies have demonstrated that these variables are related to reduced risk of developing dementia (Meng and D'Arcy, 2012; Valenzuela and Sachdev, 2006; Xu et al., 2015). Similarly, these variables have been related to slower rate of cognitive decline in healthy aging in some, e.g. (Zahodne et al., 2015b), but not all studies, e.g. (Zahodne et al., 2011). Based on these observations, these variables have been employed as proxy measures for CR. In this study, we focused on IQ as a proxy measure of CR because it is readily and reliably obtained in participants of all ages.
To yield insights into the neural implementation of CR, we and many investigators have used task-based fMRI studies to characterize how the functioning brain adapts to structural brain changes in order to maintain cognitive performance (Stern, 2009). These studies measured age-related brain changes such as atrophy (Steffener et al., 2014a), as well as disease-related features such as amyloid plaque or tau tangles (Oh et al., 2017; Rentz et al., 2017) and explored how inter-individual variability in task-related activation can account for differential task performance in the presence of the level of age- or disease-related changes. While these studies have yielded insights into how CR may be neurally implemented, for the most part they have focused on aspects of fMRI activation related to performance on a single task. Another intriguing possibility is that there exist generic, task-invariant networks that are elicited during the performance of disparate tasks (Stern et al., 2008). A task-invariant CR network would be expressed as a function of CR in the presence of varied cognitive demands. Such a network might allow people who express it to a greater degree to better maintain performance on multiple tasks in the face of age- or disease-related brain changes. Thus, in the present study we attempted to identify a network that was expressed across multiple tasks and whose expression correlates with IQ.
There are important theoretical reasons to test whether generalized neural representations of CR can be identified. In epidemiologic studies, various proxy measures of CR have been associated with lower relative risk of incident AD. In this context, CR allows people to better maintain performance in the multiple domains of cognition affected in AD, as well as activities of daily living, in the face of increasing AD brain pathology. This argues that some aspects of reserve are not task-specific, and suggests the possibility of a task-invariant CR network. In addition, identification of a task-invariant CR network would allow for direct quantification of an individual's level of CR, rather than relying on proxy measures. This would be useful clinically, and also be extremely valuable as an outcome measure in studies designed to enhance CR.
In order to identify a task-invariant CR network, we took advantage of data from the Reference Ability Neural Network (RANN) study (Stern et al., 2014), where healthy individuals age 20 through 80 were each studied with 12 different cognitive activation tasks. We used a multivariate approach, Scaled Subprofile Modeling (SSM) (Alexander and Moeller, 1994; Moeller et al., 1987) to identify a network of brain areas that was expressed during performance of all 12 tasks and whose degree of expression correlates with IQ. Two additional steps tested the network’s generalizability. The identified network was tested in held out data to see if its expression correlated with IQ. We then checked to see whether expression of this pattern correlated with IQ in fMRI data obtained during the performance of other tasks.
We then did additional tests to confirm that network expression acted like CR by mitigating the effects of age-related brain changes on cognition. CR could account for cognitive performance over and above that accounted for by brain structure, or could moderate the relationship between brain structure and cognition (Bennett et al., 2003; Jones et al., 2011; Stern et al., 1992). Both influences are conceivable, and can easily be embodied naturally in regression models containing a direct effect of CR on performance and interaction between CR and brain structure. We therefore examined whether expression of the putative task-invariant CR pattern accounted for variance in cognitive performance over that predicted by cortical thickness. In a more demanding approach, we also tested whether the CR pattern moderated the relationship between cortical thickness and cognitive performance. Meeting these demands would provide evidence that the task-invariant network is acting like CR, in helping to mitigate the effect of changes in structure on cognitive performance.
Materials and methods
Subjects
All participants were recruited through random market mailing. All participants were required to be native English speakers, strongly right-handed, and have at least a fourth grade reading level. They were screened for MRI contraindications and hearing or visual impairment that would impede testing. Participants were free of medical or psychiatric conditions that could affect cognition. Careful screening ensured that the older participants did not meet criteria for dementia or mild cognitive impairment (MCI). The primary analyses were conducted on participants from the Reference Ability Neural Network Study (Stern et al., 2014), and included 255 individuals age 20 through 80. Demographic information is presented in Table 1a. Forward application of the derived network was done using data from participants in a second study who underwent fMRI while performing executive and working memory tasks. These included 58 individuals age 20 to 32 and 91 individuals age 50 to 71. Demographic information for this group is presented in Table 1b. There was some partial overlap between participants in these two studies.
Table 1A.
Participant sample and demographics in main derivation (RANN) sample, N = 255 in total.
| Age | <30 | 30–39 | 40–49 | 50–59 | 6–69 | >70 |
|---|---|---|---|---|---|---|
| N | 35 | 44 | 38 | 40 | 62 | 36 |
| NART IQ | 113 ± 9 | 112 ± 9 | 114 ± 9 | 115 ± 8 | 118 ± 9 | 120 ± 10 |
| Education | 15.3 ± 2.3 | 16.4 ± 2.5 | 15.9 ± 2.6 | 15.5 ± 2.3 | 16.0 ± 2.5 | 17.3 ± 2.5 |
| Sex | 23 F, 12 M | 27 F, 17 M | 17 F, 21 M | 20 F, 20 M | 32 F, 30 M | 18 F, 18 M |
| DRS | 140.4 ± 2.7 | 139.8 ± 2.3 | 139.1 ± 2.9 | 140.1 ± 3.3 | 139.7 ± 3.1 | 139.7 ± 3.0 |
| Mean Cortical thickness | 2.69 ± 0.11 | 2.66 ± 0.09 | 2.65 ± 0.09 | 2.59 ± 0.08 | 2.55 ± 0.11 | 2.51 ± 0.12 |
Table 1B.
Participant sample and demographics in replication sample for ECF task, N = 149 in total.
| Age | 20–31 | 51−71 |
|---|---|---|
| N | 58 | 91 |
| NART IQ | 114.3 ± 7.5 | 117.8 ± 9.2 |
| Education | 15.7 ± 1.9 | 16.2 ± 2.4 |
| Sex | 18 M, 40 F | 44 M, 47 F |
| DRS | 140.0 ± 2.3 | 139.9 ± 2.6 |
fMRI tasks and procedures
All MR images were acquired in the same 3.0T Philips Achieva Magnet with a standard quadrature headcoil that has been used since the start of this study. For the RANN study, MR data were acquired over two 2-h imaging sessions. For the CR study all scans were acquired in one 2-h session. At the start of every session, a scout, T1-weighted image was acquired to determine patient position. In addition to the fMRI studies, all participants received MPRAGE, ASL, FLAIR and DTI scans. For the current study only fMRI and MPRAGE sequence are considered. High-resolution T1-weighted magnetization-prepared rapid gradient echo (MPRAGE) scans were collected axially for each subject (TR = 6.6 ms, TE = 3 ms, flip angle = 8°, field of view (FOV) = 256 × 256 mm, matrix size: 256 × 256 mm, slices: 165, voxel size = 1 X 1 × 1 mm3). fMRI data were acquired using T2*-weighted gradient-echo planar images (EPI) sequence (TR = 2000 ms; TE = 20 ms; flip angle = 72°; FOV = 224 × 224 mm; voxel size = 2 mm × 2 mm; slice thickness = 3 mm; duration = 3.5 min). A neuroradiologist reviewed each participant's MRI scan and confirm that there were no clinically significant findings for any of the participants.
Task administration and data collection were controlled by a computer running EPrime software, and electronically synchronized with the MR scanner. Task stimuli were back-projected onto a screen located at the foot of the MRI bed using an LCD projector. Subjects viewed the screen via a mirror system located in the head coil. For all tasks except for Picture naming, task responses were made on a LUMItouch response system and behavioral response data were recorded on the task computer.
RANN tasks
There were 12 tasks, comprising 3 tasks for each of the 4 reference abilities. These tasks are described in detail in (Stern et al., 2014). Tasks were administered over two scan sessions. Prior to each scan session, computerized training was administered for the six tasks to be administered in that session.
Vocabulary
Synonyms (Salthouse and Kersten, 1993): This task requires participants to match a given word to its synonym, or to the word most similar in meaning. Probe words are each presented in all capital letters at the top of the screen, and four numbered choices are presented below. Subjects are instructed to respond as quickly and accurately as possible. The primary dependent variable for all vocabulary tasks is proportion of correctly identified/named items. Antonyms (Salthouse and Kersten, 1993): This task requires participants to match a given word to its antonym, or to the word most different in meaning. Format is the same as for Synonyms. Synonyms and Antonyms each lasted 6 min and 26 s long, with 3 items in each of 5 blocks for a total of 15 items. Each block lasted 42 s, with each item presented for 13.5 s and a 500 ms interstimulus interval (ISI) between items. Picture Naming: This task requires subjects to verbally name pictures. Target pictures consisted of 40 colored bitmap images, adapted from the picture naming task of the WJ-R Psycho--Educational battery (Woodcock et al., 1989) (Salthouse and Kersten, 1993). The entire scan was 6 min and 16 s long, consisting of five 40 s blocks, with 8 stimuli in each block. Each stimulus was presented for 4.5 s with a 500 ms ISI. For all three tasks, a 36 s fixation cross was presented at the start of the task, then a 28 s fixation was interspersed between blocks.
Perceptual speed
Digit Symbol: A code table is presented on the top of the screen, consisting of numbers one through nine, each paired with an associated symbol. Below the code table an individual number/symbol pair is presented. Subjects are asked to indicate whether each of 90 individual pairs is the same as that in the code table using a differential button press. The entire scan was 7 min and 4 s long, consisting of 5 blocks, with 18 items in each block. Each item was presented for 2.5 s and an ISI of 250 ms. Letter Comparison (Salthouse and Babcock, 1991): Two strings of letters, each consisting of three to five letters, are presented alongside one another. Subjects indicate whether the strings are the same or different. There are 60 total items. Pattern Comparison (Salthouse and Babcock, 1991): Two figures consisting of varying numbers of lines connecting at different angles are presented alongside one another. Subjects indicated whether the figures were the same or different. There are 60 total items. Each of Letter and Pattern Comparison lasted 6 min and 26 s long, containing 5 blocks with 42 s for each block. Each block consisted of 12 items, each presented for 3 s with an ISI of 500 ms. For all three Perceptual Speed tasks, a 36 s fixation cross was presented at the start of the task, then a 28 s fixation was interspersed between blocks.
Fluid reasoning
Paper Folding (Ekstrom et al., 1976): A sequence of paper folds is presented, with final picture showing a hole punched in the folded paper. Subjects identify from 5 options the resulting pattern of holes in the unfolded paper. For all Fluid reasoning tasks, the entire scan is a fixed time, and a variable number of items are administered depending on rate of task performance. The primary dependent variable for all reasoning tasks is the number of correct trials completed. Matrix Reasoning (adapted from (Raven, 1962)): Subjects are given a matrix that is divided into nine cells, in which the figure in the bottom right cell is missing. Below the matrix, they are given eight figure choices, and they are instructed to evaluate which of the figures would best complete the missing cell. Letter Sets (Ekstrom et al., 1976) Subjects are presented with five sets of letters, where four out of the five sets have a common rule (i.e. have no vowels), with one of the sets not following this rule. Subjects are instructed to select the unique set. Timing for all three tasks were the same. Each task was 14 min and 26 s long and began with a 24 s fixation-cross, followed by the stimulus that stayed on for 11–85 s. If a response was made in the first 11 s, the stimulus terminated at the 11 s mark. However, if a response was made after 11 s, the stimulus was terminated immediately after the response. If no response was made, the stimulus terminated after 85 s. The minimum number of trials presented was 7 and a maximum of 18 trials per task, depending on each participant's response times. ISI was 35 s.
Episodic memory
Note that for the episodic memory tasks, both the encoding and retrieval phases were imaged, but only retrieval was analyzed. Logical Memory: This task requires subjects to remember specific details from stories presented on the computer screen. The subject is asked to answer detailed multiple-choice questions about the story, with four possible answer choices. The task was 7 min long, consisting of 2 stories, with ten questions per story. Each story was divided into three 1 to 2 sentence sections, with each section displayed for 10 s. Ten seconds after completion of the story, the questions were presented for 10 s with a 2.5 s ISI between questions. Thirty-second fixation-crosses were presented before and between the stories. Word Order Recognition: A list of twelve words is presented one at a time for 4 s on the screen with a variable ISI between 700 ms and 11.4 s, and subjects were instructed to remember the order in which the words are presented. Subjects are then given a probe word at the top of the screen, and four additional word choices below. Each probe was presented for 6 s followed by a 2 s ISI. They are instructed to select the word that immediately followed the word given above. The task has two word lists, with ten questions following each list. Total task duration was 7 min 2 s with 30 s fixation at the beginning of task and between the two word lists. Paired Associates: Six pairs of words are presented on the screen, one at a time for 2 s with a variable ISI of 200 ms to 5.6 s, and subjects are instructed to remember the pairs. Following the pairs, they are given a probe word at the top of the screen and four additional word choices below. The probe and choices are presented for 5 s with an ISI of 2 s. Subjects are asked to choose the word that was originally paired with the probe word. The task contains two lists of pairs, with six probe questions for each list. The task lasted a total of 3 min and 24 s, with 30 s fixation at the beginning of the task and 10s fixation between the two lists.
Scoring
When proportion correct trials was calculated for a task, trials where the participant did not respond (i.e. timed out) were not considered in the calculation. To ensure that we included data only from instances where subjects were performing the task, we eliminate data from any task where the participant's performance was at chance or lower. For the perceptual speed tasks, we required accuracy of 75% or greater because the focus was on the speed of performance as represented by reaction time.
Validation tasks
Two tasks were used for validation of the derived CR network.
Letter Sternberg (LS) task
Our implementation of the LS task for fMRI consists of a total of three runs of thirty trials each. Each trial consists of 3 components: study, retention and probe, followed by a 3 s inter trial interval (ITI). The study component consists of the simultaneous presentation for 3 s of either one, three or six uppercase letters (10 of each trial type per run) arranged in a 2×3 grid. After a retention interval (7 s), a single lowercase letter is presented in the center of the screen for 3 s. During this period participants pressed one of two keys indicating whether or not this probe was part of the stimuli set. The contrast selected from this study was the change in activation over the three set sizes (1, 3, or 6 letters) during the retention period.
Executive context (EC) task
The EC task consists of an intrinsically cued task-switching paradigm with a no-go component. Twenty-four active task blocks, each lasting 33.5 s, include an instruction cue presented for 4.7 s, followed by 12 letter-stimuli. Each stimulus was shown for 2400 ms, but terminated following a response before that deadline. In all cases, red letters indicate a lower/upper case decision trial (left press for lower, right press for upper), green letters indicate a vowel/consonant decision trial (left press for vowel, right press for consonant), and white letters indicate a no-go trial. Each block consisted of two no-switch conditions, where they perform either the vowel/consonant or the upper/lower case task, and two switch conditions, where they perform both the vowel/consonant and the upper/lower case tasks. There were 6 blocks of the 4 conditions. The contrast chosen for this study was activation during the dual task condition.
Image analysis procedures
fMRI pre-processing
We use FMRIB Software Library v5.0 (FSL) and custom-written Python code. The following steps were performed for each participant's data set: All functional images were realigned to the first volume, corrected for the order of slice acquisition, smoothed with a 5 mm3 non-linear kernel followed by intensity normalization, and high-pass filtered using a Gaussian kernel and cut-off frequency of 0.008 Hz. The first functional volume was co-registered to the template-aligned T1-weighted image using FLIRT with the normalized mutual information cost function. These obtained transformation parameters were used to transfer the statistical parametric maps of the subject level analysis to standard space.
fMRI subject-level time-series modeling.
The fMRI time-series data was pre-whitened to explicitly correct for intrinsic autocorrelations in the data. The FEAT module in FSL was used for subject-level analysis. The majority of the tasks were analyzed using block analysis; event-related analysis was used for the three memory tasks, the letter Sternberg and the executive context tasks. A first level design matrix appropriate to each task was convolved with a model of the hemodynamic response function, yielding one contrast image per subject per task.
FreeSurfer cortical thickness analysis.
Using each individual's T1-weighted MPRAGE image, cortical thickness measures were derived using the FreeSurfer software package (http://surfer.nmr.mgh.harvard.edu/). Although the estimation procedure is automated, we manually checked the accuracy of the spatial registration and the white matter and gray matter segmentations following the analytic procedures outlined in Fjell et al. (2009). Cortical thickness was measured by first reconstructing the gray/white matter boundary and the cortical surface (Dale et al., 1999), and the distances between these surfaces at each point across the cortical mantle were calculated. Using a validated automated labeling system (Fischl et al., 2004), FreeSurfer divided the cortex into 68 different gyral-based areas, and calculates the mean thickness in each area.
Derivation of the task-invariant CR activation pattern
A pattern of activation that correlated with NART IQ was derived as follows: (1) All task-subject statistical contrasts scans were gathered for analysis. (2) The scans were randomly divided into a derivation sample comprising ~60% of the scans (=150) and a replication sample of 40% of the scans (=105). For this assignment age or task-identity played no role and were not considered for any stratification and all 150*12 task maps in the derivation sample were pooled together. Because of overall collinearity of IQ and age in our sample, we imposed orthogonality of the two measures in the derivation sample such that the p-level of the correlation between NART IQ and age was p > 0.2. (3) A Principal Component Analysis was conducted in the derivation sample. (4) All N Principal Components with an Eigen value > 1 were retained and their component scores were computed for every subject-task scan in the derivation sample. (5) All-inclusive PC-sets amongst PCs, i.e. 1, 1:2, 1:3, …., 1:N, were used in linear regressions to predict the IQ associated with each subject, and the set with the lowest AIC information criterion was chosen. (6) This step served as validation of the derived patterns: component scores for the chosen set of Principal Components were then computed in the replication sample; the regression weights obtained from the model-fit in the derivation sample were applied to produce estimates of NARTIQ in the replication sample, and all resulting 12 values per subject were averaged across task; the correlation between predicted subject average NART IQ and actual NART IQ in the replication was computed. A positive correlation with p < 0.01 was counted as a successful replication. Steps (2)–(6) were repeated 1000 times. Table 2 shows the full algorithm in pseudo-code for clarity.
Table 2.
Derivation and validation in held-out data of the task-invariant CR activation pattern.
| (1) | Randomly pick a derivation sample of 200 participants and assemble their task data in matrix array Y. Y has as many rows as voxels in the analysis, and 200*12 = 2400 columns. |
| (2) | Perform PCA on this data array; this yields an array of Principal Components in the matrix V; V has as many rows as voxels and 2399 columns since there are 2399 Principal Components. (The mean image, i.e. the mean across all columns, was removed from the data array Y prior to the PCA.) |
| (3) | Compute the PC scores W according to the formula: W = Y′ V. Here ‘ indicates matrix transposition. W has 2400 rows and 2399 columns. |
| (4) | Perform linear regressions where NARTIQ is predicted from the score array W. For every one of the N participants in the derivation sample NARTIQ is stacked 12 times, resulting in a dependent variable DV that has 200 × 12 = 2400 rows. The regression can be written as: DV = [W (:,1:k) 1] *β + ε, where the first k Principal Components are used for the array of independent variables, and 1 denotes an intercept term. The number k is determined with the best-fit AIC criterion. This concludes the model-estimation in the derivation sample. |
| (5) | A corresponding pattern can be constructed according to: pattern = V(:,1:k)*β(1:k). The pattern is normalized to have a Euclidean norm = 1. |
| (6) | Form the data array of the remaining 55 subjects in the replication sample, again subjects and tasks are stacked to form the data array Z which has as many rows as voxels and 55 × 12 = 660 columns. |
| (7) | Compute the PC scores in the replication sample with respect to the pattern derived in the derivation sample: w=Z′ pattern. The score vector w is a column vector with 660 rows. This score vector is the partial prediction of NART in the replication sample (minus an intercept term).It contains 12 predictions per participant. The predictions are averaged within subject. |
| (8) | The subject-wise prediction is then correlated with the actual NARTIQ values and the lodP statistic lodP = sign (R)* log10(p) is computed for tallying the quality of the prediction. |
| (9) | Steps 1–8 are executed 1000 times -each time a different random subset of participants is chosen- to yield 1000 activation patterns and 1000 lodP-values. |
| (10) | The 1000 patterns are averaged and re-normalized to compute a point estimate value of the task-invariant NARTIQ pattern. |
| (11) | The variability of the voxel-loadings of the 1000 patterns around the point estimate value is computed as a standard deviation. A coefficient-of-variation image is computed as: CV(i) = mean(i)/std(i), where i indicates the voxel location. CV is thresholded at ∣CV∣>3 to focus on inferentially robust voxels. |
The final point-estimate pattern was computed by averaging all derived 1000 patterns. A Z-map to assess robustness of loadings was computed by dividing the loadings in the point-estimate pattern by the standard deviation of the loadings in the 1000 patterns around the point-estimate value.
Of our 255 participants, 14 (=5.5%) were missing NART IQ information. The task-activation maps of these participants were used in the PCA-step, but could not be used in the regression to predict NART IQ. For the non-PCA computation steps in both derivation and replication samples, these participants were left out.
A more detailed account of this analysis is provided in Table 2, where we supply a pseudo-code algorithm.
Forward application of task invariant CR pattern to activation data from other studies
To obtain the subject scores of the CR-pattern in the ECF and LS task data sets, the pattern was forward applied to the contrast of interest and its expression calculated. Of the 149 participants in the ECF task, 4 were missing NART IQ information, and the correlation with NARTIQ thus only included 145 participants. Of the 121 participants who performed both ECF and LS tasks, 3 were missing NART IQ information.
Influence of IQ and the task invariant CR pattern expression on structure-cognition relationships
In the 255 adults from the RANN study, we performed Scaled Subprofile Modeling (SSM) on the array of thickness data, THX for 68 ROIs (=rows) for all 255 participants (=columns), to derive a cortical-thickness pattern that best predicted the mean performance in the RANN fluid reasoning tasks. Principal Components Analysis was performed on the thickness data. Subsequently, all-inclusive PC-sets amongst the first 20PCs, i.e. PC1, 1:2, …, 1:20, were tested in a linear regression to predict the average performance of the 3 FLUID tasks. The best-fitting set, 1:N, with the lowest AIC value was selected and the regression weights for this set were used to construct a linear-combination according to
where W is a matrix of PC-scores, with rows denoting participants, and columns denoting PC indices; V is a matrix of the topographic PCs with rows denoting ROIs and columns denoting PC indices, and beta is the vector of regression weights for the set of PCs chosen. Beta has N+1 rows, with row N+1 indicating the intercept term, which is not needed for the pattern construction.
The pattern score of the derived pattern was obtained as
Where ‘ indicates matrix transposition. The pattern score was used further for moderation analysis, i.e. the slope of the relationship between fluid reasoning performance and the pattern score was tested for a dependence on expression of the task-invariant CR pattern.
Results
A task-invariant pattern can be derived that accurately predicts IQ
The process of deriving a task invariant CR pattern, explained in detail in the methods section, produced the covariance pattern illustrated in Fig. 1. This NART IQ-related covariance pattern was derived in the derivation sample, with a test of successful prediction in the replication sample. 76% of the 1000 iterations yielded replications with a positive correlations between predicted and actual NARTIQ with p < 0.01; i.e. for more than three quarters of the split-sample iterations the derived pattern could reliably predict NART IQ in the held-out data, and exceed the to-be-expected false-positive rate of 1% more than 75-fold.
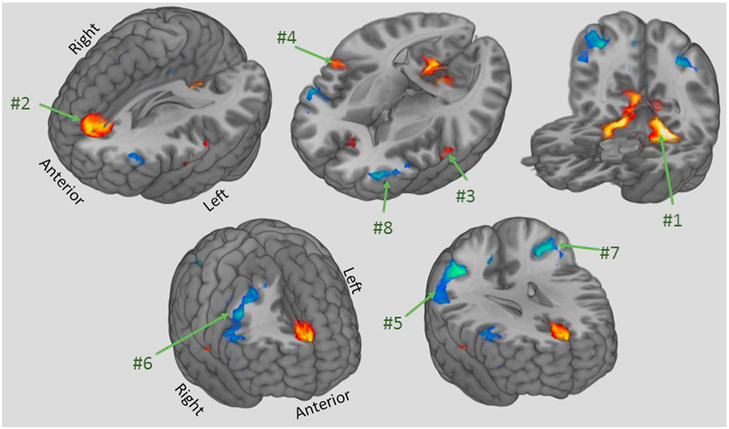
Fig. 1.
Topographic composition of the task-invariant CR pattern. Bootstrap loadings indicating statistically robust participant voxels in the covariance pattern ∣Z∣>2 with cluster size >49 voxels). Red voxels indicate positive correlation between task-activation and NART IQ, while blue voxels indicate covarying negative correlation. Numbers correspond to cluster numbers in Table 2.
Table 3 lists, and Fig. 1. illustrates, areas whose loadings significantly participate in the covariance pattern. The color coding indicates the weighting of voxel's in these areas. These voxel weights describe the covariance pattern such that areas with positive weightings increase expression and those with negative weightings decrease expression in a covarying manner. When this covariance pattern is imposed on any contrast from a task-related activation, voxel weightings are applied to the fMRI signal in that voxel, and the sum of these weighted fMRI signals yield the expression of the covariance pattern.
Table 3.
Robust loadings for the task invariant CR pattern, computed from a Bootstrap procedure. Locations with ∣Z∣>2.00 (=incorporating a correction for the number of voxels, i.e. 24,596) and a cluster size of CS > 49 are displayed, in descending order of Z for each loading direction. Anatomical labels are taken from the Talairach atlas from the program autoaq distributed as part of FSL. The cluster numbers correspond to clusters displayed in Fig. 1. BA = Brodmann Area.
| Cluster | Voxels | Max | MNI coordinates | Region labels | ||
|---|---|---|---|---|---|---|
| # | Z | X | Y | Z | ||
| Positive loadings | ||||||
| 1 | 1194 | 3.25 | 6 | −51 | 3 | Bilateral cerebellum |
| 2 | 414 | 2.97 | 0 | 36 | 18 | Bilateral medial frontal gyrus and anterior cingulate, BA 9 & 32 |
| 3 | 78 | 2.56 | −60 | −9 | 6 | Left superior temporal gyrus, BA 22 |
| 4 | 68 | 2.71 | 54 | −6 | 9 | Right superior temporal gyrus, BA 22 |
| Negative loadings | ||||||
| 5 | 912 | 3.3 | 36 | −48 | 42 | Right inferior parietal lobule, BA 40 |
| 6 | 505 | 2.91 | 39 | 12 | 39 | Right middle and inferior frontal gyri, BA 6 & 9 |
| 7 | 317 | 2.99 | −36 | −51 | 42 | Left Precuneus and inferior parietal lobule, BA 7 & 40 |
| 8 | 145 | 2.94 | −39 | 48 | 6 | Left middle and inferior frontal gyri, BA 10 & 46 |
Because age and NART IQ are correlated in our sample (r = 0.28, p < 0.0001), we tried to ensure that age did not influence the derivation of the IQ pattern by requiring that the relationship between age and NART IQ was non-significant in each derivation sample. Still, we tested to what extent pattern score predicted NART IQ when partialling for age in partial correlations. The Table 4 below shows the effect of partialling for age. Two of the Memory asks (Logical Memory and Word Order) show no independent association between pattern expression and NARTIQ.
Table 4.
Bivariate correlations and correlations partialled for age between pattern expression and NARTIQ in the full sample.
| Task | Bivariate unadjusted R (NARTIQ) |
R (NARTIQ) partialling for age |
|---|---|---|
| Logical Memory | R=0.1728 p=0.0072 | R = 0.1224 p = 0.0582 |
| Word Order | R = 0.1243 p = 0.0539 | R = 0.0729 p = 0.2606 |
| Pair Associates | R=0.2581 p=0.0001 | R=0.2175 p=0.0007 |
| Matrix Reasoning | R=0.2942 p=0.0000 | R=0.2503 p=0.0001 |
| Letter Sets | R=0.2468 p=0.0001 | R=0.1965 p=0.0022 |
| Paper Folding | R=0.3394 p=0.0000 | R=0.2795 p=0.0000 |
| Digit Symbol | R=0.4355 p=0.0000 | R=0.3793 p=0.0000 |
| Letter Comparison | R=0.3143 p=0.0000 | R=0.2738 p=0.0000 |
| Pattern Comparison | R=0.2234 p=0.0005 | R=0.1917 p=0.0029 |
| Antonyms | R=0.3214 p=0.0000 | R=0.2561 p=0.0001 |
| Picture Naming | R=0.3729 p=0.0000 | R=0.3536 p=0.0000 |
| Synonyms | R=0.3318 p=0.0000 | R=0.2752 p=0.0000 |
Bolding indicates significant R values.
Expression of the task-invariant CR pattern in separate imaging data predicts NART IQ
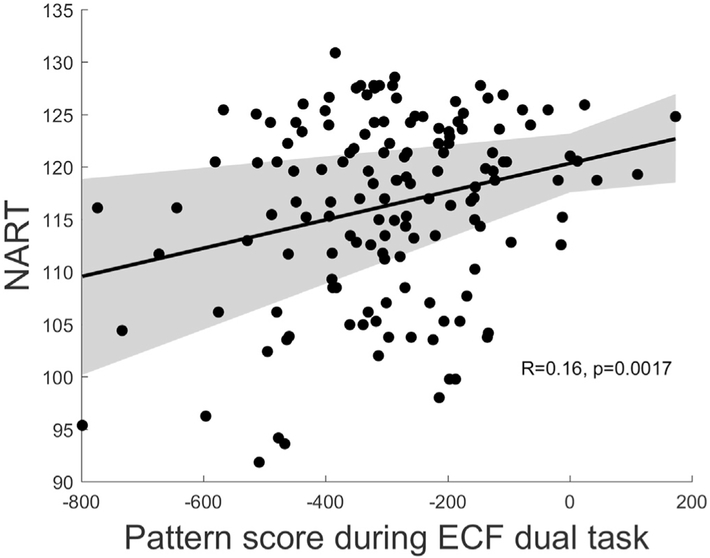
In the chosen contrast for each of the two separate activation studies, we multiplied pattern loadings of each voxel in the task-invariant CR-pattern with each subject's parametric task-maps. The subsequent sum of the products across voxels yielded one scalar number per participant for each contrast, which indicates the predicted NART IQ score. For the ECF task, we used the contrast from the dual task condition, where participants needed to switch between two selection rules. As demonstrated in Fig. 2, the derived estimated NART IQ score showed a statistically significant positive relationship with actual NART IQ even when adjusting for age (t = 3.79, p = 0.0002). For the LS task, no significant relationship between pattern-expression and NART IQ was found.
Fig. 2.
Replication success in the dual ECF task, which is separate from the RANN data set. NART IQ was predicted from the pattern score and age. Both also contributed independently: for age we obtained T = −2.79, p = 0.0059, and for the pattern score we obtained T = 3.7921, p = 0.0002.
Expression of the task-invariant CR pattern accounts for additional variance in fluid reasoning performance over cortical thickness
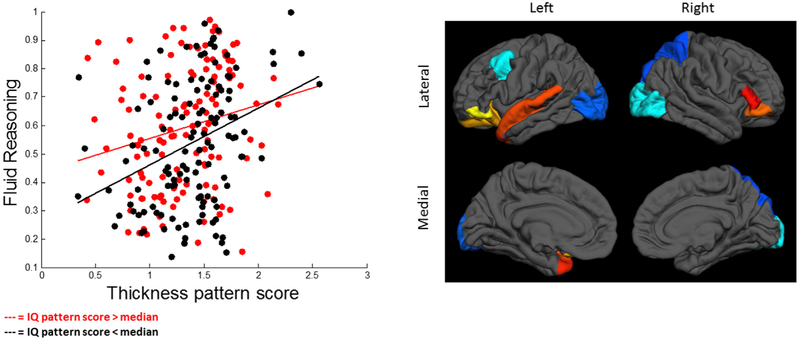
We tested whether the task invariant CR pattern accounted for additional variance in fluid reasoning performance over and above a covariance pattern that summarized the effect of cortical thickness on fluid reasoning. The derived cortical thickness covariance pattern is illustrated in Fig. 3. It comprises the following areas: positive loadings indicating a positive relationship between cortical thickness and fluid reasoning was found in the following areas: left orbitofrontal cortex, left pars orbitalis, left superior temporal cortex, left temporal pole, right pars orbitalis, and right pars triangularis. Negative loadings, indicating a negative correlation between thickness and fluid reasoning was found: caudal middle frontal cortex, left cuneus, left lateral occipital cortex, left postcentral gyrus, right lateral occipital cortex, right paracentral gyrus, and superior parietal cortex. It is worth stressing that all loadings are relative since the whole-brain mean thickness was removed prior to the PCA, thus negative loadings do not necessarily indicate that better performers have lower thickness in the corresponding areas in an absolute sense.
Fig. 3.
Moderation of the relationship between a cortical thickness covariance pattern and fluid reasoning performance by expression of the task invariant CR pattern. The ROIs contributing significantly to the cortical thickness covariance pattern are illustrated on the right, and the moderation is illustrated on the left. After dichotomizing expression of the CR pattern score around its median into high and low pattern expression, one can discern a negative difference in slope: participants with low pattern scores (black circles) show a steeper slope in the relationship of thickness and fluid reasoning (black line), while participants with high pattern scores (red circles) show a flatter slope (red line). The scatter plot in the figure shows raw data, not partial model predictions. The colors in the thickness pattern are arbitrary, to illustrate the different regions.
The structural pattern expression accounted for 7% of variance in fluid reasoning performance (t = 4.74, p < .00001). The additional variance contributed by CR pattern was 2.4% (T = 3.18, p < .0017). To assess moderation of the relationship between cortical thickness and fluid reasoning, we tested whether there was a significant interaction between cortical thickness and the CR pattern on fluid reasoning performance. The interaction effect was negative and significant, accounting for an additional 2% in the variance of fluid reasoning (T = −2.34, p < .0199). To illustrate this significant moderation, in Fig. 3, we display the thickness-cognition relationship using the summary covariance pattern, indicating high and low task-invariant CR pattern scores around a median split.
In addition to the figure display, it is instructive to consider the regression equation for this analysis. Without the intercept term, we obtained
where pattern score and thickness are Z-transformed versions of the raw pattern score and the cortical thickness measured in millimeters. We fixed the transformed pattern score at the 75th and 25th percentile and calculated the partial relationship between thickness and performance for high and low pattern expression scores, respectively:
where intercept captures main effect of the pattern expression which is now fixed at one value and the original intercept of the regression. High pattern expression at the 75th percentile reduced the slope of the main effect of thickness on cognition by a factor 0.0429/0.0623 = 0.69; low pattern expression, on the other hand, increases the slope by a factor of 0.0792/0.0623 = 1.27.
Discussion
Cognitive reserve theory posits that individual differences in how tasks are processed help some people perform better than others given comparable structural characteristics of the brain (e.g. cortical thickness), or the same amount of brain pathology (Stern, 2002). Support for the concept of CR comes from epidemiologic studies that demonstrate that specific life experiences, such as premorbid IQ, or educational/occupational attainment are associated with reduced risk of developing Alzheimer's disease (Valenzuela and Sachdev, 2006). These studies suggest that these life experiences modify active cognitive processing in a way that allows some individuals to cope better than others with AD pathology. Many studies have demonstrated that given a certain level of clinical severity of AD, individuals with higher educational/occupational attainment have more advanced AD pathology, suggesting that they are coping better with this pathology in order to maintain comparable performance with people who have lower education and less pathology (e.g. Stern et al., 1992). The concept of CR has also been applied to normal aging, where many studies, but not all, have demonstrated a slower rate of age-related cognitive decline in people with higher educational or occupational attainment (Zahodne et al., 2015b).
Imaging studies that have attempted to understand the neural implementation of cognitive reserve have typically focused on activation associated with a single particular task. Thus, we and others have reported that in individuals with higher reserve proxies, such as higher IQ or educational attainment, task-related activation is often more efficient, i.e. less activation is required to accomplish a task to a similar level of performance. Further, when tasks are made more difficult activation in people with higher CR often demonstrate greater capacity, i.e. the individuals can activate these task-related networks to a greater degree (Oh et al., 2017; Stern, 2009). These observations support the idea that CR represents the influence of lifetime exposures on cognitive networks, and that these CR-related processing differences are also present in healthy individuals.
While studies investigating individual differences in task-related activation are instructive, they do not address the possibility that life experiences may result in brain processing differences that might be applicable to multiple tasks. This consideration sparked our interest in attempting to identify a task-invariant CR network that might be expressed during the performance of multiple tasks. In a previous study, we attempted to identify a task-invariant CR network by extracting an fMRI covariance pattern that was expressed across two different, unrelated tasks, and whose degree of expression correlated with standard proxies of CR (Stern et al., 2008). With increasing CR we noted a network consisting of increased expression in right and left superior frontal gyrus and concomitant reduced expression in left medial frontal gyrus. This network was noted in young but not older participants. This study guided our current thinking, but suffered from small Ns. In addition, we previously utilized a version of a Multivariate Linear Model which operated contrast data which was the mean across multiple subjects. This is a less sensitive multivariate approach than the one we use in the current study. The current approach requires less data reduction and utilized individual differences to a greater degree.
Here, we took advantage of data from our Reference Ability Neural Network study, where we are administering 12 different tasks in the scanner. We derived a single covariance pattern that was active during the performance of all 12 tasks and whose degree of expression correlated with a CR proxy (i.e. the IQ). We therefore considered this identified pattern as a good candidate for a task-invariant CR network.
The identified CR network was very successful in predicting NART IQ in held-out data from the RANN tasks. The pattern reliably predicted NART IQ in held-out data over more than three quarters of 1000 iterations. This exceeds the to-be-expected false-positive rate of 1% more than 75-fold and helps establish the relationship between the pattern expression and IQ over 12 different tasks.
To further validate the pattern, we forward applied it to data from two different activation studies one assessing set switching, and the other assessing working memory. In the former but not the latter task, we found a significant relationship between expression of our task-invariant CR network in the forward applied data sets and IQ. It is notable that the set switching task taps a cognitive ability (executive control), that differs from those assessed in the activation tasks used to derive the CR pattern. This, along with the validation in held out data across 12 tasks, supports the idea that we have identified a task-invariant network that may be activated during the performance of multiple cognitive operations. Still, expression of the pattern in the external working memory task did not correlate with IQ, suggesting that this network may not be expressed across all activation tasks.
We and others have noted that proxy measures of CR can account for additional variance in cognitive performance after accounting for variance attributable to structural brain measures (Brayne et al., 2010; Stern et al., 1992). Further, we have noted that proxy measures of CR can moderate the relationship between measured aspects of neuroanatomy and clinical outcomes such as cognitive performance. For example, in a study using gray matter volume ROIs, we found that a CR proxy moderated the relationship between brain and cognition such that given a certain gray matter volume, individuals with higher CR performed better on cognitive tasks (Steffener et al., 2014b). This result suggests that the individuals with higher CR were better able to take advantage of this greater volume. The converse is conceivable also, and it could be that higher CR implies that brain structure is less of a determinant of good performance than in low CR. Thus we felt that an appropriate test for a putative measure of CR is whether it accounts for additional variance in the structure – cognition relationship or moderates the structure-cognition relationship. After identifying a covariance pattern comprising a set of areas where cortical thickness correlated with reasoning, which closely resembled semantic networks in the left hemisphere {Vatansever, 2017 #216}, we tested whether our CR pattern accounted for a significant amount of additional variance in cognition after controlling for cortical thickness, which it did. This provides evidence that individuals able to recruit this network perform better than can be expected simply by considering cortical thickness. We then tested whether the CR pattern moderated this structure (i.e. thickness) – cognition (i.e. fluid reasoning) relationship and found significant moderation. The cortical-thickness pattern explained 7% of the variance in fluid reasoning performance. The NART IQ pattern explained an additional 2.4% of the variance over and above cortical thickness, which is more than one third of the variance accounted for by the thickness pattern, and inferentially highly significant. Further, the pattern also moderates the effect of cortical thickness on cognition. This finding is not trivial, particularly in the context of normal cognition. Clearly cortical thickness remains a driver of performance, but expression of our CR network moderates that influence, and separately accounts for additional variance. We consider this moderation analysis an extremely demanding test because it was performed in cognitively normal individuals age 20 through 80.
It is important to note that cortical thickness itself could partly be a result of lifestyle and accumulation of experiences. This relationship may be associated with the concept of brain maintenance (Nyberg et al., 2012). Further, a correlation between cortical thickness and the fMRI results is certainly expected. Here, however, we focused on the identified networks additional contribution to performance, over and above that explained by cortical thickness. This is because the concept of cognitive reserve addresses the aspect of cognitive performance that cannot be explained simply by the underlying brain anatomy and pathology. Thus cognitive reserve should help account for individual differences in performance given the same status of the brain.
We considered whether individuals with higher IQ might have quicker reaction times and whether this could have influenced study results. When we examined time on task, we did find that individuals with higher IQ had more rapid RT for items in our activation tasks. When RT was correlated with pattern expression, there was no correlation for 6 tasks and positive one for 3 and a negative one for 2 (there were no RTs recorded for picture naming). Since we do not see a consistent relationship between RT on specific tasks and expression of the identified CR network we conclude that time on task did not influence the derivation of the task-invariant network.
The task-invariant CR network as summarized by a covariance pattern encompasses a wide set of brain regions that are involved in both basic visual and motor processes, as well as higher order frontoparietal cognitive control regions, as shown in Fig. 1. The regions with positive loadings (in orange) showed relatively greater activation with higher CR while the regions with negative loadings (in blue) showed relatively lower activation with higher CR. In the positive pattern, the largest cluster was in the cerebellum, which has been associated with not only motor coordination but also cognitive processing (Koziol et al., 2014). The second largest cluster was in the medial frontal gyrus with the center of gravity located at the dorsal anterior cingulate cortex and has been associated with error prediction (Alexander and Brown, 2011) as well as pain perception (Jahn et al., 2016). The medial frontal gyrus is also an important node in the default mode network, which has been shown to have a role in the application of learned rules in a stable mental environment {Vatansever, 2017 #215}. The last two clusters were on the anterior portion of the superior temporal gyrus for both hemispheres and were usually associated with auditory processing including speech comprehension (Ozker et al., 2017). For the negative pattern, two clusters resided in bilateral inferior parietal lobules, extending to parts of the precuneus on the left hemisphere, and two other clusters in bilateral middle and inferior frontal gyri. Large portions of these clusters are part of the frontoparietal attention network and specifically in the ventral attention network which reorients attentional processes to external stimuli that may be unexpected (Corbetta and Shulman, 2002). It is important to stress that activity in regions with positive loadings covary together such that the activity is higher for participants with higher CR, while at the same time, regions with negative loadings are relatively lower with higher CR. Combining the loading directions with functional significance of the regions in the CR task invariant pattern demonstrates that higher CR is associated with upregulation of more task-relevant processes such as motor coordination and error prediction while also downregulating the stimulus-driven attention network, which minimizes distractions that may otherwise diminish focus on the goal-oriented processes in support of the task at hand.
Localization in a pattern derived from SSM is not equivalent to most of the extant literature because most studies relate localization to the performance of specific tasks using a general linear model (GLM) procedure. GLM directly localizes voxels associated with task performance on a voxelwise basis. In contrast, the SSM procedure seeks to identify a set of voxels whose increase or decrease expression during activation covaries. A key advantage of this approach is that it directly addresses the interaction of multiple brain areas during task performance. Other advantages are that the covariance pattern can be directly applied to other fMRI data for exploration or validation, and that utilization of the covariance pattern can be directly captured with a single number. However, because of differences between GLM and SSM analyses, areas localized in SSM during the performance of a specific task may or may not be similar to those identified with GLM. Despite this difference, we did attempt to determine whether the task-invariant network included areas typically observed in standard resting BOLD networks such as the task positive network or the default mode network as described by Fox et al. (2005). Apart from the medial frontal (BA32) and the supramarginal gyrus (BA 40) activations, the network had little overlap with these two networks. BA40 activation negative correlated with IQ in our study while it was part of the task-positive network in Fox et al. (2005). BA 32 correlated positively with IQ in our task-invariant pattern but was part of both task-positive and -negative networks in Fox et al. (2005).
Similarly, apart from medial frontal activation, the network had little overlap with other “common” or task-invariant networks that have been reported. These other common or task-invariant networks have been identified or developed for various reasons and in various ways. Some investigators started by noticing that there was common activation across multiple tasks, and then proceeding to use convergence analysis and other approaches to validate this observation (Cole et al., 2014; Cole and Schneider, 2007; Duncan, 2010; Duncan and Owen, 2000; Hugdahl et al., 2015). An alternate approach, more similar to the one used here, is to identify brain areas or networks associated with specific cognitive processes, such as aspects of attention (Petersen and Posner, 2012; Posner and Petersen, 1990). Finally, others derived a network with a specific goal in mind. For example one study intended to derive a common neurobiological substrate for mental illness (Goodkind et al., 2015). Here, our overarching goal was to identify a task-invariant network whose expression correlated with a IQ, a key proxy for CR. This differs significantly from simply trying to identify a generic task-invariant network.
There are several other advantages/differences of the analysis here compared to previously identified task-invariant networks. First, we started with fMRI activation data from 12 tasks, all administered to the same people, demanding a consistent relationship with NARTIQ. Thus we did not need to rely on meta-study data. Second, we did not rely on topographic conjunction analysis or visual identification of selected brain regions. Rather, we derived a covariance pattern which described brain areas that are consistently more or less activated, in a covarying manner, by people with higher NART IQ, regardless of cognitive task in suite of 12 activation tasks. This is a more stringent requirement than topographic concordance of activation patterns. Lastly, out-of-sample validation was built into the derivation process, and the pattern successfully predicted NARTIQ in held-out data for all 12 tasks with a prediction success that far surpassed chance.
A related theoretical issue is our premise that a task-invariant CR network should exist. In addition, why would such a network be expressed in younger people who have not experienced age-related cognitive change, or in tasks such as vocabulary that typically (and in our data as well) show a positive age gradient in performance. One might expect that this network should not need to be expressed in people or for tasks with little or no negative age effect. This question has important theoretical implications. We have hypothesized that there are two broad ways in which CR may be implemented (Stern, 2009). One, which we have in the past called “neural reserve” posits that existing individual differences in the way that tasks are processed (even in healthy individuals) may allow some individuals to cope better than others with age-or disease-related brain changes. In the past we have characterized networks in terms of differing efficiency or capacity. An alternate implementation of CR is what we have called “neural compensation” where in response to pathology some people adapt new or infrequently used compensatory networks (Steffener et al., 2011). Our concept of a pre-existing, task-invariant CR network is consistent with the concept of neural reserve. That is, networks that are up and running lifelong are important for CR in that they might allow some people to cope with age-or disease-related changes when they occur. The innovation in thinking here is that neural reserve may not be task specific but may also be implemented as a network that is activated across multiple tasks with differing cognitive demands.
One might also question our approach towards identifying a CR network where we identified a set of areas whose expression correlates with IQ. If CR is associated with better performance, perhaps it would be more advisable to derive a pattern that simply is associated with better performance on most tasks. However, this approach would neglect one of the key qualities of CR, which is that it helps to provide better performance in the face of a specific degree of age- or disease-related brain changes. In the past, CR proxies such as IQ have proven to be associated with better performance in the face of brain changes, as well as to moderate between brain changes and performance. Thus our approach is in line with the original conceptualization of cognitive reserve and was geared towards identifying a pattern of activation associated with higher IQ, since such a pattern would have greater probability of providing such moderation.
Going forward, we will attempt to apply the same method to other CR proxies, such as measures of educational and occupational attainment. This is because the epidemiology suggests that each of these life exposures contributes incrementally to CR. Thus, we would predict that task invariant networks associated with these other CR proxies would encompass different brain areas, or have alternate weightings on some of the areas included in the present network. For this reason we have entitled the paper “A task-invariant CR network,” because we assume there will be others as well.
The identification of this task invariant CR network confirms the theoretical prediction that an aspect of cognitive processing is common across multiple tasks and helps influence overall task performance. We derived this network using IQ, a proxy for CR. Analyses that have investigated CR using IQ operate under the assumption that the genetics and life experience that determine IQ allow some people to maintain performance better than others in the face of age-or disease-related brain changes. We thus would like to speculate that this network captures aspects of the neural implementation of IQ's contribution to CR. Epidemiologic evidence indicates that other life experiences, including educational and occupational exposures, and late life leisure activities, may contribute separate aspects to CR. Thus, it is possible that these experiences might be associated with different task-invariant networks. Future work will use similar methods to determine whether extracting task invariant networks using other CR proxies produces additional task invariant CR networks. We expect that there may be overlap among them, but that any potential differences may be illuminating.
Besides its theoretical importance, a direct imaging measure of CR would be extremely useful. Today researchers have typically use proxies for CR, based on epidemiologic evidence that these proxies are associated with reduced risk of incident dementia or with slowing of age-related cognitive decline. While in the context of these studies these proxies represent CR, they are not direct measures of an individual's acquired CR. In response to this, a statistical residual model has been proposed to directly estimate CR (Reed et al., 2010; Zahodne et al., 2013). This approach estimates the amount of variance in cognitive performance that can be accounted for by both demographic variables and selected structural brain measures. The residual variance in performance is then considered to be a direct measure of CR. While promising, this approach relies on accurate and relatively full specification of the brain measures that account for cognitive performance, which by nature renders it relatively inaccurate. Further, we have reported that this approach can provide anomalous results in longitudinal studies (Zahodne et al., 2015a).
In contrast, expression of the reported task-invariant network could be applied to many fMRI tasks, yielding a direct, accurate estimate of CR. This approach could be used in studies intended to enhance cognitive function, and help determine whether they actually enhance CR. Further, many studies have demonstrated that once AD pathology begins to affect cognitive function, individuals with higher CR actually show more rapid rate of decline. Thus, it would be very important to estimate levels of CR in studies designed to influence the preclinical to clinical AD process. Unfortunately, this is difficult to do using proxy measures since these measures are often language and culture specific, and might not translate well across different countries. A direct imaging measure of CR might be of great use.
In summary, we have identified a covariance pattern whose expression correlates with a measure of IQ. We suggest that this pattern may be a task-invariant measure of CR. The beauty of our hypothesis is that it is directly testable in any situation where task-related activation data from any ask are available.
Acknowledgments
This work was supported by the National Institute on Aging [Grant numbers R01 AG026158 and RF1AG038465].
References
- Alexander GE, Moeller JR, 1994. Application of the Scaled Subprofile Model to functional imaging in Neuropsychiatric disorders: a principal component approach. Hum. Brain Mapp 2, 79–94. [Google Scholar]
- Alexander WH, Brown JW, 2011. Medial prefrontal cortex as an action-outcome predictor. Nat. Neurosci. 14, 1338–1344. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett DA, Wilson RS, Schneider JA, Evans DA, Mendes De Leon CF, Arnold SE, Barnes LL, Bienias JL, 2003. Education modifies the relation of AD pathology to level of cognitive function in older persons. Neurology 60 (12), 1909–1915. [DOI] [PubMed] [Google Scholar]
- Brayne C, Ince PG, Keage HAD, McKeith IG, Matthews FE, Polvikoski T, Sulkava R, 2010. Education, the brain and dementia: neuroprotection or compensation? EClipSE Collab. Members 133, 2210–2216. [DOI] [PubMed] [Google Scholar]
- Cole MW, Repovs G, Anticevic A, 2014. The frontoparietal control system: a central role in mental health. Neuroscientist 20, 652–664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cole MW, Schneider W, 2007. The cognitive control network: integrated cortical regions with dissociable functions. Neuroimage 37, 343–360. [DOI] [PubMed] [Google Scholar]
- Corbetta M, Shulman GL, 2002. Control of goal-directed and stimulus-driven attention in the brain. Nat. Rev. Neurosci. 3, 201–215. [DOI] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI, 1999. Cortical surface-based analysis. I. Segmentation and surface reconstruction. Neuroimage 9, 179–194. [DOI] [PubMed] [Google Scholar]
- Duncan J, 2010. The multiple-demand (MD) system of the primate brain: mental programs for intelligent behaviour. Trends Cogn. Sci. 14, 172–179. [DOI] [PubMed] [Google Scholar]
- Duncan J, Owen AM, 2000. Common regions of the human frontal lobe recruited by diverse cognitive demands. Trends Neurosci. 23, 475–483. [DOI] [PubMed] [Google Scholar]
- Ekstrom RB, French JW, Harman HH, Dermen D, 1976. Manual for Kit of Factor-referenced Cognitive Tests (Princeton). [Google Scholar]
- Fischl B, van der Kouwe A, Destrieux C, Halgren E, Segonne F, Salat DH, Busa E, Seidman LJ, Goldstein J, Kennedy D, Caviness V, Makris N, Rosen B, Dale AM, 2004. Automatically parcellating the human cerebral cortex. Cereb. Cortex 14, 11–22. [DOI] [PubMed] [Google Scholar]
- Fjell AM, Westlye LT, Amlien I, Espeseth T, Reinvang I, Raz N, Agartz I, Salat DH, Greve DN, Fischl B, Dale AM, Walhovd KB, 2009. High consistency of regional cortical thinning in aging across multiple samples. Cereb. Cortex 19, 2001–2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox MD, Snyder AZ, Vincent JL, Corbetta M, Van Essen DC, Raichle ME, 2005. The human brain is intrinsically organized into dynamic, anticorrelated functional networks. Proc. Natl. Acad. Sci. U. S. A. 102, 9673–9678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodkind M, Eickhoff SB, Oathes DJ, Jiang Y, Chang A, Jones-Hagata LB, Ortega BN, Zaiko YV, Roach EL, Korgaonkar MS, Grieve SM, Galatzer-Levy I, Fox PT, Etkin A, 2015. Identification of a common neurobiological substrate for mental illness. JAMA Psychiatry 72, 305–315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hugdahl K, Raichle ME, Mitra A, Specht K, 2015. On the existence of a generalized non-specific task-dependent network. Front. Hum. Neurosci. 9, 430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jahn A, Nee DE, Alexander WH, Brown JW, 2016. Distinct regions within medial prefrontal cortex process pain and cognition. J. Neurosci. 36, 12385–12392. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones RN, Manly J, Glymour MM, Rentz DM, Jefferson AL, Stern Y, 2011. Conceptual and measurement challenges in research on cognitive reserve. J. Int. Neuropsychol. Soc. 17, 593–601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koziol LF, Budding D, Andreasen N, D'Arrigo S, Bulgheroni S, Imamizu H, Ito M, Manto M, Marvel C, Parker K, Pezzulo G, Ramnani N, Riva D, Schmahmann J, Vandervert L, Yamazaki T, 2014. Consensus paper: the cerebellum's role in movement and cognition. Cerebellum 13, 151–177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meng X, D'Arcy C, 2012. Education and dementia in the context of the cognitive reserve hypothesis: a systematic review with meta-analyses and qualitative analyses. PLoS One 7 e38268. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moeller JR, Strother SC, Sidtis JJ, Rottenberg DA, 1987. Scaled subprofile model: a statistical approach to the analysis of functional patterns in positron emission tomographic data. J. Cereb. Blood Flow Metabolism 7, 649–658. [DOI] [PubMed] [Google Scholar]
- Nyberg L, Lovden M, Riklund K, Lindenberger U, Backman L, 2012. Memory aging and brain maintenance. Trends Cogn. Sci. 16, 292–305. [DOI] [PubMed] [Google Scholar]
- Oh H, Razlighi QR, Stern Y, 2017. Multiple pathways of reserve simultaneously present in cognitively normal older adults. Neurology. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ozker M, Schepers IM, Magnotti JF, Yoshor D, Beauchamp MS, 2017. A double dissociation between anterior and posterior superior temporal gyrus for processing audiovisual speech demonstrated by electrocorticography. J. Cogn. Neurosci. 29, 1044–1060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petersen SE, Posner MI, 2012. The attention system of the human brain: 20 years after. Annu. Rev. Neurosci. 35, 73–89. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Posner MI, Petersen SE, 1990. The attention system of the human brain. Annu. Rev. Neurosci. 13, 25–42. [DOI] [PubMed] [Google Scholar]
- Raven JC, 1962. Advanced Progressive Matrices, set II. H.K. Lewis, London, UK. [Google Scholar]
- Reed BR, Mungas D, Farias ST, Harvey D, Beckett L, Widaman K, Hinton L, DeCarli C, 2010. Measuring cognitive reserve based on the decomposition of episodic memory variance. Brain 133, 2196–2209. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rentz DM, Mormino EC, Papp KV, Betensky RA, Sperling RA, Johnson KA, 2017. Cognitive resilience in clinical and preclinical Alzheimer's disease: the Association of Amyloid and Tau Burden on cognitive performance. Brain Imaging Behav. 11, 383–390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salthouse TA, Babcock RL, 1991. Decomposing adult age differences in working memory. Dev. Psychol. 27, 763–776. [Google Scholar]
- Salthouse TA, Kersten AW, 1993. Decomposing adult age differences in symbol arithmetic. Mem. Cogn. 21, 699–710. [DOI] [PubMed] [Google Scholar]
- Steffener J, Barulli D, Habeck C, O'Shea D, Razlighi Q, Stern Y, 2014a. The role of education and verbal abilities in altering the effect of age-related gray matter differences on cognition. PLoS One 9 e91196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steffener J, Barulli D, Habeck C, Stern Y, 2014b. Neuroimaging explanations of age-related differences in task performance. Front. aging Neurosci. 6, 46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steffener J, Reuben A, Rakitin BC, Stern Y, 2011. Supporting performance in the face of age-related neural changes: testing mechanistic roles of cognitive reserve. Brain Imaging Behav. 22, 655–669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern Y, 2002. What is cognitive reserve? Theory and research application of the reserve concept. J. Int. Neuropsychological Soc. 8, 448–460. [PubMed] [Google Scholar]
- Stern Y, 2009. Cognitive reserve. Neuropsychologia 47, 2015–2028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern Y, Alexander GE, Prohovnik I, Mayeux R, 1992. Inverse relationship between education and parietotemporal perfusion deficit in Alzheimer's disease. Ann. Neurology 32, 371–375. [DOI] [PubMed] [Google Scholar]
- Stern Y, Habeck C, Steffener J, Barulli D, Gazes Y, Razlighi Q, Shaked D, Salthouse T,2014. The Reference Ability Neural Network Study: motivation, design, and initial feasibility analyses. Neuroimage 103, 139–151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stern Y, Zarahn E, Habeck C, Holtzer R, Rakitin BC, Kumar A, Flynn J, Steffener J, Brown T, 2008. A common neural network for cognitive reserve in verbal and object working memory in young but not old. Cereb. Cortex 18, 959–967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Valenzuela MJ, Sachdev P, 2006. Brain reserve and dementia: a systematic review. Psychol. Med. 36, 441–454. [DOI] [PubMed] [Google Scholar]
- Woodcock RW, Johnson MB, Mather N, 1989. Woodcock-Johnson Psycho-educational Battery–revised. DLM Teaching Resources. [Google Scholar]
- Xu W, Yu JT, Tan MS, Tan L, 2015. Cognitive reserve and Alzheimer’s disease. Mol. Neurobiol. 51, 187–208. [DOI] [PubMed] [Google Scholar]
- Zahodne LB, Glymour MM, Sparks C, Bontempo D, Dixon RA, MacDonald SW, Manly JJ, 2011. Education does not slow cognitive decline with aging: 12-year evidence from the victoria longitudinal study. J. Int. Neuropsychol. Soc. 17, 1039–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahodne LB, Manly JJ, Brickman AM, Narkhede A, Griffith EY, Guzman VA, Schupf N, Stern Y, 2015a. Is residual memory variance a valid method for quantifying cognitive reserve? A longitudinal application. Neuropsychologia 77, 260–266. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahodne LB, Manly JJ, Brickman AM, Siedlecki KL, Decarli C, Stern Y, 2013. Quantifying cognitive reserve in older adults by decomposing episodic memory variance: replication and extension. J. Int. Neuropsychol. Soc. 19, 854–862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zahodne LB, Stern Y, Manly JJ, 2015b. Differing effects of education on cognitive decline in diverse elders with low versus high educational attainment. Neuropsychology 29, 649–657. [DOI] [PMC free article] [PubMed] [Google Scholar]