3D conditional generative adversarial networks for high-quality PET image estimation at low dose

Abstract

Positron emission tomography (PET) is a widely used imaging modality, providing insight into both the biochemical and physiological processes of human body. Usually, a full dose radioactive tracer is required to obtain high-quality PET images for clinical needs. This inevitably raises concerns about potential health hazards. On the other hand, dose reduction may cause the increased noise in the reconstructed PET images, which impacts the image quality to a certain extent. In this paper, in order to reduce the radiation exposure while maintaining the high quality of PET images, we propose a novel method based on 3D conditional generative adversarial networks (3D c-GANs) to estimate the high-quality full-dose PET images from low-dose ones. Generative adversarial networks (GANs) include a generator network and a discriminator network which are trained simultaneously with the goal of one beating the other. Similar to GANs, in the proposed 3D c-GANs, we condition the model on an input low-dose PET image and generate a corresponding output full-dose PET image. Specifically, to render the same underlying information between the low-dose and full-dose PET images, a 3D U-net-like deep architecture which can combine hierarchical features by using skip connection is designed as the generator network to synthesize the full-dose image. In order to guarantee the synthesized PET image to be close to the real one, we take into account of the estimation error loss in addition to the discriminator feedback to train the generator network. Furthermore, a concatenated 3D c-GANs based progressive refinement scheme is also proposed to further improve the quality of estimated images. Validation was done on a real human brain dataset including both the normal subjects and the subjects diagnosed as mild cognitive impairment (MCI). Experimental results show that our proposed 3D c-GANs method outperforms the benchmark methods and achieves much better performance than the state-of-the-art methods in both qualitative and quantitative measures.

Introduction

Positron emission tomography (PET) has been widely applied in hospitals and clinics for disease diagnosis and intervention (Daerr et al.,; Mosconi et al., 2008; Huang et al., 2014; Cerami et al., 2015). Different from other imaging techniques, such as computed tomography (CT) and magnetic resonance imaging (MRI), PET is a functional imaging technique that produces three-dimensional in-vivo observation of metabolism processes of human body (Karnabi, 2017). Specifically, the PET system detects pairs of gamma rays emitted indirectly from a radioactive tracer which is injected into the human body on a biologically active molecule. Then, three-dimensional PET images of tracer concentration within the human body are constructed using computer analysis (Bailey et al., 2005).

To^† obtain high quality PET images for diagnostic needs, a full dose radioactive tracer is usually preferred. This inevitably raises concerns about potential health hazards. According to the report “Biological Effects of Ionizing Radiation (BEIR VII)”,¹ the increased risk of incidence of cancer is 10.8% per Sv, so one brain PET scan increases lifetime cancer risk by about 0.04%. Although this number is small, the risks are multiplied for the patients who experience multiple PET scans during their treatments. Moreover, these risks are more serious for pediatric patients. Although it is desirable to reduce the dose during the PET scanning, a major drawback of dose reduction is that more noise may be involved in the reconstructed PET images, resulting in poor image quality.

A range of methods have been proposed to improve the image quality and reduce noise and artifacts in PET images, while preserving crucial image details. In (Bagci and Mollura, 2013), for denoising PET images and preserving structural information simultaneously, the authors used the singular value thresholding concept and Stein's unbiased risk estimate to optimize a soft thresholding rule. In order to address the issue of resolution loss associated with denoising, Pogam et al. (2013) considered a strategy that combines the complementary wavelet and curvelet transforms. In (Mejia et al., 2014), a multi-resolution approach for noise reduction of PET images was proposed in the transform domain by modeling each sub-band as a group of different regions separated by boundaries.

The aforementioned methods are mainly designed to improve the image quality for the full-dose PET images. In contrast, the goal of this study is to estimate the high-quality full-dose PET image from the low-dose PET image, which is an innovative and promising research field. To the best of our knowledge, there are only a few works along this research direction. Specifically, Kang et al. (2015) proposed to train a regression forest to estimate the full-dose PET image in a voxel-wise strategy. In (Wang et al., 2016), a mapping based sparse representation method was adopted for full-dose PET prediction, utilizing both low-dose PET and multimodal MRI. To take advantage of a large number of missing-modality training samples, the authors further developed a semi-supervised tripled dictionary learning method for full-dose PET image prediction (Wang et al., 2017). An et al. (2016) proposed a multi-level canonical correlation analysis framework to map the low-dose and full-dose PET into a common space and perform patch-based sparse representation for estimation. Although the above sparse learning based methods showed good estimation performance, a major limitation of these methods is that they are based on small patches, and adopt a voxel-wise estimate strategy which is very time-consuming when testing on new samples. Also, the final estimation of each voxel was obtained by averaging the overlapped patches, resulting in over-smoothed images that lack the texture information within typical full-dose PET images. This smoothing effect may limit the quantification of small structures in estimated PET images.

Convolutional neural networks (CNN) have drawn a tremendous amount of attention in machine learning and medical image analysis areas (Kamnitsas et al., 2017; Kleesiek et al., 2016; Valverde et al., 2017; Dolz et al., 2017; Kawahara et al., 2017). In PET estimation research field, Xiang et al. (2017) proposed a deep auto-context CNN that estimates full-dose PET image based on local patches in low-dose PET. This regression method integrated multiple CNN modules following the auto-context strategy, to iteratively improve the tentatively estimated PET image. However, the authors just extracted the axial slices from the 3D images and treated them as separate 2D images independently for training the deep architecture. This inevitably causes the loss of information in sagittal and coronal directions and discontinuous estimation results across slices.

Recently, generative adversarial networks (GANs) have attracted widespread attention since their introduction (Goodfellow et al., 2014; Denton et al., 2015; Chen et al., 2016; Ledig et al., 2016; Wu et al., 2016). GANs are generative models which comprise two units namely generator and discriminator. The generator learns to map the input low-dimensional vectors to plausible counterfeits, according to some pre-specified distribution. The discriminator learns to distinguish between the generated distribution and the real data distribution. Using GANs, many researches have gained encouraging performance through architectural improvements and modification to the training scheme (Radford et al., 2015; Arjovsky and Bottou, 2017; Arjovsky et al., 2017; Berthelot et al., 2017; Zhao et al., 2016; Bi et al., 2017). Previous works have also explored GANs in the conditional settings, i.e., conditional GANs (Mirza and Osindero, 2014; Reed et al., 2016; Isola et al., 2016). Just like GANs learn a generative model data, the conditional GANs learn a conditional model of data. In the real world, there are numerous 3D image data such as 3D medical image, however, many applications using GANs focus on 2D images. To tackle the problem of 3D medical images, Wolterink et al. (2017) proposed a 3D conditional GANs model for noise reduction in low-dose CT images. In this paper, inspired by the remarkable success of GANs and to overcome the limitations of existing estimation methods, we propose a novel end-to-end framework based on 3D conditional GANs (3D c-GANs) to estimate the high-quality full-dose PET image from the corresponding low-dose PET image. Like the original GANs, the training procedure of our proposed 3D c-GANs is similar to a two-player min-max game in which a generator network (G) and a discriminator network (D) are trained alternatively to respectively minimize and maximize an objective function. The novelties and contributions of the paper are as follows.

1. To ensure the same size of the input and output of the generator network, we utilize both convolutional and up-convolutional layers in our generator architecture instead of using the traditional CNN network which just includes convolutional layers.

2. To render the same underlying information between low-dose and full-dose PET images, we adopt a 3D U-net-like deep architecture as the generator network and use the skip connections strategy to combine hierarchical features for generating the estimated image. The detailed U-net-like architecture will be fully described in Section 2.2.1. The trained U-net-like generator can be directly applied to test images to synthesize the corresponding full-dose PET images, which is very efficient compared with those voxel-wise estimation methods.

3. To take into account the differences between the estimated full-dose PET image and the ground truth (i.e., the real full-dose PET image), the estimation error loss is considered in the objective function to enhance the robustness of the proposed approach. Different from (Wolterink et al., 2017), we employ the L1 norm instead of L2 distance to encourage less blurring.

4. To further improve the estimated image quality, we propose a concatenated 3D c-GANs based progressive refinement scheme.

The rest of this paper is organized as follows. Section 2 introduces our proposed 3D c-GANs architecture and methodology. Experimental setup is conducted in Section 3 and Section 4 gives the experimental results. Finally, we discuss and conclude this paper in Section 5.

Methodology

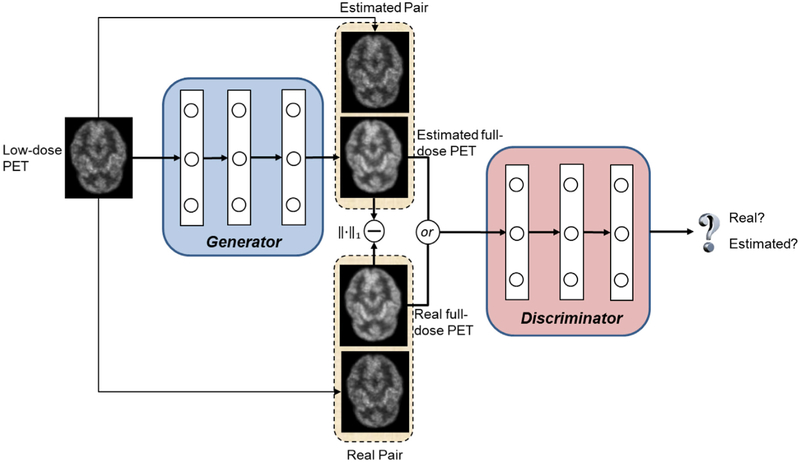
Fig. 1 illustrates the proposed 3D c-GANs training procedure, which constitutes two networks: the generator network G and the discriminator network D. The generator network takes a low-dose PET image and generates an estimated PET image that approximates its corresponding real full-dose PET image. The discriminator network takes a pair of images as input including both the low-dose PET and the corresponding real/estimated full-dose PET images, and it aims to differentiate between the real and estimated pairs. If the discriminator can easily distinguish between them, which means the estimated PET image does not resemble the real full-dose image, the generator should improve its performance and provide more realistic estimations. Otherwise, the discriminator should be enhanced. Hence, the two networks have competing tasks: one tries to synthesize full-dose PET image while the other one tries to differentiate the estimated image from the real full-dose image. To train the generator network G, we also consider the estimation error loss in addition to the discriminator feedback. The objective and details of the architecture are discussed in the following Sections 2.1 and 2.2.

Fig. 1.

Framework of training a 3D c-GANs to estimate the full-dose PET image from low-dose counterpart.

Objective

The original GANs model was first introduced by Goodfellow et al., in 2014 (Goodfellow et al., 2014). It is a framework for training deep generative model using a two-player min-max game. The goal of GANs is to learn a generator distribution P_G that matches the real data distribution P_data. In light of this, GANs learn a generator network G that generates samples by transforming a random input drawn from a probability distribution (such as Gaussian) z ~ P_noise(z) into a sample G(z). This generator is trained by playing against a discriminator network D whose task is to differentiate between samples from the true data distribution P_data and the generated distribution P_G. The objective function of the original GANs can be expressed as:

$$\text{arg}mi{n}_{G}ma{x}_{D}V(G,D)={\mathbb{E}}_{x\sim P_{data}}[\log D(x)]+{\mathbb{E}}_{z\sim P_{noise(z)}}[\log (1-D(G(z)))]$$ (1)

In our proposed 3D c-GANs, instead of using the random noise vector as the input, we condition the model on an input low-dose PET image. Specifically, given a low-dose PET image x ~ P_low(x), and the corresponding real full-dose PET image y ~ P_full(y), the objective of the conditional adversarial network can be defined as:

$$\begin{gathered} \text{arg}mi{n}_{G}ma{x}_D{V}_{c-GANs}(G,D)={\mathbb{E}}_{x\sim P_{low(x)},y\sim P_{full(y)}}[\log D(x,y)]+{\mathbb{E}}_{x\sim P_{low(x)}}[\log (1 \\ -D(x,G(x)))] \end{gathered}$$ (2)

In order to ensure the generated PET image close to the real full-dose PET image and also inspired by the latest empirical data reported in (van den Oord et al., 2016), we consider the estimation error loss in addition to the discriminator feedback for training the generator network. In this manner, the task of the discriminator remains unchanged, while the generator's task is extended to not only fool the discriminator but also to keep similar to the real full-dose image. In this paper, L1 norm estimation error is employed to encourage less blurring, as shown below.

$$V_{L1}(G)={\mathbb{E}}_{x\sim P_{low(x)},y\sim P_{full(y)}}[y-G(x){}_1]$$ (3)

In summary, our final objective function of 3D c-GANs is defined as:

$$\begin{gathered} \text{arg}mi{n}_{G}ma{x}_D(V_{c-GANs}(G,D)+\lambda V_{L1}(G)) \\ ={\mathbb{E}}_{x\sim P_{low(x)},y\sim P_{full(y)}}[\log D(x,y)]+{\mathbb{E}}_{x\sim P_{low(x)}}[\log (1-D(x,G(x)))] \\ +\lambda {\mathbb{E}}_{x\sim P_{low(x)},y\sim P_{full(y)}}[y-G(x{)}_1] \end{gathered}$$ (4)

where λ > 0 is a tunable parameter used to control the balance between two terms, V_c–gans(G, D) and V_L1(G).

3D c-GANs architecture

We present the details of our proposed 3D c-GANs architecture in this section. We first introduce the 3D U-net-like generator which maps the input of low-dose PET images to the output of full-dose ones. Then, the details of the discriminator which tries to distinguish between the real full-dose and the estimated PET images are presented. The training procedure is also discussed in Section 2.2.3.

3D U-net-like generator

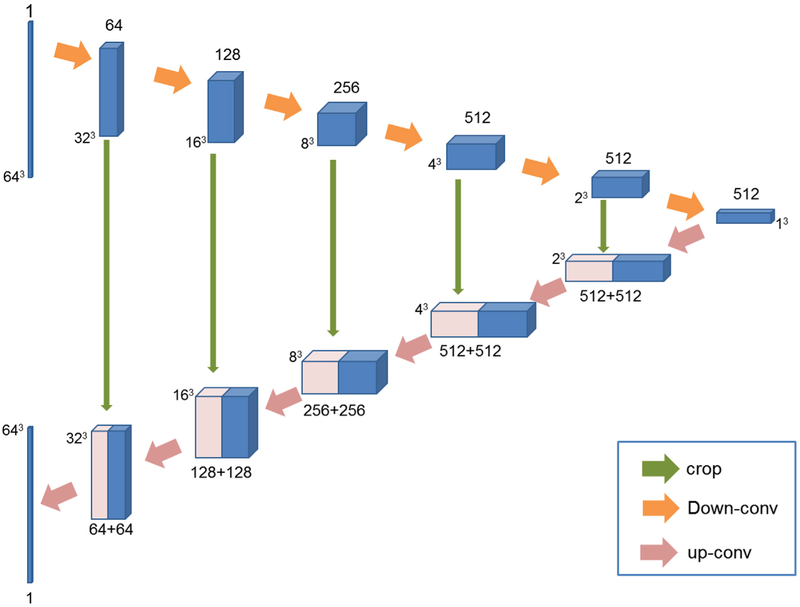
The skip connection used in U-net architecture combines the appearance feature representation from shallow encoding layers with the high-level feature representation from the deep decoding layers (Ronneberger et al., 2015). With the idea of skip connection, the U-net architecture can achieve very good performance and has been applied in many applications such as image translation (Isola et al., 2016). Since the low-dose and full-dose PET images belong to the same modality, there is a great deal of low-level information shared between them, which makes the U-net architecture particularly suitable for the PET estimation task. As a result, we propose a U-net-like architecture as the generator network in this paper. While the original U-net is an entirely 2D architecture, the generator network proposed in this paper takes 3D volumes as input and processes them with corresponding 3D operations, such as 3D down-convolutions and 3D up-convolutions. Fig. 2 illustrates the architecture of the 3D U-net-like generator network, which consists of a contracting encoder part to analyze the input low-dose image and an expansive decoder part to produce an output of estimated full-dose image.

Fig. 2.

Architecture of the 3D U-net-like generator. Blue boxes represent feature maps while the pink boxes represent copied feature maps. The number of channels is denoted above/below (contracting part/expansive part) each feature map. (·)³ around the feature maps denotes the size of the 3D volumes. The arrows denote different operations.

Current U-net architectures are usually trained on whole images or large image patches. In this paper, considering the limited number of training images, we extract large image patches of size 64 × 64 × 64 as the input, from the entire image whose size is 128 × 128 × 128. The entire network consists of 12 convolutional layers including 6 down-convolutional layers and 6 up-convolutional layers. The pooling layer is not used in this paper. The main reason is that pooling is usually used in classification or recognition tasks to reduce the dimension of feature maps and also to make the network invariant to small translation of the input (Xiang et al., 2017). Thus, it is not suitable to use pooling layers for the task of voxel-wise image quality enhancement. In the contracting encoder path, all convolutions are 4 × 4 × 4 spatial filters applied with stride 2 in each direction, and followed by a leaky ReLu with 0.2 negative slope. The number of feature maps increases from 1 to 512. In addition, we apply zero padding with 1 × 1 × 1 in each down-convolutional layer. In this manner, the output patch size of each convolutional layer would be I_output = (I_input – F + 2P)/S + 1, where I_input and I_output are the patch sizes of the input and output of the convolutional layer, F is the filter size, P represents the padding size, and S is the stride size. According to the above equation, the output of each down-convolutional layer would halve the patch size, so the size of feature maps decreases from 64 × 64 × 64 to 1 × 1 × 1. In the expansive decoder path, each layer consists of an up-convolution of 2 × 2 × 2 by stride of 2 in each dimension, followed by a ReLu. The feature maps from the contracting path are copied and cropped to concatenate with the up-convolutional feature maps. Using skip connections to combine hierarchical features can be beneficial for better estimation of PET image. Finally, the output of the network is an image patch of size 64 × 64 × 64, the same size as the input.

Meanwhile, we also introduce batch normalization in each convolutional layer. Batch normalization was first introduced by Ioffe and Szegedy to ease the training of neural networks (Ioffe and Szegedy, 2015). Specifically, each batch is normalized during the training procedure using its mean and standard deviation, and global statistics are then updated using these values. Using the batch normalization, the deep networks tend to learn more efficiently. Therefore, for each layer in Fig. 2, the output from the precedent layer is processed by batch normalization and then fed to the subsequent layer. In addition, for the second up-convolutional layer, we also use the dropout with a rate of 50% before ReLu.

Discriminator architecture

The discriminator takes either a real full-dose PET image or a synthesized one as input, and determines whether the input is real or not. The input to the discriminator is a 3D volume of size 64 × 64 × 64, which is the same size of the generator's output. The architecture consists of four convolutional layers, and each convolution layer uses 4 × 4 × 4 filters with stride 2, similar to the encoder structure of the generator network. The first convolution layer produces 64 feature maps, and then this number is doubled at each following convolution step. After the last layer, a convolution is then applied to map to a one-dimensional output, followed by a sigmoid activation to determine whether the input is a real full-dose PET image or the estimated image. In addition, we use Leaky ReLu activation in the discriminator for all layers, with slope 0.2.

Training 3D c-GANs

The generator network G and discriminator network D are trained in an alternating manner, which is the same as the standard approach of (Goodfellow et al., 2014). Specifically, we first fix G and train D for one step using gradients computed from the loss function, and then fix D and train G. As shown in Equation (4), the training of G and D is just like playing a min-max game: G tries to minimize the loss function while D tries to maximize it. With the training continuing, both the generator and discriminator become more and more powerful. Finally, the generator will be able to generate the estimated full-dose PET image that is extremely close to the real one. In the testing stage, the generator network is performed exactly the same manner as in the training stage. The only difference from the usual protocol is that we apply batch normalization using the statistics of the testing batch instead of aggregated statistics of the training batch. The Gaussian distribution is utilized to initialize the learning parameters in our network model. All networks are trained with mini-batch stochastic gradient descent (SGD) using a mini-batch size of 128. Adam solver with batch size 4 is used for training all networks. The learning rate for the first 100 epochs is fixed to 0.0002, and then linearly decays from 0.0002 to 0 in the second 100 epochs. In addition, we find leaving the weight of the estimation error term λ at the value of 300 resulting the best estimation performance.

Concatenated 3D c-GANs based progressive refinement

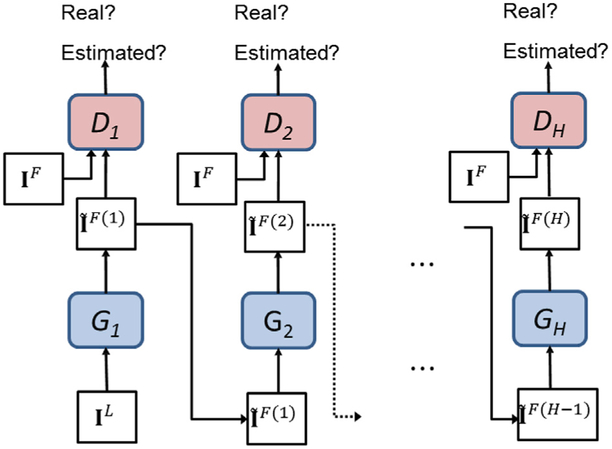
Even if the 3D c-GANs can learn the mapping between the low-dose and full-dose PET images, there may be still some discrepancies due to the large differences of feature distributions. To further mitigate the inconsistency between them, we propose a progressive refinement scheme in a concatenated manner, where a sequence of intermediate generators and discriminators can be constructed to gradually improve the estimation performance. Specifically, the estimation results from the previous 3D c-GANs are fed into a new 3D c-GANs architecture to generate a new set of estimations. The procedure can be summarized in Algorithm 1. For more intuitive understanding, the illustration of the progressive refinement procedure is shown in Fig. 3.

Fig. 3.

Progressive refinement based on the concatenated 3D c-GANs.

Algorithm 1

$$\begin{array}{cc}\hfill & 1\mathbf{Input}:\text{A set of training low-dose PET images}{\mathbf{I}}^L=\{I_1^L,I_2^L,\dots ,I_N^L\},\text{a set of training}\hfill \\ \hfill & \text{full-dose PET images}{\mathbf{I}}^F=\{I_1^F,I_2^F,\dots ,I_N^F\}.\text{N is the total number of training subjects}.\hfill \\ \hfill & \text{Parameters}:\text{concatenated number}H.\hfill \\ \hfill & 2\mathbf{Initialize}:h=1.{\mathbf{I}}^L\text{is used as the initial estimation}{\tilde{\mathbf{I}}}^{F(0)}\text{of the set of full-dose}\hfill \\ \hfill & \text{images}{\mathbf{I}}^F.\hfill \\ \hfill & 3\mathbf{while}\mathit{h}<H\hfill \\ \hfill & 4\text{Perform the 3D c-GANs between}{\tilde{\mathbf{I}}}^{F(h-1)}\text{and}{\mathbf{I}}^F\text{to obtain the generator network}{G}_h\hfill \\ \hfill & \text{and discriminator network}{D}_h\text{according to Eq.}(4).\hfill \\ \hfill & 5\text{For each training subject}i(i=1,2,\dots ,N),\text{use the above trained generator network}{G}_h\hfill \\ \hfill & \text{to generate the estimated full-dose PET image}{\tilde{I}}_i^{F(h)}.\text{Finally, get the estimations for}\hfill \\ \hfill & \text{all training subjects}{\tilde{\mathbf{I}}}^{F(h)}.\hfill \\ \hfill & 6h=h+1.\hfill \\ \hfill & 7\mathrm{End}\mathrm{while}\hfill \\ \hfill & 8\mathbf{Output}:\text{The trained generator networks}\{G_1,G_2,\dots ,G_H\}\text{and discriminator networks}\hfill \\ \hfill & \{D_1,D_2,\dots ,D_H\}.\hfill \end{array}$$

For a testing subject which just has the low-dose PET image, we can use the already trained generator networks {G₁, G₂, …, G_H} to obtain the final estimation. In this manner, the estimated full-dose PET image can be progressively refined.

Experimental setup

Data acquisition

We evaluate our 3D c-GANs based method on a real human brain dataset, including two categories: 8 normal subjects and 8 subjects diagnosed as mild cognitive impairment (MCI). The detailed demographic information of these subjects is summarized in Table 1.

Table 1.

Demographic information of the subjects.

	Normal subjects	MCI subjects
Total	8	8
Gender (Female/Male)	4/4	5/3
Age (Mean ± SD)	26.87 ± 6.29	73.37 ± 9.77
Weight/kg (Mean±SD)	86.92 ± 27.70	74.96 ± 15.18

The PET scans were acquired on the Siemens Biograph mMR PET-MR scanner. The full-dose PET scans in our cohort was administered an average of 203MBq (from 191 MBq to 229 MBq) of ¹⁸F-2-deoxyglucose (¹⁸FDG). This corresponds to an effective dose of 3.86 mSv which is in the low part of the range suggested by the Society of Nuclear Medicine and Molecular Imaging for FDG PET scans. The average time post-injection was 36 min (from 32 to 41 min). Full-dose and low-dose PET images were acquired consecutively: first 12-min full-dose PET immediately followed by 3-min low-dose PET scans. This order was necessarily fixed because we need to acquire clinical PET scans first and then the experimental scans. The order, however, creates some implications. One thing is that the standard uptake value (SUV) increases slightly for the low-dose PET scans since the uptake in the brain continues to increase measurably during the acquisition time. On the other hand, due to the radioactive decay occurs in acquisition, the effective noise level for the low-dose PET scans is slightly higher. Strictly speaking, these two effects may be not cancel out exactly, but they tend to work against each other to create low-dose PET data that are the equivalent of approximately one-quarter of the full dose. During the PET scanning, no head holders were used and the subjects were simply asked to keep still. Although the existing motion correction methods can mitigate the motion effect to some extent (Woods et al., 1992), the interpolation or resampling of voxels may distort the data, thus interfering or even invalidating the training models. Therefore, we checked the resulting images visually for apparent motion by examining the alignment between the early full-dose PET and late low-dose PET images with the attenuation map, and the subjects with unqualified PET images would be required to be rescanned to obtain new PET images. The reconstruction was performed using manufacturer-provided software with all physical corrections, including attenuation, scatter and randoms. Specifically, the reconstruction was carried out iteratively with the ordered subsets expectation maximization (OSEM) method (Hudson and Larkin, 1994), with 3 iterations, 21 subsets, and post-reconstruction filtered with a 3D Gaussian with FWHM of 2 mm. The full-dose and low-dose PET for the same subject used the same attenuation map, which was obtained prior to the full-dose PET scan. And the attenuation maps were computed by the Dixon fat-water method provided by the scanner manufacturer. Reconstructing the full-dose and low-dose images with the same reconstruction parameters and post-reconstruction filters ensures that both images have comparable spatial resolution. Each PET image has a voxel size of 2.09 × 2.09 × 2.03 mm³, and image size of 128 × 128 × 128. Non-brain tissues were removed from the entire image using skull stripping algorithm (Shi et al., 2012). In experiments, to make full use of available samples and reduce the possible bias to measure the performance, we follow the widely used “Leave-One-Subject-Out cross-validation” strategy, i.e., each time one subject is used in turn for testing and the other 15 subjects are for training. In addition, the normal and MCI data are trained together to maximally utilize the available samples. Since a great deal of parameters need to be trained in the c-GANs model, it requires that the training data should be adequate. If we directly use the entire 3D PET images to train the c-GANs model, the overfitting problem would inevitably appear. Therefore, considering the limited number of training images, we extracted large 3D image patches instead of using the entire 3D images to train the deep model. Specially, large image patches of size 64 × 64 × 64 are extracted from each PET image of size 128 × 128 × 128, with the stride of 16. In this case, 125 image patches are generated for each training image. Generally, the pair of the low-dose and full-dose PET image patches is regarded as one training sample. Therefore, there are a total of 125 × 15 = 1875 training samples in every leave-one-out case, which is sufficient to train the deep model. For the testing image, we also extract 125 testing image patches in the same manner. Then, each testing image patch is fed into the already trained generator and the corresponding estimated full-dose PET patch is obtained. Finally, all the estimated patches are merged together by averaging the overlapped estimation values to generate the whole estimated PET image of size 128 × 128 × 128. The method is implemented by PyTorch, and all the experiments are carried out on a NVIDIA GeForce GTX 1080 Ti with 11 GB memory. The code will be released through Github soon.

Evaluations measures

To evaluate the estimation performance, we use three measures in the experiments. Specifically, peak signal-to-noise (PSNR) and normalized mean squared error (NMSE) are employed to evaluate the estimated image quality. PSNR is defined as

$$\text{PSNR}=10{\log }_{10}\left(\frac{U{R}^2}{\Vert I^F-{\tilde{I}}^{{}^F_{}}{\Vert }_2^2}\right),$$ (5)

where R is the maximum intensity range of the real full-dose image I^F and the estimated full-dose image ${\tilde{I}}^{{}^F_{}}$, and U represents the total number of voxels in the image. This metric is used to evaluate the estimation accuracy in terms of the logarithmic decibel scale.

The NMSE is defined as

$$\text{NMSE}=\frac{\Vert I^F-{\tilde{I}}^{{}^F_{}}{\Vert }_2^2}{\Vert I^F{\Vert }_2^2}$$ (6)

This metric is used to measure the voxel-wise intensity differences between the real and estimated images. Theoretically, image with higher PSNR and lower NMSE represents higher quality.

In addition to image quality measure, whether the region of interests (ROIs) in an estimated full-dose PET image can be well preserved in terms of clinical quantification is also important. In light of this, we leverage another clinical measure (i.e., SUV) for specific lesion regions as the ROIs. Specifically, SUV is commonly used in clinical FDG-PET/CT oncology imaging, and has a specific role in therapy planning. As indicated by Paul E. Kinahan (Kinahan and Fletcher, 2010), the use of SUV as a measure of relative tissue uptake facilitates comparisons between patients, and has been suggested as the basis of diagnosis. We use the definition of SUV in (Kinahan and Fletcher, 2010), as

$$\text{SUV}=\frac{r}{\left(\frac{a}{w}\right)}$$ (7)

where r is the radioactivity concentration measured by the PET scanner (in kBq/ml), a is the decay-corrected amount of injected FDG dose (in kBq), and w is the weight of the subject (in g). Smaller differences in SUV are highly desirable, indicating that the estimation does not substantially change the quantitative makers of the PET images (Bagci and Mollura, 2013). Therefore, we calculate the SUV differences for specific ROIs in both low-dose and the estimated full-dose PET images, in order to investigate how the SUV in our estimated full-dose PET images deviates from the SUV in the real full-dose PET images.

Experimental results

To study the effectiveness of the proposed 3D c-GANs method, our experiment explores the following questions:

• Compared with 2D model, does the 3D c-GANs model gain better performance?

• Compared with the model just use the generator network (i.e., 3D U-net-like network), does the adversarial training in the 3D c-GANs model increase the estimation performance?

• Does the model adopting the concatenated 3D c-GANs based progressive refinement scheme improve the estimation quality?

• For the lesion regions of human brain, is the proposed method effective for specific ROIs using clinical measure?

• Can the 3D c-GANs method achieve comparable results with the existing PET estimation methods?

• Is our proposed c-GANs model superior to the state-of-the-art c-GANs models?

• Does this method have the potential of domain adaption? That is, whether the c-GANs model trained by one dataset could be used on another dataset.

To answer the first two questions, we first run our method without the progressive refinement scheme, as presented in Section 4.1 and 4.2. Then, the effectiveness of concatenated 3D c-GANs is evaluated in Section 4.3. In Section 4.4, we evaluate the clinical measure on specific ROIs (hippocampus) for both the normal subjects and the MCI patients. The proposed method is respectively compared to the existing PET estimation methods and the state-of-the-art c-GANs models (Wolterink et al., 2017) in Section 4.5 and 4.6. Finally, the potential of domain adaption of our method is investigated in Section 4.7.

Comparison with 2D based c-GANs architectures

In this section, to study the effectiveness of the 3D model, we compare it with a variant of our model using 2D c-GANs architectures. Three 2D c-GANs corresponding to the sagittal, coronal, and axial views are separately trained with the same settings used in the 3D c-GANs architecture. It is worth noting that the 2D models use the whole 2D slides as input while 3D model uses large image patches as input. For qualitative comparison, samples of the estimated full-dose PET images by 2D c-GANs and 3D c-GANs are shown in Fig. 4. The corresponding low-dose PET images (the left-most column) and the real full-dose PET images (the right-most column) are also provided. As observed, there are obvious distinctions between the low-dose and real full-dose PET images. The estimated images by all c-GANs show better image quality than low-dose images, indicating that the proposed c-GANs can reduce the noise in low-dose PET images and enhance the image quality towards the real full-dose PET images. Compared to 2D c-GANs, the proposed 3D c-GANs produce better visual quality that is close to the real full-dose image in all three views (blue block in Fig. 4). In contrast, the results obtained by 2D c-GANs only show good performance in the corresponding trained view (red circles in Fig. 4), but deteriorate in the other two views. For example, 2D axial c-GANs generate faithful axial view, but very blurry sagittal and coronal views (as indicated by red arrows in Fig. 4). This is because the 2D axial c-GANs consider the image appearance slice by slice along the axial direction, thus potentially causing discontinuous estimation across slices and thus losing 3D structural information. The similar phenomenon can be observed in the estimation results provided by 2D sagittal c-GANs and 2D coronal c-GANs, respectively.

Fig. 4.

Qualitative comparison between estimated results by 2D c-GANs and 3D c-GANs. In the axial and coronal images, the left side of the image is the right side of the brain, and the right side of the image is the left side of the brain.

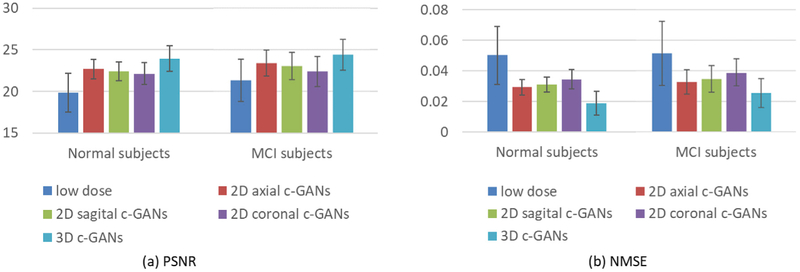
For quantitative comparison, the averaged estimation results achieved by 2D c-GANs and 3D c-GANs across both the normal and the MCI subjects are presented in Fig. 5, in terms of PSNR and NMSE. Fig. 5(a) shows that the PSNR values of all c-GANs’ estimations are improved compared with that of the low-dose images. Moreover, the proposed 3D c-GANs outperform all 2D c-GANs for both the normal subjects and the MCI subjects, indicating the 3D information learned in 3D c-GANs can boost the estimation. The NMSE results are reported in Fig. 5(b), where we can see the same conclusion. Both qualitative and quantitative results demonstrate the benefits of employing the proposed 3D c-GANs over the commonly used 2D c-GANs.

Fig. 5.

Quantitative comparison between 2D c-GANs and 3D c-GANs, in terms of PSNR and NMSE. Error bar indicates the standard deviation.

Comparison with 3D U-net-like model

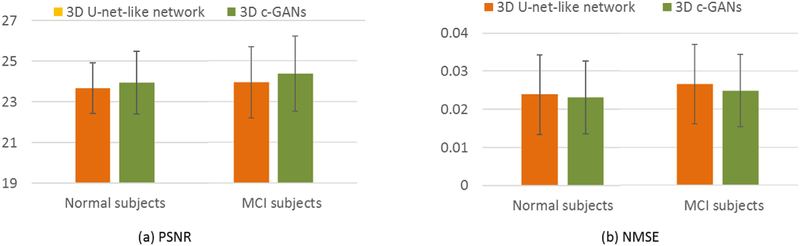
To evaluate the effectiveness of the adversarial training in 3D c-GANs model, we compare our method with the model that removes the discriminator network from our 3D c-GANs model, i.e., 3D U-net-like network. The averaged quantitative comparison for the normal subjects and the MCI subjects are given in Fig. 6.

Fig. 6.

Quantitative comparison between 3D U-net-like network and 3D c-GANs, in terms of PSNR and NMSE. Error bar indicates the standard deviation.

We can see that adversarial training brings higher PSNR and lower NMSE for both the normal and the MCI subjects. Specifically, compared with 3D U-net-like network, the averaged PSNR of our method increases approximately 0.28 for the normal subjects and 0.43 for MCI subjects. The averaged NMSE for the normal subjects decreases from 0.02417 to 0.0231, and this measurement drops by 0.0017 for MCI group. The experimental results imply that the adversarial training in the 3D c-GANs is essential for improving the estimation quality.

Effectiveness of concatenated 3D c-GANs

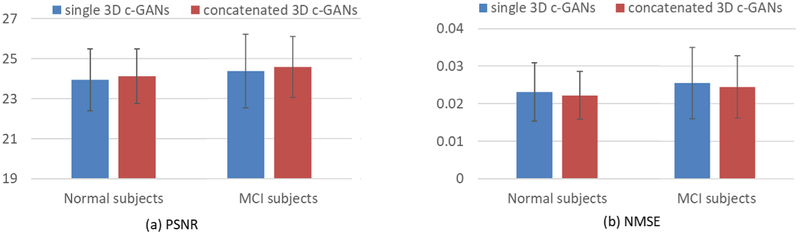
In this section, we study the performance of the concatenated 3D c-GANs based progressive refinement procedure as discussed in Section 2.3. Here, we use a concatenated architecture with two 3D c-GANs, as we observe that the use of more c-GANs does not bring significant improvement but instead increasing the computational time. As before, the averaged PSNR and NMSE for the two groups are given in Fig. 7.

Fig. 7.

Quantitative comparison between single 3D c-GANs and concatenated 3D c-GANs, in terms of PSNR and NMSE. Error bar indicates the standard deviation.

From Fig. 7(a), it can be seen that the concatenated 3D c-GANs achieve higher PSNR than single 3D c-GANs for both the normal subjects and the MCI patients. The reason triggering this improvement is that the concatenated 3D c-GANs utilize the concatenation of two GANs instead of a single GANs architecture. The reason for this improvement is that the concatenation of two GANs rather than a single GANs architecture allows iterative reduction of residuals when estimating full-dose images based on low-dose images, and the concatenation architecture could progressively mitigate the inconsistency of the feature distributions between the full-dose and low-dose PET images. This is consistent with the NMSE values shown in Fig. 7(b), indicating the concatenated 3D c-GANs based progressive refinement scheme can further improve image quality of the estimated full-dose PET image.

Clinical evaluation for specific ROIs

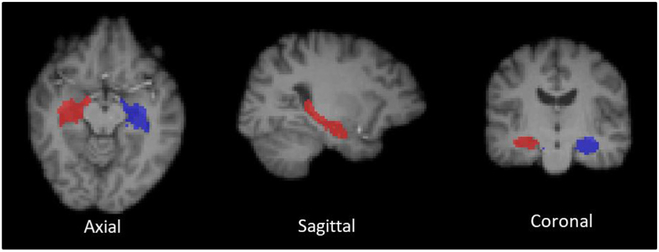
Images with abnormal uptake can be often obtained in the real-world applications and a number of factors can affect the tracer uptakes. For example, patients with brain atrophy may not normally uptake the tracer in particular ROIs. Therefore, the robustness of a PET image estimation method, tackling abnormal uptake, is a significant consideration in clinical practice. Here, we use the SUV measure to investigate the effectiveness of the proposed method for specific ROIs on both the normal subjects and the MCI subjects. Since the hippocampal regions are highly related to the MCI, it is particularly crucial that the estimated PET images can well maintain the SUV in hippocampal regions. Thus, the SUV differences are computed on both left and right hippocampi. Smaller differences in SUV are preferred, indicating that the estimation does not substantially change the quantitative makers of the PET images. We delineated the hippocampal regions based on the MRI-T1 images. Specifically, during the PET scans, a T1-weighted MRI sequence was also acquired by the Siemens Biograph PET-MR system. For each subject, the PET images are respectively co-registered to the T1 image via affine transformation (Smith et al., 2004). Then, we labeled the T1 images with hippocampal ROIs based on a multi-atlas segmentation method (Rohlfing et al., 2004). Fig. 8 shows an example of the delineated hippocampal regions in three views. The average SUV differences and standard deviation are shown in Table 2.

Fig. 8.

An example of the delineated hippocampal regions (Blue: left hippocampus; Red: right hippocampus). In the axial and coronal images, the left side of the image is the right side of the brain, and the right side of the image is the left side of the brain.

Table 2.

Average SUV differences and standard deviations in left/right hippocampal regions of the normal subjects and the MCI subjects, respectively.

	Normal subjects		MCI subjects
	Left hippocampi	Right hippocampi	Left hippocampi	Right hippocampi
Low-dose PET	0.652 ± 0.157	0.501 ± 0.135	0.218 ± 0.098	0.305 ± 0.102
Concatenated 3D c-GANs	0.037 ± 0.015	0.067 ± 0.018	0.015 ± 0.009	0.019 ± 0.010

As observed, compared to the low-dose PET image, the SUV differences between the 3D c-GANs estimated image and the real full-dose one are much smaller, suggesting the faithful preservation of tracer uptake of the proposed method. Similar conclusion can be drawn from the MCI group. In addition, the SUV differences of the MCI subjects are smaller than those of normal subjects. The main reason probably lies in that the hippocampal lesions in MCI patients lowers the metabolic activity, thus decreasing the uptake of the radioactive tracer in hippocampal regions. The above results illustrate that the estimated PET image does not significantly change the quantitative markers of the corresponding real full-dose PET image.

Comparison with the existing PET estimation methods

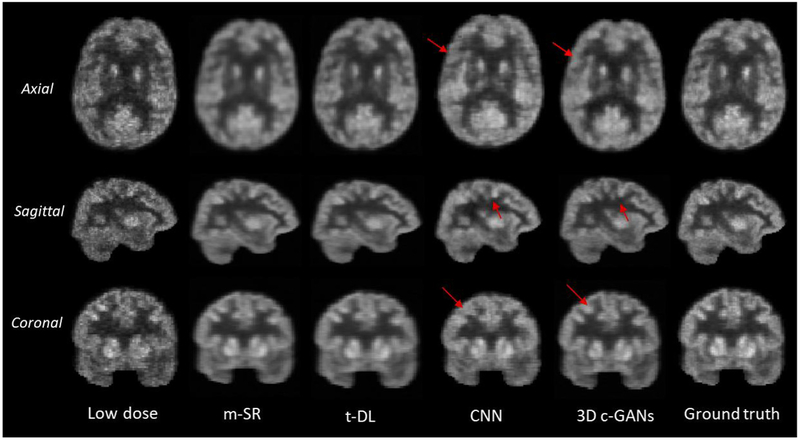
In this section, we compare our method with the existing PET estimation methods, including: 1) mapping based sparse representation method (m-SR) (Wang et al., 2016), 2) semi-supervised tripled dictionary learning method (t-DL) (Wang et al., 2017), and 3) convolutional neural networks based method (CNN) (Xiang et al., 2017). The qualitative comparison results are shown in Fig. 9.

Fig. 9.

Qualitative comparison of low-dose PET images, estimated by the mapping based sparse presentation method (m-SR), by semi-supervised tripled dictionary learning method (t-DL), by convolutional neural networks (CNN), and by the proposed concatenated 3D c-GANs method (3D c-GANs), as well as the real full-dose PET images (Ground truth). In the axial and coronal images, the left side of the image is the right side of the brain, and the right side of the image is the left side of the brain.

It can be seen from Fig. 9 that by all methods, the image qualities of all three views (axial, sagittal and coronal) have been enhanced compared with the low dose images. The estimated images by the sparse representation based methods (including m-SR and t-DL) are over-smoothed compared with the real full-dose PET images. This is because these methods estimate the full-dose PET image in a voxel-wise manner and the final estimation for each voxel is determined by averaging the results of the overlapping patches. Although the estimations by CNN based method are sharper than those of the sparse representation based methods, apparently our proposed method still performs better in all three views (as indicated by red arrows in Fig. 9). The quantitative comparison in terms of PSNR, NMSE and SUV differences is also provided in Fig. 10.

Fig. 10.

Quantitative comparison between the existing PET estimation methods and the proposed method, in terms of PSNR, NMSE and SUV differences. Error bar indicates the standard deviation.

As shown in Fig. 10 (a), m-SR, CNN and t-DL obtain similar PSNR values in the two groups of subjects, indicating their estimation results are comparable. In contrast, our proposed method achieves the highest PSNR values in both the normal and the MCI groups, which significantly outperforms the compared three methods. This can also be observed from NMSE results in Fig. 10 (b), where our proposed method achieves the lowest error. For the normal subjects, compared with t-DL which gains the second-best performance, the averaged PSNR by our method increases by approximately 0.9. For the MCI subjects, compared with the second-best performance of the CNN based method, the averaged PSNR by our method increases by about 1.1. In addition, we can see from Fig. 10 (c) that, compared with the existing methods, the SUV differences by the proposed method is the smallest. This indicates that the estimated full-dose PET images by our method can better preserve the SUV. Therefore, our method potentially improves the clinical usability as compared to the low-dose PET images or the results by the previous methods.

Compared with the existing PET estimation methods, another major advantage of our proposed method is the processing speed. Since the sparse representation based methods cannot build a predictive model, if a previously unknown subject is added into the test set, the entire algorithms would need to be retrained with all the samples. Thus, the computation is quite burdensome. In contrast, our method only needs to do the estimation with the pre-trained model, which is much more efficient. It is worth noting that, the discriminator network is only used during training, without introducing extra computational burden during the test. Specifically, our method has a runtime of less than 1 s on a 64 × 64 × 64 vol, on a NVIDIA GeForce GTX 1080 Ti with 11 GB memory.

Comparison with the state-of-the-art c-GANs models

In (Wolterink et al., 2017), Wolterink et al. proposed a method for noise reduction in low-dose CT images, which also employs 3D c-GANs model. Nevertheless, there are several major distinctions between their approach and ours. First, the network structures are significantly different. Wolterink's generator utilizes seven convolutional layers without any padding, thus causing the output size smaller than the input size. To ensure the de-noised CT image has the same size with the routine-dose CT image, they have to first apply zero padding to the input image. In contrast, our U-net-like generator architecture includes both convolutional and de-convolutional layers, which can ensure the same size of the input and the output without any additional pre-processing. Also, we use skip connections in the generator architecture to combine hierarchical features for better estimation. The skip connection strategy could relieve the vanishing gradient problem, allowing the network architecture could be much deeper. Second, Wolterink et al. used the L2 distance to measure the voxel-wise estimation error. However, as known, L2 norm error is more sensitive to outliers compared with L1. Thus, we adopted the L1 norm to encourage less blurring. Third, we also proposed a concatenated 3D c-GANs based progressive refinement scheme to further improve the estimated image quality. In Section 4.3, we have demonstrated the effectiveness of the concatenated c-GANs model. In this experiment, in order to evaluate the effect of the different network structures and loss functions between Wolterink's approach and our proposed method, we compare the proposed model with other two methods (CNN-like generator model and L2 distance based model). In CNN-like generator approach, the skip connections are removed from the generator network of our model. Since directly removing the skip connections from the very deep architecture can easily cause model collapse, we use six convolutional layers in the generator network. The L2 distance based model means that we use L2 distance instead of L1 to measure the estimation error. Fig. 11(a) shows the quantitative comparison in terms of PSNR while Fig. 11(b) gives a visual example in sagittal view.

Fig. 11.

Comparison with the state-of-the-art c-GANs models. (a) Comparison in terms of PSNR, and (b) visual comparison in sagittal view. Error bar indicates the standard deviation.

From Fig. 11(a), the advantage of using U-net-like generator over CNN-like generator can be well demonstrated by comparing the results of CNN-like generator model (blue bar) and our model (green bar). Although the performance of L2 distance based c-GANs model almost catches up with our model using L1 norm, we can clearly see from Fig. 11(b) that the L2 distance based model tends to generate blurry estimations, as indicated by the red block. Both qualitative and quantitative results suggest that, compared with Wolterink's approach, our method gains better estimation performance.

Investigation of the potential of domain adaption of our method

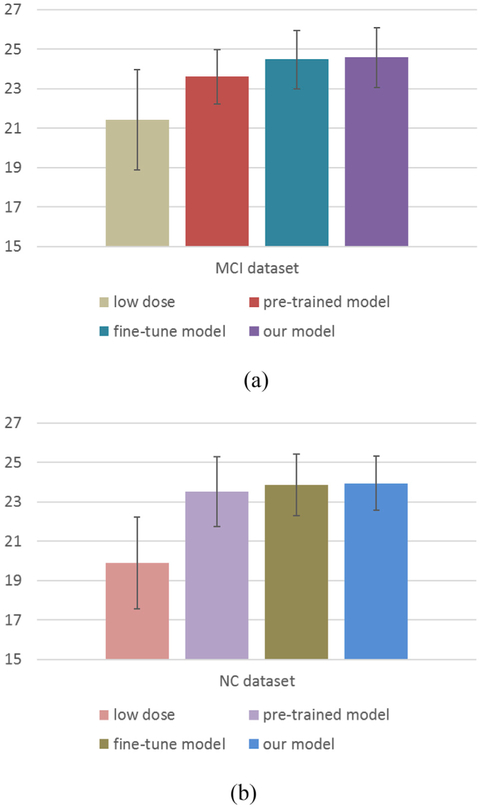
In deep learning, the potential of domain adaption is quite important, that is, whether the deep model trained using one dataset could be applied on another dataset. In order to investigate the potential of domain adaption of our method, we split our data into two non-overlapping datasets according to the clinical labels, i.e., the normal control (NC) dataset and the MCI dataset, and each dataset consists of 8 subjects. As is known, these two groups have different data distributions. We first use the NC dataset to train a c-GANs model, and then test the pre-trained model on the MCI dataset. However, due to the discrepancy of the data distributions between the two distinct datasets, directly applying the pre-trained model on the other dataset may lead to unsatisfactory performance. To tackle this problem, we further fine-tune (a type of transfer learning) the pre-trained model based on the test dataset, thus transferring the useful knowledge of the training dataset to help image estimation, and this model is named as fine-tune model. Please note that transfer learning is a common strategy used in deep learning to adapt a pre-trained model to another dataset, and takes only a small number of epochs, which is very fast in contrast to the full training procedure. Specifically, we fine-tune the pre-trained model using the MCI dataset via the leave-one-subject-out strategy. That is, one subject of the MCI dataset is reserved for test and the rest 7 subjects are used for fine-tuning the pretrained model. The averaged performance in terms of PSNR is reported in Fig. 12(a). For comparison, we also list the result of the proposed model which trained by all samples, i.e., reserve one subject for test and train the model using the rest 15 subjects. Similarly, we further use the MCI dataset to train a c-GANs model and test this model based on the NC dataset. The results are shown in Fig. 12(b).

Fig. 12.

Investigation on the potential of domain adaption of our method. (a) Using the NC dataset for training and then the MCI dataset for testing, and (b) using the MCI dataset for training and then the NC dataset for testing. Error bar indicates the standard deviation.

From Fig. 12, we can see that the PSNR results of the pre-trained model are much higher than those of the low-dose PET images, indicating that the pre-trained model using one dataset could be applied on another dataset for image synthesis. The results of the fine-tune model almost catch up with those of the proposed model, which suggests that the fine-tune strategy could decrease the discrepancy of the data distributions between the two different datasets. In addition, the pre-trained model and the fine-tune model tend to learn more efficiently with less training samples. Experimental results show that the pre-trained model and the fine-tune model can well estimate the full-dose PET images, indicating that our method has the potential of domain adaption. However, since both the NC dataset and the MCI dataset used in this paper belong to the clinical data, it might be interesting to evaluate our method using digital simulations, i.e., phantoms. Such simulations would be helpful to understand the physical performance of the proposed method, which is one of our research focuses in future.

Conclusion

In this paper, we have proposed a novel end-to-end framework based on 3D c-GANs to estimate the high-quality full-dose PET images from the low-dose PET images. Difference from the original GANs that consider the image appearance slice by slice, our proposed method is carried on in a 3D manner, avoiding the discontinuous cross-slice estimation that occurs in 2D GANs models. To render the same underlying information between the low-dose and full-dose PET images, we employ a 3D U-net-like architecture as the generator to combine hierarchical features for generating the estimated images. In addition, a concatenated GANs based progressive refinement scheme is utilized to further improve the quality of estimated images.

To train reliable 3D c-GANs model with small sample size, we use the following strategies. First, for each subject we extract 125 large 3D patches rather than directly using the entire 3D image as input. In this way, we significantly increased the number of training samples (from 16 images to 2000 patches in total), and at the same time greatly reduced the number of parameters to learn. Second, during training, to make full use of available samples and reduce the possible bias to measure the performance, we follow the widely used “Leave-One-Subject-Out” strategy, i.e, we repeat the training and test for 16 times, at each time sequentially reserve one subject (125 patches) for test and train our model on the patches from the rest 15 subjects (1875 patches), and report the average performance. Third, please note that, we can keep increasing the number of training samples by extracting more overlapping patches or smaller patches from the original 3D images as in the literature. However, we found that more overlapping or smaller patches do not further improve the performance. In contrast, they could possibly bring the problems of either over-smoothing or inter-patch discontinuity, leading to inferior performance to our current settings. Our experimental results demonstrate that the above strategies could effectively mitigate the impact of the small sample size. Certainly, involving more subjects into the study could further increase the generalization capacity of our model, and is one of our research focuses in future.

Extensive experiment has been conducted on a real dataset of human brain PET images consisting of both the normal subjects and the MCI subjects. Both the qualitative and quantitative results suggest that our proposed method outperforms the benchmark methods and the existing state-of-the-art estimation methods, for both normal subjects and subjects with abnormal uptake (MCI subjects). The estimated full-dose PET images by our method are close to the real ones. Moreover, the experimental results demonstrate that, the desired quantification measure SUV for specific ROIs can be faithfully preserved by the proposed method, compared with the real full-dose PET images. In summary, the proposed method can greatly improve the quality of PET images with low dose tracer injection. This potentially meets the requirement to reduce the radioactive tracer during PET scans.

Please note that, the PET scanner is usually combined with other imaging modalities, such as PET/CT and PET/MRI. It has been suggested that the anatomical or the structural information from CT or MRI could be utilized for improving the PET image quality. In our future work, we will extend our method to incorporate the multi-modality information for better estimation. Also, the current study is restricted to brain PET image data. It would be highly interesting to evaluate our proposed method for extended body areas and diseases, especially in pediatric patients, since they are more susceptible to the radioactive tracer. In addition, since the simulations of phantom would be helpful to understand the physical performance of the algorithm, in the future, we plan to simulate digital phantom data according to the standard PET quality assessment protocol, and involve domain adaption and transfer learning techniques to investigate the relationship between different datasets.