Single-molecule excitation–emission spectroscopy

Significance

The most popular methods of single-molecule detection are based on fixed-wavelength excitation of individual molecules combined with dispersed detection of emission. While these methods are well established, they mainly provide information on the excited-state environment of the fluorophore. Here, we introduce an approach capable of simultaneously acquiring the full information, involving both ground- and excited states, by recording a 2D excitation versus emission map for single molecules by use of a birefringent interferometer. We interpret the results in terms of optical lineshape theory. The presented approach is easily implementable and applicable to a wide range of scientific problems, ranging from spectroscopy of supramolecular biological complexes to materials science.

Abstract

Single-molecule spectroscopy (SMS) provides a detailed view of individual emitter properties and local environments without having to resort to ensemble averaging. While the last several decades have seen substantial refinement of SMS techniques, recording excitation spectra of single emitters still poses a significant challenge. Here we address this problem by demonstrating simultaneous collection of fluorescence emission and excitation spectra using a compact common-path interferometer and broadband excitation, which is implemented as an extension of a standard SMS microscope. We demonstrate the technique by simultaneously collecting room-temperature excitation and emission spectra of individual terrylene diimide molecules and donor–acceptor dyads embedded in polystyrene. We analyze the resulting spectral parameters in terms of optical lineshape theory to obtain detailed information on the interactions of the emitters with their nanoscopic environment. This analysis finally reveals that environmental fluctuations between the donor and acceptor in the dyads are not correlated.

Since its demonstration in the late 1980s (1, 2) single-molecule spectroscopy (SMS) has been widely implemented to provide detailed information about individual molecules in heterogeneous environments. This ability to address the individual members of an ensemble allows reconstruction of macroscopic observables through measurement statistics. More importantly, however, SMS preserves information about the interaction of individual molecules with their surroundings that would otherwise vanish in the ensemble average. This wealth of information is made accessible through spectral parameters such as transition frequencies and linewidths, excited-state decay times, polarization, and single-photon statistics, which report directly the properties and interactions of the individual molecule (3, 4). Hence, SMS can be used to develop a physical model for the behavior of a molecular ensemble without making assumptions on the properties of the individual molecules.

The first luminescence-based SMS experiments were realized by tunable narrow-band laser sources, and reported fluorescence excitation spectra of dyes embedded in Shpolskii matrices at subliquid helium temperatures (2, 5, 6). Meanwhile, most modern SMS implementations rely on fixed-wavelength excitation and rather report emission spectra, fluorescence lifetimes, or intensity fluctuations (7). Not only does this allow photoinduced excited-state processes to be followed, it also greatly simplifies and accelerates the experiment. A consequence of measuring emission rather than excitation spectra, however, is that most SMS experiments provide little information on the environment of ground-state molecules. Emission spectra primarily report the relaxed environment of the photoexcited molecules, and thus information on the ground-state equilibrium properties of the system is lost. Attempts at reintroducing molecular ground-state information by recording fluorescence excitation spectra have been made both by the tunable narrow-band excitation approach and by interferometry. While the narrow-band approach has been demonstrated in several experiments (8–10), a Fourier-transform (FT)–based approach has received recent attention (11–13). The principles of FT spectroscopy are well known from ensemble measurements (14, 15): Fundamentally, an FT instrument requires a broadband excitation source coupled to an interferometer capable of generating two collinear replicas of the excitation beam with a time delay t₁. Recording the emission intensity as a function of t₁ results in an interferogram, which after an FT yields the frequency-resolved excitation spectrum.

Here we use a common-path interferometer (16, 17) for the combined detection of time-resolved or dispersed emission with FT-based excitation spectroscopy of single emitters. The resulting implementation is robust with high inherent phase stability; no active phase stabilization is necessary when recording spectral interferograms of individual molecules at room temperature. The FT data yield simultaneously detected SM excitation and emission spectra in the form of a 2D excitation–emission matrix (EEM), which contains all information available in a steady-state emission experiment. We use this wealth of spectroscopic data to characterize the interactions of a simple terrylene diimide (TDI) derivative with its local nanoscopic environment in the framework of the Brownian oscillator model (18). Building on this analysis, we then investigate an intramolecular excitation-energy transfer (EET) dyad to address a question of current relevance in natural and artificial light-harvesting: Can we identify correlated bath fluctuations, analogous to those suggested as a mechanism to “protect” excitonic coherence from dephasing in photosynthetic proteins (19), in a donor–acceptor dyad?

Results and Discussion

SM Interferometry.

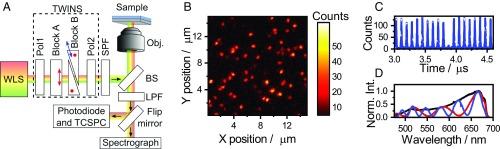
The experimental implementation, based on broadband spectral interferometry in a standard confocal microscope (20), is schematically illustrated in Fig. 1A. The instrumental details are summarized in Materials and Methods. Briefly, the output of a supercontinuum laser passes through a common-path birefringent interferometer (Translating-Wedge-based Identical pulses eNcoding System – TWINS, model GEMINI from NIREOS) and a short-pass filter (SPF), before being reflected off a beam splitter (BS) and focused on the sample with a high-N.A. oil immersion objective. The emission is collected in backscattering geometry and passes through a long-pass filter (LPF) before being directed to a pair of avalanche photodiodes (APDs) for imaging, photon antibunching, and time-correlated single-photon counting (TCSPC), or to a spectrograph-equipped CCD camera for spectroscopy. We image the sample by collecting the integrated fluorescence while raster scanning to yield a diffraction-limited map of the fluorescence intensity. A typical image acquired over a 15 × 15-μm area is shown in Fig. 1B where, as confirmed by photon-antibunching experiments (21, 22), each spot corresponds to a single TDI molecule. A typical antibunching trace is shown in Fig. 1C, where the lack of simultaneous detection events at around 3.9 μs––equal to the detection delay between the APDs––is a proof of a single-photon emitter.

Fig. 1.

(A) Schematic of the interferometry-based confocal microscope. The birefringent interferometer (TWINS) creates two time-delayed, copropagating beam replicas from the output of the white-light source (WLS). See text for details. (B) Image of a 15 × 15-μm region of the TDI sample; each “spot” corresponds to an SM. (C) Photon antibunching data from a single bright spot. The lack of signal at 3.9 μs, corresponding to the detection delay between the APD detectors, demonstrates that it originates from a single emitter. (D) Laser spectra at several interferometer wedge positions. A sinusoidal interference pattern appears in the spectrum with fringe density increasing proportionally to the time delay between the beam replicas.

The detailed operational principles of the interferometer have been described previously (16, 23). In brief, a movable birefringent wedge pair (shown as block B in Fig. 1A) is introduced in the beam path, generating two orthogonally polarized phase-locked beam replicas with tunable time delay, which are finally projected to a common polarization by a polarizer. The procedure for converting from wedge insertion to absolute time delay t₁ is outlined in ref. 21 and reported in SI Appendix. As t₁ increases, spectral interference fringes modulate the laser spectrum. We illustrate this by recording back-reflected light from a cover glass, as shown in Fig. 1D, where characteristic fringes appear as a function of wedge insertion (i.e., time delay).

The resulting simple but versatile platform allows both diffraction-limited imaging and spectroscopy of SMs. EEM data are collected by recording emission spectra as a function of wedge insertion, while conventional emission spectra (after broadband excitation) can be acquired by setting t₁ to zero. In an alternative mode of operation, we detect the TCSPC signal as a function of wedge insertion, which allows for mapping of the fluorescence decay as a function of excitation frequency (see ref. 24 and Materials and Methods for details).

EEM of Single TDI Molecules.

As a first application of our interferometric SMS approach, we investigate in detail the interactions of a simple TDI derivative (structure in SI Appendix) with its local environment––a polystyrene thin film. TDI––and related rylene dyes––are popular in SMS due to their strong absorbance, high quantum yield, and photostability (25–31). Further, for the TDI used here, we can expect the majority of the spectral differences to be due to variations in the molecule–environment interactions. We note that this is not always the case, as has been shown for bay-substituted rylene analogs (32, 33). In the vast majority of SMS studies, only emission spectra are recorded, meaning that details on the system–bath interaction in the TDI ground state are generally not available. Our approach features two main advantages: first, simultaneously recording both excitation and emission spectra (or excitation spectra and emission intensity decays) allows access to information about environmental and conformational distributions in both ground- and excited states. Second, we can correlate features in the excitation and emission spectra for individual molecules, revealing how different nanoenvironments modulate excited-state relaxation.

We note a technical complication caused by the very small Stokes shifts of rylenes: Due to the large overlap of absorption and emission, part of the spectral range in either excitation or emission is lost in filtering the excitation light from the signal. We circumvent this loss by recording full-excitation-range EEM and supplying the missing emission band by a conventional SM experiment. To assess the validity of this approach we compare spectra extracted from full-excitation-range EEM, full-emission-range EEM, and conventional SMS for a bulk TDI sample. These are, outside the regions affected by the cutoff filters, essentially identical (SI Appendix, Fig. S2), justifying our approach.

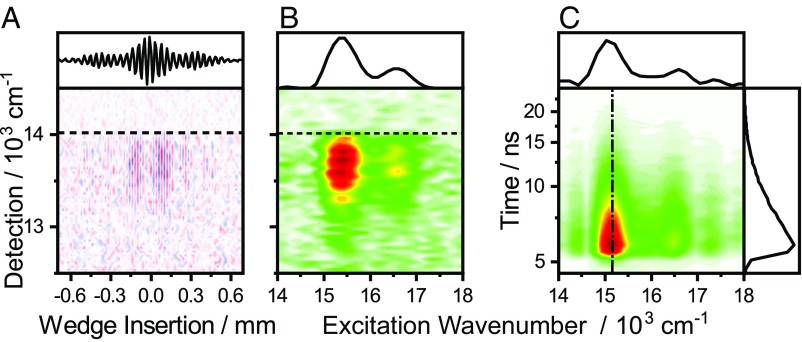
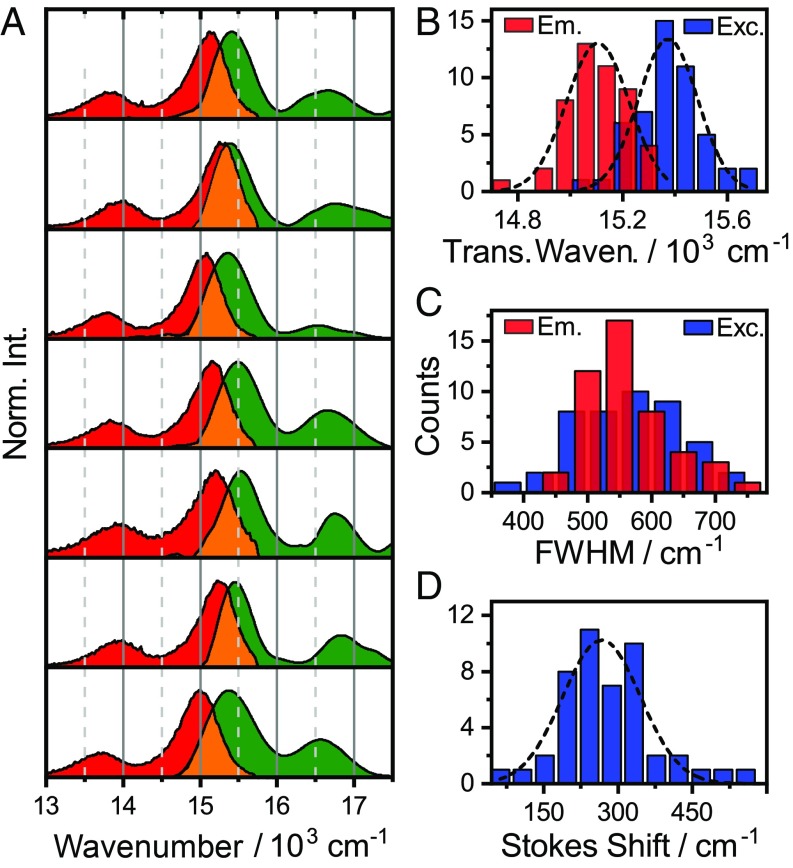
We proceed by recording SM EEMs of a polystyrene thin film containing TDI at very high dilution. Fig. 2A shows a typical SM interferogram, with the LPF cutoff denoted with a horizontal dashed line. Along the wedge-insertion axis interference fringes in the fluorescence signal appear as t₁ increases. An FT over the time delay yields the SM EEM in Fig. 2B, where the data are represented as an excitation- versus emission- wavenumber heat map. A corresponding excitation wavenumber versus time map, constructed by an FT over wedge insertion vs. TCSPC decay data, is shown in Fig. 2C. While these latter maps contain information on the variations in fluorescence lifetime across the ensemble, we here focus on spectral lineshapes. To facilitate direct comparison of individual spectra, we extract conventional excitation spectra by integrating the EEM over the detection axis. We show a representative selection of such extracted SM spectra in Fig. 3A. Significant variations from molecule to molecule in parameters such as transition frequencies, Stokes shifts, and linewidths are apparent. Notably, the parameters do not fluctuate during the measurement, implying that any relevant spectral dynamics in this system must be either much faster or much slower than the experimental readout, which is on the order of seconds. It is convenient to fit these spectra with suitable functions to extract precise transition frequencies and linewidths, where we achieve quantitative agreement with the data using a series of Gaussians (example fits in SI Appendix, Fig. S7). Using more complex lineshape functions does not improve the fit—or decrease the number of parameters, as discussed below.

Fig. 2.

SM interferogram (A) and the corresponding SM EEM (B). Excitation spectra can be extracted by integrating the interferogram over the detection frequency (A, Top) followed by an FT, or by an FT to produce the EEM followed by integration over the detection frequency (B, Top). (B). The filter cutoffs are indicated by horizontal dashed lines. (C) Excitation-energy versus emission-intensity decay for an SM constructed from a interferometric TCSPC experiment.

Fig. 3.

(A) Representative selection of SM excitation (green) and emission (red) spectra. Significant variations in transition energies, linewidths, and Stokes shifts between molecules are observed. Distribution of transition frequencies (B), 0–0 transition linewidths (C), and Stokes shifts (D).

We collect the distribution of several relevant observables in Fig. 3 B–D, which provide a direct link between the properties of the individual molecules and those of the ensemble. The transition frequencies are distributed around 15.375 cm⁻¹ (excitation) and 15.110 cm⁻¹ (emission)––which agree within 40 cm⁻¹ with the ensemble values (SI Appendix, Fig. S2). In contrast to an earlier study on single-rylene quaterrylene diimides (11), where large spectral shifts were observed, we find no bimodal frequency distribution. Rather, we observe a narrow distribution of frequencies, with an SD of 115 cm⁻¹ for emission and 120 cm⁻¹ for excitation, respectively. This is in agreement with earlier work of Liao et al. (20), who showed that large spectral shifts were due to photoconversion reactions. These narrow, single-mode distributions are consistent with the weakly interacting environment provided by polystyrene.

While transition frequencies report on site-energies, linewidths and Stokes shifts report more directly on the bath interaction dynamics (18). In particular, they report the bath fluctuations experienced by a molecule. The Stokes shift is normal distributed around 265 cm⁻¹ (σ ∼ 80 cm⁻¹), close to the ensemble value of ∼220 cm⁻¹. The linewidth distributions, as extracted from the Gaussian fits to the data, peak at 565 and 540 cm⁻¹ for excitation and emission, respectively, which is again close to the ensemble value of ∼600 cm⁻¹. This similarity of ensemble- and SM linewidths reveals that the line broadening under these conditions is largely from homogeneous rather than inhomogeneous broadening.

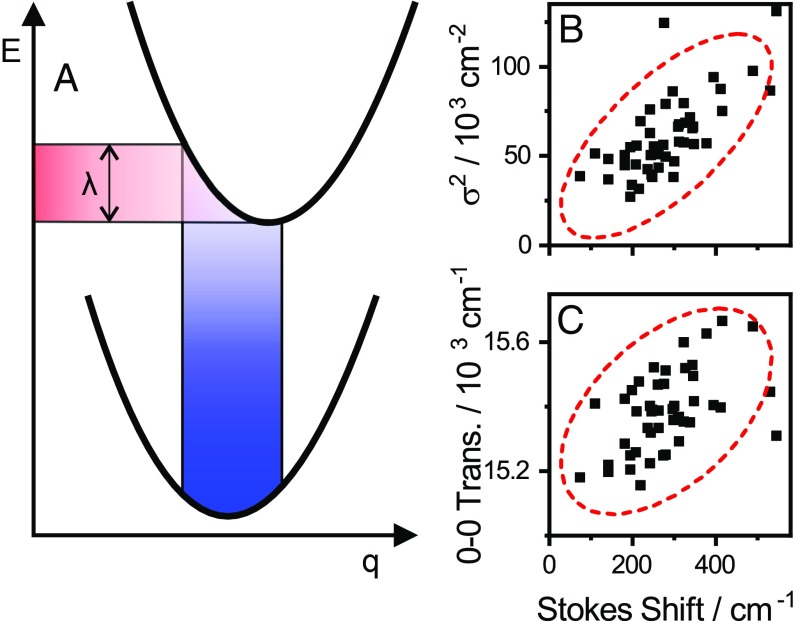
Having the EEM available for SMs provides an opportunity to apply lineshape theory to a situation that is not obscured by ensemble averaging. We here apply the common framework of the Brownian oscillator model (18) of system–bath interactions, the physical basis of which is schematically illustrated for an electronic two-level system in Fig. 4A. Herein, thermal bath fluctuations result in nuclear motion along the coordinate q, giving rise to fluctuating transition frequencies. The spectral lineshapes determined by this thermal motion are described by the correlation functions of these fluctuations. The observation of Gaussian lines implies that we are close to the high-temperature, slow-modulation limit of the model, where fluctuation frequencies are much smaller than the absorption linewidth (18). In this limit the spectral lineshapes are

$$A\left(\omega \right)\propto e^{-\left[{\left(\omega -{\omega }_a\right)}^2/2{\sigma }^2\right]}.$$

This is a Gaussian transition with a central frequency of ω_a and an SD of σ. The square of SD can be written in terms of the reorganization energy λ as

$${\sigma }^2=2\lambda \frac{k_{B}T}{\hslash }.$$

This standard lineshape analysis implies correlation between Stokes shift (2λ) and the squared excitation linewidth for TDI. Plotting ${\sigma }^2$ against 2λ in Fig. 4B we observe positive linear correlation [Pearson correlation coefficient r = 0.69 (P = 6 × 10⁻⁸)], although the agreement with the predicted slope of this dependence is not quantitative. This discrepancy may be the result of, e.g., the simple bath model used, or of deviations from the slow-modulation limit. Nevertheless, limits on the fluctuation timescales can be derived from these observations. As we observe no time-dependent spectral shifts during acquisition, any fluctuations must be fast compared with the timescale of the experiment. This sets an upper limit on the characteristic timescales in the millisecond range. A lower limit can be estimated from the slow-modulation limit assumption of a fluctuation frequency much smaller than the linewidth. With the SDs in the range of 300 cm⁻¹ observed for the lines here, this implies fluctuations that are much slower than a few hundred femtoseconds––in the general domain of low-frequency acoustic phonons, as might be expected. The positive correlation between absorption frequency and Stokes shift apparent in Fig. 4C can be qualitatively understood to arise from rapid excited-state relaxation combined with relative curve displacement (Fig. 4A). An increase of the relative potential surface displacement along q leads to both an increase in absorption frequency and reorganization energy, while fast excited-state relaxation causes loss of memory of the excitation frequency before emission takes place. As a result, excitation vs. decay maps do not yield more information about this simple system than what is available in the EEM.

Fig. 4.

(A) Potential energy surfaces in terms of a nuclear coordinate q. In the Brownian oscillator model (18) bath-induced thermal fluctuations induce a distribution in the transition frequencies. The corresponding Stokes shift is related to the reorganization energy λ as Stokes = 2λ. The optical lineshapes and -widths are ultimately determined by the amplitude and frequency of the bath fluctuations. (B) In accordance with the Brownian oscillator model, we observe linear correlation between the Stokes shift and the square of the linewidth. (C) We observe weaker, but significant correlation between the excitation transition frequency and the Stokes shift.

EEM of Energy-Transfer Dyads.

In the preceding sections, we demonstrated an SMS-EEM–based analysis of simple monomeric molecules. SMS-EEM only displays its full power for more spectrally complex systems however. One example is the intramolecular energy-transfer dyad shown in Fig. 5A. Intramolecular donor–acceptor pairs are popular both in investigations of the fundamental mechanisms of EET, and as simple model systems for the pigment protein complexes found in natural photosynthesis (e.g., ref. 34). This particular dyad is a rigidly linked perylene diimide–benzoperylene pair, forming a structurally well-defined EET pair with orthogonally polarized transitions (35, 36). It has received recent attention (37, 38) due to the substantial discrepancy between the observed and predicted EET efficiencies; the orthogonal transition moments imply vanishing donor–acceptor coupling, and thus vanishing EET rates in the simple Förster model. In experiments however, the EET proceeds on a timescale of ∼10 ps with essentially unity quantum yield. This discrepancy has been explained by modulation of couplings and transition frequencies by low-frequency vibrational motion (38).

Fig. 5.

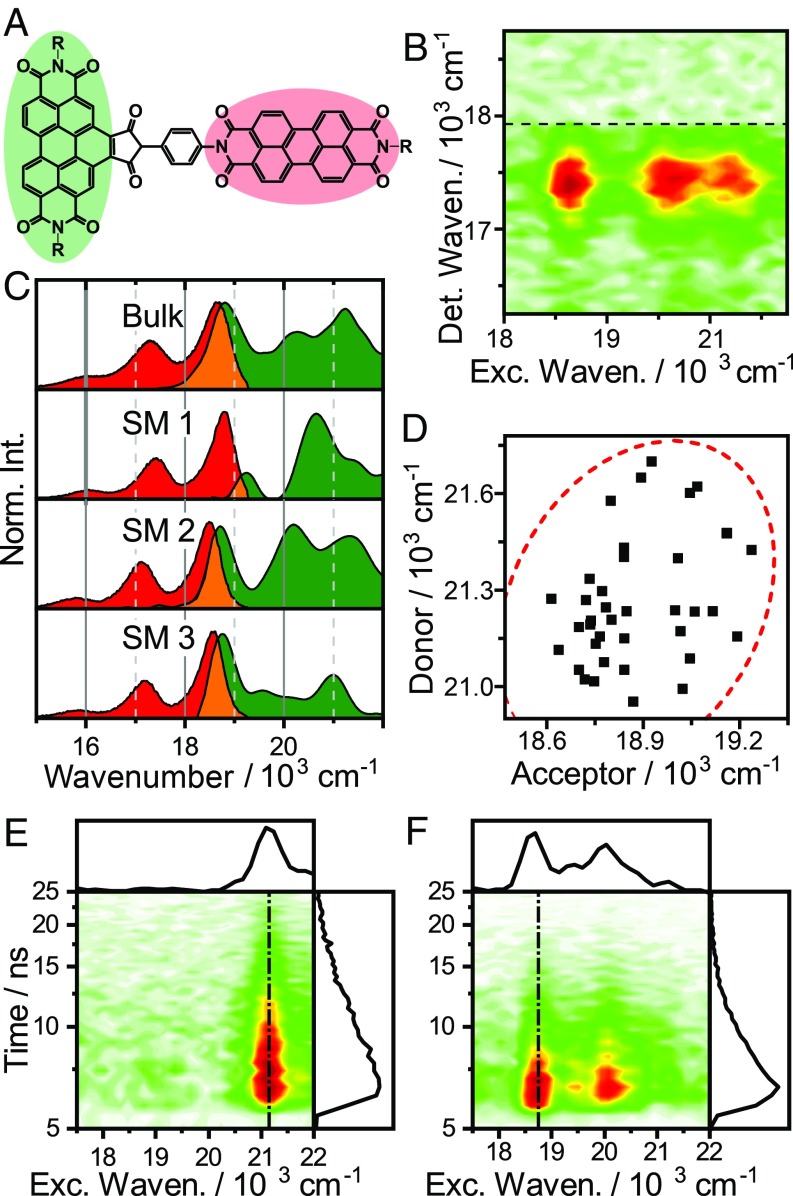
(A) Structure of the excitation-energy transfer donor–acceptor dyad. (B) EEM of a single dyad. (C) Comparison of excitation (green) and emission (red) spectra of several single dyads and the bulk spectra. (D) Correlation plot of donor- and acceptor frequencies in the dyads; 95% confidence ellipse shown as dashed red line. (E and F) Excitation versus emission intensity decay maps of two single dyads with different relative orientation to the polarization vector of the excitation light.

In the studies of several biological light-harvesting systems (39, 40), claims of unusual EET mechanisms have been made. In particular, excitonic coherence has been proposed to play a major functional role. Qualitatively, this implies that the dynamics in these systems have a significant degree of “wave-like” character. These claims have been heavily disputed, as the wave-like coherences are extremely fragile and require a specific protection mechanism for them to persist on functionally relevant timescales. One proposed mechanism invokes correlations in the environmental fluctuations experienced by the donor- and acceptor excitons (40, 41). Any such correlation must naturally lead to correlations in the spectra. The dyad investigated here presents a convenient model system to search for such correlations, and determine whether they are a general phenomenon, or extremely specific (e.g., protein-structure mediated) conditions are required.

Fig. 5B shows a typical EEM for a single dyad, where the emission arises predominantly from the acceptor, as expected given the near-unity quantum yield of EET. Along the excitation axis two distinct contributions are visible, in accordance with refs. 35 and 36: the vibronic progression of the acceptor appearing around 18.700 and 20.100 cm⁻¹, and the lowest-energy transition of the donor at ∼21.200 cm⁻¹. Proceeding as above, we present the data as conventional excitation- and emission spectra to facilitate comparisons between single dyads. The bulk- and representative SM spectra are shown in Fig. 5C. As for TDI, we observe significant spectral variations across the ensemble. The distributions of both transitions have SDs of ∼160 cm⁻¹––slightly larger than the ∼120 cm⁻¹ observed for TDI (SI Appendix, Fig. S6). This may reflect the larger range of conformational geometries possible for the dyad. Nevertheless, these energies are consistent with the weak solvent–solute interactions expected for aromatic hydrocarbons in a nonpolar matrix. Note that the large variation in relative intensity of donor- and acceptor-excitation spectra seen both in Fig. 5C and in the time-resolved maps in Fig. 5 E and F is a result of the polarization of the light source rather than an intrinsic dyad property: Due to the orthogonal orientation of the transition moments, the ratio of intensities is strongly dependent on the orientation of a particular dyad relative to the laser polarization. In experiments where the absolute orientation of chromophores is important, this geometric information is of significant interest. Here it confirms the expected molecular geometry: Since we in some cases observe exclusively donor absorption, but in all cases acceptor fluorescence, the angles between transition dipoles cannot be substantially different from orthogonal. This rules out significant structural distortions as a promotor of EET and supports the assignment of low-frequency vibrations as a primary driver in this system (38).

Turning our attention to the issue of correlated bath fluctuations, we first note that the ∼160-cm⁻¹ frequency distribution observed for the dyads is essentially the range over which the transition fluctuates as the molecules interact with their rapidly fluctuating bath. While this is small compared with the transition frequencies, it is a substantial fraction of the donor–acceptor energy-level spacing. Excitonic coherence on functionally relevant timescales requires preservation of this energy-gap magnitude during bath-induced fluctuations, which directly leads to the assumption of correlated bath fluctuations. In many biological light harvesters where excitonic coherence has been discussed, this issue is magnified, as their energy-level separations are often directly comparable to frequency fluctuations of this magnitude (42). To investigate whether these correlations manifest under generic conditions, we plot the dyad 0–0 transition frequencies against each other in Fig. 5D. Simple visual inspection reveals no obvious linear correlation, as the donor frequencies are scattered over a broad range in any given interval of acceptor frequencies. The weakness of correlation is similarly demonstrated by failing a simple statistical test at the P < 0.1 level [Pearsons correlation coefficient r = 0.24 (P = 0.11)]. The straightforward conclusion from this observation is that there is no evidence for correlated bath fluctuations in this weakly coupled EET system.

Applying these results to biological light harvesters is illuminating. In these complex systems it may be difficult to assign spectroscopic signals to specific physical processes, and the current debate is centered on whether certain ambiguous oscillatory signals in time-resolved spectra are signatures of excitonic coherence or of vibrational wavepacket motion. As outlined above, excitonic coherence is extremely fragile, and as a result there has been significant interest in identifying bath correlations that could inhibit their rapid dephasing. Indeed, if the lack of correlation observed for the dyad applied also to the excitonic states in photosynthetic proteins, we would derive dephasing times well below 100 fs––much too short for biological relevance. While a search for biological bath correlations was recently performed using Fourier analysis of photon-echo data (41), the results so far appear inconclusive. In contrast, SMS-EEM provides a straightforward and much less parameter-sensitive approach to address this question, as correlations appear directly in the spectral statistics. Taking the present results as general, one would conclude that energy-level fluctuations in weakly coupled donor–acceptor systems are uncorrelated, and thus that excitonic coherence is not maintained on biologically relevant timescales. However, from the presented experiments, we cannot however rule out the possibility of “active” protection of coherences by the protein matrix, as has been proposed (19, 40). Future studies, applying SMS-EEM to the search for correlated fluctuations in biological light harvesters, will shed light on this problem.

Conclusions

We have introduced a spectral interferometry approach that allows us to record the entire excitation and emission information of SMs in a single experiment. This forms the basis for detailed analysis of spectral lineshapes, which directly reveals the interaction between molecules and their local nanoscopic environment. We use this ability to analyze both a simple rylene dye and an EET dyad. From the statistics of the spectral data, we find that the commonly used lineshape theory is justified also from a microscopic perspective, and we use simple expressions derived from this approach to estimate the timescales and properties of the fluctuating bath. Applying this statistical analysis of transition frequencies to a dyad system with intramolecular EET, we rule out correlated bath-fluctuation dynamics for this donor–acceptor molecule. This implies that such effects, which have been proposed in natural light harvesters as a protection mechanism for excitonic coherence, cannot be generic, but must be the result of highly tuned behavior of the system. The SMS-EEM approach is directly applicable to a wide range of natural and artificial light harvesters, and can provide direct evidence for––or against––correlated bath fluctuations in systems with stronger coupling than the one targeted here. More generally, our powerful and easily implementable interferometric approach could be useful to address a wide range of problems in SM- and diffraction-limited microscopy, where the emission properties are nontrivially related to the excitation wavelength, and can thus further expand the scientific horizon of these techniques.

Materials and Methods

Sample Preparation.

TDI was bought from KU dyes ApS. The EET dyad (WAN-KF-10) was obtained from Prof. Heinz Langhals, Ludwig Maximilian University of Munich, Munich. Poly(styrene) (PS MW = 23,000 g/mol) was purchased from Sigma-Aldrich and used as supplied. About 20 mg of PS were dissolved in 0.5 mL toluene (spectroscopic grade; Sigma-Aldrich). The solution was doped with TDI at a concentration of <10⁻⁹ mol/L and spin-coated onto an annealed glass coverslip (Menzel). For bulk measurements, a higher concentration of TDI was used.

SMS.

The broadband light source was a pulsed white-light laser (SuperK EXTREME EXB-6, NKT) operating at 11 MHz. The output was cut off above 633 nm (for the full emission spectrum, BSP01-633R-25; Semrock) or 700 nm (for the full excitation spectrum, ET-700SP-2P8; Chroma Technology Corp.) by SPFs. The remainder was fed through the TWINS interferometer and reflected by a 30:70 BX (XF122 Omega Optical) into an oil immersion objective (UPLFLN 100× N.A. = 1.3; Olympus). The fluorescence was collected with the same objective and separated from the excitation light by LPFs (488- and 633-nm-long pass, LP02-488RE-25 and BLP01-633R-25; Semrock) for full-range emission spectrum and a 714-nm-long pass (TLP01-704–25 × 36; Semrock Versachrome) for the full-range excitation. The fluorescence was detected by a spectrograph (Princeton Instruments SPEC-10:100B/LN eXcelon CCD camera, SP 2356 spectrometer, 300 grooves/mm) or by two APDs (Perkin-Elmer CD3226) after splitting by a 50:50 nonpolarizing BS cube to measure photon antibunching. A 750-nm SPF (FF01-750/SP-25; Semrock) was added in front of one of the APDs to prevent cross-talk. The signals from the two APDs were collected by a single photon-counting module (Becker & Hickl SPC-830). A DG535 Delay generator (Stanford Research Systems) was used to create delay between the two APD channels. Excitation-lifetime maps were acquired by using an APD instead of the spectrometer and triggering TCSPC acquisition for every position of the TWINS interferometer.

Interferometer specifications, details on calibration, additional SMS EEMs, TDI molecular structure, and full excitation- and emission-range bulk EEMs are included in SI Appendix.