Amyloid fibril-directed synthesis of silica core–shell nanofilaments, gels, and aerogels

Significance

Proteinaceous fibrils networks are ubiquitous in nature and span most domains of living matter. Among these, amyloid networks bear a twofold significance, due to their implication in the formation of amyloid plaques and tangles in vivo, but also the remarkable width of applications in which they start to emerge when synthesized in vitro. This work provides a solid strategy to improve the mechanical properties of amyloid networks by biosilicification and demonstrates how the resulting hydrogels can be used for further material design, such as in the fabrication of ultra-high porous aerogels. This contribution also advances our fundamental understanding of complex dynamic networks by introducing a general theoretical model capable of quantitatively capturing the effects of filament bundling on gel rigidity.

Abstract

Amyloid fibrils have evolved from purely pathological materials implicated in neurodegenerative diseases to efficient templates for last-generation functional materials and nanotechnologies. Due to their high intrinsic stiffness and extreme aspect ratio, amyloid fibril hydrogels can serve as ideal building blocks for material design and synthesis. Yet, in these gels, stiffness is generally not paired by toughness, and their fragile nature hinders significantly their widespread application. Here we introduce an amyloid-assisted biosilicification process, which leads to the formation of silicified nanofibrils (fibril–silica core–shell nanofilaments) with stiffness up to and beyond $\sim$20 GPa, approaching the Young’s moduli of many metal alloys and inorganic materials. The silica shell endows the silicified fibrils with large bending rigidity, reflected in hydrogels with elasticity three orders of magnitude beyond conventional amyloid fibril hydrogels. A constitutive theoretical model is proposed that, despite its simplicity, quantitatively interprets the nonmonotonic dependence of the gel elasticity upon the filaments bundling promoted by shear stresses. The application of these hybrid silica–amyloid hydrogels is demonstrated on the fabrication of mechanically stable aerogels generated via sequential solvent exchange, supercritical ${\mathrm{C}\mathrm{O}}_2$ removal, and calcination of the amyloid core, leading to aerogels of specific surface area as high as 993 ${\mathrm{m}}^2$/g, among the highest values ever reported for aerogels. We finally show that the scope of amyloid hydrogels can be expanded considerably by generating double networks of amyloid and hydrophilic polymers, which combine excellent stiffness and toughness beyond those of each of the constitutive individual networks.

Protein amyloid fibrils, filamentous protein aggregates with highly ordered structural morphology and cross-$\beta$ strands orientation as a fingerprint can be generated from a multitude of proteins, including food-grade proteins, by unfolding and hydrolysis (1–3). Differently from the pathological homologue amyloid fibrils, which assemble in vivo from misfolding proteins and peptides (4, 5), the resulting amyloid fibrils formed from food proteins can be used in a diverse range of applications such as drug delivery platforms, cell scaffolds, ultralight aerogels, artificial bones, degradable films, and water purification filters (6–10). However, many of these applications could be hindered by the low mechanical strengths of amyloid networks. Improving their mechanical strengths at different length scales is thus of prime interest in a very broad context.

In nature, one common strategy endowing organic components with remarkable mechanical strengths is to produce organic–inorganic composites via biomineralization, among which biosilicification has been most investigated because of its wide existence in many organisms such as diatoms and sponges, and various functionalities including molecule separation, enzyme immobilization, and drug delivery (11, 12). It has been demonstrated that both in vivo and in vitro basic amino acids (lysine, histidine, and arginine) can catalyze the sol–gel transition of silica precursors, i.e., hydrolysis and condensation (11, 13–18). Some templates abundant in basic amino acids, such as polypeptides, peptide fibrils, and amphiphiles, have been prepared thereof (11, 13–18). Despite success in fabricating desired silica structures, these templates are designed with specific amino acid composition and even sequence, implying limited applications due to the associated high-cost synthesis. Therefore, it is desirable to identify a class of templates that can be tailored and have inexpensive sources but that can match the needs of practical applications. Amyloid fibrils assembled from food proteins could be a candidate, given the various types of amino acids involved and the multitude of morphologies associated with their polymorphism.

In this study, we introduce fibril–silica core–shell nanostructures formed by mixing amyloid fibrils and silica precursor tetraethyl orthosilicate (TEOS). The use of amyloid fibrils as possible support for superhydrophobic surfaces has recently been discussed, using catalyzers to carry out the silification process (19). Here, silification is templated directly by the amyloid fibrils themselves and is shown to be a general process by performing the same process on two classes of amyloids based on $\beta$-lactoglobulin and lysozyme. A theoretical framework of the network elasticity is also provided, which can be appropriately applied to explain the origins of the robust mechanical properties of silicified fibril networks. Moreover, mechanically stable aerogels and stretchable double network (DN) hydrogels based on these building blocks were also prepared and characterized. The fabrication of this class of biohybrids not only imposes amyloid fibril networks with strong mechanical properties but also brings biosilicification closer to practical applications.

Results and Discussion

Fabrication of Fibril–Silica Core–Shell Structures.

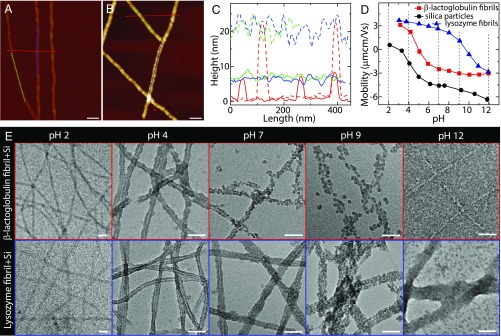
Atomic force microscopy (AFM) imaging of $\beta$-lactoglobulin amyloid fibrils shows rod-like structures with an average diameter of $\sim$5 nm and contour lengths spanning several micrometers (Fig. 1 A and C and SI Appendix, Fig. S1), which is in line with the previous observations (1). In addition, wide pH values ranging from 2 to 12 do not change the filamentous morphology of amyloid fibrils (SI Appendix, Fig. S1). One common silica precursor TEOS was used here, and it was found that its hydrolysis and condensation are accelerated by the presence of $\beta$-lactoglobulin amyloid fibrils at pH 4 (SI Appendix, Fig. S2). As mentioned above, this is understood to arise from $\beta$-lactoglobulin–enriched composition in basic amino acids (lysine, histidine, and arginine), 20 out of 162, which can promote the hydrolysis and condensation of silica precursor (11, 13–18). By further investigating the mixture of silica precursor and fibril, AFM imaging shows that almost all condensed silica is deposited on the fibril surfaces, with an average diameter of $\sim$20 nm (Fig. 1 B and C) and contour length of $\sim 1\hspace{0.17em}\mathrm{\mu }$m (SI Appendix, Fig. S3) after silicification. Amyloid fibrils successfully coated by silica were also probed by Fourier transform infrared (FTIR) spectroscopy (SI Appendix, Fig. S4), suggesting that the main composition is in the Si–O–Si form. Moreover, these silicified fibrils exhibit high rigidities: an average Young’s modulus of $\sim$20 GPa measured by peak force quantitative nanomechanical AFM (SI Appendix, Fig. S5), which is $\sim$5 times higher than the bare fibrils having a Young’s modulus of $\sim$3.7 GPa (20).

Fig. 1.

Interaction between amyloid fibril and silica. (A) AFM image of $\beta$-lactoglobulin amyloid fibrils at pH 4. (B) AFM image of the mixture of $\beta$-lactoglobulin fibril and silica precursor at pH 4: Silica deposited onto fibril surfaces lead to the formation of fibril–silica core–shell nanofilaments. (C) Height profiles of bare fibrils in A (solid lines) and silicified fibrils in B (dashed lines). (D) Electrophoretic mobility of $\beta$-lactoglobulin fibril, lysozyme fibril, and silica as a function of pH. The isoelectric points of $\beta$-lactoglobulin and lysozyme fibrils are around 5 and 10, respectively. (E) TEM images of the mixtures of fibril and silica precursor at different pHs: $\beta$-lactoglobulin (Upper) and lysozyme (Lower). The concentrations of fibril and silica precursor (TEOS) are 0.1 wt % and 20 mM, respectively. (Scale bars for A, B, and E: 50 nm.)

To reveal the formation mechanism of the fibril–silica core–shell nanofilaments, the $\beta$-lactoglobulin fibril and silica precursor were mixed and characterized in a wide pH range from 2 to 12 ( Fig. 1E, Upper and SI Appendix, Fig. S6). Note that transmission electron microscopy (TEM) imaging was applied to study the core–shell structure, due to the electron density difference between silica and amyloid fibril, yielding a light core of fibril and a dark shell of silica, as shown in the contrast experiment (SI Appendix, Fig. S7). At low and high pH values (pH 2 and 12), silica are less condensed and more separated from fibrils, which can be explained by the strong electrostatic repulsion between identically charged fibril and silica (Fig. 1D; both negative at pH 2 and both positive at pH 12) preventing the silica adsorption onto the amyloid fibrils, as well as the low self-condensation rate of silica (SI Appendix, Fig. S8) (21). In contrast, at pH 4, silica are decorated on the fibril surface with the formation of uniform core–shell structures, wherein the fibril and silica are oppositely charged. The electrostatic attraction between the oppositely charged fibril and silica is expected to yield high local silica content in the proximity of the fibril surface, while the catalytic role of basic amino acids on fibril surface and self-condensation of silica lead to uniform fibril–silica core–shell structures. At pH 7 and 9, only part of the silica could adhere to the fibrils. The adhesion for identically charged silica and fibril could be ascribed to the nucleating role of fibrils in the silica condensation process and/or net Derjaguin–Landau–Vervey–Overbeek (DLVO) attraction forces.

The morphologies of the fibril–silica hybrids at various pHs infer the crucial role of fibril charge in templating uniform fibril–silica core–shell nanofilaments, which could be further demonstrated by another class of amyloid fibrils (Fig. 1E, Lower). Differently from $\beta$-lactoglobulin fibrils, lysozyme fibrils possess a higher isoelectric point, $\sim$10. Thus, lysozyme fibril and silica are oppositely charged at pH 7 and 9, which is different from $\beta$-lactoglobulin fibril system. The uniform fibril–silica core–shell structures observed at those pHs for lysozyme fibril, as opposed to $\beta$-lactoglobulin fibrils, further confirm the mentioned role of amyloid fibril charge. This also illustrates the generality of in situ synthesizing of core–shell nanofilaments by protein amyloid fibrils. Based on the TEM observations for lysozyme and $\beta$-lactoglobulin amyloid fibril systems, it is plausible that the electrostatic attraction between fibrils and silica is the dominating factor for templating uniform fibril–silica core–shell structures.

Evolution of Core–Shell Structures.

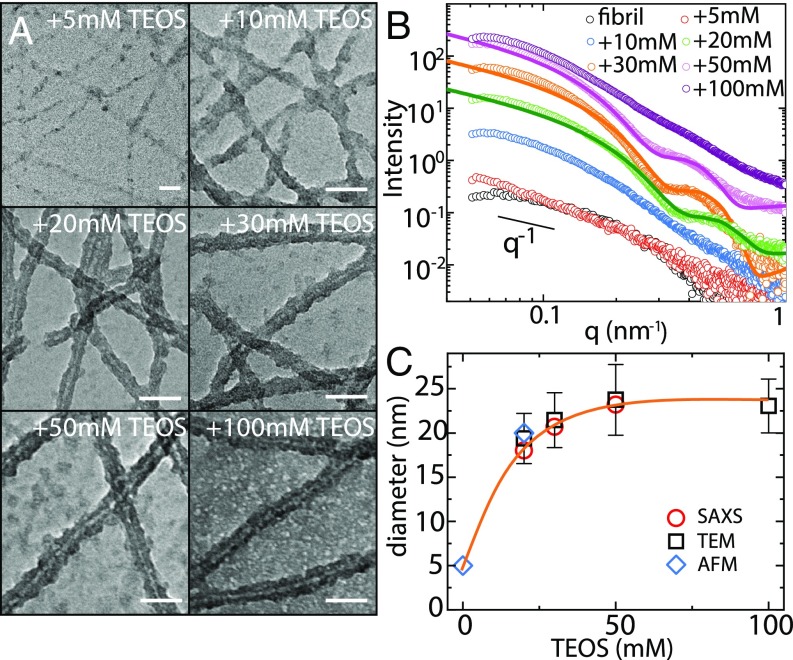
The templating versatility of $\beta$-lactoglobulin fibrils at pH 4 is further characterized by TEM and small-angle X-ray scattering (SAXS) with varying silica precursor contents but fixed fibril concentration of 0.1 wt %. TEM images (Fig. 2A) show that the fibrils are adhered by a few silica nanoparticles at low TEOS content, but start to be completely coated by silica at TEOS = 20 mM. Upon further increase of TEOS content, the shell thickness is only slightly increased (SI Appendix, Fig. S9), but the amount of nontemplated silica significantly increases. The results suggest that silica are preferably condensed and deposited on fibril surfaces at moderate concentrations, while, at high silica content, fibrils’ overall surface becomes unavailable to further template silica onto amyloids shell. This also means that the silica shell thickness can be tuned by controlling the charges balances of amyloid fibrils vs. silica.

Fig. 2.

Evolution of the fibril–silica core–shell structure. (A) TEM images of the $\beta$-lactoglobulin fibril–silica mixtures at different silica precursor contents and a fixed fibril concentration 0.1 wt % at pH 4. A statistical analysis was performed to calculate the diameters of silicified fibrils by the software ImageJ. (Scale bars, 50 nm.) (B) SAXS curves of pure fibril and silicified fibrils. Polydisperse core–shell cylinder model was applied to fit with the experimental data, as shown by the solid lines. (C) Plot of the diameters of silicified fibrils, extracted from SAXS, TEM, and AFM, as a function of silica content.

The global changes of the local structure of silicified fibrils were quantified by SAXS, as shown in Fig. 2B. The pure fibril has a relatively low scattering intensity, and a slope value of 1 is found in the low-$q$ regime, reflecting the rigid nature of $\beta$-lactoglobulin amyloid fibril (22). For the silicified fibrils, the scattering intensity increases and oscillations in the high-$q$ regime start to appear. These oscillations are typical features of the form factor of fractal objects with fairly monodisperse cross-section. In contrast, the lack of an identifiable form factor in the case TEOS = 100 mM is associated with the large amount of nontemplated silica left in the system and high background scattering, as also suggested by TEM (Fig. 2A). To capture the oscillations in the high $q$ regime, a core–shell cylinder form factor model was applied to fit the SAXS scattering profiles (23). As displayed by the solid lines of Fig. 2B, the model fits very well the experimental data, with the corresponding fitting parameters given in SI Appendix, Table S1. The slight deviation of the fitted curves at the high-$q$ regime could be induced by the existence of nontemplate silica in this scatter dimension, evidenced by less deviation for the 20-mM system (almost no dispersed silica; Fig. 2A) than for the 30- and 50-mM systems (more dispersed silica; Fig. 2A). The diameters of silicified fibrils extracted from the fitting are 18.0, 20.7, and 23.2 nm, respectively, for the 20-, 30-, and 50-mM TEOS systems. The increase in diameter is also confirmed by the shift of the shoulder toward lower $q$, i.e., larger length scale, with increasing silica content. Fig. 2C gives the diameters of the silicified fibrils extracted from SAXS as well as TEM and AFM, the different techniques being in perfect agreement.

Highly Elastic Hydrogels from Silicified Fibrils.

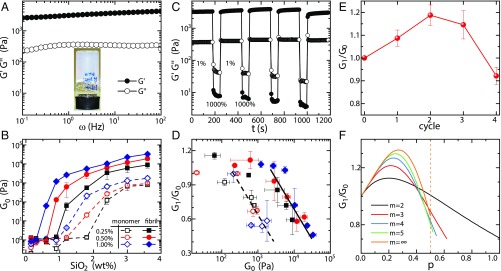
Along with the formation of fibril–silica core–shell structures at pH 4, self-supporting hydrogels are also formed ( Fig. 3A, Inset and SI Appendix, Fig. S10) upon raising fibril and silica contents. Frequency sweep, at strain 1% (in the linear region; SI Appendix, Fig. S11), shows that elastic modulus $G\prime$ is dominant over loss modulus $G\prime \prime$ and both are nearly frequency-independent across the frequency range investigated, indicating an elastic gel-like behavior (Fig. 3A). The network elasticity $G_0$ was characterized by studying the value of $G\prime$ at frequency 1 Hz. Fig. 3B plots $G_0$ as a function of silica content at three different fibril concentrations. Control experiments were performed using protein monomers. Silica content now is expressed as the weight concentration of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ rather than the molar concentration of TEOS; the full condensation of TEOS to ${\mathrm{\text{SiO}}}_2$ is illustrated in a thermogravimetric analysis (TGA) experiment (SI Appendix, Fig. S15). At low silica content, the fibril–silica mixtures remain in the liquid state, reflected in $G_0$ of the order of several pascals only. In these conditions, only a limited amount of silica existed in the system, which is insufficient to form 3D connecting networks (Fig. 2A). By raising silica content, both fibril–silica and protein–silica systems could form hydrogels, but the critical gelation concentration of silica for the fibril–silica system is much lower than that for the protein–silica system. This is due to the lower percolation threshold for elongated objects compared with spherical shapes. More importantly, the elasticities of fibril–silica hydrogels are almost two orders of magnitude higher than those of protein–silica hydrogels at the same protein and silica contents, which directly reflects the benefits of amyloid fibrils in establishing solid networks. Furthermore, fibril networks cross-linked by silica are significantly stiffer than the counterparts cross-linked by salt; for example, 1.0 wt % fibril network cross-linked by silica ($\sim$50 kPa) is almost three orders of magnitude stiffer than the same amount of fibrils cross-linked into a gel by the presence of salts ($\sim$50 Pa) (24). This can be rationalized by MacKintosh’s theory (25, 26), according to which the elasticity can be expressed as

$$G\approx \frac{{\kappa }^2}{k_{B}T{\xi }^2{l}_c^3},$$ [1]

where $k_B$ is the Boltzmann constant, $T$ is the absolute temperature, $\xi$ is the network mesh size, $l_c$ is the cross-link length, and $\kappa$ is the bending modulus, expressed as $\kappa =EI$; $E$ is the Young’s modulus, $I$ is the area moment of inertia, and $I=\pi d^4/64$ for the cross-section of cylinder with a diameter $d$. Owing to the silica coating, $E$ and $d$ of the network-building filaments are both increased, leading to a significant increase in $\kappa$, which can be quantified by measuring the persistence length $l_p=\kappa /k_{B}T$; see SI Appendix, Fig. S3. The significant increase in $\kappa$ endows the silicified fibril hydrogels with high elasticity. Note that $G_0$ trending to plateau at high silica content is in line with TEM observation: The silica shell thickness reaches a plateau, and the nontemplated silica only has negligible effects on network elasticity, compared with templated silica shell.

Fig. 3.

Elasticity of silicified fibril hydrogels. (A) Frequency sweep of 1 wt % fibril + 1.2 wt % ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ hydrogel at a strain of 1%. (Inset) Self-supporting hydrogel. (B) Elasticity evolution of the silicified fibril hydrogels with increasing silica content, with protein monomer applied as controls. (C) Recovery property of the 1 wt % fibril + 1.2 wt % ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ hydrogel evaluated by the continuous steps of oscillatory strains: 1,000% and 1% strains are applied to break gel and measure recovery property, respectively. (D) Plotting the correlation of network elasticity and recovery rate. The recovery rate is defined as the ratio of recovered elasticity after the first destruction and heal cycle, $G_1$, and initial elasticity, $G_0$. Full line is for fibril-based hybrids; dashed line is for monomer-based hybrids. (E) Elasticity changes of 1 wt % fibril + 1.2 wt % ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ hydrogel at different damage–recovery cycles. (F) Theoretical prediction of the elasticity evolution as function of the probability $p$ of single bundling event at different $m$ values, where $m$ is the maximum number of virgin filaments in one bundled filament. The dashed line shows the $p$ range when $m$ = $\infty$, i.e., $p\in \left[\mathrm{0,0.5}\right]$.

The recovery properties of silicified fibril hydrogels were also investigated by continuous steps of oscillatory strains, i.e., 1,000% and 1% strains, respectively, applied to break the hydrogel and inspect the recovery of the hydrogel. Fig. 3C shows that the elasticity of a strain-damaged network could recover within a few seconds and even exceeds its initial value (Fig. 3E). The elasticity recovery features are expressed by the recovery rate, defined as the recovery elasticity after the first destruction and healing cycle, $G_1$, over its initial elasticity $G_0$. It was found that the recovery rates of the fibril–silica and protein–silica hydrogels are, in general, comparable, although only fibril–silica hydrogels have the peculiar yet desirable feature of possessing recovery rates beyond unity (SI Appendix, Fig. S12). It is known that some hydrogels composed of spherical colloids exhibit recovery properties, due to the reversibility of the noncovalent interparticle bonds (27). Analogously, the silica shells contribute to the recovery property of silicified fibril hydrogels. Indeed, the same slope values found for two systems in the framework of the recovery rate–elasticity correlation illustrate well the vital role of silica shells (Fig. 3D).

Theoretical Calculations of Network Elasticity.

As mentioned in Highly Elastic Hydrogels from Silicified Fibrils, for silicified fibril hydrogels, the recovery elasticity could exceed the initial elasticity, i.e., recovery rate of >100% (Fig. 3E). This phenomenon has been observed before in self-assembling peptide hydrogels (28) and colloidal hydrogels (27) and, in both cases, qualitatively attributed to an increase in bending rigidity exerted by filament bundles. On a more quantitative basis, however, bundling among filaments also implies increases of the mesh size, that is, a weakening effect on network elasticity (Eq. 1), so that the final outcome of bundling on final network elasticity has nontrivial dependence, due to these two competing effects. Here we provide a theoretical framework to quantify the effects of the increase on both bending rigidity and mesh size on the network elasticity, whose predictions are in close agreement with the experimental observations. For the rigid filament network, the entanglement length $l_e$ is approximated to $\xi$. Here $l_c$ is defined as $a{l}_e$, with $a$ as the cross-linking probability (24). Thus, the network elasticity in Eq. 1 can be rewritten as $G\approx {\kappa }^2/{\xi }^5$ for a fixed $a$. Based on the calculations of mesh size and bending rigidity (SI Appendix), the elasticity recovery rate can be generalized as

$$\frac{G_1}{G_0}=\frac{{\left[1+{\sum }_{i=2}^m\left(i^2-1\right)p^{i-1}\right]}^2}{{\left[1+{\sum }_{i=2}^m\left(i-1\right)p^{i-1}\right]}^{9/2}},$$ [2]

where $m$ is the maximum number of virgin filaments in one bundled filament, $m\in \left[2,\infty \right)$, $i$ is the number of virgin filaments in the bundled filaments, $i\in \left[2,m\right]$, and $p$ is the probability of a single bundling event, so that a bundle of $i$ filaments occurs with probability $p^{i-1}$, whereas virgin filaments will occur with probability $1-{\sum }_{i=2}^m{p}^{i-1}$. Thus, for example, for $m$ = 2, the recovery rate is ${\left(1+3p\right)}^2/{\left(1+p\right)}^{9/2}$, while, for $m$ = $\infty$, the recovery rate is $\frac{{\left(1+2p^2-p^3\right)}^2{\left(1-p\right)}^3}{{\left(1-p+p^2\right)}^{9/2}}$. Fig. 3F displays the functional curves of Eq. 2 at different $m$ values. In all cases, a nonmonotonic elasticity evolution is observed, i.e., elasticity first increases and then decreases with raising the filament bundling extent $p$. This is in perfect agreement with the experimental observation during the shear damage–recovery process (Fig. 3E). Remarkably, the theoretical recovery ratio also quantitatively matches the experiments for $m$ values between 2 and 3. This theoretical tool highlights two points at least: (i) Networks having elasticity recovery properties are not only induced by reversible cross-linking bonds but may also occur by irreversible bundles; (ii) in the bundled filament network, the bending rigidity is the dominating effect at small extents of bundling (elasticity increases), while mesh size takes over at large bundling extents (elasticity decreases).

DN Hydrogels.

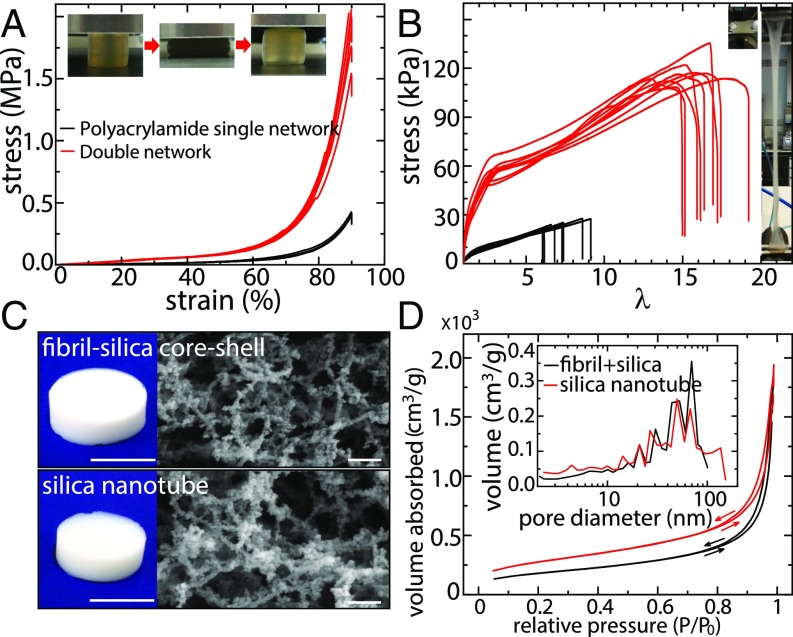
The silicified fibril hydrogels possess very high elasticities in the linear strain region, i.e., deformation of $<$10%, but, in practical applications, hydrogels are often requested to perform under high stretching and compression modes, i.e., at deformation of $\gg$10%. Hydrogels constituted by a DN can potentially achieve these mechanical properties, leading to performances comparable with natural rubbers (29, 30). A DN hydrogel based on $\beta$-lactoglobulin fibril/polyacrylamide was prepared and investigated here. Fig. 4A shows the compressive stretch–stress curves of single network (SN) and DN hydrogels. The fibril SN hydrogel fractures at extremely low strain (<10%; SI Appendix, Fig. S11), while the polyacrylamide SN hydrogel sustains a stress of $\sim$0.3 MPa at strain 90%. In contrast, the DN hydrogel reaches a stress of $\sim$2 MPa, which is much higher than its pristine forms. More importantly, the DN hydrogel could restore its original shape after unloading from a maximum 50% compression.

Fig. 4.

DN hydrogels and aerogels. (A) Compressive stress–strain curves of the polyacrylamide SN and the fibril/polyacrylamide DN hydrogels with certain repeated experiments. Insert displays that the DN hydrogel could recover even with a compression of 50% initial height. (B) Tensile stress–stretch curves of the polyacrylamide SN and the fibril/polyacrylamide DN hydrogels with certain repeated experiments. Insert shows that the DN hydrogel could be elongated to 17 times its initial length. (C) Photos and SEM images of the fibril–silica core–shell aerogel (Upper) and silica nanotube aerogel (Lower). The silica nanotube aerogel was generated by calcining the fibril–silica aerogel at $\sim$700 °C for 2 h. (Scales bars in photos and SEM images: 1 cm and 200 nm, respectively.) (D) Nitrogen gas absorption–desorption curves of the fibril–silica aerogel and silica nanotube aerogel, with the pore size distributions in Insert, derived from the nitrogen desorption.

Fig. 4B shows the tensile stretch–stress curves of SN and DN hydrogels. The stress and deformation at rupture are $\sim$110 kPa and $\sim$1,700% for DN, $\sim$24 kPa and $\sim$700% for polyacrylamide SN, and extremely low for fibril SN, so low that is difficult to quantify. Moreover, the Young’s and compressive moduli of the DN are $\sim$57.6 kPa and $\sim$142 kPa, respectively, much higher than those of the polyacrylamide SN (SI Appendix, Fig. S13). Thus, the mechanical properties of the DN based on $\beta$-lactoglobulin fibril/polyacrylamide far exceed those of either of its individual components, providing appealing opportunities in the design of functional materials made thereof.

Aerogels.

Aerogels, including amyloid fibril aerogels, show great promise in a variety of applications (31–33). However, low mechanical strength and high flammability of organic aerogels often hamper aerogel preparations and restrict the field of application (32). Amyloid fibrils coated with silica offer an appealing solution to these drawbacks: The compressive modulus and onset flammability temperature are respectively improved by $\sim$50 times and $\sim$35 °C (SI Appendix, Figs. S11 and S12 and Table S2), thanks to the high Young’s modulus and thermal insulation properties of silica shells. SEM imaging of the composite aerogel displays the filamentous network structure (Fig. 4C, Upper) confirming that the fibril–silica core–shell nanostructures remained intact in the aerogel state. A specific surface area of 648 $\pm$ 3.8 ${\mathrm{m}}^2$/g is obtained from a nitrogen sorption experiment [Brunauer–Emmett–Teller (BET) analysis; Fig. 4D], which is 2 times higher than pure $\beta$-lactoglobulin fibril aerogel (325 ${\mathrm{m}}^2$/g) (33). By considering the core–shell nanofilament structure with fibril core having a diameter of 5 nm and density of 1.3 g/${\mathrm{c}\mathrm{m}}^3$ and silica shell having a thickness of 7.5 nm and density of 0.208 g/${\mathrm{c}\mathrm{m}}^3$ as measured by TGA analysis (SI Appendix), a surface area of 724 ${\mathrm{m}}^2$/g can be estimated (SI Appendix), which is extremely close to the experimental value (648 ${\mathrm{m}}^2$/g). The silica shell density of 0.208 g/${\mathrm{c}\mathrm{m}}^3$, calculated from the mass ratio of silica and fibril obtained by TGA measurements, is significantly lower than the density of ${\mathrm{S}\mathrm{i}\mathrm{O}}_2$ solid, 2.65 g/${\mathrm{c}\mathrm{m}}^3$, suggesting a loosely packed silica in the shells of the filaments.

Moreover, we observed that the shape and size of the silicified fibril aerogel remains almost unaltered when the fibril skeleton is completely degraded (Fig. 4C). SEM image shows the calcined aerogel still with filamentous nanostructures, which can be referred to as a silica nanotube aerogel, as the calcination induces the conversion of fibril–silica core–shell structure into silica hollow nanotubes. This is further confirmed by BET analysis, which, after the calcination process, shows that the silica nanotube aerogel increases the surface specific area to 993 $\pm$ 6 ${\mathrm{m}}^2$/g, which is among the highest ever reported values for aerogels (31, 32). The pore sizes extracted from desorption curves are polydisperse for both aerogels but with remarkable similarity, which again demonstrates how the aerogel microstructure remained unaltered after removing fibril skeleton. Although silica nanotubes have been synthesized by using peptide fibrils as templates (14, 16, 18), this has never been carried out so far in the context of aerogels. Here we design an ultra-high surface area silica nanotube aerogel by using protein amyloid fibrils as sacrificial templates.

In summary, we have shown that, by using amyloid fibrils from inexpensive, nontoxic sources, it is possible to design a class of hybrid hydrogels and aerogels whose performance positions these systems at the front end of the current state of the art. We have also demonstrated that, by extending these concepts to double networks of amyloid fibrils and hydrophilic polymers, the scope of these materials can be further expanded. Finally, we have proposed an original analytical model capable of capturing, in a quantitative way, both the increase in rigidity of amyloid–silica hybrid hydrogels as a result of filaments bundling and the nonmonotonic evolution of the gel elasticity; this model bears general significance and can be applied to other classes of dynamic hydrogels. These results not only deepen our understanding of hybrid gels and complex networks but also widen significantly their application breadth, expanding their scope and making in reach the application of other classes of functional materials derived from them, such as hybrid aerogels.

Materials and Methods

Amyloid fibrils were prepared by heating protein monomer ($\beta$-lactoglobulin, lysozyme) at pH 2 and 90 °C. The mature amyloid fibrils then were mixed with different amounts of TEOS to fabricate silicified fibrils (fibril–silica core–shell nanofilaments). At low concentration, these structures were characterized by TEM, AFM, and SAXS; at high concentration, they formed gels characterized by rheology. The DN hydrogels were prepared by polymerizing acrylamide within preformed fibril gels, while the fibril–silica hybrid aerogels were prepared by supercritical ${\mathrm{C}\mathrm{O}}_2$ drying. The silica nanotube aerogels were obtained by calcination of fibril–silica aerogels. More information about materials and methods is given in SI Appendix.