Metalearners for estimating heterogeneous treatment effects using machine learning

Significance

Estimating and analyzing heterogeneous treatment effects is timely, yet challenging. We introduce a unifying framework for many conditional average treatment effect estimators, and we propose a metalearner, the X-learner, which can adapt to structural properties, such as the smoothness and sparsity of the underlying treatment effect. We present its favorable properties, using theory and simulations. We apply it, using random forests, to two field experiments in political science, where it is shown to be easy to use and to produce results that are interpretable.

Abstract

There is growing interest in estimating and analyzing heterogeneous treatment effects in experimental and observational studies. We describe a number of metaalgorithms that can take advantage of any supervised learning or regression method in machine learning and statistics to estimate the conditional average treatment effect (CATE) function. Metaalgorithms build on base algorithms—such as random forests (RFs), Bayesian additive regression trees (BARTs), or neural networks—to estimate the CATE, a function that the base algorithms are not designed to estimate directly. We introduce a metaalgorithm, the X-learner, that is provably efficient when the number of units in one treatment group is much larger than in the other and can exploit structural properties of the CATE function. For example, if the CATE function is linear and the response functions in treatment and control are Lipschitz-continuous, the X-learner can still achieve the parametric rate under regularity conditions. We then introduce versions of the X-learner that use RF and BART as base learners. In extensive simulation studies, the X-learner performs favorably, although none of the metalearners is uniformly the best. In two persuasion field experiments from political science, we demonstrate how our X-learner can be used to target treatment regimes and to shed light on underlying mechanisms. A software package is provided that implements our methods.

With the rise of large datasets containing fine-grained information about humans and their behavior, researchers, businesses, and policymakers are increasingly interested in how treatment effects vary across individuals and contexts. They wish to go beyond the information provided by estimating the average treatment effect (ATE) in randomized experiments and observational studies. Instead, they often seek to estimate the conditional ATE (CATE) to personalize treatment regimes and to better understand causal mechanisms. We introduce an estimator called the X-learner, and we characterize it and many other CATE estimators within a unified metalearner framework. Their performance is compared by using broad simulations, theory, and two datasets from randomized field experiments in political science.

In the first randomized experiment, we estimate the effect of a mailer on voter turnout (1), and, in the second, we measure the effect of door-to-door conversations on prejudice against gender-nonconforming individuals (2). In both experiments, the treatment effect is found to be nonconstant, and we quantify this heterogeneity by estimating the CATE. We obtain insights into the underlying mechanisms, and the results allow us to better target the treatment.

To estimate the CATE, we build on regression or supervised learning methods in statistics and machine learning, which are successfully used in a wide range of applications. Specifically, we study metaalgorithms (or metalearners) for estimating the CATE in a binary treatment setting. Metaalgorithms decompose estimating the CATE into several subregression problems that can be solved with any regression or supervised learning method.

The most common metaalgorithm for estimating heterogeneous treatment effects takes two steps. First, it uses so-called base learners to estimate the conditional expectations of the outcomes separately for units under control and those under treatment. Second, it takes the difference between these estimates. This approach has been analyzed when the base learners are linear-regression (3) or tree-based methods (4). When used with trees, this has been called the “two-tree” estimator, and we will therefore refer to the general mechanism of estimating the response functions separately as the “T-learner,” with “T” being short for “two.”

Closely related to the T-learner is the idea of estimating the outcome by using all of the features and the treatment indicator, without giving the treatment indicator a special role. The predicted CATE for an individual unit is then the difference between the predicted values when the treatment-assignment indicator is changed from control to treatment, with all other features held fixed. This metaalgorithm has been studied with Bayesian additive regression trees (BARTs) (5, 6) and regression trees (4) as the base learners. We refer to this metaalgorithm as the “S-learner,” since it uses a “single” estimator.

Not all methods that aim to capture the heterogeneity of treatment effects fall in the class of metaalgorithms. For example, some researchers analyze heterogeneity by estimating ATEs for meaningful subgroups (7). Another example is causal forests (8). Since causal forests are random forest (RF)-based estimators, they can be compared with metalearners with RFs in simulation studies. We will see that causal forests and the metalearners used with RFs perform comparably well, but the metalearners with other base learners can significantly outperform causal forests.

The main contribution of this work is the introduction of a metaalgorithm: the X-learner, which builds on the T-learner and uses each observation in the training set in an “X”-like shape. Suppose that we could observe the individual treatment effects (ITEs) directly. We could then estimate the CATE function by regressing the difference of ITEs on the covariates. Structural knowledge about the CATE function (e.g., linearity, sparsity, or smoothness) could be taken into account by either picking a particular regression estimator for CATE or using an adaptive estimator that could learn these structural features. Obviously, we do not observe ITEs because we observe the outcome either under control or under treatment, but never both. The X-learner uses the observed outcomes to estimate the unobserved ITEs. It then estimates the CATE function in a second step as if the ITEs were observed.

The X-learner has two key advantages over other estimators of the CATE. First, it can provably adapt to structural properties such as the sparsity or smoothness of the CATE. This is particularly useful since the CATE is often zero or approximately linear (9, 10). Secondly, it is particularly effective when the number of units in one treatment group (usually the control group) is much larger than in the other. This occurs because (control) outcomes and covariates are easy to obtain by using data collected by administrative agencies, electronic medical record systems, or online platforms. This is the case in our first data example, where election-turnout decisions in the United States are recorded by local election administrators for all registered individuals.

The rest of the paper is organized as follows. We start with a formal introduction of the metalearners and provide intuitions for why we can expect the X-learner to perform well when the CATE is smoother than the response-outcome functions and when the sample sizes between treatment and control are unequal. We then present the results of an extensive simulation study and provide advice for practitioners before we present theoretical results on the convergence rate for different metalearners. Finally, we examine two field experiments using several metaalgorithms and illustrate how the X-learner can find useful heterogeneity with fewer observations.

Framework and Definitions

We use the Neyman–Rubin potential outcome framework (11, 12) and assume a superpopulation or distribution $\mathcal{P}$ from which a realization of $N$ independent random variables is given as the training data. That is, $\left(Y_i\left(0\right),Y_i\left(1\right),X_i,W_i\right)\sim \mathcal{P}$, where $X_i\in {\mathbb{R}}^d$ is a $d$-dimensional covariate or feature vector, $W_i\in \left\{\mathrm{0,1}\right\}$ is the treatment-assignment indicator (to be defined precisely later), $Y_i\left(0\right)\in \mathbb{R}$ is the potential outcome of unit $i$ when $i$ is assigned to the control group, and $Y_i\left(1\right)$ is the potential outcome when $i$ is assigned to the treatment group. With this definition, the ATE is defined as

$$\text{ATE}\hspace{0.17em}≔\hspace{0.17em}\mathbb{E}\left[Y\left(1\right)-Y\left(0\right)\right].$$

It is also useful to define the response under control, ${\mu }_0,$ and the response under treatment, ${\mu }_1,$ as

$${\mu }_0\left(x\right)\hspace{0.17em}≔\hspace{0.17em}\mathbb{E}\left[Y\left(0\right)|X=x\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{and}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\mu }_1\left(x\right)\hspace{0.17em}≔\hspace{0.17em}\mathbb{E}\left[Y\left(1\right)|X=x\right].$$

Furthermore, we use the following representation of $\mathcal{P}$:

$$\begin{array}{cc}\hfill X& \sim \mathrm{\Lambda },\hfill \\ \hfill W& \sim \text{Bern}\left(e\left(X\right)\right),\hfill \\ \hfill Y\left(0\right)& ={\mu }_0\left(X\right)+\epsilon \left(0\right),\hfill \\ \hfill Y\left(1\right)& ={\mu }_1\left(X\right)+\epsilon \left(1\right),\hfill \end{array}$$ [1]

where $\mathrm{\Lambda }$ is the marginal distribution of $X$, $\epsilon \left(0\right)$, and $\epsilon \left(1\right)$ are zero-mean random variables and independent of $X$ and $W$, and $e\left(x\right)=\mathbb{P}\left(W=1|X=x\right)$ is the propensity score.

The fundamental problem of causal inference is that for each unit in the training dataset, we observe either the potential outcome under control ($W_i=0$) or the potential outcome under treatment ($W_i=1$) but never both. Hence, we denote the observed data as

$$\mathcal{D}={\left(Y_i,X_i,W_i\right)}_{1\le i\le N},$$

with $Y_i=Y_i\left(W_i\right)$. Note that the distribution of $\mathcal{D}$ is specified by $\mathcal{P}$. To avoid the problem that, with a small but nonzero probability all units are under control or under treatment, we will analyze the behavior of different estimators conditional on the number of treated units. That is, for a fixed $n$ with $0<n<N$, we condition on the event that

$$\sum _{i=1}^N{W}_i=n.$$

This will enable us to state the performance of an estimator in terms of the number of treated units $n$ and the number of control units $m=N-n$.

For a new unit $i$ with covariate vector $x_i$, to decide whether to give the unit the treatment, we wish to estimate the ITE of unit $i$, $D_i$, which is defined as

$$D_i\hspace{0.17em}≔\hspace{0.17em}{Y}_i\left(1\right)-Y_i\left(0\right).$$

However, we do not observe $D_i$ for any unit, and $D_i$ is not identifiable without strong additional assumptions in the sense that one can construct data-generating processes with the same distribution of the observed data, but a different $D_i$ (SI Appendix, Example SI1). Instead, we will estimate the CATE function, which is defined as

$$\tau \left(x\right)\hspace{0.17em}≔\hspace{0.17em}\mathbb{E}\left[D|X=x\right]=\mathbb{E}\left[Y\left(1\right)-Y\left(0\right)|X=x\right],$$

and we note that the best estimator for the CATE is also the best estimator for the ITE in terms of the mean squared error (MSE). To see that, let ${\widehat{\tau }}_i$ be an estimator for $D_i$ and decompose the MSE at $x_i$

$$\begin{array}{cc}\hfill \mathbb{E}& \left[{\left(D_i-{\widehat{\tau }}_i\right)}^2|X_i=x_i\right]=\mathbb{E}\left[{\left(D_i-\tau \left(x_i\right)\right)}^2|X_i=x_i\right]\hfill \\ \hfill & +\mathbb{E}\left[{\left(\tau \left(x_i\right)-{\widehat{\tau }}_i\right)}^2\right].\hfill \end{array}$$ [2]

Since we cannot influence the first term in the last expression, the estimator that minimizes the MSE for the ITE of $i$ also minimizes the MSE for the CATE at $x_i$.

In this work, we are interested in estimators with a small expected mean squared error (EMSE) for estimating the CATE,

$$\text{EMSE}\left(\mathcal{P},\widehat{\tau }\right)=\mathbb{E}\left[{\left(\tau \left(\mathcal{X}\right)-\widehat{\tau }\left(\mathcal{X}\right)\right)}^2\right].$$

The expectation is here taken over $\widehat{\tau }$ and $\mathcal{X}\sim \mathrm{\Lambda }$, where $\mathcal{X}$ is independent of $\widehat{\tau }$.

To aid our ability to estimate $\tau$, we need to assume that there are no hidden confounders (13):

Condition 1:

$$\left(\epsilon \left(0\right),\epsilon \left(1\right)\right)\hspace{0.17em}\perp \hspace{0.17em}W|X.$$

This assumption is, however, not sufficient to identify the CATE. One additional assumption that is often made to obtain identifiability of the CATE in the support of $X$ is to assume that the propensity score is bounded away from 0 and 1.

Condition 2:

There exists $e_{min}$ and $e_{max}$, such that for all $x$ in the support of $X$,

$$0<e_{min}<e\left(x\right)<e_{max}<1.$$

Metaalgorithms

In this section, we formally define a metaalgorithm (or metalearner) for the CATE as the result of combining supervised learning or regression estimators (i.e., base learners) in a specific manner while allowing the base learners to take any form. Metaalgorithms thus have the flexibility to appropriately leverage different sources of prior information in separate subproblems of the CATE estimation problem: They can be chosen to fit a particular type of data, and they can directly take advantage of existing data-analysis pipelines.

We first review both S- and T-learners, and we then propose the X-learner, which is a metaalgorithm that can take advantage of unbalanced designs (i.e., the control or the treated group is much larger than the other group) and existing structures of the CATE (e.g., smoothness or sparsity). Obviously, flexibility is a gain only if the base learners in the metaalgorithm match the features of the data and the underlying model well.

The T-learner takes two steps. First, the control response function,

$${\mu }_0\left(x\right)=\mathbb{E}\left[Y\left(0\right)|X=x\right],$$

is estimated by a base learner, which could be any supervised learning or regression estimator using the observations in the control group, ${\left\{\left(X_i,Y_i\right)\right\}}_{W_i=0}$. We denote the estimated function as ${\widehat{\mu }}_0$. Second, we estimate the treatment response function,

$${\mu }_1\left(x\right)=\mathbb{E}\left[Y\left(1\right)|X=x\right],$$

with a potentially different base learner, using the treated observations and denoting the estimator by ${\widehat{\mu }}_1$. A T-learner is then obtained as

$${\widehat{\tau }}_T\left(x\right)={\widehat{\mu }}_1\left(x\right)-{\widehat{\mu }}_0\left(x\right).$$ [3]

Pseudocode for this T-learner can be found in SI Appendix, Algorithm SI1.

In the S-learner, the treatment indicator is included as a feature similar to all of the other features without the indicator being given any special role. We thus estimate the combined response function,

$$\mu \left(x,w\right)\hspace{0.17em}≔\hspace{0.17em}\mathbb{E}\left[Y^{obs}|X=x,W=w\right],$$

using any base learner (supervised machine learning or regression algorithm) on the entire dataset. We denote the estimator as $\widehat{\mu }$. The CATE estimator is then given by

$${\widehat{\tau }}_S\left(x\right)=\widehat{\mu }\left(x,1\right)-\widehat{\mu }\left(x,0\right),$$ [4]

and pseudocode is provided in SI Appendix, Algorithm SI2.

There are other metaalgorithms in the literature, but we do not discuss them here in detail because of limited space. For example, one may transform the outcomes so that any regression method can estimate the CATE directly (SI Appendix, Algorithm SI4) (4, 14, 15). In our simulations, this algorithm performs poorly, and we do not discuss it further, but it may do well in other settings.

X-Learner.

We propose the X-learner and provide an illustrative example to highlight its motivations. The basic idea of the X-learner can be described in three stages:

• 1.Estimate the response functions

$${\mu }_0\left(x\right)=\mathbb{E}\left[\hspace{0.17em}Y\left(0\right)|X=x\right],\text{and}$$ [5]

$${\mu }_1\left(x\right)=\mathbb{E}\left[\hspace{0.17em}Y\left(1\right)|X=x\right],$$ [6]

• using any supervised learning or regression algorithm and denote the estimated functions ${\widehat{\mu }}_0$ and ${\widehat{\mu }}_1$. The algorithms used are referred to as the base learners for the first stage.

• 2.Impute the treatment effects for the individuals in the treated group, based on the control-outcome estimator, and the treatment effects for the individuals in the control group, based on the treatment-outcome estimator. That is, we define

$${\tilde{D}}_i^1\hspace{0.17em}≔\hspace{0.17em}{Y}_i^1-{\widehat{\mu }}_0\left(X_i^1\right),\text{and}$$ [7]

$${\tilde{D}}_i^0\hspace{0.17em}≔\hspace{0.17em}{\widehat{\mu }}_1\left(X_i^0\right)-Y_i^0,$$ [8]

• and we call these the imputed treatment effects. Note that if ${\widehat{\mu }}_0={\mu }_0$ and ${\widehat{\mu }}_1={\mu }_1$, then $\tau \left(x\right)=\mathbb{E}\left[{\tilde{D}}^1|X=x\right]=\mathbb{E}\left[{\tilde{D}}^0|X=x\right]$.

• Use any supervised learning or regression method(s) to estimate $\tau \left(x\right)$ in two ways: using the imputed treatment effects as the response variable in the treatment group to obtain ${\widehat{\tau }}_1\left(x\right)$ and similarly in the control group to obtain ${\widehat{\tau }}_0\left(x\right)$. Call the supervised learning or regression algorithms base learners of the second stage.

• 3.Define the CATE estimate by a weighted average of the two estimates in stage 2:

$$\widehat{\tau }\left(x\right)=g\left(x\right){\widehat{\tau }}_0\left(x\right)+\left(1-g\left(x\right)\right){\widehat{\tau }}_1\left(x\right),$$ [9]

• where $g\in \left[\mathrm{0,1}\right]$ is a weight function.

See SI Appendix, Algorithm SI3 for pseudocode.

Remark 1:

${\widehat{\tau }}_0$ and ${\widehat{\tau }}_1$ are both estimators for $\tau$, while $g$ is chosen to combine these estimators to one improved estimator $\widehat{\tau }$. Based on our experience, we observe that it is good to use an estimate of the propensity score for $g$, so that $g=ê$, but it also makes sense to choose $g=1$ or 0, if the number of treated units is very large or small compared with the number of control units. For some estimators, it might even be possible to estimate the covariance matrix of ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_0$. One may then wish to choose $g$ to minimize the variance of $\widehat{\tau }$.

Intuition Behind the Metalearners.

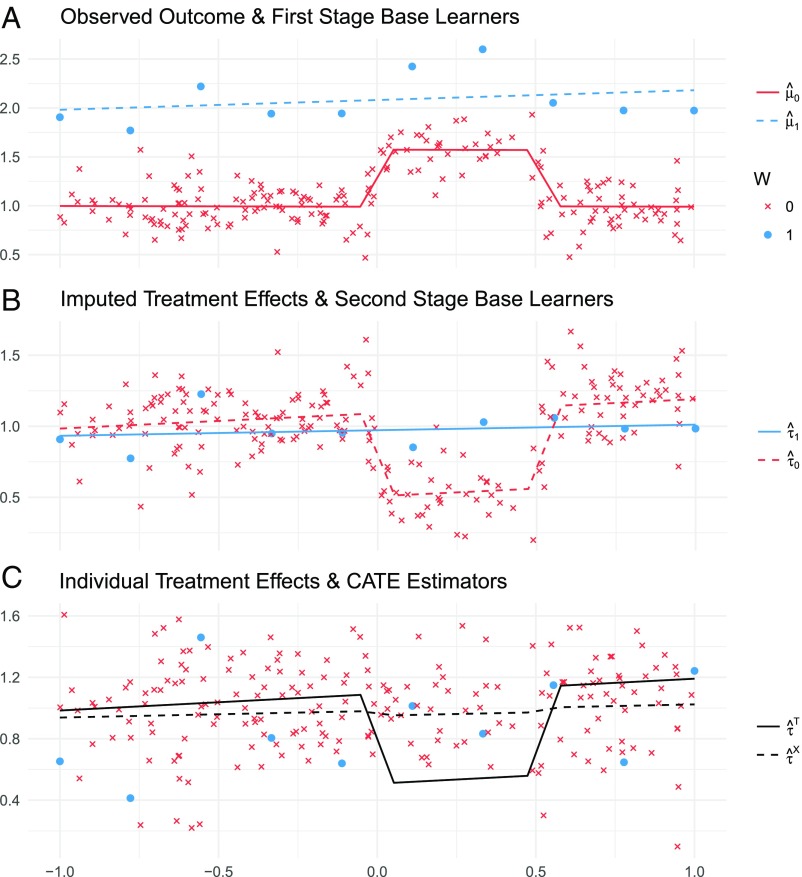
The X-learner can use information from the control group to derive better estimators for the treatment group and vice versa. We will illustrate this using a simple example. Suppose that we want to study a treatment, and we are interested in estimating the CATE as a function of one covariate $x$. We observe, however, very few units in the treatment group and many units in the control group. This situation often arises with the growth of administrative and online data sources: Data on control units are often far more plentiful than data on treated units. Fig. 1A shows the outcome for units in the treatment group (circles) and the outcome of units in the untreated group (crosses). In this example, the CATE is constant and equal to one.

Fig. 1.

Intuition behind the X-learner with an unbalanced design. (A) Observed outcome and first-stage base learners. (B) Imputed treatment effects and second-stage base learners. (C) ITEs and CATE estimators.

For the moment, let us look only at the treated outcome. When we estimate ${\mu }_1\left(x\right)=\mathbb{E}\left[Y\left(1\right)|X=x\right]$, we must be careful not to overfit the data since we observe only 10 data points. We might decide to use a linear model, ${\widehat{\mu }}_1\left(x\right)$ (dashed line) to estimate ${\mu }_1$. For the control group, we noticed that observations with $x\in \left[\mathrm{0,0.5}\right]$ seemed to be different, and we ended up modeling ${\mu }_0\left(x\right)=\mathbb{E}\left[Y\left(0\right)|X=x\right]$ with a piecewise linear function with jumps at 0 and 0.5 (solid line). This is a relatively complex function, but we are not worried about overfitting since we observe many data points.

The T-learner would now use estimator ${\widehat{\tau }}_T\left(x\right)={\widehat{\mu }}_1\left(x\right)-{\widehat{\mu }}_0\left(x\right)$ (Fig. 1C, solid line), which is a relatively complicated function with jumps at 0 and 0.5, while the true $\tau \left(x\right)$ is a constant. This is, however, problematic because we are estimating a complex CATE function, based on 10 observations in the treated group.

When choosing an estimator for the treatment group, we correctly avoided overfitting, and we found a good estimator for the treatment-response function, and, as a result, we chose a relatively complex estimator for the CATE, namely, the quantity of interest. We could have selected a piecewise linear function with jumps at 0 and 0.5, but this, of course, would have been unreasonable when looking only at the treated group. If, however, we were to also take the control group into account, this function would be a natural choice. In other words, we should change our objective for ${\widehat{\mu }}_1$ and ${\widehat{\mu }}_0$. We want to estimate ${\widehat{\mu }}_1$ and ${\widehat{\mu }}_0$ in such a way that their difference is a good estimator for $\tau$.

The X-learner enabled us to do exactly that. It allowed us to use structural information about the CATE to make efficient use of an unbalanced design. The first stage of the X-learner is the same as the first stage of the T-learner, but in its second stage, the estimator for the controls is subtracted from the observed treated outcomes, and, similarly, the observed control outcomes are subtracted from estimated treatment outcomes to obtain the imputed treatment effects,

$$\begin{array}{cc}\hfill {\tilde{D}}_i^1& \hspace{0.17em}≔\hspace{0.17em}{Y}_i^1-{\widehat{\mu }}_0\left(X_i^1\right),\hfill \\ \hfill {\tilde{D}}_i^0& \hspace{0.17em}≔\hspace{0.17em}{\widehat{\mu }}_1\left(X_i^0\right)-Y_i^0.\hfill \end{array}$$

Here, we used the notation that $Y_i^0$ and $Y_i^1$ are the $i$th observed outcome of the control and the treated group, respectively. $X_i^1$, $X_i^0$ are the corresponding feature vectors. Fig. 1B shows the imputed treatment effects, $\tilde{D}$. By choosing a simple—here, linear—function to estimate ${\tau }_1\left(x\right)=\mathbb{E}\left[{\tilde{D}}^1|X^1=x\right]$, we effectively estimated a model for ${\mu }_1\left(x\right)=\mathbb{E}\left[Y^1|X^1=x\right]$, which has a similar shape to ${\widehat{\mu }}_0$. By choosing a relatively poor model for ${\mu }_1\left(x\right)$, ${\tilde{D}}^0$ (the red crosses in Fig. 1B) are relatively far away from $\tau \left(x\right)$, which is constant and equal to 1. The model for ${\tau }_0\left(x\right)=\mathbb{E}\left[{\tilde{D}}^0|X=x\right]$ will thus be relatively poor. However, our final estimator combines these two estimators according to

$$\widehat{\tau }\left(x\right)=g\left(x\right){\widehat{\tau }}_0\left(x\right)+\left(1-g\left(x\right)\right){\widehat{\tau }}_1\left(x\right).$$

If we choose $g\left(x\right)=ê\left(x\right)$, an estimator for the propensity score, $\widehat{\tau }$ will be very similar to ${\widehat{\tau }}_1\left(x\right)$, since we have many more observations in the control group; i.e., $ê\left(x\right)$ is small. Fig. 1C shows the T-learner and the X-learner.

It is difficult to assess the general behavior of the S-learner in this example because we must choose a base learner. For example, when we use RF as the base learner for this dataset, the S-learner’s first split is on the treatment indicator in 97.5% of all trees in our simulations because the treatment assignment is very predictive of the observed outcome, $Y$ (see also SI Appendix, Fig. S10). From there on, the S- and T-learner were the same, and we observed them to perform similarly poorly in this example.

Simulation Results

In this section, we conducted a broad simulation study to compare the different metalearners. In particular, we summarize our findings and provide general remarks on the strengths and weaknesses of the S-, T-, and X-learners, while deferring the details to SI Appendix. The simulations are key to providing an understanding of the performance of the methods we consider for model classes that are not covered by our theoretical results.

Our simulation study is designed to consider a range of situations. We include conditions under which the S- or T-learner is likely to perform the best, as well as simulation setups proposed by previous researchers (8). We consider cases where the treatment effect is zero for all units (and so pooling the treatment and control groups would be beneficial) and cases where the treatment and control response functions are completely different (and so pooling would be harmful). We consider cases with and without confounding* and cases with equal and unequal sample sizes across treatment conditions. All simulations discussed in this section are based on synthetic data. For details, please see SI Appendix, section SI1. We provide additional simulations based on actual data when we discuss our applications.

We compared the S-, T-, and X-learners with RF and BART as base learners. We implemented a version of RF for which the tree structure is independent of the leaf prediction given the observed features, the so-called honest RF in an R package called hte (16). This version of RF is particularly accessible from a theoretical point of view; it performs well in noisy settings; and it is better suited for inference (8, 17). For BART, our software used the dbarts (18) implementation for the base learner.

Comparing different base learners enabled us to demonstrate two things. On the one hand, it shows that the conclusions we draw about the S-, T-, and X-learner are not specific to a particular base learner, and, on the other hand, it demonstrates that the choice of base learners can make a large difference in prediction accuracy. The latter is an important advantage of metalearners since subject knowledge can be used to choose base learners that perform well. For example, in SI Appendix, Simulations SI2 and SI4, the response functions are globally linear, and we observe that estimators that act globally such as BART have a significant advantage in these situations or when the dataset is small. If, however, there is no global structure or when the dataset is large, then more local estimators such as RF seem to have an advantage (SI Appendix, Simulations SI3 and SI5).

We observe that the choice of metalearner can make a large difference, and, for each metalearner, there exist cases where it is the best-performing estimator.

The S-learner treats the treatment indicator like any other predictor. For some base learners, such as $k$-nearest neighbors, it is not a sensible estimator, but for others, it can perform well. Since the treatment indicator is given no special role, algorithms such as the lasso and RFs can completely ignore the treatment assignment by not choosing/splitting on it. This is beneficial if the CATE is in many places 0 (SI Appendix, Simulations SI4 and SI5), but—as we will see in our second data example—the S-learner can be biased toward 0.

The T-learner, on the other hand, does not combine the treated and control groups. This can be a disadvantage when the treatment effect is simple because, by not pooling the data, it is more difficult for the T-learner to mimic a behavior that appears in both the control- and treatment-response functions (e.g., SI Appendix, Simulation SI4). If, however, the treatment effect is very complicated, and there are no common trends in ${\mu }_0$ and ${\mu }_1$, then the T-learner performs especially well (SI Appendix, Simulations SI2 and SI3).

The X-learner performs particularly well when there are structural assumptions on the CATE or when one of the treatment groups is much larger than the other (SI Appendix, Simulations SI1 and SI2). In the case where the CATE is 0, it usually does not perform as well as the S-learner, but it is significantly better than the T-learner (SI Appendix, Simulations SI4–6), and in the case of a very complex CATE, it performs better than the S-learner, and it often outperforms even the T-learner (SI Appendix, Simulations SI2 and SI3). These simulation results lead us to the conclusion that, unless one has a strong belief that the CATE is mostly 0, then, as a rule of thumb, one should use the X-learner with BART for small datasets and RF for bigger ones. In the sequel, we will further support these claims with additional theoretical results and empirical evidence from real data and data-inspired simulations.

Comparison of Convergence Rates.

In this section, we provide conditions under which the X-learner can be proven to outperform the T-learner in terms of pointwise estimation rate. These results can be viewed as attempts to rigorously formulate intuitions regarding when the X-learner is desirable. They corroborate our intuition that the X-learner outperforms the T-learner when one group is much larger than the other group and when the CATE function has a simpler form than those of the underlying response functions themselves.

Let us start by reviewing some of the basic results in the field of minimax nonparametric regression estimation (19). In the standard regression problem, one observes $N$ independent and identically distributed tuples ${\left(X_i,Y_i\right)}_i\in {\mathbb{R}}^{d\times N}\times {\mathbb{R}}^N$ generated from some distribution $\mathcal{P}$, and one is interested in estimating the conditional expectation of $Y$ given some feature vector $x$, $\mu \left(x\right)=\mathbb{E}\left[Y|X=x\right]$. The error of an estimator ${\widehat{\mu }}_N$ can be evaluated by the EMSE,

$$\text{EMSE}\left(\mathcal{P},{\widehat{\mu }}_N\right)=\mathbb{E}\left[{\left({\widehat{\mu }}_N\left(\mathcal{X}\right)-\mu \left(\mathcal{X}\right)\right)}^2\right].$$

For a fixed $\mathcal{P}$, there are always estimators that have a very small EMSE. For example, choosing ${\widehat{\mu }}_N\equiv \mu$ would have no error. However, $\mathcal{P}$, and thus $\mu$ would be unknown. Instead, one usually wants to find an estimator that achieves a small EMSE for a relevant set of distributions (such a set is relevant if it captures domain knowledge or prior information about the problem). To make this problem feasible, a typical approach is the minimax approach, where one analyzes the worst performance of an estimator over a family, $F$, of distributions (20). The goal is to find an estimator that has a small EMSE for all distributions in this family. For example, if $F_0$ is the family of distributions $\mathcal{P}$ such that $X\sim \text{Unif}\left[\mathrm{0,1}\right]$, $Y=\beta X+\epsilon$, $\epsilon \sim N\left(\mathrm{0,1}\right)$, and $\beta \in \mathbb{R}$, then it is well known that the ordinary least squares (OLS) estimator achieves the optimal parametric rate. That is, there exists a constant $C\in \mathbb{R}$ such that for all $\mathcal{P}\in F_0$,

$$\text{EMSE}\left(\mathcal{P},{\widehat{\mu }}_N^{\text{OLS}}\right)\le C{N}^{-1}.$$

If, however, $F_1$ is the family of all distributions $\mathcal{P}$ such that $X\sim \text{Unif}\left[\mathrm{0,1}\right]$, $Y\sim \mu \left(X\right)+\epsilon$, and $\mu$ is a Lipschitz continuous function with a bounded Lipschitz constant, then there exists no estimator that achieves the parametric rate uniformly for all possible distributions in $F_1$. To be precise, we can at most expect to find an estimator that achieves a rate of $N^{-2/3}$ and that there exists a constant $C\prime$, such that

$$\underset{N\to \infty }{liminf}\underset{{\widehat{\mu }}_N}{inf}\underset{\mathcal{P}\in F_1}{sup}\frac{\text{EMSE}\left(\mathcal{P},{\widehat{\mu }}_N\right)}{N^{-2/3}}>C\prime >0.$$

The Nadaraya–Watson and the $k$-nearest neighbors estimators can achieve this optimal rate (19, 21).

Crucially, the fastest rate of convergence that holds uniformly for a family $F$ is a property of the family to which the underlying data-generating distribution belongs. It will be useful for us to define sets of families for which particular rates are achieved.

Definition 1 (families with bounded minimax rate):

For $a\in \left(\mathrm{0,1}\right]$, we define $S\left(a\right)$ to be the set of all families, $F$, with a minimax rate of at most $N^{-a}$.

Note that for any family $F\in S\left(a\right)$, there exists an estimator $\widehat{\mu }$ and a constant $C$ such that for all $N\ge 1$,

$$\underset{\mathcal{P}\in F}{sup}\text{EMSE}\left(\mathcal{P},{\widehat{\mu }}_N\right)\le C{N}^{-a}.$$

From the examples above, it is clear that $F_0\in S\left(1\right)$ and $F_1\in S\left(2/3\right)$.

Even though the minimax rate of the EMSE is not very practical since one rarely knows that the true data-generating process is in some reasonable family of distributions, it is nevertheless one of the very few useful theoretical tools to compare different nonparametric estimators. If for a big class of distributions, the worst EMSE of an estimator ${\widehat{\mu }}^A$ is smaller than the worst EMSE of an estimator ${\widehat{\mu }}^B$, then one might prefer estimator ${\widehat{\mu }}^A$ over estimator ${\widehat{\mu }}^B$. Furthermore, if the estimator of choice does not have a small error for a family that we believe based on domain information could be relevant in practice, then we might expect $\widehat{\mu }$ to have a large EMSE in real data.

Implication for CATE Estimation.

Let us now apply the minimax approach to the problem of estimating the CATE. Recall that we assume a superpopulation, $\mathcal{P}$, of random variables $\left(Y\left(0\right),Y\left(1\right),X,W\right)$ according to [1], and we observe $N$ outcomes, ${\left(X_i,W_i,Y_i^{obs}\right)}_{i=1}^N$. To avoid the problem that with a small but nonzero probability all units are treated or untreated, we analyze the EMSE of an estimator given that there are $0<n<N$ treated units,

$$\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}^{mn}\right)=\mathbb{E}\left[{\left(\tau \left(\mathcal{X}\right)-{\widehat{\tau }}^{mn}\left(\mathcal{X}\right)\right)}^2|\sum _{i=1}^N{W}_i=n\right].$$

The expectation is taken over the observed data,^† ${\left(X_i,W_i,Y_i\right)}_{i=1}^N$, given that we observe $n$ treated units, and over $\mathcal{X}$, which is distributed according to $\mathcal{P}$.

As in Definition 1, we characterize families of superpopulations by the rates at which the response functions and the CATE function can be estimated.

Definition 2 (superpopulations with given rates):

For $a_{\mu },a_{\tau }\in \left(\mathrm{0,1}\right]$, we define $S\left(a_{\mu },a_{\tau }\right)$ to be the set of all families of distributions $\mathcal{P}$ of $\left(Y\left(0\right),Y\left(1\right),X,W\right)$ such that ignorability holds (Condition 1), the overlab condition (Condition 2) is satisfied, and the following conditions hold:

• 1.The distribution of $\left(X,Y\left(0\right)\right)$ given $W=0$ is in a family $F_0\in S\left(a_{\mu }\right)$;
• 2.The distribution of $\left(X,Y\left(1\right)\right)$ given $W=1$ is in a family $F_1\in S\left(a_{\mu }\right)$;
• 3.The distribution of $\left(X,{\mu }_1\left(X\right)-Y\left(0\right)\right)$ given $W=0$ is in a family $F_{\tau 0}\in S\left(a_{\tau }\right)$; and
• 4.The distribution of $\left(X,Y\left(1\right)-{\mu }_0\left(X\right)\right)$ given $W=1$ is in a family $F_{\tau 1}\in S\left(a_{\tau }\right)$.

A simple example of a family in $S\left(2/\mathrm{3,1}\right)$ is the set of distributions $\mathcal{P}$ for which $X\sim \text{Unif}\left(\left[\mathrm{0,1}\right]\right)$, $W\sim \text{Bern}\left(1/2\right)$, ${\mu }_0$ is any Lipschitz continuous function, $\tau$ is linear, and $\epsilon \left(0\right),\epsilon \left(1\right)$ are independent and standard normal-distributed.

We can also build on existing results from the literature to characterize many families in terms of smoothness conditions on the CATE and on the response functions.

Example 1:

Let $C>0$ be an arbitrary constant and consider the family, $F_2$, of distributions for which $X$ has compact support in ${\mathbb{R}}^d$, the propensity score $e$ is bounded away from 0 and 1 (Condition 2), ${\mu }_0,{\mu }_1$ are $C$ Lipschitz continuous, and the variance of $\epsilon$ is bounded. Then it follows (19) that

$$F_2\in S\left(\frac{2d}{2+d},\frac{2d}{2+d}\right).$$

Note that we don’t have any assumptions on $X$, apart from its support being bounded. If we are willing to make assumptions on the density (e.g., $X$ is uniformly distributed), then we can characterize many distributions by the smoothness conditions of ${\mu }_0$, ${\mu }_1$, and $\tau$.

Definition 3 [$\left(\mathit{p},\mathit{C}\right)$ -smooth functions (19)]:

Let $p=k+\beta$ for some $k\in \mathbb{N}$ and $0<\beta \le 1$, and let $C>0$. A function $f:{\mathbb{R}}^d\to \mathbb{R}$ is called $\left(p,C\right)$ -smooth if for every $\alpha =\left({\alpha }_1,\dots ,{\alpha }_d\right)$, ${\alpha }_i\in \mathbb{N}$, ${\sum }_{j=1}^d{\alpha }_j=k$, the partial derivative $\frac{{\partial }^{k}f}{\partial x_1^{{\alpha }_1}\dots \partial x_d^{{\alpha }_d}}$ exists and satisfies

$$\left|\frac{{\partial }^{k}f}{\partial x_1^{{\alpha }_1}\dots \partial x_d^{{\alpha }_d}}\left(x\right)-\frac{{\partial }^{k}f}{\partial x_1^{{\alpha }_1}\dots \partial x_d^{{\alpha }_d}}\left(z\right)\right|\le C{\Vert x-z\Vert }^{\beta }.$$

Example 2:

Let $C_1,C_2$ be arbitrary constants and consider the family, $F_3$, of distributions for which $X\sim \text{Unif}\left({\left[\mathrm{0,1}\right]}^d\right)$, $e\equiv c\in \left(\mathrm{0,1}\right)$, $\epsilon$ is 2D normally distributed, ${\mu }_0$ and ${\mu }_1$ are $\left(p_{\mu },C_1\right)$-smooth, and $\tau$ is $\left(p_{\tau },C_2\right)$-smooth.^‡ Then it follows (19, 24) that

$$F_3\in S\left(\frac{2d}{2p_{\mu }+d},\frac{2d}{2p_{\tau }+d}\right).$$

Let us intuitively understand the difference between the T- and X-learners. The T-learner splits the problem of estimating the CATE into the two subproblems of estimating ${\mu }_0$ and ${\mu }_1$ separately. By appropriately choosing the base learners, we can expect to achieve the minimax optimal rates of $m^{-a_{\mu }}$ and $n^{-a_{\mu }}$, respectively,

$$\begin{array}{cccc}\hfill & \underset{{\mathcal{P}}_0\in F_0}{sup}\text{EMSE}\left({\mathcal{P}}_0,{\widehat{\mu }}_0^m\right)\le C{m}^{-a_{\mu }},\hfill & \hfill & \text{and}\hfill \\ \hfill & \underset{{\mathcal{P}}_1\in F_1}{sup}\text{EMSE}\left({\mathcal{P}}_1,{\widehat{\mu }}_1^n\right)\hspace{0.17em}\le C{n}^{-a_{\mu }},\hfill \end{array}$$ [10]

where $C$ is some constant. Those rates translate immediately to rates for estimating $\tau$,

$$\underset{\mathcal{P}\in F}{sup}\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}_T^{nm}\right)\le C_{\tau }\left(m^{-a_{\mu }}+n^{-a_{\mu }}\right).$$

In general, we cannot expect to do better than this when using an estimation strategy that falls in the class of T-learners, because the subproblems in Eq. 10 are treated completely independently, and there is nothing to be learned from the treatment group about the control group and vice versa.

In SI Appendix, section SI8, we present a careful analysis of this result, and we prove the following theorem.

Theorem 1 (Minimax Rates of the T-Learner).

For a family of superpopulations, $F\in S\left(a_{\mu },a_{\tau }\right)$, there exist base learners to be used in the T-learner so that the corresponding T-learner estimates the CATE at a rate

$$\mathcal{O}\left(m^{-a_{\mu }}+n^{-a_{\mu }}\right).$$ [11]

The X-learner, on the other hand, can be seen as a locally weighted average of the two estimators, ${\widehat{\tau }}_0$ and ${\widehat{\tau }}_1$ (Eq. 9). Take, for the moment, ${\widehat{\tau }}_1$. It consists of an estimator for the outcome under control, which achieves a rate of $m^{-a_{\mu }}$, and an estimator for the imputed treatment effects, which should intuitively achieve a rate of $n^{-a_{\tau }}$. We therefore expect that under some conditions on $F\in S\left(a_{\mu },a_{\tau }\right)$, there exist base learners such that ${\widehat{\tau }}_0$ and ${\widehat{\tau }}_1$ in the X-learner achieve the rates

$$\mathcal{O}\left(m^{-a_{\tau }}+n^{-a_{\mu }}\right)\text{and}\mathcal{O}\left(m^{-a_{\mu }}+n^{-a_{\tau }}\right),$$ [12]

respectively.

Even though it is theoretically possible that $a_{\tau }$ is similar to $a_{\mu }$, our experience with real data suggests that it is often larger (i.e., the treatment effect is simpler to estimate than the potential outcomes), because the CATE function is often smoother or sparsely related to the feature vector. In this case, the X-learner converges at a faster rate than the T-learner.

Remark 2 (unbalanced groups):

In many real-world applications, we observe that the number of control units is much larger than the number of treated units, $m\gg n$. This happens, for example, if we test a new treatment and we have a large number of previous (untreated) observations that can be used as the control group. In that case, the bound on the EMSE of the T-learner will be dominated by the regression problem for the treated response function,

$$\underset{\mathcal{P}\in F}{sup}\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}_T^{nm}\right)\le C_1{n}^{-a_{\mu }}.$$ [13]

The EMSE of the X-learner, however, will be dominated by the regression problem for the imputed treatment effects and it will achieve a faster rate of $n^{-a_{\tau }}$,

$$\underset{\mathcal{P}\in F}{sup}\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}_X^{nm}\right)\le C_2{n}^{-a_{\tau }}.$$ [14]

This is a substantial improvement on [13] when $a_{\tau }>a_{\mu }$, and it demonstrates that, in contrast to the T-learner, the X-learner can exploit structural conditions on the treatment effect. We therefore expect the X-learner to perform particularly well when one of the treatment groups is larger than the other. This can also be seen in our extensive simulation study presented in SI Appendix, section SI1 and in the field experiment on social pressure on voter turnout presented in Applications.

Example When the CATE Is Linear.

It turns out to be mathematically very challenging to give a satisfying statement of the extra conditions needed on $F$ in [12]. However, they are satisfied under weak conditions when the CATE is Lipschitz continuous (cf. SI Appendix, section SI9.3) and, as we discuss in the rest of this section, when the CATE is linear. We emphasize that we believe that this result holds in much greater generality.

Let us discuss the result in the following families of distributions with a linear CATE, but without assumptions on the response functions other than that they can be estimated at some rate $a$.

Condition 3:

The treatment effect is linear, $\tau \left(x\right)=x^T\beta$, with $\beta \in {\mathbb{R}}^d$.

Condition 4:

There exists an estimator ${\widehat{\mu }}_0^m$ and constants $C_0,a>0$ with

$$\text{EMSE}\left(\mathcal{P},{\widehat{\mu }}_0^m\right)=\mathbb{E}\left[{\left({\mu }_0\left(X\right)-{\widehat{\mu }}_0^m\left(X\right)\right)}^2|W=0\right]\le C_0{m}^{-a}.$$

To help our analysis, we also assume that the noise terms are independent given $X$ and that the feature values are well behaved.

Condition 5:

The error terms ${\epsilon }_i$ are independent given $X$, with $\mathbb{E}\left[{\epsilon }_i|X=x\right]=0$ and $\text{Var}\left[{\epsilon }_i|X=x\right]\le {\sigma }^2$.

Condition 6:

$X$ has finite second moments,

$$\mathbb{E}\left[{\Vert X\Vert }_2^2\right]\le C_X,$$

and the eigenvalues of the sample covariance matrix of $X^1$ are well conditioned, in the sense that there exists an $n_0\in \mathbb{N}$ and a constant $C_{\mathrm{\Sigma }}\in \mathbb{R}$such that for all $n>n_0$,

$$\mathbb{P}\left({\gamma }_{\text{min}}^{-1}\left({\widehat{\mathrm{\Sigma }}}_n\right)\le C_{\mathrm{\Sigma }}\right)=1.$$ [15]

Under these conditions, we can prove that the X-learner achieves a rate of $O\left(m^{-a}+n^{-1}\right)$.

Theorem 2.

Assume that we observe $m$ control units and $n$ treated units from a superpopulation that satisfies Conditions 1–6; then ${\widehat{\tau }}_1$ of the X-learner with ${\widehat{\mu }}_0^m$ in the first stage and OLS in the second stage achieves a rate of $O\left(m^{-a}+n^{-1}\right)$. Specifically, for all $n>n_0,m>1$,

$$\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}_1^{mn}\right)\le C\left(m^{-a}+n^{-1}\right),$$

with $C=max\left(\frac{e_{max}-e_{max}{e}_{min}}{e_{min}-e_{max}{e}_{min}}{C}_0,{\sigma }^{2}d\right)C_X{C}_{\mathrm{\Sigma }}$.

We note that an equivalent statement also holds for the pointwise MSE (SI Appendix, Theorem SI2) and for ${\widehat{\tau }}_0$.

This example also supports Remark 2, because if there are many control units, $m\ge n^{1/a},$ then the X-learner achieves the parametric rate in $n$,

$$\text{EMSE}\left(\mathcal{P},{\widehat{\tau }}_1^{mn}\right)\le C{n}^{-1}.$$

In fact, as SI Appendix, Theorem SI3 shows, even if the number of control units is of the same order as the number of treated units, we can often achieve the parametric rate.

Applications

In this section, we consider two data examples. In the first example, we consider a large Get-Out-the-Vote experiment that explored if social pressure can be used to increase voter turnout in elections in the United States (1). In the second example, we consider an experiment that explored if door-to-door canvassing can be used to durably reduce transphobia in Miami (2). In both examples, the original authors failed to find evidence of heterogeneous treatment effects when using simple linear models without basis expansion, and subsequent researchers and policymakers have been acutely interested in treatment-effect heterogeneity that could be used to better target the interventions. We use our honest RF implementation (16) because of the importance of obtaining useful confidence intervals in these applications. Confidence intervals are obtained by using a bootstrap procedure (SI Appendix, Algorithm SI6). We have evaluated several bootstrap procedures, and we have found that the results for all of them were very similar. We explain this particular bootstrap choice in detail in SI Appendix, section SI3.

Social Pressure and Voter Turnout.

In a large field experiment, Gerber et al. (1) show that substantially higher turnout was observed among registered voters who received a mailing promising to publicize their turnout to their neighbors. In the United States, whether someone is registered to vote and their past voting turnout are a matter of public record. Of course, how individuals voted is private. The experiment has been highly influential both in the scholarly literature and in political practice. In our reanalysis, we focus on two treatment conditions: the control group, which was assigned to 191,243 individuals, and the “neighbors” treatment group, which was assigned to 38,218 individuals. Note the unequal sample sizes. The experiment was conducted in Michigan before the August 2006 primary election, which was a statewide election with a wide range of offices and proposals on the ballot. The authors randomly assigned households with registered voters to receive mailers. The outcome, whether someone voted, was observed in the primary election. The neighbors mailing opened with a message that states “DO YOUR CIVIC DUTY—VOTE!” It then continued by not only listing the household’s voting records but also the voting records of those living nearby. The mailer informed individuals that “we intend to mail an updated chart” after the primary.

The study consists of seven key individual-level covariates, most of which are discrete: gender, age, and whether the registered individual voted in the primary elections in 2000, 2002, and 2004 or the general election in 2000 and 2002. The sample was restricted to voters who had voted in the 2004 general election. The outcome of interest is turnout in the 2006 primary election, which is an indicator variable. Because compliance is not observed, all estimates are of the intention-to-treat effect, which is identified by the randomization. The ATE estimated by the authors is 0.081 with a SE of (0.003). Increasing voter turnout by 8.1% using a simple mailer is a substantive effect, especially considering that many individuals may never have seen the mailer.

Fig. 2 presents the estimated treatment effects, using X-RF where the potential voters are grouped by their voting history. Fig. 2, Upper shows the proportion of voters with a significant positive (blue) and a significant negative (red) CATE estimate. We can see that there is evidence of a negative backlash among a small number of people who voted only once in the past five elections before the general election in 2004. Applied researchers have observed a backlash from these mailers; e.g., some recipients called their Secretary of State’s office or local election registrar to complain (25, 26). Fig. 2, Lower shows the distribution of CATE estimates for each of the subgroups. Having estimates of the heterogeneity enables campaigns to better target the mailers in the future. For example, if the number of mailers is limited, one should target potential voters who voted three times during the past five elections, since this group has the highest ATE and it is a very big group of potential voters.^§

Fig. 2.

Social pressure and voter turnout. Potential voters are grouped by the number of elections they participated in, ranging from 0 (potential voters who did not vote during the past five elections) to 5 (voters who participated in all five past elections). The width of each group is proportional to the size of the group. (Upper) Positive values correspond to the percentage of voters for which the predicted CATE is significantly positive, while negative values correspond to the percentage of voters for which the predicted CATE is significantly negative. (Lower) The plot shows the CATE estimate distribution for each bin.

S-, T-, and X-RF all provide similar CATE estimates. This is unsurprising given the very large sample size, the small number of covariates, and their distributions. For example, the correlation between the CATE estimates of S- and T-RF is 0.99 (results for S- and T-RF can be found in SI Appendix, Fig. S9).

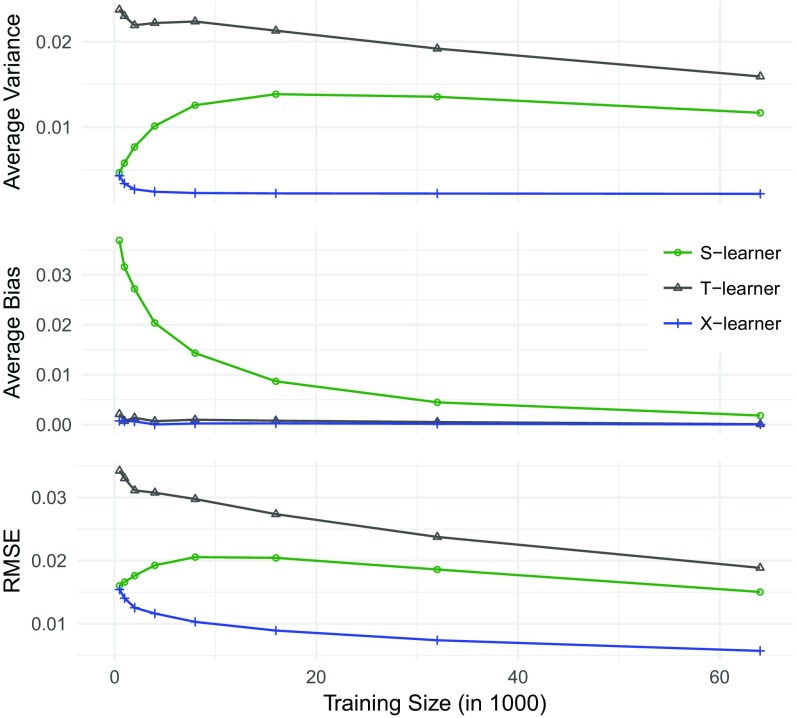
We conducted a data-inspired simulation study to see how these estimators would behave in smaller samples. We take the CATE estimates produced by T-RF, and we assume that they are the truth. We can then impute the potential outcomes under both treatment and control for every observation. We then sample training data from the complete data and predict the CATE estimates for the test data using S-, T-, and X-RF. We keep the unequal treatment proportion observed in the full data fixed—i.e., $\mathbb{P}\left(\hspace{0.17em}W=1\right)=0.167$. Fig. 3 presents the results of this simulation. They show that, in small samples, both X- and S-RF outperform T-RF, with X-RF performing the best, as one may conjecture, given the unequal sample sizes.

Fig. 3.

RMSE, bias, and variance for a simulation based on the social pressure and voter turnout experiment.

Reducing Transphobia: A Field Experiment on Door-to-Door Canvassing.

In an experiment that received widespread media attention, Broockman et al. (2, 27) show that brief (10 min) but high-quality door-to-door conversations can markedly reduce prejudice against gender-nonconforming individuals for at least 3 mo. There are important methodological differences between this example and our previous one. The experiment is a placebo-controlled experiment with a parallel survey that measures attitudes, which are the outcomes of interest. The authors follow the design of ref. 28. The authors first recruited registered voters (n = 68,378) via mail for an unrelated online survey to measure baseline outcomes. They then randomly assigned respondents of the baseline survey to either the treatment group ($n=913$) or the placebo group that was targeted with a conversation about recycling ($n=912$). Randomization was conducted at the household level (n = 1,295), and because the design uses a placebo control, the estimand of interest is the complier-average-treatment effect. Outcomes were measured by the online survey 3 d, 3 wk, 6 wk, and 3 mo after the door-to-door conversations. We analyze results for the first follow-up.

The final experimental sample consisted of only 501 observations. The experiment was well-powered despite its small sample size because it included a baseline survey of respondents as well as posttreatment surveys. The survey questions were designed to have high over-time stability. The ${\mathrm{R}}^2$ of regressing the outcomes of the placebo-control group on baseline covariates using OLS is 0.77. Therefore, covariate adjustment greatly reduces sampling variation. There are 26 baseline covariates that include basic demographics (gender, age, and ethnicity) and baseline measures of political and social attitudes and opinions about prejudice in general.

The authors find an ATE of 0.22 (SE: 0.072, t stat: 3.1) on their transgender tolerance scale.^¶ The scale is coded so that a larger number implies greater tolerance. The variance of the scale is 1.14, with a minimum observed value of −2.3 and a maximum of 2. This is a large effect given the scale. For example, the estimated decrease in transgender prejudice is greater than Americans’ average decrease in homophobia from 1998 to 2012, when both are measured as changes in standard deviations of their respective scales.

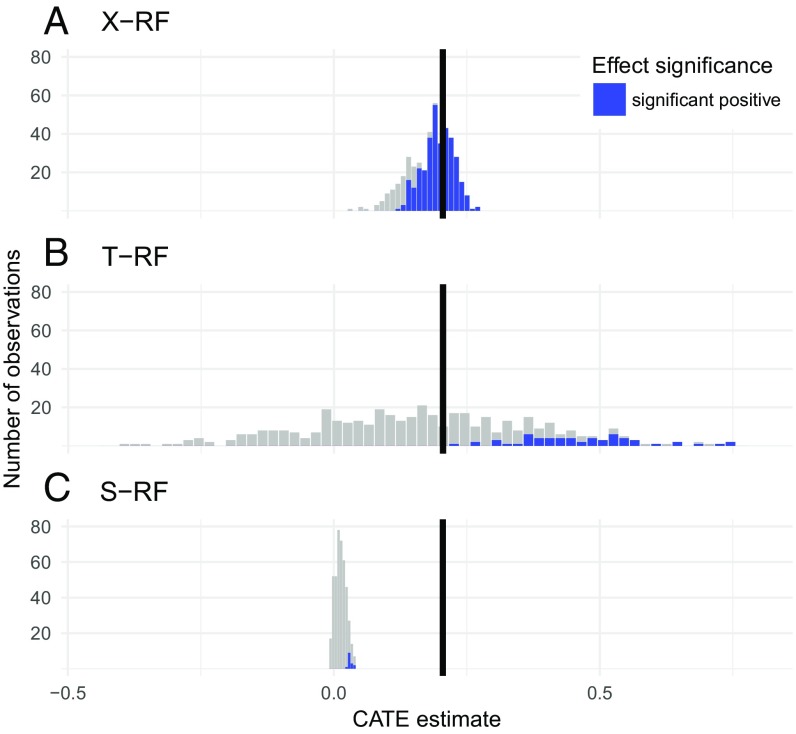
The authors report finding no evidence of heterogeneity in the treatment effect that can be explained by the observed covariates. Their analysis is based on linear models (OLS, lasso, and elastic net) without basis expansions.^∥ Fig. 4A presents our results for estimating the CATE, using X–RF. We find that there is strong evidence that the positive effect that the authors find is only found among a subset of respondents that can be targeted based on observed covariates. The average of our CATE estimates is within half a SD of the ATE that the authors report.

Fig. 4.

Histograms for the distribution of the CATE estimates in the Reducing Transphobia study. The horizontal line shows the position of the estimated ATE. (A) X-RF. (B) T-RF. (C) S-RF.

Unlike in our previous data example, there are marked differences in the treatment effects estimated by our three learners. Fig. 4B presents the estimates from T–RF. These estimates are similar to those of X-RF, but with a larger spread. Fig. 4C presents the estimates from S-RF. Note that the average CATE estimate of S-RF is much lower than the ATE reported by the original authors and the average CATE estimates of the other two learners. Almost none of the CATE estimates are significantly different from zero. Recall that the ATE in the experiment was estimated with precision and was large both substantively and statistically (t stat = 3.1).

In these data, S-RF shrinks the treatment estimates toward zero. The ordering of the estimates we see in this data application is what we have often observed in simulations: The S-learner has the least spread around zero, the T-learner has the largest spread, and the X-learner is somewhere in between. Unlike in the previous example, the covariates are strongly predictive of the outcomes, and the splits in the S-RF are mostly on the features rather than the treatment indicator, because they are more predictive of the observed outcomes than the treatment assignment (cf. SI Appendix, Fig. S10).

Conclusion

This paper reviewed metaalgorithms for CATE estimation including the S- and T-learners. It then introduced a metaalgorithm, the X-learner, that can translate any supervised learning or regression algorithm or a combination of such algorithms into a CATE estimator. The X-learner is adaptive to various settings. For example, both theory and data examples show that it performs particularly well when one of the treatment groups is much larger than the other or when the separate parts of the X-learner are able to exploit the structural properties of the response and treatment effect functions. Specifically, if the CATE function is linear, but the response functions in the treatment and control group satisfy only the Lipschitz-continuity condition, the X-learner can still achieve the parametric rate if one of the groups is much larger than the other (Theorem 2). If there are no regularity conditions on the CATE function and the response functions are Lipschitz continuous, then both the X- and T-learner obtain the same minimax optimal rate (SI Appendix, Theorem SI5). We conjecture that these results hold for more general model classes than those in our theorems.

We have presented a broad set of simulations to understand the finite sample behaviors of different implementations of these learners, especially for model classes that are not covered by our theoretical results. We have also examined two data applications. Although none of the metaalgorithms is always the best, the X-learner performs well overall, especially in the real-data examples. In practice, in finite samples, there will always be gains to be had if one accurately judges the underlying data-generating process. For example, if the treatment effect is simple, or even zero, then pooling the data across treatment and control conditions will be beneficial when estimating the response model (i.e., the S-learner will perform well). However, if the treatment effect is strongly heterogeneous and the response surfaces of the outcomes under treatment and control are very different, pooling the data will lead to worse finite sample performance (i.e., the T-learner will perform well). Other situations are possible and lead to different preferred estimators. For example, one could slightly change the S-learner so that it shrinks to the estimated ATE instead of zero, and it would then be preferred when the treatment effect is constant and nonzero. One hopes that the X-learner can adapt to these different settings. The simulations and real-data studies presented have demonstrated the X-learner’s adaptivity. However, further studies and experience with more real datasets are necessary. To enable practitioners to benchmark these learners on their own datasets, we have created an easy-to-use software library called hte. It implements several methods of selecting the best CATE estimator for a particular dataset, and it implements confidence-interval estimators for the CATE.