Artificial intelligence to support human instruction

The popular media’s recent interest in artificial intelligence (AI) has focused on autonomous systems that might ultimately replace people in fields as diverse as medicine, customer service, and transportation and logistics. Often neglected is a subfield of AI that focuses on empowering people by improving how we learn, remember, perceive, and make decisions. This human-centered focus relies on interdisciplinary research from cognitive neuroscience, psychology, and theoretical computer science.

The synergy among these fields promises to improve the microorganization of human instruction: picking the next exercise for a student to attempt, choosing what sort of hints and feedback to provide, determining when material should be reviewed, and selecting among teaching activities. These are decisions which occur on a granularity that human instructors are typically unable to monitor and individualize, and for which students have poor metacognitive strategies (1). Such microinstruction complements the strengths of human teachers and can yield significant benefits. For example, in a semester-long experiment integrated into a middle-school foreign language course, setting aside roughly 30 min per week for AI-guided personalized review of previously introduced material led to a 16.5% improvement in overall course retention on a cumulative examination administered a month after the end of the semester, relative to a time-matched control condition that reflects current educational practice (2).

In PNAS, Tabibian et al. (3) address the learning and retention of factual material such as foreign language vocabulary. They present an adaptive, data-driven method with theoretical guarantees for scheduling retrieval practice. Their work contributes to a growing body of results in algorithmic-education theory that proves properties of idealized mathematical models of educational scenarios (4–6).

Like every proposal for AI-based instruction, the approach of Tabibian et al. (3) is formalized by two models: student and teacher. The student model quantifies an individual’s current knowledge state and how it evolves based on instructional actions and the passage of time. The teacher model specifies a policy—in the control-theoretic sense—for administering instructional actions conditioned on the student model. Student models range from those motivated heavily by psychological theory (7–10) to those motivated primarily by mathematical elegance and tractability (4–6). Somewhere in the middle of this continuum are methods that mine corpora of educational data (11) to predict the influence of various teaching actions on the student’s subsequent performance (2, 12). Teacher models also lie along a continuum, from hand-constructed heuristic or expert-based approaches (2, 9, 13, 14) to those that provably optimize according to some criterion, such as the student model’s score on a postinstruction quiz (4, 15).

The ultimate aim in AI is to develop automated instruction methods based on the combination of a psychologically valid student model and a theoretically grounded teacher model. However, this goal has yet to be achieved. Research concerned with solving a tractable optimization problem has assumed a simplified student model; nonetheless, even with a naive or unrealistic student model, the formal nature of the work can provide intuitions and a deeper understanding of the computational issues. Conversely, the research most concerned with psychological fidelity of the student model has relied on heuristic teacher models; nonetheless, heuristic strategies often appear to be effective [e.g., Bjork’s (16) notion of desirable difficulty].

Tabibian et al. (3) identify a class of student models that admit a formal analysis yet are informed by human memory data. They characterize the student’s memory state in terms of stochastic differential equations with jumps: When the student reviews a particular item (e.g., a vocabulary word), the memory strength of the item is bumped up and then decays over time. Reviewing times for an item are specified via a temporal point process. The stochastic optimal control problem is to determine the point-process reviewing intensity, that is, the rate of retrieval practice, to maintain memory without excessive practice. Formally, the penalty function they optimize is quadratic in both recall failure rate and reviewing intensity. Their key result is a proof that the optimal reviewing intensity is proportional to the student model’s predicted probability of recall failure. Predicted recall probability has long been used as a heuristic measure for prioritizing material in flashcard-type schedulers, but Tabibian et al. (3) provide a compelling theoretical justification for the use of this heuristic.

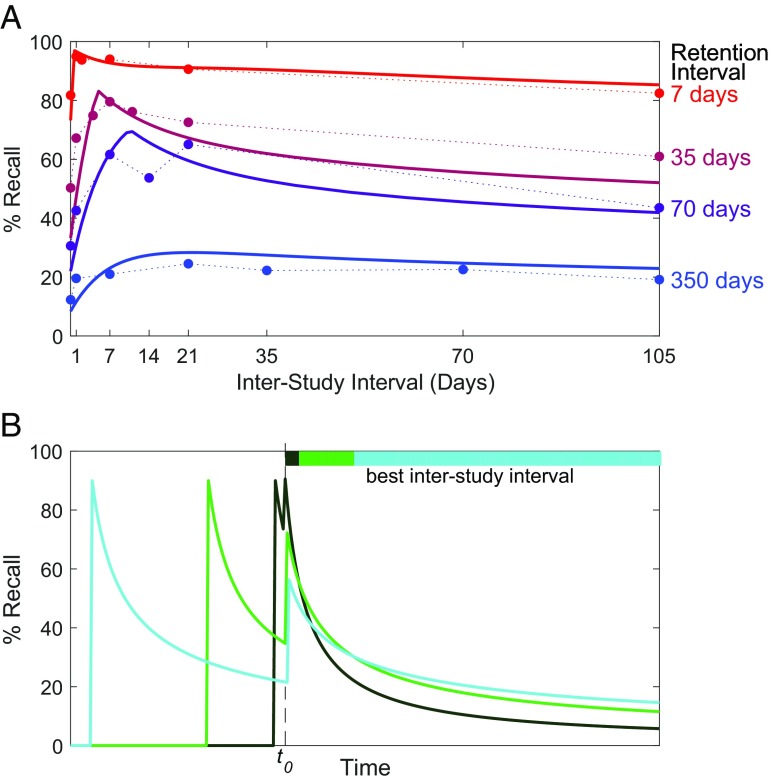
Tabibian et al.’s (3) claim that the benefit of review increases as memory decays is consonant with the spacing effect (17), the behavioral finding that temporally distributed practice leads to more robust and durable learning than massed practice. The spacing effect is often cast as “don’t cram for an examination.” Cramming can help students remember information on the examination; however, cramming also leads to rapid forgetting. The rate of forgetting is slowed by spaced practice. Fig. 1A presents results from an empirical study in which participants learned trivia facts in two sessions and were subsequently quizzed on the facts (18). In the first session, each item is practiced to criterion; in the second session, each item is practiced a fixed number of times. The lag between the first and second study sessions (the interstudy interval, ISI) is varied from minutes to 105 d, and the lag between the second study session and the quiz (the retention interval, RI) is varied from 7 to 350 d. The figure reveals an optimal ISI, and this optimum increases with the RI. This interaction between optimal ISI and RI is also found in big data corpora (19). The smooth curves in the figure are predictions from a psychological model (10). Fig. 1B shows hypothetical forgetting curves for various ISIs, consistent with the empirical results in Fig. 1A and psychological theories of the spacing effect (e.g., refs. 10 and 17).

Fig. 1.

(A) Recall accuracy at test for a given RI (7, 35, 70, or 350 d), after the learner has studied material over two sessions separated by a given ISI ($<$ to 105 d). Data points are from a human behavioral experiment (18). Solid lines are predictions of a cognitive model fit with one free parameter to the data (10). (B) Hypothetical memory strength curves consistent with experimental results in A. Each curve shows a sequence of two study sessions, aligned such that the second session of each sequence occurs at time $t_0$ (dashed line). For various $t>t_0$ (i.e., the RI $t-t_0$) the bars at the top of the graph indicate which ISI achieves the highest recall accuracy. The optimal spacing depends on the RI.

Whereas psychologists have focused on optimizing time of study given a fixed number of practice opportunities (Fig. 1A), or on prioritizing items for study given finite study time (2, 13, 14), Tabibian et al. (3) frame the challenge as determining the optimal (time-varying) reviewing rate per item. It may be unrealistic in an educational context to forego hard constraints on practice trials or time, but the cost trade-off formulation that Tabibian et al. (3) propose—standard in machine learning—is a fresh perspective for psychology. Another novelty of Tabibian et al. (3) concerns the objective of spaced practice. Experimentalists typically consider optimizing spacing for a particular RI, that is, the duration following final study over which the information must be maintained (Fig. 1A). In contrast, Tabibian et al. (3) suggest a perhaps more practical situation in which study and test phases are not distinguished and knowledge must be periodically refreshed to ensure its continuous availability. This practical, lifelong learning perspective is relatively understudied in psychology (20).

Tabibian et al. identify a class of student models that admit a formal analysis yet are informed by human memory data.

Just as cognitive psychology may find new avenues of investigation from algorithmic-instruction theory, algorithmic-instruction theory may have more practical impact as it takes into consideration the complexity of human behavioral data. For example, consider the inverted-U shape of the curves in Fig. 1A. Various psychological accounts have been proposed to explain these curves (17), most positing dual opposing mechanisms at play, one favoring short ISIs and one favoring long ISIs, and the trade-off between these opposing mechanisms gives rise to the inverted U.

Formal student models in Tabibian et al. (3) and in other theoretical work (15) presently do not capture this key dynamic of spaced practice. As Tabibian et al. (3) acknowledge, under their student model the forgetting rate is reduced at least as much by massed practice as spaced practice, inconsistent with the behavioral data. They suggest possible extensions but the theory does not at present incorporate these extensions. One might therefore expect an actual student following the schedule prescribed by their algorithm to fail to achieve optimal performance. Remarkably, Tabibian et al. (3) present evidence ameliorating this concern. They report on a natural experiment involving the reanalysis of a big-data corpus from an online-learning platform. They find that forgetting is relatively slowed following study sequences that more closely adhere to their theory’s optimum spacing. Their natural experiment is as well-conducted as one could hope for: In comparing alternative schedules, they control for the lag between first and final study, the total number of study trials, and the memory strength after the first study trial. Our explanation for the theory’s success in practice is their choice of penalty function, which imposes a cost for high review intensities (i.e., massed practice). This cost encourages long ISIs, and the inevitability of forgetting encourages short ISIs, resulting in dual opposing factors that yield an intermediate spacing. Whether the Tabibian et al. (3) theory can predict the precise peak of the spacing function (Fig. 1A) may not be terribly critical, given that for long retention periods the peak appears to be broad and flat. This fact gives us some reason to be optimistic about the ease with which the spacing effect can be leveraged to mitigate forgetting. Indeed, online platforms that perform adaptive scheduling using variants of the Leitner method (21) and SuperMemo (22) have thrived despite their heuristic nature.

Although “rote memorization” is not considered a particularly glamorous area of research in the education community, facts underpin most types of learning, and one cannot engage in critical thinking without sufficient field-specific knowledge. The notion of an automated instructor which refreshes our knowledge base at appropriate times is quite appealing. Such an instructor even has a role to play in the classroom that is complementary to that of the teacher: In the study mentioned earlier using personalized review software (2), the teacher is freed from mechanical duties to interact with smaller groups of students.

AI-guided microinstruction has other potential applications, such as selecting and ordering examples to learn complex visual concepts (e.g., bird species or skin-lesion diagnosis), determining the hints a learner requires to solve a problem and when to provide them, and recognizing when a student’s attention has wandered while reading. In each of these cases, principled approaches require a psychologically plausible student model, a quantitative measure of performance to be optimized, and a teacher model with theoretical guarantees of achieving optimal performance under the student model. The field of AI has made advances through development of its theoretical foundations and explicit formulations of system objectives. We expect this lesson to apply to human-centered AI as well, but it will occur only through collaborations between cognitive scientists who understand the intricacy of human behavior and AI researchers who can bring a new degree of clarity and elegance to cognitive models.