Abstract
A high performance, snapshot Image Mapping Spectrometer was developed that provides fast image acquisition (100 Hz) of 16 bit hyperspectral data cubes (210x210x46) over a spectral range of 515-842 nm. Essential details of the opto-mechanical design are presented. Spectral accuracy, precision, and image reconstruction metrics such as resolution are discussed. Fluorescently stained cell samples were used to directly compare the data obtained using newly developed and the reference image mapping spectrometer. Additional experimental results are provided to demonstrate the abilities of the new spectrometer to acquire highly-resolved, motion-artifact-free hyperspectral images at high temporal sampling rates.
1. Introduction
Imaging spectrometers are specialized instruments capable of simultaneously acquiring spectral and spatial signatures. Typically, these instruments provide information about the observed scene in the form of a three dimensional data cube (x,y,λ). Due to the rapid developmental process of electronic components such as solid state detectors, imaging spectrometers can operate in a broad spectral range from ultra violet (UV) [1,2] to visible (VIS) [3] to infra-red (IR) [4,5]. Hyperspectral imaging instruments found wide-spread use in industrial [6], research [7,8] and quality control [9] settings. Typically, these instruments are used to analyze chemical composition of astronomical bodies [10,11], detect explosives and aid in friend or foe decision making [7], identify vegetation [12] and its coverage [13], and quantify environmental condition factors such as canopy water content and plant stress states [14]. Furthermore, hyperspectral imagers are used to analyze forensic traces [15,16], check the condition and authenticity of artwork [17,18], study the chemical makeup of food ingredients and products [19], aid in sorting of plastics in recycling settings [20], and assist in diagnostics for a broad range of biomedical applications [21–23].
Hyperspectral imaging spectrometers can be divided based on their principle of operation into scanning and snapshot instruments. Snapshot instruments capture the entire hyperspectral data cube in a single integration event of the imaging detector. Thanks to this property, each voxel in the hyperspectral data cube can be exposed for a time that is inversely proportional to the system’s frame rate. This allows for detection of the weak fluorescent signatures at relatively high frame rates at low excitation levels, resulting in reduced phototoxicity [24]. Additionally, since data is acquired during a single exposure event, snapshot hyperspectral data cubes do not require hardware level synchronization of the detector with the scanning platform to reconstruct the observed scene. Thus, snapshot imaging spectrometers are well suited to monitor transient events such as the observation of flagellated cell movement and morphogen diffusion, which would require at least 100 and 72 fps temporal acquisition rates respectively to provide motion-artifact free data [25]. The ability to acquire data during a single integration event of the imaging detector allows for a great degree of synchronization between multiple snapshot imaging spectrometers, a feature exploited in remote sensing to acquire estimates of bidirectional reflectance-distribution function by a fleet of spatially, directionally and temporary coordinated instruments [26]. Further, direct imaging snapshot hyperspectral spectrometers, a sub category of snapshot imaging spectrometers, enjoy the advantage of simple data reconstruction algorithms [27], which reduces computational load and provides the ability to display and analyze multidimensional data cubes at high frame rates, as compared to e.g.: computationally intensive tomographic snapshot spectrometers [27]. Additionally, direct imaging snapshot spectrometers, which are based on the image mapping principle, enjoy the advantage of high light throughput [28], a critical component for light sensitive applications such as fluorescent imaging and observation of fast changing phenomena.
Our group specializes in the design and manufacturing of snapshot image mapping spectrometers (IMS) based on the image slicing principle. We have successfully built several generations of IMS systems that were optimized for microscopic applications and these systems were used to monitor both cell signaling events [29] and fluorescently stained samples [30]. We have integrated our IMS spectrometer with a fundus camera to enable direct monitoring of blood perfusion and tissue oxygenation in the eye [31]. Moreover, we used the IMS to build a snapshot optical coherence tomographic system (OCT) [32]. All systems we developed to date were built around large area detectors, comparable in terms of the image diagonal to a full frame 36x24 mm2 photographic film. The spectral range covered by instruments developed in the past varied between systems; for example, the spectrometer for hyperspectral microscopy operated in the 450-650 nm [33] range, the system designed for fluorescence microscopy acquired data in the 520-660 nm range [30], and the OCT system was optimized for the 610-645 nm spectral range [32]. The read noise of the utilized detectors was on the level of 16e- and 15 e- for the BOBCAT ICL-B4820M and the Apogee U16 camera respectively, and combined with low quantum efficiency resulted in low light sensitivity. The maximum achievable temporal resolution reached was 7.2 fps and was limited by the respective camera internal electronics and data interface bandwidth.
Previous generations of IMS systems operated in the VIS part of the electromagnetic spectrum. This allowed their use in a range of applications including the assessment of skin perfusion [34] and retinal tissue oxygenation levels [35] using the reflectance mode of operation, as well as the direct observation of a range of fluorophores such as acridine orange, proflavine, DAPI and Alexa Fluor [33]. While the visual part of the electromagnetic spectrum is preferred for direct observation of biological samples, due to low spectral absorption of tissue, contrast of exogenous fluorophores is typically limited by the background signal emitted by endogenous fluorophores e.g.: melanin, (NADH), collagen and elastin. From the perspective of multi-spectral observation, a spectrometer working on the border of the VIS and near infrared (NIR) part of the electromagnetic spectrum has several interesting properties. First, it allows deeper imaging into a tissue due to reduced scattering, which is proportional to λ−4 as described by the Rayleigh scattering law. Additionally, because absorption of the main tissue pigment, melanin, decreases with wavelength, tissue transmission increases proportionally with wavelength. Moreover, contrast of exogenous fluorophores emitting in the red and NIR part of the spectrum is not affected by the main endogenous tissue fluorophores such as NADPH, collagen and elastin, which have an emission spectra in 325-550 nm range. Furthermore, a spectrometer operating in NIR allows for the observation of new fluorophores such as indocyanine green (ICG) (Ex. 600-900nm/Em. 750-950nm), which is commonly used to diagnose heart conditions as well as to visualize blood flow in the retina. Aside from biomedical applications, a spectrometer operating within the VIS and NIR spectral bands can find multiple applications in remote sensing, as it may be used to delineate between vegetation species [9–11], identify minerals [21], and characterize urban environment landscapes (rooftop, pavement condition, and type identification) [22–24]. Additionally, due to the low absorption of atmosphere in the NIR region, all of the above measurements can be performed at extended distances.
Taking the above statements into account, a new snapshot image mapping spectrometer operating in the VIS and NIR bands was developed around a sCMOS camera to provide low noise, high dynamic range data in the spectral range of 515-842 nm. The presented system is capable of reconstructing hyperspectral data cubes (x,y,λ) of a minimal size of 210x210x46 at a temporal sampling rate of 100 Hz. The newly developed spectrometer, as compared to previous generation systems, has about 16 times lower read noise, about 20% better quantum efficiency, and can acquire data at about 14 times higher frame rate. Previously developed IMS systems utilized detectors which imaging area was close to 36x24 mm2, a size similar to “full-frame” photographic film. Presented high performance system was built around sCMOS camera with imaging area of 16.6x14 mm2. Because the photosensitive area of the detector was smaller, we re-designed and miniaturized the prism and lenslet assembly. A detailed description of the new opto-mechanical design together with a discussion of mechanical tolerances of critical components is presented in the following paragraph. Additionally, the sCMOS detector photo-electron to intensity conversion characteristic was experimentally measured and is presented in paragraph 4.1. Quantitative and qualitative performance metrics of the high performance IMS system are experimentally verified. Advantages of an extended dynamic range and an increased spectral sensitivity in VIS and NIR together with a high temporal sampling rate are demonstrated in two experiments. In the first experiment, free falling objects selectively stained with NIR dye were monitored at 50 frames per second, and images of objects accelerating in the Earth’s gravitational field were reconstructed in the VIS and NIR part of the spectrum without motion-related artifacts. In the second experiment, the emission spectrum of a halogen filament was continuously observed during an ON/OFF cycle at 100 fps to show the maximum temporal sampling rate of the newly developed system together with its potential to acquire data in the full dynamic range provided by the imaging detector. Performance of the new spectrometer is directly compared to a representative instrument from the previous generations of IMS systems in an experiment, during which a fluorescent BPAE cell sample was simultaneously observed by both systems. The presented system is to our best knowledge the first snapshot image mapping spectrometer utilizing the slicing principle that is capable of acquisition of data in the visible and near infrared part of the electromagnetic spectrum. Additionally, this is the first IMS type spectrometer with a temporal sampling rate adequate to monitor transient events.
2. Opto-mechanical design
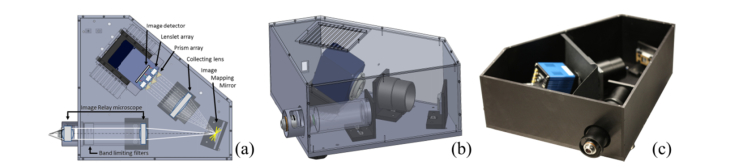
An opto-mechanical schematic of the IMS is presented in Fig. 1(a). A three dimensional visualization of the opto-mechanical model for the IMS spectrometer is presented in Fig. 1(b), with the enclosure walls drawn in a semi-transparent mode to present the internal organization of the system components, and finally, a photograph of the assembled prototype is given in Fig. 1(c). A detailed description of the operating principle for the IMS can be found in our previous publications [24,28,30,33,34]. Below, an abbreviated description of critical elements and their function is provided. The optical system of the IMS consists of three functional groups: the image relay microscope, the image mapping mirror, and the re-imaging optical system made out of a collecting lens followed by a set of prisms and an array of miniature lenslets. The image relay microscope is made out of commercially available Zeiss components: a tube lens with focal length of f = 165 mm and a 2.5x Plan-Apo NA = 0.017 microscope objective. The primary role of this system is to provide a magnified, telecentrically projected image of a target on a segmented image mapping mirror. The segmented image mapping mirror is divided into regularly spaced rows of narrow, strip like facets. Each mirror is tilted around the x and y axes in order to break the image into spatially separated lines. Light reflected by the image mapping mirror is collimated by a 1x stereomicroscope lens (MVPLAPO 1 × , NA 0.25, W.D. 65 mm, Olympus, USA) and is subsequently dispersed by a set of five prisms. An array of miniature lenses, placed directly behind the prism assembly, provides the dispersed facets images of the mapping mirror onto the image detector. In this system, the raw image is broken into spectrally dispersed lines, which are grouped together to form a matrix of five rows and six columns. The spatio-spectrally scrambled image can be reconstructed into a three-dimensional (x,y,λ) data cube, using a transformation matrix created during a dedicated calibration procedure [34].
Fig. 1.
Opto-mechanical schematic of the IMS system (a). Three-dimensional model of the complete system, with chassis walls drawn in semi-transparent mode (b). Photograph of assembled prototype with top cover removed (c).
The presented system was built around a scientific CMOS PCO.EDGE 5.5 detector. We have selected this detector due to its low read noise (median of 1e- and 2.2e- in slow and fast scan modes respectively), dynamic range of 89.5 dB, high peak QE of 60% around λ = 600nm and ability to acquire full-frame images at 100 fps rate. Those parameters compare favorably to technical specifications of detectors used in the previous generations of the IMS systems.
The primary difference between the imaging detectors used in the past and the current PCO.EDGE 5.5 is the length of the detector diagonal. The CIS2521(PCO) chip diagonal, used in the PCO camera, is 2 and 2.4 times smaller than the KAI-16000 (Bobcat) and the Kodak KAF-16801E (Apogee) detectors, respectively. Because of this, the entire re-imaging optical system was redesigned. In order to maximize detector utilization and to take into account the selection of commercially available lenses, the mapping mirror was designed to split the image into 210 lines organized in 30 groups (arranged in 5 rows and 6 columns). The re-imaging system was built using a 1x stereomicroscope lens (MVPLAPO 1 × , NA 0.25, W.D. 65 mm, Olympus, USA) followed by a stack of five custom miniature 20° wedge angle dispersive prisms made out of H-ZF62 (Tower Optical Corp., USA). Images of the dispersed, spatially separated lines of the object were provided by an array of 5x6 miniature achromatic lenslets (f = 12 mm, part #83339, Edmund Optics, USA), which were placed directly behind the prism assembly. The combined magnification of the re-imaging system was −0.13x and its optical schematic is presented in Fig. 2(a). The system’s spectral range was limited by a pair of interference filters (LP02-514RU-25 and FF01-842/SP-25, Semrock, USA). Nominal spot diagrams for 515 and 842 nm wavelengths for axial and diagonal edge field points are given in Fig. 2(b). As indicated by root-mean-squared (RMS) spot radii, the presented system was diffraction-limited close to the optical axis for both wavelengths, and the RMS spot diameter increased by 47% and 62% at the edge of the field of view for 515 and 842 nm, respectively. Please note that the PCO 5.5 edge detector has square 6.5 μm pixels, and taking this into account, point-like objects will be imaged as disks which radius will be within 0.6 and 2.1 pixels for object located at the optical axis and at the edge of the field of view respectively.
Fig. 2.
Optical model of the re-imaging system of the IMS system limited to the prism-lenslet –detector assembly (a). Nominal spot diagrams for axial (Obj: 0.0, 0.0 mm) and diagonal edge field points (Obj: 9.1, 13.5 mm) for 515 and 842 nm (b).
While the performance of the system can be improved by the use of dedicated, custom achromatic lenses, we decided to use commercially available ones to reduce cost and accelerate development.
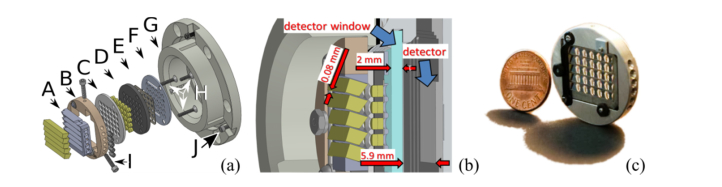
A cross-section through an arbitrarily selected part of the re-imaging assembly is given in Fig. 3(b). Separation between lenses (yellow) was controlled by a matrix of regularly spaced holes drilled in a disk made out of Delrin, part D, Fig. 3(a). Axial position of the lenses was fixed by two disks marked with C and F on Fig. 3(a), which were made from Delrin and aluminum, respectively. In order to provide proper alignment and minimize obscuration, parts C, D and F were manufactured on one numerically controlled milling machine. All critical dimensions such as hole separation and internal diameters were toleranced to be within 10 µm. The only part that was manufactured with lowered tolerance requirements was a spacer (E, Fig. 3(a)), which was made from volume blackened construction paper and was cut in an iterative process on VLS 3.60 laser cutter (Universal Laser Systems, USA). The cutting procedure was repeated multiple times, with dimensions of a spacer changed with each iteration until all holes in Delrin disk D, Fig. 3(a) aligned with apertures cut in construction paper E, Fig. 3(a). Stereomicroscope with 4.5x magnification was used to visually inspect alignment of apertures of both parts. In this design, separation between adjacent prisms was only 80 µm. In order to meet this requirement, a grid like prism enclosure A, Fig. (3), was machined from a solid piece of stainless steel using Electro Discharge Machining (EDM) technology. Distance between consecutive prism slots was kept within ± 10 µm and height of slots housing prisms tolerance was + 25 µm in order to meet prism manufacturer process limitations. The angular orientation of prisms slots was set to be within ± 0.1°. The prisms were fixed to the EMD machined frame A, Fig. 3(a), by set of five rubber tipped set screws. Spacing between prisms and lenslets was controlled by thickness of a disk C, Fig.3(a), which thickness was within standard machine shop tolerance limits of ±0.2 mm, since it was not critical from the perspective of the system performance because the prisms are nominally placed in the optical infinity space between the collector lens and lenslet array. The Assembly of lenslets and prisms was bolted together by a set of three miniature screws H, Fig. 3(a). Focus of the prism-lenslet module was controlled by custom made paper spacers placed between the base lip machined in collar G and the external disk of lenslet assembly F. Fine focus was set using three set screws I, Fig. 3(a), and correction of angular orientation of the assembly was performed by adjusting position of three 120° spaced screws J, Fig. 3(a). The Entire assembly was bolted to the camera body using interface collar G, Fig. 3(a).
Fig. 3.
Exploded view model of the lenslet assembly (a). Cross-section through the lenslet assembly with critical dimensions and elements indicated (b). Photograph of complete assembly with one-cent coin for size comparison (c).
A three-dimensional hyperspectral data cube is built from raw images using an image reorganization procedure of , which parameters are stored in the look-up table created during calibration. The look-up table contains information regarding the position of each pixel in the hyperspectral data cube in the coordinate space of the imaging detector. Entries of the look-up matrix are established during the calibration procedure previously described in detail by Bedard et al. [34]. In short, the calibration procedure is split into two parts, spatial and spectral calibration. During spatial calibration, a narrow slit illuminated by a broadband light source is moved across the field of view in two perpendicular directions. Images of the slit together with its position are simultaneously acquired, and based on these data, spatial (x, y) transformation parameters of the look-up table are calculated. In the second step, images of a broad band light source observed through set of five narrow band filters are recorded. Spectral coordinates of the look-up table which relate position of the slit with wavelength are calculated based on the location of narrow band signal within focal plane array.
3. System characterization
A series of experiments were executed to characterize the system’s performance. Spectral accuracy and repeatability were tested quantitatively using a tunable supercontinuum laser and a reference spectrometer. Lateral resolution was tested using a 1951 USAF resolution bar target; a, reconstructed image of the target integrated over 515-842 nm range is presented in Fig. 4(a). Geometric quality of the image reconstruction was tested qualitatively using a Ronchi ruling target, which the image integrated over 515-842 nm range is given in Fig. 4(b).
Fig. 4.
Reconstructed images of the 1951 USAF resolution target (a) and Ronchi ruling (c). Designed (red line) and measured (black line) system dispersion expressed in lateral shift measured in pixel/nm (c).
During all experiments the PCO.edge 5.5 camera was connected to a PC computer via PCI-Express card using two Camera Link cables. Use of a dual Camera Link interface enabled acquisition of images at 50 and 100 fps rates in global and rolling to shutter mode respectively. All images were saved using a native b16 raw format. For all experiments, the image sensor was operated at a 286 MHz pixel clock rate, to maximize temporal sampling.
The system’s dispersion was measured using a calibration transformation matrix, which was calculated using the procedure detailed by Bedard et al. [34]. Data averaged over the entire hyperspectral data cube was used to calculate the average dispersion. Nominal dispersion values were obtained from the system’s model created in OpticStudio (Zemax LLC, USA). Experimentally verified and nominal dispersion curves are given in Fig. 4(c) and are plotted using continuous black and red lines, respectively. In the spectral range of 550-780 nm, the difference between nominal and measured dispersion was below 0.01 pixel/nm and increased to 0.04 pixel/nm for 515 nm wavelength. Please note that differences between the theoretically predicted and the measured dispersion are small, and may be attributed to intrinsic material properties of the source glass as well as geometric imperfections of the prisms themselves.
Spectral performance of the IMS system was tested by measuring the spectral accuracy and precision of narrow band signals provided by an adjustable light source. A Fianium supercontinuum laser (NKT Photonics, Denmark) coupled with an acousto-optic tunable filter and controlled by AODS 20160-8 digital generator (Crystal Technology, Inc, USA) served as the light source. A beam filtered by a tunable AOTF filter was coupled to a liquid light guide, which in turn was plugged into the back illumination port of the Z1 Axio Observer microscope (Zeiss, Germany). Light reflected from an aluminum coated external mirror was measured sequentially by either the IMS or the reference spectrometer. An Ocean Optics USB2G38810 spectrometer (Ocean Optics, USA) was used as the reference spectrometer to measure the central wavelength and the Full Width at Half Maximum (FWHM) of each tested laser line. In total, nine measurements covering the 540 to 730 nm range were made. Tested spectral range was limited by technical capabilities of the acousto-optical tunable filter; please note that the Fianium supercontinuum laser can operate in wider range of wavelengths. A quantitative summary of the experimental data is given in Table 1. Please note that experimental results given for reference Ocean Optics spectrometer are for single acquisition event and data for the IMS spectrometer are averaged over the entire FOV.
Table 1. Spectral accuracy and precision of IMS system as measured against Ocean Optics USB2G38810. Ocean Optics λOO –central wavelength as measured by Ocean Optics USB2G38810; Ocean Optics FWHM – full width at half maximum of laser line as measured by the Ocean Optics spectrometer; IMS λIMS – central wavelength of laser line as measured by the IMS system; IMS ± σ – standard deviation of measured central wavelength of the laser line as measured by the IMS;IMS FWHM – full width at half maximum of the laser line as measured by the IMS system; Δλ – difference between IMS and Ocean Optics central wavelength.
| Ocean Optics λOO[nm] |
Ocean Optics FWHM [nm] |
IMS λIMS[nm] |
IMS ± 1σ [nm] |
IMS FWHM [nm] |
Δλ λOO-λIMS [nm] |
|---|---|---|---|---|---|
| 542 | 8.9 | 541.7 | 0.8 | 15.2 | 0.3 |
| 573.2 | 4.9 | 571.7 | 0.4 | 13.5 | 1.5 |
| 598.8 | 5.3 | 597.6 | 0.6 | 16.4 | 1.2 |
| 622 | 5.4 | 622.7 | 0.8 | 19.1 | −0.7 |
| 651.7 | 6.4 | 652.4 | 1.0 | 23.3 | −0.7 |
| 680.9 | 6.4 | 681.4 | 1.3 | 25.9 | −0.5 |
| 698.1 | 7.7 | 697.9 | 1.3 | 26.9 | 0.2 |
| 703.6 | 7.8 | 702.1 | 2.1 | 29.9 | 1.5 |
| 723.1 | 8.8 | 719.7 | 3.6 | 30.0 | 3.4 |
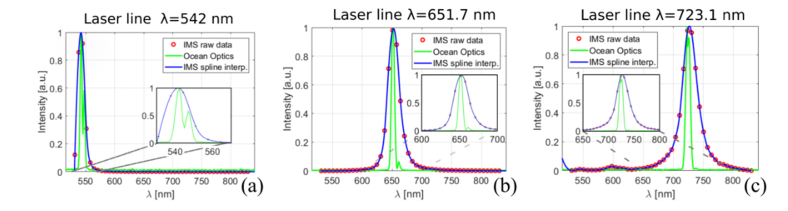
Central wavelengths and full width at half maxima (FWHM) of tested laser lines as measured by the reference spectrometer are given in the “Ocean Optics λOO[nm]” and “Ocean Optics FWHM [nm]” columns respectively. Central wavelengths of laser lines as measured by the IMS system are given in the “IMS λIMS[nm]” column. Standard deviations of central wavelengths measured over the entire field of view of the IMS system are given in the “IMS ±1σ [nm]” column. Full width at half maxima of laser lines measured by the IMS system is provided in the column labeled “IMS FWHM [nm]”. Differences between central wavelength values measured by the IMS and the reference spectrometer are provided in the column labeled “Δλ λOO-λIMS [nm]”. Central wavelengths were approximated by the abscissa of a vertex of a second degree polynomial fitted in the least square sense to three data points with the highest signal. Spectral plots obtained at 540, 650 and 730 nm laser lines for both the IMS and reference spectrometer are presented in Fig. 5 (a), (b) and (c), respectively. Spectral intensity values averaged over the field of view of the IMS system are drawn using red dots. The blue continuous line depicts a cubic spline curve fitted to the IMS data points. Raw spectra obtained from the reference Ocean Optics spectrometer are drawn with a continuous green line. All spectral profiles were normalized, and the inset in each figure shows the magnified spectra in the selected region of interest. Please note that lines filtered by the AOTF filter have secondary peaks across the visible spectrum, which amplitude decreases towards the red part of the spectrum. A set of office and flood lights was used to illuminate scene during experiment and because of directionality of the illumination a shadow of free falling balls was clearly visible in both “VIS” and “NIR” data sets, see for example Fig. 8(b).
Fig. 5.
Spectral plots at three selected emission lines of the Fianium laser. Data for nominal 540, 650 and 730 nm laser lines are presented in figures (a), (b) and (c) respectively. Red dots represent HS-IMS data averaged over the field of view, the continuous green line is for Ocean Optics spectrometer raw data, and the blue line is for HS-IMS data interpolated with a cubic spline curve. Insets in the figures depict the area in the vicinity of a laser line peak.
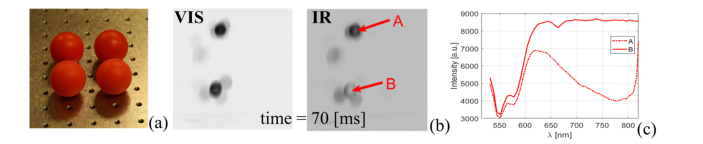
Fig. 8.
Picture of red ping pong balls dyed with Spectre 300 infrared dye (top row) and un-painted (bottom row) (a). Arbitrary selected frame, recorded at time t = 0.78 s with two ping-pong balls in free fall (b). Gray scale image sub-titled “VIS” shows hyperspectral data cube integrated over 513-605 nm and 2D image “IR” shows hyperspectral data cube integrated in range 610-777 nm. Spectral cross-sections taken at points marked with A and B through dyed (dash dotted line) and un-dyed (continuous line) (c). Movie compiled from a series of consecutive hyperspectral data cubes is given in Visualization 1 (3.2MB, avi) . Two dimensional representations of hyperspectral data cube were flat field corrected and digitally post-processed with a 5x5 median filter for visualization purposes. Presented spectral cross-sections were averaged over a 3x3 area.
The standard deviation of the signal recorded by the IMS system in the spectral range of 542-652 nm was below 1 nm, and starting from the wavelength of 681 nm, it increased monotonically, reaching 3.6 nm for the longest tested wavelength of 730 nm. The FWHM of the laser lines as measured by the IMS was on average 3.3 times wider then FWHM measured by the reference spectrometer. IMS measured FWHM increased with wavelength, with the exception of narrow band signal centered at 573.2 nm. The absolute difference between measured and the reference central wavelength was on average 0.7 nm, with a median value of 0.3 nm and fluctuated in the range of 4.1 nm. The entire 327 nm spectral range covered by the IMS systems is sampled by 46 spectral bins with an average distance of 7.1 nm between them. Taking spectrometer sampling into account, spectral precision and accuracy reached sub-pixel performance within the tested spectral range. Small wavelength dependent accuracy and precision non-linearities were due to the dispersion model (a 4th degree polynomial), which was selected for its simplicity and satisfactory performance. The measured FWHM was 15.2 nm in the short wavelength end of the spectrum and 30 nm in the longer part of the spectrum. The width of the peak in the narrow band reference signal on the detector was determined by the imaging optics resolution and dispersion of the prisms. Minute misalignments of the optical system such as decentrations and deviations from the nominal spacing negatively impacted both spatial and spectral resolution of the spectrometer. Additionally, it should be noted that due to diffractive effects, spectral and spatial resolution of imaging spectrometers based on the image slicing principle is inversely proportional to wavelength because both parameters are bound to the diameter of the Airy disk (assuming typical circular aperture of the imaging system). Moreover, decrease of spectral resolution in the longer part of the electromagnetic spectrum is adversely affected by the non-linear dependence of the refractive index from wavelength, which is an inherent and unwanted property of all refractive components.
IMS image reconstruction quality was evaluated quantitatively using a 1951 USAF resolution bar target and qualitatively using Ronchi ruling test. The limit of resolution of the IMS system was measured with the spectrometer coupled to the side port of a Zeiss Z1 inverted microscope. An image of a bar target was provided by 5x (EpiPlan Neofluar, 5x/0.15 HD, Zeiss, USA)) microscope objective in trans-illumination mode. In the above configuration, at the near-infrared end of the spectrum for the wavelength of 842 nm, the system should resolve at least element 4 from group 6, which was successfully imaged, proving correct alignment. Ronchi ruling (10 lp/mm, #38-258, Edmund Optics, USA) was used to evaluate geometric distortions of images provided by the image mapping spectrometer. Image of the bar test relayed through 10x (NA = 0.3, Plan-neofluar, Zeiss, Germany) microscope objective to the side port of the Z1 microscope served as a target for the IMS system. Test bars were rotated 45° with respect to IMS camera pixel grid in order to visualize geometric deformations in both directions simultaneously. The test revealed that lines of the Ronchi test were reconstructed without visible warping for all 46 wavelengths in 515-842 nm spectral range. The transition between dark and bright bars was uniform in length, and consistent in appearance throughout the field of view, which indicates good chromatic correction and suitable performance of image reconstruction routines. The inconsistency with the theoretically predicted lateral resolution can be ascribed to residual misalignment of the matrix of miniature lenses, which is inherently difficult to adjust using static optical components.
4. Experiments
A series of two experiments were performed to directly compare signal strength and throughput of the newly developed system to the previous generation spectrometer represented by an IMS built around an Imperx B4820M monochromatic camera. The reference system was capable of providing a (356x336x75) data cube in the spectral range of 470-670 nm at a maximum temporal sampling rate of 7.2 Hz [33]. The two experiments performed were quantitative bead imaging and qualitative BPAE cells imaging.
Additionally, two experiments were performed to showcase the capability of the newly developed system to record data at 50 and 100 fps in experimental conditions requiring acquisition of intensity samples spanning the entire detector dynamic range. In the first experiment, free falling ping-pong balls (selectively stained with a near infrared absorbing dye) were observed by the IMS system and spectral data cubes were recorded at the 50 fps rate, the maximum frame rate at which the PCO camera can operate in global shutter mode. In the second experiment, a halogen bulb filament was observed during the ON/OFF cycle at a rate of 100 Hz, the maximum temporal sampling of the PCO camera operating in full frame mode. In the first experiment, the ability of the HS-IMS to acquire motion-artifact-free hyperspectral data cubes of fast moving objects is presented, and in the second experiment, dynamic range and high rate of temporal sampling required to monitor transient phenomena are shown.
4.1 Quantitative comparative evaluation of new IMS system against previous generation spectrometer
For the purpose of this experiment, the newly developed system will be hereafter referred to as HS-IMS and the formerly developed one will be simply denoted as P-IMS [34]. The goal of this test was to quantitatively compare the reference P-IMS with the newly developed HS-IMS system. A Zeiss Z1 microscope served as the imaging platform and a mercury vapor X-Cite 120 (Excelitas, USA) provided excitation light, which was delivered to the epi-port of the microscope by a liquid guide cable. A double port adapter (T2-2x60N) with a 50/50 broadband beam splitter (operating range 400-750 nm, #21000, Chroma, USA) provided an image to both image mapping spectrometers, simultaneously. Both IMS systems used identical 2.5x (Plan-Apo 0.017 Zeiss, USA) microscope objectives in the fore-optical sub-system in order to guarantee identical light collection conditions.
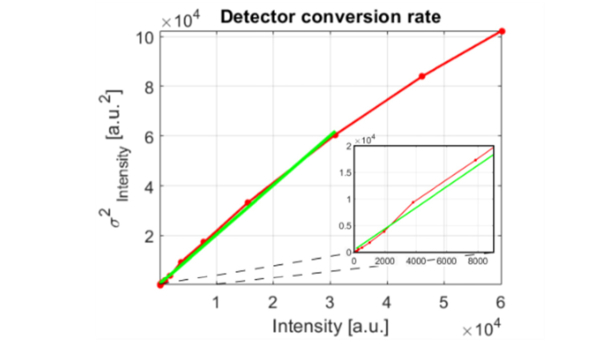
The KAI-16000 detector installed in the P-IMS system has a 16 e- read noise, 14-bit maximum nominal bit depth, and 30,000 e- full well capacity. The CIS2521 sCMOS chip used in the HS-IMS system has a maximum root mean square read noise of 2.5 e- in the fast scan mode (the root mean square read noise drops to 1.1e- in the slow scan mode), 30,000 electron full well capacity and 16-bit analog to digital converter. In order to make a comparison that will be not biased by the camera A/D converter and signal conditioning circuitry, the intensity signal returned by each detector was converted to photo-electrons. The catalog specified conversion rate for the PCO5.5 Edge camera (stated as 0.46 e-/intensity count) was verified to be 0.504 e-/intensity count. Experimentally measured read noise was 2.6 e- in the fast scanning mode. To measure the conversion rate and read noise, the PCO camera was directly attached to the side port of the Z1 microscope and a series of defocused, uniformly illuminated background images were measured at multiple exposure times. Figure 6 shows a correlogram of variance with the mean intensity as recorded by the PCO camera. Red dots on Fig. 6 represent raw data points and the red continuous line shows the raw signal linearly interpolated between sampling points. A first degree polynomial fitted to the linear part of the data set is plotted in green and its slope was used to calculate the detector conversion rate. The magnified portion of the plot (displayed as an inset in the lower right hand corner of Fig. 6) shows the transition region, where signal from two separated 11-bit A/D converters is mixed to produce a continuous 16-bit signal. Since the Imperx B4820M detector was integrated with the P-IMS system, the manufacturer provided gain/conversion values provided by the CamConfig application were used. Video amplifier gain of the Imperx camera for all experiments was set to 5.17 dB, pre-amplifier gain was set to 0 dB, and output signal bit depth was reduced to twelve bits. Based on the information above, the detector conversion rate of 1.813 e-/intensity count was calculated and a maximum output signal value was set to 4096.
Fig. 6.
Variance vs. mean intensity signal as measured for the PCO.EDGE 5.5 camera. Raw data points are marked with red dots; the red line show raw signal linearly interpolated between sampling points and the green line depicts a first degree polynomial fitted to the linear part of the data set. Inset in the right bottom of the plot depicts magnified region of correlogram, for which average signal was below 8000 counts.
To quantitatively compare the P-IMS with the HS-IMS, a test sample consisting of FluoSpheres polystyrene microspheres (catalog number F8841, ThermoFisher, USA) was utilized. A 4:1 solution was prepared using purified deionized water. The nominal excitation and emission spectra for F8841 15 µm microspheres is around 540 and 560nm respectively. A TRITC filter cube set (41002, Ex.535/50, Lp.565, Em.610/75 nm, Chroma, USA) was used to excite the target sample and to isolate the emitted fluorescent light. A Z1 microscope equipped with a 5x (EpiPlan Neofluar, 5x/0.15 HD, Zeiss, USA) was used to observe the microsphere sample. Each system recorded 168 images of fluorescent beads at 30, 20, 10, and 5 ms exposure times respectively. Since the two systems operate at different magnifications and were optimized for different spectral ranges, the only quantity compared was integrated signal, calculated for each bead as the sum of intensities over the spectral and spatial dimensions. Table 2 summarizes the experimental data. As indicated by the last column of Table 2, the newly developed HS-IMS system recorded on average 4.8 times more photo-electrons than the reference IMS system in identical imaging conditions. As per each respective systems’ camera specification, the HS-IMS detector has ~48% quantum efficiency for the wavelength of 580 nm as compared to ~35% for the P-IMS system. The difference between the quantum efficiency of both detectors at the peak emission line of the micro beads is 1.4 times higher for the HS-IMS. We attribute the remaining difference of signal strength between systems to intrinsic differences in opto-mechanical design and to unavoidable oxidation of an unprotected aluminum mirror of the P-IMS system. Please note that the re-imaging optics of the P-IMS system consists of two doublet lenses and the prism assembly is made out of Amici prims. The Fresnel reflection off of uncoated prism and lens surfaces have contributed to lower efficiency of the P-IMS system.
Table 2. Quantitative comparison of fluorescent signal level between P-IMS and HS-IMS systems. Three arbitrary selected microspheres (FluoSpheres, #F8841, Thermo-Fisher) were imaged at 30, 20, 10 and 5 ms exposure times respectively. Averaged (168 images) intensity values integrated over spatial and spectral voxels of selected beads for both systems are given in columns ItotHS-IMS and ItotM-IMS. Count of photo-electrons recorded by HS-IMS and P-IMS systems over spatio-spectral voxels of each bead is given in Ie-HS-IMS and Ie-M-IMS respectively. Please note that signal recorded by P-IMS was multiplied by 0.5 to account for 2x binning in y direction.
| Exposure time [ms] | ItotHS-IMS [a.u.] | Ie-HS-IMS [e-] | ItotM-IMS [a.u.] | Ie-M-IMS[e-] | Ie-HS-IMS/Ie-M-IMS | |
|---|---|---|---|---|---|---|
| Bead #1 | 30 | 1371800 | 664170 | 154040 | 139660 | 4.7 |
| 20 | 908570 | 457920 | 107000 | 97018 | 4.7 | |
| 10 | 464090 | 233900 | 51466 | 46664 | 5.0 | |
| 5 | 231210 | 116530 | 23784 | 21565 | 5.4 | |
| Bead #2 | 30 | 1696400 | 854990 | 190380 | 172620 | 4.9 |
| 20 | 1175200 | 592300 | 131220 | 118980 | 5.0 | |
| 10 | 594710 | 299730 | 62994 | 57117 | 5.4 | |
| 5 | 273870 | 138030 | 28272 | 25634 | 5.2 | |
| Bead #3 | 30 | 1193700 | 601620 | 149070 | 135160 | 4.4 |
| 20 | 789850 | 398080 | 103090 | 93472 | 4.3 | |
| 10 | 413270 | 208290 | 50468 | 45759 | 4.5 | |
| 5 | 194050 | 97801 | 24887 | 22565 | 4.3 | |
4.2 BPAE cells imaging using HS-IMS and P-IMS systems
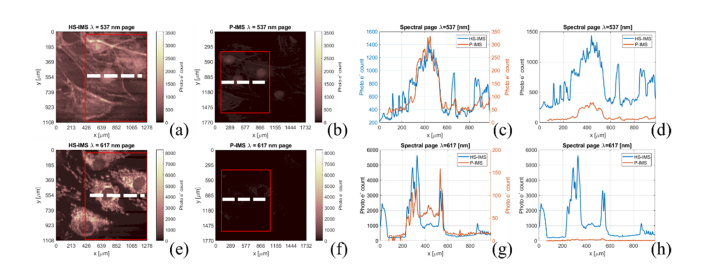
To qualitatively compare performance of the HS-IMS and P-IMS, a FluoCells slide #1 (F36924, Thermo-Fisher, USA) was observed in the setup described in the paragraph above. FluoCells slide #1 contains bovine pulmonary artery endothelial cells (BPAEC) stained with three fluorescent dyes: DAPI (λEx = 358/λEm = 461), Alexa Fluor 488 (λEx = 505/λEm = 512) and MitoTracker Red (λEx = 579/λEm = 599). Both systems are capable of operation between 515 and 670 nm wavelength, and in that range signal emitted by AlexaFluor and MitoTracker was analyzed. It should be noted that due to the spectral properties of the 515 nm long pass filter, the newly developed HS-IMS system was able to record about half of the emission spectra of the AlexaFluor. Images of fluorescently stained samples were recorded by both systems at an identical exposure time of 500 ms. Intensity signals recorded by both systems were converted to photo electron count using the procedure described in the paragraph above to facilitate direct signal comparison. Emission spectra recorded at 537 nm wavelength by the HS-IMS and the P-IMS are presented in Fig. 7(a) and Fig. 7(b), respectively. The color scale on both images was set to cover an identical range to visualize differences in sensitivity between systems. Cross-sections through the 537 nm spectral pages (in the direction indicated by the white dotted line) and acquired by the newly developed and reference spectrometers are given in Fig. 7(c) and Fig. 7(d). Continuous blue and orange lines represent signals acquired by the MS-IMS and P-IMS, respectively. Cross-sections through the BPAEC sample are scaled individually on Fig. 7(c), with the left hand y-axis for HS-IMS and right hand side y-axis for P-IMS. Both plots with identical y-scales are drawn in Fig. 7(d). Spectral signatures of the BPAEC sample recorded at λ = 617 nm for both compared systems are shown in Fig. 7(d) and 7(e) for HS-IMS and P-IMS respectively. Both 2D images share the same color scale range to facilitate direct comparison. A cross-section through the HS-IMS and P-IMS data in the direction marked by the white lines in Fig. 7(e) and Fig. 7(f) is given in Fig. 7(g) and Fig. 7(h). Presented plots are individually scaled on Fig. 7(g), with the left and right y-axis scale range set to cover the HS-IMS and P-IMS data range respectively. The range of y-axis on Fig. 7(h) was selected to simultaneously visualize both plots. Please note that all spectral cross-sections are provided for the common area of the two data sets, which is marked on all 2D images with a red rectangle. Source hyperspectral data cubes for both systems were numerically stitched from multiple laterally shifted fields of view to extend the visualized area and to eliminate a flat-field correction post-processing step [34]. Additionally, all two-dimensional images were low pass filtered to remove high frequency noise and their contrast, with the exception of cross-sectional plots that were numerically enhanced for visualization purposes. Please note, that striping and low intensity artifacts visible in the background of BPAEC cells images were artificially accentuated by the selected color map, which was used because it is capable of providing contrast rich images of data sets spanning a wide range of values.
Fig. 7.
Pseudo-colored image of a fluorescently stained sample of a bovine pulmonary artery endothelial cell sample recorded at 537 nm for a newly developed (HS-IMS) (a) and reference (P-IMS) spectrometer (b). Intensity cross-sections though both data sets in the direction marked on (a) and (b) by white lines are given in (c) and (d). HS-IMS and P-IMS signals are drawn in blue and orange lines respectively; individually scaled signals are shown in (c) and shared y-axis scale for both plots is provided in (d). Fluorescent signal from the BPAEC sample recorded at 617 nm by the newly developed (e) and reference spectrometer (f). Intensity cross-sections in the direction marked on (e) and (f) by white lines are given in (g) and (h). Individually scaled plots with left and right hand side scale for HS-IMS and P-IMS respectively (g). Plots from (g) with single y axis scale (h). Red rectangle marks area of the field of view area shared by both systems. Axis scales are given in physical units of length in the sample space.
Two-dimensional visualizations together with cross-sectional plots presented in Fig. 7 show a clear advantage of the newly developed system over the reference one. Morphological details of the BPAEC sample are clearly visible in images provided by the HS-IMS system and are barely visible in pictures from the reference spectrometer. Signal recorded by the new spectrometer was about 4 times stronger at the wavelength of 537 nm and about 16 times stronger for the wavelength of 617 nm. The differences are due to modifications in optical design between systems and sensitivity of utilized detectors. Optical magnification of the P-IMS is ~1.6 times larger than the magnification of the HS-IMS system, and due to this, signal recorded by the latter should be about 3 times stronger. Additionally, taking into account dispersion differences between systems, signal recorded by the HS-IMS due to lower spectral sampling should be ~3 times higher. Additionally, difference between quantum efficiency of the detectors utilized by both systems is on average 1.4 times higher in favor of the newly developed system. Combined influence of enumerated factors should in theory give the newly developed system about 13.5 times stronger signal, which is close to the measured 16 times difference at 617nm wavelength. The smaller ratio of signal measured at 537 nm can be due to unwanted attenuation of spectral signatures by the band-limiting long-pass filter installed on the HS-IMS spectrometer. Please note that despite differences in spatio-spectral sampling, intensity profiles recorded by both systems overlap, as presented in cross-sections in Fig. 7(d) and (h), and prove the correct geometric calibration of the two IMS systems.
4.3 Monitoring of objects free falling in the Earth gravity field
To showcase the ability of the HS-IMS system to acquire hyperspectral data over the visible and near infrared wavelengths at high temporal resolution, an experiment with free falling ping pong balls was performed. A set of eight red ping pong balls was acquired and every second ball was dyed with Spectre 300 dye (Epolin, USA). Spectre 300 has absorbance peak at 790 nm wavelength and has neutral absorption spectral characteristics in the visible part of the electromagnetic spectrum. A photograph taken with a digital DSLR camera of two dyed and unpainted ping pong balls is given in Fig. 8(a), with dyed and unaltered balls in the top and bottom rows respectively. Please note that the dyed balls have a slightly darker appearance, as short wavelength absorbance of the Spectre 300 overlaps with the spectral sensitivity of red pixels in a typical Bayer type color camera. During the experiment, mixed dyed and un-dyed balls were free falling from a height of about 2 m onto a surface of an optical table covered with clear white paper. A white screen was placed behind the optical table to provide a uniform, spectrally neutral background. A 14-42mm/1:3,5-5,6 Olympus Digital ED zoom lens was installed in front of the 2.5x Zeiss microscope objective of the HS-IMS to image roughly a 0.7x0.7 m2 field of view from a distance of ~2 m. For this experiment, the HS-IMS detector operated in global shutter mode with a 10 ms exposure time. A total of 396 images were recorded. A movie visualizing the hyperspectral data cubes reconstructed from subsequent raw images is available at the link given in the caption of Fig. 8. An arbitrarily selected frame from the movie, recorded at t = 0.78 s is presented in Fig. 8(b). The left sub-image, entitled “VIS” shows a gray scale two-dimensional representation of the hyperspectral data cube acquired over visible wavelengths (515-605nm) and was obtained by summing the respective pages of the data cube(IVIS(x,y) = SUM(x,y,λ) from λ = 515 to λ = 605). The right hand side image shows the hyperspectral data cube summed over the visible and near infra-red wavelengths in the range of 610-777 nm (IIR(x,y) = SUM(x,y,λ) from λ = 610 to λ = 777). A spectral cross-section through points marked with A and B in Fig. 8(b) are given in Fig. 8(c). Please note that the ball marked with B on Fig. 8(b) was painted with near infrared dye and exhibits the characteristic absorption of the Spectre 300 in the range of 650-810 nm. Both balls have nearly identical reflectance spectral profiles in the visible wavelengths, and as result, they cannot be easily distinguished in the left hand side “VIS” image. However, they can be clearly identified on the right hand side “IR” image as the dyed ball is clearly darker due to lower reflectance in the near infrared part of the spectrum. A set of light towers was used to illuminate scene during experiment and because of directionality of the illumination a shadow of free falling balls was clearly visible in both “VIS” and “NIR” data sets, see for example Fig. 8(b). Please note that source images were recorded at 50 fps frame rate, and due to the short 10 ms exposure time, high sensitivity of the imaging detector, and its low read noise, we were able to acquire sharp images with an average intensity on the order of 10% of the system’s dynamic range.
4.4 Monitoring halogen bulb spectra during ON/OFF cycle
To present the ability of the newly developed system to acquire data at the maximum temporal resolution in the full dynamic range of the sCMOS detector, the fast changing spectral emission of a halogen bulb during a power up and power down cycle was measured. A Zeiss Axio A1 Observer internal power supply unit was used to drive a 30W, 6V microscope type halogen bulb, which was observed through a 2.5x microscope objective installed on the newly developed imaging spectrometer. Data was acquired with the HS-IMS detector operating in rolling-shutter mode with 9 ms exposure time. In total, five hundred images were recorded during the experiment at an acquisition rate of 100 frames per second. The halogen bulb was powered on at time t = 0.6 s and was turned off at time t = 3.0 s. Images of the halogen bulb in off and on states, recorded at time t = 0.0s and t = 2.75s are presented in Fig. 9(a) and (b), respectively. Please note that color maps in both images were stretched to the dynamic range of their respective data sets to maximize contrast. Three selected spectral plots, taken at time t = 0.9s, t = 1.7s and t = 3.07s and averaged over a 5x5 area marked with red arrow on Fig. 9(b) are shown in Fig. 9(c) and Fig. 9(d). Plots presented in Fig. 9(c) are scaled to the maximum dynamic range of the data set and plots given in Fig. 9(d) are normalized to visualize the shift of the spectral peak to shorter wavelengths together with increase of intensity as predicted by the Wien’s displacement law. It should be noted that curves recorded for time t = 0.9 s and t = 1.7 s and t = 3.07 s (Fig. 9(c) and (d)) differ in signal levels by two orders of magnitude. Additionally, it should be pointed out that during this experiment detector exposure time was held constant. At time t = 0 s until the halogen lamp was turned on, the features of the emitter are visible only due to ambient light provided by the laboratory ceiling mounted fluorescent lamps. The blurred and distorted background behind the emitter in Fig. 9(a) is due to aberrations introduced by the glass bulb.
Fig. 9.
Images and spectral profiles of a halogen bulb emitter acquired during a power on/off cycle. A pseudo-colored, panchromatic image of the halogen bulb emitter in an off state acquired at time t = 0 (a). A panchromatic image of a tungsten emitter in an on state, acquired at time t = 2.75 s (b). Spectral intensity plots taken at t = 0.9 s, t = 1.7 s and t = 3.07 s scaled (to the detector’s dynamic range) and normalized are given in (c) and (d) respectively. Time laps recording of the halogen bulb during an on/off cycle is given in Visualization 2 (9.3MB, mp4) .
Please note that neutral density filters were not used and we relied entirely on the dynamic range of the detector to acquire spectral signatures of the halogen bulb over a full on/off cycle.
5. Conclusions
A new image mapping spectrometer based on a sCMOS detector is presented. The system is capable of acquiring (210x210x46) hyperspectral data cubes at 100 fps rate. The spectral range covers the VIS and NIR wavelengths in the range of 515-842 nm. Experimentally verified spectral accuracy was better than 1.5 nm in the 515-705 nm range and was on average 1.1 nm in the 515-740 nm range. Satisfactory performance was confirmed by measuring dispersion which matched designed values, and evaluating geometric distortions using a qualitative Ronchi ruling test together with a resolution test using a 1951 USAF bar target. Because the utilized detector has only 1.1 e- read noise (slow scanning mode), acquisition of data in shot noise limited mode is possible in nearly the entire 89.5 dB dynamic range. The HS-IMS system differs significantly from previous generations of image mapping spectrometers. It uses a small form factor imaging detector, has re-designed opto-mechanics, and is capable of data acquisition at a rate which is ~14 times faster compared to previous generations of the direct image mapping spectrometers.
Performance of the newly developed system was directly compared to a representative image mapping spectrometer from previous generations. Two samples were used to illustrate advantages of the newly developed system. Reference fluorescent beads and a BPAEC slide were simultaneously observed by both systems through a 50/50 beam splitter, and evidence to support superior performance of the newly developed systems was shown by directly comparing the spectral signature acquired by both compared systems. Dynamic range of the new spectrometer together with its ability to acquire data at 100 fps were presented in an experiment in which emission spectrum of a halogen bulb was continuously monitored during a power on/off cycle. The capability to monitor dynamic events in the full field of view without introduction of motion related artifacts was demonstrated in an experiment where free falling ping pong balls selectively stained with infrared dye were observed.
In the future we plan to employ the newly developed HS-IMS system to the observation of transient events in fluorescently stained living cells to study dynamic cellular processes. Additionally, we plan to take advantage of its high dynamic range by performing direct measurements of the absorbance/transmittance spectral signatures of thin pathological slides and integrate the newly developed spectrometer with a fundus camera to study retinal tissue perfusion. A small, compact version of this instrument will be developed in the future for use in remote sensing applications.
Acknowledgements
We would like to acknowledge Nathan Hagen for his analysis of manufacturability of the imaging spectrometer based on a small form factor imaging sensor. We would like to thank Richard Schwarz and Cynthia Wong for fruitful discussions and help in preparation of this manuscript.
Funding
The National Institutes of Health (NIH) (NIH P41RR0001192); St. Michaels Hospital, Toronto, CA research services agreement financed through Canada Foundation for Innovation (31326).
Disclosures
Tomasz S. Tkaczyk has financial interests in Attoris LLC focusing on hyperspectral technologies.
References
- 1.Torr M. R., Vitz R. C., “Extreme ultraviolet imaging spectrometer for thermospheric emissions,” Appl. Opt. 21(17), 3080–3090 (1982). 10.1364/AO.21.003080 [DOI] [PubMed] [Google Scholar]
- 2.Dittman M. G., Ramberg E., Chrisp M., Rodriguez J. V., Sparks A. L., Zaun N. H., Hendershot P., Dixon T., Philbrick R. H., Wasinger D., “Nadir ultraviolet imaging spectrometer for the NPOESS Ozone Mapping and Profiler Suite (OMPS),” In Earth Observing Systems VII 4814, 111–120 (2002). [Google Scholar]
- 3.Breckinridge J. B., Page N. A., Shannon R. R., Rodgers J. M., “Reflecting Schmidt imaging spectrometers,” Appl. Opt. 22(8), 1175–1180 (1983). 10.1364/AO.22.001175 [DOI] [PubMed] [Google Scholar]
- 4.Vane G., Goetz A. F. H., Wellman J. B., “Airborne imaging spectrometer: A new tool for remote sensing,” IEEE Trans. Geosci. Remote Sens. GE-22(6), 546–549 (1984). 10.1109/TGRS.1984.6499168 [DOI] [Google Scholar]
- 5.Rode J. P., Brownell M. L., Herring M., “HgCdTe infrared focal plane arrays for imaging spectrometer applications,” Advanced Infrared Sensor Technology 395, 48–54 (1983). 10.1117/12.935180 [DOI] [Google Scholar]
- 6.Willoughby C. T., Folkman M. A., Figueroa M. A., “Application of hyperspectral imaging spectrometer systems to industrial inspection,” Three-Dimensional and Unconventional Imaging for Industrial Inspection and Metrology 2599, 264–272 (1996). 10.1117/12.230385 [DOI] [Google Scholar]
- 7.Khan M. J., Khan H. S., Yousaf A., Khurshid K., Abbas A., “Modern Trends in Hyperspectral Image Analysis: A Review,” IEEE Access 6, 14118–14129 (2018). 10.1109/ACCESS.2018.2812999 [DOI] [Google Scholar]
- 8.Eismann M. T., Hyperspectral Remote Sensing,(SPIE Press, 2012). [Google Scholar]
- 9.Sun D.-W., Hyperspectral Imaging for Food Quality Analysis and Control, (Elsevier, 2010). [Google Scholar]
- 10.Keith E., O’Connell D., Johnson W., Basty S., Dereniak E. L., “Hyperspectral imaging for astronomy and space surveillance,” Proc. SPIE 5158, 380–391 (2004). [Google Scholar]
- 11.Sivakumar V., Neelakantan R., Santosh M., “Lunar surface mineralogy using hyperspectral data: implications for primordial crust in the Earth-Moon system,” Geoscience Frontiers 8(3), 457–465 (2017). 10.1016/j.gsf.2016.03.005 [DOI] [Google Scholar]
- 12.Thenkabail P. S., Lyon J. G., Huete A., Hyperspectral Remote Sensing of Vegetation, (CRC Press, 2012). [Google Scholar]
- 13.Shen L., Xu H., Guo X., “Satellite remote sensing of harmful algal blooms (HABs) and a potential synthesized framework,” Sensors (Basel) 12(6), 7778–7803 (2012). 10.3390/s120607778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Zhang F., Zhou G., “Estimation of canopy water content by means of hyperspectral indices based on drought stress gradient experiments of maize in the north plain China,” Remote Sens. 7(11), 15203–15223 (2015). 10.3390/rs71115203 [DOI] [Google Scholar]
- 15.Majda A., Wietecha-Posluszny R., Mendys A., Wojtowicz A., Lydzba-Kopczynska B., “Hyperspectral imaging and multivariate analysis in the dried blood spots investigations,” Appl. Phys., A Mater. Sci. Process. 124(4), 312 (2018). 10.1007/s00339-018-1739-6 [DOI] [Google Scholar]
- 16.Edelman G. J., Gaston E., van Leeuwen T. G., Cullen P. J., Aalders M. C. G., “Hyperspectral imaging for non-contact analysis of forensic traces,” Forensic Sci. Int. 223(1-3), 28–39 (2012). 10.1016/j.forsciint.2012.09.012 [DOI] [PubMed] [Google Scholar]
- 17.Liang H., “Advances in multispectral and hyperspectral imaging for archaeology and art conservation,” Appl. Phys., A Mater. Sci. Process. 106(2), 309–323 (2012). 10.1007/s00339-011-6689-1 [DOI] [Google Scholar]
- 18.Legrand S., Vanmeert F., van der Snickt G., Alfeld M., De Nolf W., Dik J., Janssens K., “Examination of historical paintings by state-of-the-art hyperspectral imaging methods: from scanning infra-red spectroscopy to computed X-ray laminography,” Heritage Science 2(1), 13 (2014). 10.1186/2050-7445-2-13 [DOI] [Google Scholar]
- 19.Baiano A., “Applications of hyperspectral imaging for quality assessment of liquid based and semi-liquid food products: A review,” J. Food Eng. 214, 10–15 (2017). 10.1016/j.jfoodeng.2017.06.012 [DOI] [Google Scholar]
- 20.Zheng Y., Bai J., Xu J., Li X., Zhang Y., “A discrimination model in waste plastics sorting using NIR hyperspectral imaging system,” Waste Manag. 72, 87–98 (2018). 10.1016/j.wasman.2017.10.015 [DOI] [PubMed] [Google Scholar]
- 21.Lu G., Fei B., “Medical hyperspectral imaging: a review,” J. Biomed. Opt. 19(1), 10901 (2014). 10.1117/1.JBO.19.1.010901 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Calin M. A., Parasca S. V., Savastru D., Manea D., “Hyperspectral Imaging in the Medical Field: Present and Future,” Appl. Spectrosc. Rev. 49(6), 435–447 (2013). 10.1080/05704928.2013.838678 [DOI] [Google Scholar]
- 23.Levenson R. M., Mansfield J. R., “Multispectral imaging in biology and medicine: slices of life,” Cytometry A 69A(8), 748–758 (2006). 10.1002/cyto.a.20319 [DOI] [PubMed] [Google Scholar]
- 24.Gao L., Kester R. T., Hagen N., Tkaczyk T. S., “Snapshot Image Mapping Spectrometer (IMS) with high sampling density for hyperspectral microscopy,” Opt. Express 18(14), 14330–14344 (2010). 10.1364/OE.18.014330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Vermot J., Fraser S. E., Liebling M., “Fast fluorescence microscopy for imaging the dynamics of embryonic development,” HFSP J. 2(3), 143–155 (2008). 10.2976/1.2907579 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hagen N., Kudenov M. W., “Review of snapshot spectral imaging technologies,” Opt. Eng. 52(9), 090901 (2013). 10.1117/1.OE.52.9.090901 [DOI] [Google Scholar]
- 27.Nag S., Hewagama T., Georgiev G. T., Pasquale B., Aslam S., Gatebe C. K., “Multispectral snapshot imagers onboard small satellite formations for multi-angular remote sensing,” IEEE Sensors 17(16), 5252–5268 (2017). 10.1109/JSEN.2017.2717384 [DOI] [Google Scholar]
- 28.Hagen N., Kester R. T., Gao L., Tkaczyk T. S., “Snapshot advantage: a review of the light collection improvement for parallel high-dimensional measurement systems,” Opt. Eng. 51(11), 111702 (2012). 10.1117/1.OE.51.11.111702 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Elliott A. D., Gao L., Ustione A., Bedard N., Kester R., Piston D. W., Tkaczyk T. S., “Real-time hyperspectral fluorescence imaging of pancreatic β-cell dynamics with the image mapping spectrometer,” J. Cell Sci. 125(Pt 20), 4833–4840 (2012). 10.1242/jcs.108258 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Gao L., Kester R. T., Tkaczyk T. S., “Compact Image Slicing Spectrometer (ISS) for hyperspectral fluorescence microscopy,” Opt. Express 17(15), 12293–12308 (2009). 10.1364/OE.17.012293 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gao L., Smith R. T., Tkaczyk T. S., “Snapshot hyperspectral retinal camera with the Image Mapping Spectrometer (IMS),” Biomed. Opt. Express 3(1), 48–54 (2012). 10.1364/BOE.3.000048 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Nguyen T. U., Pierce M. C., Higgins L., Tkaczyk T. S., “Snapshot 3D optical coherence tomography system using image mapping spectrometry,” Opt. Express 21(11), 13758–13772 (2013). 10.1364/OE.21.013758 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Gao L., Kester R. T., Hagen N., Tkaczyk T. S., “Snapshot Image Mapping Spectrometer (IMS) with high sampling density for hyperspectral microscopy,” Opt. Express 18(14), 14330–14344 (2010). 10.1364/OE.18.014330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bedard N., Hagen N., Gao L., Tkaczyk T. S., “Image mapping spectrometry: calibration and characterization,” Opt. Eng. 51(11), 111711 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dwight J. G., Weng C. Y., Coffee R. E., Pawlowski M. E., Tkaczyk T. S., “Hyperspectral Image Mapping Spectrometry for Retinal Oximetry Measurements in Four Diseased Eyes,” Int. Ophthalmol. Clin. 56(4), 25–38 (2016). 10.1097/IIO.0000000000000139 [DOI] [PMC free article] [PubMed] [Google Scholar]