Theory and design of Schwarzschild scan objective for Optical Coherence Tomography

Abstract

Optical coherence elastography (OCE) is one form of multi-channel imaging that combines high-resolution optical coherence tomography (OCT) imaging with mechanical tissue stimulation. This combination of structural and functional imaging can require additional space to integrate imaging capabilities with additional functional elements (e.g., optical, mechanical, or acoustic modulators) either at or near the imaging axis. We address this challenge by designing a novel scan lens based on a modified Schwarzchild objective lens, comprised of a pair of concentric mirrors with potential space to incorporate additional functional elements and minimal compromise to the available scan field. This scan objective design allows perpendicular tissue-excitation and response recording. The optimized scan lens design results in a working distance that is extended to ~140 mm (nearly 2x the focal length), an expanded central space suitable for additional functional elements (>15 mm in diameter) and diffraction-limited lateral resolution (19.33 μm) across a full annular scan field ~ ± 7.5 mm to ± 12.7 mm.

1. Introduction

A Multi-channel optical system contains several independent working channels with various functionalities, such as illumination, mechanical stimulation, imaging, etc. In biomedical and clinical studies, the independent imaging channels could include modalities, such as confocal microscopy, ultrasound, x-ray, magnetic resonance imaging, fluorescence intensity imaging, two-photon imaging, and optical coherence tomography. Compared to a specific single-channel imaging system, multi-channel optical systems can provide complementary, synergistic information, or enable rapid switching between different modes and functions [1]. The use of a multi-channel optical system is helpful to expand the potential uses of non-invasive imaging. For example, dynamic elasticity imaging systems are used to determine tissue mechanical properties (e.g., stiffness) [2,3] by combining a mechanical loading channel (a source of sample stimulation) and an imaging channel to record the sample response.

Optical coherence elastography (OCE) [4] is an emerging elasticity imaging technique that employs at least two channels. A loading channel is used to induce elastic waves in a tissue using techniques, such as optical, mechanical, or acoustic modulators for sample stimulation. Various approaches of loading methods have been developed, such as static [5,6], dynamic contact [4,7–9], audio sound [10], pulsed laser [11,12], and air puff/pulse [13–15] loading. The second channel uses optical coherence tomography (OCT) [16] imaging to record the tissue response. Compared to traditional ultrasound elastography [17–19] and magnetic resonance elastography [20,21], OCT can noninvasively obtain tissue mechanical properties with higher spatial resolution and faster speeds [22]. Phase-sensitive OCT methods [23–27] have further improved the dynamic surface displacement detection sensitivity to a sub-nanometer scale. For example, we reported a 0.24 nm resolution in our common-path OCE results [28]. More channels may be added into the OCE system for specific purposes. For example, a targeting channel and a monitoring camera can be used for locating the regions of stimulus and imaging in the tissue.

The combination of a loading mechanism and OCT imaging usually requires space between the OCT scan objective and sample, especially for dynamic/transient, non-contact OCE applications [10–15]. An optimal OCE set-up should satisfy certain criteria. First, the loading channel should be set up to deform tissue in a predictable way so that tissue mechanical properties can be derived from the deformation response. Loading normal to the surface is advantageous since it simplifies the complex modeling methods that are used to derive the mechanical properties from the observed response [4–6]. Second, measurement distance to the stimulation point should be optimized to clearly record the induced wave-propagation and to avoid near-field effects [29]. Capability of measuring around the stimulation point would also be advantageous to determine tissue anisotropy.

However, spatial conflict often occurs between the physical bulk of the loading system and a limited space provided by the OCT system. Consequently, oblique tissue-excitation has been adopted by several investigators instead of the preferred perpendicular tissue-excitation [7,8,11–14]. The axial distance between the OCT scan objective and sample is usually similar to, or shorter than, the focal length of the scan objective lens. The focal length is often relatively short to achieve a desired optical lateral resolution. For instance, the focal length of the OCT scan lens of our OCE system in [28] was 54 mm, and the total working distance was 42 mm. Therefore, designing a scan objective with a longer working distance without sacrificing optical performance is important for OCE imaging to quantify tissue biomechanics.

Here we describe a novel OCE scan objective comprised of a pair of concentric convex and concave mirrors. This reflective objective is a modification of a Schwarzschild lens design [30]. First-order theory is used to determine the general geometric parameters, especially the focal length, working distance, and dimensional constraint criteria of the Schwarzschild scan objective. Astigmatism for the marginal rays of each scan beam is derived and minimized based on the Coddington equations [31,32]. Optical path differences (OPDs) among all scan beams are reduced to provide effective OCT interference signals from reference and sample arms. The Schwarzschild scan objective extends the working distance and enables adequate free space to accommodate a loading system that can deliver force normal to the tissue surface. Since all the optical elements are mirrors, this Schwarzschild scan objective is free of chromatic aberration and is idea for applications in systems with broad bandwidth (e.g. from visible to near-infrared range that is usually applied in OCT systems).

A Schwarzschild scan objective is designed for, but not limited to, OCE imaging systems. It may also benefit other multi-channel imaging systems that combine peripheral scans with central channels of various purposes. For example, a camera situated in the center area, enclosed by the peripheral scan beams, can serve as a view-finder to guide the scan beams to specific locations. An illumination light source situated in the center of the scan beams may also benefit fluorescence or two-photon imaging.

2. Theory

2.1 Schwarzschild scan objective

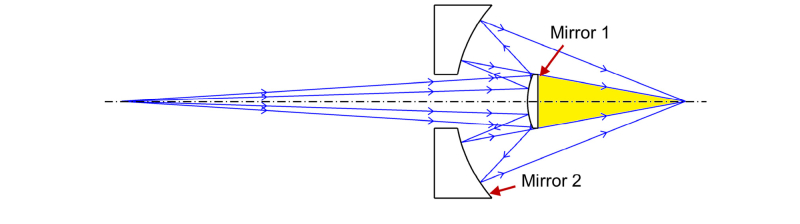
The Schwarzschild system [30] was initially designed for astronomical telescopes and was more recently adopted for use in microscope objectives [33–36].The Schwarzschild system consists of two mirrors, as demonstrated in Fig. 1. Previous publications have discussed the use of the Schwarzschild design to correct Seidel aberrations, such as spherical aberration, coma, astigmatism and distortion, and to provide a flat field when the object is either in an infinite or finite distance [33–36].

Fig. 1.

Schematic of a classic Schwarzschild objective that consists of two mirrors. The object distance is demonstrated in a finite distance. The potential space (yellow shaded region) can be used to include additional channels (e.g. functional elements) to create a multi-channel imaging system.

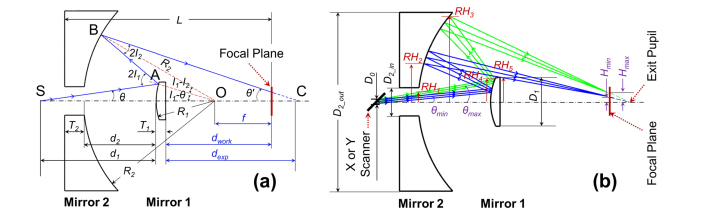
We extend the application of the Schwarzschild construction to a scan objective that will accommodate additional functional elements for multi-channel imaging (Fig. 1). As demonstrated in Fig. 2, the newly-designed Schwarzschild scan objective is based on the classic Schwarzschild system, but requires modifications to address concerns specifically related to scanning optics. Mirror 1 is a convex mirror and Mirror 2 is a concave annular mirror, these two mirrors share the same central point located at the optical axis. Two-dimensional scanners (x and y) are positioned before the scan objective. For simplifying the theory and calculations, we employ one scanner for this analysis. The collimated light beam is demonstrated by a chief-ray and two marginal rays. This beam is scanned by the scanners, is reflected by Mirror 1 and Mirror 2 in sequence, then bypasses Mirror 1 again, and finally is focused at the focal plane.

Fig. 2.

Configuration geometry of the Schwarzschild scan objective which consists of concentric Mirror 1 and Mirror 2. Only one scanner was shown here for simplicity. (a) Ray-tracing for an arbitrary chief ray with the scan angle of θ. R₁ and R₂ are the radii of curvature, and T₁ and T₂ are the center thickness for Mirror 1 and Mirror 2, respectively. O is the mutual center point of the curvatures of the mirrors. S is the pivot point of the scanner. The distance between point S and Mirror 1 is d₁, the distance between Mirror 2 and Mirror 1 is d₂. The chief ray interacts with the two mirrors at points A and B with incident angles I₁ and I₂, respectively. The chief ray is incident on the focal plane (θ’) before the point C (exit pupil position). f is the focal length of the Schwarzschild scan object, and equals to the distance from point O to the focal plane. L is the total length. d_work and d_exp are the working distance and exit pupil distance, respectively. (b) Ray-tracing of the scan beams with the minimal and the maximal scan angles (θ_min and θ_max, respectively). The reserved central area of loading is in a central zone of ± H_min, while the peripheral area of scanning is in the annular zone of ± (H_min – H_max) at the focal plane. D₀ is the input beam size, D₁ is the diameter of Mirror 1, and D_{2_out} and D_{2_in} are the outer and inner diameters of Mirror 2, respectively. RH₁ to RH₅ are the specific marginal ray heights.

Figure 2 (a) demonstrates the ray-tracing of the chief ray for a scan beam with the scan angle of θ in the Schwarzschild scan objective. O is the mutual center point of the curvatures of the mirrors. S is the pivot point of the scanner. The chief ray is incident upon the two mirrors at points A and B with angles I₁ and I₂, respectively. C is the exit pupil position. f is the focal length of the Schwarzschild scan objective, and is equal to the distance from point O to the focal plane. L is the total length; d_work and d_exp are the working distance and exit pupil distance, respectively. Figure 2 (b) demonstrates the ray-tracing of the scan beams with the minimal and the maximal scan angles (θ_min and θ_max, respectively). The central aperture at the focal plane is ± H_min, which precludes imaging within this central area and enables the space for the loading mechanism required by OCE applications. The peripheral annular area at the focal plane — ± (H_min to H_max), defined by the scan angel range (θ_min to θ_max) — is available for OCT imaging.

There are some additional concerns in the design of the Schwarzschild scan objective compared to the classic Schwarzschild construction.

• (1) The scan angles (θ_min to θ_max) and the scan zone at the focal plane ( ± H_min to ± H_max) are constrained by the physical size and distance of the two mirrors. For example, the size of Mirror 1 should be big enough to reflect the beam with the maximum scan angle (θ_max) and should be also small enough to ensure the passage of the beam with the minimum scan angle (θ_min) in a non-vignetting condition. Therefore, the modified design incorporated these additional dimensional constraints and established a new criterion to meet the spatial requirements for the Schwarzschild scan objective design.
• (2) The light path of the chief ray for each scan beam in the newly-designed Schwarzschild scan objective (Fig. 2(a)) is similar to the light path of each ray in the classic paraxial Schwarzschild construction (Fig. 1). We used methods described in previous work [33–36] to correct Seidel aberrations of the chief rays. However, the layout for each scan beam (Fig. 2(b)) is off-axis with incident angles which can be tens of degrees to the normal of each mirror. Also, the incident angles for all of the scan beams are also over a wide range (tens of degrees). In this application, astigmatism becomes the major contribution to the total aberrations [37] of each scan beam, and the value of astigmatism varies by scan location. Therefore, minimization of astigmatism across the entire scan range was a major design goal.
• (3) This Schwarzschild scan objective was developed for an OCT-based elastography application. OCT imaging is a form of low-coherence interferometry where the interference signal is generated by combining light from reference and sample arms [38]. Effective interference requires minimal optical path difference between these two arms. Therefore, the light path length difference among the chief-rays of all the scan beams was constrained to meet the requirement of OCT detection.

2.2 Key points for the Schwarzschild scan objective design

The design principles for the Schwarzschild scan objective are provided as follows:

• (1) First-order optical design principles were used to determine the general geometry of the Schwarzschild scan objective that would maximize the axial working distance (defined by the radii of the mirrors (Fig. 2)) without greatly enlarging the radial dimensions of the scan lens for a specified scan range. The extended working distance was derived by calculating the axial dimensions and the radial dimensions were primarily determined by the defined scan range.
• (2) The Coddington equations [31,32] were applied to quantify the astigmatism, defined as the difference in focal distance between the tangential and sagittal marginal rays [39,40] for each scan beam. The astigmatism value across the whole scan range was then evaluated and minimized by optimizing the design parameters.
• (3) The chief-ray optical length (OPL) was calculated for each scan beam. The optical path differences (OPDs) of all the chief-rays from all of the scan beams were estimated. The OPD values were balanced with other design requirements (e.g. size of the system, astigmatism) to enable the use of the Schwarzschild scan objective in OCT imaging.

The detailed theoretical analysis for the above design concerns are discussed in the following sections.

2.3 Axial dimensions and working distance extension

The radii of curvatures for Mirror 1 and Mirror 2 are R₁ and R₂, respectively, both are defined as positive values. The focal lengths of these two mirrors are f₁ = -R₁ / 2 and f₂ = R₂ / 2. We define R₂ = M × R₁ (M >1), where M is ratio of the raddi of curvatures as well as the ratio of focal lengths between two mirrors. The distance between scanner and Mirror 1 is d₁. The distance between Mirror 2 and Mirror 1 is d₂, where d₂ = R₂ - R₁ because Mirror 1 and Mirror 2 are concentric. The total focal length f of the objective can be calculated as:

$$f=\frac{f_1{f}_2}{f+f_2-d_2}=\frac{M{R}_1}{2\left(M-1\right)},$$ (1)

where M = 2f / (2f - R₁), R₂ = 2fR₁ / (2f - R₁), and d₂ = R₁² / (2f - R₁).

The exit pupil distance d_exp is defined as the axial distance from Mirror 1 to the exit pupil, and the working distance d_work is defined as the axial distance from Mirror 1 to the focal plane. d_exp and d_work can be expressed as:

$$d_{\exp }=\left[\frac{M{d}_1+M{R}_1}{2d_1\left(M-1\right)+R_1\left(M-2\right)}+1\right]\times R_1-T_1,$$ (2)

$$d_{work}=\left(\frac{M}{2M-2}+1\right)\times R_1-T_1,$$ (3)

where T₁ and T₂ are the center thicknesses for the two mirrors. Comparing Eq. (1) and Eq. (3), we have:

$$d_{work}=f+R_1-T_1,$$ (4)

If R₁ > T₁, then d_work > f. Therefore, the working distance can be extended to a longer value than the focal length. For the same value of f, d_work is increased by the same amount as R₁ is increased. Therefore, f is equal to the distance from the mutual center point of the two mirrors to the focal plane. The total length L from Mirror 2 to the focal plane can be expressed as:

$$L=T_1+R_2+f=\frac{\left(2M-1\right)}{2\left(M-1\right)}\times M{R}_1+T_1.$$ (5)

2.4 Radial dimensions and dimensional constraint criteria

Scan angle θ is in the range of θ_min to θ_max, its corresponding scan length H (H = f tanθ) at the focal plane is in the range of H_min to H_max. Figure 2 depicts RH₁ to RH₅, the specific marginal ray heights. RH₁ is the maximum ray height inside the center hole of Mirror 2. RH₂ and RH₃ are the inner and outer ray heights for the light annulus on Mirror 2. RH₄ is the maximum ray height at the front surface of Mirror 1, and RH₅ is the minimum ray height at the back surface of Mirror 1. These marginal ray heights can be expressed as:

$$\{\begin{array}{l}R{H}_1=\left(d_1-d_2\right)\tan {\theta }_{\max }+\frac{D_0}{2},\\ R{H}_2=\left[d_1\left(2M-1\right)+R_1\left(M-1\right)\right]\times \tan {\theta }_{\min }-\frac{\left(2M-1\right)}{2}{D}_0,\\ R{H}_3=\left[d_1\left(2M-1\right)+R_1\left(M-1\right)\right]\times \tan {\theta }_{\max }+\frac{\left(2M-1\right)}{2}{D}_0,\\ R{H}_4=d_1\tan {\theta }_{\max }+\frac{D_0}{2},\\ R{H}_5=\left\{1-\frac{\left[2d_1\left(M-1\right)+R_1\left(M-2\right)\right]\left[R_1\left(M-1\right)+T_1\right]}{M{R}_1\left[d_1\left(2M-1\right)+R_1\left(M-1\right)\right]}\right\}\\ \times \left\{\left[d_1\left(2M-1\right)+R_1\left(M-1\right)\right]\tan {\theta }_{\min }-\frac{\left(2M-1\right)}{2}{D}_0\right\},\end{array}$$ (6)

where D₀ is the entrance pupil size or beam size, D₁ is the diameter of Mirror 1, and D_{2_out} and D_{2_in} are the outer and inner diameters for Mirror 2. The expressions for RH₁ to RH₅ all consist of two components. The first component contains either tanθ_max or tanθ_min, and denotes the chief ray heights. The second component contains D₀, and denotes the half beam size at the corresponding surface.

To avoid vignetting in Mirror 1 and Mirror 2, the following dimensional criteria should be satisfied:

$$\{\begin{array}{l}\frac{2R{H}_3}{{\rho }_{2\_out}}\le D_{2\_out},\hfill \\ 2R{H}_1\le D_{2\_in}\le 2R{H}_2\times {\rho }_{2\_in},\hfill \\ \frac{2R{H}_4}{{\rho }_1}\le D_1\le 2R{H}_5,\hfill \end{array}$$ (7)

where ρ₁, ρ₂, and ρ_{2_out} are the ratios for the clear aperture (usually, ρ ≈90%). The first criterion defines the minimum requirement for D_{2_out}. The second criterion ensures the vignetting-free condition for Mirror 2 where the scan beams can go through the center hole, and the reflected beams from Mirror 1 can reach the effective optical portion of Mirror 2. The third criterion determines the vignetting-free condition for Mirror 1 so that the scan beams can be reflected by the clear aperture of Mirror 1, while the reflected light from Mirror 2 can bypass the outside diameter of Mirror 1.

2.5 Optical path length (OPL) and optical path difference (OPD)

To guarantee the effective interference between the signals from the sample arm (where OPL varies across the field of view) and the reference arm (where OPL is a constant value), the OPD from all the chief-rays across the scan field in the sample arm must be limited to a certain range. As shown in Fig. 2, The OPL for this chief ray is dominated by R₁ and θ and can be expressed as:

$$\begin{array}{l}OPL\left(R_1,\theta \right)=\left|\overrightarrow{SA}\right|+\left|\overrightarrow{AB}\right|+\left|\overrightarrow{BC}\right|\\ =\frac{\sin \left(I_1-\theta \right)\left(\sin \theta +\sin I_2\right)}{\sin \theta \sin I_2}\times R_1+\frac{1+2\left(M-1\right)\cos \left(2I_1-I_2-\theta \right)}{2\left(M-1\right)\cos \left(2I_1-2I_2-\theta \right)}\times M{R}_1,\end{array}$$ (8)

where

$$\{\begin{array}{c}{I}_1=\mathrm{arc\; sin}\left(\frac{d_1+R_1}{R_1}\times \sin \theta \right),\\ I_2=\mathrm{arc\; sin}\left(\frac{d_1+R_1}{R_2}\times \sin \theta \right).\end{array}$$ (9)

The maximum OPD from all the chief-rays across the scan field can be expressed as:

$$OP{D}_{\max }\left(R_1,\theta \right)=OPL\left(R_1,{\theta }_{\max }\right)-OPL\left(R_1,{\theta }_{\min }\right).$$ (10)

2.6 Astigmatism

As shown in Fig. 2, the layout for each scan beam is off-axis with large incident angles relative to the surface normal for each mirror. In this mirror-based, off-axis construction, the dominant aberration is astigmatism [37], defined as the difference in focal distance between the tangential and sagittal marginal rays [39,40]. Applying the Coddington equations [31,32] to Mirror 1 and Mirror 2, we can express the general astigmatism (AST) as:

$$AST(R_1,0)=\frac{M{R}_1(2M-2+\cos I_1)\cos I_2}{4(M-1)+2\cos I_1-2M\cos I_2}-\frac{M{R}_1[(2M-1)+\sec I_1]}{2\cos I_2[2(M-1)+\sec I_1-2M}$$ (11)

Corresponding to the different scan angle θ, the value of astigmatism varies across the scan field. We define a discrete mean absolute astigmatism (DMAA) equation to minimize the total amount of astigmatism in the required scan range:

$$DMAA=\frac{{\displaystyle \sum _{i=0}^k{a}_i\left|AST\left(R_1,{\theta }_i\right)\right|}}{{\displaystyle \sum _{i=0}^k{a}_i}},$$ (12)

where θ_i = θ_min + i(θ_max - θ_min)/k, k is the step number (i = 0, …, k), and α_i is the weight.

3. Quantitative simulation

We performed a quantitative simulation to demonstrate the design of the Schwarzschild scan objective. We first specified the design requirements and then computed the possible R₁ values that met each of the design requirements separately. We then optimized R₁ to simultaneously satisfy all of the requirements.

3.1 Design requirements

The design parameters for this Schwarzschild scan objective were defined by the current specifications of our clinical OCE system [28]. The spectral bandwidth of the OCT light source was 795 nm – 895 nm, D₀ = 4 mm, and f = 75 mm, the lateral resolution was 19.33 μm, calculated at the central wavelength of 845 nm. The requirements for the loading and scanning space were specified as d_work ≥ 120 mm, 2H_min ≥ 10 mm, and H_max to H_min ≈5 mm. The dimensional requirements were specified as D₁ ≤ 70 mm, D_{2_out} ≤ 200 mm, T₁ = 10 mm, T₂ = 20 mm – 30 mm, and L ≤ 300 mm. The distance requirements for the X and Y scanners were set to d_1Y - d_1X = 12.7 mm, and d_1X ≥ d₂ + T₂ + 15 mm. To simplify the calculation and keep the structure compact, we assigned d₁ = (d_1X + d_1Y)/2 = d₂ + 51.35 mm. This scan objective was designed for an OCT system with the capability of detecting 6.5 mm OPD between the sample arm and the reference arm. We specified the maximum OPD range across the entire FOV in the sample arm as 1.5 mm.

3.2 Computing R₁ values to meet each requirement

The key variable in the calculation and optimization is R₁, which is in the range of 0 to 2f. Here, we reduced its range to 0.5f to 1.5f (37.5 mm to 112.5 mm) to avoid extreme values in dimensions and aberrations.

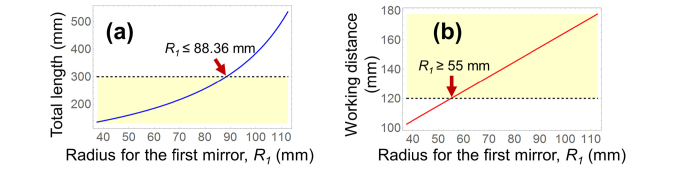
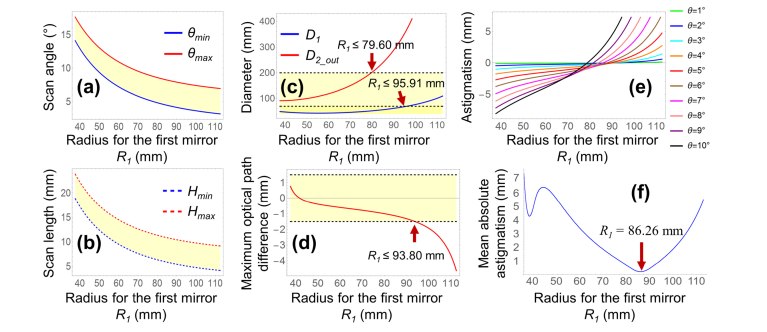
Figure 3 shows the axial dimensions for L and d_work corresponding to R₁, when f = 75 mm. To satisfy the requirements of L ≤ 300 mm and d_work ≥ 120 mm, R₁ should be in the range of 55 mm to 88.36 mm. As R₁ increased, d_work increased by the same amount, provided T₁ was kept constant (Eq. (4)).

Fig. 3.

Axial dimensions of (a) total length L and (b) working distance d_work. To meet the requirements of L ≤ 300 mm and d_work ≥120 mm, R₁ should be in the range of 55 mm – 88.36 mm (yellow-shaded areas).

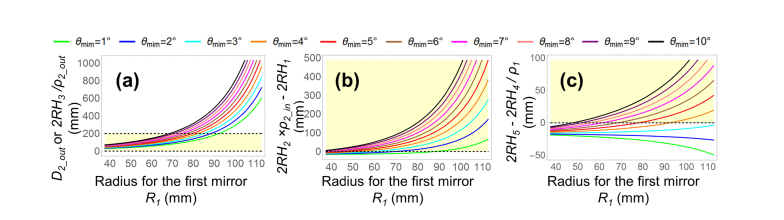
The marginal rays for RH₁ to RH₅ were traced to satisfy the dimensional criteria in Eq. (7). Figure 4 (a) corresponds to the first constraint, which defines the minimum value for D_{2_out} (ρ_{2_out} = 90%). The required D_{2_out} increased when R₁ was increased. A larger D_{2_out} would be more difficult to manufacture and result in higher manufacturing costs. Thus, limiting D_{2_out} to as small a value as possible, such as in a range smaller than 200 mm, was found to be beneficial, while still satisfying the design requirements.

Fig. 4.

Marginal ray tracing for RH₁ to RH₅, to satisfy the dimensional constraint criteria in Eq. (7) for different values of R₁ and θ_min. (a) Satisfaction of first criterion, representing the minimum diameter for D_{2_out}. (b) Satisfaction of second criterion, representing the vignetting-free condition around the center hole in Mirror 2. (c) Satisfaction of the third criterion, representing the vignetting-free condition for Mirror 1 (ρ₁ = ρ_{2_out} = ρ_{2_in} = 90%). Yellow-shaded areas show the radial dimensional constraint requirements.

Figures 4 (b) and (c) represent the second and third criteria that enable the vignetting-free conditions for Mirror 1 and the center hole region of Mirror 2, where ρ₁ = ρ_{2_in} = 90%. These two criteria are met once the marginal height differences in both criteria are no less than zero, shown as yellow-shaded areas. As shown in Fig. 4 (b), once R₁ was set to a larger value, the second criteria was met with a smaller minimum scan angle θ_min. Figure 4 (c) shows that when θ_min = 1° to 3°, 2RH₅ - 2RH₄ / ρ₁ <0, and the light beams would not bypass Mirror 1, irrespective of the value of R₁ value. When θ_min ≥ 4°, as R₁ was increased, the minimum required θ_min was decreased. For each θ_min, the desired R₁ range to meet the third criterion was found to be within the R₁ range required to meet the second criterion. Thus, the third criterion in this design was stricter than the second criterion. That is, satisfying the third criterion assured the satisfaction of the second criterion.

D_{2_in} was set to a value between 2RH₁ and 2RH₂ × ρ_{2_in}. Therefore, we utilized the minimum requirement of the third criterion (2RH₄/ρ₁ = 2RH₅) to calculate the desired scan angle range (θ_min to θ_max) and scan length range (H_min to H_max), as a function of R₁ (Fig. 3 (a) and (b)). When R₁ was increased, the minimum required θ_min was decreased. This result was consistent with Fig. 4 (c). Thus, both the scan angles and scan lengths were reduced.

Once the scan angle range (θ_min to θ_max) was determined, we computed the diameter requirements for D₁ and D_{2_out} as a function of R₁ (Fig. 5 (c)). To meet the requirement of D₁ ≤ 70 mm and D_{2_out} ≤ 200 mm, R₁ was required to be less than 79.60 mm.

Fig. 5.

The equality 2RH₄/ρ₁ = 2RH₅ was used to determine (a) θ_min to θ_max, (b) H_min to H_max, (c) D₁ and D_{2_out}, and (d) OPD_max in related to the radius of the Mirror 1 (R₁). Yellow-shaded areas in (a) to (d) represent the desired value ranges. (e) Astigmatism for general scan angles (1° to 10°, with a step of 1°) without considering the physical constraints. (f) Astigmatism minimization using DMAA method (when α_i = 1) for the constraint-determined scan angle range of θ_min to θ_max.

Figure 5 (d) shows the OPD_max curve we computed by substituting θ_min and θ_max from Fig. 5 (a) into Eqs. (8), (9), and (10). When R₁ = 41.67 mm then OPD_max = 0, when R₁ < 41.67 mm then OPD_max > 0, and when R₁ > 41.67 mm then OPD_max < 0. To restrict OPD in the range of ± 1.5 mm, R₁ was required to be in the range of 37.5 mm to 93.80 mm.

Based on Eqs. (9) and (11), the changes in astigmatism caused by R₁ and θ are shown in Fig. 5 (e). Larger values for θ were associated with a steeper slope for the relationship between astigmatism and R₁. Thus, for astigmatism reduction, the possible R₁ values were in a wider range when θ was a relatively small value, and the possible R₁ were in a narrower range when θ had a larger value. Given a certain value of θ, a corresponding R₁ can be selected to minimize astigmatism. However, given a range of θ, astigmatism cannot be fully eliminated. Thus, we computed the discrete mean absolute astigmatism (DMAA) (Eq. (12)) for the scan angle range of θ_min to θ_max, where α_i = 1, and k = (θ_max to θ_min)/0.01°. As shown in Fig. 5 (f), for the minimum value of DMAA = 0.2033 mm, R₁ equaled 86.26 mm.

If different weights (α_i) were assigned, e.g. more weight for the center field and less weight for the edge field, or vice versa, the optimal R₁ value calculated by the DMAA method was between 80 mm and 90 mm.

3.3 Calculation summary and optimization of R₁

The requirements for the key design parameter R₁ were:

• (1) To achieve the dimensional requirements of L ≤ 300 mm and d_work ≥ 120 mm, R₁ was limited to the range of 55 mm to 88.36 mm.
• (2) To relate all of the scan-related parameters (θ_min to θ_max, H_min to H_max, D₁, D_{2_out}, OPD, and astigmatism) to R₁, the minimum requirement of the third criterion in Eq. (8) was used, where 2RH₄/ρ₁ = 2RH₅.
• (3) To meet the diameter requirements of D₁ ≤ 70 mm and D_{2_out} ≤ 200 mm, R₁ was required to be less than 79.60 mm.
• (4) To restrict the absolute value of OPD_max less than 1.5 mm, R₁ was required to be in the range of 37.5mm to 93.80 mm. When R₁ = 41.67 mm, then OPD_max = 0; when 37.5 mm ≤ R₁ < 41.67 mm, then 0 < OPD_max ≤ 0.76 mm; and when 41.67 mm < R₁ ≤ 93.80 mm, then −1.5 mm ≤ OPD_max < 0.
• (5) To reduce the astigmatism for the entire scan field, R₁ was required to be in the range of 80 mm to 90 mm.

To satisfy requirements (1) to (5), R₁ was found to be optimal in the range 55 mm to 79.60 mm, where the requirements for L, d_work, D_{2_out} and OPD_max were met. However, this range of values for R₁ did not minimize astigmatism. Since the residual astigmatism decreased as the value of R₁ was increased in the range 55 mm – 79.60 mm (Fig. 5 (f)), we chose a relatively large R₁ value (75 mm). Note that, aspherical surfaces can be used to further minimize residual astigmatism and other aberrations.

4. Zemax validation and design results

We employed the optical design software Zemax (Zemax, LLC) to validate the calculation, and to finalize the design. Mirror 1 was designed as an aspherical mirror to further reduce aberrations. A low-order standard aspherical surface is given by [41]:

$$z(r)=\frac{r^2/R_1}{1+\sqrt{1-(1+k_1)r^2/R_1^2}},$$ (13)

where the optical axis is presumed in the z direction, z(r) is the sag value (the displacement of surface in the z direction from the vertex at a distance of r from the optical axis), and r is in the range 0 to 0.5ρ₁D₁. The conic constant k₁ of the aspherical Mirror 1 was set as the only variable to be optimized, along with all of the other parameters that were calculated in Section 3. The aspherical surface type is determined by k₁, and can be hyperbola (k₁ < –1), parabola (k₁ = –1), prolate ellipse (–1 < k₁ < 0), sphere (k₁ = 0), or oblate ellipse (k₁ > 0).

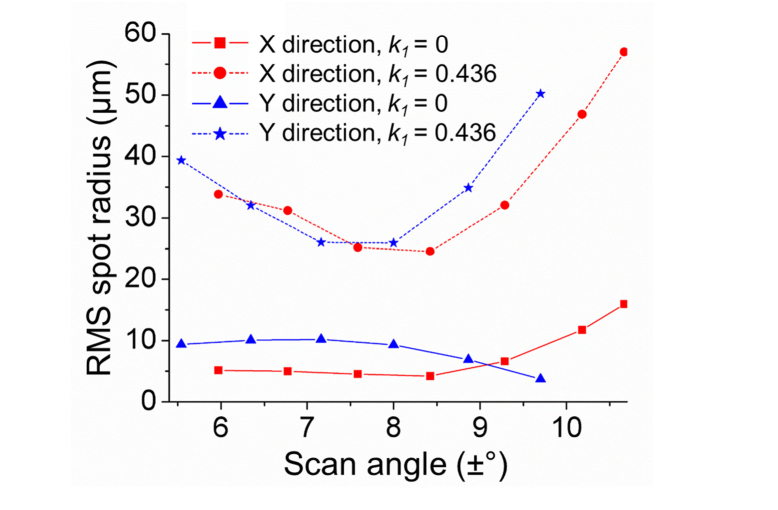
Using the damped least square algorithm in Zemax, k₁ was optimized to 0.436. For the two scanners, d_1x and d_1y were computed to be 120 mm and 134.7 mm, respectively. The scan fields in the x-direction and in y-direction were ± (5.97° to 10.67°) and ± (5.54° to 9.70°), respectively. The root mean square (RMS) spot sizes was reduced significantly across the scan field in both x and y directions when Mirror 1 was modeled as an oblate ellipsoid (since k₁ > 0), as shown in Fig. 6.

Fig. 6.

RMS spot size reduction by employing an aspherical (k₁ = 0.436, solid lines) Mirror 1, compared to when Mirror 1 is spherical (k₁ = 0, dotted lines).

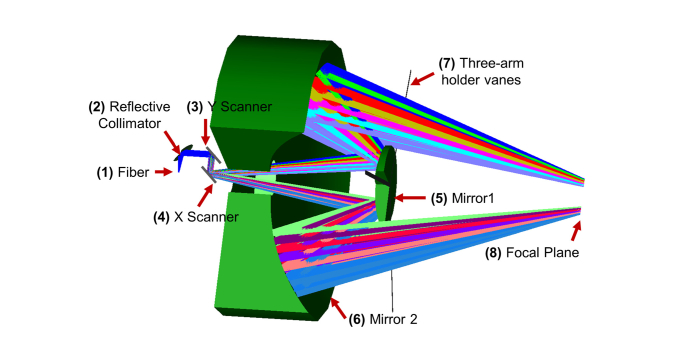
All of the optical elements in this Schwarzschild scan objective were mirrors (Fig. 7), ensuring no chromatic aberrations in broad bandwidths. The light coming out of the fiber was collimated by a parabolic reflective collimator (RC04FC-P01, Thorlabs), and then scanned by Galvo mirrors (GVS012, Thorlabs) in the x and y directions. The scan beams then passed through a 1-inch center hole in Mirror 2, were reflected by the concave Mirror 1 with 75 mm radius, and then reflected by the concave Mirror 2 with 150 mm radius. The outside diameters for Mirror 1 and Mirror 2 were 200 mm and 56 mm, respectively, and the outside clear apertures were 90% of their diameters. The distance between the two mirrors was 75 mm. The thicknesses of Mirror 1 and Mirror 2 were 10 mm and 30 mm, respectively. Mirror 1 was mounted using a three-arm holder vane. The working distance between the back of Mirror 1 to the focal plan was 139.8 mm.

Fig. 7.

Schematic of the Schwarzschild scan objective, designed using the outcome of the design requirement analysis and Zemax software simulation (drawed in 3/4 section).

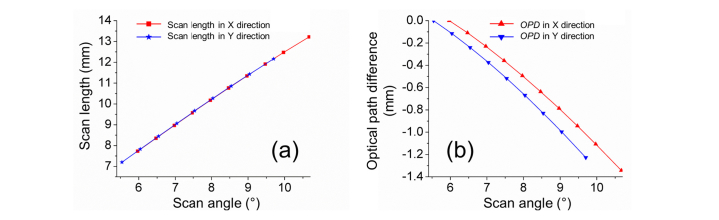
Figure 8 (a) shows a quasi-linear relation between the scan angles and scan lengths in the x and y directions, simulated in Zemax. This result was used to calibrate the lateral distortion for the objective. Figure 8 (b) shows the OPD across the scan fields, relative to the minimum scan angles, 5.97° in x direction and 5.54° in y direction. The maximum OPD across the scan field was 1.34 mm. The OPLs at bigger scan angles were found to be shorter. Figure 8 (b) can be used in the digital calibration to offset the axial distortion generated by OPD.

Fig. 8.

Distortion calibration in Zemax simulation. (a) Lateral distortion, demonstrated by the relation between scan angle and scan length. (b) Axial distortion, demonstrated by optical path difference (OPD) across the scan field.

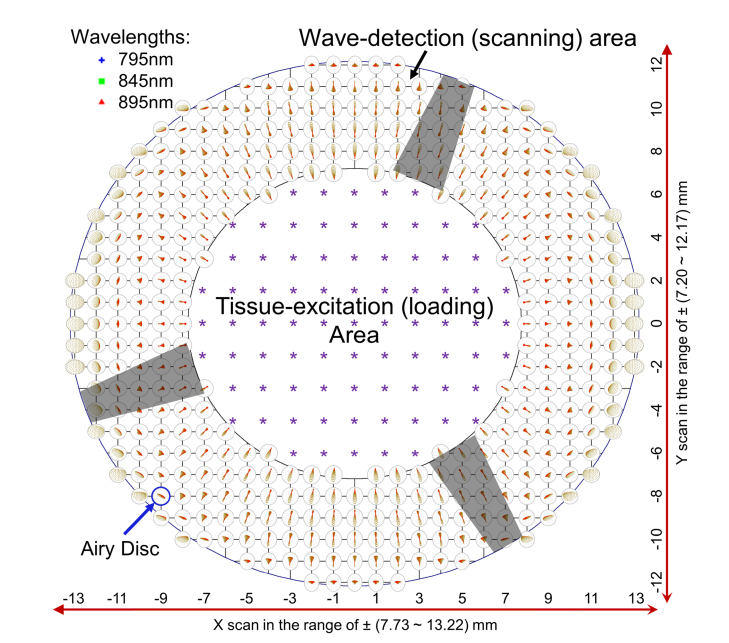
Figure 9 shows the tissue-excitation (loading) and the wave-detection (scanning) areas, as well as the spot diagrams of selected wavelengths (795 nm, 845 nm, and 895 nm) at the focal plane, simulated in Zemax. The scanning area was an elliptical annulus zone of ± (7.73 mm to 13.22 mm) in the x direction and ± (7.20 mm to 12.17 mm) in the y direction, centered at the optical axis. The loading area was an elliptical zone of ± 7.73 mm in the x direction and ± 7.20 mm in the y direction. The spots at different fields are shown as 1-mm intervals in scan length. These spots were free of chromatic aberration, and were scaled using the Airy disc at 845 nm wavelength, whose radius is theoretically 19.33 μm for a circular, uniformly illuminated entrance pupil. Therefore, the elliptical shapes of some circles are caused by non-uniform illuminations due to oblique light incidences. The radius of the Airy disc is equal to the minimum resolvable detail (diffraction-limited resolution) based on the Rayleigh criterion. If all of the rays are well within the Airy disk, then the system is often said to be diffraction-limited [41]. Except for several out-of-focus spots at the edge of the scan field, all other spots were within the Airy disk circles. The maximum RMS radius for the spots at the edge of the scan FOV was 16.49 μm, still smaller than the Airy disc radius. Thus, this scan objective was diffraction-limited. If each arm of the holder vane for Mirror 1 was 3 mm in width, the obscuration (shadow areas in Fig. 9) due to each arm is ~3 mm at the inner ellipse and ~2 mm at the outer ellipse in the scanning area.

Fig. 9.

Demonstration of the tissue-excitation (loading) and the wave-detection (scanning) areas, as well as the spot diagrams at the focal plane, simulated in Zemax. The purple stars show the possible loading locations. The distance between two spots is 1mm in the x and y directions. The shadow areas are due to the obscuration of the Mirror 1 mount.

5. Discussion

5.1 Non-uniform illumination due to angle of incidence

We used a telecentric scan lens in our previous OCE system [28] where the chief rays of scan beams were parallel to the optical axis and perpendicular to the focal plane. Compared to the non-telecentric construction, the telecentric scan lens can illuminate the sample more uniformly and collect more reflected/scattered light back to the system with a flat sample geometry (e.g. 2% agar phantom [28]).

In the Schwarzschild scan objective, scan beams are not perpendicular to the focal plane and the incident angel (θ’) varies across different scan positions. In the design example of Section 4, the incident angels at the focal plane vary from 9.88° to 19.14° in the x direction, and from 10.09° to 19.05° in the y direction. Illumination is positively correlated with cos⁴(θ’). When the sample surface was flat, the illuminance values were calculated as 94.2% – 79.7% in the x direction, and 94.0% – 79.8% in the y direction, relative to the perpendicular illumination.

Tissue samples may have any shape including convex surface geometry, such as the cornea [42]. In our previous work, we have quantified the biomechanical properties of rabbit [43–45] and porcine [46–49] corneas. We noticed that the imaging intensities and phase sensitivities dropped noticeably when imaging away from the apex or in the peripheral regions of the cornea using a telecentric scan lens. In this case, a scan lens with a convergent scan beam geometry would provide greater tissue illumination and back-light collection for better image contrast than a telecentric scan lens. The design example presented in section 4 has a larger work space relief to accommodate a loading channel for corneal OCE applications. Future designs could also include a convergent beam scan lens for other applications.

5.2 Design alternative I: optimizing d₁ to further reduce OPD

In Section 3.3, the required R₁ range was found to be 55 mm to 79.60 mm. Instead of choosing a smaller value (for example 55 mm) to reduce the OPD, we selected a value of 75 mm to reduce astigmatism. This resulted in a maximum absolute OPD of 1.34 mm, across the entire scan field (Fig. 8 (b)).

Without compromising the correction of astigmatism, another possibility for OPD reduction would be to adjust the value of d₁. Our calculations and simulations demonstrated that a smaller d₁ reduced OPD. However, the scanning mirrors in our design were big and had to be located to the left side of Mirror 2 (Fig. 7), resulting in a relatively big d₁ (120 mm and 134.7 mm, respectively for the two scanners). Using smaller scanners and mounts might reduce d₁ and further reduce OPD, if they can be located between Mirror 1 and Mirror 2.

5.3 Design alternative II: using spherical surfaces for both mirrors

For astigmatism minimization, we designed Mirror 1 as a standard aspherical mirror with a small diameter (56 mm) and small departures (k = 0.436) from a standard spherical mirror. The manufacturing cost for such a mirror is inexpensive.

If a larger R₁ value is chosen, such as 90 mm, both mirrors can be spherical surfaces and still achieve diffraction-limited performance. However, a larger R₁ will require a larger diameter Mirror 2 (> 300 mm). This would greatly increase the cost of manufacturing and mirror verification.

5.4 Design alternative III: splitting Mirror 2 as multiple small mirrors

Some specific applications may require better lateral resolution (related to D₀/f) or a need to accommodate larger scan areas (related to scan angles). Consequently, Mirror 2 with a larger aperture (e.g. > 200 mm) may be required to meet these demands. However, fabrication of a larger aperture of Mirror 2 is more difficult and expensive. A possible solution is to split Mirror 2 into multiple small mirrors, e.g. two or four mirrors. This mirror-splitting method can reduce the fabrication cost, but will require more complex construction as well as higher assembly cost.

5.5 Design alternative IV: mounting Mirror 1 onto glass to reduce obscuration

Holder vanes are commonly applied for mounting the small mirror into a two-reflector telescope, such as in the construction of Schwarzschild [30] and Cassegrain [50] lenses. Since the small mirror is usually located at the pupil plane in a conventional telescope, holder vanes do not generate blind spots at the image plane.

In our design, since Mirror 1 is not located at the pupil plane (Fig. 7), the three-arm holder vanes would induce obscurations at the focal plane (Fig. 9). Use of a flat glass window to mount Mirror 1 can effectively avoid such obscurations. We have performed the Zemax simulation using a 10-mm thick glass window (material: BK7) to mount Mirror 1 instead (wavelength: 795–895 nm). The point spread functions in the same scan areas are still diffraction-limited with only slightly increased chromatic dispersions over this wavelength range and this validates this glass window mount as a viable option. In addition, the reflective collimator used in Fig. 7 can be replaced by an achromatic lens-based collimator for this wavelength range as well. Choosing the mounting method would be determined by the specific design requirements, such as wave bandwidth, numerical number, scan angles, and complexity, as well as the preference of the designer.

6. Conclusion

We demonstrated the theory and design for an OCE reflective scan objective by employing a Schwarzschild design with two concentric convex and concave mirrors. This Schwarzschild scan objective extended the working distance, and enabled the use of central perpendicular tissue-excitation with peripheral wave-detection.

We presented a detailed theory in Section 2, where R₁ was chosen as the key value to calculate, optimize, and evaluate the main parameters, such as the axial dimensions, radial dimensions, radial constraints and dimensional criteria, OPD among chief rays, and astigmatism values for the scan beams.

In Section 3, the relation between the axial dimensions (L and d_work) and R₁ was demonstrated. The equation of 2RH₄/ρ₁ = 2RH₅ was used to further relate R₁ to other parameters, such as scan angles, scan lengths at the focal plane, OPD among chief rays, and astigmatism for the scan beams. After balancing all of these key design constraints, especially D_{2_out}, we chose R₁ = 75 mm.

In Section 4, we defined the conic constant for Mirror 1 surface as the only variable, and optimized this scan objective to further reduce astigmatism and the residual aberrations (Fig. 6). The reflective configuration provided a chromatic-aberration-free design. This feature enables its use in broad bandwidths (e.g. from visible to near-infrared range that is usually applied in OCT imaging). Lateral distortion (relation between the scan angle and scan length) and axial distortion (OPD) were presented for system calibration (Fig. 8). Regions of loading and scanning were defined and the diffraction-limited performance was achieved (Fig. 9).

In summary, a Schwarzschild scan objective was designed for broad bandwidth optical coherence elastography with a long working distance, central perpendicular tissue-excitation, and peripheral wave-detection. OPD of the chief rays and astigmatism values for the scan beams were reduced and the lateral resolution was diffraction-limited for the entire scan field. This Schwarzschild scan objective may also benefit other multi-channel imaging systems that combine peripheral scans with other central channels.

Funding

This study was supported by the following grants: NIH/NEI R01-EY022362, P30EY07551, and P30EY003039 from United States; and the Foshan University start-up fund Gg07071 from China