Do Low Levels of Blood Lead Reduce Children’s Future Test Scores?

Abstract

We construct a unique individual-level dataset linking preschool blood lead levels with third grade test scores for Rhode Island children born 1997–2005. Using two identification strategies, we show for the first time that reductions of lead from even historically low levels have significant positive effects. A one-unit decrease in average blood lead levels reduces the probability of being substantially below proficient in reading (math) by 0.96 (0.79) percentage points on a baseline of 12 (16) percent. Since disadvantaged children have greater exposure to lead, lead poisoning may be one of the causes of continuing disparities in test scores.

With recent findings of high levels of lead in the drinking water in Flint, Michigan and in schools in several urban districts, attention has focused once again on the dangers of lead poisoning. While child blood lead levels have declined dramatically over the past 30 years, current estimates suggest that 4.5 million households in the United States are exposed to high levels of lead and that half a million preschool aged children have elevated blood lead levels (BLLs). The US Public Health Service recently included the elimination of elevated blood lead levels as a goal in Healthy People 2020, the ten-year national objectives for improving the health of all Americans.

There is strong neurobiological and epidemiological evidence of a relationship between early exposure to lead and future negative cognitive and noncognitive outcomes. However, the epidemiological evidence is correlational, and almost all of it is based on studies of children with much higher blood lead levels than are common today. The CDC lowered the threshold for children to receive case-management services from 10 to 5 ug/dl in 2012 (CDC 2013). It is unclear to what extent children with blood levels that are detectable but below this threshold are being harmed. These children form the majority of children in our sample who have detectable blood lead levels.

One reason for the lack of evidence on this point is that it is rare to have longitudinal data linking preschool BLLs with future test scores. An additional difficulty for identifying the effects of lead is that even with such data, at least some of the measured correlation between blood lead levels and outcomes could reflect omitted characteristics of households that are independently correlated with negative child outcomes. Confounding arises from the fact that children with higher lead levels are more disadvantaged. They are more likely to come from minority groups, to be poor, to live in single parent homes, and to have less educated mothers. Such a bias would tend to cause researchers to overstate the dangers of small amounts of lead.

A second problem is that blood lead levels are imperfectly measured and it may be necessary to measure frequently in order to capture harmful exposures since lead does not remain in blood but is deposited in hair, bones, and other body organs. Measurement issues of this type add random noise to lead measures that could lead to underestimates of the effects of lead exposure.

Our study addresses these weaknesses in the literature using a unique dataset that we constructed for the state of Rhode Island. We start with all children who were born between January 1997 and September 2005 whose BLL was measured at least once before age six. Rhode Island had a particularly aggressive program of testing for lead, and 80 percent of all three-year-old children in the state have at least one BLL measurement. Most have repeated lead measures (an average of three tests per child). We are able to match information on preschool blood lead levels from the Rhode Island Department of Health (RIDOH) with the child’s test scores from the Rhode Island Department of Education (RIDE) in order to examine the effects of preschool blood lead levels on third grade math and reading test scores.

We are able to control for many possible confounders associated with neighborhoods and schools by including census tract fixed effects as well as measures of average test scores in the child’s own school and grade. In order to deal with residual confounding as well as errors in measured lead exposure, we develop two instrumental variables methods. The first exploits the fact that for most children we observe multiple measures of blood lead. If we regard each as a noisy measure of the child’s true lead exposure and assume that the measurement errors are uncorrelated, then we can instrument one measure with another in order to develop an estimate that is purged of measurement error.

The second strategy is based on policies implemented in Rhode Island in 1997 that required landlords to ensure that rental homes were free of lead hazards. These policies were adopted following statements from the Centers for Disease Control in 1997 urging states to prioritize lead testing and remediation that targets children at the highest risk (Jones et al. 2009). Neighborhoods with a greater share of old housing (one of the primary sources of lead paint in Rhode Island), and with higher initial child lead levels (as measured in 1997), witnessed the biggest gains in the number of lead-safe certificates issued, and the biggest reductions in child lead levels. These neighborhoods were also predominantly African American and poor and remained so after the lead clean-up.

Since the policies were rolled out in a targeted way, we construct instruments by modeling the probability that a child’s home was certified at the time of birth as a function of the number of certificates that had been issued in their census tract as of their year of birth, as well as family characteristics, and tract, year, and month of birth fixed effects. We then use these models to predict the probability that a child’s home was certified at the time of birth, and use this predicted probability as an instrument for a child’s lead level. By using the predicted certification measure we use all of the available information about certification in the census tract, abstract from the individual family’s decision to take up the certificate program (which may be endogenous), and base our estimates on the availability of the program in their census tract. We also demonstrate that the program successfully targeted poor and minority areas and that it did not result in gentrification of these areas.

Both IV strategies yield estimates that are considerably larger than OLS, suggesting that measurement error is a real concern. The first IV strategy suggests a one unit increase in a child’s average blood lead level leads to a 0.96 percentage point increase in the probability of being “substantially below proficient” in reading on a baseline of 12 percent.¹ The comparable figures for mathematics scores are a 0.79 percentage point reduction on a baseline of 16 percent. The estimates from the second IV strategy are considerably larger but also noisier so that we cannot reject the null that confidence intervals encompass both the OLS and first set of IV estimates. However larger point estimates are consistent with the fact that the certificate programs targeted poor and minority children who were most at risk of harm from lead exposure.

The rest of this paper is organized as follows. We first provide an overview of some of the previous research about the prevalence and effects of lead poisoning and background information about lead remediation in Rhode Island. This is followed by an overview of our data and estimation strategy, and then by the main results and conclusions.

I. Background

A. Lead Poisoning and the Measurement of Lead in US Children

Lead has no biological value and is toxic to the human body, regardless of the pathway of exposure (ingestion or inhalation). Lead is toxic because of its ability to inhibit or mimic the actions of calcium, thereby affecting all calcium-dependent biological processes. Many body systems including the renal, endocrine, and cardiovascular systems are affected by lead exposure, but the nervous system appears to be the most sensitive target. Within the brain, exposure leads to brain damage in the prefrontal cerebral cortex, hippocampus and cerebellum (Finkelstein, Markowitz, and Rosen 1998). Neurodevelopmental studies show that infants, children, and the developing fetus are at the greatest risk of toxicity (National Research Council 1993). This sensitivity is due to the fact that young children are more likely to ingest lead, and ingested lead is more likely to be absorbed from the gastrointestinal tract of children. Moreover, conditional on absorption, lead is more likely to affect the developing nervous system than the mature brain because the so-called “blood-brain” barrier is less effective in young children than in adults (Lidsky and Schneider 2003).

The negative health effects of lead ingestion have been known since at least Roman times. But until the mid-twentieth century, health officials considered only severe cases of lead poisoning to be harmful. In the 1960s, medical professionals recognized that less acute lead exposure also had harmful effects and began characterizing lead poisoning as epidemic (Berney 1993). In 1970, the US Surgeon General issued his first formal statement on lead poisoning, naming it a national health problem (US Deptartment of Health, Education and Welfare 1971). Since then, American children’s exposure to lead has declined dramatically, due largely to two major regulatory changes involving the elimination of lead from gasoline and from household paint.² Coincident with this decline, the share of preschool age American children with blood lead levels in excess of 10 micrograms per deciliter (ug/dl) has likewise declined from 8.6 to 1.4 percent over the period 1988 to 2004, with declines across all groups, but especially for historically high-risk groups of children (Jones et al. 2009). Note that since 10 ug/dl was the “threshold for concern” over much of this period, lower levels of exposure were not tracked and we therefore know little about trends at the low end of the distribution of exposure.

Despite substantial progress, lead has remained a significant hazard especially in urban areas due to geographic concentrations of lead paint in deteriorating older homes, residual lead in soil at former industrial sites, and residual lead in soil near high traffic areas (Lanphear et al. 1998; Levin et al. 2008). Even conditional on living in an urban setting, there may be important differences in exposure to lead by socio-economic status, which could potentially confound the estimated effects of lead exposure. For example, the hazards associated with lead-based paint can be reduced by painting over old paint and ensuring that living areas are free of paint chips and dust. To the extent that more educated or wealthier families are more likely to take these precautions, similar exposures to old housing within an urban area are more likely to more negatively affect the most disadvantaged.

For both these reasons, disparities in child BLLs by race and income remain, with African American and poor children two to three times as likely to have elevated lead levels, defined as above 5 ug/dl (CDC 2013).³ As we will see below, disadvantaged children are also more likely to have detectable lead levels that fall below the 5 threshold. And conditional on exposure, more disadvantaged children may receive less effective remediation both at home and at school. Thus, the impact of the same exposure could well be different for different children.

How many children suffer from low but detectable levels of lead exposure, and how much such exposure has affected their outcomes is not easy to determine. The best national data on exposure comes from the National Health and Nutrition Examination Survey (NHANES), which draws venous blood from a nationally representative cross-sectional sample of children. Unfortunately, the cross-sectional nature of this dataset does not allow an examination of the relationship between preschool blood lead levels and later child outcomes. A difficulty with having only a single measure of blood lead (as in the NHANES) is that the half-life of lead in blood is relatively short (36 days). As such, BLLs only capture very recent exposure and will not necessarily capture the amount of lead that has settled in body organs and bone.⁴ Hence, a single blood lead measure may be an unreliable indicator of lead exposure.

A second measurement issue making multiple measures per child useful is that error can arise from contamination of the blood sample especially when the sample is a capillary sample (also known as a finger prick). Capillary samples are common due to their lower expense and degree of discomfort to the child. Even without contamination, there is significant error in measurement, with greater error characterizing capillary measures. According to the CDC, the “ratio of imprecision to measurement value, particularly at BLLs <10ug/dL, is relatively high” (CDC 2002).⁵ Measurement error can lead to considerable attenuation bias in the estimated effect of lead, as we demonstrate below. These considerations mean that having repeated measures for most children is a signal advantage for our study.⁶

Our study contributes to a large literature on effects of lead, much of which is correlational, and almost all of which focuses on children with relatively high levels of blood lead. Chandramouli, Ellis, and Emond (2009); Canfield et al. (2003); Lanphear et al. (2005); Nigg et al. (2010); and Wasserman et al. (1997) all document a significant correlation between lead levels less than 10 milograms per deciliter (ug/ml) during childhood and cognitive and behavioral outcomes including ADHD and hyperactivity. McLaine et al. (2013) analyzes the Rhode Island data used here and shows an inverse relationship between blood lead levels and school readiness. Among children with BLLs below 5, 68 percent scored above the benchmark levels, while among children with a BLL of at least 10, only 49 percent exceeded the benchmark. However, among the children with BLLs below 5 (the majority of the sample with detectable BLLs), to date we have little idea of the correlation between lead and outcomes.

There are several studies by economists examining the causal relationship between lead and outcomes. Rao, Reyes, and Urzúa (2015) estimate the impact of a child’s proximity to a toxic waste site contaminated with lead on future academic achievement in Chile. Some of the best known studies examining the effects of high lead levels are based on cohort-level analyses of historical data. For example, Ferrie, Rolf, and Troesken (2012) exploit variation in the use of lead water pipes across time and place in the early part of the twentieth century to estimate a negative relationship between exposure to leaded water and later intelligence test scores among World War II (WWII) army enlistees. Other studies use a similar research design to link declining lead levels in US children in the 1970s and 1980s after the de-leading of gasoline to the dramatic declines in crime witnessed since the mid-1990s (see Masters, Hone, and Doshi 1998; Reyes 2015a; Nevin 2000 and 2007; Mielke and Zahran 2012; and Grönqvist, Nilsson, and Robling 2014). Reyes (2015b) also links these declines to increases in test scores.

Billings and Schnepel (2015) take advantage of the measurement error in blood lead levels and a similarly comprehensive dataset in order to evaluate the effects of intensive intervention among children who were lead poisoned in North Carolina. Children with two consecutive BLLs over 10 micrograms per deciliter were eligible for the intervention program, whereas children with levels just below these cutoffs were not. The mean BLLs for children in their treatment group were 17.9 compared to 12.09 for their control group. Nevertheless, the children in the treatment group experienced large declines in antisocial behavior relative to the control group. They also experienced large, but only marginally statistically significant gains in an index of educational performance. Baseline reading (math) test scores in the lead poisoned groups were about two-thirds (half) of a standard deviation below normal levels.

As we will show below, the mean lead levels in the Billings and Schnepel study are far above the mean lead levels found in Rhode Island children. This is typical of the literature, which has focused (understandably) on the most severely affected children. We know almost nothing about how the relatively low levels of lead that are still found in many young children’s blood affect their outcomes. Answering this question is a primary goal of this study.

B. Lead Mitigation Policies in Rhode Island

Rhode Island, and particularly its urban areas, is characterized by old housing, with much of it (43 percent) built prior to WWII, and therefore containing high concentrations of lead paint. As a result, many of the state’s children are exposed to lead through deteriorating lead-based paint, with minority and low-income children disproportionately exposed.⁷ As is the case nationally, this disproportionate exposure is due largely to the residential segregation of the poor, and especially of African Americans, in the four core urban areas of the state located within Providence County (Appendix Table 1). US census data reveals that 81 percent of the homes in Providence County were built prior to 1978 and 49 percent before WWII. Comparable numbers for the rest of the state are 68 and 27 percent.

In an effort to reduce childhood exposure to lead, in 1997 Rhode Island established two programs to encourage mitigation of lead hazards in old homes. The first required all owners of homes in which an elevated lead level was found to mitigate such hazards. Once the home was mitigated, an inspection would be performed, and the Department of Health (DOH) would issue a certificate. Noncompliant landlords were referred to the state Attorney General for prosecution. The second program was administered by the Rhode Island Housing Resources Commission (HRC) and required all landlords to mitigate lead hazards in the homes they rented—regardless of whether an elevated lead level had been reported. It is important to note that the standards of the HRC certifications were considerably lower than those of the DOH. When confirmation of mitigation was received, a lead-safe certificate was issued.

The state provided landlords with training in the importance of lead hazard mitigation, information, and training on how to reduce lead hazards in the homes in the least costly manner, and even provided low interest loans to landlords to help them comply. The state targeted this outreach to the communities with the oldest housing stock and the highest child blood lead levels. These areas were often those in which the families were the most disadvantaged. Few resources were devoted to enforcement and though noncompliance was illegal, landlords were typically not penalized for noncompliance. However, landlords who did not have a lead-safe certificate could be sued in civil court if children living in their homes were found to have elevated lead levels.

Over the period 1997 to 2010, the total number of lead-safe certificates issued to landlords increased from 333 to 47,734 (Appendix Table 2). Of these, 31,104 were HRC certificates indicating a regulatory approach that was, in practice, far more likely to involve carrots (e.g., training and assistance to landlords to help them to comply in addition to protection against civil suits) than sticks in the form of potential prosecution by the state Attorney General.

Individual blood lead levels generally declined in a household after a certificate has been issued (Rogers et al. 2014). The program was relatively inexpensive with annual government spending of approximately a half a million dollars for FY2014. If we assume the same level for each year of the program (which is an overestimate given the program ramp up in the early years), the total cost to government would be about $4 million.

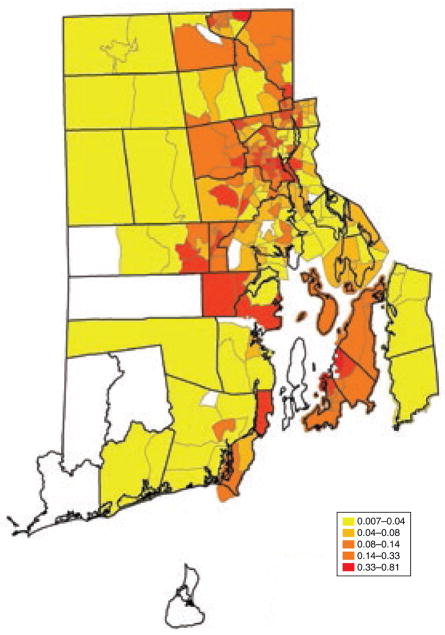
Figure 1 plots the number of certificates issued in each census tract by 2010 as a share of the pre-1978 housing stock. The figure demonstrates the uneven distribution of certificates across the state. The program did successfully target neighborhoods at highest risk of lead poisoning. The census tracts that experienced the greatest increase in certificates issued per capita were characterized by older housing stock, a greater share of children with high lead levels in 1997, a greater share of poor families, and a higher share of African American families, as shown in Figure 2, which plots the number of certificates per capita in 2010 against these characteristics of census tracts as measured in 1997.⁸

Figure 1.

Total Certifications per Pre-1979 Unit

Figure 2.

Certificates per 1,000 Population and 1997 Tract Characteristics

Notes: Each observation is a census tract. The linear fit and 95 percent confidence interval is generated from a simple regression of the number of certificates per capita in 2010 on characteristics of the tract as measured in 1997. No additional controls are included. Prewar housing share poor and share black come from census data.

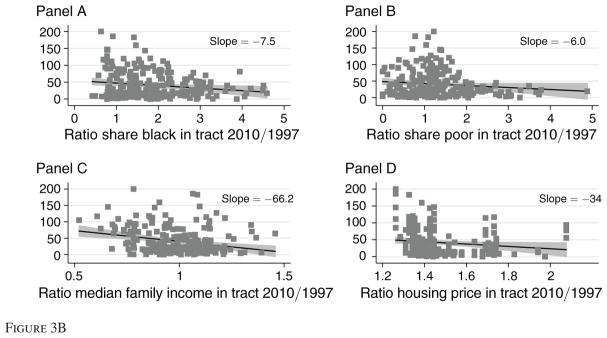
Similarly, Figure 3A examines pre-trends in important variables prior to the start of the certificate program. The figure shows that there was no relationship between the number of certificates received by 2010 and changes in the share of the census tract that was African American or the share of the census tract that was poor between 1990 and 2000. The third panel of the figure shows that tracts that received many certificates were actually more likely to have had declining income in the pre-period, a trend that would have been expected to be associated with lower test scores, other things being equal.

Figure 3.

Figure 3A. Certificates per 1,000 Population in 2010 and Changing Tract Characteristics 1990–2000

Notes: Each observation is a census tract. The linear fit and 95 percent confidence interval is generated from a simple regression of the number of certificates per capita in 2010 on the ratio of the tract characteristic in 1997 to 1990. No additional controls are included. All values on the x-axis come from census data.

Figure 3B. Certificates per 1,000 Population in 2010 and Changing Tract Characteristics, 1997–2010

Notes: Each observation is a census tract. The linear fit and 95 percent confidence interval is generated from a simple regression of the number of certificates per capita in 2010 on the ratio of the tract characteristic 2010 to 1997. No additional controls are included. All values on the x-axis come from census data except housing values which come from Zillow.

Neighborhoods with a greater increase in certificates per capita did not appear to gentrify after the program, as evidenced by similar trends across neighborhoods in the share black and the share poor, as well as in median house prices (Figure 3B). The decline in median income witnessed in the pretreatment period persisted after the certificate program was introduced.⁹ The lack of gentrification is not surprising. The majority of certificates issued during our time period were from the Housing Authority (not the Department of Health) and rarely required large renovations.

II. Data and Trends

A. Sources of Data

Our sample consists of all children born in the state of Rhode Island between January 1997 and September 2005, who have data on at least one BLL measure before the age of six, and who are enrolled in any Rhode Island public school. Note that BLL is not generally measured in children over six. The data on BLLs comes from the Rhode Island Department of Health (RIDOH) and includes the age at each test, the test method (capillary or venous), the census tract where the child lived at the time of the test, and the BLL. Educational outcomes come from the Rhode Island Department of Education (RIDE) and include NECAP¹⁰ scaled test scores in third grade, gender, race, ethnicity, and school lunch (free or reduced) status. The third source of data are birth certificates of children born in Rhode Island, which we have for 85 percent of our sample (the remainder moved to the state as young children.) We impute data for the children with missing birth certificate data in our main results, and also show results excluding these observations as a robustness check. These data include maternal education, marital status at birth, and the child’s birth order and birth weight. Since confidential versions of these data contained information about the child’s address at each blood test, we were able to merge these data with data collected on whether and when a lead-safe certificate was issued for a given dwelling.¹¹

The final sample includes roughly 71,000 Rhode Island children born between January 1997 and September 2005 with linked BLL and educational test score data. Details on construction of the sample can be found in Appendix Table 3.¹² Compared with a national lead screening rate of only 25 percent, 80 percent of all children with a Rhode Island birth certificate are screened at least once, and the screening rate remained constant throughout the study period, suggesting that the demographics of children screened also likely remained constant. Figure 4 shows that increases in the number of certificates issued were not accompanied by increases in lead screening rates.

Figure 4.

Certificates per 1,000 and the Ratio of Children Screened by Tract for Birth Cohorts 2005/1997

Notes: Each observation is a census tract. The x-axis represents the ratio of the number of children born in 2005 with a lead screen to the number of children born in 1997 with a lead screen.

Using vital statistics data to compare the maternal characteristics (race, education, and marital status) of children with a blood lead level (80 percent) to those without a blood lead level (20 percent), we find that those with at least one lead screen are slightly more disadvantaged along most measures, with the exception of birth weight, which is the same for the two groups. Appendix Table 3 also shows that among those with a lead level, those matched with RIDE data are slightly more disadvantaged than those who we were not found in RIDE data (presumably because they attended private school). However, children with matched lead-RIDE data are representative of all children in the RIDE data (that is of all public school students).

Table 1 provides an overview of our data, for the whole sample and for various subsamples. Children have on average 2.7 BLL measures over the first 72 months of life, after which they are typically not tested.¹³ Minority and disadvantaged children receive more tests, suggesting that they may be more likely to have high BLLs that call for further monitoring. In some of our analyses, we construct a single measure of BLLs using the geometric mean, reducing the influence of outliers. This procedure is consistent with the existing literature.

Table 1.

Summary Statistics for Sample

	All	White	White/Asian/other	Black	Hispanic	Never free lunch	Always free lunch
Preschool lead levels
Number of tests	2.7	2.5	2.5	3.1	3.3	2.4	3.2
Number of venous tests	1.9	1.5	1.6	2.4	2.8	1.4	2.5
Lead (geometric mean)	3.12	2.80	2.80	4.20	3.60	2.40	3.90
Share geom. mean ≥ 5	0.17	0.14	0.14	0.30	0.23	0.09	0.27
Share geom. mean ≥ 10	0.02	0.01	0.01	0.05	0.03	0.01	0.04
Share any BLL ≥ 5	0.40	0.33	0.34	0.57	0.54	0.26	0.57
Share any BLL ≥ 10	0.09	0.06	0.06	0.17	0.13	0.03	0.15
Test scores
Third grade reading	45.5	48.1	47.90	40.6	39.2	50.8	39.7
Not reading proficient	0.12	0.08	0.08	0.19	0.22	0.04	0.21
Third grade math	42.2	44.8	44.6	36.3	36.1	47.2	36.5
Not math proficient	0.16	0.10	0.11	0.29	0.29	0.06	0.28
Lead certificates
Ever certificate in home	0.17	0.10	0.10	0.31	0.35	0.05	0.32
Certificate in home at birth	0.03	0.003	0.01	0.08	0.08	0.003	0.08
Characteristics at birth
Birth weight (kg)	3.30	3.40	3.40	3.30	3.30	3.40	3.30
Mother < high school	0.15	0.08	0.09	0.24	0.33	0.02	0.33
Mother high school	0.30	0.29	0.29	0.34	0.29	0.21	0.34
Mother college	0.26	0.35	0.33	0.09	0.06	0.48	0.05
Male	0.51	0.51	0.51	0.51	0.51	0.51	0.50
Observations	70,678	47,668	50,037	6,967	13,674	30,970	19,060

Notes: BLL referes to blood lead level. Data on preschool lead levels comes from the Rhode Island Department of Health; data on reading and math test scores come from the Rhode Island Department of Education; Data on characteristics at birth come from Rhode Island vital statistics data; Data on certificates comes from the Rhode Island Departments of Health and Housing.

The mean BLL is 3.1, which is well below the CDCs threshold for medical intervention of 5 micrograms per deciliter. African American and Hispanic children both have higher mean levels, as do children who always receive free school lunch (4.2, 3.6, and 3.9, respectively).¹⁴ Minority children are also more likely to have high mean scores, with 30 percent of African American, 23 percent of Hispanic, and 27 percent of always free lunch children having levels above 5 (compared to 14 percent of white children). The corresponding numbers for mean levels above 10 micrograms per deciliter are 5, 3, and 4 percent, respectively. Note that it is not at all unusual in Rhode Island for a child to have a single BLL above 5 or even above 10 micrograms per deciliter—overall, 40 percent of children have at least one measure above 5 and 9 percent have a measure above 10. The discrepancy between single measures and mean measures likely reflects considerable measurement error in the tests.

Academic test scores range from 0 to 80, with an average score of 45.5 for reading (standard deviation of 13) and 42.2 for math (standard deviation of 13). In addition to the average scores, it is helpful to think about whether children are meeting minimum levels of proficiency in these academic subjects. Focusing on the lower tail of the distribution can also help to reveal heterogeneous impacts of lead exposure, with possibly greater effects on the children who are more likely to have low test scores to begin with. Twelve percent of children were “substantially below proficient” (defined as a score less than 30) in reading, and 16 percent in mathematics. Again, there is considerable variation by race, ethnicity, and free lunch status with, for example, the fraction of children who are substantially below proficient in reading reaching 19 percent for African Americans, 22 percent for Hispanics, and 21 percent for children who were always eligible for free lunch.

Seventeen percent of the children live in a home that received a lead-safe certificate at some point during our sample. (We consider all of the certificates together here and below unless otherwise specified). This fraction is much higher for poor and minority children at 31 percent for African Americans, 35 percent for Hispanics, and 32 percent for children who were always eligible for free lunch. These numbers suggest that the certificate program had significant penetration and that it was in fact targeted at the areas with the highest initial lead burden. The number of children whose homes had received a lead safe certificate at the time of their birth is smaller, reflecting the fact that the first birth cohorts in our data had almost no exposure to the certification program.

The rest of Table 1 summarizes characteristics drawn from the birth certificate data and shows that in addition to having higher BLLs, poor and minority children had lower birth weight, and mothers with less education. Since both of these factors have been independently shown to be associated with lower children’s test scores, the table shows the potential for confounding of the relationship between BLLs and children’s test scores.

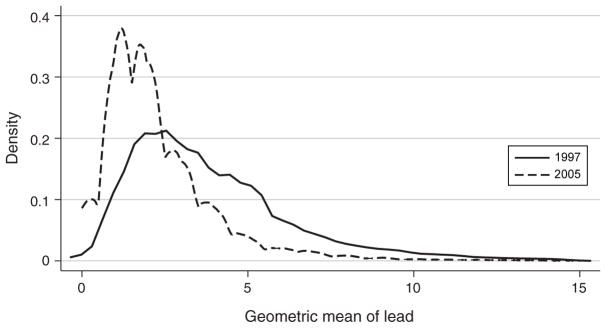
Table 1 provides a static picture. There were, however, dramatic reductions in blood lead levels in a very short period of time. Figure 5 shows the distribution of a child’s average BLLs for the cohorts born in 1997 and 2005. Clearly, the whole distribution shifted to the left, with a virtual collapse in the part of the distribution above 5 milligrams per deciliter. This shift is laudable but makes it more urgent to understand the burden of low lead levels.

Figure 5.

Distribution of Average Lead by Birth Cohort

Note: Kernel = Epanechnikov, bandwidth = 0.3378.

Table 2 therefore focuses on changes in BLLs, exposure to the housing certificate program, and test scores between the first and last birth cohorts in our data. The first two columns indicate that blood lead levels declined by 42 percent relative to base levels in eight years. This is a very rapid decline, which we attribute in part to the introduction of the lead-safe certificate program. Consistent with this interpretation, the next two columns show that the fraction of children with a certificate in place at the time of the birth increased dramatically among children in the most disadvantaged groups. For example, in the 1997 birth cohort only 2 percent of sample African American children lived in a home that had been certified lead-safe at the time of their birth; by 2005, 12 percent of sample African American children lived in a home that had been certified as lead safe from the time of their birth.

Table 2.

Lead Levels, Lead Certificates, and Test Score Results by Birth Cohort and Child Characteristic

	Geometric mean lead levels		Certificate at birth		Mean third grade reading
	1997	2005	1997	2005	1997	2005
Panel A
Child characteristic
Race
White	3.49	2.02	0.00	0.02	46.20	49.30
White/Asian/other	3.54	2.07	0.00	0.02	46.10	48.80
Black	5.77	2.95	0.02	0.12	37.80	41.54
Hispanic	4.91	2.52	0.01	0.13	36.20	40.47
Asian	4.42	2.64	0.02	0.09	44.40	47.40
Free lunch
Always free lunch	5.25	2.85	0.02	0.11	36.75	40.87
Sometimes free lunch	4.32	2.38	0.01	0.07	41.25	43.49
Never free lunch	3.04	1.79	0.00	0.01	48.94	51.84
Maternal education
≥ HS	3.73	2.18	0.01	0.04	45.03	48.73
< HS	5.12	2.82	0.01	0.12	36.67	38.27
Marital status at birth
Single	4.87	2.68	0.01	0.11	38.79	41.93
Married	3.55	2.05	0.00	0.03	45.87	48.87

	Substantially below reading proficient		Mean third grade math		Substantially below math proficient
	1997	2005	1997	2005	1997	2005
Panel B
Child characteristic
Race
White	0.10	0.07	43.00	44.40	0.12	0.11
White/Asian/other	0.10	0.08	42.90	44.00	0.13	0.12
Black	0.23	0.17	34.60	36.20	0.31	0.29
Hispanic	0.30	0.21	33.90	36.40	0.35	0.29
Asian	0.09	0.07	40.50	42.20	0.21	0.14
Free lunch
Always free lunch	0.27	0.18	34.58	36.24	0.33	0.28
Sometimes free lunch	0.17	0.17	38.53	39.26	0.21	0.22
Never free lunch	0.06	0.04	45.32	46.66	0.08	0.07
Maternal education
≥ HS	0.12	0.09	41.88	42.84	0.15	0.14
< HS	0.28	0.27	34.51	34.00	0.35	0.37
Marital status at birth
Single	0.22	0.18	36.22	37.23	0.28	0.26
Married	0.11	0.08	42.68	44.01	0.14	0.12

Notes: The row subheadings refer to birth cohort. Because only data through August is available for birth cohort 2005, the sample used in this table includes all children born between January and August of the respective years.

Third grade test scores rose across birth cohorts in all demographic groups, while the fraction scoring substantially below proficient declined. However, the gains were greatest in the groups that were most affected by the certificate program and showed the greatest declines in BLLs. For instance, among children who never participated in the free lunch program, reading test scores rose by 5.9 percent and the percent who were not proficient in reading fell from 6 to 4 percent. Among children who were always eligible for the free lunch program, reading test scores rose by 11.2 percent, and the percent who were substantially below proficient in reading fell from 27 to 18 percent, a remarkable improvement. Of course these gains might have been caused by other changes targeted at poor and minority children; the most likely alternative candidate is targeted educational policies. Hence, in our models we will also show estimates controlling for third grade reading scores in the child’s school and cohort, which should capture other efforts targeting children in these neighborhoods and schools.

III. Estimation Strategy

A. Lead Levels and Future Child Cognitive Achievement—OLS Estimates

We wish to estimate the impact of preschool lead levels on future academic achievement as measured by test scores. We begin with estimates of the following equation:

$$Y_i={\beta }_0+{\beta }_1{\mathit{Lead}}_i+{\beta }_2{\mathbf{X}}_i^c+{\beta }_3{\mathbf{X}}_i^m+{\beta }_4{\mathbf{X}}_{nt}^n+{\mathbf{\tau }}_n+{\mathbf{\tau }}_t+{\epsilon }_i,$$ (1)

where Y_i is the scaled reading or math test score in grade 3, or an indicator equal to one if the child was substantially below proficient in one of these subjects. The variable Lead_i is the geometric mean of the multiple BLLs taken for each child. The vector X^c includes the child’s race (indicators for white, black, Hispanic, Asian, and other), birth weight, gender, and a measure of the child’s free/reduced lunch status (always free lunch, sometimes free lunch, never free lunch). The vector X^m includes maternal educational attainment (indicators for less than high schoool, high school, and some college or more), and marital status at birth.¹⁵ The vector Xⁿ includes time-varying neighborhood (census tract) characteristics from census data including the share poor, median family income, and the share of housing units built post-1978.¹⁶ All variants of this model include τ_t, a vector of year of birth and month of birth fixed effects. We estimate versions of this model with and without τ_n, a vector of census tract fixed effects. As we will see below, adding the census tract fixed effects has little impact on the estimated effects of lead once individual-level variables are included in the model suggesting that there may actually be little residual confounding due to omitted variables bias in this instance.

B. Instrumental Variables Strategies

As discussed above, estimation is complicated by the fact that there may be considerable measurement error in blood lead levels. In order to explore the importance of this feature of the data, we follow Ashenfelter and Krueger (1994) and Chalfin and McCrary (forthcoming), who have multiple measures of their variables of interest and use one measure as an instrument for another in order to estimate the degree of measurement error and the extent of downward attenuation bias in OLS estimates of education on earnings and police on crime, respectively.

In our context, there are multiple ways in which this strategy can be implemented. For example, we can estimate models using the subset of children who have both venous (less noisy) and capillary (more noisy) measures, and using the former as instruments for the later. We also estimate models in which we instrument a randomly chosen test result for each child using the mean of the other available tests. Although our multiple measures of child lead exposure were taken at different times and may capture differences in the child’s underlying lead levels, each measure can still be interpreted as an (imperfect) measure of the underlying level of lead exposure during early childhood. And because the source of the measurement error is the inexactitude of the tests, and the plausibly random variation in the length of time between an exposure and a test, we believe it likely that measurement errors in subsequent tests for the same child will be largely uncorrelated. The results of these estimations suggest that measurement error is a considerable problem and that it tends to lead to significant attenuation in the estimated effect of lead exposure on test scores.

As discussed above, we also pursue a second instrumental variables strategy. For each child we know whether their place of residence during their preschool years had received a lead-safe certificate as of their birth date.¹⁷ Issuance of a certificate indicates that any lead hazard in the home had been mitigated, so it should be associated with lower BLLs. However, whether a particular residence receives a certificate or not is at least partly endogenous. We measure the presence of a certificate in the home as of the date of birth of the child so that certificate status cannot be a function of the child’s preschool lead level (i.e., parents with a child with an elevated lead level might seek out a home with a certificate and we want to rule that out), it might still be the case, for example, that among otherwise similar parents, those who seek out lead testing and lead mitigation are also more likely to have children with higher test scores.

Hence, rather than using the actual measure of whether there was a certificate or not in the child’s home as an instrument, we construct a predicted certificate measure based on census-tract level measures of the number of certificates issues in the tract in the last five years and observable characteristics of the child and family. By using the “predicted certificate,” we purge the instrument of any potential endogeneity associated with the take-up decision. The prediction equation takes the form

$$\mathit{Certificates}@{\mathit{Birth}}_i={\alpha }_0+{\alpha }_1\mathbf{Certificat}{\mathbf{e}}_{nt-5}+{\alpha }_2\mathit{EverCerti}{\mathit{ficate}}_i+{\alpha }_3{\mathbf{X}}_i^c+{\alpha }_4{\mathbf{X}}_i^m+{\alpha }_5{\mathbf{X}}_{tn}^n+{\gamma }_n+{\gamma }_t+{\mu }_i.$$ (2)

Here Certificate@Birth_i indicates that the child lived in a house that had been certified lead-safe as of the time of the child’s birth and Certificates _nt−5 is a vector of census tract-level measures of the availability of the certificate programs as of the child’s year of birth (as measured by the number of certificates issued in the past five years divided by the number of old homes in the census tract, excluding the focal child’s). The variable EverCertificate_i is an indicator equal to one if the child’s home ever received a certificate. We include this indicator in order to control for the fact that some homes require lead remediation while others do not, and given that it is a proxy for low quality housing, it is included in the second stage as well. By including this variable, we are focusing on the timing of the certificate intervention—conditional on the house needing and eventually receiving remediation, was the remediation done in time for this particular child to benefit? The other variables are as defined above and include child, mother, and census tract characteristics as well as year, month, and census tract fixed effects. Importantly, the instrument, predicted certificate, is not a function of μ_i, the unobservable characteristics of the child or family that influence certificate take-up and that might also be correlated with test scores.

Having constructed the predicted certificate instrument, we proceed with instrumental variables estimation. The first stage is given by

$${\mathit{Lead}}_i={\alpha }_0+{\alpha }_1\mathit{Certificate}@{\mathit{Birth}}_i^{\ast }+{\alpha }_2\mathit{EverCerti}{\mathit{ficate}}_i+{\alpha }_3{\mathbf{X}}_i^c+{\alpha }_4{\mathbf{X}}_i^m+{\alpha }_5{\mathbf{X}}_{tn}^n+{\gamma }_n+{\gamma }_t+{\mu }_i,$$ (3)

where $\mathit{Certificate}@{\mathit{Birth}}_i^{\ast }$ is the predicted value of Certificate@Birth_i generated by equation (2). In addition to the overall first stage, we show estimates of this equation separately for racial groups and by free lunch status in order to demonstrate that the certificate program had larger effects on disadvantaged children.

Finally, we estimate an instrumental variables version of equation (1) in which Lea d_i is replaced with the predicted geometric mean BLL from (3):

$$Y_i={\beta }_0+{\beta }_1{\mathit{Lead}}_i^{\ast }+{\beta }_2\mathit{EverCerti}{\mathit{ficate}}_i+{\beta }_3{\mathbf{X}}_i^c+{\beta }_4{\mathbf{X}}_i^m+{\beta }_5{\mathbf{X}}_{tn}^n+{\mathbf{\tau }}_n+{\mathbf{\tau }}_n+{\epsilon }_i.$$ (4)

To address concern that the areas of the state that received more certificates are the most disadvantaged and that schooling inputs in these neighborhoods may have increased over this period, we also show estimates that include a control for the average third grade reading test scores in the child’s school (calculated as the leave out mean, i.e., leaving out the index child in each case, for all children with third grade test scores in the same school and cohort). To address concerns that these unobserved improvements occurred not within the school but in the neighborhood, we also estimate models including a linear trend for each initial 1997 census tract reading score. This control is intended to capture the idea that tracts that started with the lowest scores may have improved the fastest because of other unobserved investments targeted to these tracts.

IV. Results: Effects of BLLs on Third Grade Test Scores

OLS estimates of the effect of preschool BLLs on third grade test scores are shown in Table 3A (for reading) and Table 3B (for math). The first column shows estimates that control only for gender, race and free/reduced lunch status (that is, the information available from the Rhode Island Department of Education). The second column adds information obtained from the birth certificate, as well as time varying census tract characteristics. These additions reduce the estimated effects of lead from −0.456 per unit of lead to −0.326 for reading and from −0.348 to −0.216 for math, suggesting that confounding could be a concern in studies with inadequate controls for family background.

Table 3A.

OLS and Neighborhood FE Estimates: Preschool Lead and Third Grade Reading Scores

	(1)	(2)	(3)	(4)	(5)
Geometric mean of lead	−0.456 [0.0256]	−0.326 [0.0241]	−0.335 [0.0228]	−0.306 [0.0225]	−0.326 [0.0230]
Avg. third grade reading score in school × grade				0.421 [0.0140]
Tract 1997 reading score × year					−0.0252 [0.00501]
African American	1.029 [0.959]	1.580 [0.939]	1.618 [0.933]	1.819 [0.898]	1.748 [0.942]
White	3.910 [0.997]	3.210 [0.957]	3.263 [0.950]	2.810 [0.910]	3.420 [0.958]
Hispanic	−0.178 [0.984]	0.777 [0.943]	0.795 [0.927]	1.155 [0.896]	0.966 [0.935]
Asian	4.276 [1.049]	4.915 [1.010]	4.980 [1.009]	4.868 [0.979]	5.140 [1.017]
Always free/reduced lunch	−8.224 [0.197]	−4.806 [0.177]	−4.687 [0.179]	−3.834 [0.179]	−4.705 [0.180]
Sometimes free/reduced lunch	−6.163 [0.188]	−3.759 [0.151]	−3.664 [0.149]	−3.206 [0.141]	−3.653 [0.149]
Male	−3.162 [0.0820]	−3.333 [0.0814]	−3.320 [0.0813]	−3.287 [0.0804]	−3.323 [0.0813]
Birth weight in kg		1.195 [0.0846]	1.179 [0.0842]	1.164 [0.0842]	1.176 [0.0842]
Mother < high school		−3.590 [0.186]	−3.546 [0.188]	−3.204 [0.183]	−3.550 [0.188]
Mother high school graduate		−1.475 [0.153]	−1.444 [0.152]	−1.344 [0.149]	−1.450 [0.152]
Mother college +		1.750 [0.155]	1.664 [0.156]	1.578 [0.155]	1.676 [0.156]
Married at birth		0.521 [0.129]	0.531 [0.127]	0.472 [0.129]	0.531 [0.127]
Birth order		−0.670 [0.0491]	−0.671 [0.0496]	−0.641 [0.0495]	−0.671 [0.0497]
Birth weight missing—imputed		0.721 [0.310]	0.703 [0.305]	0.617 [0.299]	0.739 [0.307]
Maternal education—imputed		−1.588 [0.328]	−1.624 [0.327]	−1.390 [0.316]	−1.631 [0.329]
Families with income in 2010 below poverty		−0.947 [1.071]	2.755 [5.220]	3.482 [4.533]	4.896 [5.768]
Median family income (in $1,000 (2010))		5.41e–05 [5.18e–06]	−5.32e–05 [3.84e–05]	−2.97e–05 [3.25e–05]	1.29e–05 [3.95e–05]
Share of housing built post-1978		−2.900 [0.695]	4.783 [4.028]	2.212 [3.450]	11.14 [4.342]
Observations	70,678	70,678	70,678	70,635	70,658
R2	0.187	0.215	0.223	0.237	0.224
Fixed effect	none	none	census tract	census tract	census tract
Number of fixed effects			233	233	230

Notes: Standard errors clustered on tract are shown in brackets. Estimates from a regression of a child’s third grade reading test score on the child’s average preschool blood lead level. All regressions also include year and month of birth fixed effects.

Table 3B.

OLS and Neighborhood FE Estimates: Preschool Lead and Third Grade Math Scores

	(1)	(2)	(3)	(4)	(5)
Geometric mean of lead	−0.348 [0.0245]	−0.216 [0.0224]	−0.220 [0.0218]	−0.193 [0.0215]	−0.210 [0.0216]
Average third grade math score for school × grade				0.489 [0.0134]
Tract 1997 math score × year					−0.0294 [0.00585]
African American	0.605 [1.020]	1.198 [0.995]	1.181 [0.975]	1.372 [0.922]	1.326 [0.982]
White	4.764 [1.001]	4.049 [0.958]	3.824 [0.941]	3.232 [0.879]	3.997 [0.948]
Hispanic	0.550 [0.989]	1.507 [0.952]	1.533 [0.943]	1.844 [0.891]	1.718 [0.949]
Asian	4.788 [1.033]	5.434 [1.009]	5.555 [0.996]	5.409 [0.940]	5.731 [1.005]
Always free/reduced lunch	−7.632 [0.199]	−4.152 [0.170]	−4.136 [0.167]	−3.239 [0.163]	−4.154 [0.167]
Sometimes free/reduced lunch	−5.992 [0.185]	−3.465 [0.133]	−3.410 [0.129]	−2.925 [0.121]	−3.401 [0.129]
Male	0.0668 [0.0826]	−0.132 [0.0813]	−0.123 [0.0814]	−0.0909 [0.0796]	−0.129 [0.0812]
Birth weight in kg		1.501 [0.0792]	1.489 [0.0782]	1.487 [0.0774]	1.487 [0.0782]
Mother < high school		−3.196 [0.188]	−3.214 [0.191]	−2.821 [0.185]	−3.220 [0.191]
Mother high school graduate		−1.300 [0.151]	−1.320 [0.150]	−1.196 [0.148]	−1.326 [0.151]
Mother college+		1.931 [0.146]	1.851 [0.147]	1.723 [0.143]	1.859 [0.147]
Married at birth		0.706 [0.117]	0.764 [0.115]	0.690 [0.113]	0.763 [0.115]
Birth order		−0.403 [0.0436]	−0.418 [0.0438]	−0.384 [0.0430]	−0.420 [0.0438]
Birth weight missing—imputed		0.637 [0.296]	0.450 [0.284]	0.379 [0.282]	0.484 [0.287]
Maternal education—imputed		−1.344 [0.282]	−1.405 [0.276]	−1.159 [0.271]	−1.409 [0.278]
Families with income in 2010 below poverty		−0.257 [1.043]	6.687 [6.420]	7.552 [5.000]	8.855 [6.779]
Median family income (in $1,000 (2010))		5.78e–05 [5.06e–06]	−2.97e–05 [4.49e–05]	−1.01e–05 [3.19e–05]	5.26e–05 [4.18e–05]
Share of housing built post-1978		−1.753 [0.912]	8.404 [4.531]	4.572 [3.378]	15.13 [4.850]
Observations	70,625	70,625	70,625	70,584	70,605
R2	0.181	0.213	0.225	0.246	0.225
Fixed effect	none	none	census tract	census tract	census tract
Number of fixed effects			233	233	230

Notes: Standard errors clustered on tract are shown in brackets. Estimates from a regression of a child’s third grade math test score on the child’s average preschool blood lead level. All regressions also include year and month of birth fixed effects.

Columns 3, 4, and 5 add census tract fixed effects as well as school- and grade-level measures (column 4) and linear trends in the 1997 census tract test scores. These additions have relatively little impact on the coefficient estimates, providing some reassurance that bias due to omitted confounders may be small in models with this rich set of controls.¹⁸ This finding is consistent with a meta-analysis of eight studies conducted by epidemiologists in which they reported that adding more family controls to a relatively parsimonious set (maternal schooling and IQ, the HOME score, birth weight, and city) did little to alter the relationship between lead and IQ in children (Rothenberg and Rothenberg 2005).

The estimated effects of lead in these models are strongly statistically significant but relatively small. The column 3 estimates suggest that a 1 point increase in mean BLLs is estimated to reduce reading scores by −0.335, and math scores by −0.220. The finding of larger effect sizes for reading relative to math is consistent with some epidemiological studies that have also documented stronger relationships between lead and verbal functioning (e.g., see Bellinger, Stiles, and Needleman 1992 as an example and CDC 2004 for a review of estimated effects of lead on verbal IQ and performance IQ). However, as discussed above, results for both reading and math may well be underestimates of the true effect given the difficulties of properly measuring lead exposures from BLLs.

Table 4 explores the issue of measurement error in these data. The first two columns focus on the subset of 12,002 children who had both capillary and venous tests. Venous tests are known to be far more accurate than capillary (finger prick) tests. Consistent with this, we see that estimating the effects of lead using the average of all capillary tests (column 1) produces a much lower estimate of the effect of lead than using the average of all venous tests (column 2).

Table 4.

Exploring Effects of Measurement Error in Lead Levels

	OLS (1)	OLS (2)	OLS (3)	OLS (4)
Panel A. Outcome = third grade reading score
Average of all capillary tests	−0.141 [0.0310]
Average of all venous tests		−0.313 [0.0470]
Single random draw of blood lead levels			−0.186 [0.0188]
Average all other blood lead levels				−0.278 [0.0238]
Observations	12,012	12,012	54,491	54,491
R2	0.226	0.229	0.233	0.234
Panel B. Outcome = third grade math score
Average of all capillary tests	−0.102 [0.0320]
Average of all venous tests		−0.201 [0.0477]
Single random draw of blood lead levels			−0.124 [0.0171]
Average all other blood lead levels				−0.189 [0.0212]
Observations	12,002	12,002	54,449	54,449
R2	0.221	0.223	0.232	0.233

Notes: Standard errors clustered on census tract are shown in brackets. Sample for columns 1–2 is limited to children from whom there are both capillary and venous measures of blood lead levels. Sample for columns 3–4 limited to children with at least two blood lead tests. All models include census tract, year of birth and month of birth fixed effects, as well as all other covariates listed in Table 3, column 3.

Columns 3 and 4 demonstrate this measurement error issue in another way, using the subsample of 54,491 children who had more than one test. Column 3 shows estimates based on a single randomly drawn test. Column 4 shows estimates based on the average of all other tests. The latter are somewhat larger in absolute value than those in column 3 consistent with averaging reducing the effects of random measurement errors.¹⁹

Given two noisy measures of the same underlying concept, and assuming that the measurement errors in the two tests are independent, we can use one set of tests as an instrument for the other set of tests, as is done Table 5. Here, we focus on instrumenting one random lead measurement with the average of the remaining estimates. The first column of Table 5 shows OLS estimates based on the same specification as column 3 of Tables 3A and 3B, but using the smaller sample of children with at least two tests. In addition to showing estimates using the continuous test scores as dependent variables, we also examine the probability that the child is below the proficiency standard in reading or math. The point estimates in this sample are smaller than those shown in the full sample and based on the geometric mean (Tables 3A and 3B), consistent with an average being less noisy than a single measure.

Table 5.

OLS and IV Estimates of Lead and Third Grade Scores Instrument Is the Remaing Blood Lead Levels

	OLS (1)	IV (2)	IV (3)
Dependent variable: Below proficient in reading
Single random draw of blood lead levels	0.00465 [0.000600]	0.00961 [0.00121]	0.00873 [0.00120]
Observations	54,491	54,491	54,458
R2	0.093	0.037	0.047
Dependent variable: Reading score
Single random draw of blood lead levels	−0.186 [0.0188]	−0.442 [0.0372]	−0.396 [0.0372]
Observations	54,491	54,491	54,458
R2	0.233	0.107	0.123
Dependent variable: Below proficient in math
Single random draw of blood lead levels	0.00383 [0.000656]	0.00792 [0.00119]	0.00682 [0.00119]
Observations	54,449	54,449	54,416
R2	0.105	0.034	0.049
Dependent variable: Math score
Single random draw of blood lead levels	−0.124 [0.0171]	−0.305 [0.0351]	−0.266 [0.0347]
Observations	54,449	54,449	54,416
R2	0.232
Additional controls
Census tract, year of birth, month of birth fixed effects	Yes	Yes	Yes
Average score in grade × school (leave-out mean)			Yes
Percent below proficient in grade × school (leave-out mean)			Yes
Race specific linear time trend			Yes
Free lunch specific linear time trend			Yes

Notes: Standard errors clustered on census tract are in brackets. Instrument for child’s lead level is the average of the child’s other blood lead levels. All covariates in Table 3, column 3, also included. are relatively large effects compared to the baseline rates of 12 and 16 percent below proficiency in these subjects.

The IV estimates shown in Table 5, column 2 are much larger than the OLS estimates. For reading the estimated coefficient rises from −0.186 to −0.442; for math the value rises from −0.124 to −0.305. The estimated increase in the probability of being less than proficient rises from 0.47 percentage points to 0.96 percentage points in reading. The corresponding increase for math is from 0.38 to 0.79. These

Column 3 probes the robustness of these estimates to the inclusion of additional controls. We add the average score in the grade and school (leaving out the index child’s score); the percentage of children who were below proficiency in the grade and school (again leaving out the index child), a race-specific linear time-trend and a free lunch-specific linear time trend (to account for changes in education policy that might have had a differential effect by race or income). These additions attenuate our estimates only slightly.

As discussed above, our second instrumental variables strategy relies on the introduction of the lead-free certificate programs. Whereas the first strategy estimates the average effect of lead in all children with multiple lead measures, an instrument based on the certificate program will estimate the effect of lead on the children most likely to be impacted by the program. The same “dose” of lead could have larger effects on these poor and minority children if their families and schools are less likely to be able to remediate the effects of lead.

Table 6 shows three different models of whether the child’s preschool home had a lead safe certificate at the time of the child’s birth (estimates of equation (2)). Column 1 has the total number of certificates, and the number of certificates squared. Column 2 includes interactions of the total number of certificates with the characteristics of the household, allowing for the fact that different types of households might be more likely to receive certificates within a census tract. Column 3 differentiates between the two types of certificates.

Table 6.

Predicting Certificate in Own Housing Unit at Time of First Lead Test

	(1)	(2)	(3)
Certificates in tract at birth	0.898 [0.0544]	0.469 [0.0615]
Certificates in tract at birth squared	−1.400 [0.136]	−1.276 [0.137]
Certificates × free lunch		0.264 [0.0374]
Certificates × black		0.292 [0.0386]
Certificates × Hispanic		0.297 [0.0329]
HRC Certificates at birth			0.707 [0.0706]
HRC Certificates at birth squared			−1.178 [0.288]
DOH Certificates at birth			1.166 [0.0911]
DOH Certificates at birth squared			−2.528 [0.214]
African American	0.0153 [0.0131]	−0.00356 [0.0133]	0.0175 [0.0131]
White	0.00305 [0.0130]	−0.00599 [0.0130]	0.00570 [0.0130]
Hispanic	0.00997 [0.0130]	−0.00977 [0.0132]	0.0128 [0.0130]
Asian	0.000413 [0.0134]	−0.00419 [0.0134]	0.00338 [0.0134]
Always free/reduced lunch	0.00627 [0.00217]	0.00137 [0.00228]	0.00627 [0.00217]
Sometimes free/reduced lunch	−0.00278 [0.00178]	−0.00662 [0.00187]	−0.00277 [0.00178]
Male	−0.000470 [0.00123]	−0.000508 [0.00122]	−0.000487 [0.00122]
Birth weight in kg	3.15e–05 [0.00113]	−9.31e–05 [0.00113]	2.27e–05 [0.00113]
Mother < high school	0.00566 [0.00264]	0.00551 [0.00264]	0.00556 [0.00264]
Mother high school graduate	−0.000103 [0.00220]	−0.000193 [0.00220]	−0.000114 [0.00220]
Mother college+	−0.00122 [0.00226]	−0.00118 [0.00226]	−0.00118 [0.00226]
Married at birth	−0.00910 [0.00169]	−0.00923 [0.00169]	−0.00917 [0.00169]
Birth order	0.00181 [0.000651]	0.00186 [0.000650]	0.00180 [0.000650]
Birth weight missing—imputed	−0.0168 [0.00391]	−0.0156 [0.00391]	−0.0160 [0.00391]
Maternal education—imputed	0.00999 [0.00397]	0.00937 [0.00396]	0.00946 [0.00396]
Families: Income in 2012 below poverty	−0.00255 [0.0687]	0.0229 [0.0686]	0.0788 [0.0692]
Median family income (in $1,000 (2010))	−1.07e–06 [4.08e–07]	−1.05e–06 [4.08e–07]	−9.26e–07 [4.08e–07]
Share of housing built post-1978	−0.340 [0.0486]	−0.243 [0.0489]	−0.304 [0.0486]
Home ever had a certificate	0.105 [0.00177]	0.105 [0.00177]	0.105 [0.00177]
Observations	70,678	70,678	70,678
R2	0.139	0.142	0.140

Notes: Standard errors clustered on census tract are in brackets. Outcome is an indicator for whether the child lived in a house with a certificate as of the date of the first blood test for the child. Certificates in tract is the number of certificates in the census tract of the child’s home (at the first lead test of the child). In columns 1 and 2, “certificates in tract” refers to the total number of certificates (DOH and HRC, combined). In column 3, we estimate the effects of the two different certificate types (DOH and HRC) separately.

All three specifications show that census tract-level measures of certificate program activity are strongly predictive of whether there was a certificate in the child’s preschool home as of the child’s birth. The interactions in column 2 further suggest that the total number of certificates in the tract was more highly predictive of having a certificate in the child’s home if the child was African American or Hispanic, or always eligible for free lunch. That is, the interactions demonstrate that these children were more likely to be affected by the program even within census tract. Of course, whether the home ever received a certificate over the course of our sample period is also highly predictive as are some of the census tract-level variables such as median family income and the share of newer housing, both of which are negatively associated with having a certificate in the home.

Table 7 shows the results of using a predicted certificate measure based on the model in column 3 of Table 6 in the first-stage equation (3). The overall estimated effect of a predicted certificate on blood lead levels is strongly negative, and is much more strongly negative for the groups with high initial BLLs consistent with these groups being the most impacted by the new lead mitigation policies enacted in 1997. Among white children in the 2005 birth cohort, 2 percent lived in a house where a certificate had been issued as of the time of birth. Thus, the overall coefficient of −8.388 suggests that a certificate reduced blood lead levels by only 0.17 micrograms per deciliter. In contrast, among African Americans in the 2005 birth cohort, Table 2 shows that 12 percent of children lived in homes that had been certified by the time of the child’s birth. The coefficient of −15.49 for African Americans suggests that blood lead levels would be reduced by almost two micrograms per deciliter in these certified homes. This number can be compared to the coefficient of 1.958 on the indicator for whether the “home ever had a certificate.” This comparison suggests that black children in homes that had not yet received a certificate had BLLs two micrograms per deciliter higher than other black children and that this gap was reduced to zero when a certificate was obtained.

Table 7.

First-Stage Estimates

	All (1)	White (2)	White/Asian/other (3)	Black (4)	Hispanic (5)	Paid lunch (6)	Free lunch (7)
Predicted certificate in home at time of birth	−8.388 [0.904]	−4.619 [1.401]	−5.302 [1.207]	−15.49 [2.219]	−3.389 [1.211]	−3.490 [1.402]	−7.199 [1.027]
Home ever had a certificate	1.165 [0.106]	0.653 [0.157]	0.756 [0.134]	1.958 [0.245]	0.729 [0.143]	0.516 [0.164]	1.063 [0.117]
Observations	70,678	47,668	50,035	6,967	13,674	30,970	39,708
R2	0.200	0.185	0.186	0.210	0.149	0.135	0.155

Notes: Dependent variable is the average blood lead level of the child. Standard errors clustered at the census tract shown are in brackets. The predicted certificate is the instrument for the child’s average blood lead level. Whether the child lived in a home that ever receives a certificate is not an instrument as it is also included in the second stage. The predicted certificate is based on the results presented in Table 5 in which whether a child lives in a home with a certificate is predicted as a function of the child’s family characteristics and the number of certificates issued in the census tract of residence as of the date of the child’s first blood lead test. All covariates listed in Table 3, column 3, included.

Table 8 presents IV estimates based on this second instrumental variables strategy. The format is the same as in Table 5. The first column shows OLS, the second the baseline IV estimate, and the third column probes the robustness of the estimates to the addition of an even richer set of controls.

Table 8.

OLS and IV Estimates of Lead and Third Grade Scores Instrument Is Predicted Certificate

	OLS (1)	IV (2)	IV (3)
Dependent variable: Below proficient in reading
Geometric mean of lead	0.0075 [0.0005]	0.0352 [0.00938]	0.0270 [0.0144]
Observations	70,678	70,678	70,637
R2	0.090
Dependent variable: Reading score
Geometric mean of lead	−0.332 [0.0199]	−0.936 [0.340]	−0.931 [0.516]
Observations	70,678	70,678	70,637
R2	0.223
Dependent variable: Below proficient in math
Geometric mean of lead	0.0056 [0.0006]	0.0143 [0.0104]	0.00999 [0.0157]
Observations	70,625	70,625	70,584
R2	0.103
Dependent variable: Math score
Geometric mean of lead	−0.217 [0.0187]	−0.149 [0.317]	−0.431 [0.471]
Observations	70,625	70,625	70,584
R2	0.225
Additional controls:
Census tract, year of birth, month of birth fixed effects	Yes	Yes	Yes
Average score in grade × school (leave-out mean)			Yes
Percent below proficient in grade × school (leave-out mean)			Yes
Race specific linear time trend			Yes
Free lunch specific linear time trend			Yes

Notes: Standard errors clustered on census tract are shown in brackets. Instrument for child’s lead level is whether the child is predicted to live in a home with a lead certificate at the time they were first tested, based on the regression presented in Table 5, column 2. All other covariates in Table 3, column 3, also included.

The second column of Table 8 shows that for reading, the IV estimates are statistically significant and roughly three times as large as the OLS estimates in the first column. They are also about double the size of the corresponding IV estimates in Table 5. For mathematics, the estimates are unfortunately imprecise, and for both math and reading the confidence intervals encompass both the OLS estimates and the corresponding IV estimates from Table 5. Thus, we must be cautious in interpreting the large estimated effects for reading scores, though it is possible that the large estimates reflect the larger impact of the certificate program on the individuals most likely to be “treated” by the certificate program.

Hausman tests of the equality of the OLS and the two IV estimates suggest that while estimates based on the first instrument (alternative measures for the same child) differ significantly from the OLS estimates, the confidence intervals are wide enough that the IV estimates based on the certificate program instrument do not differ significantly from the OLS estimates (Appendix Table 4).²⁰

Table 9 probes the robustness of the third grade reading test score results to several changes in sample and specification. About 15 percent of our sample are missing birth information, primarily because they were born outside of Rhode Island. Column 1 of Table 9 shows OLS and the two sets of IV estimates from a sample that excludes these observations. The OLS and first set of IV estimates are quite similar to those reported above. The predicted certificate IV specification is still larger that the first IV specification, but is no longer statistically significant.

Table 9.

Lead and Reading Test Scores—Robustness

	Drop obs. with imputed natality (1)	Include address FE (2)	Impute all pre-school lead (3)	Weight earlier exposure more (4)
Panel A. Ordinary least squares
Single random draw of blood lead levels	−0.295 [0.0252]	−0.262 [0.0657]
Geometric mean of lead (imputed)			−0.296 [0.0230]
Geometric mean of lead (weighted)				−0.320 [0.0345]
Observations	59,877	26,131	70,678	70,678
R2	0.224	0.640	0.223	0.221
Fixed effect	Tract	Address	Tract	Tract
Number of fixed effects	233	10,157	233	233
Panel B. IV with first random draw as dependent variable and average of other draws as instrument
Single random draw of blood lead levels	−0.373 [0.0328]	−0.340 [0.0791]
Observations	47,603	20,521
Fixed effect	Tract	Address
Number of fixed effects	233	10,157
Panel C. IV with geometric mean of lead as dependent variable and predicted certificate as instrument
Geometric mean of lead	−0.600 [0.415]	−1.390 [0.643]
Geometric mean of lead (imputed)			−1.097 [0.390]
Geometric mean of lead (weighted)				−2.470 [0.898]
Observations	59,877	26,131	70,678	70,678
R2	0.224	0.640
Fixed effect	Tract	Address	Tract	Tract
Number of fixed effects	233	11,298	233	233

Notes: Standard errors clustered at the tract level are shown in brackets. Fifteen percent of the children in our sample were not born in Rhode Island and therefore there is no natality data available for them. They are dropped in column 1. Column 2 shows estimates for the sample of addresses with more than one child and including address fixed effects. Column 3 uses an alternative measure of lead exposure: we impute lead levels for months with no lead test based on an average of the two nearest months with measured lead levels. Column 4 shows estimates based on an imputed lead measure where we give greater weight to measures taken at younger ages (see text for more detail on imputation and weighting methods).

The second column exploits the fact that for some addresses we observe multiple children over time. Focusing on this subsample reduces the sample size to 26,131 children. Column 2 shows estimates using this subsample and including address fixed effects. Again, the results are remarkably similar to those presented above, although now the IV specification based on predicted certificates is somewhat larger than before.

Column 3 of Table 9 shows estimates using a measure that imputes total lead exposure over the child’s preschool years using the lead measures that we have. In order to create this measure we interpolate lead measures for each month of the sample using the nearest adjacent measures to the month in question.²¹ While this measure should better reflect duration of lead exposure, in practice the measure is very similar to the simple geometric mean (correlation of 0.96). Given this high degree of correlation in the measures, it is not surprising that the OLS estimate based on these imputed values shown in panel A is quite similar to the estimate shown in Table 3A. Since now we have only one imputed measure, this method does not lend itself to our first IV strategy, but the estimate using the predicted certificate instrument is also quite similar to that shown in Table 5.

In column 4, we experiment with an imputed measure of lead exposure over the child’s lifetime, which weights earlier exposure more heavily than later exposure.²² The OLS estimate is again quite similar to that discussed above, while the IV based on the predicted certificate is much larger than any of the previous estimates. This could indicate that exposure in early life is more harmful than later exposure or it could simply reflect the fact that the instrument is calculated based on the address at the first blood test and thus is more predictive of early BLLs.

The same set of robustness exercises were performed for the third grade math scores and shown in Appendix Table 6. The OLS and instrumental variable estimates based on multiple measures of lead are roughly similar to, though in some cases smaller than, the main set of estimates presented in Tables 3B and 5. However, the IV results based on the certificate program, which were already quite imprecise, are generally not robust to the above described modifications to sample or measurement of lead.

With regard to our second instrumental variables strategy, it could be argued that since all the variation in the certificate program is at the census tract level, we could perform the same estimation aggregating the data to that level. This estimation is shown for reading test scores in Appendix Table 5. The estimated effects are similar but slightly larger than those described in Table 8. A one unit increase in BLLs is estimated to reduce reading scores by −1.251. However, the effects for math (not shown) are small and imprecisely estimated.

V. Conclusions

Our study contributes to an evolving understanding of the hazards of low levels of lead exposure among young children. It is to our knowledge the first study to utilize a dataset that links preschool blood lead levels in a representative group of all public school children in a state to their future school test scores, and to develop a research design aimed at overcoming threats to inference posed by confounding and measurement error. While the issues associated with confounding have been understood, the literature to date has largely ignored the measurement error problem.

In order to address these issues, we develop two instrumental variables strategies. The first exploits the fact that there are multiple measures of blood lead levels for most of the children in our data. Using this instrument increases the estimated impact of a unit of blood lead on reading (math) from −0.188 (−0.124) to −0.436 (−0.305). These figures suggest that for the average public school child, eliminating lead (by reducing lead levels from 2.7 to zero micrograms per deciliter) increased mean reading and math scores by 1.18 and 0.82 points, respectively, corresponding to 9 and 6 percent of a standard deviation. These are relatively modest gains. However, the effects are larger at the tails of the distribution. The same reduction in lead reduced the probability of being below proficiency in reading by 2.6 percentage points, or 22 percent. For math the comparable figure is 2.1 percentage points or 13 percent. These estimates seem generally consistent with estimates in the epidemiological literature, though direct comparisons are difficult because of differences in methods, adjustments for measurement error, and the higher lead levels examined in previous work.²³

Table 2 showed that African Americans and children eligible for free lunch experienced greater average reductions in blood lead levels over the period we examine. This may be in part because as Table 7 shows, the lead-safe certificate program had a disproportionate impact on these children. Our second IV method focused on using the certificate program as an instrument, and therefore measures the impact of lead reductions on the vulnerable children targeted by that program. Although these estimates are imprecise, they are substantially larger than those generated by our first IV method, which perhaps provides some preliminary evidence for heterogeneity in the impact of lead. Disadvantaged children may suffer double jeopardy in the sense that they are both exposed to greater levels of lead and experience greater impacts of the same exposure. This question is an important topic for future research.

Appendix

Appendix Table 1.

Age of Housing and Child Characteristics

Panel A. Concentration of children by race and income living in old housing in the United States and Rhode Island
	US share in housing built		RI share in housing built
	Pre-1978	Pre-1945	Pre-1978	Pre-1945
Black	0.72	0.22	0.83	0.52
White	0.63	0.22	0.74	0.37
Hispanic	0.68	0.2	0.83	0.53
≤100% FPL			0.81	0.43
≥200% FPL			0.76	0.4
<200% FPL and Black			0.83	0.5
<200% FPL and White			0.84	0.48
Black
2010	0.58	0.18	0.82	0.58
2000	0.7	0.21	0.85	0.47
1990	0.81	0.26	0.82	0.52
White
2010	0.5	0.18	0.62	0.41
2000	0.59	0.21	0.71	0.34
1990	0.73	0.25	0.8	0.32
Panel B. Concentration of children by race and income living in Providence, Rhode Island
	Providence	Rest of RI
Share housing built pre-1978	0.81	0.68
Share housing built pre-1945	0.49	0.27
Share black population living in:	0.86	0.14
Share white population living in:	0.51	0.49
Share population < 100% FPL living in:	0.77	0.23
Share population > 100% FPL living in:	0.55	0.45
Share population < 100% FPL and black living in:	0.89	0.11
Share population < 100% FPL and white living in:	0.6	0.4

Notes: Calculations from US census IPUMS data for 1990, 2000, and 2010. Sample includes all children ten and under.

Appendix Table 2.

Certificates Granted by End of 2010 by County

Panel A. Total certificates
	Population	Old housing	Certificates			Certificates per old housing unit
			Total	DOH	HRC	Total	DOH	HRC
Bristol	49,875	8,602	634	0	634	0.07	—	0.07
Kent	166,155	22,249	4,336	3,122	1,214	0.19	0.14	0.05
Newport	75,400	13,514	3,204	707	2,497	0.24	0.05	0.18
Providence	626,667	128,225	37,059	11,452	25,607	0.29	0.09	0.20
Washington	118,269	13,265	1,501	349	1,152	0.11	0.03	0.09
Panel B. Certificates in past 5 years
Bristol			597	0	426	0.24	—	0.17
Kent			3,661	2,427	936	0.13	0.09	0.03
Newport			2,943	577	2,372	0.52	0.10	0.42
Providence			24,724	7,421	17,483	0.06	0.02	0.04
Washington			1,072	254	823	0.08	0.02	0.06

Note: Data on population and housing age from ACS data; data on certificates based on authors’ calculations of data from the Rhode Island Departments of Health and Housing.

Appendix Table 3.

Sample Construction

	RIDE (n = 122,786)			RIDE-Lead (w/test score) (n = 77,777)		RIDE w/test scores (n = 91,456)
	No lead (n =30,795)	Lead (n = 91,991)
		No test score (n =14,214)	Test score (n=77,777)	No VS (n = 12,008)	VS (n = 65,769)
From RIDE or VS:
Black	0.15	0.1	0.1	0.11	0.09	0.1
White	0.5	0.67	0.68	0.55	0.71	0.69
Hispanic	0.23	0.19	0.19	0.27	0.17	0.19
Asian	0.06	0.04	0.03	0.05	0.03	0.03
Never free lunch	0.4	0.45	0.44	0.4	0.45	0.43
Always free lunch	0.39	0.27	0.27	0.31	0.26	0.27
From VS:
Maternal education		13.2	13.2		13.2	13.2
Married at birth		0.57	0.61		0.61	0.61
Maternal age at birth		28.1	28.6		28.6	28.6
Birth order		1.9	1.9		1.9	1.9
Birth weight		3,311	3,341		3,341	3,340
From RIDOH:
Lead—average		3.1	3.1	3.25	3.1	3.1
Third grade reading scores			45.6	46.2	45.7	45.2

Notes: For column 1 (education data but no lead test) we do not present means for vital statistics data because there are few observations with such data. The sample used for analysis is shown in column 3 and includes imputations of some variables drawn from the vital statistics data. Columns 4 and 5 show means for the non-imputed sample.

Appendix Table 4.

Hausman Tests for the Equivalence of OLS and IV Estimates

	OLS (1)	IV1 (2)	IV2 (3)
Single random draw of blood lead levels	−0.186 [0.0188]	−0.442 [0.0372]	−0.924 [0.426]
Observations	54,491	54,491	54,491
R2	0.233
Instrument	None	Average of other BLLs	Predicted certificate
Hausman test (chi squared) comparing OLS and IV estimates		12.1	0.53

Notes: Sample restricted to children with at least two BLLs. Also included are all covariates listed in Table 3A, column 3, whether the home has/will ever receive a certificate, year of birth and month of birth, and census tract fixed effects. The null hypothesis for the Hausman test is that the difference in the coefficients is not systematic. The test statistics indicate that the IV1 and OLS coefficients are different, but that the IV2 and OLS coefficients are not.

Appendix Table 5.

Estimates of Lead and Reading Scores Based on Aggregate Means

	Outcome = reading score		Outcome = average lead level first stage (3)
	OLS weighted (1)	IV (2)
Geometric mean of lead	−0.408 [0.148]	−1.251 [0.422]
African American	11.82 [6.567]	13.67 [5.673]	0.922 [1.042]
White	13.04 [6.373]	15.09 [5.655]	1.001 [1.051]
Hispanic	11.28 [6.428]	13.03 [5.540]	0.457 [1.026]
Asian	15.16 [6.660]	16.83 [5.847]	0.548 [1.079]
Always free/reduced lunch	−5.477 [1.045]	−5.344 [0.995]	0.250 [0.204]
Sometimes free/reduced lunch	−4.329 [0.857]	−4.032 [0.814]	0.289 [0.172]
Male	−3.335 [0.605]	−3.291 [0.569]	0.0499 [0.0980]
Birth weight in kg	1.703 [0.546]	1.553 [0.527]	−0.158 [0.113]
Mother < high school	−4.603 [1.258]	−4.385 [1.265]	0.266 [0.283]
Mother high school grad	−2.476 [0.937]	−2.828 [1.014]	−0.239 [0.184]
Mother college+	1.163 [1.012]	1.172 [1.005]	−0.0619 [0.193]
Married at birth	−1.178 [0.920]	−1.571 [0.841]	−0.475 [0.165]
Birth order	−0.615 [0.369]	−0.498 [0.330]	0.154 [0.0690]
Birth weight missing—imputed	2.358 [1.909]	3.163 [1.860]	0.425 [0.385]
Maternal education	−3.558 [1.835]	−3.879 [1.838]	−0.159 [0.373]
Families: Income in 2012 below poverty level	2.703 [5.647]	3.707 [5.216]	0.497 [1.563]
Median family income (in 2010 inflation adjusted dollars)	−4.59e–05 [4.15e–05]	−2.51e–05 [3.21e–05]	1.25e–05 [9.18e–06]
Share of housing built post-1978	4.704 [4.350]	8.252 [4.112]	3.891 [1.260]
HRC certificates at birth			−8.275 [1.760]
HRC certificates at birth squared			20.38 [8.086]
DOH certificates at birth			−8.308 [2.245]
DOH certificates at birth squared			17.57 [4.889]
Share of housing to ever receive a certificate	−0.993 [0.870]	−0.765 [0.911]	0.235 [0.207]
Observations	1,989	1,989	1,989
R2	0.865		0.885

Notes: Each observation is a birth year × census tract cell. All variables represent the average for that year of birth and census tract. For example, the outcome (reading test scores) is the average third grade reading test score of all children born in a given year living in a given tract as of the first lead test. All covariates similarly defined (i.e., lead is the average lead level for these children; African American is the share African American in that year of birth and census tract). All regressions weighted by the number of children in each cell.

Appendix Table 6.

Lead and Math Test Scores—Robustness

	Drop obs. with imputed natality (1)	Include address FE (2)	Impute all preschool lead (3)	Weight earlier exposure more (4)
Panel A. Ordinary least squares
Single random draw of blood lead levels	−0.111 [0.0158]	−0.0737 [0.0390]
Geometric mean of lead (imputed)			−0.188 [0.0218]
Geometric mean of lead (weighted)				−0.175 [0.0327]
Observations	59,834	26,112	70,625	70,625
R2	0.227	0.659	0.225	0.224
Fixed effect	Tract	Address	Tract	Tract
Number of fixed effects	233	10,157	233	233
Panel B. IV with first random draw as dependent variable and average of other draws as instrument
Single random draw of blood lead levels	−0.264 [0.0306]	−0.177 [0.0704]
Observations	47,566	18,310
Fixed effect	Tract	Address
Number of fixed effects	233	10,157
Panel C. IV with geometric mean of lead as dependent variable and predicted certificate as instrument
Geometric mean of lead	0.321 [0.501]	−0.640 [0.495]
Geometric mean of lead (imputed)			0.0208 [0.524]
Geometric mean of lead (weighted)				0.0468 [1.179]
Observations	59,834	26,102	70,625	70,625
R2
Fixed effect	Tract	Address	Tract	Tract
Number of fixed effects	233	11,298	233	233

Notes: Standard errors clustered at the tract level are shown in brackets. Fifteen percent of the children in our sample were not born in Rhode Island and therefore there is no natality data available for them. They are dropped in column 1. Column 2 shows estimates for the sample of addresses with more than one child and including address fixed effects. Column 3 uses an alternative measure of lead exposure: we impute lead levels for months with no lead test based on an average of the two nearest months with measured lead levels. Column 4 shows estimates based on an imputed lead measure where we give greater weight to measures taken at younger ages (see text for more detail on imputation and weighting methods).