When Are Metabolic Ratios Superior to Absolute Quantification? A Statistical Analysis

Abstract

Metabolite levels measured using magnetic resonance spectroscopy (MRS) are often expressed as ratios rather than as absolute concentrations. However, the inter-subject variability of the denominator metabolite can introduce uncertainty into a metabolite ratio. In a clinical setting, there are no guidelines on whether ratios or absolute quantification should be used for a more accurate classification of normal versus abnormal results based on their statistical properties. In a research setting, choosing one over the other can have significant implications on sample size, which must be factored in at the study design stage. Herein, we derive the probability distribution function for the ratio of two normally distributed random variables, and present analytical expressions for comparing ratios to absolute quantification in terms of both sample size and area under the receiver operator characteristic curve. The two approaches are compared for typical metabolite values found in the literature, and their respective merits are illustrated using previously acquired clinical MRS data in two pathologies: mild traumatic brain injury and multiple sclerosis. Our analysis shows that deciding between ratios and absolute quantification is non-trivial: in some cases, ratios might offer a reduction in sample size, while in others, absolute quantification might prove more desirable for individual (i.e. clinical) use. The decision is straightforward and exact guidelines are provided in the text, given that population means and standard deviations of numerator and denominator can be reliably estimated.

Graphical Abstract

Metabolite ratios can either improve or diminish the usefulness of MRS, compared to absolute quantification, depending on the change in the ratio’s numerator and denominator. An analysis of when to choose one over the other is presented, based on considerations of sample size requirements and area under the receiver operator characteristic (AUROC).

Introduction

The quantification of MRS data requires some form of reference signal. This signal can be external, as in a replacement phantom (1,2) or stable signal injected into the coil’s RF system (3,4); It can also be internal, as in the water signal from an unsuppressed acquisition (1,5) or another metabolite present in the spectrum, as seen in clinical applications (6-11). If the concentration of the reference signal is known, a statement can be made about the absolute concentration of the metabolite being quantified; otherwise, only a ratio can be reported. Since ratios do not reveal whether an observed difference is due to a change in the numerator or in the denominator, absolute quantification is deemed preferable whenever possible, despite often requiring additional scans and calibration steps (12,13). This increased complexity sometimes leads practitioners to instead favor metabolic ratios, which also account for hardware imperfections and cerebrospinal fluid content.

Another instance when metabolic ratios are preferred is in cases when metabolites are expected to shift in opposing directions, as reported with proton MRS (¹H-MRS) in many neurological pathologies, including multiple sclerosis (MS) in which the n-acetyl-aspartate (NAA) levels decrease while creatine (Cr), myo-inositol (mI) and choline (Cho) increase (14); dementia, in which NAA decreases while Cr increases (15); and brain tumors, in which Cr and NAA often decrease while Cho increases (16). Metabolite ratios capitalize on this trend, since the ratio of two such quantities A/B will change in pathology A/B → (A+ΔA)/(B-ΔB) markedly more than either numerator (A→A+ΔA) or denominator (B→B-ΔB).

As previously noted (17,18), some metabolic ratios display increased coefficients of variation (CVs) compared to absolute quantification due to the combined variances of both numerator and denominator. To adequately decide whether ratios are statistically superior to absolute quantification, however, CVs alone are insufficient and one must examine the expected change and the CVs simultaneously. Despite the prevalence of ratios in the research and clinical literature, no attempt has been made to examine this question in depth. Herein we contrast absolute quantification with metabolite ratios by examining their statistical properties. We begin by deriving a simplified probability distribution function (pdf) of the ratio of two metabolites. This is used to determine two key quantities: the reduction in sample size required to observe a change in a cohort study, and the total area underneath the Receiver Operator Characteristic (AUROC). Minimizing sample size reduces both the cost and complexity of studies which use ¹H-MRS to define clinical end points. The AUROC equals the probability that a test correctly classifies those with and without the disease (19,20); it is often used as indicator of the quality of a classifier. Both metrics are numerically computed and examined for a range of physiologically relevant metabolite values, based on literature reports and on two previously acquired datasets from MS (14) and mild traumatic brain injury (mTBI) (21).

Theory

The Probability Distribution of a Metabolic Ratio

The distribution of most metabolites is approximately normal. The probability distribution function p(R) of the ratio R=X₁/X₂ of two normally distributed random variables, $X_1\sim N\left({\mu }_1,{\sigma }_1^2\right),X_2\sim N\left({\mu }_2,{\sigma }_2^2\right)$ has been previously derived (22):

$$\begin{array}{cc}\hfill & p(R)=g(R)\text{exp}\left[h(R)\right]\hfill \\ \hfill & g(R)=\frac{b(R)}{\sqrt{2\pi }{\sigma }_1{\sigma }_{2}a{}^{{}^3}(R)}\hfill \\ \hfill & h(R)=\frac{b^{{}^2}(R)-c\cdot a^2(R)}{2(1-{\rho }^2)a^{{}^2}(R)}\hfill \\ \hfill & b(R)=\frac{{\mu }_1}{{\sigma }_1^2}R-\frac{\rho ({\mu }_1+{\mu }_{2}R)}{{\sigma }_1{\sigma }_2}+\frac{{\mu }_2}{{\sigma }_2^2}\hfill \\ \hfill & a(R)=\sqrt{\frac{R^2}{{\sigma }_1^2}-\frac{2\rho R}{{\sigma }_1{\sigma }_2}+\frac{1}{{\sigma }_2^2}}\hfill \\ \hfill & c=\frac{{\mu }_1^2}{{\sigma }_1^2}-\frac{2\rho {\mu }_1{\mu }_2}{{\sigma }_1{\sigma }_2}+\frac{{\mu }_2^2}{{\sigma }_2^2}\hfill \end{array}$$ [1]

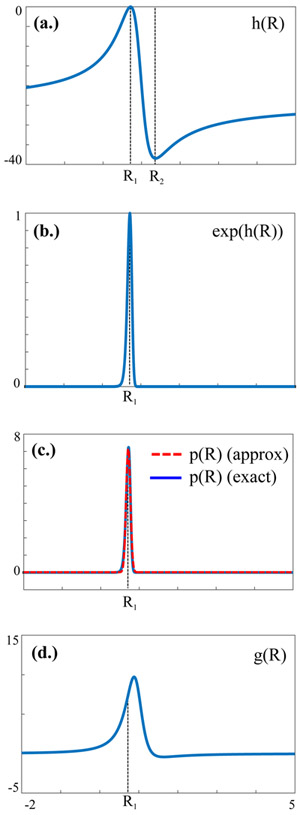
where −1 ≤ ρ ≤ 1 is the correlation coefficient between X₁ and X₂. Often, clinical data will have CVs ≤ 0.25. Under this assumption, Eq. [1] can be simplified as follows: The function h(R) in the exponent has two extremal points, R₁ and R₂ (solutions of h’(R)=0), at which (Fig. 1a):

$$\begin{array}{cc}\hfill & h\left(R_1=\frac{{\mu }_1}{{\mu }_2}\right)=0\hfill \\ \hfill & h\left(R_2=-\frac{{\sigma }_1}{{\sigma }_2}\frac{c{v}_1-\rho \cdot c{v}_2}{c{v}_2-\rho \cdot c{v}_1}\right)=\frac{c{v}_2^2-2\rho \cdot c{v}_{1}c{v}_2+c{v}_1^2}{2c{v}_1^{2}c{v}_2^2\left({\rho }^2-1\right)}\hfill \end{array}$$ [2]

with CV_i=σ_i/μ_i the coefficient of variation for the numerator (i=1) or denominator (i=2). Second derivatives indicate R₁ is a maximum while R₂ is a minimum (Fig. 1a). Furthermore, taking the limits, one finds $h(R)\stackrel{R\to \pm \infty }{\to }-\frac{1}{2c{v}_2{}^2}$. Under the assumption CV₂<<1, this implies exp(h(R)) becomes non-negligible only in the vicinity of the maximum R=R₁ (Fig. 1b). We can therefore expand h(R) in a series around R₁, $h\left(R\right)\approx h\left(R_1\right)+\frac{1}{2}h{}^{{}^{″}}(R_1){\left(R-\frac{{\mu }_1}{{\mu }_2}\right)}^2$, with negligible higher order terms since h(R) is heavily damped by the exponent. The slowly-varying function g(R), shown in Fig. 1d, can simply be substituted by its value at the extremum, g(R)≈g(R₁). Following normalization, ${\int }_{-\infty }^{\infty }p\left(R\right)dR=1$, a Gaussian distribution is obtained:

$$R\sim N\left(\frac{{\mu }_1}{{\mu }_2},{\left(\frac{{\mu }_1}{{\mu }_2}\right)}^2\left(c{v}_1^2-2\rho \cdot c{v}_1\cdot c{v}_2+c{v}_2^2\right)\right).$$ [3]

Fig. 1.

Plots of (a.) h(R), (b.) exp(h(R)) and (c.) the normal approximation (red) to the exact probability distribution function p(R) (blue) defined in Eq. [1], for μ₁=10, σ₁=2, μ₂=14, σ₂=2 (CV₂≈14%). Also shown in (d.) is the function g(R).

The approximate distribution (Eq. [3]) is plotted in Fig. 1c against the true distribution, p(R) (Eq. [1]). The assumptions used to derive Eq. [3], namely CV₂<<1 and normality, will be examined below.

Metrics For Assessing Patient and Control Distributions

A normally distributed ratio allows one to easily calculate other quantities of statistical interest. Given normal patient and control ratio distributions, $R_p\sim N\left({\mu }_p,{\sigma }_p^2\right),R_c\sim N\left({\mu }_c,{\sigma }_c^2\right)$, the sample size required to observe a one-sided change in the mean, Δμ = μ_p – μ_c, is:

$$N=\frac{{\left(z_{1-\alpha }{\sigma }_p-z_{\beta }{\sigma }_c\right)}^2}{\Delta {\mu }^2}$$ [4]

where α, 1-β are the statistical significance and power of the study, respectively, and μ_p, μ_c, σ_c and σ_p can be calculated using Eq. [3] given the means and variances of the numerator and denominator metabolites. z_x is the inverse of the normal cumulative distribution function. In many studies one sets α=0.05, β=0.2, and so z_0.2=−0.842, z_0.95=1.645.

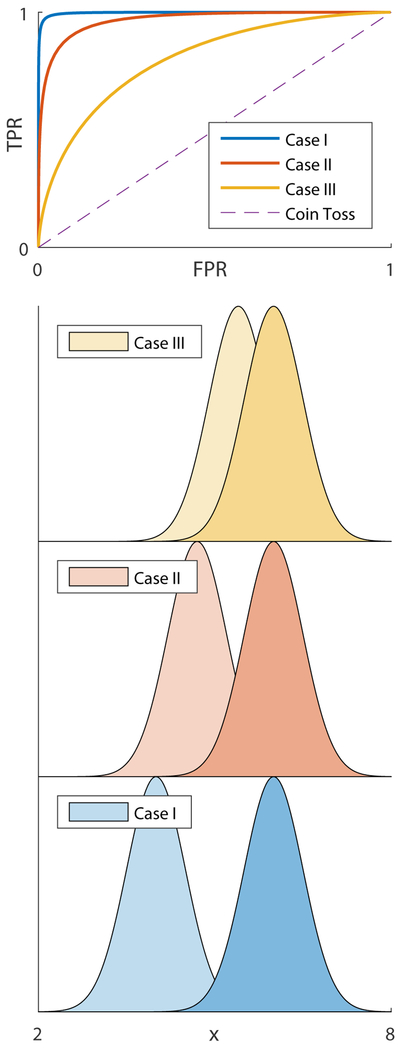
A second quantity of interest is the area underneath the receiver operator characteristic (AUROC). Receiver operating characteristic (ROC) curves are often used to assess the performance of a classifier which decides whether a given result is true (e.g. pathological) or false (e.g. healthy), by plotting its true positive rate (sensitivity) as a function of its false positive rate (1-specificity) (23). A coin toss is characterized by a straight line, with an area under the curve of AUROC=0.5, while any non-random useful classifier will deviate from a straight line and have AUROC>0.5 (Fig. 2). The AUROC is bounded from above by unity, and a higher value indicates a superior classifier. The AUROC equals its discrimination: the probability that a randomly chosen true positive (pathological) specimen outranks a randomly chosen true negative (control) (19). Given two uncorrelated normal distributions for controls and patients, $R_c\sim N\left({\mu }_c,{\sigma }_c^2\right),R_p\sim N\left({\mu }_p,{\sigma }_p^2\right)$, the AUROC can be shown to equal:

$$\text{AUROC}=\Phi \left(\frac{\mid {\mu }_C-{\mu }_P}{\sqrt{{\sigma }_C^2+{\sigma }_P^2}}\right)$$ [5]

where Φ(z) is the cumulative distribution function of the Gaussian distribution N(0,1).

Fig 2.

Receiver operating characteristic (ROC) curves: a visual overview. Shown are three pairs of normal distributions (Case I: 4±0.5 vs 6±0.5; Case II: 4.7±0.5 vs. 6±0.5; Case III: 5.4±0.5 vs. 6±0.5), possibly corresponding to patient and control distributions of some biomarker x. ROC curves for all three cases are plotted above as follows: a classifier value μ_c is selected, with all values above it classified as “pathological” and below it as “healthy”; random values are generated from each distribution and classified, and the rate of true positives (TPR) and false positive (FPR) is recorded; μ_c is swept from μ_c=2 to μ_c=8, and the processes is repeated at each step, until one is able to construct a continuous curve of TPR as a function of FPR, which is the ROC curve. The dashed line corresponds to a coin toss, where cases are classified as pathological or healthy randomly with equal probability. As the distance between the two distributions decreases, classification becomes more prone to error and the ROC curve becomes more diagonal-like. The areas under the ROC curves are AUROC=0.99, 0.97 and 0.80 for cases I, II and III, respectively, reflecting how classification becomes more difficult as the distributions become closer (AUROC=0.5 for the random coin toss).

Materials and Methods

Absolute Quantification vs. Ratios: Numerical Simulations

To determine when metabolite ratios improve sample size requirements and diagnostic value, we computed N (Eq. [4]) and the AUROC (Eq. [5]), respectively, for NAA, Cr and NAA/Cr. Literature values for white matter (WM) NAA (7.7±0.6 mM) and Cr (4.9±0.5 mM) in healthy controls were used (24). We have confined ourselves to the regime in which NAA decreased and Cr increased, for which ratios would normally be deemed statistically beneficial. Three cases were examined, in which patient standard deviations decreased (σ_NAA,P=0.4, σ_Cr,P=0.3), remained unchanged (σ_NAA,P=0.6, σ_Cr,P=0.5) and increased (σ_NAA,P=0.9, σ_Cr,P=0.9) standard deviations in the patient population. The patient WM NAA and Cr values were varied by up to 40% (typical of many pathologies), keeping the inter-subject coefficient of variation smaller than 25% for the denominator, Cr, and hence validating use of Eq. [3]. The sample sizes N_NAA, N_Cr and N_ratio required to observe the single-sided change between controls and patients were computed using a statistical significance of 5% and power of 80%.

Absolute Quantification vs. Ratios: In-Vivo Comparisons

Global WM changes in NAA, Cr and NAA/Cr were examined using data from two previously acquired datasets: a longitudinal study of relapsing-remitting MS, and a cross-sectional mTBI study. The cohort and data analysis pipeline are described elsewhere (14,21). To briefly summarize: the MS cohort consists of eighteen patients (5 men, 13 women) aged 21-45, scanned every 6 months for a period of 3 years, and 10 age- and gender-matched healthy controls scanned yearly; the mTBI cohort consists of twenty-six patients with closed-head trauma (5 women, 21 men) aged 33 ± 11 years, scanned up to 55 days from injury, and thirteen age- and gender-matched healthy controls (5 women, 8 men). All scans were approved by the Institutional Review Board of New York University School of Medicine. Both cohorts were scanned on a 3T whole-body MR imager (Tim-Trio, Siemens AG, Erlangen Germany) using hybrid Hadamard-PRESS 3D ¹H-MRS covering a 360 cm³ volume. Linear regression was used to calculate the global WM values of NAA, Cr, Cho and mI (24). Data was processed using in-house software and fit using SITools-FITT (25), and phantom replacement was used for absolute quantification, based on the signal formula

$$s={\Lambda }_0\cdot c\cdot v_{{}_{ref}}\cdot v_{{}_{voxel}}\cdot \left(1-e^{{}^{-TR∕T_1}}\right)\cdot e^{{}^{-TE∕T_2}}$$ [6]

where Λ₀ is a proportionality constant which depends on the electronics and coils; C the concentration, in mM; V_voxel the voxel volume, in mL; V_ref the reference voltage, in volts; and T₁, T₂ the metabolite-specific relaxation constants in question, in either the phantom or the in-vivo tissue. B₁₊ and B₁₋ variations in the 360 mL spectroscopic volume were not accounted for. Note that Eq. [6] implies taking the ratio of two absolutely quantified metabolites is completely equivalent to the ratio of the original metabolic signals following T₁, T₂ correction, since the phantom contributions cancel out among both metabolites.

A Shapiro-Wilks test with a significance level of α=0.05 was used to validate the normality of numerator, denominator and ratio. A two-sided t-test at α=0.05 was used to verify whether one can assume ρ = 0 in Eq. [3]. Estimated population means and standard deviations for NAA and Cr were used to compute required sample sizes and AUROC using Eqs. [4], [5] for NAA, Cr and NAA/Cr (in MS) and NAA, mI and NAA/mI (in mTBI).

Results

Absolute Quantification vs. Ratios: Numerical Simulations

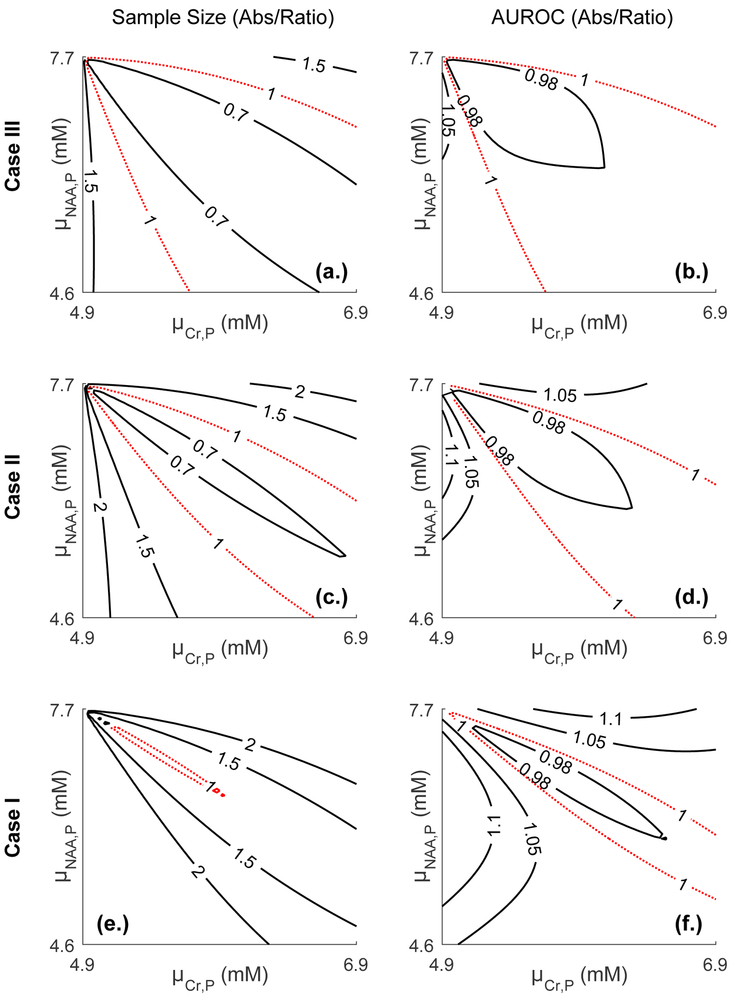
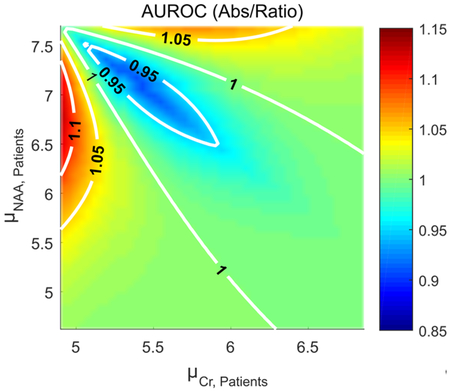
Fig. 3 compares both sample size requirements and the AUROC between absolute quantification and metabolite ratios, for all three cases: decreased, unchanged and increased population standard deviations. Plotted are two quantities in the $\left({\mu }_{NAA}^{(\text{patient})},{\mu }_{Cr}^{(\text{patient})}\right)$ plane: the ratio min(N_NAA,N_Cr)/N_ratio (Figs. 3a,c,e) and max(AUROC_NAA, AUROC_Cr)/AUROC_ratio (Figs. 3b,d,f), with several contours. A ratio of unity (dashed, red) corresponds to the case in which ratios and absolute quantification perform equally. Ratios are preferable in the strip within the unity contour, while absolute quantification is preferable outside the strip. The plots reveal several general behaviors of ratios.

Fig. 3.

Contour plots comparing sample sizes and AUROC curves between absolute quantification and ratios in the ($\left({\mu }_{NAA,patients},{\mu }_{Cr,patients}\right)$) plane. Physiologically relevant metabolite values and standard deviations for averaged WM NAA (7.7±0.6 mM) and Cr (4.9±0.5 mM) were employed for controls. Patient metabolite values were varied by up to 40%, with NAA decreasing and Cr increasing. Three cases were examined: decreased (case I: σ_NAA,P=0.4, σ_Cr,P=0.3), unchanged (case II) and increased (case III: σ_NAA,P=0.9, σ_Cr,P=0.9) patient standard deviations. Left: the ratio of sample sizes N_ratio/min(N_NAA,N_Cr) is plotted, where N_NAA, N_Cr, N_ratio, are the sample sizes required for NAA, Cr, and their ratio, assuming statistical significance of 5% and power of 80% and a single-sided change. The unity contour (red, dashed line) implies both require the same sample size. The region inside the unity contour indicates absolute quantification is preferable, while ratios are preferable outside the unity contour. Right: the ratio AUROC_ratio/max(AUROC_NAA, AUROC_Cr). Here, again, a ratio of unity (red, dashed line) indicates both absolute quantification and ratios are equivalent in terms of their AUROC. Ratios are superior outside the unity contour.

First, a non-trivial relationship exists between numerator, denominator and ratio distributions, and one must carefully consider both changes in mean values and standard deviations before opting for one or the other. For example, for the case of unchanged standard deviations, when NAA declines by 5% and Cr rises by 5%, ⎾N_Cr⏋=27, ⎾N_NAA⏋=15 and ⎾N_ratio⏋=11, AUROC_Cr=0.63, AUROC_NAA=0.68, AUROC_ratio=0.71 (here ⎾x⏋ denotes the smallest possible integer larger than or equal to x). While ratios are superior to absolute quantification in both cases, they clearly have a much more pronounced advantage when considering sample sizes. An opposite situation arises when NAA declines by 15% and Cr rises by 15%, where ⎾N_Cr⏋=3, ⎾N_NAA⏋=2 and ⎾N_ratio⏋=2, AUROC_Cr=0.85, AUROC_NAA=0.91, AUROC_ratio=0.95; here, sample size requirements are equal but diagnostically, the ratio NAA/Cr still presents an improvement over both NAA and Cr. These examples illustrate a second point: as shown by all cases, the relative merit of ratios vs. absolute quantification depend on the metric considered. The regions within which ratios are preferable to absolute quantification are similar but not equivalent.

Third, ratios become more favorable as the standard deviation in the patient population decreases relative to controls. This is a direct consequence of the decreased variability introduced into the ratio NAA/Cr by dividing by Cr: as the denominator’s variability decreases, ratios become more statistically appealing. This same behavior can also be seen by, e.g., considering case II with NAA declining by 10% and Cr remaining unchanged: here, ⎾N_Cr⏋=∞, ⎾N_NAA⏋=4 and ⎾N_ratio⏋=10, AUROC_Cr=0.5, AUROC_NAA=0.82, AUROC_ratio=0.72. NAA/Cr displays decreased performance compared to NAA due to division by the Cr value, which does not change on average but has a non-zero standard deviation (owing to inter-subject variability).

A two-sided sample size calculation would simply scale these numbers, but not change the overall form of Fig. 3.

Absolute Quantification vs. Ratios: In-Vivo Comparisons

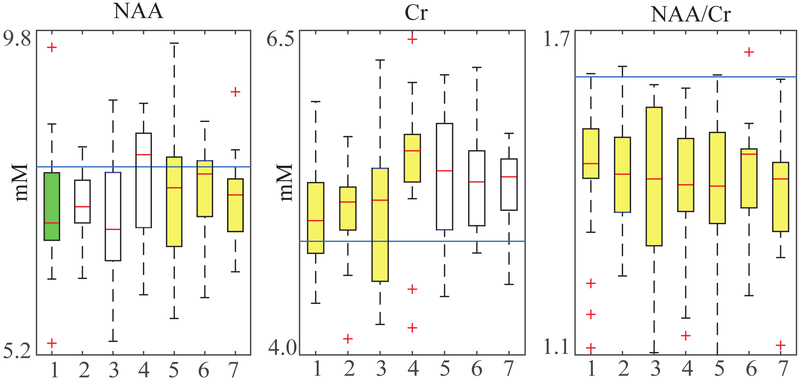
All metabolite distributions examined were normally distributed as revealed by the Shapiro-Wilks test for normality. For the ratios considered, none of the metabolite pairs exhibited statistically significant correlation, leading us to assume ρ=0. Statistically significant (α=0.05) reduction in WM NAA and increase in WM Cho, Cr and mI concentrations were observed in several - but not all - time points in MS patients compared with the pooled mean of controls, in accordance with previously reported results (14) (Table 1). In contrast, the ratio NAA/Cr differs significantly at all time points between patients and controls (Fig. 4); all time points remain significant even as the significance level is lowered to a strict α=0.01 level. Despite its more pronounced statistical significance, NAA/Cr actually underperforms compared to absolute quantification in three of the seven time points (4, 5 and 6), at which the sole Cr measurement offers marginally better sample sizes and AUROCs. This clearly illustrates that statistical significance does not imply statistical superiority in terms of sample size or diagnostic quality, although differences in question might be small.

Table 1.

Metabolite global WM means for NAA, Cr and NAA/Cr, over seven time points, at 6 month intervals, for both patients and control in MS (taken from (14)). This data reflects the boxplots in Fig. 4. Greyed out columns indicate statistical significance (p-value≤0.05 with α=0.05). All absolute quantities are in millimoles/L of tissue water. The control values over all time points were pooled to create a global μ_control, σ_control, following (14). For each metabolite, the sample size requirement (rounded up) and AUROC are displayed. Note that, even though Cr is not statistically significant at time points 5, 6 and 7, it actually yields smaller sample size requirements and AUROC compared to NAA/Cr which is statistically significant.

Time Pt.	1	2	3	4	5	6	7
NAA (μcontrol=7.87, σcontrol=0.71)
μpatient	7.26	7.30	7.14	7.70	7.50	7.58	7.39
σpatient	0.94	0.53	1.02	0.82	0.90	0.61	0.61
⎾N⏋	11	9	8	131	28	35	13
AUROC×100	69	74	72	56	63	62	69
Cr (μcontrol=4.88, σcontrol=0.38)
μpatient	5.09	5.09	5.09	5.49	5.37	5.34	5.30
σpatient	0.46	0.39	0.63	0.54	0.51	0.41	0.31
⎾N⏋	24	19	28	4	5	5	5
AUROC×100	63	66	62	82	78	80	81
NAA/Cr (μcontrol=1.61, σcontrol=0.19)
μpatient	1.43	1.43	1.40	1.40	1.40	1.42	1.39
σpatient	0.23	0.15	0.26	0.20	0.21	0.16	0.14
⎾N⏋	8	7	7	6	6	6	4
AUROC×100	73	77	74	77	77	78	82

Fig. 4.

Statistical significance of NAA, Cr, and NAA/Cr in longitudinally studied MS patients and controls. Data taken from (14). The straight line represents the controls’ means, assumed unaltered throughout, while the boxplots represent the patient metabolite distributions. Highlighted boxes represent a statistically significant difference between controls and patients at that particular time point, as determined by a two-tailed t-test using α=0.05 (green and yellow) and α=0.01 (yellow). Note that, while neither NAA nor Cr remain statistically significant throughout, their ratio does. Population and control metabolite means and standard deviations for all time points can be found in Table 1.

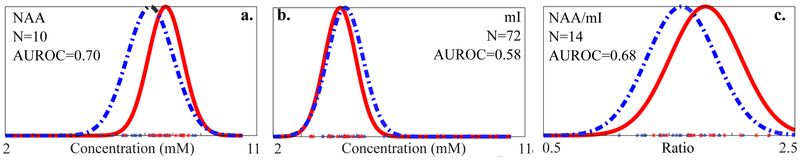
For the mTBI cohort, only WM NAA was statistically different between patients and controls (α=0.05) (Fig. 5). Sample size and AUROC calculations based on the estimated population variance and mean yielded the smallest sample size (⎾N_NAA⏋=10) and largest AUROC=0.7 for NAA, and slightly inferior results for the ratio NAA/mI (⎾N_mI⏋=14, AUROC=0.68). This clearly illustrates a second point: even though NAA and mI change in opposing directions, their ratio is not preferable to absolute quantification due to the additional variance introduced by dividing by mI.

Fig. 5.

Metabolite data from mTBI patients (blue stars) and controls (red asterisks) for (a.) global WM NAA, (b.) mI and (c.) NAA/mI, with fitted normal distributions (solid red: controls; dashed blue: patients): ${\mu }_{\text{NAA}}^{(\text{controls})}=7.74\pm 0.62\text{mM}$, ${\mu }_{\text{NAA}}^{(\text{patients})}=7.19\pm 0.83\text{mM}$, ${\mu }_{\text{mI}}^{(\text{controls})}=4.4\pm 0.56\text{mM}$, ${\mu }_{\text{mI}}^{(\text{patients})}=4.574\pm 0.65\text{mM}$, ${\mu }_{\text{ratio}}^{(\text{controls})}=1.76\pm 0.27$, ${\mu }_{\text{ratio}}^{(\text{patients})}=1.57\pm 0.29$. NAA decreases and mI slightly increases, with the only statistically significant change being that of NAA as determined by a double-sided t-test (p=0.042). Note the increased variability of the ratio distribution in (c), introduced by dividing by mI. The sample sizes required to observe each change (Eq. [4]) are N_NAA=10, N_mI=72, N_NAA/mI=14, and the AUROCs are AUROC_NAA=0.70, AUROC_mI=0.58, AUROC_NAA/mI=0.68, showing absolute quantification is superior to metabolic ratios in detecting mTBI WM injury.

Discussion

Normally distributed random variables and their ratios are found throughout science, and their ratios appear in fields as diverse as analog circuit design (26), telecommunications (27), industrial process monitoring (28) and econometrics (29). The statistical literature contains exact derivations (30-34), as well as various application-driven approximations to these ratios, probability distribution functions, moments and confidence intervals (35-37), for both the correlated and uncorrelated case. Herein, we have derived one particular normal approximation valid for typical, normally-distributed MRS data (Eq. [3]), where metabolite CVs rarely exceed 20-25%. This approximation lends itself to comparing absolute quantification to metabolite ratios in terms of their relevant statistical properties.

It is often implicitly assumed that whenever two metabolites’ means shift in an opposing manner, their ratio must improve detection. Herein we have shown that, depending on the means and variances of both numerator and denominator, metabolic ratios can either enhance or diminish the AUROC and sample size requirements in a non-trivial manner. On the one hand, ratios of metabolites with opposite behavior exhibit a greater change to the mean; on the other hand, any inter-subject variability present in the reference metabolite carries over to the ratio. Our conclusions can be considered an extension of previous studies, which have already noted the increased CVs exhibited by ratios, albeit without examining their effect on either sample size or contribution to clinical diagnosis (17).

When Are Ratios Preferable?

Choosing ratios over absolute quantification – from a statistical point of view – should be weighted carefully, especially since in many pathologies MRS peak areas change only modestly and it is not a-priori clear which metric is better; put differently, the change in the metabolite ratio’s mean is on the order of the variability inherent in the denominator. We have provided the reader with concrete tools for assessing precisely which distribution is favorable, depending on whether study design (Eq. [4]) or clinical diagnosis (Eq. [5]) are concerned.

We also note that there are multiple other considerations that affect one’s choice: absolute quantification often requires additional scan time and adds complexity, but allows for a clearer physiological interpretation of the underlying changes (albeit not always a statistically superior one). However, whether one should even consider adding this complexity should ultimately rest upon the measurement’s usage. For example, in a clinical setting where diagnosis is of paramount importance, ratios might offer greater AUROCs in some cases, rendering absolute quantification unnecessary. It should be stressed that deciding between the two requires knowledge of the mean and standard deviation of both numerator and denominator – e.g., from a previous study which did use absolute quantification.

Caveats And Pitfalls

Statistical significance should not be assumed to indicate statistical superiority. This was demonstrated in the MS cohort (Table 1). Even though Cr did not show statistical significance at three time points, it still offered both smaller sample sizes and better AUROCs compared to NAA/Cr which was statistically significant at the same three points. This should not be surprising: sample size and AUROCs are calculated using a population’s distribution, while statistical significance depends on the sampling distribution; indeed, by sufficiently lowering the significance level (α) any result can be rendered statistically non-significant, without affecting our sample size and AUROC estimations.

When using Eqs. [4], [5], one must know a-priori the means and standard deviations of both numerator and denominator metabolites, as well as their correlation coefficient, for both patient and control populations. These must be obtained from a previous MRS study which has employed absolute quantification for the same pathology. It is important to select reliable studies which employ high quality, robust methodology, in which mean and standard deviation estimates are dominated by inter-subject variation, with a minimal intra-subject component related to measurement error. This can be done by focusing on studies with high intraclass correlation coefficient (ICC≈1), which quantifies the agreement of measurements on the same subject (38).

Our derivations have assumed both numerator and denominator are normally distributed inter-subject, which must be tested on a per-case basis. All metabolite distributions used herein from the mTBI and MS cohorts, as well as their matched controls, were verified to be normally distributed using the Shapiro-Wilks test. There are multiple tests for normality, and the interested reader is referred to the literature for a comprehensive overview (39,40).

Absolute quantification itself is obtained by taking the ratio of a metabolite to a reference signal, and the preceding framework can be used to analyze the uncertainty these ratios introduce, such as the random physiological variation inherent to reference unsuppressed water scans or inter-subject variability in tissue water content. For example, when performing absolute quantification of liver fat content, the ratio of hepatic fat content to liver water content is sometimes used, with an assumed water content of 0.711 g water/g normal tissue (41). However, this does not take into account an inter-subject variation of approximately 10% (42). This variation enters into the ratio distribution as described by Eq. [3], contributes to the standard deviation of the reported metabolite values and should be accounted for when performing sample size estimation and other statistical analyses.

In the case two metabolites simultaneously increase or decrease, their ratio will always be statistically unfavorable compared to absolute quantification.

Conclusions

Metabolite ratios reduce sample size requirements and increase statistical significance compared to absolute quantification in almost all cases the numerator and denominator shift in opposition in pathology, despite increases in CVs reported by other authors (17,18). Nevertheless, care must be taken when the shifts are small in size, in which case the denominator’s variance may become dominant, making absolute quantification statistically favorable. A precise determination of whether ratios are favorable can be made on a per-case basis using Eqs. [3] and [4].

Abbreviations:

MS

Multiple Sclerosis

mTBI

mild traumatic brain injury

NAA

n-acetyl-aspartate

Cr

creatine, Cho-choline

mI

myo-inositol

CV

coefficient of variation

pdf

probability distribution function

AUROC

area underneath the Receiver Operator Characteristic

ROC

Receiver operating characteristic

WM

white matter