Abstract
Phase-based optical coherence tomography (OCT), such as OCT angiography (OCTA) and Doppler OCT, is sensitive to the confounding phase shift introduced by subject bulk motion. Traditional bulk motion compensation methods are limited by their accuracy and computing cost-effectiveness. In this Letter, to the best of our knowledge, we present a novel bulk motion compensation method for phase-based functional OCT. Bulk motion associated phase shift can be directly derived by solving its equation using a standard deviation of phase-based OCTA and Doppler OCT flow signals. This method was evaluated on rodent retinal images acquired by a prototype visible light OCT and human retinal images acquired by a commercial system. The image quality and computational speed were significantly improved, compared to two conventional phase compensation methods.
OCIS codes: (170.4500) Optical coherence tomography, (170.0110) Imaging systems, (170.3880) Medical and biological imaging
Optical coherence tomography (OCT) is a three-dimensional imaging technique used to image biological tissues with micrometer resolution [1]. With the advent of Fourier domain OCT [2,3], the larger speed and sensitivity of this technology have enabled new functional capabilities, such as flow imaging by Doppler OCT and OCT angiography (OCTA). Doppler OCT detects the phase shift between adjacent A-scans to provide flow velocity along the axial direction within the macro-vasculature. More recently, OCTA was developed to extract intrinsic blood flow signals within the microvasculature by subtracting the OCT signal of adjacent B-scans acquired at the same position. OCTA algorithms based on amplitude [4,5] or phase [6–8] signals have been successfully adopted by commercial systems and are routinely used by clinicians for ocular imaging.
However, one major challenge for phase-based functional OCT (e.g., phase-resolved Doppler OCT, phase-based OCTA) is the additional phase shift (difference) caused by bulk motion induced by breathing, heartbeats, and other involuntary motion. Phase-based methods are more vulnerable to bulk motion artifacts than amplitude-based methods, so the step to remove bulk motion phase shift is essential for accurately detecting the flow signal.
Two phase compensation methods have been previously reported and widely used. One is the “average” (AVG) method, which estimates bulk motion phase shift by averaging the phase shift along each A-line in the B-frame within the retinal tissue slab. This method may introduce a large error when vessels and their shadows occupy a relatively large portion of tissue. The other is the “histogram” (HIST) method, which estimates this artifact by finding the phase shift with the highest bin number (peak density) in the HIST of all values crossing the tissue on each A-line [6,7,9,10]. The HIST method can be more accurate than the AVG method by iteratively subtracting estimated bulk motion phase shift on each A-line. However, it requires a large computational budget.
In this Letter, we propose, to the best of our knowledge, a novel bulk motion compensation method based on the standard deviation (STD) of the phase shift signal on phase-based functional OCT imaging. Retinal Doppler OCT and OCTA scans were acquired on rats and healthy human volunteers to validate the theoretical framework. The performance of the algorithm, including image quality and computational needs, was evaluated.
A prototype visible light spectral-domain OCT system was used for imaging rodents. It was built at the Casey Eye Institute of Oregon Health & Science University (OHSU) with a 50 kHz scanning rate, a center wavelength at 560 nm, and axial resolution of 1.53 μm [11]. A total 12 eyes from six rats were imaged using this system. The scanning pattern was set to 1024 pixels per A-line, 512 A-lines per B-scan, and 512 B-scans per volume times three repeats. The scanning size is 2.1 mm × 2.1 mm, and the lateral resolution is 6 μm. Ten human retinal scans were acquired from five volunteers using a commercial spectral-domain OCT system (RTVue-XR Avanti; Optovue, Inc., Fremont, CA) with a 70 kHz scanning rate, a center wavelength at 840 nm, and an axial resolution of 5 μm. The scanning pattern was set to 1024 pixels per A-line, 304 A-lines per B-scan, and 304 B-scans per volume times two repeats. The scanning size is 3.0 mm × 3.0 mm, and the lateral resolution for this system is 10 μm. Written informed consent was obtained from all volunteers. All the experimental procedures were approved by the Institutional Review Board/Ethics Committee, as well as the Institutional Animal Care and Use Committee (IACUC) of OHSU.
The theory of the proposed compensation method was first verified on phase-based OCTA. According to Ref. [8], an OCT complex signal (amplitude and phase) at one specific lateral location, axial location z, and time t can be described as
| (1) |
where Boct(t, z) is a complex signal, A (t, z) is the amplitude, and ϕ is the phase. The phase term includes three components and can be expanded as
| (2) |
where ϕP(t, z) is the phase shift caused by the moving red blood cell inside vessels, ϕB(t, z) is the phase shift caused by the projection of the bulk motion on the axial direction (along beam direction) and ϕM(t, z) is the phase shift caused by the system’s modulation frequency. The absolute value of the difference between two repeated B-scans can be expressed as
| (3) |
Here the time coordinate of the second scan can be represented as t2 = t1 + Δt. The system modulation phase difference is assumed to be a constant for all A-scans and can be removed [8]. The term of ΔϕB can be expressed in the STD analysis of Bdiff:
| (4) |
Plugging Eq. (3) into Eq. (4), we have
| (5) |
where C1 and C2 are constants. The phase shift contribution from the vessels is relatively small compared to that of the tissue, so ΔϕP can be ignored from the calculation. Accordingly, the variance υ is shown as
| (6) |
Based on the explicit bulk motion equation, we can directly solve the bulk motion phase. Because it is contained inside a cosine function, the contribution of the bulk motion phase is affected by phase wrapping. In order to solve this equation, we need to artificially subtract a phase θ to the complex signal Boct(t + Δt, z):
| (7) |
The variance becomes
| (8) |
Then the variance is a cosine function with the phase θ. The bulk motion phase ΔϕB can be directly solved by variance values at four θ with π/2 interval. For example, θ = 0, π/2, π, 3π/2, can be chosen to initiate the computation:
| (9) |
| (10) |
| (11) |
| (12) |
Here An is the nth repeated A-line from the nth consecutive B-frames at the same location. Then the bulk motion phase shift can be written as
| (13) |
where the atan2 is the four-quadrant inverse tangent. Thus, based on Eq. (13), we can directly solve the bulk motion phase shift. However, in order to increase the calculation accuracy, in this Letter, we solved the equation m = 5 times by shifting the four sampling points, together with a random θm:θm, θm + π/2, θm + π and θm + 3π/2. Five ΔϕBm were calculated and averaged to obtain the final bulk motion phase shift ΔϕB for each A-line. The detailed procedure is shown in Fig. 1.
Fig. 1.
Flow chart of the proposed method to compensate for a bulk motion phase shift on phase-based OCTA. (A) Summary of the flow chart and (B) a detailed flow chart showing the estimation of bulk motion phase shift ΔϕBm on base phase θm.
Next, this theory was verified and demonstrated on OCTA scans. The raw OCT spectrum was first converted to a complex OCT signal, including the wavelength-to-frequency conversion and fast Fourier transform steps. Bulk motion was then estimated using an STD method and compensated for on each A-line. The accuracy of the proposed method relies on how the experimental results correlate with the cosine curve predicted by Eq. (8). If they are not well fitted, we are not able to retrieve an accurate bulk motion phase shift at the first lowest value of cosine function. To verify this, we randomly chose a single A-scan from three different locations (static tissue and large vessels) and investigated the relationship between the variances calculated at various θ from data and the variance derived directly from Eq. (8). They fit well, suggesting that Eq. (8) is correct, and the bulk motion phase shift can be directly solved using Eq. (13).
The bulk motion-introduced phase shift signal on OCTA scans was substantially removed by the STD method (Fig. 2B). The improvement of the tissue-vessel contrast was observed in the phase-based OCTA images (Fig. 2D). The STD method can also be applied to remove the bulk motion artifact in Doppler OCT, which is based on the phase difference between adjacent A-lines on the same B-frames. Accordingly, the bulk motion phase shift is also calculated from adjacent A-lines. Our results indicate that the STD method is also applicable to phase-resolved Doppler OCT (Fig. 2F).
Fig. 2.
Cross-sectional OCT images (A), (B), (C), and (D) were acquired from the same volumetric scan as shown in Fig. 3D, the position of which is indicated by the yellow line. The Doppler OCT images (E) and (F) were acquired from the circular scan indicated by the blue circle in Fig. 3D. (A) Phase difference image before bulk motion compensation. The colored fringes indicate the bulk motion phase shift. (B) Phase difference image after bulk motion compensation with the STD method. (C) Phase-based OCTA image without bulk motion compensation showing retinal flow signals indistinguishable from a motion artifact. (D) Phase-based OCTA image after bulk motion compensation with the STD method showing distinguishable flow signals. (The examples are indicated by yellow arrows.) (E) Doppler OCT image before bulk motion compensation, showing a large amount of motion signals and low Doppler signal contrast. (F) Doppler OCT image after bulk motion compensation with the STD method, showing improved Doppler signal contrast. The range of color bars in (A), (B), (E), and (F) is the phase from −π to π or from –π/2 to π/2, whereas in (C) and (D), the range is the normalized amplitude from 0 to 0.2.
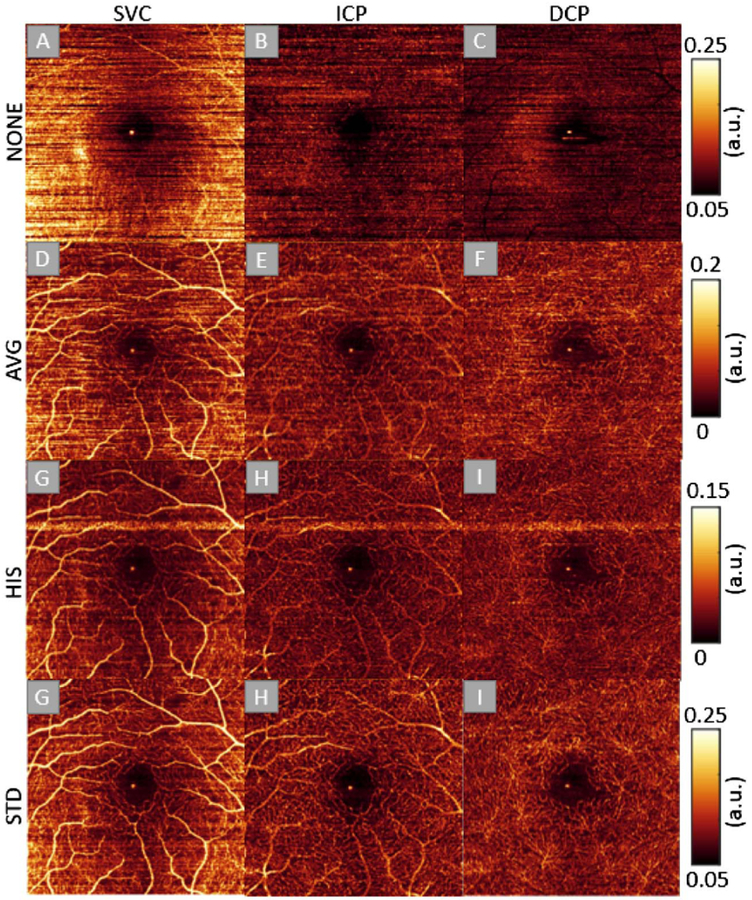
Here the proposed method was qualitatively and quantitatively evaluated on en face angiograms by comparing to two conventional methods on the same datasets from rat (Fig. 4) and human retinas (Fig. 5). All data were processed in the same way, except for the phase compensation methods. The superficial vascular complex (SVC), intermediate capillary plexuses (ICPs), and deep capillary plexus (DCP) images were generated using our automatic segmentation software [12].
Fig. 4.
2.1 mm × 2.1 mm en face maximum projection of the flow signal within the SVC of a rat retina. (A) Flow signal calculated without bulk motion compensation (NONE). (B) Flow signal calculated using the AVG method. (C) Flow signal compensated for using the HIST method. (D) Flow signal compensated for using the STD method. The white arrows are used to indicate where a motion artifact in some place can be suppressed by (B), (D) the AVG and STD methods, respectively, and (C) can be mistakenly enhanced by the HIST method.
Fig. 5.
Representative 3 mm × 3 mm scan of the human macula, showing the effect of different bulk motion compensation methods on en face maximum projection of flow in three different slabs. The first column shows the SVC, the second column shows the ICP, and the third column shows the DCP. The first row was calculated without bulk motion compensation (NONE), the second row was calculated using the AVG method, the third row was calculated using the HIST method, and the fourth row was calculated using the STD method. A bright horizontal streak on the HIST method appears at the B-scan positions where it failed to approximate the bulk motion phase value, whereas other methods are more stable and never showed bright streaks.
Compared to OCTA without compensation step (Fig. 4A), the image compensated for by the AVG method (Fig. 4B) reveals some microvascular details, but retains high background noise (bulk motion artifacts). The HIST method (Fig. 4C) suppressed artifacts and improved image contrast, but some errors were introduced by the compensation step (Fig. 4C, white arrows). Overall, the image processed by the STD method (Fig. 4D) shows the best image quality for rodent retinal imaging. Human retina images were also inspected.
The results show that the STD method can produce superior image quality in the SVC, as well as the intermediate and DCPs (Fig. 5).
Image quality after bulk motion compensation was also investigated by calculating the flow signal-to-noise ratio (SNR). Since the foveal avascular zone (FAZ) is a known landmark devoid of flow, it is a good noise reference in the healthy retina, and the SNR can be calculated by the ratio of parafoveal flow to the FAZ signal; details can be found in Ref. [4]. The ganglion cell layer plexus was the only slab used to analyze SNR, in order to remove the interference of a large amount of residual motion signal within nerve fiber layer. Our calculations show that the STD method has an image quality improvement over 62%, compared to the AVG method (Table 1).
Table 1.
SNRs of Three Bulk Motion Compensation Methods
| Method | AVG | HIST | STD |
|---|---|---|---|
| SNR (mean+std) | 1.08 ± 0.55 | 1.32 ± 0.40 | 1.75 ± 0.58 |
| Improvement | - | 22% | 62% |
The computational budget is an important factor in evaluating algorithm performance. The AVG method had the lowest computational budget, but also the lowest image quality (Fig. 6). The HIST method had a higher image quality compared to the AVG method but, due to the required number of iterations, it had the highest computational budget. The STD method had a relatively low computational budget, as well as the best image quality. In our benchmark, the STD method for bulk motion calculation is almost five times faster than that of the HIST method.
Fig. 6.
Computational budget (time to generate one OCTA B-scan) of three different bulk motion phase compensation algorithms. (Computing platform: Matlab 2017a, Intel Core i7 6700k, 32GB RAM)
In summary, we present, to the best of our knowledge, a novel method of bulk motion compensation based on the STD of the flow signals. The explicit equation of the bulk motion has been derived and subtracted from phase-based functional OCT. This method was more effective and time-saving than previous methods and can be used in tandem with bulk motion subtraction algorithms that operate a posteriori on an OCTA flow signal.
Fig. 3.
(A)–(C) are the plots of υ versus θ at different points A–C; “+” are the calculated variances, normalized to −1 to 1. The red curve is the cosine function derived from the Eq. (8); the yellow region indicates the phase shift caused by the bulk motion. (A) is the A-line chosen from a point that contains capillaries only; (B) and (C) are chosen from points that contain large vessels. (D) is the en face OCT mean projection of a scan on a rat eye. Positions A–C correspond to plots (A)–(C); the yellow straight line and the blue circle indicate the B-scan used for comparison and the Doppler circular scan position.
Funding.
National Institutes of Health (NIH) (DP3 DK104397, P30 EY010572, R01 EY010145, R01 EY023285, R01 EY024544, R01 EY027833); William & Mary Greve Special Scholar Award from Research to Prevent Blindness (RPB); unrestricted departmental funding grant.
REFERENCES
- 1.Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, and Puliafito CA, Science (New York) 254, 1178 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Choma MA, Sarunic MV, Yang C, and Izatt JA, Opt. Express 11, 2183 (2003). [DOI] [PubMed] [Google Scholar]
- 3.Watanabe Y and Itagaki T, J. Biomed. Opt 14, 060506 (2009). [DOI] [PubMed] [Google Scholar]
- 4.Jia Y, Tan O, Tokayer J, Potsaid B, Wang Y, Liu JJ, Kraus MF, Subhash H, Fujimoto JG, and Hornegger J, Opt. Express 20, 4710 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Gao SS, Jia Y, Zhang M, Su JP, Liu G, Hwang TS, Bailey ST, and Huang D, Invest. Ophthalmol. Visual Sci 57, OCT27 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Yang VX, Gordon ML, Mok A, Zhao Y, Chen Z, Cobbold RS, Wilson BC, and Vitkin IA, Opt. Commun 208, 209 (2002). [Google Scholar]
- 7.Makita S, Hong Y, Yamanari M, Yatagai T, and Yasuno Y, Opt. Express 14, 7821 (2006). [DOI] [PubMed] [Google Scholar]
- 8.An L and Wang RK, Opt. Express 16, 11438 (2008). [DOI] [PubMed] [Google Scholar]
- 9.An L, Shen TT, and Wang RK, J. Biomed. Opt 16, 106013 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cheng Y, Guo L, Pan C, Lu T, Hong T, Ding Z, and Li P, J. Biomed. Opt 20, 116004 (2015). [DOI] [PubMed] [Google Scholar]
- 11.Pi S, Camino A, Zhang M, Cepurna W, Liu G, Huang D, Morrison J, and Jia Y, Biomed. Opt. Express 8, 4595 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Zhang M, Wang J, Pechauer AD, Hwang TS, Gao SS, Liu L, Liu L, Bailey ST, Wilson DJ, and Huang D, Biomed. Opt. Express 6, 4661 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]