Calorimetric studies of interactions between low molecular weight salts and bovine serum albumin in water at pH values below and above the isoionic point

Abstract

Isothermal titration calorimetry was used to determine the temperature and salt concentration dependence of the enthalpy of mixing, Δ_mixH, of bovine serum albumin (BSA) in aqueous buffer solutions with several low molecular weight salts. Three buffers were used: acetate (pH = 4.0), MOPS (7.2), and borate (9.2). Since the isoionic point of BSA is at pI ≈ 4.7, the net charge of BSA in acetate buffer was positive (≈ +20), while in the other two buffer solutions it was negative (≈ −15 in MOPS and ≈ −25 in borate). The majority of the recorded heat effects were exothermic, while only at pH = 9.2 a weak endothermic effect upon mixing BSA with LiCl, NaCl, and KCl was observed. For all buffer solutions the absolute values of Δ_mixH of sodium salts followed the order: NaCl < NaBr < NaNO₃ < NaI < NaSCN, which is the reverse Hofmeister series for anions. The magnitude of the effects was the largest in acetate buffer and decreased with an increasing pH value of the solution. While the effect of varying the anion of the added salts was strongly pronounced at all pH values, the effect of the cation (LiCl, NaCl, KCl, RbCl and CsCl salts) was weak. The most interesting feature of the results obtained for pH > pI was the fact that Δ_mixH were considerably more sensitive to the anion (co-ion to the net BSA charge) than to the cation species. This indicated that anions interacted quite strongly with the BSA even at pH values where the net charge of the protein was negative. We showed that Δ_mixH at high addition of salts correlated well with the enthalpy of hydration of the corresponding salt anion. This finding suggested, consistently with some previous studies, that a part of the exothermic contribution to Δ_mixH originated from the hydration changes upon the protein–salt interaction. Theoretical analysis, based on the primitive model of highly asymmetric electrolyte solutions solved within the mean spherical approximation, was used to estimate Coulomb effects upon mixing.

1. Introduction

Aqueous solutions of proteins most commonly contain buffers to control the formulation’s pH and to ensure their stability. In addition, low molecular weight salts are often present in mixture as well. Better predictive ability of salt and buffer effects on the protein-protein interactions is needed to understand the solution’s properties, in particular the protein self-association and its conformational stability. It is well known that protein aggregation is posing serious problems in pharmaceutical industry [1]; the bio-pharmaceutical formulations must be free of aggregates to maintain high efficacy, low viscosity, and required shelf-life.

Proteins possess ionizable amino-acid residues on their surfaces. These functional groups become charged at a certain pH and accordingly proteins exhibit certain polyelectrolyte-like properties. Most importantly, they are sensitive to the amount of added low molecular weight electrolyte (i.e. salt) as also to its chemical nature; many phenomena involving protein solutions are salt-specific [2–7]. Membrane transport, salting in and out, crystallization, and other properties being of significance for industrial and technological processes, are affected by addition of salts. These facts stimulated a renewed interest in studying of the so-called Hofmeister series [2, 8], defined as a list of ions ranked in terms of their efficiency to affect the solubility of proteins. For anions the series orders as: ${\mathrm{F}}^{-}>{\mathrm{Cl}}^{-}>{\mathrm{Br}}^{-}>{\text{NO}}_3^{-}>{\mathrm{I}}^{-}>{\text{SCN}}^{-}$. This means that F⁻ ion is more efficient in precipitation of proteins than all the other ions in the list including SCN⁻. For cations, the order is: Ca²⁺ > Ba²⁺ > Na⁺ > K⁺ > Cs⁺. The above two series are named direct Hofmeister series. The specific effects of buffers, at the same nominal pH of protein solutions, were recently critically examined by Salis and Monduzzi [9]. These authors have shown how adsorption of buffer species can modify the properties of proteins (for example, the effective surface charges). Buffer ions, namely, compete with ions of the added strong electrolyte for the adsorption at protein surface, what can lead to the modulations in the Hofmeister effects.

In the present work, the isothermal titration calorimetry (ITC) was chosen as a principle method of investigation toward better understanding of interactions in aqueous buffer-salt-protein mixtures. This approach was found to provide useful information about interactions in various biological systems. The work reported here is related to our previous studies of protein [10] and polyelectrolyte solutions [11, 12]. Here, we employed ITC to measure the heat effects caused by mixing bovine serum albumin (BSA) in aqueous buffer environment with low molecular weight salts. Three different buffers were examined: (i) acetate buffer having pH = 4.0, (ii) MOPS buffer with pH = 7.2, and (iii) borate buffer with pH = 9.2. The isoionic point (pI) of BSA, i.e. the pH at which BSA molecule has the same number of positive and negative charges without any adsorbed ionic species, is at pI ≈ 4.7. Literature values for the pI somewhat vary, depending on the experimental method and conditions used [13]. However, for pH < pI (acetate buffer in our case) the net protein charge is positive, whereas at pH > pI (MOPS and borate buffers in our case) it is negative. From the experimental titration curves of BSA [13], the number of charges per protein in a 0.01 M NaCl solution was found to be ≈ +20 at pH = 4.0, ≈ −15 at pH = 7.2, and ≈ −25 at pH = 9.2. The task of the present study is to examine the effects of anions and cations of the added salt on the heat effects upon mixing BSA with salts at pH values below and above the pI.

In the first part of this contribution we present the measurements of the enthalpies of mixing of BSA in acetate buffer (pH = 4.0) with NaCl, NaBr, NaI, NaNO₃, and NaSCN at three different temperatures (5, 20, and 35 °C). The experiments are compared with the results of a similar study of lysozyme solution in acetate buffer for the same range of temperatures and the same salts. Relation of the measured enthalpies of mixing with the results of measurements, obtained for cationic polyelectrolytes (ionenes), is briefly discussed [11, 12]. In the second part of the study we report the salt–BSA interaction enthalpies obtained for solutions in MOPS and borate buffers, that is under conditions where BSA is carrying negative net charge. Interestingly, while in literature there is an abundance of studies under the conditions where the net charge of proteins is positive, there is much less studies for the pH values above the isoionic point. In this region it is expected for the carboxylic groups to dictate properties of solutions. We have explored the situation from the standpoint of the enthalpy measurements. An appreciable cation-specific effect is expected under conditions where carboxylic groups dominate in number, but just an opposite appears to be true. We observe strong anion-specific effect up to the pH value equal to 9.2. The measurements presented here suggest that anions upon interaction with BSA produce much stronger heat effects than the cations (Li, Na, K, Rb, and Cs chlorides were tested); high negative charge on the protein seem to be needed to reverse such a behavior.

In the last part of this paper, a theoretical analysis of the Coulomb contribution of enthalpy of mixing, based on the Ornstein-Zernike integral equation theory within the mean-spherical approximation (MSA) closure [14], is presented.

2. Experimental Part

2.1. Chemicals, solution preparation, and measurements

Bovine serum albumin (BSA, M_w ≈ 66 kDa) was purchased from Sigma Aldrich (lot number: SLBM9552V). Other chemicals were supplied by Merck (LiCl, NaCl, KCl, RbCl, CsCl, NaBr, NaNO₃, Na₂B₄O₇ · 10H₂O, 100% acetic acid and 1 M NaOH solution), and by Sigma Aldrich (NaI, NaSCN, and MOPS). All solutions were prepared with Mili Q water.

An appropriate amount of the solid buffer component (MOPS, borate) was weighed and dissolved in a smaller amount of water, while acetic acid was measured volumetrically and then diluted with water. The solutions were adjusted to the desired pH value with 1 M NaOH solution. pH was measured by Iskra pH meter model MA5740 (Ljubljana, Slovenia), using a combined glass microelectrode InLab 423 by Mettler Toledo (Schwerzenbach, Switzerland). Water was added to the solution to match the total buffer concentration to 20 mM. All solutions were prepared at 20 °C.

All low molecular weight salts were first dried for 1.5 hours at 105 °C and then left in the desiccator to cool down. 150 mM salt solutions were prepared by weighting an appropriate amount of the dry salt and dissolving it in the 20 mM buffer solution (acetate, MOPS, and borate).

BSA-buffer solutions were prepared by weighting the dry protein and dissolving it in 20 mM aqueous buffer solutions (acetic, MOPS, and borate). All solutions were filtered through 0.45 µm Minisart Sartorious filters. After BSA was dissolved in the buffer solution, the solution was extensively dialyzed (three changes of fresh buffer solutions every 8 hours) against the same buffer using a dialysis cassette (Slide-A-Lyser Dialysis Cassete G2 Thermo Scientific, M_w cutoff 3.5 kDa). The concentration of BSA was determined by UV-VIS spectrophotometer (Varian Cary 100 Bio) at 280 nm using extinction coefficient 0.667 mL cm⁻¹ mg⁻¹ [15]. The concentration of the BSA solutions used was ≈ 0.3 mM.

2.2. Isothermal Titration Calorimetry (ITC)

ITC experiments were performed by TA-ITC isothermal titration calorimeter (Nano Isothermal Titration Calorimeter, cell volume 950 µL). Titrant (salt-buffer solution) was added in increments of 12 µL from a syringe into the solution containing the solute (BSA-buffer solution) at 5, 20, and 35 °C. 20 additions of titrant in 10 minute intervals were performed after the initial 4 µL pre-injection. Initial concentration of BSA in the sample cell was 20 mg mL⁻¹ (≈ 0.3 mM), while the concentration of the salt which was added into protein solution was 150 mM. The reference cell of the calorimeter was filled with water. At the final injection of the titrant the concentration of the protein in the sample cell was approximately 0.2 mM, and the concentration of the salt was 35 mM. By taking into account the net charge of the protein in a given buffer [13], i.e. +20 (acetate), −15 (MOPS) and −25 (borate buffer), we estimated that the final counterion to protein charge molar ratio was between 6 and 10.

The area under the peak following each injection of the titrant, i.e. the enthalpy change for a given addition of salt to the protein, was obtained by integration of the raw signal (the heat power required to maintain equal temperatures of the sample and reference cells). It is expressed per mole of the added titrant per injection to give the corresponding enthalpy changes at a given temperature. By subtraction of the salt-buffer enthalpy change, obtained in a separate ITC experiment by titration of salt-buffer solution into buffer solution (no protein present), one obtains the enthalpy change corresponding to the protein-salt interaction (cf. Figure 1 of Ref. [10]).

3. Enthalpies of BSA-Salt Mixing

In the following two subsections, we present calorimetric measurements of the enthalpies of mixing, Δ_mixH, of aqueous buffer-BSA solutions with low molecular weight salts. Buffers were chosen in such a way that the adjusted value of the solution’s pH was below (subsection 3.1) or above (subsection 3.2) the isoionic point of the protein, pI. The net charge of the protein in these buffers was either positive (pH < pI, acetate buffer) or negative (pH > pI for MOPS and borate buffers). Interactions of anions (salts of Na⁺ and Cl⁻, Br⁻, I⁻, ${\text{NO}}_3^{-}$, and SCN⁻) and of cations (salts of Cl⁻ and Li⁺, Na⁺, K⁺, Rb⁺, and Cs⁺), as reflected in enthalpies of mixing, were investigated below and above the BSA pI point.

3.1. Enthalpies of mixing under conditions where protein has a positive net charge (pH < pI). Experiments in acetate buffer

Before we analyze the present ITC measurements for BSA solutions, it may be instructive to review some results obtained for simpler systems, i.e. for nitrogen based cationic polyelectrolytes, called ionenes. These chain-like polyelectrolytes can be prepared with varying degrees of hydrophobicity by changing the numbers of methylene groups between the adjacent quaternary ammonium groups. We reported the heat effects, caused by the polyelectrolyte-salt mixing, in several papers [11, 12, 16, 17]. One of the conclusions of these studies was: purely Coulomb polyelectrolyte theories [18], treating solvent as a dielectric continuum, predicted for the enthalpy of mixing to be endothermic, while in contrast to this, in most situations release of the heat was observed experimentaly. In a yet another previous ITC study we examined mixing of aqueous lysozyme solutions with the low molecular weight salts in acetate buffer at pH = 4.0 [10]. Note that at this pH lysozyme has a positive net charge. Bončina et al. showed [10] that enthalpies of mixing were exothermic for all the investigated salts and increased in the order: NaCl < NaBr < NaNO₃ < NaI < NaSCN.

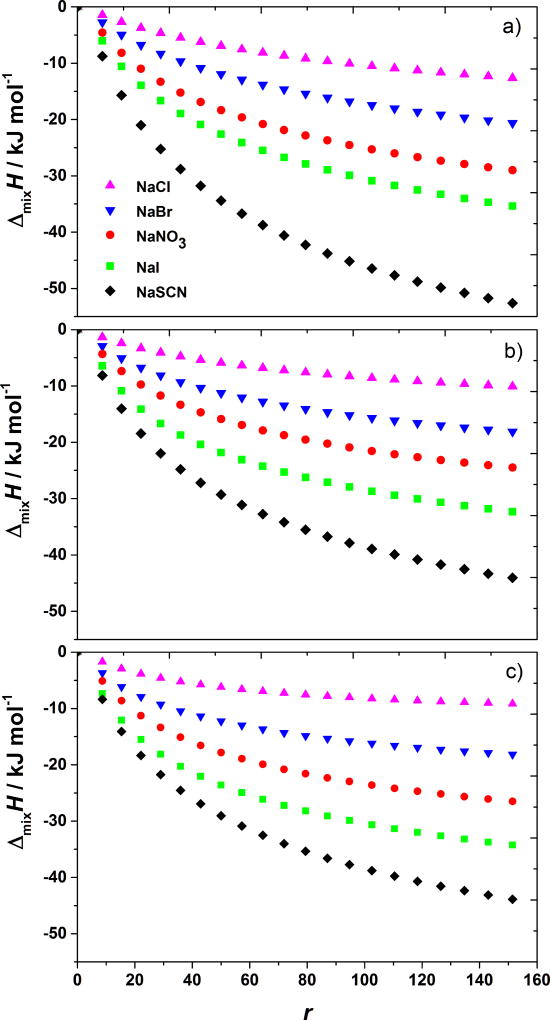
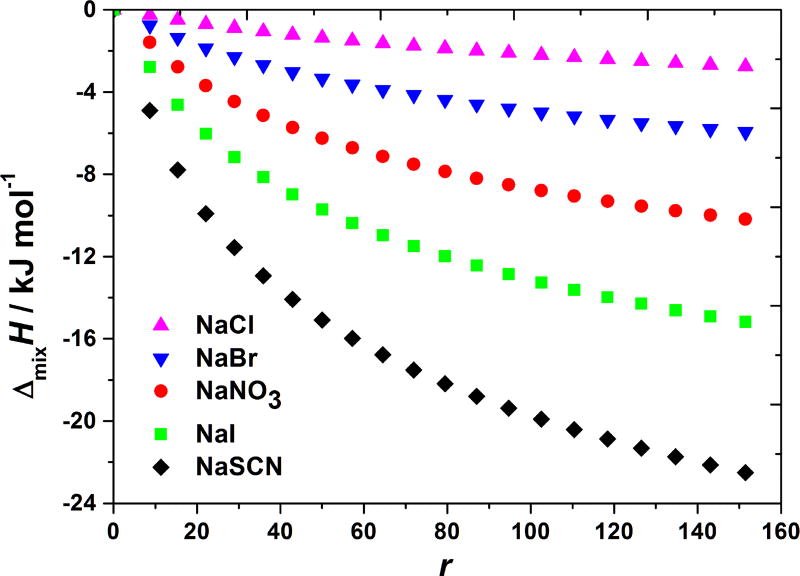
With this background information we turn now to the results of the BSA-salt titrations in acetate buffer solutions (pH = 4.0). In Figure 1 we show the cumulative heat effects of mixing of BSA in acetate buffer with various low molecular weight sodium salt solutions as a function of the molar ratio between the added salt and BSA (r = n_salt/n_BSA) and at three temperature (5, 20, and 30 °C). As seen from these results the effect is exothermic, Δ_mixH < 0: upon addition of salts to the BSA solution the heat is released. The salts are ordered in the series from NaCl (giving the least exothermic effect) to NaSCN (giving the most exothermic effect): NaCl < NaBr < NaNO₃ < NaI < NaSCN. The sequence is exactly the reverse Hofmeister series for anions. Such sequence of salts is the same as in the case of lysozyme solutions [10]. However, the magnitude of the enthalpic effect upon mixing is in the case of BSA considerably larger than for lysozyme solution. As we see, the salt anion variations examined here (Cl⁻, Br⁻, ${\text{NO}}_3^{-}$, I⁻, and SCN⁻), yield significant salt-specific effect.

Figure 1. BSA–salt mixing enthalpies at pH < pI depend on the nature of salt’s anion.

Shown are the cumulative enthalpy changes, Δ_mixH, at 5 (panel a), 20 (panel b), and 35 °C (panel c) as a function of r (the molar ratio between the added salt and BSA) for adding NaCl, NaBr, NaNO₃, NaI, and NaSCN solutions to aqueous BSA solution with pH = 4.0 (acetate buffer).

At this point we wish to mention experimental study of BSA solutions published by Sarangapani and co-workers [19, 20]. These authors, among other properties, determined also the second virial coefficient for a range of pH values. According to their data (see Figure 3B of Ref. [20]) the second virial coefficient is for pH = 4.0 positive, what indicates electrostatic repulsion and suggests stability of these solutions. The same holds true for the pH values above 6.0.

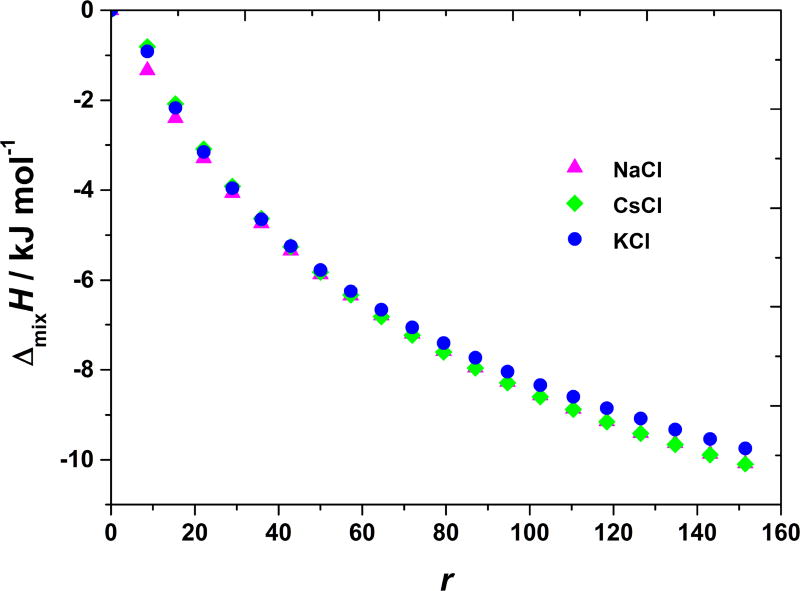
In contrast to anions (counterions with respect to the BSA net charge, which is positive at pH = 4.0), small differences in the enthalpies obtained upon the titration with NaCl, KCl, and CsCl salts were observed (see Figure 2). In addition, the magnitudes of the enthalpies, obtained by the cation variations, are much smaller than in case of anions. Effects of the cation variation (Na⁺, K⁺, and Cs⁺ ion) are small, practically within the experimental error. Notice that cations are co-ions to the net BSA charge at this pH. The effect of chloride ion interaction (when in combination with different cations, NaCl, KCl, and CsCl salts), is similar as for lysozyme solutions [10]. The fact that anions produce much stronger ion-specific effects in comparison to cations is most often explained by the fact that BSA carries net positive charge at this pH. At pH = 4.0 (this is below the isoionic point of BSA) amino groups are protonated $(-{\text{NH}}_3^{+})$ and interaction of salts with BSA molecules is mainly through anions of the salt. However, as we will see in the next section, this is merely a part of the story.

Figure 2. BSA-salt mixing enthalpies at pH < pI are almost independent on the nature of salt’s cation.

Δ_mixH vs. r at 20 °C for adding NaCl, KCl, and CsCl solutions to aqueous BSA solution at pH = 4.0 (acetate buffer).

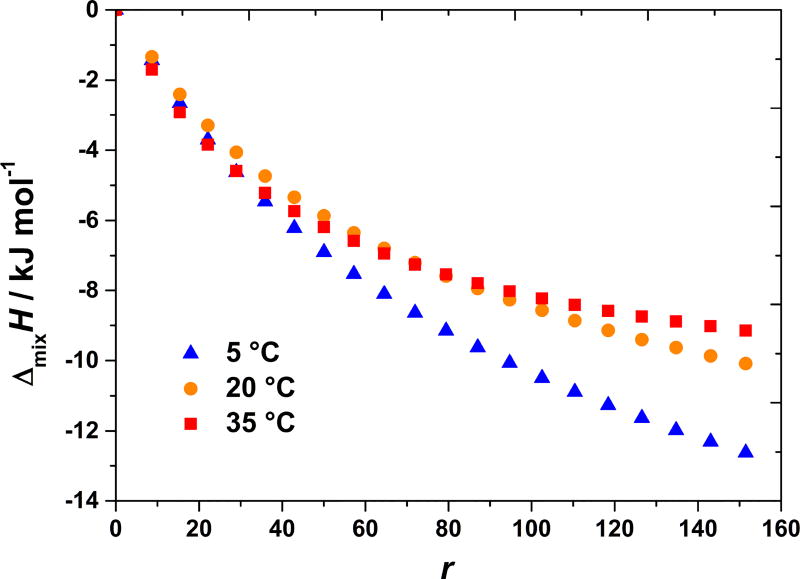
Temperature dependence of the enthalpies of mixing is not exactly as for lysozyme solutions [10]. In case of BSA solutions, the magnitude of exothermic effect depends, not only on the nature of the salt, but also on its concentration in mixture, that is on r value. An example of BSA–NaCl heat effects upon mixing at 5, 20, and 35 °C is shown in Figure 3. Notice that the most exothermic enthalpies apply to 5 °C. As seen from this Figure and from Figure 1, the differences in heat effects measured at 20 and 35 °C are relatively small. For large r values (salt/protein ratio) more heat is released at 20 °C than at 30 °C.

Figure 3. Exothermic heat effect is somewhat larger at lower temperatures and the difference diminishes with increasing temperature.

Shown are cumulative enthalpy changes, Δ_mixH, as a function of r for BSA–NaCl mixing at 5, 20, and 35 °C in acetate buffer at pH = 4.0.

3.2. BSA–salt mixing under conditions where pH > pI. Experiments in MOPS and borate buffers

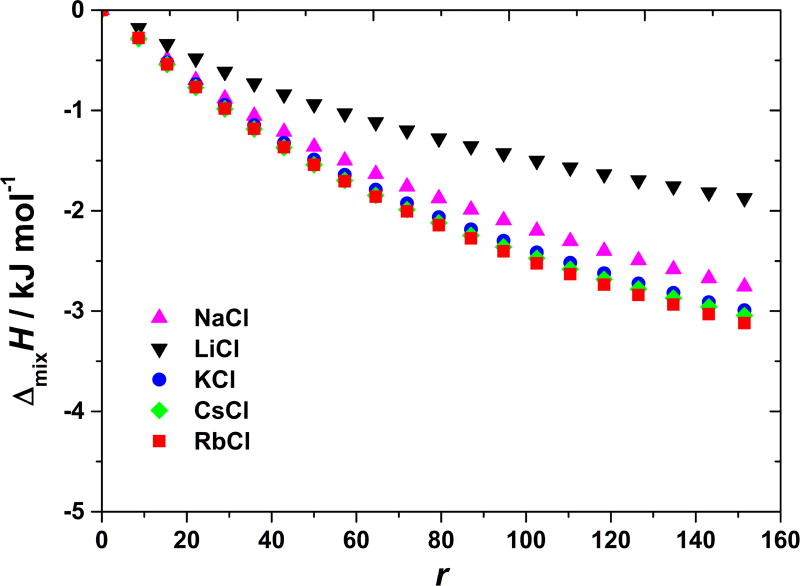
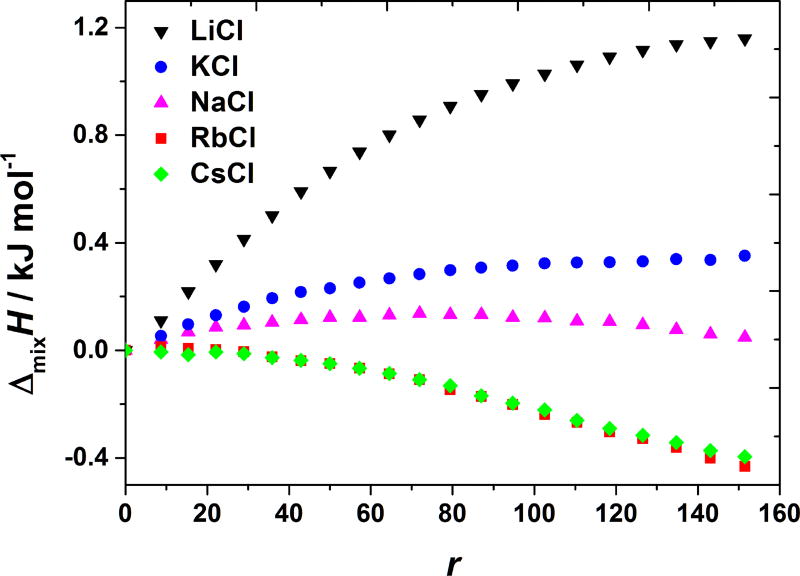
Above the isoionic point of the BSA the protein molecule possesses a net negative charge. We determined the enthalpies of mixing of BSA with various salts in MOPS (pH = 7.2) and borate buffers (pH = 9.2). We would expect for protein in these solutions to behave as polyanion and accordingly the salt cations would have stronger influence on the results as anions. Again the alkali halide salts were used: cations were varied while the chloride anion was present in all the combinations. These measurements are for MOPS buffer shown in Figure 4. As we see from Figure 4 the heat is released in this process, Δ_mixH < 0. It is easy to notice that LiCl differs from other salts; it produces a somewhat weaker exothermic effect than the others (note that the experimental error at r ≈ 150 was estimated to be ±0.2 kJ mol⁻¹).

Figure 4. BSA-salt mixing enthalpies at pH > pI are not strongly dependent on the nature of salt’s cation.

The Δ_mixH at 20 °C are shown as a function of r for adding NaCl, LiCl, KCl, CsCl, and RbCl to aqueous BSA solution at pH = 7.2 (MOPS buffer).

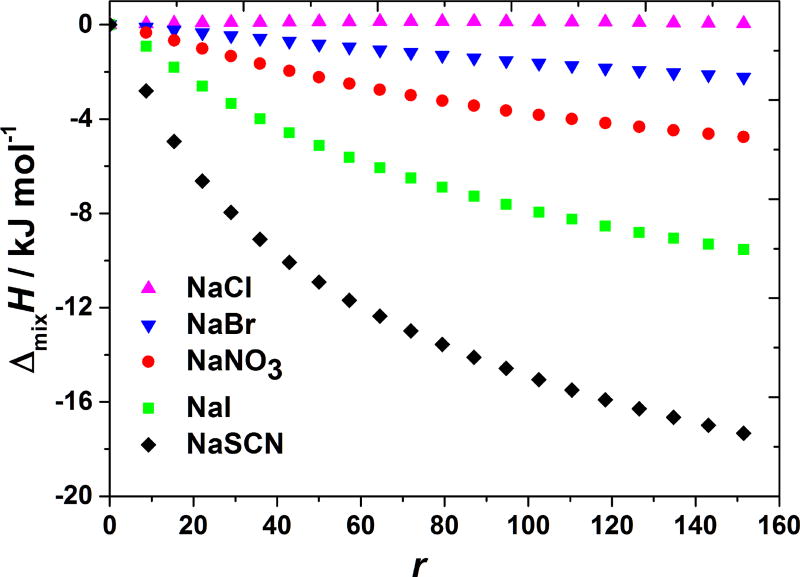
The same set of salts as studied before in case of the acetic buffer solutions (anions in the sodium salts were varied) were titrated into the buffer–BSA mixture, see Figure 5. Here the salt-specific effects are more pronounced and the enthalpies of mixing are more negative than those shown in Figure 4, where the cations are varied while the anionic species (chloride in this case) is kept constant. In view of the fact that BSA has a negative net charge for these pH values this is, at least at the first sight, a surprising result.

Figure 5. BSA-salt mixing enthalpies at pH > pI depend on the nature of the salt’s anion.

The Δ_mixH at 20 °C are shown as a function of r for adding NaCl, NaBr, NaNO₃, NaI, and NaSCN solutions to aqueous BSA solution with pH = 7.2 (MOPS buffer).

In literature there are not many articles in which proteins are studied in the region where their net charge is negative. Few exceptions we noticed are studies published in Refs. [13, 21–23]. For example, Medda et al. [23] studied BSA solutions via potentiometric titration and electrophoretic light scattering methods for a range of pH values. They found an appreciable salt specific effects for the added salt at physiological concentration of 0.1 M. They also found that anions bind to the protein surface, below and above the isoionic point, according to the same reverse Hofmeister series ${\mathrm{Cl}}^{-}<{\mathrm{Br}}^{-}<{\text{NO}}_3^{-}<{\mathrm{I}}^{-}<{\text{SCN}}^{-}$. This is exactly the same ordering as it applies to the enthalpies of mixing presented in Figures 1 and 5. Another finding of relevance for our study is their observation that ”the number of bound cations exceeds that of anions only at pH > 8.5” [23]. This finding stimulated us to perform also the enthalpy of mixing measurements for pH = 9.2 (borate buffer) at 20 °C. The results are shown in Figures 6 and 7. What is particularly interesting here is the fact that titrations with LiCl, KCl, and NaCl yield small endothermic effects, Δ_mixH > 0. The heat effects at this pH are smaller than for the cases of lower pH values. In conclusion to this subsection, our results are consistent with those of Medda et al. [23].

Figure 6. BSA-salt mixing enthalpies at pH >> pI are weakly dependent on the nature of salt’s cation.

Same as in Figure 4 but for solutions with pH = 9.2 (borate buffer).

Figure 7. BSA-salt mixing enthalpies even at pH >> pI depend on the nature of the salt’s anion.

Same as in Figure 5 but for solutions with pH = 9.2 (borate buffer).

At the end it is worth mentioning that enthalpic measurements do not provide the same information as “ion binding” data, which are derived from the solution free energy and accordingly contain also the entropic contribution. It is therefore possible that enthalpy of mixing and the “ion binding” results do not follow the same trend [24].

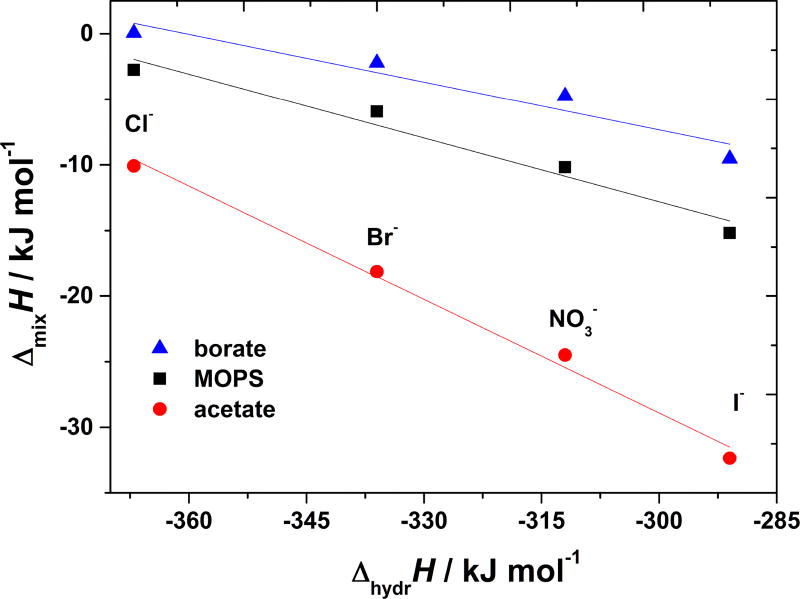
In order to see where the salt specific effects come from it is useful to examine Figure 8. Here we show the enthalpies of mixing for an excess of added salt, the latter is indicated by high value of r ≈ 150, as a function of the enthalpy of hydration, ΔH_hydr, of the salt anion. At this high r value the enthalpy changes practically reach a saturation point. As stated in the Experimental part the final counterion to protein charge molar ratio is estimated to be between 6 to 10, depending on the solution pH. For this conditions, the counterion concentration with respect to that of the charged residues is sufficient for effective screening of the electrostatic repulsions. As we see in Figure 8, linear correlation is observed for all the buffers and the salts shown in the graph. NaSCN, which provides the strongest negative effect in all three cases, is an outlier and not shown in the Figure. For this salt in acetate buffer at 20 °C Δ_mixH at r ≈ 150 is −44.0 kJ mol⁻¹, in MOPS buffer it is −22.5 kJ mol⁻¹, and in borate buffer it is −17.3 kJ mol⁻¹ while Δ_hydrH_SCN⁻ ≈ −311 kJ mol⁻¹. Similar correlations were previously observed for cationic polyelectrolytes (see for example, Refs. [11, 16, 17]). We may consider the results shown in Figure 8 as an indication of the solute dehydration, caused by the salt-protein interaction. The latter effect yields a negative contribution to the enthalpy of mixing and seem to be a leading cause of the salt-specific effect.

Figure 8. Enthalpy of mixing, Δ_mixH, is correlated with the enthalpy of hydration of the added salt’s anions, Δ_hydrH.

Data for Δ_mixH correspond to the cumulative enthalpy change at the highest amount of the added salt (r ≈ 151) at 20 °C. Shown are the results in acetate (pH = 4.0), MOPS (pH = 7.2), and borate buffers (pH = 9.2).

As mentioned in the introduction, not just the chemical nature of the salt but also that of the buffer may be important. The values of properties, measured at identical nominal pH values [9] but in different buffers, may be different. Although such a study is beyond the scope of the present manuscript, we tested these effects on a small set of experimental conditions. In the Supporting Information (SI) file, we show the enthalpy changes upon titrating BSA with NaCl and NaBr in two different buffer solutions, having the same pH value, equal to 7.35. For this purpose MOPS and HEPES buffers were used. The comparison of titration curves shows that there is slightly more negative enthalpic effect in case of HEPES buffer, compared to MOPS but the order with respect to the identity of the added salt remains the same as shown before (see SI).

4. Mean–Spherical Approximation for Asymmetric Electrolytes

Proteins have charges on the surface and accordingly their properties in solution are influenced by presence of additional charged species. The net charge of the protein depends on the pH of the solution and may be influenced by the amount of the adsorbed ions as well. Here, we are interested in the magnitude and sign of the Coulomb contribution to the enthalpy of salt–protein mixing. We modeled the protein as a large rigid spherical particle of radius 3.0 nm with the charge located in the center. The radius used is an estimated radius of gyration of BSA as suggested in literature [25, 26]. We show the results for the case where the valency of the protein particle was +20 (this is, for example, an estimate for BSA at pH = 4.0 and in presence of a 0.01 M NaCl [13]). The low molecular weight salt ions present in the solution are pictured as rigid spheres having smaller size (radius 0.2 nm), and the cations and anions are assumed to be of equal size. Also, they both had charges in their centers to model the restricted primitive +1 : −1 electrolytes. Counterions of the protein were modeled in the same way as the ions of the low molecular weight salt ions (radius of 0.2 nm and valency −1). In this calculations we did not discriminate between the buffer and salt ions. The model system representing the solution was a dielectric continuum with relative permitivity equal to that of pure water at 20 °C.

General mathematical solution of the Ornstein-Zernike (OZ) integral equation for such system of ions was obtained by Lesser Blum within the mean spherical approximation (MSA) closure [14, 27]. On the McMillan-Mayer level of description the excess electrostatic energy reads:

$$E^{\text{ex}}=[1+\frac{\text{d ln }{\epsilon }_r}{\text{d ln }T}]·E_{\text{MSA}}^{\text{ex}}$$ (1)

where $E_{\text{MSA}}^{\text{ex}}$ is the excess electrostatic energy (per unit volume) valid within the MSA closure [14, 27]:

$$\beta E_{\text{MSA}}^{\text{ex}}=-{\lambda }_{\mathrm{B}}\left[\mathrm{\Gamma }\sum _i\right(\frac{{\rho }_i{z}_i^2}{1+\mathrm{\Gamma }{a}_i})+\frac{\pi }{2\mathrm{\Delta }}\mathrm{\Omega }{P}_n^2]$$ (2)

In Equation (2) $\mathrm{\Delta }=1-\frac{\pi }{6}{\sum }_i{\rho }_i{a}_i^3$, and

$$\mathrm{\Omega }=1+\frac{\pi }{2\mathrm{\Delta }}\sum _i\frac{{\rho }_i{a}_i^3}{1+\mathrm{\Gamma }{a}_i}$$

$$P_n=\frac{1}{\mathrm{\Omega }}\sum _i\frac{{\rho }_i{a}_i{z}_i}{1+\mathrm{\Gamma }{a}_i}$$

$$4{\mathrm{\Gamma }}^2=4\pi {\lambda }_{\mathrm{B}}\sum _i{\rho }_i{\left[\frac{z_i-\frac{\pi }{2\mathrm{\Delta }}{a}_2^i{P}_n}{1+\mathrm{\Gamma }{a}_i}\right]}^2$$

Here λ_B = e₀²/ (4πε_rε₀k_BT) stands for the Bjerrum length, where e₀ is the elementary charge, ε₀ the permittivity of vacuum, ε_r the relative permittivity, k_B the Boltzmann constant, and T denotes the absolute temperature. The number density of species i of diameter a_i and charge z_i is denoted by ρ_i. It is related to the molar concentration, c_i, via the relation ρ_i = c_iN_A, where N_A is the Avogadro constant. For water at 20 °C λ_B = 7.10 Å and the term [1 + d ln ε_r/d ln T] in Equation (1) equals to −0.325. An assumption that enthalpy of the solution can be approximated by its electrostatic energy E^ex, yields for the enthalpy of mixing

$${\mathrm{\Delta }}_{\text{mix}}H=H(c_{\text{protein}}^{\mathrm{f}},c_{\text{salt}}^{\mathrm{f}})-H(c_{\text{protein}}^{\mathrm{i}},c_{\text{salt}}^{\mathrm{i}})$$ (3)

where indices ”f” and ”i” denote the final and initial states, respectively.

The model suggested above may not always be a realistic description of the actual protein solution. First, the model assumes that the net charge at a particular pH value is located at the center of a hard sphere representing the protein. But proteins are polyampholytes and patches of charges of both signs are present on the surface of the molecule for all pH values studied here. Second, for the BSA molecule studied here, spherical shape is a rather crude approximation. Third, in comparing theory with experiment one has to be aware of the fact that proteins are not rigid, they may unwind, what renders (if this happens) such models useless [19, 28]. Finally, the model takes into account only excluded volume due to the rigidity of the spherical ions and Coulomb forces acting between the ions mediated by the dielectric medium representing water implicitly. So the results of the model calculations presented here are expected to provide merely an estimate of the Coulomb contribution to the enthalpy of mixing. A more realistic model, taking into account surface heteregeneity of charge and the presence of water molecules explicitly, has been proposed recently [21, 29], but no enthalpy calculations have been reported yet.

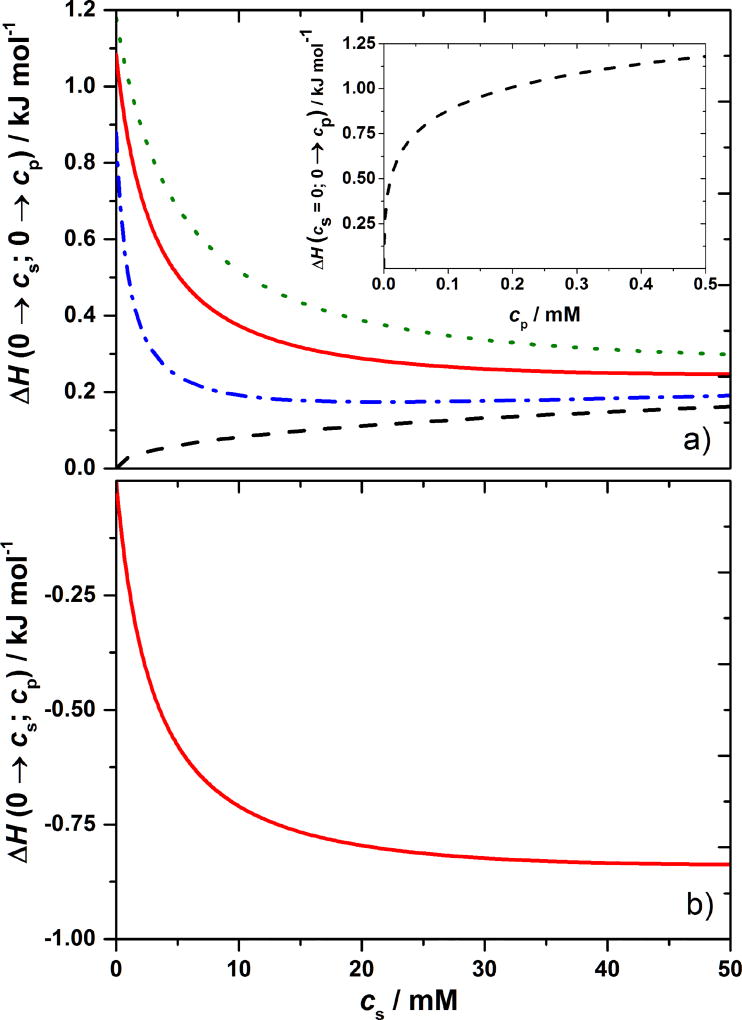
A sample of numerical results (Equations 1–3), is presented in Figure 9. Here we show how the enthalpy of the system is evolving when the concentration of protein in water increases from zero to c_p and the concentration of low molecular weight salt increases from zero to c_s as well. Black broken line at the bottom of panel (a) represents the enthalpy change per mole of solution when salt is added to pure water (no protein present); the effect is endothermic as for LiCl, NaCl, and other salts found experimentally [30, 31]. In contrast to this, the colored lines are showing the effects when salt is added to the aqueous protein solution with concentration c_p. Green (short dash) curve applies to c_p = 0.5 mM, the red (continuous) one to c_p = 0.3 mM, and the blue (dash-dotted) curve to the protein concentration equal to 0.1 mM. In all cases an addition of +1 : −1 electrolyte representing salt, decreases the enthalpy of the pure protein in water. Inset shows the enthalpy of formation of pure protein solution, c_s = 0 mM in this example, as a function of c_p. Calculated enthalpy changes upon an addition of the salt to a given concentration of a model protein in water are exothermic. This is in accord with most of the experimentally obtained results for Δ_mixH. However, in comparison with experiment, the magnitude of the effect is much too small. In view of the correlations shown in Figure 8, the Coulomb effect calculated above, is clearly not the only negative contribution to the enthalpy change upon mixing.

Figure 9. OZ/MSA theory predicts that enthalpy of mixing a protein solution with salt solution is exothermic.

Panel (a) shows enthalpy changes upon forming a solution with protein concentration c_p and salt concentration c_s starting from pure water. Black dashed line is for c_p = 0, i.e. enthalpy of formation of salt solution. Other three curves apply to constant c_p = 0.1 (blue dash-dotted line), 0.3 (red continuous line), and 0.5 mM (green dotted line) and increasing c_s. Inset: Enthalpy of formation of pure protein solution (c_s = 0 mM) as a function of c_p. Panel (b) shows enthalpy change upon adding salt to an aqueous protein solution of concentration c_p = 0.3 mM as a function of the concentration of added salt, c_s. The charge and diameter of a model protein particle are +20 and 60 Å, respectively, while counterions with charge −1 and added +1 : −1 electrolyte are all of diameter 4 Å.

5. Conclusions

The conclusions of this study can be sumarized as follows: (i) enthalpies of BSA-salt mixing, measured in three different buffer solutions are in the explored experimental range mostly exothermic. Exceptions are LiCl, KCl, and NaCl salts in borate buffer. (ii) Surprisingly, the ion-specific effects of anions are much more pronounced than those of cations even at conditions where the protein has a net negative charge. (iii) Coulomb contribution to the enthalpy of mixing is estimated within the primitive model (treating solvent as continuous dielectric) using the Ornstein-Zernike integral equation theory in the MSA closure. The calculated enthalpy change upon mixing is negative, but too small to explain the experimental results. (iv) Correlation between the enthalpy of mixing, obtained at large excess of the added salt, and the enthalpy of hydration of salt anion indicates, that change of the solvation/desolvation equilibrium is partly responsible for the exothermic effects observed in experiments. The results are consistent with similar measurements performed for lysozyme solutions and for solutions of cationic polyelectrolytes. (v) The results for mixing enthalpies point toward strong BSA–anion interaction for all the experimental conditions examined here, i.e. up to pH = 9.2.

Highlights.

• Mixing solutions BSA with low molecular weight salts is (in most cases) exothermic.

• Compared to cations, ion-specific effects of anions are much stronger even when protein has negative net charge.

• Correlation between the BSA-salt mixing enthalpy and the hydration enthalpy of the corresponding salt’s anion is linear.

• Mean spherical approximation theory predicts the sign but not the magnitude of the experimentally observed heat effects.