SAFETY: Secure gwAs in Federated Environment Through a hYbrid solution

Abstract

Recent studies demonstrate that effective healthcare can benefit from using the human genomic information. Consequently, many institutions are using statistical analysis of genomic data, which are mostly based on genome-wide association studies (GWAS). GWAS analyze genome sequence variations in order to identify genetic risk factors for diseases. These studies often require pooling data from different sources together in order to unravel statistical patterns, relationships between genetic variants and diseases. Here, the primary challenge is to fulfill one major objective: accessing multiple genomic data repositories for collaborative research in a privacy-preserving manner. Due to the privacy concerns regarding the genomic data, multi-jurisdictional laws and policies of cross-border genomic data sharing are enforced among different countries. In this article, we present SAFETY, a hybrid framework, which can securely perform GWAS on federated genomic datasets using homomorphic encryption and recently introduced secure hardware component of Intel Software Guard Extensions to ensure high efficiency and privacy at the same time. Different experimental settings show the efficacy and applicability of such hybrid framework in secure conduction of GWAS. To the best of our knowledge, this hybrid use of homomorphic encryption along with Intel SGX is not proposed to this date. SAFETY is up to 4.82 times faster than the best existing secure computation technique.

1. Introduction

Rapid advancement in human genome sequencing has led us to a genomic era where human genomic data play an ever-important role in clinical research [1]. As cost-effective and efficient genome sequencing technologies are readily available, the research community can conduct experiments on different genomic data repositories for scientific discovery [2]. As a result of this massive data availability, Genome-Wide Association Studies (GWAS) are gaining popularity as they answer critical questions like susceptibility towards a disease or a physical trait by analyzing genome sequence variations in different individuals. GWAS examine genetic architecture of a disease to identify genetic risk factors associated with it. In other words, GWAS aims at finding if there is any correlation between a certain gene and a specific disease. Another fundamental goal of GWAS is to identify biological factors responsible for disease susceptibility in order to develop more effective diagnosis, treatment, and prevention techniques.

A larger genomic dataset is quintessential to perform any analytical study such as GWAS. Different research organizations or healthcare facilities often sequence genomes of different patients or participants for this reason. Researchers are interested in executing queries over these massive genomic datasets for unraveling new pieces of information about diseases under study. Oftentimes, the accuracy of this evaluation relies on the quantity and quality of the data used in the analysis– but a single organization often does not possess adequate genomic data (collection, processing, and storing of large-scale data is non-trivial) to perform a comprehensive or meaningful experiment. Because more data can reduce the sampling errors and improve the power of the analysis (for instance, statistical strength of GWAS increases with the quantity of data [3]), organizations tend to collect as much data as possible to meet data analysis needs.

Because sharing genomic data in plaintext possesses serious privacy implications for the participants [11], [12], in addition to the approval from an institutional review board (IRB), collaborative research on shared genomic data often needs to satisfy two criteria at the same time — a) authorizing access to genomic data for research and b) preserving participants’ privacy and protecting the confidentiality of their genomic information [13]. That is why strict policies regarding genomic data sharing have been enforced, and generally, these policies are different in different regions of the world. This difference in the regulations of cross-border genomic data sharing greatly impedes international research projects [14]. It is imperative to address the reality challenge with practical solutions to promote health science discoveries.

1.1. Existing Techniques.

To ensure the security and privacy of shared genomic data, different privacy-preserving techniques (for instance, homomorphic encryption [15], garbled circuit [16], secure hardware [10], secret sharing [17], differential privacy [18] etc.) have been proposed. Some applications of these techniques in secure GWAS, are demonstrated in Table 1. Each of these techniques has some advantages as they allow some functions to be computed on the data without compromising confidentiality and integrity of it [19]. For instance, homomorphic encryption allows to perform some computation (i.e. addition and multiplication) on encrypted data. Hence, encrypting the data before sharing and then executing the required computation on encrypted data is an intuitive solution. However, homomorphic encryption based solutions have significant computational and storage overhead, which makes them often impractical for real life applications [20].

TABLE 1:

Previous research works in secure and privacy-preserving GWAS in chronological order

Existing Techniques	Year	Secret Sharing	Homomorphic Encryption	Differential Privacy	Intel SGX
Bogdanov et al. [4]	2014	✓
Lauter et al. [5]	2014		✓
Tramèr et al. [6]	2015			✓
FORESEE [7]	2015		✓
Simmons et al. [8]	2016			✓
Shahbazi et al. [9]	2016	✓
PRINCESS [10]	2017				✓
SAFETY (our proposal)	2017		✓		✓

Secure multiparty computation (garbled circuit and secret sharing) is also a prospective solution because of their lower computational overhead. However, garbled circuit based solutions need complex circuit design and optimization, which limit its flexibility and usability greatly. Another technique of this genre, secret sharing involves huge communication overhead. Besides, it is not suitable for client server architecture [21].

Differential privacy based techniques add noise to the data in order to protect individual privacy. But, this noise reduces data utility, and makes accurate statistical analysis much harder. In addition, differential privacy requires one trusted party who has access to the integrated dataset. This requirement is not applicable to our scenario.

Intel SGX [22], [23] is an extension to the Intel architecture which allows an application to run inside protected execution areas of CPU. Although, SGX is efficient from computation and storage perspective, the security of SGX is yet to be fully established due to the recent discovery of side-channel attacks against SGX [24].

1.2. Contributions.

In this paper, we propose a hybrid framework, SAFETY, for secure execution of some popular statistical tests used in GWAS in a federated environment. Our proposed hybrid model incorporates security and efficiency of two different cryptographic schemes in a single system. More precisely, it is the first attempt to infuse homomorphic encryption with SGX to develop a secure and scalable genomic data computation model. The experimental results clearly demonstrate that it performs consistently irrespective of the number of data owners making it highly scalable (see Section 5 for details). This hybrid model captures the essence of both techniques: ability of computing some functions on encrypted data (homomorphic encryption) and performing sophisticated mathematical operation in the secure execution area of an SGX enabled CPU. Our primary goal behind proposing a hybrid model relies on better security guarantee from existing secure computation schemes, and faster and scalable execution for any number of data owners. From our experimental results, it is evident that the proposed hybrid model provides better efficiency and security than pure secure hardware or homomorphic encryption based solutions.

SAFETY utilizes an architecture [25] to execute secure count query on federated genomic datasets. Similar federated architectures are available in literature [4], [26]. In our adopted architecture [7], [25], genomic data resides in the local premises of individual data owners in plaintext (see Figure 1). Data owners have their own database systems which are geographically distributed and have different policy compliance for the data usage. An overview of data representation for each data owner is shown in Table 2. Proper authentication allows any researcher to execute queries on their data.

Fig. 1:

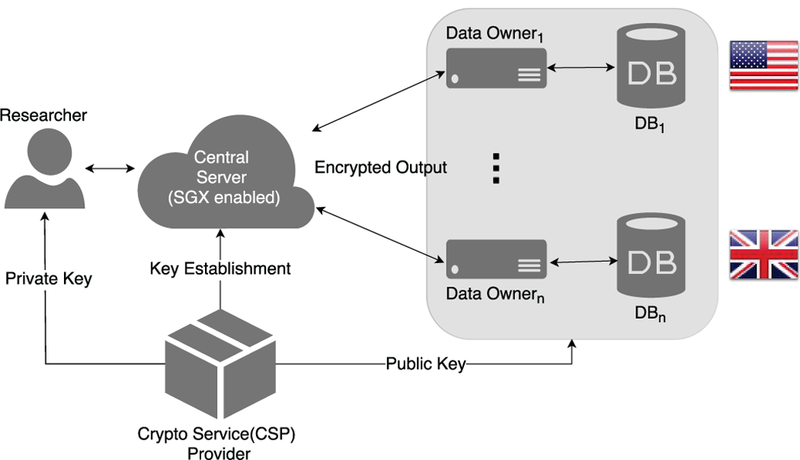
Diagram of the federated architecture where data owners are geographically distributed.

TABLE 2:

Data representation in each party

		Sequence
#	Case	rs4426	rs4305	rs4630		Cancer
Data Owner 1	1	CC	CT	GG	…	Negative
	2	CT	CT	AG	…	Negative
	3	CC	CT	GG	…	Negative
Data Owner 2	1	CC	CT	GG	…	Negative
	2	CT	CC	GG	…	Positive
	3	CC	CT	GG	…	Positive
Data Owner 3	1	CT	CC	AG	…	Positive
	2	CT	CT	AG	…	Negative
	3	TT	CC	GG	…	Positive
Data Owner 4	1	TT	CC	AA	…	Positive
	2	CC	CC	GG	…	Positive
	3	CC	CT	GG	…	Positive

Among the existing secure computation techniques, SGX is the most efficient. For instance, an implementation of SGX-based MapReduce framework [27] shows a very modest overhead of 8% to achieve read/write integrity. This is a great advantage of SGX in comparison to other secure computation schemes like garbled circuit and homomorphic encryption, which generally increase the computational overhead to a great extent. However, our proposed hybrid model is 1.7 to 4.82 times faster than SGX (see Section 5). This comparative efficiency increases with the number of data owners. The contributions of this article are summarized as follows:

1. We propose a hybrid cryptographic framework, SAFETY, which uses homomorphic encryption along with secure hardware features of the Intel SGX. SAFETY is not only secure and efficient, but also overcomes the limitations of solely homomorphic encryption based solutions which often come with higher computational overhead for processing higher order polynomials. In addition, SAFETY also simplifies solely SGX based solutions, which require pairwise attestation and secure key distributions between server and data owners.

2. Using SAFETY, we securely execute and evaluate some of the major functions of GWAS in federated architecture where genomic data are distributed and owned by different parties. We performed four statistical tests: Linkage Disequilibrium (LD), Hardy-Weinberg Equilibrium (HWE), Cochran-Armitage Test for Trend (CATT), Fisher’s Exact Test (FET) to evaluate SAFETY over a variety of settings. However, our framework SAFETY can incorporate any GWAS functions (i.e., transmission disequilibrium test [10], EigenSTRAT [28], linear mixed model [8], etc.) and not limited to the GWAS functions mentioned previously. The methodology to perform these statistical tests securely is discussed in Section 4.

3. SAFETY ensures that each data owner is completely unaware of the contributions from the other data owners, who are participating in the same analysis. Moreover, the final result is revealed only to the researchers without disclosing individual contribution of data owners. This allows us to preserve the privacy of the output of each data owner.

4. We conduct multiple experiments in different realistic setting in a federated environment varying the data size and the geographic locations of data owners (see Section 5 for details).

2. System Overview

In this section, we discuss the system architecture and the threat model.

2.1. System Architecture

There are four entities in the proposed system architecture as shown in Figure 1:

• Researchers (authorized): Individuals or organizations who want to execute queries over genomic databases. This party sends queries to the central server and expects encrypted results of different GWAS functions.

• Data Owners: These parties are geographically distributed and possess databases upon which queries are performed. These data owners might be hospitals or government organizations who want to share their genomic data and have different policies regarding the data sharing. The proposed model supports any number of data owners where they can execute any aggregate query locally.

• Crypto Service Provider (CSP): CSP manages the cryptographic keys that will be used for data encryption and decryption in various steps of the system protocol. Each data owner receives a public key from the CSP and encrypts its output using that public key. CSP also issues the private key to an authorized researcher who can decrypt the final result.

• Central Server: The central server maintains communications with all other entities of the system architecture. It receives queries from the researcher, sends them to the data owners, and collects individual encrypted results from each data owner. Individual encrypted results from data owners are securely combined by the central server to compute the final result of the query with the help of homomorphic encryption and SGX.

2.2. Threat Model

In this paper, our goal is to ensure the confidentiality of individual contributions or data from different geographically distributed data owners. Researchers can decrypt only the final result provided by the central server. We assume the CSP to be a trusted entity while the central server is a semi-honest entity (also known as honest-but-curious) where it follows the protocol but may attempt to derive additional information from the server logs or received defined protocols [29].

We assume that the computations (required for statistical tests of GWAS) run in an SGX enabled central server. SGX architecture facilitates the central server to perform any computation securely on data provided by multiple data owners. We assume that the processor works properly, and is not compromised. We trust the design and implementation of SGX including all cryptographic operations performed by it.

It should be mentioned that there are some recently proposed side-channel attacks against SGX [24], [30], [31]. All of these attacks are software attack. To the best of our knowledge, there is no known physical attack against SGX. The attack proposed in [24], is a limited or controlled side-channel attack against a particular SGX based framework [32]. This is basically a page-fault attack. Another software attack proposed in [30] (known as synchronization bugs), is applicable only for multi-threaded applications.

Existing defense mechanisms are proposed targeting only the page-fault side-channel attacks [33]–[35]. However, these defense mechanisms may not prevent the future attacks. Further research is required to better understand the potential vulnerability of SGX, consequence of different side-channel attacks, and possible defense mechanisms.

Addressing these side-channel attacks against SGX, SAFETY protects the institutional privacy of the participating data owners by aggregating their local statistics without decrypting them. This approach provides a higher layer of data security.

3. Background

In this section, we will introduce some of the concepts, which are required to understand the proposed methods in Section 4.

3.1. Intel SGX

Intel SGX is a set of extensions to the Intel architecture which mainly focuses on the problem of running applications on a remote machine administered by an untrusted party. SGX allows parts of an application to be executed inside secure segments of the CPU called enclaves. Untrusted entities including privileged software (kernel, hypervisor, etc.) cannot access enclave. SGX ensures that the code and data within an enclave cannot be read or modified from outside the enclave.

There are two SGX features that play a vital role in provisioning of sensitive data to an enclave. These are called attestation and sealing.

• Attestation: SGX enclaves are created without privacy-sensitive data. Privacy-sensitive data are delivered after the enclave has been properly instantiated on the platform. The process of demonstrating that a piece of software has been properly instantiated within an enclave on an enabled platform is called attestation [36].

  Attestation demonstrates to a user that he is communicating with an application running inside an enclave. This demonstration is accomplished via a cryptographic signature that certifies the hash of the enclave’s contents. The remote computer’s administrator is able to load any program in an enclave. However, the user (who uses the remote computation service) will deny to load his data into an enclave if the hash of the contents does not match the desired value [37].

• Sealing: When an enclave is instantiated, SGX provides protections to its data until it is maintained inside the enclave. However, when the enclave process exits, the enclave will be destroyed and all associated data will be lost. If the data is required later, it needs to be stored outside the enclave. Sealing is the process of encrypting and storing data in a way such that only the same enclave would be able un-seal them back to their original form. In our framework, data sealing is not required since the data owners do not necessarily outsource their data to the central server. Instead, they send certain local counts in response to researcher’s query.

Memory partition in Intel SGX is described in Appendix B.

3.2. Homomorphic Encryption

Homomorphic encryption allows performing computation on encrypted data without decrypting the data. Homomorphic encryption in a nutshell is: if c₁ = ξ(m₁) and c₂ = ξ(m₂) (where m₁ and m₂ are the plaintexts, c₁ and c₂ are the ciphertexts, and ξ is any randomized encryption function), we can perform computation on c₁, c₂ and get the same output as if we were performing computation on m₁ and m₂.

In SAFETY, we have used a partial homomorphic system named Paillier cryptosystem [38]. Paillier cryptosystem has two important properties that we utilized in SAFETY.

• Probabilistic encryption: If we encrypt the same message several times using Paillier cryptosystem, it generates different ciphertexts for the same plaintext.

• Addition homomorphism: For any public key n and arbitrary messages m₁, m₂,

  $$\xi \left(m_1+m_2\right)=\left(\xi (m_1\right)*\xi \left(m_2)\right)\mathrm{mod}{n}^2$$

  which denotes that we can do an addition operation over ciphertexts.

4. Methodology

In this section, we discuss how to perform the statistical tests (LD, HWE, CATT, and FET) securely. Please see Appendix B for a brief introduction of the corresponding GWAS functions. To explain our proposed methods we use the data from Table 2.

As mentioned earlier, we consider the use of Intel SGX in two ways — 1) Hybrid approach: using Intel SGX along with homomorphic encryption 2) Secure hardware approach: using only Intel SGX. SAFETY is based on the hybrid approach.

4.1. Hybrid Approach (SAFETY)

Suppose, there are total n number of data owners (D₁, D₂, … , D_n) connected in the federated environment where a researcher wants to execute a statistical query. The query result should follow or represent as if the query is being executed on the combined dataset. Here, each data owner will have their own individual outputs. For example, data owners D₁, D₂, … , D_n will have outputs x₁, x₂,…, x_n respectively. These outputs can be haplotype or genotype counts (encrypted) for a specific SNP locus based on the query from a researcher.

These outputs are encrypted by the public keys provided beforehand by the CSP. Data owners get the public keys from the CSP before any computation. The data owners generate their encrypted outputs c₁, c₂, … , c_n (from x₁, x₂, … , x_n) using the public keys provided by the CSP and send them to the central server for further computation.

The central server then performs homomorphic addition on the individual encrypted outputs c₁, c₂, … , c_n with the Paillier cryptosystem [38]. After homomorphic addition, it hands over the total encrypted counts to Intel SGX for further computation required to perform different statistical tests like LD, HWE, CATT, and FET. Then, the total counts are decrypted inside enclave, and further computation is also performed inside enclave where no untrusted application can access these data. The sequence diagram of this protocol is shown in Figure 2.

Fig. 2:

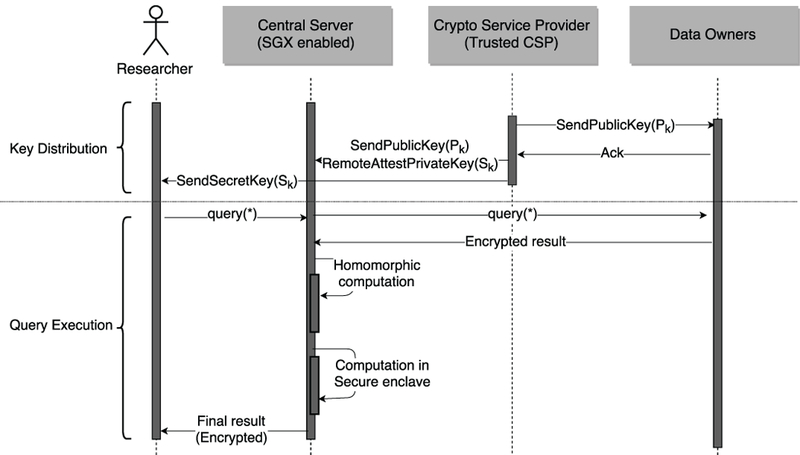
Sequence diagram for the hybrid approach.

It is noteworthy that due to the use of homomorphic addition operation, the number of decryptions required to perform statistical tests is greatly reduced (shown in Table 7). Also the individual contributions from the data owners are secured since their values are encrypted. Figure 3 demonstrates the use of homomorphic encryption and Intel SGX in a hybrid architecture.

TABLE 7:

Number of decryptions required to perform a statistical test for different number of data owners

Test	Number of data owners
	One		Three		Five
	Hybrid	Secure h/w	Hybrid	Secure h/w	Hybrid	Secure h/w
LD	4	4	4	12	4	20
HWE	3	3	3	9	3	15
CATT	6	6	6	18	6	30
FET	6	6	6	18	6	30

Fig. 3:

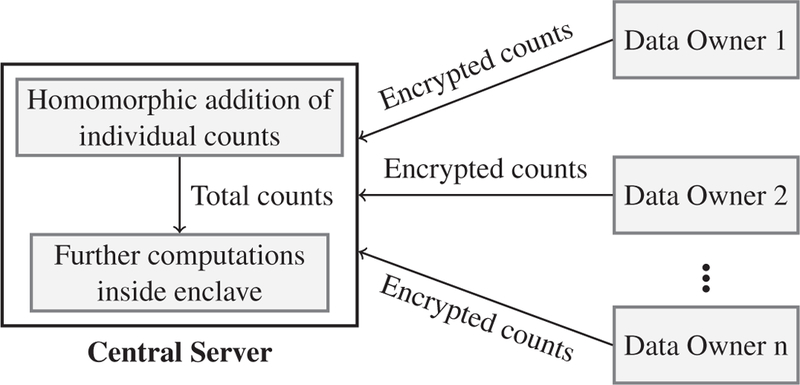
Usage of homomorphic addition in our framework.

4.2. Secure Hardware Approach

In secure hardware approach, after receiving individual outputs from different data owners, the central server decrypts them inside the enclave and performs further computation on plaintext. The fundamental difference between a hybrid approach and a secure hardware approach is, not using the homomorphic addition on ciphertext. Since in this approach, all the individual homomorphically encrypted outputs need to be decrypted, the computational overhead is quite large.

In the following subsections, we discuss the methods for securely performing LD, HWE, CATT, and FET according to the hybrid approach. We use the data from Table 2 to explain the methods.

4.3. Secure Linkage Disequilibrium (LD)

A sample query from researcher regarding LD may look like: Are rs4305 and rs4630 at linkage disequilibrium?

Both SNPs are bi-allelic. So, there are four possible haplotypes: CA, TA, CG, and TG.

Each data owners send their haplotype counts, which are encrypted by Paillier cryptosystem [38]. For instance, data owner 1 sends $N_{C{A}_{\text{1}}}=E\left(1\right)$ where the count of haplotype CA is 1 and E is the encryption function. After receiving the encrypted counts of CA from all the data owners, the central server performs homomorphic addition operation on them to obtain the total encrypted count for CA. For n data owners,

$$N_{CA}=N_{C{A}_1}+N_{C{A}_2}+\dots +N_{C{A}_n}$$

Similarly, total count for TA, CG, and TG are computed. Then the central server instantiates a secure enclave and provisions these encrypted values as input there. As the decryption key (private key) is sealed by the enclave, it can decrypt the counts and calculate the haplotype frequencies. The haplotype frequencies are calculated in enclave to avoid division of encrypted numbers, which is expensive even in fully homomorphic encryption. Finally, coefficient of the LD is computed, and researcher gets the result of her query from this. We discuss detailed procedure for computing LD coefficient in Appendix A.2.

4.4. Secure Hardy-Weinberg Equilibrium (HWE)

A sample query regarding HWE is: Does HWE holds at SNP rs4305?

Possible genotypes at SNP rs4305: CC, CT, and TT. Each data owner will send their individual count for CC, CT, and TT genotypes. After receiving these encrypted genotype counts from all data owners, the central server performs homomorphic addition operation using Paillier cryptosystem [38] to obtain total encrypted counts for corresponding genotypes.

Now, all the counts are decrypted inside the enclave to calculate the frequencies $P_C$ and $P_T$. $P_C$ is calculated using, $P_C=\frac{n_{CC}}{n}+\frac{1}{2}\times \frac{n_{CT}}{n}$. Then, P_T = 1 − P_C.

Further discussion is available in Appendix A.3.

4.5. Secure Cochran-Armitage Test for Trend (CATT)

A typical query from researcher regarding CATT is: Determine if CATT can be inferred at rs4426?

Possible genotypes at SNP rs4426 are: CC, CT, and TT. For cases and controls (Cancer positives and negatives respectively), all the data owners send their encrypted genotype counts for both categories to the central server. Homomorphic addition operations are performed to calculate row total and column total using Paillier cryptosystem [38]. A contingency table needs to be constructed, which is described in the Appendix A.4. This table is then sent to the enclave where all these row totals and column totals are decrypted for further computation.

4.6. Secure Fisher’s Exact Test (FET)

Like CATT, FET also operates on a contingency table. So, for FET, data flow is similar to CATT. Here, the p − value is calculated in enclave after securely aggregating the individual encrypted inputs from the data owners. Please see Appendix A.5 for further discussion.

4.7. Pre-computation table for GWAS

As we have seen, all the statistical tests mentioned before (LD, HWE, CATT, and FET) require processing data in a tabular format. Data owner can keep their data in this format. Consequently, when central server requests for data, data owner can respond readily. It is noteworthy that each data owner has to build the table only once. Thus, pre-computation of the table enhances the efficiency of SAFETY.

Table 3 represents pre-computation table of data owner 1 for performing HWE, CATT, and FET at rs4426.

TABLE 3:

Sample pre-computation table for HWE, CATT, and FET

CC		CT		TT
Case	Control	Case	Control	Case	Control
2	0	1	0	0	0
2		1		0

Since performing LD involves two SNP loci, a different pre-computation table is required. Table 4 represents pre-computation table of data owner 1 for performing LD at rs4305 and rs4630.

TABLE 4:

Sample pre-computation table for LD

	rs4630
rs4305	Allele	A	G
	C	CA (1)	CG (2)
	T	TA (0)	TG (3)

5. Experimental Results

In this section, we extensively evaluate aforementioned hybrid approach and secure hardware based approach in a federated environment using Amazon cloud and demonstrate their applicability in a real world setting. Our proposed framework SAFETY is based on hybrid approach where we use SGX along with homomorphic encryption. However, secure hardware based approach uses only SGX.

5.1. Experimental Setting

In our experimental setup, the researcher, CSP, and central server were located in Manitoba, Canada. Our central server was hosted on a machine with Intel Core i7–6700 (3.40 GHz) processor and 8 GB memory. However, we emulate data owners in different locations of the world to evaluate the propriety of our proposed framework in a real world environment. We used Amazon EC2 cloud servers having the same configuration for all data owners. Table 5 shows the location, IP address, and the latency of these servers used in our experiment. In our experiments, we used 80 bit security (size of the public key is 1024 bits) on the public-key cryptosystem. The security can be improved by increasing the key length.

TABLE 5:

Server locations and average latency

Server Location	IP Address	Network Latency (ms)
Canada (Manitoba)	130.179.30.133	<1
USA (Oregon)	52.32.83.223	37
London	52.56.65.221	105
Seoul	52.78.100.194	170
Sydney	54.206.67.251	233

We performed four experiments with different settings. The number of data owners was different for different experiments which allowed us to evaluate the scalability of both methods. Table 6 shows different settings used in the experiments. For instance, in experiment 1, two data owners were in USA and Canada while in experiment 4, five data owners were residing in all the locations mentioned in Table 5. Experiments were performed using synthetic data which were generated according to the allele frequency of CHB, CHS, JPT and MXL populations from 1000genomes dataset (August 2010 Release) [39].

TABLE 6:

Location of different data owners in different experimental settings

Exp. #	Canada	USA	London	Seoul	Sydney
Exp. 1	✓	✓	✗	✗	✗
Exp. 2	✓	✓	✓	✗	✗
Exp. 3	✓	✓	✓	✓	✗
Exp. 4	✓	✓	✓	✓	✓

5.2. Results and Discussions

Prior to analyzing the running times of our proposed methods, we evaluate the required time to compute the four statistical tests on plaintext (i.e. without any security protection). We calculate the exact results for the GWAS calculations without loosing any accuracy.

In Figure 4, we show the running time (in milliseconds) for performing the four statistical tests on plaintext. We observed that in any single experimental setup, the running time is almost the same for all the statistical tests. However, running times for different experiments are different because different experiments involve different number of data owners (as shown in Table 6). As a result, higher communication overhead is added in these experiments. For instance, experiment 2 involves more data owners than experiment 1, which yields more communication overhead and results in greater running time.

Fig. 4:

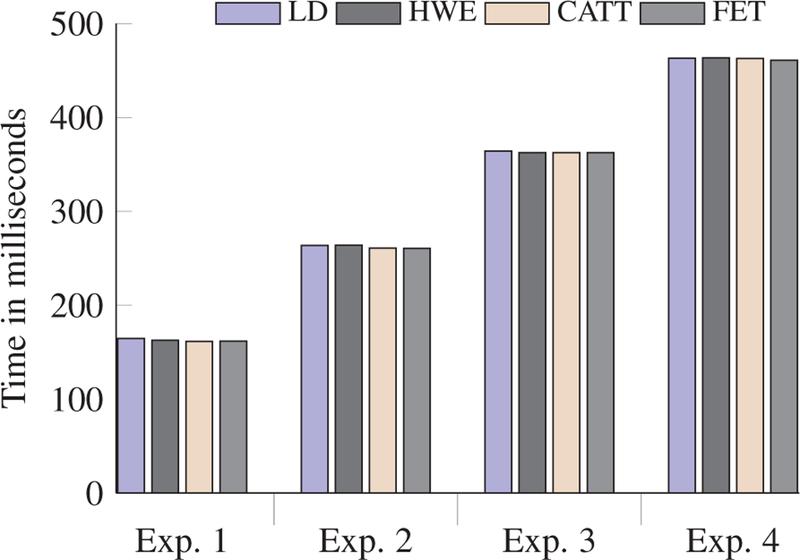
Experimental results for plaintext.

The running time for computing LD on ciphertexts is shown in Figure 5(a). Here, running time is decomposed into communication overhead in the network and time required for secure computation of the method. It is noteworthy that,

Communication overhead ∝ Number of data owners

Fig. 5:

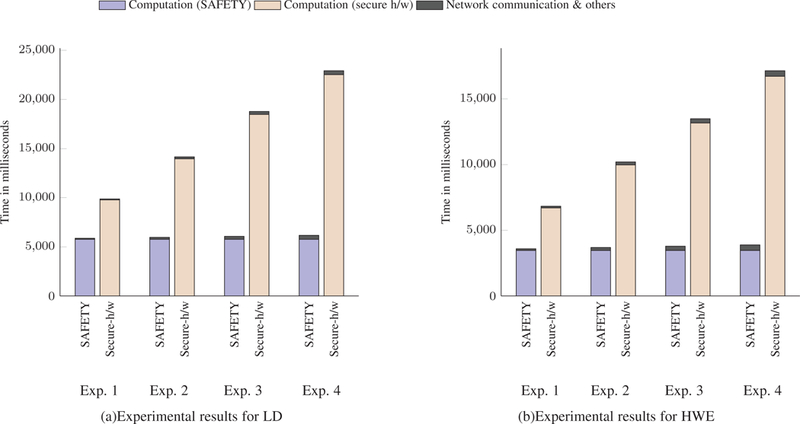
Experimental results for LD and HWE. (a) and (b) compare computation time and communication costs of conducing Linkage Disequilibrium (LD) and Hardy-Weinberg Equilibrium (HWE) test using SAFETY and purely secure hardware approach.

SAFETY requires 5,770 ms to compute LD coefficient for two data owners, which is 1.7 times faster than secure hardware approach. Rest of the time is due to the communication overhead in the network. Figure 5(b), 6(a), and 6(b) illustrate the experimental results for performing HWE, CATT, and FET respectively on ciphertexts. Experimental results illustrate that SAFETY is much faster than solely secure hardware based approach. For instance, for HWE, SAFETY is 1.93, 2.87, 3.8, and 4.82 times faster than solely secure hardware based approach in Experiment 1, 2, 3, and 4 respectively (see Figure 5(b)). It is noteworthy that SAFETY and the secure h/w approach both utilize the asymmetric encryption and decryption.

Fig. 6:

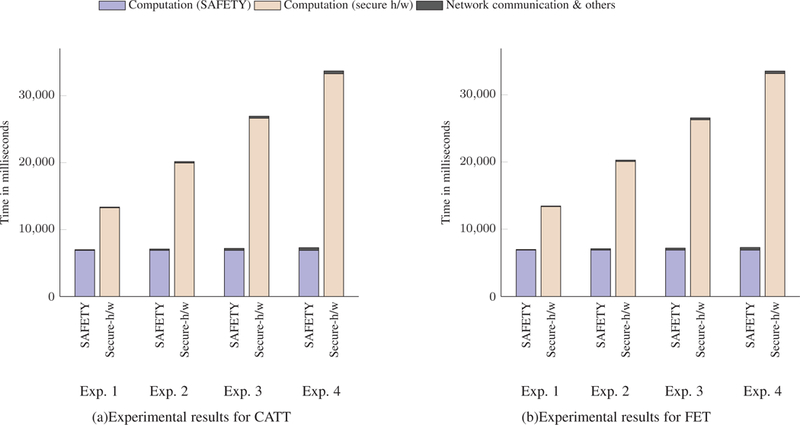
Experimental results for CATT and FET. (a) and (b) compare computation time and communication costs of conducing Cochran-Armitage Test for Trend (CATT) and Fisher’s Exact Test (FET) using SAFETY and purely secure hardware approach.

The experimental results demonstrate that the performance of the secure hardware approach does not scale well with the number of data owners. As the number of data owner increases, the running time of secure hardware approach increases rapidly. On the contrary, the hybrid approach (SAFETY) performs consistently irrespective of the number of data owners due to its hybrid properties (homomorphic addition followed by computation inside enclave). In this case, only the communication overhead increases which is very small considering the total running time.

Another important analysis regarding the methods is the number of decryptions needed for any statistical tests. It is evident that LD requires more time than HWE while CATT and FET require more time than the other two. The reason behind this is, the time required to perform a statistical test is proportional to the number of decryptions required. Moreover, for secure hardware approach, all the individual contributions of data owners need to be decrypted inside the secure enclave. As the number of the data owner increases, the number of decryptions also increases which results into higher running time. Table 7 demonstrates how the required number of decryptions increases with the number of data owners.

6. Discussions

In this section, we discuss some of the other security and privacy concerns regarding the secure computation of GWAS in our hybrid model.

6.1. Query Privacy

In the proposed methods, we do not consider the query privacy of the researcher. In other words, we consider the queries from researcher to be public and data owners, central servers know the targeted position (locus) from the researcher. This issue can be resolved by some of the query privacy or private information retrieval techniques [40]–[42].

6.2. Output Privacy

SAFETY does not guarantee the privacy of the final result as that only gets decrypted by researcher. We are aware that there are some differential privacy based approaches [8], [43], [44], those address this issue and generate differentially private outputs for GWAS. However, as we consider this researcher to be semi-honest, this issue is beyond the scope of the paper.

6.3. Assumption Regarding CSP

In our threat model, we assumed that the Crypto Service Provider (CSP) is a trusted entity, and does not collude with any other party. In other words, if the CSP leaks the secret keys, the proposed framework will not be deemed secure.

To ensure the security and integrity of the CSP, we should employ good security practices (software security, OS security etc.). However, if it is not the case, then our proposed system will fall apart. Our situation is similar to the public-key system, where there are CAs (they are assumed to be trusted).

6.4. Consideration of Symmetric Cryptography

We are not using symmetric cryptography (like AES) for a couple of reasons:

• Achieving randomized encryption (initialization vector management issue): One major drawback of using any symmetric cryptography scheme, (i.e., AES) is achieving randomized or probabilistic encryption. This randomness can be introduced by choosing initialization vectors which needs to be managed by the central server or CSP for multiple data owners. However, SAFETY is based on homomorphic encryption whose encryption is probabilistic by definition, which reduces the burden of managing initialization vectors.

• Risk of individual contribution leakage: One of the major concerns in addressing the security of the federated environment is hiding the individual contributions from data owners. As we perform the additions over encrypted data, these contributions are never revealed. As a result, in our proposed framework the possibility of such leakage is highly unlikely.

• Requires n remote attestations for n data owners (key distribution problem): Symmetric cryptography schemes like AES require key distribution/setup with every data owners which results in many network communications, which might be prone to attack. On the contrary, our proposed framework is based on public-key cryptography where the data owners use a public key to encrypt their data published by the CSP. As a result, key distribution is much simpler and our framework incurs less communication overhead.

7. Conclusion

Homomorphic encryption and Intel SGX have their own strengths to utilize. Homomorphic encryption can perform some computational operations without decrypting the ciphertext, and Intel SGX can perform any secure computation efficiently after decrypting ciphertext. However, a hybrid model where homomorphic encryption and secure hardware are used in appropriate use cases provides a good trade-off in terms of efficiency and computational support for secure statistical analysis. The outstanding performance of SAFETY attests this hypothesis.

Recently, some data analytics and machine learning applications [27], [45], [46] have adopted Intel SGX for secure computation. However, little work has been done using Intel SGX for analyzing genomic data. We think, using secure and efficient computation capability of Intel SGX to analyze genomic data is very promising for healthcare and medical research.

Biographies

Md Nazmus Sadat received his B.Sc. degree in Computer Science and Engineering from Bangladesh University of Engineering and Technology (BUET) in 2014. He is currently pursuing M.Sc. in Computer Science at University of Manitoba. His primary research interests include trusted hardware assisted secure computation techniques, privacy-preserving data analytics.

Md Momin Al Aziz received his B.Sc. degree in Computer Science and Engineering from Bangladesh University of Engineering and Technology (BUET) in 2014. He is currently a research assistant in Computer Science at University of Manitoba pursuing his PhD degree. His primary interest is in secure computation over genomic data, privacy preserving data sharing and protien structures.

Noman Mohammed received a Ph.D. degree in Computer Science from Concordia University in 2012. He is currently an Assistant Professor in the Department of Computer Science at University of Manitoba, Manitoba, Canada. Before coming to UofM, he was an NSERC postdoctoral fellow in the School of Computer Science at McGill University and a member of the Cryptography, Security, & Privacy (CrySP) Research Group at the University of Waterloo. His research interests include private data sharing, privacy-preserving data mining, secure distributed systems, and applied cryptography.

Feng Chen received a Ph.D. degree in Electrical and Computer Engineering from University of Oklahoma. Currently, Feng Chen is a Post-doctoral researcher at Division of Biomedical Informatics (DBMI), University of California, San Diego (UCSD). His research interests include privacy-preserving machine learning, secure data sharing, and computation techniques.

Xiaoqian Jiang is an assistant professor in the Department of Biomedical Informatics at University of California San Diego. He received his PhD in Computer Science from Carnegie Mellon University. He is an associate editor of BMC Medical Informatics and Decision Making and serves as an editorial board member of Journal of American Medical Informatics Association. He works primarily in health data privacy and predictive models in biomedicine. Dr. Jiang is a recipient of distinguished paper award from American Medical Informatics Association (AMIA) Clinical Research Informatics (CRI) Summit in 2012 and 2013.

Shuang Wang received the B.S. degree in Applied Physics and M.S. degree in Biomedical Engineering from the Dalian University of Technology, and M.S. and Ph.D. degrees in Electrical and Computer Engineering from the University of Oklahoma. Currently, Shuang Wang is an Assistant Professor at Department of Biomedical Informatics, University of California, San Diego. His research interests include Data Privacy, Pattern recognition, Machine Learning, GPU based high performace computing.