Skip to main content
NCBI home page
NeuroImage : Clinical logoLink to NeuroImage : Clinical
. 2018 Dec 10;21:101637. doi: 10.1016/j.nicl.2018.101637

Prognosis of conversion of mild cognitive impairment to Alzheimer's dementia by voxel-wise Cox regression based on FDG PET data

Arnd Sörensen a,⁎, Ganna Blazhenets a, Gerta Rücker b, Florian Schiller a, Philipp Tobias Meyer a, Lars Frings a,c; for the Alzheimer's Disease Neuroimaging Initiative1
PMCID: PMC6411907  PMID: 30553760

Abstract

Aim

The value of 18F-fluorodeoxyglucose (FDG) PET for the prognosis of conversion from mild cognitive impairment (MCI) to Alzheimer's dementia (AD) is controversial. In the present work, the identification of cerebral metabolic patterns with significant prognostic value for conversion of MCI patients to AD is investigated with voxel-based Cox regression, which in contrast to common categorical comparisons also utilizes time information.

Methods

FDG PET data of 544 MCI patients from the Alzheimer's Disease Neuroimaging Initiative (ADNI) database were randomly split into two equally-sized datasets (training and test). Within a median follow-up duration of 47 months (95% CI: 46–48 months) 181 patients developed AD. In the training dataset, voxel-wise Cox regressions were used to identify regions associated with conversion of MCI to AD. These were compared to regions identified by a classical group comparison (analysis of covariance (ANCOVA) with statistical parametric mapping (SPM) 8) between converters and non-converters (both adjusted for apolipoprotein E (APOE) genotype, mini-mental state examination (MMSE) score, age, sex and education). In the test dataset, normalized FDG uptake within significant brain regions from voxel-wise Cox- and ANCOVA analyses (Cox- and ANCOVA- regions of interest (ROI), respectively) and clinical variables APOE status, MMSE score and education were tested in different Cox models (adjusted for age, sex) including: (1) only clinical variables, (2) only normalized FDG uptake in ANCOVA-ROI, (3) only normalized FDG uptake from Cox-ROI, (4) clinical variables plus FDG uptake in ANCOVA-ROI, (5) clinical variables plus FDG uptake from Cox-ROI.

Results

Conversion-related regions with relative hypometabolism comprised parts of the temporo-parietal and posterior cingulate cortex/precuneus for voxel-wise ANCOVA, plus frontal regions for voxel-wise Cox regression (both p < .01, false discovery rate (FDR) corrected). The clinical-only model (1) and the models based on normalized FDG uptake from Cox-ROI only (2) and ANCOVA-ROI only (3) all significantly predicted conversion to AD (Wald Test (WT): p < .001). The clinical model (1) was significantly improved by adding imaging information in model (4) (Akaike information criterion (AIC) relative likelihood (RL) (1) vs (4): RL < 0.018). There were no significant differences between models (2) and (3), as well as (4) and (5).

Conclusions

Voxel-wise Cox regression identifies conversion-related patterns of cerebral glucose metabolism, but is not superior to classical group contrasts in this regard. With imaging information from both FDG PET patterns, the prediction of conversion to AD was improved.

Keywords: Cox model, Mild cognitive impairment, Alzheimer's dementia, FDG PET

Highlights

  • •

    Voxel-wise Cox regression identifies regions relevant for development AD.

  • •

    Hypometabolism of these regions poses a significant hazard for AD development.

  • •

    Inclusion of FDG PET data improves the accuracy of prognosis significantly.

1. Introduction

In recent years, the prognostic accuracy of 18F-fluorodeoxyglucose (FDG) PET concerning conversion from mild cognitive impairment (MCI) to Alzheimer's dementia (AD) has been discussed controversially. Some studies reported uninformative prediction accuracies of 50% (Grimmer et al., 2016) to 57% (Schmand et al., 2012) and a recent Cochrane review (Smailagic et al., 2015) did not recommend FDG PET for clinical use for this purpose. This has been criticized (Morbelli et al., 2015), and other studies have shown that FDG PET is a significant predictor of conversion to AD (Drzezga et al., 2005; Lange et al., 2015; Prestia et al., 2015).

The majority of previous FDG PET studies were limited as they used only a-priori defined region of interest (ROI)-based survival analyses (Gray et al., 2012; Landau et al., 2010; Torosyan et al., 2017) or voxel-based analyses that disregarded observation time information (Chen et al., 2011). In addition, previous MRI studies have shown advantages of the well-established Cox proportional hazard regression (Cox, 1972) over traditional group comparisons (Vemuri et al., 2011; Zeifman et al., 2015), when applied at voxel level.

In the present work, we aimed to use voxel-wise Cox regression to identify patterns of cerebral glucose metabolism that are significantly related to MCI to AD conversion without a-priori knowledge about typical AD patterns. The predictive value of the normalized FDG uptake within these hypometabolic clusters was evaluated and compared against other predictors in a test-dataset, using multivariate Cox regression.

To this end, we used the large imaging data collected in the scope of the Alzheimer's Disease Neuroimaging Initiative (ADNI, http://adni.loni.usc.edu), which enables a combination of voxel level analysis of FDG PET with observation time information.

2. Materials and methods

2.1. Subjects

The data used in the present study is provided by the ADNI project, which is a large multi-center study with approximately 50 sites participating in the United States and Canada. It was launched in 2003 as a public-private partnership and is led by Principal Investigator Michael W. Weiner, MD. The primary goal of the ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessments could be combined to measure the progression of MCI and early AD. Comprehensive information about the ADNI project can be found at the official website.

For the present work 576 FDG PET scans of MCI patients were retrieved from the ADNI database (August 2016) with the following inclusion criteria: all patients were clinically diagnosed as MCI (DX-score 2) and had an FDG PET at baseline. A mini-mental state examination (MMSE) score of at least 24 points (n = 6 excluded), minimal follow-up of at least 6 months (n = 20 excluded, of these n = 10 had no follow-up) and no bidirectional change of DX-scores (e.g. between different ADNI phases, n = 6 excluded) were requested. The remaining 544 subjects were randomly split into equally sized cohorts A and B, see Table 1.

Table 1.

Clinical and demographic characteristics of the included Alzheimer's Disease Neuroimaging Initiative (ADNI) participants.

Training dataset Test dataset
Subjects 272 272
Age mean (±S.D.) [years] 74 ± 8 73 ± 8
Sex [M/F] 172/100 163/109
Education (±S.D.) [years] 15.6 ± 4 15.7 ± 4
MMSE score mean (±S.D.) 28 ± 2 28 ± 2
APOE ε4 positive rate 49% 52%
Conversion rate 32% 34%
Median follow-up (±S.D.) [months] 48 ± 1 47 ± 1
Open in a new tab

Apolipoprotein E (APOE) ε4 status is defined as positive if at least one epsilon 4 allele is present. The median follow-up was calculated as the reversed Kaplan-Meier estimate. MMSE = mini-mental score examination.

2.2. FDG PET data and image preprocessing

The scans were acquired at 57 different sites and across 22 scanner types. In 468 cases the images had been recorded with a dynamic protocol of 6 frames of 5-min duration, starting at 30–35 min. after injection, while the remaining 76 were scanned with a static 30-min acquisition. The reconstructed files were downloaded in their original format (DICOM, ECAT, Interfile) for meta-information and as Nifti which was ultimately used for analysis.

The preprocessing steps for the ADNI MCI scans followed recommendations for optimal statistical analysis of brain FDG PET scans in the context of MCI to AD conversion prognosis, previously described elsewhere (Lange et al., 2015). This processing pipeline utilized MATLAB (The MathWorks, Inc., Natick, Massachusetts, United States) and the freely available Statistical Parametric Mapping (SPM 8) framework (Friston et al., 2007).

In case of dynamic scans, first a frame-by-frame motion correction to the first frame was applied and realigned frames were summed into a final static uptake image. In a second step the images were regularized into MNI space and subsequently stereotactically normalized onto an in-house FDG PET template, obtained from healthy elderly controls. Finally, the scans were proportionally scaled to brain parenchyma and a Gaussian smoothing of 12 mm full-width at half maximum (FWHM) was applied.

2.3. Region of interest derivation

Two fundamentally different methods were applied to the training dataset in order to identify conversion-related ROIs of cerebral glucose metabolism on FDG PET. In both cases the calculations were restricted to brain parenchyma voxels.

First, a voxel-wise analysis of covariance (ANCOVA) was performed to identify voxels with significantly reduced FDG uptake in converters (n = 86) versus non-converters (n = 194) in the training dataset, adjusted for age, sex, mini-mental state examination (MMSE) score and apolipoprotein E (APOE) genotype using statistical parametric mapping (SPM) 8 software. The subsequent region of interest (ANCOVA-ROI, Fig. 1), containing all voxels with significant hypometabolism in converters compared to non-converters, was thresholded at p < .01 (false discovery rate (FDR) corrected).

Fig. 1.

Fig. 1

Open in a new tab

MRI template and ROI overlays showing significant regions from the Cox model (Cox-ROI, cyan) and the analysis of covariance (ANCOVA-ROI, red). Both were derived in the training dataset (p < .01, false discovery rate (FDR)-corrected).

Second, a Cox model was fit independently for each voxel within MATLAB, with normalized and subsequently z-scaled FDG uptake as predictor variable, adjusted for sex, age, MMSE score and APOE genotype. Voxels that showed a significant (FDR-corrected p < .01) association between hypometabolism and (earlier) conversion were combined to a ‘Cox-ROI’ (Fig. 1). In order to match the common convention that hazard ratios above one correspond to a risk increase, the measure ‘hypometabolism’ was defined as a positive value. Hazard ratios below one, indicating a protective effect, were excluded for the final analysis as these seemingly hypermetabolic regions were actually due to proportional scaling (i.e. relative preserved areas like cortices).

2.4. Cox regressions in the test dataset

Using the ANCOVA- and Cox-ROIs derived from the training dataset, Cox regressions were carried out in the test dataset. First, the average normalized FDG uptake within both ROIs were read out for each subject in the test dataset, and used together with clinical data as covariates for five Cox models (see Table 2). Multicollinearity was addressed by the usage of ridge regression. For all five Cox models, a validation of the proportional hazard assumption has been performed for all covariates by testing for multiple fractional polynomials transformation, using the R package mfp (R Core Team, 2017; Ambler, 2015). As all covariates satisfied the proportional hazard assumption, transformations would have been only linear and were thus omitted.

Table 2.

Variables chosen as covariates for Cox regressions in the test dataset.

Model Cox-ROI ANCOVA-ROI Age Sex MMSE score Education APOE status
1 – – X X X X X
2 – X – – – – –
3 X – – – – – –
4 – X X X X X X
5 X – X X X X X
Open in a new tab

The variables sex (male = 1, female = 0) and APOE status (positive if at least one epsilon 4 allele present) are dichotomous. (ROI = region of interest, ANCOVA = analysis of covariance).

In order to be able to assign a given MCI patient to a risk group, the feasibility of risk stratification was tested and illustrated using Kaplan-Meier survival curves. To this end, we calculated a prognostic index (PI) as proposed by (Royston and Altman, 2013) as follows:

PIp=HRc1∗c1p+…+HRc6∗c6p

with HRci = hazard ratio corresponding to ci = covariate and PI = individual prognostic index for patient p.

The resulting continuous distribution of the PI was stratified into three equally-sized groups: corresponding to low, medium and high risk for conversion. For those three groups Kaplan-Meier survival curves were analyzed.

3. Results

Using the categorical group comparison (SPM ANCOVA), significantly decreased metabolism in converters compared to non-converters in the training dataset was observed in the parietal cortex, posterior cingulate cortex and the precuneus bilaterally (Fig. 1, red regions).

Voxel-wise Cox regressions identified an association between (earlier) conversion and hypometabolism of the bilateral temporo-parietal cortex, posterior cingulate cortex/precuneus, and frontal cortex in the training dataset (Fig. 1, cyan regions; see Fig. 2 for topography of voxel-wise HR). As shown in Fig. 1, regions identified by voxel-wise Cox regressions (66 cm3) considerably extended beyond those identified by SPM ANCOVA (6 cm3).

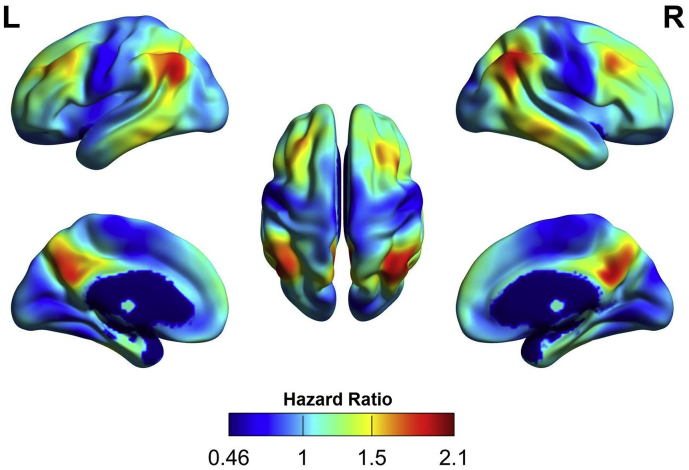
Fig. 2.

Fig. 2

Open in a new tab

Surface projection of the hazard ratios from the voxel-wise Cox model in the training dataset. Hazard ratios above one correspond to one-unit decrease in the normalized and z-scaled 18F-fluorodeoxyglucose (FDG) uptake.

For the test dataset, model 1 yielded APOE (HR = 1.6 [95% C.I.: 1.2–2.1], p < .001) and MMSE (HR = 1.24 [95% C.I.: 1.1–1.4], p < .001) as independent predictors with an Akaike information criterion (Akaike, 1974) (AIC) of 883 (Wald test (WT) p < .001).

Model 2, using only the normalized FDG uptake within the ANCOVA-ROI, also significantly predicted MCI to AD conversion with a HR = 1.35 [95% C.I.: 1.2–1.5] and AIC = 901 (WT: p < .001).

Model 3 (Cox-ROI-only) yielded comparable results with a HR = 1.29 [95% C.I.: 1.2–1.4] and AIC = 904 (WT: p < .001).

Model 4, consisting of the clinical variables and normalized FDG uptake from the ANCOVA-ROI yielded all three as independent predictors, with an AIC of 875 (WT: p < .001): FDG uptake from ANCOVA-ROI (HR = 1.2 [95% C.I.: 1.1–1.4], p < .001), APOE (HR = 1.6 [95% C.I.: 1.2–2.1], p < .001) and MMSE (HR = 1.2 [95% C.I.: 1.1–1.4], p < .003), see also Fig. 3.

Fig. 3.

Fig. 3

Open in a new tab

Resulting hazard ratios for models 4 (left) and 5 (right). All covariates have been transformed to z-scores, except for sex and APOE status which are dichotomous. The MMSE has been multiplied by −1 to yield a positive HR, in order to increase comparability.

Comparable results were found for model 5, with the normalized FDG uptake, APOE and MMSE as independent predictors (HR = 1.2 [95% C.I.: 1.1–1.3], HR = 1.6 [95% C.I.: 1.2–2.1], HR = 1.2 [95% C.I.: 1.1–1.4], respectively; all p < .001) with an AIC = 878 (WT: p < .001), see also Fig. 3.

The clinical-only model (1) was significantly improved by adding normalized FDG uptake in the ANCOVA-ROI in model 4 (relative likelihood (1) to (4): L = 0.018). Similarly, it was improved by adding normalized FDG uptake in the Cox-ROI in model 5 (at trend level, relative likelihood (1) to (5): L = 0.08).

A change between model 4 and 5 was not beneficial: relative likelihood (4) vs (5): L = 0.22.

Finally, changing from either model 2 or 3 towards model 4 or 5 yielded a strong improvement, all relative Likelihood tests yielded L < 0.001.

The prognostic value of the Cox models in the test dataset was evaluated by comparing survival curves for the three risk groups. A comparison of Fig. 4 (model 1, clinical-only) and Fig. 5 (model 4, clinical plus normalized FDG uptake on ANCOVA-ROI) showed that the inclusion of imaging data improved the separation in between the different risk groups. As indicated by median conversion times, separation of the high- from the medium-risk group was worse in model 1 (48 [95% C.I.: 35-n/a] months vs. 60 [95% C.I.: 51-n/a] months), than in model 4 (36 [95% C.I.: 27–49] months vs. 85 [95% C.I.: 60-n/a] months). Likewise, the hazard ratios of the high-risk groups were 8.1 compared to 4.9 but 3.2 and 3.4 for the median-risk group (with low-risk group as reference, see Fig. 4, Fig. 5), respectively. After about 60 months, the number of subjects left is too small to draw conclusions. Very comparable results were found for model 5 (clinical plus normalized FDG uptake on Cox-ROI), see Fig. 6.

Fig. 4.

Fig. 4

Open in a new tab

Survival curves for model 1 including only clinical covariates sex, age, MMSE score and APOE genotype. Three risk groups were defined corresponding to the lower, middle and upper thirds of subjects in the prognostic index (PI) distribution. With the low-risk group defined as reference, the hazard ratios are 3.4 [95% C.I.: 1.8–6.4, p < .001] and 4.9 [95% C.I.: 2.6–9.1, p < .001] for the medium- and high-risk group, respectively.

Fig. 5.

Fig. 5

Open in a new tab

Survival curves for model 4 including clinical covariates and normalized FDG uptake values from within the ANCOVA-ROI. Three risk groups were defined corresponding to the lower, middle and upper thirds of subjects in the PI distribution. With the low-risk group defined as reference, the hazard ratios are 3.2 [95% C.I.: 1.6–6.3, p < .001] and 8.1 [95% C.I.: 4.2–15.6, p < .001] for the medium- and high-risk group, respectively.

Fig. 6.

Fig. 6

Open in a new tab

Survival curves for model 5 including clinical covariates and normalized FDG uptake from the Cox-ROI. Three risk groups were defined corresponding to the lower, middle and upper thirds of subjects in the PI distribution. With the low-risk group defined as reference, the hazard ratios are 3.6 [95% C.I.: 1.8–7.1, p < .001] and 7.7 [95% C.I.: 4.0–14.8, p < .001] for the medium- and high-risk group, respectively.

The survival curves for models 2 and 3 can also be found in the supplementary material, see Fig. 7, Fig. 8. Both show a very good separation of the high-risk group, whereas the low- and medium-risk groups were less satisfactorily separated.

Fig. 7.

Fig. 7

Open in a new tab

Survival curves for model 2 including only normalized FDG uptake within the ANCOVA-ROI. Three risk groups were defined corresponding to the lower, middle and upper thirds of subjects in the PI distribution. With the low-risk group defined as reference, the hazard ratios are 2.2 [95% C.I.: 1.1–4.4, p < .001] and 6.8 [95% C.I.: 3.7–13, p < .001] for the medium- and high-risk group, respectively.

Fig. 8.

Fig. 8

Open in a new tab

Survival curves for model 3 with only normalized FDG uptake within the Cox-ROI. Three risk groups were defined corresponding to the lower, middle and upper thirds of subjects in the PI distribution. With the low-risk group defined as reference, the hazard ratios are 2 [95% C.I.: 1–4, p < .001] and 9.2 [95% C.I.: 4.8–17.7, p < .001] for the medium- and high-risk group, respectively.

Finally, Table 3 shows the annual conversion rates for all models and risk groups after 1, 3 and 5 years.

Table 3.

Conversion rates [%] after 1, 3 and 5 years for all models and risk groups.

Risk group Low Medium High
Time [years] 1 3 5 1 3 5 1 3 5
Model 1 3.5 8.6 13.1 7.9 33.3 52.8 15.8 41.9 63.2
2 4.6 9.9 19.7 4.6 22.2 29.4 18.2 50.2 78.4
3 4.6 9.6 15.2 3.4 17.2 29.6 19.3 56.1 89.1
4 3.4 9.9 19.7 5.7 22.2 29.4 18.0 50.2 78.4
5 3.4 6.0 10.2 6.9 27.3 46.4 16.7 50.2 76.0
Open in a new tab

4. Discussion

In the present study, voxel-wise Cox regression identified brain regions for which decreased metabolism was significantly associated with MCI to AD conversion. This pattern included the hypometabolic clusters derived from the reference method (ANCOVA SPM), but was more widespread and (at the same selected significance threshold) also involved the frontal cortex. The identified conversion-related brain regions (Fig. 1), including frontal cortex, coincided with the well-established regions of cerebral hypometabolism in MCI (Dukart et al., 2013) and AD (Bohnen et al., 2012; Langbaum et al., 2009). Although the Cox-ROI was noticeably larger than the ANCOVA-ROI, both covered similar brain regions and the normalized FDG uptake within the two regions was highly correlated. Consequently, the Cox model pairs 2 and 3 as well as 4 and 5 in the test dataset led to comparable results, respectively. Apparently, the classical group comparison already identified the most relevant areas, and the additional information contained in the slightly larger Cox-ROI had no added value concerning the prediction of conversion to AD. Therefore, the inclusion of observation time information via voxel-wise Cox regression, used to identify the Cox-ROI, was not superior to traditional group contrasts for identification of conversion-related regions.

Of note, the prognosis of conversion to AD by APOE genotype and MMSE score was significantly improved when imaging information (normalized FDG uptake based on either method) was included.

Identification of conversion-related hypometabolism in frontal regions might indicate greater sensitivity of the Cox regression method. However, notably the predictive power of models including the Cox regression-derived FDG uptake (and hence frontal metabolism) was not superior to those including FDG uptake from conventionally derived regions (excluding frontal regions), which might also indicate that frontal regions play only a minor role in conversion to AD.

The applied stratification into risk groups based on the calculated prognostic index has the advantage of individual predictions of conversion probability within arbitrarily chosen time frames (e.g., 1, 3, or 5 years, see Table 3). This might be of value for patient counseling in clinical routine.

Limitations for the Cox regression method, as applied in both datasets, include the fact that the set of chosen predictor variables was not comprehensive: For instance, it did not include information about beta-amyloid or tau from PET imaging, cerebrospinal fluid (CSF), or structural information from MRI. Also, more detailed cognitive performance data (e.g. Montreal Cognitive Assessment, which has not been available for about half of the patients in this study) might be important covariates. In addition, comorbid diseases like vascular pathologies may both obscure and mimic an AD-pathology.

However, the current study aimed at testing the method of voxel-wise Cox regressions and hence results were only compared to those of conventional group contrasts and adjusted for commonly used clinical covariates.

Concerning the predictive value of FDG PET in the context of MCI to AD conversion, the literature shows a large heterogeneity. While the current study and Lange et al. (2015) found a significant predictive value for FDG PET within the ADNI data, others did not (Schmand et al., 2012; Trzepacz et al., 2014). Beyond differences in employed methods, reasons for this obvious discrepancy might be different subsets of the constantly growing ADNI sample, based on the time of download and inclusion criteria. This is apparent when comparing annual conversion rates of different ADNI samples: while the current study used a dataset with an annual conversion rate of 8.7%, in (Landau et al., 2010) it was 17.2%, in (Trzepacz et al., 2014) even 20% and (Lange et al., 2017, Lange et al., 2015) report about 9.5% and 6.3%, respectively. It has been pointed out that the ADNI database does not represent the general population (Whitwell et al., 2012). Therefore, the predictive value of FDG PET that we found might not necessarily apply to other samples tested. In line with this, smaller studies (Grimmer et al., 2016; Trzepacz et al., 2014), (Frings et al., 2018) did not support this, although a meta-analysis of (Frisoni et al., 2013) showed a clear advantage of FDG PET for conversion prediction over other modalities.

5. Conclusions

We demonstrated that voxel-wise Cox regression can be used to identify MCI to AD conversion-related patterns of cerebral glucose metabolism, but does not outperform classical group contrasts in this regard. With imaging information from these patterns on FDG PET, the prediction of conversion to AD was improved in the ADNI dataset.

The following are the supplementary data related to this article.

Acknowledgments

Acknowledgements

Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Lumosity; Lundbeck; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.

Conflict of interest

The authors declare that they have no conflict of interest.

Ethical approval

All procedures performed in studies involving human participants were in accordance with the ethical standards of the institutional and/or national research committee and with the 1964 Helsinki declaration and its later amendments or comparable ethical standards.

References

  1. Akaike H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 1974;19:716–723. [Google Scholar]
  2. Ambler G. mfp: Multivariable Fractional Polynomials. 2015. (original) and modified by A. Benner. [Google Scholar]
  3. Bohnen N.I., Djang D.S.W., Herholz K., Anzai Y., Minoshima S. Effectiveness and safety of 18F-FDG PET in the evaluation of dementia: a review of the recent literature. J. Nucl. Med. 2012;53:59–71. doi: 10.2967/jnumed.111.096578. [DOI] [PubMed] [Google Scholar]
  4. Chen K., Ayutyanont N., Langbaum J.B.S., Fleisher A.S., Reschke C., Lee W., Liu X., Bandy D., Alexander G.E., Thompson P.M., Shaw L., Trojanowski J.Q., Jack C.R., Landau S.M., Foster N.L., Harvey D.J., Weiner M.W., Koeppe R.A., Jagust W.J. Characterizing Alzheimer's disease using a hypometabolic convergence index. NeuroImage. 2011;56:52–60. doi: 10.1016/j.neuroimage.2011.01.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cox D.R. Regression models and life-tables. J. R. Stat. Soc. 1972;34:187–220. [Google Scholar]
  6. Drzezga A., Grimmer T., Riemenschneider M., Lautenschlager N., Siebner H., Alexopoulus P., Minoshima S., Schwaiger M., Kurz A. Prediction of individual clinical outcome in MCI by means of genetic assessment and (18)F-FDG PET. J. Nucl. Med. 2005;46:1625–1632. https://doi.org/46/10/1625 [pii] [PubMed] [Google Scholar]
  7. Dukart J., Mueller K., Villringer A., Kherif F., Draganski B., Frackowiak R., Schroeter M.L. Relationship between imaging biomarkers, age, progression and symptom severity in Alzheimer's disease. NeuroImage Clin. 2013;3:84–94. doi: 10.1016/j.nicl.2013.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Frings L., Hellwig S., Bormann T., Spehl T.S., Buchert R., Meyer P.T. Amyloid load but not regional glucose metabolism predicts conversion to Alzheimer's dementia in a memory clinic population. Eur. J. Nucl. Med. Mol. Imaging. 2018 doi: 10.1007/s00259-018-3983-6. [DOI] [PubMed] [Google Scholar]
  9. Frisoni G.B., Bocchetta M., Chetelat G., Rabinovici G.D., de Leon M.J., Kaye J., Reiman E.M., Scheltens P., Barkhof F., Black S.E., Brooks D.J., Carrillo M.C., Fox N.C., Herholz K., Nordberg A., Jack C.R., Jagust W.J., Johnson K.A., Rowe C.C., Sperling R.A., Thies W., Wahlund L.-O., Weiner M.W., Pasqualetti P., Decarli C. Imaging markers for Alzheimer disease: which vs how. Neurology. 2013;81:487–500. doi: 10.1212/WNL.0b013e31829d86e8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Friston K.J., Ashburner J., Kiebel S., Nichols T., Penny W.D. Elsevier/Academic Press; 2007. Statistical Parametric Mapping : The Analysis of Funtional Brain Images. [Google Scholar]
  11. Gray K.R., Wolz R., Heckemann R.A., Aljabar P., Hammers A., Rueckert D. Multi-region analysis of longitudinal FDG-PET for the classification of Alzheimer's disease. NeuroImage. 2012;60:221–229. doi: 10.1016/j.neuroimage.2011.12.071. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Grimmer T., Wutz C., Alexopoulos P., Drzezga A., Forster S., Forstl H., Goldhardt O., Ortner M., Sorg C., Kurz A. Visual versus fully automated analyses of 18F-FDG and amyloid PET for prediction of dementia due to Alzheimer disease in mild cognitive impairment. J. Nucl. Med. 2016;57:204–207. doi: 10.2967/jnumed.115.163717. [DOI] [PubMed] [Google Scholar]
  13. Landau S.M., Harvey D., Madison C.M., Reiman E.M., Foster N.L., Aisen P.S., Petersen R.C., Shaw L.M., Trojanowski J.Q., Jack C.R., Weiner M.W., Jagust W.J. Comparing predictors of conversion and decline in mild cognitive impairment. Neurology. 2010;75:230–238. doi: 10.1212/WNL.0b013e3181e8e8b8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Langbaum J.B.S., Chen K., Lee W., Reschke C., Bandy D., Fleisher A.S., Alexander G.E., Foster N.L., Weiner M.W., Koeppe R.A., Jagust W.J., Reiman E.M. Categorical and correlational analyses of baseline fluorodeoxyglucose positron emission tomography images from the Alzheimer's Disease Neuroimaging Initiative (ADNI) NeuroImage. 2009;45:1107–1116. doi: 10.1016/j.neuroimage.2008.12.072. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Lange C., Suppa P., Frings L., Brenner W., Spies L., Buchert R. Optimization of statistical single subject analysis of brain FDG PET for the Prognosis of mild cognitive impairment-to-Alzheimer's disease conversion. J. Alzheimers Dis. 2015;49:945–959. doi: 10.3233/JAD-150814. [DOI] [PubMed] [Google Scholar]
  16. Lange C., Suppa P., Pietrzyk U., Makowski M.R., Spies L., Peters O., Buchert R. Prediction of Alzheimer's dementia in patients with amnestic mild cognitive impairment in clinical routine: incremental value of biomarkers of neurodegeneration and brain amyloidosis added stepwise to cognitive status. J. Alzheimers Dis. 2017;61:373–388. doi: 10.3233/JAD-170705. [DOI] [PubMed] [Google Scholar]
  17. Morbelli S., Garibotto V., Van De Giessen E., Arbizu J., Chételat G., Drezgza A., Hesse S., Lammertsma A.A., Law I., Pappata S., Payoux P., Pagani M. A Cochrane review on brain [18F]FDG PET in dementia: limitations and future perspectives. Eur. J. Nucl. Med. Mol. Imaging. 2015;42:1487–1491. doi: 10.1007/s00259-015-3098-2. [DOI] [PubMed] [Google Scholar]
  18. Prestia A., Caroli A., Wade S.K., van der Flier W.M., Ossenkoppele R., Van Berckel B., Barkhof F., Teunissen C.E., Wall A., Carter S.F., Schöll M., Choo I.H., Nordberg A., Scheltens P., Frisoni G.B. Prediction of AD dementia by biomarkers following the NIA-AA and IWG diagnostic criteria in MCI patients from three European memory clinics. Alzheimers Dement. 2015;11:1191–1201. doi: 10.1016/j.jalz.2014.12.001. [DOI] [PubMed] [Google Scholar]
  19. Royston P., Altman D.G. External validation of a Cox prognostic model: principles and methods. BMC Med. Res. Methodol. 2013;13:33. doi: 10.1186/1471-2288-13-33. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Schmand B., Eikelenboom P., van Gool W.A., Alzheimer's Disease Neuroimaging Initiative Value of diagnostic tests to predict conversion to Alzheimer's disease in young and old patients with amnestic mild cognitive impairment. J. Alzheimers Dis. 2012;29:641–648. doi: 10.3233/JAD-2012-111703. [DOI] [PubMed] [Google Scholar]
  21. Smailagic N., Vacante M., Hyde C., Martin S., Ukoumunne O., Sachpekidis C. 18 F-FDG PET for the early diagnosis of Alzheimer's disease dementia and other dementias in people with mild cognitive impairment (MCI) Cochrane Database Syst. Rev. 2015 doi: 10.1002/14651858.CD010632.pub2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Team, R Core . 2017. R: A Language and Environment for Statistical Computing. [Google Scholar]
  23. Torosyan N., Mason K., Dahlbom M., Silverman D.H.S. Value of FDG-PET scans of non-demented patients in predicting rates of future cognitive and functional decline. Eur. J. Nucl. Med. Mol. Imaging. 2017;44:1355–1363. doi: 10.1007/s00259-017-3634-3. [DOI] [PubMed] [Google Scholar]
  24. Trzepacz P.T., Yu P., Sun J., Schuh K., Case M., Witte M.M., Hochstetler H., Hake A. Comparison of neuroimaging modalities for the prediction of conversion from mild cognitive impairment to Alzheimer's dementia. Neurobiol. Aging. 2014;35:143–151. doi: 10.1016/j.neurobiolaging.2013.06.018. [DOI] [PubMed] [Google Scholar]
  25. Vemuri P., Weigand S.D., Knopman D.S., Kantarci K., Boeve B.F., Petersen R.C., Jack C.R. Time-to-event voxel-based techniques to assess regional atrophy associated with MCI risk of progression to AD. NeuroImage. 2011;54:985–991. doi: 10.1016/j.neuroimage.2010.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Whitwell J.L., Wiste H.J., Weigand S.D., Rocca W.A., Knopman D.S., Roberts R.O., Boeve B.F., Petersen R.C., Jack C.R., Alzheimer Disease Neuroimaging Initiative Comparison of imaging biomarkers in the Alzheimer Disease Neuroimaging Initiative and the Mayo Clinic Study of Aging. Arch. Neurol. 2012;69:614–622. doi: 10.1001/archneurol.2011.3029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zeifman L.E., Eddy W.F., Lopez O.L., Kuller L.H., Raji C., Thompson P.M., Becker J.T. Voxel level survival analysis of grey matter volume and incident mild cognitive impairment or Alzheimer's disease. J. Alzheimers Dis. 2015;46:167–178. doi: 10.3233/JAD-150047. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from NeuroImage : Clinical are provided here courtesy of Elsevier

RESOURCES