Abstract
This study examines the atrophy rates of subjects with mild cognitive impairment (MCI) compared to controls in four regions within the medial temporal lobe: the transentorhinal cortex (TEC), entorhinal cortex (ERC), hippocampus, and amygdala. These regions were manually segmented and then corrected for undesirable longitudinal variability via Large Deformation Diffeomorphic Metric Mapping (LDDMM) based longitudinal diffeomorphometry. Diffeomorphometry techniques were used to compare thickness measurements in the TEC with the ERC. There were more significant changes in thickness atrophy rate in the TEC than medial regions of the entorhinal cortex. Volume measures were also calculated for all four regions. Classifiers were constructed using linear discriminant analysis to demonstrate that average thickness and atrophy rate of TEC together was the most discriminating measure compared to the thickness and volume measures in the areas examined, in differentiating MCI from controls. These findings are consistent with autopsy findings demonstrating that initial neuronal changes are found in TEC before spreading more medially in the ERC and to other regions in the medial temporal lobe. These findings suggest that the TEC thickness could serve as a biomarker for Alzheimer's disease in the prodromal phase of the disease.
Keywords: Entorhinal cortex, Transentorhinal cortex, Mild cognitive impairment, Braak staging, Cortical thickness, Shape analysis, Longitudinal analysis
Highlights
-
•
The transentorhinal cortex is significantly thinner in subjects with mild cognitive impairment than controls.
-
•
Mildly cognitively impaired subjects show a significantly greater atrophy rate in the transentorhinal cortex than controls.
1. Background
Current research criteria for a diagnosis of mild cognitive impairment (MCI) or dementia due to Alzheimer's disease (AD) recommend the use of biomarkers to improve the accuracy of diagnosis. These recommendations include the use of imaging biomarkers, but emphasize the importance of developing additional more sensitive and specific imaging markers for AD (Albert et al., 2011; McKhann et al., 2010). Braak's neuropathological staging of AD proposes that accumulation of pathology first begins in the transentorhinal cortex (TEC) before spreading along the lamina to the medial regions of the entorhinal cortex (ERC) and subsequently involves the hippocampus and amygdala (Braak and Braak, 1991). These findings are supported by other autopsy studies that indicate that well-characterized subjects in the early phases of AD demonstrate neuronal loss in selective layers of the ERC and TEC (Gómez-Isla et al., 1996; Kordower et al., 2001; Price et al., 2001). This neuronal loss and injury can be indirectly measured through the analysis of structural magnetic resonance imaging (MRI) (Atiya et al., 2003; Kantarci and Jack Jr, 2004). ERC atrophy as measured on structural MRI scans has been associated with greater clinical disease severity (Devanand et al., 2007; Kerchner et al., 2012; La Joie et al., 2012; Miller et al., 2013) impairment on memory tests (Varon et al., 2011), and are predictive of progression from normal cognition to MCI (Younes et al., 2014). In addition, numerous MRI studies have shown an association of hippocampal atrophy associated with disease severity (Csernansky et al., 2005; Devanand et al., 2007; Kerchner et al., 2012; La Joie et al., 2012; Platero et al., 2018). In comparison, relatively few MRI studies have distinguished the TEC from the ERC or have examined the amygdala (Miller et al., 2015b; Miller et al., 2012). From the few recent studies on transentorhinal atrophy, there is evidence of a correlation between neurofibrillary tangle (NFT) burden measured from PET and atrophy rate measured from MRI in the transentorhinal cortex, as well as enhanced discrimination from healthy controls and early stages of AD using transentorhinal atrophy (Wolk et al., 2017; Xie et al., 2018a). In previous work (Tward et al., 2017b), we found significant thickness and volume differences in the TEC of MCI subjects. In this study, we have introduced a new, unbiased, low variance method for estimating the thickness and curvature of the laminar neocortex based on diffeomorphic flows. This has allowed us to further investigate the differences in the local change of the volume measure by separating the detection of baseline differences from differences in atrophy rate and incorporating a protocol that provides measures of absolute thickness in addition to changes in thickness. Furthermore, we examine four regions of interest in this population to put our findings in context of the wealth of studies performed on the hippocampus: the TEC, the ERC, the hippocampus, and the amygdala.
The field of computational anatomy has worked to establish quantitative, robust structural imaging biomarkers for neurodegenerative disease (Grenander and Miller, 1998). Evidence of neuronal loss in the ERC and accumulation of pathology within the TEC motivate a local, laminar study of this region. However, segmentation of the ERC and TEC presents two technical hurdles. First, the proximity of the meninges and oculomotor nerve make accurate automated segmentation of the ERC difficult. Here we address this following a protocol to manually segment and then automatically correct for undesirable longitudinal variability in segmentation boundaries through a technique called longitudinal diffeomorphometry (Tward et al., 2017b). The second hurdle results from the difficulty in accurately and consistently measuring distances across curved manifolds in the human cortex. We utilize a method that maps the pial surface to the grey matter-white matter boundary surface along a flow of diffeomorphisms constrained to move in a direction normal to the surface (Ratnanather et al., 2018). Here we assess local changes in cortical thickness over time and compute the atrophy rate and spatial distribution of these changes in the ERC and TEC separately. Different atrophy rates between groups were identified using permutation testing and high field atlasing of the regions of interest.
2. Methods
2.1. Data collection
Data was obtained from the ADNI database (adni.loni.usc.edu). Subjects in this study were selected for having at least 3 time points over 2 years with 3 T MRI scans, typically scanned at 6, 12, and 24 months after baseline. Inclusion criteria for subjects with MCI included evidence of impaired performance on the Logical Memory Subtest of the Wechsler Memory Scale (based on age and education adjusted norms) and a score of ≥0.5 on the clinical dementia rating scale (CDR). MCI subjects were all selected to be amyloid β positive based on cerebrospinal fluid cutoff values established by the ADNI Biospecimen Core (i.e., less than a cutoff score of 192 pg/mL) and between 55 and 85 years old.
The criteria for control status in ADNI included evidence of performance within the normal range on the Logical Memory Subtest of the Wechsler Memory Scale (based on age and education adjusted norms), a baseline score of CDR = 0, and the absence of a diagnosis of MCI or dementia. Control subjects were included only if they were amyloid β negative (greater than a cutoff of 192 pg/mL). In total, 35 subjects with MCI and 21 control subjects were selected. Their baseline demographics are summarized in Table 1.
Table 1.
Baseline demographic information for control and MCI groups with mean ± standard deviation.
| Parameter | Control | MCI | P⁎⁎ |
|---|---|---|---|
| Number | 21 | 35 | |
| Age (years) | 71.0 ± 5.42 | 71.0 ± 7.2 | 0.995 |
| Sex (% female) | 61.9% | 57.1% | 0.732 |
| CDR-SB | 0 ± 0 | 1.6 ± 0.76 | <0.0001 |
| Mini-Mental State Examination | 29.6 ± 0.5 | 27.1 ± 1.6 | <0.0001 |
| WMS⁎ Logical Memory (Immediate) | 15.2 ± 2.8 | 7.2 ± 3.5 | <0.0001 |
| WMS Logical Memory (Delayed) | 14.4 ± 2.7 | 3.1 ± 2.6 | <0.0001 |
| Follow-up Period (years) | 2.02 ± 0.07 | 1.75 ± 0.45 | 0.573 |
⁎Wechsler Memory Scale, ⁎⁎p-values of group comparisons using a two-sample t-test.
2.2. High field atlasing for coordinatizing the medial temporal lobe
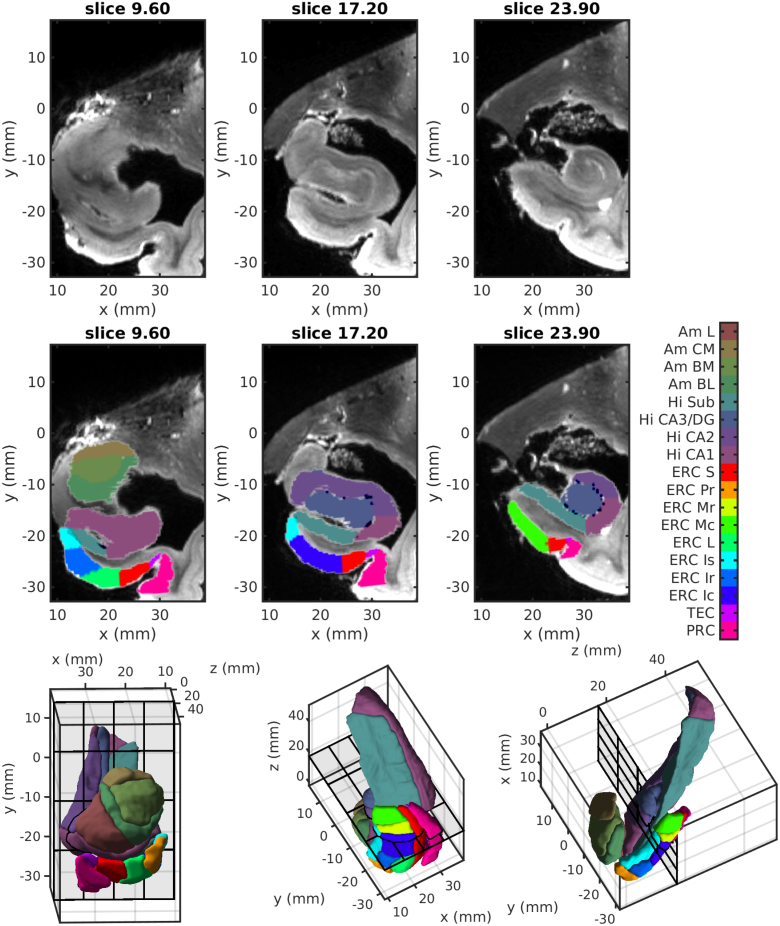
To label structures of interest on the MRI images in this study, we utilized a high field strength (11 T) MRI as depicted in Fig. 1. We used partitions defined by Krimer et al. (Krimer et al., 1997) to guide the boundaries for our measurements of the ERC. This Krimer partition, as it is referred to through out this paper, divides the ERC into 9 subregions. This framework was used to construct the lateral to medial coordinates for the 9 subregions, using an established protocol (Insausti et al., 1998; Krimer et al., 1997; Miller et al., 2015a). MRI studies of the ERC typically define the lateral boundary of the ERC at the apex of the gyrus (Devanand et al., 2007; Kerchner et al., 2012; La Joie et al., 2012; Miller et al., 2013; Varon et al., 2011; Younes et al., 2014), whereas histological studies typically extend past the apex (Gómez-Isla et al., 1996; Kordower et al., 2001; Price et al., 2001). In this study, we define the following 7 Krimer regions together as the ERC: (1) intermediate superior, (2) intermediate rostral, (3) intermediate caudal, (4) prorhinal, (5) medial rostral, (6) medial caudal, and (7) lateral. This definition corresponds well to how the ERC is typically defined for most MRI studies. We define the Krimer sulcal and transentorhinal regions together as the TEC; these are the sections often not included in prior MRI studies. We map the region from the subjects onto this atlas using the LDDMM framework (Beg et al., 2005) to visualize and evaluate subregional thickness. All thickness results in the ERC and TEC are shown projected onto the high field atlas of Fig. 1 to localize information within the subregions.
Fig. 1.
Top row: Coronal views of the high-field atlas from anterior (left) to posterior (right) in Mai coordinates (Mai et al., 2007). Middle row: Segmentations superimposed on the high-field atlas views. Bottom row: High-field 3D model of ERC, hippocampus, and amygdala. On the left is a coronal view with the subject facing forward; middle is an axial view from the inferior side with the subject facing down; right is a sagittal view from the medial side with the subject facing down. Krimer regions of ERC: Transentorhinal cortex (TEC), Sulcal ERC (ERC S), Intermediate Superior ERC (ERC Is), Intermediate Rostral ERC (ERC Ir), Intermediate Caudal ERC (ERC Ic), Prorhinal ERC (ERC Pr), Medial rostral ERC (ERC Mr), Medial caudal ERC (ERC Mc), and Lateral ERC (ERC L).
2.3. Manual segmentation and surface-based morphometry
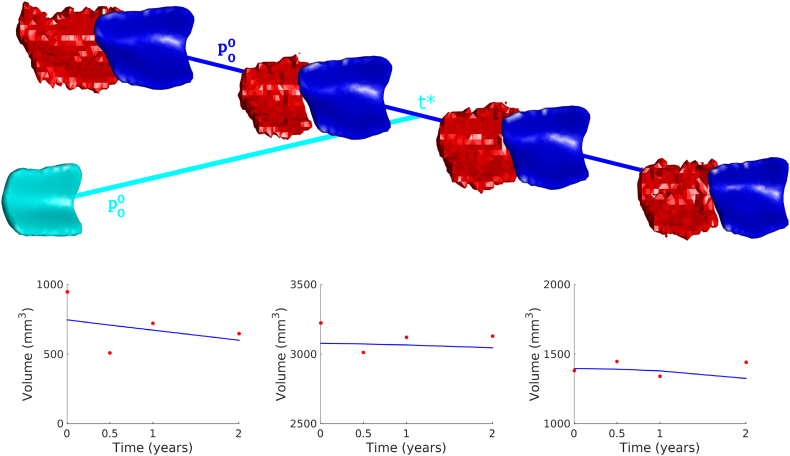
We followed an established procedure for segmentation and delineation of the ERC and TEC (Tward et al., 2017b). Most subjects examined had a continuous collateral sulcus in the left hemisphere, whereas a higher proportion had a discontinuous collateral sulcus in the right hemisphere. Given the goals of the current analyses, we restricted the analysis to the left hemisphere and excluded subjects with a discontinuity in the left collateral sulcus. Manual segmentations for 35 MCI subjects that met the criteria were completed in alphanumerical order, with priority given to subjects with 4 scan times. ERC and TEC were segmented manually by one expert (C.S.) and reviewed by another expert (T.B.) using the Seg3D software (Center for Integrative Biomedical Computing, 2016). For hippocampus and amygdala segmentations, we processed the same subjects through an automated segmentation pipeline called MRICloud (Mori et al., 2016) using a set of 26 adult atlases specifically for 50–90 year old adults. The atlases were fused following a previously established label fusion algorithm (Wang et al., 2013). Left hippocampus and left amygdala segmentations were extracted and manually corrected by an expert (T.B.) using neuroanatomical boundaries previously described (Csernansky et al., 1998; Miller et al., 2013; Munn et al., 2007). All regions were adjusted for variability in segmentation boundaries over time by mapping a population template simultaneously onto each scan of a time series as shown in Fig. 1. The template surface is estimated as a triangulated mesh from the population of controls and MCI subjects (Ma et al., 2008). Denote this mesh representation as q(i) ∈ ℝ3, i = 1, …, N, a collection of vertices representing points in 3D-space with smoothly varying normals, and we denote qkobserved as a subject's mesh at time tk, where k = 1, …, M indexes through scans of a subject. Each region's population template was mapped onto each subjects time-series as follows. First, the template was deformed to a subject-specific average mesh at an average time t∗, not necessarily one of the observed scan times. Second, it was deformed along a continuous geodesic trajectory (Miller et al., 2006), both forwards and backwards in time, to closely match each of the observed segmentations. The three parameters, consisting of the subject specific map, the average time t∗, and the continuous trajectory, were all estimated simultaneously by maximizing a penalized log-likelihood (Tward and Miller, 2017a). Fig. 2 shows an example of volumes obtained from manual segmentations of a subject and volumes obtained after longitudinal diffeomorphometry.
Fig. 2.
Geodesic longitudinal diffeomorphometry matching the template (cyan) onto the set of surfaces (red) and depicting the deformed smooth surfaces (blue). Volumetric fits using longitudinal diffeomorphometry (blue) on manual segmentations (red) for the ERC plus TEC (left), hippocampus (middle), and amygdala (right) are shown. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The deformations are generated as a flow of diffeomorphisms . The vector field vt is generated to be smooth using a Gaussian kernel K(⋅, ⋅) with a standard deviation of 5mm according to:
| (1) |
Here, the Hamiltonian momentum pt and deforming surface vertices q satisfies the Euler-Lagrange equations for initial conditions q0 = initial mesh:
| (2) |
We motivate our method using an analogy to linear regression, “y(t) = aΔt + b”, where i) b represents a shift from the origin and ii) aΔt represents a time-dependent shift from b. In our case, shifts are replaced by geodesic flows of Eqs. (1), (2), with resulting deformations combined using composition ∘ rather than vector addition. We i) define ϕp00 as the diffeomorphism generated with initial conditions q0 and p00, which plays a role analogous to “b”. We ii) define ϕp01Δt as the diffeomorphism generated with initial conditions ϕp00(q0) and p01Δt, which plays a role analogous to “aΔt”. In particular, our template is deformed to match observed data at time tk according to ϕp01Δtk ∘ ϕp00(q0), where Δtk = tk − t∗. We estimate the parameters p00, p01, and t∗ by minimizing the cost:
| (3) |
with
| (4) |
We chose this specific form of cost function because it is the same as used in population template estimation (Ma et al., 2010), with the added constraint that each deformed surface lies along a single geodesic trajectory. This type of procedure is often called geodesic regression (Fletcher, 2013). The volume of a structure – amygdala, ERC, hippocampus – is calculated from the set of faces of the surface. To calculate volume, let F be the number of faces where the f-th face is defined as a set of three vertices {vf, 1, vf, 2, vf, 3} and vertex v ∈ ℝ3: .
2.4. Cortical thickness of TEC and ERC
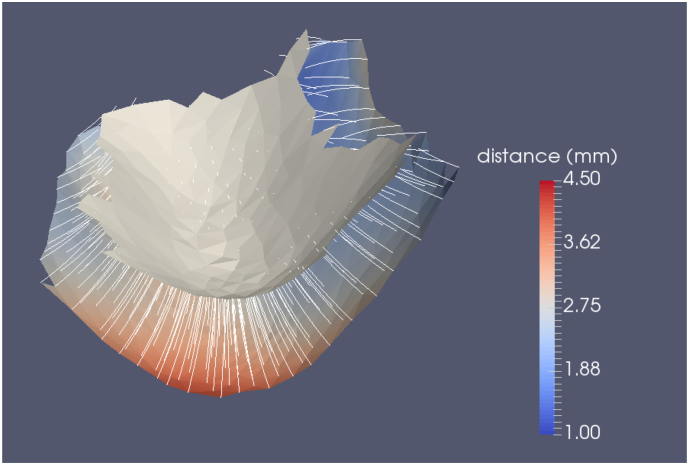
For estimating the cortical thickness of the ERC and TEC, we used LDDMM to generate a normal geodesic flow of the pial surface to the grey matter-white matter boundary surface. The ERC plus TEC surface template calculated in the previous section is manually cut into two surfaces: the pial surface and the grey matter-white matter boundary surface. Specifically, the boundaries were defined using dynamic programming to find the shortest geodesic path between user-defined landmarks (Ratnanather et al., 2003). Landmarks were chosen to be the points spaced along the inferior and superior sides of the surface at the most lateral, medial, rostral and caudal extents. These two surface cuts were then mapped to subjects using the diffeomorphic mapping described in the previous section. One surface is then deformed to the other surface within the constrained LDDMM framework (Arguillère et al., 2015) with an additional imposed constraint that the surface must flow in the direction normal to its current surface. For details on implementation, please see (Ratnanather et al., 2018). Local cortical thickness is then estimated as the distance a vertex travels along the trajectory of this surface deformation as shown in Fig. 3. Due to variability of measures along the boundary, we excluded distance measures on vertices at boundary of surface cuts. A paired t-test was performed on average TEC thickness versus average ERC thickness in controls. A one-way ANCOVA were conducted on baseline TEC thickness and baseline ERC thickness to determine statistically significant differences between diagnostic groups while controlling for age and sex. Finally, Spearman rank correlation tests were performed on TEC thickness and ERC thickness stratified by CDR Sum of Boxes (CDR-SB) and results were corrected for multiple comparisons using a Bonferroni correction.
Fig. 3.
Generation of normal coordinates via the pial surface (colored) as it is deformed to the grey matter-white matter boundary surface (grey) along the normal constraints. The vertex paths are shown in white. The geodesic distance defining the cortical thickness measured at each surface vertex is calculated along the normal geodesic flow shown in color on pial surface.
2.5. Mixed effects modeling
The log-linear mixed effects model under the null hypothesis can be written as Eq. (5) and Eq. (6) for thickness and volume, respectively.
| (5) |
| (6) |
with subject i, scan j, and vertex k. The constants μ, δ, α, β, γ and the variance of ei, k are estimated by maximum likelihood. The variable ei, k is the subject-specific random effect from a 0-mean Gaussian distribution, which explains correlations between measurements of the same subject over time. Including between-subject variability as a random effect allows us to separate cross-sectional variability (subject-specific differences from the population average, independent of time) from longitudinal effects. The variables εi, j, k is independent identically distributed Gaussian noise, isFemalei is a binary variable indicating sex of subject i, ICV is the intracranial volume, and Δtj is the change in time since a subject's baseline scan. Age, sex, and intracranial volume were treated as fixed effects.
We first test whether a model including diagnostic groups to modulate cross-sectional differences and differences in atrophy rate fit the data significantly better than the model under the null hypothesis. The model under the alternate hypothesis can be written as Eq. (7) and Eq. (8) for thickness and volume, respectively.
| (7) |
| (8) |
where isMCIi is a binary variable indicating diagnostic group of subject i. We use a likelihood ratio test statistic and permutation testing on the residuals with 10,000 permutations and correct for multiple comparisons using the maximum test statistic to control familywise error rate at 5% as shown (Nichols and Hayasaka, 2003).
We then visualized diagnostic group-dependent effects on thickness and volume under the alternate hypothesis as shown in Eq. (9) and Eq. (10) for average thickness over vertices and volume, respectively.
| (9) |
| (10) |
where the bar indicates average baseline value over all subjects.
If the alternate model proved to be a significantly better fit for the data than the null model, we follow up with two hypothesis tests. First, we determine whether there were significant cross-sectional diagnostic group differences at baseline and how much they differ by testing the alternate model in Eq. (7) and Eq. (8) against a new null hypothesis, setting μ′ = 0 in Eq. (7) and Eq. (8). Next, we determined whether there were significant diagnostic group differences in atrophy rate and how much they differ by testing the alternate model in Eq. (7) and Eq. (8) against another null hypothesis, setting δ′ = 0 in Eq. (7) and Eq. (8). We then correct for testing these two hypotheses with a Bonferroni correction. Note that the value δ + δ′ isMCI is related to annual atrophy rate percentage by the following equation:
| (11) |
For small values this can be approximated as:
| (12) |
2.6. Comparison of diagnostic accuracy using imaging measures
A comparison of the accuracy with which the two groups could be distinguished from one another based on measures from baseline and the linear rate of change was evaluated for the following measures: (1) TEC thickness, (2) ERC thickness, (3) ERC thickness plus TEC thickness, (4) ERC volume plus TEC volume, (5) hippocampal volume, (6) amygdalar volume. Linear discriminant analysis was also conducted in which all the available measures (e.g., thickness measures and volume measures) were combined to determine which measures provided complementary information in classification. Leave-one-out linear discriminant analysis was performed on all combinations of N − 1 subjects as training data to classify the remaining 1 subject into a diagnostic group. Sensitivity and specificity were calculated as the rate of true positives and true negatives, respectively, over all the combinations.
3. Results
3.1. Cross-sectional differences of cortical thickness and volume
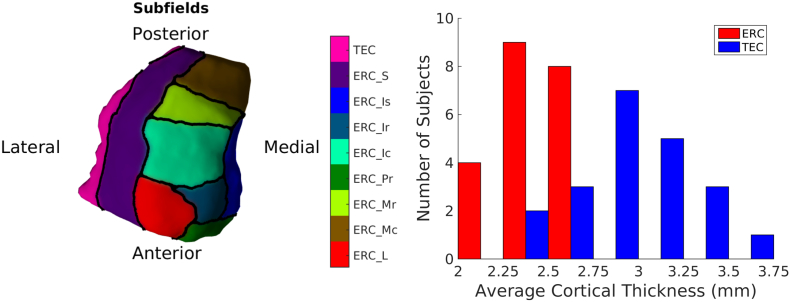
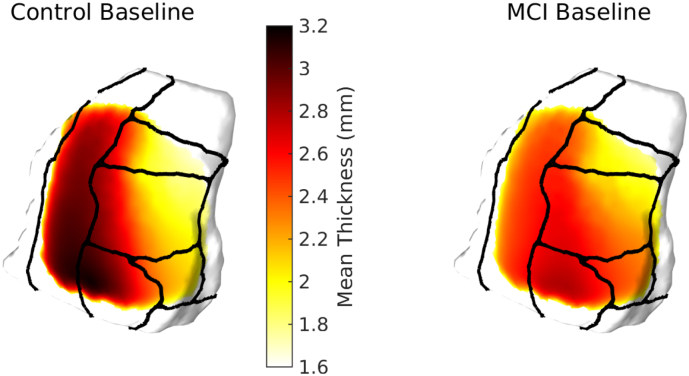
Cortical thickness and volume stratified by scan time are found in Table 2 and Table 3, respectively. Results show that the cortical thickness is not uniform across the ERC and TEC in controls. The histogram of cortical thickness measured at each vertex stratified by ERC and TEC shows that the control population has a markedly thicker TEC than the ERC (Fig. 4). A paired t-test on baseline average TEC thickness versus average ERC thickness in control subjects rejected the null hypothesis with p ≪ 0.0001, showing that at baseline, control participants had a significantly larger average TEC thickness compared to average ERC thickness. Fig. 5 shows the average TEC and ERC thickness of the control group and the MCI group. Note that after excluding vertices on the surface boundary and mapping to the 11 T high-field atlas, there are regions with no cortical thickness data (indicated in white in Fig. 5).
Table 2.
Cortical thickness by scan time (Mean ± standard deviation in mm, mean difference from baseline in parenthesis).
| Region | Diagnosis | 0 | Scan |
time |
(months) |
24 |
|---|---|---|---|---|---|---|
| 6 | 12 | 18 | ||||
| TEC | Control | 2.96 ± 0.32 | 2.95 ± 0.32 | 2.93 ± 0.33 | 2.90 ± 0.34 | |
| (−0.0189) | (−0.0364) | (−0.0668) | ||||
| MCI | 2.47 ± 0.28 | 2.42 ± 0.27 | 2.38 ± 0.27 | 2.45 ± 0.05 | 2.24 ± 0.23 | |
| (−0.0463) | (−0.0896) | (−0.1041) | (−0.1761) | |||
| ERC | Control | 2.43 ± 0.16 | 2.42 ± 0.17 | 2.40 ± 0.18 | 2.37 ± 0.22 | |
| (−0.0165) | (−0.0322) | (−0.0603) | ||||
| MCI | 2.46 ± 0.27 | 2.42 ± 0.26 | 2.38 ± 0.25 | 2.33 ± 0.34 | 2.28 ± 0.26 | |
| (−0.0426) | (−0.0826) | (−0.0428) | (−0.1642) |
Table 3.
Volume by scan time (Mean ± standard deviation in mm3, mean difference from baseline in parenthesis).
| Region | Diagnosis | 0 | Scan |
time |
(months) |
24 |
|---|---|---|---|---|---|---|
| 6 | 12 | 18 | ||||
| ERC + TEC | Control | 1093 ± 266 | 1087 ± 271 | 1080 ± 277 | 1066 ± 290 | |
| (−6.45) | (−13.2427) | (−27.5562) | ||||
| MCI | 860 ± 230 | 832 ± 219 | 803 ± 211 | 790 ± 165 | 736 ± 196 | |
| (−28.5095) | (−57.8032) | (6.1131) | (−90.3126) | |||
| Hippocampus | Control | 2935 ± 412 | 2924 ± 409 | 2911 ± 408 | 2891 ± 417 | |
| (−11.3376) | (−24.0392) | (−47.5090) | ||||
| MCI | 2705 ± 438 | 2692 ± 430 | 2673 ± 426 | 2692 ± 520 | 2586 ± 407 | |
| (−13.1303) | (−32.0696) | (23.8482) | (−83.3799) | |||
| Amygdala | Control | 1409 ± 212 | 1412 ± 217 | 1408 ± 220 | 1378 ± 225 | |
| (2.9082) | (−1.7) | (−31.6153) | ||||
| MCI | 1194 ± 192 | 1187 ± 194 | 1171 ± 195 | 1169 ± 220 | 1103 ± 181 | |
| (−7.4868) | (−22.5044) | (−8.6961) | (−75.3710) |
Fig. 4.
An inferior view of ERC overlayed with Krimer partitions. A histogram of cortical thickness in control subjects for TEC (Krimer's sulcal and transentorhinal partitions) and other ERC partitions including LS, LR, LC, PR, MR, MC.
Fig. 5.
Control and MCI disribution of ERC plus TEC cortical thickness at baseline. Areas in white have no cortical thickness data.
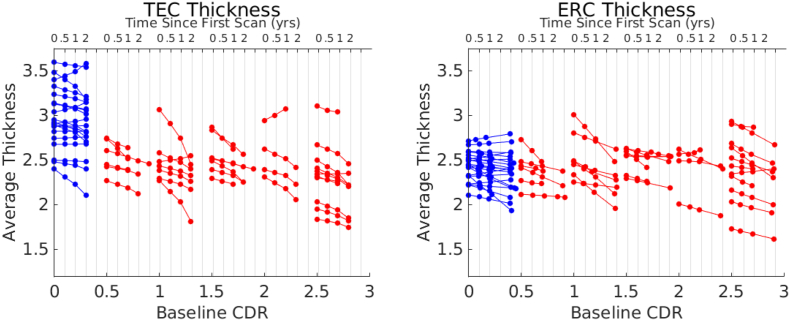
One-way ANCOVA showed there was a significant difference in baseline TEC thickness in subjects with MCI compared to controls (p ≪ 0.0001, F = − 5.611), whereas no diagnostic difference was detected in baseline ERC thickness (p = 0.85, F = 0.187). CDR-SB was used to approximate the distribution of disease severity (Fig. 6). To assess the potential clinical relevance of these findings, we examine the relationship between baseline thickness measures and the CDR-SB. The Spearman rank correlation test indicated a significant correlation between TEC thickness and CDR-SB (p ≪ 0.0001) with a correlation coefficient of ρ = − 0.6187. For ERC thickness, the Spearman rank correlation test did not indicate any significant correlation (p = 0.1818).
Fig. 6.
Average thickness over the TEC and ERC stratified by baseline CDR Sum of Boxes score over time. In blue are controls, in red are MCI. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2. Cross-sectional and longitudinal differences based on mixed effects models
3.2.1. Cortical thickness
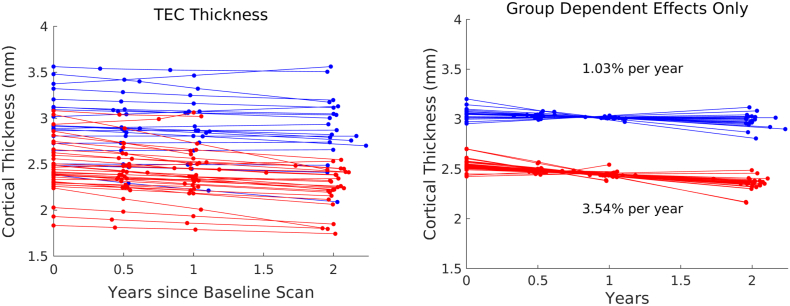
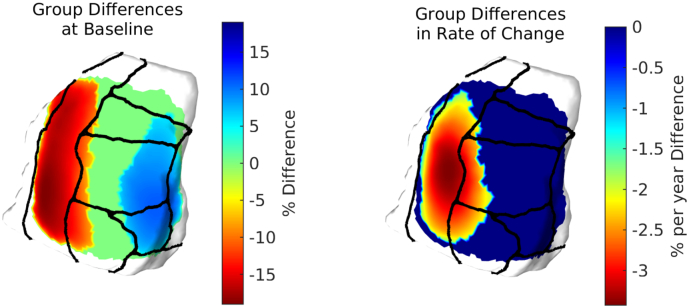
We rejected the null hypothesis in Eq. (5) with global p < 0.0001 and concluded that the alternate model with diagnostic group information fits the data significantly better. Fig. 7 shows average cortical thickness of the TEC and a visualization of group dependent effects using Eq. (9). We rejected the null hypothesis in both follow up tests and concluded there are significant cross-sectional differences at baseline with global p < 0.0002 and significant differences in atrophy rate with global p = 0.0044. Significant group differences are visualized in Fig. 8. MCI baseline cortical thickness was as much as 20.44% significantly thinner than control group's baseline cortical thickness in the TEC. Results also indicated an up to 12.60% significantly thicker MCI cortex in portions of the intermediate rostral and caudal ERC. Significant difference in atrophy rates of cortical thickness is shown in Fig. 8. Note that additional atrophy rate seen in MCI subjects was as high as 3.57% more than control atrophy rate, with the differences localized to the TEC.
Fig. 7.
Average TEC thickness over time with controls in blue, MCI in red. Shown is the thickness and the group dependent effects under the alternate hypothesis. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 8.
Thickness differences cross-sectionally, and thickness differences in atrophy rate from control to MCI over ERC and TEC.
3.2.2. Volume
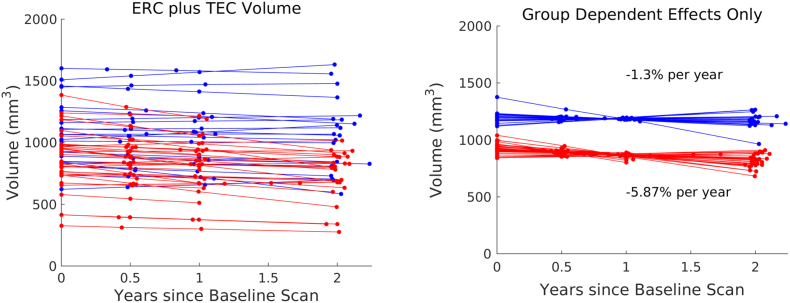
In the analysis of volumes of the combined ERC plus TEC region, we rejected the null hypothesis with p = 0.0014 and concluded that the alternate model with diagnostic group information fits the data significantly better. We also rejected the null hypothesis in both follow up tests and concluded that we can detect significant cross-sectional differences at baseline with p = 0.0020 and significant differences in atrophy rate with p = 0.0112. Specifically, MCI subjects had 22.70% smaller ERC and TEC volume than controls at baseline, and while controls experienced atrophy at a rate of 1.45% per year, MCI subjects experienced an additional 4.67% per year. Fig. 9 visualizes ERC plus TEC volume and the group dependent effects under the alternate model from Eq. (8).
Fig. 9.
ERC with TEC volume over time with controls in blue, MCI in red. Shown is the volume and the group dependent effects on volume under the alternate hypothesis. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
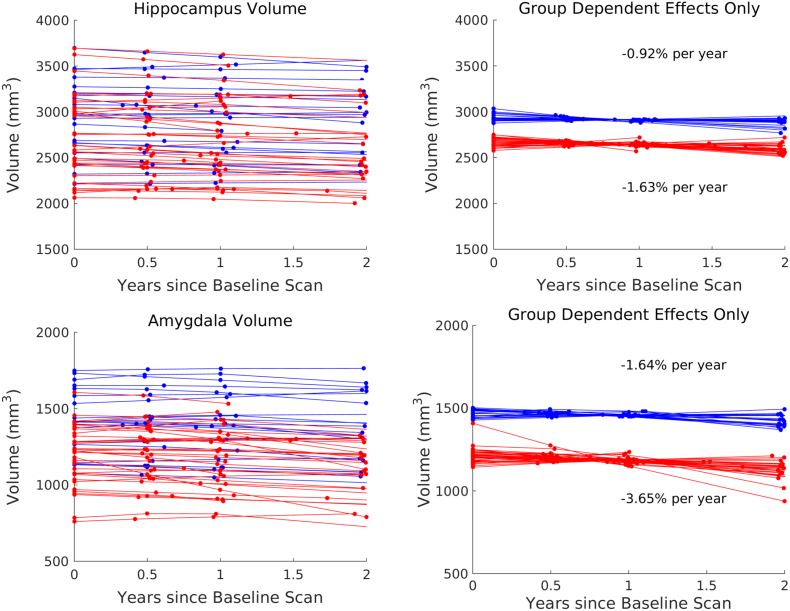
In the analysis of hippocampal volumes, we failed to reject the null hypothesis, but see a strong trend with p = 0.0503. Under the alternate hypothesis, MCI subjects were 8.72% smaller than controls at baseline and experienced an additional 0.71% per year atrophy compared to controls (0.92% per year). Fig. 10 visualizes hippocampal volume and group dependent effects under the alternate model.
Fig. 10.
Hippocampal and amygdalar volume over time with controls in blue, MCI in red. Shown is the volume and the group dependent effects on volume under the alternate hypothesis. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
In the analysis of amygdalar volumes, we rejected the null hypothesis with p = 0.0004 and concluded that the alternate model fits significantly better. We rejected the null hypothesis for the first follow up test with p < 0.0002 and concluded MCI subjects show 17.32% smaller amygdalar volumes than controls at baseline. However, we failed to rigorously reject the null hypothesis for the second follow up test with p = 0.0886 and concluded we cannot detect significant differences in atrophy rate by diagnostic group. Under the alternate model, MCI subjects experienced an additional 2.02% per year atrophy compared to controls (1.64% per year). Fig. 10 visualizes amygdalar volume and group dependent effects under the alternate model (Table 4).
Table 4.
Linear discriminant analysis of various shape measures.
| Measure | Sensitivity | Specificity |
|---|---|---|
| TEC Thickness | 0.8857 | 0.8095 |
| ERC Thickness | 0.5143 | 0.7619 |
| ERC + TEC Thickness | 0.7714 | 0.7143 |
| ERC + TEC Volume | 0.8263 | 0.6667 |
| Hippocampus Volume | 0.6571 | 0.5238 |
| Amygdala Volume | 0.6571 | 0.6667 |
3.3. Differentiating groups using linear discriminant analysis
The results of linear discriminant analysis on the baseline value and atrophy rate of the various thickness and volume metrics are shown in Table 5. TEC thickness showed higher sensitivity and higher specificity in discriminating controls from MCI than the other MRI measures, including: ERC thickness, ERC plus TEC thickness and volume, hippocampal volume, and amygdalar volume. The results of the linear discriminant function analysis, in which all of the available measures were combined showed that the ERC thickness and TEC thickness together improved specificity of diagnosis beyond TEC thickness alone. Addition of volume measures did not improve specificity or accuracy.
Table 5.
Linear discriminant analysis of combinations of shape measures.
| Measure | Sensitivity | Specificity |
|---|---|---|
| ERC and TEC Thicknesses | 0.8857 | 0.9048 |
| All Volumes | 0.80 | 0.8095 |
| All Thicknesses and Volumes | 0.8857 | 0.9048 |
4. Discussion
The primary finding in this study is that the TEC demonstrates more striking changes in thickness compared with the ERC during the MCI phase of AD. Results showed significant differences in TEC thickness between MCI subjects and controls cross-sectionally whereas the ERC thickness was not significantly different between the groups. Additionally, the atrophy rate of the TEC over 2 years was significantly greater in MCI subjects compared to controls. For example, the atrophy rate in the TEC of the MCI group was approximately 3.5 times greater than controls, whereas the atrophy rate of the ERC was considerably smaller.
The volumetric measure for the region that combined the TEC and the ERC together were also different cross-sectionally between MCI subjects and controls. The volume of the amygdala was also significantly different between these groups.
Discriminant function analysis was also performed to determine which of the thickness and volumetric measures described above best differentiated MCI subjects from controls. The TEC thickness had the largest sensitivity and specificity than any of the other regions (0.89 and 0.81, respectively). The clinical relevance of these MRI findings was reflected by examining the relationship between the TEC and the CDR-SB. There was a significant correlation between the CDR-SB and TEC thickness in the MCI subjects, but there was no significant correlation between the CDR-SB and ERC thickness.
Taken together, these findings demonstrate that the TEC thickness appears to be differentially affected during the early phase of AD. Cortical thickness atrophy in the TEC corresponds well with the localization of early neurofibrillary tangle accumulation previously reported (Braak and Braak, 1991). This study adds to the growing evidence that the thickness of the TEC could function as a biomarker for early AD. The subjects selected for this analysis were specifically chosen with strict criteria for MCI due to AD in order to reduce the confounding effects of MCI due to other conditions. Given the marked difference in cross-sectional analysis of the TEC, ERC, and amygdala, one future direction is to implement this analysis on a population of subjects earlier in the disease course as well as cognitively normal older adults following previous findings in the TEC in this population (Maass et al., 2018). Another future direction is to implement this analysis on a larger population of subjects to determine whether significant longitudinal diagnostic differences can be detected for amygdalar volume and hippocampal volume. A larger sample size may also show hippocampal volume differences between the groups. While the volume of the hippocampus did not differ between diagnostic groups in the present study, the estimated volume of the hippocampus is similar to previous reports (Chao et al., 2005; Csernansky et al., 2005; Du et al., 2001; Müller et al., 2005). For example, in this study the hippocampal volume for MCI subjects was 248 mm3 smaller than controls on the left hippocampus while in another study the hippocampus was 240 mm3 smaller than controls in the left hippocampus (Csernansky et al., 2005).
This study has a number of strengths. This includes: the careful selection of subjects in order to maximize the likelihood that any differences observed were the result of underlying AD pathology and the use of 11 T MRI to place coordinates on the images.
The study also has some limitations. Measures of cortical thickness along the boundaries of the ERC were excluded due to inaccuracy of trajectories. Extension of surface laterally into the perirhinal cortex may yield a more complete understanding of changes in the thickness profile of this region. The analysis was restricted to subjects with a continuous collateral sulcus in the left hemisphere. Restriction to the left hemisphere was based on previous findings showing that functional and structural changes in MCI were primarily observed in the left medial temporal lobe (Bakker et al., 2015; Bakker et al., 2012; Yassa et al., 2010). This may be due to a functional specialization of left medial temporal lobe structures relevant to the behavioral impairments observed in subjects with MCI (El-Gaby et al., 2015). In the future, this work could be extended to other well-characterized variants of the collateral sulcus (Ding and Van Hoesen, 2010) using a multi-atlas approach (Xie et al., 2018b). Without histology as a gold standard, the accuracy of Krimer region placement on longitudinal data cannot be validated. Using mappings to the high field atlas is our best available alternative, and has been used in other studies (Mahon et al., 2015; Miller et al., 2015a; Miller et al., 2015b; Yushkevich et al., 2009). While it remains unclear whether these regional differences could be observed without the use of 11 T MRI to improve accuracy of coordinate placement, the distribution of thickness differences in Fig. 8 can still be considered valid independent of the Krimer partition labels. The current study provides evidence that changes in the TEC thickness provide a sensitive measure of disease progression associated with functional decline in the MCI phase of AD, providing a potential outcome measure of disease modification in clinical trials for AD.
Funding
This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by the National Science Foundation (ACI-1548562). This work was supported by the National Institutes of Health (P41-EB015909, R01-AG048349, R01-DC016784 and R01-EB020062); the Phyllis F. Albstein Fund; and the Kavli Neuroscience Discovery Institute. Michela Gallagher is the founder of AgeneBio, Inc. and has a financial interest in the company, which is managed by the Johns Hopkins University. Michela Gallagher and Arnold Bakker are inventors of technology licensed by Johns Hopkins University to the company. Michael Miller reports personal fees from AnatomyWorks, LLC, outside the submitted work, and jointly owns AnatomyWorks. Dr. Miller's relationship with AnatomyWorks is being handled under full disclosure by the Johns Hopkins University.
Acknowledgments
Data collection and sharing for this project was funded by the Alzheimer's Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DODADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: AbbVie, Alzheimer's Association; Alzheimer's Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen; Bristol-Myers Squibb Company; CereSpir, Inc.; Cogstate; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC; Johnson & Johnson Pharmaceutical Research & Development LLC; Lumosity; Lundbeck; Merck & Co, Inc.; Meso Scale Diagnostics, LLC; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Takeda Pharmaceutical Company; and Transition Therapeutics. The Canadian Institutes of Health Research is providing funds to supportADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer's Therapeutic Research Institute at the University of Southern California. ADNI data are disseminated by the Laboratory for Neuroimaging at the University of Southern California.
References
- Albert M.S., Dekosky S.T., Dickson D., Dubois B., Feldman H.H., Fox N.C., Gamst A., Holtzman D.M., Jagust W.J., Petersen R.C., Snyder P.J. The diagnosis of mild cognitive impairment due to Alzheimer's disease: Recommendations from the National Institute on Aging-Alzheimers Association workgroups on diagnostic guidelines for Alzheimer's disease. Alzheimers Dement. 2011;7(3):270–279. doi: 10.1016/j.jalz.2011.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arguillère S., Trélat E., Trouvé A., Younes L. Shape deformation analysis from the optimal control viewpoint. J. Math. Pures Appl. 2015;104(1):139–178. [Google Scholar]
- Atiya M., Hyman B.T., Albert M.S., Killiany R. Structural magnetic resonance imaging in established and prodromal Alzheimer disease: a review. Alzheimer Dis. Assoc. Disord. 2003;17(3):177–195. doi: 10.1097/00002093-200307000-00010. [DOI] [PubMed] [Google Scholar]
- Bakker A., Krauss G.L., Albert M.S., Speck C.L., Jones L.R., Stark C.E., Yassa M.A., Bassett S.S., Shelton A.L., Gallagher M. Reduction of hippocampal hyperactivity improves cognition in amnestic mild cognitive impairment. Neuron. 2012;74(3):467–474. doi: 10.1016/j.neuron.2012.03.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakker A., Albert M.S., Krauss G., Speck C.L., Gallagher M. Response of the medial temporal lobe network in amnestic mild cognitive impairment to therapeutic intervention assessed by fmri and memory task performance. NeuroImage. 2015;7:688–698. doi: 10.1016/j.nicl.2015.02.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beg M.F., Miller M.I., Trouvé A., Younes L. Computing large deformation metric mappings via geodesic flows of diffeomorphisms. Int. J. Comput. Vis. 2005;61(2):139–157. [Google Scholar]
- Braak H., Braak E. Neuropathological stageing of Alzheimer-related changes. Acta Neuropathol. 1991;82(4):239259. doi: 10.1007/BF00308809. [DOI] [PubMed] [Google Scholar]
- Center for Integrative Biomedical Computing Seg3D: Volumetric image Segmentation and Visualization. Scientific Computing and Imaging Institute (SCI) 2016. http://www.seg3d.org Download from.
- Chao L.L., Schuff N., Kramer J.H., Du A.T., Capizzano A.A., O'Neill J., Wolkowitz O.M., Jagust W.J., Chui H.C., Miller B.L., Yaffe K., Weiner M.W. Reduced medial temporal lobe n-acetylaspartate in cognitively impaired but nondemented patients. Neurology. 2005;64(2):282–289. doi: 10.1212/01.WNL.0000149638.45635.FF. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csernansky J.G., Joshi S., Wang L., Haller J.W., Gado M., Miller J.P., Grenander U., Miller M.I. Hippocampal morphometry in schizophrenia by high dimensional brain mapping. Proc. Natl. Acad. Sci. 1998;95(19):11406–11411. doi: 10.1073/pnas.95.19.11406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Csernansky J.G., Wang L., Swank J., Miller J.P., Gado M., McKeel D., Miller M.I., Morris J.C. Preclinical detection of Alzheimer's disease: hippocampal shape and volume predict dementia onset in the elderly. NeuroImage. 2005;25(3):783–792. doi: 10.1016/j.neuroimage.2004.12.036. [DOI] [PubMed] [Google Scholar]
- Devanand D.P., Pradhaban G., Liu X., Khandji A., De Santi S., Segal S., Rusinek H., Pelton G.H., Honig L.S., Mayeux R., Stern Y. Hippocampal and entorhinal atrophy in mild cognitive impairment prediction of Alzheimer disease. Neurology. 2007;68(11):828–836. doi: 10.1212/01.wnl.0000256697.20968.d7. [DOI] [PubMed] [Google Scholar]
- Ding S.-L., Van Hoesen G.W. Borders, extent, and topography of human perirhinal cortex as revealed using multiple modern neuroanatomical and pathological markers. Hum. Brain Mapp. 2010;31(9):1359–1379. doi: 10.1002/hbm.20940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du A., Schuff N., Amend D., Laakso M., Hsu Y., Jagust W., Yaffe K., Kramer J., Reed B., Norman D., Chui H.C. Magnetic resonance imaging of the entorhinal cortex and hippocampus in mild cognitive impairment and Alzheimer's disease. J. Neurol. Neurosurg. Psychiatry. 2001;71(4):441–447. doi: 10.1136/jnnp.71.4.441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- El-Gaby M., Shipton O.A., Paulsen O. Synaptic plasticity and memory: new insights from hippocampal left–right asymmetries. Neuroscientist. 2015;21(5):490–502. doi: 10.1177/1073858414550658. [DOI] [PubMed] [Google Scholar]
- Fletcher P.T. Geodesic regression and the theory of least squares on Riemannian manifolds. Int. J. Comput. Vis. 2013;105(2):171–185. [Google Scholar]
- Gómez-Isla T., Price J.L., McKeel Jr D.W., Morris J.C., Growdon J.H., Hyman B.T. Profound loss of layer II entorhinal cortex neurons occurs in very mild Alzheimer's disease. J. Neurosci. 1996;16(14):4491–4500. doi: 10.1523/JNEUROSCI.16-14-04491.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grenander U., Miller M.I. Computational anatomy: an emerging discipline. Q. Appl. Math. 1998;56(4):617–694. [Google Scholar]
- Insausti R., Juottonen K., Soininen H., Insausti A.M., Partanen K., Vainio P., Laakso M.P., Pitkänen A. MR volumetric analysis of the human entorhinal, perirhinal, and temporopolar cortices. Am. J. Neuroradiol. 1998;19(4):659–671. [PMC free article] [PubMed] [Google Scholar]
- Kantarci K., Jack C.R., Jr. Quantitative magnetic resonance techniques as surrogate markers of Alzheimer's disease. NeuroRx. 2004;1(2):196–205. doi: 10.1602/neurorx.1.2.196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kerchner G.A., Deutsch G.K., Zeineh M., Dougherty R.F., Saranathan M., Rutt B.K. Hippocampal CA1 apical neuropil atrophy and memory performance in Alzheimer's disease. NeuroImage. 2012;63(1):194–202. doi: 10.1016/j.neuroimage.2012.06.048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kordower J.H., Chu Y., Stebbins G.T., Dekosky S.T., Cochran E.J., Bennett D., Mufson E.J. Loss and atrophy of layer II entorhinal cortex neurons in elderly people with mild cognitive impairment. Ann. Neurol. 2001;49(2):202–213. [PubMed] [Google Scholar]
- Krimer L.S., Hyde T.M., Herman M.M., Saunders R.C. The entorhinal cortex: an examination of cyto-and myeloarchitectonic organization in humans. Cereb. Cortex. 1997;7(8):722–731. doi: 10.1093/cercor/7.8.722. [DOI] [PubMed] [Google Scholar]
- La Joie R., Perrotin A., Barre L., Hommet C., Mezenge F., Ibazizene M. Region-specific hierarchy between atrophy, hypometabolism, and beta-amyloid (Abeta) load in Alzheimer's disease dementia. J. Neurosci. 2012;46(32) doi: 10.1523/JNEUROSCI.2170-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J., Miller M.I., Trouvé A., Younes L. Bayesian template estimation in computational anatomy. NeuroImage. 2008;42(1):252–261. doi: 10.1016/j.neuroimage.2008.03.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma J., Miller M.I., Younes L. A bayesian generative model for surface template estimation. J. Biomed. Imaging. 2010:16. doi: 10.1155/2010/974957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maass A., Lockhart S.N., Harrison T.M., Bell R.K., Mellinger T., Swinnerton K., Baker S.L., Rabinovici G.D., Jagust W.J. Entorhinal tau pathology, episodic memory decline, and neurodegeneration in aging. J. Neurosci. 2018;38(3):530–543. doi: 10.1523/JNEUROSCI.2028-17.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahon P.B., Lee D.S., Trinh H., Tward D., Miller M.I., Younes L., Barta P.E., Ratnanather J.T. Morphometry of the amygdala in schizophrenia and psychotic bipolar disorder. Schizophr. Res. 2015;164(1–3):199–202. doi: 10.1016/j.schres.2015.02.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mai J.K., Paxinos G., Voss T. 3rd edition. Academic Press; 2007. The Atlas of the Human Brain. [Google Scholar]
- McKhann G.M., Knopman D.S., Chertkow H., Hyman B.T., Jack C.R., Kawas C.H., Klunk W.E., Koroshetz W.J., Manly J.J., Mayeux R., Mohs R.C. The diagnosis of dementia due to Alzheimer's disease: Recommendations from the National Institute on Aging-Alzheimers Association workgroups on diagnostic guidelines for Alzheimers disease. Alzheimers Dement. 2010;7(3):263–269. doi: 10.1016/j.jalz.2011.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller M.I., Trouvé A., Younes L. Geodesic Shooting for Computational Anatomy. J. Math. Imaging Vis. 2006;24(2):209–228. doi: 10.1007/s10851-005-3624-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller M.I., Younes L., Ratnanather T., Brown T., Reigel T., Trinh H., Tang X., Barker P., Mori S., Albert M. MICCAI-NIBAD; October 2012. Amygdala Atrophy in MCI/Alzheimer's Disease in the BIOCARD Cohort Based on Diffeomorphic Morphometry; pp. 155–166. [PMC free article] [PubMed] [Google Scholar]
- Miller M.I., Younes L., Ratnanather J.T., Brown T., Trinh H., Postell E., Lee D.S., Wang M.C., Mori S., O'Brien R., Albert M., BIOCARD Research Team The diffeomorphometry of temporal lobe structures in preclinical Alzheimer's disease. Neuroimage Clin. September 16 2013;3:352–360. doi: 10.1016/j.nicl.2013.09.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller M.I., Ratnanather J.T., Tward D.J., Brown T., Lee D.S., Ketcha M., Mori K., Wang M.-C., Mori S., Albert M.S., Younes L. Network neurodegeneration in Alzheimer's disease via MRI based shape diffeomorphometry and high-field atlasing. Front. Bioeng. Biotechnol. 2015;3(54) doi: 10.3389/fbioe.2015.00054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller M.I., Younes L., Ratnanather J.T., Brown T., Trinh H., Lee D.S., Tward D., Mahon P.B., Mori S., Albert M. Amygdalar atrophy in symptomatic Alzheimer's disease based on diffeomorphometry: the BIOCARD cohort. Neurobiol. Aging. 2015;36:S3–S10. doi: 10.1016/j.neurobiolaging.2014.06.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mori S., Wu D., Ceritoglu C., Li Y., Kolasny A., Vaillant M.A., Faria A.V., Oishi K., Miller M.I. MRICloud: delivering high-throughput MRI neuroinformatics as cloud-based software as a service. Comput. Sci. Eng. 2016;18(5):21–35. [Google Scholar]
- Müller M.J., Greverus D., Dellani P.R., Weibrich C., Wille P.R., Scheurich A., Stoeter P., Fellgiebel A. Functional implications of hippocampal volume and diffusivity in mild cognitive impairment. NeuroImage. 2005;28(4):1033–1042. doi: 10.1016/j.neuroimage.2005.06.029. [DOI] [PubMed] [Google Scholar]
- Munn M.A., Alexopoulos J., Nishino T., Babb C.M., Flake L.A., Singer T., Ratnanather J.T., Huang H., Todd R.D., Miller M.I. Amygdala volume analysis in female twins with major depression. Biol. Psychiatry. 2007;62(5):415–422. doi: 10.1016/j.biopsych.2006.11.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nichols T., Hayasaka S. Controlling the familywise error rate in functional neuroimaging: a comparative review. Stat. Methods Med. Res. 2003;12(5):419–446. doi: 10.1191/0962280203sm341ra. [DOI] [PubMed] [Google Scholar]
- Platero C., Lin L., Tobar M.C. Longitudinal neuroimaging hippocampal markers for diagnosing alzheimer's disease. Neuroinformatics. 2018:1–19. doi: 10.1007/s12021-018-9380-2. [DOI] [PubMed] [Google Scholar]
- Price J., Ko A., Wade M., Tsou S., McKeel D., Morris J. Neuron number in the entorhinal cortex and CA1 in preclinical Alzheimer disease. Arch. Neurol. 2001;9(58):13951402. doi: 10.1001/archneur.58.9.1395. [DOI] [PubMed] [Google Scholar]
- Ratnanather J.T., Barta P.E., Honeycutt N.A., Lee N., Morris H.M., Dziorny A.C., Hurdal M.K., Pearlson G.D., Miller M.I. Dynamic programming generation of boundaries of local coordinatized submanifolds in the neocortex: application to the planum temporale. NeuroImage. 2003;20(1):359–377. doi: 10.1016/s1053-8119(03)00238-6. [DOI] [PubMed] [Google Scholar]
- Ratnanather J.T., Arguillère S., Kutten K.S., Hubka P., Kral A., Younes L. 2018. 3d Normal Coordinate Systems for Cortical Areas. [Google Scholar]
- Tward D.J., Miller M.I., Alzheimers Disease Neuroimaging Initiative Unbiased diffeomorphic mapping of longitudinal data with simultaneous subject specific template estimation. Graphs Biomed Image Anal. Comput. Anat. Imaging Genet. 2017:125–136. [Google Scholar]
- Tward D.J., Sicat C.S., Brown T., Bakker A., Gallagher M., Albert M., Miller M.I., Alzheimer's Disease Neuroimaging Initiative Entorhinal and transentorhinal atrophy in mild cognitive impairment using longitudinal diffeomorphometry. Alzheimers Dement. 2017;9:41–50. doi: 10.1016/j.dadm.2017.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Varon D., Loewenstein D.A., Potter E., Greig M.T., Agron J., Shen Q., Zhao W., Ramirez M.C., Santos I., Barker W. Minimal atrophy of the entorhinal cortex and hippocampus: progression of cognitive impairment. Dement. Geriatr. Cogn. Disord. 2011;31(4):276–283. doi: 10.1159/000324711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang H., Pouch A., Takabe M., Jackson B., Gorman J., Gorman R., Yushkevich P.A. International Conference on Information Processing in Medical Imaging. Springer; 2013. Multi-atlas segmentation with robust label transfer and label fusion; pp. 548–559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolk D.A., Das S.R., Mueller S.G., Weiner M.W., Yushkevich P.A., Initiative A.D.N. Medial temporal lobe subregional morphometry using high resolution mri in alzheimer's disease. Neurobiol. Aging. 2017;49:204–213. doi: 10.1016/j.neurobiolaging.2016.09.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L., Das S.R., Wisse L.E., Ittyerah R., Yushkevich P.A., Wolk D.A., Initiative A.D.N. Early tau burden correlates with higher rate of atrophy in transentorhinal cortex. J. Alzheimers Dis. 2018;62(1):85–92. doi: 10.3233/JAD-170945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie L., Wisse L., Das S.R., Ittyerah R., Yushkevich P.A., Wolk D.A. Pattern of cortical thinning and shape variability related to alzheimers disease in regions affected by earliest neurofibrillary tangle pathology. Alzheimer's Dementia. 2018;14(7):P146–P148. [Google Scholar]
- Yassa M.A., Stark S.M., Bakker A., Albert M.S., Gallagher M., Stark C.E. High-resolution structural and functional mri of hippocampal ca3 and dentate gyrus in patients with amnestic mild cognitive impairment. NeuroImage. 2010;51(3):1242–1252. doi: 10.1016/j.neuroimage.2010.03.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Younes L., Albert M., Miller M.I., BIOCARD Research Team Inferring changepoint times of medial temporal lobe morphometric change in preclinical Alzheimer's disease. Neuroimage Clin. 2014;5:178187. doi: 10.1016/j.nicl.2014.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yushkevich P.A., Avants B.B., Pluta J., Das S., Minkoff D., Mechanic-Hamilton D., Glynn S., Pickup S., Liu W., Gee J.C. A high-resolution computational atlas of the human hippocampus from postmortem magnetic resonance imaging at 9.4 T. NeuroImage. 2009;44(2):385–398. doi: 10.1016/j.neuroimage.2008.08.04. [DOI] [PMC free article] [PubMed] [Google Scholar]