Spatial correlations exploitation based on nonlocal voxel-wise GWAS for biomarker detection of AD

Abstract

Potential biomarker detection is a crucial area of study for the prediction, diagnosis, and monitoring of Alzheimer's disease (AD). The voxelwise genome-wide association study (vGWAS) is widely used in imaging genomics studies that is usually applied to the detection of AD biomarkers in both imaging and genetic data. However, performing vGWAS remains a challenge because of the computational complexity of the technique and our ignorance of the spatial correlations within the imaging data. In this paper, we propose a novel method based on the exploitation of spatial correlations that may help to detect potential AD biomarkers using a fast vGWAS. To incorporate spatial correlations, we applied a nonlocal method that supposed that a given voxel could be represented by weighting the sum of the other voxels. Three commonly used weighting methods were adopted to calculate the weights among different voxels in this study. Then, a fast vGWAS approach was used to assess the association between the image and the genetic data. The proposed method was estimated using both simulated and real data. In the simulation studies, we designed a set of experiments to evaluate the effectiveness of the nonlocal method for incorporating spatial correlations in vGWAS. The experiments showed that incorporating spatial correlations by the nonlocal method could improve the detecting accuracy of AD biomarkers. For real data, we successfully identified three genes, namely, ANK3, MEIS2, and TLR4, which have significant associations with mental retardation, learning disabilities and age according to previous research. These genes have profound impacts on AD or other neurodegenerative diseases. Our results indicated that our method might be an effective and valuable tool for detecting potential biomarkers of AD.

Highlights

• •Exploiting spatial correlations in neuroimaging data holds the potential to improve detecting accuracy of AD biomarkers.
• •GS weighted method applied in the nonlocal operation performs best than other classic weighted methods.
• •Proposed method accelerates the whole calculation of traditional vGWAS.
• •Several AD-related genes and brain regions have been identified successfully.

1. Introduction

Alzheimer's disease (AD) is a complex neurodegenerative disease and the main cause of age-related dementia (Huang et al., 2017a), so far affecting millions of people worldwide. Moreover, the underlying pathological mechanism of AD is not well understood. Fortunately, recent studies have shown that the detection of AD biomarkers can contribute substantially to AD prediction, diagnosis, and monitoring (Bolkan et al., 2015; Hugon et al., 2016; Li et al., 2011; Mayeux & Schupf, 2011).

Imaging genomics is a new field that has developed over the past two decades. It can be used to detect potential biomarkers of AD, helping to develop new treatments, monitor their effectiveness, and reduce the duration of clinical trials (Stein et al., 2010; Tairyan & Illes, 2009). In addition, discovering the biomarkers within both imaging and genetic data has at least three advantages. First, it helps us to gain insight into the underlying pathologic processes of AD or other neuropsychiatric and neurodegenerative diseases (Chauhan et al., 2014; Xuan et al., 2017). Second, the genetic pathways by which relevant genes affect these diseases can be discovered with the help of neuroimaging under the assumption that we could, in some ways, identify the significant but hidden associations between causal genes and specific variations drawn from the brain regions (Liu et al., 2014; Lu et al., 2017; Peper et al., 2007; Scharinger et al., 2010). Third, morphometric changes in the brain areas in neuropsychiatric and neurodegenerative diseases can be detected, which is rather straightforward in clinical practice and can be an indicator of functional changes in diseases.

Until now, many methods have been proposed to solve a variety of problems in the field of imaging genomics studies. Among these methods, the voxel-wise genome-wide association analysis (vGWAS) approach offers a holistic perspective, and in recent years, it has become the most common way to analyze brain images and genetic data simultaneously. In contrast to traditional methods, which are based on candidate phenotype and/or candidate genotype analyses, a vGWAS detects potential biomarkers of neuropsychiatric and neurodegenerative diseases by combining multiple phenotypic variables (e.g., voxels in imaging space) and the whole genome (e.g., single nucleotide polymorphism, SNP) (Bedő et al., 2014). Therefore, a vGWAS does not require a priori pathological knowledge of diseases to select the candidate phenotypes and/or candidate genotypes of interest, thereby reducing the probability of missing both important genes and brain clusters (Braskie et al., 2011; Hibar et al., 2015; Liu & Calhoun, 2013). However, a vGWAS is typically impossible without the support of large amounts of data of approximately 10⁶ voxels and 10⁶ SNPs for a subject because of its global reach as indicated in our previous study (Huang et al., 2015), thus creating a heavy computational burden.

To tackle the computational complexity issue, we proposed a more efficient method, namely, the fast voxel-wise genome-wide association analysis (FVGWAS), to accelerate the calculation of traditional vGWAS in our previous study (Huang et al., 2015). FVGWAS includes the following two steps: 1) A global sure independence screening (GSIS) procedure to eliminate many ‘noisy’ loci that had a weak association with the image phenotypes. 2) A detection procedure based on wild bootstrap methods that is intended to prevent the repeated analyses of simulated datasets. By decreasing both the data size and experimental times together, the FVGWAS has greatly alleviated the computational burden. To be specific, FVGWAS is dozens of times faster than traditional vGWAS.

The vGWAS is known to rely on the assumption that the voxels are independent of one another, and each voxel is treated as an individual unit to estimate the gene-voxel pairwise significance. Therefore, the correlations among voxels commonly known as spatial correlations in images is ignored in typical vGWAS methods (Ge et al., 2012; Stein et al., 2010; Tao et al., 2017) as well as in our FVGWAS.

Biologically speaking, the disease-related regions in the brain are usually not separate but are actually contiguous because of the inherent biological structure and function of the organ. In other words, structural changes caused by disease always refer to a relatively large region in the brain (Hinrichs et al., 2009) rather than the independent voxel or small clusters. In terms of image processing, the spatial correlations in images has been proven to contribute to different image-related tasks (Gong et al., 2012; Li et al., 2013; Moser et al., 2013; Tarabalka et al., 2010). Hence, exploiting spatial correlations within data provides a new way to approach neuroimaging studies. For example, Polzehl (Polzehl et al., 2010) proposed a structural adaptive segmentation method for structure denoising and signal detection in fMRI, which is conducted by iteratively updating the smoothing parameters. In addition, some studies (Li et al., 2011; Li et al., 2012; Liu & Calhoun, 2013) have flexibly incorporated the neighboring areas of each voxel by using a multiscale adaptive regression approach whose parameters are iteratively updated in a sequence of hierarchically nested spheres with increasing radii. Tao (Tao et al., 2017) proposed a generalized reduced rank latent factor (GRRLF) regression approach, which works by smoothing the tensor fields that are parameterized by smoothing the basis functions in the model, to exploit the spatial structure of the neuroimaging data indirectly. Recently, a functional genome wide association analysis (FGWAS) (Huang et al., 2017b), exploiting the spatial correlations in imaging data based on a multivariate varying coefficient model, can effectively detect crucial genetic and functional biomarkers. Thus, based on the biological mechanism of disease and previous studies, exploiting the spatial correlations in images is expected to provide a new and effective point of view to improve the detection accuracy in vGWAS. However, most of the abovementioned methods incorporated the spatial correlations within imaging data by fitting a regression model and smoothing all the parameters for group analyses of the image phenotype, leading to high computational complexity.

In this paper, we introduce an alternative strategy to our framework for neuroimaging studies, which is known as nonlocal methods in the field of image processing. Due to the redundancy of the images, nonlocal methods employ local similarities between the patch centered at a given voxel and the patch centered at a neighboring voxel (or between the given voxel and its neighboring voxel) to approximately represent the given voxel. Note that the similarities identified here are expected to reflect the complex correlations among high-dimensional voxels. In that case, it is reasonable to consider the nonlocal method within our framework to exploit the spatial correlations in neuroimaging data. In practice, the nonlocal method quantifies similarities with weightings. Therefore, the key to this method is how to assign weights to neighboring voxels. Here, we selected three kinds of weighted functions, namely, the Gaussian (GS) function, nonlocal means (NLM), and block-matching and 3D/4D filtering (i.e., BM3D for 2-dimensional images and BM4D for 3-dimensional images). In fact, the similarities in both NLM and BM3D/BM4D are based on the image patches, whereas the similarities in the GS function are based on voxels. All these weighted methods are widely used in the field of image processing, and have achieved good results. They are clearly representative enough to incorporate the spatial correlations in images.

In this study, we proposed a novel method using vGWAS based on spatial correlations exploitation with the aim of detecting more biomarkers of AD. A schematic overview of the proposed method is given in Fig. 1. Our method includes two major steps, 1) a nonlocal method is used to integrate the correlations among voxels, which supposes that the given voxel can be represented by weighting the sum of its neighboring voxels; and 2) finding the potential AD biomarkers from images (phenotypes) and genetic data (genotypes) by using FVGWAS, which actually makes the computation more rapid. To validate our method, we designed both simulation studies and analyses with real data. For the simulation studies, we presented experiments to evaluate the effectiveness of the nonlocal method and compared the performance of three weighted approaches. For the analyses with real data, we empirically evaluated our proposed method with three different weighted approaches to detect potential biomarkers, and we successfully detected the three significant AD-related genes ANK3, MEIS2, and TLR4. The results showed that our method is very promising for detecting more biomarkers, and it may provide a new way to gain insight into the underlying pathological mechanism of AD.

Fig. 1.

The schematic of our proposed method, which includes three main parts: (1) exploiting spatial correlations, (2) performing FVGWAS procedure, and (3) obtaining associated SNPs and Clusters (FVGWAS: fast voxel-wise genome-wide association analysis; GSIS: global sure independence screening procedure).

2. Materials and methods

2.1. Data preprocessing

In preparation for our analysis, both genetic data and anatomical MRI scans of the human brain were obtained from the ADNI database (http://adni.loni.usc.edu/).

The ADNI was launched in 2003, and it has been running since 2004; it is currently funded until 2021. This funding has been provided by the National Institute on Aging (NIA), the National Institute of Biomedical Image and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and nonprofit organizations as a $60 million, 5-year public-private partnership. The primary goal of the ADNI has been to test whether serial image (MRI, PET) and nonimage (other biological markers) measures can be combined to measure the progression of mild cognitive impairment (MCI) and early AD. The determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians in developing new treatments and in monitoring their effectiveness, in addition to decreasing the time and money needed for clinical trials. Data are collected at a range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the United States and Canada. The complete background and methodological detail of the ADNI data as well as up-to-date information can be found on the project website.

A total of 708 (421 men and 287 women, age 75.61 ± 6.76 years) subjects with anatomical MRI scans were involved, including 164 AD, 346 MCI, and 198 healthy subjects. These MRI scan were obtained on a 1.5 T MRI scanner using a 3D MPRAGE sequence in the sagittal plane. The scan parameters were as follows: the repetition time (TR) was 2400 ms, the inversion time (TI) was 1000 ms, the flip angle was 8°, and the field of view (FOV) was 24 cm with a 256 × 256 × 170 acquisition matrix (x-, y-, and z-dimensions), which yielded a voxel size of 1.25 × 1.26 × 1.2 mm³.

The standard process of approaching the MRI data included the following: (a) The use of a nonparametric nonuniform bias correction (N3) for image intensity inhomogeneity correction (Sled et al., 1998). (b) Skull stripping (Wang et al., 2014) and warping a labeled template to each skull-stripped image to remove the cerebellum (aBEAT in version 1.0, http://www.nitrc.org/projects/abeat). (c) The segmentation of each brain image into four different tissues, i.e., white matter (WM), gray matter (GM), cerebrospinal fluid (CSF), and ventricles (VN), using the FAST method (Zhang et al., 2001) (FAST in FMRIB Software Library version 5.0, https://fsl.fmrib.ox.ac.uk/fsl/fslwiki/). (d) All the images were registered to the common template using the 4D-HAMMER method proposed in (Shen & Davatzikos, 2004) (HAMMER in version 1.0, https://www.nitrc.org/projects/hammer/). (e) Finally, the use of the deformation field to generate the RAVENS maps (Davatzikos et al., 2001), which can be used to quantify the local volumetric group differences for the whole brain volume and for each of the tissue types (WM, GM, CSF, and VN).

We used the Human 610-quad Beadchip (Illumina, Inc., San Diego, CA) to acquire the genotype data of 818 subjects, including 620,901 SNPs, all of which were provided by the ADNI dataset. To avoid the effect of population stratification, we used only 749 Caucasians (selected from the 818 subjects) with both genetic data and imaging data at the baseline in our study. Then, quality control procedures (QCP), including the steps presented below, were performed to exclude unsatisfactory data through a (1) gender check; (2) population stratification; (3) sibling pair identification; (4) call rate check for each subject and each SNP marker; (5) marker removal according to the minor allele frequency; and (6) the Hardy-Weinberg equilibrium test.

Next, we screened the SNPs for the following: (1) at least 95% retention values; (2) at least 95% minor allele frequency; and (3) Hardy-Weinberg equilibrium p-values >10⁻⁶. We input the remaining missing genetic data as the modal value. After the QCP and SNPs screening procedures, there were 708 subjects remaining, and each subject obtained 501,584 SNPs during the analysis to follow.

2.2. Spatial correlations exploitation

We will begin our methods with a brief symbol introduction. Suppose that we observe imaging data, clinical variables, and genetic markers from n dependent subjects. Let V be a selected brain region that contains N_V voxels, and let v be a voxel in V(v ∈ V). Let C be the set of genetic loci containing N_C SNPs, and let c be a locus in C(c ∈ C). We denote Y_i = {y_i(v); i = 1, …, n} ∈ R^1×N_v as the image measurement vector of interest for the i-th subject at voxel v under observation. Here, x_i = {(x_i1, …, x_iK)^T; i = 1, …, n} ∈ R^1×K is denoted as the clinical covariates for the i-th subject, where x_ik is the k-th clinical covariate, and K is the dimensions of the clinical covariates. Additionally, we denote z_i(c) = {(z_i1(c), …, z_iL(c))^T; i = 1, …, n} ∈ R^1×L as the genetic data for the i-th subject at locus c, where z_il is the l-th genetic data and L is the dimensions of genetic data. In particular, we assign values of 0 (major homozygous alleles), 1 (heterozygote) and 2 (homozygotes of minor alleles) to the three types of SNPs.

To apply the spatial correlations reasonably in a vGWAS, the nonlocal method we broadly presented above should be introduced to our framework. The assumption of the nonlocal method is that an unknown voxel can be estimated by the neighboring voxels. The model is designed as follows:

$$y\left(v_i\right)={\sum }_{i,j\in \mathrm{\Theta }}\mathit{\Psi }\left(v_j\right)y\left(v_j\right)$$ (1)

where y(v_j) denotes the value of voxel j in neighborhood Θ centered at voxel i, and Ψ(v) denotes the weighted function. Obviously, the key to this model is to find a suitable function for fitting the weights of the neighboring voxels as well as possible. This strategy, which is always regarded as a nonlocal method, is applied during our first step, and we selected three commonly weighted functions to incorporate the spatial correlations in the images. The first weighted function was the GS function, which is most commonly used in image weighting processing (Vliet et al., 1998; Young & Vliet, 1995). The second one was performed by NLM, which is known as the data-adaptive image process technique (Buades et al., 2005a; Buades et al., 2005b). Moreover, the last function involved BM3D/BM4D to process the imaging data because of its superior effect on image processing (Dabov et al., 2007; Dabov et al., 2008; Dabov et al., 2015). After that, the FVGWAS procedures, including the GSIS and detection procedures, were performed to detect significant biomarkers efficiently.

In the introduction section, we sketched our entire framework consisting of the nonlocal method and FVGWAS under the assumption that a given voxel could be recovered using its neighboring voxels. To verify this assumption, we designed controlled trials by setting whether Ψ(⋅) was zero in the simulation studies. The result that applied the nonlocal method was supposed to be better if the assumption was valid. Moreover, in the analyses with real data, we performed our method with the nonlocal process to select the significant biomarkers. Considering that different weighted functions lead to different effects on correlations among voxels, here we selected three different weighted functions, namely, the GS function, NLM and BM3D/BM4D to perform our method, and their underlying theories are detailed below.

2.2.1. GS weight

Empirically speaking, the correlation between two voxels depends on their distance because the voxels in the images are not isolated from one another. This distance leads in a direction for assigning the weights, and it is just what the GS function relies on. The 2-dimensional GS function has been widely used for image processing. It assumes that the weights of the voxels decay by the distance from the given voxel. In a square neighborhood Θ centered at a given voxel, the GS function configures a weight matrix to convolve with the voxels (Kumar, 2013) for estimating the given one.

The weights calculated by the GS function are denoted as Ψ_G, and in the same way Ψ_N and Ψ_B are for NLM and BM3D/4D, respectively. The Ψ_G(⋅) is described as.

$${\mathit{\Psi }}_G\left(i,j\right)=\frac{1}{H}{e}^{\frac{-\left({v_i}^2+{v_j}^2\right)}{2h^2}}$$ (2)

where v_k denotes voxel k belonging to domain Θ_G^m x m, H is a normalization constant, and h is the standard deviation. Specifically, a larger h leads to a stronger dependence between voxels. The optimal h could be set in the range of $\frac{m-1}{6}\le h\le \frac{m-1}{4}$ (Seibold, 2010), where m was one dimension of the square neighborhood Θ_G^m x m.

2.2.2. NLM weight

As the most popular application of the nonlocal method, the NLM approach proposed by Buades (Buades et al., 2005a) is efficient and has provided an incredible breakthrough in image processing. In this paper, we scanned a search window (Ω_N1) of the image in search of similar patches (similar windows Ω_N2) that clearly resemble the given patch of interest.

The weights for similar patches in the NLM are defined as.

$${\mathit{\Psi }}_N\left(i,j\right)=\frac{1}{T}{e}^{-\frac{{‖y\left({\mathcal{N}}_{v_i}\right)-y\left({\mathcal{N}}_{v_j}\right)‖}_{2,a}^2}{2t^2}}$$ (3)

where T is the normalizing constant, t is the standard deviation that controls the degree of weighting, and a > 0 is the standard deviation of the GS kernel. Note that $y\left({\mathcal{N}}_{v_i}\right)$ and $y\left({\mathcal{N}}_{v_j}\right)$ indicate the values of voxel vectors belonging to a given patch centered at voxel i and a similar patch centered at voxel j, respectively. It is therefore clear that the interpatch similarities are weighted by the Euclidean distance. Specifically, all the voxels in a similar patch have the same importance; that is, the weights of all the voxels in the same patch are shared.

2.2.3. BM3D/BM4D weight

BM3D (for 2-dimensional data in our simulation studies) or BM4D (for 3-dimensional data in our analyses with real data) are based on an enhanced sparse representation in the transform-domain, and each was proposed as a novel image processing method. Similar to NLM, BM3D/BM4D is based on the same assumption that there are mutually similar blocks in images (Dabov et al., 2007; Dabov et al., 2008; Dabov et al., 2015). To calculate the weight for each voxel, BM3D/BM4D has the following two major steps: basic estimate and final estimate; then there are three operations within both steps, namely, grouping, collaborative hard-thresholding (or Wiener filtering) and aggregation. Therefore, the formulation of weights is hard to describe, with details in (Dabov et al., 2007). Compared to the two other weighted methods, this strategy clearly has a higher computational cost.

2.3. FVGWAS procedure

During this step, we attempted to find the association between the genotypes and imaging phenotypes by using the FVGWAS framework. Here, we briefly introduce the rationales and the scientific basis of FVGWAS, and more details can be found in (Huang et al., 2015).

The FVGWAS model formulation was as follows:

$$\mathbf{Y}=\mathbf{XB}+\mathbf{Z\Gamma }+\mathbf{E}$$ (4)

where X ∈ R^n×K, Y ∈ R^n×Vand Z ∈ R^n×L corresponded to the matrix of clinical covariates, the matrix of image measurements, and the matrix of genetic data, respectively. B ∈ R^K×V and Γ ∈ R^L×V were the coefficient matrices and they referred to the covariate effect and the genetic effect, respectively. E ∈ R^n×V is the measurement error.

Note that it was crucial to test the null hypothesis. Here, for all (voxel, locus) pairs, we need to test the following:

$$H_0:\mathbf{\gamma }\left(c,v\right)=0\mathit{versus}{H}_1:\mathbf{\gamma }\left(c,v\right)\ne 0$$ (5)

where H₀ represents that there is no association between the genetic data and the imaging data. We then introduce the standard Wald-type test statistic to obtain the p-values to test the null hypothesis.

$$W\left(c,v\right)=\tilde{\mathbf{\gamma }}{\left(c,v\right)}^T{\left\{\mathit{Cov}\left(\tilde{\mathbf{\gamma }}\left(c,v\right)\right)\right\}}^{-1}\tilde{\mathbf{\gamma }}\left(c,v\right)$$ (6)

The calculation of the Wald-type test statistic for the entire genome is computationally intensive. To solve this problem, the FVGWAS introduced a GSIS procedure to speed up the calculation. The primary idea of GSIS is to reduce the dimension from a very large scale to an appropriate scale by eliminating many ‘noisy’ loci (no-effect loci). Since detecting widespread genetic effects is more powerful and meaningful than testing for local effects during neuroimaging, we calculated a global Wald-type statistic at locus c as follows:

$$W\left(c\right)=N_V^{-1}{\sum }_{v\in V}W\left(c,v\right)$$ (7)

We then used an approximation method to select significant voxel-locus pairs, in virtue of sorting the −log₁₀(p)-value of all of the global Wald-type test statistics for the entire genome, and then we selected the top N₀ loci, denoted as ${\tilde{\mathbf{C}}}_0=\left\{{\tilde{c}}_1,\dots ,{\tilde{c}}_{N_0}\right\}$, as the significant candidate locus set.

The detection procedure for FVGWAS contained two primary wild bootstrap methods. One was used to simultaneously detect the significant (voxel, locus) pairs by calculating a maximum statistic over all of the voxels for the top N₀ loci. The other was used to simultaneously detect the significant (cluster, locus) pairs by calculating a maximum cluster size statistic for the top N₀ loci. As discussed before, the wild bootstrap can prevent the repeated analyses of simulated datasets and that is why it can considerably reduce the computational.

3. Results

3.1. Simulation studies

In this section, we executed simulation studies by using Monte Carlo simulation studies to evaluate the prediction performance of vGWAS with the nonlocal method. For simplicity, we considered only 2D imaging data during the simulation studies. All these numerical computations were performed on an IBMServer3 with MATLAB.

The simulated imaging data contained N_V = 3355 pixels in the brain region of 128 × 128 images, which corresponded to the middle slice of the 3D brain images obtained from ADNI. With the assumption that the SNPs were additive and homogeneous, the simulation of imaging data y_i(v) was, therefore, generated using the following model.

$$y_i\left(v\right)={\mathbf{x}}_i^T\mathbf{\beta }\left(v\right)+{\sum }_{j=1}^{N_c}\mathbf{\gamma }\left(c_j,v\right){\mathbf{z}}_i\left(c_j\right)+e_i\left(v\right)$$ (8)

where x_i = (1, x_i1, …, x_i9)^T were the simulated clinical covariates that were generated from either the binomial distribution with the probability of 0.5 (for discrete variables, e.g., gender) or U(0, 1) (for continuous variables, e.g., age). The variables z_i(c_j) were the simulated genetic data generated by the linkage disequilibrium blocks defined by the default method (Gabriel et al., 2002) of Haploview (Barrett et al., 2004) and PLINK (Purcell et al., 2007). The estimate values of β(v) were generated by fitting the FVGWAS model in Eq. (5) without the genetic data. The fixed genetic effects γ(c_j, v), which corresponded to the prespecified pairs of the affected Regions of Interest (ROI) and causal SNPs, were set to magnitude γ∗. Moreover, the size of the affected ROIs was set at 10 × 10. The measured error satisfied the normal distribution, e_i(v)~N(0, σ²).

For the other parameters of the FVGWAS framework, we chose the first q SNPs as the causal SNPs and set q as 100. The sample size (n), the standard deviation of the measurement error (σ) and the number of bootstrap samples were set to 1000, 1 and 100, respectively.

We performed a series of experiments to optimize the parameters of the three types of weight. For each experiment, we tuned only one parameter and fixed the other parameters. We then used the Receiver Operating Characteristic (ROC) curves to evaluate the effectiveness of the weight setting with different parameters for detecting the causal voxel-SNP pairs. The parameter that resulted in the highest Area Under Curve (AUC) value was regarded as the optimal value.

3.1.1. Optimal parameters of three weighted functions

For weight setting by the GS function, the parameters Ω_G (the size of the GS window) and h (the degree of the GS) were set based on Seibold's introduction manual for optimal GS parameters (Seibold, 2010). During our experiment, we fixed h = 3 and changed Ω_G to the range (17 × 17, 21 × 21, 25 × 25, 29 × 29, 33 × 33). As shown in Fig. 2A, Ω_G = 25 × 25 had the highest AUC, whereas the AUC decreased with the value of Ω_G was higher or lower than 25 × 25. We then fixed Ω_G = 25 × 25, and changed h to a range of (3, 4, 4.3, 4.5, 4.7, 5). As shown in Fig. 2B, the AUC decreased with the value of h was higher or lower than 4.3. Therefore, to achieve the best GS performance, the parameters Ω_G and h were set to 25 × 25 and 4.3, respectively.

Fig. 2.

The optimized parameters and the selected results. A, the size of the GS window (Ω_G); B, the degree of GS (h); C, the size of the NLM search window (Ω_N1); D, the size of the NLM similar window (Ω_N2); E, the degree of NLM (t); and F, the degree of BM3D (f) (GS: Gaussian; NLM: Nonlocal means; and BM3D: Block-matching and 3D filtering). For simplicity, we denoted the Ω = ∗ as Ω = ∗ × ∗ in the legend of Fig. 2A, C and D.

For weight setting by NLM, the parameters Ω_N1 (the size of the search window), Ω_N2 (the size of the similar window), and t (the degree of the NLM) were set based on Buades' study (Buades et al., 2005a). In our experiment, we first fixed Ω_N2 = 7 × 7, t = 0.05, and changed Ω_N1 to a range of (9 × 9, 11 × 11, 13 × 13, 17 × 17, 21 × 21). As shown in Fig. 2C, the AUC decreased with the value of Ω_N1 was higher or lower than 11 × 11. Therefore, Ω_N1 was set to 11 × 11 for the following experiments. We then fixed Ω_N1 = 11 × 11, t = 0.05, and changed Ω_N2 to a range of (5 × 5, 7 × 7, 9 × 9, 11 × 11, 13 × 13). As shown in Fig. 2D, the NLM achieved the highest AUC when Ω_N2 = 7 × 7. Next, we fixed Ω_N1 = 11 × 11, Ω_N2 = 7 × 7, and changed t to a range of (0.01, 0.03, 0.05, 0.07, 0.09). When t = 0.05, the NLM achieved the highest AUC (Fig. 2E). Therefore, to achieve the best performance of NLM, the parameters Ω_N1, Ω_N2, and t were set to 11 × 11, 7 × 7, and 0.05, respectively.

For weight setting by BM3D, the parameter f (the degree of BM3D) was set based on Dabov's study (Dabov et al., 2007). We changed f to a range of (2, 6, 10, 14, 18). As shown in Fig. 2F, BM3D performed best when f = 10. Therefore, f was set to 10 for the BM3D.The optimal parameter settings used in the three weights are summarized in Table 1.

Table 1.

Summary of the optimal parameter settings used in the three weights (GS: Gaussian; NLM: Nonlocal means; BM3D: Block-matching and 3D filtering).

Parameter	Description	Setting
ΩG	Size of the GS window	25 × 25
h	The degree of GS	4.3
ΩN1	Size of the NLM search window	11 × 11
ΩN2	Size of the NLM similar window	7 × 7
t	The degree of NLM	0.05
f	The degree of BM3D	10

3.1.2. The effect of nonlocal method

Table 2 lists the computational costs of the nonlocal method mentioned above for either 2D simulation data or 3D real data. For the 2D imaging data process, NLM had a cost of close to 10⁴ s, which took a hundred times slower than GS or BM3D. It was expected to have a higher computational cost for the 3D images. Due to the excessive computational burden of NLM, we excluded it from the real 3D data analysis procedure.

Table 2.

Computation time for different weights in the nonlocal method for 2D simulation data and 3D real data for all n subjects (GS: Gaussian; NLM: Nonlocal means; BM3D/BM4D: Block-matching and 3D/4D filtering).

Weighted method	GS	NLM	BM3D/BM4D
2D Time (s)	22.776	2109.400	74.315
3D Time (s)	377.234	–	179,760

‘–’ stands for not conducting the corresponding operation.

To evaluate the performance of the nonlocal method in detecting casual SNP rate, we set γ∗ = 0.0005, 0.001, 0.005, and 0.01, which correspond to the weak genetic signal (0.0005 and 0.001) and the moderate/strong signal (0.005 and 0.01), respectively. The top N₀ SNPs were set to a range from 100 to 2000. In addition, the number of causal SNPs (q) was set to 100. The causal SNP rate R_casual was calculated as.

$$R_{\mathit{causal}}=\frac{N_{{\tilde{\mathbf{c}}}_0}}{N_q}$$ (9)

where $N_{{\tilde{\mathbf{c}}}_0}$ was the number of causal SNPs in the candidate significant locus set ${\tilde{\mathbf{C}}}_0$, and N_q was the total number of causal SNPs. As shown in Table 3, the application of the nonlocal method presented larger causal SNP rates than not applying the nonlocal method, which indicated that more causal SNPs were included in set ${\tilde{C}}_0$, and the nonlocal method whose weight setting was done by the GS function had the best result for a weak genetic signal. For medium/strong signals, the results were close to one another.

Table 3.

Causal SNP rates results (in different N₀ values and γ∗ values) (N-weight: method without nonlocal operation; GS: Gaussian; NLM: Nonlocal means; BM3D: Block-matching and 3D filtering).

γ⁎	Weighted Method	N0
		100	200	300	400	500	600	700	800	900	1000	1200	1400	1600	1800	2000
0.0005	N-weight	0	0	0	0.01	0.01	0.01	0.02	0.02	0.02	0.03	0.05	0.07	0.07	0.11	0.12
	GS	0.02	0.03	0.04	0.04	0.05	0.06	0.09	0.09	0.09	0.09	0.11	0.14	0.16	0.18	0.18
	NLM	0.03	0.03	0.03	0.03	0.03	0.03	0.04	0.04	0.04	0.05	0.06	0.07	0.08	0.09	0.1
	BM3D	0.01	0.03	0.03	0.04	0.04	0.04	0.05	0.06	0.07	0.07	0.09	0.1	0.11	0.14	0.17
0.001	N-weight	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.02	0.04	0.04	0.05	0.06	0.09	0.11	0.11
	GS	0.04	0.06	0.06	0.08	0.11	0.12	0.14	0.15	0.16	0.18	0.19	0.24	0.26	0.27	0.28
	NLM	0.02	0.05	0.08	0.09	0.09	0.1	0.13	0.14	0.15	0.16	0.19	0.21	0.22	0.23	0.24
	BM3D	0.02	0.04	0.04	0.04	0.06	0.07	0.09	0.09	0.1	0.1	0.14	0.16	0.2	0.21	0.22
0.005	N-weight	0.27	0.39	0.5	0.59	0.71	0.81	0.89	0.95	0.97	1	1	1	1	1	1
	GS	0.27	0.39	0.57	0.69	0.74	0.83	0.88	0.93	0.96	1	1	1	1	1	1
	NLM	0.31	0.45	0.51	0.6	0.69	0.76	0.85	0.94	1	1	1	1	1	1	1
	BM3D	0.32	0.43	0.55	0.65	0.75	0.78	0.85	0.9	0.98	1	1	1	1	1	1
0.01	N-weight	0.33	0.46	0.61	0.7	0.76	0.82	0.91	0.95	0.97	1	1	1	1	1	1
	GS	0.34	0.48	0.62	0.7	0.76	0.83	0.9	0.93	0.98	1	1	1	1	1	1
	NLM	0.34	0.5	0.61	0.68	0.76	0.84	0.91	0.94	0.97	1	1	1	1	1	1
	BM3D	0.33	0.52	0.6	0.71	0.76	0.82	0.91	0.94	0.97	1	1	1	1	1	1

To evaluate the performance of the nonlocal method in detecting the causal voxel-SNP pairs in the affected ROIs, we used the ROC curves as an evaluation approach. The parameters N₀, γ and q were set to 100, 0.01 and 100, respectively. To eliminate the effect of the location of the ROI, we chose three different brain areas with a size of 10 × 10 as the prefixed effect ROIs for analysis, as shown in the first column of Fig. 3. The second column of Fig. 3 presents the ROC curves that correspond to the three ROIs. As expected, at the three locations of the affected ROIs that we chose, the AUC values of applying the nonlocal method (GS, NLM, BM3D/4D) were larger than the values when not applying the nonlocal method (N-Weight). Moreover, the nonlocal method setting weights by the GS function, always obtained the best results for the three ROIs. From comparison of the three ROC curves, we can see that there was only slight difference among the three locations of the affected ROIs.

Fig. 3.

Simulation results for the association between SNPs and voxels: the first column shows three different ROI locations with a size of 10 × 10. The second column contains the ROC curves of the nonlocal method and the lack of applied nonlocal method corresponding to the three different ROIs shown in the first column (N-weight: method without nonlocal operation; GS: Gaussian; NLM: Nonlocal means; and BM3D: Block-matching and 3D filtering).

To evaluate the performance of the nonlocal method in detecting the causal cluster-SNP pairs, we identified the clusters of the contiguous suprathreshold pixels using an uncorrected 0.01 p-value threshold. In addition, the other parameters n,  q,  σ,  γ and ROI were set to 1000, 100, 1, 0.01 and 10 × 10, respectively. We used a number of “false positive” clusters (a threshold cluster that did not overlap with any pixels of the prefixed, affected ROI at any causal SNP) and the size of the number of pixels in the false positive clusters to demonstrate the accuracy of our detection method. In addition, we used the dice overlap ratio (DOR), which was the ratio of the number of true positive pixels to the size of the affected ROI, to compare the nonlocal method and the absence of nonlocal method application results. A larger average DOR value corresponded to more effective detection power. As shown in Fig. 4A and B, no false positive cluster was detected by our method either with nonlocal operation or without nonlocal operation. Fig. 4C shows that the nonlocal method has a larger average DOR value than the result of not applying the nonlocal method. Besides, the nonlocal method with weight setting by the GS function, had the largest average DOR value (Fig. 4C) and was thus believed to have the most effective detection power.

Fig. 4.

Simulation results for the association between SNPs and clusters. A: the number of false positive clusters in each causal SNP; B: the size in the number of pixels of false positive clusters in each causal SNP; C: the DOR in each causal SNP; (N-weight: method without nonlocal operation; GS: Gaussian; NLM: Nonlocal means; and BM3D: Block-matching and 3D filtering).

To evaluate the overall Type I error rates (that is, the rate of rejecting the null hypothesis when it is true) of the nonlocal method, we set γ = 0 (null hypothesis) and calculated the familywise error rate (FWER) at the level of both the (voxel, locus) pairs and the (cluster, locus) pairs (Dudoit et al., 2003; Shaffer, 1995). For each weight, we conducted 1000 replications in a test to assess the FWERs, and the significance level (α) was varied between 0.1 and 0.5. For any particular multiple testing procedure, it is said that a particular Type I error rate must be controlled for at the level of α_I. If the FWER was no larger than α_I then the test was deemed conservative; otherwise, the test was deemed anticonservative or liberal (Dudoit et al., 2003). Here, we set α_I = 0.005. As shown in Table 4, we list the results of FWERs that corresponded to different significance levels of α to detect significant voxel-SNP pairs and significant cluster-SNP pairs. Applying the nonlocal method has larger rejection rates, indicated that it was more accurate for detecting significant voxel-SNP pairs and significant cluster-SNP pairs. Moreover, the nonlocal method with the weight setting by the GS function, always has the largest rejection rates.

Table 4.

Percentage of times when significant voxel-SNP pairs or cluster-SNP pairs were found at different thresholds (the ratio of repeat times to the total times of significant pairs). (N-weight: method without nonlocal operation; GS: Gaussian; NLM: Nonlocal means; and BM3D: Block-matching and 3D filtering).

Replication = 1000	Weighted method	α
		0.01	0.02	0.03	0.04	0.05
voxel-SNP pairs	N-Weight	0.15	0.029	0.044	0.06	0.077
	GS	0.026	0.044	0.058	0.069	0.081
	NLM	0.019	0.031	0.04	0.057	0.068
	BM3D	0.014	0.033	0.045	0.057	0.07
cluster-SNP pairs	N-Weight	0.052	0.067	0.092	0.163	0.381
	GS	0.05	0.063	0.1	0.176	0.413
	NLM	0.047	0.065	0.092	0.156	0.399
	BM3D	0.056	0.072	0.096	0.178	0.384

Finally, we compared our proposed method with the FGWAS method (Huang et al., 2017b) in terms of the power for detecting casual SNPs in the candidate significant locus set ${\tilde{\mathbf{C}}}_0$. With the same simulated data, we set the number of casual SNPs q = 100 and γ^∗ = 0.01,  0.001. Table 5 showed R_causal with different top N₀ SNPs. We found that the performance of applying the nonlocal method (GS, NLM, and BM3D) was better than that of FGWAS in terms of weak and moderate/strong signals, indicating that our method achieved a strong power to detect casual SNPs.

Table 5.

The comparison of causal SNP rate between the proposed method and FGWAS method. (N-weight: method without nonlocal operation; GS: Gaussian; NLM: Nonlocal means; BM3D: Block-matching and 3D filtering).

γ⁎	Method	N0
		100	300	500	700	900	1200	1600	2000
0.01	GS	0.34	0.62	0.76	0.9	0.98	1	1	1
	NLM	0.34	0.61	0.76	0.91	0.97	1	1	1
	BM3D	0.33	0.6	0.76	0.91	0.97	1	1	1
	FGWAS	0.26	0.51	0.74	0.84	0.97	1	1	1
0.001	GS	0.04	0.06	0.11	0.14	0.16	0.19	0.26	0.28
	NLM	0.02	0.08	0.09	0.13	0.15	0.19	0.22	0.24
	BM3D	0.02	0.04	0.06	0.09	0.1	0.14	0.2	0.22
	FGWAS	0.02	0.04	0.04	0.06	0.09	0.1	0.12	0.16

3.2. Analyses with real data

Here, we considered the RAVENS maps to illustrate the power of the proposed method with 708 subjects, including 193,275 voxels and 501,584 SNPs. The clinical covariates included the age, gender, intercept, and whole brain volume as well as the top 5 principal component scores for the SNPs in the ADNI data analysis. When N₀ = 1000, the computational time of integrating the spatial correlations for all 708 subjects is given in Table 2. Moreover, our whole framework with the weighted function of GS function and BM4D required 23,211 and 202,594 s, respectively.

The strategy of the optimal parameters selection for the three weighted functions should differ from that in simulation studies. With simulated data, we can prespecify the SNPs that remarkably contribute to the imaging measures and the affected ROIs, such as like prior knowledge in statistics. However, exact SNP-voxel/cluster pairs in GWAS have yet to be verified. In this case, without the assistance of prespecified values (ground truth), we addressed this problem based on statistics in this section. In the GSIS procedure, we defined W(c) as the global Wald-type statistic at c locus, and used an approximation method to calculate the p-value of all W(c)s. We sorted the −log₁₀(p) − values and selected the top N₀ loci with the highest −log₁₀(p) − values. Biologically, it is expected that important genetic markers should be associated with relatively large ROIs (Huang et al., 2015; Huang et al., 2017b). Therefore, we could use the p-values of W(c)s to estimate the association strength between the whole brain and the genetic data and to select the most relative loci. In this study, we applied a nonlocal method to process the images to incorporate spatial correlations. We hoped that incorporating the spatial correlations could strengthen the associations between the whole brain and the genetic data, leading to a reduced p-value of W(c). Therefore, we used the p-values of W(c)s to select the optimal parameters of the three different weighted functions. The optimal parameter settings used for the weights and the results are summarized in Table 6.

• (1)For weight setting by the GS function, we fixed h = 4.3, and changed Ω_G to a range of (11 × 11, 15 × 15, 19 × 19, 23 × 23, 25 × 25). As shown in Table 6, Ω_G = 15 × 15 had the smallest p-values, whereas the p-value increased with the value of Ω_G was higher or lower than 15 × 15. Then, we fixed Ω_G = 15 × 15, and changed h to a range of (0.3, 0.5, 1.5, 2.5, 3.5). As shown in Table 6, the p-values increased with the value of h was higher than 0.5. Therefore, the parameters Ω_G and h were set to 15 × 15 and 0.5, respectively. (2) For weight setting by BM4D, we changed the parameter f to a range of (6, 8, 10, 12, 14). As shown in Table 6, BM4D performed best when f = 8. Therefore, f was set to 8 for BM4D.

Table 6.

The parameters and select results for the weight setting by the GS function and the weight setting by BM4D. The bold font corresponds to the parameter we selected (W is the GS window; h is the degree of GS; and f is the degree of BM4D) (GS: Gaussian; BM4D: Block-matching and 4D filtering).

	ΩG (h = 4.3)	p-value	h (ΩG = 15 × 15)	p-value
GS	11*11	1.5783E-07	0.3	7.15979E-08
	15*15	4.1590E-08	0.5	6.13960E-08
	19*19	4.9311E-08	1.5	1.01940E-07
	23*23	5.2805E-08	2.5	2.8267E-07
	25*25	5.2805E-08	3.5	2.8556E-07
BM4D	f	p-value
	6	1.4118E-07
	8	1.3797E-07
	10	1.4203E-07
	12	1.6345E-07
	14	1.7239E-07

Fig. 5 shows the Manhattan and QQ plots of GWAS for the whole region of the brain's RAVENS maps. Fig. 5A shows the Manhattan plots with the weight setting by the GS function and we found that there was one detected SNP in chromosome 10 near the widely used threshold 5 × 10⁻⁸ in the GWAS. In Fig. 5C (the QQ plot), shows that the distribution of the observed p-values fit the expected p-values well for most p-values when the null hypothesis was true. Moreover, the distribution of the observed p-values in the upper tail could be compared against that of the expected p-values, which has an obvious deviation and indicates a strong association between these SNPs and the imaging data. Fig. 5B shows the Manhattan plot with the weight setting by BM4D and we found no SNP was detected to pass the threshold of 5 × 10⁻⁸. Fig. 5D shows the QQ plot with the weight setting by BM4D, which has a similar result to that of the GS function. However, there was slightly smaller deviation in the upper tail than deviation in Fig. 5C, demonstrating that the association between SNPs and imaging data found with BM4D is weaker than the association found with GS function.

Fig. 5.

Manhattan and QQ plots. A and C correspond to the weight setting by the GS function; B and D correspond to the weight setting by BM4D (GS: Gaussian; BM4D: block-matching and 4D filtering).

In Table 7, we report the top 10 SNPs that were associated with the entire region of the RAVENS brain maps, including the corresponding SNPs, chromosome IDs, base pair (BP) values, p-values, and gene. As reported in Table 7, all of the SNPs surpassed the significance level of 10⁻⁵ with both the weight setting by GS function and the BM4D. The gene ANK3 (chr10) has been known to be associated with mental retardation. The mutations in the ANK3 gene could be involved in bipolar disorder and/or intellectual disability. The gene TYK2 (chr2) is known to be associated with immunodeficiency 35 and lymphomatoid papulosis. TLR4 (chr10) is an age-related gene. MEIS2 (chr15) is associated with learning disabilities and was found by the nonlocal method with weight setting by the GS function. ANK3 and TYK2 could be found by the nonlocal method with weight setting by BM4D.

Table 7.

ADNI whole-brain GWAS: top 10 SNPs that were selected for association with the brain-wide conditions (GS: Gaussian; BM4D: Block-matching and 4D filtering).

Weighted method	SNP	CHR	BP	p-Value	Gene	Diseases associated
GS	rs10761514	10	62,276,317	6.14e-08	ANK3	Mental Retardation, Autosomal recessive and Neuroma
	rs2901788	2	65,908,706	1.20e-07	LOC105369166	–
	rs2068043	10	62,320,330	3.47e-07	ANK3	Mental Retardation, Autosomal recessive and Neuroma
	rs2765480	10	131,844,235	3.88e-07	–	–
	rs2304259	19	10,491,352	1.29e-06	TYK2	Immunodeficiency 35, Lymphomatoid Papulosis
	rs1927914	9	120,464,725	1.36e-06	TLR4	Macular Degeneration, Age-Related, and Colorectal Cancer
	rs5754850	22	34,546,682	1.64e-06	LL22NC03-86d4.1	–
	rs885720	12	12,248,099	1.80e-06	BCL2L14	–
	rs11857187	15	37,317,545	2.20e-06	MEIS2	15Q14 Microdeletion Syndrome, Learning Disability
	rs10445654	2	144,879,660	2.48e-06	GTDC1
BM4D	rs10761514	10	62,276,317	1.32e-07	ANK3	Mental Retardation, Autosomal recessive and Neuroma
	rs10445654	2	144,879,660	4.65e-07	GTDC1	Colon Adenocarcinoma
	rs2068043	10	62,320,330	6.14e-07	ANK3	Mental Retardation, Autosomal recessive and Neuroma
	rs2901788	2	65,908,706	6.23e-07	LOC105369166	–
	rs2444861	8	99,100,932	1.35e-06	ERICH5	–
	rs12275375	11	13,802,919	2.21e-06	–	–
	rs2304259	19	10,491,352	2.27e-06	TYK2	Immunodeficiency 35, Lymphomatoid Papulosis
	rs845016	21	33,998,284	2.52e-06	–	–
	rs2765480	10	131,844,235	2.62e-06	–	–
	rs2420936	10	123,208,881	2.69e-06	–	–

‘–’ in the table indicates the item was not found to correspond to genes or not found to be associated with diseases.

To detect significant voxel-SNP pairs, we calculated the raw p-values of the Wald-type test statistic against the top N₀ = 1000 SNPs in ${\tilde{\mathit{C}}}_0$, and the significance level was set to 10⁻⁵. As shown in Fig. 6A and B, both weight settings could detect some significant voxel-locus pairs with different N₀. Using multiple comparisons, we calculated the corrected p-values of the Wald-type test statistic, with the significance levels set to 0.5 and 0.8, respectively. As shown in Fig. 6C-F, after correcting the p-values, a few significant voxel-locus pairs were detected. Fig. 6A, C and E correspond to the weight setting by the GS function, while Fig. 6B, D and F correspond to the weight setting by BM4D.

Fig. 6.

The number of significant voxel-locus pairs based on the raw p-values (rawpv) of the Wald-type test statistic at the 10⁻⁵ significance level with the top N₀ = 1000 SNPs. The number of significant voxel-locus pairs based on the corrected p-values (corpv) of the Wald-type test statistic at the 0.5 or 0.8 significance level with the top N₀ = 1000 SNPs. A, B and C correspond to the weights setting by the GS function; D, E and F correspond to the weights setting by BM4D (GS: Gaussian; BM4D: block-matching and 4D filtering).

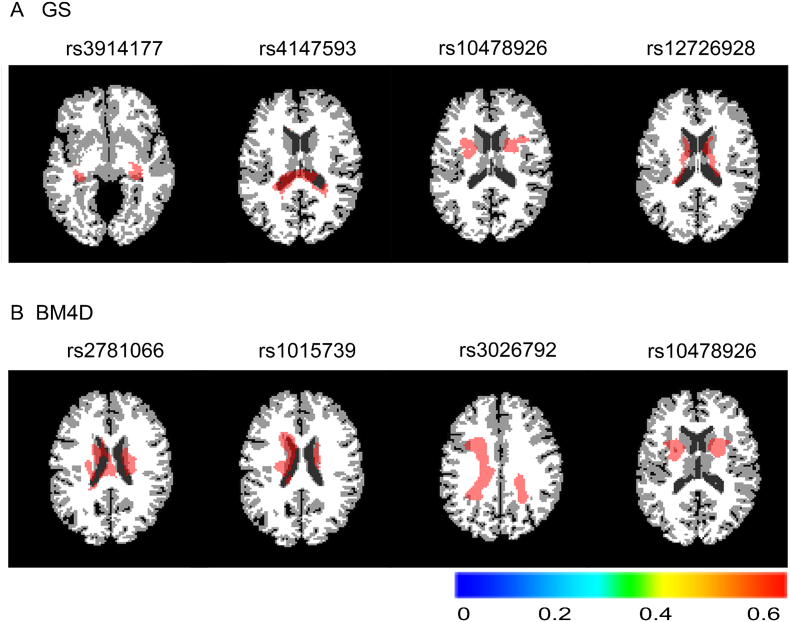
Fig. 7 shows some slice maps of the −log₁₀(p)-value for the significant clusters corresponding to some of SNPs within the top N₀. Several major clusters, including major ROIs and their corresponding SNPs for the nonlocal method, which involve weight setting by GS and BM4D function, are listed in Table 8. Fig. 7 shows some symmetric clusters that were observed; it could be biologically plausible to observe the symmetric associations between the SNPs and the clusters.

Fig. 7.

ADNI whole-brain GWAS: selected slice maps of −log₁₀(p)-value for significant clusters corresponding to some SNPs within the topN₀. Fig. 8A corresponds to the weight setting by the GS function, and B corresponds to the weight setting by BM4D (GS: Gaussian; BM4D: block-matching and 4D filtering).

Table 8.

Significant clusters, including major ROIs and their corresponding SNPs, for the weight setting by GS and BM4D (GS: Gaussian; BM4D: Block-matching and 4D filtering).

Weighted method	Clusters	SNP
GS	Hippocampus Left/Right.	rs3914177
	Thalamus Left/Right; Precuneus Left.	rs4147593
	Inferior Frontal Gyrus Right; Insula Left/Right; Caudate Nucleus Right; Putamen Left/Right.	rs10478926
	Caudate Nucleus Left/Right; Thalamus Left/Right.	rs12726928
BM4D	Caudate Nucleus Left/Right.	rs2781066
	Caudate Nucleus Left/Right.	rs1015739
	Inferior Frontal Gyrus Left.	rs3026792
	Insula Left/Right; Caudate Nucleus Left/Right; Putamen Left/Right; Superior Temporal Gyrus Right.	rs10478926

4. Conclusions and discussion

In this paper, we proposed a novel vGWAS method based on spatial correlations exploitation that is expected to boost the power of detecting potential AD biomarkers. On the one hand, the importance of spatial correlations in neuroimaging studies cannot be neglected, especially those that had been demonstrated many times in previous studies (Bedő et al., 2014; Ge et al., 2012; Li et al., 2013; Moser et al., 2013; Tao et al., 2017). Therefore, in our paper, a nonlocal method has been employed to integrate the complex correlations among voxels in imaging data. It is actually a widely used strategy in the field of image processing, and it achieved good results. As we discussed before, the key of this method is the weighted function. Thus, we selected three representative weighted functions, including the GS function, NLM and BM4D, to integrate the neighboring information around each voxel. On the other hand, FVGWAS was proposed in our previous studies (Huang et al., 2015) and has been applied within our framework to alleviate the computational burden. Considering the advanced acceleration of FVGWAS (Huang et al., 2015), we did not compare our proposed method with the traditional vGWAS in terms of computational time in this study. Thus, our method not only retained low complexity and a fast calculation ability but also addressed the important spatial correlations issues that were ignored in previous work. In addition, the nonlocal method was supposed to have the potential to target a much larger number of significant AD-associated biomarkers in neuroimaging. Consequently, the exploitation of nonlocal method in vGWAS is meaningful for AD prediction, diagnosis, and monitoring.

In the simulation studies, we designed experiments to evaluate whether the nonlocal method applying in our framework work or not. For the results of the causal SNP rate shown in Table 3, there are significant differences between the methods with nonlocal operation (GS function, NLM and BM3D) and those without nonlocal operation (procedure-weight) for a weak genetic signal, whereas for a moderate/strong signal, their results were close to one another. Therefore, it can be considered that the nonlocal method is effective within our framework, especially for the weak signal that was usually difficult to detect in other previous studies. In fact, the assumption of the nonlocal method, i.e., an unknown voxel can be estimated by the neighboring voxels, exactly satisfies the inherent characteristic of an image in which the information in the image is so redundant that we can even utilize the neighboring voxels to represent the unknown voxel. In other words, the results of the causal SNP rate verified this assumption further, as we mentioned in method section. On the other hand, we compared the three weighted functions in both the simulation studies and the analyses with real data. In Table 3, the nonlocal method with weight setting by the GS function achieved the largest causal SNP rates when the genetic signal was weak, presenting a strong power to detect causal SNPs. In Fig. 3, at the different ROI locations, the ROC curve with GS function outperformed the other methods, indicating a strong power to detect causal voxel-SNP pairs in the affected ROIs. In Fig. 4C, the nonlocal method with weight setting by the GS function also obtained the largest average DOR, suggesting that this method could detect the ROI correctly. In Table 4, the nonlocal method with weight setting by the GS function had the largest rejection rates, implying that it was accurate for detecting significant voxel-SNP pairs and cluster-SNP pairs. In the analyses with real data, the QQ plot with GS function had a slightly larger deviation in the upper tail than that shown in the QQ plot with BM4D, demonstrating that the association between SNPs and the imaging data found with GS function was stronger than the association found with BM4D (Fig. 5). Therefore, the weights set by the GS function always had the best performance among the three weighted functions possibly because of the following reasons: 1) For a given voxel, the neighboring voxels are assigned weights that are decaying by distance in the GS function. This approach exactly conforms to the law of pathology present in neuroimaging in which disease-related regions are generally perceived to be contiguous. 2) In contrast to the GS function, which depends on the similarity among voxels, the weights set by NLM and BM3D/BM4D incorporate spatial correlations depending on the similarity among patches. Their worse performance compared with the GS function may be attributed to a lack of strong correlations between similar patches in the brain MRI scans. 3) The MRI data collected in the spatial frequency space are usually corrupted by Gaussian noise (Mahmood et al., 2016), and GS can help reduce the effect of Gaussian noise by exploiting the spatial correlations. Therefore, the nonlocal method with weight setting by the GS function always obtained the best results.

Besides, there was a slight difference in the ROC curves among the three locations of the affected ROIs in Fig. 3, presumably because of the gray difference degree at different locations in the brain. This finding could affect the weights setting and thus affect the estimate results.

In our method, some new risk genes and clusters were detected, which will contribute to the prevention and earlier treatment for AD. As listed in Table 7, the genes that we detected included ANK3 (chr10), which is associated with mental retardation; MEIS2 (chr15), which is associated with learning disabilities; and TLR4 (chr10), which is an age-related gene. Therefore, we can conclude that those genes could affect the occurrence of AD. As shown in Table 8, we found that the following areas of the brain that exhibited changes would be affected by the progression of AD: the hippocampus, which is related to memory and cognition (Voineskos et al., 2015); the inferior frontal gyrus, which is associated with language comprehension and production; the insula, which is involved in consciousness and plays a role in both self-awareness and cognitive functioning; the precuneus, which is involved in episodic memory, reflections on the self, and aspects of consciousness; the caudate nucleus, which experiences a ‘significant reduction in the caudate volume’ in AD patients (Jiji et al., 2013) and is linked with patients diagnosed with schizophrenia; the putamen, which is associated with cognitive decline in AD and is also correlated with schizophrenia and depression; the thalamus, which provides differentiation in the functioning of recollective and familiarity memory; and the temporal gyrus, which is connected to memory, emotion, language comprehension and recognition.

Many issues remain to be solved. Some unobservable and latent factors accounting for the final analyses have been completely ignored, as elucidated in some studies (Bhattacharya & Dunson, 2011; Montagna et al., 2012). To address this problem, for example, Zhu (Zhu et al., 2014) proposed a Bayesian generalized low rank regression model (GLRR) based on a Markov chain Monte Carlo algorithm, but the cost of the computational complexity would be difficult to overcome. Overall, we can attempt to introduce unobservable latent factors into our model in some way to improve its performance. In addition, because of a variety of image phenotype characteristics drawn from different neuroimaging modalities (e.g., functional MRI, PET, and diffusion tensor imaging), different image phenotypes combined with our research would probably achieve better results.

Conflicts of interest

We declare no conflicts of interest with this paper.