Longitudinal changes in the genetic and environmental influences on the epigenetic clocks across old age: Evidence from two twin cohorts

Abstract

Background

Measures based on DNA methylation, epigenetic clocks, have recently gained attraction as predictors of mortality and age-related pathologies. However, the origins of variation in these measures are not well understood.

Methods

In a pooled sample of 104 Swedish and Danish twin pairs, we estimated, at the mean age of 70 (baseline) and 79 years (follow-up), the genetic and environmental influences on the Horvath and Levine clocks.

Findings

A model incorporating additive genetic (A) and person-specific environmental (E) influences best explained the variation in both clocks. Heritability was estimated at 55% at baseline and at 51% at follow-up for the Horvath clock and 34% at baseline and 41% at follow-up for the Levine clock. For the Horvath clock, new sources of A influences emerged at follow-up, whereas for the Levine clock, the same A influences accounted for the genetic variance at both measurement occasions. The cross-time phenotypic correlations, 0·52 for the Horvath clock and 0·36 for the Levine clock, were mediated primarily by genetic factors, whereas the person-specific environmental factors were completely different at the two measurement occasions.

Interpretation

For both clocks, new sources of person-specific environmental influences emerge with age. The epigenetic clocks might thus be responsive to new environmental stimuli even at old age.

Fund

NIH (R01;AG04563;AG10175;AG028555) the MacArthur Foundation Research Network on Successful Aging, FAS/FORTE (97:0147:1B;2009-0795), Swedish Research Council (825-2007-7460;825-2009-6141;521-2013-8689;2015-03255;2015-06796;2018-02077), FORTE (2013-2292), the Strategic Research Program in Epidemiology at KI, VELUX FOUNDATION, NIA (P01-AG08761), the EU (FP7/2007-2011;259679) and The Danish National Program for Research Infrastructure 2007 (9-063256).

Research in context.

Evidence before this study

Epigenetic clocks are well-established independent predictors of mortality. To date, only a limited number of studies have estimated their heritability and no longitudinal studies exist to show how genetic and environmental influences change with age. Moreover, it is unknown whether the sources of person-specific environmental influences change with age.

Added value of this study

We show that the Horvath ad Levine epigenetic clocks are moderately heritable at and across old age. For the Horvath clock, new genetic influences emerge with age but for the Levine clock, the same genetic factors explained the genetic variation across old age. Most importantly however, new person-specific environmental influences emerged with age for both clocks.

Implications of all the available evidence

Establishing the extent to which the genetic and environmental sources of variation act upon the epigenetic clocks at different stages of aging creates a foreground for prevention and intervention. Our findings on the emergence of new sources of person-specific environmental influences for both Horvath and Levine clocks with age would suggest that the clocks are amenable for such measures even at old age.

Alt-text: Unlabelled Box

1. Introduction

Two measures of DNA methylation age (DNAmAge), the Horvath and the Levine epigenetic clocks, the latter also called DNAm PhenoAge, have recently emerged as compelling markers of biological aging [1]. It has been observed that individuals with the same chronological age may differ in their biological age; hence, such markers have utility in tracking inter-individual differences in the rate of biological aging [2]. Besides providing an accurate prediction of an individual's biological age, both the Horvath and Levine clocks predict mortality independent of other risk factors [1,3,4]. Both clocks are composite measures of methylation levels of a selected set of CpG sites. The Horvath clock includes 353 CpG sites that best predicted chronological age [5], whereas the 513 CpG sites in the Levine clock were regressed against chronological age and nine markers of phenotypic aging: albumin, creatinine, glucose, C-reactive protein, lymphocyte percentage, mean cell volume, red blood cell distribution width, alkaline phosphatase and white blood cell count [3]. In this way, by tapping into physiological dysregulation, the Levine clock yielded improved predictions for all-cause mortality and age-related diseases compared to the Horvath clock [3].

However, little is known about what controls the clocks. The strongest evidence available might be from a recent genome-wide genetic analysis of epigenetic aging rates [6]. Associations with life style factors, such as smoking, diet and physical activity have been rather modest for the Horvath clock [7] but stronger for the Levine clock [3]. On the other hand, associations of the clock measures with lifestyle factors may differ across developmental periods as has been observed for obesity and the Horvath clock [8]. Twin and pedigree-based studies have estimated the Horvath clock heritability at approximately 40% [9] and the Levine clock at 33% [3]. However, as these are cross-sectional estimates, they may not inform about potential changes in genetic and environmental influences across time. Elucidating the sources of variation longitudinally in the same individuals provides insights not only on aging-associated changes, but also on how much of the trait's cross-time stability is explained by genetic and environmental factors. Such a design also reveals whether new sources of variation emerge with increasing age.

This study was undertaken to examine longitudinally the genetic and environmental contributions to the Horvath and Levine clocks, measured in the same individuals at two occasions on average nine years apart, at the mean ages of 70 (baseline) and 79 (follow-up) years. By using biometric modeling, we estimated the contribution of genetic and environmental influences to the variation in the clocks at each occasion as well as across time (nine years of follow-up). This approach could also identify new genetic and environmental influences at follow-up that were independent of genetic and environmental effects at baseline. A pooled sample of Swedish and Danish twins was used in the analysis.

2. Materials and methods

2.1. Study samples

The samples were drawn from two longitudinal twin studies: the Swedish Adoption/Twin Study of Aging (SATSA) and the Longitudinal Study of Aging Danish Twins (LSADT). Begun in 1984 and finished in 2014, SATSA is a population-based study drawn from the Swedish Twin Registry that includes same-sex pairs of twins reared together and pairs separated before the age of 11, with both mailed questionnaires and in-person testing (IPT) waves that assess a broad spectrum of biological, psychological and social domains. A total of nine questionnaire waves and ten IPT waves have been performed. The timeline of the SATSA data collection, sampling procedures and the data sets until the seventh questionnaire and seventh IPT wave have been previously described and are publicly available [10]. Please see the “Availability of data and materials” section for the availability of the methylation data. The samples included in the present study consist of 126 individual twins (63 intact pairs; 26 monozygotic [MZ] pairs and 37 dizygotic [DZ] pairs) who have DNA methylation and covariate data available on two measurement occasions on average 9 (SD ± 3) years apart. The methylation data for clock measures came from IPTs 3, 5, 7, 8 and 9. As follows, the follow-up times varied to some extent between pairs, but within a pair, both members contributed their baseline and follow-up measurements at the same IPT wave, being thus matched for age.

The LSADT cohort, drawn from the Danish Twin Registry, was initiated in 1995 with the assessment of all same-sex Danish twins at least 75 years of age [11]. The surviving members were followed-up every second year through 2007, and additional twin cohorts were added consecutively with the age requirement reduced to 70 years of age. Each survey comprises multidimensional face-to-face interviews focusing on health and lifestyle issues, and including assessment of cognitive and physical abilities. In 1997 and 2007, whole blood samples were collected from same-sex twin pairs, and the samples included in the current study consist of those 82 individual twins (41 intact pairs; 16 MZ and 25 DZ pairs) who participated in both the baseline assessment in 1997 and the follow-up in 2007. Please see the “Availability of data and materials” section for the availability of the methylation data.

2.2. DNA methylation data

In both samples, whole blood methylation data were obtained using the Infinium 450 K HumanMethylation BeadChip (Illumina, San Diego, CA, USA). As previously described in more detail [12], the SATSA samples were preprocessed using the R package RnBeads [13]. Samples with low quality and probes overlapping with a single nucleotide polymorphism and non-CpG probes were excluded. Additionally, a greedy-cut algorithm that iteratively filters out probes and samples was used; it was employed by maximizing false positive rate minus sensitivity with a detection p-value cutoff of 0·05. After preprocessing 390,894 probes were retained. The data were normalized using ‘dasen’ [14]. Detection and removal of technical variance, we performed using a Sammon mapping method [15] to produce a lower-dimension projection preserving the original data structure. These data were then corrected for batch effects using the ComBat method in the sva package [16]. Preprocessing of the LSADT methylation data was performed using the R-package MethylAid [17] as previously described in more detail [18]. Samples not meeting the quality requirements were excluded and probes with detection p-value>0·01, no signal, or bead count<3 were filtered out. CpG sites with >5% missing values, probes mapping to sex chromosomes, and cross-reactive probes were removed. Data were normalized using functional normalization [19] with four principal components. Batch effect -correction was part of the functional normalization method. After preprocessing, 452,920 CpG sites remained for further analysis.

The Horvath and the Levine epigenetic clocks are composite measures of 353⁵ and 513³ CpG sites, respectively, and have 41 CpG sites in common. The Horvath DNA methylation age (DNAmAge) was assessed using the algorithm described by Horvath [5] and available at https://dnamage.genetics.ucla.edu/home. The algorithm for the Levine DNAmAge was obtained from Levine et al. by request. Normalized data (beta values) were used as input to derive the DNAmAges, and the values were further adjusted for blood cell distributions and chronological age to yield the epigenetic clock residuals. These residuals, hereafter denoted as the Horvath and Levine (epigenetic) clocks, were used as the final values in the modeling. By definition, the residuals generated this way have a mean and sum equal or very close to zero. Per recommendation, we used normalized methylation data (personal communication with S. Horvath), which resulted in SDs that were comparable between the datasets. We used these values to derive the age and cell count -adjusted Horvath clock residuals. The blood cell type distributions (monocytes, granulocytes, B cells, CD4 and CD8 and NK cells) for both cohorts were assessed using the Houseman method [20].

2.3. Statistical methods

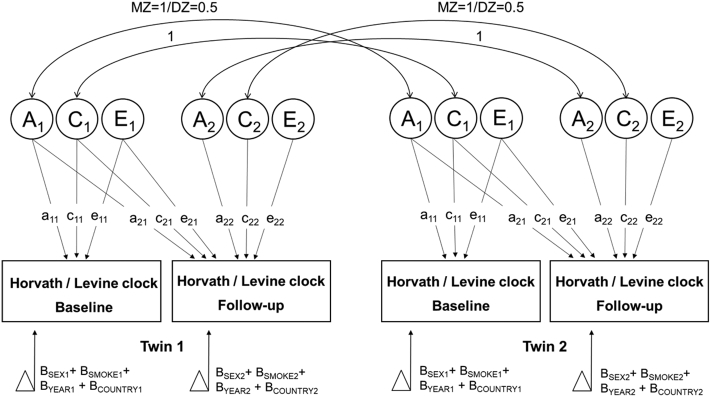
Longitudinal biometric twin models, such as the bivariate Cholesky for two measurement occasions, can be used to estimate genetic and environmental influences that are shared between different ages (or measurement occasions) versus those that are specific to certain ages [21]. That is, in addition to partitioning the phenotypic variation in the epigenetic clocks at the two occasions into additive genetic (A), dominant or non-additive genetic (D), common environmental (i.e., shared among family members; C), and unique environmental (i.e. person-specific; E), we can evaluate the covariation between these sources of variation, i.e., stability across time. Fig. 1 illustrates the bivariate Cholesky decomposition model that we used to partition the sources of variance in the Horvath and Levine clocks at baseline and follow-up, as well as the sources of covariance across time. This model specifies two sets of three latent factors (dominant genetic influences not shown); A₁, C₁, and E₁ that influence the clocks at both baseline and follow-up, and A₂, C₂, and E₂ that are specific to follow-up (Fig. 1). The magnitudes of the variance components at the two measurement occasions and cross time can be calculated from the path coefficients using path tracing rules [21]. The analyses were adjusted for sex (0 = male, 1 = female), current smoking status (0 = no, 1 = yes), cohort effects (birth year) and country (0 = Sweden, 1 = Denmark) (Fig. 1). Age was not included as a covariate as the effect of age was already regressed out from the clock residuals. Medical conditions were not considered as covariates; hence, the results are interpretable as general population estimates in old individuals of which many have co-morbidity.

Fig. 1.

The bivariate Cholesky decomposition model. This model estimates the latent additive genetic (A), shared environmental (C), and person-specific environmental (E) variance components that affect the clocks at both time points (A₁, C₁, E₁) yet possibly at different magnitude, and those that are unique to time 2 (A₂, C₂, E₂). Replacing C by dominant genetic effects (D) would fix the correlation between DZ twins to 0.25. The path coefficients are; a11 genetic path for clock at time 1; c11, shared environmental path for clock at time 1; e11, non-shared environmental path for clock at time 1; a21, genetic covariance between clock at time 1 and time 2; c21, shared environmental covariance between clock at time 1 and time 1; e21, non-shared environmental covariance between clock at time 1 and time 2; a22, genetic path unique to clock at time 2; c22, shared environmental path unique clock at time 2; e22, non-shared environmental path unique to clock at time 2. The clock values are adjusted for sex (0 = male, 1 = female), current smoking status (0 = no, 1 = yes), cohort effects (birth year) and country (0 = Sweden,1 = Denmark).

The bivariate design provides a more powerful method than two univariate analyses to assess variance components' contributions on two correlated traits, i.e., the baseline and follow-up clock measures in our case, since it exploits the extra information of the cross-time (CT) and the cross-twin cross-time (CTCT) correlations. The CTCT correlation is the within-pair correlation between the twin A's clock value at baseline and twin B's clock value at follow-up and vice versa, and it informs about the relative importance of genetic and environmental contributions to the phenotypic correlation of the clocks across time. If the CTCT is greater for MZ twins than for DZ twins, it suggests that genetic factors contribute to stability of the clock across time. The bivariate design also allows us to estimate the extent to which the estimated sources of variation (A, C/D and E) overlap across time. That is, we can obtain the genetic correlation (rA or rD), common environmental correlation (rC) and c unique environmental correlation (rE). For example, if the rA = 1, it indicates that the same genetic factors influence the clock at both baseline and follow-up and no new genetic influences emerge with time.

We fitted a fully saturated model that perfectly captures the mean levels, variance and covariance of the observed data. To evaluate whether an ACE or ADE model and sub-models, i.e. AE, CE and E provided a better more parsimonious fit to the data, comparisons of the Akaike index and likelihood ratio testing were performed [21]. The slightly greater variances for both clocks in the Swedish sample were accounted for using a scalar correction, i.e., by multiplying the Danish data so that the variances across the countries became equal. Descriptive statistics and twin correlations for the clocks were assessed separately for the Swedish and Danish samples using Stata (version 15·1, College Station, TX: StataCorp LP). For the bivariate modeling, the samples were pooled to obtain more power. The models were run using the structural equation model program Mplus 8.1. P-values <0·05 were considered statistically significant.

2.4. Ethics approval and consent to participate

All participants in both cohorts have given their informed consent to participate. The SATSA study was approved by the Regional Ethics Review Board in Stockholm (Dnr 2015/1729-31/5). The LSADT study was approved by the Regional Committees on Health Research Ethics for Southern Denmark (S-VF-20040241).

3. Results

3.1. Descriptive statistics

Characteristics of the study sample are presented in Table 1. The mean age of SATSA participants was 65·3 (standard deviation [SD] ± 8·3) years at baseline and 74·1 (SD ± 7·3) years at follow-up. The mean age of the LSADT sample was 76·2 (SD ± 1·8) years at baseline and 86·1 (SD ± 1·8) years at follow-up. The derived Horvath clock residuals demonstrated mean levels in the expected range (mean close to zero; Table 1). We also assessed the correlation between the Horvath and Levine clocks at baseline and follow-up. The clock residuals were moderately correlated with each other at each occasion (r = 0·36, p < 0·001) and (r = 0·31, p < 0·001).

Table 1.

Characteristics of the study population.

	Swedish twins, SATSA		Danish twins, LSADT		Pooled		p across time
	Mean (SD)		Mean (SD)		Mean (SD)
	Baseline	Follow-up	Baseline	Follow-up	Baseline	Follow-up
aMZ pairs	26 (41·3)		16 (39·0)		42 (40·4)
aDZ pairs	37 (58·7)		25 (61·0)		62 (59·6)
aWomen	70 (55·6)		58 (70·7)		128 (61·5)
bBirth year	1915–1947		1915–1923		1915–1947
aCurrent smokers	27 (21·4)	16 (12·7)	18 (22·0)	10 (12·2)	45 (21·6)	26 (12·5)
Age	65·6 (8·3)	74·1 (7·3)	76·3 (1·8)	86·2 (1·8)	69·8 (8·4)	78·9 (8·3)
Horvath DNAmAge	44·3 (6·7)	49·2 (7·7)	71·3 (4·8)	79·0 (5·2)	55·0 (14·5)	64·4 (20·2)	<0·001
Horvath clock residual	0·10 (5·9)	0·33 (6·9)	−0·44 (4·2)	−0·02 (4·8)	−0·11 (5·3)	0·19 (6·2)	0·466
Levine DNAmAge	63·6 (9·6)	69·8 (8·3)	66·6 (6·1)	76·7 (7·1)	64·8 (8·3)	72·5 (8·7)	<0·001
Levine clock residual	−0·54 (7·2)	0·48 (6·8)	−0·40 (5·7)	0·04 (6·9)	−0·49 (6·6)	0·31 (6·8)	0·146

Note. The DNAmAge values are years. The somewhat lower than expected mean value for the Horvath DNAmAge in SATSA is explained in the Methods. The clock residuals are derived from adjusting the Horvath and Levine DNAmAges for blood cell counts and chronological age. The p-value for the across-time difference in the pooled sample was assessed using paired samples t-test. Abbreviations: DNAmAge, DNA methylation age; DZ, dizygotic; MZ, monozygotic; SD, standard deviation.

^aNumbers are N (%).

^bNumbers are range (min-max).

3.2. Twin correlations

The sex, smoking, birth year and sample origin -adjusted twin correlations and phenotypic correlations across age for the Horvath and Levine clocks are shown in Table 2. Corresponding unadjusted correlations, excluding the CTCT correlations, also assessed separately for both samples, are presented in Supplementary Table S1. Both the within-time and CTCT correlations were greater for the MZ twins than for DZ twins for both clocks (Table 2), suggesting genetic influences on within-time variation and cross-time covariance (stability). The phenotypic cross-time correlation was moderate for the Horvath clock (r = 0·52) and modest for the Levine clock (r = 0·36), indicating greater longitudinal stability for the former (Table 2).

Table 2.

The twin pair, phenotypic and cross-twin cross-trait correlations (95% CI) for the Horvath and Levine epigenetic clocks. The correlations are adjusted for sex, smoking, birth year and sample origin (country).

		Pooled sample of SATSA and LSADT
		Baseline	Follow-up	CTCT r	Phenotypic r
Horvath clock	MZ	0·54 (0·29, 0·79)	0·55 (0·35, 0·75)	0·37 (0·18, 0·53)	0·52
	DZ	0·31 (0·12, 0·51)	0·19 (−0·04, 0·42)	0·25 (0·08, 0·41)	(0·41, 0·63)
Levine clock	MZ	0·41 (0·07, 0·75)	0·38 (0·10, 0·67)	0·44 (0·23, 0·65)	0·36
	DZ	0·10 (−0·11, 0·31)	0·19 (−0·03, 0·41)	0·11 (−0·05, 0·27)	(0·24, 0·49)

Note. Phenotypic correlation represents the cross-time correlation for the trait in the sample. The CTCT correlation is the within-pair correlation between the twin A's clock value at time 1 and twin B's clock value at time 2 and vice versa.

Abbreviations: CI, confidence interval; CTCT, cross-twin cross-trait; MZ, monozygotic; DZ, dizygotic.

3.3. Quantitative genetic modeling

Fig. 1 describes the Cholesky biometric model of within-pair correlations in MZ and DZ twin pairs to derive the sources of A, D, C and E variation in the clocks at each occasion as well as across time (approximately 9 years). Prior to the modeling, we verified that the assumptions of equal means, variances and regression coefficients across zygosity and twin order were met. These parameters could thus be constrained to be equal in subsequent analyses. The full ACE and ADE Cholesky models did not provide a significantly worse fit than the fully saturated model. Based on the Akaike's information criterion (AIC), the ADE model provided a slightly better fit than ACE for both clocks (Supplementary Table S2). Subsequent comparison for the nested sub-models indicated that the AE model provided the most parsimonious fit to the data for both clocks (Supplementary Table S2). That is, although the twin correlations at baseline suggest a contribution from D, we could drop the D effects without significantly reducing the model fit. However, significant loss of fit was observed when dropping A effects from the AE model (Supplementary Table S2). Thus, the path coefficients (Fig. 2) and the magnitudes of the variance components (Table 3) are presented for the AE model for both clocks.

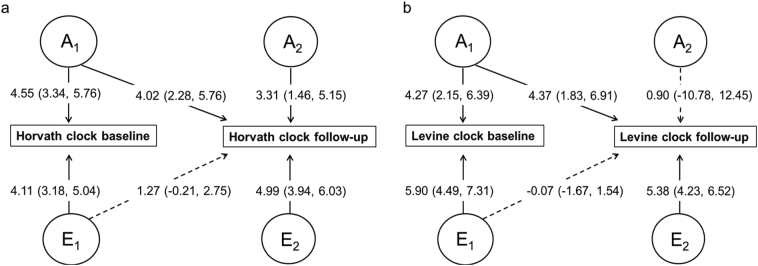
Fig. 2.

Unstandardized parameter estimates for the Horvath clock (A) and Levine clock (B) from the Cholesky AE model. Significant paths are indicated with solid lines and non-significant with dashed lines. The numbers in parentheses indicate 95% confidence intervals. The models are adjusted for sex, current smoking status, cohort (birth year) and country (not shown, see Fig. 1).

Table 3.

Proportions of variance explained by genetic (a [2]) and non-shared environmental (e [2]) factors for the Horvath and Levine clocks at time 1 and time 2 in the pooled sample of SATSA and LSADT. The genetic and environmental correlations, rA and rE, indicate the extent of overlap in A and E between time 1 and time 2.

		a2	e2	Cross-time a2	Cross-time e2	rA	rE
Horvath clock	Baseline	0·55 (0·34, 0·76)	0·45 (0·24, 0·66)	0·78 (0·51, 1·05)	0·22 (−0·05, 0·49)	0·77 (0·52, 1·03)	0·25 (−0·02, 0·52)
	Follow-up	0·51 (0·30, 0·71)	0·49 (0·29, 0·70)
Levine clock	Baseline	0·34 (0·04, 0·65)	0·66 (0·35, 0·97)	1·02 (0·50, 1·54)	−0·02 (−0·54, 0·50)	0·98 (0·45, 1·51)	−0·01 (−0·31, 0·29)
	Follow-up	0·41 (0·17, 0·65)	0·59 (0·36, 0·83)

Note. Numbers in parentheses indicate 95% confidence intervals. The analyses were adjusted for sex (0 = male, 1 = female), current smoking status (0 = no, 1 = yes), cohort effects (birth year) and country (0 = Sweden,1 = Denmark).

Changes in total (raw) variance components under the Cholesky AE model for both clocks separately for the Swedish and the Danish sample are presented in Supplementary Fig. S1. For the Horvath clock, the total variation increased from 37·55 at baseline to 53·59 at follow-up in the Swedish sample, and was a consequence of A increasing by 31% and E increasing by 57%. In the Danish sample, the total variation increased from 14·77 to 18·15, and the increase was a consequence of A increasing by 13% and E increasing by 35% (Supplementary Fig. S1a). For the Levine clock, the total variation marginally decreased from 53·04 at baseline to 48·79 at follow-up in the Swedish sample, and was a consequence of E decreasing by 17% while A increased by 8%. In the Danish sample, the total variation increased from 30·87 to 41·52, and it was a consequence of A increasing by 69% and E increasing by 21% (Supplementary Fig. S1b). Scalars of 0·63 at baseline and 0·58 at follow-up for the Horvath clock and 0·76 at baseline and 0·92 at follow-up for the Levine clock were used to allow for scalar (proportional) differences in total (raw) variation at each measurement while the relative contributions of A, C/D; and E were equated between the Danish and Swedish samples.

The unstandardized Cholesky path coefficients are presented in Fig. 2. For the Horvath clock, the same genetic factors, i.e. those that overlap between baseline and follow-up (A₁), account a little over half of the genetic variation at follow-up (path a_21,Fig. 2). Consequently, significant amounts of new A emerge at follow-up (path a₂₂), accounting for a bit less than half of the genetic variation at follow-up (Fig. 2). The person-specific E effects are specific to each occasion as the amount of overlap indicated by path e₂₁ is non-significant (Fig. 2). For the Levine clock, the same genetic factors (A₁, paths a₁₁ and a₂₁) account for the genetic variance at both baseline and follow-up and no new significant A influences emerge at follow-up (path a₂₂, Fig. 2). Similar to the Horvath clock, there were no significant person-specific E influences common to both times (path e₂₁, Fig. 2). The estimated genetic correlation was high for the Horvath clock (rA = 0·77) and almost perfect for the Levine clock (rA = 0·98), indicating that the genetic factors contributing to the variance at baseline and follow-up were largely the same for Horvath and practically identical for the Levine (Table 3). Regression coefficients for the model covariates are presented in Supplementary Table S3. All covariates were entered into all the models regardless of whether they were significant or not.

The standardized AE model results indicate that the heritability (a [2]; the proportion of variance explained by A) was similar at 55% and 51% for the Horvath clock and 36% and 41% for the Levine clock at baseline and follow-up, respectively (Table 3). The remaining variance was accounted for by person-specific environmental effects (e [2]) that were greater for the Levine clock than for Horvath at both times. This finding is reflected by the cross-time a² estimates of 78% for Horvath and 102% for Levine (Table 3). The negligible rE for the Levine clock indicates that the person-specific environmental influences are completely different at baseline and follow-up. For the Horvath clock, the rE of 0·25 (Table 2) suggests some degree of overlap in the person-specific environmental effects, but the estimate was not statistically significantly different from zero.

4. Discussion

In this longitudinal twin study, demonstrated that the Horvath and Levine epigenetic clocks in whole blood are moderately heritable at and across old age. For the Horvath clock, the total (raw) variance increased from baseline to follow-up with both A and E increasing absolute values in both samples. For the Levine clock, the raw variance explained by A increased from baseline to follow-up in absolute and relative values, whereas the variance explained by E was attenuated across time with scalar differences in absolute values across the Swedish and Danish samples. Increases in the raw variances would indicate that the individuals become more heterogeneous with time and also suggest that people may not only vary in their level but also in their slope. For the Horvath clock, new genetic influences emerged across time, whereas for the Levine clock, the same genetic factors acted upon the clock at both occasions. Although the genetic variation for the Levine clock was more stable than that of the Horvath clock, the Horvath clock showed greater longitudinal phenotypic stability than the Levine clock. For both clocks, the longitudinal stability was nevertheless driven by genetic factors. Consequently, essentially all the person-specific environmental influences were unique to each measurement occasion.

Previous twin studies that looked into the variance components of the clocks are rather limited in number. Heritability of the Horvath clock was first assessed in one of the data sets used to derive the clock and was estimated at 39% in 31 female twin pairs aged between 49 and 74 years [5]. Marioni et al. (2015) used family data including adolescent twins, their siblings and parents, and estimated the Horvath clock heritability at 43% [9]. Pedigree and single nucleotide polymorphism (SNP)-based estimates for the Horvath clock reported in a recent genome-wide association study (GWAS) have been somewhat lower, 37% and 19%, respectively [6]. Previous results for the Levine clock heritability are available only as pedigree and SNP-based estimates from a GWAS that demonstrate heritabilities of 33% and 51%, respectively, the latter being obtained in a cohort of postmenopausal women [3]. Our heritability estimates for the Levine clock at baseline align well with the pedigree-based estimates. For the Horvath clock, our heritability estimates of 55% and 51%, are higher than previously reported. One reason for the higher values might be our selection of individuals with two measurement occasions available. Moreover, many of the SATSA participants and all the LSADT participants had their follow-up measurement at advanced ages. Hence, the sample is by design homogenous for survival into old age – an aspect that may lead to lower variance and higher heritability for survival-related traits. However, the lack of comparable longitudinal studies across the same age periods hampers effective comparisons for the moment.

Given that the epigenetic clocks have been proposed as candidate markers to monitor healthy aging and assess the need for preventive measures against chronic disorders [1], our findings may inform about the prospects of such plans. Contribution of the person-specific environmental effects, which were sizeable especially for the Levine clock, would suggest that the clocks are responsive to environmental cues even at old age, which in turn may be in part due to genetic mediation. That is, methylation may reflect altered gene expression that is at the nexus of gene-environment (GE) interplay. Where genetic variance increases, amplification of genetic influences on altered expression may be at play, whereas increased E may partly reflect an increasing modulation of expression that depends partly on the exposure and partly on the genetic modulation of sensitivity to that environment (i.e., may index some GxE). Moreover, the Levine clock showed also more longitudinal variation (lower stability) than the Horvath. Since it has been shown to outperform the Horvath clock in predicting mortality, aging-associated diseases and functional performance [3], the Levine clock may contain CpG sites that are more plausible targets for monitoring. However, person-specific environmental effects were non-stable, i.e., specific to each measurement occasion, suggests that these factors vary within a relatively short period in old age.

It is worth highlighting that twin modeling assesses the influences of the latent factors (A and E in our study) on trait variances and not on means. With this in mind, it is interesting that new sources of genetic influences come into play with age for the Horvath clock. As our samples largely align with the post-menopausal period, sex hormone withdrawal and the associated changes in gene expression might be contributing mechanisms. Sex steroid mediated regulation for the Horvath clock has previously been demonstrated in a Mendelian randomization analysis; a causal association was found between early timing of menarche and menopause and higher Horvath clock [6]. Although a GWAS-based genetic correlation between the Horvath clock and age at menopause has been shown to be rather weak [6], menopause and its associated traits might have been captured by the A in our study, rather than E, as the age at menopause is highly heritable, up to 87% [22]. Interestingly, genetic variants underlying leukocyte telomere length have also been shown to be associated with the Horvath clock, yet the alleles associated with longer telomeres were associated with higher Horvath clock [6]. The genetic component for the Horvath clock appears thus complex and pleiotropic.

As the Levine clock by definition captures (bio)physiological regulation of the nine biomarkers used to create the measure, it is not surprising that it had a larger person-specific variance component and lower cross-time stability than the Horvath clock. Associations with environmental and life style factors, such as smoking, exercise and dietary habits as well with functional performance and age-associated disease have indeed been stronger and more numerous for the Levine clock than for the Horvath [1,3]. Genetic variants underlying the Levine clock are yet to be identified as the clock was very recently introduced. Our observation that the same genetic factors influence the Levine clock across old age would nevertheless suggest a stable genetic component. The almost perfect genetic cross-time correlation can be due to either the same genes directly influencing the Levine clock at the two occasions or the genes influencing the clock at baseline create a series of events that lead to continuation in the Levine clock at follow-up. The former scenario is perhaps more plausible in our data. The genetic factors were, however found to increase their absolute and relative impact with age. If this finding is corroborated in further studies, it will be pertinent to study its underpinnings. In specific, if it is the same genes directly affecting the clock across time, as physiologic and homeostatic resources become depleted with age, genetics would play a greater role in keeping the Levine clock (and its constituting biomarkers) at an optimal level. In this scenario, common genetic variants would show less pronounced effects on the Levine clock in younger ages when the resources are higher.

A limitation of our study was the lack of power to demonstrate whether the variance components are different between the clocks as the confidence intervals overlapped. We could also not examine potential quantitative or qualitative sex differences in the variance components, as we did not have enough power to stratify the analysis by sex or opposite sex pairs available for a sex-limitation model. Another issue worth noting is that although the baseline twin correlation for the Horvath clock suggests C (shared familial environmental) influences, we tested this in the bivariate models, and the C was non-significant for both clocks (Supplementary Table S2). A study by Li et al. (2015) has in fact examined the differences in the Horvath clock correlations between middle-aged MZ and DZ twins and their sisters, and suggested that some part of the genetic variation might actually be due to C [23]. They did not, however, estimate the variance components or provide an estimate of heritability in their data. However, even if an ACE model was selected in our study, the classical twin design has relatively low power to detect C compared to A, and to do so requires a very large sample. A major strength of our study is nevertheless the follow-up design with the same individuals providing measures of both clocks at the same occasions, enabling meaningful comparison of the clocks' variance components longitudinally. It should be noted, however, that our data do not allow assessment of the variance components for the clock trajectories i.e., the slope; for that purpose we would have needed at least three measurement occasions. Furthermore, as twin modeling assesses latent factors, further research is needed to identify the specific genetic and environmental factors that act upon the variances and means.

In conclusion, the results of this longitudinal study demonstrate that the Horvath and Levine clocks are moderately heritable at and across old age. The somewhat striking finding that the person-specific environmental effects were specific to each measurement occasion warrants further analysis into these potentially age-varying factors. The magnitudes of these components nevertheless suggest that both clocks may be responsive to environmental stimuli by means of intervention, even at old age. However, as our results concern whole blood, further studies are needed to demonstrate whether similar results are obtained in other tissues and cell types.

Availability of data and material

For the SATSA study, the methylation data are available in the ArrayExpress database at EMBL-EBI (www.ebi.ac.uk/arrayexpress) under accession number E-MTAB-7309. SATSA covariate data used in the present analysis are available from the authors upon request.

For the LSADT study, according to Danish legislation, transfer and sharing of individual-level data requires prior approval from the Danish Data Protection Agency and requires that data sharing requests be dealt with on a case-by-case basis. For this reason, the data cannot be deposited in a public database. However, we welcome any enquiries regarding collaboration and individual requests for data sharing.

Conflict of interest

None.

Funding

The SATSA study was supported by NIH grants R01 AG04563, AG10175, AG028555, the MacArthur Foundation Research Network on Successful Aging, the Swedish Council for Working Life and Social Research (FAS/FORTE) (97:0147:1B, 2009-0795), and the Swedish Research Council (825-2007-7460, 825-2009-6141). This study is supported by the Swedish Research Council (521-2013-8689, 2015-03255), JPND/Swedish Research Council (2015-06796), FORTE (2013-2292), the Loo & Hans Osterman Foundation, the Foundation for Geriatric Diseases, the Magnus Bergwall Foundation, and the Strategic Research Program in Epidemiology at Karolinska Institutet. The LSADT study has been supported by grants from the VELUX FOUNDATION, the U.S. National Institute on Aging (P01-AG08761), the European Union's Seventh Framework Programme (FP7/2007-2011) under grant agreement no. 259679, and The Danish National Program for Research Infrastructure 2007 (9-063256). The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. The corresponding author had full access to all the data in the study and had final responsibility for the decision to submit the work for publication.

Author contributions

JJ and CAR analyzed data and drafted the manuscript. NLP is the director of the SATSA study, and LC and KC are directors of the LSADT study. NLP and SH contributed to the coordination of the study and acquisition of the SATSA methylation data. JH participated in interpretation of the results and together with MS, QT and JMF, coordinated the LSADT data acquisition. EM and RKH provided advice in scripting. All authors participated in interpretation of the data, have read and commented on the manuscript and approved the final version.

Appendix A. Supplementary data

Supplementary material