Hydronium Ions Accompanying Buried Acidic Residues Lead to High Apparent Dielectric Constants in the Interior of Proteins

Abstract

Internal ionizable groups are known to play important roles in protein functions. A mystery that has attracted decades of extensive experimental and theoretical studies is the apparent dielectric constants experienced by buried ionizable groups, which are much higher than values expected for protein interiors. Many interpretations have been proposed, such as water penetration, conformational relaxation, local unfolding, protein intrinsic backbone fluctuations, etc. However, these interpretations conflict with many experimental observations. The virtual mixture of multiple states (VMMS) simulation method developed in our lab provides a direct approach for studying the equilibrium of multiple chemical states and can monitor pK_a values along simulation trajectories. Through VMMS simulations of staphylococcal nuclease (SNase) variants with internal Asp or Glu residues, we discovered that cations were attracted to buried deprotonated acidic groups and the presence of the nearby cations were essential to reproduce experimentally measured pK_a values. This finding, combined with structural analysis and validation simulations, suggests that the proton released from a deprotonation process stays near the deprotonated group inside proteins, possibly in the form of a hydronium ion. The existence of a proton near a buried charge has many implications in our understanding of protein functions.

Graphical Abstract

INTRODUCTION

Buried ionizable groups are important for biomolecular functions, such as catalysis,¹ redox reactions,^2,3 proton transport,^4,5 and proton-coupled-electron-transfer reactions.⁶ During biomolecular function cycles, ionizable groups that experience microenvironment changes may adopt different protonation states.

A major mystery that remains after decades of studies is the high apparent dielectric constants experienced by buried ionizable groups. pK_a is a property that measures the tendency of deprotonation. When an ionizable group transfers from aqueous solution to the hydrophobic environment inside proteins, its pK_a shifts. The pK_a shift reflects the difference in dielectric behaviors between aqueous solution and the environment of the protein interior and can be converted to the apparent dielectric constant. The pK_a values of many ionizable groups in proteins have been measured via NMR spectroscopy,^7,8 from which it has been determined that the apparent dielectric constants around internal ionizable groups can be as high as 10–20, which is much higher than 2–4 expected inside proteins.⁹

Over the decades, to explain the high apparent dielectric constants, many experimental and theoretical studies have been performed. Among many labs studying buried ionizable groups, Garcia-Moreno’s lab has systematically engineered a series of staphylococcal nuclease (SNase) variants with ionizable residue mutations at various positions.^10–15 These variants provide systematic targets for studies on the properties of the internal environment of proteins.

Many interpretations for the high apparent dielectric constants around buried ionizable groups have been proposed. Water penetration is thought to be a major factor,^16–21 even though some crystal structures do not show water molecules around ionizable groups and long-lived water penetration is not observed in certain variants.²² Another interpretation is conformational relaxation and local unfolding.^{13,17,18,22–25} However, many studies found no detectable conformational changes upon charging buried ionizable groups.^10,26–29 A high apparent dielectric constant has also been suggested as being a property resulting from the intrinsic backbone fluctuations originating from its structural architecture.¹¹ In addition, some studies show that the structural responses involving ionization of buried ionizable groups are in a time scale beyond microseconds,^30,31 implying that the mystery of the high apparent dielectric constants is difficult to address with nanosecond-scale molecular dynamics simulations.

Many computational methods for structure-based calculation of pK_a values have been developed to examine pK_a’s molecular determinants.^9,32–40 The large energy barriers between different charge states when simulating with explicit solvent makes sequential sampling of all charge states highly inefficient. The virtual mixture of multiple states (VMMS) method⁴¹ was designed to directly simulate chemical state equilibrium and can sample different charge states efficiently in explicit solvent. VMMS simulations produce instantaneous pK_a values along simulation trajectories and are convenient for deciphering molecular determinants behind pK_a shifts. This method has been applied to calculate the pK_a values of SNase variants with lysine mutations, and the results agree with experimental measurements reasonably well.⁴² Water penetration was found to be the major reason for the high apparent dielectric constants around buried lysine residues.

In this work, we performed VMMS simulations for SNase variants with buried acidic residues, Asp and Glu. Our simulation results show that water penetration and conformation relaxation are not enough to account for the high apparent dielectric constants. Surprisingly, we found that cations floated into the buried charges and brought pK_a close to experiment values. This finding, combined with additional chemical, energetic, structural, and simulation analysis, led us to believe that nearby protons, possibly in the form of hydronium ions, are a main contributor to the high apparent dielectric constants around buried acidic residues.

METHODS

SNase Variants.

The initial conformations of the 10 SNase variants, listed in Table I, were taken from PDB database when available. For the Asp mutation variants that did not have crystal structures, we built their initial conformations from the PDB structures of their corresponding Glu mutation variants. All variants contain a SNase protein, a thymidine-3′,5′-diphosphate ligand, and a calcium ion. The VMMS systems were constructed by dissolving the initial conformations into a box of TIP3P water together with several ions to produce a neutral system in a cubic box of 46.655 × 46.655 × 46.655 ų. The number of water molecules and ions in the deprotonated states are listed in Table I. The protonated state has one sodium ion replaced with a water molecule. In the simulations with a hydronium ion, the deprotonated state was created from the protonated state by replacing a water near the acidic group with a hydronium ion.

Table I.

VMMS Simulation Systems and the Hydronium Interaction Energies^a

systems	structureb	pKa (exp.)	systemd (TIP3P,Na+ + H3O+,Cl−)	$E_{{\text{H}}_3\text{O}}$ kcal/mol	$\delta E_{{\text{H}}_3\text{O}}$ kcal/mol
Aspc	model	4.0	(980,5,4)	−116.61 ± 0.14 (−121.60 ± 0.15)	7.30 (7.41)
Gluc	model	4.4	(977,5,4)	−116.50 ± 0.15 (−121.46 ± 0.19)	7.52 (7.32)
V66D	5egtb	9.025	(2831,7,15)	−119.83 ± 0.07	7.29
V66E	5egt	9.125	(2803,8,15)	−119.60 ± 0.07	5.62
L25D	4ky6	6.829	(2820,8,15)	−128.27 ± 0.08	7.57
L25E	3evq	7.528	(2809,8,15)	−124.18 ± 0.07	7.32
L38D	5isrb	7.213	(2823,8,15)	−126.59 ± 0.09	9.39
L38E	5isr	7.013	(2817,8,15)	−132.78 ± 0.08	5.35
I72D	4eqp	7.629	(2825,8,15)	−126.54 ± 0.15	7.99
I72E	3ero	7.328	(2824,8,15)	−129.78 ± 0.08	8.50
I92D	5kixb	7.549	(2815,12,15)	−120.95 ± 0.07	7.36
I92E	5kix	9.028	(2777,7,15)	−129.71 ± 0.06	6.43

^aSNase variants are named by their mutations.

^bSome variants with Asp mutations have no X-ray structure and were created by mutating Glu to Asp from the corresponding variant crystal structures.

^cThe hydronium interaction energies for the model compounds are for the noncomplexing states. Their complexing state hydronium interaction energies are shown in parenthesis.

^dNumbers of water molecules, sodium plus hydronium ions, chloride ions in the deprotonated state are listed for each system.

The deprotonated state has a dummy hydrogen so that the SNase variants in both states have the same number of atoms. The dummy hydrogen atom is identical to a hydrogen atom except that it has no charge. The atomic charges of the ionizable residues can be found in ref 41.

The reference deprotonation free energies $\left(\Delta G_{\text{HD}}^{\text{ref}}\right)$ of Asp and Glu, which are needed to calculate the pK_a values of these residues in the SNase variants, were obtained with model compounds. The model compounds consist of an ionizable residue, Asp or Glu, with an acetyl group (ACE) at the N-terminal and a methyl amide group (NME) at the C-terminal: ACE-Asp-NME or ACE-Glu-NME. The reference systems were built by dissolving the model compounds into a cubic TIP3P⁴³ water box, including several chloride and sodium ions. The box side was 31.1 Å.

Equal-Molar VMMS Simulations.

An equal-molar VMMS system contains two subsystems, one for the protonated state and one for the deprotonated state. At every time step, interaction forces at each subsystem are calculated independently. The solvent forces at each state are used to drive the motion of the solvent atoms. The solute forces from both states are averaged (50% from each state) to produce combined forces that drive the motion of the solute atoms. Therefore, solvent atoms in different subsystems experience different forces and sample their conformations differently, whereas solute atoms in all subsystems experience the same combined forces and sample their conformational space the same way. At every specific interval (10 fs in simulations presented here), the energy changes of the solute in transition from the current state to another state were calculated to evaluate the quantities for free-energy calculation. More details can be found in our previous work.1^41,42

All simulations presented here were performed with a modified version 39 of CHARMM^44,45 with the VMMS method implemented. The all-atom CHARMM36 force field⁴⁶ was used for energy calculation. All simulations were performed in a constant volume and a constant temperature of 300 K using the self-guided Langevin dynamics via generalized Langevin equation method⁴⁷ with a local averaging time t_L = 0.2 ps, a guiding factor λ =1, and a friction constant ξ = 10/ps. A time step of 1 fs was used, and the SHAKE algorithm⁴⁸ was employed to fix hydrogen connecting bond lengths.

RESULTS AND DISCUSSION

VMMS Simulations Show Low Dielectric Constants inside Many SNase Variants.

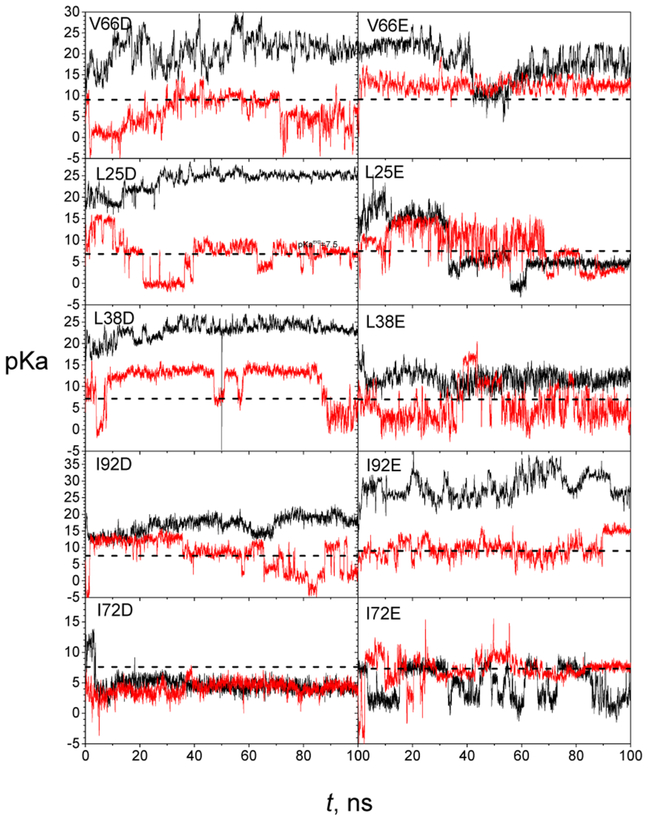
Table I lists the 10 SNase variants simulated in this work. Their pK_a values have been measured experimentally and can be compared with our simulation results. The pK_a profiles of these variants during our VMMS simulations are shown in Figure 1 (black curves). Not surprisingly, we see large discrepancies between the calculated pK_a values and the experimental results (dashed lines) for many variants. As can be seen in Figure 1, V66D, L25D, L38D, I92D, and I92E’s pK_a values fluctuate between 15 and 40, much higher than their experimental values ranging between 5 and 10. These large discrepancies indicate that the apparent dielectric constants in the simulations are significantly lower than those observed in experiments. In other words, the high apparent dielectric constants observed in experiment are not captured in these simulation systems.

Figure 1.

pK_a profiles of the SNase variants during VMMS simulations. The variant names are labeled in their panels. Simulations without hydronium ions are shown with the black lines and simulations with nearby hydronium ions are shown with the red lines. Experimental values are marked by the horizontal dashed lines.

Conformational Relaxation and Water Penetration Are Not Enough To Account for the High Apparent Dielectric Constants.

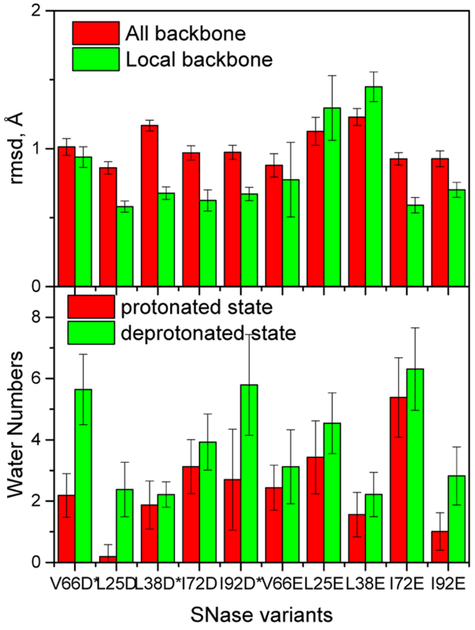
The conformational changes and numbers of water molecules around the ionizable groups are shown in Figure 2. The root-mean-square deviations (rmsd) of the backbones from X-ray structures are all under 1.5 Å, indicating conformational changes are minimal, especially for the local structures around the ionizable groups. There are water penetrations in both the protonated and deprotonated states for all variants, and the deprotonated states have more water molecules than the protonated states. The large discrepancies in pK_a values indicate that the water penetration and the conformational relaxation observed in these simulations cannot account for the high apparent dielectric constants. Although water penetration can increase the apparent dielectric constant, without significant local conformational change, the few water molecules that can be accommodated around the ionizable groups are not enough to increase the apparent dielectric constants to experimental values.

Figure 2.

Conformational changes (top panel) and penetrated water molecules (bottom panel) around the ionizable groups. The root-mean-square deviations (rmsd) are calculated against the X-ray structures. Local residues are those with any atom within 6 Å from the ionizable groups. Penetrated water molecules are counted within 6 Å from the ionizable groups. The error bars represent the standard deviations of the water numbers.

Force field inaccuracy could be a reason for the inability to reproduce the high apparent dielectric constants at buried ionizable groups. However, more accurate force fields, such as polarizable force fields, will not make too much difference inside proteins where the hydrophobic microenvironment provides little polarizability to increase the apparent dielectric constant.

Examining the simulation trajectories, we found that the large fluctuations in pK_a values shown in Figure 1 are due to changes in the number of penetrated water molecules in both the protonated and deprotonated states. The standard deviations of the penetrated water molecule numbers are shown in Figure 2 as error bars.

Discovery of Nearby Cations and Their Correlation with High Apparent Dielectric Constants.

Although large discrepancies in pK_a values are seen for many variants, there are several cases where the pK_a values from the simulations are close to the experimental values. As shown in Figure 1, the pK_a value of V66E is around 20 at the beginning, but approaches the experimental value of 9.1 at 42 ns and remains there until 55 ns. For L25E, its pK_a fluctuates between 15 and 25 until 33 ns, when its pK_a drops below the experimental value of 7.5. I72D shows a pK_a around 12 for about 3.2 ns before dropping to values below the experimental value of 7.6. I72E’s pK_a is very close to the experimental value of 7.3, but frequently drops to around 2. A drop in pK_a values corresponds to an increase in the apparent dielectric constant. These simulation trajectories with pK_a approaching experimental values provide us opportunities to examine atomic details behind the high apparent dielectric constants.

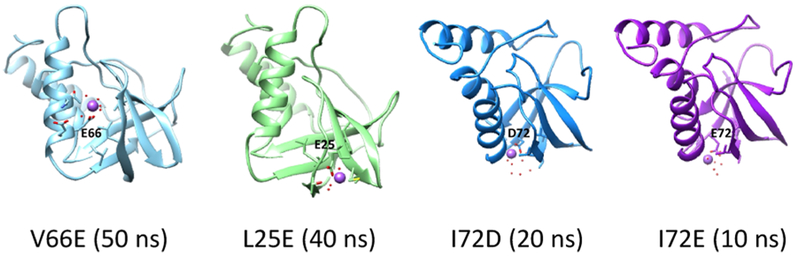
Examining the conformations where pK_a values are low, we found one common phenomenon: there is always a sodium ion near the deprotonated acidic groups. Figure 3 shows the conformations of these variants with low pK_a values where a sodium ion can be seen near the deprotonated acidic group. The correlation between presence of a nearby cation and the low pK_a values indicates that a nearby sodium ion can bring down the pK_a value. For V66E, L25E, and I72D, the lower pK_a values resulting from the nearby sodium ions agree more with their experimental results. For I72E, on the other hand, the higher pK_a values without a nearby sodium ion are more consistent with the experimental result. Examining the conformations reveals that the sidechain of E72 extends into the solvent and becomes unburied. These results tell us that a deprotonated acidic group is likely to have a nearby sodium ion when buried inside proteins, but not when unburied. This is understandable because for unburied charge groups, a nearby sodium ion can easily diffuse into bulk solvent. Therefore, the presence of a nearby sodium ion may be a reason for the high apparent dielectric constants. It is common to see that naturally buried ionizable residues interact with metal ions, such as in the crystal structures of ATPase (PDB code: 1SU4) and cytochrome C oxidase (PDB code: 5DJQ) where Ca²⁺ ions are buried and interact with charged Asp or Glu residues.

Figure 3.

Sodium ions (purple spheres) are found near the deprotonated acidic groups (labeled with residue name and number) in V66E, L25E, I72D, and I72E when their pK_a values are low, or when the apparent dielectric constants are high.

Nearby Proton Hypothesis.

Because sodium ions are the only available cations in these simulation systems, sodium ions are found near deprotonated acidic groups do not mean that only sodium ions can lead to the high apparent dielectric constants. Cations other than sodium ions would have a similar effect.

Examining both the protonated and deprotonated states of these simulation systems, we find that sodium ions exist near the acidic groups only in the deprotonated state. This is understandable because a deprotonated group has charge–charge interactions with cations, whereas a protonated group is neutral and does not have charge–charge interactions. Even though metal ions are often found in protein structures, there is no metal ion near the buried acidic groups in the crystal structures of these proteins. A proton is a natural product of the deprotonation process and is possibly hydrated to form a hydronium

$$\text{AH}\text{+}{\text{H}}_{\text{2}}\text{O}\iff {\text{A}}^{-}+{\text{H}}_{\text{3}}{\text{O}}^{+}$$ (1)

Therefore, the nearby cation is mostly likely a proton, possibly in the form of a hydronium, instead of a metal ion. On the basis of this rationale, we propose a hypothesis that a deprotonated acidic group can be stabilized by a nearby proton, possibly in the form of a hydronium ion, when buried in an apolar environment.

Why we do not see protons near acidic groups in crystal structures of these SNase variants? First, most of the X-ray structures are obtained under conditions, in which the acidic groups are in a protonated state. A protonated acidic group is neutral and has no charge–charge interactions with protons, agreeing with what was seen in our VMMS simulations. Second, protons cannot be seen with X-rays. X-rays are scattered by electrons, and hydrogen is the smallest of atoms with just one electron, making it very difficult to see. Electron-bare protons are completely invisible. Third, hydronium ions could be mistaken as water molecules due to the invisibility of protons. Even though protons cannot be seen by X-ray crystallography, the short distance between a water oxygen atom and its hydrogen-bonding acceptor implies possible hydronium ions.^50,51 An existing example of a buried ionizable residue interacting with water molecules is Glu-109 in chymosin, with one crystal water molecule and a serine hydroxyl group within hydrogen-bonding distance.⁵¹ The buried water molecule has three oxygen atoms within 2.9 Å, with the shortest of these contacts, 2.5–2.6 Å, being one of the carboxyl oxygens of the buried glutamate. The geometric features prompted the suggestion that this water molecule might be a hydronium ion (H₃O⁺). Alternatively, neutrons are scattered by atomic nuclei and can be used to visualize hydrogen atoms and protons, which can distinguish hydronium ions from water molecules. Using neutron crystallography, hydronium ions have been successfully observed in some protein structures.^52–56 Through quantum mechanics/molecular mechanics calculations, Ikeda et al. have shown that isolated hydronium ion can stably exist in the interior of proteins when hydrogen bonded with acidic residues, such as aspartic and glutamic acids.⁵⁷

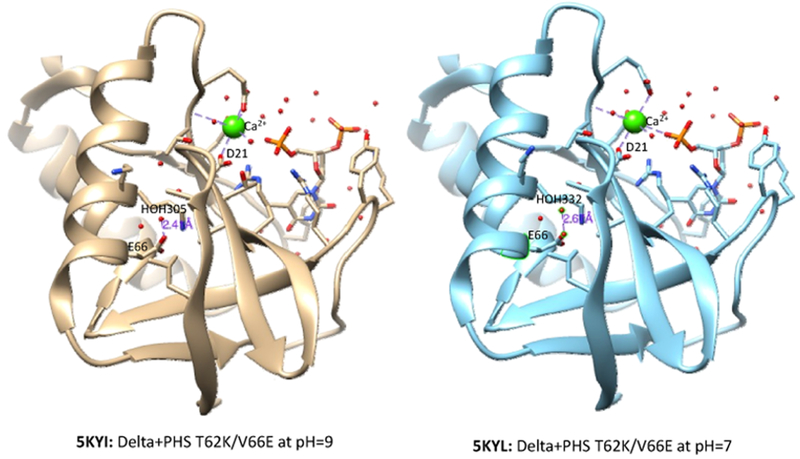
In the X-ray crystal structures of some SNase variants, we do see some crystal water molecules that are very close to the ionizable groups. For example, as shown in Figure 4, in the structure of Δ+PHS T62K/V66E at pH = 9 (PDB code: 5KYI), water A332 is 2.67 Å from E66 atom OE2, and in the structure of the same variant at pH = 7 (PDB code: 5KYL), water A305 is only 2.41 Å from E66 atom OE1. Because a typical hydrogen bond length is around 3 Å, a short distance around 2.5 Å would suggest the existence of a hydronium ion.

Figure 4.

Crystal structures of Δ+PHS T62K/V66E at pH = 9 (5KYI) and at pH = 7 (5KYL). The water molecules around the sidechain of E66 are shown as the red balls and the calcium ion near the sidechain of D21 is shown as a green sphere. In 5KYI, water molecule A305 is only 2.41 Å from E66 atom OE2, and in 5KYL, water molecule A332 is only 2.67 Å from E66 atom OE1.

Nearby Proton Hypothesis is Supported by VMMS Simulations with Added Hydronium Ions.

To verify this hypothesis, we performed VMMS simulations with a hydronium ion added near the deprotonated acidic groups. The pK_a profiles of these VMMS simulations are also shown in Figure 1 with the red curves. Clearly, it can be seen that with the nearby hydronium ions, all pK_a values from the VMMS simulations approach experimental values. Large fluctuations in the pK_a values are due to water penetrations in both protonated and deprotonated states. These results clearly demonstrate that the nearby hydronium ion can account for the high apparent dielectric constants. Without the nearby hydronium ions or other cations, pK_a values obtained from our VMMS simulations are significantly higher than the experimental results, as indicated by the black curves were also observed in Figure 1. Similar results in simulations with the AMBER force field⁵⁸ and we believe the nearby proton hypothesis is a generalizable concept.

Nearby Protons are Energetically Favored for Buried Acidic Groups.

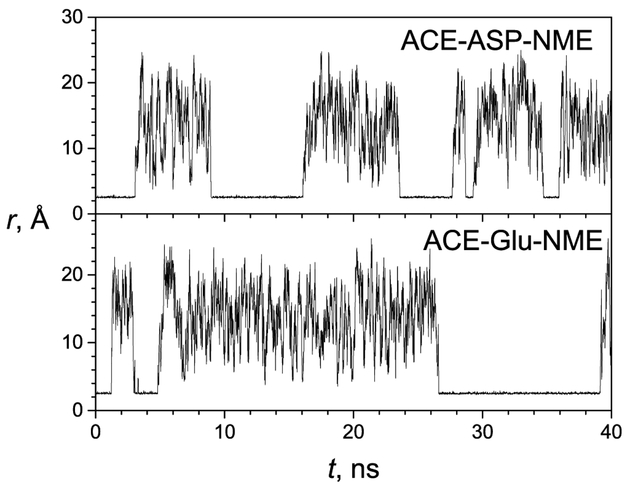
The proton produced from a deprotonation process can either stay near the deprotonated group or difluse into the bulk solvent. For the nearby proton hypothesis to stand, a proton needs to energetically favor the nearby placement. To calculate the interaction energies of hydronium ions in bulk solvent, we performed simulations of the model compounds, ACE–Asp–NME and ACE–Glu–NME, with a hydronium ion added. Figure 5 shows the distances between a hydronium ion and the ionizable groups of the model compounds during the VMMS simulations. As can be seen from Figure 5, the hydronium ions frequently move away from the deprotonated ionizable groups of the model compounds. These distance changes correspond to transitions between the complexing (nearby) state (r ~ 2.5 Å) and the noncomplexing state (r > 6 Å). The interaction energies of both states are calculated and are listed in Table I. The hydronium interaction energy in bulk water is the interaction energy of the noncomplexing state, which are −116.61 ± 0.14 and −116.50 ± 0.15 kcal/mol, for the Asp and Glu model compound systems, respectively.

Figure 5.

Distances between the hydronium ion and the charge groups during the VMMS simulations of the model compounds, ACE-Asp-NME and ACE-Glu-NME.

In the simulations of the variants, the hydronium ions stay near the deprotonated ionizable groups throughout the 100 ns simulations for all 10 variants. As shown in Table I, the hydronium interactions in all variants are stronger than interactions in bulk water. With the exceptions of V66D, V66E, and I92D, the hydronium interactions are even stronger than those of the complexing state of the model compounds. These strong interactions force the hydronium ions to stay near the buried acidic groups.

The nearby proton hypothesis does not apply to nonburied acidic groups. For ionizable residues on protein surfaces, the proton released from deprotonation would diffuse into bulk solvent, as that occurs in the model compound simulations shown in Figure 5. The model compounds, ACE-Asp-NME and ACE-Glu-NME, resemble residues on a protein surface. Therefore, there is not much difference if a hydronium ion is included for a surface ionizable group. As can be seen from Figure 5, the hydronium ions frequently move away from the deprotonated ionizable groups of the model compounds and under physiologic conditions (pH ~ 7) where the proton concentration is low, the hydronium ions will be mainly in the noncomplexing state.

The movement of cations toward the buried charge groups in the VMMS simulations of V66E, L25E, I72D, and I72E implies that the nearby placements of cations are low free-energy states. For the other variants, the simulations may be too short to see the move-in events. These move-in processes themselves indicate that cations prefer to stay near the buried charges. The interaction energies, shown in Table I, provide a quantitative support of the nearby proton hypothesis.

A nearby hydronium ion not only has stronger interactions with its surroundings, including with protein, penetrated water, and the deprotonated acidic group, but can also significantly reduce the deprotonation free energy of the buried acidic groups, which in turn lead to the high apparent dielectric constants. This is the energetic basis for a hydronium ion to favor a nearby placement. In other words, the proton produced from deprotonation prefers to stay nearby where it has a lower potential energy, which stabilizes the deprotonated state.

With a Nearby Hydronium Ion, Buried Ionizable Sidechains Show Better Agreement with X-ray Structures.

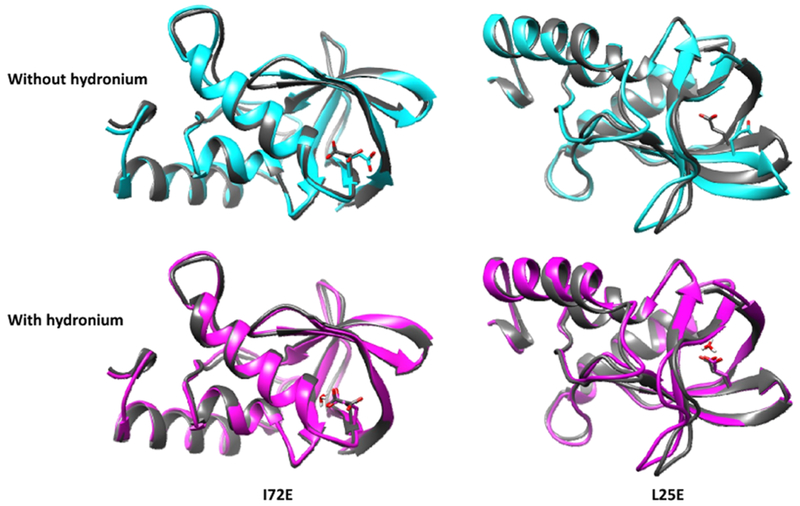
As a further support of the existence of protons near buried deprotonated acidic groups, we examined the conformations of these variants in the simulations with and without hydronium ions. We found that the buried ionizable residues kept a similar conformation to the X-ray structures when hydronium ions were added, whereas without the hydronium ions, the ionizable residues changed their conformation so that they could reach solvent. Figure 6 shows the conformations of L25E and I72E obtained from the simulations with and without a nearby hydronium ion. With nearby hydronium ions, the conformations of L25E and I72E are very similar to their X-ray structures, 3EVQ and 3ERO, respectively. In the X-ray structures, I72E is half buried and I25E is fully buried. Without a nearby hydronium ion, the carboxyl groups turn toward the solvent and become unburied, which are clearly different from the X-ray structures where the carboxyl groups point away from the solvent. For L25E, to allow the ionizable group to reach solvent, the β-sheet must break up to allow the E25 sidechain to pass through, further distorting the protein structure. In other words, without a nearby hydronium, the X-ray structure of L25E is not stable.

Figure 6.

Conformations of the ionizable residues, buried in SNase variants in simulations with and without hydronium ions. I72E is half buried and I25E is fully buried. X-ray structures are shown in dark gray. The simulation conformations are shown in cyan (without hydronium) and purple (with hydronium).

The nearby hydronium ions neutralize the deprotonated groups, allowing them to be stably buried inside proteins. This could be the reason why proteins often show little conformational change with buried charges. For acidic residues inside proteins, their deprotonation may proceed in two steps. First, the proton goes to a nearby water molecule to form a hydronium ion. Second, the proton transfers from a hydronium ion to bulk solvent. At the first stage, the overall buried group is neutral and the protein structure remains stable. At the second stage, the overall buried group is charged and could cause large-scale conformational relaxation and local unfolding. NMR measurement very likely reports the deprotonation at the first stage, where the nearby proton produces a high apparent dielectric constant without noticeable conformational relaxation or local unfolding.

Our simulation study is distinct from other simulation studies of the SNase variants due to the explicit treatment of the solvent environment. Because of the large energy barrier involving the reorientation of water molecules between different charge states, most of pK_a related simulations were performed with implicit solvation models. Implicit solvation models do not have molecular details, like the protons nearby, and cannot correctly describe the microenvironment necessary for pK_a determination. For example, Liu et al.⁵⁹ performed pH replica exchange molecular dynamics simulations using the generalized Born solvation model to study SNase variants with internal Lys, Glu, or Asp residues. With implicit solvation models, conformational change is the only way to shift pK_a to match experiment measurement. Not only pK_a values in the buried and exposed states are needed, the equilibrium constants between the buried and exposed states are also introduced as additional parameters to fit experimental pK_a values. The lack of details in implicit solvation models leads them to conclude that a coupled-ionization-conformational equilibrium is required to understand the properties of interior ionizable residues. The pK_as of introduced buried residues in staphylococcal nuclease were also analyzed with the multi-conformation continuum electrostatic program.⁶⁰ The results depend on parameters, such as the protein dielectric constant (ε_prot). An ε_prot of 8–10 and a Lennard-Jones scaling of 0.25 produce the best match with experimental values.

The idea that the proton from deprotonation can linger near the charged sidechains has been mentioned by many studies.^61–63 The nearby proton concept played a role to explain proton pumping mechanisms in bacteriorhodopsin.⁶⁴ Hydronium ions have been shown to have an important role in proton channels to transfer protons.⁵⁰ These examples illustrate that the existence of hydronium ions near deprotonated acidic groups inside proteins could be a generalizable concept and has many implications in understanding protein functions.

This simulation study was performed with a highly stable form of SNase known as Δ+PHS. The stability of these variants may play a role to accommodate nearby hydronium ions without noticeable conformational relaxation or local unfolding. For other less stable proteins, deprotonation of buried acidic groups may result in conformational relaxation or local unfolding and let hydronium ions diffuse into the bulk solvent. Therefore, the nearby hydronium ions may only exist in stable proteins like Δ+PHS and bacteriorhodopsin.

CONCLUSIONS

We applied the VMMS method to simulate SNase variants with Asp or Glu mutations. As expected, large discrepancies between the calculated and experimental pK_a values were observed for many variants. Of the 10 variants simulated, some variants showed pK_a values very close to experimental results, which provide clues to the molecular determinants behind the high apparent dielectric constants. Conformational analysis reveals the presence of cations near the deprotonated acidic groups when the pK_a approaches experimental values. This finding relates the high apparent dielectric constants to nearby cations. On the basis of available X-ray crystallography structures and deprotonation chemistry, we proposed a nearby proton hypothesis that the proton produced in a deprotonation process remains nearby to have stronger interactions with and stabilize the deprotonated group in an apolar environment. On the basis of this hypothesis, we set up VMMS simulations with a hydronium ion placed near the deprotonated group. The pK_a values produced in these simulations correlate excellently with experimental observations. Energy analysis shows that it is energetically favorable for the hydronium ion to stay near the buried deprotonated group. Although other mechanisms, such as water penetration and conformational relaxation, play important roles, protons near buried deprotonated acidic groups should be a natural way to elevate apparent dielectric constants without significant conformational relaxation or local unfolding.