Enhanced Sampling in Free Energy Calculations: Combining SGLD with the Bennett’s Acceptance Ratio and Enveloping Distribution Sampling Methods

Abstract

One of the key requirements for the accurate calculation of free energy differences is proper sampling of conformational space. Especially in biological applications, molecular dynamics simulations are often confronted with rugged energy surfaces and high energy barriers, leading to insufficient sampling and, in turn, poor convergence of the free energy results. In this work, we address this problem by employing enhanced sampling methods. We explore the possibility of using self-guided Langevin dynamics (SGLD) to speed up the exploration process in free energy simulations. To obtain improved free energy differences from such simulations, it is necessary to account for the effects of the bias due to the guiding forces. We demonstrate how this can be accomplished for the Bennett’s acceptance ratio (BAR) and the enveloping distribution sampling (EDS) methods. While BAR is considered among the most efficient methods available for free energy calculations, the EDS method developed by Christ and van Gunsteren is a promising development that reduces the computational costs of free energy calculations by simulating a single reference state. To evaluate the accuracy of both approaches in connection with enhanced sampling, EDS was implemented in CHARMM. For testing, we employ benchmark systems with analytical reference results and the mutation of alanine to serine. We find that SGLD with reweighting can provide accurate results for BAR and EDS where conventional molecular dynamics simulations fail. In addition, we compare the performance of EDS with other free energy methods. We briefly discuss the implications of our results and provide practical guidelines for conducting free energy simulations with SGLD.

1. INTRODUCTION

The determination of free energy differences has become an essential part of the toolbox of computational chemists. Free energy simulations (FES) provide means to calculate relative binding affinities of different ligands to a receptor,^1,2 guide drug development,³ or study enzymatic reactions⁴ and protein synthesis in the ribosome.⁵ Despite many successful applications, one has to keep in mind that the accuracy of FES is limited by two factors. First, the quality of the force field has a direct impact on the correctness of the calculated free energy differences.⁶ Second, it is necessary to adequately sample the important parts of the phase spaces at the end points of a FES. The recent SAMPL3 binding affinity prediction competition highlights that, even for the binding of relatively small host–guest complexes, sampling is still an issue that accounts for a significant part of the deviations from experimental results.^7–11 An insightful discussion of the importance of sampling in molecular simulation was recently published;¹² furthermore, we refer the reader to an overview of the state of the art of FES, which addresses both of these limitations.³

In this work, we explore the utility of a recent method to accelerate sampling, self-guided Langevin dynamics (SGLD),¹³ in connection with FES. Originally presented in 2003, SGLD has been successfully applied to a variety of problems.^14–18 However, since the effect of the guiding force on ensemble distributions was initially poorly understood, SGLD has so far been restricted to applications that primarily focus on enhancing sampling; it was considered unsuitable for FES, where simulating a well-defined statistical mechanical ensemble is essential. Recently, Wu and Brooks have shown how to obtain a canonical ensemble distribution from SGLD,¹⁹ which makes it possible to use SGLD in FES. SGLD certainly is an interesting option to enhance sampling: the overhead above unmodified Langevin dynamics is minimal, and no prior knowledge of the system is required. SGLD enhances the (slow) low frequency degrees of freedom that are usually considered more biologically relevant by redistributing energy into them from high frequency motions; the amount of redistribution is controlled by the user. There is no need to run multiple simulations at different temperatures, and the method is equally applicable to gas phase, implicit solvent, and explicit solvent simulations. Reference ¹⁹ demonstrates that SGLD can be considered a simulation in the presence of weighting factors that are derived from the SGLD trajectory and a reference LD simulation. Once the weighting factors w^SGLD are known for each frame of the trajectory, any (canonical) ensemble average 〈X〉 can be obtained from SGLD simulations according to

$$\langle X\rangle =\frac{{\langle X{w}^{\text{SGID}}\rangle }_{\text{SGLD}}}{{\langle w^{\text{SGLD}}\rangle }_{\text{SGLD}}}$$ (1)

by the well-known Torrie–Valleau reweighting formula for simulations in the presence of a biasing potential.²⁰

All of the standard methods to compute free energy differences, thermodynamic perturbation (TP),²¹ thermodynamic integration (TI),²² and Bennett’s acceptance ratio method (BAR),²³ are based on the calculation of ensemble averages 〈X〉. Therefore, eq 1 makes it possible to use SGLD as the underlying sampling method in FES. One focus of this work is the combination of SGLD with BAR, since BAR and its derivatives are widely considered the computationally most efficient FES techniques.^24–27 However, SGLD could be coupled with thermodynamic perturbation and integration equally well.

A practical limitation of all standard techniques to compute free energy differences is the large amount of computational resources required.²⁸ In addition to simulations at the end states, i.e., the states corresponding to the physical systems, simulations of several artificial (“alchemical”) intermediate states, typically 10–20, are needed. This makes FES prohibitively expensive in many molecular modeling applications, in particular for high-throughput screening. One way to mitigate the computational cost of FES is to use special techniques to compute multiple free energy differences from a single simulation. A recent promising development in this direction is the enveloping distribution sampling (EDS) method developed by Christ and van Gunsteren.^29–32 Instead of computing individual free energy differences between N states as in standard FES methods, EDS computes the free energy differences of the N states relative to a common reference state R. This can be accomplished from a single simulation, though some exploratory calculations to optimize the reference state may be necessary. Methods such as EDS represent a trade-off between gains in computational efficiency and a loss in accuracy compared to the direct calculation of the free energy differences. The most important factor determining the accuracy of EDS is the choice of parameters characterizing the reference state R. The simulation of R not only has to explore the phase space of the hypothetical hybrid state itself but also must sample regions of phase space relevant for each of the real systems of interest. Therefore, sampling may be even more important in EDS than in traditional FES, which suggests testing SGLD in conjunction with both BAR and EDS.

Clearly, any combination of an enhanced sampling method with FES should be tested carefully. In particular, it is prudent to verify the correctness of the approach with simple systems for which free energy differences of interest can be computed either analytically or by direct integration of the partition function. While neither approach is feasible for biological systems, it is well-known how to compute partition functions of polyatomic molecules in the gas phase.^33,34 These types of systems have been successfully employed in earlier methodological work.^35–39 In addition, we compute relative solvation free energy differences of model systems. To test the combination of SGLD with BAR and EDS in the simplest possible manner, we proceed in four steps: First, we test the treatment of bonded terms in FES with SGLD by studying a four-atomic benchmark system (system I), for which analytical reference results are available. Second, we demonstrate that SGLD allows the calculation of free energy differences in cases where normal MD fails. For this purpose, we calculate the free energy difference between two five-atomic benchmark systems (systems II and III). These were designed to have no significant phase space overlap, and the relevant energy minima are separated by high energy barriers of more than 10 kcal/mol (16 kT).³⁹ Third, we explore the capability of SGLD to be used with explicit solvent by mutating “ethan-1-ol” to “ethan-2-ol” (i.e., moving the hydroxyl group from carbon 1 to carbon 2) in aqueous solution. This system was selected since the end states are equivalent and the total free energy change is zero, and no reference results are required. Fourth, we present the practicability of our approach for the biologically relevant mutation of Alanine to Serine and study the solvation free energy difference between the two amino acids. As shown recently, this free energy difference of solvation is very sensitive to the “secondary structure”⁴⁰ of the blocked amino acids. Thus, it represents a good test for the correct sampling of a nontrivial free energy surface. In addition, we employ this system to compare the performance of EDS with BAR and three different kinds of thermodynamic perturbation.

The remainder of the manuscript is organized as follows. First, we outline the theory of SGLD, BAR, and EDS, including the equations to perform BAR and EDS with reweighted SGLD data. Next, the implementation of EDS in CHARMM version 36 and the methodological details of the simulations are presented. We then proceed to the results for the four benchmark systems as outlined above and conclude with a short discussion concerning the usefulness of these types of calculations. In the Appendix, we lay out the equations for the analytical reference results and a short extract from a CHARMM script that uses EDS.

2. THEORY

2.1. Self-Guided Langevin Dynamics.

2.1.1. Basics.

The principal idea of SGLD is to selectively enhance the sampling of slow degrees of freedom by using information about the low frequency motions from the history of the simulation.¹³ This is done by adding a guiding force g to the Langevin equation of motion

$$\frac{\partial p_i}{\partial t}=f_i+g_i-{\gamma }_i{p}_i+R_i$$ (2)

where p denotes the momentum, f the force, γ the collision frequency, and R the random forces applied to maintain a temperature T; i is the atom index. The guiding force depends on three factors

$$g_i={\lambda }_{\text{g}}{\gamma }_i\left({\langle p_i\rangle }_{\text{L}}-\xi p_i\right)$$ (3)

where the guiding factor λ_g sets the strength of the guiding force. For λ_g = 0, eq 2 reduces to normal LD. 〈p_i〉_L represents a local time average of the momenta over a time period t_L. The factor ξ ensures the conservation of energy.

The local (time) average 〈·〉_L serves as a low-pass filter. By an appropriate choice of the averaging time t_L, it is possible to divide the motion contributions of the fast degrees of freedom (such as bond stretching and angle bending terms, which exhibit a high frequency) from those of the slow degrees of freedom (e.g., dihedral angles that change with low frequency motions). Fast, high frequency fluctuations of the momenta cancel during the averaging process, while slow motions pass through the filter. Thus, the guiding force is automatically applied in the direction of systematic motions and accelerates the conformational change caused by low frequency motions. The averaging time t_L defines which motions are considered high or low frequency, i.e., those with a frequency lower than (t_L)⁻¹ are enhanced by the guiding force. For example, bond and angle vibrations usually happen on a subpicosecond timescale, while conformational changes of a protein take nanoseconds or microseconds. Therefore, the optimal t_L for a specific application has to be estimated by the user (e.g., a t_L = 0.2 ps is used for enhanced sampling of changes of the secondary structure, while a t_L = 1 ps is employed for interdomain motions).

2.1.2. Reweighting with SGLD.

It is clear that SGLD does not preserve the canonical ensemble, because low frequency motions are accelerated by λ_gγ_i(p_i)_L, while the high frequency motions are dampened by − λ_gγ_ip_i to conserve energy. Hence, SGLD constantly transfers kinetic energy from the fast to the slow degrees of freedom. At the same time, the slow degrees of freedom lose kinetic energy via the coupling to the fast degrees of freedom. The balance between the two opposing effects leads to two separate “effective” temperatures, one for the high frequency motions and one for the low frequency motions. Recently, Wu and Brooks derived reweighting factors to account for those deviations by employing eq 1. Here, we present a short outline of the derivation found in ref 19.

The conceptional basis of the derivation lies in reformulating the configurational partition function Θ in terms of contributions from low and high frequency motions. It starts from the assumption that the local time average of the total potential energy 〈U〉_L represents the potential energy associated with the slow degrees of freedom

$$U^{\text{lf}}\approx {\eta }^{\text{lf}}{\langle U\rangle }_{\text{L}}$$ (4)

where n^lf is a correction factor for the bias introduced to the energy surface of the low frequency motions due to the guiding force. This bias of the potential energies can be determined from the projection of guiding forces g on the forces 〈f〉_L in the SGLD trajectory. If the two variables are uncorrelated, n^lf is 1, and the guiding force can be regarded as a random factor added to the forces (for the selected examples in this paper, n^lf was ~0.93 ± 0.03).

Conversely, the bias introduced by the high frequency motions to the energy surface is approximated by the difference between the total potential energy and 〈U〉_L

$$U^{\text{hf}}\approx {\eta }^{\text{hf}}\left(U-{\langle U\rangle }_{\text{L}}\right)$$ (5)

where n^hf is the correction factor for the bias due to the guiding force. It can be calculated from the covariance of the scalar products of the guiding forces and the internal forces (for the selected examples in this paper, n^hf was ~0.993 ± 0.002).

To account for the differences of the effective temperature, the low frequency collision factor χ^lf f is introduced. It is the ratio of the effective temperature of the low frequency motions T^lf to the reference temperature of these motions, $T_0^{\text{lf}}$

$${\chi }^{\text{lf}}=\frac{T_0^{\text{lf}}}{T^{\text{lf}}}$$ (6)

where the effective low frequency temperature can be calculated from the SGLD trajectory with

$$T^{\text{lf}}={\left(N_{\text{dof}}\cdot k_{\text{B}}\right)}^{-1}{\langle \sum _i\frac{{\langle p\rangle }_{\text{L}}^2}{m_i}\rangle }_{\text{SGLD}}$$ (7)

employing the number of degrees of freedom, N_dof, the Boltzmann constant, k_B, and the atomic masses, m_i. For LD simulations, T^lf equals $T_0^{\text{lf}}$. While $T_0^{\text{lf}}$ can be estimated on the basis of an SGLD simulation according to ref 19, practical experience shows that the results are more accurate if $T_0^{\text{lf}}$ is determined from a LD simulation (using the average of the TREFLF output in CHARMM).

The collision factor for the high frequency motions is defined on the basis of the difference between the total temperature of the system T and the effective temperature of the low frequency motions

$${\chi }^{\text{hf}}=\frac{T-T_0^{\text{lf}}}{T-T^{\text{lf}}}$$ (8)

thus accounting for the lowered effective temperature of the fast high frequency motions.

With the equations above, it possible to formulate a partition function for SGLD in terms of low frequency and high frequency contributions

$${\mathrm{\Theta }}_{\text{SGLD}}=\sum _s{\text{e}}^{-\beta \left({\chi }^{\text{lf}}{U}_s^{\text{lf}}+{\chi }^{\text{hf}}{U}_s^{\text{hf}}\right)}$$ (9)

where β has the usual meaning of 1/k_BT. The summation runs over all combinations of microstates and, additionally, possible pathways for the local time average 〈·〉_L to that microstate s. The microstates, therefore, not only depend on the conformational degrees of freedom but also on their history. However, the main difference from the classical partition function is the use of two different effective temperatures (χ^lfβ and χ^hfβ) for the low and high frequency motions.

The calculation of the weighting factor for eq 1 requires the unnormalized probabilities of a microstate s in an LD simulation $\left({\tilde{p}}_s^{\text{LD}}\right)$ and in an SGLD simulation $\left({\tilde{p}}_s^{\text{SGLD}}\right)$, which are given by

$${\tilde{p}}_s^{\text{LD}}={\text{e}}^{-\beta \left(U_s\right)}\text{and}{\tilde{p}}_s^{\text{SGLD}}={\text{e}}^{-\beta \left({\chi }^{\text{lf}}{U}_s^{\text{lf}}+{\chi }^{\text{hf}}{U}_s^{\text{hf}}\right)}$$ (10)

The weighting factor w^SGLD is calculated from the ratio of these two probabilities

$$w_s^{\text{SGLD}}=\frac{{\tilde{p}}_s^{\text{LD}}}{{\tilde{p}}_s^{\text{SGLD}}}={\text{e}}^{-\beta \left(U_s-{\chi }^{\text{lf}}{U}_s^{\text{lf}}-{\chi }^{\text{hf}}{U}_s^{\text{hf}}\right)}$$ (11)

To summarize, determining the weighting factors for an SGLD trajectory requires the measurement of two different kinds of contributions. First, the contribution of the guiding force to the energy is accounted for by calculating U^lf and U^hf at each time step. Second, the bias due to the two effective temperatures must be calculated. This requires the determination of the effective temperature T^lf over the whole SGLD trajectory, as well as measuring the reference low frequency temperature $T_0^{\text{lf}}$ from a reference LD simulation.

2.2. Free Energy Methods.

2.2.1. Bennett’s Acceptance Ratio Method.

To compute the free energy difference between two states, 0 and 1, BAR utilizes the information obtained from simulations of both states.²³ The free energy difference ΔA between states 0 (potential energy function U₀) and 1 (potential energy function U₁) is given by

$$\mathrm{\Delta }{A}^{0\to 1}={\beta }^{-1}\left(\text{ln}\frac{{\langle f\left(U_0-U_1+C\right)\rangle }_1}{{\langle f\left(U_1-U_0-C\right)\rangle }_0}\right)+C$$ (12)

The subscripts 0 and 1 in eq 12 indicate that the ensemble averages 〈·〉 are calculated from the trajectories of the initial (0) and final states (1), respectively. The symbol f denotes the Fermi function

$$f(x)=\frac{1}{1+\text{exp}(\beta x)}$$ (13)

and

$$C={\beta }^{-1}\text{ln}\frac{Q_0{n}_1}{Q_1{n}_0}$$ (14)

where Q denotes the respective partition function and n₀ and n₁ are the numbers of configurations of states 0 and 1 from which the ensemble averages are evaluated. The unknown constant C, which corresponds essentially to the free energy difference of interest, is found iteratively. Starting from an initial guess, a value of C is found so that the argument of the logarithm in eq 12 equals unity, since in this case the free energy difference is given by

$$\mathrm{\Delta }{A}^{0\to 1}=-{\beta }^{-1}\text{ln}\frac{n_1}{n_0}+C$$ (15)

As shown in refs ⁴¹ and ⁴², BAR can conveniently be extended to employ weighted averages, leading to

$$\mathrm{\Delta }{A}^{0\to 1}=k_{\text{B}}T\text{ln}\left(\frac{{\langle f\left(U_0-U_1+C\right)w_1\rangle }_1}{{\langle f\left(U_1-U_0-C\right)w_0\rangle }_0}\frac{{\langle w_0\rangle }_0}{{\langle w_1\rangle }_1}\right)+C$$ (16)

where the indices 0 and 1 refer to the respective end state. This method is referred to as non-Boltzmann Bennett (NBB)⁴¹ or weighted Bennett’s acceptance ratio (w-BAR).⁴²

To use eq 16, it is necessary to evaluate three quantities for each frame of each state’s trajectories: For the biased trajectory of state 0, U₀, U₁, and the SGLD weight w₀ must be computed, while for state 1, U₀, U₁, and w₁ are required. Thus, the computational overhead is limited to the determination of the w^SGLD for both trajectories.

2.2.2. Enveloping Distributions Sampling.

Enveloping distribution sampling^29–32 relies on the simulation of a single reference state R to calculate the free energy differences between N end points. The potential energy of the reference state U_R mixes the potential energies of all end points according to

$$U_{\text{R}}=-{(\beta s)}^{-1}\text{ln}\sum _{k=0}^N{\text{e}}^{-\beta s\left(U_k-E_k^{\text{R}}\right)}$$ (17)

where U_k denotes the potential energy of end point k, $E_k^{\text{R}}$ is the energy offset parameter that ensures equal sampling of all end states, and s is the smoothness factor. Note that the EDS equation presented here employs only a single s for all end points. Thus, it resembles the EDS implementation in ref 30 rather than more recent versions of EDS (e.g., in refs ³¹ and ³²), which are considerably more general. Depending on the choice of s and $E_k^{\text{R}}$, the reference state can be used for different purposes.^30,31 A reference state with s = −1 and $E_k^{\text{R}}=A_k$ corresponds to the virtual state that is generated by the perturbations in Bennett’s acceptance ratio method. However, when this state is actually simulated, U_R will be dominated by the end state with the highest $\left(U_k-E_k^{\text{R}}\right)$. For example, if two imaginary end points are used, one with low potential energy (U₁ = 1) and one with high potential energy (U₂ = 10), using s = −1, $E_1^{\text{R}}=0$, and $E_2^{\text{R}}=0$ will lead to a reference state potential of U_R = 10.001, which corresponds to the state with higher energy. This approach will lead to significant sampling problems and, therefore, poor convergence. Therefore, negative values of s should not be used in EDS.

On the other hand, a reference state with s = +1 and $E_k^{\text{R}}=A_k$ corresponds to enveloping all important parts of phase space of the end states. U_R will be dominated by the end state with the smallest $U_k-E_k^{\text{R}}$. Returning to our example with two imaginary end points above, using s = +1 will lead to U_R = 0.99, which corresponds to the state with lower energy. In this case, high energy barriers may remain due to interactions with the environment of the free energy calculation. In practice, the efficiency of EDS can be tuned by the smoothness parameter s, and it can be further improved by introducing two-dimensional smoothness parameters s_kl for pairs of end states k and l.^31,32

The energy offsets $E_k^{\text{R}}$ can be optimized by selecting a good estimate for the free energy difference between the reference state and the respective end state i. This estimate can be obtained from an LD simulation. In connection with SGLD, the same LD simulation can be used to determine $T_0^{\text{lf}}$ for the reweighing of SGLD and an initial guess of $E_k^{\text{R}}$. However, since efficient protocols are available to update s and ER in an optimal way,^30–32 we focus on testing the advantages of advanced sampling for the simplified version of EDS described in eq 17. Our results should be regarded as a worst-case scenario of an EDS implementation.

The free energy difference between two arbitrary end states, X and Y, is evaluated by their free energy differences from the reference state:

$$\mathrm{\Delta }{A}^{\text{X}\to \text{Y}}=-{\beta }^{-1}\text{ln}\frac{{\langle {\text{e}}^{-\beta \left(U_{\text{Y}}-U_{\text{R}}\right)}\rangle }_{\text{R}}}{{\langle {\text{e}}^{-\beta \left(U_{\text{X}}-U_{\text{R}}\right)}\rangle }_{\text{R}}}$$ (18)

Reweighing can be implemented in a straightforward fashion by combining eq 18 with eq 1, which leads to

$$\mathrm{\Delta }{A}^{\text{X}\to \text{Y}}=-{\beta }^{-1}\text{ln}\frac{{\langle {\text{e}}^{-\beta \left(U_{\text{Y}}-U_{\text{R}}\right)}{w}_{\text{R}}\rangle }_{\text{R}}}{{\langle {\text{e}}^{-\beta \left(U_{\text{X}}-U_{\text{R}}\right)}{w}_{\text{R}}\rangle }_{\text{R}}}$$ (19)

3. METHODS

Except for the four-atomic benchmark system and the ethanol mutation, four different approaches were used to calculate the free energy differences: BAR with LD simulations (BAR/LD), EDS with LD simulations (EDS/LD), BAR with SGLD and reweighting based on eq 16 (BAR/SGLD), and EDS with SGLD based on eq 19 (EDS/SGLD). Unless stated otherwise, the BAR calculations were conducted without any intermediate points, relying on simulations of the end points only, and EDS calculations used only a single reference state with an EDS smoothness parameter s = 1. The energy offset parameters $E_k^{\text{R}}$ were determined from short LD equilibration simulations with a simulation time of less that 10% of the production run. The same $E_k^{\text{R}}$ values were used for production of both EDS/LD and EDS/SGLD; i.e., $E_k^{\text{R}}$ values were never updated after the initial estimate. To calculate the weights w^SGLD for BAR/SGLD and EDS/SGLD, the low frequency reference temperature $T_0^{\text{lf}}$ was determined from reference LD simulations that had equal length and identical energy parameters.

3.1. EDS-Implementation in CHARMM Using MSCALE.

We have implemented the simulation of EDS reference states in CHARMM,^43,44 making use of the MSCALE module.⁴⁵ MSCALE is a communications protocol that has been developed for CHARMM and other programs to facilitate the combination of different simulation methods into a single calculation. The system can be arbitrarily divided into one or more subsystems, allowing for the possibility of overlapping atom selections for the subsystems. For example, it is possible to set up three subsystems, where the first subsystem contains a core region, the second subsystem the environment around the core, and the third subsystem both the core region and the environment.

It is possible to employ a different Hamiltonian for each subsystem with MSCALE. For this purpose, the main process, called the client, spawns a new calculation for each of the subsystems. The spawned processes are called servers and may run any program for which an MSCALE interface has been developed. At each energy and force evaluation, the client sends each server the coordinates that its subsystem requires, and the server returns the energies and forces (as well as other data that might be relevant for the simulation). Therefore, all subsystems are coupled over the main process, and energies and forces from the various subsystems may be combined in an arbitrary manner.

The EDS implementation in CHARMM follows eq 17. It is, therefore, based on a simplified version of EDS with single smoothness parameter s for all end states, as described in ref 30. Instead of using s explicitly, the user has to specify a so-called “EDS temperature” (T_EDS). The EDS temperature is given by

$$T_{\text{EDS}}=\frac{T}{s}$$ (20)

Based om T_EDS eq 17 becomes

$$U_{\text{R}}=-k_{\text{B}}{T}_{\text{EDS}}\text{ln}\sum _{k=0}^N\text{exp}\left(-\frac{U_k-E_k^{\text{R}}}{k_{\text{B}}{T}_{\text{EDS}}}\right)$$ (21)

To perform an EDS simulation, the MSCALE command is invoked by the user, followed by SUBSystem commands that define each end state of the simulation. The use of different atom selections allows both single and multi-topology approaches to free energy calculations while using a common set of coordinates. After the specification of the end states in MSCALE, the EDS command is invoked. It requires the specification of the EDS TEMPerature (T_EDS), the number of end states, the names of the MSCALE subsystems that will be used as end states, as well as their corresponding energy offsets $E_k^{\text{R}}$. An extract from an example CHARMM script that calls EDS is shown in the Appendix.

The internal communication of the EDS implementation is structured as follows. The main process sends the current atomic coordinates to the subsystem processes. Each subsystem calculates the energies U_k and atomic forces f_kfor its corresponding end state and reports them to the main process. Instead of just combining the resulting energies and forces as is normally done in MSCALE, the main process is responsible for calculating the potential energy of the reference state U_R as well as its corresponding forces (c.f. eq 10 in ref 31), based on the information from the subsystems. The forces of the reference state are then used to conduct a molecular dynamics step that leads to the next set of atomic coordinates. For optimal performance, all interactions that are not affected by the mutation should be calculated in the main process.⁴⁶

3.2. Simulation Details.

All calculations were conducted with CHARMM version 36, using the CHARMM22 all-atom force field.⁴⁷ Images of the mutations were generated with VMD.⁴⁸ Random forces for both LD and SGLD were applied according to a target temperature of 300 K. Except for the four-atomic benchmark system, either all atomic masses were set to at least 10 amu or SHAKE⁴⁹ was employed to keep the bonds rigid, allowing for a time step between 1 and 2 fs. A cutoff radius of 998 Å was employed for the gas phase simulations, which is considerably larger than the size of the molecule. Trajectories were written every 10 steps for the four-atomic benchmark system and every 100 steps for all other benchmarks. Further details of the simulations follow when describing the respective system. Tables 1 and 2 give an overview of the simulation details and the EDS parameters. Unless stated otherwise, the reported standard deviations were determined by repeating each free energy simulation four times, starting with different initial random velocities. The energies of the respective states required for BAR and EDS were extracted with the UPEN command of the MSCALE module of CHARMM; the BAR/EDS analysis was carried out by a Perl program.

Table 1.

Simulation Types and Details

benchmark	descriptiona	nsb	tsc	λgd	γe	$T_0^{\text{lf}}$f
four-atomic	BAR gas	880g	0.2	—	5	X
	BAR gas	880g	0.2	—	5
	BAR gas	880g	0.2	1.0	5
five-atomic	BAR II gas	4	50	—	5	X
	BAR II gas	4	50	—	300
	BAR II gas	4	50	1.0	300
	BAR III gas	4	50	—	5	X
	BAR III gas	4	50	—	300
	BAR III gas	4	50	1.0	300
	EDS II/III gas	4	50	—	5	X
	EDS II/III gas	4	50	—	300
	EDS II/III gas	4	50	1.0	300
ethanol	BAR solv	44	0.2	—	5	X
	BAR solv	44	0.2	1.0	5
Ala–Ser	BAR Ala gas	4	0.2	—	5	X
	BAR Ala gas	4	75	—	100
	BAR Ala gas	4	75	0.75	100
	BAR Ala GBMV	4	75	—	5	X
	BAR Ala GBMV	4	75	—	100
	BAR Ala GBMV	4	75	0.75	100
	BAR Ser gas	4	75	—	5	X
	BAR Ser gas	4	75	—	100
	BAR Ser gas	4	75	0.75	100
	BAR Ser GBMV	4	75	—	5	X
	BAR Ser GBMV	4	75	—	100
	BAR Ser GBMV	4	75	0.75	100
	EDS Ala/Ser gas	4	75	—	5	X
	EDS Ala/Ser gas	4	75	—	100
	EDS Ala/Ser gas	4	75	0.75	100
	EDS Ala/Ser GBMV	4	75	—	5	X
	EDS Ala/Ser GBMV	4	75	—	100
	EDS Ala/Ser GBMV	4	75	0.75	100
	TP0.5 Ala/2+Ser/2 gas	4	75	—	5	X
	TP0.5 Ala/2+Ser/2 gas	4	75	—	100
	TP0.5 Ala/2+Ser/2 gas	4	75	0.75	100
	TP0.5 Ala/2+Ser/2 GBMV	4	75	—	5	X
	TP0.5 Ala/2+Ser/2 GBMV	4	75	—	100
	TP0.5 Ala/2+Ser/2 GBMV	4	75	0.75	100

^aBAR marks simulations used for BAR calculations marks simulations using an EDS reference state, followed by a description EDS of the end states. The abbreviation “gas” marks gas phase simulations. “solv” means simulations with explicit solvent, and “GBMV” marks implicit solvent simulations using GBMV.

^bNumber of simulations.

^cSimulation time in nanoseconds.

^dSGLD guiding factor, a “—” marks LD simulations.

^eFriction constant in picoseconds⁻¹.

^fX marks LD reference calculations to determine $T_0^{\text{lf}}$ for the reweighting of SGLD trajectories.

^gBenchmark involves eight mutations (see corresponding sections in the Methods), each using the two end states and nine intermediate states, each being repeated 10 times.

Table 2.

EDS Details

benchmark	description	U1a	U2b	s	$E_1^{\text{R}}$c	$E_2^{\text{R}}$d	tope
2	ΔAII→III	II	III	1	0	0	S
2	ΔAII→III	II	III	0.1	0	0	S
2	ΔAII→III	II	III	0.01	0	0	S
4	$\mathrm{\Delta }{A}_{\text{gas}}^{\text{Ala}\to \text{Ser}}$f	Ala	Ser	1	4.17	13.27	D
	$\mathrm{\Delta }{A}_{\text{GBMV}}^{\text{Ala}\to \text{Ser}}$g	Ala	Ser	1	4.21	11.28	D

^aFirst end state.

^bSecond end state.

^cEnergy offset of first subsystem.

^dEnergy offset of second subsystem.

^eTopology of FES. S = single topology, D = dual topology.

^fFree energy difference in gas phase.

^gFree energy difference using the GBMV implicit solvent.

3.2.1. Four-Atomic Benchmark Systems.

The calculations on the four-atomic benchmark system test whether BAR in combination with SGLD can reproduce analytically calculable free energy differences of bonded terms. The theoretical background concerning the partition function of small polyatomic molecules is summarized in the Appendix. As demonstrated in refs ^{35, 36}, and ³⁸, free energy differences between small molecules in the gas phase can be computed with high accuracy and precision by MD based FES. The most important practical detail is the choice of the thermostat since (i) such small systems clearly are far from the thermodynamic limit, and (ii) their stiff harmonic nature when represented by a typical force field causes the initial kinetic energy introduced by the assignment of random velocities to not redistribute unless special precautions are taken. Simulations with a Berendsen or a single Nose–Hoover thermostat fail to reproduce the analytical result. In earlier work, we, therefore, used individual Nose–Hoover thermostats for each atom;^35,36 in this work, we employed Langevin dynamics (LD) in the reference simulations. Further, the overall rotation of the molecules must not be removed.³⁵ The high sensitivity of the free energy results to small deviations from the original ensemble makes them a very useful benchmark for the SGLD reweighting scheme.

The alchemical free energy simulation with LD was carried out with the PERT module of CHARMM,⁴³ using a single topology approach for the alchemical intermediates.³⁶ Each free energy difference was calculated using 21 λ intermediate states, λ = 0.00, 0.05, 0.10, …0.95, 1.00 with BAR (note that λ intermediate states are not connected with the guiding factor λ_g). A friction coefficient of 5 ps⁻¹ was applied to all atoms. For SGLD, an averaging time (t_L) of 0.2 ps and a guiding factor λ_g = 1 were used. The time step was 1 fs. At each λ, 10 ps were discarded as equilibration, while the free energy data were accumulated over the following 190 ps. Although this is an extremely short protocol, longer simulation lengths had only a minuscule impact on the results (data not shown). The statistical uncertainty was estimated by computing each free energy difference 10 times using independent simulations with different initial random velocities. The results reported in Table 3 are the mean and standard deviations of these 10 individual values.

Table 3.

Free Energy Differences of Dummy Atoms in Four-Atomic Benchmark Systems in Kilocalories Per Mole

type of changea	refb	LDc	SGLDd	SGLDrwe	SGLDnrf
1. r34	−0.483	−0.491	−0.112	−0.141	−0.504
2. K34	0.207	0.208	0.118	0.115	0.196
3. r34,K34	−0.277	−0.268	−0.505	−0.521	−0.301
4. K234	0.207	0.206	0.118	0.114	0.196
5. θ234	0.376	0.366	0.231	0.201	0.381
6. θ234,K234	0.583	0.513	0.421	0.404	0.595
7. r34,K34,θ234,K234,k1234	0.550	0.544	0.156	0.108	0.612
8. r34,K34, θ234,K234,k1234,n1234	0.550	0.569	0.110	0.026	0.586
RMSDg		0.009	0.250	0.288	0.030

^aThe internal parameters changed are indicated. For the abbreviations used and values of the changed parameters, see the Methods.

^bAnalytical results (cf. Appendix).

^cRegular BAR results with Langevin dynamics, average standard deviation = 0.033 kcal/mol.

^dBAR/SGLD results without reweighting, average standard deviation = 0.037 kcal/mol.

^eReweighted SGLD/BAR results, average standard deviation = 0.036 kcal/mol.

^fReweighted SGLD/BAR results if net translation and rotation are removed from the guiding force (SGNONET command), average standard deviation = 0.034 kcal/mol.

^gRoot mean square deviations from analytical results.

An identical initial state was used in all free energy calculations: The equilibrium bond lengths r₁₂ = r₂₃ = r₃₄ were set to 2 Å; the indices denote the atom numbers. The force constant for all bonds was K_bond = 200 kcal/(mol Ų). Similarly, equal equilibrium bond angles θ₁₂₃ = θ₂₃₄ =110° and angle force constants K_angle = 50 kcal/(mol rad²) were employed. The dihedral force constant was k₁₂₃₄ = 1 kcal/mol with a multiplicity n₁₂₃₄ = 3. We computed the free energy differences to end states with the following changes relative to this initial state analytically, using both regular BAR and BAR in combination with SGLD (see Table 3): (1) r₃₄ = 3 Å; (2) K₃₄ = 400 kcal/(mol Ų); (3) r₃₄ = 3 Å, K₃₄ = 400 kcal/(mol Ų); (4) K₂₃₄ = 100 kcal/(mol rad²); (5) θ₂₃₄ = 150°; (6) θ₂₃₄ = 150°, K₂₃₄ = 100 kcal/(mol rad²); (7) r₃₄ = 3 Å, K₃₄ = 400 kcal/(mol Ų), θ₂₃₄ = 150°, K₂₃₄ = 100 kcal/(mol rad²), k₁₂₃₄ = 2 kcal/mol; (8) r₃₄ = 3 Å, K₃₄ = 400 kcal/(mol A2), θ₂₃₄ = 150°, K₂₃₄ = 100 kcal/(mol rad²), k₁₂₃₄ = 2 kcal/mol, n₁₂₃₄ = 2.

3.2.2. Five-Atomic Benchmark Systems.

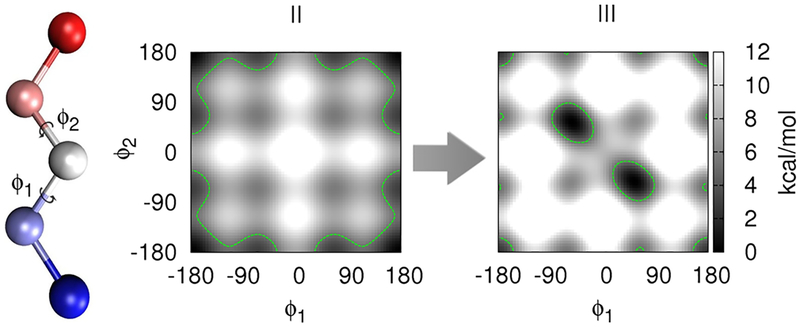
Two five-atomic benchmark systems developed by Leitgeb et al. were employed (systems II and III of reference ³⁹), using a single topology setup for the FES. They are unbranched, nonlinear five-atomic molecules. The two systems are designed to have small phase space overlap and large energy barriers, thus representing a worst case scenario for free energy calculations. Due to the smallness of the systems, quasi-analytical reference results are available (c.f. Appendix 1). The equilibrium bond length is 1.53 Å, and all bond angles are 111°. Two dihedral angle terms (ϕ₁, ϕ₂) are present.

In system II, the sum of two potentials was applied simultaneously to each dihedral (n_1,1 = 3, k_1,1 = 2 kcal/mol, n_1,2 = 1, k_1,2 = 2 kcal/mol; n_2,1 = 3, k_2,1 = 2 kcal/mol, n_2,2 = 1, k_2,2 = 2 kcal/mol). This results in one global minimum and four local minima (cf Figure 2). The dihedral potentials were identical for system III, but the dihedral force constants were raised (n_1,1 = 3, k_1,1 = 3.5 kcal/mol, n_1,2 = 1, k_1,2 = 3 kcal/mol; n_2,1 = 3, k_2,1 = 3.5 kcal/mol, n_2,2 = 1, k_2,2 = 3 kcal/mol). Furthermore, intramolecular electrostatic and Lennard-Jones interactions were added to the system, resulting in two equivalent global minima and one local minimum for system III. However, the three minima are separated by high energy barriers (Figure 2).

Figure 2.

Potentials of mean force of the five-atomic benchmark systems II and III as a function of the dihedral angles ϕ₁ and ϕ₂. Dark areas represent energy minima. A green dashed line encircles the areas with energy levels below 9 k_BT.

For all computations involving the five-atomic benchmark systems, simulation lengths of 50 ns and a time step of 1 fs were employed. Free energy differences were computed with BAR and EDS using three different sets of parameters: LD with a friction coefficient of 5 ps⁻¹ on all atoms, LD with a friction coefficient of 300 ps⁻¹ on all atoms to determine the reference low frequency temperature, and SGLD with a friction coefficient of 300 ps⁻¹ on all atoms and a guiding factor of 1. The different friction constants in LD (γ =5 ps⁻¹) and SGLD (γ = 300 ps⁻¹) are motivated by the increase of the guiding force with larger values of γ (eq 3).

3.2.3. Ethanol.

The solvation free energy difference between ethan-1-ol and ethan-2-ol was calculated in explicit water, using the standard thermodynamic cycle to compute solvation free energies.⁵⁰ Alchemical free energy differences between the end states were calculated both in the gas phase (yielding ΔA_gas) and with explicit solvent (yielding $\mathrm{\Delta }{A}_{{\text{H}}_2\text{O}}$), employing 11 λ points and a dual topology setup. The solvation free energy difference (ΔΔA_solv)is given by $\mathrm{\Delta }\mathrm{\Delta }{A}_{\text{ solv }}=\mathrm{\Delta }{A}_{{\text{H}}_2\text{O}}-\mathrm{\Delta }{A}_{\text{gas}}$. The gas phase simulations were set up as described in ref 40. However, since the free energy results for LD and SGLD in the gas phase were well converged and close to zero (<0.0008 ± 0.011 kcal/mol), the solvation free energy difference results shown in Table 5 are practically the same as the free energy differences in solution (i.e., $\mathrm{\Delta }\mathrm{\Delta }{A}_{\text{ solv }}\approx \mathrm{\Delta }{A}_{{\text{H}}_2\text{O}}$).

Table 5.

Free Energy Differences (ΔΔA_solv) between Ethan-1-ol and Ethan-2-ol in Explicit Solvent in Kilocalories Per Mole

	ΔΔAsolv
LD	−0.04 ± 0.05
SGLDall	−0.03 ± 0.04
SGLDEtOH	0.02 ± 0.03
${\text{SGLD}}_{\text{rw}}^{\text{all}}$	−0.51 ± 1.24
${\text{SGLD}}_{\text{rw}}^{\text{EtOH}}$	−0.11 ± 0.05

A total of 766 TIP3P water molecules^51,52 were present in the solvent simulations. The simulation box was a truncated octahedron. The side length L of the cube from which the octahedron was generated was L = 35.75 Å, which was the average box size from a 200 ps constant pressure simulation. For the determination of the free energy difference, we used constant volume simulations with a friction coefficient of 5 ps⁻¹ on all atoms. The time step was 1 fs, and SHAKE⁴⁹ was used to keep the water geometry rigid. Lennard-Jones interactions were switched off between 10 and 12 Å, while electrostatic interactions were computed with the particle mesh Ewald method.⁵³ Each system was equilibrated for 100 ps at every λ value, followed by 1 ns of production dynamics. For SGLD, two different setups were employed to evaluate the efficiency of the reweighting scheme for large systems. In the first case, the guiding force was applied to all atoms, thus acting on both solute and solvent (SGLD^all). In the second setup, the application of guiding forces was restricted to the solute by using the ISGSTA and ISGEND commands (SGLD^EtOH).

3.2.4. Alanine–Serine.

The solvation free energy differences between Ala and Ser shown in Table 6 were calculated with the same thermodynamic cycle as in the ethanol example, but using a dual topology approach. Free energy differences between Ala and Ser were calculated both in the gas phase (yielding $\mathrm{\Delta }{A}_{\text{gas}}^{\text{Ala}\to \text{Ser}}$) and with implicit solvent (yielding $\mathrm{\Delta }{A}_{\text{imp}}^{\text{Ala}\to \text{Ser}}$). The solvation free energy difference is given by $\mathrm{\Delta }\mathrm{\Delta }{A}_{\text{ solv }}^{\text{Ala}\to \text{Ser}}=\mathrm{\Delta }{A}_{\text{imp}}^{\text{Ala}\to \text{Ser}}-\mathrm{\Delta }{A}_{\text{gas}}^{\text{Ala}\to \text{Ser}}$. The implicit solvent simulations utilized GBMv,⁵⁴ as described in ref 40. This choice is motivated by the good agreement between GBMV and explicit solvent results. GBMV is able to reproduce the dependency of the solvation free energy difference between Ala and Ser on the backbone conformation with a root-mean-square error (RMSE) of 0.27 kcal/mol compared to explicit solvent. Moreover, GBMV yielded an RMSE of 0.41 for eight solvation free energy differences between the amino acids Ala, Ser, Val, Thr, Phe, and Tyr (compared to explicit solvent).⁴⁰

Table 6.

Solvation Free Energy Differences between Alanine and Serine in Kilocalories Per Mole

	LD	SGLDrw
BAR	−2.98 ± 0.04	−3.12 ± 0.03
EDS	−2.97 ± 0.04	−3.01 ± 0.03
TPfwa	−2.88 ± 0.89	−2.84 ± 1.07
TPbwb	−2.50 ± 0.69	−3.10 ± 0.43
TP0.5c	−2.82 ± 0.28	−2.82 ± 0.21

^aThermodynamic perturbation based on trajectories of Ala.

^bThermodynamic perturbation based on trajectories of Ser.

^cThermodynamic perturbation based on trajectories of U_R = U_Ala/2 + U_Ser/2.

For all simulations, a time step of 1.5 fs was chosen. Free energy differences were calculated with EDS and BAR, based on simulations of 75 ns length. The parameters for GBMV were those recommended in gbmv.doc in the CHARMM documentation at www.charmm.org. The thermodynamic perturbation (TP) results for TP_fw and TP_bw in Table 6 were calculated from the same trajectories as BAR. For TP_0.5, MSCALE generated a reference state with U_R = U_Ala/2 + U_Ser/2. All other simulation details were identical to those used for BAR. The respective SGLD results for TP were generated on the basis of eq 9 given in ref 39 for non-Boltzmann thermodynamic perturbation.

4. RESULTS AND DISCUSSION

4.1. Four-Atomic Benchmark Systems.

In this example, we test the effect of SGLD on the treatment of bonded terms of dummy atoms in FES (Figure 1). Table 3 summarizes results of FES for four-atomic model systems without nonbonded interactions. The results of regular LD simulations (third column) are compared with those obtained from SGLD simulations with (fifth column) and without reweighting (fourth column). The column “ref’ lists the analytical results, which are calculated as outlined in the Appendix. The agreement between the analytical and LD results is excellent, with the largest absolute deviation being ~0.02 kcal/mol. Similarly, the standard deviations of the simulation results are very low (on average, ~0.03 kcal/mol). The results of the SGLD simulations with and without reweighting (columns four and five in Table 3) deviate significantly from the reference results (with absolute deviations of up to ~0.4 kcal/mol). This finding is not surprising, considering that SGLD is designed to transfer energy from fast degrees of freedom (such as bond and angle terms) to slow degrees of freedom and, hence, does not correspond to the canonical ensemble. The results illustrate the sensitivity of this simple model system to the details of the simulation setup. Similar deviations can also be found for two- and three-atomic systems (data not shown). Therefore, we investigated further potential sources of error.

Figure 1.

Illustration of the four-atomic benchmark system to test the treatment of bonded terms (for example, changes of bond length and bond angle) in free energy simulations with SGLD.

If the net translational force and torque for the whole system is removed from the guiding force in SGLD simulations by using the SGNONET command (SGLD_nr), the results (rightmost column of Table 3) are in agreement with the analytical results, exhibiting a root-mean-square difference of 0.030 kcal/mol. Although the RMSD of SGLD_nr is slightly higher than that with LD, the deviations are not statistically significant (the average standard devation is 0.034). The difference between SGLD and SGLD_nr indicates that, for small systems, the default parameters of SGLD lead to distributions of the kinetic energy that do not correspond to the canonical ensemble. Specifically, SGLD increases the rotational motions of the molecule. This side effect leads to artifacts in the contributions to the free energy difference from the change in moment of inertia (cf. pp. 5150–5151 of ref 35). This essentially kinetic contribution to the free energy difference is presently not accounted for by using the reweighting scheme in eq 11. For the remainder of this paper, only simulations with the SGNONET keyword (i.e., without enhanced translation and rotation) will be employed. Future versions of SGLD in CHARMM will automatically remove all net translation and rotation from the guiding force.

An alternative way to avoid contributions to the free energy difference from the change in moment of inertia is to set up the mutation with a so-called dual topology approach. Dual topology simulations use three separate groups of atoms in the coordinate set: (a) atoms that do not change during the FES (the environment), (b) atoms corresponding to the initial state, and (c) atoms corresponding to the target state. Atoms in groups b and c do not interact with each other. For example, in a FES of the mutation of Ala to Ser, the backbone, which corresponds to the environment group a, is connected to both a CH₃ group (corresponding to Ala) and a CH₂OH group (corresponding to Ser). A dual topology setup was used in the ethanol and Ala → Ser examples presented in this work, avoiding complications resulting from changes of bonded terms that could potentially arise in single topology.

4.2. Five-Atomic Benchmark Systems.

This example considers the effect of high energy barriers on FES by employing two five-atomic benchmark systems having both bonded and nonbonded interactions. In contrast to the four-atomic benchmark system, the bond and angle terms are not changed during the mutation, and SHAKE is applied to the bonds. Thus, no contributions to the free energy difference arise from changes of the “hard” bond or angle terms. In addition, the net translation and rotation was removed from the guiding force to avoid unphysical contributions to the free energy. Figure 2 presents the potentials of mean force (PMF) around the two dihedral angles, ϕ₁ and ϕ₂ of the two five-atomic benchmark systems II and III. Dark areas signify energy minima, while bright areas represent energy barriers. A dashed green line encircles the energy minima at an energy level of about 9 k_BT, representing the areas of phase space that can usually be accessed by normal LD simulations within a few nanoseconds. It is evident that the two systems are designed to have little phase space overlap. The global energy minima of both states do not overlap; instead, the minima of system II are located in high energy regions of III and vice versa. In addition, the minima are separated by energy barriers greater than 10 kcal/mol. The five-atomic benchmark systems thus are one of the simplest possible systems for which enhanced sampling in one form or the other is essential to obtaining converged free energy results.

Table 4 lists the free energy difference results between II and III based on LD (second column) and reweighted SGLD (third column) simulations. For LD, regular BAR simulations fail to converge, since there is no phase space overlap between the two end points. For EDS with LD, the deviations depend on the chosen s. For s =1 and 0.1 (corresponding to T_EDS = 300 and 3000 K), the free energy results deviate from the reference results by 2 and 1.5 kcal/mol. Using thermodynamic integration, Leitgeb et al. found similar deviations for simulations that were trapped in a local energy minimum.³⁹ This demonstrates that, for values of s close to 1, EDS can also be afflicted by sampling problems. Starting from an s lower than 0.01 (which corresponds to an T_EDS > 30 000 K), EDS with LD is able to reproduce the reference results, but with relatively high standard deviations of greater than 0.45 kcal/mol.

Table 4.

Free Energy Difference of Five-Atomic Benchmark Systems in Kilocalories Per Mole

	LD	SGLDrw
reference	−14.28
BAR	no convergence	−14.28 ± 0.10
EDS (s = 1)	−11.91 ± 0.54	−14.13 ± 0.12
EDS (s = 0.1)	−12.83 ± 0.16	−14.11 ± 0.20
EDS (s = 0.01)	−14.05 ± 0.45	−14.08 ± 0.16
EDS (s = 0.001)	−14.20 ± 0.52	−14.25 ± 0.21

Without reweighting, the SGLD results are 12.31 ± 0.06 for BAR and 12.08 ± 0.10 for EDS with s =1 (an error of 2 kcal/mol), thus reflecting the bias introduced by SGLD. However, after reweighting, the BAR result is in excellent agreement with the analytical reference, while the deviations of EDS are minuscule (ranging between 0.03 to 0.2 kcal/mol). In addition, all SGLD results exhibit low standard deviations. This demonstrates that reweighting considerably improves the result. Although no energy offsets were used for these EDS calculations, the FES with SGLD still yields accurate results. This feature can be exploited for more advanced versions of EDS that include a parameter update scheme (e.g., ref 32). The key step for the fast convergence of EDS is finding the optimal value of the smoothing parameter s and the energy offsets $E_k^{\text{R}}$. The use of SGLD allows higher values of s and, thus, increases the efficiency of the calculations. While SGLD is probably not able to obtain accurate free energy results in all cases, our data demonstrate that it can improve the convergence during the search for the correct $E_k^{\text{R}}$ parameters, which reduces the time required for EDS.

In the following, we compare the present results with previously reported results by other FES methods with advanced sampling. In ref 39, non-Boltzmann thermodynamic integration with 11 intermediate steps and a total simulation time of 52 ns yielded a free energy difference of −14.43 ± 0.17 by using adaptive umbrella potentials. In ref 41, non-Boltzmann Bennett with a special umbrella potential and a total simulation time of 84 ns yielded a result of −14.38 ± 0.20. This indicates that SGLD is able to improve the sampling compared to LD with an efficiency that is equal or superior to umbrella potentials.

4.2.1. Ethanol.

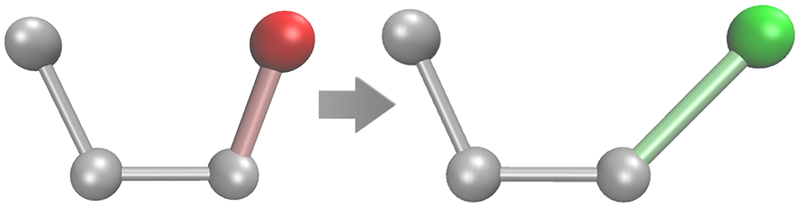
In this section, we test the efficiency of the reweighting scheme in explicit solvent. For this purpose, we employ a benchmark system where the two end states are equivalent, and therefore, the total free energy difference is zero. Thus, no reference data are required. In particular, we focus on the alchemical mutation of ethan-1-ol to ethan-2-ol in a box of 766 TIP3P water molecules. In this mutation, the hydroxyl group is transferred from one carbon atom of ethanol to the opposite carbon atom (Figure 3), causing the hydration shell to adapt to the new charge distribution. Since this happens on the time scale of a few picoseconds, sampling is not a limiting factor for the accuracy of this FES. However, the primary objective of this benchmark system is to illustrate the limitations of the reweighting scheme in free energy calculations. For this purpose, two different forms of SGLD are employed: In the first case (SGLD^all), the guiding force is applied to all atoms, thus enhancing the motions of both solute and solvent. In the second setup (SGLD^EtOH), the application of guiding forces is restricted to the solute, leaving the water unaffected.

Figure 3.

Mutation of ethan-1-ol to ethan-2-ol in explicit water. Since the end states are equivalent, the free energy difference is zero.

The solvation free energy differences (ΔΔA_solv) between ethan-1-ol and ethan-2-ol in explicit solvent are listed in Table 5. The first three rows show the results without reweighting. The accuracy and precision of the LD results indicate that the simulation times used in this example are long enough to obtain converged results (exhibiting a deviation of −0.04 kcal/mol from the ideal result). The unreweighted SGLD results in rows two and three illustrate that the use of SGLD does not introduce any substatial additional errors (yielding deviations <0.03 kcal/mol). However, when the reweighting equation is employed (indicated by the subscript “rw” in rows four and five), both errors and standard deviations increase dramatically. In particular, the application of the reweighting scheme to all atoms of the system (${\text{SGLD}}_{\text{rw}}^{\text{all}}$) leads to an error of −0.51 kcal/mol, which is 10 times higher than that of LD. In addition, the standard deviations amount to 1.24 kcal/mol, which is ~30 times higher than in LD.

This truly terrifying result can be explained in terms of the variance of the weighting factors w^SGLD. The weighting factors for ${\text{SGLD}}_{\text{rw}}^{\text{all}}$ range between 10⁻¹⁰ and 10⁺⁴⁰. Since a few data points carry weights that are several orders of magnitude above average, they dominate in the calculation of the reweighted free energy result. For example, the results for ${\text{SGLD}}_{\text{rw}}^{\text{all}}$ are largely determined from three data points out of the whole trajectory. This finding highlights that SGLD is not size-extensive; i.e., the employment of reweighting becomes more inefficient as the number of atoms of the system increases. Therefore, the use of SGLD should be restricted to the environment directly surrounding the site of interest in the FES. For example, if the application of SGLD is restricted to the solute (${\text{SGLD}}_{\text{rw}}^{\text{EtOH}}$), the weighting factors vary only between 0.1 and 10, leading to a reduction of the deviation to acceptable levels (0.11 kcal/mol) as well as yielding a standard deviation that is comparable to that of LD (0.05 kcal/mol).

4.3. Alanine–Serine.

In the final example, we compare the performance of BAR and EDS in connection with SGLD for a more biologically relevant system. Here, we mutate Ala into Ser (see Figure 4) both in the gas phase and implicit solvent to compute the solvation free energy difference between the two amino acids. Since a dual topology setup is employed, no contributions from changes of the bond angles arise. The choice of this system is motivated by the high sensitivity of the free energy difference between Ala and Ser to the secondary structure of the backbone. Limited or biased sampling of the backbone can lead to free energy differences between −1.47 and −4.45 kcal/mol.⁴⁰ The mutation, therefore, provides means to test SGLD for biases in the sampling of secondary structures.

Figure 4.

Illustration of the mutation of N-acetyl-methylamide alanine to serine.

Table 6 lists the solvation free energy differences between Ala and Ser based on LD (second column) and reweighted SGLD (third column) simulations. Focusing on the upper half of Table 6, the solvation free energy differences from BAR and EDS are in excellent agreement. In addition, the results are in fair agreement with explicit and implicit solvent results in refs ^{40, 41}, and ⁵⁵. However, when comparing the LD results with the SGLD results, there is a subtle, but statistically significant deviation between the two BAR results. Although this deviation amounts to about 5% of the LD results, it should be perfectly acceptable in normal applications, especially considering that errors due to insufficient sampling can be significantly larger.

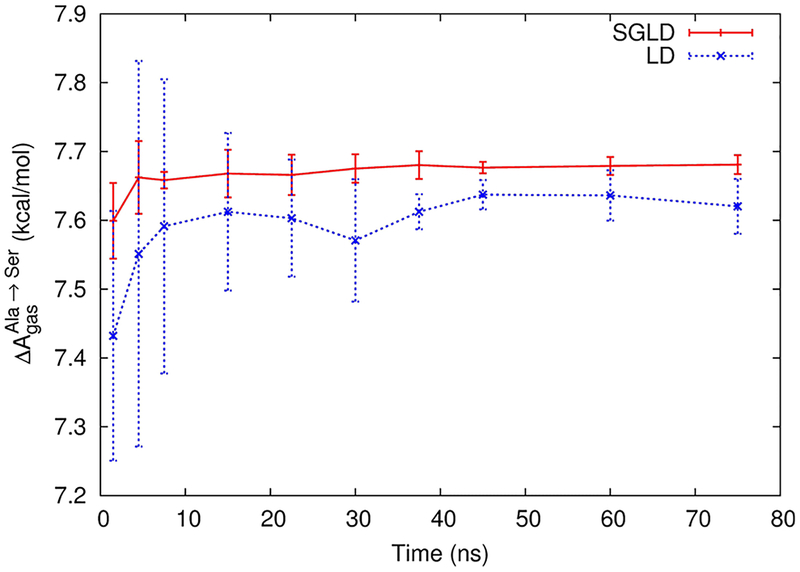
The effect of SGLD on sampling for this benchmark system is shown in Figure 5. The plot compares the convergence and standard deviations of LD and SGLD FES. Gas phase free energy differences ($\mathrm{\Delta }{A}_{\text{gas}}^{\text{Ala}\to \text{Ser}}$) between alanine and serine resulting from BAR are plotted over simulation time. While both LD and SGLD results converge in 10 ns to ΔA_gas values that are within 0.05 kcal/mol of the final result, the standard devations are significantly lower when using SGLD (0.05 compared to 0.28 kcal/mol after ~5 ns). This demonstrates that, even for relatively unproblematic systems like alanine and serine, the use of SGLD can increase the performance of FES.

Figure 5.

Comparison of the convergence of free energy simulations based on SGLD (red) and LD (blue). Gas phase free energy differences ($\mathrm{\Delta }{A}_{\text{gas}}^{\text{Ala}\to \text{Ser}}$) between alanine and serine resulting from BAR are plotted over time. The error bars at each data point are calculated from four different simulations.

The other motivation to employ this benchmark system is the capability of BAR to calculate its free energy difference in a single step. As shown previously,⁵⁵ the phase space overlap between alanine and serine is not a limiting factor for the accuracy of FES. Our aim here is a fair comparison of the efficiency of several free energy methods without the use of λ intermediate states. In the following, we rely on BAR as a reference. In particular, we compare the performance of EDS with BAR and thermodynamic perturbation based on trajectories of Ala (TP_fw), Ser (TP_bw), and a simple half of a d-half mixture of both end states (TP_0.5). The results for those methods are shown in the lower part of Table 6.

On the basis of the EDS equation to calculate free energies, eq 18, one could wrongly assume that the performance of EDS resembles TP since the end states are connected to the reference state by two TP steps. However, due to the characteristics of the reference state, the sampling and convergence properties of EDS and TP are different. The data in Table 6 show that EDS is more closely related to BAR than to the three different TP methods, both in terms of absolute value and standard deviations. While EDS is in almost perfect agreement with BAR, the deviations of the TP methods from the reference results range between 0.1 and 0.4 kcal/mol. The standard deviations of TP range between 0.28 and 0.89, while EDS yields the same standard deviations as BAR (0.04 kcal/mol). The close relationship between BAR and EDS was recently derived by theoretical means by Christ and van Gunsteren in ref 30.

5. CONCLUSIONS

From the results in this paper, it is possible to provide a few general guidelines for the use of SGLD in FES. The results for the four-atomic benchmark system show that the use of SGLD changes free energy differences of bonded terms of dummy atoms. These errors can be eliminated if the net rotation and translation is removed from the guiding force, reducing the RMSD of SGLD simulations from 0.250 to 0.03 kcal/mol. Therefore, this option will become the default of all future versions of SGLD in CHARMM. Alternatively, errors resulting from changes of the bonded terms can also be avoided by employing dual topology setups.

The results for the five-atomic benchmark system highlight that BAR is not able to yield correct results with LD due to the lack ofphase space overlap between the two end points and the high energy barriers of over 10 kcal/mol (~16k_BT). Even higher energy barriers are quite common in biological systems, e.g., in the rearrangement of protein side chains.³⁹ In order to become a standard technique, FES will have to be able to deal with such an energy barrier without human intervention on a case by case basis. Considering that side chain motions or conformation changes in proteins can happen on a scale of microseconds to milliseconds, it becomes evident that sampling problems in MD simulations cannot be addressed by a simple increase of computer power (as was hoped for during past decades). With SGLD, both BAR and EDS lead to the correct results. Considering that SGLD does not require any prior knowledge about the system, it is an attractive choice for (semi)automatic FES protocols. For the examples presented here, the additional effort required for running SGLD with reweighting consisted in equilibrating the system with LD and executing an awk script after the termination of the SGLD simulation.

Notably, EDS simulations with LD yield the correct results for the five-atomic benchmark system if the s parameter is lower than 0.01. However, this comes at the cost of greater standard deviations than in any corresponding SGLD simulation. This indicates that SGLD can be used to improve the convergence of EDS. In addition, SGLD allows the use of higher s values, which allows a more efficient use of the EDS update scheme. Another interesting aspect of the results for the five-atomic benchmark systems is that we did not use any energy offsets to balance the sampling between the two end states. This suggests that SGLD can improve the convergence of the more advanced versions of EDS such as used in refs ³¹ and ³².

The next example, which involves an FES of ethanol in explicit solvent, shows that the performance of SGLD is limited by the size of the system since the variance of the weighting factors increases with system size. This leads to excessively high standard deviations and inaccuracies of the free energy results, as computed ensemble averages are dominated by the outliers with the highest weight. In extreme cases, the final free energy result will be determined by a single data point. This is a general limitation of FESs that rely on biased sampling followed by reweighting. For optimal performance, it could be necessary to limit the application of SGLD to the solute and, in protein simulations, to atoms close to the site of interest. Alternatively, it might be interesting to explore size-extensive methods.⁵⁶

The last example, involving the mutation of Ala to Ser, is a very sensitive benchmark for the sampling of the backbone by SGLD. As shown recently, the correct generation of the backbone probability distributions is essential for reproducing experimental results.⁵⁷ Previous studies demonstrate that the solvation free energies of Ala and Ser are very sensitive to the secondary structure of the backbone, causing deviations of up to 2.57 kcal/mol.⁴⁰ For BAR, we find a statistically significant difference of 0.14 kcal/mol between LD and SGLD, which suggests a slight bias due to SGLD. However, this deviation can be considered small in comparison to other sources of error, and the detected loss of accuracy is outweighed by a faster convergence of the results.

In addition, we employ the mutation of Ala to Ser to compare the performance of EDS with BAR and three different kinds of TP. In particular, we focus on TP based on the trajectories of Ala and Ser, as well as on an intermediate state based on U_R = U_Ala/2 + U_Ser/2. Our data support the hypothesis that the sampling and convergence properties of EDS are different from TP and more closely related to BAR. Even the simplified version of EDS exhibits smaller deviations from the BAR reference results than all versions of TP considered here. The standard deviations from EDS are considerably smaller than those of TP, being equal to the results from BAR. Our results indicate that EDS is a viable method for performing free energy calculations from a single simulation. In particular, EDS is a valuable tool in cases where the simulation of multiple intermediate states would be prohibitively expensive in terms of computational time or human resources. However, it is necessary to keep in mind that the convergence of the EDS results will become poorer with decreasing overlap of the phase spaces of the end points involved. In such cases, the performance of EDS can be improved by optimizing the EDS reference state Hamiltonian (e.g., using an s < 1) as well as by increasing the sampling with SGLD.

APPENDIX 1: ANALYTICAL CALCULATION OF FREE ENERGY DIFFERENCES BETWEEN POLYATOMIC MOLECULES

As reference results for the free energy calculations of the four-and five-atomic benchmark systems, we employ analytical results based on the derivations by Herschbach, Johnston, and Rapp (HJR). In work completely unrelated to computer simulations, HJR introduced an alternative formulation of how to compute the configurational partition function of a polyatomic molecule,⁵⁸ which turned out to be extremely useful for computing alchemical free energy differences between such moieties analytically.³⁵ Summarizing the result of ref 58, the configurational partition function Z of a polyatomic molecule in the rigid rotator harmonic oscillator (RRHO) approximation is given by

$$Z\approx Z^{\text{RRHO}}=\frac{{\left(2\pi k_{\text{B}}T\right)}^{(3N-6)/2}}{|F{|}^{1/2}}J$$ (22)

where N is the number of atoms and k_B and T are the Boltzmann constant and the temperature. J is the Jacobian factor arising from the change of Cartesian to internal coordinates. The crucial element of HJR was to show that J can be computed as a simple product of factors, one for each atom, i.e., $J={\mathrm{\Pi }}_{a=1}^N{J}_{\alpha }$ (see Table 1 of ref 58). F is the force matrix, and in the simple cases considered here (unbranched four- and five-atomic molecules) its determinant is just the product of all force constants present in the system. Equation 22 implicitly assumes dihedral angles to be harmonic as well; however, HJR also show how hindered rotation can be accounted for correctly.

In the RRHO approximation, i.e., assuming that all bonded energy terms are harmonic, the alchemical free energy difference between two molecules (i, f) with the same number of atoms is, therefore, given by

$$\mathrm{\Delta }A=-k_{\text{B}}T\text{ln}\frac{{\mathrm{\prod }}_{\alpha =1}^N{J}_{\alpha }^f}{{\mathrm{\prod }}_{\alpha =1}^N{J}_{\alpha }^i}-k_{\text{B}}T\text{ln}{\left(\frac{\left|F^i\right|}{\left|F^f\right|}\right)}^{1/2}$$ (23)

Keeping in mind that IFI in simple situations is just a product of force constants, only those parts of the system that are different between states i and f contribute to ΔA. Suppose that two unbranched, nonlinear four-atomic molecules are mostly identical but differ by the bond length between atoms 3 and 4 (r₃₄) and by the force constants for the bond stretching term between atoms 3 and 4 (K₃₄), as well as the angle bending term for atoms 2, 3, and 4 (K₂₃₄), then the free energy difference between the two hypothetical molecules is given by (see refs ³⁵, ³⁶, and ⁵⁸, for more details and further examples)

$$\mathrm{\Delta }A=-k_{\text{B}}T\text{ln}{\left(\frac{r_{34}^f}{r_{34}^i}\right)}^2-k_{\text{B}}T\text{ln}{\left(\frac{K_{234}^i{K}_{34}^i}{K_{234}^f{K}_{34}^f}\right)}^{1/2}$$ (24)

In the present work, we even went beyond the RRHO approximation and treated the dihedral terms exactly. Following HJR, the terms are taken out of the force matrix, and their contribution to the partition function is obtained by numerical integration, i.e., for a four-atomic molecule with one dihedral angle term

$$Z=Z^{\text{RRHO}}\int \text{d}\phi \text{exp}\left(-\frac{U_{\text{dine}}}{k_{\text{B}}T}\right)$$ (25)

Here, Z^RRHO accounts for the bond stretching and bond angle terms in excellent approximation, whereas the explicit integration over the dihedral angle takes care of the anharmonic dihedral potential. For the five-atomic model systems, there are two dihedral degrees of freedom, and the intramolecular nonbonded interactions were included as well by expressing the distances between atom pairs 1–4, 2–5, and 1–5 in terms of internal coordinates (see ref 39 for further details).

APPENDIX 2: EXAMPLE SCRIPT TO USE EDS WITH MSCALE

Here, we show an extract from an example script for the use of the EDS implementation in CHARMM. First, two end points called “first” and “second” are set up with MSCALE, spawning two processes that will use one processor each (nproc). The Hamiltonians of each end point are defined in the input scripts sub1.inp and sub2.inp:

mscale nsubs 2
 subs first coef 1.0 prog “../exec/gnu/charmm” –
   outp “sub1.out” inpu “sub1.inp” –
   nproc 1 sele all end
 subs second coef 1.0 prog “../exec/gnu/charmm” –
   outp “sub2.out” inpu “sub2.inp” –
   nproc 1 sele all end
 end

After setting up the end points with MSCALE, the EDS command has to be invoked. Here, an EDS temperature T_EDS = 300 is chosen, which is equivalent to an s = 1 at T = 300. The number of subsystems for EDS (neds) is two, followed by the names of the subsystems and their energy offsets (with $E_{\text{first}}^{\text{R}}=1.1$ and $E_{\text{Second}}^{\text{R}}=2.2$).

eds temp 300. neds 2 term first 1.1 term second 2.2

After the EDS command, the normal CHARMM commands to start a simulation may be used.