Multimodal imaging of brain connectivity reveals predictors of individual decision strategy in statistical learning

Abstract

Successful human behaviour depends on the brain’s ability to extract meaningful structure from information streams and make predictions about future events. Individuals can differ markedly in the decision strategies they use to learn the environment’s statistics, yet we have little idea why. Here, we investigate whether the brain networks involved in learning temporal sequences without explicit reward differ depending on the decision strategy that individuals adopt. We demonstrate that individuals alter their decision strategy in response to changes in temporal statistics and engage dissociable circuits: extracting the exact sequence statistics relates to plasticity in motor corticostriatal circuits, while selecting the most probable outcomes relates to plasticity in visual, motivational and executive corticostriatal circuits. Combining graph metrics of functional and structural connectivity, we provide evidence that learning-dependent changes in these circuits predict individual decision strategy. Our findings propose brain plasticity mechanisms that mediate individual ability for interpreting the structure of variable environments.

Learning and experience are known to facilitate our ability to extract meaningful structure from streams of information and interpret complex environments. Despite the general consensus that ‘practice makes perfect’, there is striking variability among individuals in the extent to which they take advantage of past experience. In the laboratory, this variability has been demonstrated in tasks such as perceptual decision-making^1,2 or statistical learning of regularities (that is, learning of probabilistic spatial or temporal structures) through mere exposure to the environment^3,4. Previous work examining individual variability in decision-making and probabilistic learning tasks has highlighted the role of individual decision strategies^5–10. In particular, humans and animals have been shown to engage in probability matching or maximization when making choices in probabilistic environments (for example, refs. ^9,11,12). Probability matching involves making choices stochastically to match the probabilistic distribution of all possible outcomes, while probability maximization involves choosing the most probable or frequently rewarded outcome in a given context.

Individual variability in these decision strategies has mainly been investigated in the context of reward learning (for example, refs. ^9,11,12). Yet, reward-based learning captures only one aspect of human flexibility in natural environments, as feedback and rewards are often not explicit. Here, we test the role of decision strategies in statistical learning. In particular, we designed a statistical learning task that tests whether individuals learn to extract temporal structure from mere exposure to unfamiliar sequences without explicit reward (that is, trial-by-trial feedback). We changed the temporal sequence statistics unbeknown to the participants, to simulate structure in natural environments that may vary from simple regularities to more complex probabilistic combinations. Participants were first exposed to sequences determined by frequency statistics (that is, one item in the sequence occurred more frequently than others) and then sequences that were determined by context-based statistics (that is, some item combinations were more frequent than others). Participants predicted which item would appear next in the sequence. We modelled the participant responses to interrogate the decision strategy that individuals adopt during learning (that is, how individuals extract temporal structure). We reasoned that individuals would adapt their decision strategies in response to changes in the temporal sequence statistics and the learning goal (that is, learning frequency versus context-based statistics).

Previous work has implicated corticostriatal circuits in sequence and probabilistic learning^13–16. Here, we sought to determine whether these circuits are involved in statistical learning of temporal structures without explicit reward. We ask whether individual decision strategies (from matching to maximization) involve distinct corticostriatal circuits and whether learning-dependent plasticity in these circuits can account for individual variability in learning to extract the environment’s statistics. We reasoned that brain plasticity, as expressed by learning-dependent connectivity changes in corticostriatal circuits, would predict changes in decision strategy when learning frequency versus context-based statistics.

To test these hypotheses, we combined our statistical learning task with multi-session (before versus after training) measurements of functional (resting-state functional MRI (rs-fMRI)) and structural (diffusion tensor imaging (DTI)) connectivity. rs-fMRI has been shown to reveal functional connectivity within and across brain networks that subserve task performance^17,18. Moreover, there is accumulating evidence for changes in both functional and structural brain connectivity due to training (for example, see refs. ^19,20), suggesting learning-dependent plasticity in human brain networks that mediate adaptive behaviour. To map corticostriatal circuits at a fine scale, we employed DTI-based segmentation analysis²¹ of the striatum into finer subregions and computed the functional connectivity between these striatal regions and cortical networks, as revealed by analysis of the rs-fMRI data. Our results show that individuals adapt their decision strategies (from matching towards maximization) in response to changes in the temporal statistics. These adaptive decision strategies relate to distinct corticostriatal circuits for learning temporal statistics. That is, adopting a strategy closer to matching when learning frequency statistics relates to learning-dependent connectivity changes in the motor circuit. In contrast, deviating from matching towards maximization when learning context-based statistics relates to functional connectivity changes in the visual corticostriatal circuit.

Next, we combined graph theory analysis with a multivariate statistical analysis (partial least squares (PLS) regression) to determine multimodal predictors of decision strategy. This approach allows us to: (1) combine information from multivariate signals (rs-fMRI and DTI)—rather than using data from each MRI modality alone; and (2) test whether plasticity in functional and/or structural connectivity in corticostriatal circuits predicts—rather than simply relates to—individual decision strategy. In particular, we employed graph theory to extract metrics of brain connectivity that are comparable across brain imaging modalities and have been suggested to relate to learning and brain plasticity^22,23. We then used PLS modelling to combine these multimodal graph metrics and identify brain connectivity predictors (rs-fMRI and DTI) of individual decision strategy when learning temporal statistics. Our results demonstrate learning-dependent changes in resting corticostriatal connectivity (functional and structural) that predict individual decision strategy for statistical learning. In particular, we discern distinct brain plasticity mechanisms that predict: (1) changes in individual decision strategy in response to changes in the environment’s statistics; and (2) individual variability in decision strategy independent of temporal statistics. Our findings provide evidence for adaptive decision strategies that involve distinct brain routes for statistical learning, proposing a strong link between learning-dependent plasticity in brain connectivity and individual learning ability.

Results

Behavioural improvement in learning temporal statistics

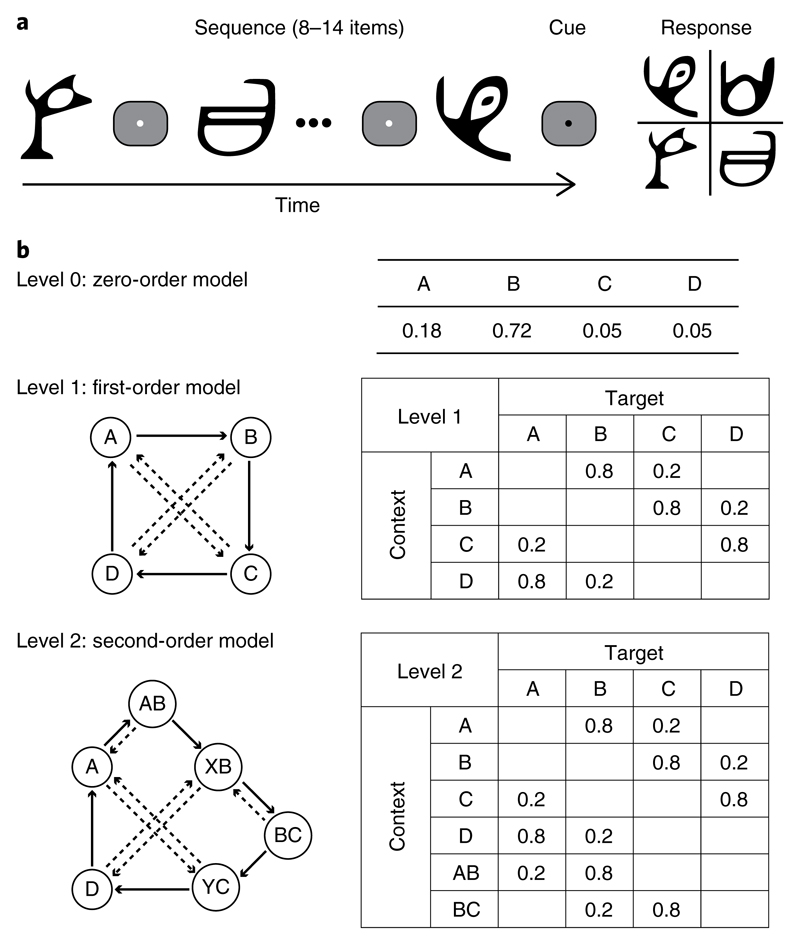
To investigate learning of temporal structures, we generated temporal sequences of different Markov orders (that is, level 0, level 1 and level 2: context lengths of 0, 1 or 2 previous items, respectively) (Fig. 1a,b). We simulated event structures that typically vary in their complexity in natural environments by exposing participants to sequences of unfamiliar symbols that increased in context length unbeknown to the participants. Participants were first trained on sequences determined by frequency statistics (that is, level 0: occurrence probability per symbol) and then on sequences determined by context-based statistics (that is, levels 1 and 2: the probability of the next symbol depends on the preceding symbol(s)). Participants were asked to predict which symbol they expected to appear next in the sequence. Participants were not given trial-by-trial feedback, consistent with statistical learning paradigms.

Fig. 1. Trial and sequence design.

a, Trial design: stimuli comprised four symbols chosen from Ndjuká syllabary. A temporal sequence of 8–14 symbols was presented, followed by a cue and the test display. b, Sequence design: the three Markov models used in the study. In the zero-order model (level 0), each of the four symbols (A, B, C and D) constitutes a different state that occurred with a different probability. In the first-order (level 1) and second-order (level 2) models, each state (indicated by a circle) is associated with two transitional probabilities—one high probability (solid arrow) and one low probability (dashed arrow). Rows in the conditional probability matrix represent the temporal context, whereas columns represent the corresponding target.

We quantified participants’ performance in this prediction task by measuring how closely the probability distribution of the participant responses matched the distribution of the presented symbols¹⁰. This performance index (see Supplementary Information) is preferable to a simple measure of accuracy as the probabilistic nature of the sequences means that the ‘correct’ upcoming symbol is not uniquely specified.

We then computed a normalized performance index by subtracting performance for random guessing. Comparing the normalized performance index across sessions and levels (two-way repeated-measures analysis of variance (ANOVA) with session (pre- and post-training) and level (levels 0, 1 and 2)) showed a significant main effect of session (F(1,20) = 117.9; P < 0.001; partial eta squared: η_p² = 0.855) and level (F(2,40) = 17.9; P < 0.001; η_p² = 0.473), but no significant interaction between session and level (F(1.44,28.71) = 2.7; P = 0.098; η_p² = 0.120; Greenhouse–Geisser corrected), suggesting that participants improved significantly after training and showed similar improvement across levels (Fig. 2a).

Fig. 2. Behavioural performance.

a, Normalized performance index for the training group (n = 21) per level and test session (pre-training, grey bars; post-training, black bars). Error bars indicate s.e.m. across participants. b, Box plots of strategy index show individual variability for each level (levels 0, 1 and 2). The upper and lower error bars display the minimum and maximum data values, and the central boxes represent the interquartile range (25th–75th percentiles). The thick line in the central boxes represents the median. The open circle denotes an outlier. The strategy index for frequency statistics was not significantly different from matching (that is, zero strategy index; t(20) = −0.23; P = 0.82; CI = −0.08 to 0.07; Cohen’s d = −0.050). Note that the variability across participants around zero could be due to the fact that the task is probabilistic and the participants were not given trial-by-trial feedback. In contrast, the strategy index for context-based statistics (mean strategy index for levels 1 and 2) was significantly higher than zero (t(20) = 4.01; P<0.001; CI = 0.08 to 0.26; Cohen’s d = 0.874). c, Scatter plot of strategy index for frequency and context-based statistics. Individual participant data are shown with open circles (n = 21). Points below the diagonal indicate participants who showed a higher strategy index for context-based compared with frequency statistics.

Decision strategies for learning: from matching to maximization

Previous work on probabilistic learning^8–10 and decision-making in the context of sensorimotor tasks^5–7 has shown that individuals adopt decision strategies (from matching to maximization) when making probabilistic choices. Here, we test the role of these decision strategies in statistical learning (that is, without explicit feedback or reward). In our statistical learning task, participants were exposed to stochastic sequences and therefore needed to learn the probabilities of different outcomes. Modelling the participants’ responses allows us to quantify their decision strategy, reflecting how the participants extract and respond to context-target contingencies in probabilistic sequences. In particular, participants may adopt: (1) probability matching (that is, match their choices to the relative probabilities of the context-target contingencies presented in the sequences); or (2) deviate from matching towards maximization (that is, choose the most likely outcome in a given context).

We quantified each participant’s decision strategy during training by comparing individual participant responses to two models: (1) a probability matching model, where probabilistic distributions of possible outcomes were derived from the Markov models that generated the presented sequences; and (2) a probability maximization model, where only the most likely outcome was allowed for each context. We quantified each participant’s strategy choice during training based on the distance of the participant response distribution from the matching and maximization model. We then computed a single measure of strategy index as the integral between the participant’s strategy choice and the matching model across trials and training blocks. Therefore, strategy index is a continuous measure that captures the strategy that individuals adopt over time (that is, during training) on a continuous scale between matching and maximization (Fig. 2b and Supplementary Figs. 1 and 2). Zero strategy index indicates that the participant response distribution matches the probability distribution of the presented sequence (that is, exact matching). A participant’s performance deviating from the matching model may result in a positive or negative strategy index. Overestimating the probability of the most probable context-target contingency in the sequence results in a positive strategy index, indicating that the participant’s strategy ranges between matching and maximization. In contrast, underestimating the probability of the most probable context-target contingency in the sequence results in a negative strategy index, indicating that the participant’s strategy ranges between matching and a random model of response (that is, participants choose all context-target contingencies with equal probability). Thus, we interpret strategy index values close to zero as strategy closer to matching, and higher positive values as strategy deviating from matching towards maximization.

Fig. 2b,c shows differences in strategy index across sequence levels and individual participants. A one-way repeated-measures ANOVA with level (level 0, 1 or 2) showed a significant main effect of level (F(1.44,28.79) = 8.0; P = 0.004; η_p² = 0.286; Greenhouse–Geisser corrected), indicating higher strategy index for increasing context length. In particular, the strategy index for level 1 was higher than the strategy index for level 0 (t(19) = 2.5; P = 0.020; confidence interval (CI) = 0.03 to 0.30; Cohen’s d = 0.567), but not for level 2 compared with level 1 (t(19) = 1.9; P = 0.066; CI = −0.01 to 0.13; Cohen’s d = 0.435). Furthermore, the strategy indices for levels 1 and 2 were highly correlated (r(19) = 0.72; P < 0.001; CI = 0.42 to 0.89), while no significant correlations were found for level 0 (level 0 versus level 1: r(19) = −0.21; P = 0.35; CI = −0.71 to 0.28; level 0 versus level 2: r(19) = −0.15; P = 0.52; CI = −0.55 to 0.34). To avoid collinearity²⁴, we computed a mean strategy index for levels 1 and 2 to generate a single predictor of learning context-based statistics for further regression analyses. This mean strategy index for context-based statistics was significantly higher than the strategy index for frequency statistics (t(19) = 3.2; P = 0.005; CI = 0.07 to 0.32; Cohen’s d = 0.711). Furthermore, the strategy index for frequency statistics was not significantly different from matching (that is, zero; one-sample t-test: t(20) = −0.23; P = 0.82; CI = −0.08 to 0.07; Cohen’s d = −0.050). In contrast, the strategy index for context-based statistics was significantly higher than zero (one-sample t-test: t(20) = 4.01; P < 0.001; CI = 0.08 to 0.26; Cohen’s d = 0.874). Taken together, these results provide evidence that participants adapted their decision strategy in response to changes in temporal statistics across sequence levels; that is, individuals adopted a strategy that deviated from matching towards maximization for learning first frequency and then context-based statistics.

These differences in decision strategy across sequence levels could not be simply explained by changes in reward processing, cognitive strategy training or differences in performance improvement across sequence levels. Specifically, the participants were not given explicit reward (that is, no trial-by-trial feedback) or explicitly trained on effective cognitive strategies to boost task performance. Furthermore, there were no significant differences in performance index across levels after training (see ‘Behavioural improvement in learning temporal statistics’), and participant performance after training did not correlate significantly with decision strategy (level 0: r(19) = 0.21; P = 0.36; CI = −0.21 to 0.58; level 1: r(19) = 0.06; P = 0.81; CI = −0.37 to 0.42; level 2: r(19) = 0.15; P = 0.52; CI = −0.37 to 0.52). In contrast, we have previously shown that individual decision strategy is positively correlated with learning rate (that is, how fast participants extract the correct sequence structure) in our statistical learning task¹⁰. Taken together, these results suggest that the adaptive decision strategies we observed in response to changes in temporal statistics reflect changes in the learning process (that is, how individuals extract temporal sequence structure) rather than overall changes in task training.

Learning-dependent changes in DTI-informed resting-state connectivity

Previous work has established distinct corticostriatal circuits with dissociable functions²⁵ that have been implicated in a range of learning tasks, including sequence and probabilistic learning^13–15. Here, we investigated whether brain plasticity in these corticostriatal circuits relates to individual decision strategy in statistical learning (that is, without trial-by-trial feedback). In particular, to determine functional connectivity at rest, we used: (1) DTI-based segmentation to define striatal regions; and (2) independent component analysis (ICA) for decomposition of the rs-fMRI time course to define functional cortical networks.

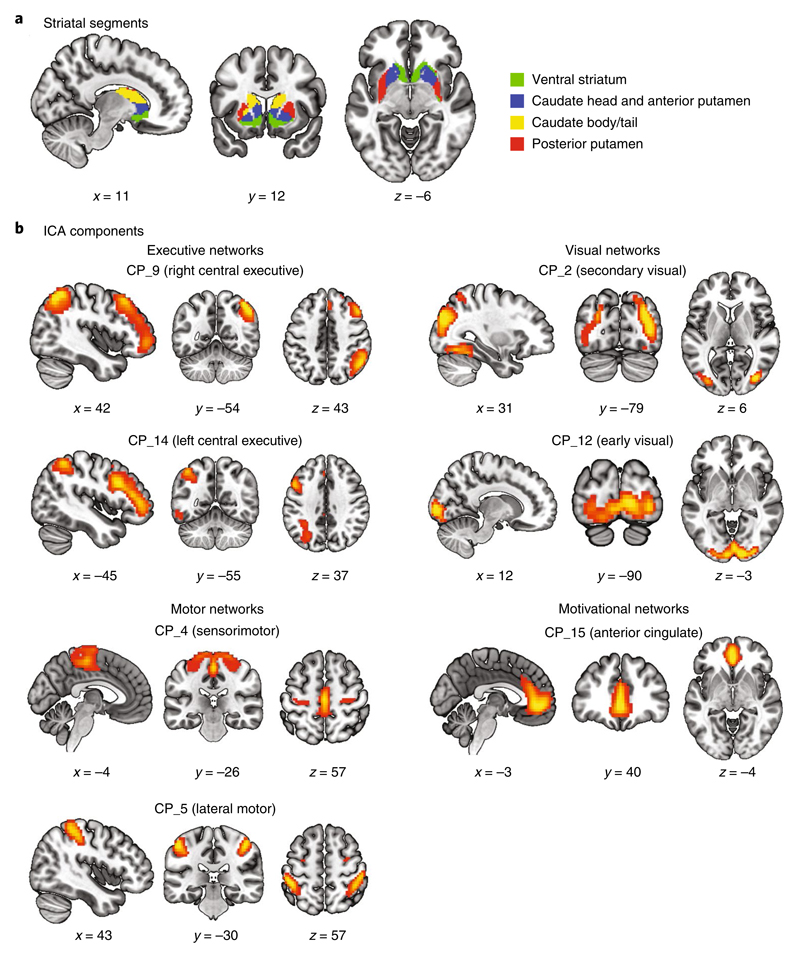
First, we used DTI data to segment the striatum into finer subregions that would then serve as regions of interest for the functional connectivity analysis of the rs-fMRI data (see Supplementary Information). In particular, we defined striatum (that is, caudate and putamen) anatomically from the Automated Anatomical Labeling (AAL) atlas²⁶ and segmented it into subregions based on their structural connectivity profile (Supplementary Fig. 3). We derived four segments per hemisphere that corresponded to: (1) the ventral striatum; (2) the head of the caudate and anterior putamen; (3) the body and tail of the caudate; and (4) the posterior putamen (Fig. 3a and Supplementary Table 1). This segmentation is in agreement with previous histological studies²⁵.

Fig. 3. Striatal segments and iCA components.

a, Four striatal segments as estimated by a DTI connectivity-based and hypothesis-free classification method. Segments are displayed in neurological convention (left is left) and overlaid on the Montreal Neurological Institute (MNI) template (green, ventral striatum; blue, caudate head and anterior putamen; yellow, caudate body/tail; red, posterior putamen). b, The seven selected ICA components are depicted, organized into known cortical networks. Group spatial maps are thresholded at z = 1.96 for visualization purposes and displayed in neurological convention on the MNI template. The x, y and z coordinates denote the location of the sagittal, coronal and axial slices, respectively.

We then identified functional brain networks during rest by decomposing the rs-fMRI time course into functionally connected components (that is, components comprising voxel clusters with a correlated time course) using group independent component analysis (GICA; see Supplementary Information). We followed the standard pipeline to perform the preprocessing on the rs-fMRI data for GICA (see Supplementary Information). Following GICA, we selected components associated with known corticostriatal circuits that have been implicated in learning²⁵ (Fig. 3b and Supplementary Table 2): (1) the right central executive network (CP_9; peak activations in the right middle frontal gyrus (MFG) and right inferior parietal lobule); (2) the left central executive network (CP_14; peak activations in the left inferior frontal gyrus (IFG) and left inferior parietal lobule); (3) the sensorimotor network (CP_4; peak activations in the bilateral supplementary motor area); (4) the lateral motor network (CP_5; peak activations in the bilateral postcentral gyrus); (5) the secondary visual network (CP_2; peak activations in the bilateral middle occipital gyrus); (6) the early visual network (CP_12; peak activations in the bilateral calcarine sulcus); and (7) the anterior cingulate network (CP_15; peak activations in the bilateral anterior cingulate gyrus (ACC)).

Next, we tested whether learning-dependent changes in intrinsic and extrinsic functional connectivity within corticostriatal circuits (that is, between DTI-defined striatal segments and ICA-defined cortical components) relate to individual decision strategy. As the strategy index is a continuous measure of decision strategy, we correlated changes in functional connectivity with individual strategy index, rather than comparing between separate groups of participants (that is, matchers versus maximizers). Positive correlations indicate that a higher increase in connectivity after training relates to maximization (top-right quadrant of the correlation plots), whereas negative correlations indicate that a higher increase in connectivity relates to matching (top-left quadrant of the correlation plots).

Correlating intrinsic connectivity with strategy

Intrinsic connectivity is a measure of signal coherence within a local network and quantifies activity correlation across voxels within the network. Previous work has shown that functional networks during task and rest are highly similar²⁷, suggesting that task-related blood-oxygen-level-dependent (BOLD) activity relates to intrinsic connectivity at rest. Furthermore, variability in intrinsic connectivity has been suggested to explain task performance²⁸. Here, we ask whether learning-dependent changes in intrinsic connectivity within each cortical network relate to individual decision strategy when learning temporal statistics.

We calculated an intrinsic connectivity measure for each cortical network indicating its local connectivity strength (n = 7). We then correlated intrinsic connectivity change (post- minus pre-training) with strategy for frequency and context-based statistics (Supplementary Table 3a). For frequency statistics, learning-dependent changes in connectivity in the lateral motor network correlated positively with strategy index (r(19) = 0.77; P < 0.001; CI = 0.60 to 0.89; surviving false coverage rate (FCR) correction) (Fig. 4a). For context-based statistics, learning-dependent changes in connectivity in the secondary visual network correlated negatively with strategy index (r(19) = −0.49; P = 0.025; CI = −0.74 to −0.10) (Fig. 4a). In contrast, we observed positive (marginally significant) correlations of learning-dependent changes in connectivity in the left central executive network (LCEN) and anterior cingulate network(ACN) with strategy index (LCEN: r(19) = 0.42; P = 0.059; CI = 0.01 to 0.68; ACN: r(19) = 0.35; P = 0.121; CI = 0.04 to 0.63) (Supplementary Fig. 4).

Fig. 4. Intrinsic and extrinsic connectivity analysis.

a,b, Significant skipped Pearson correlations (two-sided; n = 21) of the intrinsic connectivity change (post- minus pre-training) (a) and the extrinsic connectivity change (b) with strategy index for frequency (top) and context-based statistics (bottom). Open circles denote outliers as detected by the Robust Correlation Toolbox.

Correlating extrinsic connectivity with strategy

Extrinsic connectivity is a measure of functional connectivity between brain regions. In particular, it is computed as the correlation of the brain signals in typically distant regions across time, and quantifies the coherence of their activity^17,29. Previous work suggests that extrinsic connectivity changes with training and relates to behavioural performance¹⁹. Here, we test whether learning-dependent changes in corticostriatal extrinsic connectivity relate to individual decision strategy.

We selected pairs of striatal (Fig. 3a and Supplementary Table 1) and cortical areas (Fig. 3b and Supplementary Table 2) based on known corticostriatal circuits²⁵ (n = 14): (1) motivational: ventral striatum to ACN; (2) executive: caudate head and anterior putamen to right central executive network (RCEN) and LCEN (that is, the dorsolateral prefrontal and parietal cortex); (3) visual: caudate body and tail to secondary visual and early visual networks; and (4) motor: posterior putamen to sensorimotor and lateral motor networks (Supplementary Table 3b). These pathways have been identified by previous functional^30,31 and structural connectivity^32,33 studies. We calculated the Pearson correlation between the time courses in these corticostriatal areas, as a measure of extrinsic functional connectivity. We then correlated connectivity change (post- minus pre-training; after Fisher z-transform) with the strategy index for frequency and context-based statistics. For learning frequency statistics, learning-dependent changes in connectivity between the right posterior putamen and lateral motor network (r(19) = 0.51; P = 0.018; CI = 0.20 to 0.74; surviving FCR correction) correlated positively with strategy index (Fig. 4b). In contrast, for context-based statistics, learning-dependent changes in connectivity between the left body and tail of the caudate and the early visual network (r(19) = −0.46; P = 0.034; CI = −0.83 to −0.13; surviving FCR correction) correlated negatively with strategy index (Fig. 4b).

Relating adaptive decision strategies to brain plasticity

Taken together, our results provide evidence that plasticity in distinct corticostriatal circuits—as expressed by changes in intrinsic and extrinsic connectivity—relates to adaptive decision strategies when learning temporal statistics. We interpret this brain plasticity in the context of our behavioural findings showing that participants adapted their strategy from matching towards maximization when learning first frequency and then context-based statistics.

Our results showed that matching when learning frequency statistics relates to decreased intrinsic connectivity within the lateral motor network and decreased extrinsic connectivity between this network and the posterior putamen. Previous work has implicated the motor circuit in habitual learning^34,35 and stimulus–response associations³⁶. Thus, decreased connectivity in this circuit may facilitate matching that involves learning the exact sequence statistics rather than reinforcing habitual responses.

In contrast, deviating from matching towards maximization when learning context-based statistics relates to decreased connectivity within the visual corticostriatal circuit (intrinsic connectivity in the secondary visual network, and extrinsic connectivity between the body and tail of the caudate and the early visual network). Previous work has implicated the visual corticostriatal circuit in learning predictive associations16 and decision-making^37,38, highlighting its role in higher cognitive functions rather than simply the processing of low-level sensory information. Thus, decreased connectivity in this circuit may facilitate selecting the most probable outcome when learning complex context-target contingencies rather than learning the exact probability distributions.

Multimodal predictors of decision strategy

Our results so far provide evidence that learning-dependent changes in resting functional connectivity relate to adaptive changes in decision strategies. Next, we test whether learning-dependent plasticity in both functional and structural connectivity in these circuits predicts individual decision strategy, extending beyond the univariate and correlational approach we followed for our rs-fMRI connectivity analysis.

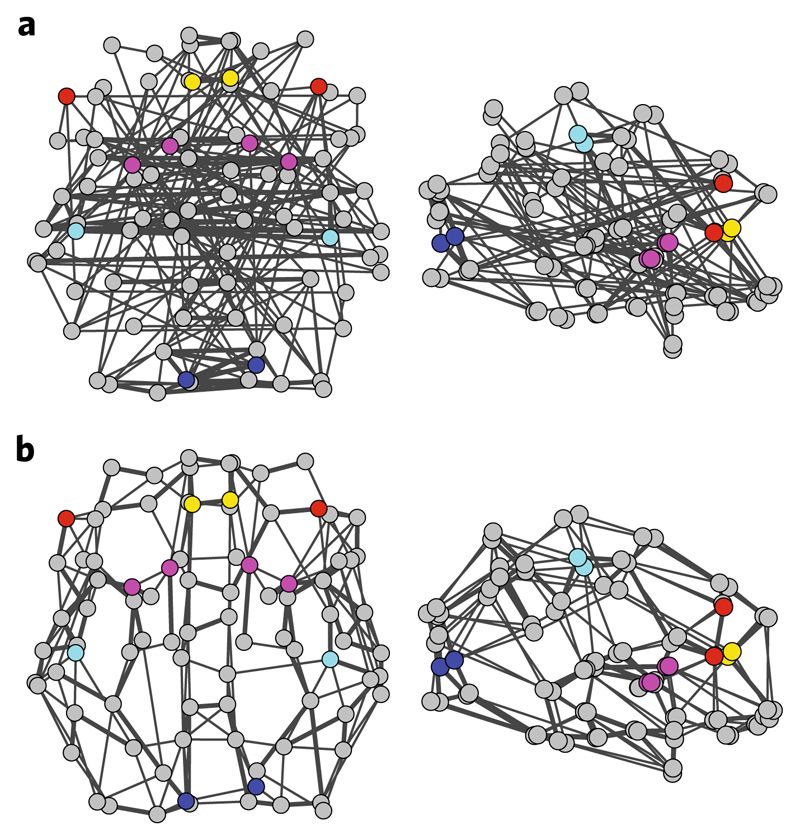
To combine data from rs-fMRI and DTI, we employed graph theory that allows us to extract comparable metrics across participants and brain imaging modalities using the same topological brain structure (for example, AAL parcellation). In particular, we constructed participant-specific whole-brain binary graphs for each brain imaging modality (rs-fMRI and DTI). We then selected 12 nodes from these graphs per imaging modality corresponding to the corticostriatal circuits in the rs-fMRI analysis (Figs. 3b and 4): (1) the striatum (the bilateral caudate and bilateral putamen); (2) the RCEN network (the right MFG); (3) the LCEN network (the triangular part of the left IFG); (4) the lateral motor network (the bilateral postcentral gyrus); (5) the early visual network (the bilateral calcarine sulcus); and (6) the ACN network (the bilateral ACC) (Fig. 5a,b).

Fig. 5. rs-fMRI and DTI graphs.

a,b, Whole-brain graphs for rs-fMRI (a) and DTI data (b). Graphs were generated based on the AAL parcellation (90 areas excluding the cerebellum and vermis) and displayed at 5% density for visualization. The thickness of the edges is proportional to the average functional and structural connectivity, respectively. The selected nodes are coloured to represent regions within known corticostriatal circuits: caudate and putamen (magenta); right MFG and left IFG (red); postcentral gyrus (cyan); calcarine sulcus (blue); and ACC (yellow). Graphs are displayed in neurological convention (left is left) in axial (left) and sagittal (right) views. Three-dimensional videos illustrating the rs-fMRI and DTI graphs are included in the Supplementary Information.

For each selected node, we computed a measure of global and local integration. In networks, global integration describes the extent to which nodes integrate information from the whole graph. Different metrics have been used to quantify global integration (for example, regions with high global integration may have many connections to the rest of the brain (that is, high degree) or fast routes to all other brain regions (that is, low path length)). Here, we focus on the nodal degree (that is, the number of a node’s connections to the whole brain), as high-degree nodes (also known as hubs) have been shown to play a key role in learning (for example, see ref. 39). In contrast, local integration quantifies the regional organization of a graph (for example, modules are defined as brain nodes that are highly connected with each other but less strongly connected to the rest of the brain, therefore forming a community⁴⁰). Here, we focus on the clustering coefficient, which measures the proportion of a node’s first neighbours that are also connected to one another⁴¹. Both the degree and clustering coefficient have previously been shown to relate to learning and brain plasticity^22,23.

Next, we asked whether learning-dependent changes in the local and global integration of corticostriatal networks predict variability in decision strategy across sequence levels (that is, frequency versus context-based statistics) and individuals. To identify the linear combinations of regional metrics of functional and structural brain connectivity that best predict individual strategy, we entered into a PLS regression model the difference in rs-fMRI and DTI graph metrics (degree and clustering coefficient) before versus after training (that is, post- minus pre-training values for the degree and clustering coefficient). PLS regression⁴² is a statistical method that is used to relate a set of predictors to a set of response variables. It identifies a set of independent components from the predictors (that is, linear combinations of the rs-fMRI and DTI graph metrics) that show the strongest association (that is, the maximum covariance) with the response variables of interest (that is, the strategy index for frequency and context-based statistics)⁴². This statistical method has previously been used in neuroimaging studies^43,44 with multi-collinear predictors or high data dimensionality (that is, the number of predictors exceeds the number of samples). We followed this methodology to combine nodal graph metrics derived from rs-fMRI and DTI data and identify predictors of strategy, as the number of predictors exceeds our sample size (that is, 48 predictors and 21 participants).

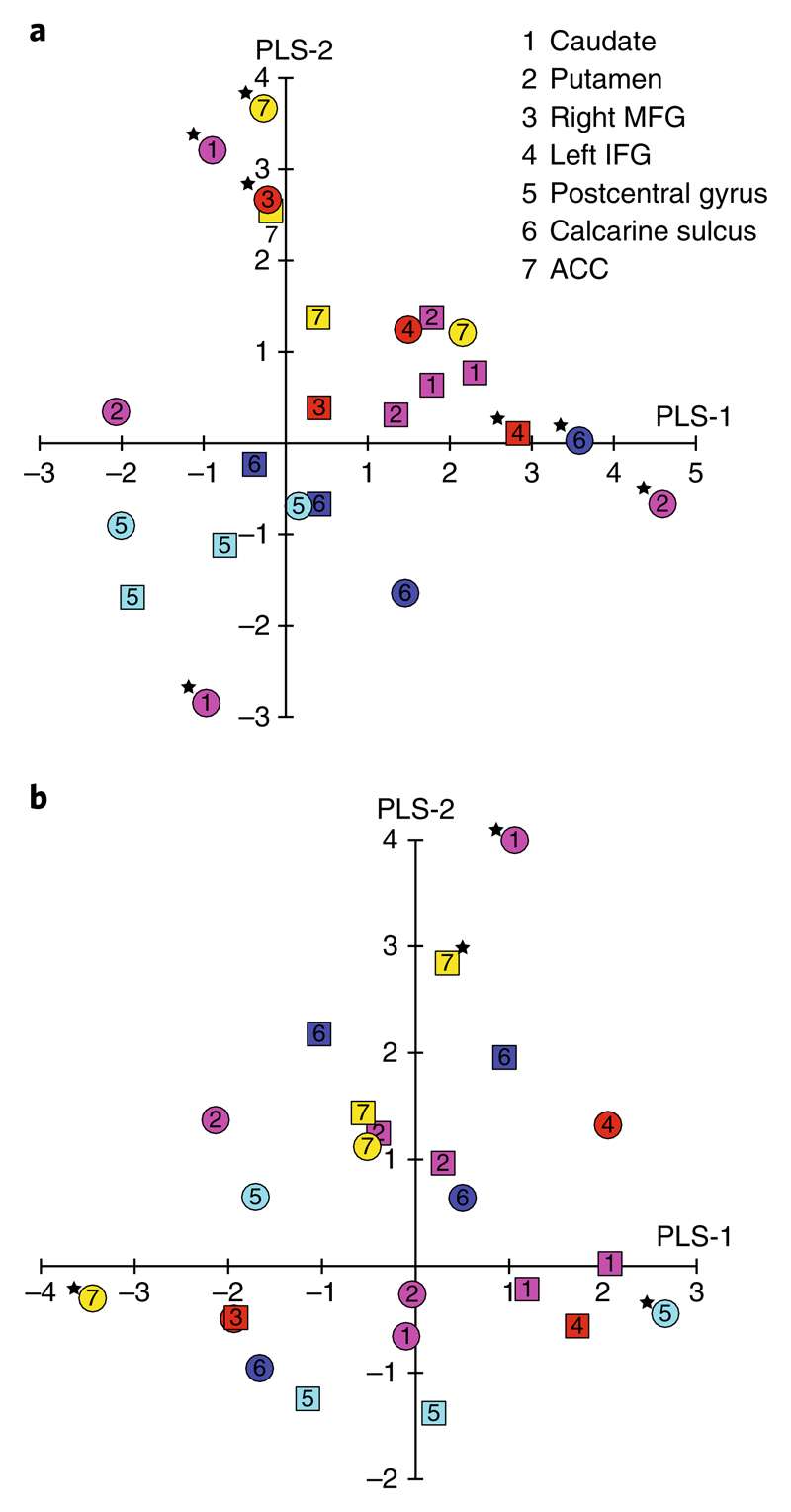
We found that the first three PLS components (PLS-1, PLS-2 and PLS-3) significantly predicted the strategy index for frequency and context-based statistics compared with a null model (P = 0.024 for 10,000 permutations). These three components together explained 85% of the variance in strategy index (Supplementary Fig. 5). For further analysis, we focused on the first two components (Supplementary Table 4), as they were robustly estimated across a range of density levels (10–30% density; Supplementary Fig. 6) and two additional atlases (the Shen and Brainnetome atlases) (see Supplementary Information). Fig. 6a,b summarizes the weights (combinations of nodes and metrics) for PLS-1 and PLS-2 at 20% density (|z| > 2.576 indicates significant predictors (P = 0.01)⁴²).

Fig. 6. PLS weights for degree and clustering coefficient.

a,b, Scatter plot of PLS-1 and PLS-2 weights for change (that is, post- minus pre-training) in degree (a) and clustering coefficient (b). PLS predictor weights for each selected node are indicated by symbols separately for DTI (circles) and rs-fMRI data (squares). The colour of the symbols corresponds to the nodes (see Fig. 5) in corticostriatal circuits: caudate and putamen (magenta); right MFG and left IFG (red); postcentral gyrus (cyan); calcarine sulcus (blue); and ACC (yellow). PLS predictor weights with |z| > 2.576 (P = 0.01) are marked by an asterisk to denote significant predictors for the respective PLS component. Supplementary Table 4a shows the numerical values of the PLS weights for each predictor.

Our analyses showed that these PLS components predict: (1) differences in decision strategy across sequence levels (that is, frequency versus context-based statistics); and (2) differences in decision strategy across individuals independent of sequence statistics. Fig, 7a shows that PLS-1 dissociates strategy across sequence levels: a negative weight is assigned for frequency statistics versus a positive weight for context-based statistics (that is, the two strategies are separated by the y = 0 axis). In contrast, PLS-2 predicts individual variability in strategy independent of the sequence statistics (that is, positive weights are assigned for both frequency and context-based statistics) (Fig. 7a).

Fig. 7. PLS components predicting decision strategy.

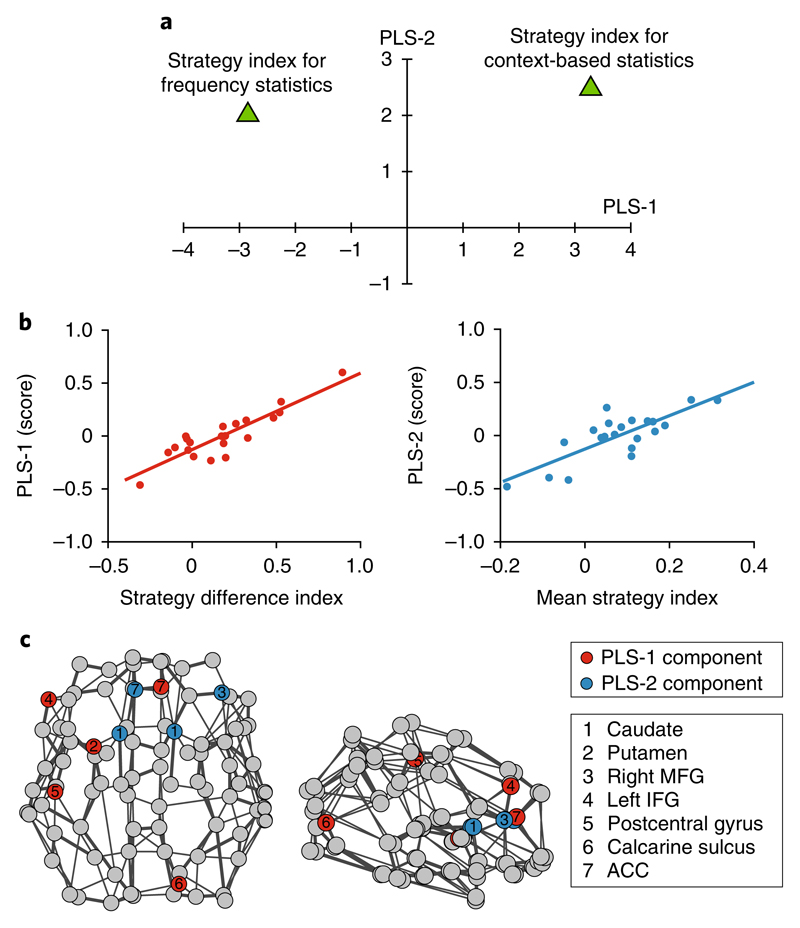
a, Scatter plot of PLS-1 and PLS-2 weights (values akin to the z-score) for the response variables (that is, the strategy index for frequency versus context-based statistics). Supplementary Table 4b shows the numerical values of the PLS weights for each response variable. PLS-1 separates decision strategies for frequency versus context-based statistics (that is, negative versus positive weight), capturing changes in decision strategy across sequence levels. PLS-2 weights equally the strategy for frequency and context-based statistics, capturing variability in decision strategy across participants independent of the sequence levels. b, Pearson correlations (two-sided; n = 21) of PLS-1 score with difference in strategy index for frequency and context-based statistics (r(19) = 0.89; P < 0.001; CI = 0.68 to 0.96) (left) and PLS-2 score with mean strategy index (r(19) = 0.79; P < 0.001; CI = 0.49 to 0.92) (right). c, Significant predictors (|z| > 2.576; P = 0.01) for the first two PLS components are shown on axial (left) and sagittal (right) views of the DTI graph for illustration purposes only (neurological convention: left is left). Red nodes indicate the significant predictors for PLS-1 and blue nodes the significant predictors for PLS-2, irrespective of imaging modality (rs-fMRI or DTI) or graph metric (degree change or clustering coefficient change).

To further quantify these findings, we computed two complementary indices. First, we calculated a strategy difference index by subtracting the strategy index for frequency statistics from the strategy index for context-based statistics (that is, higher values indicate strategy closer to maximization for context-based than frequency statistics). Second, we calculated a mean strategy index by averaging the strategy index for frequency and context-based statistics (that is, higher values indicate strategy closer to maximization across sequence levels). We found that PLS-1 correlates positively with the strategy difference index (r(19) = 0.89; P < 0.001; CI = 0.68 to 0.96) but not with the mean strategy index (r(19) = 0.18; P = 0.44; CI = −0.27 to 0.51), suggesting that this component captures learning-dependent changes in brain connectivity that predict changes in strategy in response to changes in the sequence statistics (Fig. 7b). In contrast, PLS-2 correlates positively with the mean strategy index (r(19) = 0.79; P < 0.001; CI = 0.49 to 0.92) but not with the strategy difference index (r(19) = 0.13; P = 0.58; CI = −0.25 to 0.48), suggesting that this component captures learning-dependent changes in brain connectivity that predict variability in decision strategy across individuals, independent of the sequence structure (Fig. 7b). Supplementary Fig. 7 provides a complementary illustration of the relationship between each PLS component (PLS-1 and PLS-2) and decision strategy for frequency versus context-based statistics.

Fig. 7c summarizes the brain nodes that correspond to significant predictors (|z| > 2.576; P = 0.01 (ref. ⁴²)) for PLS-1 and PLS-2 across imaging modalities (rs-fMRI and DTI) and graph metrics (degree change and clustering coefficient change). For PLS-1, the brain metrics that significantly predict change in decision strategy in response to changes in the sequence statistics include: (1) degree change in the left putamen (DTI), right calcarine (DTI) and left IFG (rs-fMRI); and (2) clustering change in the left postcentral gyrus (DTI) and right ACC (DTI) (Fig. 7c and Supplementary Table 4a). That is, global integration in the visual and left executive circuits, and local integration within the motor and motivational circuits, predict changes in decision strategy in response to changes in sequence structure (learning frequency versus context-based statistics), as indicated by the positive correlation of PLS-1 with the strategy difference index (Fig. 7b). In contrast, for PLS-2, the brain metrics that significantly predict individual variability in decision strategy independent of the temporal statistics include: (1) degree change in the left ACC (DTI), bilateral caudate (DTI) and right MFG (DTI); and (2) clustering change in the left caudate (DTI) and left ACC (rs-fMRI) (Fig. 7c and Supplementary Table 4a). Therefore, global integration in the motivational and right executive circuits, and local integration within the motivational circuit, support learning by maximizing, as indicated by the positive correlation of PLS-2 with the mean strategy index (Fig. 7b).

These results showing that graph metrics in the visual and motor corticostriatal circuits predict decision strategy are consistent with our previous correlational analyses (Fig. 4), suggesting that learning-dependent plasticity in these circuits may facilitate switching from matching towards maximization for learning more complex context-based statistics. Furthermore, the multivariate treatment of the data afforded by the PLS analysis supports the role of regions in motivational and executive corticostriatal circuits in decision strategy, corroborating our correlational analyses that showed marginal effects for these regions (Supplementary Fig. 4). These findings are consistent with previous work implicating the motivational circuit in goal-directed actions^34,45 and individual strategy choice³⁵, and the executive circuit in updating task rules^46,47.

Finally, our findings generalized to other graph metrics that relate to global and local integration (see Supplementary Information). In particular, we tested: (1) the average shortest path length and betweenness centrality as measures of global integration; and (2) the local efficiency as a measure of local integration. The first two components of models including these measures were highly correlated with the components of the main model we tested that included degree and clustering coefficient (Supplementary Table 5).

Comparing training versus no-training control groups

We conducted a no-training control experiment to investigate whether the brain connectivity changes we observed were training specific rather than due to repeated exposure to the task. Participants in this group were tested with structured sequences in two test sessions (26.1 ± 5.2 d apart) but did not receive training between sessions.

Comparing behavioural performance in the two test sessions for the no-training control group, we found no significant main effect of session (F(1,20) = 0.1; P = 0.740; η_p² = 0.006), nor a significant interaction between session and level (F(1.33,26.56) = 0.2; P = 0.695; η_p² = 0.012; Greenhouse–Geisser corrected). Furthermore, comparing performance between the two groups (training versus no-training control) showed a significant main effect of group (F(1,40) = 39.0; P < 0.001; η_p² = 0.493) and a significant interaction between group and session (F(1,40) = 73.0; P < 0.001; η_p² = 0.646). Taken together, these results suggest that behavioural improvement was specific to the trained group rather than the result of repeated exposure during the two test sessions.

Furthermore, we tested whether the learning-dependent changes we observed in the intrinsic and extrinsic connectivity analyses were specific to training. We conducted these analyses for the no-training control group and for the areas that showed significant correlations of brain connectivity changes with strategy for the training group (Fig. 4). We computed a strategy index for the control group from the post-training session, as there were no training data for this group. None of the correlations observed for the training group were significant for the no-training control group for either the intrinsic or extrinsic connectivity analysis. To compare these correlations of intrinsic and extrinsic connectivity with strategy index directly between groups, we performed a linear regression analysis with an interaction term (group × strategy). We observed significant differences between groups in key networks: (1) intrinsic connectivity change in the lateral motor network (group × strategy interaction: F(2,35) = 8.0; P = 0.001; η_p² = 0.316) and in the secondary visual network (group × strategy interaction: F(2,34) = 5.6; P = 0.008; η_p² = 0.249); and (2) extrinsic connectivity change between the right posterior putamen and the lateral motor network (group × strategy interaction: F(2,34) = 3.8; P = 0.031; η_p² = 0.184).

Finally, we conducted a PLS regression analysis to test whether changes in degree and clustering predict individual strategy for the no-training control group. This analysis did not show any significant model compared with the null model (10,000 permutations) for any number of PLS components. Furthermore, we found no significant correlations when correlating each of the first two PLS components from the training group with the corresponding PLS components from the no-training control group (PLS-1: r(19) = −0.22; P = 0.34; CI = −0.48 to 0.11; PLS-2: r(19) = −0.10; P = 0.66; CI = −0.50 to 0.19). Taken together, these results suggest that predicting individual strategy from changes in graph metrics of brain connectivity (degree and clustering coefficient) is specific to the training group.

Discussion

Here, we sought to identify the human brain plasticity mechanisms that mediate individual ability to learn probabilistic temporal structures and make predictions in variable environments. Linking multimodal brain imaging measures (rs-fMRI and DTI) to individual behaviour, we demonstrate that these task-free measures of plasticity in brain connectivity predict individual decision strategy when learning temporal statistics. Our findings advance our understanding of the brain plasticity mechanisms that mediate our ability to learn temporal statistics in variable environments.

First, modelling the participants’ predictions in our statistical learning task provides a window into the mental processes that support learning (that is, how participants extract temporal statistics and make choices in variable environments). Learning studies typically test changes in overall task performance (that is, accuracy and learning rate) due to training. In contrast, characterizing individual decision strategy provides insight into the learning process (that is, what information participants learn and how they make choices), extending beyond measures of overall behavioural improvement due to task training. We demonstrate that individuals adapt their decision strategy in response to changes in the environment’s statistics (that is, changes in the sequence structure). In particular, participants deviate from matching towards maximization when learning more complex structures (that is, context-based statistics). Our results could not be simply explained by task difficulty, as participants reached similar performance after training when learning frequency or context-based statistics. In contrast, our results reveal that individuals alter their choices to meet the learning goal in different contexts (that is, learning frequency versus context-based statistics). Although our experimental design does not allow us to dissociate sequence structure from decision strategy, considering variability in decision strategy across participants allows us to test the case where sequence structure remains the same but decision strategy differs across participants. The complementary case of the same decision strategy for different sequence structures could be tested by providing the participants with trial-by-trial feedback that has been shown to encourage maximization irrespective of sequence level⁹.

Second, previous work has investigated these decision strategies in the context of reward learning (for example, refs. ^9,11,12). Here, we test the role of decision strategy in statistical learning (that is, without explicit feedback or reward). Our results demonstrate that learning predictive statistics proceeds without explicit trial-by-trial feedback, and reveal adaptive decision strategies that cannot be simply explained by changes in reward processing or training on explicit cognitive strategies that aim to boost task performance, as we did not provide trial-by-trial feedback nor instruct the participants to adopt a given strategy. Consistent with previous studies, we show that when making choices in stochastic environments, individuals adopt a decision strategy (matching or maximizing) without having been explicitly instructed to follow one or the other (for example, ref. 11). Furthermore, previous work has shown that training results in changes in resting functional connectivity in a range of tasks (for example, ref. 19), such as perceptual^48,49 and motor learning^50,51. Yet, most of the previous work examining learning-dependent changes in functional connectivity has focused on reward-based rather than statistical learning (that is, training without trial-by-trial feedback). Here, we demonstrate that statistical learning by mere exposure to temporal sequences involves corticostriatal circuits that have previously been implicated in probabilistic^13–15 and reward-based learning^34,52. We provide evidence that these circuits support adaptive decision strategies and learning even when the reward structure is uncertain.

Third, combining modelling of individual behaviour with functional brain connectivity analysis (that is, DTI-informed analysis of rs-fMRI data), we investigate the brain plasticity mechanisms that relate to adaptive decision strategies. Using this approach, we extend beyond previous brain imaging studies that have typically investigated whether changes in task performance (that is, accuracy and learning rate) due to training relate to learning-dependent changes in brain function. Our results demonstrate that changes in individual decision strategies in response to changes in the environment’s statistics relate to learning-dependent plasticity in distinct corticostriatal circuits. That is, decreased connectivity in the motor circuit, which is known to be involved in associative and habitual learning^34–36, may facilitate matching for learning the exact frequency statistics rather than reinforcing habitual responses. In contrast, decreased connectivity in the visual corticostriatal circuit, which has been implicated in learning predictive associations¹⁶, may facilitate learning complex context-target contingencies by selecting the most probable outcome rather than learning the exact probability distributions.

Fourth, we provide evidence that plasticity in these corticostriatal circuits—as indicated by learning-dependent changes in functional and structural connectivity at rest—predicts individual decision strategy when learning temporal statistics. To identify multimodal imaging predictors of individual decision strategy, we extracted graph metrics from each imaging modality (rs-fMRI and DTI) and combined them in a multivariate analysis method (PLS regression). Our results demonstrate that graph metrics reflecting interactions within (as indicated by local integration metrics) and between (as indicated by global integration metrics) corticostriatal circuits predict 85% of individual variability in decision strategy. In particular, this analysis reveals distinct brain plasticity mechanisms that predict: (1) changes in the decision strategy from matching to maximization in response to changes in the environment’s statistics; and (2) variability in decision strategy across participants independent of the sequence statistics. These mechanisms involve both functional and structural connectivity changes in motor and visual corticostriatal circuits, in line with our rs-fMRI connectivity findings, as well as executive and motivational circuits, consistent with the role of these circuits in flexible rule learning (for example, ref. 52).

In summary, by interrogating individual decision strategy, we provide insights into individual variability in statistical learning. Our results provide evidence for distinct brain plasticity mechanisms that predict adaptive decision strategies to flexibly solve the same learning problem (that is, learn temporal statistics). Importantly, brain plasticity in functional and structural connectivity accounts for variability in individual strategy when learning temporal statistics. This evidence for a strong link between plasticity in brain connectivity and behavioural choice demonstrates the brain’s capacity to adapt in variable environments and solve problems flexibly that could be harnessed to optimize adaptive human behaviour.

Methods

Observers and study design

A total of 44 healthy volunteers (15 females and 29 males aged 23.54 ± 3 years) took part in the experiment: half in the training group and half in the no-training control group. The sample size was determined based on previous rs-fMRI studies of learning-dependent plasticity that employed similar data analysis methods^49,50,53. Data collection and analysis were not performed blind to the experimental groups. Participants were randomly allocated into the two experimental groups and recruited by advertising to university students. The only exclusion criterion during recruitment was MRI safety. Data from one participant per group were excluded from further analyses due to excessive head movement, resulting in 21 participants in each group. All participants were naïve to the study, had normal or corrected-to-normal vision and signed an informed consent form. Experiments were approved by the University of Birmingham Ethics Committee.

Participants in the training group took part in multiple behavioural training and test sessions that were conducted on different days. In addition, they participated in two MRI sessions: one before the first training session and one after the last training session. During the training sessions, participants were presented with structured sequences of unfamiliar symbols that were determined by three different Markov order models. To test whether the training was specific to the trained sequences, participants were presented with both structured and random sequences during the test sessions (see Supplementary Information).

MRI data analysis

Intrinsic connectivity analysis

Following GICA (see Supplementary Information), we assessed the temporal coherence of cortical components by calculating intrinsic functional connectivity⁵⁴. Intrinsic connectivity quantifies how correlated the activity across voxels within a network is. Therefore, we correlated the filtered time course of each voxel with every other voxel in the participant-specific component. We then applied Fisher z-transform to the correlation matrix and averaged the z-values across voxels, resulting in one component connectivity value for each participant and run. Lastly, we averaged the intrinsic connectivity values across runs to derive a single value for each participant and session.

We then tested whether changes in intrinsic connectivity with training (post- minus pre-training) relate to individual decision strategy. In particular, we performed a semipartial correlation of intrinsic connectivity change with a strategy index for frequency and context-based statistics. We computed skipped Pearson correlations using the Robust Correlation Toolbox⁵⁵. This method accounts for potential outliers and determines statistical significance using bootstrapped CIs for 1,000 permutations.

To correct for multiple comparisons, we used FCR⁵⁶. FCR is equivalent to the false discovery rate correction for multiple comparisons when significance is determined by CIs rather than P values. In particular, for n tests, we sorted the P values for all statistical tests in ascending order (that is, P(1) ≤ … ≤ P(n)). We then computed the parameter R for significance level at a = 0.05: R = max{i: P(i) ≤ i × a/n}. Finally, we assessed significance after multiple comparison correction based on the adjusted CI at 1 − R × a/n (%)⁵⁶. In particular, we found R = 1 for the n = 7 tests; therefore, FCR-corrected significance for intrinsic connectivity correlations was determined at the 99.3% CI.

Extrinsic connectivity analysis

To investigate changes in corticostriatal functional connectivity due to training, we correlated the resting-state time course of striatal segments (as determined by the DTI-based segmentation) with the time course of cortical components (as determined by the ICA of the rs-fMRI signals). We then standardized the correlation coefficients (Fisher z-transform) and averaged the z-values across runs to derive a single extrinsic connectivity value for each participant and session.

We followed the same semipartial correlation method as before (see ‘Intrinsic connectivity analysis’) to test for learning-dependent changes in corticostriatal functional connectivity that relate to individual decision strategy. We used the Robust Correlation Toolbox⁵⁵ to test for correlations between extrinsic connectivity change (post- minus pre-training) and strategy index for frequency and context-based statistics. We tested whether these correlations were significant after FCR correction. FCR-corrected significance for extrinsic connectivity correlations was determined at the 99.3% CI (R = 2 for n = 14 tests).

Partial least-squares regression analysis

To test for significant predictors of decision strategy, we used PLS regression. PLS regression applies a decomposition on a set of predictors to create orthogonal latent variables that show the maximum covariance with the response variables^42,57. In particular, we selected 12 graph nodes (that is, AAL areas) from: (1) the striatum (the bilateral caudate and bilateral putamen); (2) the RCEN network (the right MFG); (3) the LCEN network (the triangular part of left IFG); (4) the lateral motor network (the bilateral postcentral gyrus); (5) the early visual network (the bilateral calcarine sulcus); and (6) the ACN network (the bilateral ACC). For each selected node, we computed degree as a measure of global integration and clustering coefficient as a measure of local integration, respectively⁵⁸. We then entered the change in degree and clustering (post- minus pre-training) of the selected nodes as predictors in the PLS model and strategy index for learning frequency and context-based statistics as response variables. Predictors and response variables were standardized (z-scored) before being entered in the PLS model.

To test the significance of the model, we permutated the response variables 10,000 times and performed a PLS regression for each permutation to generate a null distribution from our data⁴². We then tested whether our sample explains more variance in the response variables than the 95th percentile of the permutated samples. We computed the significance as a function of the number of latent variables (that is, PLS components) to select significant components for further analysis.

Next, we assessed the stability of the predictor loadings (that is, weights) to determine the significant predictors of the response variables. We generated 1,000 bootstrap samples from our data by sampling with replacement. We then performed a PLS regression for each bootstrap sample to generate a distribution per weight. To generate these distributions, we first corrected the estimated components for axis rotation and reflection across bootstrap samples using Procrustes rotation⁵⁹. We normalized the weights of the observed sample (that is, original data) to the standard deviation of the bootstrapped weights, resulting in z-score-like weights. We accepted as significant the predictors showing |z| > 2.576 (P = 0.01)⁴² for each component independently.

Statistical analysis

The sample size for all statistical tests was n = 21 (that is, the number of participants per group) unless stated otherwise. All statistical tests were two tailed and tested for normality. Correlational analyses were also tested for heteroscedasticity within the Robust Correlation Toolbox⁵⁵ and validated by bootstrapping (1,000 permutations), as non-parametric testing is more appropriate than standard Pearson correlation (parametric test) under heteroscedasticity conditions⁵⁵. All confidence intervals are reported at the 95% level.

Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.