Summary
All living systems function out of equilibrium and exchange energy in the form of heat with their environment. Thus, heat flow can inform on the energetic costs of cellular processes, which are largely unknown. Here, we have repurposed an isothermal calorimeter to measure heat flow between developing zebrafish embryos and the surrounding medium. Heat flow increased over time with cell number. Unexpectedly, a prominent oscillatory component of the heat flow, with periods matching the synchronous early reductive cleavage divisions, persisted even when DNA synthesis and mitosis were blocked by inhibitors. Instead, the heat flow oscillations were driven by the phosphorylation and dephosphorylation reactions catalyzed by the cell cycle oscillator, the biochemical network controlling mitotic entry and exit. We propose that the high energetic cost of cell cycle signaling reflects the significant thermodynamic burden of imposing accurate and robust timing on cell proliferation during development.
Introduction
In all metazoans, fertilization leads to a period of rapid cell divisions that expand the number of pluripotent cells. These dividing cells differ from cancer cells and post-implantation embryonic cells: they lack growth phases and thus become smaller as the cells divide, producing a multi-cellular embryo with the same volume as the fertilized egg (O’Farrell, 2015). During these reductive cleavage divisions, cells progress through a coordinated and tightly regulated sequence of processes—DNA replication, mitosis and cytokinesis—that define the embryonic cell cycle. Increasing embryonic cell number demands precursors (e.g. nucleotides, fatty acids and amino acids) for DNA replication, the increase in plasma membranes, and protein synthesis. Each cell of the embryo must also expend energy to assemble and disassemble cellular machineries (e.g. chromatin, mitotic spindles), to generate forces needed to segregate the chromosomes and divide the cell, and to change the activity of signaling pathways that enforce cell cycle phasing (Ferrell et al., 2011; Morgan, 2007; Murray and Hunt, 1993; Song et al., 2017; Tyson and Novák, 2013; Yang and Ferrell, 2013). In this work, we address the question of the relative energetic costs of these processes in the context of early development.
Proliferating cells use a variety of metabolic strategies to satisfy the energetic requirements of cell growth and division. Otto Warburg discovered that many types of cancer cells derive energy from glycolysis rather than oxidative phosphorylation, even in the presence of oxygen (Warburg, 1925). It has since been recognized that aerobic glycolysis (Warburg metabolism) likely supports the production of biomass and energy conversion during the proliferation of cancer cells, stem cells, and late embryonic cells during post-implantation mammalian development (Lunt and Vander Heiden, 2011; Pavlova and Thompson, 2016; Ward and Thompson, 2012). Growing bacterial and eukaryotic cells are thought to expend most of their energy on protein synthesis, which exceeds the energetic cost of other cellular processes such as cell motility, DNA replication and transcription (Flamholz et al., 2014; Lynch and Marinov, 2015; Stouthamer, 1973; Wagner, 2005). Interestingly, a different metabolic strategy, namely oxidative phosphorylation, is taken during early embryogenesis in most species (e.g. pre-implantation mammalian development) when the embryo is autonomous (Gardner, 1998; Gardner and Leese, 1990; Houghton et al., 1996; Leese, 2012). However, we do not know how metabolic energy is partitioned among the complex array of cellular processes that take place during early development.
Here, we develop an approach to quantify the overall energetics of an embryonic system and to dissect the relative costs of the underlying cellular events. The size of a cell, its rate of proliferation, and its health are controlled by the balance between energy uptake in the form of nutrients and energy drain by synthesis and degradation of macromolecules and metabolites (Jusup et al., 2016). This energy balance can be measured as the flow of heat between the system and its surroundings, which is equal to the net change in enthalpy of the all reactions taking place in the system. Therefore, we developed a method of measuring heat flow during early zebrafish embryogenesis, which offers several experimental advantages. First, as noted earlier, the embryo volume remains approximately constant during cleavage stage, providing a unique opportunity to investigate the energetics of non-growth-related cellular processes as the enthalpic changes associated with net biosynthesis are minimized. Second, pharmacological perturbations can be made by adding agents to the water. Third, the large size of the eggs, which undergo ten reductive cleavage divisions, allow for sufficient material to measure comparatively small amounts of heat flow. And finally, the high temporal precision of the cell divisions allows for the synchronization of many cells so that heat flows can be analyzed with respect to the phases of the cell cycle.
Results
Isothermal calorimetry measures dynamic heat flow during early embryonic development
To measure heat flow during zebrafish cleavage stage development, we adapted isothermal calorimetry (ITC) to detect the rate of heat transfer from the embryos to the surrounding medium during the first 3 hours after fertilization (Figure 1A). Thirty embryos were synchronized at the 2-cell stage and placed into one chamber of the calorimeter. The differential heat signal was recorded relative to the control chamber over time. Introduction of embryos into the ITC chamber led to a positive heat flow. In contrast, E3 medium alone or paraformaldehyde (PFA)-killed embryos did not exchange any detectable heat with their surroundings (Figures 1A, 1B and S1A). This indicates that the net reactions are exothermic with heat flowing from the embryos to the bath. ITC measurements had no effect on embryonic development, because embryos were viable and developed normally when recovered from the instrument at the end of the experiment (Figure S1B). Thus, ITC can be used to measure the heat produced by developing zebrafish embryos.
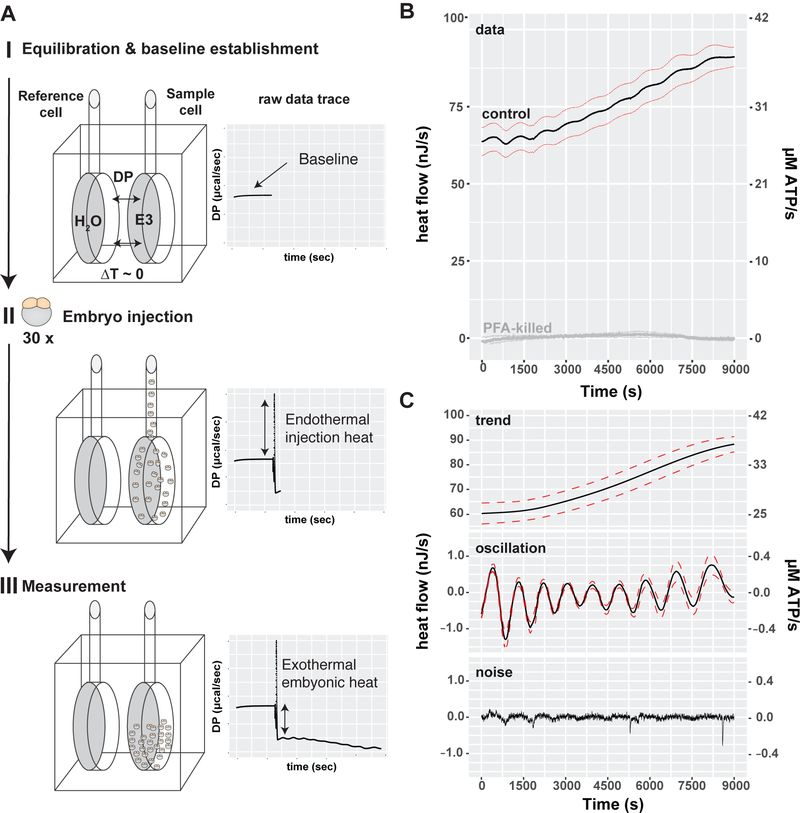
Figure 1. Isothermal micro-calorimetry of synchronized cleavage stage embryos reveals oscillatory heat flow atop an increasing trend.
(A) Schematic of an ITC experiment. (I) Calorimeter equilibration of H2O in the reference cell against E3 medium alone in the experimental cell. The temperature difference between the reference cell and experimental cell was recorded to establish a baseline reading. (II) 30 zebrafish embryos were staged at the 2-cell stage and injected into the experimental cell which caused a reproducible endothermic injection peak. (III) Measurement of the embryonic heat flow after embryo injection. The negative difference between the initial baseline and the new signal indicates heat flow from the experimental to the reference cell. (B) Mean heat flow per embryo (black & gray lines) during embryonic cleavage development plotted against time. Dashed lines=SEM. Control embryos (black line, n=10), paraformaldehyde-killed embryos (gray line, n=4). (C) Decomposition of the observed heat flow into its trend, oscillatory and noise component. Mean (black line), SEM (dashed red lines), n=10. See also Figure S1.
Although the embryo remains the same size during the first 2.5h of development, heat flow was not static (Figure 1B). A 2-cell stage embryo exchanged heat at an average rate of 60 nJ/s, which increased to 84 nJ/s by the end of cleavage stage (1024 cells). Normalizing the heat flow to the embryo’s wet weight (excluding the yolk) indicates that the embryos’ metabolic rate increased from 1W/kg to 1.4 W/kg during the measured time period. As a point of reference, the value of 1W/kg is similar to the standard metabolic rate of resting adult fish (Makarieva et al., 2008). For example, the Indian flying barb (Esomus danricus), a small fish of the Danioninae subfamily, weighs 620 mg and has the standard metabolic rate corrected to 25ºC of 1.66 W/kg (Makarieva et al., 2008). By comparison, the more distantly related medaka (Japanese rice fish, Oryzias latipes) has a weight of 270 mg and standard metabolic rate of 0.72 W/kg at 25 C. 1W/kg is also equal to the standard metabolic rate of adult humans (Makarieva et al., 2008). A second way to express metabolic rates is as the equivalent amount of ATP hydrolyzed per unit time: 60 nJ/s is equivalent to 25 µM ATP/s (∆HATP = 40 kJ/mol, (Alberty and Goldberg, 2002; Curtin and Woledge, 1978)), which roughly corresponds to the turnover of total cellular ATP in one minute. Thus, the metabolism of cleavage stage embryos is approximately equal to the standard metabolic rate of adult fish and increases slowly over time, although total embryo volume and mass remains approximately constant (Joseph et al., 2017; Mesbah Oskui et al., 2017; Olivier et al., 2010).
Heat flow oscillates with the embryonic cell cycle
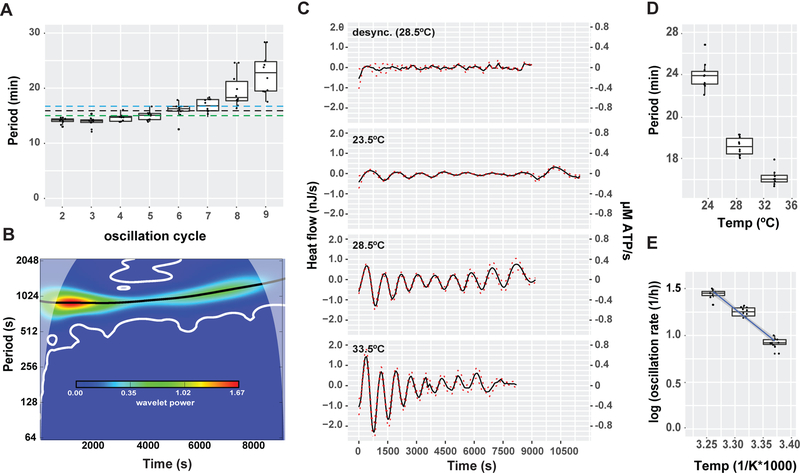
Remarkably, we detected oscillations superimposed on the increasing trend (Figure 1B). We therefore decomposed the embryonic heat flow into trend, oscillatory and noise components (Figure 1C). The oscillations suggest the presence of cyclic energetic events associated with embryonic cell proliferation, leading us to wonder if the oscillations are associated with the embryonic cell cycle. After fertilization, zebrafish embryos undergo ten synchronous divisions composed of alternating DNA synthesis (S) and mitosis (M) phases. Following the delayed first cell division (45 min), each subsequent cell cycle lasts ~15 min and lengthens slightly over time (Kane and Kimmel, 1993; Kimmel et al., 1995; Olivier et al., 2010). The midblastula transition (MBT) begins after the 10th cell cycle, and cell divisions gradually lose synchrony (Kane and Kimmel, 1993). The number and period of the heat oscillations suggested that heat might be generated by active processes during specific phases of the cell cycle. To test this, the periods of the heat oscillations were measured as the time difference between the minima (Figure S2). The period increased from 16.1 min at cycle 2 to 20.2 min at cycle 9 (Figure 2A). Similar results were obtained by wavelet analysis (Figures 2B and S2). Thus, the oscillatory period correlates well with the previously measured cell cycle period, including the lengthening of the cell cycle overtime (Kane and Kimmel, 1993).
Figure 2. Heat flow oscillates with the embryonic cell cycle.
(A) Boxplot of the oscillatory cycle period plotted against oscillation cycle number, determined by inter-trough distance, n=10, Mean oscillation period determined by wavelet transformation (black dotted line=16.4 min) and by inter-trough distance (blue dotted line=17.2 min) compared to the reported cell cycle period (dotted green line=15min) (B) Wavelet-power spectrum of the mean oscillatory heat flow plotted against time (C). Decomposed oscillatory heat flow of synchronized embryos measured at 23.5ºC, 28.5ºC, 33.5ºC (n>9) and desynchronized embryos (n=6) at 28.5ºC plotted against time. Mean (black line), SEM (dashed red lines) (D) Boxplot of the average oscillatory heat flow period plotted against temperature, n>9. (E) Arrhenius plot of (C), black line=linear fit, R2=0.984, blue shade= 95% confidence interval, activation energy=18.3 kJ/mol). See also Figures S2 and S3.
Two further lines of experimentation tested whether the oscillatory component of the heat flow was associated with the cell cycle. First, desynchronized embryos displayed a strong reduction in the mean oscillatory amplitude without a change in the trend component (Figures 2C and S3). Second, the oscillatory period decreased with increasing temperature (Figures 2D-E and S3), in accordance with the known temperature dependence of the cell cycle period (Begasse et al., 2015; Gillooly et al., 2001). Taken together, these findings indicate that embryonic heat flow oscillates with the cell cycle.
Heat flow is highest during mitotic entry and lowest during mitotic exit
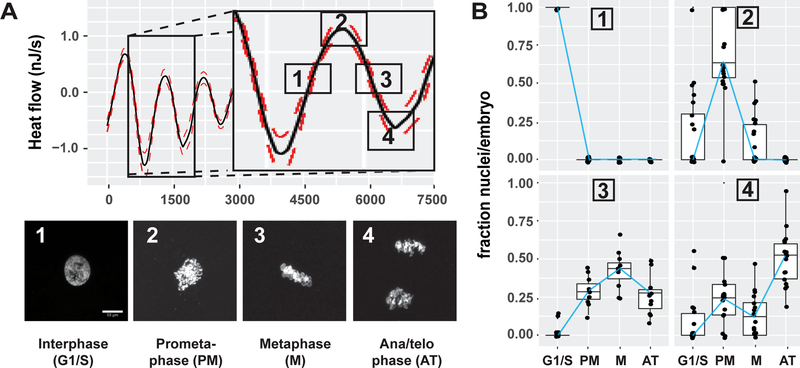
The association of the heat flow oscillations with the cell cycle implies that energetic demands are significant and vary with cell cycle phase. To associate the phase of the oscillations with specific phases of the cell cycle, embryos were chemically fixed with PFA at 4 different times during the second oscillation (Figure 3A, upper). DNA staining followed by imaging revealed that cells were in interphase during the increasing phase of the oscillation (Figure 3A [phase 1 and panel 1], and Figure 3B upper left). At the peak, most cells were in prometaphase (Figure 3A [phase 1 and panel 2], and Figure 3B upper right). During the decreasing phase, most cells were in metaphase (Figure 3A [phase 3 and panel 3], and Figure 3B lower left). At the trough, most cells were in anaphase or telophase (Figure 3A [phase 4 and panel 4,] and Figure 3B lower right). These cytological measurements show that the oscillatory heat flow is tightly linked to the phases of the cell cycle; yet the maxima and minima do not correspond to the peaks of replication or mitosis, i.e. S or M phase, per se. Instead, the oscillations peak at mitotic entry, the transition from S to M phase. These findings suggest that oscillatory heat flow may not be due to the biosynthetic or mechanochemical energy demands of replication or cell division.
Figure 3. Heat flow is highest during mitotic entry and lowest during mitotic exit.
(A) Mapping of heat flow oscillations to the cell cycle. Embryos were fixed at the indicated times spanning the second oscillation cycle and stained with Hoechst to assess cell cycle status by DNA morphology, (1) interphase (G1/S), (2) Prometaphase, (3) Metaphase and (4) Anaphase/telophase. Scale bar=5μm (B) Quantification of (A). DNA-morphology in all the nuclei was counted per embryo and plotted as a fraction of nuclei per embryo in a boxplot, blue line connects the medians, n>150 nuclei per condition.
Oscillatory heat flow depends on cell cycle signaling
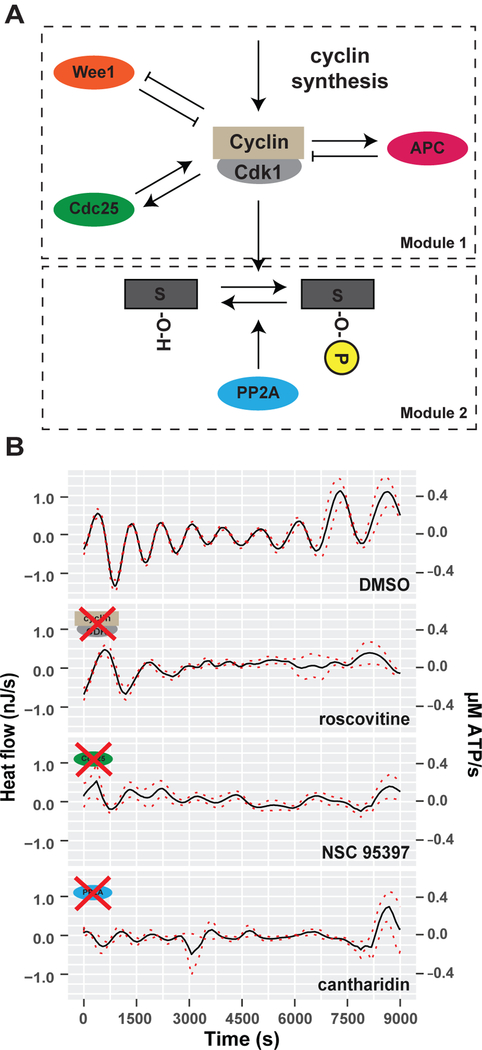
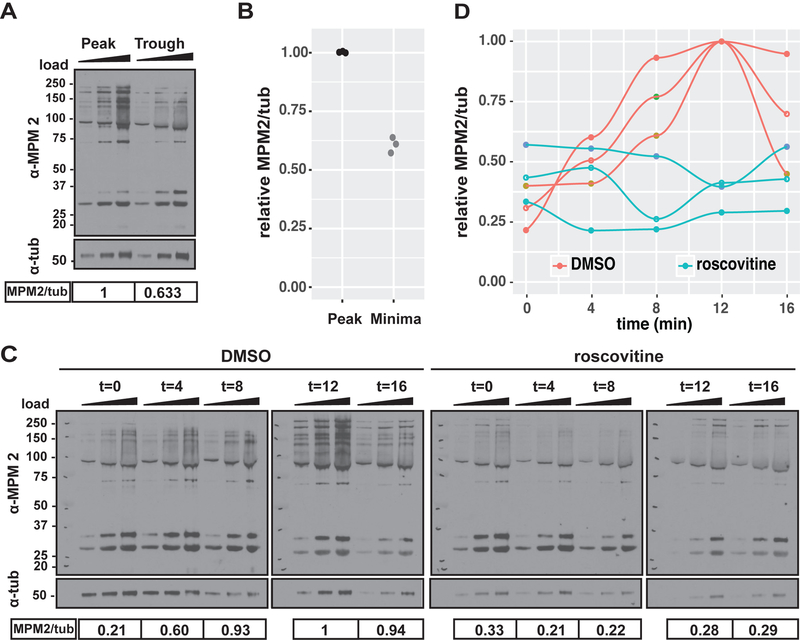
The peak of the heat flow oscillations corresponded to mitotic entry, which is the phase at which the cell cycle oscillator is most active. This biochemical network is centered on the activity of cyclin-dependent kinase 1 (Cdk1) in a complex with cyclin B (Figure 4A). Oscillations in Cdk1/Cyclin B1 activity are achieved by positive and negative feedback loops mediated by the kinase Wee1, the phosphatase Cdc25, and the activation of anaphase promoting complex (APC) (Tsai et al., 2014). This suggests the hypothesis that the cell cycle oscillator itself could underlie the oscillations in heat flow. A prediction of this hypothesis is that altering the activity of Cdk1 and its counteracting phosphatases will perturb the oscillatory heat flow. To test this, we inhibited various cell cycle protein kinases with chemical inhibitors. We titrated each individual drug to concentrations that allow embryonic viability over the duration of the experiments, although they later cause developmental arrest and death (Figure S4B). First, we inhibited Cdk1/Cyclin B1 with roscovitine. Strikingly, roscovitine-treated embryos showed almost no heat oscillations after the first few cycles (Figures 4B and S4A). This indicates that the oscillatory heat flow depends on Cdk1 activity. Next, the phosphatase Cdc25, which positively regulates Cdk1 activity, was inhibited with NSC95397 (Lazo et al., 2002; Pestell et al., 2000). The phosphatase PP2A, which dephosphorylates targets of Cdk1 phosphorylation, was inhibited with cantharidin (Li et al., 2010). Both treatments strongly decreased the oscillatory heat flow without affecting viability over the course of the experiment. (Figures 4B, S4A and S4B). These data indicate that the activity of the cell cycle oscillator is required for heat oscillations during embryonic cleavage divisions.
Figure 4. Oscillatory heat flow depends on cell cycle signaling.
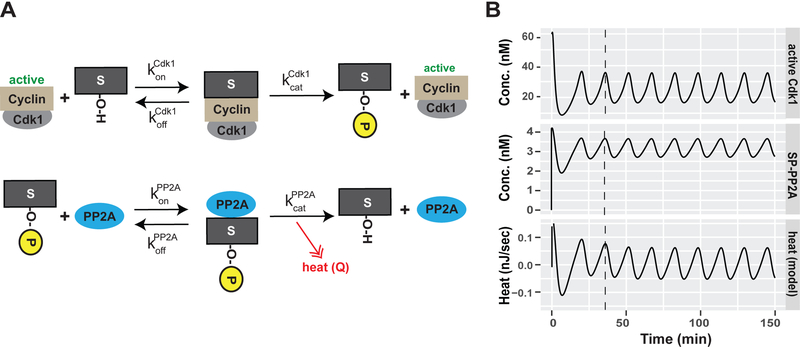
(A) Schematic depiction of the embryonic cell cycle signaling oscillator. Module 1 describes the core cell cycle oscillator based on cyclin synthesis, its Wee1 based negative and Cdc25 based positive feedback loops as well as its time-delayed Cyclin/Cdk1 degradation by APC. Module 2 describes the phosphorylation/de-phosphorylation of Cdk1 targets by active Cdk1 (output Module 1) and the phosphatase PP2A.(B) Decomposed mean oscillatory heat flow of DMSO (control), roscovitine (Cdk inhibitor), NSC95397 (Cdc25 inhibitor), cantharidin (PP2A inhibitor) treated embryos plotted against time. Mean (black line), SEM (dashed red lines), n=6. See also Figure S4.
Cell cycle-dependent phosphorylation and dephosphorylation accounts for oscillatory heat flow
We were intrigued by the possibility that the cell cycle oscillator itself could dissipate energy in the form of heat. Recent theoretical studies have demonstrated that the sensitivity and accuracy of biochemical signaling oscillations have a thermodynamic cost and depend on energy dissipation (Cao et al., 2015). The cell cycle oscillator imposes a temporal ordering on hundreds of different phosphorylation-dephosphorylation reactions, and controls many biochemical pathways such as DNA synthesis and mitosis (Godfrey et al., 2017; Swaffer et al., 2016). In these reactions, a high-energy phosphate is transferred to a target amino acid by the kinase Cdk1 and then removed by the phosphatase PP2A. Thus, these phosphorylation/dephosphorylation reactions could be responsible for the heat oscillations. To test this, we employed the anti-MPM2 monoclonal antibody, which recognizes proteins that are phosphorylated on Cdk1/2 consensus motifs (Davis et al., 1983; Westendorf et al., 1994; Yaffe et al., 1997), to investigate the phase relationship between total Cdk1-dependent protein phosphorylation and the heat oscillations (Figure 5A). We measured a 40% difference in total Cdk1-dependent phosphorylation between the oscillatory heat flow peaks and troughs (Figure 5B). Thus, the net phosphorylation levels of Cdk1 targets change during the heat flow oscillations, as expected. Given this, Cdk1 inhibition by roscovitine, which strongly inhibited the oscillatory heat flow (Figure 4B), should elicit corresponding changes in total Cdk1-dependent protein phosphorylation (Figure 5C). Indeed, roscovitine treated embryos lacked detectable oscillations in protein phosphorylation compared to control embryos (Figure 5D). Taken together, these data indicate that the oscillatory heat flow could depend on protein phosphorylation/dephosphorylation reactions mediated by the cell cycle oscillator.
Figure 5. Cell cycle-dependent protein phosphorylation and dephosphorylation correspond to oscillations in heat flow.
(A) Western blot of total embryo lysate for MPM2 and ß-tubulin. Embryo samples were collected at the peak and trough of the heat flow oscillation. (B) quantification of (A), each data point represents one biological replicate relative to the highest MPM2/tub signal (peak samples), n=3. (C) Western blot of total embryo lysate for MPM2 and ß-tubulin. Control and roscovitine-treated embryo samples collected over the course of one cell cycle in 4 min time intervals. In A and C, triangle indicates increasing protein amount loaded per sample and replicate for quantification by densitometry. Numbers under the blot show the normalized MPM2/tub signal which are represented as a fraction of to each other. Scale is molecular weight in kD. (D) quantification of (C), each data point and corresponding line represents one cell cycle time course for total cdk1-dependent protein phosphorylation in control and roscovitine treated embryos. MPM2/tub signal is displayed relative to the highest MPM2/tub signal (control 12 min), n=3.
To investigate the potential of reactions taking place during the cell cycle to generate heat, we used a previously published model developed for the Xenopus embryonic cell cycle to calculate the expected phase of the heat flow by these reactions (Tsai et al., 2014). The model incorporated the synthesis and degradation of mitotic cyclins, the regulation of the Cdk1/cyclinB1 complex by Wee1 and Cdc25, and the two-step activation of APC (Figure 4A, module 1). The oscillation period in the model was adjusted to the zebrafish cell cycle length (Figure S5A). The output of this module, namely the change in Cdk1 activity, was the input for a second module describing the phosphorylation of substrates by Cdk1 and their subsequent dephosphorylation by PP2A (Figures 4A, module 2, and Figure 6A). To determine the phase of phosphorylation and dephosphorylation, rate constants and protein concentrations were obtained from the literature or the BRENDA enzyme database (Placzek et al., 2017). Our model generated oscillations in the levels of phosphorylation and dephosphorylation of Cdk1 substrates (Figure S5B), as expected.
Figure 6. Cell cycle-dependent protein phosphorylation and dephosphorylation can account for the oscillations in heat flow.
(A) Schematic depiction of the second module of our embryonic cell cycle signaling oscillator describing the phosphorylation/de-phosphorylation of Cdk1 targets (S or S-P when phosphorylated) by Cdk1 and PPP2a, respectively =Cdk1 on rate for substrate binding, = off rate for Cdk1 target binding, = catalytic rate of Cdk1, = PP2A on rate for substrate binding, = off rate for PP2A target binding, = catalytic rate of PP2A. (B) Modeling of active Cdk1 (Module 1), phosphorylated-substrate phosphatase complex (SP-PP2A) and theoretical heat flow by PP2A-dependent dephosphorylation events during the embryonic cell cycle. See also Figure S5.
To calculate the phase of the heat flow oscillations from the above model, information about the energetics of phosphorylation-dephosphorylation reactions is needed. Previous studies have shown that dephosphorylation of phospho-serine and phospho-threonine releases 35–42 kJ/mol Gibbs free energy, which is close to the 40–60 kJ/mol released by ATP hydrolysis (Fukami and Lipmann, 1983; Stock et al., 1990). Thus, phosphopeptides in proteins harbor high energy bonds, which are expected to yield the bulk of the dissipated heat during dephosphorylation. Therefore, we assumed that the heat generated by cell cycle dephosphorylation events is proportional to concentration of the phosphorylated substrate-PP2A complex and calculated the expected heat flow (Figure 6B). Remarkably, cell cycle reactions predicted heat flow oscillations with phases similar to those we observed (Figure 6B). The model predicted that the heat oscillations should attain their maxima close to the Cdk1-Cyclin B1 activity peaks (prophase), because phosphatase activity is expected to closely follow phosphorylation (Mochida et al., 2016; Swaffer et al., 2016). This agrees with our measurements showing that heat flow oscillations peak at prometaphase when kinase activity peaks (Figures 3A and3B).
Oscillatory heat flow does not correspond to DNA replication or mitosis
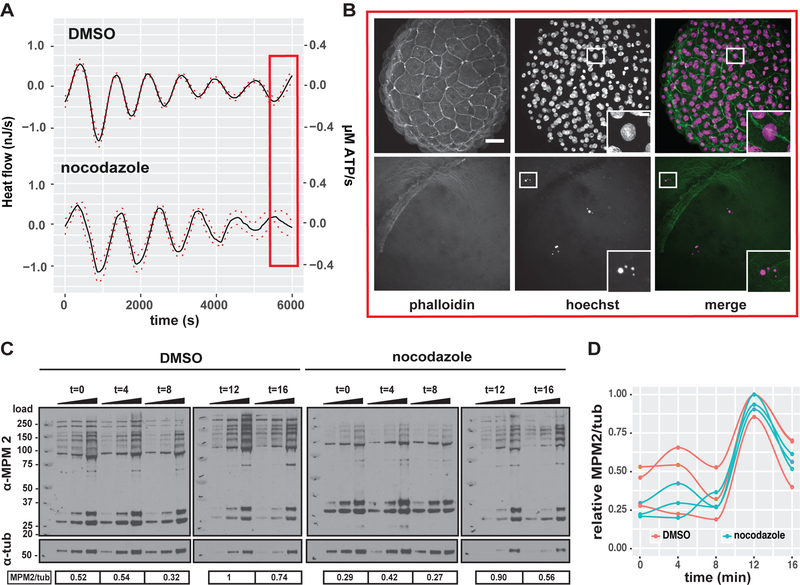
Our calculations suggest that the cell cycle oscillator itself could generate heat during cleavage stage development. Yet, the model does not address possible contributions from the major cytological processes to the heat oscillations. To investigate the contributions of DNA replication and/or mitosis directly, both phases were pharmacologically perturbed using the microtubule polymerization inhibitor, nocodazole. Treated embryos arrested between the 2- and 4-cell stages and failed to replicate their DNA (Figure 7B). Strikingly, embryonic heat flow continued to oscillate with similar periods and amplitudes during nocodazole treatment, although the increasing component was inhibited (Figures 7A, S6A and S6B). Furthermore, Western blotting and probing with MPM-2 showed that the cell cycle dependent protein phosphorylation events continue to oscillate in nocodazole treated embryos when compared to DMSO treated embryos (Figures 7C and7D). Thus, the heat flow oscillations are independent of DNA replication, mitosis and cell division, indicating that cell cycle signaling and/or other cell cycle dependent metabolic reactions account for the observed oscillatory heat flow in embryos.
Figure 7. Oscillatory heat flow in embryos does not correspond to DNA replication or mitosis.
(A) Decomposed mean oscillatory heat flow component of DMSO and nocodazole treated embryos plotted against time, Mean (black line), SEM (dashed red lines) n=6. The arrow indicates the time of drug treatment. (B) Micrographs of DMSO (top row) and nocodazole treated embryos stained for f-actin (phalloidin) and DNA (Hoechst). Embryos were fixed at times corresponding to the red box in (A). Scale bar= 50μm. Islet shows magnified nuclear DNA staining, Scale bar = 5μm. (C) Western blot of total embryo lysate for MPM2 and ß-tubulin of control and nocodazole treated embryo samples collected over the course of one cell cycle with 4 min time intervals. Triangle indicates increasing protein amount loaded per sample and replicate for quantification by densitometry. Numbers under the blot show the normalized MPM2/tub signal which are represented as a fraction of to each other. (D) quantification of (C), each data point and corresponding line represents one cell cycle time course for total cdk1 dependent protein phosphorylation of control and nocodazole treated embryos. MPM2/tub signal is displayed relative to the highest MPM2/tub signal (control 12 min), n=3. See also Figure S6.
Energetic cost estimates for cell cycle-dependent processes during cleavage stage development.
Our results suggest that cell cycle signaling could account for the observed oscillatory heat flow in embryos undergoing cleavage stage development. How does the measured oscillatory heat flow amplitude compare to the energetic cost of cell cycle signaling and other cell cycle dependent processes and reactions? To address this question, we estimated the ATP equivalents hydrolyzed due to DNA replication, mitosis, protein degradation and synthesis, and cdk1-cyclin-dependent phosphorylation and dephosphorylation cycles. We compare these estimated energetic costs to the measured average oscillatory amplitude of ~1 nJ/s, which is equivalent to ~400 nM ATP/s.
Regarding DNA replication, the zebrafish genome has ~1.5 × 109 base pairs, which corresponds to ~0.08 µM nucleotides in the one-cell embryo, using the animal cap volume of 60 × 106 µm3 and the conversion factor 1 nM ≈ 0.6 molecules/µm3. Replication of the genome therefore requires ~0.3 µM ATP equivalents, given 2 ATP equivalents for polymerization of each base, 0.5 per base for unwinding and 1.5 per base for priming the Okazaki fragments (Lynch and Marinov, 2015). This calculation assumes that nucleotides are available and do not need to be synthesized, which is reasonable given that even the 1000 genomes needed to be replicated during the 10th cycle will require a total of only ~0.1 mM nucleotides. Furthermore, Xenopus and Drosophila embryos have sufficient nucleotide stores for at least 1000 genomes (Song et al., 2017; Vastag et al., 2011). Given that the period of the cell cycle is about 1000 s, replicating one genome corresponds to ~0.6 nM ATP/s, if we assume that synthesis takes place during only half the cycle. For the 2nd cell division cycle, when two genomes are replicated, ~1 nM ATP equivalents per second are needed (ignoring histone synthesis – see next paragraph). This value is very small compared to the average peak-to-peak amplitude of the heat oscillations, which is equivalent to ~400 nM ATP/s (Figure 1C). During the 10th cell division cycle, however, the cost of DNA synthesis is expected to be roughly equal to the amplitude of the heat oscillations. In summary, except for the last cycles, the enthalpic cost of DNA synthesis is small compared to the size of the heat oscillations.
The above estimate of the energetic cost of genome replication assumed that sufficient histones are available in the oocyte and do not need to be synthesized during S phase. This is justified as follows. There is one nucleosome (9 histone proteins) per 180 base pairs, so the total bound histone concentration at the one cell stage is ~2 nM. At the 1024 cell stage, the concentration is ~2 µM (or ~30 ng/ml), which is much less than the total measured concentration of histone in the embryo (Joseph et al., 2017). However, if these histones had to be synthesized by elongation of extant amino acids, the cost would be 4 ATP equivalents per amino acid (Lynch and Marinov, 2015). Because there are ~6 histone amino acids per base pair, histone synthesis would increase the oscillation amplitude ~3-fold (using a similar calculation to the previous paragraph), assuming histone synthesis only occurred during S phase. While this is true for slower cell divisions such as tissue culture cells it need not be the case for the rapid cleavage divisions. In summary, histone synthesis is not likely to contribute to the oscillatory heat flow because the histone requirement during a cleavage division is small, and histone synthesis may occur throughout the cell cycle.
To estimate the energetics of mitosis, we first consider the GTPase activity associated with tubulin turnover during mitotic spindle assembly and disassembly. We assume that the free tubulin concentration in embryos is ~20 µM, as found for Xenopus oocytes (Gard and Kirschner, 1987). During the cleavage divisions, the volume of each mitotic spindle decreases, but the total volume of spindles increases as the number of cells increase; for Xenopus, where this has been studied in some detail (Wühr et al., 2008), the total spindle volume increases roughly 100-fold over the first 9 divisions. If we assume that the spindles in the latter divisions contain 20 µM of polymerized tubulin (an upper limit) and that the lifetime of tubulin in the spindle microtubules is ~20 s (Reber et al., 2013), then the GTPase rate is ~1 µM GTP/s. Because the energy dissipated by GTP hydrolysis is similar to that by ATP hydrolysis, an upper limit on the oscillatory heat flow during mitosis due to spindle tubulin turnover is about 1000 nM ATP equivalents per second, similar to the measured heat flow of ~400 nM ATP/s. For the early divisions, the heat flow will be much less. Spindle ATPases such as motor proteins will contribute to the heat oscillations, but to a lesser extent. For microtubules several micrometers long, the concentration of microtubule ends is about four orders of magnitude smaller than that of polymerized tubulin; the number of motor proteins on the lattice is about two orders of magnitude less than the number of polymerized tubulins. Therefore, ATPases with turnover rates of 1–10 per second, are expected to contribute no more than the tubulin GTPase. Thus, except for the last cycles, the enthalpic cost of mitosis is small compared to the amplitude of the heat flow oscillations.
The synthesis of cyclin and its degradation by APC/C-complex will generate heat, though synthesis occurs throughout the cell cycle and should not contribute to the oscillatory component. To estimate how much heat flow is generated by cyclin degradation, we note that ~1 ATP equivalent is required per amino acid (Lynch and Marinov, 2015). Degrading all 60 nM of the 400-aa cyclin B1 bound to Cdk1 during half the cell cycle will therefore lead to an oscillation amplitude of ~50 nM ATP equivalents per second. Thus, cyclin degradation is expected to make only a small contribution to the measured heat flow amplitude.
In this final paragraph, we calculate the ATP turnover associated with cdk1-cyclin-dependent phosphorylation and dephosphorylation. 60 nM of active Cdk1 will phosphorylate substrate at a rate of 180 nM/s, assuming a catalytic rate of 3 s−1 (see Supplementary Information). Because dephosphorylation follows shortly thereafter, the turnover of ATP will occur at a rate of ~180 nM/s. This value is close to the measured value of 400 nM/s. Similar calculations using the full mathematical model, which considers that only a fraction of the total 60 nM Cdk1 is active and oscillates during the cell cycle, leads to ATP turnover rate of ~60 nM/s at peaks of active Cdk1. If the model assumes that heat flow is only generated by the dephosphorylation of Cdk1 targets catalyzed by PP2A, the predicted ATP turnover is ~40 nM ATP/s or 0.1 nJ/s, which is 10-fold smaller than the measured amplitude. This may imply that other Cdk1-dependent reactions are responsible for the oscillatory heat flow. However, our uncertainty in the predicted amplitude is large due to uncertainties in enzyme concentrations and rates. Furthermore, if cell cycle reactions take place in the yolk, their predicted contribution to the total oscillatory heat will be even larger. Thus, it is possible that most of the oscillatory heat flow arises from the reactions catalyzed by the cell cycle oscillator. We conclude, therefore, that the activity of the cell cycle oscillator alone is sufficient to generate heat flow oscillations with a phase and, possibly, amplitude similar to those observed by ITC in living zebrafish embryos.
Discussion
Using ITC, we observed heat flow oscillations during the reductive cleavage stage of zebrafish embryogenesis that are in phase with the cell cycle. The oscillations have the same frequency and temperature-dependence as the cell cycle, and the oscillations peak at a characteristic part of the cell cycle, namely prometaphase. The heat flow oscillations are abolished when the cell cycle is inhibited pharmacologically (e.g. using roscovitine, NSC 95397 or cantharidin) and are not inhibited by nocodazole, which blocks prominent cytological process that define the cell cycle such as DNA synthesis, mitosis and cell division. Thus, the amplitude of the heat flow oscillations does not correlate with cell number, but rather with cell cycle activity.
The heat flow oscillations are small relative to total heat flow, with a peak-to-peak amplitude equal to about 2% of the mean. This shows that the net enthalpy change from all metabolic activity has only a small cell cycle associated component during early development. This contrasts with yeast and tissue culture cells, which display relatively larger enthalpic changes associated with cell cycle (Ahn et al., 2017; Ewald et al., 2016; Mitra et al., 2009; Papagiannakis et al., 2016; Slavov and Botstein, 2011; Tu et al., 2005). Thus, metabolism during embryonic cleavage divisions is unique. A likely explanation for this difference is the lack of growth phases (G1 and G2) during embryonic reductive cleavage divisions (Paranjpe and Veenstra, 2015).
We investigated several potential contributions to the heat oscillations both experimentally and theoretically. These include DNA synthesis, mitosis and cell division, synthesis and breakdown of cyclins, and the cycles of phosphorylation and dephosphorylation associated the cyclin-dependent Cdk1 kinase. Cdk1 is at the center of the biochemical signaling network controlling the temporal ordering of the cell cycle, known as the cell cycle oscillator. Below, we will discuss these potential energetic contributions individually, leading to our primary conclusion that the heat flow oscillations likely have a major contribution from enthalpic changes associated with repeated rounds of phosphorylation and dephosphorylation of targets of the cell cycle oscillator. Although other uncharacterized metabolic processes downstream of the cell cycle oscillator may also contribute, our findings show that the cells of the embryo expend significant energy in enforcing the accuracy of cell cycle periodicity.
The heat flow oscillations are not due to the DNA synthesis during S phase. First, the peaks of oscillatory heat flow occur during prometaphase, after the DNA has been replicated. Second, the oscillations remain when S-phase is blocked by nocodazole. Third, the amplitudes of the heat oscillations are approximately constant; if the oscillations were due to the replication of DNA and the synthesis of histones, then the amplitude would increase exponentially and double every cell cycle. This is not observed. And fourth, the enthalpy change associated with DNA replication is negligible compared to the size of the heat oscillations, except during the very last cleavage divisions as MBT approaches (see Results section). Thus, the heat oscillations are not attributable to S phase.
Similar arguments apply to mitosis and cell division. First, the peak of the heat flow oscillations occurs during prometaphase, before metaphase and cell division. Second, the oscillations remain when M phase and cell division are inhibited by nocodazole. Third, the amplitudes of the heat oscillations are approximately constant; if the oscillations were due to mitotic spindle assembly, chromosome segregation or cell division, then the amplitude would increase exponentially and double every cell cycle. This is not observed. And fourth, the enthalpy change associated with tubulin turnover in the mitotic spindle, which is likely to be one of the largest energetic demands during mitosis, is small compared to the size of the heat oscillations, except possibly during the very last cleavage divisions. Thus, the heat oscillations are not attributable to M phase or cell division.
Which molecular events within the cell cycle oscillator emit heat? Prior studies indicate that the energetic costs of protein synthesis exceeds the costs of other cellular processes such as cell motility, DNA replication and transcription (Flamholz et al., 2014; Lynch and Marinov, 2015; Wagner, 2005). The cell cycle oscillator depends on translation and degradation of cyclin B1. Therefore, cyclin B1 protein synthesis and degradation could contribute the oscillatory heat flow generated during the cell cycle. The synthesis rate of cyclin B1 is thought to be constant and will not contribute to the oscillatory component. However, cyclin B1 degradation by APC/C-complex oscillates due to the activity of Cdk1 on the proteasome. Thus, the energetic cost of cyclin B1 degradation could contribute to the oscillatory heat flow. If so, the expected amplitude would stay constant, and be inhibited by cell cycle signaling inhibitors but not by nocodazole. This was observed. However, we would expect cyclin B1 degradation to take place after active Cdk1 peaks with some time delay. This is inconsistent with the observed phase of the heat flow oscillations, which peak during mitotic entry. Furthermore, the estimated amplitude of ATP hydrolysis due to degradation is small (see Results section). Thus, the heat oscillations are not attributable to cyclin B1 protein degradation.
We arrive at the conclusion that the heat flow oscillations are in phase with the activity of Cdk1 and likely have a major contribution from enthalpic changes associated with repeated rounds of phosphorylation and dephosphorylation of targets of the cell cycle oscillator. Our modeling, based on recent biochemical data, shows that the combination of cell cycle kinase and phosphatase activities can account for the phase of the measured oscillatory heat flow. The heat flow oscillations peak during mitotic entry, which is consistent with phosphorylation of hundreds of proteins during entry into mitosis by Cdk1 (Domingo-Sananes et al., 2011; Mochida and Hunt, 2012). The turnover of phosphates on Cdk1 substrates is fast with a mean phosphate half-life of ~1 minute in fission yeast (Swaffer et al., 2016). This suggests that the peak of dephosphorylation activity should lag only slightly behind the peak of phosphorylation by Cdk1. A 1-minute half-time corresponds to only 7% of the 15-minute cell cycle period, leading to the expectation that peak heat flow should occur at mitotic entry; this is precisely what we observe experimentally and predict in our model. The intuitive reason that both kinase and phosphatase activity rise and fall together in near synchrony is that the higher the kinase activity, the higher the phosphorylated substrate, and therefore the higher the rate of removal of high-energy phosphates from protein substrates. Thus, Cdk1 substrates undergo rapid phosphorylation and dephosphorylation during the transition from S to M phase, and the net Cdk1/phosphatase activity determines the energetic costs that we measure as heat.
A recent study in Xenopus egg extracts showed that the stable switching on of mitotic protein phosphorylation at mitotic entry is accomplished by the simultaneous upregulation of Cdk1 kinase activity and downregulation of PP2A phosphatase activity; the kinase and phosphatase activities are linked through the Greatwall kinase-endosulfine (ENSA) pathway (Mochida et al., 2016). Depending on the relative strengths of these antagonistic activities, the phosphorylation/dephosphorylation turnover would be higher at mitotic entry, if activation of Cdk1 dominates (as assumed in our modeling), or lower, if inhibition of PP2A dominates. In yeast, it appears that turnover is higher as PP2A is active at mitotic entry (Godfrey et al., 2017; Swaffer et al., 2016). However, in vertebrate embryos there is still much uncertainty about the details of the cell cycle oscillator and our estimates of phospho-turnover will need to be tested experimentally.
The average peak-to-peak amplitude of the heat flow oscillations is equivalent to ~400 nM ATP/s (Figure 1C and results section). We reason that a majority of this turnover can be attributed to cell cycle oscillator, which is centered around Cdk1-cyclin-dependent phosphorylation and dephosphorylation reactions. We estimate the ATP turnover of these reactions to lie within a range of ~40 nM ATP/s to ~180 nM ATP/s (see Results section). How does this the amplitude of the heat flow oscillations compare with the measured biochemistry of the cell cycle oscillator? Though quantitative information about the absolute levels, number and phosphorylation dynamics of Cdk1 and PP2A targets during cleavage divisions is currently lacking, a recent quantitative proteomic study measured the total change in phosphorylation during Xenopus egg activation to be ~7 μM (Presler et al., 2017). These measurements give us an estimate of the total phosphate turnover of ~ 80 nM ATP/s if all of these sites have a half-life of one minute (see above). Our estimated range of ~40 nM ATP /s to ~180 nM ATP/s turnover is, therefore, close to the value derived from these measurements in frog eggs. Thus, the cell cycle oscillator can generate heat oscillations of similar magnitude that we measure.
Both our experiments and modeling suggest that the biochemistry of the cell cycle oscillator is energetically costlier than DNA replication, mitosis or cytokinesis. The enthalpic changes associated with repeated rounds of phosphorylation and dephosphorylation of targets of the cell cycle oscillator are likely to make a major contribution to the oscillatory heat flow during embryonic cleavage stage development. The phosphoester bonds of phosphorylated serine and threonine in Cdk1 targets contain high energy bonds gained from the transfer of the gamma phosphate from ATP. We therefore reason that dephosphorylation releases a significant fraction of the measured heat. However, given the uncertainties in our estimates, we cannot rule out other contributions by unspecified metabolic pathways in phase with Cdk1-dependent phosphorylation reactions.
Why does the embryo expend this much of its energy budget on the cell cycle oscillator? Above, we have argued that most of the oscillatory heat flow arises from the dephosphorylation step. Therefore, the peaks in the observed heat oscillations are associated with the erasure of cell cycle timing information contained in protein phosphoester bonds. This cost of erasing biological information is akin to Landauer’s limit in computer systems, which states that there is a minimum theoretical energetic cost for the loss of information (Landauer, 1961). In computer systems this minimum cost is kT∙ln2 (~ 3 × 10−21 J at room temperature) per bit of information, though the practical cost is higher by orders of magnitude (Koomey et al., 2011). We cannot compare our measurements directly to the Landauer limit, because we do not know how much information is encoded by the cell cycle oscillator. However, theoretical studies have estimated the amount of energy dissipation needed to drive biological oscillators robustly, such that the period remains relatively constant over time (Cao et al., 2015). Our heat flow measurements show that many orders of magnitude more energy is dissipated than predicted by the Landauer limit, indicating that coordinating the cell cycle spatially as well as temporally during the cleavage divisions entails a high energetic cost. This insight, which is likely generalizable to all cells due to the conservation of the underlying system, implies that the accuracy of cell cycle timing reflects the biological importance of coordinating cellular activities in proliferating cells.
STAR Methods
Contact of Reagent and Resource Sharing
Further information and requests for resources and reagents should be directed to and will be fulfilled by the co-corresponding author, J. Rodenfels (jonathan.rodenfels@gmail.com).
Experimental model and subject details
Ethics statement
Animal research using zebrafish embryos was conducted under a protocol approved by according to the specific rules specified by Institutional Animal Care and Use Committee (IACUC) in compliance with the Animal Welfare Act and other federal statutes and regulations relating to animals and experiments involving animals.
Zebrafish husbandry and staging
Adult zebrafish were maintained and bred under standard conditions. Wild-type (AB) embryos were left to develop in E3 medium (5 mM NaCl, 0.17 mM KCl, 0.33 mM CaCl, 0.33 mM MgSO4) to the desired stage at 28.5C or otherwise indicated. Staging was done based on morphology. It was not possible to record the sex of the embryos examined due to their developmental stage.
Method details
Staging for heat flow measurements by isothermal calorimetry
Multiple pairs of fish were paired for a maximum of ten minutes after which eggs were collected and allowed to develop for 30 minutes at 28.5ºC. 30 embryos with an appearing first cleavage furrow were selected within 3 minutes to stage and synchronized the population of embryos at the 2-cell stage. For ITC measurements, 30 embryos were injected into the isothermal micro-calorimeter within 5 minutes after staging. To manually desynchronize the population of embryos, two populations of 25 randomly selected eggs where collected and incubated at room-temperature or 28.5ºC for 10 minutes, respectively. The two populations embryos were combined and allowed to develop for an additional 30 minutes at 28.5ºC after which and non-developing embryos were removed. From the remaining embryos, 30 were randomly selected for ITC measurements and injected into the isothermal micro-calorimeter.
Isothermal calorimetry
ITC experiments were carried out using a Malvern MicroCal VP-ITC high sensitivity titration calorimeter (Malvern Instruments Ltd, Worcestershire, UK) and the raw data was extracted using VP-Viewer2000 software. The temperature in the instrument was set to desired temperature of 28.5ºC or otherwise indicated. The reference power (µcal s−1) was set to 11.5, the initial injection delay after calibration was set at 240s, the feedback mode/gain was set to high, and the ITC equilibration option were set to “fast equilibration & auto”. The ITC experiments were performed without the injection syringe and stirring and the ITC camber injection ports were covered with a plastic lid. Due to operational software requirements the injection syringe parameter was set as follows. Injection volume was set to 2 µl, the duration of 2 seconds with a spacing of 14400 s (240 min) and the number of injections was set to 3 to cover the desired timeframe of the experiment. The sample cell was filled with either 1.57 ml of E3 medium or E3 medium with the desired concentration of chemical inhibitors. Nanopure water was used in the reference cell. Each experiment began with the equilibration of the calorimeter and an initial baseline recording for at least 10 minutes. 30 embryos of were manually injected into the sample cell opening using a cut off micro-pipette tip. The embryos were allowed to sink down into the sample cell and the additional pipetting volume of 200 µl was removed using a Hamilton syringe. The embryo injection and pipetting led to a reproducible endothermic peak lasting 1–2 minutes after which signal was recorded covering cleavage stage development.
Embryo staining
Zebrafish embryos at the indicated times where fixed in 4% paraformaldehyde (w/v) in E3 for 40 min at RT, rinsed in H2O and frozen in pre-chilled acetone, (−20ºC, 10 min) to permeabilize the embryo. Embryo were washed 3× 5 min with PBST (PBS contain 0.2% Triton X-100) and were manually dechorionated and deyolked using forceps. Then embryos were blocked for 45 min in 10% NGS/PBST and incubated with the Alexa488-phallodin (Invitrogen) at 1/250 (v/v) and Hoechst overnight at 4ºC. Embryos were washed 3×10 min with PBST, transferred through a glycerol series (25%, 50%, 80% in PBS) and mounted in 80% glycerol.
Microscopy
Documentation of embryo morphology and development upon drug treatment was performed using a Leica M165C stereo microscope equipped with a Leica DFC7000 camera. Imaging of stained embryos was performed using a Leica SP8 laser scanning confocal microscope and a 40× 1.2 NA objective.
Mapping heat oscillations to the cell cycle
Groups of 30 stages wild-type embryos at the 2-cell stage were injected into the calorimeter and the live heat flow oscillations were observed until the desired oscillation cycle. Once the heat flow oscillations reached the increase, peak, minima and decrease of the 2nd observable oscillation cycle 0.75 ml of E3 medium was carefully removed and immediately replaced with 0.75 ml of 8% PFA in E3. Embryos were fixed within the experimental cell of the calorimeter for 25 min, recovered and stained with Hoechst to assess the nuclear morphology. Nuclear morphology in each embryo was assessed and plotted as a fraction of the total number of nuclei per embryo
Chemical inhibition
Chemical inhibition was performed at the 2-cell stage in a dish or at the time of embryo injection into the calorimeter containing drug treated E3 media. Embryos were placed in these solutions with their chorion intact. The following chemical compounds and experimental concentrations where used: Nocodazole (10 µM), roscovitine (30 µM), cantharidin (10 µM) and NSC 95397 (15 µM). All stock solutions were prepared in DMSO.
Protein extractions and western blotting
Three embryos per experimental condition were collected per sample and biological replicate and immediately frozen in liquid nitrogen after excess embryo media was removed and stored at −80ºC. Frozen embryos were homogenized and suspended using a pipet tip containing 40 µl SDS-buffer, heated to 95ºC for 6 minutes, vortexed for 2 mins, and the equivalents of 0.5–1 embryo were loaded on each lane of 4–12% Bis-Tris Gels, and proteins were separated by SDS-PAGE. Protein detection by western blotting was performed using 5%-BSA TBST and TBST as blocking and washing buffer, respectively. The following antibodies were used – Primary antibodies: anti-MPM-2 (mouse monoclonal to Mitotic proteins, Abcam #ab14581) 1:1000, anti-ß-tubulin (rabbit polyclonal, Abcam # ab6046), 1 :3000. Secondary antibodies: horseradish peroxidase-conjugated goat anti-mouse IgM 1:8000 (Sigma, #A8786), horseradish peroxidase-conjugated goat donkey anti-rabbit IgG 1:10000 (GE Healthcare, #NA934). Signal was detected using Amersham ECL Western Blotting Detection Reagent (GE Healthcare). Control and drug treated samples where developed on the same film for each biological replicate. Western blot intensities were quantified by normalizing the most intense α-MPM2 and α-tubulin signal on the respective film to 100%, respectively. The MPM2 signal was subsequently normalized by the its tubulin signal and the strongest MPM2/tub signal on the film was set to 100%. All other MPM2/tub signals are represented as a fraction thereof.
Quantification and statistical analysis
Data analysis
Data analysis was performed in R version 3.3.1 “Bug in Your Hair” in RStudio version 1.0.136 with the additional libraries “ggplot2”, “tidyr”, “WaveletComp” and “deSolve”. All R scripts and calorimetry data can be found on zenodo (https://doi.org/10.5281/zenodo.1589353). Statistical parameters including the exact value of n and precision measures (mean ± standard error of the mean (SEM)) are reported in the Figure Legends. For ITC experiments, n represents the number of biological replicates (groups of 30 staged zebrafish embryos). Data from biological replicates with identical conditions were combined and mean ITC data ± SEM are presented in the figures. Heat oscillation periods are represented with a boxplot based on data from each biological replicate. Experiments mapping the heat oscillations to the cell cycle were performed in 3 biological replicates. The data from each biological replicate were combined, and the nuclear morphology in each embryo was assessed blind. Each phase contains n>15 embryos and a total of n>150 nuclei. Nuclear morphology was plotted as a fraction of the total number of nuclei per embryo and represented as a boxplot.
Analysis of isothermal calorimeter data
We used TextWrangler version 5.5.2 to removed meta data form VP-ITC *.itc raw data and converted it into *.csv leaving the raw data structured as time, differential power (µcal s−1), temperature. The initial baseline was subtracted and the raw power normalized per embryo was converted into (nJ/s). This was followed by manual time-normalization to the embryo injection peak of the experiment. Raw data for each replicate were normalized to t=0 using the first detectable minima in the heat flow oscillations and the mean, standard deviation and standard error of the mean of all the replicates was calculated. The measured time normalized data was decomposed into its trend, oscillation and noise component. First, we used lowess smoothing of the observed data to determine the trend component. We then subtracted the trend from the measured data to obtain the noise containing oscillatory component, which was smoothed using lowess filtering to determine the oscillatory heat flow component. Subtraction of the smoothed oscillatory component led to the noise component. To determine the minima and maxima in the heat flow oscillations we subtracted a moving average from the raw data and smoothed the remaining oscillations using a lowess filter. The minima and maxima were identified using the custom function find_peaks, manually checked, and the inter minima/maxima distance in time was calculated to determine the period of the heat oscillations. The mean period of all observed oscillation cycles per replicate was calculated.
Wavelet transformation was performed using the R package “Wavelet Comp”. A Morlet wavelet was used to compute the wavelet-power spectrum of the smoothed oscillatory component of each biological replicate. The peak in the detected significant oscillation periods was detected in order to determine the heat oscillation period for each biological replicate.
Mathematical modeling
Constructing a mathematical model for module 1 (core cell cycle oscillator)
We constructed our mathematical model for the cell cycle dependent phosphorylation and de-phosphorylation events in zebrafish by combining two modules. Module 1decribes the embryonic cell cycle oscillator. Module 2 describes the phosphorylation/de-phosphorylation events based on the output of the activity of module 1. The cell cycle oscillator has been modelled based on the work of Tyson and Novak (Tyson, 1991) by many groups. We set out to base our mathematical model for Module 1 one relative simple ordinary-differential equation (ODE) model proposed by Tsai and Ferrell (Tsai et al., 2014) for the Xenopus cell cycle oscillator. We assumed that core cell cycle oscillator is conserved between frog and zebrafish. The model details for module 1 have been extensively described in Tsai et al (Tsai et al., 2014). It accounts for the synthesis and degradation of cyclin B and the activation and inactivation of the cyclin B1-Cdk1 complex by its positive and negative feedback loop via the phosphatase Cdc25 and the kinase Wee1, respectively. It is also assumed that the Cdk1 cyclin B1 complex is further inactivated by APC and the proteasome. The switch like activation of APC by Cdk1 is time-delayed and is integrated into the ODE-framework by a two-step function. First Plx1 is activated then APC. This leads to a 4-ODE model for the cell cycle oscillator in Module 1:
The parameter p defines the maximal-activated Cdc25 and Wee1 activities relative to their basal activities. The rates of cyclin B-Cdk1 activation and inactivation are can be adjusted by r assuming that cdc25 and Wee1 each change by the same factor.
We used the same initial conditions as Tsai et al. to reproduce the Xenopus cell cycle oscillator:
cdk1a[0]=60 nM
cdk1i[0]=0 nM
plxa[0]=0
apca[0]=0
The parameters chosen can be found in Tsai et al. and are also listed below (Parameter table 1).
Parameter table 1.
Model parameters used to solve the 4-ODE Module 1
| Parameter | Value | Meaning | Justification |
|---|---|---|---|
| ksynth | 1.5 nM/min | Rate of synthesis of cyclin B1 | (Tsai et al., 2014) |
| kdest | 0.4 nM/min | Degradation of cyclin B1 by APC | (Tsai et al., 2014) |
| kcdk1on | 0.0354 | Rate of Cdk1 activation | (Tsai et al., 2014) |
| kcdk1off | 0.0354 | Rate of Cdk1 inactivation | (Tsai et al., 2014) |
| kplxon | 1.5 | Rate of activation of Plx1 | (Tsai et al., 2014) |
| kplxoff | 0.125 | Rate of inactivation of Plx1 | (Tsai et al., 2014) |
| kapcon | 1.5 | Rate of APC activation by Plx1 | (Tsai et al., 2014) |
| kapcoff | 0.15 | Rate of APC inactivation after Plx1 is inactivated | (Tsai et al., 2014) |
| r | 1/32 | Ratio of rate of Cdk1 activation and inactivation by Cdc25 and Wee1 | (Tsai et al., 2014) |
| p | 5 | Is the ratio active Wee1 vs Wee1 basal activity or active Cdc25 vs Cdc25 basal activity. It means either Wee1 or Cdc25 is p time more active than its basal activity | (Kumagai and Dunphy, 1992; Tsai et al., 2014) |
| ncdc25 | 11 | Hill exponent for the response of cdc25 to Cdk1 | (Trunnell et al., 2011) |
| nwee1 | 3.5 | Hill exponent for response of Wee1 to Cdk1 | (Kim and Ferrell, 2007) |
| ec50cdc25 | 30 nM | EC50 for the response of CDC25 to Cdk1 | (Kim and Ferrell, 2007) |
| ec50wee1 | 35 nM | EC50 for the response of Wee1 Cdk1 | (Kim and Ferrell, 2007) |
| ec50plx1 | 60 nM | EC50 for the response for Cdk1 to activate Plx1 | (Yang and Ferrell, 2013) |
| ec50apc | 0.5 | EC50 for the response of APC to Plx1 | (Yang and Ferrell, 2013) |
| napc | 4 | Hill exponent for response of APC | (Yang and Ferrell, 2013) |
| nplx | 5 | Hill exponent for response of Plx1 to Cdk1 | (Yang and Ferrell, 2013) |
Adjustment of Module 1 from Xenopus to D. rerio
The Xenopus cell cycle period (25–30) min differs from the reported cell cycle length in zebrafish (~15 min). To match the cell cycle oscillator period to the cell cycle length in zebrafish we increased the cyclin synthesis rate and destruction rate, and the maximal rates of Plx1 and Cdk1 activation and inactivation by a factor of 1.9
Constructing a mathematical model for phosphorylation/de-phosphorylation cycles of Cdk1 substrates by Cdk1 and PP2A.
The model accounts for the reversible binding of Cdk1 to its substrate (S) forming a substrate/Cdk1 complex (SCdk1) and the irreversible formation of phosphorylated substrate (SP) by Cdk1. Active Cdk1 levels were modeled in module 1 and regulated by the cell cycle oscillator. We then assumed that SP can reversibly associate with the phosphatase PP2A to form the phosphorylated substrate phosphatase complex SPPP2A, and is irreversibly hydrolyzed to regenerate free S and PP2A. Phosphorylated substrate can be produced form the dephosphorylated substrate. We assumed mass action kinetics for all of these processes. This yielded 6 ODEs:
For the initial conditions we chose:
| [Cdk1a] | = output of modul 1) |
| S[0] | = 60 nM |
| SCdk1[0] | = 0 nM |
| SP[0] | = 0 nM |
| PP2A[0] | = 60 nM |
| SPPP2A[0] | = 0 nM |
| Stotal | = 60 nM |
The parameters chosen are listed below (Parameter table 2). The on and off rates for substrate binding by active Cdk1 and PP2A were not constrained. We assumed that the on rate is much fast then their off rate and we empirically determined their parameter space which generated oscillations in the phosphorylation/de-phosphorylation cycle of the Cdk1 substrates.
Parameter table 2:
Parameters for used to solve the 5-ODE module 2
| Parameter | Value | Meaning | Justification |
|---|---|---|---|
| kcdkon | 10 | Rate of substrate binding by active Cdk1 | We expect the on rate for substrate binding by Cdk1 to be faster than the off rate. On and off rates were not constrained and empirically determine to generate oscillations in the phosphorylation/de-phosphorylation cycles of the substrate |
| kcdkoff | 1 | Rate of substrate unbinding by active Cdk1 | We expect the on rate for substrate binding by Cdk1 to be faster than the off rate. On and off rates were not constrained and empirically determine to generate oscillations in the phosphorylation/de-phosphorylation cycles of the substrate |
| kcatcdk1 | 180*min−1 (3*s−1) | Catalytic rate of Cdk1 | (Loog and Morgan, 2005) |
| kpp2on | 100 | Rate of substrate binding by PP2A | We expect the on rate for substrate binding by PP2A to be faster than the off rate. On and off rates were not constrained and empirically determine to generate oscillations in the phosphorylation/de-phosphorylation cycles of the substrate |
| kpp2off | 0.01 | Rate of substrate unbinding by PP2A | We expect the on rate for substrate binding by PP2A to be faster than the off rate. On and off rates were not constrained and empirically determine to generate oscillations in the phosphorylation/de-phosphorylation cycles of the substrate |
| Kcatpp2 | 1800*min−1 (30*s−1) | Catalytic rate of PP2A | (Gopishetty et al., 2008; Ren et al., 2011) |
The 4-ODE module 1 and 6-ODE module 2 was calculated and solved together in R.
Using these parameters, our model generated oscillations in active Cdk1, in its substrate complex SCdk1, in phosphorylated substrate, SP, as well as, in free PP2A, its phosphorylated substrates complex SPPP2A and free non-phosphorylated substrate S (fig S5B). Thus, our model generates oscillations in the phosphorylation statues of Cdk1 substrates.
Estimation of the theoretical heat flow
We assumed that the majority of the heat during the phosphorylation/de-phosphorylation cycles of Cdk1 substrates is dissipated by the de-phosphorylation of the substrate by PP2A. Therefore, is seems reasonable that the heat released is proportional to change in phosphorylated substrate/PP2A complex . The model heat flow can be calculated as follows:
, with: Vembryo= embryo volume = 60 ×106 µm3 (Joseph et al., 2017) ∆Hdesphos= Enthalpy change of protein de-phosphorylation = 40 kJ*mol−1, kcatPP2= reaction rate of PP2A= 30*s−1
Supplementary Material
Acknowledgments
We thank Drs. Hugo Bowne-Anderson, Gerald Shulman, Mustafa Khokha and Emre Seli for helpful discussions. We thank Manuel Razo and Mathjiis Veugel for their participation in the early stage of this project during the 2015 Marine Biology Laboratory Physiology course at Woods Hole, MA. We thank Dahyana Arias Escayola for help with blind data acquisition in mapping the heat oscillations to the cell cycle. We thank Stefania Nicoli and Meredith S. Cavanaugh for their help with fish breeding in the time of need. We thank Vladimir Despic for his help with zebrafish embryo illustrations. This work was supported by funding from EMBO ALTF 754-2015 (to JR), from NIH R01 GM110386 (to JH) from the NIGMS, and from NIH R21 HD094013 (to KMN) from the NICHD. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of the NIH.
Footnotes
Declaration of Interests
The authors declare no competing interests
References
- Ahn E, Kumar P, Mukha D, Tzur A, and Shlomi T (2017). Temporal fluxomics reveals oscillations in TCA cycle flux throughout the mammalian cell cycle. Mol. Syst. Biol 13, 953–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alberty RA, and Goldberg RN (2002). Standard thermodynamic formation properties for the adenosine 5’-triphosphate series. Biochemistry 31, 10610–10615. [DOI] [PubMed] [Google Scholar]
- Begasse ML, Leaver M, Vazquez F, Grill SW, and Hyman AA (2015). Temperature Dependence of Cell Division Timing Accounts for a Shift in the Thermal Limits of C. elegans and C. briggsae. Cell Reports 10, 647–653. [DOI] [PubMed] [Google Scholar]
- Cao Y, Wang H, Ouyang Q, and Tu Y (2015). The free-energy cost of accurate biochemical oscillations. Nat Phys 11, 772–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Curtin NA, and Woledge RC (1978). Energy changes and muscular contraction. Physiological Reviews 58, 690–761 [DOI] [PubMed] [Google Scholar]
- Davis FM, Tsao TY, Fowler SK, and Rao PN (1983). Monoclonal antibodies to mitotic cells. Proc Natl Acad Sci USA 80, 2926–2930. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Domingo-Sananes MR, Kapuy O, Hunt T, and Novak B (2011). Switches and latches: a biochemical tug-of-war between the kinases and phosphatases that control mitosis. Philosophical Transactions of the Royal Society B: Biological Sciences 366, 3584–3594. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ewald JC, Kuehne A, Zamboni N, and Skotheim JM (2016). The Yeast Cyclin-Dependent Kinase Routes Carbon Fluxes to Fuel Cell Cycle Progression. Mol. Cell 62, 532–545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ferrell JE Jr., Tsai TY-C, and Yang Q (2011). Modeling the Cell Cycle: Why Do Certain Circuits Oscillate? Cell 144, 874–885. [DOI] [PubMed] [Google Scholar]
- Flamholz A, Phillips R, and Milo R (2014). The quantified cell. Mol Biol Cell 25, 3497–3500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fukami Y, and Lipmann F (1983). Reversal of Rous sarcoma-specific immunoglobulin phosphorylation on tyrosine (ADP as phosphate acceptor) catalyzed by the src gene kinase. Proc Natl Acad Sci USA 80, 1872–1876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gard DL, and Kirschner MW (1987). Microtubule assembly in cytoplasmic extracts of Xenopus oocytes and eggs. J Cell Biol 105, 2191–2201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gardner DK (1998). Changes in requirements and utilization of nutrients during mammalian preimplantation embryo development and their significance in embryo culture. Theriogenology 49, 83–102. [DOI] [PubMed] [Google Scholar]
- Gardner DK, and Leese HJ (1990). Concentrations of nutrients in mouse oviduct fluid and their effects on embryo development and metabolism in vitro. J. Reprod. Fertil 88, 361–368. [DOI] [PubMed] [Google Scholar]
- Gillooly JF, Brown JH, West GB, Savage Van M, and Charnov EL (2001). Effects of Size and Temperature on Metabolic Rate. Science 293, 2248–2251. [DOI] [PubMed] [Google Scholar]
- Godfrey M, Touati SA, Kataria M, Jones A, Snijders AP, and Uhlmann F (2017). PP2ACdc55 Phosphatase Imposes Ordered Cell-Cycle Phosphorylation by Opposing Threonine Phosphorylation. Mol. Cell 65, 393–402.e393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gopishetty B, Ren L, Waller TM, Wavreille A-S, Lopez M, Thakkar A, Zhu J, and Pei D (2008). Synthesis of 3,5-Difluorotyrosine-Containing Peptides: Application in Substrate Profiling of Protein Tyrosine Phosphatases. Org. Lett 10, 4605–4608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Houghton FD, Thompson JG, Kennedy CJ, and Leese HJ (1996). Oxygen consumption and energy metabolism of the early mouse embryo. Mol. Reprod. Dev 44, 476–485. [DOI] [PubMed] [Google Scholar]
- Joseph SR, Pálfy M, Hilbert L, Kumar M, Karschau J, Zaburdaev V, Shevchenko A, and Vastenhouw NL (2017). Competition between histone and transcription factor binding regulates the onset of transcription in zebrafish embryos. Elife 6, 1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jusup M, Sousa T, Domingos T, Labinac V, Marn N, Wang Z, and Klanjšček T (2016). Physics of metabolic organization. Physics of Life Review 20, 1–39. [DOI] [PubMed] [Google Scholar]
- Kane DA, and Kimmel CB (1993). The zebrafish midblastula transition. Development 119, 447–456. [DOI] [PubMed] [Google Scholar]
- Kim SY, and Ferrell JE (2007). Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell 128, 1133–1145. [DOI] [PubMed] [Google Scholar]
- Kimmel CB, Ballard WW, Kimmel SR, Ullmann B, and Schilling TF (1995). Stages of embryonic development of the zebrafish. Developmental Dynamics 203, 253–310. [DOI] [PubMed] [Google Scholar]
- Koomey J, Berard S, (null) MS, and Wong H (2011). Implications of historical trends in the electrical efficiency of computing. IEEE Annals of the History of Computing 33, 46–54. [Google Scholar]
- Kumagai A, and Dunphy WG (1992). Regulation of the cdc25 protein during the cell cycle in Xenopus extracts. Cell 70, 139–151. [DOI] [PubMed] [Google Scholar]
- Landauer R (1961). Irreversibility and Heat Generation in the Computing Process. IBM J. Res. & Dev 5, 183–191. [Google Scholar]
- Lazo JS, Nemoto K, Pestell KE, Cooley K, Southwick EC, Mitchell DA, Furey W, Gussio R, Zaharevitz DW, Joo B, et al. (2002). Identification of a Potent and Selective Pharmacophore for Cdc25 Dual Specificity Phosphatase Inhibitors. Mol Pharmacol 61, 720–728. [DOI] [PubMed] [Google Scholar]
- Leese HJ (2012). Metabolism of the preimplantation embryo: 40 years on. Reproduction 143, 417–427. [DOI] [PubMed] [Google Scholar]
- Li W, Xie L, Chen Z, Zhu Y, Sun Y, Miao Y, Xu Z, and Han X (2010). Cantharidin, a potent and selective PP2A inhibitor, induces an oxidative stress-independent growth inhibition of pancreatic cancer cells through G2/M cell-cycle arrest and apoptosis. Cancer Sci 101, 1226–1233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loog M, and Morgan DO (2005). Cyclin specificity in the phosphorylation of cyclin-dependent kinase substrates. Nature 434, 104–108. [DOI] [PubMed] [Google Scholar]
- Lunt SY, and Vander Heiden MG (2011). Aerobic Glycolysis: Meeting the Metabolic Requirements of Cell Proliferation. Annu. Rev. Cell Dev. Biol 27, 441–464. [DOI] [PubMed] [Google Scholar]
- Lynch M, and Marinov GK (2015). The bioenergetic costs of a gene. Proc Natl Acad Sci USA 112, 15690–15695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Makarieva AM, Gorshkov VG, Li B-L, Chown SL, Reich PB, and Gavrilov VM (2008). Mean mass-specific metabolic rates are strikingly similar across life’s major domains: Evidence for life’s metabolic optimum. Proc Natl Acad Sci USA 105, 16994–16999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mesbah Oskui S, Bhakta HC, Diamante G, Liu H, Schlenk D, and Grover WH (2017). Measuring the mass, volume, and density of microgram-sized objects in fluid. PLoS ONE 12, e0174068–17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mitra K, Wunder C, Roysam B, Lin G, and Lippincott-Schwartz J (2009). A hyperfused mitochondrial state achieved at G1-S regulates cyclin E buildup and entry into S phase. Proceedings of the National Academy of Sciences 106, 11960–11965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mochida S, and Hunt T (2012). Protein phosphatases and their regulation in the control of mitosis. EMBO Rep 13, 197–203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mochida S, Rata S, Hino H, Nagai T, and Novák B (2016). Two Bistable Switches Govern M Phase Entry. Current Biology 26, 3361–3367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morgan DO (2007). The Cell Cycle (New Science Press)
- Murray AW, and Hunt T (1993). The Cell Cycle (Oxford University Press on Demand)
- Olivier N, Luengo-Oroz MA, Duloquin L, Faure E, Savy T, Veilleux I, Solinas X, Débarre D, Bourgine P, Santos A, et al. (2010). Cell Lineage Reconstruction of Early Zebrafish Embryos Using Label-Free Nonlinear Microscopy. Science 329, 967–971. [DOI] [PubMed] [Google Scholar]
- O’Farrell PH (2015). Growing an Embryo from a Single Cell: A Hurdle in Animal Life. Cold Spring Harb Perspect Biol 7, a019042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Papagiannakis A, Niebel B, Wit EC, and Heinemann M (2016). Autonomous Metabolic Oscillations Robustly Gate the Early and Late Cell Cycle. Mol. Cell 1–12. [DOI] [PubMed]
- Paranjpe SS, and Veenstra GJC (2015). Establishing pluripotency in early development. Biochimica Et Biophysica Acta (BBA) - Gene Regulatory Mechanisms 1849, 626–636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavlova NN, and Thompson CB (2016). The Emerging Hallmarks of Cancer Metabolism. Cell Metab 23, 27–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pestell KE, Ducruet AP, Wipf P, and Lazo JS (2000). Small molecule inhibitors of dual specificity protein phosphatases. Oncogene 19, 6607–6612. [DOI] [PubMed] [Google Scholar]
- Placzek S, Schomburg I, Chang A, Jeske L, Ulbrich M, Tillack J, and Schomburg D (2017). BRENDA in 2017: new perspectives and new tools in BRENDA. Nucleic Acids Research 45, D380–D388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Presler M, Van Itallie E, Klein AM, Kunz R, Coughlin ML, Peshkin L, Gygi SP, Wühr M, and Kirschner MW (2017). Proteomics of phosphorylation and protein dynamics during fertilization and meiotic exit in theXenopusegg. Proceedings of the National Academy of Sciences 114, E10838–E10847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reber SB, Baumgart J, Widlund PO, Pozniakovsky A, Howard J, Hyman AA, and Jülicher F (2013). XMAP215 activity sets spindle length by controlling the total mass of spindle microtubules. Nat Cell Biol 15, 1116. [DOI] [PubMed] [Google Scholar]
- Ren L, Chen X, Luechapanichkul R, Selner NG, Meyer TM, Wavreille A-S, Chan R, Iorio C, Zhou X, Neel BG, et al. (2011). Substrate Specificity of Protein Tyrosine Phosphatases 1B, RPTPα, SHP-1, and SHP-2. Biochemistry 50, 2339–2356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Slavov N, and Botstein D (2011). Coupling among growth rate response, metabolic cycle, and cell division cycle in yeast. Mol Biol Cell 22, 1997–2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song Y, Marmion RA, Park JO, Biswas D, Rabinowitz JD, and Shvartsman SY (2017). Dynamic Control of dNTP Synthesis in Early Embryos. Dev Cell 42, 301–308.e303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stock JB, Stock AM, and Mottonen JM (1990). Signal transduction in bacteria. Nature 344, 395–400. [DOI] [PubMed] [Google Scholar]
- Stouthamer AH (1973). A theoretical study on the amount of ATP required for synthesis of microbial cell material. Antonie Van Leeuwenhoek 39, 545–565. [DOI] [PubMed] [Google Scholar]
- Swaffer MP, Jones AW, Flynn HR, Snijders AP, and Nurse P (2016). CDK Substrate Phosphorylation and Ordering the Cell Cycle. Cell 167, 1750–1750.e16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trunnell NB, Poon AC, Kim SY, and Ferrell JE (2011). Ultrasensitivity in the Regulation of Cdc25C by Cdk1. Mol. Cell 41, 263–274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tsai TYC, Theriot JA, and Ferrell JE (2014). Changes in Oscillatory Dynamics in the Cell Cycle of Early Xenopus laevis Embryos. PLoS Biol 12, e1001788–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tu BP, Kudlicki A, Rowicka M, and McKnight SL (2005). Logic of the Yeast Metabolic Cycle: Temporal Compartmentalization of Cellular Processes. Science 310, 1152–1158. [DOI] [PubMed] [Google Scholar]
- Tyson JJ (1991). Modeling the cell division cycle: cdc2 and cyclin interactions. Proc Natl Acad Sci USA 88, 7328–7332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tyson JJ, and Novák B (2013). Irreversible Transitions, Bistability and Checkpoint Controls in the Eukaryotic Cell Cycle. In Handbook of Systems Biology, (Elsevier), pp. 265–285.
- Vastag L, Jorgensen P, Peshkin L, Wei R, Rabinowitz JD, and Kirschner MW (2011). Remodeling of the Metabolome during Early Frog Development. PLoS ONE 6, e16881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner A (2005). Energy Constraints on the Evolution of Gene Expression. Molecular Biology and Evolution 22, 1365–1374. [DOI] [PubMed] [Google Scholar]
- Warburg O (1925). The Metabolism of Carcinoma Cells. The Journal of Cancer Research 9, 148–163. [Google Scholar]
- Ward PS, and Thompson CB (2012). Metabolic Reprogramming: A Cancer Hallmark Even Warburg Did Not Anticipate. Cancer Cell 21, 297–308. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westendorf JM, Rao PN, and Gerace L (1994). Cloning of cDNAs for M-phase phosphoproteins recognized by the MPM2 monoclonal antibody and determination of the phosphorylated epitope. Proc Natl Acad Sci USA 91, 714–718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wühr M, Chen Y, Dumont S, Groen AC, Needleman DJ, Salic A, and Mitchison TJ (2008). Evidence for an upper limit to mitotic spindle length. Current Biology 18, 1256–1261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yaffe MB, Schutkowski M, Shen M, Zhou XZ, Stukenberg PT, Rahfeld J-U, Xu J, Kuang J, Kirschner MW, Fischer G, et al. (1997). Sequence-Specific and Phosphorylation-Dependent Proline Isomerization: A Potential Mitotic Regulatory Mechanism. Science 278, 1957–1960. [DOI] [PubMed] [Google Scholar]
- Yang Q, and Ferrell JE Jr. (2013). The Cdk1--APC/C cell cycle oscillator circuit functions as a time-delayed, ultrasensitive switch. Nat Cell Biol 15, 519–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.