Parameter map error due to normal noise and aliasing artifacts in Magnetic Resonance Fingerprinting

Abstract

Purpose:

To introduce a quantitative tool that enables rapid forecasting of T₁ and T₂ parameter map errors due to normal and aliasing noise as a function of the MRF sequence, which can be used in sequence optimization.

Theory and Methods:

The variances of normal noise and aliasing artifacts in the collected signal are related to the variances in T₁ and T₂ maps through derived quality factors. This analytical result is tested against the results of a Monte-Carlo approach for analyzing MRF sequence encoding capability in the presence of aliasing noise, and verified with phantom experiments at 3T. To further show the utility of our approach, our quality factors are used to find efficient MRF sequences for fewer repetitions.

Results:

Experimental results verify the ability of our quality factors to rapidly assess the efficiency of an MRF sequence in the presence of both normal and aliasing noise. Quality factor assessment of MRF sequences is in agreement with the results of a Monte-Carlo approach. Analysis of MRF parameter map errors from phantom experiments is consistent with the derived quality factors, with T₁ (T₂) data yielding goodness of fit R² ≥ 0.92 (0.80). In phantom and in vivo experiments, the efficient pulse sequence, determined through quality factor maximization, led to comparable or improved accuracy and precision relative to a longer sequence, demonstrating quality factor utility in MRF sequence design.

Conclusion:

The here introduced quality factor framework allows for rapid analysis and optimization of MRF sequence design through T₁ and T₂ error forecasting.

Introduction

MRI has long been used as a diagnostic tool, taking advantage of the MR signal’s dependence on underlying tissue properties, such as relaxation times and spin density, to provide natural contrast between tissue types. While many MR experiments are designed to provide qualitative weighting for a particular property, quantitative mapping is a useful diagnostic tool [1], for example, in oncology [2][3], cardiology [4][5], and neurology [6][7].

The desire for quantitative MRI has led to the introduction of Magnetic Resonance Fingerprinting (MRF), which allows for fast, simultaneous quantization of intrinsic tissue properties, including spin density and relaxation times (T₁, T₂) [8]. Improving upon previously developed quantitative MR techniques, MRF can be performed on a clinically relevant time scale and produces maps of multiple tissue parameters from a single data set. This is achieved by varying imaging parameters such as the flip angle, repetition time (TR), and echo time (TE) over N repetitions (time steps), causing tissues with different underlying characteristics to produce unique signal evolutions. The obtained signals are then matched to a dictionary to generate maps.

It has recently been shown that MRF parameter maps are reliably reproducible given a particular sequence design [9]. However, it is also known that the precision of parameter quantification depends on the chosen imaging sequence (flip angles, TRs, TEs, and N) [10]–[16]. For example, there are known structures that have been implemented in MRF sequence design to enhance T₁ or T₂ sensitivity, such as inversion pulses to improve T₁ sensitivity, time steps with zero degree flip angles to allow for signal recovery, RF phase alternation to build bSSFP signal, and π/2 pulses to improve T₂ sensitivity [17][18].

The dependence of T₁ and T₂ mapping on the sequence design raises the question of optimality. High degrees of freedom in the pulse sequence design add to the challenge of determining an experiment that will result in minimal mapping error. To this end, a number of techniques have been proposed for assessing MRF sequence designs. In Cohen et al. and Sommer et al., techniques are proposed for judging encoding capability, and thus pulse sequence design optimality, based on the correlation between local and global dictionary entries[13][14]. However, Sommer et al. found inconsistency in this method in the presence of undersampling artifacts. With a rich history in statistical estimation theory, several groups have used the Cramer-Rao lower bound to assess MRF parameter estimation in the presence of Gaussian white noise [11][15][16][19]. However, Gaussian white noise does not accurately characterize the undersampling noise that is prevalent in MRF and dependent on signal amplitude.

To address the problem of signal amplitude dependent aliasing noise, Sommer et al. have successfully proposed a trial and error, Monte Carlo technique for assessing MRF sequence performance [13]. While able to accurately predict the efficacy of a given experimental design, the Monte Carlo approach does not provide an analytical tool for quickly understanding errors in MRF maps due to aliasing noise.

In this work we introduce a mathematical framework that relates parameter map errors due to both Gaussian white noise and correlated undersampling artifacts to the MRF signal, and thus to the chosen imaging sequence (N, TR series, flip angle series). As a result of this framework, “quality factors” are found that are inversely related to parameter map variance. These quality factors are compared to the results of the Monte Carlo approach presented by Sommer et al. and experimentally validated. To show further the utility of the approach, our quality factors are used to find an efficient flip angle distribution, requiring fewer acquisitions than the best sequence from the Monte Carlo approach, yet achieving a similar encoding capability. This analytical approach offers increased understandability and usability compared to the previously presented Monte Carlo method.

Theory

In the MRF framework, a dictionary (D) of potential signals (d(θ)) given an experimental design is generated for a range of relevant tissue parameters (θ). Then, the experimentally acquired signal (s) is matched to a dictionary entry to determine tissue properties per voxel. Matching is often performed with maximization of the complex valued dot product between the normalized signal $(\widehat{s})$ and the dictionary $(\widehat{D})$ composed of normalized entries $(\widehat{d}(\theta ))$,

$${\text{max}}_{\theta }\left|\widehat{s}\cdot {\widehat{D}}^{*}\right|$$ [1]

To understand errors in MRF parameter mapping, this work analyzes Eq. [1] using appropriate models for ideal and noisy MRF signals. This work specifically concentrates on the case where θ = [T₁, T₂]; therefore, we focus on FISP-MRF based sequences, which have been shown to be insensitive to off-resonance frequency. [20]

The MRF signal, which behaves according to the Bloch equations, is dependent on a variety of experimental parameters and intrinsic tissue properties. In general, at each RF pulse the magnetization is rotated, then longitudinal magnetization recovers exponentially at a rate determined by R₁=1/T₁ and transverse magnetization decays exponentially at a rate determined by R₂=1/T₂ up to the time of the subsequent RF pulse. If the repetition time is short and the signal is not spoiled between RF pulses, the signal contains the magnetization’s history and is dependent on both T₁ and T₂. In a FISP-MRF experiment, where gradients in the slice select direction are applied at the end of each TR to generate a phase twist greater than 2π, the overall signal from a given voxel is dephased and thus insensitive to off-resonance frequency. [20]

Therefore, the solution to the Bloch equations at each time step in an FISP-MRF experiment is a complicated function of R₁, R₂, repetition times, echo times, and flip angles. In MRF experiments, typical TE and TR values are short relative to T₁ and T₂. Therefore, the signal at each time step can be represented by a first-order Taylor Series expansion about chosen values of R₁ and R₂, R_1,0=1/T_1,0 and R_2,0=1/T_2,0. Then, each dictionary entry (corresponding to relaxation rates R₁ and R₂) is a 1×N dimensional vector that follows the model:

$$\mathit{d}\left(R_1,R_2\right)\approx {\mathit{d}}_0+{\mathit{c}}_1\left(R_1-R_{1,0}\right)+{\mathit{c}}_2\left(R_2-R_{2,0}\right)$$ [2]

where d₀ = d(R_1,0, R_2,0) is the dictionary entry corresponding to the relaxation rates R_1,0 and R_2,0, and the 1×N dimensional coefficients c₁ and c₂ contain the first derivatives of the transverse magnetization with respect to R₁ and R₂ respectively at each time step.

The acquired signal in an MRF experiment will, in general, contain both Gaussian white noise (η) as the result of thermal contributions, and correlated aliasing noise (α) due to undersampling artifacts. Therefore, a noisy acquired signal from a voxel with R₁=R_1,0 and R₂=R_2,0 is expected to be

$$\begin{gathered} \mathit{s}=\mathit{d}\left(R_{1,0},R_{2,0}\right)+\mathit{\eta }+\mathit{\alpha } \\ ={\mathit{d}}_0+\mathit{\eta }+\mathit{\alpha } \end{gathered}$$ [3]

The thermal noise in the acquired signal is assumed to have zero mean, variance ${{\sigma }_{\eta }}^2$, and to be uncorrelated between real and imaginary channels. Thermal noise is taken to be Gaussian rather than Rician due to the high SNR in fully sampled data [21].

Motivated by the work in [13], we model the aliasing noise as proportional to the MRF signal at each time step, with a coefficient of proportionality that is taken to be zero-mean Gaussian noise (ω) with variance ${{\sigma }_{\omega }}^2$. This modeled approximation of aliasing noise is an ansatz, based on the pseudo-randomization of k-space coverage (for example, through golden angle rotation between sparse, variable density spiral acquisitions), and is shown a posteriori to serve as a good approximation of experimentally observed aliasing noise (see Supporting Information Fig. [S1]). Specifically, the n^th component of the complex aliasing noise in our model is given by

$${(\mathit{\alpha })}_n=\left|{\left({\mathit{d}}_0\right)}_n\right|{(\mathit{\omega })}_n$$ [4]

The components of ω are assumed to be uncorrelated, as are η and ω.

With the presented dictionary and acquired signal models and Eq. [1] expressed as $\frac{\partial }{\partial R_i}\left|\widehat{S}\cdot \widehat{d}{\left(R_1,R_2\right)}^{*}\right|$ for i=1,2, evaluation of the derivatives with respect to R₁ and R₂ yields two independent equations with which it is possible to solve for (R₁-R_1,0) and (R₂-R_2,0). From the resulting equations, we find expressions for the variance in R₁ and R₂ [see appendix for a detailed derivation]:

$${{\sigma }_{R_{\text{i}}}}^2=\frac{{{\sigma }_{\eta }}^2}{Q_i}+\frac{{{\sigma }_{\omega }}^2}{q_i}i=1,2$$ [5]

with the quality factors relating to thermal noise given by

$$Q_i=\frac{a_i{a}_j-b^2}{{d_0}^2{a}_j}i=1,2j=2,1$$ [6]

and the quality factors relating to aliasing noise given by

$$q_i=\frac{{\left(a_i{a}_j-b^2\right)}^2}{{d_0}^4{\sum }_{n=1}^N{\left|{\left({\mathit{d}}_0\right)}_n\right|}^2{\left(a_j{\left({\mathit{c}}_i\right)}_n-b{\left({\mathit{c}}_j\right)}_n+{\gamma }_i{\left({\mathit{d}}_0\right)}_n\right)}^2}i=1,2j=2,1$$ [7]

where

$$a_i={\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)}^2-{d_0}^2{c_i}^2$$

$$b=\left({\mathit{d}}_0\cdot {{\mathit{c}}_1}^{*}\right)\left({\mathit{d}}_0\cdot {{\mathit{c}}_2}^{*}\right)-{d_0}^2\left({\mathit{c}}_1\cdot {c_2}^{*}\right)$$

$${\gamma }_i={c_j}^2\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)-\left({\mathit{c}}_i\cdot {{\mathit{c}}_j}^{*}\right)\left({\mathit{d}}_0\cdot {{\mathit{c}}_j}^{*}\right)$$

Our quality factors due to both thermal and aliasing noise contain dependence on R_1,0 and R_2,0 through d₀ and the determination of c₁ and c₂. Additionally, because the signal components (d₀, c₁, c₂) depend on experimental design parameters (flip angle series, TR series, TE, N), the quality factors are indicative of the ability with which a given experiment can match the noisy acquired signal from a voxel with R₁=R_1,0 and R₂=R_2,0 to the appropriate dictionary entry for a given level of noise. Therefore, the comparison of quality factors for different experimental designs allows for the determination of more optimal sequence parameters.

Additionally, noting that c₁ and c₂ are the derivatives of the MRF signal with respect to R₁ and R₂, the quality factors for thermal noise (Q_i) are determined to be consistent with the Cramer-Rao bounds evaluated for a FISP-MRF experiment. For a complete derivation, please see the Supporting Information. Numerical results can be found in reference [22].

If either thermal noise (i.e. fully sampled data) or aliasing noise (i.e. highly undersampled data) dominates Eq. [5], the variance in parameter quantification becomes approximately proportional to the dominant term. Because MRF is generally performed with large undersampling acceleration factors, this work focuses on the case where aliasing noise is dominant so that

$${{\sigma }_{R_{\text{i}}}}^2\cong \frac{{{\sigma }_{\omega }}^2}{q_i}\left({{\sigma }_{\omega }}^2\gg {{\sigma }_{\eta }}^2\right)i=1,2$$ [8]

Methods

Verification Experiments

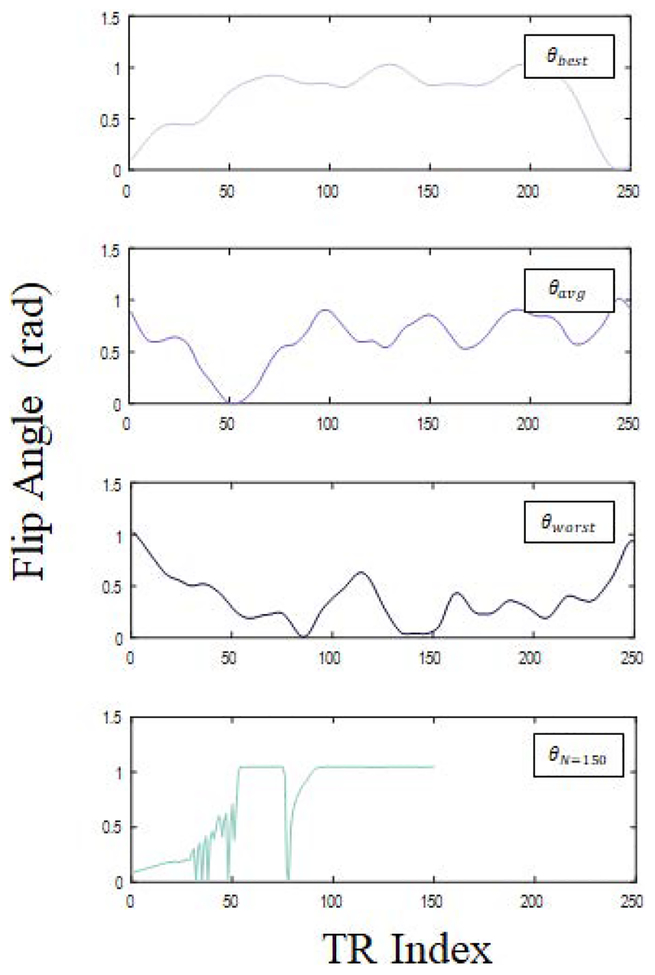
To verify the ability of Eq. [5] to predict the encoding capabilities of a given sequence design, FISP-MRF experiments predicated on the findings of Sommer et al. were performed with a 10-compartment phantom. For these experiments, three FISP-MRF sequences were tested, each containing an inversion pulse (inversion time, TI = 21 ms), constant repetition times (TR = 6.98 ms) and echo times (TE = 2.93 ms), and flip angle patterns with N=250 repetitions. The chosen flip angle distributions (θ_best, θ_average, θ_worst) are based on the three patterns presented in Sommer et al., which were determined to have varying encoding capabilities (best, average, and worst) through their Monte-Carlo approach and with experimental verification (see Fig. [1]) [13].

Figure 1.

Flip angle distributions used in verification and optimization experiments. (a)-(c) Flip angle distributions based on Sommer et al., (θ_best, θ_average, θ_worst), which were determined to have varying encoding capabilities: (a) best, (b) average, and (c) worst. (d) Efficient flip angle distribution with N=150 acquisitions, determined through maximization of aliasing noise quality factors.

Optimization Experiments

As a result of the inverse relationship between ${{\sigma }_{R_i}}^2$ and q_i, the error in mapping T₁ and T₂ with MRF in the presence of aliasing noise can be minimized by designing an experiment with maximized q₁ and q₂, respectively. Optimization of the flip angle sequence through maximization of the herein introduced aliasing noise quality factors was performed in MATLAB (MathWorks, Natick, Massachusetts, USA) with the genetic algorithm. For simplicity, aliasing noise quality factor maximization was performed while allowing the flip angle distribution to vary over the range [0, 60] degrees, fixing TE = 2.93 ms, TR = 6.98 ms, and RF phase = 0°, and executing an initial inversion pulse (T_I = 21 ms). Optimization was initially performed with N=250, resulting in a flip angle distribution achieving a small (20%) forecasted improvement in mapping error relative to already optimized θ_best as determined by Sommer et al. Therefore, to show the utility of our quality factors, the presented optimization was performed for N=150 to determine a sequence with comparable error and shorter scan time, and therefore improved efficiency, relative to the N=250 step experiment with θ_best.

The initial population of the genetic algorithm, containing 900 random entries, was created with a colored noise generator so that 300 entries each had a power spectral density 1/|f|^a with a = 20, 50, and 100 to filter out high frequencies [13]. Although the initial population contained relatively smoothly varying flip angle distributions, distributions in future generations could contain rapid variations due to the processes of mutation and crossover employed by the genetic algorithm.

Quality factors are dependent on underlying relaxation time values (T_1,0, T_2,0) through the calculation of zeroth and first order terms in Eq. [2]; thus, to have an effective formula for use over a large range of relaxation times, optimization was performed by minimizing the weighted sum: ${\sum }_{T_{1,0},T_{2,0}}\left[\frac{T_{1,0}}{\sqrt{q_1\left(T_{1,0},T_{2,0}\right)}}+\frac{T_{2,0}}{\sqrt{q_2\left(T_{1,0},T_{2,0}\right)}}\right]$ with T_1,0 = [600, 850, 1300] ms and T_2,0 = [45 70 100] ms. Weighting the quality factor terms by T_1,0 and T_2,0 for this optimization acts to normalize the terms in the sum, preventing any one term from dominating. The T_1,0 and T_2,0 values chosen for the optimization cover the range of reference relaxation times for white and gray matter at 3T (see Table [1]). The resulting optimized flip angle distribution, θ_N=150, is shown in Fig. [1]. The results of flip angle optimization for normal noise through maximization of Q_i can be found in reference [23].

Table 1.

Relaxation times in white and gray matter at 3T from literature [29] and the results of ROI and nRMSE analysis on in vivo parameter maps obtained with FISP-MRF experiments using θ_best, θ_N=150, and a reference scan based on Jiang et al.

	White Matter		Gray Matter
Sequence	$T_1\pm {\sigma }_{T_1}(\text{ms})$	$T_2\pm {\sigma }_{T_2}(\text{ms})$	$T_1\pm {\sigma }_{T_1}(\text{ms})$	$T_2\pm {\sigma }_{T_2}(\text{ms})$	nRMSET1 (ms)	nRMSET2 (ms)
Literature	(812.3–1110.0)	(49.5–79.6)	(1275.0–1763.0)	(66.0–110.0)	-	-
Reference Scan	1066 ± 91	59 ± 5	1610 ± 128	78 ± 10	-	-
θbest	1033 ± 88	53 ± 4	1579 ± 133	71 ± 7	0.09	0.15
θN=150	993 ± 89	49 ± 4	1629 ± 95	73 ± 10	0.10	0.22

Dictionary and Quality Factor Calculation

Dictionaries containing signal time courses for a range of relevant tissue parameters are generated in MATLAB using the Bloch equations. Because these dictionaries are used to fit d₀, c₁, and c₂ for the calculation of quality factors as defined in Eqs. [6] and [7], the array of T₁ and T₂ values chosen should have small enough increments to perform a linear regression while spanning the typical physiological values of the samples to be imaged. For this work, T₁ was chosen to vary over [35, 1000] ms in 5 ms increments and [1010, 2800] ms in 10 ms increments. T₂ was chosen to vary over [2, 24] ms in 1 ms increments, [26, 40] ms in 2 ms increments, and [45, 800] ms in 5 ms increments, resulting in 56,659 dictionary entries.

To ensure matching accuracy to experimental data, FISP-MRF dictionaries were calculated with slice profile corrections [24]. This calculation was performed based on work by Hargreaves using RF-pulse and gradient information specific to the performed experiments [25]. Using Bloch simulations over 250 spins per voxel, a slice profile corrected FISP-MRF dictionary with 250 time steps for each entry was generated in three hours with MATLAB on the CWRU High Performance Cluster.

Both normal noise and aliasing noise quality factors were then calculated in MATLAB with Eqs. [6] and [7], using linear regressions over nearest neighbors from the calculated dictionary entries for chosen T_1,0 and T_2,0 values to determine d₀, c₁, and c₂.

Experimental Design and Image Reconstruction

FISP-MRF experiments were performed on a 3T Siemens Skyra (Siemens Healthcare, Erlangen, Germany) with a 20-channel head-neck array coil. For phantom experiments, an 8 mm slice was excited with an apodized sinc pulse (n_z=8, τ_RF=2 ms) during application of slice select (G_ss = 11.74 mT/m, slew rate=117.4 T/m/s) and rephasing (G_rephase =−27.4 mT/m, slew rate=119.1 T/m/s) gradients. For in vivo experiments, a 5 mm slice was excited with an apodized sinc pulse (n_z=8, τ_RF=2 ms) during application of slice select (G_ss = 11.74 mT/m, slew rate=117.4 T/m/s) and rephasing (G_rephase =−27.4 mT/m, slew rate=119.1 T/m/s) gradients. Additionally, a spoiler gradient (G_spoil =27.4 mT/m, slew rate=119.1 T/m/s) was applied at the end of each TR to create a phase twist of 8π in the slice select direction.

Data was collected using a variable density spiral k-space trajectory, which required 48 interleaves to fully cover k-space (192×192, 300 mm² FOV for phantom experiments; 256×256, 300 mm² FOV for in vivo experiments) [26]. Fully sampled data sets were acquired for each experiment. Then, data was retrospectively undersampled to achieve acceleration factors ranging from R=5 to R=48, employing golden angle rotation of interleaves within each time step and relative to neighboring time steps [27]. Image reconstruction was performed using the non-uniform fast Fourier transform (NUFFT) [28] and the adaptive method for combining images from multiple coils [29].

Phantom Experiments

Both verification experiments, based on the results of Sommer et al., and optimization experiments, derived through maximization of our aliasing noise quality factors, were performed as described in Experimental Design and Image Reconstruction to image a 10-compartment phantom. Reference T_1,0 and T_2,0 values for each of the ten phantom compartments were determined with inversion recovery and spin echo sequences, respectively (see Supporting Information Table [1]). For additional comparison to the optimization experiments, reference T₁ and T₂ maps were obtained using an undersampled (R=48) 1000 step FISP-MRF sequence based on Jiang et al. [20]

Parameter maps (T₁ and T₂) were generated through complex valued dot product matching with the fully sampled and undersampled data from each experiment. A 5×5 ROI was drawn in each of the ten phantom compartments for calculation of mean $\left({\overline{\text{T}}}_1,{\overline{\text{T}}}_2\right)$ and standard deviation $\left({\sigma }_{T_1},{\sigma }_{T_2}\right)$ values. The obtained mean values were used to calculate q_i and Q_i for each experiment, and errors in the ${\sigma }_{T_i}$ data were propagated based on the changes in q_i and Q_i as the result of mean error relative to the reference T_1,0 and T_2,0 values in Table [1].

In vivo Experiments

Experiments with θ_best and θ_N=150 were performed in vivo as described in Experimental Design and Image Reconstruction to generate T₁ and T₂ maps from volunteer head scans. Reference T₁ and T₂ maps were obtained using a 1000 step FISP-MRF sequence based on Jiang et al., which was shown to reliably yield comparable results to standard T₁ and T₂ mapping techniques [20].

The in vivo parameter maps resulting from experiments with θ_best and θ_N=150 were analyzed through calculations of the relative error in each parameter map compared to the reference map, and the resulting normalized root mean squared errors in T₁ and T₂ (nRMSE_T1, nRMSE_T2), defined as ${\text{nRMSE}}_{\text{Ti}}\text{=}\sqrt{{\sum }_{j=1}^n\frac{1}{n}{\left(\frac{T_{i,j}-T_{i,j}^{ref}}{T_{i,j}^{ref}}\right)}^2}$, with n total voxels, the matched value of T_i in the j^th voxel given by T_i,j, and the T_i value in the j^th voxel of the reference scan given by $T_{i,j}^{ref}$. Regions of interest were drawn in areas of white and gray matter for calculation of mean $\left({\overline{\text{T}}}_1,{\overline{\text{T}}}_2\right)$, standard deviation $\left({\sigma }_{T_1},{\sigma }_{T_2}\right)$ values for additional parameter map comparison to reference map and literature values [30].

Results

Verification Experiments: Quality Factors as Functions of T₁ and T₂

With the generated dictionaries, both aliasing and normal noise quality factors for the three experiments based on Sommer et al. [13] were calculated in MATLAB with T_1,0 varying over [350, 1710] ms in increments of 10 ms and T_2,0 varying over [30, 110] ms in increments of 2 ms.

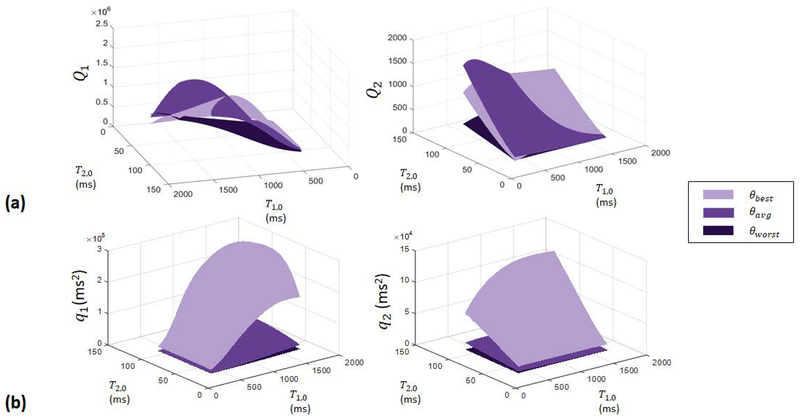
The resulting surface plots of the normal noise quality factor, Q_i, versus T_1,0 and T_2,0 are shown in Fig. [2a], demonstrating that the encoding capability of the three sequences in the presence of normal noise does not necessarily follow the θ_best > θ_average > θ_worst hierarchy predicted for aliasing noise by Sommer et al., but instead the sequences should tend to perform comparably well [13]. Surface plots of q_i versus T_1,0 and T_2,0 shown in Fig. [2b] reveal that θ_best results in the highest valued aliasing noise quality factors and θ_worst results in the lowest valued aliasing noise quality factors over the entire tested range, in agreement with the encoding capability predicted by Sommer et al.

Figure 2.

Surface plots of (a) normal and (b) aliasing noise quality factors as functions of T_1,0 and T_2,0 over the range T_1,0=[350,1710] ms and T_2,0=[30,110] ms, for experiments using θ_best, θ_average, and θ_worst. Figure [2a] demonstrates that the three flip angle distributions, which achieve comparable normal noise quality factors over the tested range in relaxation times, are expected to perform similarly in the presence of normal noise. Figure [2b] shows that experiments with θ_best yield the highest aliasing noise quality factors and experiments with θ_worst yield the lowest aliasing noise quality factors over the tested range, in agreement with the encoding capabilities demonstrated by Sommer et al.

Verification Experiments: Phantom Data

The results of ROI analysis on the T₁ and T₂ maps obtained with phantom experiments using θ_best, θ_average, and θ_worst based on Sommer et al. are presented. Analysis of parameter maps obtained with fully sampled data show that the three experiments perform comparably well in the absence of aliasing noise. This result is in agreement with the T₁ and T₂ error forecasted by the normal noise quality factors (see Fig [2a]), which are expected to dominate the relationship presented in Eq. [5] in the absence of aliasing noise. Error in the parameter maps obtained with undersampled data achieving acceleration factors between R=5 and R=10 were determined to be dependent on both normal noise and aliasing noise quality factors, with neither term dominating the relationship between parameter map error and the derived quality factors presented in Eq. [5]. See the attached Supporting Information Figs. [S2] and [S3] for further details regarding parameter map error at low acceleration factors (R≤10).

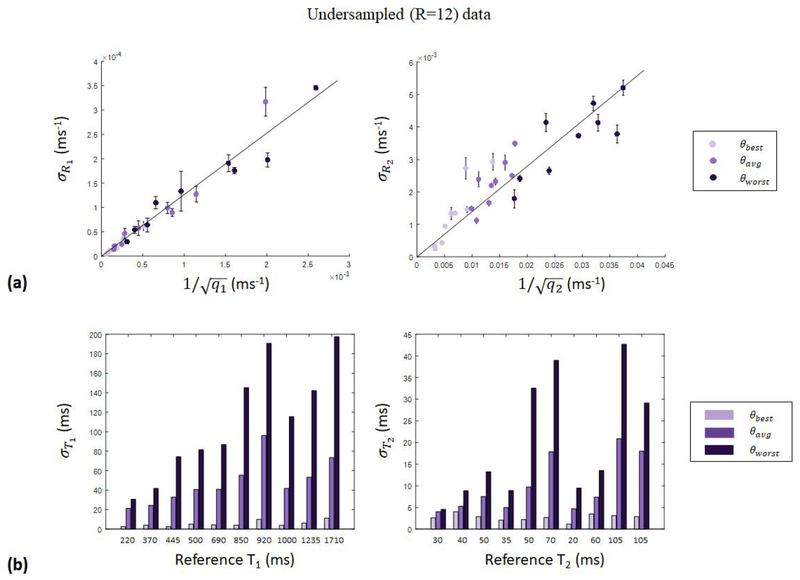
ROI analysis of the T₁ and T₂ maps obtained with undersampled data achieving acceleration factors R=12 and higher showed that the relationship between parameter map error and quality factors derived in Eq. [5] is dominated by the aliasing noise quality factors, so that the approximation taken in Eq. [8] is appropriate. As a representative example, Fig. [3a] shows the parameter map error $\left({\sigma }_{R_i}\right)$ per ROI, obtained with undersampled (R=12) data, plotted as a function of the calculated aliasing noise quality factor $\left(1/\sqrt{q_i}\right)$ for the three tested sequences (θ_best, θ_average, and θ_worst). In agreement with Eq. [8], the parameter map error achieves good linearity (R²=0.92 for ${\sigma }_{R_1}$ and R²=0.80 for ${\sigma }_{R_2}$) in $1/\sqrt{q_i}$. The variance of the aliasing noise, corresponding to the slope of the fitted data as a result of Eq. [8], is determined to be σ_ω = 0.12,0.15 from the ${\sigma }_{R_1}$ and ${\sigma }_{R_2}$ data, respectively, agreeing to within 20%. Bar graphs (see Fig. [3b]) of the parameter map error $\left({\sigma }_{T_i}\right)$ per ROI, obtained with undersampled (R=12) data, show further agreement with the results of Sommer et al. and the surface plots of aliasing noise quality factors as functions of relaxation times presented in Fig. [3a], with θ_best achieving the lowest parameter map error and θ_worst achieving the highest parameter map error in each of the tested ROIs. At higher acceleration factors, parameter map errors continue to show agreement with the quality factor framework in the case where aliasing noise is dominant. For R=16 and R=24, parameter map errors are very well characterized by Eq. [8], with goodness of fit greater than or equal to 0.94 (0.89) for ${\sigma }_{R_1}\left({\sigma }_{R_2}\right)$ data (see Supporting Information Fig. [S4] for details).

Figure 3.

Results of undersampled (R=12) verification experiments. (a) Parameter map error $\left({\sigma }_{R_i}\right)$ per ROI, plotted as a function of the calculated aliasing noise quality factor $\left(1/\sqrt{q_i}\right)$ for the three tested sequences (θ_best, θ_average, and θ_worst), achieving goodness of fit R²=0.92 and R²=0.80 in ${\sigma }_{R_1}$ and ${\sigma }_{R_2}$, respectively. (b) Bar graphs of the parameter map error $\left({\sigma }_{T_i}\right)$ per ROI, showing further agreement with quality factor analysis, with θ_best experiments achieving the lowest error and θ_worst experiments achieving the highest error, as expected.

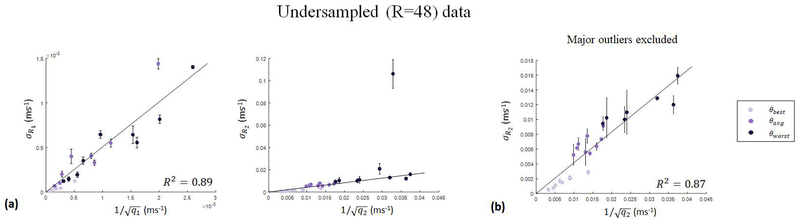
At very high acceleration factors (R=48), while parameter map errors continue to show relative agreement with the presented quality factor framework in the case where aliasing noise is dominant, deviations from the expected results begin to arise. The results of ROI analysis on parameter maps obtained from data at the highest available acceleration factor in this work, R=48, are presented in Fig. [4]. Although the ${\sigma }_{R_1}$ data continues to be well modeled by the aliasing noise quality factors, achieving R²=0.89, the ${\sigma }_{R_2}$ data contains obvious outliers relative to $1/\sqrt{q_2}$. The divergence from the quality factor framework is, in part, explained by the large mean error in T₂ quantification, as verified by the large error bars on the outlying data points. Additional sources of error arise from the first-order approximation of aliasing noise used in the quality factor derivation (see Discussion). Excluding major outliers from the ${\sigma }_{R_2}$ data, the quality factor model is in good agreement with the obtained data, achieving R²=0.87 (see Fig. [4b]).

Figure 4.

Results of undersampled (R=48) verification experiments, plotting parameter map error $\left({\sigma }_{R_i}\right)$ per ROI as a function of the calculated aliasing noise quality factor $\left(1/\sqrt{q_i}\right)$ for the three tested sequences (θ_best, θ_average, and θ_worst). In (a), all data points are included achieving goodness of fit R²=0.89 and R²=0.20 in ${\sigma }_{R_1}$ and ${\sigma }_{R_2}$, respectively. In (b), obvious outliers from the ${\sigma }_{R_2}$ are excluded, resulting in goodness of fit R²=0.87.

Optimization Experiments: Quality Factors as Functions of T₁ and T₂

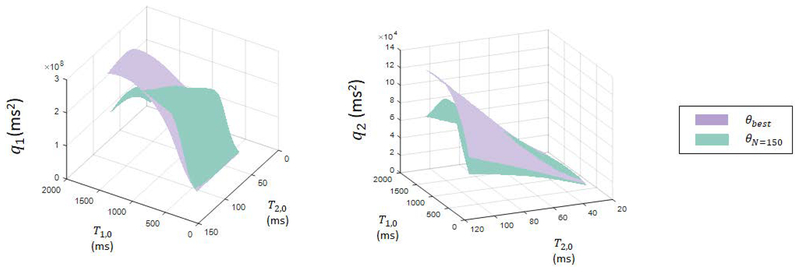
Aliasing noise quality factors for the 250 step experiment with θ_best based on Sommer et al. and the efficient experiment with θ_N=150 derived through maximization of the aliasing noise quality factors were calculated in MATLAB using Eq. [7]. The resulting surface plots of quality factors for aliasing noise as functions of T_1,0 and T_2,0 (see Fig. [5]) reveal that the θ_best and θ_N=150 experiments yield comparable values of q_i, and therefore comparable forecasted errors, over a large range in T₁ and T₂ values. With comparable error and decreased scan time due to fewer acquisitions, θ_N=150 is expected to be more efficient in T₁ and T₂ mapping than θ_best. Note, however, the θ_N=150 experiment is expected to perform poorly at large values of T₁ (>1500 ms), which is likely due to the short total scan time relative to T_1,0 at high values.

Figure 5.

Surface plots of aliasing noise quality factors as functions of T_1,0 and T_2,0 over the range T_1,0=[350,1710] ms and T_2,0=[30,110] ms, comparing experiments using θ_best and θ_N=150. The two experiments yield comparable aliasing noise quality factors, except at large T₁, where θ_N=150 is expected to yield large errors.

Optimization Experiments: Phantom Data

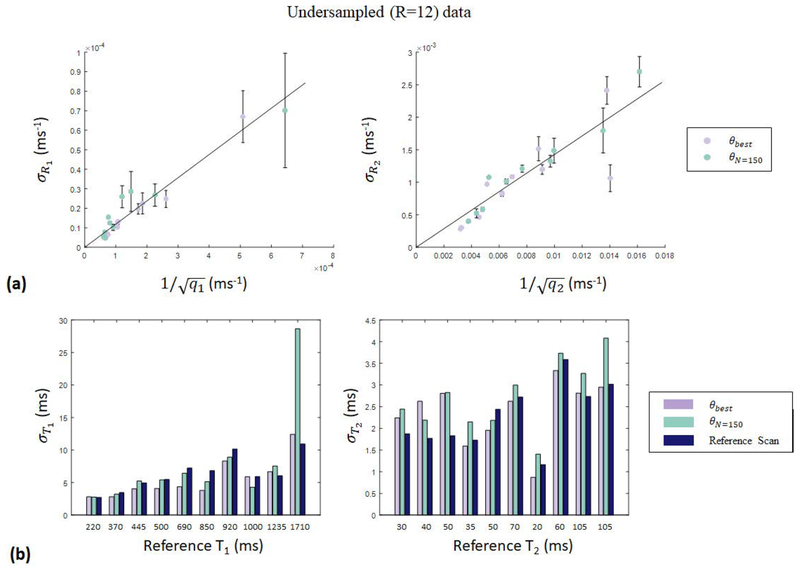
The results of ROI analysis on the T₁ and T₂ maps obtained with phantom experiments using the 250 step θ_best based on Sommer et al. and the 150 step θ_N=150 derived through quality factor maximization are presented. Because θ_N=150 was designed to achieve aliasing noise quality factors comparable to θ_best, error analysis was designed to specifically probe the relationship between q_i and ${\sigma }_{R_i}$. In agreement with the results of verification experiments, plots of the obtained parameter map error per ROI as functions of aliasing noise quality factors showed that the q_i term dominates the relationship in Eq. [5] for undersampled data with acceleration factors at and above R=12. As a representative case, Fig. [6a] shows the parameter map error $\left({\sigma }_{R_i}\right)$ per ROI, obtained with undersampled (R=12) data, plotted as a function of the calculated aliasing noise quality factor $\left(1/\sqrt{q_i}\right)$, achieving R²=0.92 and R²=0.70 for ${\sigma }_{R_1}$ and for ${\sigma }_{R_2}$ data, respectively. (We note that without the outlying data point (related to a very low valued T_2,0 for which the first order approximation taken in Eq. [2] is less accurate) in the plot comparing our ${\sigma }_{R_2}$ data to $1/\sqrt{q_i}$, the goodness of fit is increased from 0.70 to 0.92, so that both plots demonstrate excellent agreement with the expected linear relationship in Eq. [8]). Bar graphs of the parameter map error $\left({\sigma }_{T_i}\right)$ per ROI, obtained with undersampled (R=12) data from experiments using θ_best and θ_N=150 are presented in Fig. [6b]. For additional comparison, Fig. [6b] also shows ${\sigma }_{T_i}$ per ROI, obtained with the reference scan based on the FISP-MRF sequence presented in Jiang et al. and performed at the usual acceleration factor R=48. The graphs in Fig. [6b] continue to show agreement with parameter map error forecasted by aliasing noise quality factors, with generally comparable parameter map error per ROI for θ_best and θ_N=150, except at large T₁, where the 150 step experiment is expected to incur high mapping errors. In addition, Fig. [6b] demonstrates that the parameter map error from undersampled data (R=12) obtained with the two short sequences (θ_best and θ_N=150) is comparable to that from the reference sequence.

Figure 6.

Results of undersampled (R=12) phantom optimization experiments. (a) Parameter map error $\left({\sigma }_{R_i}\right)$ per ROI, plotted as a function of the calculated aliasing noise quality factor $\left(1/\sqrt{q_i}\right)$ for experiments with θ_best and θ_N=150. achieving goodness of fit R²=0.92 and R²=0.70 in ${\sigma }_{R_1}$ and ${\sigma }_{R_2}$, respectively. (b) Bar graphs of parameter map error $\left({\sigma }_{T_i}\right)$ per ROI, showing that experiments with θ_best and θ_N=150 performed at R=12, and the standard FISP-MRF experiment based on Jiang et al. yield comparable errors. With fewer acquisitions (shorter scan time) and comparable error, θ_N=150 is more efficient than θ_best.

Optimization Experiments: In Vivo Data

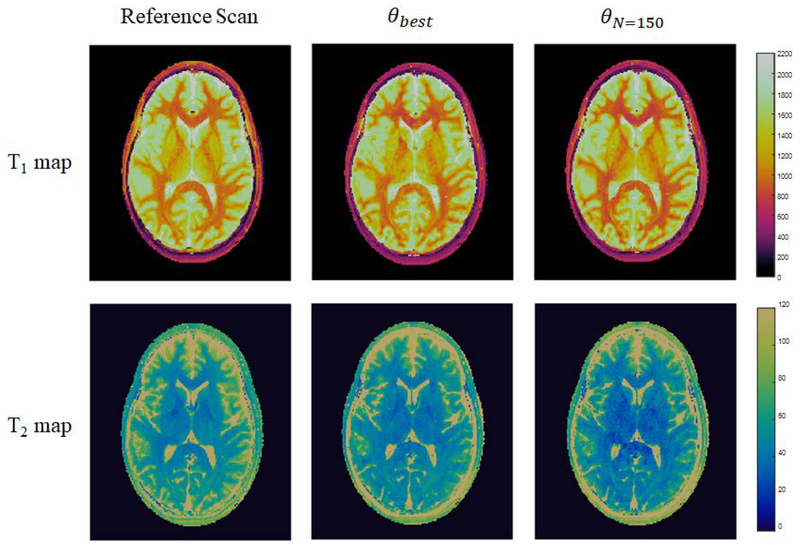
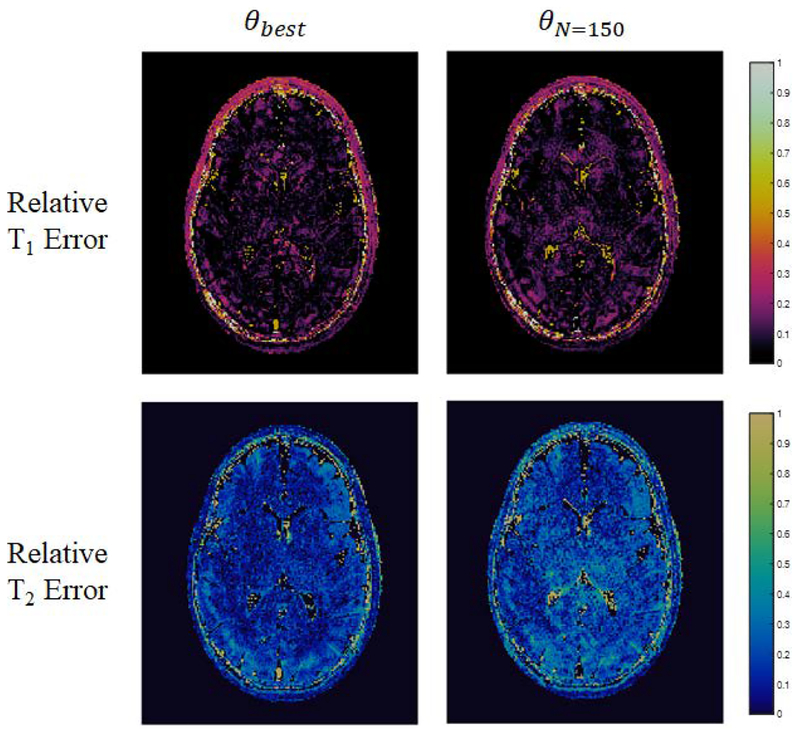
The results of in vivo experiments using the 250 step θ_best based on Sommer et al. and the 150 step θ_N=150 derived through quality factor maximization are presented. As a representative example for the case where the aliasing noise term is expected to dominate Eq. [5] based on the findings of Optimization Experiments: Phantom Data, all presented results were obtained with an acceleration factor R=12. Parameter maps from experiments using θ_best and θ_N=150, as well as reference maps from a FISP-MRF scan based on Jiang et al., are presented in Fig. [7]. Relative error maps from experiments using θ_best and θ_N=150 compared to the reference maps are presented in Fig. [8]. Both the parameter maps and the relative error maps demonstrate the expected comparable mapping capabilities of θ_best and θ_N=150. The results of nRMSE and ROI analysis on maps from the two sequences, detailed in Table [1], further demonstrate the comparable performance of the 150 step experiment to the 250 step experiment in terms of mean and standard deviation relaxation time values. White matter and gray matter ROI analysis on parameter maps from both sequences are in agreement with the reference maps and in agreement with literature values [29]. In addition, θ_best and θ_N=150 are found to have comparable nRMSE in both T₁ (0.09, 0.10) and T₂ (0.15, 0.22). Due to its comparable performance and decreased scan time, the results of the in vivo experiments with θ_N=150 continue to demonstrate the utility of the quality factor framework in designing efficient MRF experiments.

Figure 7.

In vivo T₁ and T₂ maps from experiments using θ_best and θ_N=150, as well as reference maps from a FISP-MRF scan based on Jiang et al., demonstrating the expected comparable mapping capabilities of θ_best and θ_N=150.

Figure 8.

Relative error maps from experiments using θ_best and θ_N=150 compared to a reference scan based on Jiang et al., demonstrating the expected comparable mapping capabilities of θ_best and θ_N=150.

Discussion

In this work, the genetic algorithm was chosen for aliasing noise quality factor optimization, with an initial population of 900 sequences. Optimization was initially performed with N=250, reaching agreement with the already optimized θ_best as determined by Sommer et al. within the first iteration (approximately 1 minute). Convergence to a result similar in encoding capability to θ_best on this first iteration was anticipated due to the similarity between our initial population and the population of sequences tested by Sommer et al. Allowing further iteration, the optimization produced sequences with incremental improvements over the best sequence at the initial iteration, producing an MRF sequence leading to an approximately 20% improvement in forecasted error relative to θ_best. This result suggests two advantages of the quality factor framework in MRF sequence evaluation and optimization. Due to this demonstrated ability to quickly evaluate given MRF sequences, the quality factor framework is expected to provide significant advantages in computation time compared to other, trial and error approaches. In addition, while trial and error approaches are limited to the initial population of MRF sequences, optimizations with our quality factors can produce effective sequences that are dissimilar from the initial population, and therefore do not require a priori knowledge.

To show the efficacy of our approach, optimization was performed for N=150, to determine a sequence with comparable error and therefore improved efficiency relative to the N=250 step experiment with θ_best. While still fast (1 minute), the initial iteration of the optimization over 150 steps did not yield a sequence with forecasted error comparable to the 250 step θ_best, suggesting that the initial population created with a colored noise generator did not contain the required qualities for an efficient MRF sequence. Therefore, the ability to diverge from the initial population provided by our quality factor framework was required to find an MRF sequence comparable to θ_best. As in the optimization over 250 steps, not having a priori information built into our initial population did not affect the capability of the quality factor approach to find an efficient MRF sequence; however, thousands of iterations (approximately 26 hours) were required to find θ_N=150.

The flip angle distribution optimized for aliasing noise (θ_N=150) is observed to contain some rapid variation, resulting in a correspondingly varying signal time course (see Fig. [1]). In contrast to the common belief that MRF sequences should be smoothly varying [11][16], this result suggests that while flip angle distributions used in MRF with undersampling should not contain significant and very rapid variations to prevent the unequal weighting of aliasing noise at various time steps, some controlled rapid variations in the flip angle distribution may be beneficial.

The error assessment and optimization in this work has been focused on comparisons with the MRF sequences presented in Sommer et al. For example, we find a 150-step sequence that performs as well as the best, 250-step sequence found with Monte Carlo methods at equal acceleration factors, and, therefore, θ_N=150 is more efficient than θ_best. Short sequences at lower acceleration factors may not be as efficient as longer sequences at higher acceleration factors. This decreased efficiency can be mitigated, for example, in multi-slice imaging where the wait time between k-space acquisitions can be used to acquire data in other slices. In addition, sequences with fewer steps, are expected to be useful in specialized applications, for example in imaging patients for whom breath holds are challenging.

As an example, it is of interest to discuss experiments with the standard 1000-step distribution based on Jiang et al. acquired at R=48. At lower acceleration factors (R=12), the short sequences (θ_N=150 and θ_best) have comparable T1 and T2 mapping error to the standard sequence performed at R=48, as evidenced by both the phantom and the in vivo data presented herein (Fig. [6b], Table 1). Although θ_N=150 and θ_best have fewer time steps than the standard sequence, necessary wait times between the k-space trajectories, required to achieve the reduced acceleration factor, result in a less efficient scan in terms of total sequence duration. However, outside the aforementioned focus of this work, our quality factors can be employed to find new distributions with increased efficiency relative to the standard sequence. In an example, the presented framework has been used to find a flip angle distribution with 500 time steps, achieving higher q₁ (reduced T₁ mapping error) and comparable q₂ (comparable T₂ mapping error) relative to the standard sequence in [20]. Other examples employing our quality factors to analyze and optimize MRF sequences with larger number of time steps have been reported in [23][31][32].

Results in this work demonstrate that the aliasing noise term dominates Eq. [5] for acceleration factors R=12 and above. Parameter map error is found to be in very good agreement with the relationship in Eq. [8] for acceleration factors between R=12 and 24; however, at the highest available acceleration factor in this work, R=48, deviations from the derived model arise (see Fig. [4]). These deviations are believed to result, in part, from the first-order approximation of the aliasing noise taken in the quality factor derivation, which is not accurate for the large aliasing artifacts (approximately equal to the signal amplitude) present in the undersampled data for R=48. Therefore, at very large acceleration factors, the derived parameter map model in terms of aliasing noise quality factors is an appropriate guide in forecasting the parameter map error of an MRF sequence, serving as a first approximation to the true, more complicated relationship. Further investigation into improving the derived quality factor model for very large acceleration factors will be a topic for future work.

While the quality factors defined by Eqs. [6–7] are specific to T₁ and T₂ mapping, there are several additional imaging parameters that can be mapped with MRF. In addition to off-resonance frequency mapping, which is necessary in bSSFP-MRF, MRF has expanded into the quantification of properties such as B₁⁺ [24][33][34] and diffusion parameters [35][36]. Therefore, broadening the quality factor framework to include these additional parameters is of great interest.

Because the quality factor framework derived herein is based on the theory of small perturbations to a system, specifically those arising from TR/T_i << 1, the expansion of quality factors to include a third mapping parameter is straightforward if the added parameter of interest can also be modeled as a small perturbation. For example, initial investigations have successfully quantified the error in T₁, T₂, and B₁⁺ mapping when the flip angle distribution is required to be small (<15°). Alternatively, an expansion can be made assuming a small variation about a central value of B₁⁺. Then quality factors can be calculated at various central B₁⁺ values to analyze mapping capability over a large range in B₁⁺ values, analogous to the procedure for comparing quality factors over a large range of relaxation times used in this work. In addition, initial investigation into the application of quality factors to T₁, T₂, and ADC mapping is promising. However, more work is required for a robust expansion of the quality factor framework to include added properties such as off-resonance frequency and B₁⁺, which in general do not produce small perturbations to the system.

Conclusion

In this work, quality factors for the assessment of MRF pulse sequence designs in the presence of normal noise and aliasing artifacts were derived, tested, and shown to accurately forecast parameter map error. Due to quality factor dependence on the MRF signal, optimized MRF sequences can be rapidly evaluated and optimized relative to normal and aliasing noise through quality factor maximization, to yield efficient MRF experiments.

Appendix

Quality Factor Derivation

With presented models for the dictionary entries and acquired signal, as detailed in the theory section,

$$\mathbf{d}\left({\text{R}}_1,{\text{R}}_2\right)\approx {\mathbf{d}}_0+{\mathbf{c}}_1\left({\text{R}}_1-{\text{R}}_{1,0}\right)+{\mathbf{c}}_2\left({\text{R}}_2-{\text{R}}_{2,0}\right)$$

$$\mathit{s}={\mathit{d}}_0+\mathit{\eta }+\mathit{\alpha }$$

the initial step in our quality factor derivation involves noting that matching through maximization of the complex dot product implies that the derivative of the dot product between the normalized signal and the matched normalized dictionary entry will be zero:

$$\underset{R_1,R_2}{\text{max}}\left|\widehat{s}\cdot {\widehat{D}}^{*}\right|\to \frac{\partial }{\partial R_i}\left|\widehat{s}\cdot \widehat{d}{\left(R_1,R_2\right)}^{*}\right|=0$$

$$\Rightarrow \text{Re}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)\frac{\partial }{\partial R_i}\text{Re}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)+\text{Im}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)\frac{\partial }{\partial R_i}\text{Im}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)=0$$ (A.1)

In a FISP-MRF experiment where spoiler gradients are applied at the end of each TR to create a phase twist greater than 2π in the slice select direction and excitation pulses are applied along a single axis (ex. along x), the complex signal (d = d_x + id_y) will be dominated by either the real or the imaginary component (ex. d ≈ id_y). Therefore, the imaginary components of Eq. [A.1] vanish, leaving

$$\frac{\partial }{\partial R_i}\left|\widehat{s}\cdot \widehat{d}{\left(R_1,R_2\right)}^{*}\right|\approx \text{Re}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)\frac{\partial }{\partial R_i}\text{Re}\left(\widehat{s}\cdot {\widehat{d}}^{*}\right)=0(\text{single excitation axis FISP-MRF})$$ (A.2)

For ease of notation, now let (a⋅b*) indicate the real part of the complex dot product. Using Eq. [A.2] and noting that s is related to the ground truth relaxation rates (R_1,0 and R_2,0), and thus independent of R_i, to first order in R_i and R_j we find,

$$\frac{1}{\left|\mathit{s}\right||\mathit{d}{|}^3}\left[|\mathit{d}{|}^2\left(\mathit{s}\cdot {{\mathit{c}}_i}^{*}\right)-\left(\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)+{c_i}^2\left({\text{R}}_{\text{i}}-{\text{R}}_{\text{i},0}\right)+\left({\mathit{c}}_i\cdot {{\mathit{c}}_j}^{*}\right)\left({\text{R}}_{\text{j}}-{\text{R}}_{\text{j},0}\right)\right)\left(\mathit{s}\cdot {\mathit{d}}^{*}\right)\right]=0$$ (A.3)

Using Eq. [2] to write Eq. [A.3] in terms of d₀, c_i, c_j, η, and α, keeping only first order terms in R_i, R_j, η, and α:

$$\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)\left[\left(\mathit{\eta }\cdot {{\mathit{d}}_0}^{*}\right)+\left(\mathit{\alpha }\cdot {{\mathit{d}}_0}^{*}\right)\right]-{d_0}^2\left[\left(\mathit{\eta }\cdot {{\mathit{c}}_i}^{*}\right)+\left(\mathit{\alpha }\cdot {{\mathit{c}}_i}^{*}\right)\right]=a_i\left({\text{R}}_{\text{i}}-{\text{R}}_{\text{i},0}\right)+b\left({\text{R}}_{\text{j}}-{\text{R}}_{\text{j},0}\right)$$ (A.4)

With

$$a_i={\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)}^2-{d_0}^2{c_i}^2$$

$$b=\left({\mathit{d}}_0\cdot {{\mathit{c}}_1}^{*}\right)\left({\mathit{d}}_0\cdot {{\mathit{c}}_2}^{*}\right)-{d_0}^2\left({\mathit{c}}_1\cdot {{\mathit{c}}_2}^{*}\right)$$

Using the two equations (i=1,2 and j=2,1) to solve for (R₁ – R_1,0) and (R₂ – R_2,0):

$$\left[a_i{a}_j-b\right]\left({\text{R}}_{\text{i}}-{\text{R}}_{\text{i},\text{0}}\right)=-{d_0}^2\left[a_j\left(\left(\mathit{\eta }\cdot {{\mathit{c}}_i}^{*}\right)+\left(\mathit{\alpha }\cdot {{\mathit{c}}_i}^{*}\right)\right)-b\left(\left(\mathit{\eta }\cdot {{\mathit{c}}_j}^{*}\right)+\left(\mathit{\alpha }\cdot {{\mathit{c}}_j}^{*}\right)\right)+{\gamma }_i\left(\left(\mathit{\eta }\cdot {{\mathit{d}}_0}^{*}\right)+\left(\mathit{\alpha }\cdot {{\mathit{d}}_0}^{*}\right)\right)\right]$$ (A.5)

Where

$${\gamma }_i={c_j}^2\left({\mathit{d}}_0\cdot {{\mathit{c}}_i}^{*}\right)-\left({\mathit{c}}_i\cdot {{\mathit{c}}_j}^{*}\right)\left({\mathit{d}}_0\cdot {{\mathit{c}}_j}^{*}\right)$$

Because ω and α have zero mean and are uncorrelated, averaging Eq. [A.5] over the time-step population yields a vanishing result on the right-hand side of the equation, leading to R₁=R_1,0. Averaging over the square of both sides leads to the following variance relationships:

$$\text{Var}[LHS[A.5]]={{\sigma }_{R_i}}^2{\left[a_i{a}_j-b\right]}^2$$ (A.6)

$$\text{Var}[RHS[A.5]]={d_0}^4\langle {\left(a_j\left(\mathit{\eta }\cdot {{\mathit{c}}_i}^{*}\right)-b\left(\mathit{\eta }\cdot {{\mathit{c}}_j}^{*}\right)+{\gamma }_i\left(\mathit{\eta }\cdot {{\mathit{d}}_0}^{*}\right)\right)}^2\rangle +{d_0}^4\langle {\left(a_j\left(\mathit{\alpha }\cdot {{\mathit{c}}_i}^{*}\right)-b\left(\mathit{\alpha }\cdot {{\mathit{c}}_j}^{*}\right)+{\gamma }_i\left(\mathit{\alpha }\cdot {{\mathit{d}}_0}^{*}\right)\right)}^2\rangle$$ (A.7)

In general, for vectors u = iu_y and ν = iν_y with vanishing real components and Gaussian white noise η with 〈(η)_m(η)_n〉 = σ_η²δ_m,n:

$$\langle \left(\mathit{\eta }\cdot {\mathit{u}}^{*}\right)\left(\mathit{\eta }\cdot {\mathit{v}}^{*}\right)\rangle ={\sum }_{m,n}\langle {\left({\mathit{\eta }}_y\right)}_m{\left({\mathit{\eta }}_y\right)}_n\rangle {\left({\mathit{u}}_y\right)}_m{\left({\mathit{v}}_y\right)}_n={\sum }_{m,n}{{\sigma }_{\eta }}^2{\delta }_{m,n}{\left({\mathit{u}}_y\right)}_m{\left({\mathit{v}}_y\right)}_n={{\sigma }_{\eta }}^2\left(\mathit{u}\cdot {\mathit{v}}^{*}\right)$$

In the case of aliasing noise with (α)_n = |(d₀)_n|(ω)_n and 〈(ω)_m(ω)_n〉 = σ_ω²δ_m,n:

$$\begin{gathered} \langle \left(\mathit{\alpha }\cdot {\mathit{u}}^{*}\right)\left(\mathit{\alpha }\cdot {\mathit{v}}^{*}\right)\rangle ={\sum }_{m,n}\langle {\left({\mathit{\alpha }}_y\right)}_m{\left({\mathit{\alpha }}_y\right)}_n\rangle {\left({\mathit{u}}_y\right)}_m{\left({\mathit{v}}_y\right)}_n \\ ={\sum }_{m,n}|{\left({\mathit{d}}_0\right)}_m\Vert {\left({\mathit{d}}_0\right)}_n|\langle {(\mathit{\omega })}_m{(\mathit{\omega })}_n\rangle {\left({\mathit{u}}_y\right)}_m{\left({\mathit{v}}_y\right)}_n \\ ={\sum }_{m,n}{{\sigma }_{\omega }}^2{\delta }_{m,n}|{\left({\mathit{d}}_0\right)}_m\Vert {\left({\mathit{d}}_0\right)}_n|{\left({\mathit{u}}_y\right)}_m{\left({\mathit{v}}_y\right)}_n={{\sigma }_{\omega }}^2{\sum }_n{\left|{\left({\mathit{d}}_0\right)}_n\right|}^2({(\mathit{u})}_n\cdot {{(\mathit{v})}_n}^{*}) \end{gathered}$$

Therefore, we find

$$\text{Var}[RHS[A.5]]={{\sigma }_{\eta }}^2{d_0}^2{a}_j\left(a_i{a}_j-b^2\right)+{{\sigma }_{\omega }}^2{d_0}^4{\sum }_n{\left|{\left({\mathit{d}}_0\right)}_n\right|}^2{\left(a_j{\left({\mathit{c}}_i\right)}_n-b{\left({\mathit{c}}_j\right)}_n+{\gamma }_i{\left({\mathit{d}}_0\right)}_n\right)}^2$$ (A.8)

Finally, combining Eqs. [A.6] and [A.8],

$${{\sigma }_{R_{\text{i}}}}^2=\frac{{{\sigma }_{\eta }}^2}{Q_i}+\frac{{{\sigma }_{\omega }}^2}{q_i}i=1,2$$

With the quality factors relating to thermal noise given by

$$Q_i=\frac{a_i{a}_j-b^2}{{d_0}^2{a}_j}i=1,2j=2,1$$

And the quality factors relating to aliasing noise given by

$$q_i=\frac{{\left(a_i{a}_j-b^2\right)}^2}{{d_0}^4{\mathrm{\Sigma }}_{n=1}^N|{\left({\mathit{d}}_0\right)}_n{|}^2{\left(a_j{\left({\mathit{c}}_i\right)}_n-b{\left({\mathit{c}}_j\right)}_n+{\gamma }_i{\left({\mathit{d}}_0\right)}_n\right)}^2}i=1,2j=2,1$$