Decorrelating Kinetic and Relaxation Parameters in Exchange Saturation Transfer NMR: A Case Study of N‑Terminal Huntingtin Peptides Binding to Unilamellar Lipid Vesicles

ABSTRACT:

Dark state exchange saturation transfer (DEST) and lifetime line-broadening (ΔR₂, the difference in the measured transverse relaxation rates for the observable species in the presence and absence of exchange with a species characterized by very large intrinsic transverse relaxation rates) have proven to be powerful NMR tools for studying exchange phenomena between a NMR visible species and a high-molecular weight, “dark”, NMR invisible state. However, in the exchange regime, where the transverse spin relaxation rates in the bound state $\left({\text{R}}_{\text{2}}^{\text{bound}}\right)$ are smaller than the strength of the DEST saturation radio frequency field, typically corresponding to systems below ∼6 MDa, the combination of DEST and ΔR₂ data, while sufficient to define the apparent association rate unambiguously constant, cannot determine the population of the bound state p_B and ${\text{R}}_{\text{2}}^{\text{bound}}$ values independently. We show that the latter exchange and relaxation parameters can be decorrelated by the measurement of the maximal value of the contribution of the fast-relaxing magnetization component to the total NMR signal, ${\text{C}}_{\text{fast}}^{\text{max}}$ , an observable that is directly proportional to p_B. When integrated into the analysis of DEST/ΔR₂ data, ${\text{C}}_{\text{fast}}^{\text{max}}$ provides an indispensable source of information for quantitative studies of exchange involving high-molecular-weight dark states. We demonstrate the utility of this approach by investigating the binding kinetics of two huntingtin exon-1-derived peptides to small unilamellar lipid vesicles (SUV), ∼ 31 nm in diameter and 4.3 MDa in molecular weight. The interaction of the N-terminal amphiphilic domain of huntingtin exon-1 with membrane surfaces promotes polyglutamine-mediated aggregation and, as such, is thought to play a role in the etiology of Huntington’s disease, an autosomal dominant fatal neurodegenerative condition. The first peptide comprises the 16-residue N-terminal amphiphilic domain (htt^NT) alone, while the second contains an additional seven residue polyglutamine tract at the C-terminus (htt^NTQ₇). At a peptide-to-lipid molar ratio of 1:4, the population of peptide bound to the SUV surface is substantial, ∼ 7−8%, while exchange between the free and SUV-bound peptide is slow on the relaxation time-scale (k_ex ∼ 200 s⁻¹). The last two C-terminal residues of htt^NT and the last 9 of htt^NTQ₇ remain flexible in the SUV-bound form due to transient detachment from the lipid surface that occurs on a time-scale several-fold faster than binding.

Graphical Abstract

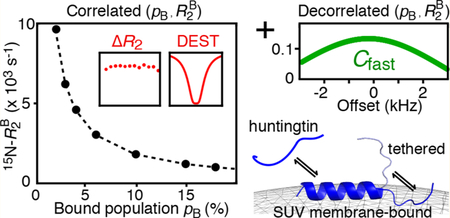
INTRODUCTION

Dark state exchange saturation transfer (DEST) and lifetime line broadening (ΔR₂) provide a powerful means of probing exchange dynamics and atomic resolution dynamics involving the interaction of a NMR visible species with a very high-molecular weight NMR invisible “dark” state.^1,2 (Note that ΔR₂ is defined as the difference in transverse relaxation rates measured on the observable species in the presence and absence of exchange, arising from a significantly higher intrinsic transverse relaxation rate in the “dark” state.) Typically, DEST profiles acquired at two radio frequency (RF) saturation fields and ΔR₂ values measured at two static spectrometer fields are analyzed together with the aim of quantitatively describing the exchange equilibrium in question; namely, extracting the rate constants of all involved processes, the populations of all states, and the residue-specific transverse spin relaxation rates of the minor, “dark” species.³ Initial applications of the DEST/ΔR₂ methodology focused on exchange between monomeric amyloid-β peptides free in solution and bound to the surface of amyloid-β protofibrils.^1,2,4 More recent examples have involved the interaction of intrinsically disordered peptides and small protein domains with the ∼800 kDa chaperonin GroEL.^5–7 In these latter studies, however, full characterization of the exchanging system required supplementing the DEST and ΔR₂ data with exchange-induced chemical shift and/or Carr−Purcell−Meiboom−Gill (CPMG) relaxation dispersion measurements. ^8–10 In this article, we illustrate some limitations of the DEST/ΔR₂ methodology in applications involving exchanging systems with medium-sized dark states (1−6 MDa), provide a semiquantitative explanation of their origin, and describe the manner and conditions under which these limitations can be overcome.

Here we focus on the characterization of the binding kinetics of two peptides derived from exon-1 of the huntingtin gene (htt) to unilamellar lipid vesicles. Polyglutamine expansion of more than 35 glutamines, immediately C-terminal to the 16-residue N-terminal amphiphilic sequence (htt^NT), results in a fatal neurodegerative condition known as Huntington’s disease.¹¹ The two peptides are htt^NT and htt^NTQ₇, the latter containing a seven-residue glutamine repeat. Interaction of the htt^NT domain with membrane surfaces promotes polyglut-amine-mediated aggregation.^12,13 Recently, we showed, using chemical exchange saturation transfer (CEST) NMR and Q-band-pulsed electron paramagnetic resonance (EPR), that both peptides form a well-defined α-helical structure when bound to lipid micelles and, in addition, can dimerize in the bound state.¹⁴ As small unilamelar lipid vesicles (SUV) have a molecular weight of ∼4.3 MDa and are ∼4-fold larger in diameter than micelles (∼31 versus ∼8 nm), the same experimental approach cannot be used to study the exchange of htt^NT and htt^NTQ₇ with their SUV-bound form, and hence, experiments such as DEST and ΔR₂ are required. However, in the exchange regime where the transverse spin relaxation rate $R_2^B$ of the bound state is smaller than the strength of the RF saturation field, DEST and ΔR₂ data are only sensitive to the product of $R_2^B$ and the population p_B of the bound state, and hence, $R_2^B$ and p_B cannot be determined independently. We show that this problem can be resolved by supplementing the DEST and ΔR₂ data with the measurement of residue-specific maximal (on-resonance) values of the contribution of the fast-relaxing component of magnetization, ${\text{C}}_{\text{fast}}^{\text{max}}$ , to the total NMR signal undergoing slow chemical exchange.¹⁵ As ${\text{C}}_{\text{fast}}^{\text{max}}$ provides a good measure of p_B, simultaneous analysis of DEST, ΔR₂, and ${\text{C}}_{\text{fast}}^{\text{max}}$ allows p_B and $R_{\text{2}}^{\text{B}}$ to be decorrelated from one another. In the absence of other experimental data on the exchanging system under consideration, such as chemical exchange induced shifts and/or CPMG relaxation dispersions,^5,7 which may not be readily available for systems in exchange with very high-molecular weight (>1 MDa) dark states, ${\text{C}}_{\text{fast}}^{\text{max}}$ serves as a valuable addition to the array of existing NMR observables that report on the parameters of exchange involving NMR-dark systems.

EXPERIMENTAL SECTION

Expression and Purification of htt^NTQ_n Peptides.

Huntingtin exon-1 peptides htt^NTQ_n (n = 0 or 7, where n is the number of C-terminal polyglutamine repeats) were expressed and ¹⁵N-labeled in E. coli as GB1−htt^NTQ_n fusion proteins and purified as described previously.¹⁴ NMR samples comprised uniformly ¹⁵N-labeled peptides at a final concentration of 300 μM (after the addition of liposome solutions). All NMR samples were prepared in 20 mM phosphate buffer (Na₂HPO₄/NaH₂PO₄) pH 6.5, 50 mM NaCl, and 10% D₂O/ 90% H₂O (v/v). Peptide concentrations were determined by UV absorption at a wavelength of 205 nm.¹⁶

Preparation and Characterization of SUVs.

The sodium salts of 1-palmitoyl-2-oleoyl-sn-glycero-3-phospho(1′-rac-glycerol) (POPG), 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC), and cholesterol were purchased from Avanti Polar Lipids (Alabaster, AL). SUV particles were prepared by dissolving the same amount (35% mol/mol) of POPG and POPC in a round-bottom flask. Cholesterol (30% mol/mol) was added to the lipid mixture to reduce the permeability of vesicles upon htt^NTQ_n binding.¹³ Homogenous SUV preparations were obtained by sonication as described previously.¹⁷ The size distribution of the SUV particles (mean diameter ∼31 nm with a polydispersity index PDI = 0.22) was obtained on 1 mM samples (in lipids) at 10 °C from analysis of dynamic light scattering (DLS) data obtained with a Zetasizer Nano ZS (Malvern Instruments, 4 mW He−Ne laser, λ₀ = 633 nm, θ = 173°).

NMR Measurements.

NMR experiments were recorded at 10 °C using a Bruker Avance-III spectrometer equipped with a TCI z-axis gradient cryogenic probe operating at a ¹H Larmor frequency of 600.82 MHz. All measurements were performed on a 300 μM htt^NTQ_n (n = 0 or 7) peptide in the presence of SUVs at a 1:4 peptide:lipid molar ratio. On-resonance ¹⁵N-R_1ρ measurements were carried out using the pulse sequence described by Yuwen et al.¹⁵ A ¹⁵N spin-lock field strength of 2.0 kHz was applied for spin-lock durations (T_relax) of 20, 40, 60, 80, and 100 ms. The values of the constant time during which longitudinal relaxation occurs (T_relax,max) and the equilibration delay (τ_ex) were set to 120 and 50 ms, respectively. A reference spectrum (T_relax = 0) was acquired with the ¹⁵N spin-lock as well as adiabatic half-passage (AHP) pulses prior to and after each spin-lock period omitted. Two spin-lock elements were used in each relaxation delay (see the pulse-scheme in Figure S5 of Yuwen et al.¹⁵), effectively amplifying the value of ${\text{C}}_{\text{fast}}^{\text{max}}$ approximately 2-fold. Each 2D experiment comprised 128* × 512* complex points in the indirect (¹⁵N) and direct (¹H) dimensions, respectively. Sixty-four scans per increment, with an interscan delay of 2.5 s, were used, resulting in a total acquisition time of ∼11.4 h per 2D experiment. The values of ${\text{C}}_{\text{fast}}^{\text{max}}$ were measured by extrapolation of the exponential decays to time zero.¹⁵ The values of T_relax were corrected for the duration of the two AHP pulses (2.4 ms total). ¹⁵N-R₂ values for the htt^NTQ_n peptides in the absence and presence of SUVs were obtained from ¹⁵N-R_1ρ and R₁ measurements recorded at both 600 and 800 MHz as described previously.^6,17 ΔR₂ values were calculated as the difference between ¹⁵N-R₂ values obtained in the presence and absence of SUVs.

Two-dimensional ¹⁵N-DEST measurements were performed by applying continuous wave (CW) saturation at RF field strengths of 500 and 750 Hz for a duration of 0.7 s at the following offsets from the carrier frequency (in kHz): −22.0, −20.0, −18.0, −16.0, −14.0, −12.0, −10.0, −8.0, −6.0, −5.0, −4.0, −3.0, −2.0, −1.0, −0.5, 0.0, 0.5, 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0, 18.0, 20.0, and 22.0. The carrier was set to 121.5 ppm for ¹⁵N and 4.7 ppm for ¹H. Reference experiments were performed applying the same RF field strengths but with the offset moved to −1 MHz. A total of 110* × 512* complex data points were acquired in the indirect (¹⁵N) and direct (¹H) dimensions with respective acquisition times of 71 and 64 ms, resulting in a total measurement time of ∼3 h per 2D experiment.

NMR spectra were processed with the nmrPipe/nmrDraw suite of programs, and uncertainties in the extracted relaxation rates were estimated from Monte Carlo simulations.¹⁸

Simultaneous Analysis of 15N-DEST, ΔR₂, and ${\text{C}}_{\text{fast}}^{\text{max}}$ Data.

All experimental data (¹⁵N- DEST, ΔR₂, and ${\text{C}}_{\text{fast}}^{\text{max}}$) were fit simultaneously by minimizing the following error function:

$$\begin{gathered} F={\alpha }_1{{\displaystyle \sum _i\left(\frac{\Delta R_{\text{2}}^{\text{obs,}i}-\Delta R_{\text{2}}^{\text{calc,}i}}{{\sigma }_{\Delta R_2}^i}\right)}}^{\text{2}} \\ \hspace{1em}\hspace{1em}+{\alpha }_2{\displaystyle \sum _i{\displaystyle \sum _k{\displaystyle \sum _{j=1}^{\text{2}}{\left(\frac{K_{\text{DEST}}^{\text{obs,}i,k,j}-K_{\text{DEST}}^{\text{calc,}i,k,j}}{{\sigma }_{{}^K}^i}\right)}^2}}} \\ \hspace{1em}\hspace{1em}+{\alpha }_3{{\displaystyle \sum _i\left(\frac{{\text{C}}_{\text{fast}}^{\max ,\text{obs,}i}-{\text{C}}_{\text{fast}}^{\max ,\text{calc,}i}}{{\sigma }_{{}^{{\text{C}}_{f\text{ast}}^{\text{max}}}}^i}\right)}}^{\text{2}} \end{gathered}$$ (1)

where the first term accounts for the ΔR₂ data, the second for the DEST normalized intensities κ, and the third for ${\text{C}}_{\text{fast}}^{\text{max}}$ . The indices i, k, and j refer to the residue number, DEST offset, and saturation RF field strength (500 and 750 Hz), respectively; α₁₋₃ represent empirically determined factors used to appropriately weight the different data types and have values of 3, 0.5, and 1000, respectively; and σ denotes the uncertainty of each data type. The high value of the weighting factor used for the term that accounts for ${\text{C}}_{\text{fast}}^{\text{max}}$ in eq 1 is justified by the apparent absence of contradictions between the information content of ${\text{C}}_{\text{fast}}^{\text{max}}$ and the other two types of data, i.e., the information content of the DEST/ΔR₂ data may be considered to be “separated” from that of ${\text{C}}_{\text{fast}}^{\text{max}}$. The set of global variable parameters for the ${\text{P}}_{\text{coil}}^{\text{A}}\rightleftharpoons {\text{P}}_{\text{helical}}^{\text{B}}$ interconversion comprised $\left\{k_1=k_{\text{on}}^{\text{app}};p_{\text{B}}\right\}.$ The set of global variable parameters for the ${\text{P}}_{\text{coil}}^{\text{A}}\rightleftharpoons {\text{P}}_{\text{tethered}}^{\text{B}}$ equilibrium comprised $\left\{k_{\text{on}}^{\text{overall}};k_{\text{off}}^{\text{overall}}\right\}.$ The uncertainties in the values of the optimized parameters, corresponding to confidence intervals of ±1 standard deviation, were determined from the variance−covariance matrix of the nonlinear fits. Minimization of the error function F was performed using an in-house Matlab program (Math-Works Inc., MA).

RESULTS AND DISCUSSION

Problem of Correlated Parameters in DEST/ΔR₂ Analysis of Exchange Data.

The first applications of the DEST/ΔR₂ methodology focused on systems where the transverse relaxation rate of the “dark” state, $R_{\text{2}}^{\text{B}}$ , was very large, typically reaching tens of thousands per second, so that $R_{\text{2}}^{\text{B}}$ ≫ 2πω₁, where ω₁ is the strength of the applied RF field in the DEST experiments, with saturation RF field strengths typically not exceeding ∼750 Hz (∼4700 rad/s).^1,2,4 The very high transverse relaxation rates in the dark state ensured that accurate kinetic parameters of exchange, as well as the $R_{\text{2}}^{\text{B}}$ values themselves, could be extracted from the combined analysis of DEST profiles acquired at two RF field strengths and ΔR₂ profiles acquired at two spectrometer fields. When the DEST/ΔR₂ methodology is applied to exchanging systems with $R_{\text{2}}^{\text{B}}$ ≪ 2πω₁, such as complexes of the 800 kDa chaperonin GroEL with amyloid-β peptide⁵ and Fyn-SH3 domains,^6,7 where the typical average ¹⁵N-$R_{\text{2}}^{\text{B}}$ value is ∼900 s⁻¹ (at 10 °C and 900 MHz spectrometer field) and the lowest ω₁ field strength is typically ∼500 Hz (∼3140 rad/s), simultaneous extraction of the kinetic parameters of exchange (namely, the dissociation rate constant, k_off, and consequently the population of the dark, bound state, p_B) together with the $R_{\text{2}}^{\text{B}}$ values in the bound state is no longer possible without additional information. The latter can come, for example, from CPMG relaxation dispersion and exchange-induced chemical shift measurements.^5–7 In terms of data modeling, the problem boils down to the high degree of correlation between the fitted parameters, p_B ∼ 1/k_off and $R_{\text{2}}^{\text{B}}$, so that only a quantity proportional to the product p_B $R_{\text{2}}^{\text{B}}$ can be derived from analysis of the DEST/ΔR₂ data.

Exactly the same underlying problem is apparent in the current studies of the binding of huntingtin exon-1 peptides, htt^NT and htt^NTQ₇, to SUV lipid vesicles. The SUVs used here are 31 nm in diameter and have a molecular weight of ∼4.3 MDa, and exchange arising from the binding is slow on both the chemical shift and relaxation time scales. For this particle size range and exchange regime, CPMG dispersion and exchange-induced shift data, even in the presence of large differences in chemical shifts between free and bound states of the peptides, are of little utility as their magnitudes are predicted to be unmeasurably small.

Examples of ¹⁵N-DEST profiles for Lys⁵ and Ser¹² of htt^NT in the presence of SUVs at two RF field strengths are shown in Figure 1A, and ¹⁵N-ΔR₂ profiles for both htt^NT and htt^NTQ₇ are displayed in Figure 1B. With the exception of the C-terminal residues (15−16 for htt^NT and 15−23 for htt^NTQ₇ are displayed in Figure 1B. With the exception of the C-terminal residues (15−16 for htt^NT and 15−23 for htt^NTQ₇ that require a separate treatment), the ¹⁵N-DEST and ΔR₂ data for residues 3−14 can be well fit simultaneously to a two-state exchange model between free (A) and bound (B) states (Scheme 1) by propagation of a set of Bloch-McConnell differential equations¹⁹ to yield apparent association rates, $k_{\text{on}}^{\text{app}}$, of 14.1 ± 0.03 and 17.1 ± 0.05 s⁻¹ for htt^NT and htt^NTQ₇, respectively. However, the dissociation rate constant (k_off), and hence p_B, as well as the residue specific $R_{\text{2}}^{\text{B}}$ values are associated with very large uncertainties. This is due to the fact that the ¹⁵N-DEST/ΔR₂ data can be fit equally well (with practically the same value of the resulting χ²) by a continuum of {p_B;$R_{\text{2}}^{\text{B}}$} combinations, as shown in Figure 2, where a series of fits were performed with p_B fixed at different values (x-axis), and the resulting average $R_{\text{2}}^{\text{B}}$ values, ${\langle }^{15}\text{N-}{R}_2^{\text{B}}\rangle$, are plotted on the y-axis.

Figure 1.

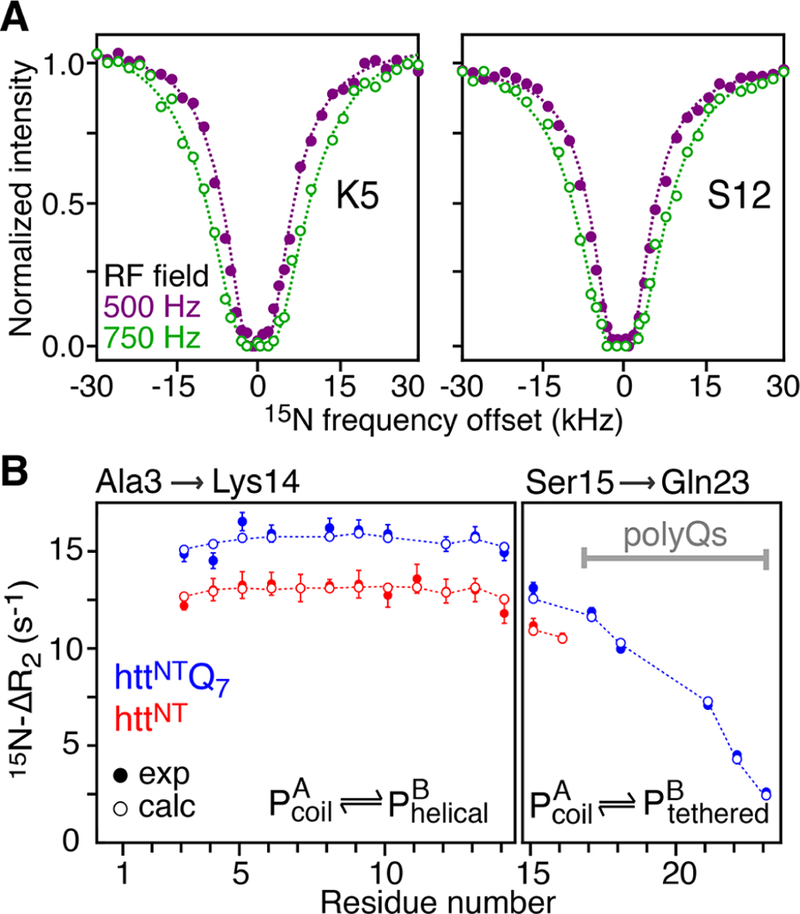
Binding of htt^NT and htt^NTQ₇ to SUVs characterized by relaxation-based NMR experiments. (A) Examples of ¹⁵N-DEST profiles acquired on Lys⁵ and Ser¹² of htt^NT in the presence of SUVs at RF field strengths of 500 and 750 Hz shown as filled-in purple and open green circles, respectively. (B) ¹⁵N-ΔR₂ profiles for htt^NT and htt^NTQ₇ in the presence of SUVs. Experimental data are shown as red and blue filled-in circles for htt^NT and htt^NTQ₇, respectively. Dashed lines in (A) and open circles in (B) represent best-fits of the ¹⁵N-DEST and ¹⁵N-ΔR₂ data to a two-state exchange model. Residues that do not fit well to this model and required a separate treatment (see text) are shown in the right panel. The data were recorded at 600 MHz and 10 °C on a 300 μM peptide sample in the presence of SUVs at a 1:4 molar ratio of peptide to lipid (on a lipid molecule basis).

Figure 2.

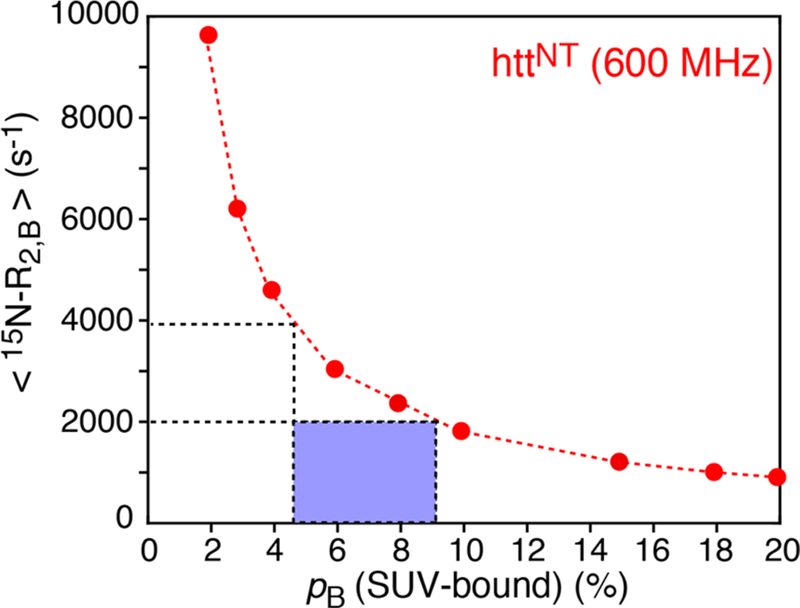
Average ${\langle }^{15}\text{N-}{R}_2^{\text{B}}\rangle$ values obtained from a fit of the ¹⁵N-DEST/ΔR₂ data of htt^NT in the presence of SUVs (600 MHz; 10 °C) to a two-state exchange model (y-axis), plotted versus the population of SUV-bound htt^NT (p_B) which was fixed in the fit (x-axis). For a particle of 31 nm in diameter, one can estimate a range of 4.5−9 μs for the rotational correlation time, corresponding to ⟨¹⁵N-$R_2^{\text{B}}$⟩ values of 2000−4000 s⁻¹. The bound population p_B for this range of ⟨¹⁵N‑$R_2^{\text{B}}$⟩ values spans ∼9−4.5% (enclosed in the blue box).

Thus, without prior knowledge of $R_{\text{2}}^{\text{B}}$, the value of p_B (and therefore k_off) cannot be determined unambiguously. Of note, the same indeterminacy was described in our earlier studies on the interaction of the Δ57^VPL mutant of the Fyn-SH3 domain with GroEL.⁷ The problem is akin to that arising with the interpretation of ΔR₂ data in the limit of fast exchange on the transverse relaxation time scale, where ΔR₂ = p_B $R_{\text{2}}^{\text{B}}$, and only the product of the two parameters can be extracted. Numerical simulations using synthetic data sets comprising well-digitized ¹⁵N-DEST profiles at three saturation field strengths and ΔR₂ at a single spectrometer field, generated using the parameters of exchange of htt^NT binding to SUVs with 1% random noise superimposed on the data, show that accurate values of p_B and $R_{\text{2}}^{\text{B}}$ can be reliably extracted from the DEST/ΔR₂ fits when $R_{\text{2}}^{\text{B}}$ is at least a factor of approximately four times higher than the maximal RF field strength used in the DEST experiments Β_1,max = 2πω_1,max (i.e., $R_{\text{2}}^{\text{B}}$ larger than ∼20 000 s⁻¹ for a maximal RF saturation field strength of 750 Hz). However, we would predict, on the basis of these simulations, that as long as $R_{\text{2}}^{\text{B}}$ just exceeds B_1,max ($R_{\text{2}}^{\text{B}}$ > 2πω_1,max) for high-quality ¹⁵N-DEST profiles acquired with at least two RF field strengths, the errors in the values of p_B, k_off, and $R_{\text{2}}^{\text{B}}$ will remain relatively small and likely within the uncertainties of the fit.

Given the molecular size of the SUVs, ${\langle }^{15}\text{N-}{R}_2^{\text{B}}\rangle$ is predicted to lie within a range of 2000−4000 s⁻¹, with values of 4.5−9% for p_B (as shown by the dashed lines and blue box in Figure 2). The corresponding range for k_off is ∼350−180 s⁻¹, indicating that exchange is slow on the relaxation time-scale, which is in agreement with the observed absence of the dependence of ΔR₂ on the static spectrometer field.

Quantitative Analysis and Resolution of the Uncertainties.

To gain deeper quantitative insight into the nature of the uncertainty described above, we draw an analogy with the recent work of Kay and co-workers,¹⁵ who probed a slowly exchanging system involving two unequally populated states of a protein via off-resonance R_1ρ experiments. In the limit where ω₁ ≫$R_{\text{2}}^{\text{B}}$ and in the absence of chemical shift differences between the interconverting species (Δω = 0), the 6 × 6 Bloch-McConnell exchange matrix describing the evolution of magnetization in a two-state system (Scheme 1) that exchanges slowly (ω₁ ≫ k_off) can be approximated by¹⁵

$$\frac{d}{dt}\left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]=-\lfloor \begin{array}{cc}{k}_{\text{on}}^{\text{app}}& -k_{\text{off}}\\ -k_{\text{on}}^{\text{app}}& k_{\text{off}}+R_2^B{\sin }^2\theta \end{array}\rfloor \left[\begin{array}{c}{M}^{\text{A}}\\ M^{\text{B}}\end{array}\right]$$ (2)

where M^A and M^B are the transverse magnetizations of states A (free) and B (bound), respectively, and θ is the angle between the spin-locked magnetization and the z-axis of the laboratory frame. The longitudinal relaxation rates of states A and B ($R_1^{\text{A}}$ and $R_1^{\text{B}}$) as well as the transverse relaxation rate of state A, $R_2^{\text{A}}$ , are assumed to be zero in this approximation. The solutions of this set of equations are

$$\begin{gathered} M^{\text{A}}(t)=A{e}^{{\lambda }_{s}t}+B{e}^{{\lambda }_{\text{f}}t} \\ {M}^{\text{B}}(t)=C{e}^{{\lambda }_{s}t}+D{e}^{{\lambda }_{\text{f}}t} \end{gathered}$$ (3)

with small (“slow”) and large (“fast”) eigenvalues, λ_s and λ_f, given by

$$\begin{gathered} {\lambda }_{\text{f,s}}=-\frac{1}{2}\left(k_{\text{ex}}+R_2^B{\sin }^2\theta \\ \hspace{1em}\hspace{1em}\pm \sqrt{{\left(k_{\text{ex}}+R_2^B{\sin }^2\theta \right)}^2-4p_{\text{B}}{k}_{\text{ex}}{R}_2^B{\sin }^2\theta }\right) \end{gathered}$$ (4)

where the exchange rate $k_{\text{ex}}=k_{\text{on}}^{\text{app}}+k_{\text{off,}}$ and the population of state B, $p_{\text{B}}=k_{\text{on}}^{\text{app}}/k_{\text{ex}}.$ Expressions for the coefficients A−D in eq 3 in the absence of chemical shift differences between states $(\Delta \omega =0)$ are given by

$$\begin{gathered} A={\lambda }_{\text{f}}(1-p_{\text{B}})/({\lambda }_{\text{f}}-{\lambda }_{\text{s}}) \\ B=-{\lambda }_{\text{s}}(1-p_{\text{B}})/({\lambda }_{\text{f}}-{\lambda }_{\text{s}}) \\ C=p_{\text{B}}({\lambda }_{\text{f}}+R_2^{\text{B}}{\sin }^2\theta )/({\lambda }_{\text{f}}-{\lambda }_{\text{s}}) \\ D=-p_{\text{B}}({\lambda }_{\text{s}}+R_2^{\text{B}}{\sin }^2\theta )/({\lambda }_{\text{f}}-{\lambda }_{\text{s}}) \end{gathered}$$ (5)

From eqs 2–4, given that −λ_s represents the effective relaxation rate measured as a function of the offset angle θ, it follows that the contribution to the transverse relaxation rate arising from exchange, R_ex, in the limit of skewed populations (p_B ≪ p_A) can be expressed as¹⁵

$$\begin{gathered} R_{\text{ex}}=-{\lambda }_{\text{s}}/{\sin }^2\theta \approx {\left[\frac{1}{p_{\text{B}}{R}_2^{\text{B}}}+\frac{{\sin }^2\theta }{p_{\text{B}}{k}_{\text{ex}}}\right]}^{-1} \\ \hspace{1em}={\left[\frac{1}{p_{\text{B}}{R}_2^{\text{B}}}+\frac{{\sin }^2\theta }{k_{\text{on}}^{\text{app}}}\right]}^{-1} \end{gathered}$$ (6)

Equation 2 and its solutions in eqs 3–5 are a good approximation to the full Bloch-McConnell equations in the ω₁ ≫ $R_{\text{2}}^{\text{B}}$,k_ex for analysis of off-resonance R_1ρ experiments where for each value of the offset angle θ, the magnetization is aligned along the effective RF field (i.e., “locked”).¹⁵ In contrast, in exchange saturation transfer experiments, such as DEST, the magnetization is saturated in the course of the relaxation period by application of a continuous RF field resulting in the angle between the magnetization and the z-axis of the laboratory frame becoming time-dependent. Therefore, we use the approximations above solely for illustrative purposes. Nevertheless, using the expressions for relaxation rates in the rotating frame, R_1ρ = R₁cos² θ + R_2,eff sin² θ, where R_2,eff = $R_{\text{2}}^{\text{A}}$ + R_ex, and R_ex is calculated using eq 6, we can quantitatively reproduce the DEST profiles generated using the full set of Bloch-McConnell equations as long as the $R_{\text{2}}^{\text{B}}$ values are sufficiently large (> ∼500 s⁻¹), indicating that the relationships above in general and eq 6 in particular serve as good approximations for reproducing DEST profiles under conditions that are relevant for the present study, i.e., when ω₁ > $R_{\text{2}}^{\text{B}}$ > k_ex and $R_{\text{2}}^{\text{B}}$ > ∼ 500 s⁻¹. Equation 6 is especially useful in this regard as it shows that whereas the value of $k_{\text{on}}^{\text{app}}=p_{\text{B}}{k}_{\text{ex}}$ in the denominator of the second term is largely defined by the ΔR₂ data, the product p_{B$R_{\text{2}}^{\text{B}}$} in the denominator of the first term is the only quantity that can be determined with certainty from DEST profiles. (Note that ΔR₂ in our notation is the measured difference between the transverse relaxation rates measured on the observable species in the presence and the absence of exchange, as opposed to the difference $R_{\text{2}}^{\text{B}}$−$R_{\text{2}}^{\text{A}}$ in Yuwen et al.¹⁵) Equation 6 thus serves as a clear illustration of the uncertainties in the values of p_B and $R_{\text{2}}^{\text{B}}$ derived from the DEST data as described above.

To decorrelate p_B and $R_{\text{2}}^{\text{B}}$ , we make use of another observable quantity introduced by Kay and co-workers, C_fast,¹⁵ that relates to the fractional contribution of the fast decaying component to the total signal intensity, namely, (B + D) in eq 3 if the sum of all components (A + B + C + D) is normalized to unity. As can be seen from eq 3, the decay of “spin-locked” magnetization for each state in the R_1ρ experiments is inherently biphasic. Since the magnetization is carefully equilibrated before and after each relaxation period (“spin-lock” element) of the R_1ρ measurements such that after each relaxation period $M_{\text{eq}}^{\text{A}}(T)=(1-p_B)[M^{\text{A}}(T)+M^{\text{B}}(T)]$ and $M_{\text{eq}}^{\text{A}}(T)=p_B[M^{\text{A}}(T)+M^{\text{B}}(T)]$ ,¹⁵ where T is the duration of relaxation delay, the C_fast component can be reliably estimated by extrapolation of the R_1ρ decay curve to zero time, provided that normalization of signal intensities is performed relative to those measured in the absence of relaxation period (i.e., at T = 0, corresponding to A + B + C + D in eq 3). Using the expressions in eqs 4 and 5, it is straightforward to show that in the limit Δω = 0, C_fast has the form

$${\text{C}}_{\text{fast}}=\text{B+D=}\frac{p_{\text{B}}{\sin }^4\theta }{{(k_{\text{ex}}/R_{\text{2}}^{\text{B}}+{\sin }^2\theta )}^2-(2p_{\text{B}}{k}_{\text{ex}}/R_2^{\text{B}}){\sin }^2\theta }$$ (7)

Note that eq 7 is different from the corresponding eq 11 in Yuwen et al.¹⁵ by a factor of “2” in the second term of the denominator, as no assumptions about λ_f were made in its derivation (the full expression for λ_s,f in eq 4 was used). Equation 7 shows that C_fast is directly proportional to p_B and, importantly, p_B is not “mixed” with $R_2^{\text{B}}$ anywhere in this relationship.

The variation of C_fast as a function of offset frequency (angle θ) is predicated on the value of k_ex/$R_2^{\text{B}}$ (eq 7). For small values of k_ex/$R_2^{\text{B}}$, as is the case in the present study (typically, k_ex/$R_2^{\text{B}}$ < 0.1 for the htt^NT and htt^NTQ₇ peptides in the presence of SUVs), the profiles of C_fast versus offset frequency show little variability. Figure 3A shows the profiles of C_fast as a function of ¹⁵N-frequency offset simulated using a variant of eq 7, where the assumption that Δω = 0 is dropped (see eq 12 in Yuwen et al.¹⁵) for Lys⁵ of htt^NT and htt^NTQ₇. The simulations were performed using two spin-lock periods effectively amplifying the value of C_fast approximately 2-fold, and using the chemical shifts of the bound state of Lys⁵ available from our previous study of htt^NTQ_n peptides binding to lipid micelles.¹⁴ The curves obtained via propagation of the full Bloch-McConnell matrix are practically indistinguishable from those shown in Figure 3A. The maxima of the C_fast profiles are only very slightly shifted from the position of the carrier (assumed to be at 0 Hz, which coincides with the chemical shift of the major free state A) toward the chemical shifts of the minor bound state (Δω/2π = −212 Hz for Lys⁵). In this context, it is important to note that although htt^NTQ_n peptides are known to form helices on the surfaces of lipid-based particles¹⁴ resulting in large (and negative) ¹⁵N chemical shift changes in the bound state, the difference in chemical shifts between the free and bound states is largely of no consequence in the present study, as all the experimental techniques employed here are either insensitive to chemical shift changes, such as DEST and C_fast, or the effect of these changes is suppressed by strong spin-lock RF fields, as in the case of ΔR₂ measurements.

Figure 3.

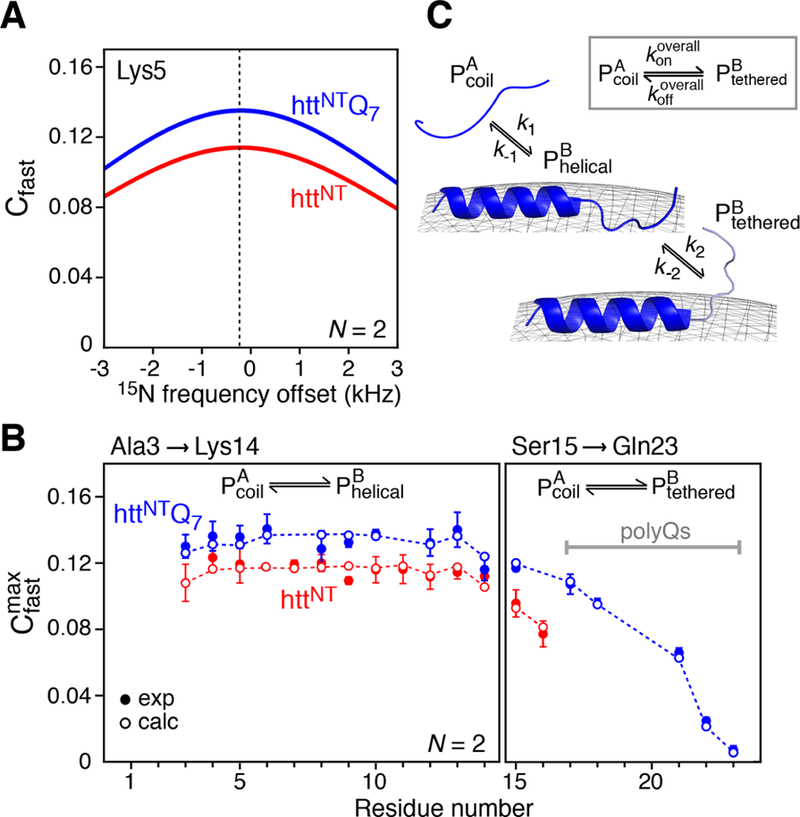
Simulated and experimental C_fast profiles for the binding of htt^NT and htt^NTQ₇ to SUVs. (A) Simulated profiles of C_fast as a function of ¹⁵N frequency offset for Lys⁵ of htt^NT (red) and htt^NTQ₇ (blue) in the presence of SUV vesicles at a molar ratio of 1:4 peptide to lipid. The curves were calculated using a variant of eq 7 that accounts for Δω ≠ 0¹⁵) with the following values for the exchange parameters (where the first value refers to htt^NT and the second to htt^NTQ₇): k_ex = 204.7/208.3 s⁻¹, p_B = 0.07/0.08, $R_1^{\text{A}}-R_1^{\text{B}}$ = 1.5/1.5 s^{− 1}, $R_2^{\text{A}}$= 2.4/3.6 s^{− 1}, $R_2^{\text{B}}$ = 2300/2300 s⁻¹, ω₁ field strength = 2000 Hz, number of spin locks N = 2, and Δω/(2π) = −211.8 Hz (−3.47 ppm at 600 MHz). (B) Experimental ¹⁵N-${\text{C}}_{\text{fast}}^{\max }$ profiles measured for htt^NT (red filled-in circles) and htt^NTQ₇ (blue filled circles) in the presence of SUVs. The open circles are the best-fit profiles obtained by including ${\text{C}}_{\text{fast}}^{\max }$ into the target function together with the DEST and ΔR₂ data (see Experimental Section). (C) Kinetic scheme used for modeling the binding of htt^NT and htt^NTQ₇ to the surface of SUVs. The data for residues 3−14 are fit to a two-state exchange between the free peptide $\left({\text{P}}_{\text{coil}}^{\text{A}}\right)$ and membrane-bound helical peptide $\left({\text{P}}_{\text{helix}}^{\text{B}}\right).$ For residues 15−16 of htt^NT and 15−23 of htt^NTQ₇, there is an additional process involving the interconversion between ${\text{P}}_{\text{helix}}^{\text{B}}$ and ${\text{P}}_{\text{tethered}}^{\text{B}}$, where the residues in the ${\text{P}}_{\text{tethered}}^{\text{B}}$ state are not attached to the membrane but tethered via the membrane-bound helical residues. The overall process for the conversion of ${\text{P}}_{\text{coil}}^{\text{A}}$ to ${\text{P}}_{\text{tethered}}^{\text{B}}$ (via ${\text{P}}_{\text{helix}}^{\text{B}}$ ) is shown in the inset.

As practically no information can be gleaned from the dependence of C_fast on the frequency offset for the exchange parameters of htt^NT and htt^NTQ₇ peptides binding to SUVs, we opted for the measurement of a single C_fast value per residue at or close to the on-resonance frequency. As follows from eq 7, C_fast reaches its maximal value, ${\text{C}}_{\text{fast}}^{\max }$, on resonance (sin θ = 1). For skewed populations (p_B ≪ p_A), the expression for ${\text{C}}_{\text{fast}}^{\max }$ can be simplified to

$$\begin{gathered} {\text{C}}_{\text{fast}}^{\max }=\frac{p_{\text{B}}}{1+{(k_{\text{ex}}/R_2^{\text{B}})}^2+(2k_{\text{ex}}/R_2^{\text{B}})(1-p_{\text{B}})} \\ \hspace{1em}\hspace{1em}\approx \frac{p_{\text{B}}}{{(1+k_{\text{ex}}/R_2^{\text{B}})}^2} \end{gathered}$$ (8)

Equation 8 shows that as long as $k_{\text{ex}}/R_2^{\text{B}}<1,{\text{C}}_{\text{fast}}^{\max }$ provides a good measure of the population of the bound state p_B, even if only a single on-resonance measurement of C_fast is available. Only when the ratio k_ex/$R_2^{\text{B}}$ becomes significantly larger than unity does ${\text{C}}_{\text{fast}}^{\max }$ decrease to unmeasurably low values.

Impact of Incorporation of ${\text{C}}_{\text{fast}}^{\max }$ Data in the Analysis of DEST/ ΔR₂ Data.

The measurements of ${\text{C}}_{\text{fast}}^{\max }$ for htt^NT and htt^NTQ₇ peptides in the presence of SUVs were conducted as described in the Experimental section and closely followed the procedures of Yuwen et al.¹⁵ To amplify the value of ${\text{C}}_{\text{fast}}^{\max }$ approximately 2-fold, two spin-lock periods were used in the total relaxation delay, each preceded and followed by the magnetization equilibration delay τ_eq ≥ 2/k_ex. The experimental ¹⁵N-${\text{C}}_{\text{fast}}^{\max }$ profiles are shown in Figure 3B. Inclusion of an additional term that accounts for the ${\text{C}}_{\text{fast}}^{\max }$ data into the DEST/ΔR₂ target function (see the Experimental section for details of the calculations) enables unambiguous determination of p_B, and hence k_off, as well as the set of residue-specific ¹⁵N-$R_2^{\text{B}}$ values, without compromising the quality of the fit for either the DEST (Figure 1A) or ΔR₂ (Figure 1B) data.

The ¹⁵N-DEST, ΔR₂, and ${\text{C}}_{\text{fast}}^{\max }$ data for Ala³−Lys¹⁴ were fitted simultaneously to a two-state exchange model (defined by the rate constants k₁ and k₋₁ in Figure 3C) to yield the following exchange parameters: $k_1=k_{\text{on}}^{\text{app}}$ = 14.1 ± 0.03 and 17.1 ± 0.04 s⁻¹, and k₋₁ = k_off = 190.6 ± 1.3 and 191.2 ± 1.3 s⁻¹ for htt^NT and htt^NTQ₇, respectively (corresponding to p_B values of 6.9 ± 0.1 and 8.2 ± 0.1%).

The C-terminal region for both peptides, comprising residues 15−16 of htt^NT and 15−23 (encompassing the polyglutamine tract) of htt^NTQ₇ required a separate treatment: the same overall two- state exchange model (shown in the inset of Figure 3C) was used to fit the data for these residues, keeping in mind that the overall exchange process is more complex for these sites and involves initial binding to the surface of SUVs followed by transient, reversible detachment from the lipid surface depicted as the ${\text{P}}_{\text{tethered}}^{\text{B}}$ state in Figure 3C. The fits for these residues to the model shown in the inset to Figure 3C yielded $k_{\text{on}}^{\text{overall}}$ = 9.2 ± 0.2 and 13.2 ± 0.1 s⁻¹, and $k_{\text{off}}^{\text{overall}}$ = 144 ± 3 and 157 ± 2 s⁻¹ for htt^NT and htt^NTQ₇, respectively. The rate constants k₂ and k₋₂ describing the exchange process between membrane-bound (direct-contact) and tethered states $\left({\text{P}}_{\text{tethered}}^{\text{B}}\right)$ of the C-terminal residues can be calculated from the relationships

$$\begin{gathered} k_2=k_{\text{on}}^{\text{overall}}\frac{k_{-1}}{k_1-k_{\text{on}}^{\text{overall}}} \\ {k}_{-2}=k_{\text{off}}^{\text{overall}}\left(1+\frac{k_2}{k_{-1}}\right) \end{gathered}$$ (9)

yielding k₂ = 358 ± 13 and 635 ± 14 s⁻¹, and k₋₂ = 413 ± 22 and 680 ± 24 s⁻¹ for htt^NT and htt^NTQ₇, respectively. From the values of these rate constants, it follows that reversible detachment of the C-terminal residues from the SUV surface occurs ∼4-to-6-fold faster than the binding itself (first stage of the global process). Further, exchange between the direct-contact and tethered states of the C-terminal residues occurs ∼1.7-fold faster in htt^NTQ₇ than in htt^NT, consistent with the presence of the seven-residue polyglutamine C-terminal tail, while the slight preference for the direct-contact state is apparent for both peptides.

The ¹⁵N-$R_2^{\text{B}}$ values for SUV-bound htt^NT and htt^NTQ₇, derived from the combined analysis of ¹⁵N-DEST, ΔR₂, and ${\text{C}}_{\text{fast}}^{\max }$ data, are shown in Figure 4 as a function of residue number. The average ${\langle }^{15}\text{N-}{R}_2^{\text{B}}\rangle$ values of 2550 and 2340 s⁻¹ for the membrane-bound states $\left({\text{P}}_{\text{helix}}^{\text{B}}\right)$ of htt^NT and htt^NTQ₇ lie within the range predicted for a particle of 31 nm in diameter (Figure 2). The corresponding $R_2^{\text{B}}$ values for the tethered $\left({\text{P}}_{\text{tethered}}^{\text{B}}\right)$ state are on average 3-to-4-fold lower for both complexes (right panel of Figure 4), as expected since the C-terminal residues are semi-detached from the lipid surface, do not form a helical structure, and are therefore at least partially disordered.

Figure 4.

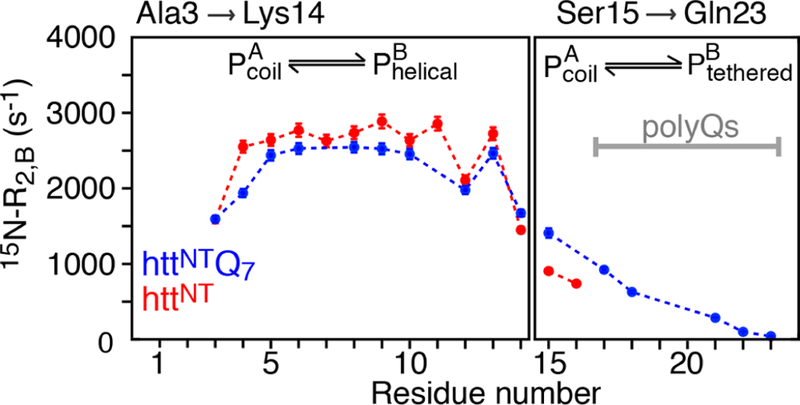
¹⁵N-$R_2^{\text{B}}$ profiles for htt^NT (red circles) and htt^NTQ₇ (blue circles) bound to SUVs, obtained from combined analysis of ¹⁵N-DEST,¹⁵N-ΔR₂, and ¹⁵N-${\text{C}}_{\text{fast}}^{\max }$ data.

CONCLUSIONS

In summary, we have characterized the binding kinetics of two peptides derived from exon-1 of the huntingtin gene, htt^NT and htt^NTQ₇, to SUV particles 31 nm in diameter and 4.3 MDa in molecular weight, using DEST and lifetime line broadening (ΔR₂) supplemented with the measurement of the maximal (on-resonance) value of the contribution of the fast-relaxing component of magnetization, ${\text{C}}_{\text{fast}}^{\max }$. We show that the measurement of DEST and ΔR₂ is not sufficient to unambiguously determine both the transverse relaxation rates in the bound state, $R_2^{\text{B}}$, and the population of the bound state, p_B, simultaneously in the exchange regime where $R_2^{\text{B}}$ is smaller than the strength of the DEST saturation RF field (see Figure 2). The measurement of ${\text{C}}_{\text{fast}}^{\max }$, an observable that is directly proportional to p_B, allows one to decorrelate $R_2^{\text{B}}$ and p_B from one another. ${\text{C}}_{\text{fast}}^{\max }$ thus serves as a valuable addition to the array of available experimental NMR observables for studying exchanging systems involving binding to high-molecular-weight, dark states in the 2−6 MDa range, where exchange-induced chemical shifts and/or CPMG relaxation dispersions are not measurable. Under the experimental conditions employed (300 μM peptide at a 1:4 molar ratio of peptide to lipid), exchange between the free huntingtin peptides and the SUV-bound states is slow on the relaxation time-scale (τ_ex ∼ 5 ms, mean < T₂ > ∼ 400 μs for the bound state) with bound populations of 7−8%. While the peptide core (residues 3−14) is stably bound to the SUV surface, the C-terminal region of both peptides (residues 15−16 of htt^NT and residues 15−23 of htt^NTQ₇ encompassing the polyglutamine region) remain flexible in the bound form due to reversible detachment from the surface of SUV particles that occurs on a time-scale ∼4-to-6-fold faster than the binding to the SUV.

Scheme 1