Abstract
In this work, mixed-matrix membranes (MMMs) for gas separation in the form of thick films were prepared via the combination of the polymer Matrimid® 5218 and activated carbons (AC). The AC particles had a mean particle size of 1.5 μm and a mean pore diameter of 1.9 nm. The films were prepared by slow solvent evaporation from casting solutions in chloroform, which had a varying polymer–AC ratio. It was possible to produce stable films with up to a content of 50 vol % of AC. Thorough characterization experiments were accomplished via differential scanning calorimetry and thermogravimetric analysis, while the morphology of the MMMs was also investigated via scanning electron microscopy. The gas transport properties were revealed by employing time-lag measurements for different pure gases as well as sorption balance experiments for the filler particles. It was found that defect free Matrimid® MMMs with AC were prepared and the increase of the filler content led to a higher effective permeability for different gases. The single gas selectivity αij of different gas pairs maintained stable values with the increase of AC content, regardless of the steep increase in the effective permeability of the pure gases. Estimation of the solubilities and the diffusivities of the Matrimid®, AC, and MMMs allowed for the explanation of the increasing permeabilities of the MMMs, with the increase of AC content by modelling.
Keywords: mixed-matrix membranes, Matrimid®, activated carbon, time-lag, permeability, gas separation
1. Introduction
Membranes offer attractive opportunities for many gas separation applications, e.g., in hydrogen recovery, natural gas processing, etc. [1]. In comparison to conventional gas separation processes like adsorption, absorption, or condensation, membrane technology offers an easier separation process. For membranes, polymers allowing for mass transfer according to the solution–diffusion mechanism are often used [1]. The benefits of using polymers are that they have a good processability and a low price, whereas they also have a low stability at high temperatures and aggressive chemical compounds. Robeson compiled in his work the separation capacity for polymeric membranes for the gas pairs consisting of He, H2, O2, N2, CO2, and CH4. As a result, it was shown that the maximal selectivity inversely correlates with the permeability: with increasing the permeability, the selectivity decreases. This upper limit is called “Robeson Upper Bound” and was first established in 1991 [2] and updated in 2008 [3]. In contrast to polymers, inorganic membranes made of zeolites or carbon exhibit high permeabilities and selectivities [4,5]. Nevertheless, the disadvantage for industrial use complies that they are often mechanically and chemically very unstable and cost-intensive. Because of this, an alternative approach was proposed, in which inorganic particles are dispersed in the polymeric matrix to combine the positive properties of the two material classes. This kind of membranes is often called mixed-matrix membranes (MMMs) [6,7], which are based in most of the cases on a polymer matrix and inorganic fillers (porous or non-porous). These components are optimally combined to exhibit enhanced separation and mechanical properties in comparison to the pure materials. In principle, almost all polymers can be used for the fabrication of MMMs, as far as they can be easily processed, e.g., in solution. Usually, the solution method is favored for the dispersion of the inorganic fillers since the polymers are relaxed in the solution and the inorganic fillers can be easily incorporated. Removing the solvent in a proper way results in the formation of the MMMs. Numerous combinations of polymers and fillers have already been studied and extensive reviews have been published [8,9,10]. Elastomers, as well as semi-crystalline polymers (e.g., polydimethylsiloxane polyethylene respectively), have been used for such applications. Also, a variety of filler materials have been studied, among them, metal–organic frameworks (MOFs), polyoctahedral silsesquioxanes, zeolites, carbon nanotubes, activated carbon, as well as ceramic, metal oxide particles (e.g., γ-alumina, titanium dioxide nanoparticles) and metallic nanoparticles, e.g., palladium [7,11,12,13,14,15,16,17,18].
Polyimides are a class of polymers that are prepared via polycondensation reaction between a dianhydride and a diamine or diisocyanate [19], and they usually exhibit high glass transition temperatures. Matrimid® 5218 (further Matrimid®) belongs to this category of polymers and is well-known for its attractive gas separation properties, in particular for a good gas separation performance in the separation of CO2 from CH4 or for hydrogen recovery [20]. There is a variety of works on Matrimid® MMMs. Vinoba et al. give a good overview on recent fillers used in MMMs [9], while Wang et al. recently gave an overview of the use of mixed matrix membranes for CO2 separation applications [10]. Khan et al. published a work on Matrimid® MMMs with silica particles exhibiting a decreasing trend for the activation energy of permeation of CO2 with increasing silica particles content [21]. Naseri et al. reported the fabrication of Matrimid® MMMs with metal–organic frameworks (MOFs) and found that the selectivity of the composite material was improved for the pair of gases CO2/CH4 and CO2/N2 in comparison to the pure Matrimid® for a content of MOFs equal to 30 wt % [22]. Similar are the results published by Dong et al. with the use of a different MOF. In this case, they observed that the selectivity for CO2 increases but they also studied the morphology of the membranes and found a “crater” structure of the Matrimid® matrix phase around the MOF particles. In this work, the thermal stability of Matrimid® was also investigated and found to be better since the glass transition temperature showed a significant increase due to the introduction of the inorganic particles [23]. Last but not least, significant results were reported by Zhang et al. on MMMs with mesoporous ZSM-5 zeolite particles. In this case, the micropores of the ZSM-5 crystals provided size and shape selectivity especially for the gas pairs of H2/N2 and O2/N2 [24].
Activated carbons (AC) are materials also well known for gas separation processes. Recently, our group published works on MMMs prepared as thin film composite membranes based on polydimethylsiloxane (PDMS) or polyoctomethylsiloxane (POMS) with AC. With the use of AC, it was possible to increase the separation performance towards higher hydrocarbons. The selectivity for a binary mixture of n-C4H10/CH4 was increased [25,26].
In this work, we present the fabrication of MMMs based on Matrimid® and AC. The target of this work is to identify the properties of the prepared MMMs not only regarding the gas transport performance but also concerning the material characteristics. The analysis was done via a variety of experiments, which are presented below. The correlation of the material properties, as well as the gas transport properties, e.g., the morphology and the thermal properties, with the permeability, revealed interesting characteristics for the overall separation performance.
2. Materials and Methods
2.1. Materials
The Matrimid® 5218 (Matrimid®), a polyimide of 3,3′,4,4′-benzophenone tetracarboxylic dianhydride and diamino-phenylindane, was purchased from Huntsman Advanced Materials GmbH (Bergkamen, Germany) in powder form and it was used as the matrix for the mixed matrix membranes. The bulk density of Matrimid® is 1.24 g cm−3.
The activated carbon (AC) was used as inorganic filler and was kindly provided by the company Blücher GmbH (Erkrath, Germany). The AC particles were produced from a polymeric precursor that leads to clean carbon particles with reproducible pore structure. The initially prepared spherical particles of 100 μm diameter were milled and fractioned to a final mean particle size d50 = 1.5 μm without changes of the pore characteristics according to the producer. The apparent density of the particles was 0.89 g cm−3 and the mean pore size was 1.87 nm [25].
The solvent and non-solvent used for Matrimid® membrane production were chloroform (analytical grade, Merck GmbH, Darmstadt, Germany) and methanol (analytical grade, Merck GmbH, Darmstadt, Germany), respectively.
2.2. Preparation of Membranes
Thick films of Matrimid® and MMMs of Matrimid® and AC were fabricated by solution casting using chloroform as a solvent. Solutions with different contents of AC were prepared while maintaining the same amount of polymer. The polymer solution prepared had a concentration 4 wt %. The films produced by the solution casting had an activated carbon content of 0–50 vol %. The typical procedure to prepare the films was as follows: first, the dried powder of Matrimid® together with the activated carbon particles were dissolved—dispersed in chloroform (CH3Cl) and stirred for two hours. Following that, the solution was ultrasonicated using an Elmasonic ultrasonication device (Elma Schmidbauer GmbH, Singen, Germany), which did not affect the molecular weight of the polymer. In the next step, the solution was directly cast into a leveled Teflon® mold and solvent evaporation was carried out with a constant nitrogen flow under ambient conditions. The dried membranes were processed with methanol for 8 h to remove the residues of chloroform via solvent exchange [27]. In the last step, the membranes were dried at 60 °C for 24 h under vacuum in order to completely remove solvent residues. The thickness of the obtained membranes was in the range of 80 up to 160 μm, dependent on the amount of AC. The thickness was measured using a Deltascope FMP10 (Helmut Fischer GmbH, Sindelfingen, Germany), in order to obtain accurate values.
2.3. Characterization Methods
2.3.1. Thermal Analysis
Differential Scanning Calorimetry. Differential scanning calorimetry (DSC) experiments were carried out using the calorimeter DSC 1 (Mettler-Toledo, Gießen, Germany), in a nitrogen atmosphere, with a heating rate of 10 K/min, within a temperature range from room temperature to 380 °C. Three heating–cooling cycles were accomplished with a five minutes isotherm interval between the heating and the cooling. The first heating interval served for erasing the sample thermal history from the preparation and started from room temperature up to 380 °C, while the two other cycles were used for the determination of thermal properties and they were accomplished in the temperature range from 200 °C up to 380 °C. The second heating interval was used for the evaluation of the glass transition and the third heating interval was used to verify it. The glass transition temperature Tg was assessed as the inflection point of the heat flow as a function of the temperature with the onset method using the instrumentation software. The DIN midpoint was calculated with the use of the software of the instrumentation. Approximately 10 mg of the polymer and the grounded composites were placed in an aluminum pan of 10 μL after having been dried for several days under vacuum.
Thermogravimetric Analysis. Thermogravimetric analysis (TGA) was performed using a TG 209 F1 Iris (Netzsch, Selb, Germany). The experiments were carried out within a temperature range from 25 °C up to 1000 °C at a heating rate of 10 K/min. The measurements were performed under argon atmosphere. Approximately 10 mg of the membrane was placed in a ceramic pan for the measurements.
2.3.2. Morphological Characterization
Scanning Electron Microscopy (SEM). The morphology of the membranes was investigated with the scanning electron microscope Merlin (Carl ZEISS GmbH, Oberkochen, Germany). The samples were cryo-fractured in liquid nitrogen to examine the dispersion of the filler particles in the cross-section. The surface morphology was investigated as well. The samples were sputter-coated with approximately 2 nm Pt. The images were obtained at an acceleration voltage in the range of 3–5 kV.
2.3.3. Gas Sorption Measurements
The sorption of pure gases He, H2, O2, N2, CO2, and CH4 on AC was accomplished with the gravimetric sorption analyzer IsoSORP® Static (Rubotherm GmbH, Bochum, Germany). The system is equipped with a precision pressure sensor DPI 282 of ±0.006 bar accuracy. The experimental temperature was maintained with a cryo-compact circulator (Julabo GmbH, Seelbach, Germany) with an accuracy of ±0.03 °C. Adsorption isotherms were recorded at 30 °C in a pressure range from ~0 up to 30 bar. The resolution and reproducibility of the magnetic suspension balance (MSB, Rubotherm GmbH, Bochum, Germany) was 0.01 mg and ±0.03 mg, respectively. In order to correlate with the real gas behavior, the fugacities of the different gases were determined according to the Soave–Redlich–Kwong equation of state [28] using the chemical process simulation and optimization software Aspen Plus® (AspenTech, Bedford, MA, USA).
2.3.4. Gas Transport Characteristics Determination
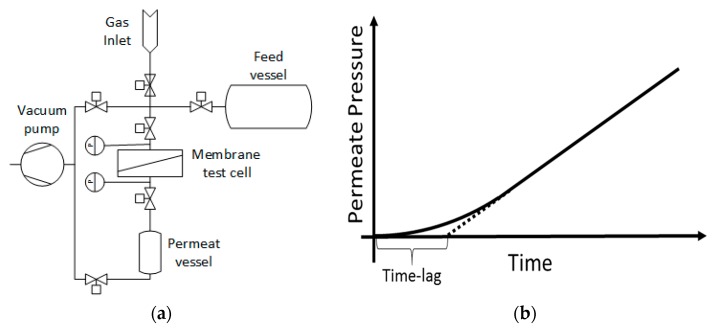
The gas transport parameters were determined with the time-lag (variable pressure, constant volume [29]) method at 30 °C and 1000 mbar feed pressure for He, H2, N2, O2, CO2, and CH4 [30]. The method relies on maintaining a constant feed pressure and measuring the permeate pressure changing as a function of time due to the diffusion of gas molecules through the membrane film of known thickness. The membrane under investigation was placed into the measurement cell and sealed with a Viton® O-ring, which served as a barrier between the feed and permeate side of the measurement instrumentation. Prior to the measurement, the apparatus was evacuated to a state where no evidence of desorption was observed anymore, i.e., no pressure increase was recorded. The pressure increase in the permeate chamber with known constant volume was monitored from the moment the gas at a constant pressure was brought in contact with the membrane. From the obtained curve, the time-lag, θ, was determined by extrapolating the slope of the linear increase to its intersection with the time axis and the gas permeability coefficient of the membrane was calculated from the linear part of the curve [31]. The employed experimental apparatus as well as the schematic representation of the experimental result is depicted in Figure 1. The diffusion coefficient of component i (Deff,i) was calculated by the following equation [32]:
| (1) |
where l is the membrane film thickness and Deff the effective diffusion coefficient of the penetrant in the studied material. The permeability (Peff,i) of a gas penetrant i is the pressure or fugacity difference (i.e., driving force) and thickness-normalized flux of the component through the membrane and is defined by:
| (2) |
where Pi is the permeability of component i, Ni is the component i’s volumetric flowrate at standard conditions (STP) through the membrane, Am is the membrane area, and Δpi the partial pressure (or fugacity) difference between feed and permeate sides. The volumetric flowrate was determined from the permeate pressure change with time assuming that in a pressure range 0–10 mbar the ideal gas law is applicable. The solubility (Seff,i) coefficient can be calculated from the following equation:
| (3) |
Figure 1.
(a) Sketch of the time-lag measurement setup and (b) the schematic representative of the experimental result (solid curve: permeate pressure; dotted line: tangent at large time).
The selectivity of a dense gas separation membrane is defined as:
| (4) |
Here Pi and Pj are the permeabilities of gas i and j.
For the time-lag measurements, a custom-made machine was used. The gases used for the experiments (Linde AG, Munich, Germany) were of high purity, while a thermostat, similar to the one employed in the sorption experiments, was used to maintain the temperature. The vacuum was generated by a turbomolecular pump (Pfeiffer GmbH, Asslar, Germany). A LabView based custom software (National Instruments, Austin, TX, USA) was used for the control of the time-lag experiments as well as for the evaluation of the data. It should be noted that the placement of the Viton® O-ring involves relatively hard pressing of the O-ring onto the membrane. The O-ring has a 65 Shore hardness. The pressing ensures a good sealing of the membrane in the measurement cell, whilst it is also an indication of the membrane mechanical stability, which is necessary for the accomplishment of the measurement.
3. Results and Discussion
3.1. Thermal Analysis
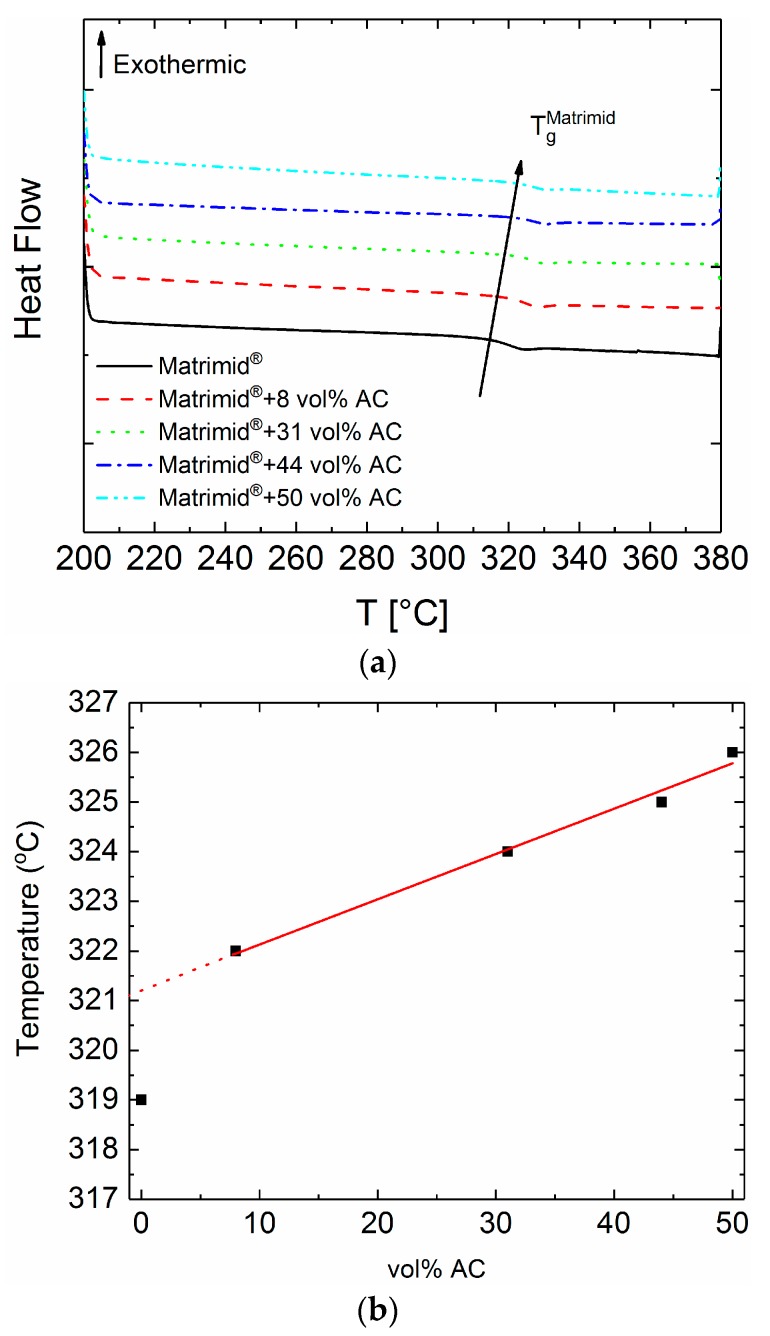
Differential Scanning Calorimetry. The differential scanning calorimetry of the pure Matrimid® and the Matrimid®–AC MMMs shows a small difference between the glass transition temperature of the pure polymer and the MMMs. More in detail, as it can be seen from the values in Table 1, the glass transition temperature is slightly but gradually affected by the incorporation of AC into Matrimid®. This indicates that there is some interaction of the polymer with the AC [33,34]. The pure Matrimid® shows a glass transition temperature at 319 °C and it is increasing with the increase of activated carbon content up to the value of 326 °C for the MMM with 50 vol % filler content. The slight interaction of the filler particles with the polymer matrix was expected, since the carbon particles are not chemically modified (e.g., containing functional groups, hydrophobically or hydrophilically modified) and therefore a strong bonding of the polymer matrix with the particles is not to be expected. The results are presented in Figure 2a. In other cases, incorporation of chemically modified fillers have shown a significant effect on the glass transition temperature of Matrimid®, attributed to the chemical bonding—hydrogen bonds mostly—occurring at the interface between the polymer and the filler particles [24]. It is important to mention that the increase of the glass transition with the increase of the AC volume content (Figure 2b) is linear for the MMMs, but the extrapolation of the linear fit to 0 vol % AC indicates a difference. A slight increase of 2 °C for the theoretically expected glass transition temperature for the pure Matrimid® (extrapolated value is 321 °C), in comparison to the experimentally estimated value of 319 °C, is observed. This indicates that the polymer incorporates well the particles into its matrix, as it is also pointed out in literature [33,34].
Table 1.
Glass transition temperature of Matrimid® in Matrimid®–AC MMMs.
| Membrane—Activated Carbon Content | Tg [°C] |
|---|---|
| Matrimid® | 319 |
| Matrimid® + 8 vol % AC | 322 |
| Matrimid® + 31 vol % AC | 324 |
| Matrimid® + 44 vol % AC | 325 |
| Matrimid® + 50 vol % AC | 326 |
Figure 2.
(a) DSC thermographs for the pure Matrimid® and the Matrimid®–activated carbon (AC) mixed-matrix members (MMMs). The data are vertically shifted for clarity. (b) Glass transition as a function of the AC volume content. The linear fit for the MMMs indicates the slight linear increase of the glass transition due to the well adaption of the AC particles in the polymer matrix.
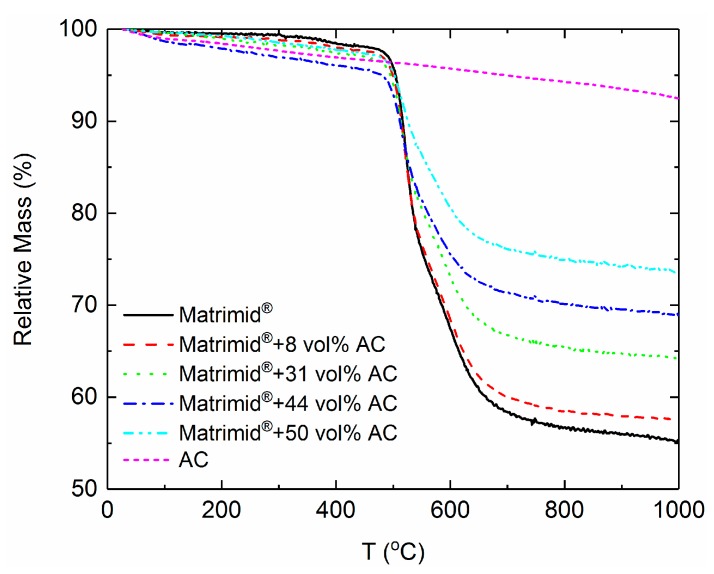
Thermogravimetric analysis. In Figure 3, the results of the TGA are presented for the pure Matrimid® as well as the Matrimid®–AC MMM prepared in this work. It is indicated that the membranes show a high thermal stability since the degradation processes start above 400 °C. The initial mass-losses indicate changes of the polyimide polymer as well as small changes of the AC.
Figure 3.
TGA thermographs of the MMMs prepared in this work. The pure Matrimid® is also shown for comparison.
From the TGA curves, it is observed that the AC presence in the MMMs does not significantly influence the onset of the Matrimid® decomposition. As it follows from the polymer decomposition curve, the process of polymer decomposition does not occur in one-step and the shape of the curve changes when the AC is present in the polymer. The remaining weight of the sample at 1000 °C was used to determine the real weight content of the AC in the Matrimid® MMMs according to the following Equation (5):
| (5) |
where mr,i is the remaining relative mass of Matrimid®, AC, and MMMs, and wAC is the weight content of AC in the MMMs. In order to calculate the volume content of the AC in the films, the densities of the pure materials are needed. The calculation is done following the Equation (6):
| (6) |
where ρPolymer is the density of Matrimid® and ρAC is the density of AC. In Table 2, the theoretical and the estimated values of AC content from the TGA are given for all the MMMs studied in this work. The small deviation from the initial content of the AC that was used for the membrane fabrication is caused by the sample preparation.
Table 2.
AC content of the MMMs according to the fabrication process and the TGA analysis. The volume content of AC included in the last column is calculated from the weight content determined from the TGA measurement.
| wACTheoretical [%] | wACTGA [%] | [%] |
|---|---|---|
| 4.70 | 6.00 | 8.20 |
| 20.00 | 23.94 | 30.50 |
| 33.33 | 36.32 | 44.20 |
| 42.85 | 42.11 | 50.30 |
3.2. Morphology of the Membranes
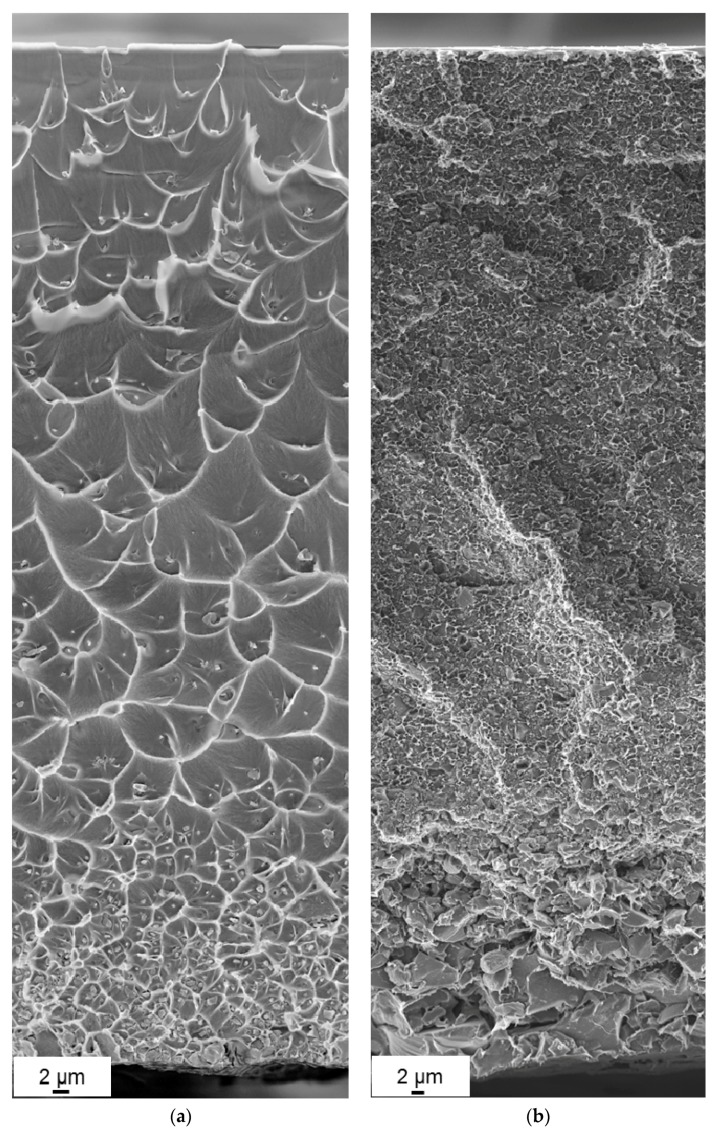
Surface and cross-section morphologies for the MMMs of Matrimid® and AC have been analyzed. In Figure 4a,b, representative SEM surface images of the pure Matrimid® and the filled MMMs are shown. The topography is smooth in case of the pure Matrimid® membrane while due to the incorporation of the AC in the MMMs the roughness is increased. The surface of the membranes does not exhibit defects that could affect the gas separation properties. The filler particles are covered by a thin layer of polymer, which indicates the good compatibility of these different materials as it was already concluded from the thermal analysis. Additional information was revealed from the cross-section images. In Figure 5, it is shown that the AC particles are well incorporated into the polymer matrix as already indicated by the surface view of Figure 4b. A continuous solid interface between the carbon particles and the polymer was found from the SEM. This is in agreement with literature [23,24].
Figure 4.
SEM images of (a) the surface of a pure Matrimid® membrane; (b) surface of a Matrimid® MMM with 44 vol % AC.
Figure 5.
SEM image of a fracture surface of a Matrimid® MMM with (a) 8 vol % AC and (b) 50 vol % AC. The increased concentration of the AC particles at the bottom of the membrane due to the membrane preparation is visible. The “crater”-like morphology is observed in the case of the 8 vol % AC while it is not visible for the 50 vol % AC due to the high content of fillers.
Figure 5a of the MMM with 8 vol % of AC shows an interesting type of morphology of the composite is indicated. This morphology is the “crater” like morphology deriving from the inclusion of the activated carbon into the polymer matrix, which is also referred to in literature [22,35,36]. Also, the ductile behavior during fracture of the Matrimid® MMM is visible. The particles act as the centers of the ductile fracture and this is also in agreement with literature [37]. Furthermore, the morphology is affected strongly by the incorporation of a high amount of filler particles. As can be seen in Figure 5b of the MMM with 50 vol %, the polymer domains that include the filler particles are now significantly smaller and almost not detectable. A closer observation of the bottom part of Figure 5a—bottom part of the cast membrane with 8 vol % AC particles—indicates an increase of particle concentration in that area, similar to what is also mentioned by Fernández-Barquín et al. in case of mixed-matrix membranes of zeolite with poly(1-trimethylsilyl-1-propyne) (PTMSP) [38]. This can be explained by the method of the membrane fabrication through solvent evaporation. The solvent does not evaporate instantly; rather, the controlled solvent evaporation is effected over a period of more than 24 h by applying a small nitrogen flowrate through the covering compartment above the membrane preparation mold. This gives the solvent enough time to penetrate into the small pores of the filler particles. In that way, the particles are filled up with chloroform and obtain higher density so that they partially sediment. Nevertheless, since the polymer and the particles are well compatible, the polymer keeps the particles in place and the membrane is absolutely stable, allowing for easy handling. Another indication of the good stability is that the membranes were not raptured during the gas transport measurement. Hence, there is a prospect of further AC modification by incorporation of substances able to interact specifically with components of the gas mixture to be separated into the porous structure and thus increase membrane performance.
3.3. Gas Transport Characterization Results
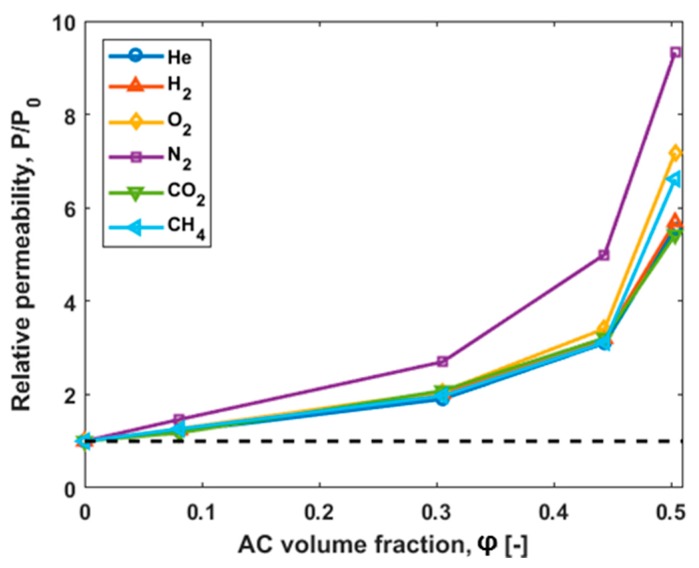
The time-lag method was used for the evaluation of the permeability, the diffusivity and the solubility coefficients of the MMMs for the gases He, H2, O2, N2, CO2, and CH4. The pure gas permeability data determined for Matrimid® and the MMMs at 30 °C and 1000 mbar feed pressure are presented in Table 3. The gas permeabilities of filled Matrimid® are higher than those of pure Matrimid® and increase as the filler volume fraction increases. The trend for all gases is shown in Figure 6, which presents the relative permeability of Matrimid® compared to the filled Matrimid® MMMs as a function of the volume fraction.
Table 3.
Permeability of the different MMMs with the different volume fraction of activated carbon φAC at 30 °C.
| [%] | P [Barrer] * | |||||
|---|---|---|---|---|---|---|
| He | H2 | O2 | N2 | CO2 | CH4 | |
| 0 | 28.3 | 31.6 | 2.41 | 0.30 | 12.3 | 0.34 |
| 8 | 34.2 | 39.0 | 3.06 | 0.44 | 14.5 | 0.43 |
| 31 | 53.8 | 63.8 | 4.97 | 0.81 | 25.6 | 0.67 |
| 44 | 87.8 | 101 | 8.22 | 1.50 | 39.5 | 1.06 |
| 50 | 157 | 180 | 17.3 | 2.80 | 66.7 | 2.25 |
* 1 Barrer = 10−10 [cm3STP/(cm s cmHg)] = 2.7 × 10−9 [Nm3/(m h bar)].
Figure 6.
Ratio of permeability of MMMs (P) to that of unfilled polymer (P0) as a function of the AC volume fraction. The relative enhancement of permeability of MMMs as a function of AC volume fraction at 30 °C depends on the gas (dotted line: relative permeability for Matrimid®).
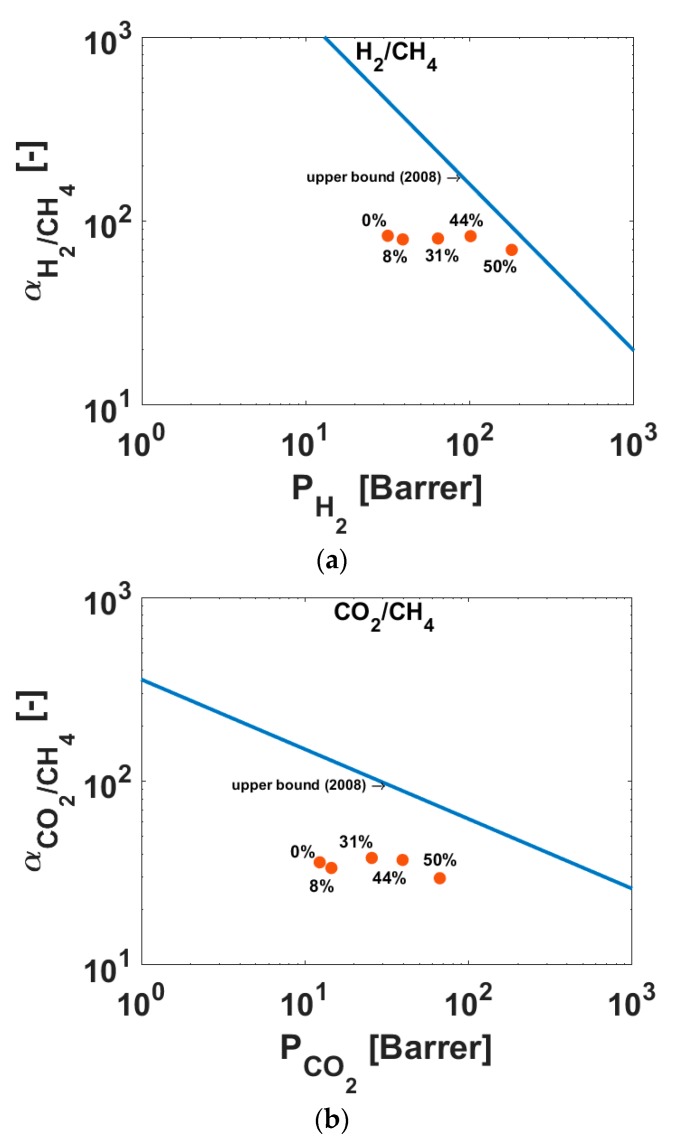
With an AC content of 50 vol %, strongly increasing permeabilities for all gases are observed. For example, the permeability coefficient of hydrogen changes from 31.6 Barrer in case of the pure Matrimid® to 180 Barrer for the MMM with 50 vol % AC content; here the permeability increases by a factor of 5.7. The permeability of CH4 increases from 0.34 Barrer (pure Matrimid®) to 2.25 Barrer (50 vol % AC in Matrimid®), meaning that the permeability increases with a factor of 6.6. This means that a slight change in the permselectivities of H2/CH4 occurs. In Figure 7a, the permselectivities of H2/CH4 over the permeabilities of H2 are shown for the different membranes. In the same plot, the Robeson upper bound (2008) [3] is presented and it is observed that the performance of the produced membranes approaches this bound with increasing amounts of activated carbon in the MMMs compared to pure Matrimid®.
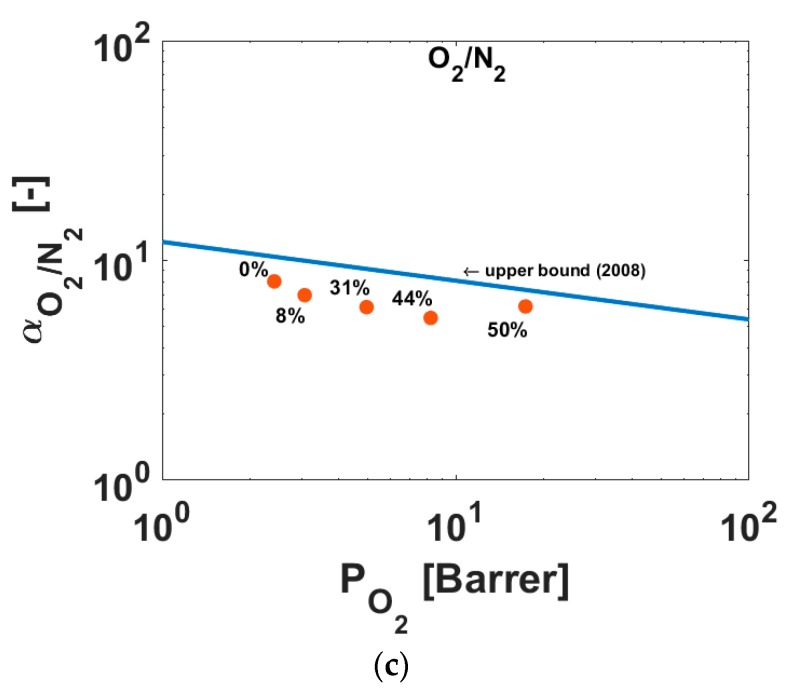
Figure 7.
(a) H2/CH4, (b) CO2/CH4 and (c) O2/N2 permselectivities of MMMs for different loadings of AC particles at 30 °C.
In Figure 6, the increase of the permeabilities of the MMMs compared to the permeability of the pure Matrimid® is presented. For the gases CO2, H2, and He, the same increasing trend of the permeabilities was found. The permeabilities of CH4 and O2 increase slightly more while N2 has the highest increase.
For CO2/CH4, a slight decrease of permselectivity over the amount of fillers is observed, due to the higher increase of CH4 permeability, but both permeabilities rise with the amount of filler. In Figure 7b the permselectivity of the gas pair CO2/CH4 is shown. Even though the permselectivity is decreasing, a closer approach to the Robeson bound (2008) with a higher amount of AC in the MMMs compared to pure Matrimid® is observed, because of the highly increasing permeabilities of the gases. In Figure 7c, the permselectivity of O2/N2 over the permeability of O2 is shown and the same trend is observed. For the gas pairs H2/CH4, CO2/CH4, and O2/N2, the permselectivities are listed in Table 4.
Table 4.
Permselectivities for the gas pairs H2/CH4, CO2/CH4, and O2/N2 at 30 °C for the MMMs with different AC volume content and the corresponding Knudsen selectivity.
| [%] | Permselectivity [-] | ||
|---|---|---|---|
| H2/CH4 | CO2/CH4 | O2/N2 | |
| 0 | 94.4 | 36.8 | 8.11 |
| 8 | 90.2 | 33.4 | 7.04 |
| 31 | 95.7 | 38.3 | 6.16 |
| 44 | 95.8 | 37.4 | 5.48 |
| 50 | 80.2 | 29.7 | 6.19 |
| Knudsen selectivity | 2.82 | 0.60 | 0.94 |
Furthermore, in order to investigate the existence of defects on the membranes, the Knudsen selectivity was calculated employing Equation (7):
| (7) |
where M is the molecular mass of the gas.
Comparing the permselectivities values with the calculated Knudsen selectivity values (Table 4) indicates that the values are not in agreement. Hence, the gas transport in the membranes is still controlled by the solution–diffusion mechanism of the polymer and the contribution of the dispersed AC particles. The trend of the increase of the permeabilities in the MMMs is based on the solubilities and diffusivities (see Equation (3)), and it will be explained further below.
3.4. Sorption Results
The pure gas solubility coefficients of the investigated gases in Matrimid® 5218 and the MMMs determined according to Equation (3) from time-lag experiments at 30 °C are presented in Table 5.
Table 5.
Solubility coefficient Seff of the different MMMs at 30 °C for the different AC volume content.
| [%] | Seff [10−3 cm3STP/(cm3 cm Hg)] | |||||
|---|---|---|---|---|---|---|
| He | H2 | O2 | N2 | CO2 | CH4 | |
| 0 | 0.35 | 2.02 | 13.2 | 7.80 | 248 | 46.6 |
| 8 | 0.55 | 2.35 | 14.0 | 9.71 | 282 | 41.3 |
| 31 | 1.01 | 3.21 | 17.7 | 15.6 | 289 | 60.2 |
| 44 | 1.56 | 4.13 | 20.9 | 17.4 | 287 | 60.2 |
| 50 | 1.70 | 4.78 | 25.7 | 22.2 | 242 | 74.0 |
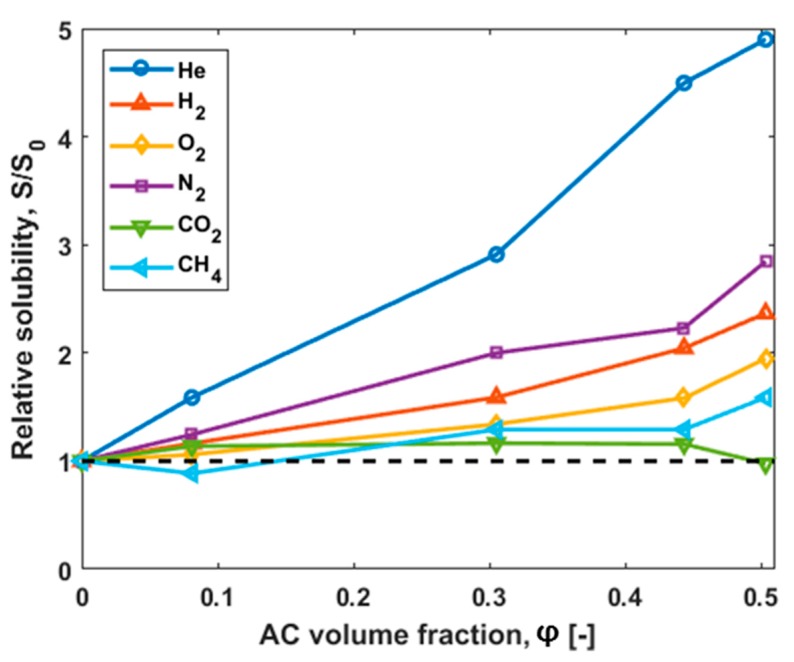
The increasing trend of the relative solubility of the investigated gases in the MMMs with the increase of the AC content compared to the pure Matrimid® is shown in Figure 8.
Figure 8.
Ratio of solubility of MMMs (S) to that of unfilled polymer (S0) as a function of the AC volume fraction. The relative enhancement of solubility of gases in MMMs as a function of AC volume fraction at 30 °C depends on the gas (dotted line: relative permeability of Matrimid®).
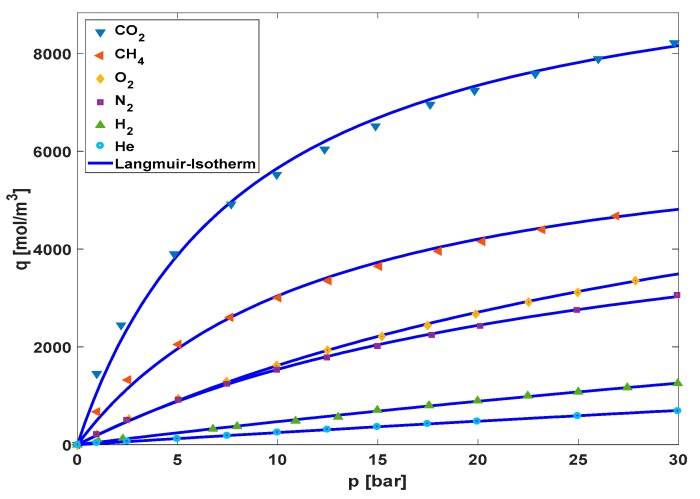
To explain the trend for the sorption coefficient Seff in the MMMs, one should consider the adsorption isotherms of the activated carbon, which are crucial for the separation performance of the resulting MMMs. Adsorption isotherms of He, H2, O2, N2, CO2, and CH4 have been measured at 30 °C. The equilibrium can be described by the Langmuir-isotherm Equation (8) [39]. The equation for the isotherm is given as:
| (8) |
where q is the adsorbate concentration, p the pressure, and qmax the maximum adsorbate concentration possible for a monolayer coverage of the considered component on the investigated adsorbent. The parameter b also is specific for an adsorbate–adsorbent pair.
In Figure 9, the adsorption isotherms for the different gases are shown, and in Table 6 the Langmuir parameters are listed.
Figure 9.
Experimentally measured concentrations for the different gases over the pressure and the corresponding adsorption-isotherm at 30 °C.
Table 6.
Langmuir-isotherm equation parameters at 30 °C.
| Gases | qmax [mol/m3] | b [1/bar] |
|---|---|---|
| He | 8069 | 0.0032 |
| H2 | 7500 | 0.0067 |
| O2 | 8270 | 0.0244 |
| N2 | 5864 | 0.0357 |
| CO2 | 10,479 | 0.1174 |
| CH4 | 6788 | 0.0813 |
As expected for AC adsorbents, CO2 has the highest maximum loading combined with the fastest kinetics, followed by methane, as an example for a light hydrocarbon gas. The permanent gases helium, hydrogen, oxygen, and nitrogen all show considerably smaller adsorption tendency. The difference between oxygen and nitrogen appears to be governed by the high maximum loading of oxygen. In contrast, the favorable adsorption of hydrogen in the investigated pressure range is assumed to be due to the faster kinetics, when compared to helium.
The time lag experiments were done at low feed pressure (1000 mbar), which means that a Henry coefficient for the gas adsorption-isotherm can be obtained. At zero loading the Langmuir-isotherm Equation (8) simplified to the Henry Equation (9) [39].
| (9) |
where the Henry constant H is qmaxb.
In the most simple form, the adsorption in glassy polymers can also be assumed to show linear behavior (Equation (10)) [1],
| (10) |
where S is the solubility coefficient of the pure Matrimid®, c the concentration which is adsorbed and p the pressure.
The comparison of the two adsorption coefficients for the pure materials is possible. In Table 7, the Henry and the solubility coefficients for all gases are shown. The ratio between H and S follows the same trend as for the time-lag measurements. In more detail, the H/S ratio for CO2 is the smallest, and for He the ratio is the highest. As a result, the trend of the ratio of the pure materials follows the trend observed from the time-lag measurements (Figure 8) described in the following series:
| CO2 < CH4 < O2 < H2 < N2 < He |
Table 7.
Henry coefficient H, solubility coefficient S, and the ratio of them (H/S) for the studied gases at 30 °C.
| Gases | H [mol/(m3·bar)] | S [mol/(m3·bar)] | H/S [-] |
|---|---|---|---|
| He | 25.7 | 1.16 | 22.3 |
| H2 | 50.3 | 6.76 | 7.43 |
| O2 | 202 | 44.4 | 4.54 |
| N2 | 209 | 26.2 | 7.99 |
| CO2 | 1230 | 831 | 1.48 |
| CH4 | 552 | 156 | 3.54 |
3.5. Diffusion Coefficient
Analyzing the diffusion coefficients presented in Table 8 for all the studied membranes allows an estimation of the influence of the AC on the gas transport properties.
Table 8.
Diffusion coefficients Deff of MMMs with different AC loading at 30°.
| [%] | Deff [10−7 cm2/s] | |||||
|---|---|---|---|---|---|---|
| He | H2 | O2 | N2 | CO2 | CH4 | |
| 0 | 81.5 | 15.7 | 0.182 | 0.0381 | 0.0497 | 0.00719 |
| 8 | 62.0 | 16.6 | 0.219 | 0.0448 | 0.0512 | 0.0105 |
| 31 | 54.6 | 19.9 | 0.282 | 0.0518 | 0.0885 | 0.0111 |
| 44 | 56.4 | 24.5 | 0.393 | 0.0864 | 0.138 | 0.0176 |
| 50 | 92.9 | 37.7 | 0.673 | 0.126 | 0.275 | 0.0304 |
The AC has pores below 2 nm, meaning that the samples belong to the region of microporous materials and below the region of Knudsen diffusion [39]. Also, the gas component diameter is not much bigger than the AC pore diameter, leading to the conclusion that the AC behaves as a material where configurational diffusion is the dominant transport mechanism, i.e., the diffusion coefficient can be described by surface diffusion [40].
Since it was not possible to measure the diffusion coefficient of the AC directly, due to the feature of the powder and the experimental set up used, the diffusion coefficient was estimated from the time-lag measurements of the Matrimid® MMMs. To calculate the diffusion coefficient for the AC, the values of pure Matrimid® and the MMMs with 50 vol % are compared. The assumption is that the diffusion coefficient of AC has an influence of 50% in the MMMs with 50 vol % AC inside. This leads to the values of Table 9 for the diffusion coefficient of AC.
Table 9.
Diffusion coefficient estimated by the time-lag measurements and permeability of the AC particles at 1000 mbar feed pressure as estimated by the diffusion and the Henry coefficients from the time-lag and sorption measurements, respectively.
| Coefficients | He | H2 | O2 | N2 | CO2 | CH4 |
|---|---|---|---|---|---|---|
| DAC [cm2/s] | 1.0 × 10−5 | 6.0 × 10−6 | 1.2 × 10−7 | 2.1 × 10−8 | 5.0 × 10−8 | 5.4 × 10−9 |
| PAC [Barrer] | 800 | 898 | 70.2 | 13.4 | 184 | 8.84 |
With Equation (11), it is possible to get a permeability for the inorganic filler for small pressures, since HAC is only valid for small pressures.
| (11) |
3.6. Permeability Predictions
To predict the permeability of MMMs, a number of models have been suggested. Shimekit et al. as well as Vinh-Thang and Laliagiune give an overview of existing models and by using experimental data they predict the permeability of MMMs for different gases [41,42]. The simplest model to be applied is the Maxwell model. The Maxwell model was originally developed to simulate the electrical conductivity of composite materials [43]. It was shown that the equation is also valid for the flux through membranes containing a dispersed phase in the matrix of a polymer [44]. The Maxwell model provides values valid only for low particle loadings (0 < φd < 0.2). The description of the Maxwell model is given by the following Equation (12):
| (12) |
where Peff is the effective permeability, Pc is the permeability of the continuous phase (Matrimid®), Pd the permeability of the dispersed phase (AC), and φd the volume fraction of the disperse phase (AC).
For medium particle loadings, the Bruggeman model is better suited to predict the permeability. The Bruggeman equation was developed for the prediction of the dielectric constant of composite materials and has been adopted to simulate the gas transport properties of MMMs [45].
The Bruggeman model is described in Equation (13) below:
| (13) |
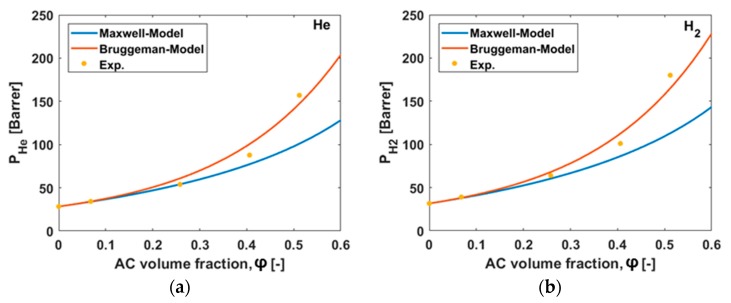
In Figure 10, the model predictions for the gases He, H2, O2, N2, CO2, and CH4 compared to the experimental values are shown. Both models provide good predictions of the permeability for small AC volume fraction (0 < φd < 0.2), while at a medium volume fraction (0 < φd < 0.4) the Bruggeman model assumptions are still reasonable. At high AC volume fractions, the deviations for both models become more significant, but the trend reflects the experimental data. It should be mentioned that in the literature, many different approaches and models exist for the interpretation of the permeability of different gases in MMM [46,47,48,49], nevertheless for this work the simplest models of Maxwell and Bruggeman are used in order to avoid more assumptions. For example, the Lewis–Nielsen model can be applied, but the estimation of an accurate maximum packing volume fraction of the filler particles would be an additional assumption [50,51]. Most of the newer ideal models are enhancements of the Maxwell or Bruggeman models, and therefore the initial models were used to avoid additional assumptions.
Figure 10.
(a–f) Comparison of the experimental results (points) with the predictions of the Maxwell model (blue line) and the Bruggeman model (orange line) at 30 °C for the different gases and the different AC volume fraction used in this work.
Since both models predict the MMMs permeabilities in the valid regions for both models quite well, the hypotheses for predicting the permeability of AC is valid. By combining the results of the adsorption measurements for solubility with the results of the time-lag experiments, involving a contribution hypothesis for diffusivity, the results indicate that the overall MMM permeability is greatly influenced by the AC. That means that the experimental results for the permeability of the MMMs for the different gases are valid as well.
4. Conclusions
Matrimid® MMMs were prepared by introducing microporous AC particles up to a high volume content to investigate the effect of filler on the transport properties, thermal properties, and morphology. The obtained experimental results demonstrate that it is possible to form defect-free MMMs of Matrimid® and AC. From the thermal analysis, the influence of AC content on the polymer was revealed. A small increase in the glass transition temperature was observed, indicating that the particles were well incorporated into the polymer matrix. The thermogravimetric analysis allowed for the estimation of the AC content with a better accuracy, which is important for the correlation of the results of the gas transport properties. The characterization by scanning electron microscopy indicated the good adaption of the AC in the polymer matrix, while the increase of AC content led to the partial concentration of the particles on the bottom side of the membranes without a decrease in the membrane stability, as it was also verified by the successful time-lag experiments. Both components are very well compatible when chloroform is used as a solvent and do not form any significant gaps on the AC particle and glassy polymer interface during the solvent evaporation even when the filler particles have very sharp edges and non-uniform shape. The filler particles have a significant influence on the gas transport properties of the studied membranes. The permeability coefficients of all gases increase with increasing the AC content while the selectivity remains stable for most of the gas pairs. The effect of the increasing permeabilities derives from the adsorption of the gases on the AC. With increasing content of AC in the MMMs, the influence on the sorption and diffusion, and finally the relative permeability increases. Hence, the results clearly demonstrate that the selected approach improves the membrane performance and allows for the fabrication of membrane materials closely approaching the upper bound identified by Robeson [3] for the investigated gas pairs. A prospect for further application is the preparation of MMMs with AC particles that incorporate into their porous structure substances, which are able to interact specifically with components of the gas mixture under separation. Hence, a further increase of the membrane performance appears to be possible.
Acknowledgments
We gratefully acknowledge financial support from the Federal Ministry of Education and Research of Germany (BMBF) via the project HyScore (FKZ: 03SF0532A-D). We are grateful to Blücher GmbH (Erkrath, Germany) for the supply of high performance activated carbon adsorbents. The authors thank Ivonne Ternes and Silvio Neumann for thermal analysis experiments, Jelena Lillepärg for assistance on the sorption balance experiments, and Clarissa Abetz and Anke-Lisa Metze for the scanning electron microscopy experiments.
Nomenclature
| θ | time-lag, [s] |
| l | membrane film thickness, [m] |
| Deff,i | effective diffusion coefficient of component i, [cm2/s] |
| Peff,i | effective permeability of component i, [Barrer] |
| Ni | volumetric flowrate of component i, [Nm3/h] |
| Am | membrane area, [m2] |
| Δpi | partial pressure difference between feed an permeate side of component i, [bar] |
| Seff,i | effective solubility coefficient of component i, [cm3STP/(cm3 cmHg)]; [mol/(m3 bar)] |
| αij | selectivity of component i and j, [-] |
| Tg | glass transition temperature, [°C] |
| T | temperature, [°C] |
| wAC | weight content of AC in MMM, [%] |
| mr,i | remaining relative mass of AC, MMM or Matrimid®, [%] |
| φAC | volume content of AC in MMM, [%] |
| ρi | density of component i, [kg/m3] |
| Mi | molecular mass of the component i, [kg/mol] |
| q | adsorption concentration, [mol/m3] |
| qmax | the maximum adsorbed concentration possible for a monolayer coverage, [mol/m3] |
| p | pressure, [bar] |
| b | parameter for an adsorbate-adsorbent pair, [1/bar] |
| H | Henry coefficient, [mol/(m3 bar)] |
| c | concentration, [mol/m3] |
| Pc | permeability continuous phase, [Barrer] |
| Pd | permeability dispersed phase, [Barrer] |
| φd | volume fraction dispersed phase, [-] |
Subscripts
| eff | effective |
| AC | activated carbon |
| MMM | mixed-matrix membrane |
| g | glass transition |
| i,j | gas component i or j (He, H2, O2, N2, CO2 or CH4) |
| c | continuous phase |
| d | dispersed phase |
| Kn | Knudsen |
| r | remaining relative mass |
Author Contributions
Prokopios Georgopanos, Volkan Filiz, Torsten Brinkmann, and Volker Abetz conceived the idea; Prokopios Georgopanos and Fynn Weigelt designed, performed and/or evaluated the experiments; Sergey Shishatskiy, Volkan Filiz, Torsten Brinkmann, and Volker Abetz assisted on the evaluations of the experiments; Fynn Weigelt and Prokopios Georgopanos wrote the paper while all the authors contributed to the scientific discussion, revision, and finalization of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Baker R.W. Membrane Technology and Applications. John Wiley & Sons; Hoboken, NJ, USA: 2000. [Google Scholar]
- 2.Robeson L.M. Correlation of separation factor versus permeability for polymeric membranes. J. Membr. Sci. 1991;62:165–185. doi: 10.1016/0376-7388(91)80060-J. [DOI] [Google Scholar]
- 3.Robeson L.M. The upper bound revisited. J. Membr. Sci. 2008;320:390–400. doi: 10.1016/j.memsci.2008.04.030. [DOI] [Google Scholar]
- 4.Freeman B., Yampolskii Y., Pinnau I. Materials Science of Membranes for Gas and Vapor Separation. John Wiley & Sons; Hoboken, NJ, USA: 2006. [Google Scholar]
- 5.Gascon J., Kapteijn F., Zornoza B., Sebastián V., Casado C., Coronas J. Practical approach to zeolitic membranes and coatings: State of the art, opportunities, barriers, and future perspectives. Chem. Mater. 2012;24:2829–2844. doi: 10.1021/cm301435j. [DOI] [Google Scholar]
- 6.Aroon M., Ismail A., Matsuura T., Montazer-Rahmati M. Performance studies of mixed matrix membranes for gas separation: A review. Sep. Purif. Technol. 2010;75:229–242. doi: 10.1016/j.seppur.2010.08.023. [DOI] [Google Scholar]
- 7.Chung T.-S., Jiang L.Y., Li Y., Kulprathipanja S. Mixed matrix membranes (MMMS) comprising organic polymers with dispersed inorganic fillers for gas separation. Prog. Polym. Sci. 2007;32:483–507. doi: 10.1016/j.progpolymsci.2007.01.008. [DOI] [Google Scholar]
- 8.Rezakazemi M., Amooghin A.E., Montazer-Rahmati M.M., Ismail A.F., Matsuura T. State-of-the-art membrane based CO2 separation using mixed matrix membranes (MMMS): An overview on current status and future directions. Prog. Polym. Sci. 2014;39:817–861. doi: 10.1016/j.progpolymsci.2014.01.003. [DOI] [Google Scholar]
- 9.Vinoba M., Bhagiyalakshmi M., Alqaheem Y., Alomair A.A., Pérez A., Rana M.S. Recent progress of fillers in mixed matrix membranes for CO2 separation: A review. Sep. Purif. Technol. 2017;188:431–450. doi: 10.1016/j.seppur.2017.07.051. [DOI] [Google Scholar]
- 10.Wang M., Wang Z., Zhao S., Wang J., Wang S. Recent advances on mixed matrix membranes for CO2 separation. Chin. J. Chem. Eng. 2017;25:1581–1597. doi: 10.1016/j.cjche.2017.07.006. [DOI] [Google Scholar]
- 11.Galizia M., Chi W.S., Smith Z.P., Merkel T.C., Baker R.W., Freeman B.D. 50th anniversary perspective: Polymers and mixed matrix membranes for gas and vapor separation: A review and prospective opportunities. Macromolecules. 2017;50:7809–7843. doi: 10.1021/acs.macromol.7b01718. [DOI] [Google Scholar]
- 12.Tena A., Fernández L., Sánchez M., Palacio L., Lozano A., Hernández A., Prádanos P. Mixed matrix membranes of 6FDA-6FpDA with surface functionalized γ-alumina particles. An analysis of the improvement of permselectivity for several gas pairs. Chem. Eng. Sci. 2010;65:2227–2235. doi: 10.1016/j.ces.2009.12.023. [DOI] [Google Scholar]
- 13.Rahman M.M., Filiz V., Shishatskiy S., Abetz C., Georgopanos P., Khan M.M., Neumann S., Abetz V. Influence of poly (ethylene glycol) segment length on CO2 permeation and stability of polyactive membranes and their nanocomposites with peg poss. ACS Appl. Mater. Interfaces. 2015;7:12289–12298. doi: 10.1021/am504223f. [DOI] [PubMed] [Google Scholar]
- 14.Rahman M.M., Shishatskiy S., Abetz C., Georgopanos P., Neumann S., Khan M.M., Filiz V., Abetz V. Influence of temperature upon properties of tailor-made PEBAX® Mh 1657 nanocomposite membranes for post-combustion CO2 capture. J. Membr. Sci. 2014;469:344–354. doi: 10.1016/j.memsci.2014.06.048. [DOI] [Google Scholar]
- 15.Khan M.M., Filiz V., Bengtson G., Rahman M.M., Shishatskiy S., Abetz V. Functionalized carbon nanotube mixed matrix membranes of polymers of intrinsic microporosity (PIMs) for gas separation. Procedia Eng. 2012;44:1899–1901. doi: 10.1016/j.proeng.2012.08.997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Moghadam F., Omidkhah M., Vasheghani-Farahani E., Pedram M., Dorosti F. The effect of tio2 nanoparticles on gas transport properties of matrimid5218-based mixed matrix membranes. Sep. Purif. Technol. 2011;77:128–136. doi: 10.1016/j.seppur.2010.11.032. [DOI] [Google Scholar]
- 17.Bengtson G., Oehring M., Fritsch D. Improved dense catalytically active polymer membranes of different configuration to separate and react organics simultaneously by pervaporation. Chem. Eng. Process. Process Intensif. 2004;43:1159–1170. doi: 10.1016/j.cep.2004.01.009. [DOI] [Google Scholar]
- 18.Kanehashi S., Chen G.Q., Scholes C.A., Ozcelik B., Hua C., Ciddor L., Southon P.D., D’Alessandro D.M., Kentish S.E. Enhancing gas permeability in mixed matrix membranes through tuning the nanoparticle properties. J. Membr. Sci. 2015;482:49–55. doi: 10.1016/j.memsci.2015.01.046. [DOI] [Google Scholar]
- 19.Wright W.W., Hallden-Abberton M. Ullmann’s Encyclopedia of Industrial Chemistry. John Wiley & Sons; Hoboken, NJ, USA: 2002. Polyimides. [Google Scholar]
- 20.David O.C., Gorri D., Urtiaga A., Ortiz I. Mixed gas separation study for the hydrogen recovery from H2/CO/N2/CO2 post combustion mixtures using a matrimid membrane. J. Membr. Sci. 2011;378:359–368. doi: 10.1016/j.memsci.2011.05.029. [DOI] [Google Scholar]
- 21.Khan A.L., Sree S.P., Martens J.A., Raza M.T., Vankelecom I.F. Mixed matrix membranes comprising of matrimid and mesoporous COK-12: Preparation and gas separation properties. J. Membr. Sci. 2015;495:471–478. doi: 10.1016/j.memsci.2015.08.008. [DOI] [Google Scholar]
- 22.Naseri M., Mousavi S.F., Mohammadi T., Bakhtiari O. Synthesis and gas transport performance of mil-101/matrimid mixed matrix membranes. J. Ind. Eng. Chem. 2015;29:249–256. doi: 10.1016/j.jiec.2015.04.007. [DOI] [Google Scholar]
- 23.Dong X., Liu Q., Huang A. Highly permselective MIL-68 (Al)/matrimid mixed matrix membranes for CO2/CH4 separation. J. Appl. Polym. Sci. 2016;133 doi: 10.1002/app.43485. [DOI] [Google Scholar]
- 24.Zhang Y., Balkus K.J., Musselman I.H., Ferraris J.P. Mixed-matrix membranes composed of Matrimid® and mesoporous ZSM-5 nanoparticles. J. Membr. Sci. 2008;325:28–39. doi: 10.1016/j.memsci.2008.04.063. [DOI] [Google Scholar]
- 25.Mushardt H., Kramer V., Hülagü D., Brinkmann T., Kraume M. Development of solubility selective mixed matrix membranes for gas separation. Chem. Ing. Tech. 2014;86:83–91. doi: 10.1002/cite.201300074. [DOI] [Google Scholar]
- 26.Mushardt H., Müller M., Shishatskiy S., Wind J., Brinkmann T. Detailed investigation of separation performance of a MMM for removal of higher hydrocarbons under varying operating conditions. Membranes. 2016;6:16. doi: 10.3390/membranes6010016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Ghanem B.S., McKeown N.B., Budd P.M., Al-Harbi N.M., Fritsch D., Heinrich K., Starannikova L., Tokarev A., Yampolskii Y. Synthesis, characterization, and gas permeation properties of a novel group of polymers with intrinsic microporosity: PIM-polyimides. Macromolecules. 2009;42:7881–7888. doi: 10.1021/ma901430q. [DOI] [Google Scholar]
- 28.Soave G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972;27:1197–1203. doi: 10.1016/0009-2509(72)80096-4. [DOI] [Google Scholar]
- 29.Pye D., Hoehn H., Panar M. Measurement of gas permeability of polymers. I. Permeabilities in constant volume/variable pressure apparatus. J. Appl. Polym. Sci. 1976;20:1921–1931. doi: 10.1002/app.1976.070200719. [DOI] [Google Scholar]
- 30.Shishatskiy S., Nistor C., Popa M., Nunes S.P., Peinemann K.V. Polyimide asymmetric membranes for hydrogen separation: Influence of formation conditions on gas transport properties. Adv. Eng. Mater. 2006;8:390–397. doi: 10.1002/adem.200600024. [DOI] [Google Scholar]
- 31.Blume I., Smit E., Wessling M., Smolders C. Macromolecular Symposia. Wiley Online Library; Hoboken, NJ, USA: 1991. Diffusion through Rubbery and Glassy Polymer Membranes; pp. 237–257. [Google Scholar]
- 32.Frisch H.L. The time lag in diffusion. J. Phys. Chem. 1957;61:93–95. doi: 10.1021/j150547a018. [DOI] [Google Scholar]
- 33.Bansal A., Yang H., Li C., Cho K., Benicewicz B.C., Kumar S.K., Schadler L.S. Quantitative equivalence between polymer nanocomposites and thin polymer films. Nat. Mater. 2005;4:693–698. doi: 10.1038/nmat1447. [DOI] [PubMed] [Google Scholar]
- 34.Schadler L.S., Kumar S.K., Benicewicz B.C., Lewis S.L., Harton S.E. Designed interfaces in polymer nanocomposites: A fundamental viewpoint. MRS Bull. 2007;32:335–340. doi: 10.1557/mrs2007.232. [DOI] [Google Scholar]
- 35.Perez E.V., Balkus K.J., Ferraris J.P., Musselman I.H. Mixed-matrix membranes containing MOF-5 for gas separations. J. Membr. Sci. 2009;328:165–173. doi: 10.1016/j.memsci.2008.12.006. [DOI] [Google Scholar]
- 36.Ordonez M.J.C., Balkus K.J., Ferraris J.P., Musselman I.H. Molecular sieving realized with ZIF-8/Matrimid® mixed-matrix membranes. J. Membr. Sci. 2010;361:28–37. doi: 10.1016/j.memsci.2010.06.017. [DOI] [Google Scholar]
- 37.Mahdi E.M., Tan J.-C. Mixed-matrix membranes of zeolitic imidazolate framework (ZIF-8)/Matrimid nanocomposite: Thermo-mechanical stability and viscoelasticity underpinning membrane separation performance. J. Membr. Sci. 2016;498:276–290. doi: 10.1016/j.memsci.2015.09.066. [DOI] [Google Scholar]
- 38.Fernández-Barquín A., Casado-Coterillo C., Palomino M., Valencia S., Irabien A. Lta/poly (1-trimethylsilyl-1-propyne) mixed-matrix membranes for high-temperature CO2/N2 separation. Chem. Eng. Technol. 2015;38:658–666. doi: 10.1002/ceat.201400641. [DOI] [Google Scholar]
- 39.Do D.D. Adsorption Analysis: Equilibria and Kinetics. Volume 2 World Scientific; Singapore: 1998. [Google Scholar]
- 40.Choi J.-G., Do D., Do H. Surface diffusion of adsorbed molecules in porous media: Monolayer, multilayer, and capillary condensation regimes. Ind. Eng. Chem. Res. 2001;40:4005–4031. doi: 10.1021/ie010195z. [DOI] [Google Scholar]
- 41.Shimekit B., Mukhtar H., Murugesan T. Prediction of the relative permeability of gases in mixed matrix membranes. J. Membr. Sci. 2011;373:152–159. doi: 10.1016/j.memsci.2011.02.038. [DOI] [Google Scholar]
- 42.Vinh-Thang H., Kaliaguine S. Predictive models for mixed-matrix membrane performance: A review. Chem. Rev. 2013;113:4980–5028. doi: 10.1021/cr3003888. [DOI] [PubMed] [Google Scholar]
- 43.Maxwell J.C. A Treatise on Electricity and Magnetism. Volume 1 Clarendon Press; Wotton-under-Edge, UK: 1881. [Google Scholar]
- 44.Bouma R., Checchetti A., Chidichimo G., Drioli E. Permeation through a heterogeneous membrane: The effect of the dispersed phase. J. Membr. Sci. 1997;128:141–149. doi: 10.1016/S0376-7388(96)00303-1. [DOI] [Google Scholar]
- 45.Banhegyi G. Comparison of electrical mixture rules for composites. Colloid Polym. Sci. 1986;264:1030–1050. doi: 10.1007/BF01410321. [DOI] [Google Scholar]
- 46.Moore T.T., Mahajan R., Vu D.Q., Koros W.J. Hybrid membrane materials comprising organic polymers with rigid dispersed phases. AIChE J. 2004;50:311–321. doi: 10.1002/aic.10029. [DOI] [Google Scholar]
- 47.Li Y., Guan H.-M., Chung T.-S., Kulprathipanja S. Effects of novel silane modification of zeolite surface on polymer chain rigidification and partial pore blockage in polyethersulfone (PES)–zeolite a mixed matrix membranes. J. Membr. Sci. 2006;275:17–28. doi: 10.1016/j.memsci.2005.08.015. [DOI] [Google Scholar]
- 48.Casado-Coterillo C., Soto J., Jimaré M.T., Valencia S., Corma A., Téllez C., Coronas J. Preparation and characterization of ITQ-29/polysulfone mixed-matrix membranes for gas separation: Effect of zeolite composition and crystal size. Chem. Eng. Sci. 2012;73:116–122. doi: 10.1016/j.ces.2012.01.024. [DOI] [Google Scholar]
- 49.Casado-Coterillo C., Fernández-Barquín A., Zornoza B., Téllez C., Coronas J., Irabien Á. Synthesis and characterisation of MOF/ionic liquid/chitosan mixed matrix membranes for CO2/N2 separation. RSC Adv. 2015;5:102350–102361. doi: 10.1039/C5RA19331A. [DOI] [Google Scholar]
- 50.Lewis T., Nielsen L. Dynamic mechanical properties of particulate-filled composites. J. Appl. Polym. Sci. 1970;14:1449–1471. doi: 10.1002/app.1970.070140604. [DOI] [Google Scholar]
- 51.Shen Y., Lua A.C. Theoretical and experimental studies on the gas transport properties of mixed matrix membranes based on polyvinylidene fluoride. AIChE J. 2013;59:4715–4726. doi: 10.1002/aic.14186. [DOI] [Google Scholar]