Abstract
The influence of maleated polypropylene (MAPP) on the non-isothermal crystallization behavior of wood fiber (WF)-reinforced PP composites (WPCs) was investigated by a differential scanning calorimeter (DSC). The results showed that MAPP as a nucleation agent accelerated the crystallization rate of the PP matrix in WPC under the cooling process. The corresponding crystallization kinetics and activation energy were further analyzed using the Avrami method, Avrami–Ozawa method, Kissinger method, and Friedman method. The results demonstrated that MAPP significantly changed the crystal growth mechanism of the PP matrix to heterogeneous nucleation for acicular and tabular crystal growth during the annealing step. A remarkably lower cooling rate can achieve a certain relative crystallinity degree at the unit crystallization time for WPC with 3 wt % MAPP (WPCM3). Similarly, the lowest crystallization activation energy was observed for the WPCM3 among all WPCs by the Kissinger method. Furthermore, based on the Friedman method, the addition of MAPP easily caused the PP matrix to crystallize in the WPC at the initial stage of relative crystallinity.
Keywords: wood fiber, maleated polypropylene (MAPP), polypropylene (PP), cooling rate, non-isothermal crystallization, crystallization kinetics
1. Introduction
Over the last decade, wood fiber (WF)-reinforced polymer matrices, consisting of petroleum-based and renewable resources, have gained interest for the manufacture of products in a number of fields, such as fencing, decking, and automotive components, due to sustainability, relatively high strength and stiffness, low maintenance and cost, and good durability [1,2,3,4,5]. However, the incompatibility between hydrophilic lignocellulosics and hydrophobic thermoplastics has been found to limit the applicability of wood–plastic composites (WPCs). This deficiency produces insufficient interfacial adhesion, which may lead to moisture intrusion and biological attack [6,7]; in addition, this incompatibility results in decreased mechanical properties due to poor stress transition from the matrix to the fibers [8,9]. To enhance the interfacial adhesion and to improve the properties of the composites, many physical and chemical approaches, such as the addition of coupling agents [8,9,10,11,12], silane treatment [10,13,14], alkaline treatment [13,15,16], esterification [15,17], and heat treatment [18,19], have been used. Under the consideration of usability and eco-effectiveness, the use of coupling agents has been attractive since some coupling agents can create significant bonds between the WF and the polymer matrix and improve the composite compatibility. Among the coupling agents, copolymers containing maleic anhydride, such as maleated polypropylene (MAPP), are commonly and widely used in WPCs [8,9,10,11,12]. Until recently, a hypothetical coupling mechanism of the wood–polymer interface was that anhydride molecules can react to form covalent bonds with the hydroxyl groups of the WF, and the other end of the maleic anhydrides of the copolymers entangle and cohere with the polymer matrix. This reaction makes the surface energy of the polypropylene (PP) matrix much closer to that of the WF, further resulting in better interfacial interactions between the PP matrix, WFs, and wettability [11,20,21]. Therefore, after the addition of MAPP as a coupling agent in WPCs, the improvement of their dimensional stability, mechanical properties, and impact strength has been reported in several studies [22,23,24,25]. To date, investigations on WPCs have primarily focused on the effects of various attributes to the performances of the composites, such as fiber type, fiber loading, and fiber modification. However, the quality and properties of the end products have been significantly influenced by the resulting microstructure, especially the crystallization of the polymer matrix, which is dependent on the thermal and press history during processing [26]. In addition, polymer composites are invariably solidified under non-isothermal conditions in industrial processing, e.g., extrusion and compression moldings. Therefore, information on the non-isothermal crystallization behavior of WPCs is still indispensable to understand the crystallization mechanism of the final composite material. Thus far, the kinetic aspects of the crystallization process have been examined by alternative methods, such as the Avrami theory, to investigate the non-isothermal crystallization behavior of polymer composites with various natural fibers [21,27,28,29,30]. On the other hand, a few studies have reported the crystallization kinetics of WPCs with a constant amount of coupling agent under non-isothermal conditions [29,31]. However, to the best of our knowledge, no clear indication of the effect of different MAPP concentrations on the non-isothermal crystallization behavior of WF/polymer composites has been obtained. Therefore, the aim of the present study was to examine the crystallization behaviors of WPCs with various amounts of MAPP under non-isothermal conditions by differential scanning calorimetry (DSC) analysis. Investigations of the nucleation mechanism and the required crystallization rate were analyzed by the Avrami method and the Avrami–Ozawa method, respectively. Additionally, the Kissinger method and Friedman method were applied to obtain the activation energy of non-isothermal crystallization.
2. Materials and Methods
2.1. Materials
PP pellets (Globalene 7633) were purchased from LCY Chemical Co. (Taipei, Taiwan), and their density, melting point (MP), and melt flow index (MFI) were 896 kg/m3, 170 °C, and 2 g/10 min, respectively. The commercially available coupling agent MAPP (density: 934 kg/m3; MP: 156 °C; MFI: 115 g/10 min) was purchased from Sigma-Aldrich Chemical Co. (St. Louis, MO, USA). WFs were prepared from a 52-year-old China fir (Cunninghamia lanceolata), which was kindly provided by the experimental forest of National Chung Hsing University (Nantou, Taiwan), via hammer-milling and sieving to obtain fibers between 16 and 24 mesh (1.00–0.71 mm). As shown in Table 1, the weight ratios of oven-dried WF, PP, and MAPP were 0/100/0, 60/40/0, 60/39/1, 60/37/3, 60/35/5, and 60/33/7 (wt %), designated Neat PP, WPC0, WPCM1, WPCM3, WPCM5, and WPCM7, respectively. Each composition was compounded at 200 °C for 5 min by a YKI-3 Banbury mixer (Goldspring Enterprise Inc., Taichung, Taiwan) at a rotor speed of 50 rpm and consequently extruded and pelleted into 4–5 mm diameters and 5–7 mm length pellets.
Table 1.
Sample code and composition of the neat polypropylene (PP) and its composites.
| Code | WF (wt %) | PP (wt %) | MAPP (wt %) |
|---|---|---|---|
| Neat PP | 0 | 100 | 0 |
| WPC0 | 60 | 40 | 0 |
| WPCM1 | 60 | 39 | 1 |
| WPCM3 | 60 | 37 | 3 |
| WPCM5 | 60 | 35 | 5 |
| WPCM7 | 60 | 33 | 7 |
2.2. Differential Scanning Calorimetry Measurement
Neat PP and various WPC pellets were ground in an attrition mill, and a total of 3–5 mg of each sample was prepared directly in DSC aluminum pans with lid. The non-isothermal crystallization was executed in nitrogen at a flow rate of 20 mL/min using a PerkinElmer DSC-6 (Beaconsfield, UK). To eliminate the thermal and mechanical history and to ensure a nuclei-free melt, the first step was preliminary heating of the samples to 200 °C with a heating rate of 10 °C/min, and the temperature was held for 5 min. Afterward, the samples were cooled to 50 °C at different constant cooling rates of 2.5, 5, 10, 15, 20 and 25 °C/min. The exothermic flow curves as a function of temperature were recorded to analyze the non-isothermal crystallization kinetics. Two individual samples for each composition were tested. The PP crystallinity (Xc) was obtained as a function of the cooling rate using the following expression:
| (1) |
where ΔHm is the melting enthalpy for the sample at a given cooling rate, ΔHm0 denotes the melting enthalpy of 100% crystalline PP, the value of which is 209 J/g [32], and Wp denotes the weight percentage of the PP in the samples.
2.3. Crystallization Kinetics
The relative crystallinity (X) as a function of crystallization temperature (T) can be formulated based on the non-isothermal DSC data by using the following equation:
| (2) |
where T0 and T∞ are the onset and offset temperatures of crystallization, respectively, and dHc/dT is the heat flow rate. The crystallization time (t) at a given cooling rate can be calculated as follows:
| (3) |
where T0 is the onset temperature at crystallization time t = 0, T is the temperature at time t, and ϕ is the cooling rate.
The crystallization kinetics could be determined based on the Avrami (Equation (4)) [33,34,35] and Ozawa (Equation (5)) approaches [36] using the following equations:
| (4) |
| (5) |
where X(t) is the relative crystallinity at time t, K is the Avrami crystallization rate constant indicating nucleation and growth rate parameters, n denotes a mechanism constant that explains the nucleation and growing geometry of the crystallites, X(T) is the relative crystallinity at temperature T, k(T) is the cooling crystallization function, m is the Ozawa exponent, which depends on the nucleation mechanism and the crystal growth, and ϕ is the constant cooling rate. Furthermore, by taking a logarithm of both sides, Equations (4) and (5) can be converted into Equations (6) and (7), respectively:
| (6) |
| (7) |
However, the Ozawa equation has been proven to be inappropriate for describing the non-isothermal crystallization kinetics of some polymer systems [37,38,39]. Therefore, by combining the Avrami and Ozawa equations, an equation related to the cooling crystallization rate ϕ and time t could be generated at a given degree of crystallization under dynamic crystallization conditions [40,41] as follows:
| (8) |
where F(T) = [k(T)/K]1/m denotes the value of the cooling rate at the unit crystallization time under a given degree of crystallinity, and α denotes the ratio of the Avrami exponent n to the Ozawa exponent m.
Moreover, the crystallization activation energy was calculated by the Kissinger equation (Equation (9)) and the Friedman equation (Equation (10)), and these equations are expressed as follows [42,43]:
| (9) |
| (10) |
where Tp is the crystallization peak, ΔE is the activation energy, which characterizes the transport process of macromolecular segments to the surface of crystal growth, R is the universal gas constant, X is the relative degree of crystallinity, t is the time, f(X) is the function of the reaction mechanism, and AX, EX, and TX are the pre-exponential factor, the activation energy, and the temperature at a given X value, respectively.
3. Results and Discussion
3.1. Non-Isothermal Crystallization Behavior
As shown in Figure 1a, the onset temperature (To) and the crystallization peak (Tp) can be obtained from the DSC exothermic curves of the non-isothermal crystallization of neat PP for a range of cooling rates from 2.5 to 25 °C/min. It can be seen that the To and Tp shifted to lower temperatures, and the range of crystallization temperatures broadened for all samples with an increasing cooling rate. This result is attributed to the fact that the motion of the PP chains lagged at higher cooling rates, and crystallization occurred at lower temperatures. In contrast, sufficient time to induce nuclei was available at lower cooling rates, resulting in the initiation of crystallization at higher temperatures [29,44]. In Figure 2a,b, at the given cooling rate, the To and Tp values of WPC0 and MAPP-containing WPCs were higher than those of neat PP, especially for the WPC0. These results indicated that the WF or MAPP could act as a heterogeneous nucleation agent for the crystallization of PP and accelerate the crystallization process. On the other hand, as shown in Figure 2c, the crystallinity (Xc) value of the neat PP decreased from 54.7% (2.5 °C/min) to 45.2% (25 °C/min) with an increase in the cooling rate, and the other samples showed the same tendency. This result indicated that a higher crystallinity of the PP matrix was produced at a lower cooling rate. When WFs were incorporated in the PP matrix, the Xc value increased by 11–22%, especially at a lower cooling rate (<15 °C/min), indicating that the WF could significantly increase the crystallinity of the PP matrix. However, the Xc values of the MAPP-containing WPCs were slightly lower than those of the neat PP at various cooling rates. This result probably suggested that the transport of PP molecular chains was impeded at the crystal surface due to the high density of nuclei for PP with WF and MAPP [29,45].
Figure 1.
Non-isothermal crystallization behaviors of the neat PP. (a) Differential scanning calorimetry (DSC) thermograms. (b) Relative crystallinity as a function of time.
Figure 2.
Non-isothermal crystallization parameters as a function of the cooling rate for the neat PP and wood–plastic composites (WPCs) with various maleated polypropylene (MAPP) concentrations. (a) The onset temperature (To); (b) The crystallization peak (Tp); (c) Crystallinity (Xc); (d) The half-time (t1/2).
Figure 1b shows the relative crystallinity (X) as a function of the crystallization time (t) for the neat PP at various cooling rates. It can be seen that the curves showed sigmoidal growth, and this trend is essentially the same for all samples with different cooling rates. This result clearly indicated the lag effect of the cooling rate on the crystallization [31]. In many previous studies [37,40,46], the trend of these curves was attributed to two crystallization processes including the initial stage of a fast crystallization process and the later stage of a slower crystallization process. During the later stage of the curve (Figure 1b), it can be seen that the crystallization rate significantly decreased, which resulted from the impingement of spherulites [37,40]. Additionally, at the slower cooling rate, the curve ramp was decreased compared to the higher cooling rate, indicating that the time for crystallization completion decreased with increasing cooling rates. This phenomenon was further determined for each sample by the half-time of crystallization (t1/2), which is defined as the period corresponding to an X of 50%. As shown in Figure 2d, the t1/2 values of all samples were reduced with increasing cooling rates. For instance, it can be seen that the t1/2 value of the neat PP decreased from 3.85 min at 2.5 °C/min to 0.52 min at 25 °C/min. Furthermore, the t1/2 value of various WPCs was lower than that of the neat PP, and the effect of MAPP is clearly seen in the case of lower cooling rates. At a cooling rate of 2.5 °C/min, the t1/2 value decreased to 3.66 min when WFs were added to the PP matrix (WPC0), and this value further decreased to 3.04 min as MAPP content increased up to 3 wt %. Once the MAPP content exceeded 3 wt %, however, an increased t1/2 value was observed, e.g., 3.34 min for WPCM7. This result is attributed to the fact that the rearrangement of molecular chains is hindered due to the greatest number of nucleation sites, resulting in a reduced crystallization rate of the PP matrix.
3.2. Kinetic Analysis with the Avrami Approach
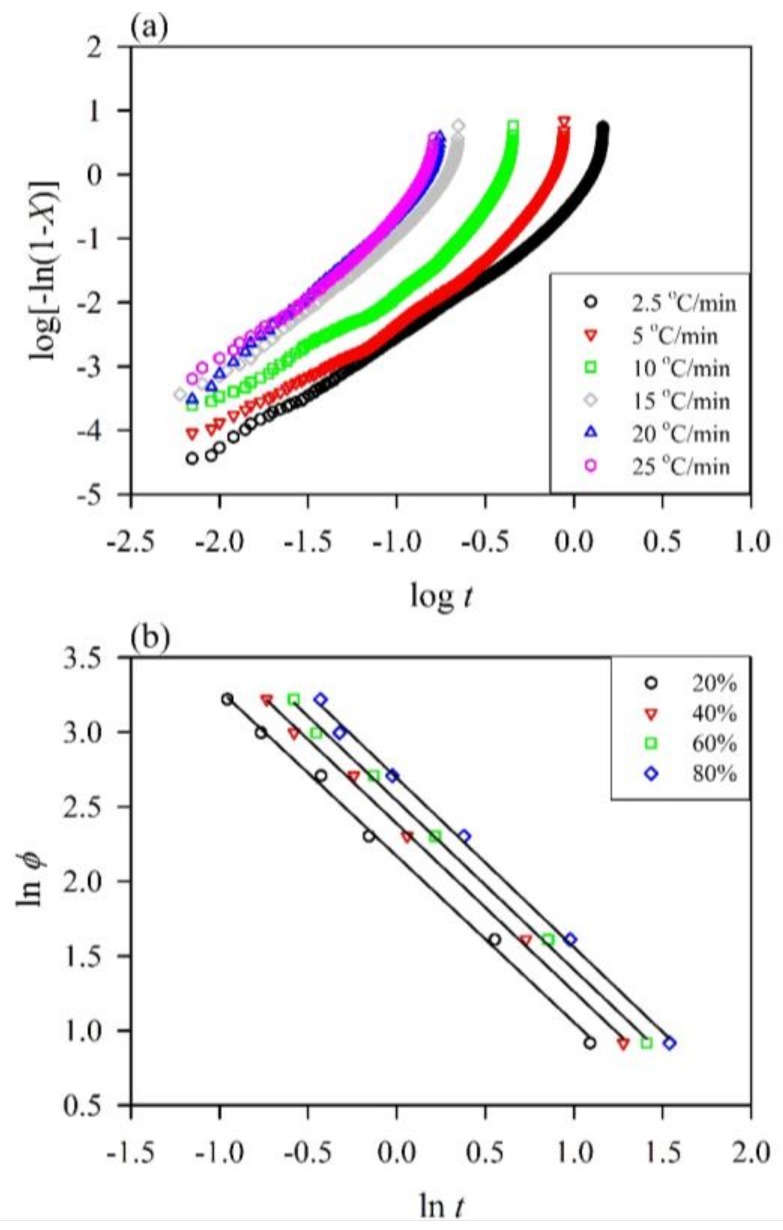
The nucleation mechanisms were further analyzed with the Avrami approach. According to the assumption that the crystallization temperature is constant, the Avrami model is widely applied to the isothermal crystallization kinetics of polymers to describe the initial stage of crystallization. At a given cooling rate, a plot of log[–ln(1–X(t))] versus log t can be used to obtain the values of n and K from the slope of the linear portion and intercept of the curve according to Equation (6). As shown in Figure 3a, linear fits of the plots describing the initial stage of crystallization were conducted for the log[–ln(1–X(t))] values. A linear regression was performed on the slope for all samples as validated by the square of the correlation coefficient (R2) value which was greater than 0.94 (Table 2). The fitting lines of each section were nearly parallel for the neat PP, implying that the nucleation mechanism and geometry of crystal growth at different cooling rates were similar, and the same tendency for various WPCs was observed (not shown). On the other hand, the n values ranged from 1.67 to 1.99 for the neat PP at different cooling rates, suggesting that its non-isothermal crystallization corresponded to acicular crystal growth with homogeneous nucleation [47]. The following n values of all WPCs were in the range of 1.28–2.04, suggesting that their non-isothermal crystallization mechanisms were acicular and tabular crystal growth with heterogeneous nucleation [30,47]. These results indicated that the addition of WF and MAPP significantly changed the nucleation mechanism of the PP matrix in WPCs under the crystallization process. Moreover, the crystallization rate constant (K) was corrected to obtain the crystallization rate (KJ) as a function of the cooling rate (ϕ) according to the following equation [48]:
| (11) |
Figure 3.
The non-isothermal crystallization kinetics of the neat PP. (a) Avrami plots of log[–ln(1–X)] versus log t; (b) Avrami–Ozawa plots of ln ϕ versus ln t.
Table 2.
The parameters calculated at various cooling rates based on the Avrami model.
| Code | Cooling Rate (°C/min) | K | KJ | n | R2 |
|---|---|---|---|---|---|
| Neat PP | 2.5 | 0.19 ± 0.01 | 0.52 ± 0.01 | 1.77 ± 0.05 | 0.9856 |
| 5 | 0.28 ± 0.02 | 0.78 ± 0.01 | 1.74 ± 0.04 | 0.9873 | |
| 10 | 0.69 ± 0.10 | 0.96 ± 0.01 | 1.67 ± 0.06 | 0.9823 | |
| 15 | 1.31 ± 0.59 | 1.01 ± 0.03 | 1.83 ± 0.02 | 0.9817 | |
| 20 | 5.17 ± 1.51 | 1.08 ± 0.02 | 1.87 ± 0.22 | 0.9878 | |
| 25 | 14.23 ± 0.52 | 1.11 ± 0.00 | 1.99 ± 0.05 | 0.9931 | |
| WPC0 | 2.5 | 0.63 ± 0.04 | 0.83 ± 0.02 | 2.04 ± 0.35 | 0.9889 |
| 5 | 0.14 ± 0.04 | 0.67 ± 0.04 | 1.84 ± 0.00 | 0.9885 | |
| 10 | 1.08 ± 0.26 | 1.00 ± 0.02 | 1.77 ± 0.70 | 0.9923 | |
| 15 | 0.73 ± 0.03 | 0.98 ± 0.01 | 1.70 ± 0.16 | 0.9836 | |
| 20 | 1.12 ± 0.05 | 1.01 ± 0.02 | 1.73 ± 0.13 | 0.9854 | |
| 25 | 5.74 ± 1.62 | 1.07 ± 0.01 | 1.65 ± 0.32 | 0.9951 | |
| WPCM1 | 2.5 | 0.20 ± 0.04 | 0.52 ± 0.05 | 1.57 ± 0.10 | 0.9770 |
| 5 | 0.26 ± 0.03 | 0.76 ± 0.02 | 1.62 ± 0.12 | 0.9776 | |
| 10 | 0.63 ± 0.05 | 0.96 ± 0.01 | 1.82 ± 0.29 | 0.9487 | |
| 15 | 3.08 ± 1.14 | 1.07 ± 0.03 | 1.93 ± 0.11 | 0.9807 | |
| 20 | 1.24 ± 0.39 | 1.01 ± 0.02 | 1.71 ± 0.08 | 0.9673 | |
| 25 | 1.59 ± 0.52 | 1.02 ± 0.01 | 1.93 ± 0.01 | 0.9925 | |
| WPCM3 | 2.5 | 0.79 ± 0.47 | 0.87 ± 0.23 | 2.03 ± 0.88 | 0.9984 |
| 5 | 0.40 ± 0.01 | 0.83 ± 0.00 | 1.75 ± 0.28 | 0.9660 | |
| 10 | 1.82 ± 0.30 | 1.06 ± 0.02 | 1.61 ± 0.25 | 0.9655 | |
| 15 | 3.33 ± 0.07 | 1.08 ± 0.00 | 1.99 ± 0.09 | 0.9859 | |
| 20 | 2.27 ± 0.06 | 1.04 ± 0.00 | 1.42 ± 0.08 | 0.9886 | |
| 25 | 2.27 ± 0.09 | 1.03 ± 0.00 | 1.50 ± 0.20 | 0.9819 | |
| WPCM5 | 2.5 | 0.22 ± 0.02 | 0.55 ± 0.02 | 1.55 ± 0.03 | 0.9872 |
| 5 | 0.16 ± 0.10 | 0.67 ± 0.09 | 1.43 ± 0.10 | 0.9385 | |
| 10 | 0.92 ± 0.21 | 0.99 ± 0.02 | 1.89 ± 0.04 | 0.9679 | |
| 15 | 0.78 ± 0.07 | 0.98 ± 0.01 | 1.40 ± 0.55 | 0.9711 | |
| 20 | 1.11 ± 0.31 | 1.00 ± 0.01 | 1.37 ± 0.27 | 0.9449 | |
| 25 | 2.77 ± 0.20 | 1.04 ± 0.00 | 1.61 ± 0.44 | 0.9906 | |
| WPCM7 | 2.5 | 0.11 ± 0.01 | 0.42 ± 0.01 | 1.56 ± 0.18 | 0.9697 |
| 5 | 0.17 ± 0.02 | 0.70 ± 0.01 | 1.28 ± 0.03 | 0.9808 | |
| 10 | 0.63 ± 0.11 | 0.95 ± 0.02 | 1.32 ± 0.03 | 0.9752 | |
| 15 | 5.35 ± 0.44 | 1.12 ± 0.01 | 1.68 ± 0.40 | 0.9848 | |
| 20 | 1.21 ± 0.35 | 1.01 ± 0.02 | 1.77 ± 0.52 | 0.9476 | |
| 25 | 4.09 ± 1.61 | 1.05 ± 0.02 | 2.03 ± 0.22 | 0.9762 |
Values are the means ± SD (n = 2).
As shown in Table 2, the KJ values for all samples markedly increased with increasing cooling rates up to 10–15 °C/min, indicating that the highest cold crystallization rate occurs at 10–15 °C/min. Furthermore, it can be seen that the WPCM3 almost exhibited the highest KJ value among all WPCs at any given cooling rate. The KJ values were in the ranges of 0.67–1.07, 0.52–1.07, 0.83–1.08, 0.55–1.04, and 0.42–1.12 for WPC0, WPCM1, WPCM3, WPCM5, and WPCM7, respectively, at cooling rates of 2.5–25 °C/min. This result is related to the fact that an appropriate MAPP concentration could be offered as nuclei to promote the crystallization of the PP matrix.
3.3. Kinetic Analysis with the Avrami–Ozawa Approach
To further validate the crystallization behavior, the overall non-isothermal crystallization kinetics of the neat PP and WPCs were analyzed by the Avrami–Ozawa approach. The F(T) and α can be determined from the intercept and the slope, respectively, of a series of straight lines at a given relative crystallinity in the plot of ln ϕ against ln t according to Equation (8). Figure 3b presents the characteristic plot of ln ϕ versus ln t of the neat PP at various relative crystallinities. Additionally, the corresponding data for each sample are listed in Table 3. The data for each crystallization stage were fitted with a straight line, and the R2 value was greater than 0.96, indicating that this method is applicable for describing the non-isothermal crystallization kinetics of the neat PP and its composites. The F(T) of all samples steadily increased with increasing X, but the values of α were almost constant. Accordingly, a higher crystallinity degree was obtained by using a higher cooling rate at the unit crystallization time. Furthermore, the F(T) values of all WPCs were lower than those of the neat PP at a given relative crystallinity. This result indicated that a slower cooling rate can achieve a higher degree of crystallinity due to the faster crystallization of WPCs. Among all samples, the WPCM3 showed the lowest F(T) value at a given relative crystallinity. This is consistent with the results of the Avrami approach given above.
Table 3.
The parameters calculated at various relative crystallinities (X) based on the Avrami–Ozawa model.
| Code | X (%) | F(T) | α | R2 |
|---|---|---|---|---|
| Neat PP | 20 | 8.8 ± 0.1 | 1.2 ± 0.0 | 0.9891 |
| 40 | 10.8 ± 0.1 | 1.1 ± 0.0 | 0.9952 | |
| 60 | 12.6 ± 0.1 | 1.1 ± 0.0 | 0.9954 | |
| 80 | 14.7 ± 0.1 | 1.1 ± 0.0 | 0.9941 | |
| WPC0 | 20 | 7.4 ± 0.2 | 1.0 ± 0.1 | 0.9611 |
| 40 | 8.8 ± 0.4 | 1.0 ± 0.0 | 0.9636 | |
| 60 | 9.9 ± 0.4 | 1.1 ± 0.1 | 0.9687 | |
| 80 | 11.5 ± 0.5 | 1.1 ± 0.0 | 0.9661 | |
| WPCM1 | 20 | 7.6 ± 0.3 | 1.2 ± 0.0 | 0.9685 |
| 40 | 9.7 ± 0.1 | 1.2 ± 0.1 | 0.9869 | |
| 60 | 11.1 ± 0.1 | 1.2 ± 0.1 | 0.9885 | |
| 80 | 12.9 ± 0.2 | 1.3 ± 0.1 | 0.9898 | |
| WPCM3 | 20 | 7.1 ± 0.0 | 1.1 ± 0.1 | 0.9711 |
| 40 | 8.5 ± 0.1 | 1.1 ± 0.1 | 0.9765 | |
| 60 | 9.4 ± 0.1 | 1.1 ± 0.1 | 0.9774 | |
| 80 | 11.3 ± 0.2 | 1.2 ± 0.1 | 0.9786 | |
| WPCM5 | 20 | 7.9 ± 0.7 | 1.0 ± 0.1 | 0.9705 |
| 40 | 9.3 ± 0.9 | 1.1 ± 0.1 | 0.9780 | |
| 60 | 10.8 ± 1.3 | 1.1 ± 0.1 | 0.9821 | |
| 80 | 12.4 ± 1.4 | 1.2 ± 0.1 | 0.9846 | |
| WPCM7 | 20 | 8.6 ± 0.2 | 1.2 ± 0.0 | 0.9818 |
| 40 | 10.3 ± 0.2 | 1.2 ± 0.0 | 0.9846 | |
| 60 | 11.7 ± 0.2 | 1.2 ± 0.0 | 0.9853 | |
| 80 | 13.7 ± 0.0 | 1.2 ± 0.0 | 0.9849 |
Values are the means ± SD (n = 2).
3.4. Activation Energy of Non-Isothermal Crystallization by the Kissinger Method and the Friedman Method
One of the indispensable parameters is the crystallization activation energy in polymer systems. The crystallization of a polymer matrix in composites is influenced by the following two factors: the static factor, which is related to the free barrier energy of nucleation, and the dynamic factor, which corresponds to the activation energy for the transport of the macromolecular segments to the surface of crystal growth [49]. Among the various kinetic models, the Kissinger method has successfully been used to estimate the crystallization activation energy for polymers. The crystallization activation energy (ΔE) can be calculated according to the Kissinger equation (Equation (9)). Figure 4a shows the Kissinger plots of ln (ϕ/Tp2) versus 1/Tp2 for the neat PP and WPCs, enabling the determination of the ΔE values from the slopes of the good linear regression for all samples. Accordingly, as shown in Figure 4b, the ΔE value of the WPC0 was −207 kJ/mol, which is lower than that of the neat PP (−172 kJ/mol) due to the nucleating effect of the WFs. Clearly, the ΔE value was further decreased to −224 kJ/mol when 3 wt % MAPP was added to the WPC. However, the crystallization activation energy increased to −218 kJ/mol and −216 kJ/mol for the WPCM5 and WPCM7, respectively. This result indicated that optimal MAPP concentrations could accelerate the crystal growth of the polymer matrix, while excessive MAPP loading would increase the crystallization activation energy to hinder the transport of polymer chains for its crystallization, as further verified by the results described above.
Figure 4.
The non-isothermal crystallization kinetics of the neat PP and WPCs using the Kissinger method. (a) Kissinger plots of ln (ϕ/Tp2) versus 1/Tp2; (b) the crystallization activation energy.
Furthermore, the isoconventional Friedman method was also used in this study since it is considered for non-isothermal crystallization as a function of the relative crystallinity. The ln (dX/dt)X versus 1/TX plots for the neat PP at different relative crystallinities are illustrated in Figure 5a. According to the Friedman equation (Equation (10)), the activation energies at a given relative crystallinity, EX, can be obtained from the slopes of the straight line of the Friedman plots for the neat PP and WPCs as shown in Figure 5b. The EX value of the neat PP varied in the finite range from −160 to −130 kJ/mol. In contrast, the EX values of all WPCs increased with increasing X from 5 to 80%. The resulting activation energies are in the ranges from −214 to −74 kJ/mol, from −212 to −80 kJ/mol, from −232 to −86 kJ/mol, from −230 to −88 kJ/mol, and from −217 to −90 kJ/mol for WPC0, WPCM1, WPCM3, WPCM5, and WPCM7, respectively. These findings suggest that the crystallization process easily proceeded at the initial stages of crystallization, while it became more difficult to crystallize as higher crystallinity was achieved. A similar result was observed for the short carbon fiber/poly(trimethylene terephthalate) composites [50]. Additionally, in comparison with the neat PP, a significant decrease in the EX values for all WPCs was observed when X was below 30%. Among them, the WPC0 exhibited the highest energy barrier at the given X, while the addition of MAPP into the WPC resulted in a decrease of the EX value in a dose-dependent manner, except at lower X (<20%) values. It can be noted that the EX values of the WPCM7 were higher than those of the WPCM3 and WPCM5 at X values of 5–20%. These results confirmed that MAPP could act as a heterogeneous nucleation agent to accelerate the crystallization process of the PP, but excessive MAPP loading would restrain the formation of crystals.
Figure 5.
The non-isothermal crystallization kinetics of the neat PP and WPCs using the Friedman method. (a) Friedman plots of ln (dX/dt)X versus 1/TX for the neat PP; (b) dependence of the effective activation energy on the relative crystallinities for the neat PP and WPCs.
4. Conclusions
The non-isothermal crystallization kinetics of WPCs with various MAPP concentrations were determined by DSC and analyzed by the Avrami method, Avrami–Ozawa method, Kissinger method, and Friedman method. According to the Avrami method, the addition of MAPP into WPC significantly changed the nucleation mechanism of the PP matrix from homogeneous nucleation for acicular crystal growth to heterogeneous nucleation for acicular and tabular crystal growth under the cooling process. Additionally, the Avrami–Ozawa method indicated that a higher crystallinity of the PP matrix could be obtained for WPCs compared to the neat PP at a lower cooling rate, and the WPC with 3 wt % MAPP (WPCM3) showed the highest crystallization rate at a given relative crystallinity among all samples. Furthermore, the Kissinger method indicated that the crystallization activation energy (ΔE) decreased when WFs and MAPP were added to the PP matrix, and the WPCM3 exhibited the lowest ΔE value among all WPCs. On the other hand, using the iso-conversional Friedman method, the results showed that the addition of WF and MAPP easily induced the PP matrix to crystallize at the initial stages, while crystallization was difficult to achieve at a higher crystallization. Overall, these results indicated that the 3 wt % MAPP addition could optimally contribute to the acceleration of the crystal growth of the polymer matrix; however, excessive MAPP loading would hinder the crystallization of polymer chains. From these methods, it was observed that the crystallization mechanism, crystallization rate, and activation energy for the PP matrix were influenced by the cooling rate and MAPP content. The addition of different MAPP concentrations can affect the crystallization behavior of the PP by either improving or hindering crystal growth, leading to competition between heterogeneous nucleation and crystal growth in the restricted interspaces between the WFs and MAPP. Therefore, for optimizing the polymer morphology in a composite, these results offer information regarding the conditions of the manufacturing process.
Acknowledgments
This work was financially supported by a research grant from the Ministry of Science and Technology, Taiwan (MOST 105-2628-B-005-002-MY3).
Author Contributions
Chung-Wei Huang and Jyh-Horng Wu conceived and designed the experiments; Chung-Wei Huang, Teng-Chun Yang, Ke-Chang Hung, Jin-Wei Xu, and Jyh-Horng Wu carried out the laboratory experiments; Chung-Wei Huang, Teng-Chun Yang, and Jyh-Horng Wu analyzed the data, interpreted the results, prepared the figures, and wrote the manuscript. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- 1.Bledzki A.K., Reihmane S., Gassan J. Thermoplastics reinforced with wood fillers: A literature review. Polym. Plast. Technol. Eng. 1998;37:451–468. doi: 10.1080/03602559808001373. [DOI] [Google Scholar]
- 2.Stark N.M., Matuana L.M. Characterization of weathered wood-plastic composite surfaces using FTIR spectroscopy, contact angle, and XPS. Polym. Degrad. Stab. 2007;92:1883–1890. doi: 10.1016/j.polymdegradstab.2007.06.017. [DOI] [Google Scholar]
- 3.Alsaeed T., Yousif B.F., Ku H. The potential of using date palm fibres as reinforcement for polymeric composites. Mater. Des. 2013;43:177–184. doi: 10.1016/j.matdes.2012.06.061. [DOI] [Google Scholar]
- 4.Hung K.-C., Yeh H., Yang T.-C., Wu T.-L., Xu J.-W., Wu J.-H. Characterization of Wood-plastic composites made different lignocellulosic materials that vary in their morphology, chemical composition and thermal stability. Polymers. 2017;9:726. doi: 10.3390/polym9120726. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Georgiopoulos P., Kontou E. The effect of wood-fiber type on the thermomechanical performance of biodegradable polymer matrix. J. Appl. Polym. Sci. 2015;132 doi: 10.1002/app.42185. [DOI] [Google Scholar]
- 6.Mahlberg R., Paajanen L., Nurmi A., Kivistö A., Koskela K., Rowell R.M. Effects of chemical modification of wood on the mechanical and adhesion properties of wood fiber/polypropylene fiber and polypropylene/veneer composites. Holz als Roh- und Werkstoff. 2001;59:319–326. doi: 10.1007/s001070100232. [DOI] [Google Scholar]
- 7.Pendleton D.E., Hoffard T.A., Adcock T., Woodward B., Wolcott M.P. Durability of an extruded HDPE/wood composite. For. Prod. J. 2002;52:21–27. [Google Scholar]
- 8.Kazayawoko M., Balatinecz J.J., Matuana L.M. Surface modification and adhesion mechanisms in wood fiber-polypropylene composites. J. Mater. Sci. 1999;34:6189–6199. doi: 10.1023/A:1004790409158. [DOI] [Google Scholar]
- 9.Hosseinaei O., Wang S., Enayati A.A., Rials T.G. Effect of hemicellulose extraction on properties of wood flour and wood–plastic composites. Compos. A Appl. Sci. Manuf. 2012;43:686–694. doi: 10.1016/j.compositesa.2012.01.007. [DOI] [Google Scholar]
- 10.Georgiopoulos P., Christopoulos A., Koutsoumpis S., Kontou E. The effect of surface treatment on the performance of flax/biodegradable composites. Compos. B Eng. 2016;106:88–98. doi: 10.1016/j.compositesb.2016.09.027. [DOI] [Google Scholar]
- 11.Fleix J.M., Gatenholm P. The nature of adhesion in composites of modified cellulose fibers and polypropylene. J. Appl. Polym. Sci. 1991;42:609–620. doi: 10.1002/app.1991.070420307. [DOI] [Google Scholar]
- 12.Keener T.J., Stuart R.K., Brown T.K. Maleated coupling agents for natural fibre composites. Compos. A Appl. Sci. Manuf. 2004;35:357–362. doi: 10.1016/j.compositesa.2003.09.014. [DOI] [Google Scholar]
- 13.Ichazo M.N., Albano C., González J., Perera R., Candal M.V. Polypropylene/wood flour composites: Treatments and properties. Compos. Struct. 2001;54:207–214. doi: 10.1016/S0263-8223(01)00089-7. [DOI] [Google Scholar]
- 14.Lee S.H., Wang S. Biodegradable polymers/bamboo fiber biocomposite with bio-based coupling agent. Compos. A Appl. Sci. Manuf. 2006;37:80–91. doi: 10.1016/j.compositesa.2005.04.015. [DOI] [Google Scholar]
- 15.Mwaikambo L.Y., Ansell M.P. The effect of chemical treatment on the properties of hemp, sisal, jute and kapok for composite reinforcement. Macromol. Mater. Eng. 1999;272:108–116. doi: 10.1002/(SICI)1522-9505(19991201)272:1<108::AID-APMC108>3.0.CO;2-9. [DOI] [Google Scholar]
- 16.Das M., Chakraborty D. Evaluation of improvement of physical and mechanical properties of bamboo fibers due to alkali treatment. J. Appl. Polym. Sci. 2008;107:522–527. doi: 10.1002/app.26155. [DOI] [Google Scholar]
- 17.Hung K.-C., Wu J.-H. Mechanical and interfacial properties of plastic composite panels made from esterified bamboo particles. J. Wood Sci. 2010;56:216–221. doi: 10.1007/s10086-009-1090-9. [DOI] [Google Scholar]
- 18.Ayrilmis N., Jarusombuti S., Fueangvivat V., Bauchongkol P. Effect of thermal-treatment of wood fibers on properties of flat–pressed wood plastic composites. Polym. Degrad. Stab. 2011;96:818–822. doi: 10.1016/j.polymdegradstab.2011.02.005. [DOI] [Google Scholar]
- 19.Yang T.-C., Chien Y.-C., Wu T.-L., Hung K.-C., Wu J.-H. Effects of heat-treated wood particles on the physico-mechanical properties and extended creep behavior of wood/recycled-HDPE composites using the time-temperature superposition principle. Materials. 2017;10:365. doi: 10.3390/ma10040365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Li X., Tabil L.G., Panigrahi S. Chemical treatments of natural fiber for use in natural fiber-reinforced composites: A review. J. Polym. Environ. 2007;15:25–33. doi: 10.1007/s10924-006-0042-3. [DOI] [Google Scholar]
- 21.Ou R., Guo C., Xie Y., Wang Q. Non-isothermal crystallization kinetics of kevlar fiber-reinforced wood flour/HDPE composites. BioResources. 2011;6:4547–4565. [Google Scholar]
- 22.Mishra S., Naik J.B., Patil Y.P. The compatibilising effect of maleic anhydride on swelling and mechanical properties of plant-fiber-reinforced novolac composites. Compos. Sci. Technol. 2000;60:1729–1735. doi: 10.1016/S0266-3538(00)00056-7. [DOI] [Google Scholar]
- 23.Qiu W., Zhang F., Endo T., Hirotsu T. Preparation and characteristics of composites of high-crystalline cellulose with polypropylene: Effects of maleated polypropylene and cellulose content. J. Appl. Polym. Sci. 2003;87:337–345. doi: 10.1002/app.11446. [DOI] [Google Scholar]
- 24.Mohanty S., Nayak S.K., Verma S.K., Tripathy S.S. Effect of MAPP as a coupling agent on the performance of jute-PP composites. J. Reinf. Plast. Compos. 2004;23:625–637. doi: 10.1177/0731684404032868. [DOI] [Google Scholar]
- 25.Bledzki A.K., Letman M., Viksne A., Rence L. A comparison of compounding processes and wood type for wood fibre-PP composites. Compos. A Appl. Sci. Manuf. 2005;36:789–797. doi: 10.1016/j.compositesa.2004.10.029. [DOI] [Google Scholar]
- 26.Kamal M.R., Chu E. Isothermal and nonisothermal crystallization of polyethylene. Polym. Eng. Sci. 1983;23:27–31. doi: 10.1002/pen.760230107. [DOI] [Google Scholar]
- 27.Arbelaiz A., Fernández B., Ramos J.A., Mondragon I. Thermal and crystallization studies of short flax fibre reinforced polypropylene matrix composites: Effect of treatments. Thermochim. Acta. 2006;440:111–121. doi: 10.1016/j.tca.2005.10.016. [DOI] [Google Scholar]
- 28.Buzarovska A., Bogoeva-Gaceva G., Grozdanov A., Avella M. Crystallization behavior of polyhydroxybutyrate in model composites with kenaf fibers. J. Appl. Polym. Sci. 2006;102:804–809. doi: 10.1002/app.24139. [DOI] [Google Scholar]
- 29.Niu P., Wang X., Liu B., Long S., Yang J. Melting and nonisothermal crystallization behavior of polypropylene/hemp fiber composites. J. Compos. Mater. 2012;46:203–210. doi: 10.1177/0021998311410494. [DOI] [Google Scholar]
- 30.Hsu C.-Y., Yang T.-C., Wu T.-L., Hung K.-C., Wu J.-H. The influence of bamboo fiber content on the non-isothermal crystallization kinetics of bamboo fiber-reinforced polypropylene composites (BPCs) Holzforschung. 2018;72:329–336. doi: 10.1515/hf-2017-0046. [DOI] [Google Scholar]
- 31.Phuong N.T., Gilbert V. Non-isothermal crystallization kinetics of short bamboo fiber-reinforced recycled polypropylene composites. J. Reinf. Plast. Compos. 2010;29:2576–2591. doi: 10.1177/0731684409355604. [DOI] [Google Scholar]
- 32.Marinelli A.L., Bretas R.E.S. Blends of polypropylene resins with a liquid crystalline polymer. I. Isothermal crystallization. J. Appl. Polym. Sci. 2003;87:916–930. doi: 10.1002/app.11386. [DOI] [Google Scholar]
- 33.Avrami M. Kinetics of phase change. I: General theory. J. Chem. Phys. 1939;7:1103–1112. doi: 10.1063/1.1750380. [DOI] [Google Scholar]
- 34.Avrami M. Kinetics of phase change. II: Transformation-time relations for random distribution of nuclei. J. Chem. Phys. 1940;8:212–224. doi: 10.1063/1.1750631. [DOI] [Google Scholar]
- 35.Avrami M. Kinetics of phase change. III: Granulation, phase change, and microstructure. J. Chem. Phys. 1941;9:177–184. doi: 10.1063/1.1750872. [DOI] [Google Scholar]
- 36.Ozawa T. Kinetics of non-isothermal crystallization. Polymer. 1971;12:150–158. doi: 10.1016/0032-3861(71)90041-3. [DOI] [Google Scholar]
- 37.Cebe P., Hong S.D. Crystallization behaviour of poly(ether-ether-ketone) Polymer. 1986;27:1183–1192. doi: 10.1016/0032-3861(86)90006-6. [DOI] [Google Scholar]
- 38.Eder M., Wlochowicz A. Kinetics of non-isothermal crystallization of polyethylene and polypropylene. Polymer. 1983;24:1593–1595. doi: 10.1016/0032-3861(83)90177-5. [DOI] [Google Scholar]
- 39.Hao W., Yang W., Cai H., Huang Y. Non-isothermal crystallization kinetics of polypropylene/silicon nitride nanocomposites. Polym. Test. 2010;29:527–533. doi: 10.1016/j.polymertesting.2010.03.004. [DOI] [Google Scholar]
- 40.Liu T., Mo Z., Wang S., Zhang H. Nonisothermal melt and cold crystallization kinetics of poly(aryl ether ether ketone ketone) Polym. Eng. Sci. 1997;37:568–575. doi: 10.1002/pen.11700. [DOI] [Google Scholar]
- 41.Liu T., Mo Z., Zhang H. Nonisothermal crystallization behavior of a novel poly(aryl ether ketone): PEDEKmK. J. Appl. Polym. Sci. 1998;67:815–821. doi: 10.1002/(SICI)1097-4628(19980131)67:5<815::AID-APP6>3.0.CO;2-W. [DOI] [Google Scholar]
- 42.Kissinger H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Nat. Inst. Stand. Technol. 1956;57:217–221. doi: 10.6028/jres.057.026. [DOI] [Google Scholar]
- 43.Friedman H.L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. Polym. Symp. 1964;6:183–195. doi: 10.1002/polc.5070060121. [DOI] [Google Scholar]
- 44.Grozdanov A., Buzarovska A., Bogoeva-Gaceva G., Avella M., Errico M.E., Gentile G. Nonisothermal crystallization kinetics of kenaf fiber/polypropylene composites. Polym. Eng. Sci. 2007;47:745–749. doi: 10.1002/pen.20749. [DOI] [Google Scholar]
- 45.Lei Y., Wu Q., Clemons C.M., Yao F., Xu Y. Influence of nanoclay on properties of HDPE/wood composites. J. Appl. Polym. Sci. 2007;106:3958–3966. doi: 10.1002/app.27048. [DOI] [Google Scholar]
- 46.Regis M., Zanetti M., Pressacco M., Bracco P. Opposite role of different carbon reinforcements on the non-isothermal crystallization behavior of poly(etheretherketone) Mater. Chem. Phys. 2016;179:223–231. doi: 10.1016/j.matchemphys.2016.05.034. [DOI] [Google Scholar]
- 47.Lee S.-H., Ohkita T. Bamboo fiber (BF)-filled poly(butylenes succinate) bio-composite—Effect of BF-e-MA on the properties and crystallization kinetics. Holzforschung. 2004;58:537–543. doi: 10.1515/HF.2004.081. [DOI] [Google Scholar]
- 48.Jeziorny A. Parameters characterizing the kinetics of the non-isothermal crystallization of poly(ethylene terephthalate) determined by d.s.c. Polymer. 1978;19:1142–1144. doi: 10.1016/0032-3861(78)90060-5. [DOI] [Google Scholar]
- 49.Yuan Q., Awate S., Misra R.D.K. Nonisothermal crystallization behavior of polypropylene-clay nanocomposites. Eur. Polym. J. 2006;42:1994–2003. doi: 10.1016/j.eurpolymj.2006.03.012. [DOI] [Google Scholar]
- 50.Run M., Song H., Yao C., Wang Y. Crystal morphology and nonisothermal crystallization kinetics of short carbon fiber/poly(trimethylene terephthalate) composites. J. Appl. Polym. Sci. 2007;106:868–877. doi: 10.1002/app.26661. [DOI] [Google Scholar]