False signals induced by single-cell imputation

Tallulah S Andrews; Martin Hemberg

doi:10.12688/f1000research.16613.2

. 2019 Mar 5;7:1740. Originally published 2018 Nov 2. [Version 2] doi: 10.12688/f1000research.16613.2

False signals induced by single-cell imputation

Tallulah S Andrews ¹, Martin Hemberg ^1,^a

PMCID: PMC6415334 PMID: 30906525

Version Changes

Revised. Amendments from Version 1

In the results, we have added a recently published auto-encoder based imputation method, dca, to our comparison. In addition, we have revised the splatter simulation dropout parameters to be more representative of real single-cell RNASeq data and have included a figure in the supplementary material to show the lower range of values used result in simulated data resembling 10X data whereas higher values resemble Smart-seq2 data. We also revised several main text figures and added some supplementary figures for clarity and added an ROC plot to Figure 2 to show the trade-off between sensitivity and specificity that is realized by each of the imputation methods. We have added recommendations that imputation can be useful for visualizing single-cell data, and that SAVER is generally the safest method to use, but that all statistical tests, be the gene-gene correlations, cluster-specific marker genes, or differential expression, should be applied to un-imputed data. We have revised the text for clarity, as well as to give additional emphasis to the increases in sensitivity achieved by imputation, and made the code used in this publication publicly available on github: https://github.com/tallulandrews/F1000Imputation. The Chan Zuckerberg Initiative (grant reference 183501) is added to the Grant information section, as this was left out of the version 1.

Abstract

Background: Single-cell RNA-seq is a powerful tool for measuring gene expression at the resolution of individual cells. A challenge in the analysis of this data is the large amount of zero values, representing either missing data or no expression. Several imputation approaches have been proposed to address this issue, but they generally rely on structure inherent to the dataset under consideration they may not provide any additional information, hence, are limited by the information contained therein and the validity of their assumptions.

Methods: We evaluated the risk of generating false positive or irreproducible differential expression when imputing data with six different methods. We applied each method to a variety of simulated datasets as well as to permuted real single-cell RNA-seq datasets and consider the number of false positive gene-gene correlations and differentially expressed genes. Using matched 10X and Smart-seq2 data we examined whether cell-type specific markers were reproducible across datasets derived from the same tissue before and after imputation.

Results: The extent of false-positives introduced by imputation varied considerably by method. Data smoothing based methods, MAGIC, knn-smooth and dca, generated many false-positives in both real and simulated data. Model-based imputation methods typically generated fewer false-positives but this varied greatly depending on the diversity of cell-types in the sample. All imputation methods decreased the reproducibility of cell-type specific markers, although this could be mitigated by selecting markers with large effect size and significance.

Conclusions: Imputation of single-cell RNA-seq data introduces circularity that can generate false-positive results. Thus, statistical tests applied to imputed data should be treated with care. Additional filtering by effect size can reduce but not fully eliminate these effects. Of the methods we considered, SAVER was the least likely to generate false or irreproducible results, thus should be favoured over alternatives if imputation is necessary.

Keywords: Gene expression, single-cell, RNA-seq, Imputation, Type 1 errors, Reproducibility

Introduction

Single-cell RNA-seq (scRNA-seq) is a powerful technique for assaying the whole transcriptome at the resolution of individual cells. Although experimental protocols have evolved rapidly, there is still no strong consensus on how to best analyse the data. An important challenge to analysing scRNA-seq data is the high frequency of zero values, often referred to as dropouts, and the overall high levels of noise due to the low amounts of input RNA obtained from individual cells. Recently there have been four methods published ( Gong et al., 2018; Huang et al., 2018; Li & Li, 2018; van Dijk et al., 2018) which attempt to address these challenges though imputation, with several more under development ( Deng et al., 2018; Mongia et al., 2018; Moussa & Mandoiu, 2018; Wagner et al., 2017). Several recently introduced methods employ deep learning autoencoders for processing scRNA-seq data, including imputation and data-smoothing ( Eraslan et al., 2019; Hu & Greene, 2018; Wang & Gu, 2018; Wang et al., 2018).

Imputation is a common approach when dealing with sparse genomics data. A notable example has been the improvements to GWAS sensitivity and resolution when using haplotype information to impute unobserved SNPs ( Visscher et al., 2017). Unlike scRNA-seq data, this imputation employs an external reference dataset, often the 1000 Genomes project, to infer the missing values ( Chou et al., 2016). Such a reference does not yet exist for scRNA-seq data, and thus imputation methods can only use information internal to the dataset to be imputed. As a result there is a degree of circularity introduced into the dataset following imputation which could result in false positive results when identifying marker genes, gene-gene correlations, or testing differential expression. Zero values in scRNA-seq may arise due to low experimental sensitivity, e.g. sequencing sampling noise, technical dropouts during library preparation, or because biologically the gene is not expressed in the particular cell. Thus, one challenge when imputing expression values is to distinguish true zeros from missing values.

Many imputation methods, such as SAVER ( Huang et al., 2018), DrImpute ( Gong et al., 2018) and scImpute ( Li & Li, 2018), use models of the expected gene expression distribution to distinguish true biological zeros from zeros originating from technical noise. Because these gene expression distributions assume homogenous cell populations, they first identify clusters of similar cells to which an appropriate mixture model is fitted. Values falling above a given probability threshold to originate from technical effects are subsequently imputed. For example, scImpute models log-normalized expression values as a mixture of gamma-distributed dropouts and normally-distributed true observations. Alternatively some scRNA-seq imputation methods perform data smoothing. In contrast to imputation, which only attempt to infer values of missing data, smoothing reduces noise present in observed values by using information from neighbouring data points. Both MAGIC ( van Dijk et al., 2018) and knn-smooth ( Wagner et al., 2017) perform data smoothing for single-cell data using each cell’s k nearest neighbours either through the application of diffusion models or weighted sums respectively.

Previous benchmarking of these imputation methods was based on positive controls, i.e. the ability to recover true signals within noisy data ( Zhang & Zhang, 2018); the potential for false signals to be introduced into a dataset by these imputation methods was not considered, and it was concluded that most imputation methods provide a small improvement. We consider negative controls to evaluate the risks of introducing false positive when using imputation for single-cell datasets. Testing of the four published imputation methods, MAGIC, SAVER, scImpute, and DrImpute and one currently unpublished method, knn-smooth, revealed that all methods can introduce false positive signals into data. While some methods, performed well on simulated data, permuting real scRNA-seq data revealed high variability in performance on different datasets. We show that statistical tests applied to imputed data should be treated with care, and that results found in imputed data may not be reproducible across datasets.

Methods

Six different single-cell RNASeq imputation methods were tested: SAVER ( Huang et al., 2018), DrImpute ( Gong et al., 2018), scImpute ( Li & Li, 2018), dca ( Eraslan et al., 2019), MAGIC ( van Dijk et al., 2018) and knn-smooth ( Wagner et al., 2017). These include all of the published imputation methods, at present, an additional data smoothing approach, knn-smooth, to contrast to the only published data smoothing method, MAGIC. We have also included a single autoencoder-based method, dca ( Eraslan et al., 2019). Unless specified otherwise these were run with default parameters ( Table 1). Each method was applied to either the raw-counts or log2 counts per million normalized data, as calculated scater ( McCarthy et al., 2017), as appropriate.

Table 1. Imputation methods.

Method	Model	Parameter(s)	Range	Reference
scImpute	Log-normal	Dropout threshold Number of clusters	0-1 (default: 0.5) Correct value given the simulation	( Li & Li, 2018)
DrImpute *	ZINB	Remaining zeros Number of clusters	0-1 (default: 0) Correct value given the simulation	( Gong et al., 2018)
SAVER	ZINB	Which genes to impute	Top 1%–100% most highly expressed (default: 100%)	( Huang et al., 2018)
MAGIC	NA	Diffusion time, K neighbours	1–8 (default: allow algorithm to choose) 5–100 (default: 12)	( van Dijk et al., 2018)
knn-smooth	NA	K neighbours	5–100 (default: number of cells / 20)	( Wagner et al., 2017)
dca	ZINB	Hidden layer size +5 others	2–64 (default: 32) Software defaults	( Eraslan et al., 2019)

Open in a new tab

*Note: All methods were applied to raw counts as intended by the authors and returned values on that scale, except for DrImpute which as per the documentation was applied to log2(CPM+1) and returned log-scaled values. CPM = counts per million.

Negative binomial simulations

As an initial test of imputation methods and to understand the effect of various method-specific parameters on imputation we simulated data from a negative binomial model, which is known to be a good model of bulk and single-cell RNA-seq data ( Grün et al., 2014; Robinson & Smyth, 2007). Expression matrices containing 1000 cells, equally spread across two cell-types, and 500 genes, with mean expression ranging from 10 ^-3-10 ⁴, were simulated. Half of the genes were differentially expressed (DE) by an order of magnitude between the two cell-types, half were drawn independently. Since there are no added dropouts in these simulations the desired behavior for model-based imputation methods is to leave the data as is. Whereas for data-smoothing the desired behaviour would be to assign non-DE genes a constant value across all cells. Ten such expression matrices were independently simulated. Each imputation method was run on each replicate with a range of parameter values ( Table 1). Significant gene-gene correlations were identified using Spearman correlation with a conservative Bonferroni multiple testing correction (q < 0.05) to avoid distributional assumptions on the imputed values. We specifically choose the Bonferroni correction to avoid issues arising from an abundance of very low p-values resulting from imputation of the strong DE genes present in these simulations. A distorted p-value distribution would be problematic as it violates the assumptions of the more typical false discovery rate correction ( Benjamini & Hochberg, 1995).

Correlations were calculated directly on the output of the imputation methods which was on the count-scale for all methods except DrImpute for which both the input and output are on a log-scale. However, since we used the non-parametric Spearman correlation the effect of different scales is minimal and largely restricted to distortions due to normalization biases and the addition of a pseudo-count. Correlations involving not DE genes or in the incorrect direction were considered false positives.

Splatter simulations

Splatter ( Zappia et al., 2017) was used to generate 60 simulated single-cell RNASeq count matrices using different combinations of parameters ( Table 2). Each simulated dataset contained 1,000 cells split into 2–10 groups and 1,000–5,000 genes of which 1–30% were differentially expressed across the groups. For simplicity all groups were equally sized and were equally different from one another. Half the simulations assumed discrete differentiated groups, whereas the other half used the continuous differentiation path model. We also considered the effect of four different amounts of added dropouts plus the no-added dropout model. These simulation parameters broadly matched real scRNA-seq data, with lower dropout rates being more similar to 10X Chromium data and higher dropout rates being more similar to Smart-seq2 data ( Figure S1). Each simulated dataset was imputed with each method using default parameters.

Table 2. Splatter parameters.

nGenes *	%DE (total) *	Dropouts (midpoint) **	nGroups	Method	Seed
1000 2000 5000	1% 10% 30%	None (45%) 1 (70%) 2 (80%) 3 (88%) 4 (94%)	2 5 10	Groups	8298 2900

Open in a new tab

*Randomly selected for each possible combination of the other four parameters.

** Numbers in parentheses indicate proportion of the expression matrix that was “0” values.

Accuracy of each imputation method was evaluated by testing for differentially expressed (DE) genes between the groups used to simulate the data. To avoid issues of different imputation methods resulting in data best approximated by different probability distribution, we employed the non-parametric Kruskal-Wallis test ( Kruskal & Wallis, 1952) with a 5% FDR to identify significant DE genes. The Kruskal-Wallis test is the multi-group extension of the Mann-Whitney-U test that performs a single test per gene regardless of the number of groups to compare ensuring equivalent power and multiple-testing corrections across simulations. Since this test is relatively low-power it is likely to underestimate the number of DE genes compared to alternatives. To filter DE results by effect size, in addition to significance, the magnitude of the DE (i.e. effect size) was estimated as the maximum log2-fold-change across all pairs of clusters. Only genes where the magnitude of the DE exceeded a specified threshold and were significant after a 5% FDR were called as DE in this case.

Permuted Tabula Muris datasets

Six 10X Chromium and 12 Smart-seq2 datasets were chosen from the Tabula Muris (8) consortium data such that: i) there were at least two cell types containing >5% of the total cells and ii) there were between 500–5,000 cells after filtering ( Table S1). Each dataset was preprocessed to remove cell-types accounting for <5% of total cells, and any cells not assigned to a named cell-type. Genes were filtered to remove those detected in fewer than 5% of cells.

We selected the two most similar cell-types in each dataset using the Euclidean distance between their mean expression profiles. Differential expression of each gene between these cell-types was evaluated using a Mann-Whitney-U test, which is the two-sample equivalent of the Kruskal-Wallis test, on the log2 library size normalized counts (pseudo-count of 1). Genes with a raw p-value > 0.2 were then permuted across the selected cell-types to eliminate any residual biological signals. Permuted raw counts were obtained by de-logging and de-normalizing the permuted log2-normalized expression to avoid library-size confounders.

Each imputation method was applied to the full dataset after permutation using default parameters ( Table 1). False-positives introduced by each imputation was assessed by applying the Mann-Whitney-U test to test for differential expression between the two chosen cell-types. A Bonferroni multiple-testing correction was applied to ensure a consistent level of expected total false positives of less than 1.

Reproducibility of markers

We utilized the six tissues for which there exists matching Smart-seq2 and 10X Chromium data from the Tabula Muris (8) to evaluate the reproducibility of imputation results. These datasets were filtered as described above, and any cell-types not present in both pairs of the matching datasets were excluded. Each imputation method was applied to the datasets without any permutation.

Marker genes were identified in each imputed dataset using a Mann-Whitney-U test, which is the two-sample version of the Kruskal-Wallis test, to compare each cell-type against all others, and effect size was calculated as the area under the ROC curve for predicting each cell-type from the others ( Kiselev et al., 2017). Genes were assigned to the cell-type for which they had the highest AUC. Significant marker genes were defined for each imputed dataset using a 5% FDR and an AUC over a particular threshold. Reproducibility was evaluated by determining the number of genes that were significant markers in both of a matching pair of datasets and were markers of the same cell-type. We used marker genes rather than DE genes to simplify the evaluation of reproducibility, since each gene was assigned to a single cell-type per dataset rather than a matrix of fold-changes across all pairs of cell-types. In addition, since these datasets contained clearly distinct cell-types nearly all genes were differentially expressed between some pairs of cell-types (e.g. B-cells and lung stromal cells). The presence of such outliers could potentially distort overall DE reproducibility measures.

Results

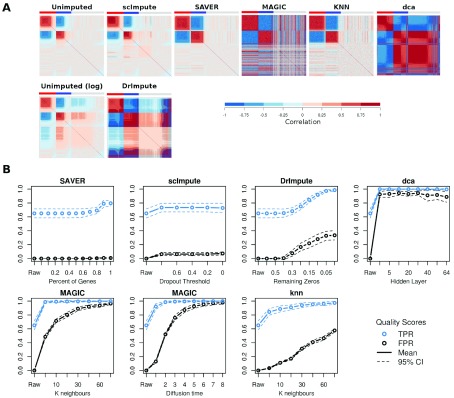
We tested three published imputation methods, SAVER ( Huang et al., 2018), scImpute ( Li & Li, 2018) and DrImpute ( Gong et al., 2018), two data-smoothing methods MAGIC ( van Dijk et al., 2018) and knn-smooth ( Wagner et al., 2017) and one autoencoder-based method dca ( Eraslan et al., 2019). We applied each method with the default parameter values ( Table 1) to data simulated from a simple negative binomial, since technical noise in scRNA-seq data has been observed to follow a negative binomial distribution since technical noise in scRNA-seq data has been observed to follow a negative binomial distribution ( Grün et al., 2014). All the imputation methods increased the sensitivity to detect gene-gene correlations between the lowly expressed DE genes. However, only SAVER strengthened the correlations between lowly expressed DE genes without generating false positive gene-gene correlations between independently drawn genes ( Figure 1A). Since SAVER models expression data using a negative binomial, it is expected to perform well on this simulated data. MAGIC and dca generated very strong false positive correlations ( r > 0.75) at all expression levels, whereas DrImpute, which only imputes zero values, created false positive correlations mostly among lowly expressed genes. Knn-smooth and scImpute produced a few false-positive correlations among moderately-expressed genes using default parameters.

Choice of parameter values has a large influence imputation results ( Figure 1B). Five of the imputation methods required the user to set at least one parameter a priori, only SAVER did not. We varied the thresholds scImpute and DrImpute use to determine which zeros to impute. For scImpute some of the lower and moderate expression values were imputed even at a very strict probability threshold ( p > 0.8), but changing the threshold had little effect on the imputation. As expected for DrImpute, imputing a greater proportion of zeros generated more false positive gene-gene correlations. Knn-smooth and MAGIC both perform data smoothing using a k-nearest-neighbour graphs between cells. Increasing the number of nearest-neighbours ( k) produces smoother data and more false-positive correlations ( Figure 1B). MAGIC provides a default value for k but no indication of how this parameter should be adjusted for different sized datasets, whereas knn-smooth provided no default value but a rough suggestion to scale the value depending on the total number of cells. MAGIC also utilizes a second parameter, time ( t), for the diffusion process acting on the graph which by default is algorithmically estimated for the dataset. Longer diffusion times produce smoother data and more false positives. Autoencoders involve a large number of parameters and these can have a large effect on performance ( Hu & Greene, 2018). For simplicity, we only considered the size of the hidden layer in this study. A larger hidden layer slightly reduced the tendency to generate false-positive gene-gene correlations.

These simple simulations contained only two cell-types and no technical confounders such as library-size or inflated dropout rates that are observed in some scRNA-seq datasets. For a more comprehensive evaluation of imputation methods we simulated data using Splatter ( Zappia et al., 2017). We simulated data with 1,000 cells split into 2–10 groups and 1,000–5,000 genes of which 1–30% were differentially expressed across the groups. We considered four different levels of zero inflation and no zero inflation ( Table 2). Each simulated dataset was imputed with each method using the default parameters ( Table 1). To score each imputation we considered the accuracy of identifying differentially expressed genes between the groups using the non-parametric Kruskal-Wallis test ( Kruskal & Wallis, 1952).

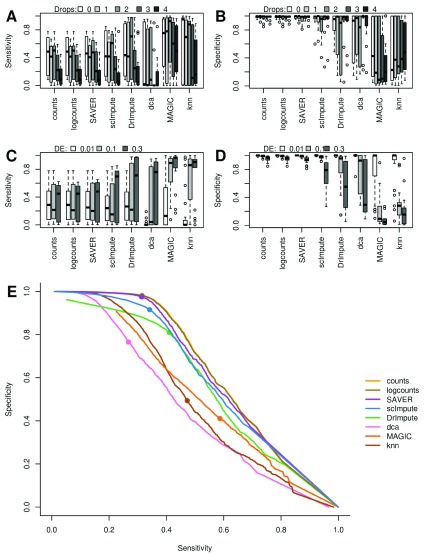
None of the imputation methods significantly outperformed the others or the unimputed data based on the sensitivity and specificity. While both knn-smooth and MAGIC have increased sensitivity, they have very low specificity, whereas SAVER and scImpute are very similar to the unimputed data with high specificity but relatively low sensitivity ( Figure 2A & B). DrImpute and dca were in between the two extremes with somewhat higher sensitivity and lower specificity than SAVER and scImpute. Both scImpute and DrImpute are designed specifically to only impute excess zeros but neither showed a clear improvement over the raw counts when the simulations contained various levels of zero inflation ( Figure 2A & B). By contrast, both smoothing methods, MAGIC and knn-smooth, retained relatively high sensitivity even at high dropout-rates, albeit with low specificity.

Figure 2. — ( A & B) Zero inflation decreases sensitivity of DE which most imputation methods fail to correct. ( C & D) Strong true signals (high proportion of DE genes) decreases specificity particularly for data-smoothing methods. ( E) Average ROC curves across all simulations, solid dots indicate 5% FDR. Counts were normalized by total library size prior to testing DE, and “logcounts” are log2(normalized counts+1).

All methods except SAVER readily introduced false-positive differential expression, as demonstrated by a drop in specificity, when 30% of genes were DE ( Figure 2D). We also observe a significant but smaller drop in specificity for the normalized but unimputed data. We hypothesize that slight biases when correcting for library-size in the presence of strong biological differences may be amplified by the imputation methods. Biases due to counts-per-million library-size normalization, in the presence of strong DE are a known issue from bulk RNASeq analysis ( Bullard et al., 2010). Both MAGIC and knn-smooth automatically use counts-per-million to normalize data before smoothing, and dca using log-transformed data to estimate library-size in its model which explains why it displays similar bias to DrImpute, which imputes log2-normalized data ( Figure 1A).

Importantly, when the trade-off between sensitivity and specificity was considered across significance thresholds we found that imputation methods generally performed worse than the raw data ( Figure 2E). This indicates that similar sensitivities to those observed in imputed data could be achieved with a higher specificity by simply lowering the significance threshold for the DE test. The only exception is SAVER which performed almost identically to the unimputed data. Overall, model-based methods performed better than smoothing-methods when both sensitivity and specificity are taken into account.

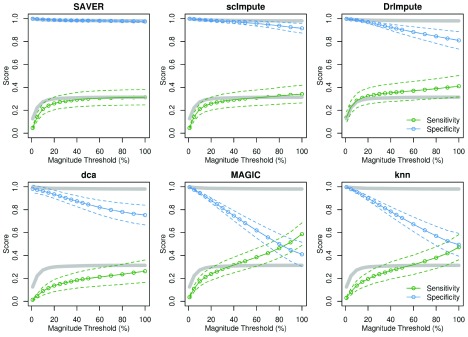
It is possible that the bulk of false-positives generated by imputation methods result from small biases or sampling noise being amplified to reach statistical significance. If this is true, then filtering DE genes by magnitude in addition to significance should restore the specificity of such tests on imputed data. We observed this to be the case when an additional threshold was set based on the Xth percentile highest log2 fold-change across the whole dataset ( Figure 3). However, sensitivity also declined as the fold-change threshold was made more stringent. Again, we observe that data-smoothing offers a worse trade-off between sensitivity and specificity than the un-imputed data, whereas model-based imputation is very close to the un-imputed data.

Figure 3. — Sensitivity (green) and specificity (blue) of each imputation method applied to the splatter-simulated data, when restricting to only the top X% of genes by fold-change. Dashed lines indicate 95% CI. Grey lines indicate results for the un-imputed data.

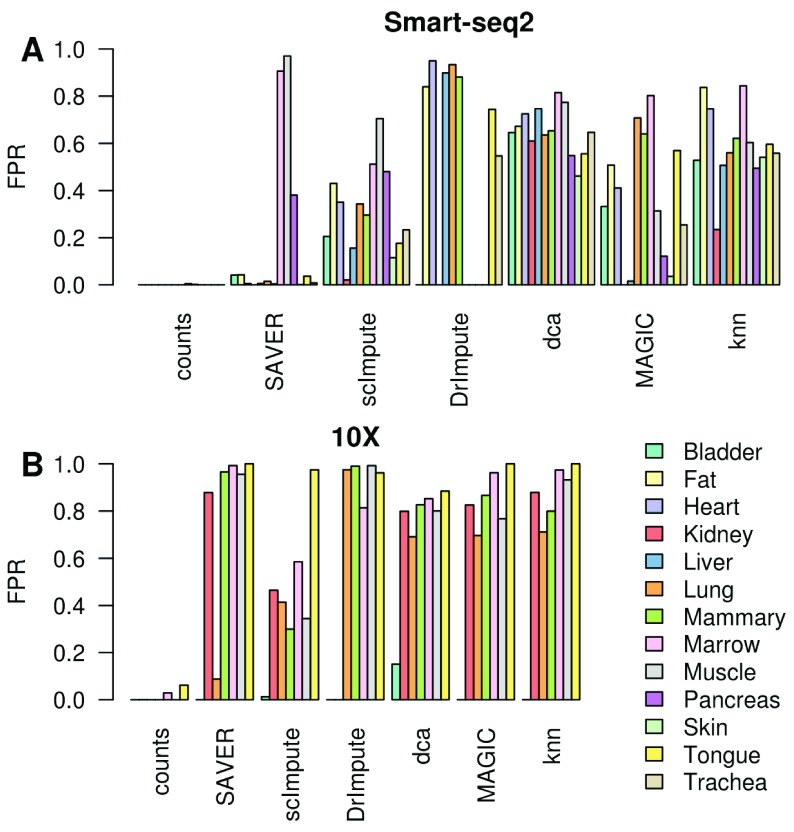
Splatter is a widely used simulation framework for scRNA-seq but may not fully capture the complexities of real scRNA-seq data. To test the performance of each imputation method on real scRNA-seq data we selected 12 tissues from the Tabula Muris database ( Tabula Muris Consortium et al., 2018) and applied the imputation methods to the Smart-seq2 and 10X data separately. Since the ground truth is not known for these data, we selected two cell-types from each dataset and permuted the expression of those genes that were not differentially expressed between them (p > 0.2) to generate a set of genes that we could confidently consider as being not differentially expressed (Methods). Using these as ground truth we could estimate the number of false positive differentially expressed genes introduced by each imputation method. Strikingly, we observed a very high variability between datasets which appears to be unrelated to the experimental platform ( Figure 4A & B). MAGIC, dca and knn-smooth consistently produced large numbers of false positives (20–80%). Whereas, DrImpute and SAVER were extremely variable producing few to no false positives in some datasets and over 90% false positives in others.

Figure 4. — ( A) Smart-seq2 datasets, ( B) 10X Chromium datasets. Non-differentially expressed genes were permuted prior to imputation.

Imputation methods generated more false-positives in the sparser 10X Chromium data than on the higher depth Smart-seq2 data. This was not due to genes failing to conform to the negative binomial distribution ( Figure S2). Rather, it is likely due to relatively stronger real signals and greater power in the large 10X datasets as seen in our splatter simulations ( Figure 2C & D), or due to biases in library size correction. We found that dca, MAGIC, knn-smooth, SAVER and scImpute tend to bias all the permuted genes in the same direction ( Figure S3), though interestingly the direction of the bias depends on the method with MAGIC and SAVER biased in one direction and knn-smooth and scImpute biased in the opposite direction. Dca was less consistent, sometimes being more similar to MAGIC and sometimes more similar to knn-smooth. This suggests an error in library-size correction is responsible for their poor performance on some datasets. In contrast, DrImpute imputed genes in random directions suggesting it is amplifying random noise in the dataset.

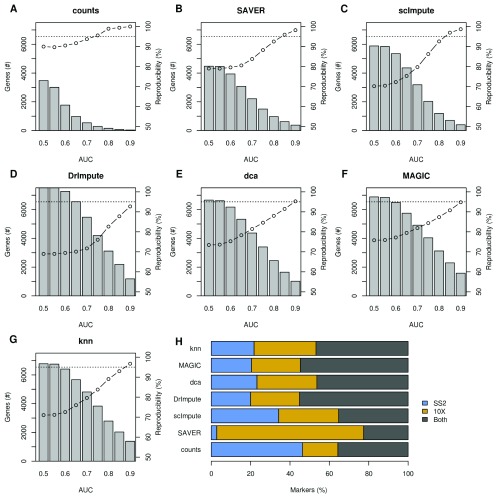
To complement the false positives in the permuted data, we used a marker being associated with the same cell-type in both 10X and Smart-seq2 data as evidence that a gene is a “true” marker. This was a necessary but flawed assumption, since the complete list of true markers is not known. Systematic differences in cell-size, and hence gene-detection rates, may result in reproducible biases in imputation across multiple datasets. In addition, even if markers are randomly associated to cell-types, a portion will agree just by chance. Thus, the proportion of irreproducible markers should be considered an underestimation of the true number of erroneous markers. We identified marker genes using a Mann-Whitney-U test, comparing one cell-type to the others in that tissue. Markers were selected by significance (5% FDR) and magnitude (AUC > T). Each marker was assigned to the cell-type for which it had the highest AUC. To prevent differences in power from affecting the results, reproducibility was measured as the fraction of those markers that were significant in both dataset that were also markers for the same cell-type ( Figure 5).

Figure 5. — ( A– G) Markers were identified in 10X Chromium and Smart-seq2 data for six different mouse tissues. The average number of markers (bars, left axis) and proportion reproducible across both datasets (line, right axis) are plotted. Only significant markers (5% FDR) exceeding the AUC threshold were considered. ( H) Proportion of markers that were unique to the Smart-seq2 (blue, SS2), or 10X Chromium (yellow), or both (dark grey).

All of the imputation methods increased the absolute number of reproducible significant markers ( Figure S4). However, these were mixed in with a larger number of irreproducible markers ( Figure 5). Without imputation, 95% of genes that were significant markers in both datasets were highly expressed in the same cell-type. After imputation, this dropped considerably depending on the AUC threshold. Decreasing the magnitude threshold led to more markers assigned to contradictory cell-types in the imputed Smart-seq2 and 10X Chromium datasets. Unimputed data retained >90% concordance in cell-type assignments of significant markers regardless of the AUC threshold, this fell to 70–80% in imputed data when a low AUC threshold is used. However, employing an AUC threshold of 0.9 increased reproducibility in imputed data back to 95% while retaining more markers than in the un-imputed data. When we considered the overall concordance of the marker test results across dataset, we found that the un-imputed data had the highest concordance in every tissue ( Figure S5).

When comparing across imputation methods applied to the same Tabula Muris dataset, we found variable concordance between methods ( Figure S6). Overall 5–35% of markers were assigned to different cell-types depending on the imputation method(s) used. As we observed for the permuted genes, imputation methods tended to two different groups depending on their particular bias, one containing MAGIC, SAVER and dca, the other containing scImpute, DrImpute and knn-smooth. This discrepancy is concerning, since it could cause the biological interpretation of a dataset to depend on the choice of imputation method.

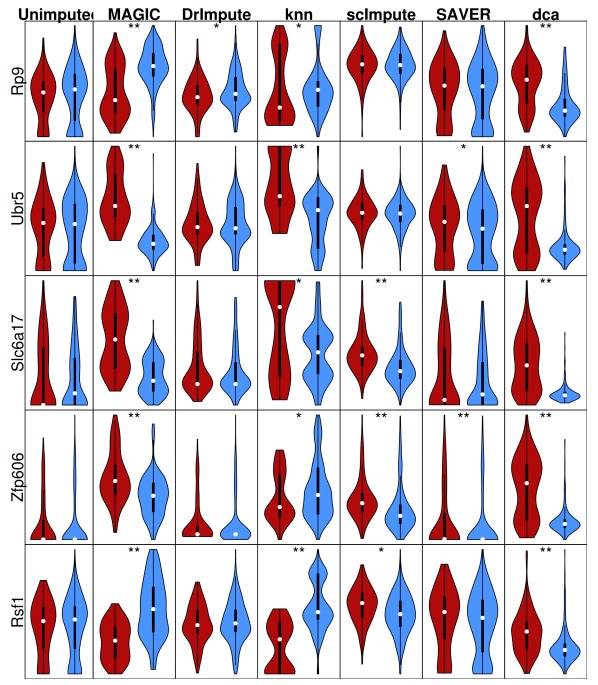
Inspection of the false positives generated by imputation of the permuted real data revealed method-specific distortions of the gene expression values ( Figure 6). SAVER had little effect on the distribution shape, but did eliminate zeros from the data. scImpute and DrImpute both tended to make the distribution more gaussian. In contrast, MAGIC and knn-smooth tended to generate bimodal expression distributions. The tendency towards bimodality could be problematic for downstream analysis since many methods, e.g. PCA and differential expression, assume either negative binomial or gaussian distributions. Many of these genes were differentially expressed after imputation, despite being permuted previously. Interestingly, the direction of differential expression was not always consistent across imputation methods, for instance Zfp606 was more highly expressed in PP cells than A cells after imputation using MAGIC but the inverse was true after imputing with knn-smooth.

Figure 6. — Unimputed indicates the permuted normalized log-transformed expression. Red = PP cell, Blue = A cell. * = p < 0.05, ** = significant after Bonferroni (q < 0.05) correction.

Discussion

We have shown that imputation for scRNA-seq data may introduce false-positive results when no signal is present. On simulated data all the methods except SAVER generated some degree of false positives ( Figure 1 & Figure 2). We find the fundamental trade-off between sensitivity and specificity, inherent to their definition, cannot be overcome with imputation ( Figure 2 & Figure 3). On permuted real data, imputation results were more variable ( Figure 4), and even SAVER generated large numbers of false positives in some datasets. Considering a scenario where a signal is present, we found that imputation also reduced the reproducibility of marker genes, unless strict magnitude thresholds were imposed ( Figure 4 & Figure 5). In addition to false-positives, distortions in expression distributions ( Figure 6) may cause imputed data to violate assumptions of some statistical tests.

We found that different imputation methods favour either sensitivity or specificity but that none of them result in an overall improvement for detecting differential expression ( Figure 2). MAGIC, dca and knn-smooth which are data-smoothing methods, as such they adjust all expression values not just zeros. Since they impose larger alterations on the data, these methods generate many more false positives than methods which only impute zero values. They also have a greater sensitivity, although a similar sensitivity could be achieved by simply reducing stringency of the significance test which would generate fewer false positives. In contrast, model-based methods which only impute low expression values, generated fewer false positives but had minimal improvements to sensitivity. Adding an effect size threshold can reduce false positives generated by imputation and shift the trade off back to lower sensitivity but higher specificity ( Figure 3, Figure 5).

These trade-offs reflect the fundamental limitation of current approaches to single-cell RNASeq imputation, namely that the methods considered here only use the information present in the original data. Hence no new information is gained, making it analogous to simply lowering the significance threshold of any statistical test applied to the data ( Fawcett, 2006). However, as large reference datasets such as the Human Cell Atlas ( Regev et al., 2017; Rozenblatt-Rosen et al., 2017), and equivalent projects in other species ( Han et al., 2018; Plass et al., 2018; Tabula Muris Consortium et al., 2018; Zeisel et al., 2018) are completed it will be possible to employ methods which borrow information from them for imputation such as the recently released SAVER-X method ( Wang et al., 2018). However, reference-based imputation is limited by the completeness of the external dataset. Alternatively, models could be developed to use gene-gene correlations derived from large external databases of expression data ( Obayashi et al., 2008), while more generalizable such methods may not capture cell-type specific relationships.

In our simulations, we have employed the conservative Bonferroni correction and we have ignored potential confounders, such as batch-effects, that imputation methods could mistake for the true structure. Thus, the false-positive rates shown here should be considered underestimates of the true false-positive rates. Similarly, technical confounders and random chance will generate some degree of agreement between markers found in two dataset, which we did not account for in the analysis of Smart-seq2 and 10X Chromium datasets, which again results in underestimating the false-positive rates in imputed data. False-positives resulting from imputation may be much higher than those observed here in the worse case scenario of strong batch-effects, differing cell-size within a sample, and confounding variability such as stress response. Since imputation will amplify any and all possible signals, including random noise, we expect confounding signals to be amplified as well.

We have shown that the circularity induced by imputation causes the outputs of imputation methods to violate the assumptions of statistical tests commonly applied to single-cell RNA-seq. This inflates the number of false-positive gene-gene correlations, cell-type markers, and differentially expressed genes. In general, our results suggest that it is better to decrease the significance threshold applied to the test than to apply an imputation method to increase sensitivity in sparse datasets. However, imputation may still be useful for visualization of single-cell RNA-seq data since it exaggerates existing structure within the data. Of the methods we tested, SAVER was the least likely to generate false positives, but its performance was variable when tested on real data.

If imputation is used, combining SAVER with an effect size threshold is the best option to avoid irreproducible results. Alternatively, verifying the reproducibility of results across multiple datasets or multiple imputation methods can eliminate some false positives. However, our results highlight that statistical tests applied to imputed data should be treated with care. Moreover, as our study only focused on the expression levels, we cannot exclude the possibility that imputation will be beneficial when considering other aspects, e.g. clustering or pseudotime alignment. Although a previous benchmarking study showed good results for positive controls, our study highlights the importance of considering negative controls when evaluating imputation methods.

Data and software availability

Tabula Muris data

Smart-seq2 https://doi.org/10.6084/m9.figshare.5715040.v1 ( Consortium, The Tabula Muris, 2017a).

10X Chromium https://doi.org/10.6084/m9.figshare.5715040.v1 ( Consortium, The Tabula Muris, 2017b).

R packages

MAGIC: Rmagic (v0.1.0) https://github.com/KrishnaswamyLab/MAGIC

DrImpute: DrImpute (v1.0) https://github.com/ikwak2/DrImpute

scImpute: scImpute(v0.0.8) https://github.com/Vivianstats/scImpute

SAVER: SAVER(v1.0.0) https://github.com/mohuangx/SAVER

Knn-smooth: knn_smooth.R (Version 2) https://github.com/yanailab/knn-smoothing

Scater: scater(v1.6.3) : https://www.bioconductor.org/packages/release/bioc/html/scater.html

Splatter: splatter(v1.2.2) : https://bioconductor.org/packages/release/bioc/html/splatter.html

Permute: permute(v0.9-4) : https://cran.r-project.org/web/packages/permute/index.html

Python/anaconda packages:

Dca : dca(v0.2.2): https://github.com/theislab/dca

Custom scripts: https://github.com/tallulandrews/F1000Imputation

Funding Statement

Funding was provided by the Wellcome Trust Sanger Institute Core Funding and the Chan Zuckerberg Initiative (grant reference 183501).

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

[version 2; peer review: 4 approved]

Supplementary material

Supplementary File 1: File containing Table S1 (Tabula Muris permuted datasets) and Figure S1 (Comparison of splatter simulations to real scRNA-seq data), Figure S2 (Distribution fits of false-positives among permuted genes), Figure S3 (Heatmap visualization of false-positives among permuted genes), Figure S4 (Absolute number of reproducible markers after imputation), Figure S5 (Correlation between marker significant tests across 10X and Smart-seq2), Figure S6 (Proportion of markers that are assigned to different cell-types by different imputation methods).

Click here for additional data file.^{(2.4MB, tgz)}

References

Benjamini Y, Hochberg Y: Controlling the false discovery rate: A practical and powerful approach to multiple testing. J Roy Stat Soc B Met. 1995;57(1):289–300. 10.1111/j.2517-6161.1995.tb02031.x [DOI] [Google Scholar]
Bullard JH, Purdom E, Hansen KD, et al. : Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010;11:94. 10.1186/1471-2105-11-94 [DOI] [PMC free article] [PubMed] [Google Scholar]
Chou WC, Zheng HF, Cheng CH, et al. : A combined reference panel from the 1000 Genomes and UK10K projects improved rare variant imputation in European and Chinese samples. Sci Rep. 2016;6:39313. 10.1038/srep39313 [DOI] [PMC free article] [PubMed] [Google Scholar]
Consortium, The Tabula Muris: Single-cell RNA-seq data from Smart-seq2 sequencing of FACS sorted cells. figshare.Fileset.2017a. 10.6084/m9.figshare.5715040.v1 [DOI] [Google Scholar]
Consortium, The Tabula Muris: Single-cell RNA-seq data from Smart-seq2 sequencing of FACS sorted cells. figshare.Fileset.2017b. 10.6084/m9.figshare.5715040.v1 [DOI] [Google Scholar]
Deng Y, Bao F, Dai Q, et al. : Massive single-cell RNA-seq analysis and imputation via deep learning. bioRxiv. 2018. 10.1101/315556 [DOI] [Google Scholar]
Eraslan G, Simon LM, Mircea M, et al. : Single-cell RNA-seq denoising using a deep count autoencoder. Nat Commun. 2019;10(1):390. 10.1038/s41467-018-07931-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
Fawcett T: An introduction to ROC analysis. Pattern Recognit Lett. 2006;27(8):861–874. 10.1016/j.patrec.2005.10.010 [DOI] [Google Scholar]
Gong W, Kwak IY, Pota P, et al. : DrImpute: imputing dropout events in single cell RNA sequencing data. BMC Bioinformatics. 2018;19(1):220. 10.1186/s12859-018-2226-y [DOI] [PMC free article] [PubMed] [Google Scholar]
Grün D, Kester L, van Oudenaarden A: Validation of noise models for single-cell transcriptomics. Nat Methods. 2014;11(6):637–640. 10.1038/nmeth.2930 [DOI] [PubMed] [Google Scholar]
Han X, Wang R, Zhou Y, et al. : Mapping the Mouse Cell Atlas by Microwell-Seq. Cell. 2018;173(5):1307. 10.1016/j.cell.2018.05.012 [DOI] [PubMed] [Google Scholar]
Hu Q, Greene CS: Parameter tuning is a key part of dimensionality reduction via deep variational autoencoders for single cell RNA transcriptomics. bioRxiv. 2018. 10.1101/385534 [DOI] [PMC free article] [PubMed] [Google Scholar]
Huang M, Wang J, Torre E, et al. : SAVER: gene expression recovery for single-cell RNA sequencing. Nat Methods. 2018;15(7):539–542. 10.1038/s41592-018-0033-z [DOI] [PMC free article] [PubMed] [Google Scholar]
Kiselev VY, Kirschner K, Schaub MT, et al. : SC3: consensus clustering of single-cell RNA-seq data. Nat Methods. 2017;14(5):483–486. 10.1038/nmeth.4236 [DOI] [PMC free article] [PubMed] [Google Scholar]
Kruskal WH, Wallis WA: Use of Ranks in One-Criterion Variance Analysis. J Am Stat Assoc. 1952;47(260):583–621. 10.1080/01621459.1952.10483441 [DOI] [Google Scholar]
Li WV, Li JJ: An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat Commun. 2018;9(1):997. 10.1038/s41467-018-03405-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
McCarthy DJ, Campbell KR, Lun AT, et al. : Scater: pre-processing, quality control, normalization and visualization of single-cell RNA-seq data in R. Bioinformatics. 2017;33(8):1179–1186. 10.1093/bioinformatics/btw777 [DOI] [PMC free article] [PubMed] [Google Scholar]
Mongia A, Sengupta D, Majumdar A: McImpute: Matrix completion based imputation for single cell RNA-seq data. bioRxiv. 2018. 10.1101/361980 [DOI] [PMC free article] [PubMed] [Google Scholar]
Moussa M, Mandoiu I: Locality Sensitive Imputation for Single-Cell RNA-Seq Data. bioRxiv. 2018. 10.1101/291807 [DOI] [PMC free article] [PubMed] [Google Scholar]
Obayashi T, Hayashi S, Shibaoka M, et al. : COXPRESdb: a database of coexpressed gene networks in mammals. Nucleic Acids Res. 2008;36(Database issue):D77–82. 10.1093/nar/gkm840 [DOI] [PMC free article] [PubMed] [Google Scholar]
Plass M, Solana J, Wolf FA, et al. : Cell type atlas and lineage tree of a whole complex animal by single-cell transcriptomics. Science. 2018;360(6391): pii: eaaq1723. 10.1126/science.aaq1723 [DOI] [PubMed] [Google Scholar]
Regev A, Teichmann S, Lander ES, et al. : The human cell atlas. bioRxiv. 2017. 10.1101/121202 [DOI] [Google Scholar]
Robinson MD, Smyth GK: Moderated statistical tests for assessing differences in tag abundance. Bioinformatics. 2007;23(21):2881–2887. 10.1093/bioinformatics/btm453 [DOI] [PubMed] [Google Scholar]
Rozenblatt-Rosen O, Stubbington MJT, Regev A, et al. : The Human Cell Atlas: from vision to reality. Nature. 2017;550(7677):451–453. 10.1038/550451a [DOI] [PubMed] [Google Scholar]
Tabula Muris Consortium, . Overall coordination, . Logistical coordination, et al. : Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature. 2018;562(7727):367–372. 10.1038/s41586-018-0590-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
van Dijk D, Sharma R, Nainys J, et al. : Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell. 2018;174(3):716–729.e27. 10.1016/j.cell.2018.05.061 [DOI] [PMC free article] [PubMed] [Google Scholar]
Visscher PM, Wray NR, Zhang Q, et al. : 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 2017;101(1):5–22. 10.1016/j.ajhg.2017.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wagner F, Yan Y, Yanai I: K-nearest neighbor smoothing for high-throughput single-cell RNA-Seq data. bioRxiv. 2017. 10.1101/217737 [DOI] [Google Scholar]
Wang D, Gu J: VASC: Dimension Reduction and Visualization of Single-cell RNA-seq Data by Deep Variational Autoencoder. Genomics Proteomics Bioinformatics. 2018;16(5):320–331. 10.1016/j.gpb.2018.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
Wang J, Agarwal D, Huang M, et al. : Transfer learning in single-cell transcriptomics improves data denoising and pattern discovery. bioRxiv. 2018. 10.1101/457879 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zappia L, Phipson B, Oshlack A: Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017;18(1):174. 10.1186/s13059-017-1305-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zeisel A, Hochgerner H, Lönnerberg P, et al. : Molecular Architecture of the Mouse Nervous System. Cell. 2018;174(4):999–1014.e22. 10.1016/j.cell.2018.06.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
Zhang L, Zhang S: Comparison of computational methods for imputing single-cell RNA-sequencing data. IEEE/ACM Trans Comput Biol Bioinform. 2018. 10.1109/TCBB.2018.2848633 [DOI] [PubMed] [Google Scholar]

F1000Res. 2019 Apr 25. doi: 10.5256/f1000research.20056.r45285

Reviewer response for version 2

Simone Tiberi ¹

The authors have addressed all the comments I made to Version 1.

In my initial review I made numerous comments: I would like to thank the authors for their replies and for the time spent addressing them.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2019 Mar 15. doi: 10.5256/f1000research.20056.r45284

Reviewer response for version 2

Charlotte Soneson ¹

In the revised version, the authors have nicely addressed all my comments from version 1.

There are a few places in the manuscript where the text should be updated to reflect the inclusion of an additional method, e.g. in the last paragraph of the Introduction.

Also, the last sentence in the Background section of the Abstract seems to be missing a word (or should rather be split into two sentences), and the second sentence of the Results has the same passage repeated twice.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2019 Mar 12. doi: 10.5256/f1000research.20056.r45283

Reviewer response for version 2

Jean Fan ^1,²

The authors have done an excellent job addressing my concerns in this review. I have the following minor comments, primarily for clarification in the text:

Comments:

I find it very difficult to distinguish the colored lines used in the new Figure 2E and Figure S4 (in particular, the counts, log counts, and knn lines). Please change one of these lines to red or another more spectrally distinguishable color. For example, the colors in Figure 4 are easier to distinguish.
SAVER, MAGIC, and dca seem to introduce more contradictory markers compared to knn, DrImpute, and scImpute (Figure S6). Is this because of the underlying methodological biases discussed on page 9? Or should users be aware that using SAVER, MAGIC, and dca may introduce more contradictory differential expression results? Please clarify how users should interpret and act on these findings.
The authors note that filtering by effect size restores specificity of identified differentially expressed genes in the imputed data. Does this effect size filtering also fix the contradictory genes issue? Or are there still contradictory genes even after the effect size filtering? Please clarify.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2019 Mar 11. doi: 10.5256/f1000research.20056.r45286

Reviewer response for version 2

Stephanie Hicks ¹

The authors have addressed all of my comments from Version 1. Also, I want to thank the authors for their thoughtful responses to my comments.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard.

F1000Res. 2018 Dec 6. doi: 10.5256/f1000research.18156.r40239

Reviewer response for version 1

Stephanie Hicks ¹

The authors Andrews and Hemberg provided an insightful analysis assessing whether or not false positives (or capturing false signals) are introduced by imputation methods into scRNA-seq data. Previous papers have only assessed true positives (or positive controls or ability to recover true signal). The authors considered both model-based (SAVER, DrImpute, scImpute) and smoothing-based (knn-smooth, MAGIC) imputation approaches where the former infers only the missing values and the latter smooths all the data (nonzero and zeros).

I have a few suggestions and questions that I believe would help the manuscript:

In the simulations (negative binomial and/or Splatter), my understanding is that the authors did not consider a simulation with batch effects (linear or non-linear, global effect or just a portion of the genes), and only considered dropouts in the Splatter simulation. An example with batch effects might be more realistic for scRNA-seq data from real biological experiments because batch effects have been shown to introduce false signals in data (Leek, 2010 ¹). My concern is that the false positive signals reported here would actually be larger or more extreme in real scRNA-seq data.
Could the authors explain the reason for using Bonferroni instead of Benjamini-Hochberg (BH) in correcting for multiple testing? I believe that BH is more commonly used in the context of high-throughput computational biology and genomics. Was it an intentional choice to impose a very conservative correction? Also, it would be interesting to use e.g. BH or even a more modern-controlling FDR methods (e.g. IHW from Wolfgang Huber's group). Hopefully this would only improve the ability to detect the true positives (e.g. positive controls), which leads me to my next question.
As sensitivity and specificity was considered in the Splatter simulations (Figure 2), could the authors show an ROC curve (e.g. averaged across the 60 scRNA-seq count matrices)?
In the 'Permuted Tabula Muris datasets' section, the authors noted they used Euclidean distance as a form of similarity between two cell types. What about using correlation-based similarity measures instead of Euclidean which has been shown to be highly susceptible to the number of dropouts?
For the approaches that were applied to the log2 transformed and normalized datasets, did the authors consider normalization methods specific for single-cell (e.g. scnorm or scran)? CPM has been shown to be not appropriate for scRNA-seq data (Vallejos et al., 2017 ²), so I'm wondering if using a more appropriate normalization method improves the results any?
I think one of the biggest concerns is the lack of reproducibility from certain imputation methods (as a side note, Figure 4C was confusing for me and I might suggest the authors consider illustrating this result a different way). This suggests more development is needed to make imputation methods more robust or an external dataset is needed (similar to using haplotype information for GWAS data). Could the authors comment on what they recommend? As this is a good example of a benchmarking paper comparing different imputation methods, I think it would be really useful for the authors to provide a set of recommendations for users.

I have read this submission. I believe that I have an appropriate level of expertise to confirm that it is of an acceptable scientific standard, however I have significant reservations, as outlined above.

References

1. Leek JT, Scharpf RB, Bravo HC, Simcha D, Langmead B, Johnson WE, Geman D, Baggerly K, Irizarry RA: Tackling the widespread and critical impact of batch effects in high-throughput data. Nat Rev Genet.11(10) : 10.1038/nrg2825 733-9 10.1038/nrg2825 [DOI] [PMC free article] [PubMed] [Google Scholar]
2. Vallejos CA, Risso D, Scialdone A, Dudoit S, Marioni JC: Normalizing single-cell RNA sequencing data: challenges and opportunities. Nat Methods.2017;14(6) : 10.1038/nmeth.4292 565-571 10.1038/nmeth.4292 [DOI] [PMC free article] [PubMed] [Google Scholar]

F1000Res. 2019 Feb 18.

Tallulah Andrews ¹

Thank you for the helpful suggestions, we have addressed all comments below and in the updated version of the manuscript:

1. The Reviewer raises a very important point regarding batch effects. We agree that they are likely to make the situation worse for real datasets. However, they are still not well understood and differ greatly between studies in magnitude and genes affected making it difficult to simulate them well. We used Splatter to add small batch effects to all genes in our simulated datasets but this had relatively little effect on the imputation methods’ overall efficiency, however manual inspection of some of them showed that in some cases imputation methods can mistake batch effects for the real underlying structure. We have added this consideration to the Discussion.

2. This was a deliberate choice both (a) to be conservative and (b) to reduce the impact of imputation methods distorting the p-value distribution. We have clarified this in the text (Discussion: paragraph 4, Methods: Negative Binomial Simulations). This was specifically used for the Negative Binomial simulation as they did not mimic real single-cell datasets very well since they had many genes with very sharp differences between cell-types, and for testing the false-negatives in the permuted Tabula Muris datasets to avoid biases resulting from how the imputation methods affected genes that were actually differentially expressed in those datasets. For the splatter simulations and reproducibility of marker genes we used the more typical Benjamini-Hochberg/FDR correction since these better reflect real single-cell datasets and we were considering the ability to call true positives not specifically focusing on false positives. This has been clarified in the text (Methods: Splatter Simulations).

3. This was requested by another reviewer as well and we have added ROC curves to Figure 2.

4. We agree with the reviewer that Euclidean distance is susceptible to the number of dropouts. However, we only used the Euclidean distance only for picking which two cell-types to consider for the permutations thus has very little importance to our analysis, we could just as easily have picked cell-types at random, we only chose the two most similar to increase the number of genes that are not differentially expressed between the cell-types.

5. Only one method was designed to be run on already log2 transformed and normalized datasets (DrImpute), while several others (MAGIC, knn) internally apply CPM normalization. Thus, for consistency we used CPM for DrImpute. In addition, SCnorm is slow and scran frequently returns negative size factors unless one manually tunes its parameters for each dataset. Because of the high-throughput nature of our benchmarks we chose not to use these methods.

6. We have added recommendations for when and which imputation methods should be used to the Discussion (paragraph 5-6).

F1000Res. 2018 Dec 6. doi: 10.5256/f1000research.18156.r40875

Reviewer response for version 1

Charlotte Soneson ¹

Andrews and Hemberg present an interesting evaluation of imputation and smoothing methods for scRNA-seq, focusing on false positive signals. Five recent imputation/smoothing methods are compared based on whether they:

Introduce false correlations between genes in a Negative Binomial simulation without dropouts.
Accurately identify differentially expressed genes in simulated data with different degrees of dropout.
Induce false positives in differential expression analysis of permuted real scRNA-seq data.
Lead to reproducible sets of differentially expressed genes in data sets generated with different platforms.

The paper treats a relevant subject and is generally well written and easy to follow. Below are suggestions for clarifications and a few additions, which I feel would strengthen the paper and provide additional guidance for the reader in determining which, if any, method to use.

Major comments:

As the authors note, the evaluated methods are based on different distributional assumptions. Since the goal of the imputation is to retrieve the "true underlying signal", performance is likely to be strongly affected by the distribution of the data used for evaluation. In the evaluation of falsely induced correlations (a), it would thus be informative to consider different plausible distributions (not only the Negative Binomial), and compare the performance of the methods. In order to avoid making distributional assumptions, perhaps an appropriate bulk RNA-seq data set could also be useful at this stage.
It would be useful to explicitly spell out the underlying models used by each of the methods, as well as the type of input that they were provided with (raw counts or log-transformed normalized values) and the scale of the output (count or log-count scale) in Table 1. I was also wondering whether correlations in (a) were always calculated on the count scale, or whether they were calculated on the log-scale for some methods. It might be useful to also show the correlations with unimputed log-transformed data in Figure 1A, since not all cells have exactly the same library size/size factor.
Depending on the type of protocol used for the library preparation, scRNA-seq data could have different distributional properties. Since the authors include both SmartSeq2 and 10x data, it would be interesting to see a discussion of the relative merits of the different methods related to the platform used to generate the data. In particular, I was wondering what type of data that the Splatter simulations most resemble, and whether simulations similar to different types of scRNA-seq data could be generated. It would be helpful to see a comparison of the main characteristics of the simulated data and those of real scRNA-seq data, to know to what extent the conclusions drawn from the simulations can be expected to be generalizable to real data sets.
No attempt is made at explaining the large differences between the Tabula Muris tissues in terms of the number of false positives in the permuted data. Are there any apparent differences between the data sets that might (at least partly) explain this? I think it would also be useful to include the results from unimputed data in Figure 4A-B.
Given that there are already several imputation/smoothing methods available that were not explicitly evaluated in this study, and that it is likely that this number will increase quickly, it would be very useful if the evaluation would be easily extendable. As a minimum, it would be useful to make the code available, preferably structured in a modular way so that new methods can be easily substituted. Depending on the time and effort required to generate and process the data sets, these could also be made available.

Minor comments:

It is not immediately clear what the numbers in the "Dropouts (midpoint)" column in Table 2 represent.
I think it would be worth briefly mentioning Figure S1 in the text, rather than just referring to it in the caption of Figure 1, without discussing its content further.
For the reproducibility evaluation, only the number of significant genes shared between SmartSeq2 and 10x are reported. How many genes were found to be significant in one data set only?
The panels in Figure 5 would be easier to compare if the y-axes were the same.
There are a few typos and inconsistencies (e.g., knn-smooth/knn smooth, raw-counts/raw counts, Smart-seq2/Smartseq2, cell-types/cell types) throughout the text.
It is not always clear how the statistical tests were applied. For the count-scale data, were the values somehow normalized between cells before the tests were applied? Also, for the log-normalization of the data, what pseudo-count was used, and how were the size factors calculated?

F1000Res. 2019 Feb 18.

Tallulah Andrews ¹

Thank you for the helpful suggestions, we have made all suggested Minor corrections and have addressed the Major corrections here and in the revised version of the text:

1. It has been established that read counts from scRNA-seq and bulk RNA-seq (or indeed other -seq protocols) are well described by some variant of the negative binomial distribution e.g. (Grün et al. 2014; Robinson and Smyth 2007), which is why that is the model used here for the simulations. We have added Figure S1 to the supplementary material showing the Splatter simulations are a good match for real scRNA-seq data. However, it should be noted that we find that 10X data was best simulated as a pure negative binomial, whereas Smart-seq2 was best simulated with a zero-inflated negative binomial as has been remarked upon previously (see: http://www.nxn.se/valent/2017/11/16/droplet-scrna-seq-is-not-zero-inflated). In addition, when comparing the fits of the zero-inflated negative binomial distribution and zero-inflated normal distribution to the Tabula Muris raw counts and log-normalized counts respectively we found the negative binomial fits the vast majority of genes better than the normal distribution (Table S1). Thus, we believe the negative binomial to be the most sensible distribution for simulating scRNA-seq data.

While we agree bulk RNA-seq intuitively seems like a good ‘ground truth’ for scRNA-seq it is difficult to use it to evaluate imputation since in general simply summing scRNA-seq data is the closest approximation to bulk RNA-seq by the nature of the experiments. The use of bulk RNA-seq as a ground truth assumes that the assayed cell-populations are in truth completely homogeneous. If the “pure” cell populations are a result of sorting this is almost certainly not correct because there is always a fraction of contaminating cells which will result in a bias towards greater smoothing. Although cell populations obtained by growing cells in culture are more likely to be homogenous, they are a poor model for scRNA-seq data obtained from complex tissue samples. There are also reasons to believe that bulk RNA-seq is not a gold standard for identifying truly differentially expressed genes. Bulk RNA-seq is generally limited by its low power due to a small number of samples and the homogenizing effect of bulk samples. Thus, genes that are simply not-detected as differentially expressed using bulk RNA-seq may in truth be differentially expressed just in a small subset of cells or with a low fold-change. Moreover, even though there are many common steps in the experimental protocols for generating bulk and scRNA-seq, it is likely that there will be effects that are specific to each method. For example: with respect to GC content biases or gene-length biases, bulk RNA-seq may not be more correct than scRNA-seq. There is no reason to believe reproducibility across bulk and scRNA-seq is a more reliable method of benchmarking than reproducibility across different scRNA-seq datasets which we have performed using the Tabula Muris data.

2. We thank the Reviewer for this suggestion. We have added information about the input, output and underlying model to Table 1 and we have also clarified in the Methods how the correlations were calculated.We have also added the unimputed log-transformed data to Figure 1A.

3. We have added Figure S1 comparing the general properties of the real Smart-seq2 and 10X datasets with the Splatter simulations. Generally they are a good match, though the 10X data more closely resemble data simulated with few/no added dropouts, whereas the Smart-seq2 data more closely resembles data with relatively high numbers of added dropouts.

In another recent publication from the group (Westoby et al. 2018, Genome Biology), we carried out extensive simulations for comparing isoform quantification methods. We concluded that the splatter simulations did a very good job at resembling the Smart-seq2 data, but the comparisons to Drop-seq data were more tenuous (the discussions on the Drop-seq data were removed from the final version but can be found in the Biorxiv version). 10x data closely resembles Drop-seq data, so those conclusions are likely to hold.

4. This was also requested by another reviewer and we have included the unimputed data in Fig 4A and B. We considered the diversity of cell-types, average sequencing depth, number of detected genes, and number of cells, and the goodness of fit of genes to a zero-inflated negative binomial distribution (in table S1) as possible explanation for the variability between datasets but none of them were particularly associated with number of false positives by different methods. However manual inspection of the effect of imputation on the Tabula Muris data (Figure S4) suggests the variable performance across datasets is related to biases in correcting for library size, which would be a combination of differences in cell-size and degree of difference (DE) between cell-types.

5. We have made the scripts in a modular structure for the comparison available on github. Thus, it should be straightforward to add methods and re-run the study.

F1000Res. 2018 Dec 3. doi: 10.5256/f1000research.18156.r40894

Reviewer response for version 1

Jean Fan ^1,²

Overview:

Analysis of single-cell RNA-seq data is often complicated by large amounts of zeros, of some which represent true lack of expression, while others are reflective of poor capture efficiency or other technical limitations. Several methods have been developed to impute the zeros and recover the true gene expression values. Here, Andrews and Hemberg compare the performance of 5 of these single-cell imputation methods using both simulated data and artificially permuted single-cell RNA-seq data. They evaluate the extent to which these methods introduce false differential expression. A number of clarifications are needed to improve the understandability of the manuscript. Performance benchmarks using additional datasets are also needed to ensure that observed performance differences between methods are not biased by how well the datasets conform to underlying distributions assumed by each method.

Major comments:

The authors conclude that SAVER is the least likely to generate false positives and should be favored over the other 4 imputation methods. However, the scImpute manuscript compared its performance with SAVER to draw conflicting conclusions. I am concerned that the conclusion of which method is better is being biased by the way the benchmark data has been simulated in both cases. Here, the authors simulate data using a negative binomial distribution and find that SAVER had the lowest false positive rate. However, as the authors note, this may be expected, since SAVER models expression data using a negative binomial model. In this manner, the simulation results appear rather circular: the method that uses the same model as the simulated data performs best. In contrast, in the scImpute paper, the authors simulate data using a normal distribution with drop-outs introduced using a Bernoulli distribution and find that SAVER imputation does not alter the data by much or improve downstream clustering whereas scImpute recapitulates the complete data. Please discuss this discrepancy.
There are genes that are not detected in most single-cells due to poor capture efficiency but we know must be expressed, albeit at low levels, based on bulk RNA-seq, FISH, RT-qPCR, or other approaches for measuring gene expression. As a result, most previous methods have assessed performance by comparing imputed values from single-cell RNA-seq against these bulk RNA-seq, FISH, or RT-qPCR datasets, typically focusing, as the authors note, on the imputation method's ability to recover true signals. How often does imputation introduce a significantly differentially expressed gene in single-cell data that we know should not be differentially expressed based on bulk RNA-seq, FISH, RT-qPCR, or etc? Bulk RNA-seq and single-cell RNA-seq datasets exist for both ESC and DEC cells, which were used for benchmarking in the scImpute paper. Both sorted and unsorted PBMCs are also widely available in both bulk and single-cell RNA-seq form. A number of cell lines have also been sequenced by both bulk and single-cell RNA-seq. In general, the manuscript would greatly benefit from the inclusion of additional benchmarks based on at least one of these datasets. Including additional datasets will also help mitigate the concern that SAVER's superior performance over the other methods is simply the result of both the simulated and the Tabula Muris dataset conforming to the negative binomial model.
The authors find that many randomly permuted genes were differentially expressed after imputation and furthermore, the direction of the differential expression after imputation was different for different imputation methods. How frequently do these different imputation methods lead to these different directions of differential expression and therefore conflicting biological interpretations? Is Zfp606 the only gene that exhibits this issue suggesting this is a rare event? Or do conflicts arise frequently?
The authors identify marker genes prior to imputation and note that 95% of marker genes are significant markers in both SmartSeq2 and 10X datasets for the same tissues. They use this comparison between SmartSeq2 and 10X datasets to quantify reproducibility. After imputation, only 80% or so of marker genes were significant in both datasets i.e. decreased reproducibility. Is this decreased reproducibility just due to significance thresholds being reached in one dataset but not the other? Are the -log10(p-values) from the Mann-Whitney-U tests correlated before and after imputation? How do the -log10(p-values) from the Mann-Whitney-U tests correlate between SmartSeq2 and 10X? Before and after imputation?

Minor comments:

The terms "false positive", "false signal", and "false positive signal" are used throughout the early components of the manuscript, including the abstract, before it is defined in the "Permuted Tabula Muris datasets" section. I initially interpreted "false positive signal" loosely to mean genes that are not supposed to be expressed but become non-zero after imputation. However, the definition that the authors are using appears more stringent in that not only does a gene become non-zero after imputation but it becomes significantly differentially expressed. I appreciate this more stringent definition since it more directly impacts biological interpretation. Please define "false positive signal" earlier or use a more specific term like "false differential expression" to minimize confusion due to terminology.
The terms "irreproducible results", "reproducibility", etc. are used throughout the early components of the manuscript, including the abstract before it is defined in the "Reproducibility of markers" section. I initially interpreted "reproducibility" to mean whether I would get the same results from running the same imputation algorithm multiple times. Please define these terms earlier or use a more specific term to minimize confusion due to terminology.
The authors note that many imputed markers were assigned to "contradictory cell-types" (page 8). Please clarify what this means. What fraction of identified markers does this affect? Does this tend to affect one cell-type i.e. are the markers consistently mixed up between two cell-types?
Please clarify which methods were run on raw counts and which were run on log2 CPM in Table 1. Was a pseudocount used in the log transformation?
The authors state that "scRNASeq imputation only draws on structure within the dataset itself" but this statement should be limited to the scope of the 5 methods currently tested. scRNAseq imputation methods in the future may draw on external datasets.
Figure 1A is very telling. Could a similar figure be included for the Tabula Muris datasets to visualize the effects of imputation?
Readers would greatly benefit from a discussion on when imputation should be used, if at all, given this observed propensity to introduce false differential expression.

F1000Res. 2019 Feb 18.

Tallulah Andrews ¹

Thank you for the helpful suggestions, we have made all suggested Minor corrections and have addressed the Major corrections here and in the revised version of the text:

1. Our results broadly agree with the results presented in the scImpute paper, in that SAVER makes modest adjustments to the data, and MAGIC introduces many false signals, whereas scImpute falls in between. However, the scImpute paper focuses on the ability of the method to amplify true signals, such as the tightness of clusters, and the strength/detection of true differential expression, within the data. Whereas, our analysis focused on the tendency to introduce false-positives. Thus it provides complementary rather than contradictory information.

Since scImpute uses a zero-inflated normal distribution to approximate log-transformed normalized counts it is expected that it would outperform other methods when that model is used for the simulations as in the scImpute paper. However, RNA-seq data is fundamentally a discrete non-negative process, thus violating the assumptions of the normal distribution. It has been established that read counts from scRNA-seq and bulk RNA-seq (or indeed other -seq protocols) are well described by some variant of the negative binomial distribution e.g. (Grün et al. 2014; Robinson and Smyth 2007), which is why that is the model used here for the simulations. We have added Figure S1 to the supplementary material showing the Splatter simulations (zero-inflated negative binomial) are a good match for real scRNA-seq data. However, it should be noted that we find that 10X data was best simulated as a pure negative binomial, whereas Smartseq2 was best simulated with a zero-inflated negative binomial as has been remarked upon previously (see: http://www.nxn.se/valent/2017/11/16/droplet-scrna-seq-is-not-zero-inflated). In addition, when comparing the fits of the zero-inflated negative binomial distribution and zero-inflated normal distribution to the Tabula Muris raw counts and log-normalized counts respectively we found the negative binomial fits most genes better than the normal distribution (Table S1). Thus, we believe the negative binomial based simulations used here are more relevant to real single-cell RNA-seq data than the simulations used in the scImpute paper.

2. While we agree bulk RNA-seq intuitively seems like a good ‘ground truth’ for scRNA-seq it is difficult to use it to evaluate imputation since in general simply summing scRNA-seq data is the closest approximation to bulk RNA-seq by the nature of the experiments. The use of bulk RNA-seq as a ground truth assumes that the assayed cell-populations are in truth completely homogeneous. If the “pure” cell populations are a result of sorting this is almost certainly not correct because there is always a fraction of contaminating cells which will result in a bias towards greater smoothing. Although cell populations obtained by growing cells in culture are more likely to be homogenous, they are a poor model for scRNA-seq data obtained from complex tissue samples. There are also reasons to believe that bulk RNA-seq is not a gold standard for identifying truly differentially expressed genes. Bulk RNA-seq is generally limited by its low power due to a small number of samples and the homogenizing effect of bulk samples. Thus, genes that are simply not-detected as differentially expressed using bulk RNA-seq may in truth be differentially expressed just in a small subset of cells or with a low fold-change. Moreover, even though there are many common steps in the experimental protocols for generating bulk and scRNA-seq, it is likely that there will be effects that are specific to each method. For example: with respect to GC content biases or gene-length biases, bulk RNA-seq may not be more correct than scRNA-seq. There is no reason to believe reproducibility across bulk and scRNA-seq is a more reliable method of benchmarking than reproducibility across different scRNA-seq datasets which we have performed using the Tabula Muris data. We attempted to use two datasets (Kolodziejczyk et al. 2015; Tung et al. 2017) for which matching bulk data was available but the results were inconsistent which is not surprising considering the variability we saw with the Tabula Muris datasets.

3. We have added Figure S6 which shows that the proportion of markers with conflicting directions across all the Tabula Muris datasets varies from 5% to 35%. We considered the full imputed Tabula Muris dataset since most genes should have some real differential expression, and thus be more likely to be consistent across imputation methods than the permuted genes, which contain no true signal.

4. We apologize that this analysis was not explained clearly. The 95% and 80% are not related to differences in power or significance thresholds, they refer to the percent of markers that were most highly expressed in the same cell-type given that the gene was a significant marker in both datasets. We have clarified this in the text (Results: page 13-14). We appreciate the suggestion for comparing p-values directly and have added a supplementary figure S5 that displays these correlations, further reinforcing our original conclusions that imputation results in poorer reproducibility.

F1000Res. 2018 Nov 29. doi: 10.5256/f1000research.18156.r40895

Reviewer response for version 1

Simone Tiberi ¹

The article investigates how imputation methods of 0 counts in single-cell RNA-seq (scRNA-seq) can introduce false signals, and hence false positives in downstream analyses. The authors explain how scRNA-seq data can present an excess of 0 counts, i.e. dropouts, due to technical artefacts, and introduce a few recent methods that can be used to impute these values. Andrews and Hemberg focus on a sub-set of 5 imputation methods and investigate, in three scenarios, if these methods introduce false signals between genes:

First, data are simulated from a simple negative binomial (NB) model: most imputation methods introduce false signals in the data by increasing the correlation between independent genes.
Secondly, the authors study the effect of imputation methods on downstream differential gene expression (DGE) analyses on 60 scRNA-seq datasets simulated via Splatter (with varying degrees of dropouts and DGE). They find that, compared to the original un-imputed data, albeit some imputation methods result in higher Sensitivity (i.e. true positive rate), all of them have lower the Specificity (i.e. true negative rate).
Thirdly, they consider several real scRNA-seq datasets, where counts are permuted to obtain approximately uncorrelated genes, and investigate how imputation methods affect the ability to identify marker genes. The authors find that, compared to the un-imputed data, imputation tools distort expression patterns and increase the number of identified marker genes, although some of these are likely to be false detections.

The article treats a relevant problem and provides a comprehensive benchmarking of imputation methods. Overall, the manuscript is clear and its scientific quality is adequate. Below, I suggest several corrections (and identify a few typos) that hopefully will contribute to improving the quality and clarity of the work.

Major Comments:

In some cases it is unclear to me why you take certain decisions: I feel you should motivate more your choices (see Minor comments for specific examples).
Please provide source code to reproduce all the analysis you present (including obtaining the simulated and permuted data).
There is some redundancy in the description of the data: you first describe in detail how you obtained the simulated data and the permuted real data in the Methods section, and then you repeat it again (although with fewer sentences) in the Results section. I would avoid or shorten the second description in the Results section.
Although the paper aims at investigating on false signals introduced by imputation methods, I feel too much emphasis has been given to false positive results as opposed to jointly considering false and true positive results. Indeed, the paper shows that imputation methods result in increased FPs/Specificity, particularly when the original data are not affected by dropouts, but it only marginally focuses on the increase in TPs/Sensitivity.

More informally, I think you should try to show both sides of the coin and avoid (over-)interpreting FP results alone. In this regard, to get a joint picture of Sensitivity and Specificity, I think you should provide (at least for the Splatter simulation) ROC and FDR curves (eventually, also as Supplementary figures). Since you perform 60 simulations from Splatter, you might consider global ROC and FDR plots based on the results from all simulations.
I think that the limitations of the study should be explained more clearly:

5.1) In the permuted real data analysis, all imputation methods find many more marker genes than the un-imputed data, but the authors mostly focus on the fact that the percentage of “reliable” identifications decreases. I think that: 1) importance should be given also to the fact that many more “reliable” marker genes are identified (also referring to the comment above about FPs and TPs) and: 2) it is essential to explicitly acknowledge that the true state of marker genes is unknown. Importantly, in Figure 4 A) and B) please add the FPR obtained on the un-imputed data to provide a baseline comparison.

5.2) In the NB simulation you don’t simulate any dropouts, which represents the worst case scenario for imputation methods. In this context, I would expect all imputation methods to worsen downstream results, because there are no dropouts to impute at all. I think you should mention this more explicitly.
In Splatter simulations you “considered the effect of four different amounts of added dropouts”. How mild or extreme were these dropout levels compared to real scRNA-seq data? I would expect imputation methods to improve the quality of the data as the number of dropouts increases. Did you try to consider more “extreme” dropout rates?
In Figures 2C and 2D you provide Sensitivity boxplots stratified by dropout rates and Specificity boxplots stratified by DE. Sensitivity and Specificity should always be examined jointly: for both stratification cases, please provide both Sensitivity and Specificity plots (eventually, also as Supplementary figures).
I suggest another round of polish to improve writing and clarity in some parts of the paper. In particular: adding few commas would facilitate the reading in long sentences; past and present tenses are sometimes mixed; some sentences seem a bit out of place and could be better integrated in the flow; I found the last two paragraphs of the Results section a bit hard to follow.
You refer a few times to the fact that you “find a fundamental trade-off between sensitivity and specificity which imputation cannot overcome”: reading the paper it seems that imputation methods might be responsible for this. But this trade-off is due to the nature of Sensitivity and Specificity; indeed, Sensitivity and Specificity are positively correlated by construction: as one moves the significance threshold, both will increase or decrease. Clearly an ideal method will have Sensitivity 0 and Specificity 1. I think you should remove or edit the sentences referring to this trade-off (particularly in the Discussion) to clarify that imputation methods are not the cause of this trade-off.
In the Discussion you say that “While imputation in other fields often uses external references or relationships for the imputation, scRNASeq imputation only draws on structure within the dataset itself.”. Actually, “canonical” imputation methods do not require an external reference and only use the available data. While having an additional reference can increase the information at disposal and hence, potentially, improve the accuracy of imputation tools, I don’t think this is the main reason why they result in increased false signals. Besides, there are other issues with using an external reference; e.g. if the reference is not “similar” to the data-set under study, particularly concerning their dropouts. I think you could clarify that using an external reference is one of the possible ways to improve imputation methods, but keeping in mind that imputation (in general) can also work without a reference.

Minor Comments:

1) General:

Throughout the text, you use both “Smart-seq2” and “Smartseq2“; I suggest you use only one, for consistency.

2) Abstract:

“since these methods generally rely on structure inherent to the dataset under consideration they may not provide any additional information.” You clarify this point later in the text but, when I read the abstract, it was not clear to me what you were referring to. Maybe you could try to be more explicit here or remove the sentence.

3) Introduction:

You cite 4 imputation methods as “under development“ but you only test one. I think you’d motivate this choice.
Typo: “though imputation” -> “through imputation”.
GWAS not defined before.
Typo: “imputation, which only attempt to infer” -> “imputation, which only attempts to infer”.

4) Methods:

Fig S1: “aka” -> “i.e.” (I would use something more elegant than aka).
Typo: “as calculated scater” -> “as calculated by scater” ?
“ranging from 10^3-10^4” -> “ranging 10^3-10^4” or “ranging from 10^3 to 10^4”.
Typo: “different probability distribution” -> “different probability distributions”.
“When filtering DE genes by effect size, in addition to significance”. This sentence is quite vague, please be more specific.
“Six 10X Chromium and 12 Smartseq2 datasets”. You use words (Six) and digits (12) in the same sentence to refer to numbers: I’d choose one for consistency.
You use two distinct types of DGE tests for the simulated data (Splatter) and the permuted real data. Please motivate your choice.
Typo (?): “for which there exists matching Smart-seq2 and 10X Chromium” -> “for which there exists matching for Smart-seq2 and 10X Chromium” ?

5) Results:

“MAGIC provides … whereas knn smooth provided …”. Present and past tenses are mixed here: I suggest you replace “provided” with “provides” to keep consistency with the rest of the manuscript.
In the NB simulation, provide more details on the implementation of the correlation test: how did you test correlations? What significance level was used to define a significant correlation in Fig 1B and S1? 0.05?
In Figure 1B and S1, I guess that “Raw” refers to the original (un-imputed) data; did I understand correctly? It was not obvious to me at a first glance, please make it explicit (in the text or in the Figure caption).
Fig 2: typo (?): “Different imputation methods choose a different trade-off ...“; I didn’t understand the use of “choose” in the sentence: is this a typo? If not, can you re-write the sentence in a clearer way?
Fig 2: “genes DE” -> “DE genes”.
In the permutation real data analysis, please clarify the concept of filtering genes: do you refer to independent filtering of genes (based on their estimated FC)?
Typo: “the bulk of false-positives ... result” -> “the bulk of false-positives … results”.
“It’s possible” -> “It is possible”.
“Xth percentile” -> “X-th percentile”.
“Xth percentile highest log2 fold-change“ -> “highest log2 fold-change X-th percentile”.
Fig 4 (A) caption: “SmartSeq2 datasets,” -> “SmartSeq2 datasets.” (a comma separates two Figure descriptions instead of a full stop).
Fig 4 (C) caption: “the proportion that were markers” -> “the proportions that were markers”.
I would change “many of the imputed markers are incorrect” to “some of the imputed markers are incorrect”. “some” seems more appropriate than “many”, considering that 80-90% of them are estimated to be true marker genes.
The second last paragraph of Results sounded a bit contorted to me: I would rephrase it in a clearer way.
“The imputation methods produced different distortions of the gene expression values ( Figure 6).” Can you better integrate this sentence in the flow? It seems a bit out of place.
“PCA and differential expression” -> “PCA and most differential expression tools/methods”. Tools/methods is missing. I would also add “most” because not all DE methods require NB or Gaussian distributions (e.g. non parametric methods).
To facilitate a visual comparison, in Figure 5 I would adjust the left y-axis (Genes #) to have the same limits in all examples.
Fig 6 caption: “significant after Bonferroni correction”; please add the significance level (I assume 0.05).

6) Discussion:

In the second paragraph you first use “these methods generate” and then “MAGIC generated” mixing present and past tenses; I’d use “generate” in both cases.
The subject is missing in this sentence: “MAGIC and knn-smooth which are data-smoothing methods, as such they adjust all expression values not just zeros.” -> I would write something like: “MAGIC and knn-smooth are data-smoothing methods, as such they adjust all expression values not just zeros.” Or alternatively, “MAGIC and knn-smooth, which are data-smoothing methods, adjust all expression values not just zeros.”
“it’s performance” -> “its performance”.

F1000Res. 2019 Feb 18.

Tallulah Andrews ¹

Thank you for the helpful suggestions, we have made all suggested Minor corrections and have addressed the Major corrections here and in the revised version of the text:

1. We have revised the text and tried to provide motivations for the key decisions.

2. The github repo accompanying the study now contains scripts that can be run to reproduce the results reported here.

3. We have followed the Reviewer’s suggestion and shortened the descriptions in the Results section.

4. We have added the true positive rate to Figure 1B, have added Figure S4 showing the increase in reproducible markers in Tabula Muris datasets, and modified the text to put greater emphasis of the increase in sensitivity provided by imputation (last paragraph of page 6, p9 paragraph 2, p14 paragraph 1) to clarify that sensitivity is increased by using imputation at the cost of specificity, however as the ROC plots show (Figure 2 E), to address the reviewer’s concern below, this increase in sensitivity could be achieved by simply lowing the significance threshold applied to the statistical test and result in fewer false positives than using an imputation method.

The reviewer raises a good point and we have calculated and included the ROC for the simulated data in Figure 2 E.

5.1.

We have updated the text to highlight the advantage of having a larger number of markers from imputed data (Figure S4, p14 paragraph 1).
We have added the FPRs for the un-imputed data (counts) to both Fig 4A and B, as expected there were almost none since we used the conservative Bonferroni multiple testing correction.

5.2. We have highlighted the lack of dropouts in the NB simulations in the text, and explicitly mentioned the desired behaviour for both model-based imputation and data-smoothing in this context (Methods: Negative Binomial Simulations).

6. We have adjusted the dropout parameters tested to be more similar to those observed in real single-cell RNA-seq data (Figure S1 A) and added the average proportion of zeros in the entire expression matrix for each value to Table 2 to help the readers understand what the different scenarios correspond to. At the highest level of added dropouts 94% of the matrix was composed on zeros and all the methods other than MAGIC and knn-smooth had sensitivity < 0.2, and the resilience of data-smoothing to high dropout rates has been noted in the text (Results: p9, paragraph 1).

7. We have followed the Reviewer’s suggestion and now include both Sensitivity and Specificity plots stratified by dropout rate and proportion of DE genes in Figure 2.

8. We have tried to improve the clarity of the text with a specific focus on paragraphs highlighted by the Reviewer.

9. The Reviewer raises an important point regarding the fundamental relationship between sensitivity and specificity. One of the central aims of our paper was to highlight this particular trade-off and that the effect of most imputation methods is simply to shift the balance between these quantities. Our goal was to say that this is indeed a relationship that is caused by how these quantities are constructed and that imputation methods simply favour one side of the trade off or the other not create it. We have edited the text to better clarify this (Discussion: paragraph 1).

10. The Reviewer raises a good point, we have edited the text appropriately (Discussion: paragraph 3).

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Click here for additional data file.^{(2.4MB, tgz)}

Data Availability Statement

Tabula Muris data

Smart-seq2 https://doi.org/10.6084/m9.figshare.5715040.v1 ( Consortium, The Tabula Muris, 2017a).

10X Chromium https://doi.org/10.6084/m9.figshare.5715040.v1 ( Consortium, The Tabula Muris, 2017b).

R packages

MAGIC: Rmagic (v0.1.0) https://github.com/KrishnaswamyLab/MAGIC

DrImpute: DrImpute (v1.0) https://github.com/ikwak2/DrImpute

scImpute: scImpute(v0.0.8) https://github.com/Vivianstats/scImpute

SAVER: SAVER(v1.0.0) https://github.com/mohuangx/SAVER

Knn-smooth: knn_smooth.R (Version 2) https://github.com/yanailab/knn-smoothing

Scater: scater(v1.6.3) : https://www.bioconductor.org/packages/release/bioc/html/scater.html

Splatter: splatter(v1.2.2) : https://bioconductor.org/packages/release/bioc/html/splatter.html

Permute: permute(v0.9-4) : https://cran.r-project.org/web/packages/permute/index.html

Python/anaconda packages:

Dca : dca(v0.2.2): https://github.com/theislab/dca

Custom scripts: https://github.com/tallulandrews/F1000Imputation

[ref-26] Benjamini Y, Hochberg Y: Controlling the false discovery rate: A practical and powerful approach to multiple testing. J Roy Stat Soc B Met. 1995;57(1):289–300. 10.1111/j.2517-6161.1995.tb02031.x [DOI] [Google Scholar]

[ref-1] Bullard JH, Purdom E, Hansen KD, et al. : Evaluation of statistical methods for normalization and differential expression in mRNA-Seq experiments. BMC Bioinformatics. 2010;11:94. 10.1186/1471-2105-11-94 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-2] Chou WC, Zheng HF, Cheng CH, et al. : A combined reference panel from the 1000 Genomes and UK10K projects improved rare variant imputation in European and Chinese samples. Sci Rep. 2016;6:39313. 10.1038/srep39313 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-35] Consortium, The Tabula Muris: Single-cell RNA-seq data from Smart-seq2 sequencing of FACS sorted cells. figshare.Fileset.2017a. 10.6084/m9.figshare.5715040.v1 [DOI] [Google Scholar]

[ref-36] Consortium, The Tabula Muris: Single-cell RNA-seq data from Smart-seq2 sequencing of FACS sorted cells. figshare.Fileset.2017b. 10.6084/m9.figshare.5715040.v1 [DOI] [Google Scholar]

[ref-5] Deng Y, Bao F, Dai Q, et al. : Massive single-cell RNA-seq analysis and imputation via deep learning. bioRxiv. 2018. 10.1101/315556 [DOI] [Google Scholar]

[ref-27] Eraslan G, Simon LM, Mircea M, et al. : Single-cell RNA-seq denoising using a deep count autoencoder. Nat Commun. 2019;10(1):390. 10.1038/s41467-018-07931-2 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-7] Fawcett T: An introduction to ROC analysis. Pattern Recognit Lett. 2006;27(8):861–874. 10.1016/j.patrec.2005.10.010 [DOI] [Google Scholar]

[ref-8] Gong W, Kwak IY, Pota P, et al. : DrImpute: imputing dropout events in single cell RNA sequencing data. BMC Bioinformatics. 2018;19(1):220. 10.1186/s12859-018-2226-y [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-9] Grün D, Kester L, van Oudenaarden A: Validation of noise models for single-cell transcriptomics. Nat Methods. 2014;11(6):637–640. 10.1038/nmeth.2930 [DOI] [PubMed] [Google Scholar]

[ref-10] Han X, Wang R, Zhou Y, et al. : Mapping the Mouse Cell Atlas by Microwell-Seq. Cell. 2018;173(5):1307. 10.1016/j.cell.2018.05.012 [DOI] [PubMed] [Google Scholar]

[ref-28] Hu Q, Greene CS: Parameter tuning is a key part of dimensionality reduction via deep variational autoencoders for single cell RNA transcriptomics. bioRxiv. 2018. 10.1101/385534 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-11] Huang M, Wang J, Torre E, et al. : SAVER: gene expression recovery for single-cell RNA sequencing. Nat Methods. 2018;15(7):539–542. 10.1038/s41592-018-0033-z [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-12] Kiselev VY, Kirschner K, Schaub MT, et al. : SC3: consensus clustering of single-cell RNA-seq data. Nat Methods. 2017;14(5):483–486. 10.1038/nmeth.4236 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-13] Kruskal WH, Wallis WA: Use of Ranks in One-Criterion Variance Analysis. J Am Stat Assoc. 1952;47(260):583–621. 10.1080/01621459.1952.10483441 [DOI] [Google Scholar]

[ref-14] Li WV, Li JJ: An accurate and robust imputation method scImpute for single-cell RNA-seq data. Nat Commun. 2018;9(1):997. 10.1038/s41467-018-03405-7 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-15] McCarthy DJ, Campbell KR, Lun AT, et al. : Scater: pre-processing, quality control, normalization and visualization of single-cell RNA-seq data in R. Bioinformatics. 2017;33(8):1179–1186. 10.1093/bioinformatics/btw777 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-16] Mongia A, Sengupta D, Majumdar A: McImpute: Matrix completion based imputation for single cell RNA-seq data. bioRxiv. 2018. 10.1101/361980 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-17] Moussa M, Mandoiu I: Locality Sensitive Imputation for Single-Cell RNA-Seq Data. bioRxiv. 2018. 10.1101/291807 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-18] Obayashi T, Hayashi S, Shibaoka M, et al. : COXPRESdb: a database of coexpressed gene networks in mammals. Nucleic Acids Res. 2008;36(Database issue):D77–82. 10.1093/nar/gkm840 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-29] Plass M, Solana J, Wolf FA, et al. : Cell type atlas and lineage tree of a whole complex animal by single-cell transcriptomics. Science. 2018;360(6391): pii: eaaq1723. 10.1126/science.aaq1723 [DOI] [PubMed] [Google Scholar]

[ref-30] Regev A, Teichmann S, Lander ES, et al. : The human cell atlas. bioRxiv. 2017. 10.1101/121202 [DOI] [Google Scholar]

[ref-31] Robinson MD, Smyth GK: Moderated statistical tests for assessing differences in tag abundance. Bioinformatics. 2007;23(21):2881–2887. 10.1093/bioinformatics/btm453 [DOI] [PubMed] [Google Scholar]

[ref-19] Rozenblatt-Rosen O, Stubbington MJT, Regev A, et al. : The Human Cell Atlas: from vision to reality. Nature. 2017;550(7677):451–453. 10.1038/550451a [DOI] [PubMed] [Google Scholar]

[ref-32] Tabula Muris Consortium, . Overall coordination, . Logistical coordination, et al. : Single-cell transcriptomics of 20 mouse organs creates a Tabula Muris. Nature. 2018;562(7727):367–372. 10.1038/s41586-018-0590-4 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-6] van Dijk D, Sharma R, Nainys J, et al. : Recovering Gene Interactions from Single-Cell Data Using Data Diffusion. Cell. 2018;174(3):716–729.e27. 10.1016/j.cell.2018.05.061 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-21] Visscher PM, Wray NR, Zhang Q, et al. : 10 years of GWAS discovery: biology, function, and translation. Am J Hum Genet. 2017;101(1):5–22. 10.1016/j.ajhg.2017.06.005 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-22] Wagner F, Yan Y, Yanai I: K-nearest neighbor smoothing for high-throughput single-cell RNA-Seq data. bioRxiv. 2017. 10.1101/217737 [DOI] [Google Scholar]

[ref-33] Wang D, Gu J: VASC: Dimension Reduction and Visualization of Single-cell RNA-seq Data by Deep Variational Autoencoder. Genomics Proteomics Bioinformatics. 2018;16(5):320–331. 10.1016/j.gpb.2018.08.003 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-20] Wang J, Agarwal D, Huang M, et al. : Transfer learning in single-cell transcriptomics improves data denoising and pattern discovery. bioRxiv. 2018. 10.1101/457879 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-23] Zappia L, Phipson B, Oshlack A: Splatter: simulation of single-cell RNA sequencing data. Genome Biol. 2017;18(1):174. 10.1186/s13059-017-1305-0 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-24] Zeisel A, Hochgerner H, Lönnerberg P, et al. : Molecular Architecture of the Mouse Nervous System. Cell. 2018;174(4):999–1014.e22. 10.1016/j.cell.2018.06.021 [DOI] [PMC free article] [PubMed] [Google Scholar]

[ref-25] Zhang L, Zhang S: Comparison of computational methods for imputing single-cell RNA-sequencing data. IEEE/ACM Trans Comput Biol Bioinform. 2018. 10.1109/TCBB.2018.2848633 [DOI] [PubMed] [Google Scholar]

PERMALINK

False signals induced by single-cell imputation

Tallulah S Andrews

Martin Hemberg

Roles

Version Changes

Revised. Amendments from Version 1

Abstract

Introduction

Methods

Table 1. Imputation methods.

Negative binomial simulations

Splatter simulations

Table 2. Splatter parameters.

Permuted Tabula Muris datasets

Reproducibility of markers

Results

Figure 1. False gene-gene correlations induced by single-cell imputation methods.

Figure 2. Accuracy of detecting differentially expressed (DE) genes in splatter simulations before and after imputation with each method.

Figure 3. Filtering by the magnitude of expression differences restores specificity in imputed data.

Figure 4. High variability in false positives induced by imputation across datasets regardless of sequencing technology.

Figure 5. Reproducibility of marker genes can be restored in imputed data using a strict effect-size threshold.

Figure 6. Examples of false positive DE induced by imputation of Pancreas Smart-seq2 data.

Discussion

Data and software availability

Funding Statement

Supplementary material

References

Reviewer response for version 2

Simone Tiberi

Roles

Reviewer response for version 2

Charlotte Soneson

Roles

Reviewer response for version 2

Jean Fan

Roles

Reviewer response for version 2

Stephanie Hicks

Roles

Reviewer response for version 1

Stephanie Hicks

Roles

References

Tallulah Andrews

Reviewer response for version 1

Charlotte Soneson

Roles

Tallulah Andrews

Reviewer response for version 1

Jean Fan

Roles

Tallulah Andrews

Reviewer response for version 1

Simone Tiberi

Roles

Tallulah Andrews

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases