Purpose-Driven Reconciliation of Approaches to Estimate Chemical Releases

Abstract

A framework is presented to address the toolbox of chemical release estimation methods available for manufacturing processes. Although scientists and engineers often strive for increased accuracy, the development of fit-for-purpose release estimates can speed results that could otherwise delay decisions important to protecting human health and the environment. A number of release estimation approaches are presented, with the newest using decision trees for regression and prediction. Each method is evaluated in a case study for cumene production to study the reconciliation of data quality concerns and requirements for time, resources, training, and knowledge. The evaluation of these decision support criteria and the lessons learned are used to develop a purpose-driven framework for estimating chemical releases.

Graphical Abstract

Reconciliation of methods applied to manufacturing processes to estimate chemical releases, useful for exposure, risk, and other sustainability assessments.

Introduction

The chemical industry’s contributions to all sectors of the economy and society are significant. Although a chemical may be designed and used for a very specific purpose, it has the potential to create environmental impact at each of its life cycle stages (i.e., manufacture, processing, distribution, use, and disposal or end-of-life). To address the summation of these impacts, an assessment of the releases of and exposures to a chemical at each life stage is needed. This can be accomplished using methods such as risk assessment.¹ With its focus on exposure and hazard, a risk assessment approach can yield insights on chemical safety and the need to mitigate exposure risk. At each life cycle stage, conceptual models can consider the release(s) of a chemical and estimate the resulting exposures as well as the resulting hazards to human and ecological environments. The quantities of a chemical release at each stage must be collected prior to employing these conceptual models. The emphasis of this contribution is to examine different approaches to quantifying the estimated releases of a chemical which are attributed to its manufacturing stage.

To determine the risk associated with chemical hazards, a first step is to understand the flows of material that can be potentially released. One method for understanding those flows completely is material flow analysis,² which when confined to a single substance is known as substance flow analysis. A substance of interest may flow through various processes, where it may be manufactured, processed, distributed, used, enter commerce in articles, and undergo end-of-life processes. The substance may accumulate in anthropologic stocks (e.g., storage) and in environmental stocks including media of biota, air, water, and land. Evaluating the releases as a substance flows through these processes and accumulating or dissipating stocks is an initial step toward risk assessment. When focusing on processes to manufacture or process a substance, the study of material (substance) flow analysis may require only an approximation of the rate of manufacture or processing and the amount of storage. Once these manufacturing, processing, and storage amounts are determined an estimation of releases can be undertaken.

Different methods for quantifying releases are described in the literature. An algorithm for developing a release assessment based on process flowsheets, identifying relevant streams, and quantifying releases was developed by Allen et al.³ The U.S. Environmental Protection Agency (EPA) has compiled air pollution estimates, or emission factors, for over 200 air pollution source categories in their AP-42 handbook using source test data, material balance studies, and engineering estimates.⁴ Additional methods focus on modeling process operations such as vessel filling, heating, condensing, etc., to quantify potential releases.⁵ Another method for quantifying releases while addressing error is rectification, using reconciliation in this context to reduce random errors and gross error compensation for systematic errors.⁶ These methods work when data can be confined to a single process with multiple scales offering redundant measurements for conservation of mass; otherwise gross error detection is difficult.^7,8

From a different perspective, regulations allow the use of surrogates for emissions, for instance, when particulate matter can be a surrogate for metallic hazardous air pollutants.⁹ Therefore, one could possibly consider surrogates or proxies as another method for quantifying chemical releases. An extension of this idea is not to pick a specific proxy chemical, but to use existing data on releases, physicochemical properties, and manufacturing flows for a wide range of chemicals to parametrize a predictive statistical model. Such a model often takes the form of a statistical classification tool known as a decision tree that subdivides the response variable (i.e. release quantity) into regions of descriptor space (e.g., water solubility, production volume) that can be used to predict releases of chemicals based on key descriptors (i.e., physicochemical and manufacturing properties). Periera et al.¹⁰ have used classification trees with reaction and process information to predict steam consumption in batch chemical manufacturing processes.

Methods for estimating releases that were developed at the EPA’s Office of Research and Development can be applied toward efforts at evaluating specific chemicals. A bottom-up process design and simulation method by Smith et al.¹¹ uses modeling to calculate input-output flows of materials and emission factors to estimate uncontrolled air emissions. These results can be augmented by pollution control modules that refine the emission inventory.¹² The approach can generate a complete multipollutant emission inventory or be narrowly focused on a single chemical of interest.¹³ The top-down data mining methodology by Cashman et al.¹⁴ uses EPA databases to develop releases of air emissions, water discharges, and solid waste based on industry supplied information. Although initially developed for life cycle inventory modeling to support life cycle assessment (LCA), the method can focus on specific facilities manufacturing a specific chemical, so the results are tailored to the emission of a specific chemical of interest.

Chemicals being assessed can be classified as either new chemicals or existing chemicals. New chemicals can be more difficult to model because much less is known about their industrial scale production. However, both classes can involve gaps regarding knowledge of the various releases during manufacturing, especially when considering fugitive emissions, venting, and storage. Given the numerous methods discussed above that can be used to estimate chemical releases, the challenge is deciding which approach to use. A clear set of criteria is necessary for this purpose. Some guidance along these lines can be taken from the systematic review process implemented for chemical assessments under the Toxic Substances Control Act (TSCA).¹⁵ The systematic review process evaluates the quality of environmental release data based on seven categories: methodology, geographic scope, applicability, temporal representativeness, sample size, metadata completeness informing the accessibility and clarity domain, and metadata completeness informing the variability and uncertainty domain. These categories provide a good starting point when trying to decide among the various approaches. Similar guidance has been developed for multi-impact assessment by Edelen and Ingwersen.¹⁶ Additional considerations must be added to address specific assessment constraints such as the decision timeline and resource availability. With this in mind, the objectives of this contribution are to (1) demonstrate the use of classification tools (i.e., decision trees) as a means for chemical release modeling; (2) analyze the quality and utility trade-offs of the top-down, bottom-up, and classification modeling approaches when applied to the case study of cumene production; and (3) identify a logical method to select the most appropriate approach for release modeling in chemical assessment when considering a range of decision constraints.

Methodology

This section first describes a case study of air releases, or emissions, during cumene manufacturing that are quantified using three methods: bottom-up simulation, top-down data mining, and statistical classification and regression. The intent of the case study is to identify the strengths and challenges of each method based on a set of evaluation criteria. Whereas the top-down and bottom-up methods have been previously described, the use of classification and regression is new to this work and, as such, is described in detail. The section concludes with an overview of the evaluation criteria developed for this work.

Cumene System Description

The process for making cumene has been well documented and the chemical itself is tracked in numerous top-down data sources. Thus, cumene presents an interesting example for estimating releases and building the foundation of a reconciliation decision framework for logically selecting appropriate estimation methods. For the case study, the three approaches were used to estimate the air emissions of cumene associated with a manufacturing facility having a production rate of 98,000 metric tons of cumene per year. Although the three approaches are capable of addressing releases to all environmental media, the analysis was limited to air emissions because there were insufficient cumene data to support modeling the other compartments using regression tree analysis. Ancillary processes, such as wastewater treatment and fuel combustion, were not specifically modeled in the bottom-up and top-down approaches, even if the activity occurred onsite. The facility-level data used for regression tree analysis did include such processes, but no attempts were made to characterize emissions by specific activity.

Bottom-Up Simulation

Cumene ((1-methylethyl)benzene) is synthesized through the Friedel-Crafts alkylation of benzene by propylene. 1,4-Di-isopropyl benzene (DIPB) is produced as a byproduct of the reaction. The overall reaction for cumene production is

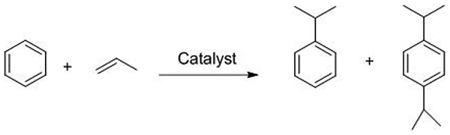
The bottom-up approach uses a process flow diagram (PFD) and process model (i.e., simulation) to estimate chemical releases. A cumene production process model utilizing solid phosphoric acid catalyst was originally developed by Turton.¹⁷ Luyben¹⁸ optimized the reaction temperature (to reduce transalkylation) and benzene recycle rate of Turton’s process. A simulation of Luyben’s cumene production process flowsheet developed by ChemSep¹⁹ was used in this analysis, and a flowsheet for a production rate of 98,000 metric tons per year is available. The process model was developed in the free-of-charge CAPE-OPEN to CAPE-OPEN (COCO) Simulation Environment²⁰ using the 64-bit CAPE-OPEN Flowsheeting Environment (COFE 64) and the Peng-Robinson equation of state from the Thermodynamics for Engineering Applications (TEA) thermodynamics property package. A fixed conversion reactor was selected because it had conversions similar to those obtained by the kinetic reactor used by Luyben. ChemSep distillation columns were used to model the separations and product purification.

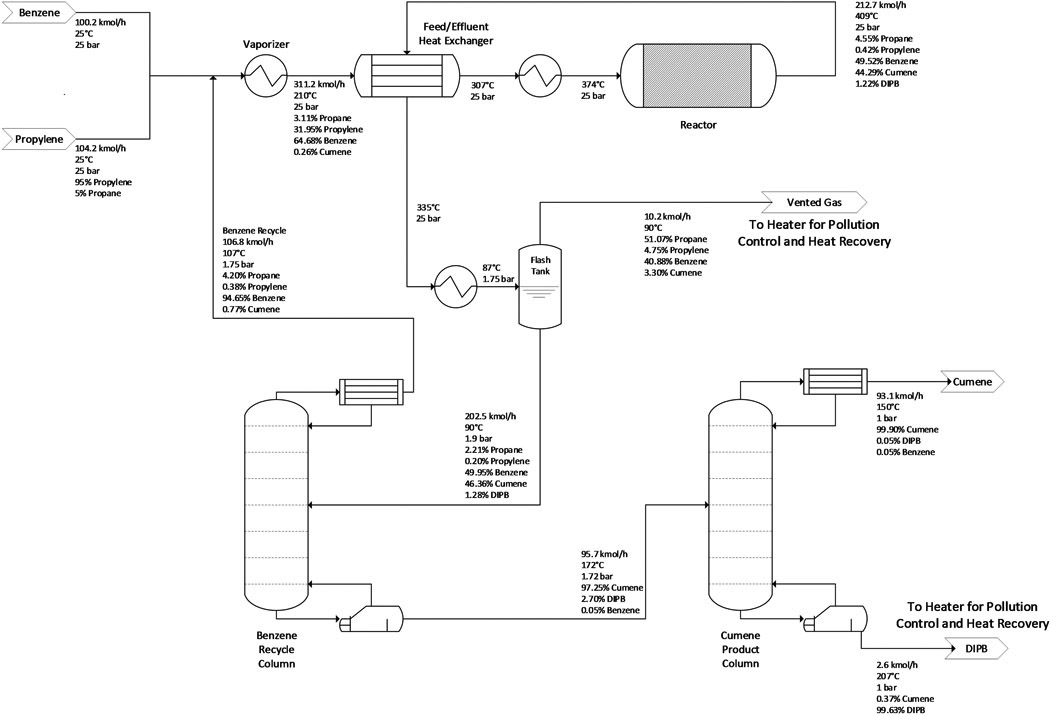
Cumene is present in the three output streams of the process flow diagram (PFD) as shown in Figure 1: the gas phase stream leaving the flash tank, and the distillate and bottom streams leaving the second distillation column (“Cumene Product Column”). The distillate stream is the net produced cumene (98,000 ton/yr), and the bottom stream is the net produced DIPB, which is an undesired byproduct. The flash gas stream (“Vented Gas” in Figure 1) and the DIPB stream are waste streams for disposal or recycling for further use. Control system data obtained from U.S. EPA’s Emissions Inventory System²¹ included diverse types of pollution control equipment being employed to treat cumene during manufacturing, including carbon adsorption (99.5% removal), catalytic thermal oxidizers (99%), enclosed vapor combustors (99.5%), and flares (99.5%). According to Luyben¹⁸ and Turton et al.,¹⁷ the cumene process waste streams are both used as fuel for process heaters because of their heating value content. Therefore, the controlled emissions of cumene were calculated assuming these waste streams are burned in a process heater operating at 99% removal. The fugitive and storage emissions were estimated from the PFD based on the approach described by Smith et al.¹¹ Storage emissions for cumene assumed a 30-day storage inventory time, a 99.9% purity of cumene, and a pollution control device (e.g., a floating roof tank) with a control efficiency of 80%.

Figure 1.

Cumene manufacturing process, based on propylene and benzene feeds. The Flash Tank gas stream and the Cumene Product Column DIPB stream are waste streams for disposal or recycling for further use. Compositions shown are in mol%.

Top-Down Data Mining

National-average cumene emissions from cumene manufacturing were generated using the steps for developing air emissions outlined in Cashman et al.¹⁴ The method was refined by incorporating additional filtering of National Emissions Inventory (NEI)²² data based on metadata for source classification and process and unit descriptions. The metadata enabled emission data to be excluded if they were associated with on-site activities other than cumene manufacturing (e.g., wastewater treatment emissions were not considered for this case study). Production volume data were obtained from EPA’s 2012 Chemical Data Reporting (CDR)²³ database while emission data were obtained from the 2011 NEI and Toxics Release Inventory (TRI).²⁴ The analysis included seven of the eight facilities that do not claim production volume data as confidential business information when reporting to the CDR, with the eighth being omitted because it did not include cumene emissions as part of its reporting. An average emission factor describing the mass of cumene emitted per mass produced was multiplied by the desired production rate to obtain the final emission estimate.

Regression Tree Analysis

A statistical learning approach for estimating chemical releases was explored by using existing chemical release and production data to train decision tree models. The purpose of introducing this approach for the current work is to demonstrate a potentially quick method that can predict releases for data-poor chemicals or new chemicals. To obtain training data, air emissions were taken from EPA’s 2011 NEI and 2011 TRI. Chemical production data were obtained from EPA’s 2012 CDR database, with production volume (PV) data corresponding to 2011. A training set of 45 common substances was developed by comparing the substance coverage list for the three data sources. Physicochemical properties for each chemical were obtained from U.S. EPA’s Chemistry Dashboard²⁵ and PubChem.²⁶

The Standardized Emission and Waste Inventories (StEWI) system²⁷ was used along with customized Python scripts to extract the release data for the training set. This system provides automated EPA inventory database data extraction, standardization, and linkage across facilities and chemicals. Three StEWI modules were used: stewi, which is the core module that standardizes inventory outputs; chemicalmatcher, which matches chemicals across inventories; and facilitymatcher, which matches facilities across inventories. Production facilities and PVs for each chemical in the training set were first manually retrieved from CDR. The primary EPA identification number for each production facility was obtained using manual searches of EPA’s Facility Registry Service (FRS).²⁸ The chemicals from the chemical-facility pairs, in CAS-FRS ID format, were input to the chemicalmatcher to fetch common chemical identification numbers that could be used to identify these chemicals in the NEI and TRI. The facilitymatcher was used to gather inventory specific facility IDs for the FRS IDs in the list. Inventory data were then retrieved from customized versions of the NEI.py and TRI.py processing scripts within stewi. The NEI script returns point-source emission data grouped by an EPA Source Classification Code (SCC) at the facility unit level, with all emissions standardized to consistent metric units and described by uniform metadata. The TRI script outputs standardized stack and fugitive air emissions. The NEI and TRI stewi outputs were then filtered to only include the chemical-facility pairs of interest. The output NEI and TRI emission data were assigned data reliability scores²⁹ from 1 (most reliable) to 5 (least reliable) using the basis-of-estimate codes contained in the metadata for each emission.

In total, 348 facilities were identified for which air emission and production volume data were available. The resulting production and emission data were combined with physicochemical property data (chosen based on their use for release estimation in ChemSTEER³⁰) describing molecular weight, vapor pressure, density, and water solubility at room temperature to create a training set for model development. In cases where a facility reported emissions to NEI and TRI that differed by greater than 100% for the same substance, the source with the lowest reliability score was dropped from the training set to reduce noise. The training set was loaded into R Studio³¹ Version 1.1.456 and randomly split using an 80:20 ratio such that 80% of the data could be used for training and 20% could be used for testing the model predictions. The decision tree models developed include a single tree, identified here as a Classification and Regression Tree (CART),³² and an ensemble method, which uses more than one tree, known as Random Forest (RF).³³

For the CART model, regression was performed using the R Language and Environment for Statistical Computing³⁴ “rpart” routine and the analysis of variance (ANOVA) method. Rpart creates a regression tree that partitions the predictor space into regions (called nodes, or leaves) where observations included in a node are averaged for that node. Additional splits of nodes lead to finer partitioning of the observations to form a decision tree. The five descriptors specified for the model are PV, molecular weight, vapor pressure, density, and water solubility. PV is a continuous variable and had a broadly reported range, with some chemicals reporting from one thousand to one billion pounds of production across various facilities. PV was hypothesized to be the most important descriptor when considering data for single chemicals from multiple facilities because only the PV differed within the descriptor set. For multiple chemicals, although the chemicals could have similar PVs, the remaining four descriptors were different. As a starting point, the minimum number of observations in a node before a further split was attempted (i.e., minsplit) was set to two while the complexity parameter was set to zero. Default settings in the R routine were applied for the remaining CART parameters. Further optimization and pruning of the raw tree were attempted by tuning the complexity parameter, minsplit, and number of splits.

The RF approach³⁴ is an extension of CART that attempts to yield improved prediction accuracy by using a randomly-generated forest of decision trees as the basis for analysis. Whereas a single tree might have a large mean square error (MSE) due to the variance of using certain training data, a forest of low-correlation trees can be averaged to lower the average error.³⁵ To reduce the correlation among trees, a random subset of descriptors is chosen for each branch split. The initial RF model was trained using the same training set described above for the CART model. The model was developed using default values for the RF parameters and 2,000 trees in the forest. Optimization included tuning the number of descriptors for a split (mtry), the minimum observations per node (Nodesize), and the number of trees.³⁶ A user can obtain an emission prediction for the RF model by implementing the code shown in the Supporting Information using PV and physicochemical properties.

For both approaches, the trained model was used to predict emissions for both the training set and the remaining 20% of the data set, hereafter referred to as the test set. The training set analysis provides information for optimization, while the test set analysis provides a measure of the predictive power of the model. A third out-of-sample data set was created for five additional chemicals using the data collection methods described above. An out-of-sample data set is a good example of how such a model could be applied to support chemical assessments. For the case study, cumene emissions were predicted using the CART and RF models by feeding the trained models the target PV (9.8E+07 kg per year) and the physicochemical properties of cumene. Given cumene was part of the training set, the models were expected to provide reasonable estimates. The R code and emission data used to create the CART and RF models are provided as Supporting Information. These resources can be used to recreate the models for further testing and use, as well as to recreate the case study results.

Criteria to Evaluate Estimation Methods

The set of criteria used to evaluate release estimation methods in this work is provided in Table 1, where the seven metrics for data quality defined in EPA’s Application of Systematic Review in TSCA Risk Evaluations have been lumped into a single data quality score based on the methodology outlined in the report.¹⁵ The criteria were developed by considering both potential use scenarios for the data and the actual application of various estimation methods. The intent is to capture aspects beyond data quality that can influence which approach is most suited to a specific data need. In addition to data quality, we consider the time and resources available for the work and the skill set (i.e., training) and knowledge required to apply a method. We note here that this set of criteria is not meant to be exhaustive or definitive because considerations beyond data quality can often be subjective. Instead, we define these additional criteria in a demonstrative capacity.

Table 1.

Example Criteria to Select an Approach to Estimate Chemical Releases

	LOW	MEDIUM	HIGH
Data Quality* Concern	DQ Score ≤ 1.7	1.7 < DQ Score < 2.3	DQ Score ≥ 2.3
Required Time	< 5 days	5–20 days	> 20 days
Required Resources	< $2,000	$2,000–$10,000	> $10,000
Required Training	novice scientific/engineering background required (bachelor’s degree with no experience)	moderate scientific/engineering background required (bachelor’s degree with 1–5 years experience)	advanced scientific/engineering background required (MS/PhD; bachelor’s degree with >5 years experience)
Required Knowledge	no activity-specific or data source knowledge required	either activity-specific or data source knowledge required	both activity-specific and data source knowledge required

^*The overall Data Quality score has a range of 1–3 and is a weighted summation of scores for Reliability, Representativeness, Accessibility/Clarity, and Variability and Uncertainty based on procedures outlined in EPA Report¹⁵ 740-P1-8001

The rating of ‘LOW”, “MEDIUM”, and “HIGH” have been transposed because here the concern for data quality is being captured.

The data quality methodology was adapted from EPA’s Application of Systematic Review in TSCA Risk Evaluations because this methodology represents a more stringent set of data quality requirements based on the application of the data in a regulatory capacity. The additional criteria were developed through a consensus process with the project team, which consisted of engineers and chemists. The time criterion considers the amount of time typically needed to apply a method. Team responses varied from one hour to multiple months. The indicated range corresponds to one work week (5 working days) and one month (20 working days). The minimal resources required for any method were approximated from the time of the person performing the work. The typical salaries for an engineer and chemist were averaged together and used to calculate the equivalent salary cost for each time interval. Additional resource needs, such as software packages or contractor support, can be added to the salary costs when necessary to obtain the total resources. Required training gauges the level of education and/or the amount of experience an individual should possess to successfully apply a method, although it is understood that exceptions can exist. The team considered the minimum requirement to be a bachelor’s degree in science or engineering to guarantee a person had adequate knowledge to model the release scenario. Increasing skill set requirements are indicative of more complex estimation techniques such as statistical classification and regression or advanced process simulation. The final criterion, knowledge, gauges how much detail would be required to apply a method and includes both details about the release scenario being modeled and the data sources needed to apply the approach. For example, top-down methods involving data mining often require intimate knowledge of database reporting requirements to make sure the data are used correctly. The proposed set of criteria will be applied and further explored as part of the case study.

Results

Regression Tree Models

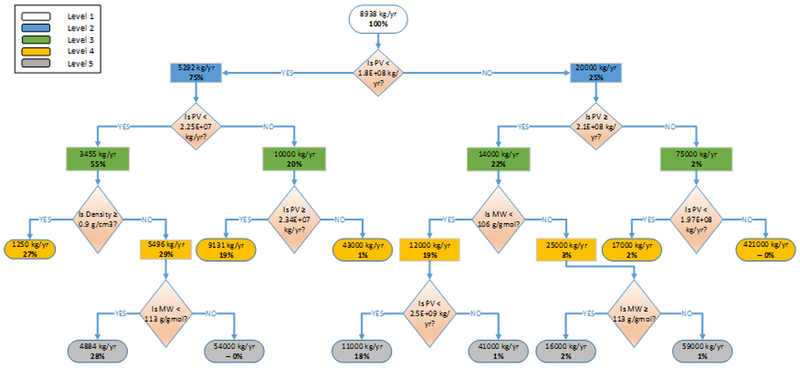
Typical tuning and pruning of a CART model is based on first identifying the complexity parameter (cp) that produces a cross-validation prediction error within one standard error of the minimum prediction error when considering the error at each split level within the tree.³⁷ The error results for the CART model developed here were indicative of a quite noisy data set and suggested that making any split was no better than making no split and using the average emission for the entire data set. Given the model was developed for demonstration purposes only, the decision was made to create a tuned tree using a cp value of 5.13E-03, a minsplit of 2, and 10 splits. These conditions produce a tree (Figure 2) that incorporates PV, molecular weight, and density and provides an example of how emissions can be predicted using a decision tree. Specifying the number of splits is a trade-off between using a large number of splits that overspecifies the classification set to obtain nodes for individual data points and using a small number of splits that minimizes the effects of descriptors and yields coarser estimates of the data. A user can implement specific PV and physicochemical properties through the decisions in Figure 2 to obtain predictions of emissions.

Figure 2.

Decision tree obtained from the CART analysis using a cp value of 5.13E-03, a minsplit of 2, and a maximum of 10 splits. The values in the nodes represent the emission prediction for that point in the tree, while the percentage indicates the fraction of the training set represented by that node.

The trained CART model was used to predict emissions for three data sets: train, test, and out-of-sample. Selected error parameters describing each set of predictions are summarized in Table 2. The mean absolute percentage error (MAPE) is typically calculated based on the absolute percentage error between the true value (reported emission) and predicted value and used as the basis to evaluate model accuracy.³⁸ However, this parameter can be misleading when some of the reported values are near zero, which is true of the emissions training set. The extremely small denominator in the MAPE calculation leads to large error values such as the 90,430% shown in Table 2. For this reason, the mean absolute error (MAE) and symmetric MAPE (SMAPE) are included. As one would expect, the MAE increases for the test and out-of-sample predictions. The issues with fitting the data are evident when considering the magnitude of the MAE, which is the same as or larger than many of the reported emissions. The SMAPE slightly decreased from training to out-of-sample predictions and suggests an actual well-trained model built with better curated data could indeed provide a simple and quick method for predicting emissions of data-poor and new chemicals. Improvements in the CART model will require the development of much better data sets for training.

Table 2.

Selected Error Parameters Describing the CART and RF Models

Data Set	Mean Absolute Error	Mean Absolute Percent Error	Symmetric Mean Absolute Percent Error
CART Train	4.6E+03	90430%	84%
CART Test	4.6E+03	653%	82%
CART Out of Sample	1.1E+04	250%	80%
RF Train	4.9E+03	128601%	67%
RF Test	4.2E+03	950%	72%
RF Out of Sample	1.2E+04	348%	92%

Varying the key tuning parameters for the RF model resulted in little, if any, change to the model error. The optimum tuned model was obtained using a minimum node size of 1 and 2 descriptors per split (mtry). Selected error parameters for the RF prediction results are presented in Table 2. Again, the MAPE value for the training set was much greater than 100% based on the presence of near-zero emissions in the training set. The MAEs for the various RF predictions were nearly identical to the CART model and again highlight the issues with the training data. For the RF model, the SMAPE increases from the training set to the out-of-sample predictions, which may suggest the RF model, as is, would be better suited for chemicals in the training set.

A benefit of the RF model is the ability to evaluate the relative importance of the descriptors to the predicted emissions values. This is accomplished by evaluating increases in the mean square error (MSE) of the model based on perturbations to the descriptors. Larger increases in MSE indicate more important descriptors. As shown in Table 3, the most important descriptor is molecular weight with a 15.1% increase in MSE, while vapor pressure, with only a 4.8% increase, is the least important. A possible explanation for the low importance of water solubility and vapor pressure could be the lack of definition of the operations and their sources/activities, which if similar could find a stronger dependence on these chemical properties. An interesting outcome of the two models created here would be to take the relative importance of descriptors identified from the RF model and create a tree using only the significant descriptors. The benefit of interpreting such single tree models in descriptor space is the outcomes could provide insights into reasons for the RF behavior.

Table 3.

Importance of Model Descriptors for the RF Model.

Descriptor	% Increase in MSE
Molecular Weight (g/mol)	15.12
PV (kg/yr)	8.20
Density (g/cm3)	6.08
Water Solubility (mol/L)	5.34
Vapor Pressure (mm Hg)	4.77

Although the CART and RF approaches have been applied to air quality modeling, their use in this paper to predict chemical emissions during manufacturing, with a direct correlation to physicochemical properties, appears to be the first of such an endeavor. Even though the results are less than ideal, they should be expected given the nature of the input data. The error analysis highlights the importance of reducing the potential noise in the data to improve the accuracy of the predictions. Here, data filtering was applied postprocessing using logical reasoning and manual inspection. The value of machine learning for predicting chemical emissions will significantly increase if automated data filtering methods can be developed to preprocess the data. The input data is split into 80–20 ratio and is used for training and testing. Any change in input data will create a different set of training and testing data and, therefore, different predictions. These variations can be minimized by making sure a large enough training set is used for the analysis to enable the same input data to give similar results. The predictive power of the models also depends on the coverage in the database. If the combination of descriptors for a chemical of interest are similar to data contained in the training set, the resulting prediction will be more accurate. Thus, a training set should be constructed such that the quality of the data in terms of representativeness and data sampling is sufficient to make the model applicable to a wide range of descriptors. This will maximize the value of the models for chemical assessment.

Case Study Emission Estimates

The estimated emissions for the case study are summarized in Table 4, with approaches listed in order of increasing emissions. The bottom-up and regression tree approaches yield emission estimates on the same order of magnitude (~1E+04 kg/yr) while the estimate from the top-down approach is an order of magnitude less. The variation in emissions is best explained by understanding the individual results.

Table 4.

Estimated Annual Cumene Emissions by Method for 9.8E+07 kg/yr Cumene Production

Approach	Cumene Emission Factor (kg/kg)	Total Cumene Emissions (kg)
Top-Down Data Mining	2.0E-05	2.0E+03
CART	9.3E-05	9.1E+03
Bottom-Up Simulation	1.3E-04	1.3E+04
RF	2.0E-04	1.9E+04

The bottom-up releases are a combination of controlled byproduct, fugitive, and storage emissions. The original byproduct streams, prior to application of pollution abatement technology, had 40.45 kg/h and 1.08 kg/h of cumene for the flash tank and DIPB streams (Figure 1), respectively. With the assumption of 99% removal in process heaters, 3,638 kg of cumene per year are released as controlled air emissions. The fugitive emissions based on the simulation and the PFD are 8,790 kg of cumene per year, while the emissions from storage are 297 kg per year. The three emission types presented here account for all possible emission sources typically reported in top-down data sources. However, the calculations apply to a single process configuration while top-down data sources may include many configurations.

The CART and RF approaches provide estimates by matching the desired production volume and chemical properties to data within the classification tree. The trees used for the case study were built using data for 45 chemicals, including cumene. For all chemicals, total facility emissions were used, which means emissions associated with on-site activities other than the manufacturing process may be included. When estimating releases, this may potentially lead to overestimation when considering a single on-site activity and would explain why the CART and RF results are larger than the top-down result obtained using the same data sources. Furthermore, the CART model developed here could not be successfully optimized based on the large variations in the training data. The arbitrary use of 10 splits may have overpruned the tree and produced much coarser estimates.

As opposed to the other approaches, the top-down estimate uses an average emission factor that is calculated based on weighted data from multiple facilities. The implications of this approach on the average emission factor are shown in Table 5 for cumene. The raw emission data spans an order-of-magnitude range, much like the predictions in Table 4. When normalized by production volume to obtain an emission factor, the facilities with data from NEI all have emission factors within the range of 4.8E-06 to 6.2E-05 kg of cumene emitted per kg of cumene produced, while the factors based on TRI data are much larger. Once allocation is applied to try to remove emissions not associated with the activity of interest at the facility, the emission factors using TRI data are much closer to the rest of the facilities. Once weighted by PV and summed, the average emission factor is an order of magnitude less than the other approaches, which is why the predicted emissions are smaller by an order of magnitude.

Table 5.

The Impact of Allocation and Weighting During the Top-Down Approach

Facility	Production Volume (kg)	Raw Release Data		Raw Emission Factor (kg/kg)	Allocated Emission Factor (kg/kg)	Weighted Emission Factor (kg/kg)
		Emission (kg)	Source
1	6.6E+08	2.1E+04	NEI	3.1E-05	3.1E-05	7.8E-06
2	6.3E+08	3.9E+04	NEI	6.2E-05	2.3E-05	5.6E-06
3	5.9E+08	2.8E+03	NEI	4.8E-06	1.1E-06	2.4E-07
4	3.9E+08	1.9E+04	NEI	5.0E-05	2.0E-05	3.0E-06
5	2.9E+08	7.2E+03	NEI	2.5E-05	2.5E-05	2.7E-06
6	5.3E+07	8.7E+03	TRI	1.7E-04	4.9E-05	9.9E-07
7	4.7E+05	5.4E+04	TRI	1.2E-01	1.3E-04	2.3E-08
Total US Emission Factor (kg/kg)						2.0E-05

All three approaches are not without their limitations. The top-down approach is only applicable to existing chemicals that are subject to reporting requirements for release data. Even when data exist, the quality of the data is dependent on how the data were generated by the reporting facility. While measured data is ideal, facilities can choose to use estimates or engineering judgments, which will lead to release estimates of lower quality. Regression tree analysis should only be applied when large curated data sets can be assembled. Like the top-down method, the quality of estimates from this approach will depend on the how the original data were generated. The use of secondary data in general can also be limited if the resolution of the data, e.g., facility-level, is coarser than the desired resolution of the assessment, e.g. activity-specific. The bottom-up approach will be most effective when sufficient details of the manufacturing process are known. The quality of the resulting estimates will depend on the ability to develop simulations that are representative of real-world operation. Given these limitations, understanding how and when to apply the three approaches will be best served by considering the decision context.

The results of evaluating each approach based on the decision-factor criteria are summarized in Table 6. It is important to note these results represent the application of the various approaches to the case study and should not be construed as the absolute scoring of the methods in general for the criteria. The top-down and CART approaches have low data quality concerns because they are based on recent release data reported to EPA by cumene manufacturers. For the bottom-up method, the data quality concern was scored as 1.8, just crossing into the medium rating, primarily because the process simulation obtained from ChemSep is older than ten years.

Table 6.

Evaluation of Approaches Using Decision Support Criteria

	Top Down	Bottom Up	CART	RF
Data Quality Concern	LOW	MEDIUM	LOW	LOW
Required Time	LOW	LOW	LOW	LOW
Required Resources	MEDIUM	LOW	MEDIUM	MEDIUM
Required Training	LOW	HIGH	HIGH	HIGH
Required Knowledge	HIGH	HIGH	LOW	LOW

For the case study, the required time for all methods was low, requiring fewer than five working days to obtain the estimates. For each approach, there were contributing factors that may or may not be unique to the case study. Without these factors, the approaches could easily reach a rating of high. For the bottom-up method, the base PFD and simulation results for cumene manufacturing were readily available and merely needed to be adapted to apply the emission calculations. Such simulations may not exist for many chemicals. For the top-down approach, only eight facilities manufactured cumene and publicly reported the production volume. Pulling the associated emissions from NEI and TRI was manageable for this small number, especially given one facility did not report cumene emission data and was omitted. Other chemicals may have a much larger number of facilities and require more time to process. Because of the large time commitment for each chemical studied by all of the methods, only the one case study for cumene was detailed for this effort. The CART and RF models used total facility emissions and did not require filtering the data based on metadata. This allowed the data to be pulled using automated routines. If more activity-specific estimates are desired, more time would be needed to process the metadata and build an activity-specific classification tree.

The resource requirements were rated as medium for all approaches except the bottom-up, which was rated as low. For the top down approach, enough resources were needed to cover the time of two people working to generate the estimate within the low time requirement. For the CART and RF approaches, the resource requirements included both the time for the person performing the analysis and the cost of the software required to perform the analysis. The bottom-up approach was carried out by a single person using freely available simulation software, which is why the resource requirement rating matched the time requirement rating – both low. As with time requirements, resource requirements will vary based on factors such as the analysis time and the ability to use freely available computational tools.

Evaluation of the training requirements was fairly straightforward. The top-down method primarily requires an understanding of how to search the Internet and navigate databases, as well as a rudimentary understanding of chemical processes. These skills are more indicative of a novice engineer or scientist, which is consistent with a low rating for the proposed criterion. The other approaches were evaluated as high because of the more sophisticated skills and experience required to apply them. For example, the bottom-up approach is best suited for someone with ample experience in process design and simulation while the use of decision trees requires training in advanced statistical analysis and programming. Even if a lesser trained person performed the actual methods, the work would need to be supervised by someone with a high level of training and/or experience. A medium or high rating for the top-down method could become necessary if the approach is automated.

For the final criterion, the knowledge requirements for the top-down and bottom-up approaches were evaluated as high while the CART and RF approaches were given a low rating. The rating for the top-down approach is based on the details required to perform the allocation of emissions while the bottom-up rating stems from the intricate process knowledge required to simulate the manufacturing process. On the other hand, the CART and RF approaches were developed to be applied with little knowledge. Assuming a decision tree is available, one needs the desired production volume and a few key properties of the chemical to obtain an estimate. The low rating could easily become medium or high if the decision tree had to be developed first.

Discussion

The final objective of this work is to identify a logical framework for reconciling the use of the various approaches that can be used to estimate chemical releases, including approaches not included in this work such as chemical read across based on the structural similarity of chemicals³⁹ and the use of proxies. As previously discussed, modelers will most often value data quality more than anything else. However, it makes no sense spending months to obtain a high-quality release estimate based on process simulation if the intended assessment is screening in nature. Similarly, why attempt the top-down approach with metadata filtering if you do not have the necessary process knowledge or the resources to obtain it? These are just a few examples of why it is important to consider the decision constraints and not just the data when deciding how to estimate releases. And what if more than one release estimate is needed? Should you apply the same method to generate all estimates or is it appropriate to use multiple tools from the toolbox? A purpose-driven reconciliation framework can address all of these challenges and promote more efficient release modeling for chemical assessments.

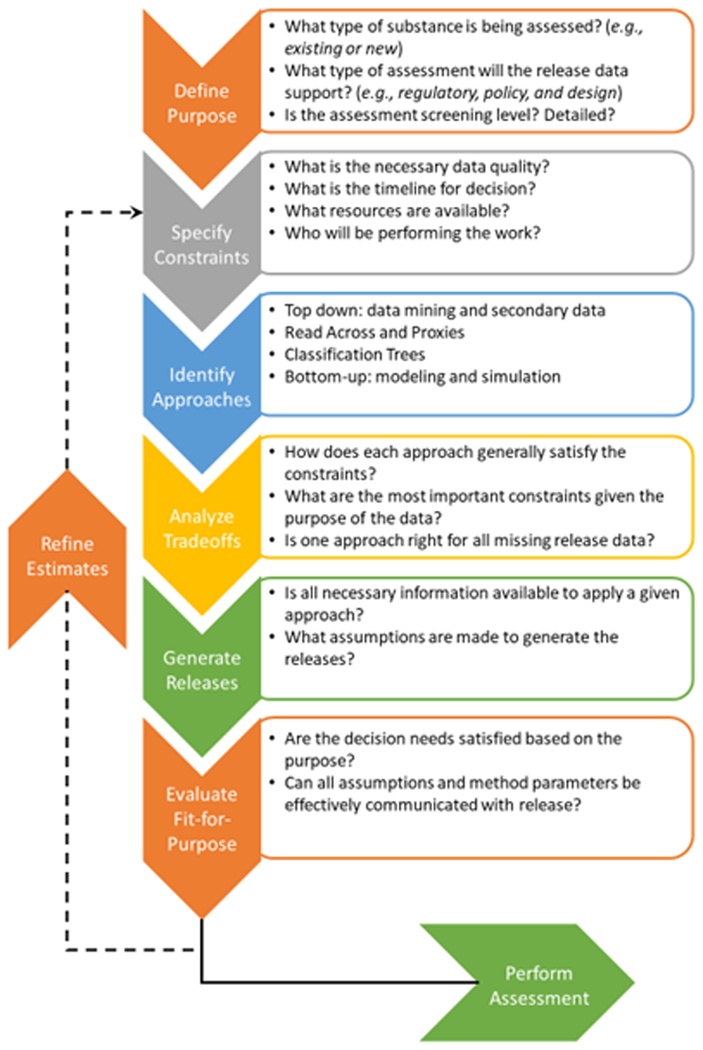
The lessons learned throughout the case study were used to synthesize an approach to purpose-driven reconciliation, with the emphasis on being able to make decisions regarding the approach before performing the calculations. The resulting framework, shown in Figure 3, involves six steps and is designed to be iterative in nature to ensure the resulting release estimate is adequate for the subsequent assessment. The process begins by defining the purpose of the required estimates(s). It is important for this step to consider all information that may impact the effectiveness of a given approach. For example, existing chemicals may be included in top-down databases and have a wealth of reported release data, which makes them well suited for the top-down approach. Conversely, new chemicals will not yet be covered in such data sources and would not be able to be modeled using the top-down approach. Thus, by adequately defining the data need, the subsequent steps to select the desired approach will be easier.

Figure 3.

Purpose-driven reconciliation framework for estimating source releases as a part of exposure or risk assessments.

The second and third steps of the framework establish the constraints that will help determine which approach is best suited for the data need and the list of possible approaches. For the case study, we developed an example set of criteria that balanced data quality needs with other factors such as the analysis time and the required knowledge. The primary objective when defining criteria should be to maximize the quality of the release estimate while minimizing the time and resources required because this will best support chemical assessment activities where there may be a number of data gaps to fill. Although listing approaches may seem obvious, the purpose of the third step is to ensure individuals are considering all options.

The next step in the framework evaluates the constraints and analyzes the trade-offs to select the best approach for the given decision need. The purpose of the case study was to compare multiple approaches, and so the evaluation of criteria was performed independently for each method while it was being applied. The purpose of the framework is to help decision makers make informed choices about how to fill data gaps and so the evaluation is performed before the actual calculations. The expectation here is not that the evaluation will be perfect. Instead, the decision maker should provide a best estimate of each criterion based on a basic understanding of the various approaches, much like when a project manager develops a project plan using limited input. Ultimately, as was demonstrated in the case study, there are trade-offs when comparing the various approaches and the onus is on the decision maker to understand the decision need and appropriately weight the importance of each criterion. Can data quality be sacrificed to make a decision deadline or can the decision timeline be extended to accommodate data quality needs? Questions like this will clearly highlight what are the most important trade-offs and enable the decision maker to select the most appropriate approach.

The final steps of the framework focus on applying the approach to obtain a release estimate and determining if the estimate satisfies the decision need. When preparing to generate the estimate, there are a few items to consider. First, is all the required information available if this was anticipated during the evaluation? If not, is the missing information readily obtained from credible sources? There will often be a need for specific information when applying a given approach. If this information is more difficult to obtain than originally thought, cannot be obtained from credible sources, or is not available, it may be necessary to revisit the approach decision and look at the next “best approach” based on the trade-offs. Assuming all information is available, are there underlying assumptions involved in the application of the approach and are these assumptions clear and justified? There will typically be the need for assumptions when estimating releases and the decision maker must be aware of these to ensure the resulting release estimates are used appropriately.

Knowledge of data sources and assumptions are key because they will impact the fit-for-purpose determination of the release estimate in the final step of the framework. The concept of fit-for-purpose was introduced by EPA to describe risk assessments and supporting products that are “suitable and useful” for the intended decision.¹ The objective is to optimize the time and resources needed to complete an assessment. Chemical release estimates can be treated as supporting products of assessments and, therefore, should adhere to this approach. At this step of the framework, the decision maker must first consider the quality of the estimate based on data quality metrics, paying particular attention to any assumptions used to generate it. This includes examining what, if anything, is known about the uncertainty of the estimate and how best to communicate it to stakeholders when justifying any decisions involving the estimate. If the resulting data quality or assumptions do not support the intended use of the data identified in the first step of the framework, the decision maker must continually revise the estimate until an acceptable chemical release estimate is obtained. This iterative concept is shown in Figure 3 as a loop to restep through the framework from the second step onward, which represents the highest level of revision. It is possible the revision process could be as simple as improving the input data or assumptions for the selected estimate approach to reduce the uncertainty of the estimate. Once an estimate has been deemed fit-for-purpose, it can be applied in subsequent assessments.

The intent of this work and the resulting framework is to address the growing toolbox of how chemical releases can be estimated. In a world that often fixates on perfection, it can be easy to lose sight of the purpose at hand when estimating chemical releases and become sidetracked trying to obtain the “perfect” estimate. The consequence of this is an assessment can take longer, delaying decisions that are important to protecting human health and the environment. Newer estimation approaches such as the decision trees demonstrated here should not be discounted in favor of more established methods like simulation or data mining merely because simulated results may be more accurate. Instead, decision makers should reconcile their use of the various estimation approaches based on the intended purpose.