Predicting location of recurrence using FDG, FLT, and Cu-ATSM PET in canine sinonasal tumors treated with radiotherapy

Abstract

Dose painting relies on the ability of functional imaging to identify resistant tumor subvolumes to be targeted for additional boosting. This work assessed the ability of FDG, FLT, and Cu-ATSM PET imaging to predict the locations of residual FDG PET in canine tumors following radiotherapy. Nineteen canines with spontaneous sinonasal tumors underwent PET/CT imaging with radiotracers FDG, FLT, and Cu-ATSM prior to hypofractionated radiotherapy. Therapy consisted of 10 fractions of 4.2 Gy to the sinonasal cavity with or without an integrated boost of 0.8 Gy to the GTV. Patients had an additional FLT PET/CT scan after fraction 2, a Cu-ATSM PET/CT scan after fraction 3, and follow-up FDG PET/CT scans after radiotherapy. Following image registration, simple and multiple linear and logistic voxel regressions were performed to assess how well pre- and mid-treatment PET imaging predicted post-treatment FDG uptake. R² and pseudo R² were used to assess the goodness of fits. For simple linear regression models, regression coefficients for all pre- and mid-treatment PET images were significantly positive across the population (P < 0.05). However, there was large variability among patients in goodness of fits: R² ranged from 0.00 to 0.85, with a median of 0.12. Results for logistic regression models were similar. Multiple linear regression models resulted in better fits (median R² = 0.31), but there was still large variability between patients in R². The R² from regression models for different predictor variables were highly correlated across patients (R ≈ 0.8), indicating tumors that were poorly predicted with one tracer were also poorly predicted by other tracers. In conclusion, the high inter-patient variability in goodness of fits indicates that PET was able to predict locations of residual tumor in some patients, but not others. This suggests not all patients would be good candidates for dose painting based on a single biological target.

Introduction

The practice of administering biologically conformal radiation therapy, or dose painting, is based on the principle that highly resistant tumor subvolumes can be identified using biological imaging, and thereby targeted for additional boosting. The success of dose painting is contingent on the ability of biological imaging to reliably and consistently identify resistant tumor subvolumes before (or during) radiation therapy. While several dose painting clinical trials have been conducted, and several more are currently underway, the largest uncertainty in dose painting has yet to be resolved—how to identify tumor subregions that are resistant to radiation.

Unlike conventional imaging biomarkers of resistance in which summary statistics from tumor imaging (e.g. maximum standardized uptake value) are correlated with clinical outcome, imaging targets for dose painting should be spatially correlated with spatial patterns of resistance. As tumor radioresistance cannot be directly measured, location of tumor recurrence is often used as a surrogate measure of tumor resistance (Aerts et al 2012, Vogelius et al 2013, Shusharina et al 2014). Pre- and post-treatment images are coregistered, and the locations of tumor recurrence on the post-treatment image are mapped back to the pre-treatment image. Patterns of recurrence are then compared to pre-treatment imaging patterns. For example, using positron emission tomography (PET) imaging in non-small cell lung cancer tumors, Aerts et al found high spatial overlap between post-treatment 2-deoxy-2-[¹⁸F]fluoro-D-glucose (FDG) uptake and pre-treatment FDG uptake (Aerts et al 2009, Aerts et al 2012). In head-and-neck tumors, Soto et al found that 8 out of 9 patients’ recurrence volumes resided primarily within regions of high pre-treatment FDG uptake (Soto et al 2008). Results such as these have encouraged the use of FDG as a target for dose painting, as clinical trials of FDG dose painting have been conducted in head-and-neck and lung tumors (Madani et al 2007, Duprez et al 2011, van Elmpt et al 2012). On the other hand, FDG uptake has also been shown to be influenced by other biological properties not directly related to resistance, such as inflammation and perfusion (Bos et al 2002), which may confound its utility as a reliable dose painting target.

Besides FDG PET, other potential biological targets for dose painting exist. Hypoxia is a known cause of radioresistance (Nordsmark and Overgaard 2000), making PET imaging of hypoxia a promising method for guiding dose distributions (Chao et al 2001). Uptake levels of copper(II)-diacetyl-bis(N4-methylthiosemicarbazone) (Cu-ATSM), a PET radiotracer for hypoxia, have been shown to be prognostic in patients undergoing radiation therapy with cervical (Dehdashti et al 2003a, Dehdashti et al 2008), head-and-neck (Minagawa et al 2011, Sato et al 2014), lung (Dehdashti et al 2003b), and rectal (Dietz et al 2008) cancer. Tumor proliferation maps may also prove useful in guiding dose distributions, especially those acquired during treatment, as accelerated repopulation of irradiated cancer cells has been shown to have deleterious effects on patient outcome (Kim and Tannock 2005, Kishino et al 2012).

In addition to PET imaging at a single time point, imaging before and during the course of treatment can provide spatially-resolved biological response information. Patterns of early biological response may correlate with patterns of overall resistance, allowing one to adapt dose distributions according to early changes in PET uptake (Brahme 2003). A comparison of tumor recurrence patterns to patterns of biological response during treatment has yet to be reported in literature.

The goal of this work was to assess how accurately pre-treatment FDG, FLT, and Cu-ATSM PET imaging, as well as mid-treatment FLT and Cu-ATSM PET imaging, predicts the location of residual or recurrent tumor in canine sinonasal tumors. This work builds off of a previous exploratory study, in which we performed voxel regressions of pre-treatment FDG, FLT, and Cu-ATSM uptake values against 3 month post-treatment FDG uptake values in 9 canine patients (Bowen et al 2012). In that study, pre-treatment FDG PET was found to perform better than FLT and Cu-ATSM PET at predicting post-treatment FDG PET distributions. The work reported herein builds on these results by increasing the number of patients from 9 to 19, adding mid-treatment FLT and Cu-ATSM PET images as additional predictor variables, and expanding the statistical methods of analysis.

Methods

Patients

The trial included 22 canine veterinary patients referred to the University of Wisconsin Veterinary Medical Teaching Hospital, 19 of whom were evaluable for this study. Three patients were excluded from analysis: two because no recurrent tumor was visible in follow-up PET/CT images, and one because the tumor did not shrink following treatment. The research protocol was approved by the Animal Care and Use Committee of the University of Wisconsin, and all canine owners signed a written informed consent. Patients were diagnosed using CT and biopsied for histopathological evaluation. All dogs had treatment-naive nasal or paranasal sinus tumors with no evidence of distant metastases or intracranial extension. Histopathology results were 10 adenocarcinoma, 7 chondrosarcoma, 1 squamous cell carcinoma, and 1 osteosarcoma.

Imaging and treatment

Patients received intensity-modulated radiation therapy (IMRT) delivered by helical tomotherapy with curative intent. Patients were divided into two treatment groups as part of a larger study investigating dose escalation. The first group received the veterinary standard-of-care prescription at our institution: 10 fractions of 4.2 Gy to the planning target volume (PTV) for a total of 42 Gy. The second group was prescribed 10 fractions of 4.2 Gy to the PTV with an integrated boost of 0.8 Gy per fraction to the gross tumor volume (GTV), for a total of 50 Gy to the GTV.

The imaging and treatment schedules were as follows: Patients had pretreatment FDG, FLT, and [⁶¹Cu]Cu-ATSM PET/CT scans on consecutive days beginning 3 d before the onset of IMRT. Patients received a second FLT PET/CT scan after two fractions of IMRT (8.4 or 10 Gy) and a weekend break. Patients received a second Cu-ATSM PET/CT scan following the third fraction of IMRT (12.6 or 15 Gy). One patient missed the midtreatment FLT scan due to equipment failure (resulting in 18 patients with complete data sets). Patients were injected with 150–370 MBq of tracer. After injection, patients were kept in a kennel to limit physical activity. PET/CT scans were acquired on a Discovery VCT (GE Healthcare, Waukesha, WI) scanner. FDG and Cu-ATSM PET scans were acquired 60 min and 180 min post-injection, respectively; both were 20 min 3D static acquisitions over a single 15 cm bed position. FLT PET scans were 90 min 3D dynamic acquisitions over a single 15 cm bed position. Patients were anesthetized during imaging and treatment with an initial propofol bolus injection, and then maintained on isoflurane inhalation plus 100% oxygen. Emission data were attenuation, decay, and deadtime corrected and reconstructed using 3D ordered subset expectation maximization (2 iterations, 35 subsets, and 3 mm postfiltering). The image grid was 256 × 256 × 47 with 2.0 × 2.0 × 3.3 mm³ voxel sizes. Voxel activity measurements were converted to standardized uptake values (SUVs) for analysis. For FLT PET scans, SUVs were calculated by averaging frames between 60–90 min. To achieve reproducible positioning across PET/CT scans and IMRT treatment sessions, patients’ maxillae were positioned into custom dental molds that were affixed to the scanner and treatment couches, and patients’ bodies were immobilized with vacuum mattresses (Kubicek et al 2012).

Following therapy, patients were scheduled for follow-up FDG PET/CT scans at 3 and 6 months, with an additional CT scan at 9 months. Patients without progressive disease within the first 9 months (evaluated according to RECIST criteria) received an additional PET/CT scan whenever they presented with clinical signs suspicious of recurrence (e.g. epistaxis).

Patient CT scans were rigidly registered, and transformations were subsequently applied to their respective PET images. The GTV was segmented by a veterinarian based on the planning CT, and subsequently propagated to the PET images. The ethmoturbinates of the nasal cavity were manually segmented and excluded from analysis due to non-specific uptake of FDG and Cu-ATSM.

Regression analysis

Similar to Bowen et al (Bowen et al 2012), we used voxel regression methods to assess how well PET uptake patterns predicted the location of tumor recurrence. For each tumor, the predictor variables were pre-treatment FDG (FDG_pre), FLT (FLT_pre), Cu-ATSM (Cu-ATSM_pre) and mid-treatment FLT (FLT_mid) and Cu-ATSM (Cu-ATSM_mid) PET voxel SUVs, and the response variable was follow-up FDG PET voxel values (FDG_post), which was used as a surrogate for residual/recurrent tumor (for this paper, the terms recurrent tumor and residual tumor will be used interchangeably). Ratio maps of mid-treatment voxel values to pre-treatment voxel values for FLT (R_FLT) and Cu-ATSM (R_Cu-ATSM) PET images were also used as predictor variables. Two types of regression were considered. In linear regression models, voxel SUVs from patients’ post-treatment FDG PET images were used as response variables. In logistic regression models, recurrent tumor was segmented in the post-treatment FDG PET image, and the response variables were converted to binary variables—1 if the voxel was within the segmented volume, and 0 otherwise. The segmentation of post-treatment PET images was performed using an in-house automatic segmentation algorithm that combines gradient, region-growing, and textural feature methods (Galavis 2013). Both simple regression and multiple regression models were created for each patient. For multiple regression models, all 5 PET images were included as predictor variables (ratio variables were not included, as the regression model already accounts for absolute differences between pre- and mid-treatment voxel values). As patients had multiple follow-up FDG PET scans, the time point at which the tumor was the smallest was used for the response variable. In most cases (N = 13), response was measured at 3 months.

To evaluate how well pre- and mid-treatment PET distributions predicted recurrent tumor, goodness of fits of the regression models were calculated. For linear regression models, the coefficient of determination (R²) was calculated. For logistic regression models, pseudo R² was used. Pseudo R² was calculated according to the correlation between the model’s predicted response and measured response values:

$$\text{Pseudo}{R}^2=1-\frac{{\sum }_{i=1}^N{\left(y_i-{\widehat{\pi }}_i\right)}^2}{{\sum }_{i=1}^N{\left(y_i-\overline{y}\right)}^2},$$ (1)

where y_i is the ith response value, ${\widehat{\pi }}_i$ is the model-predicted probability, and $\overline{y}$ is the mean response value. It should also be noted that pseudo R² for logistic regression and R² from linear regression are not directly comparable, but do have similar interpretations. Significance testing of the regression coefficients was not performed due to the very high spatial correlations between neighboring voxels, which resulted in exaggerated significance values. However, similar to Bowen et al, two-tailed t-tests were used to assess if the population of regression coefficients from all patients were significantly different from zero.

Using correlation analysis, we investigated if any clinical measures or imaging biomarkers could predict which patients would have high or low R² (i.e. which patients would be good or poor candidates for dose painting). Clinical measures that were tested as predictors of R² values included histologic tumor type and dose level. Imaging biomarkers that were tested included tumor volume, maximum and mean SUV from pre- and mid-treatment PET images, relative changes in maximum and mean SUV from pre- to mid-treatment, and relative change in 1D tumor size (i.e. RECIST measurements) from pre- to post-treatment.

Predictive modeling

Given the limitations of linear regression (e.g. assumption of linearity), we also created more advanced prediction models to evaluate how accurately the location of recurrence for a ‘new’ patient could be predicted given the imaging data of all the other patients. For each patient, 4 prediction models were created/trained based on the other 17 patients’ combined data, and then applied to the test patient (i.e. leave-one-out cross validation). One patient was excluded due to a missing FLT_mid data. The 4 models included a multiple linear regression (LR) model (as a basis for comparison), a classification and regression tree (CART) model (Breiman et al 1984, Loh 2011), a linear mixed-effects regression (LMER) model, and a multiple linear regression model that included neighborhood structures surrounding each voxel as additional covariates to account for autocorrelation between neighboring voxels.

For all predictive models, FDG_pre, FLT_pre, Cu-ATSM_pre, FLT_mid, and Cu-ATSM_mid were used as continuous predictor variables. Patient-level variables of tumor histologic type, tumor volume, and dose level were also used as predictor variables. FDG_post was used as the response variable. The multiple linear regression (LR) model was defined according to

$${\text{FDG}}_i^{\text{post}}={\beta }_0+{\beta }_1{\text{PET}}_{1i}+{\beta }_2{\text{PET}}_{2i}+\dots +{\beta }_5{\text{PET}}_{5i}+{\epsilon }_i,$$ (2)

where ${\text{FDG}}_i^{\text{post}}$ is the post-treatment FDG SUV at voxel i, PET_mi is the SUV at voxel i for the mth PET image, β_k are the 6 regression coefficients, including an intercept, and ε_i is the error term. In leave-one-out cross-validation fashion, β_k values were determined by pooling together 17 of the patients’ imaging and response data and running regression on the pooled data. Prediction accuracy was then evaluated according to R² by fitting the testing data set (i.e. the one patient excluded from the training data set) with the coefficients calculated from the training data set. Each patient was likewise evaluated for prediction accuracy.

For the classification and regression tree (CART) model, the same 5 PET images were used as predictor variables as were used in the LR regression model. Patient-level variables of histologic tumor type, tumor volume, and dose level were also included as patient-level factors. Like the LR model, the model was trained on the pooled image data and tested for each patient in a leave-one-out cross-validation manner.

The linear mixed effects (LME) regression model was similar to the LR model, but with the intercept of different patients defined as a random effect. This assumes the baseline FDG_post values for different patients are normally distributed, with the mean of the distribution used as intercept for the pooled data. All other predictors were used as fixed effects. This model and the CART model were implemented in R using the packages lme4 and rpart, respectively (R Development Core Team 2014).

The autocorrelation model was defined similar to the LR model, but with added neighborhood structures as additional predictor variables for each PET image:

$${\text{FDG}}_i^{\text{post}}={\beta }_0+{\beta }_1{\text{PET}}_{1i}+{\beta }_2\sum _{jϵ{\mathcal{N}}_i}{\text{PET}}_{1j}+\dots +{\beta }_9{\text{PET}}_{5i}+{\beta }_{10}\sum _{jϵ{\mathcal{N}}_i}{\text{PET}}_{5j}+{\epsilon }_i,$$ (3)

where β_k now include 11 regression coefficients (2 for each PET image), N_i is the neighborhood surrounding voxel i, and PET_mj is the SUV of the jth voxel in N_i for PET image m. For this study, we used the first-order neighborhood surrounding voxel i to define N_i, meaning only those voxels sharing a side with voxel i (Fu et al 2013).

When pooling the 17 patients’ data for training the models, only 249 voxels were randomly sampled and used from each patient so that each tumor in the training set was equally represented in the pooled model, regardless of tumor size (249 voxels was the size of the smallest tumor). Fitted R² values were calculated based on the model fit of the 17 patients × 249 voxels = 4 233 voxels. For testing prediction accuracy, prediction R² was calculated by applying the fitted model to all the voxels of the tested patient. The procedure was repeated 100 times for each patient, and the average of the resulting R² values are reported.

In addition to the continuous prediction models, the 4 prediction models were also created for each patient using dichotomized FDG_post as the response variable, and using logistic regression instead of linear regression. Results for logistic regression models are reported in terms of pseudo R² and sensitivity.

Results

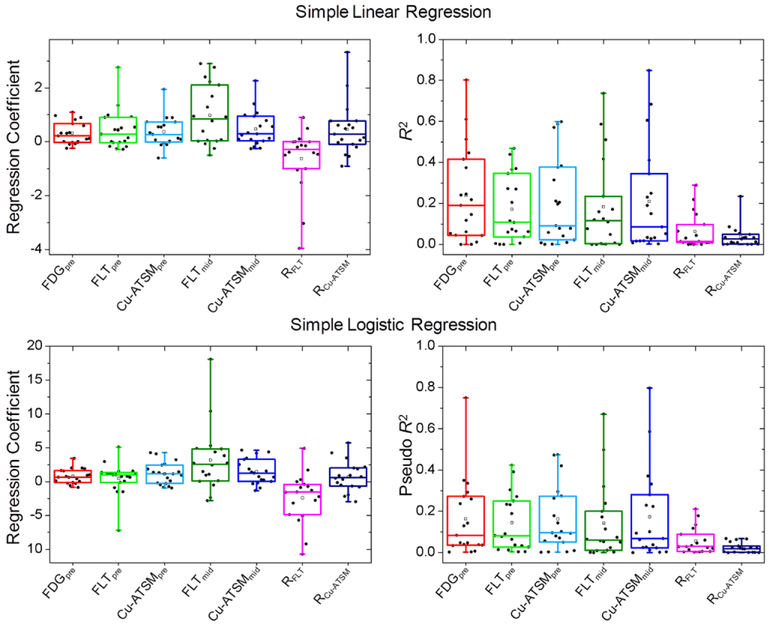
An example patient’s PET/CT images and simple linear regression plots are shown in figure 1. The fitted regression coefficients from simple linear and logistic regressions for all patients are shown in figure 2. Overall, linear regression coefficients were significantly different from zero across the population for all pre- and mid-treatment tracers (P < 0.05), with FDG_pre, FLT_mid, and Cu-ATSM_mid being the most significant (P < 0.005). R_FLT coefficients were significantly less than zero (P = 0.038), whereas R_Cu-ATSM coefficients were not significantly different from zero (P = 0.055). Likewise, for logistic regression, regression coefficients for all pre- and mid-treatment tracers were significantly different from zero (P < 0.05), except for FLT_pre (P = 0.38). Again, R_FLT coefficients were significantly less than zero (P = 0.028), whereas R_Cu-ATSM coefficients were not (P = 0.33).

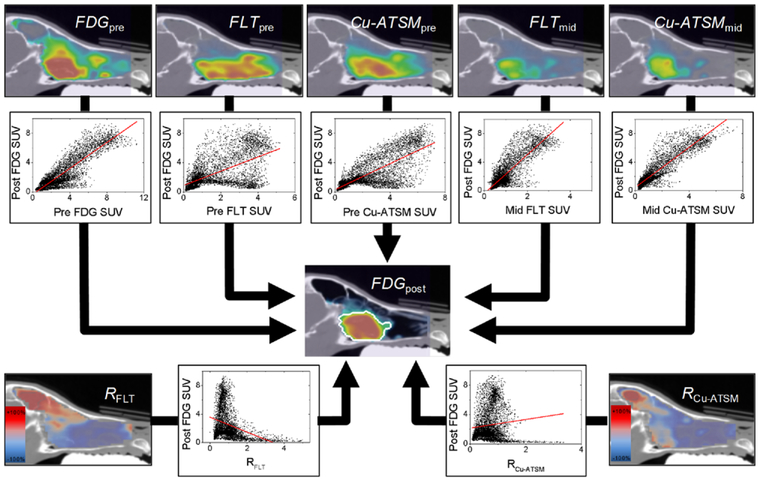
Figure 1.

An example patient is shown, illustrating the simple linear voxel regression method. Pre- and mid-treatment PET voxel values (top row) were regressed against follow-up FDG voxel values. Response maps (R_FLT and R_Cu-ATSM; bottom row) were also regressed against follow-up FDG. For logistic regression, post-treatment voxel values were dichotomized using an in-house segmentation method (outlined in white).

Figure 2.

Results from simple linear (top row) and logistic (bottom row) voxel regressions for all patients. Regression coefficients (left) and goodness of fits (right) are shown.

Figure 2 also shows R² and pseudo R² for all patients’ linear and logistic simple regression models. There was large variability between patients in goodness of fits, with R² and pseudo R² values ranging from 0.00 to 0.85, with an overall median of 0.12. For linear regression, the median R² for FDG_pre was 0.19, while the median R² values for FLT_pre, Cu-ATSM_pre, FLT_mid, and Cu-ATSM_mid were all around 0.10. Median R² for R_FLT and R_Cu-ATSM were less than 0.05. For logistic regression, median pseudo R² values for FDG_pre, FLT_pre, Cu-ATSM_pre, FLT_mid, and Cu-ATSM_mid varied between 0.06 to 0.10, and R_FLT and R_Cu-ATSM had median pseudo R² less than 0.03.

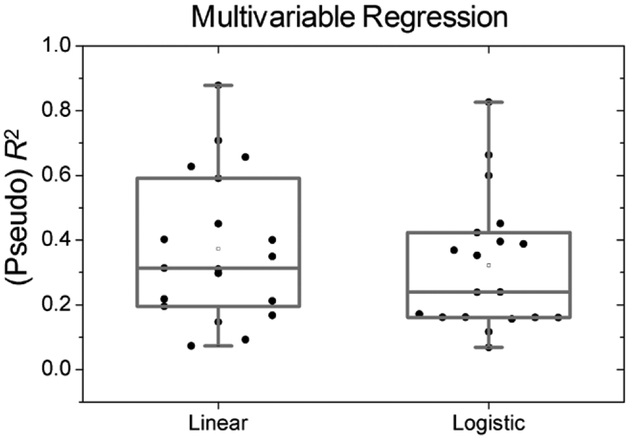
Figure 3 shows all patients’ R² and pseudo R² from both linear and logistic multiple regression models, respectively. Multiple regression models had better goodness of fits than simple regression models: the median R² for the linear model was 0.31, and median pseudo R² for the logistic model was 0.24.

Figure 3.

R² and a pseudo R² for each patient’s linear and logistic multiple regression models, respectively.

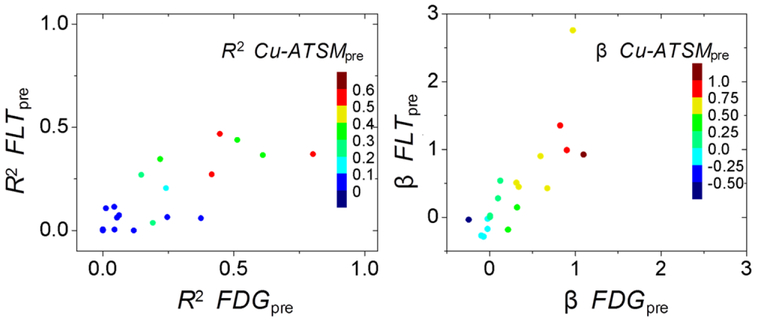
No clinical measures (e.g. dose level and tumor histology) or imaging biomarkers were correlated with patients’ respective R² (R < 0.3). We found that the R² of different regression models (for different predictor variables) were correlated across patients (R > 0.75). In other words, patients with low R² for a single predictor variable had similarly low R² for all predictor variables, even for multiple regression models. This is illustrated for all three pre-treatment simple linear regression models in figure 4. Likewise, if a patient had low regression coefficient for a single predictor variables, the other predictor variables were likely to also have low regression coefficients (see figure 4).

Figure 4.

Scatter plots illustrating that different predictor variables’ R² were correlated across patients (left). Likewise, regression coefficients for different predictor variables were correlated across patients (right). Only results from pre-treatment simple linear models are shown here.

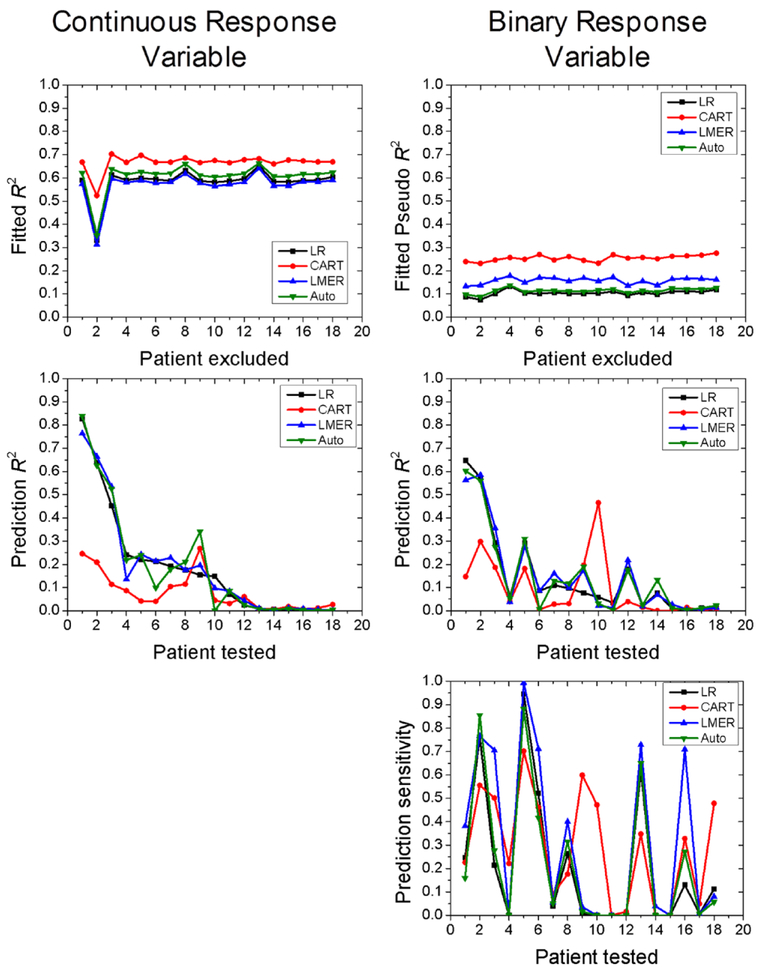
Figure 5 shows results from each patient’s predictive modeling. For each patient, the fitted R² and fitted pseudo R² are shown—these indicate how well the models described the other 17 patients’ data. The prediction R² and prediction pseudo R² indicate how well the prediction models performed when applied to the test patient. In general, CART outperformed the other models in fitting the patients’ data, but often had the worst performance in predicting a ‘new’ test patient. Overall, advanced prediction models did not improve the prediction accuracy when compared to multiple linear regression models.

Figure 5.

Prediction modeling results for each patient, for both continuous response variables (left column) and binary response variables (right column). For each patient, fitted R² are shown, indicating how well the four models fit the training data set, which consisted of all patients but one. Prediction R² are also shown, indicating how well the trained models predicted the response values for the test patient. For binary response models, the prediction sensitivity is also shown. Patients are sorted according to the prediction R² for the linear regression model, from high to low. LR = multiple linear regression, CART = classification and regression tree, LMER = linear mixed effects regression, Auto = regression with neighborhood structures.

Discussion

In this study, we used canine sinonasal tumors undergoing radiation therapy as models for evaluating which radiotracer uptake distribution—FDG, FLT, or Cu-ATSM—best correlated with location of tumor recurrence as a surrogate for measuring spatially-resolved resistance to radiation therapy. A characteristic of canine sinonasal tumors that made them especially well-suited for this study was the fact that tumors were enclosed by the bony sinonasal cavity, making image registration very accurate, thus enabling voxel-wise comparisons of PET images across different scans and time points. In our previously published exploratory voxel regression study evaluating 9 of the patient used in this study, pre-treatment FDG uptake distributions were found to be the best predictors of post-treatment FDG uptake distributions (Bowen et al 2012). In this study, we made several additions to the methods of analysis, including the addition of mid-treatment FLT and Cu-ATSM PET images as predictor variables, implementing logistic regression with segmented follow-up FDG PET images as binary response variables (removing potential autocorrelation between pre- and post-treatment FDG voxel values), and creating advanced prediction models accounting for non-linearity, patient-level variables, and autocorrelation among neighboring voxels. We also increased the statistical power of the study by increasing the number of evaluable canine patients from 9 to 19.

Overall, we found large variability among patients in how well pre- and mid-treatment PET imaging predicted the locations of tumor recurrence. For simple linear regression models, none of the predictor variables were significantly better than the other variables. FDG_pre, however, had the highest median and mean R² values of the tested predictor variables, suggesting it might be the most suitable target for dose painting. This is in agreement with the results reported by Bowen et al (Bowen et al 2012). On the other hand, when FDG_post was dichotomized and logistic regression was performed, the R² values for FDG_pre were nearly identical to those of the other predictor variable. Unsurprisingly, we found that multiple regression models resulted in better goodness of fits (R² and pseudo R²) than simple regression models. However, there was a cluster of 5 patients whose R² were at or below 0.20, regardless of regression method. We hypothesized that perhaps smaller tumors or tumors with more pronounced anatomical response were those that had lower R² values. This, however, was not the case, as patients’ R² values were not correlated with any imaging biomarkers or clinical measures that we tested, including dose level, tumor volume, and histologic tumor type. Biomarkers or patient characteristics that could predict which patients would ‘behave well’ under dose painting would be valuable for selecting patients most likely to benefit from dose painting.

The interpretation and implications of a low or high R² for such regression models, or the thresholds at which an R² could be considered adequate for dose painting, are not straightforward. In redistribution-based dose painting, total dose to the target volume is not increased but rather redistributed such that more sensitive regions receive less dose and more resistance regions receive more dose. Under such a scenario, an imprecise dose painting target (i.e. low R²) that is unable to differentiate sensitive and resistant regions could actually result in worse outcomes than standard uniform dose treatments. Bender addressed these issues using a tumor control probability model, and reported that when the voxel-based correlation coefficient between a particular imaging method and the theoretical probability of recurrence risk was greater than 0.45 (corresponding to an R² of 0.20), voxel-based dose painting would result in greater tumor control than uniform dose prescriptions (Bender 2012). Clearly, the measure of post-treatment FDG SUV used in our study was not a direct measure of recurrence risk, but if we were to use an R² threshold of 0.20 for the simple linear regression models, we would find that roughly half of the 19 patients would benefit from dose painting. For the other half of the population, however, dose painting might actually be worse than uniform dose prescriptions. These results, of course, depend on the tracer used (see figure 2), and regression method (linear vs. logistic versus multivariable), but do suggest that not all patients are good candidates for dose painting. These results highlight the need to identify alternative objective measures that can predict which patients would make good or poor candidates for dose painting based on a given biological imaging target.

Voxel-based predictors based on ratios of PET images from pre- to mid-treatment (R_FLT and R_Cu-ATSM) were not good at predicting recurrent tumor location: R² and pseudo R² values were close to 0 for simple linear and logistic regression models. We originally hypothesized that biological changes occurring early during radiation therapy might correlate with tumor resistance. This hypothesis was supported by recent analysis of clinical outcome for the canine patients included in this study: mid-treatment FLT SUV_max and relative changes in FLT SUV_max from pre-treatment to mid-treatment were the most predictive of progression-free survival (Bradshaw et al 2015). The caveat, however, was that tumors with large relative decreases in FLT SUV_max actually had a worse prognosis. In this study, we did not find response maps of FLT uptake to be significant spatial predictors of recurrent tumor location. A mathematical problem with ratio maps, however, is that response values can become inflated in regions with initially-low voxel values (i.e. denominators close to zero), so that even small fluctuations in image values due to statistical noise can appear as large response values. This may have confounded the utility of R_FLT and R_Cu-ATSM as predictors. Furthermore, we previously demonstrated in these patients that image patterns for FLT PET, and especially for Cu-ATSM PET, were spatially stable from pre-treatment to mid-treatment (Bradshaw et al 2014). Other techniques of quantifying spatially-resolved changes in longitudinal PET images may be more appropriate, such as absolute SUV changes (although these were included in the multiple regression models), or other methods (Kinoshita et al 2012).

Advanced predictive models did not provide an improvement over multiple linear regression models at predicting a ‘new’ patient’s post-treatment FDG values. These prediction models were used to account for potentially confounding factors that are not accounted for in linear regression, such as patient categorical variables, non-linearity, and autocorrelation among neighboring voxels. For the models with continuous response data, the fitted R² for the pooled data were generally higher than for the multiple linear models shown in figure 3. However, the better fitting did not result in high prediction accuracy, as median prediction R² values for the different models were less than 0.15. CART performed the best at describing the training data (see figure 5), but often having the poorest prediction performance—likely a consequence of over fitting. Overall, prediction R² were approximately the same as the regression R² shown in figure 3, and contained large interpatient variability.

Several other studies have correlated imaging patterns to recurrent tumor location. The studies by Aerts et al and Soto et al in lung and head-and-neck tumors, respectively, have already been discussed in the introduction (Soto et al 2008, Aerts et al 2009, Aerts et al 2012). Abramyuk et al and Shusharina et al performed similar studies in 10 and 19 patients, respectively, who had lung cancer and experienced loco-regional failure following radiation therapy. Both studies found high degrees of spatial overlap between recurrence volumes and pre-treatment FDG uptake (Abramyuk et al 2009, Shusharina et al 2014). Petit et al used logistic voxel regression to relate pre-treatment FDG uptake to post-treatment FDG uptake in 39 NSCLC tumors, and found increased FDG uptake at baseline predicted a greater probability of post-treatment FDG uptake (Petit et al 2009). Vogelius et al found that recurrent tumor was most likely to originate in the regions of elevated FDG uptake in 39 HN cancer patients undergoing radiation therapy (Vogelius et al 2013).

A primary assumption to the methods of this study—which is a common assumption to all of the previously-mentioned spatial analysis studies—is that, following image registration, the tumor cells in a voxel location do not change or move location between pre-treatment imaging and post-treatment imaging. It is unclear how frequently this assumption is valid. Deformable registration methods attempt to account for tumor morphological changes over time, but deformable registration algorithms assume that the tumor’s mass is preserved over time, which is not the case for tumors undergoing treatment. For this reason, we used rigid registration. Canine sinonasal tumors benefit from the fact that rigid registration can be very accurate due to the surrounding bony nasal cavity, and (based on our experience) the turbinates inside the nasal cavity help to hold the tumor in its place, restricting tumor movement over time. An additional limitation of the study is the degree to which post-treatment FDG uptake is a valid marker of recurrent or residual tumor, and whether or not it corresponds to resistant tumor. Numerous studies have found that post-treatment FDG uptake does correlate with poor clinical outcome (Inoue et al 1995, Levine et al 2006, Bollineni et al 2012, Machtay et al 2013). However, non-specific uptake of FDG, including radiation-induced inflammation, could still be a confounding factor in studies such as this. A further limitation to the study is the uncertainty regarding the specificity of Cu-ATSM uptake as a marker for tumor hypoxia (Hueting et al 2014), especially under conditions of anesthesia and oxygen breathing (Kersemans et al 2011).

Conclusion

Using multi-tracer PET imaging and voxel regression models, we found that FDG, FLT, and Cu-ATSM PET were able to predict the locations of recurrence in some canine tumors, but they were poor predictors of recurrence locations in other tumors. We also showed that no individual PET tracer significantly outperformed the other PET tracers in how well they predicted patterns of recurrence. No patient characteristics or imaging biomarkers that we tested could predict which patients would be good candidates for dose painting (i.e. have a high prediction R²). These results highlight the need for methods of pre-selecting patients who would be good candidates for dose painting, and for the development of better molecular imaging probes of resistance.