Enforcing Co-expression Within a Brain-Imaging Genomics Regression Framework

Abstract

Among the challenges arising in brain imaging genetic studies, estimating the potential links between neurological and genetic variability within a population is key. In this work, we propose a multivariate, multimodal formulation for variable selection that leverages co-expression patterns across various data modalities. Our approach is based on an intuitive combination of two widely used statistical models: sparse regression and canonical correlation analysis (CCA). While the former seeks multivariate linear relationships between a given phenotype and associated observations, the latter searches to extract co-expression patterns between sets of variables belonging to different modalities. In the following, we propose to rely on a ‘CCA-type’ formulation in order to regularize the classical multimodal sparse regression problem (essentially incorporating both CCA and regression models within a unified formulation). The underlying motivation is to extract discriminative variables that are also co-expressed across modalities. We first show that the simplest formulation of such model can be expressed as a special case of collaborative learning methods. After discussing its limitation, we propose an extended, more flexible formulation, and introduce a simple and efficient alternating minimization algorithm to solve the associated optimization problem. We explore the parameter space and provide some guidelines regarding parameter selection. Both the original and extended versions are then compared on a simple toy dataset and a more advanced simulated imaging genomics dataset in order to illustrate the benefits of the latter. Finally, we validate the proposed formulation using single nucleotide polymorphisms (SNP) data and functional magnetic resonance imaging (fMRI) data from a population of adolescents (n = 362 subjects, age 16.9 ± 1.9 years from the Philadelphia Neurodevelopmental Cohort) for the study of learning ability. Furthermore, we carry out a significance analysis of the resulting features that allow us to carefully extract brain regions and genes linked to learning and cognitive ability.

I. Introduction

An increasing amount of high-dimensional biomedical data, such as genome sequencing or brain imaging scans, is collected every day. Classical unimodal analysis, by definition, are less likely to capture potential links between brain regions and genetic variability when studying diseases such as schizophrenia, Alzheimer’s disease, or various neurocognitive phenotypes. Bridging both genomics and imaging factors has the potential to help the research community extract meaningful bio-markers, improve clinical outcome prediction or identify key associations across these modalities[1]. As a consequence, developing integrative statistical models to carry out joint analysis of genomic data together with neuroimaging data has become an active research topic[2].

Despite being an emerging field, imaging genomics has been rapidly evolving over the last decade. From early studies carrying out pairwise analysis between genomic markers and imaging endophenotypes, many advanced multivariate methods have been proposed and successfully used by the research community. For example, the concept of genomewide association studies (GWAS), has been extended by Stein et al.[3] to extract relationships between genetic sequence data and various imaging endophenotypes (referred to as voxel-wise genome-wide association study, or vGWAS). Jahanshad et al.[4] proposed to further extend vGWAS using diffusion-base MRI to study the link between genetic variants and aberrant brain connectivity structures. Besides vGWAS, many other multimodal methods have been designed to extract latent variables from both genetic and imaging data using various strategies including maximization of independence [5], [6] or the use of sparse multivariate models. In this work we focus on the latter. Le Floch et al.[7] combined univariate filtering and partial least squares (PLS) to identify SNPs co-varying with various neuroimaging phenotypes. In their recent paper, Cao et al.[8] proposed a sparse representation based variable selection algorithm relying on sparse regression model to integrate both SNP and fMRI in order to perform biomarker selection for the study of schizophrenia. Lin[9] proposed a group sparse canonical correlation analysis (CCA) method based on SNP and fMRI data to extract correlation between genes and brain regions. More recently, Jian et al.[10] and Du et al.[11] proposed interesting extensions of canonical correlation analysis (CCA) method based on SNP and fMRI data.

As mentioned by Lin in[12], one limitation that one often faces when trying to analyze imaging genomics dataset is poor biomarker reproducibility across studies. Although this issue remains an open problem, one may hope that using appropriate priors over the solution will lead to an improved consistency of the result across different studies. Given that, as discussed above, both regression and CCA lead to promising results in the context of imaging genomics, we propose in this work to use a CCA penalty term in order to further regularize the standard LASSO formulation. The underlying motivation is to extract features (in this case, brain regions and SNPs) that associate with a given phenotype while displaying a significant level of co-expression (measured by their cross-correlation). Interestingly, in a recent paper, Gross et al.[13] propose a simple additive model encompassing both CCA and Lasso terms. However, as it will be discussed in Section III, we think that such formulation might prove to be too restrictive in practice.

In this work, we propose an extended model that, to our opinion, is more flexible and provides a wider scope when it comes to perform feature selection in a multimodal framework. In our previous work[14], we applied the proposed model to the study of schizophrenia. In the present work, we focus instead on the study of cognitive functions related to learning ability and educational attainment. Additional contributions (compared to our earlier work of [14]) are presented in this updated version. While the complete and detailed algorithmic procedure is now provided, we also perform a more indepth exploration of the parameter space associated with the model on both synthetic and real data. The resulting parameter tuning procedure has been updated, as we now rely on cross-correlation instead of stability selection. This practical choice is carefully justified later in this paper. Several improvements regarding the experimental results are also presented: a much higher significance threshold (0.9 v.s. 0.3 in [14], c.f. Section IV-B3) is used for feature selection, which significantly increases the overall analysis power. We then evaluate the performances of the selected features for classification purposes, and discuss the advantages of our method over standard Lasso using the cross-correlation heatmap associated with those features.

The rest of this paper is organized as follows: we introduce in Section II some of the relevant methods as well as the motivation for this work. A novel approach to multivariate regression problems, extending a recently proposed simpler model, is then introduced in Section III. Such method is then evaluated on both synthetic and real datasets in Section IV, followed by some discussions and concluding remarks in Section V.

II. Methods

A. Learning with L ₁ penalty

We consider $M\in {\mathbb{N}}^{+}$ distinct (i.e., from different modalities) datasets with n samples and $p_m\in {\mathbb{N}}^{+}$ (m = 1, .., M) variables each. The m-th dataset is represented by a matrix ${\mathbf{X}}_m\in {\mathbb{R}}^{n\times p_m}$. Additionally, each sample is assigned a class label (e.g., case/controls) y_i ∈ {−1, 1}, i = 1, .., n. Note that instead of binary class labels, a continuous phenotype vector can also be used for y. In order to extract a linear link between y and the M data matrices, we may rely on the following regression model:

$$\underset{\beta }{\text{min}}\sum _{m=1}^M\Vert \mathbf{y}-{\mathbf{X}}_m{\beta }_m{\Vert }_2^2+\lambda \Vert \beta {\Vert }_1$$ (1)

The model described by Eq. 1 performs both variable selection and regularization. It often improves the prediction accuracy and interpretability of the results compared to the use of classical ℓ₂ norm regularization terms, especially when the number of variables is far greater than the number of observations. In some situations, we have several output vectors y_m, ∀m = 1, .., M and the m datasets belong to the same modality. In order to capture shared structures among the various regression vectors, multi-task Lasso was proposed by Obozinski et al.[15]:

$$\underset{\beta }{\text{min}}\sum _{m=1}^M\Vert {\mathbf{y}}_m-{\mathbf{X}}_m{\beta }_m{\Vert }_2^2+\lambda \sum _{p=1}^P\Vert {\beta }^p{\Vert }_2$$ (2)

where P is the dimension of the problem and β^p is the p-th row of the matrix β = [β₁, .., β_m] (i.e., the β₃ are stacked horizontally). Such norm is also referred to as the ℓ₁/ℓ₂ norm, and is used to both enforce joint sparsity across the multiple β_m and estimate only a few non-zero coefficients. Similar model such as the group-Lasso[16] try to enforce the selection of grouped features, where each group is previously defined by the user. Others enforce regularity within a modality[17], [18] (and across tasks) to increase the reliability of the results. In the next section, we briefly review some of the most commonly used methods to extract statistical links between variables belonging to different modalities.

B. Extracting relationship between datasets

A wide variety of problems amount to the joint analysis of multimodal datasets describing the same set of observations. One approach to perform such analysis is to learn projection subspaces using paired samples such that structures of interest appear more clearly. Some of these methods include: canonical correlation analysis[19] (CCA), partial least squares[7] (PLS) or cross-modal factor analysis (CFA). Among them, CCA is probably the most widely used. Its goal is to extract linear combinations of variables with maximal correlation between two (or more) datasets. Using similar notations as in the previous section, and assuming M = 2 for the sake of simplicity, one formulation of CCA is expressed as follows:

$$\underset{{\beta }_1,{\beta }_2}{\text{argmin}}{J}_{cca}({\beta }_1,{\beta }_2)=\Vert {\mathbf{X}}_1{\beta }_1-{\mathbf{X}}_2{\beta }_2{\Vert }_2^2$$ (3)

to which a constraint on the norm of canonical vectors β₁, β₂ is added to avoid the trivial null solution. In recent years, CCA has been widely applied to genomic data analysis. As a consequence, many studies on sparse versions of CCA (sCCA) have been proposed[9], [20], [21], [11], [22] to cope with the high dimension but low sample size problem.

C. Collaborative learning

For most of the methods previously mentioned in Section II-A, pair-wise or group-wise closeness is optimized in the common subspace. As a consequence these methods often fail to capture relationships across modalities. To address this issue, collaborative (or co-regularized) methods[23] are based on the optimization of measures of agreement across multi-modal datasets, where smoothness across modalities is enforced through a joint regularization term. The general formulation can be expressed as follows:

$$\begin{gathered} J(\beta )=\sum _{m=1}^M\Vert \mathbf{y}-{\mathbf{X}}_m{\beta }_m{\Vert }_2^2+\lambda \Vert \beta {\Vert }_1 \\ +\gamma \sum _{m,q=1}^M\Vert {\mathbf{U}}_m{\beta }_m-{\mathbf{U}}_q{\beta }_q{\Vert }_2^2 \end{gathered}$$ (4)

where the U_m, m = 1, .., M are arbitrary matrices whose role is to control the cross-view joint regularization between each pair of vectors (β_m, β_q), m, q = 1, .., M. Scalar parameter γ ≥ 0 controls the influence of the cross-regularization term. Notice that if γ = 0, Eq.4 is equivalent to the original Lasso formulation. Collaborative learning is an interesting extension of Eq.1 allowing the user to explicitly enforce regularization across modalities. Interestingly, we show later in this paper (c.f. the proposed model in Section III) that a proper choice for the matrices U_m, m = 1, .., M is able to incorporate Lasso and CCA formulations together within the collaborative learning framework. In the next section, such model will be introduced to address the following aspects in sparse regression: (i) enforce regularization across modalities; (ii) assume that relationships between variables are not available as a prior knowledge (as opposed, e.g., to Xin[17]); (iii) define these links between features from different modalities using cross-correlation measure.

III. Enforcing cross-correlation in regression problems

A. MT-CoReg formulation

As discussed in the previous sections, numerous methods have been proposed to estimate links between a phenotype and observations while extracting relationships between coupled datasets from different modalities. In this section, we propose to incorporate both the regression and ccA formulations into a unified framework. We hope that, by using CCA as a regularization term, we will be able to extract features that explain the phenotypic variance while displaying a significant amount of correlation with features from other modalities. A simple way to combine Lasso and sparse CCA is to consider the following weighted combination of Eq.(1) and Eq.(3):

$$\begin{gathered} \underset{\beta }{\text{min}}J(\beta )=(1-\gamma )\sum _{m=1}^M\Vert \mathbf{y}-{\mathbf{X}}_m{\beta }_m{\Vert }_2^2 \\ +\gamma \sum _{m,q=1}^M\Vert {\mathbf{X}}_m{\beta }_m-{\mathbf{X}}_q{\beta }_q{\Vert }_2^2+\lambda \Vert \beta {\Vert }_1 \end{gathered}$$ (5)

where γ ∈ [0, 1] is a weight parameter. Notice that Eq.(5) can be expressed within the collaborative framework introduced in Section II-C: setting U_m = X_m ∀m = 1, .., M in Eq.4, we fall back on Eq.(5). Let us call this model CoReg for Collaborative Regression. An equivalent formulation (up to a proper rescaling) has been considered before by Gross et al. [13] to perform breast cancer prediction. However, in their paper, the weight of the regression term is set to 1 and $\gamma \in {\mathbb{R}}^{+}$. In our opinion, while promising, both formulations from either Eq.5 or [13] might prove to be too restrictive: it essentially amounts to forcing each component of the β_m’s to fit both the regression term and the CCA one at the same time. However, in practice, there is no reason to assume that the regression coefficients and the CCA ones will share the same components values. As a result, we may want to allow the model to be slightly more flexible, and relax this assumption. Instead, since our goal is to perform feature selection, we propose to only enforce shared sparsity patterns for both the regression vector and the CCA decomposition. We then propose to first duplicate each β_m into two components such that:

$${\beta }_m=[{\alpha }_m,{\theta }_m],\forall m=1,..,M$$ (6)

where α_m, θ_m are vectors from ${\mathbb{R}}^{p_m}$. As a consequence, the β_m’s are now matrices such that ${\beta }_m\in {\mathbb{R}}^{p_m\times 2}\forall m=1,..,M$. We then propose the following ‘Multi-Task Collaborative Regression’ (MT-CoReg) formulation:

$$\begin{gathered} \underset{\beta }{\text{min}}J(\beta )=(1-\gamma )\sum _{m=1}^M\Vert \mathbf{y}-{\mathbf{X}}_m{\alpha }_m{\Vert }_2^2 \\ +\gamma \sum _{m,q=1}^M\Vert {\mathbf{X}}_m{\theta }_m-{\mathbf{X}}_q{\theta }_q{\Vert }^2+\lambda \sum _{m=1}^M\sum _{i=1}^{p_m}\Vert {\beta }_m^i{\Vert }_2 \end{gathered}$$ (7)

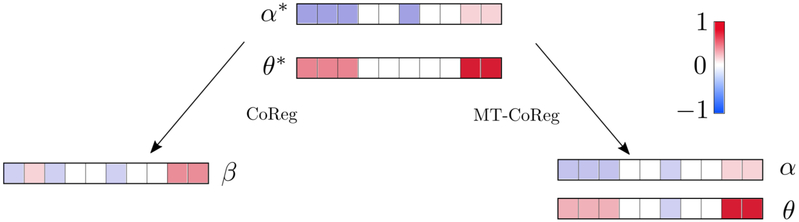
where ${\beta }_m^i$ is the i-th row of β_m, i.e., ${\beta }_m^i=[{\alpha }_m(i),{\theta }_m(i)]\in {\mathbb{R}}^2$, i = 1, .., p_m. The third term of Eq.(7) is simply the ℓ₁/ℓ₂ norm of each of the β_m We can see in Eq.(7) that each ‘component’ (i.e., column of β_m will be involved in separate parts of the functional J: (i) components α_m will fit the regression term; (ii) components θ_m will fit the CCA term. Each pair (α_m, θ_m), m = 1, .., M is coupled through the use of the ℓ₁/ℓ₂ norm: although their components values are different, shared sparsity patterns are encouraged within each pair (α_m, θ_m). As a consequence, we allow the method to be significantly more flexible than the CoReg model of Gross[13]. We hope that such framework will encourage the selection of features that are discriminative (via the regression part) but also co-expressed across modalities (via the CCA part). Note that when γ = 0, MT-CoReg essentially reduces to the initial regression problem of Eq.(1), while setting γ = 1 amounts to solving a conventional sparse CCA problem. A schematic illustration of the differences between MT-CoReg and CoReg can be seen in fig.(1).

Fig. 1: An illustrative comparison between MT-CoReg and CoReg [13].

α*, θ* are the ideal regression and canonical vectors for one dataset (M = 2 here). CoReg produces a single solution β, while MT-CoReg estimation is represented by two components α, θ. In this situation, where coefficients between the predictive and cross-correlated components (e.g. first 3 and last 2 features) are different, CoReg fails by trying to simultaneously represent both with a single component. On the other hand, MT-CoReg is flexible enough to properly estimate both components correctly.

As mentioned earlier, both CoReg and MT-CorReg encourage the method to select cross-correlated variables to solve the regression problem. Intuitively, one can argue that not all variables that are helpful for the prediction task are coexpressed with other modalities. As a consequence, a desirable property would be to retain these ‘modality-specific’ variables. This observation allows us to point out another advantage of MT-CoReg over CoReg. While using CoReg, it is more difficult to keep modality-specific variables in the model since the associated regression and cross-correlation coefficients are, by definition, given equal values. As a consequence, if a given variable significantly improves the fit to the phenotype, it will have a fairly high weight in the cross-correlation term in Eq.(5) as well. However, if that same variable is not co-expressed with other modalities, it will likely produce a poor fit. On the other hand, when using MT-CorReg, the modality specific information can be, to a certain extent, better retained. Indeed, let us take a look at the penalty term for the i-th variable in a given view m, i.e., $\Vert {\beta }_m^i{\Vert }_2=\Vert [{\alpha }_m(i),{\theta }_m(i)]{\Vert }_2$. It allows, to a certain extent, a high value for α_m(i) (regression component) and a low insignificant value for θ_m(i) (cross-correlation component). As a consequence, MT-CoReg provides a much more flexible framework in order to retain modality-specific variables. This issue is further addressed using a toy dataset in Section III-D.

In the next section, we explain how to solve the problem described in Eq.(7).

B. Optimization

Similar to the sCCA optimization procedure of Wilms et al. [24], we solve the problem from Eq.(7) by optimizing the β_m’s alternatively over the iterations until convergence. Suppose we have initial values ${\beta }_1^{\ast },..,{\beta }_{m-1}^{\ast }$, ${\beta }_{m+1}^{\ast },..,{\beta }_M^{\ast }$ foe each modality except the m-th one, and we want to estimate β_m.

$$\begin{gathered} \underset{{\beta }_m}{\text{min}}J({\beta }_m\mid {\beta }_{[1:M]\setminus m}^{\ast })=\Vert {\tilde{\mathbf{y}}}_m-{\tilde{\mathbf{X}}}_m{\alpha }_m{\Vert }_2^2 \\ +\sum _{\begin{array}{c}\hfill q=1\hfill \\ \hfill q\ne m\hfill \end{array}}^M\Vert {\widehat{\mathbf{y}}}_q-{\widehat{\mathbf{X}}}_m{\theta }_m{\Vert }_2^2+\lambda \sum _{i=1}^{p_m}\Vert {\beta }_m^i{\Vert }_2 \end{gathered}$$ (8)

where we define the following relevant quantities:

$$\left\{\begin{array}{cc}{\tilde{\mathbf{y}}}_m=\hfill & \sqrt{(1-\gamma )}\mathbf{y}\hfill \\ {\widehat{\mathbf{y}}}_q=\hfill & \sqrt{\gamma }{\mathbf{X}}_q{\theta }_q^{\ast }\hfill \end{array}\phantom{\}}\text{and}\right\{\begin{array}{cc}{\tilde{\mathbf{X}}}_m=\hfill & \sqrt{(1-\gamma )}{\mathbf{X}}_m\hfill \\ {\widehat{\mathbf{X}}}_m=\hfill & \sqrt{\gamma }{\mathbf{X}}_m\hfill \end{array}\phantom{\}}$$ (9)

Obviously, Eq.(8) is a classical group-lasso regression problem[16] (cf. Eq.(2)). It is easy to show that updating β₁ reduces to solving a similar problem. The general optimization procedure to apply MT-CoReg is described in Algorithm 1.

Algorithm 1: MT-CoReg Algorithm: alternate minimization are performed, which consist of successive multi-task regression problems.

$$\begin{array}{cc}\hfill & 1:\mathbf{Input}:\text{Standardized data matrices}{\mathbf{X}}_1,{\mathbf{X}}_2,\text{phenotype}\hfill \\ \hfill & \text{vector y},\text{and}\text{parameters}\lambda ,\gamma .\hfill \\ \hfill & 2:\mathbf{Initialize}:{\alpha }_1,..,{\alpha }_M\text{using ridge regression and}{\beta }_1,..,{\beta }_M\hfill \\ \hfill & \text{using ridge CCA}.\hfill \\ \hfill & 3:\mathbf{for}k=0\text{to Convergence}\mathbf{do}\hfill \\ \hfill & 4:\mathbf{for}m=1:1:M\mathbf{do}\hfill \\ \hfill & 5:\text{Solve for}{\beta }_m=[{\alpha }_m,{\theta }_m]\hfill \\ \hfill & \underset{{\beta }_m}{\text{min}}J({\beta }_m\mid {\beta }_{[1:M]\setminus m]}^{\ast })=\Vert {\tilde{\mathbf{y}}}_m-{\tilde{\mathbf{X}}}_m{\alpha }_m{\Vert }_2^2\hfill \\ \hfill & +\sum _{\begin{array}{c}\hfill q=1\hfill \\ \hfill q\ne m\hfill \end{array}}^M\Vert {\widehat{\mathbf{y}}}_q-{\widehat{\mathbf{X}}}_m{\theta }_m{\Vert }_2^2+\lambda \sum _{i=1}^{p_m}\Vert {\beta }_m^i{\Vert }_2(10)\hfill \\ \hfill & \text{where}\hfill \\ \hfill & \left\{\begin{array}{cc}{\tilde{\mathbf{y}}}_m=\hfill & \sqrt{(1-\gamma )}\mathbf{y}\hfill \\ {\widehat{\mathbf{y}}}_q=\hfill & \sqrt{\gamma }{\mathbf{X}}_q{\theta }_q^{\ast }\hfill \end{array}\phantom{\}}\text{and}\right\{\begin{array}{cc}{\tilde{\mathbf{X}}}_m=\hfill & \sqrt{(1-\gamma )}{\mathbf{X}}_m\hfill \\ {\widehat{\mathbf{X}}}_m=\hfill & \sqrt{\gamma }{\mathbf{X}}_m\hfill \end{array}\phantom{\}}(11)\hfill \\ \hfill & 6:\mathrm{end}\mathrm{for}\hfill \\ \hfill & 7:\mathrm{end}\mathrm{for}\hfill \end{array}$$

C. Parameter selection

Solving problem from Eq.(7) requires the estimation of the two key parameters λ and γ, which respectively control the weights of the sparsity and the co-expression regularization terms. Several strategies can be considered for their estimation: cross-validation, Bayesian/Akaike Information Criterion (BIC, AIC), or stability selection. In this work, we rely on cross-validation, which is probably one of the most commonly used methods for model selection. Indeed, cross-validation has the advantage of providing a direct estimate of the error using the resulting features as predicting variables. Interestingly, it has been shown[25] that under a few assumptions cross-validation and AIC are asymptotically equivalent. Another motivation to use cross-validation over AIC/BIC is that the latter depends on prior knowledge, e.g., making the assumption that the population at hand is a good representative of the real population’s distribution. On the other hand, cross-validation simulates the behavior of our method when facing ‘new’ data. Finally, although we relied on stability selection in our previous work[14] using MT-CoReg in the context of schizophrenia, it proved to be computationally more expensive. Indeed, stability selection usually require a substantial amount of resampling (compared to a standard k-fold cross-validation scheme).

D. MT-CoReg VS. CoReg

As mentioned earlier in Section III-A, the proposed MT-CoReg estimator can be seen as an extension of the previously introduced model (CoReg) by Gross et al. [13]. In order to illustrate the advantages of MT-CoReg vs. CoReg, we propose to first use a simple toy dataset and compare the results obtained by both methods. We generated M = 2 data matrices X₁, X₂ from Normal distribution made of p₁ = p₂ = 25 variables and n = 25 observations. We used a latent variable model to simulate cross-correlated components so that columns i ∈ [10, .. 15] of X₁, X₂ are mutually co-expressed, i.e., there exist θ₁, ${\theta }_2\in {\mathbb{R}}^{25}$ such that corr(X₁θ₁, X₂θ₂) is non zero. We further use columns i ∈ [1, ..5] ∪ [10, ..15] to generate a phenotype vector y, i.e., there exist α₁, ${\alpha }_2\in {\mathbb{R}}^{25}$ such that y ≈ X₁α₁ + X₂α₂. With such setup, columns i ∈ [10, ..15] correspond to both non-zeros values in the true canonical vectors θ₁, θ₂ and the true regression vectors α₁, α₂. However, their values are different. Profiles of each true vectors ${\theta }_1^{\ast }$, ${\theta }_2^{\ast }$, ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$ can be seen in fig.2(a-b) (and replicated in fig.2(c-d) for ease of comparison with the estimations bellow), where the blue and red curves are the values taken by the canonical and regression coefficients respectively. Solutions produced by MT-CoReg for γ = 0, γ = 0.25 and γ = 1 can respectively be seen in fig.2(e-f), fig.2(i-j) and fig.2(m-n). Solutions produced by CoReg for the same γ values can respectively be seen in fig.2(g-h), fig.2(k-l) and fig.2(o-p). As expected, it can be observed that for γ ∈ {0; 1}, both MT-CoReg and CoReg produce identical solutions and are essentially equivalent to Lasso or sparse CCA. It is however more interesting to compare both methods for γ ∈]0,1[. In such case indeed, both correlated and predictive components are jointly estimated. When comparing fig.2(i-j) and fig.2(k-l), it is obvious that, in such setup, relaxing the assumption that regression and canonical coefficients have identical values allows a finer estimation of each true factors ${\theta }_1^{\ast }$, ${\theta }_2^{\ast }$, ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$. This can be further observed as the AUC values for predictive components and cross-correlated components are respectively (0.99, 0.9850) for MT-CoReg, and (0.94,0.78) for CoReg. In our opinion, this illustrates the fact that MT-CoReg has a wider scope than the original CoReg estimator.

Fig. 2: A comparison between MT-CoReg (left side of the vertical line) and CoReg (right side of the vertical line) on a toy dataset.

(a-b) and (c-d): true canonical vectors (red) and regression vectors (blue) for each view (replicated for easier comparison with estimations bellow). (e-f): solution produced by MT-CoReg for γ = 0. (g-h): solution produced by CoReg for γ = 0. (i-j) solution produced by MT-CoReg for γ = 0.25. (k-l): solution produced by CoReg for γ = 0.25. (m-n) : solution produced by MT-CoReg for γ = 1. (o-p): solution produced by CoReg for γ = 1. Components i ∈ [10, .. 15] correspond to both non-zeros values in the true regression and canonical coefficients, although their coefficient values are different. By relaxing the assumption that regression and canonical coefficients have identical values, MT-CoReg allows a finer joint estimation of both components (i.e., regression and correlation) compared to CoReg for 0 < γ < 1. For γ ∈ {0; 1}, both methods produce identical solutions and are essentially equivalent to Lasso (γ = 0) or sparse CCA (γ = 1).

Going back to the issue raised in Section III-A, we can further compare results from fig.2(i)-(l). In both modalities, the first five variables have non zero components in the regression parameters, and are also ‘modality-specific’ as their cross-correlation with variables from the other view is zero. However, we can observe in fig.2(i)-(j) that they are still properly estimated by MT-CorReg’s α components (at least, as well estimated as when using regression), while the associated θ values are near zeros. In comparison, the estimation of the first 5 variables produced by CoReg in fig.2(k)-(l) is much more distorted or contains more noise. This illustrates the greater flexibility provided by MT-CoReg regarding the estimation of modality-specific variables.

IV. Experiments

In this section, we evaluate the proposed MT-CoReg estimator from Eq.7. Performance is assessed in terms of feature selection relevance on both simulated and real data.

A. Results on synthetic data

For our first test, to further validate MT-CoReg, we simulate both fMRI and SNP datasets, made of n = 200 subjects and respectively p₁ = p₂ = 1000 components. Genomic values are coded as 0 (no minor allele), 1 (one minor allele), and 2 (two minor allele), while voxels values are drawn from the Normal distribution. Similar to the toy dataset from Section III-D, we start by generating two sparse canonical vectors ${\theta }_1\in {\mathbb{R}}^{p_1}$, ${\theta }_2\in {\mathbb{R}}^{p_2}$ such that their first 100 components are from the Normal distribution while the rest is zero. Cross-correlated voxels are drawn from $\mathcal{N}({\theta }_1^{\ast }\mathbf{y},I_{p_1})$, while cross-correlated SNP are drawn from $\mathcal{B}(2,{\mathrm{logit}}^{-1}(-a_i+\mathrm{logit}({\eta }_i)))$ where a is issued from $\mathcal{N}({\theta }_2^{\ast }\mathbf{y},I_{p_2})$, and η represents the minor allele frequency and is drawn from a uniform distribution $\mathcal{U}([0.2,0.4])$. In addition, regression vectors ${\alpha }_1^{\ast }\in {\mathbb{R}}^{p_1}$, ${\alpha }_2^{\ast }\in {\mathbb{R}}^{p_2}$ for both genomic and brain imaging data are also generated: components i ∈ [1, 100] ∪ [500, 600] of ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$ are drawn from Normal distribution, while the rest is set to zero. Furthermore, binary phenotype vector y is generated from $\mathcal{B}(1,d_i)$, where $d_i=\frac{exp(5{\sum }_{m=1}^M{\mathbf{X}}_m{\alpha }_m^{\ast })}{1+exp(5{\sum }_{m=1}^M{\mathbf{X}}_m{\alpha }_m^{\ast })}$ Finally, the noise level is adjusted so that corr(X₁θ₁, X₂θ₂) ≈ 0.3. The resulting datasets are such that their first 100 components are both predictive and cross-correlated. However, their respective coefficients in the regression and cross-correlation parts have different values.

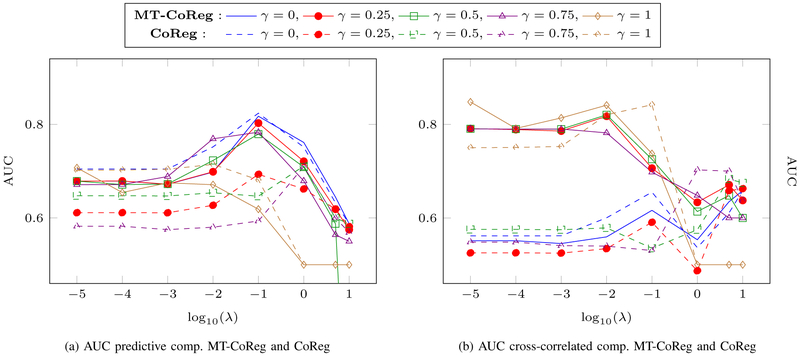
A common way to assess the performance of a model when it comes to feature selection is to measure the true positive rate (TPR) and false positive rate (FPR). TPR reflects the proportion of variables that are correctly identified, while FDR reflects the proportion of variables that are incorrectly selected by the model. We can further combine both of these metrics by plotting the receiver operating characteristic curve, or ROC curve, with the FPR values on the x-axis and the TPR values on the y-axis. Finally, one can compute the area under the (ROC) curve, or AUC, in order to further summarize the selection power of a model. We apply both MT-CoReg and CoReg to 100 random generations of the dataset described above. A range of values is considered such that γ ∈ {0, 0.25, 0.5, 0.75, 1} from Eq.(7) that weights the CCA term against the regression one. The AUC values for MT-CoReg and CoReg for both predictive and cross-correlated components can respectively be seen in fig.3(a) and fig.3(b) for different γ and λ values.

Fig. 3: A comparison between MT-CoReg (solid lines) and CoReg (dashed lines) on a simulated dataset for variable selection.

AUC values for each cross-correlated and predictive components, for various values of the parameter γ are used. (a): AUC value relative to predictive components ${\alpha }_1^{\ast }$, ${\alpha }_2^{\ast }$ for both MT-CoReg and CoReg. (b): AUC value relative to cross-correlated components ${\theta }_1^{\ast }$, ${\theta }_2^{\ast }$ for both MT-CoReg and CoReg. We can observe from (a-b) that 0 < γ < 1 produce interesting solutions compared to γ = 0 (standard Lasso) and γ = 1 (sparse CCA). For example, when γ = 0.25, MT-CoReg is able to efficiently select the real non zero features from both predictive and cross-correlated components. Overall, when comparing solid and dashed lines, we can observe that MT-CoReg produces higher AUC values that CoReg.

By comparing AUC curves from fig.3(a), we can observe that, as expected, Lasso (i.e., γ = 0) performs better when it comes to selecting the predictive features, while sparse CCA (i.e., γ = 1) is doing rather poorly. On the other hand, we can see in fig.3(b) that sparse CCA selection accuracy when it comes to the cross correlated components is much higher than the one from Lasso. Interestingly, we can observe that, for 0 < γ < 1, MT-CoReg effectively combines both CCA and Lasso models. Indeed, both predictive and cross-correlated features are reasonably well estimated. This confirms our hypothesis that using a mix of both Lasso and sparse CCA may lead to an efficient feature selection accuracy. In addition, when comparing results from MT-CoReg and the ones obtained using CoReg (solid lines vs. dashed lines), we can see that AUC values are on average higher when using MT-CoReg. To our opinion, this also illustrate the benefits provided by the proposed multi-task model MT-CoReg. By providing more flexibility to the model, we are able to obtain more accurate estimates. In the next section, we apply MT-CoReg to a real dataset of fMRI and SNP data for the study of learning ability.

B. Results on real imaging genetics data

1). Data acquisition:

The Philadelphia Neurodevelopmental Cohort[26] (PNC) is a large-scale collaborative study between the Brain Behaviour Laboratory at the University of Pennsylvania and the Children’s Hospital of Philadelphia. It contains, among other modalities, a fractal n-back fMRI task, SNP arrays and computerized neurocognitive battery (CNB) performances data for nearly 900 adolescents with age from 8 to 21 years. In order to limit the influence of age over the results, we selected a subset of the full dataset such that the remaining ages are above 160 months (n = 571 subjects).

Standard brain imaging preprocessing steps were applied to the fractal n-back fMRI data using SPM12¹, including motion correction, spatial normalization to standard MNI space (spatial resolution of 2 × 2 × 2mm, adult template) and spatial/temporal smoothing with a 3mm FWHM Gaussian kernel. Stimulus-on versus stimulus-off contrast images were extracted. After removing voxels missing more than 1% data, p₁ = 85796 voxels were left for analysis.

SNP arrays were acquired using 6 different platforms. We kept subjects genotyped by the 4 most commonly used platforms, all manufactured by Illumina. After standard data cleaning and preprocessing steps using the PLINK software package², p₂ = 98804 SNP were left for analysis. Each SNP was categorized into three clusters based on their genotype and was represented with discrete numbers: 0 for no minor allele, 1 for one minor allele and 2 for minor alleles. Merging data from different SNP chips in order to jointly analyze them is a well-known difficult problem, as it may result in spurious associations due to chip effects. This issue is addressed in the supplementary material³ (Appendix A. SNP Chip effects on the real data analysis).

Finally, all subjects underwent a 1-hour long computerized assessment battery adapted from tasks applied in functional neuroimaging studies to evaluate a broad range of cognitive domains. Data include both accuracy and speed information for each test. For this work, we relied on performance scores (ratio of total correct responses) from the wide range achievement test (WRAT), which measures an individual’s learning ability (reading, spelling, and mathematics) and provides an estimate of IQ. We first convert WRAT scores to z-scores based upon each subject’s raw score and the sample mean in order to provide a standard metric. We then only keep subjects whose absolute z-score value for PVRT test was above z* = 0.5. Our motivation was to perform feature selection using MT-CoReg on a population made of exclusively low and high achievers in terms of learning ability. This way, we hope to extract features that explain the variance between these two groups in a more robust way than if the whole spectrum is considered. After all these steps, we were left with n = 362 subjects separated in two groups: low achievers at WRAT (age 16.7 ± 1.91 years, 104 females out of 175 subjects) and high achievers (age 17.1 ± 1.92 years, 98 females out of 187 subjects). Differences among a population in terms of cognitive function are (at least partially) due to both genomic heritability and neurological attributes. On the one hand, GWAS studies have been conducted[27] to investigate links between SNP data and cognitive measures. On the other hand, numerous neuroimaging studies[28], [29] have been relying on working memory activity patterns using n-back task fMRI data, as working memory is hypothesized to be closely related to general fluid intelligence learning performances. In this work, we perform a joint analysis using both genomic and brain imaging data.

2). Quantitative analysis:

As mentioned in Section.III-C, we rely on cross-validation to chose appropriate values for parameters γ and λ. Since the proposed MT-CoReg model is a combination of Lasso and sparse CCA, we can rely on two classical error metrics:

• The ‘normalized’ Residual Sum of Squares (RSS) i.e., $\frac{1}{n}\frac{{\sum }_{i=1}^n(y_i-f(x_i){)}^2}{{\sum }_{i=1}^n(y_i-\stackrel{‒}{y}{)}^2}$ where f(x_i) is the predicted value for the i-th sample and $\stackrel{‒}{y}$ is the sample mean of the y_i, i = 1, .., n.

• The cross-correlation corr(X₁θ₁, X₂θ₂).

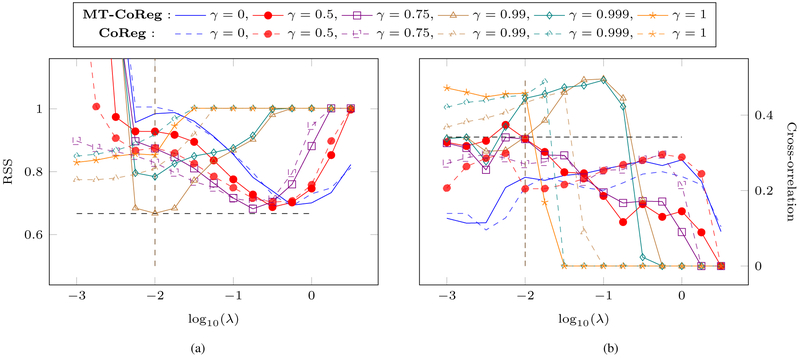
Both of these metrics are estimated on a test set that hasn’t been used during training. We display in fig.4 the associated RSS (c.f. fig.4(a)) and cross-correlation (c.f. fig.4(b)) values averaged over a cyclical 10-fold cross-validation setup for both MT-CoReg (solid lines) and CoReg (dashed lines). The respective parameters’ search ranges are λ ∈ [10⁻⁶, 10¹] and γ = {0, 0.5, 0.75, 0.99, 0.999, 1}. One main issue of sparse learning based approaches such as MT-CoReg is the instability. To address this issue, standard error values for fig.4 are provided as supplementary material⁴ in Appendix B.

Fig. 4: Error metrics (averaged over 10-fold cross-validation) on the test sets for different parameter (γ, λ) values, for both MT-CoReg (solid lines) and CoReg (dashed lines).

(a) Normalized RSS (b) Cross-correlation values. The crossing straight, black dashed lines indicate the RSS and cross-correlation values corresponding to the parameters values we retain (γ* = 0.99, λ* = 10⁻²) for our analysis. While the resulting RSS value is comparable (and even slightly lower than) the one produced by Lasso (γ = 0), the associated cross-correlation value is significantly higher.

The authors would like to point out that in practice, relying on a nested cross-validation over the hyper-parameters is likely to further improve the results. However, in the context of this paper we decided to provide error values for fixed choices of both parameters. One advantage is that it provides a detailed parameter space exploration and allows one to clearly observe the effects of various parameter choices over the results. Furthermore, such analysis can provide a well motivated starting point to further derive a reasonable range for the parameter space, in order to reduce the computational burden of a nested cross-validation scheme over the full parameter space. Another interesting point is that, in order to perform a nested cross-validation, one needs to define a single ‘optimality metric’. Such metric will likely combine both RSS and cross-correlation values (although other metrics can be defined). However, a proper combination of both these quantities is likely to strongly depend on the specific type of analysis one is carrying out. Indeed, in the case of imaging genomics, correlation between SNP and neuroimaging data is usually fairly low. But, for a different application on other data types, such correlation might be much stronger. In that case, depending on the behavior of the RSS error, proper scaling between both RSS and cross-correlation might be required.

We can first observe from fig.4(a) that, apart from γ values very close to 1, very similar minimal RSS values are obtained, although for various sparsity level. Indeed, it appears that the higher γ is, the lower the optimal λ value should be. This can probably be explained due to the fact that for a given fixed λ value, increasing γ will lead to sparser solutions, as we noticed during our tests on this dataset. In addition, we can observe that γ ≈ 1 does not allow the model to select features producing low RSS values. This make sense, as in this case, we are essentially applying a CCA model to the data. Looking at fig.4(b), we can observe that, as expected, increasing γ leads to higher cross-correlation values on the test set. We can observe that for γ ∈ {0.5, 0.75}, we do obtain higher cross-correlation values than for standard Lasso (i.e., γ = 0) when the sparsity weight is low. However, when looking at the corresponding RSS values from the similar range in terms of λ values in fig.4(a), we can see that the price to pay for an increase in cross-correlation is a significant increase in terms of RSS. Interestingly, we can pay more attention to the point (γ*, λ*) = (0.99, 10⁻²) in the parameter space, at which both straight, black dashed lines cross: while its associated RSS value is similar to the one of Lasso (and even slightly lower), the correlation value is such that corr(X₁θ₁, X₂θ₂) ≈ 0.35. This is significantly higher than the maximal cross-correlation value produced by Lasso over the whole λ range, which is the benchmark we are principally trying to compare MT-CoReg with. Furthermore, we can also compare MT-CoReg to standard sparse CCA (i.e., γ = 1). We can see that the maximal cross-correlation values produced by both methods (c.f λ ≈ 10⁻¹ for MT-CoReg and λ ≈ 10⁻² for sparse CCA) are similar. However, for such λ value, the increase in RSS for MT-CoReg is significant. Since in this work, we essentially rely on the CCA term as a regularization term to the standard Lasso, we think prioritizing a drop in RSS makes more sense. As a consequence, for our test on the PNC dataset, we retain (γ*, λ*) = (0.99,10⁻²) as optimal parameter values, since it provides both low RSS and high cross-correlation values.

It is interesting to further compare the performances of MT-CoReg and CoReg on the real data when looking at fig.4. From fig.4(a), we can observe that both methods display similar behavior for γ ∈ [0, 0.75]. However, for higher γ values, it is obvious thatMT-CoReg outperforms CoReg in term of predictive power. In our opinion, this demonstrates the benefit of a using a more flexible model that allows discrepancies between regression and CCA components. On the other hand, as it can be observed in fig.4(a), cross-correlation performances are fairly similar for both methods.

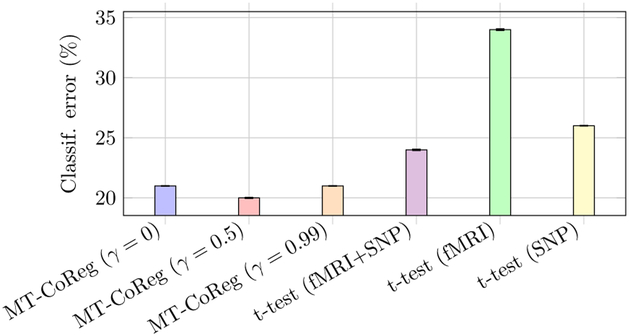
In addition to comparing RSS and cross-correlation values, we further analyzed the features retained by MT-CoReg using a support vector machine[30] (SVM) classifier. fig.5 shows the results of a ten-fold cross validation using MT-CoReg. We also provide classification results obtained using a simple uni-variate feature selection scheme: for each feature, a t-test is applied to look for differences across classes. We then rank the features according to the resulting p-values, and apply a threshold so that we only keep the features that appear to be the best at separating classes (the threshold is chosen so that the resulting number of features is the same as the one selected by a standard Lasso model). We can observe that the value of γ seems to have little influence over the classification results. However, it is interesting to note that MT-CoReg appears to be better than a simple t-test based procedure in terms of selecting features that properly separate both classes. Furthermore, when looking at classification error rates resulting from the t-test based procedure, we can observe that using both fMRI and SNP together is more efficient than performing unimodal classification.

Fig. 5:

Classification error (%) for different γ values, and comparison with unimodal and multimodal t-test based (univariate) feature selection. We can observe that the value of γ seems to have little influence over the classification results.

3). Significance analysis:

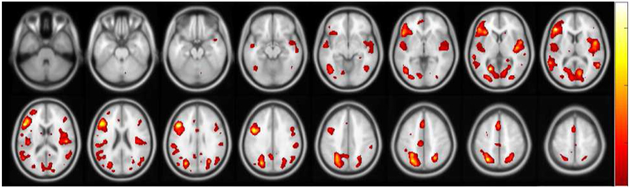
In order to achieve a stable feature selection process, we perform N = 100 random resamplings with replacement out of the 362 total subjects. At the k-th random sampling, we can calculate a set of solution vectors ${\widehat{\beta }}_m^k$, m ∈ {1, 2}. It is then possible to define a measure of relevance $p_m^i$ for the i-th feature in the m-th dataset such that: $p_m^i=\frac{1}{N}{\sum }_{k=1}^{N}I({\widehat{\beta }}_m^k(i)\ne 0)$ where i = 1, .., d_m is the feature index and I(·) is the indicator function. We can then rank each SNP and voxel based on their associated relevance measure and apply a cut-off threshold of 0.9 (i.e., each of the final features have been selected at least in 90% of the runs). After applying this significance test, we were left with a subset of 5 SNPs spanning 5 genes and 25 voxels. Following the ROI definition of the AAL parcellation map[31], the selected voxels mostly come from regions such as the inferior frontal gyri, the occipital gyri, and the right rolandic operculum. A more inclusive list of selected brain regions can be seen in fig.6, where we displayed the voxels selection heatmap across the 100 runs of MT-CoReg on the resampled data. In addition to the previously mentioned ROIs, we can see that the selected voxels mostly come from areas such as the medial frontal gyri, superior temporal gyrus, superior parietal lobules and calcarine.

Fig. 6:

Voxel selection probability heatmap (spatially smoothed for the sake of visualization). Some of the most highlighted regions include: inferior and medial frontal gyri, superior temporal gyrus, superior parietal lobules, right rolandic operculum, and calcarine.

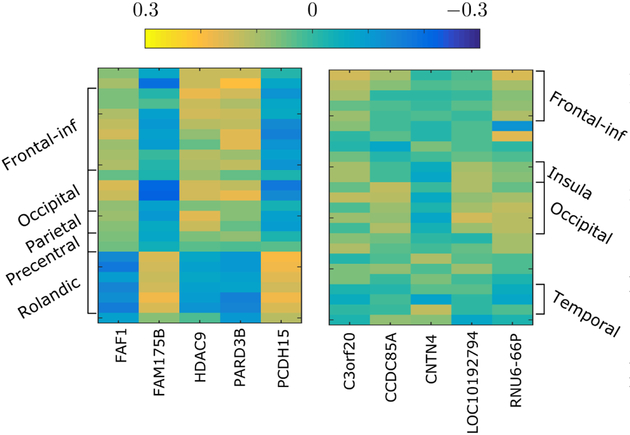
Based on the two sets of features from each modality selected by MT-CoReg, we compute in fig.7 the resulting pairwise SNP-voxel cross-correlation heatmap. In addition, we display a similar heatmap for the features resulting from a standard Lasso estimator. Note that in the case of Lasso, no features were left after applying the 0.9 threshold to each $p_m^i$. As a consequence, in order to perform a fair comparison, we simply retained the 5 most selected SNP and the 25 most selected voxels. First of all, we can observe that the heatmap resulting from MT-CoReg displays significantly higher absolute cross-correlation values than the one produced by Lasso. Additionally, the heatmap associated with MT-CoReg appears much more structured: we can clearly see various ‘blocks’ of positive and negative correlation values that seem to somehow follow the voxels group definition from the AAL template.

Fig. 7:

Cross-correlation heatmaps between selected voxels (rows) and genes (columns). (left) heatmap associated with MT-CoReg. (right) heatmap associated with standard Lasso. We can observe that the heatmap resulting from MT-CoReg displays much higher absolute values compared to the one resulting from Lasso. Additionally, it is also much more structured, as blocks of positive and negative correlation values following the brain ROIs definition can be seen.

Interestingly, there seems to be two specific correlation patterns among the features selected by MT-CoReg. For a given gene, the correlation values with the frontal, occipital, parietal and pre-central ROIs will systematically be of opposite sign than the correlation between the same gene and the rolandic operculum⁵. Such interesting behavior cannot be observed from the correlation heatmap associated with Lasso, as in that case no voxels from the rolandic operculum belong to the final list of selected features. To opinion, this illustrates one of the advantages provided by using a CCA regularization term within a standard Lasso formulation.

Some of the selected features have been reported by other similar studies. For example, the role of the prefrontal cortex in working memory and general fluid intelligence has been established by Kane et al.[29]. In addition, Li et al.[32] reported positive correlation between working memory scores (a key component of general fluid intelligence and learning ability) and gray matter volumes from Rolandic and Inferior frontal areas. The role of histone lysine acetylation deacetylases (HDACs) as a negative cognition regulator in multiple brain regions has been characterized by Penney[33]. HDAC inhibitors are considered as promising candidates to establish treatment to prevent cognitive decline associated with aging, as well as various neurodegenerative diseases. Finally, Kim et al. found that SNPs associated with PARD3 gene were significantly associated with neurological diseases such as schizophrenia[34].

V. Conclusions

The main contributions of this paper can be summarized as follows. First, we proposed a novel variable selection approach using a CCA-inspired regularization term in order to enforce co-expression between modalities when using standard Lasso estimator. Secondly, we present an efficient algorithm to optimize the associated minimization problem, as well as potential strategies to estimate the tuning parameters. Using simulation studies, we demonstrate the advantages of MT-CoReg over a previous formulation (CoReg) from Gross et al.[13]. On top of that, detailed experiments were conducted on a real dataset of adolescents for the study of learning ability and cognitive potential. Sets of SNP and voxels were identified, which can be further validated from associated studies. A comparison of the resulting cross-correlation heatmap demonstrated the benefits of our approach compared to standard Lasso in terms of feature selection.

A definite and robust parameter selection for MT-CoReg still remains an open problem. In our previous work[14], stability selection provided a satisfactory operating point. Here cross-validation turned out to be simpler and more stable. This might be due to the fact that the correlation between SNP and brain data is overall stronger in this dataset. Although cross-validation provided good practical results, we will continue to work on improving this aspect of the model.

We can further develop the MT-CoReg model and replace the standard Lasso fit term with a logistic or hinge loss one[30]. Such terms have indeed been specifically developed to perform classification tasks, and would potentially avoid the use of an ‘a posteriori’ classification step. Finally, the interpretation of the resulting SNP-Voxels interactions should be further confirmed via replication studies as well as the use of more robust and general neurocognitive phenotypes.